Benchmarking and performance evaluation of a novel deformable image registration software for radiotherapy CT images

Highlights

• •Benchmarking and evaluating a novel deformable image registration (DIR) software, DirOne, against two commercial systems, MIM and VelocityAI.
• •The study followed AAPM TG-132 guidelines, ensuring rigorous evaluation and quality assurance of the DIR software.
• •Three publicly available datasets were used for comprehensive performance analysis, including pelvic, thoracic, and head and neck CT scans.
• •DirOne demonstrated clinically acceptable accuracy in terms of TRE, DSC, and MDA.
• •Results support the potential use of DirOne for radiotherapy treatment planning applications.

Abstract

Purpose

We evaluated and benchmarked a novel deformable image registration (DIR) software functionality (DirOne, Cosylab d.d., Ljubljana, Slovenia) by comparing it to two commercial systems, MIM and VelocityAI, following AAPM task group 132 (TG-132) guidelines.

Methods

Three publicly available datasets were used for evaluation. The first dataset includes primary and deformed phantom images for a male pelvis. The second, from DIR-Lab, contains ten sets of 4D CT thoracic scans. The third dataset, from the DIR Evaluation Project (DIREP), includes ten head and neck CTs. VelocityAI and MIM served as benchmarks to assess DirOne’s performance. Target registration error (TRE), dice similarity coefficient (DSC), and mean distance to agreement (MDA) were the evaluation metrics.

Results

For TRE, the average results for DirOne, MIM, and VelocityAI were 3.3 ± 3.1 mm, 2.7 ± 3.7 mm, and 3.4 ± 2.4 mm, respectively. For DSC, DirOne achieved 0.96 ± 0.02, MIM 0.98 ± 0.02, and VelocityAI 0.98 ± 0.01 across the first and second datasets. In the DIREP dataset, DirOne achieved 0.73 ± 0.34 for MDA and 0.91 ± 0.03 for DSC; MIM achieved 0.54 ± 0.36 and 0.93 ± 0.02, and VelocityAI 0.93 ± 0.38 and 0.90 ± 0.03.

Conclusion

The novel DIR software demonstrated clinically acceptable accuracy compared to other commercial systems, supporting its potential use in radiotherapy treatment planning applications such as automatic image segmentation, 4D segmentation propagation, and dose warping.

Introduction

In modern radiotherapy, CT is central to treatment planning, providing a detailed 3D model of the patient's anatomy. However, as treatment progresses, changes such as tumor shrinkage, organ movement, or weight loss can affect the accuracy of the original plan. Deformable image registration (DIR) between CT scans is essential for tracking these changes, enabling adaptive replanning, accurate dose accumulation, and automatic contour propagation [1], [2], [3]. By accommodating anatomical shifts, DIR ensures precise targeting and effective treatment throughout the course of therapy.

To implement DIR in a clinical environment, it is important to thoroughly test and evaluate any new DIR software to ensure high precision in radiotherapy [4]. Multi-institutional studies have validated DIR algorithms but revealed performance variations across institutions due to differences in clinical workflows, making DIR accuracy specific to each site [5], [6], [7], [8]. A recent study by Viergever et al. emphasized the importance of validating DIR algorithms, reinforcing this need [9].

The American Association of Physicists in Medicine (AAPM) Task Group 132 (TG-132) report provides guidelines for quality assurance (QA) and quality control of image registration in clinical practice [10]. TG-132 recommends assessing DIR accuracy using the target registration error (TRE) metric, which measures the difference between landmark positions in the deformed and reference images calculated through the deformation vector field (DVF). Additionally, for evaluating auto-contouring accuracy, TG-132 recommends using the dice similarity coefficient (DSC) and mean distance to agreement (MDA) as key metrics to assess how well anatomical structures align between deformed images and reference images.

In this study, we evaluated the performance of DirOne - a new DIR functionality of the OncologyOne software suite (Cosylab d.d., Ljubljana, Slovenia) - following the recommendations of AAPM TG-132. Additionally, we benchmarked the performance of the new DIR algorithm with two commercially available platforms: MIM (MIM Software Inc., Cleveland, OH) and VelocityAI (Varian Medical Systems, Palo Alto, CA). The original CT datasets for a male pelvis phantom, as provided by AAPM TG-132, were used for testing. We also employed publicly available CT datasets of the thoracic region from DIR-Lab (https://www.DIR-lab.com) [11], [12] and head and neck region from DIREP (https://sites.google.com/site/dirphantoms) [13] to further assess the algorithm’s performance.

Methods and materials

Original datasets and contour generation

In this study, three CT datasets were utilized. The first dataset from AAPM TG-132 [10] includes two CTs of a male pelvis phantom, the primary dataset (CT 1), and its derived counterpart (CT 2). CT 1 serves as the original CT image, while CT 2 represents the reference image for DIR assessment. CT 2 was generated from CT 1 through deformation, artificial noise enhancement, and minor rigid shifts. The resolution of the CT images is 0.91 × 0.91 × 3 mm³. Three fiducial markers located in the bladder, rectum, and prostate were used as landmarks for DIR accuracy evaluation.

The second dataset consists of thoracic CT images from ten patients diagnosed with esophageal and lung cancers, obtained from DIR-Lab [11], [12]. These patients underwent a 4-dimensional CT (4DCT) scan, which was used for their treatment planning. The image resolution is 1.16 × 1.16 × 3 mm³. For this study, only two phases from the 4DCT set, the extreme inhale and exhale phases, were utilized. The dataset includes 300 anatomical landmarks per case, identified and registered in both phases of the original dataset, serving as references for assessing DIR algorithm accuracy.

The third dataset is from the Deformable Image Registration Evaluation Project (DIREP) [13] and consists of CT images from 10 head-and-neck cancer patients with voxel dimensions of 0.97 × 0.97 × 3 mm³. These images were acquired at two distinct time points during radiation therapy for each patient: at the start (pre-treatment, SOT) and the end (post-treatment, EOT) of the treatment course. The dataset captures anatomical changes due to tumor shrinkage, tissue deformation, and variations in patient positioning throughout treatment. Since fiducial markers were not available, this dataset was used exclusively to assess the accuracy of deformed contour propagation rather than to evaluate landmark DVF accuracy.

The original DIREP datasets, SOT and EOT, were initially processed through the AutoContour tool (Radformation, New York, NY) to generate contours on both the primary and secondary image datasets. The generated contours were then reviewed and adjusted by board-certified clinicians. These finalized contours were used as the gold standard for evaluating contour propagation.

DIR algorithm

The datasets mentioned above were imported into each system for registration. Various metrics were utilized to evaluate the performance of each software. A brief description of the DIR algorithm for each software is provided below.

• •DirOne

DirOne DIR algorithm utilizes a global minimum spanning tree (MST) optimization approach [14], [15], combined with a self-similarity measure, to achieve robust and accurate image alignment. This method effectively maps image similarities at discrete locations and compares these maps between the fixed and moving images to compute the optimization cost function. The MST optimization ensures that the registration process is global, accounting for the entire image rather than just local regions, minimizing total dissimilarity across all feature points, and avoiding local minima. Feature points are extracted based on intrinsic characteristics, and edge weights between them are calculated using a self-similarity measure, which relies on internal structural patterns rather than absolute intensity values. This makes the DIR algorithm particularly effective for registering images with varying intensity ranges and contrasts. To ensure smooth and accurate transformations, the algorithm employs a B-spline method for image interpolation [16]. This approach is particularly advantageous for adaptive radiotherapy [17], allowing for dynamic adjustments of treatment plans in response to anatomical changes over time. Furthermore, it supports the propagation of planning structures onto different phases of 4DCT images and enables predictive extrapolation of tissue movement and deformation.

• •MIM

In MIM (version 7.3.6), deformable registration was performed using the VoxAlign Deformation Engine®, an intensity-based, free-form DIR algorithm for CT-CT registration [18], [19]. The similarity metric is calculated by summing the squared differences of normalized intensities, which is minimized using a modified gradient descent method. The process began with an initial rigid registration, followed by deformable registration. This algorithm enables the deformable transformation of contours, making it useful for applications such as adaptive recontouring for replanning and propagating contours across different phases in 4DCT.

• •VelocityAI

VelocityAI (version 4.1) utilizes an intensity-based DIR algorithm with a B-spline model, chosen for its simplicity and efficiency, based on Mattes formulation of mutual information [20], [21]. VelocityAI implemented two DIR strategies: Deformable and Deformable multipass [22]. The Deformable approach performs a single-stage image deformation at a user-specified resolution, while the Deformable multipass approach conducts DIR sequentially, progressing from low to high resolution, with each stage's resolution determined automatically. The output from one stage serves as the initial condition for the next. Since the vendor recommends Deformable multipass for clinical use, we adopted this approach in our study.

Evaluation metrics

Following TG-132 guidelines for algorithm evaluation, two categories were assessed for accuracy: spatial and segmentation propagation accuracy. For spatial accuracy, the TRE metric was used to measure the accuracy of landmark positions in the deformed image compared to the gold standard. For segmentation propagation accuracy, both the DSC and MDA metrics were employed. DSC quantifies the overlap between segmented structures in the deformed images and the gold standard, while MDA calculates the average distance between corresponding surfaces in the deformed and reference images, focusing on how well the structure surfaces, such as organ boundaries, align after registration. Detailed mathematical descriptions for TRE, DSC, and MDA are provided below for better understanding.

• •Target Registration Error (TRE)

The TRE was defined as the Euclidean distance (vector error) between the corresponding landmark locations in the deformed images ($x_{\text{def}}$, $y_{\text{def}}$, $z_{\text{def}}$) and the ground truth in the reference images ($x_{\text{true}}$, $y_{\text{true}}$, $z_{\text{true}}$), as shown in Eq. (1).

$$\text{TRE}=\sqrt{{\left(x_{\text{def}}-x_{\text{true}}\right)}^2+{\left(y_{\text{def}}-y_{\text{true}}\right)}^2+{\left(z_{\text{def}}-z_{\text{true}}\right)}^2}$$ (1)

The coordinates ($x_{\text{def}}$, $y_{\text{def}}$, $z_{\text{def}}$) were calculated using the DVF ($u$, $v$, $w)$ acquired from the deformation process, from the primary image marker location ($x_{\text{prim}},y_{\text{prim}},z_{\text{prim}}$), listed as Eq. (2)

$$x_{\text{def}}=x_{\text{prim}}+u,y_{\text{def}}=y_{\text{prim}}+v,and{z}_{\mathit{def}}=z_{\text{prim}}+w$$ (2)

When multiple landmarks are used, the average TRE is calculated by averaging the TRE values for all landmarks, shown in Eq. (3)

$$\text{Average TRE}=\frac{{\sum }_{i=1}^n{\text{TRE}}_i}{n}$$ (3)

• •Dice Similarity Coefficient (DSC)

The DSC is calculated by determining the number of overlapping voxels between two volumes and normalizing this count by half the sum of the non-zero voxels in both volumes. Mathematically, the DSC is expressed as:

$$\mathit{DSC}=\frac{2\ast \left(A\cap B\right)}{\left|A\right|+\left|B\right|}$$ (4)

where $\left(A\cap B\right)$ represents the number of voxels common to both volumes A and B, and $\left|A\right|+\left|B\right|$ is the sum of the voxels in each volume. The DSC value ranges from 0 to 1, with 0 indicating no overlap and 1 representing perfect overlap between the two volumes.

• •Mean Distance to Agreement (MDA)

The MDA is calculated as the average of the shortest distances from each point on a contour in one image to the nearest point on the corresponding contour in another image. This involves a point-by-point analysis, where each point on a contour in the deformed image is matched to the nearest point on the corresponding contour in the reference image, as described in Eq. (5).

$$\mathrm{M}\mathrm{D}\mathrm{A}=\frac{1}{\mathrm{N}}\sum _{\mathrm{i}=1}^{\mathrm{N}}\underset{\mathrm{j}}{\min }\sqrt{{\left({\mathrm{x}}_{\mathrm{i}}-{\mathrm{x}}_{\mathrm{j}}\right)}^2+{\left({\mathrm{y}}_{\mathrm{i}}-{\mathrm{y}}_{\mathrm{j}}\right)}^2+{\left({\mathrm{z}}_{\mathrm{i}}-{\mathrm{z}}_{\mathrm{j}}\right)}^2}$$ (5)

where N represents the number of points on the contour of the deformed image.$({\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}},{\mathrm{z}}_{\mathrm{i}})$ are the coordinates of a point i in the deformed image while $(x_{\mathrm{j}},y_{\mathrm{j}},z_{\mathrm{j}})$ are the coordinates of point j in the reference image. The min function finds the point j in the reference image closest to point i in the registered image.

Evaluation methods

TRE was calculated on the first (male pelvic phantom) and second datasets (4D thoracic cases). The DVFs for the registered landmarks were obtained from all three DIR software, and the TRE calculation, which was depicted in Eqs. 1, 2, and 3. was performed using MATLAB (MathWorks Inc., Natick, MA) codes. The extraction of DVF from commercial software was done using a code written in Python (version 3.12).

DSC and MDA were calculated for all three datasets (AAPM TG-132 male pelvic phantom, DIR-Lab 4D thoracic case, and the DIREP Head and Neck cases) across various organ contours for all three DIR software. To assess deformation consistency, registration between the start of treatment (SOT) and the end of treatment (EOT) images was performed in both directions for the third dataset (DIREP Head and Neck). The DSC and MDA values from both directions were evaluated and compared.

Results

Table 1, Table 2 present the TRE results for datasets 1 and 2, respectively. Table 1 lists the TRE values for three fiducial markers, one in each of the bladder, rectum, and prostate, across all three software. In Table 2, the mean and standard deviation of TRE for all 300 landmarks across the 10 cases are provided.

Table 1.

Target registration error (mm) statistics for the first dataset.

Structure	DirOne	MIM	VelocityAI
Bladder	0.60	0.40	0.70
Rectum	1.40	1.30	1.20
Prostate	0.94	0.81	1.10

Table 2.

Target registration error (mm) statistics for the second dataset.

Case	DirOne	MIM	VelocityAI
1	1.75 ± 1.12	1.20 ± 0.73	1.78 ± 0.91
2	2.07 ± 1.35	1.30 ± 2.16	1.97 ± 1.56
3	3.07 ± 2.31	1.80 ± 1.33	2.88 ± 1.87
4	2.95 ± 1.95	2.43 ± 1.73	3.82 ± 3.22
5	3.34 ± 2.62	2.67 ± 1.62	3.30 ± 2.47
6	3.81 ± 2.73	3.36 ± 3.10	3.62 ± 2.40
7	3.73 ± 2.05	2.78 ± 5.00	3.10 ± 1.70
8	7.21 ± 6.65	7.56 ± 8.80	7.52 ± 3.40
9	2.03 ± 3.30	1.25 ± 1.90	2.94 ± 2.10
10	3.43 ± 3.02	2.53 ± 3.29	2.63 ± 3.10
Average	3.34 ± 3.08	2.69 ± 3.73	3.36 ± 2.40

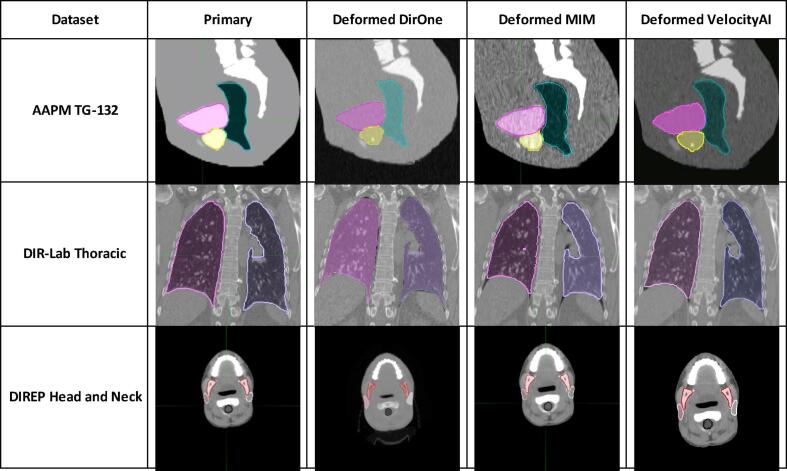
To visually demonstrate the deformation effects of all three software, we present 2D slice images and contours of sample cases from each dataset in Fig. 1. The three rows in Fig. 1 correspond to sample cases from three different datasets. The first column shows the primary images and contours before deformation, while the second, third, and fourth columns display the deformed images and contours produced by DirOne, MIM, and VelocityAI, respectively.

Fig. 1.

Example cases from three different datasets.

Table 3 lists the DSC and MDA values of dataset 1, which quantify the similarity between the deformed organ contours and the reference contours across all three software.

Table 3.

The DSC and MDA between the directly drawn and deformably propagated contours for the first dataset.

Structure	DSC			MDA (mm)
	DirOne	MIM	VelocityAI	DirOne	MIM	VelocityAI
Bladder	0.96	0.95	0.96	0.90	0.93	0.68
Rectum	0.92	0.90	0.91	1.42	1.51	1.17
Prostate	0.86	0.88	0.94	1.10	1.11	0.87

Table 4 presents the mean and standard deviation of DSC and MDA values across all 10 cases in dataset 2 for four different organ contours.

Table 4.

The Average DSC and MDA between the directly drawn and deformably propagated contours for the second dataset.

Structure	DSC			MDA (mm)
	DirOne	MIM	VelocityAI	DirOne	MIM	VelocityAI
Lung-LT	0.97 ± 0.01	0.98 ± 0.01	0.98 ± 0.01	0.74 ± 0.32	0.71 ± 0.76	0.73 ± 0.51
Lung-RT	0.98 ± 0.01	0.99 ± 0.01	0.99 ± 0.01	0.76 ± 0.30	0.74 ± 0.67	0.75 ± 0.34
Heart	0.93 ± 0.02	0.95 ± 0.02	0.96 ± 0.02	2.44 ± 1.15	2.11 ± 1.10	2.27 ± 1.19
Spinal Cord	0.98 ± 0.01	0.99 ± 0.01	0.98 ± 0.01	0.28 ± 0.11	0.24 ± 0.18	0.26 ± 0.22

For dataset 3, due to the large amount of data, results are presented in separate tables and figures. Table 5 shows the mean and standard deviation values of DSC and MDA for 6 deformed contours across 10 head and neck cases for all three software.

Table 5.

Average DSC and MDA across all patients for all software.

Structure	Direction	Average DSC			Average MDA (mm)
		DirOne	MIM	VelocityAI	DirOne	MIM	VelocityAI
Parotid-RT	EOT → SOT	0.87 ± 0.08	0.89 ± 0.07	0.88 ± 0.07	1.22 ± 0.77	1.05 ± 0.76	1.21 ± 0.86
	SOT → EOT	0.88 ± 0.08	0.89 ± 0.07	0.87 ± 0.07	1.00 ± 0.60	0.94 ± 0.62	1.45 ± 0.93
Parotid-LT	EOT → SOT	0.88 ± 0.07	0.90 ± 0.05	0.88 ± 0.06	1.03 ± 0.53	0.87 ± 0.44	1.13 ± 0.50
	SOT → EOT	0.88 ± 0.08	0.90 ± 0.05	0.88 ± 0.05	0.99 ± 0.55	0.78 ± 0.36	1.18 ± 0.51
Mandible	EOT → SOT	0.92 ± 0.01	0.94 ± 0.01	0.91 ± 0.01	0.57 ± 0.07	0.38 ± 0.05	0.67 ± 0.17
	SOT → EOT	0.92 ± 0.01	0.94 ± 0.01	0.91 ± 0.03	0.53 ± 0.06	0.36 ± 0.04	0.71 ± 0.17
Eye-RT	EOT → SOT	0.91 ± 0.02	0.95 ± 0.03	0.89 ± 0.02	0.57 ± 0.13	0.33 ± 0.15	0.72 ± 0.18
	SOT → EOT	0.91 ± 0.04	0.95 ± 0.02	0.90 ± 0.04	0.55 ± 0.22	0.31 ± 0.13	0.77 ± 0.40
Eye-LT	EOT → SOT	0.91 ± 0.01	0.95 ± 0.02	0.89 ± 0.03	0.59 ± 0.09	0.37 ± 0.11	0.83 ± 0.22
	SOT → EOT	0.91 ± 0.03	0.95 ± 0.02	0.90 ± 0.03	0.56 ± 0.17	0.35 ± 0.10	0.67 ± 0.27
Spinal Cord	EOT → SOT	0.92 ± 0.02	0.94 ± 0.01	0.90 ± 0.02	0.46 ± 0.16	0.31 ± 0.08	0.73 ± 0.22
	SOT → EOT	0.91 ± 0.04	0.94 ± 0.02	0.90 ± 0.02	0.54 ± 0.25	0.35 ± 0.19	0.67 ± 0.17

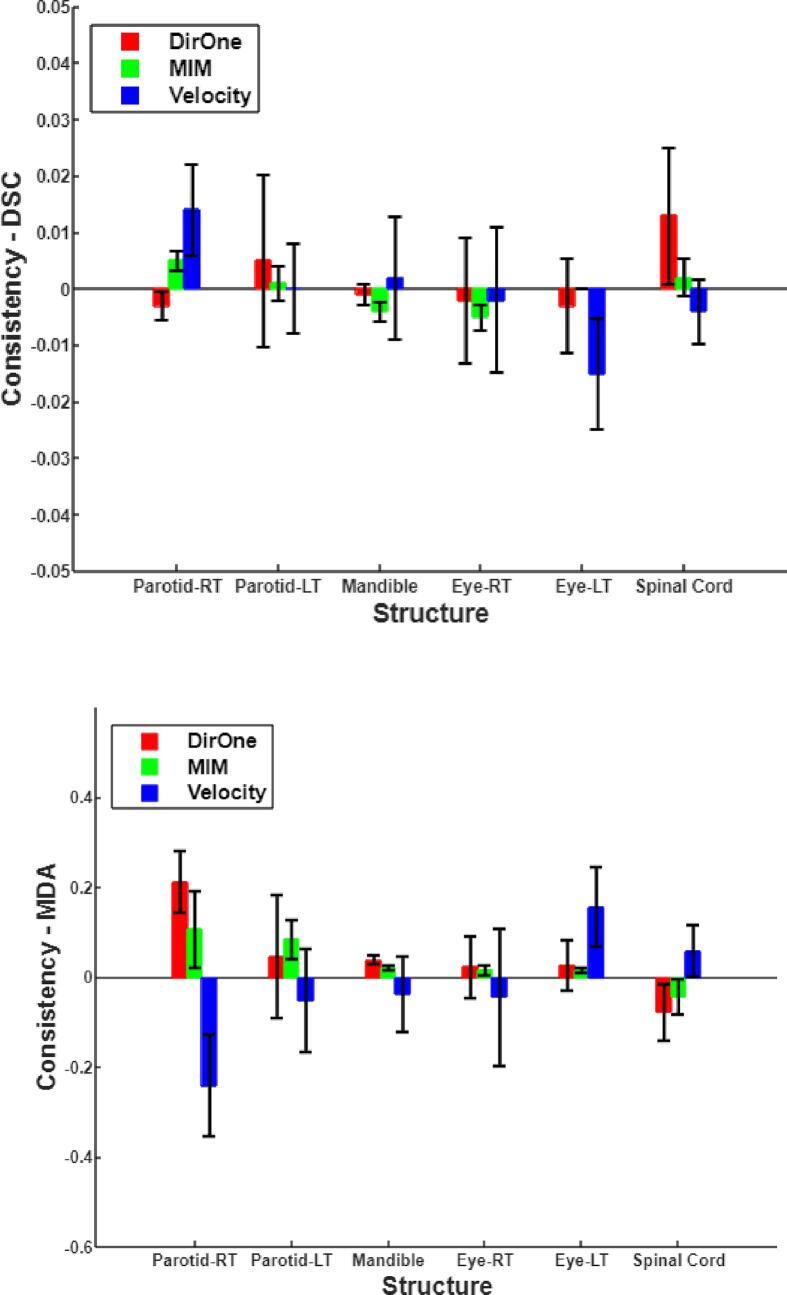
Fig. 2 shows the differences in DSC and MDA between the deformation processes in the two opposite directions (SOT → EOT and EOT → SOT).

Fig. 2.

The differences in DSC and MDA between the deformation processes in the two opposite directions.

Table 6 lists the two-sample t-test results (EOT → SOT and SOT → EOT), including t-statistic values and associated p-values for DSC and MDA metrics in dataset 3.

Table 6.

The consistency Statistics of DIR performance in both deformation directions.

Metric	Statistics	DirOne	MIM	VelocityAI
MDA	t-statistic	0.64	0.92	0.39
	p-value	0.54	0.39	0.71
DSC	t-statistic	0.91	0.59	1.31
	p-value	0.39	0.58	0.23

Discussion

In this study, we performed a comprehensive evaluation and benchmarking of the new DIR algorithm, DirOne, against established commercial platforms, including MIM and VelocityAI. DirOne employs an advanced deformation model and optimization strategy, called MST, setting it apart from traditional methods and enabling enhanced registration accuracy in specific clinical scenarios. While previous evaluations of DIR algorithms have typically focused on single anatomical sites [5], [6], our study expands this scope by assessing DirOne's performance across multiple anatomical regions, including the pelvis, thoracic, and head and neck areas. Adhering to the AAPM TG-132 guidelines, our methodology offers a robust and standardized framework for evaluating DIR performance in diverse clinical applications. This study not only highlights DirOne’s strengths relative to existing tools but also provides a template for the systematic evaluation of future DIR software, offering valuable insights into their clinical utility.

First dataset evaluation: male pelvic phantom

The first dataset included the basic anatomical and deformation datasets, which introduced controlled deformations and noise to the CT images. All three software platforms—DirOne, MIM, and VelocityAI—performed well in this initial test, achieving TRE that were within the acceptable range set by TG-132. Specifically, bladder TREs were 0.6 mm for DirOne, 0.4 mm for MIM, and 0.7 mm for VelocityAI. Similarly, rectal and prostate TREs showed minor discrepancies among the three software, with DirOne exhibiting slightly higher values in some cases, but overall maintaining accuracy comparable to the other platforms.

The comparison of DSC values further confirmed the efficacy of DirOne in contour propagation. With average DSC values exceeding 0.95, the results indicated high anatomical overlap between the deformed and reference images, matching the performance of MIM and VelocityAI. This outcome underscores the reliability of DirOne DIR algorithm for handling basic deformations and ensuring accurate contour alignment.

Second dataset evaluation: thoracic 4DCT cases

The second dataset comprised imaging data from ten thoracic cancer patients, a more complex dataset due to respiratory-induced deformations. All three software platforms exhibited good performance, with average TREs of 3.34 ± 3.08 mm for DirOne, 2.69 ± 3.73 mm for MIM, and 3.36 ± 2.40 mm for VelocityAI. While DirOne had slightly higher TREs than MIM and VelocityAI in terms of mean values, the differences were minor and within clinically acceptable limits.

One notable outlier was Case 8, where all three software platforms struggled, showing increased TRE, with reported values exceeding 7 mm. This case presented significant anatomical changes due to large respiratory motion and potential artifacts in the 4DCT scan. These factors likely contributed to the difficulty in accurately registering the anatomical structures, even with advanced DIR algorithms. Such cases highlight the challenges of handling extreme deformations and emphasize the need for continued refinement of DIR algorithms to improve performance in highly variable anatomical regions.

Third dataset evaluation: head and neck cases

The third dataset, involving head and neck phantoms from the DIREP collection, was used to assess the consistency of DIR performance in both deformation directions: from SOT to EOT and vice versa. The evaluation focused on DSC and MDA metrics, demonstrating that all three software platforms maintained strong consistency between the two registration directions. For DirOne, the mean DSC was 0.91 ± 0.03, and the MDA was well within the acceptable range, indicating robust contour alignment.

Statistical analysis, including paired t-tests for DSC and MDA between the two directions, further reinforced the reliability of the software. DirOne’s t-test results for DSC (t = 0.91, p = 0.392) and MDA (t = 0.64, p = 0.541) showed no significant differences between the SOT-to-EOT and EOT-to-SOT directions, confirming its directional consistency. Similar results were observed for MIM and VelocityAI, suggesting that all three software platforms are equally effective at handling bidirectional deformations. This level of consistency is crucial for clinical applications that require accurate registration in both directions, such as adaptive radiotherapy and dose accumulation.

Clinical implications and future work

The successful benchmarking of DirOne against MIM and VelocityAI demonstrates its clinical viability. As radiotherapy increasingly relies on DIR for accurate dose delivery, contour propagation, and adaptive planning, the need for reliable and efficient DIR systems becomes even more critical. DirOne performance, particularly in maintaining accuracy and consistency across different datasets, supports its integration into clinical workflows.

However, there are areas where further optimization is needed. For example, the increased TRE observed in Case 8 of the thoracic dataset points to challenges in cases involving large deformations and artifacts. These limitations suggest the potential for further refinement of the DIR algorithm, particularly for cases involving significant respiratory motion or anatomical variability.

Additional testing of DirOne with other imaging modalities, such as MRI and PET, will be essential to validate its versatility and robustness. Given the increasing integration of multimodality imaging in radiotherapy, the ability to accurately register images from different modalities is important. Future work will also explore the use of DirOne in adaptive radiotherapy workflow, assessing its impact on treatment accuracy, efficiency, and clinical outcomes.

Conclusion

In conclusion, the new DIR functionality, DirOne from Cosylab’s software suite OncologyOne, has demonstrated performance comparable to that of MIM and VelocityAI, meeting the accuracy standards of AAPM TG-132 across multiple datasets. Its high accuracy in spatial registration and consistent performance in both deformation directions suggest it is well-suited for clinical applications in radiotherapy. While some challenges remain, such as handling extreme anatomical deformations, DirOne holds promise as a valuable addition to the radiotherapy toolkit. Future studies will focus on validating its performance with additional imaging modalities and integrating it into adaptive treatment workflow to enhance patient care.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.