Extended target tracking with mobility based on GPR-AUKF

Abstract

Simultaneously estimating the kinematic state and extent of extended targets is a nonlinear and high-dimensional problem. While the extended Kalman filter (EKF) is widely employed to achieve this goal, it may not be sufficient for mobility targets. To address this issue, this paper first proposes to embed unscented Kalman filter (UKF) into Gaussian process regression (GPR) since the superiority of UKF to high nonlinear. Furthermore, given the widely-existed environment with time-varying noise, it is crucial to study the change of measurement noise covariance caused by time-varying noise for high-precision tracking of extended targets. However, traditional UKF filter considers measurement noise covariance as constant value. To this end, an adaptive unscented Kalman filter (AUKF) algorithm combining with GPR model (GPR-AUKF) is proposed to address the issue. Specifically, the GPR-AUKF algorithm is built based on expectation maximization (EM) algorithm to track the target state and covariance, and which updates the measurement noise covariance in real-time. Experimental results show that GPR-AUKF is more accurate and robust than other methods for tracking extended targets.

1. Introduction

Traditional target tracking algorithms are typically based on the point target model, where a target produces only a single measurement at each scan. However, with advancements in sensor technology, the resolution accuracy of sensors has significantly improved [1], [2], [3]. Consequently, the target that could be returned a set of measurements by one sensor [4], [5] is referred to as an extended target (ET). Extended target tracking (ETT) problems [6] have gained widespread applications, including maritime monitoring and surveillance [7], [8], autonomous driving [9], [10], etc. By using a series of measurements, we can simultaneously track the state of target and identify its extent information.

K. Granström et al. [11], [12], [13] proposed simple shape model, which predefined shapes such as circles, rectangles, and lines based on the contours of extended targets. Koch et al. [14], [15], [16] introduced the random matrix model (RMM) to describe the shape of the extended target. The RMM is simple and effective in tracking extended target with basic geometric shapes, such as ellipse, star-convex, etc. Based on the RMM, Baum et al. [17], [18], [19] suggested a random hyper surface model (RHM) that employs the curve fitting method to parameterize shape boundary, making it suitable for basic geometric shapes, such as ellipse, star-convex, and three-dimensional graphics. In the RHM, shape parameters are estimated using Gaussian estimator, which provides high flexibility, but comes with the downsides of requiring extensive computation and complex calculations. However, those targets with irregular shape are commonly-existed in practical applications, and this is where Gaussian Process (GP) comes in. GP is a random process that consists of infinite dimensional normal distribution functions and is widely used in machine learning [20], [21]. Wahlström et al. [22] presumed that the values of the target radial function under different angles follow a multidimensional normal distribution, and integrated Gaussian process regression (GPR) into the Bayes formula for the first time. Hence, the extended Kalman filter (EKF) algorithm combined with GPR for single extended target tracking is proposed under ideal environment. Lee et al. [23] applied the GP measurement model for extended target tracking with LiDAR measurement, which was combined with positive and negative information fusion to track vehicle targets on the road. The GPR model is capable of tracking not only convex extended targets, but also a variety of targets with different shapes within the scanning region. Therefore, this paper applies the GPR to model the extent of the extended target.

Although EKF in combination with GPR can effectively track the kinematic state and extent of extended targets [22], it may produce unsatisfactory estimation results with respect to targets with mobility due to issue of nonlinearity and dimensionality. To address this issue, the unscented Kalman filter (UKF) is a more appropriate solution for tracking extended targets. Therefore, in this paper, we focus on deducing derivatives by combining UKF and GPR to track maneuverable extended target. However, in practical target tracking environments, measurement noise may be time-varying [24]. However, current filters used to deal with variable measurement noise are applied to navigation systems of point targets [25], [26], [27]. Therefore, this paper proposes an adaptive unscented Kalman filter (AUKF) algorithm, which is based on the GPR to tackle the problem of time-varying measurement noise in extended target tracking. By incorporating expectation maximization (EM) algorithm, AUKF computes the optimal solution for the unknown noise in the model. Compared with traditional methods, the proposed algorithm has superior robustness and estimation accuracy.

In this paper, we model the extended target based on GPR and propose AUKF to update the state and covariance of the target in real-time. Therefore, the theory proposed in this paper is called GPR-AUKF.

The contributions of this paper can be summarized as follows: 1) To solve the problem of extended target tracking with mobility, we propose GPR-UKF by combining UKF with GPR, which has better robustness and adaptability for maneuverable target tracking; 2) To alleviate the problem of variable measurement covariance caused by time-varying measurement noise, we further propose GPR-AUKF based on EM algorithm to simultaneously track the state of the extended target and update the measurement noise covariance in real-time; 3) We conduct extensive simulation experiments to compare the proposed GPR-UKF and GPR-AUKF with another competing method, i.e., GPR-EKF. Experimental results demonstrate the superior performance of both GPR-UKF and GPR-AUKF.

This paper is structured as follows: The next section introduces the dynamic model and measurement model with GPR. The following Section 3 is devoted to the derivation of the GPR-UKF algorithm and GPR-AUKF algorithm. Section 4 discusses the advantages and disadvantages of the proposed algorithm through experimental simulations. Subsequently, the paper concludes in Section 5.

2. Extended target model based on GPR

In this section, we will derive the state space model based on GPR [22], which includes dynamic and measurement equations as Eq. (1) ∼ Eq. (2).

$$x_{k+1}=f(x_k)+w_k,w_k\sim N(0,Q_k)$$ (1)

$$y_k=h(x_k)+v_k,v_k\sim N(0,R_k)$$ (2)

where $w_k$ is process noise and $Q_k$ is process noise covariance, $v_k$ is measurement noise and $R_k$ is measurement noise covariance. $x_k$ is target state, it includes the kinematic state $x_{ki,k}$ and extent state $x_{e,k}$.

$$x_k={[{(x_{ki,k})}^{\mathrm{T}},{(x_{e,k})}^{\mathrm{T}}]}^{\mathrm{T}}$$ (3)

$$x_{ki,k}={[{(x_{c,k})}^{\mathrm{T}},x_{\phi ,k},{(x_{⁎,k})}^{\mathrm{T}}]}^{\mathrm{T}}$$ (4)

The target kinematic state and the target extent state are jointly estimated, we define the target position $x_{c,k}$, orientation $x_{\phi ,k}$, and any additional optional state ${(x_{⁎,k})}^{\mathrm{T}}$ separately within the $x_{ki,k}$. The optional additional state ${(x_{⁎,k})}^{\mathrm{T}}$ represents the remaining state variables. In this work, it denotes the kinematic state (velocity and angular velocity) of the target.

2.1. Dynamic model

The target state $x_k=[x_{c,k};x_{\phi ,k};x_{c,k}^{\prime };x_{\phi ,k}^{\prime };x_{e,k}]$ is described in dynamic equation.

$$x_{k+1}=F⁎x_k+w_k,w_k\sim N(0,Q_k)$$ (5)

where $F=\left[\begin{array}{cc}\hfill F_{ki,k}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill F_{e,k}\hfill \end{array}\right]$, $w_k=\left[\begin{array}{c}\hfill w_{ki,k}\hfill \\ \hfill w_{e,k}\hfill \end{array}\right]$,

$$Q=\left[\begin{array}{cc}\hfill Q_{ki,k}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill Q_{e,k}\hfill \end{array}\right].$$

The dynamic equation of extended target consists of two parts: kinematic state transition equation and extent state transition equation. The kinematic state transition equation is:

$$x_{ki,k+1}=F_{ki,k}{x}_{ki,k}+w_{ki,k},w_{ki,k}\sim N(0,Q_{ki,k})$$ (6)

where $F_{ki,k}$ and $Q_{ki,k}$ are the kinematic state transition matrix and the process noise covariance matrix respectively. The extent state transition equation is:

$$x_{e,k+1}=F_{e,k}{x}_{e,k}+w_{e,k},w_{e,k}\sim N(0,Q_{e,k})$$ (7)

$F_{e,k}$ and $Q_{e,k}$ are the extent state transition matrix and the process noise covariance matrix respectively, which could be expressed as follows:

$$F_{e,k}=e^{-\alpha T}{I}_M$$ (8)

$$Q_{e,k}=(1-e^{-2\alpha T})k(\theta ,\theta )$$ (9)

where $I_M$ is the unit matrix of dimension M and M denotes dimension of the extent, the parameter $\alpha \ge 0$ will determine the speed of the dynamics and can be considered as a forgetting factor. With $\alpha =0$, all measurements that have been collected will be of equal importance, and older measurements will be given less weight as time increases; $k(\theta ,\theta )$ is the Gaussian process covariance function. The Gaussian process covariance function determines the relationship between different function values, thereby decisively influencing the results of GPR. Currently, the most commonly used Gaussian process covariance function is with a period of 2π:

$$k_{2\pi }(\theta ,{\theta }^{\prime })={\sigma }_f^2{e}^{-\frac{2{\sin }^2(\frac{|\theta -{\theta }^{\prime }|}{2})}{l^2}}+{\sigma }_r^2$$ (10)

where ${\sigma }_f^2$ is the prior variance of the signal amplitude and l is the length scale of the function that we want to learn. ${\sigma }_r^2$ is Gaussian prior covariance, and the 2π periodic covariance function is that it satisfies the characteristics of arbitrary target radial function, and for any θ value, $f(\theta )$ and $f(\theta +2\pi )$ are completely positive correlation.

2.2. Measurement model

Under the measurement, the $i-th$ measurement at time k can be expressed as follows:

$$y_k^{(i)}=x_{c,k}+s_k^{(i)}{p}_k^{(i)}f\left({\theta }_{L,k}^{(i)}\right)+e_k^{(i)}=:g(x_k,e_k^{(i)}),e_k\sim N(0,R_k)$$ (11)

the radial function $f(•)$ represents the distance between the center and the contour at each angle. So $f\left({\theta }_{L,k}^{(i)}\right)$ represents the radial function at ${\theta }_{L,k}^{(i)}={\theta }_{G,k}^{(i)}-x_{\phi ,k}$ under the prior condition; ${\theta }_{G,k}^{(i)}$ is an angle in the global coordinate system, which is between the straight line from predicted position of the target to the measurement $y_k^{(i)}$ and the positive direction of the axis; ${\theta }_{L,k}^{(i)}$ is in the local coordinate system. $x_{c,k}$ is the position of the target (see Fig. 1), $e_k^{(i)}$ is the sensor noise, and its covariance matrix $R_k$ is the zero mean noise; $p_k^{(i)}={\left[\begin{array}{cc}\hfill \cos ({\theta }_{G,k}^{(i)})\hfill & \hfill \sin ({\theta }_{G,k}^{(i)})\hfill \end{array}\right]}^T$ is an orientation vector; $s_k^{(i)}$ is the scaling factor, $s\in \left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \end{array}\right]$, when $s_k^{(i)}=1$, $y_k^{(i)}$ is the target contour measurement; when $0\le s_k^{(i)}<1$, $y_k^{(i)}$ represents surface measurement. Through GPR, the distribution function of $f\left({\theta }_{L,k}^{(i)}\right)$ under the prior condition of the target extent can be calculated as:

$$f({\theta }_{L,k}^{(i)})\sim N(H_{p,k}^{(i)}{x}_{e,k},R_{p,k}^{(i)})$$ (12)

where

$$H_{p,k}^{(i)}=k({\theta }_{L,k}^{(i)},\theta ){[k(\theta ,\theta )]}^{-1}$$ (13)

$$R_{p,k}^{(i)}=k({\theta }_{L,k}^{(i)},{\theta }_{L,k}^{(i)})-H_{p,k}^{(i)}k(\theta ,{\theta }_{L,k}^{(i)})$$ (14)

Figure 1.

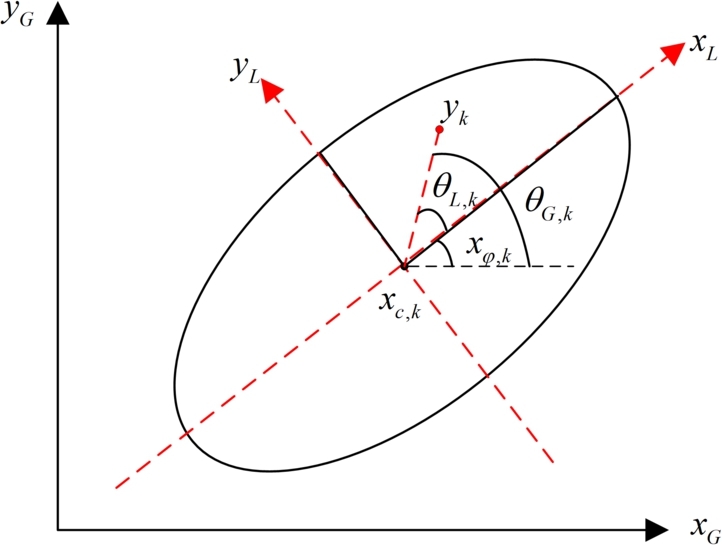
Illustration of the parameterization and measurement model. We omit the time index k. The location of the object is x_c,k. y_k is measurement source corrupted with measurement noise e_k. By anticlockwise rotating coordinates system x-y through an angle of x_φ,k, we have the depicted ellipse axes-aligned in reference frame [22].

If Eq. (12) is brought into Eq. (11), measurement equation of extended target based on GPR can be obtained:

$$y_k^{(i)}=\underset{H_k^{(i)}{x}_k}{\underbrace{x_{c,k}+s_k^{(i)}{p}_k^{(i)}{H}_{p,k}^{(i)}{x}_{e,k}}}+\underset{e_{tr,k}^{(i)}\sim N(0,R_{tr,k}^{(i)})}{\underbrace{s_k^{(i)}{p}_k^{(i)}[f({\theta }_{L,k}^{(i)})-H_{p.k}^{(i)}{x}_{e,k}]+e_k^{(i)}}}$$ (15)

the covariance $R_k$ of the pole diameter is determined by the measurement noise of the sensor; $H_{p,k}^{(i)}$ is the measurement matrix of target state to $y_k^{(i)}$; $e_{tr,k}^{(i)}$ is the zero mean Gaussian noise in the measurement equation. When the noise in GPR and the sensor measurement noise are assumed to be independent of each other, the covariance matrix of $e_{tr,k}^{(i)}$ is:

$$R_{GP,k}^{(i)}=(s_k^{(i)}{p}_k^{(i)})R_{p,k}^{(i)}{(s_k^{(i)}{p}_k^{(i)})}^T=:R(s_k^{(i)},x_k)$$ (16)

$$R_{tr,k}^{(i)}=R_{GP,k}^{(i)}+R_k$$ (17)

3. Inference

In this section, we first derive the time and measurement update step utilizing the UKF. By leveraging the recursive estimation of kinematic parameters and extent information of the extended target, we propose GPR-AUKF combining EM algorithm with GPR-UKF to achieve real-time online tracking for time-varying measurement noise covariance. Since multiple measurements are generated at each time step, we are able to process each one independently and in any order we choose.

3.1. GPR-UKF algorithm

3.1.1. Time update

Since the time update of kinematic state and extent state follows a linear model, the time update can be performed with the standard UKF [28]. Let ${\chi }_k$ be the set of sigma points for the $x_k$, these sigma points ${\chi }_k$ are positioned at the mean of the target state $x_k$ and are symmetrically along the main axes of the covariance $P_{xx,k}$. The $2n+1$ sigma points should be chosen as:

$${\chi }_k=[x_k,x_k+\sqrt{m{P}_{xx,k}},x_k-\sqrt{m{P}_{xx,k}}]$$ (18)

where m is the weight coefficient, $m=n+\lambda$, and $\lambda ={\alpha }^2(n+\kappa )-n$ is a scaling parameter, which is used to reduce the total predicted error, and n is the dimension of variables $x_k$. The selection of α controls the distribution state of sampling points. Generally, $\alpha =1$, κ is the parameter to be selected, and there is no limit on its specific value. To find the predicted state, the state transition function Eq. (5) is applied to the sigma points ${\chi }_k$, generating a new set of sigma points $X_k$ . The predicted state $x_{k+1}^{-}$, and the predicted covariance $P_{xx,k+1}^{-}$ are the weighted sample statistics of $X_k$.

$$X_k=F{\chi }_k$$ (19)

$$x_{k+1}^{-}=\sum _{i=0}^{2n}{w}_m{X}_k$$ (20)

$$P_{xx,k+1}^{-}=\sum _{i=0}^{2n}{w}_c(X_k-x_k){(X_k-x_k)}^T+Q_k$$ (21)

$$\{\begin{array}{c}{w}_m(0)=\frac{\lambda }{n+\lambda }\hfill \\ w_c(0)=\frac{\lambda }{n+\lambda }+(1-{\alpha }^2+\beta )\hfill \\ w_m(h)=w_c(h)=\frac{\lambda }{2(n+\lambda )},h=1\sim 2n\hfill \end{array}$$ (22)

where $w_m$ is the weight coefficient of the mean, and $w_c$ is the weight coefficient of covariance. The parameter of $\beta \ge 0$ is a non-negative weight coefficient, which can combine the dynamic difference of higher-order terms in the equation, so that the influence of higher-order terms can be included, generally, $\beta =2$.

3.1.2. Measurement update

The measurements $y_k={\left\{y_k^{(j)}\right\}}_{j=1}^{n_k}$ from time step k are incorporated sequentially in the measurement update, where $n_k$ is the number of measurements generated at each time. For this purpose, let $x_{k+1}^{(i-1)}$ and $P_{xx,k+1}^{(i-1)}$ denote the estimates for the state $x_k$ and covariance matrix $P_{xx,k}$, which have incorporated all measurements up to time k and the measurements ${\{y_{k+1}^{(j)}\}}_{j=1}^{i-1}$ from time $k+1$. In the measurement update, the next measurement $y_{k+1}^{(i)}$ is incorporated in order to obtain the updated estimates $x_{k+1}^{(i)}$ and $P_{xx,k+1}^{(i)}$. Note that the predicted estimate of time is recorded as ${(•)}_k^{(0)}$. The measurements of a single scan are combined in any order, and slightly different results may be obtained for different orderings.

In our approach, we utilize a UKF to update the predicted state $x_{k+1}^{-}$ and covariance $P_{xx,k+1}^{-}$. When $i=1$, $x_{k+1}^{(i-1)}=x_{k+1}^{-},P_{xx,k+1}^{(i-1)}=P_{xx,k+1}^{-}$. We apply the unscented transform (UT) to take ${\mathrm{\Upsilon }}_{k+1}^{(i)}$ into Eq. (15) and Eq. (16), which generate a set sigma points $Y_{k+1}^{(i)}$ to represent the predicted observation ${\overline{Y}}_{k+1}^{(i)}$ and GPR model error ${\overline{R}}_{GP,k+1}^{(i)}$.

$${\mathrm{\Upsilon }}_{k+1}^{(i)}=\left[\begin{array}{c}(x_{k+1}^{(i-1)}){}^T\hfill \\ {(x_{k+1}^{(i-1)}+\sqrt{m{P}_{xx,k+1}^{(i-1)}})}^T\hfill \\ {(x_{k+1}^{(i-1)}-\sqrt{m{P}_{xx,k+1}^{(i-1)}})}^T\hfill \end{array}\right]{}^T$$ (23)

$$Y_{k+1}^{(i)}=g({\mathrm{\Upsilon }}_{k+1}^{(i)},e_k^{(i)})$$ (24)

$${\overline{Y}}_{k+1}^{(i)}=\sum _{i=0}^{2n}{w}_m{Y}_{k+1}^{(i)}$$ (25)

It is important to note that when using the GPR model, the difference from the measurement update of standard UKF is the noise error which includes both GPR model error and measurement noise (see Eq. (17)). Therefore, when calculating the covariance of the error, including the covariance of the GPR model error ${\overline{R}}_{GP,k+1}^{(i)}$ and the measurement noise $R_k$.

$$R_{GP,k+1}^{(i)}=(s_k^{(i)}{p}_k^{(i)})R_{p,k}^{(i)}{(s_k^{(i)}{p}_k^{(i)})}^T=:R(s_k^{(i)},{\mathrm{\Upsilon }}_{k+1}^{(i)})$$ (26)

$${\overline{R}}_{GP,k+1}^{(i)}=\sum _{i=0}^{2n}{w}_c{R}_{GP,k+1}^{(i)}$$ (27)

$$R_{tr,k+1}^{(i)}={\overline{R}}_{GP,k+1}^{(i)}+R_k$$ (28)

The weighted sample statistics of $Y_{k+1}^{(i)}$, i.e., is given by

$$P_{YY,k+1}^{(i)}=\sum _{i=0}^{2n+1}{w}_c(Y_{k+1}^{(i)}-{\overline{Y}}_{k+1}^{(i)}){(Y_{k+1}^{(i)}-{\overline{Y}}_{k+1}^{(i)})}^T+R_{tr,k+1}^{(i)}$$ (29)

The predicted cross correlation $P_{xY,k+1}^{(i)}$ is the sample cross correlation of $X_{k+1}^{(i)}$ and $Y_{k+1}^{(i)}$.

$$P_{xY,k+1}^{(i)}=\sum _{i=0}^{2n+1}{w}_c(X_{k+1}^{(i)}-x_{k+1}^{-}){(Y_{k+1}^{(i)}-{\overline{Y}}_{k+1}^{(i)})}^T$$ (30)

The Kalman filter gain is

$$K_{k+1}^{(i)}=P_{xY,k+1}^{(i)}{P}_{YY,k+1}^{(i)-1}$$ (31)

and the estimates of the state and covariance are

$$\{\begin{array}{c}{x}_{k+1}^{(i)}=x_{k+1}^{(i-1)}+K_{k+1}^{(i)}{(y_{k+1}^{(i)}-{\overline{Y}}_{k+1}^{(i)})}^T)\hfill \\ P_{xx,k+1}^{(i)}=P_{xx,k+1}^{(i-1)}-K_{k+1}^{(i)}{P}_{YY,k+1}^{(i)}{K}_{k+1}^{(i)T}\hfill \end{array}$$ (32)

$$\{\begin{array}{c}{x}_{k+1}=x_{k+1}^{(n_k)}\hfill \\ P_{xx,k+1}=P_{xx,k+1}^{(n_k)}\hfill \end{array}$$ (33)

3.2. GPR-AUKF algorithm

The EM algorithm can solve the maximum likelihood estimation problem with latent variables. We take the state of target as a latent variable that cannot be directly observed, and regard measurement noise covariance as the current estimated parameter. Based on the EM algorithm, the posterior probability distribution of the state of target is calculated based on the initial measurement noise covariance. Then, measurement noise covariance is updated through the obtained posterior probability distribution.

To alleviate the problem caused by variable measurement noise covariance. By applying EM algorithm, we update the measurement noise covariance of the extended target at each moment. The maximum likelihood estimation of measurement noise covariance $R_{k+1}$ is written as ${\hat{R}}_{k+1}$, which is described as follows:

$$\begin{array}{c}{\hat{R}}_{k+1}=\underset{R_{k+1}}{\arg \max }{p}_{R_{k+1}}(y_{k+1})\hfill \\ =\underset{R_{k+1}}{\arg \max \log }{p}_{R_{k+1}}(y_{k+1})\hfill \end{array}$$ (34)

where $p_{R_{k+1}}(•)$ is the probability density function (PDF) related to the parameter $R_{k+1}$. We only iterate once to obtain the local optimal solution of $R_{k+1}$. Then, the minimum variance estimation $Q(R_{k+1},R_{k+1}^{[0])})$ is used to approximate $\log p_{R_{k+1}}(x_{k+1},y_{k+1})$.

$$L_{R_{k+1}}(x_{k+1},y_{k+1})\stackrel{.}{=}Q(R_{k+1},R_{k+1}^{[0])})=E_X[\log p_{R_{k+1}}(x_{k+1},y_{k+1})|R_{k+1}^{[0]},y_{k+1}]=\int \log p_{R_{k+1}}(x_{k+1},y_{k+1})p_{R_{k+1}^{[0]}}(x_{k+1},y_{k+1})d{x}_{k+1}$$ (35)

where $E_X[•]$ is an expectation of $x_{k+1}$; $R_{k+1}^{[0]}$ is an approximate solution of ${\hat{R}}_{k+1}$ at iteration 0, $Q(R_{k+1},R_{k+1}^{[0]})$ is defined as the conditional expectation of $\log p_{R_{k+1}}(x_{k+1},y_{k+1})$.

3.2.1. The expectation approach

$\log p_{R_{k+1}}(x_{k+1},y_{k+1})$ is factored using Eq. (36):

$$\log p_{R_{k+1}}(x_{k+1},y_{k+1})=\log [p_{R_{k+1}}(y_{k+1}|x_{k+1},y_{1:k})⁎p_{R_{k+1}}(x_{k+1}|y_{1:k})p(y_k)]=\log [p_{R_{k+1}}(y_{k+1}|x_{k+1},y_{1:k})]+\log [p_{R_{k+1}}(x_{k+1}|y_{1:k})]+\log [p(y_{1:k})]$$ (36)

where $p_{R_{k+1}}(y_{k+1}|x_{k+1},y_{1:k})=p_{R_{k+1}}(y_{k+1}|x_{k+1})$, because includes all of the information in $y_{1:k}$.

Remark: The predicted PDF$p_{R_{k+1}}(x_{k+1}|y_{1:k})$is approximated to follow the Gaussian distribution; then, the$2n+1$sigma points are selected, and the moment estimation of$p_{R_k}(x_{k+1}|y_{1:k})$is calculated using the unscented transformation. The mean and covariance matrix of$p_{R_k}(x_{k+1}|y_{1:k})$with higher accuracy are acquired for the nonlinear state equation.

$$p_{R_k}(x_{k+1}|y_{1:k})=N(x_{k+1};x_{k+1}^{-},P_{xx,k+1}^{-})$$ (37)

where $N(•,\mu ,{\sigma }^2)$ is the Gaussian distribution with the mean μ and covariance ${\sigma }^2$. Calculating the state vector $x_{k+1}^{-}$ and covariance matrix $P_{xx,k+1}^{-}$ are the same as Eqs. (18) ∼ (22).

When $i=1$, $x_{k+1}^{(i-1)}=x_{k+1}^{-},P_{xx,k+1}^{(i-1)}=P_{xx,k+1}^{-}$. Similarly, $p_{R_k}(y_{k+1}^{(i)}|x_{k+1}^{(i)})$ is approximated as

$$p_{R_k}(y_{k+1}^{(i)}|x_{k+1}^{(i)})=N(y_{k+1}^{(i)};{\overline{Y}}_{k+1}^{(i)},R_{k+1})$$ (38)

where the predicted measurement vector ${\overline{Y}}_{k+1}^{(n_k)}$ is calculated as Eq. (25). The measurement error covariance matrix $P_{YY,k+1}^{(i)}$ and cross error covariance matrix $P_{xY,k+1}^{(i)}$ are calculated as follows:

$$P_{YY,k+1}^{(i)}=\sum _{i=0}^{2n+1}{w}_c(Y_{k+1}^{(i)}-{\overline{Y}}_{k+1}^{(i)}){(Y_{k+1}^{(i)}-{\overline{Y}}_{k+1}^{(i)})}^T+R_{GP,k+1}^{(i)}+R_k$$ (39)

Then updating the estimates of the state $x_{k+1}$ and covariance $P_{xx,k+1}$ as Eqs. (30) ∼ (33).

The posterior PDF is $p_{R_{k+1}}(x_{k+1},y_{k+1})$ while $R_{k+1}=R_{k+1}^{[0]}$ is approximated as the Gaussian PDF:

$$p_{R_{k+1}^{(0)}}(x_{k+1},y_{k+1})=N(x_{k+1};x_{k+1}^{[1]},P_{k+1}^{[1]})$$ (40)

where the mean and covariance of $x_{k+1}$ are $x_{k+1}^{[1]}$ and $P_{k+1}^{[1]}$. Different from the linearization method mentioned above, the unscented transformation is employed in the measurement process update. The integration calculation for the nonlinear function is transformed into the weight sum for sigma points so that the negative effect caused by the truncation error is reduced. The computational procedure is presented.

Employing Eqs. (35) ∼ (38), $\log p_{R_{k+1}}(x_{k+1},y_{k+1})$ can be deduced using Eq. (40):

$$\log p_{R_{k+1}}(x_{k+1},y_{k+1})=-0.5{(y_{k+1}^{(1:n_k)}-{\overline{Y}}_{k+1}^{(1:n_k)})}^T{R}_{k+1}^{-1}(y_{k+1}^{(1:n_k)}-{\overline{Y}}_{k+1}^{(1:n_k)})-0.5{(x_{k+1}^{(1:n_k)}-{\hat{x}}_{k+1}^{-})}^T{(P_{xx,k+1}^{-})}^{-1}(x_{k+1}^{(1:n_k)}-{\hat{x}}_{k+1}^{-})-0.5\log \left|R_{k+1}\right|-0.5\log \left|P_{xx,k+1}^{-}\right|+c$$ (41)

where $|•|$ represents the determinant operation of a matrix, and c represents a constant value with regard to the variable $R_{k+1}$. Eventually, $Q(R_{k+1},R_{k+1}^{[0]})$ can be simplified as

$$Q(R_{k+1},R_{k+1}^{[0]})=-0.5\log \left|R_{k+1}\right|-0.5tr(M_{k+1}{R}_{k+1}^{-1})-0.5\log \left|P_{xx,k+1}^{-}\right|-0.5tr[N_{k+1}{(P_{xx,k+1}^{-})}^{-1}]+c$$ (42)

where $tr(•)$ represents the trace operation of a matrix, $M_{k+1}$ and $N_{k+1}$ are obtained by

$$M_{k+1}=\int (y_{k+1}^{(1:n_k)}-{\overline{Y}}_{k+1}^{(1:n_k)}){(y_{k+1}^{(1:n_k)}-{\overline{Y}}_{k+1}^{(1:n_k)})}^{T}N(x_{k+1};x_{k+1}^{[1]},P_{k+1}^{[1]})d{x}_{k+1}$$ (43)

$$N_{k+1}=\int (x_{k+1}^{(1:n_k)}-x_{k+1}^{-}){(x_{k+1}^{(1:n_k)}-x_{k+1}^{-})}^{T}N(x_{k+1};x_{k+1}^{[1]},P_{k+1}^{[1]})d{x}_{k+1}$$ (44)

3.2.2. The maximization approach

The maximization step includes the maximization of $Q(R_{k+1},R_{k+1}^{[0]})$. In order to find the extreme point, the first-order derivative of $Q(R_{k+1},R_{k+1}^{[0]})$ should be obtained and set as equal to 0.

$$\frac{\partial Q(R_{k+1},R_{k+1}^{[0]})}{\partial R_{k+1}}=-0.5R_{k+1}^{-1}+0.5R_{k+1}^{-1}{M}_{k+1}{R}_{k+1}^{-1}=0$$ (45)

solving Eq. (45), then

$$R_{k+1}=M_{k+1}$$ (46)

as a result,

$$R_{k+1}=(y_{k+1}^{(1:n_k)}-{\overline{Y}}_{k+1}^{(1:n_k)}){(y_{k+1}^{(1:n_k)}-{\overline{Y}}_{k+1}^{(1:n_k)})}^T$$ (47)

Thus, the measurement noise covariance is updated.

4. Simulation

In this section, we will first introduce the indexes for tracking targets. During the experiments, we thoroughly evaluate the tracking performance of the proposed method.

4.1. Evaluation index

4.1.1. RMSE

The position and orientation errors of target can be measured using Root Mean Square Error (RMSE).

4.1.2. IOU

IOU reflects the accuracy of the algorithm in estimating the extent of the target. Assuming that S and $\hat{S}$ are the true extent and estimated extent of the target respectively, the calculation method of IOU is as follows:

$$IOU(S,\hat{S})=\frac{area(S\cap \hat{S})}{area(S\cup \hat{S})}$$ (48)

where $area(•)$ represents the calculated area, so the value of $IOU(S,\hat{S})$ is within the interval $[0,1]$. When $IOU(S,\hat{S})=1$, it indicates that the estimated target shape completely coincides with the actual target extent; when $IOU(S,\hat{S})=0$, the estimated extent and the real extent of the target is non-intersect. IOU is easily affected by the accuracy of target kinetic state estimation, and the large error of position can easily lead to $IOU(S,\hat{S})=0$.

4.2. Experimental results and analysis

In this section, we evaluate the performance of the proposed method and compare it with relevant extended target tracking algorithms in the literature. We set up two groups of simulation experiments, the first group involves setting up moving targets with different levels of mobility and the second is to track maneuvering target under varying measurement noise. The results of the experiments demonstrate that GPR-AUKF is suitable for tracking targets with different levels of mobility and varying measurement noise. The presented results are the average of the 100 Monte Carlo runs.

4.2.1. Distinct maneuverability

During the simulation experiment, the ellipse targets with different levels of maneuverability follow different trajectories. The first scenario involves the constant velocity (CV) model for target motion trajectory and the second scenario uses both the CV and constant turn rate and velocity (CTRV) models, the last scenario uses the collaborative turning (CT) model.

For the proposed model, the hyper-parameters of the Gaussian process have been set to ${\sigma }_r=0.8$, ${\sigma }_f=2$ and the length scale of the function is set to $l=\pi /8$ (see Eq. (10)). The initial measurement noise covariance is set to $R_0=4I_2$, and the sampling time is set to $T=1$ and w represents the turning radius.

We test the algorithms on moving objects with different maneuverability, i.e., a CV model(S1), a model combining CV and CTRV (S2), and a CT model(S3). The first scenario is CV model which involves a linear path with a constant velocity of $0.14m/s$; and the second scenario, which is a combination of linear paths and turns, is generated. The object first moves on a linear path with $0.14m/s$ in the horizontal orientation, then makes a turn with $0.14m/s$ and runs with a change in direction of $\pi /300rad/s$, and again follows a linear path, maintaining the original velocity. The last scenario is CT model, for a maneuvering target, its velocity is $1m/s$ which remains unchanged, and its orientation is variable in real-time. Assuming that the size of the extended object is constant (plus noise), a target that follows a variable turn-rate model is simulated, its turn rate starts with $\pi /300(rad/s)$ in the first 150k and increases to $\pi /250(rad/s)$ from $150k-463k$, then ends with $\pi /200(rad/s)$ in the last 50k.

The number of measurements at each scan follows Poisson distributed. The measurement noise covariance of GPR-EKF and GPR-UKF is constantly set to $R=4I_2$. The measurement covariance of GPR-AUKF is updated in real-time with the update of the state and covariance of the target. The object is an ellipse with a semi-major axis of 17m and a semi-minor axis of 4m. As shown in [26], we set the real measurement noise covariance of the target as

$$R_k=30⁎(0.1+0.05⁎\cos (\frac{\pi ⁎k}{t}))⁎\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$ (49)

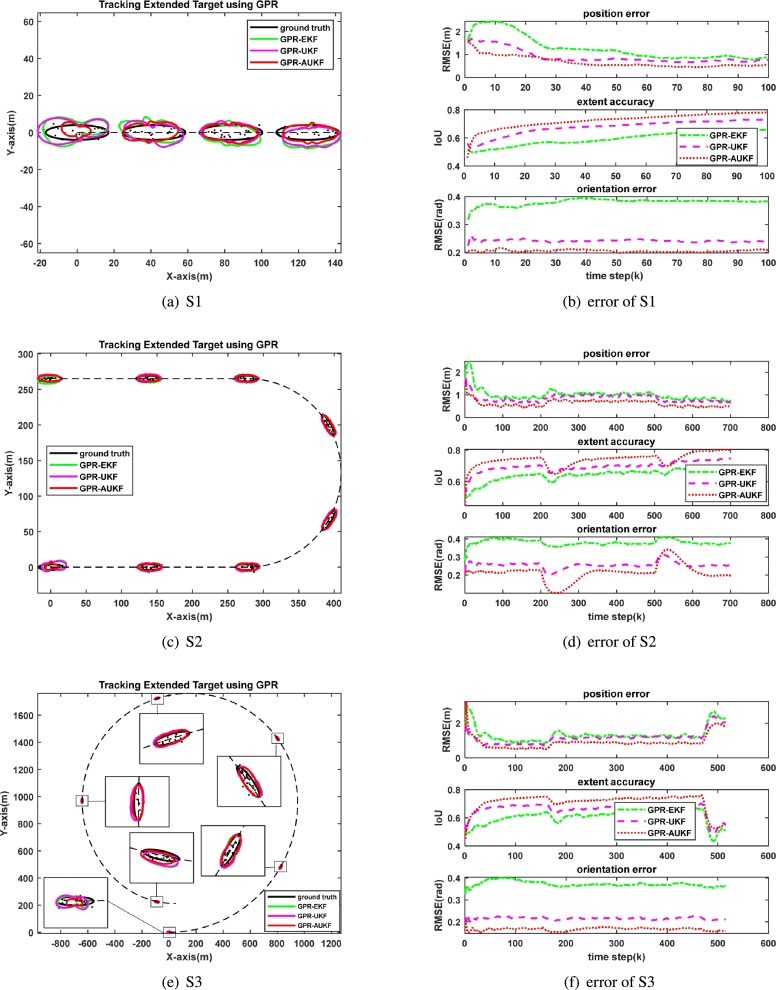
Fig. 2 presents the comparison results of trajectory (left column) and error results (right column) for GPR-UKF, GPR-AUKF, and GPR-EKF. Additionally, Table 1 displays the target tracking error.

Figure 2.

Example results for tracking target with different maneuverability. The moving trajectories are in the left column and the tracking errors of the target position, extent, and orientation are shown in the right column. True target (black contour) is compared with the proposed two methods, i.e., GPR-UKF (magenta contour) and GPR-AUKF (red contour), and other competing method, GPR-EKF (green contour). The black dashed line represents the moving trajectory which is connected by the center position of the target at each moment, and the measurements are depicted as black dots. (a) Motion model: S1, (c) Motion model: S2, (e) Motion model: S3, (b) Tracking error of S1, (d) Tracking error of S2, (f) Tracking error of S3.

Table 1.

RMSE of the target position, orientation and intersection-over-union (IOU) with respect to different tracking algorithms. The numbers are averaged over 100 MC runs.

Trajectory	S1			S2			S3
Method	GPR-EKF	GPR-UKF	GPR-AUKF	GPR-EKF	GPR-UKF	GPR-AUKF	GPR-EKF	GPR-UKF	GPR-AUKF
Center(m)	1.1056	0.7441	0.7039	1.1945	0.8970	0.7052	1.9486	1.4625	1.1868
IOU	0.6137	0.6681	0.6670	0.5965	0.6359	0.6432	0.5399	0.5802	0.6178
Orientation(rad)	0.2357	0.2138	0.2110	0.2442	0.2239	0.2183	0.2585	0.2179	0.1746

Looking at Fig. 2, it is evident that the performance of the proposed GPR-AUKF is superior to both GPR-EKF and GPR-UKF. Moreover, GPR-UKF shows better robustness than GPR-EKF in extended target tracking. In combination with Table 1, we analyze the error in Fig. 2. In Fig. 2(b), under the CV model, the tracking error is relatively smooth. For our proposed GPR-UKF, the position error is reduced to 0.7441m, the IOU is increased to 0.6681, and the orientation error is decreased to $0.2138rad$. Compared to GPR-EKF, this method exhibits better robustness. With our proposed GPR-AUKF, the position error is further reduced to 0.7039m, the IOU is increased to 0.6670, and the orientation error is reduced to $0.2110rad$. When compared to GPR-EKF and GPR-UKF, GPR-AUKF achieves the highest tracking performance. In Fig. 2(d), the error will jitter as the target maneuverability shifts and then remain smooth. Compared to GPR-EKF, by employing the proposed GPR-UKF, the position error is reduced by 0.2975m, the IOU is increased by 0.0394, and the orientation error is decreased by $0.0332rad$. Compared to GPR-UKF, by adopting GPR-AUKF, the position error is reduced by 0.1918m, the IOU is increased by 0.0073, and the orientation error is decreased by $0.0056rad$. In Fig. 2(f), as the target maneuverability increases, the tracking error becomes larger. The tracking accuracy of GPR-AUKF is further improved compared to the other two filter algorithms. It can be clearly seen that the proposed GPR-UKF outperforms GPR-EKF for targets with stronger mobility, and the proposed GPR-AUKF performs better than GPR-UKF in all aspects of tracking performance.

Moreover, for each time step k, GPR-EKF runs for 0.0055s, GPR-UKF runs for 0.04s, and GPR-AUKF runs for 0.05s. Although GPR-EKF is superior in running time compared to GPR-UKF and GPR-AUKF, its accuracy in estimating the shape and position of extended targets is limited.

4.2.2. Different measurement noises

As we focus on the variable measurement noise of the target tracking, we restrict trajectory to S3 in the Section 4.2.1. The only change is the measurement noise covariance. We set the covariance of low measurement noise as

$$R_k=3⁎(0.1+0.05⁎\cos (\frac{\pi ⁎k}{t}))⁎\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$ (50)

and the high measurement noise covariance as

$$R_k=30⁎(0.1+0.05⁎\cos (\frac{\pi ⁎k}{t}))⁎\left[\begin{array}{cc}\hfill 4\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$ (51)

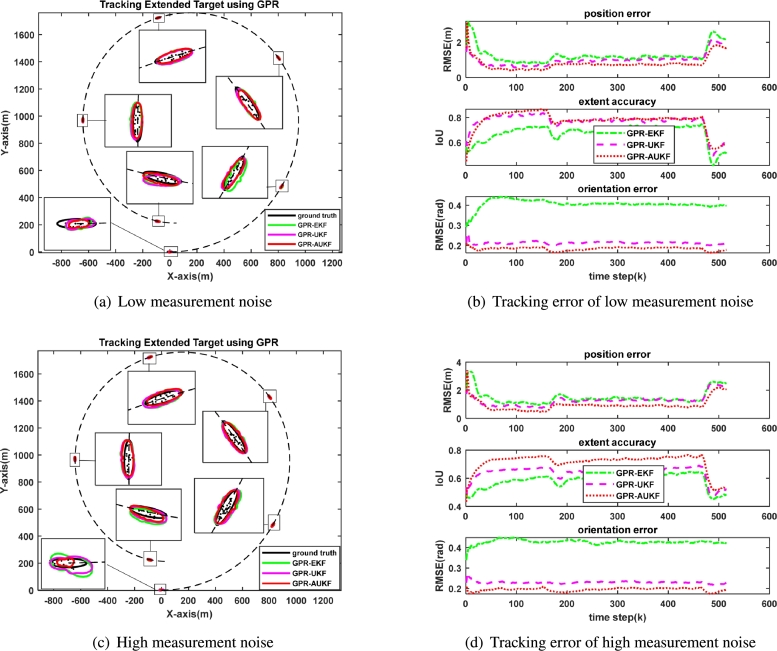
The simulation results are presented in Fig. 3. Table 2 shows the RMSM of position, orientation, and the IOU of tracking results. As can be clearly seen from Table 2, under low measurement noise, by adopting GPR-UKF, the position error is decreased from 1.7368m to 1.1711m. At the same time, the IOU is increased from 0.6156 to 0.6820, and the orientation error is reduced from $0.2265rad$ to $0.1995rad$. When employing GPR-AUKF, the position error further decreases from 1.1711m to 0.9106m, the IOU increases from 0.6820 to 0.7282, and the orientation error is reduced from $0.1995rad$ to $0.1721rad$. In the case of high measurement noise, when comparing GPR-UKF with GPR-EKF, the position error is reduced by 0.4940m, the IOU is increased by 0.0451, and the orientation error is reduced by $0.0111rad$. When comparing GPR-AUKF with GPR-UKF, the position error is reduced by 0.3586m, the IOU is increased by 0.0584, and the orientation error is reduced by $0.0318rad$. Simultaneously, when considering the tracking results under the measurement noise covariance of S3 in Section 4.2.1, it is evident that GPR-AUKF is more robust in tracking the position, extent, and orientation of the extended target both at low and high measurement noise. Moreover, GPR-UKF has better performance than GPR-EKF. From Fig. 3(b) and Fig. 3(d), it can be concluded that GPR-AUKF has more obvious advantages over GPR-EKF and GPR-UKF in the case of high measurement noise.

Figure 3.

Example results for tracking target with different measurement noises. The moving trajectories are in the left column and the tracking errors of the target position, extent, and orientation are shown in the right column. True target (black contour) is compared with the proposed two methods, i.e., GPR-UKF (magenta contour) and GPR-AUKF (red contour), and other competing method, GPR-EKF (green contour). The black dashed line represents the moving trajectory which is connected by the center position of the target at each moment, and the measurements are depicted as black dots. (a) Low measurement noise, (c) High measurement noise, (b) Tracking error of low measurement noise, (d) Tracking error of high measurement noise.

Table 2.

RMSE of the target position, orientation and intersection-over-union (IOU) with respect to different tracking algorithms. the numbers are averaged over 100 MC runs.

Trajectory	Low measurement noise			High measurement noise
Method	GPR-EKF	GPR-UKF	GPR-AUKF	GPR-EKF	GPR-UKF	GPR-AUKF
Center(m)	1.7368	1.1711	0.9106	2.1166	1.6226	1.2640
IOU	0.6156	0.6820	0.7282	0.5098	0.5549	0.6133
Orientation(rad)	0.2265	0.1995	0.1721	0.2159	0.2048	0.1730

We can see that the entire system is very stable regardless of different maneuverability conditions or environments with different measurement noises.

There are two main reasons for this: First, the measurement noise changes over time during target tracking, which leads to larger measurement error if the measurement noise covariance is not updated in real time. However, the measurement noise covariance of GPR-EKF and GPR-UKF is fixed value while GPR-AUKF realizes the real-time update. Second, the target state is not linearized in GPR-AUKF and GPR-UKF, so the truncation error may be eliminated, and thus the performance of GPR-AUKF and GPR-UKF is better than that of GPR-EKF.

5. Conclusion

The conventional EKF faces challenges in unknown and variable environments. To address this issue, a new closed form tracker called GPR-AUKF is proposed in this paper for the estimation of extended targets. The process of tracking algorithm focuses on two key points: 1) combining the GPR with UKF to achieve high-precision tracking of extended targets with maneuverability; 2) utilizing EM to update measurement noise covariance. Experimental simulation results show that GPR-AUKF outperforms GPR-EKF in terms of kinematic state and extent estimation.

In the future, we will expand this method to tracking extended targets in three-dimensional environment or embed it into multiple target trackers, such as PHD filter.

CRediT authorship contribution statement

Renli Zhang: Writing – review & editing, Writing – original draft, Software, Resources, Methodology, Investigation. Yan Zhang: Supervision, Funding acquisition. Jintao Chen: Methodology. Ziwen Sun: Methodology. Jing Li: Conceptualization. Zhuangbin Tan: Software, Conceptualization. Zhongxing Jiao: Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability statement

No additional data was used for the research describe in the article.