Plant coexistence depends on ecosystem nutrient cycles: Extension of the resource-ratio theory

Abstract

We present a model of plant-nutrient interactions that extends classical resource competition theory to environments in which essential nutrients (resources) are recycled between plant and soil pools and dissolved nutrients are lost through plant-available (i.e., inorganic forms) or plant-unavailable (i.e., complex organic forms) pathways. Losses by dissolved organic pathways can alter ratios of nutrients that are recycled and supplied within the plant-soil system, thereby influencing competition and coexistence among plant species. In special cases, our extended model does not differ from classical models, but in more realistic cases our model introduces new dynamical behavior that influences competitive outcomes. At equilibrium, coexistence still depends on nutrient supply and consumption, but nutrient supply includes recycling and is highly sensitive to whether a species promotes more organic losses of the nutrient that limits its own growth than of nutrients that limit its competitors. Because recycling operates with a time delay compared with consumption, recycling-mediated effects on competition can, under certain conditions, lead to sustained population oscillations. Our findings have implications for how we understand nutrient competition, nutrient cycles, and plant evolutionary strategies.

Essential resources, such as nitrogen or phosphorus, can limit primary production of individual plants as well as entire ecosystems (1-2) and can play an essential role in plant community assembly (3-6). Therefore, understanding plant-nutrient interactions constitutes a major challenge for plant community ecology and ecosystem biology.

Classical models (3, 6) of exploitative competition in plant communities have long assumed that individual plants affect the abundance of nutrients only through consumption (7-9). The system of interest involves two classes of nutrients that define two functionally different compartments (Fig. 1a): nutrients that are bound within plant biomass and inorganic nutrients (e.g., 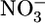or 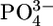) that are available for immediate plant uptake in the environmental matrix. For simplicity, the system is usually assumed to follow simple chemostat resource supply dynamics that do not incorporate species-specific effects on recycling, nutrient loss, and other such factors (9).

Fig. 1.

Plant-nutrient system. (a) In classical models, nutrients are supplied as a function of external nutrient supply (θ) and lost by plant-available inorganic pathways (LI); there is no explicit plant-detritus recycling feedback. Plants consume inorganic nutrients (C) and export biomass in particulate form through mortality (M). (b) Assuming two inorganic nutrients N₁ and N₂, the ZNGI (9) for a species x represents the nutrient level (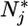) at which net plant growth is null. The equilibrium condition for inorganic nutrients is represented by the vector equation 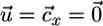, where the external supply vector 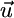represents the flux θ - LI, and the consumption vector represents the flux C. The external supply point S represents the equilibrium levels of inorganic nutrients in absence of plants. Assuming chemostat dynamics for nutrients and plants, S also represents the total capital of nutrients in the system. The slope indicates the trajectory of consumption (driven by the ratio of nutrients consumed α_x), hence the location of the equilibrium point E on the ZNGI. If several species compete, this graph is a convenient tool to predict competitive outcomes (3). (c) Our model introduces a plant-soil feedback in which nutrients made available through mortality are recycled within the ecosystem and a plant-unavailable pathway of nutrient export. Plant detritus accumulates and is partially recycled (R) and partially lost (LO) in dissolved organic forms. (d) The classical graph is modified by recycling, and the vector equation becomes , where represents the recycled flux (R). Combining 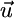and 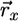into a net supply vector u′ (18) we obtain . The location of the equilibrium point E′ along the ZNGI is determined by the trajectory of the consumption (ratio α_x) relative to the net supply point S′. S′ thus represents the virtual levels that inorganic nutrients would reach in the absence of consumption but in the presence of recycling. If the ratio recycled is different from the ratio consumed, it follows that E′ differs from E.

Plant-nutrient interactions have been extensively studied from this perspective (7-10). The impact of plants on nutrients, mediated through consumption, can be illustrated (Fig. 1b) by using the traditional graphical method of the resource-ratio theory (3). If several plant species compete for two nutrients, this graphical method provides a convenient way to predict competitive outcomes as a function of nutrient supplies (3, 4, 11).

On the contrary, ecosystem biology considers consumption as only one part of a larger plant-nutrient system in which nutrients cycle between plants and their environment (11-13) (Fig. 1c). This approach typically focuses on mechanisms that control inorganic supplies to plants, most notably biological mineralization of nutrients from plant detritus but also abiotic vectors of atmospheric and weathering inputs (14, 15). To the extent that mineralization is the major proximate nutrient source for plants in terrestrial ecosystems [especially in systems with well developed detritus pools (15)], local supplies of nutrients to plants do not rely only on external abiotic constraints (e.g., atmospheric and weathering inputs) but also on an internal recycling feedback that is critical for the long-term development of nutrient budgets within the ecosystem (13-16).

Hence, to address plant competition for nutrients in a more realistic context than traditional two-compartment models, it is necessary to consider mechanisms that ultimately govern nutrient budgets and recycling within the larger plant-nutrient-environmental system. As such mechanisms modify the system-level mass balance of nutrients and their rates of supply (Fig. 1d), they will influence the outcome of the competition as well (17, 18).

Recent empirical and theoretical studies (12-14, 19, 20) have brought new understanding of how the long-term development of nutrient budgets in terrestrial ecosystems is influenced by nutrient losses from the ecosystem as a whole. Specifically, losses of chemically complex dissolved organic forms of nutrients have been proposed (19) as a key mechanism that can regulate input-output budgets and the efficiency of recycling: significant amounts of nutrients bound in dissolved organic molecules (e.g., dissolved organic nitrogen and dissolved organic phosphorus) can be lost hydrologically during the process of soil humification and leave the system without being mineralized. Such losses can effectively prevent part of the detrital nutrient pool from being recycled into inorganic forms available for plant uptake. The recycling efficiency (i.e., the proportion of nutrients contained in the detritus that is not lost during the recycling processes) for a given nutrient likely depends on such factors as the quality of detritus produced by plants and appears to differ across nutrients, such as nitrogen and phosphorus (14).

Building on these results, we seek to build a bridge between community and ecosystem ecology by addressing the mechanisms of plant competition within the context of nutrient cycles. We expand on classical models of plant competition by including nutrient recycling and organic loss processes within the system of interest.

Our approach differs from earlier studies of how recycling influences plant coexistence (11, 17, 18, 21-24) in that we consider recycling not to be necessarily herbivore-driven but more broadly to depend on the pathway of losses of nutrients at the ecosystem scale. Although we focus on terrestrial plant-soil systems, our model is applicable to any ecological system (terrestrial or aquatic) characterized by recycling and diverse paths of nutrient loss.

With a simple model and graphical representations derived from the resource-ratio theory (3) illustrated in Fig. 1, we explore competitive outcomes and, more specifically, the constraints required for the coexistence of two species competing for two essential nutrients. Despite its simple formulation, our model contains the main steps of nutrient recycling in terrestrial ecosystems: production of detritus by living plants, mineralization, and losses of nutrients by plant-available and plant-unavailable paths along the recycling pathway. For simplicity, we assume that inorganic nutrients are the only form available for direct plant uptake, whereas organic nutrients are not available unless they first undergo mineralization. Dissolved export of organic nutrients across ecosystem boundaries therefore constitutes a plant-unavailable pathway (14) for nutrient loss. Therefore, in this paper, inorganic must be read as synonymous with available and organic as synonymous with unavailable. In reality, this separation is more nuanced, with simple amino acids (a minor fraction of “dissolved organic nitrogen” in most soils) behaving in a manner similar to available, inorganic nutrients (14, 25).

Model

Our model is stoichiometrically explicit by virtue of maintaining mass balance for each nutrient.

We assume a classical dynamic equation (3) for plant biomass:

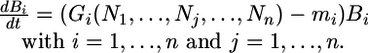[1]

B_i represents the biomass of plant species i, G_i is the growth as a function of the inorganic (available) limiting nutrient N_j, and m_i is the mortality rate. B_i is the sum of the pools of all of the different nutrients involved in plant structure: B_i = ∑_j P_ij. Here P_ij represents the pool of nutrient j bound in the biomass. We assume that nutrients are allocated in strict quotas in the biomass:

[2]

The growth function G_i depends on the availability of nutrients relative to plant demand. Because of the requirement of biomass homeostasis, plants are assumed to consume nutrients in fixed ratios, so that G_i follows a Liebig's law of the minimum:

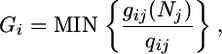[3]

where g_ij represents the growth function of plant i when limited by a nutrient j. g_ij is monotone, and it increases with the level of nutrient [such as the Monod function (11)].

Through mortality, plants generate a pool of detritus which, in turn, is processed by soil decomposers:

[4]

Here D_ij represents the nutrient j contained in detritus biomass provided by plant i, and d_ij is the rate of decomposition of the detritus. We assume d_ij to be constant (13, 26).

The dynamics of the inorganic nutrient pool involves external inputs, internal recycling, consumption by plants, and loss from the ecosystem:

[5]

Supplies and losses of nutrients to and from the inorganic nutrient pool follow a chemostat dynamic (3) in which a represents the dilution rate and S_j represents the pool of inorganic nutrient in the supply flux from external sources. ϕ_ij represents the fraction of a nutrient j that is lost from the soil in the form of dissolved organic molecules during the mineralization process. Therefore, the flux of nutrient that is effectively recycled is the fraction (1 - ϕ_ij) of the decomposition flux d_ij D_ij. Note that ϕ_ij and d_ij are species- and nutrient-specific.

From Eqs. 2-5, we derive the dynamics of the total (i.e., the sum of all of the pools of a nutrient in the system) pool T_j of a nutrient j. The dynamics only depend on the inorganic supply, that is, the input from external sources minus the inorganic loss a(S_j - N_j), and the organic loss ∑_iϕ_ijd_ijD_ij from the ecosystem:

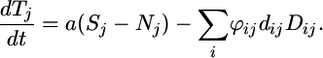[6]

Results

In this section we will address the outcomes of competition for two plant species consuming two nutrients (N₁ and N₂). Specifically, we are interested in comparing the conditions required for coexistence with vs. without recycling. That is, we want to explore whether internal recycling changes competitive outcomes given a particular external nutrient supply to the ecosystem.

Coexistence at Equilibrium Depends on How Each Competitor Influences Organic Losses. Let us consider species x and y competing for N₁ and N₂, with each species consuming nutrients according to its specific biomass quota. As for classical models, we find that our model has several equilibria. There is a unique equilibrium in which both x and y coexist (see Supporting Appendix, which is published as supporting information on the PNAS web site); here, we will discuss the conditions required for this equilibrium to be feasible and stable. The system is at equilibrium when each nutrient pool (species biomass, detritus, and inorganic pools) has reached equilibrium, i.e., when Eqs. 1, 4, and 5 are set to zero. For species biomass, detritus, and inorganic pools, respectively, equilibrium requires the three following conditions (the hat designates a variable or a function at equilibrium):

1. Ĝ_i = m_i, with i = x,y.

2. d_ijD̂_ij = q_ijm_iB̂_i, with i = x,y and j = 1,2.

3. a(S_j - N̂_j) = ∑_iĜ_iq_ijB̂_i - ∑_i(1-ϕ_ij)d_ijD̂_ij with i = x,y and j = 1,2.

To be consistent with the resource-ratio theory (3), we can represent conditions 1 and 3 on the two-dimensional space of N₁ and N₂ (Fig. 2). Condition 2 only concerns nutrients in organic form. We will see later that although condition 2 cannot be represented on the N₁, N₂ space, it establishes the link between competitive outcomes and nutrient budgets at the ecosystem scale.

Fig. 2.

Coexistence of two species. (a) The properties of Fig. 1d also apply in the case of two species (x and y) competing for two nutrients (N₁ and N₂). The coexistence equilibrium E is located at the intersection of the two species' ZNGIs. The consumption vector is the sum of each species vector 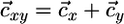. In absence of recycling, the external supply vector 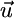points toward the external supply point S. The slopes α_x and α_y of and , respectively, bind the slopes for all external supply vectors for which coexistence is physically possible. Therefore, all external supply points S within the area defined by α_x and α_y (the “area of coexistence”) allow coexistence. (b) The presence of recycling causes a shift in the supply point that affects plants from the external point S to the net supply point S′ (which includes the recycling effect). If the ratio of nutrients recycled differs from the one consumed, a point S outside the area of coexistence may translate into a point S′ lying inside (as illustrated). The opposite case may arise as well, depending on conditions discussed in the text. The dashed lines with slopes β_x and β_y determine the area of all external supply points S that, given a particular recycling efficiency, translate into net supply points S′ within the area of coexistence.

As for classical models (8, 9) condition 1 translates into zero net growth isoclines (ZNGIs) that represent break-even levels of each nutrient 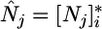[the R^* sensu Tilman (3, 27)], at which point plant growth balances mortality (3). The presence of both competitors at equilibrium requires that the ZNGIs cross one another (Fig. 2), which leads to the first classical (3, 8) feasibility condition for coexistence; that is, competitors must be limited by different nutrients. In the example treated in Fig. 2, x is a better competitor for 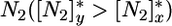and remains limited by N₁, whereas y is a better competitor for 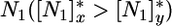and remains limited by N₂.

Thus far, coexistence is not influenced by internal recycling. However, examining condition 3 leads to a second feasibility condition that depends on recycling. On the two-dimensional space of N₁, N₂, condition 3 translates into the vector equation (Fig. 2):

[7]

where 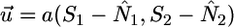is the external supply vector to the ecosystem; 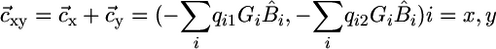, is the plant consumption vector, and , is the internal recycling vector.

We illustrate in Fig. 2a that 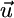points toward the external supply point S. To incorporate the recycling effect, we pool 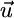and and, thus, obtain a supply-consumption equation that differs from classical models (3). The resulting vector is a net supply vector that depends on detritus dynamics and points to a net supply point (S′ in Fig. 2b) that will differ from S (discussed below):

[8]

where is the net supply vector.

In absence of recycling the net supply vector equals the external supply vector 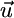, and Eq. 8 is congruent with classical models. In this case, Eq. 8 implies that and 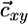share the same slope, which is physically possible only if the slope of 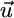lies between α_x = q_x2/q_x1 and α_y = q_y2/q_y1 (i.e., between the slopes of the species-specific components 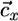and 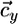of the consumption vector). In this case, these consumption boundaries (α_x and α_y) define the second feasibility criterion for coexistence (3).

In presence of recycling, however, the slope of differs from if the recycling efficiency (1 - ϕ_ij) differs between the two nutrients (i.e., the ratio of recycled nutrients differs from the biomass ratio). Differential recycling (caused by organic losses) therefore acts to modify the conditions of coexistence. For instance, an external supply vector may lie outside the area of coexistence, whereas the recycling-enhanced net supply vector 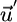falls within the area (Fig. 2b). In this case, recycling therefore permits coexistence.

Ecosystem ecologists are concerned with how recycling will affect coexistence given the range of external supply points defined by variations in weathering or atmospheric inputs across ecosystems. Therefore, we need to understand how recycling acts to modify the range of external supply vectors that permit coexistence. From Eq. 7, we can pool the combined impact of consumption and recycling by combining the consumption and recycling vectors (). It follows that, for coexistence to be physically possible, the external supply vector 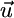must be bound by the species-specific components () and (). The area defined by the vectors () and () embeds the range of external supply vectors 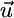, which, when influenced by recycling, translate into net supply vectors 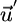that lie into the area where coexistence is feasible.

If we let β_i designate the slope of (), and assume that x is a better competitor for N₂ and y is a better competitor for N₁, the feasibility condition for coexistence reads

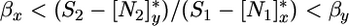[9a]

or

[9b]

This condition guarantees that the biomass for x and y is positive at equilibrium (see Supporting Appendix for the biomass equilibrium formula). Note that the recycling component of (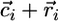) depends on the detritus dynamics and, hence, on organic losses: We show in the Supporting Appendix that because of condition 2, the slope β_i equals the ratio of nutrients in the organic loss from the ecosystem:

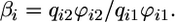[10]

Hence, condition 9 can also be interpreted at the ecosystem level: At equilibrium the total pool of nutrient T_j must remain constant (Eq. 6 set to zero). Therefore the external nutrient supply a(S_j - N̂_j) must equal the loss of nutrient in organic form (i.e., ϕ_xjd_xjD̂_xj + ϕ_yjd_yjD̂_yj), and the ratio of nutrient supplied must lie between the ratios of nutrient lost in organic form from each species' detritus (i.e., β_x and β_y).

Assuming that these two feasibility conditions are fulfilled, coexistence is granted only if each competitor has the ability to invade the system when the other competitor is resident at equilibrium. We show in Supporting Appendix that in the case for which x is a better competitor for N₂ and y for N₁, coexistence is granted provided that β_x < β_y. In such cases, Eq. 9a alone represents the condition required for coexistence. If instead β_x > β_y, none of the competitors can invade the system when the other is resident. Coexistence is therefore never met, and whether species x or y becomes the resident depends on the initial conditions of the system. For the particular case in which there is no recycling, nutrient ratios in organic losses are equal to consumption ratios (β_x = α_x and β_y = α_y) and Eq. 9a becomes the condition of coexistence for classical models (8, 9).

Because β_i is sensitive to the propensities ϕ_ij of nutrients for organic loss (Eq. 10), we can examine how these parameters influence the conditions of coexistence. In the case of recycling with propensities that are equal across nutrients and species (ϕ_x1 = ϕ_x2 = ϕ_y1 = ϕ_y2) but not at unity, the situation remains as in classical models. In any other case, nutrient recycling acts to modify the conditions of coexistence.

An important result is that recycling permits coexistence for a wider range of nutrient supply ratios if competitors increase the propensity of organic loss for the nutrient that limits their own growth (e.g., x is limited by N₁ and ϕ_x1 > ϕ_x2), as illustrated in Fig. 3a. In contrast, coexistence occurs in a more narrow range of nutrient supplies if competitors increase the propensity of organic loss for the nutrient that limits their opponent's growth (Fig. 3b). In addition to the cases depicted in Fig. 3, there also exists cases in which coexistence is not possible without recycling yet possible with recycling (e.g., x better competitor for N₁, y better competitor for N₂, α_x > α_y, and β_x < β_y), or the reverse (e.g., x better competitor for N₁, y better competitor for N₂, α_x < α_y, and β_x > β_y). As we show in the next paragraph and in Fig. 4, the first case may lead to fluctuating coexistence.

Fig. 3.

Comparison of coexistence conditions with and without recycling. Recycling can influence external supply points (specific conditions are reviewed and categorized in the text), by either increasing or decreasing the likelihood of coexistence. (a) If a species promotes organic losses (i.e., prevents efficient recycling) of a nutrient that limits itself, it acts to increase the area of external supply points that permit coexistence at equilibrium: The area with recycling (area between β_x and β_y) is greater than the area without recycling (area between α_x and α_y). (b) If a species promotes organic losses of a nutrient that limits a competitor but not itself, it acts to decrease the area of external supply points that permit coexistence at equilibrium. The area between β_x and β_y is therefore smaller than the area of coexistence in absence of recycling (between α_x and α_y).

Fig. 4.

Coexistence dynamics of two species (x, black; y, gray). The addition of a recycling feedback within traditional competition models introduces the possibility of lack of a stable equilibrium, if recycling permits coexistence of competitors that cannot coexist without recycling. (a) Illustrated is such a case: x is a better competitor for N₂, and y is a better competitor for N₁. Because α_x > α_y, coexistence is impossible without recycling (see text); however, in the presence of recycling, β_x < β_y, coexistence becomes physically possible. In case of low supplies (S₁), coexistence is stable. For higher supplies (S₂), fluctuating coexistence occurs. (b) A fast internal recycling feedback (high d_ij) causes coexistence of species x (gray) and y (black) within a short period-limit cycle. (c) A slow internal recycling feedback (low d_ij) causes a long period-limit cycle in which pseudoexclusion phases can develop.

Coexistence Dynamics Depend on the Time Scale of Consumption vs. Recycling. Reciprocal invasion (x can invade if y is resident, and y can invade if x is resident) provides a sufficient condition for coexistence, although it does not guarantee the stability of the equilibrium. We show in the Supporting Appendix that local stability is granted if the coinvasion criteria are met even in the absence of recycling (e.g., Fig. 3). In the reverse case, in which competitors are unable to coexist without the positive effect of recycling (Fig. 4), the coexistence equilibrium is not necessarily locally stable. In fact, low external nutrient supply rates lead to stable coexistence, whereas high supply rates lead to limit cycles. The period and the amplitude of these endogenous oscillations vary with the time delay of recycling. We show in Fig. 4 that, in case of long delays (e.g., slow decomposition rates d_ij), the oscillations lead to pseudoexclusion phases, in which a dominant species drives its competitor to very low biomass values for an extended period. As discussed later, pseudoexclusion raises some questions about the long term validity of the coexistence.

Discussion

Our model extends classical resource competition theory by including a detrital nutrient pool that is partly recycled, but also partly lost in forms that are not available to plant uptake. Our approach further differs from classical treatments in that plants indirectly influence rates and ratios of nutrient recycling, and there can be species-specific differences in the propensity of such effects. Through plant consumption, nutrients enter a plant-soil detritus feedback in which recycling acts to augment nutrient supplies from sources external to the ecosystem. The propensity for a nutrient to be recycled, in turn, is controlled by losses through dissolved organic pathways that occur independent of the ecosystem's overall nutrient limitation status [i.e., “system leaks” (12, 14, 19)].

Most broadly, our results show that the stoichiometry of recycling and organic nutrient losses can be critically important determinants of the conditions of coexistence/exclusion. If the propensity for organic loss does not differ between two nutrients, their ratio in dissolved organic export remains equal to the ratio consumed by plants (as defined by biomass), and conditions for coexistence at equilibrium do not qualitatively differ from classical models. On the contrary, if propensity for organic loss is nutrient-specific (i.e., differs across nutrients) and/or species-specific (i.e., varies across plant species) recycling can dramatically change conditions for coexistence relative to classical models. That is, as detrital pools and internal nutrient recycling grow larger relative to external supplies, nutrient supply ratios become increasingly influenced by recycling and organic losses, which, in turn, can act to either promote or prevent coexistence.

Coexistence is promoted if organic losses from a competitor's recycling path are higher for the nutrient that limits its own growth but prevented if they are higher for the nutrient that limits its competitor (Fig. 3). The organic export ratio of nutrients from one competitor's detritus therefore influences conditions of coexistence/exclusion for both species. We conclude that the geometries that define coexistence and exclusion in classical graphical representations are sensitive to nutrient-specific and species-specific differences in propensities for organic nutrient loss.

What Determines Propensity for Plant-Unavailable Loss? A number of factors may influence whether nutrients are mineralized locally (and thereby made available for plant uptake) or lost through organic or other unavailable pathways from ecosystems. For example, the activity of grazers can cause nutrients to be lost across system boundaries by means of plant-unavailable pathways. Examples include sedimentation of nutrient-rich particles from pelagic ecosystems due to selective assimilation processes (28, 29), vertical migration of zooplankton causing spatially decoupled assimilation and excretion of key nutrients (cf. ref. 28, dissolved organic nitrogen pump) or net nitrogen transfer by large herbivores from nutrient-poor to nutrient-rich grasslands in the Serengeti (30). Abiotic factors can also induce plant-unavailable paths of nutrient loss. In addition to sedimentation of particulate organic nutrients in aquatic ecosystems (discussed above), examples include volatilization of nitrogen during fires that are common in xeric ecosystems (31) and erosion of particulate organic matter from hillslopes.

In the case of the plant-soil systems considered here, little is known about determinants of the propensity for nutrient loss by means of dissolved organic pathways. Abiotic factors, such as whether shallow and organic-rich soil horizons are in contact with soil water flow paths (19, 25) are likely important, and biotic influences include the formation of refractory dissolved organic nutrients during microbial and root metabolism (20). It appears reasonable, however, that individual plant species differ in their local effects on organic nutrient losses. For example, plants that invest heavily in complex polyphenols and tannin compounds in leaves (e.g., Pinus sp.) may promote organic nitrogen losses from soils while minimizing inorganic nitrogen losses (32, 33). In contrast, species with more rapidly decomposing leaf tissues (e.g., Liquidambar sp.) may minimize organic losses while promoting locally efficient mineralization and recycling of nitrogen.

The propensity for organic loss likely varies across nutrients. Whereas nitrogen is readily incorporated into structurally complex and polyphenol-rich organic compounds, phosphorus occurs in more simple P—O bonds that are biochemically more available to extracellular enzymes and biotic mineralization (34). Empirical studies support these predictions, in that dissolved nutrient losses from forests tend to favor organic nitrogen over organic phosphorus (compared to either biomass or soil organic matter), indicating more efficient internal recycling of phosphorus than nitrogen (14).

What Are Time Scales for Nutrient Recycling vs. Plant Growth? Our findings (Fig. 4) highlight the coexistence dynamics that result from consumption and recycling/loss processes. If these two processes have antagonistic effects (i.e., consumption prevents coexistence, whereas recycling promotes coexistence), the time delay for recycling may promote instability and lead to limit cycles. We found that such oscillations more likely occur in conditions of high supplies of nutrients. For long time delays (e.g., for low recycling rate d), these cycles turn into pseudoexclusion phases in which a single competitor dominates the system at a given time.

It is worth noticing that because the model presented here is purely deterministic, the pseudoexcluded species can recover once the recycling effect again makes the nutrient environment favorable. In reality, however, stochastic extinction could occur during the phase of quasiexclusion, which would prevent coexistence at equilibrium. It should be noted that our model assumes fixed ratios of nutrients in plant biomass. This condition is more nuanced in reality, and future work should consider how flexible nutrient ratios would impact the oscillatory dynamics. Nevertheless, such time delays between consumption and recycling may influence transient phenomena in plant communities and may offer a mechanism for species replacement during processes of plant succession or the development of ecosystem nutrient cycles.

More generally, our model offers theoretical evidence that nutrient recycling may promote oscillations in plant community dynamics. This observation should be seriously considered in the current debate about oscillatory phenomena in plant communities (35-37) and their consequences for plant diversity (38). Indeed, preliminary extensions of our model have illustrated that oscillations may promote coexistence of more than two species on two limiting nutrients (T.D., unpublished results). Our findings in Fig. 4 should therefore be seen as a first step toward a better understanding of transient dynamics induced by plant-nutrient interactions.

Can Species “Manipulate” Nutrient Cycles? If plant individuals possess traits that influence whether dissolved organic nutrients are lost from local soil-detritus-microbe systems and if such traits are heritable, we can examine the possibility of Darwinian selective feedback between plant strategies and aggregate nutrient economies of local environments. Simply put, can plant species “engineer” local nutrient cycles for their own benefit?

In theory, we can distinguish two strategies by which plants manipulate organic losses to influence local competitive outcomes. A “nasty neighbor” could increase organic losses of the nutrient that limits a neighboring species, but not itself (i.e., for species i, the propensity for organic loss ϕ_ij is higher for the nutrient j that limits its neighbor than for the nutrient that limits its own growth). This strategy would promote competitive exclusion and decreases the coexistence range depicted in Fig. 3. In contrast, a “nice neighbor” could increase organic loss of the nutrient that limits itself, but not its neighbor. This strategy would increase the size of the region of coexistence range of Fig. 3.

In terrestrial ecosystems, the fact that nitrogen appears to be more readily lost than phosphorus in dissolved organic forms (discussed above) suggests that such losses generally promote nitrogen over phosphorus limitation in plant-soil communities. However, individuals in species adapted to persist in nitrogen-poor conditions (i.e., good competitors for nitrogen) still could enjoy selective advantage by increasing organic nitrogen losses. An example are species of pines that compete well in nitrogen-poor soils and display an evolved ability to assimilate inorganic nitrogen or amino acids at low concentrations by ectomycorrhizal symbioses (32, 33, 39). Such species could benefit from elevated organic nitrogen losses as long as they remain the strongest local competitor for nitrogen and neighboring species are limited by nitrogen. This illustrates the possibility for selfish Nash-type strategies mediated by minimizing (rather than maximizing) an essential nutrient resource.

These musings on evolved strategies for engineering nutrient cycles are admittedly speculative at this point. Because our model includes processes of recycling and species-specific nutrient losses, it permits expansion of traditional competition theory to include the emergence of local evolutionary feedbacks. Spatial heterogeneity is essential for such feedbacks (40). To us, this represents an exciting interface between community ecology/stoichiometry (41), ecosystem biogeochemistry, and evolutionary biology.