The bacterial chemotactic response reflects a compromise between transient and steady-state behavior

Abstract

Swimming bacteria detect chemical gradients by performing temporal comparisons of recent measurements of chemical concentration. These comparisons are described quantitatively by the chemotactic response function, which we expect to optimize chemotactic behavioral performance. We identify two independent chemotactic performance criteria: In the short run, a favorable response function should move bacteria up chemoattractant gradients; in the long run, bacteria should aggregate at peaks of chemoattractant concentration. Surprisingly, these two criteria conflict, so that when one performance criterion is most favorable, the other is unfavorable. Because both types of behavior are biologically relevant, we include both behaviors in a composite optimization that yields a response function that closely resembles experimental measurements. Our work suggests that the bacterial chemotactic response function can be derived from simple behavioral considerations and sheds light on how the response function contributes to chemotactic performance.

The bacterium Escherichia coli moves up gradients to regions of high chemoattractant concentration by performing a biased random walk. The random walk consists of alternating runs (periods of forward movement) and tumbles (sudden reorientations) that arise from changes in flagellar rotation (1, 2). When the flagella rotate counterclockwise, they form a bundle, and the bacterium swims more or less in a straight line at a roughly uniform speed. When one or more flagella rotate clockwise, they leave the bundle, and the bacterium tumbles, randomly reorienting itself (3, 4). Bacteria bias the random walk by modulating the run duration in response to measurements of chemoattractant concentration that are made at the cell surface (5, 6). They do not perform spatial comparisons between points along the cell body because of the fast diffusion across such short distances (7).

The chemotactic response function describes how bacteria process concentration measurements to produce their behavioral run-biasing decisions. It has been measured experimentally by monitoring the rotation of single flagella on bacteria stimulated by instantaneous chemoattractant pulses (8). The empirical response function is biphasic: The pulse provokes an immediate brief elevation of the counterclockwise probability followed by a longer depression. We expect the shape of the chemotactic response function to deliver optimal behavioral performance.

We consider the chemotactic behavior of a bacterium at some specific position on a gradient of attractant. As it wanders up and down the gradient, the distribution of its positions approaches a steady state. We choose performance criteria that quantitatively characterize the performance of the bacterium at early times in the non-steady-state regime and at late times in steady state. Both of these regimes are biologically relevant. If the system navigated by the bacterium is small compared with the distance the bacterium could explore in the time between cell divisions [an example is bacterial aggregation into clusters (9)], then it is the steady-state behavior that matters most to the bacterium. If, however, the system is large (more than a few millimeters in size) or varies in time, the bacterium will not come to a steady state before dividing, and a single cell might never reach a steady state. Bacteria have no a priori knowledge of the size of their system, so their chemotactic strategy should benefit them in either the steady-state or non-steady-state regime. Following foraging theory (10, 11), we will assume that the chemotactic strategy maximizes the attractant seen by the bacterium on the timescale of bacterial divisions.

Our first performance criterion reflects the expected velocity of bacteria at early times, before they have reached the boundaries of the system. It is quantified by 𝒯, a measure of the early time transient velocity of bacteria with a given response function. This velocity was previously calculated by de Gennes (12). Optimizing 𝒯 leads to a single-lobed response function, which causes bacteria to have transient average velocities up gradients at early times. Contrary to intuition, this optimization leads to an unfavorable steady-state distribution with bacteria accumulated in regions of low attractant. The second performance criterion, 𝒮, quantifies how strongly the bacteria aggregate about chemoattractant maxima when in steady state. Optimizing 𝒮 leads to a bacterium that has a mean velocity down gradients at early times but whose position distribution peaks at high concentrations at long times. The two performance criteria conflict: When one is maximal, the other is unfavorable. If both performance criteria are used to calculate the response function, the theoretical function closely matches the empirical biphasic bias curve measured by Segall et al. (8). The optimization procedure explains the curve's structure.

Our work contributes to a body of theoretical investigations of bacterial chemotaxis. Schnitzer et al. (13) used Monte Carlo simulations to confirm the favorable performance of a biphasic response function compared with a monophasic one. Our approach supports their end result, although we show that aggregation can occur without a positive lobe on the response function. Schnitzer (14) adopted a kinetic approach and derived results about steady-state behavior in a variety of cases. He distinguished between “nonadaptive pseudochemotaxis” and “true adaptive chemotaxis.” In contrast, our approach emphasizes both transient and steady-state behavior in evaluating chemotaxis. In a different approach, Strong et al. (15) adopted a deterministic model for tumbling and examined optimality in the presence of signal noise. Work by de Gennes (12) focused on the mean bacterial velocity due to a given response function. We show that this mean velocity only applies at early times, and we extend the framework used by de Gennes (12) to examine steady-state performance and performance optimization.

Model Details

We adopt the stochastic framework used by de Gennes (12). In this model, bacteria continuously modulate their instantaneous probability of tumbling as a function of a differential weighting of past measurements of chemoattractant concentration. The differential weighting constitutes the chemotactic response function, R(t).

We assume that the chemical landscape is static and that chemoattractant concentration is defined at every point by a function c(x). Bacteria swim along individual paths x(t) at a uniform speed v. The probability, P, that a bacterium tumbles in an interval between t and t + dt is dictated by its entire previous path, the chemical landscape, and the chemotactic response function

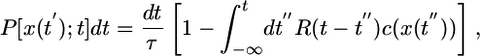[1]

where τ is the mean run duration in the absence of a perturbation. In a uniform concentration, this model describes tumbling as an unbiased Poisson process with a constant rate of tumbling 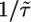given by 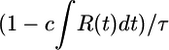. In a concentration gradient, P depends on the bacterium's history. By choosing particular forms of the response function, bacteria can bias their random walk so that they climb gradients and remain in regions of high c. We will consider first-order perturbations of the Poisson process by defining R(t) ∝ α/τ, with α small such that 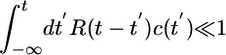. The constant α has units of volume. We expand equations as power series of such integrals and discard higher-order terms involving products of such integrals. Eq. 1 can itself be regarded as the first-order expansion of some monotonic function of 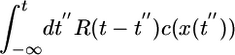that remains positive for all concentrations.

In our analysis, we neglect the effects of noise due to fluctuations of c(x). Noise averages to zero in all of our first-order expansions. The first noise contribution that does not average to zero is proportional to the variance of the concentration and is of order α²c/V, where V is the cell volume. To neglect this term with respect to the first-order term, we require α ≪ V. The experimental conditions described by Segall et al. (8) correspond to the regime in which bacterial responses are linear and the bacteria can detect c without being overwhelmed by noise.

Berg and Purcell (7) argued that measurement integration times of ∼1 s account for observed sensitivity to concentrations and gradients in the presence of noise. The response functions resulting from our analysis vary on the timescale τ, ∼1 s, so they will display biological sensitivity without explicitly requiring long integration times.

We assume that the length scale of variations in the concentration gradient is longer than the average run length, so that over one run, the gradient appears linear. We consider bacteria in one dimension and assume that tumbles are instantaneous and randomize orientation. Of course, real bacteria navigate in three dimensions, and their run directions are not completely decor-related by tumbles (1, 4). Further, in real bacteria, runs directed up attractant gradients lengthen, whereas those directed downward are the same length as runs in constant concentrations (1). Nonetheless, this simplified model gives insight into real bacterial behavior.

Transient Chemotaxis

The strategic goal of a bacterium navigating a chemoattractant landscape is arguably as simple as producing an average velocity up the attractant gradient. De Gennes (12) showed that a mean velocity can be produced when, after a tumble, a run up the gradient lasts longer than a run down the gradient. For a population of bacteria starting at the same position, the expected velocity at early times will be

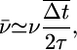[2]

where Δt is the difference in run times moving up and down the gradient, and the bars are averages over possible trajectories. The model presented in Eq. 1 dictates that the probability of next tumbling at time t_f after having previously tumbled at time t₀ is

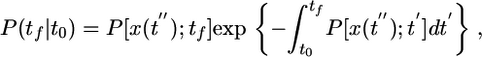[3]

where P[x(t″);t_f] is the probability of tumbling at time t_f, given a path x(t″).

Following de Gennes (12), we consider the expected time until the next tumble

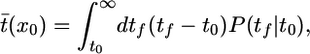[4]

where the average is taken over possible future trajectories and the bacterium is at x₀ at time t₀. We define t̄^±(x₀) as the mean time until the next tumble for bacteria moving up (+) and down (-) the gradient. We expand c(x(t)) into , where v is the constant speed of a run. After expanding in α and then using the identity 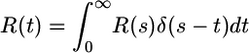, where δ(s - t) is a Dirac delta function, we find de Gennes's result that

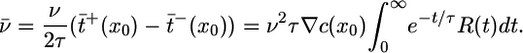[5]

Fig. 1 illustrates this integral over future paths. For bacteria to behave most favorably at early times, v̄ should be maximal.

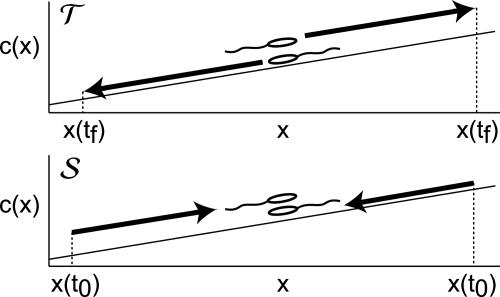
Fig. 1.

Comparison of the two performance calculations. (Upper) The integration in the expression for 𝒯 (Eq. 6). Two bacteria that have both just tumbled are considered as they move in different directions along the gradient until they tumble again at position x(t_f). (Lower) The integration in the expression for 𝒮 (Eq. 13). In this case, two bacteria meet that last tumbled at points x(t₀). One finds the expectation of their respective tumbling probabilities, P̄^±, by averaging over possible histories.

To gain intuition about this mean velocity, consider 1,000 bacteria all taking exactly average steps, beginning at a point x₀ on an infinitely long gradient, as illustrated in Fig. 2. Initially, 500 bacteria move up the gradient until the time t̄⁺; 500 bacteria move down until time t̄^-. The average position of the bacteria is simply x₀ until time t̄^-, when the 500 bacteria moving down split into 250 moving up and 250 moving down. From this time until the upward-moving bacteria tumble at time t̄⁺, the mean position of the bacteria moves up at v/2. This phenomenon is repeated after every tumble, creating the mean velocity up the gradient (Eq. 2). In Fig. 2, this mean velocity is reflected by the thick tail of bacteria on the upward-moving branch and the thinner tail on the downward-moving branch. When the upward-moving tail encounters a boundary on the system, bacteria are forced to tumble, and the mean velocity up the gradient dies away as the bacteria move toward their steady-state distribution. Fig. 3b shows the results of a simulation that demonstrates this transient behavior.

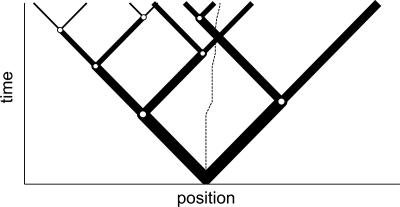
Fig. 2.

Cartoon showing origin of transient velocity. Solid lines indicate possible paths taken by bacteria that all execute exactly average paths; line thickness gives a sense of the probability weighting of each path segment. The chemoattractant gradient in this case is positive, and t̄⁺ > t̄^-. The dotted line shows the average position over time: It moves to the right, indicating an expected velocity up the gradient. Note that after the time elapsed in this figure, more bacteria on average will have reached the farthest right point than the farthest left point, because they have tumbled less frequently.

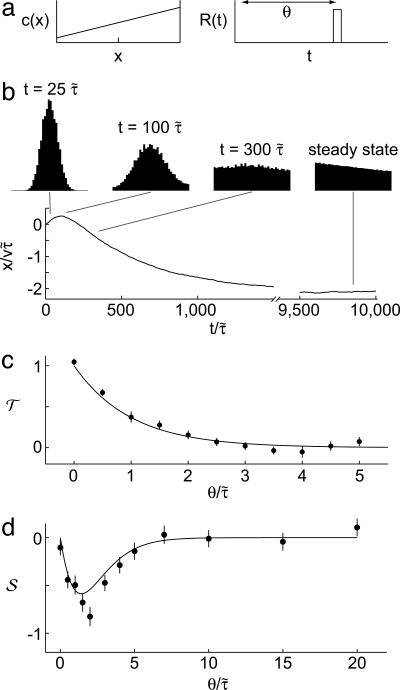
Fig. 3.

Simulations of the model. We performed discrete time simulations of the model on a positive concentration gradient with reflective boundary conditions to see the result of different R(t) on transient and steady-state behaviors. (a) Bacteria were released from the center of the gradient (Left) and evolved until they arrived at a steady-state distribution. R(t) was chosen to weight positively only at θ seconds before the current time, t (Right); that is, it weights only c(t - θ). It was further chosen so that the maximum perturbation from the average tumbling probability was 30%. (b) In a gradient of length 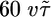, bacterial distributions and the mean position of bacteria were found by using a response function with 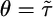, where 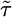is the run duration averaged over the box. At early times, bacteria are clustered and have a mean velocity up the gradient. After the bacteria hit the boundary, they approach a steady state peaked at low c. Note that more bacteria have reached the right-hand wall than the left-hand wall at 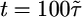. For this response function, 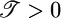and 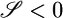; both results are reflected in the bacterial behavior. (c) We varied θ and calculated 𝒯 from the initial slope of the lower plot in b. The result shows the contribution of R(θ) to 𝒯. The solid line is the transient performance kernel, 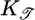, derived in the text. (d) In a short-length scale gradient (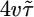), we varied θ and calculated 𝒮 from the bacterial distributions at long times. The contribution of R(θ) to 𝒮 is shown. The solid line is the steady-state performance kernel, 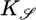, derived for a similar situation (see the supporting information). Error bars in c and d are 1 SEM.

We divide out the constants in Eq. 5 and introduce the dimensionless performance measure,

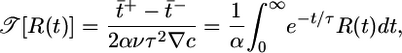[6]

to quantify the transient chemotactic behavior at early times. This quantity is an overlap integral of R(t) against a performance kernel 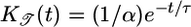. The performance kernel shows the effect of the response function on the mean velocity at early times. The form of this kernel can be understood qualitatively. The mean velocity is proportional to the difference in run times between two bacteria with the same starting point that are moving in different directions (see Fig. 1). As upward- and downward-moving bacteria move away from each other, the difference in the concentrations they measure grows until the bacteria tumble. A response that weights c(t) heavily in the immediate past will contribute more to increasing 𝒯 than a weighting further in the past where concentration differences were smaller. Therefore, the performance kernel prefers recent weighting. The shape of the performance kernel matches simulations of the model system (Fig. 3c). The exponential decrease in influence of R(t) on 𝒯 is due to the exponential run length of the unperturbed Poisson process. Note that this heuristic argument is not strongly dependent on the form of P chosen in Eq. 1. Any positive decreasing function of 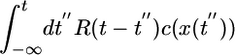would yield a kernel that weights the most recent measurements most heavily.

We can maximize 𝒯 over a constrained set of response functions. We assume the response function to be finite and to decay to 0 at large t. The simplest way to include both restrictions is to hold the integral 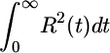constant, which amounts to maximizing over a set of response functions that have the same rms deviation from 0. We impose the constraint

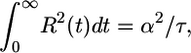[7]

and maximize 𝒯 subject to this constraint by using a Lagrange multiplier and taking a functional derivative

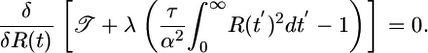[8]

Solving this condition, we calculate the optimized response function

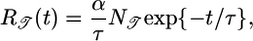[9]

where 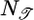is a normalization constant. This response function is proportional to the performance kernel 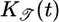used to determine 𝒯; it is positive everywhere but weighted toward most recent times (shown in Fig. 4a). Using this response function, bacteria moving up and down the gradient are progressively less and more likely to tumble, respectively. Given a particular tumbling position x, this response function results in maximally longer runs up the gradient than down it. A similar effect has been termed “pseudochemotaxis” (16). We call it “transient chemotaxis,” because, unlike in pseudochemotaxis, P[x(t′); t] in transient chemotaxis has a history dependence, and, moreover, we argue that short-term performance is relevant for bacteria in large or changing chemical gradients. Surprisingly, although 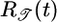maximizes the expected velocity up the gradient, it leads to an unfavorable steady-state distribution in which the bacteria spend more time in low chemoattractant concentration regions. The simulation in Fig. 3b shows the initial favorable transient velocity and the unfavorable steady state for an all-positive response function. This counterintuitive result can be explained as follows. Imagine two bacteria passing each other on a linear concentration gradient (see Fig. 1). The one heading down the gradient has high c in its past, so its value of 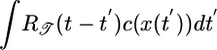is larger, on average, than that of an upward-moving one at the same position. Eq. 1 then shows that the probability of tumbling is lower for the bacterium moving down the gradient. Because this statement is true at all points on the gradient, more bacteria will accumulate in the low concentration areas. The unfavorable steady state of a positive response function was previously shown in numerical simulations (13) and noted in Schnitzer's analysis (14).

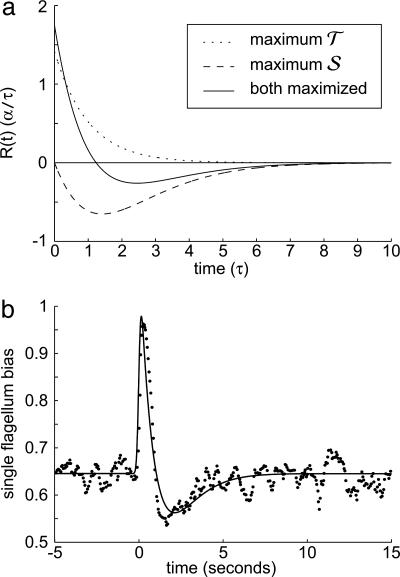
Fig. 4.

Optimized response functions and comparison with data. (a) Response functions that optimize the performance measures 𝒯, 𝒮, and 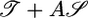, where A = 1/2. Note that all three functions are normalized such that 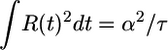. (b) The points are data from figure 1 of ref. 8 showing the counterclockwise bias in flagellar motor rotation after a very short impulse of chemoattractant at time t = 0. The bias response is linear in this experiment's regime. The solid line is a best fit of 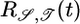to the data, using a 10-Hz low-pass Gaussian filter to realistically smooth discontinuities. The fitting parameters were A, τ, and an overall amplitude, and the least-squares fit was A = 0.56 and τ = 0.9 s. The bias of a single flagellum is related to the tumbling probability P[x(t′); t] but is not identical, because multiple flagella are involved in running and tumbling (4), and cooperative effects could be involved.

Initial velocity need not indicate the eventual steady-state distribution, as the following thought experiment shows [discussed by Lapidus (16), Schnitzer et al. (13), and Schnitzer (14)]. Consider a closed tube containing steel wool with a graded density such that one end contains dense wool and the other contains sparse wool. At one end of the tube, mean free paths of a molecule are short, whereas at the other end, they are long. After each collision, because of the gradient in the wool, a molecule has an expected net displacement toward the sparse end of the tube. In steady state, however, gas molecules are distributed evenly throughout the free volume of the tube. Therefore, although the expected net displacement after each collision creates an initial mean velocity toward the sparse end, it does not determine the steady-state distribution. For gas molecules, the collision probability is determined by a particle's instantaneous position. For bacteria using an all-positive response function, both t̄⁺ and t̄^- are longer in higher c regions because 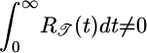, making path length depend on position. It is the history-dependence of 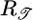that causes the bacteria to aggregate in regions of low c.

Steady-State Bacterial Distribution

Here, we show how the steady-state distribution of bacteria depends on expected tumbling rates. The expected tumbling rate for a bacterium at position x depends on whether it is moving up or down the gradient and is given by P̄⁺(x) or P̄^-(x), respectively, where bars are averages over possible histories ending at x. In steady state, these averages will not be functions of t.

In steady state, bacterial flux is zero, and the bacterial steady-state concentration, b(x), can be written in terms of the probabilities P̄^±(x) (see the supporting information, which is published on the PNAS web site):

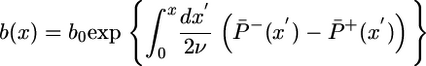[10]

This equation reproduces a more general result derived in ref. 14.

With net flux equal to zero, the number of upward-moving bacteria must equal the number of downward-moving bacteria at any point x. If P̄⁺(x) ≠ P̄^-(x), then the fraction of bacteria passing through a point from the left will not equal that passing through from the right. To keep the number fluxes equal, the number of bacteria on each side of that point must be different. Maintaining this balance generates the form of the distribution in Eq. 10. When the tumbling rate is higher for downward-moving bacteria arriving at point x, bacteria aggregate at the top of the gradient in steady state.

We now express the tumbling probabilities in terms of R(t). To calculate P̄^±(x), we must consider all possible histories of bacteria reaching point x. Histories and instantaneous tumbling probabilities both depend on R(t), so the difference P̄^-(x) - P̄⁺(x) that governs steady-state aggregation can be expressed in terms of the response function. By integrating over paths for bacteria arriving at x (details of the derivation are in the supporting information), we find that

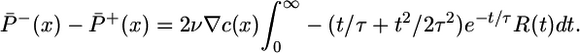[11]

This integral should be positive to obtain an advantageous steady-state distribution with more bacteria at high chemoattractant concentrations. The x dependence in Eq. 11 comes through the 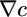factor, which integrates immediately to c(x), giving the steady-state distribution

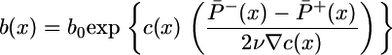[12]

The quantity in round brackets does not depend on x. We introduce the dimensionless version of this quantity,

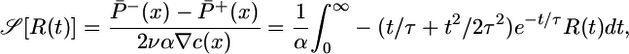[13]

as a performance measure of the steady-state distribution. This expression is an overlap integral, with a performance kernel 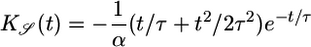. A response with large 𝒮 yields a steady-state distribution with the bacteria aggregated favorably in high c regions. When 𝒮 is maximized by the same procedure used in Eq. 8, one finds a response function

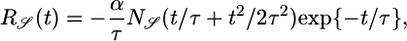[14]

which is negative everywhere, zero at t = 0 and at long times, and peaked at 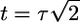(see Fig. 4a). The negative values of this response function mean that bacteria moving down the gradient at point x with high concentrations in their past have higher tumbling probabilities than bacteria moving up the gradient at x with lower concentrations in their past.

Because 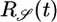is negative, it results in t̄^-(x) > t̄⁺(x), creating a transient velocity down the gradient at early times. Although this response function gives a beneficial steady-state distribution, it yields detrimental behavior at early times.

One can understand the steady-state performance kernel qualitatively. The performance measure 𝒮 considers the difference in tumbling probability between two bacteria at the same point in space but coming from opposite directions (see Fig. 1). In this case, measurements of c are most different in the past, whereas the most recent concentration measurement, c(x), is the same for both bacteria. This weighting is reflected in the performance kernel 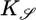and in the optimal response 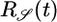, in which concentrations in the past are more heavily weighted. Concentration measurements in the more distant past could have been made where 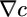was different from the current 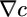and cannot be reliably related to the current gradient. Therefore, such distant information is not useful for making run-biasing decisions and is not weighted heavily by the kernel (17). Fig. 3d shows the derived performance kernel and results of simulations of the model in a small system.

Optimizing the Response Function

The response functions resulting from optimizing the two performance criteria have opposite signs, so that optimizing 𝒯 leads to an unfavorable 𝒮 and vice versa. Both aspects of performance are biologically relevant: Bacteria should move up gradients when not in steady state and remain at high concentrations as they approach steady state. We expect bacteria to optimize a composite criterion that preserves both aspects of performance. One can imagine a variety of ways to maximize a combination of the two quantities, but maximizing any positive increasing function of both 𝒯 and 𝒮 will produce a solution that is a linear combination of 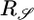and 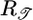. We therefore adopt the most straightforward way and maximize the quantity

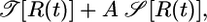[15]

where A is some unknown weighting factor of the two performance measures. As before, we constrain R(t) and take the functional derivative of this equation to find a response function that compromises between maximizing the transient velocity up gradients and the steady-state bacterial distribution. That response function is

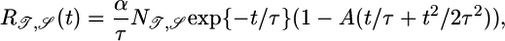[16]

which is proportional to .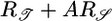

It is reasonable to set ∫ R = 0 because there are physical bounds placed on the run length of real bacteria. Purcell (18) pointed out that run duration should be chosen at least large enough so that, for a given v, a bacterium outruns the diffusion of the chemoattractant c during its run. For real values of v, ∼30 μm/s, this lower bound on run duration is ∼1 s. Further, in real situations, runs longer than ∼10 s are turned 90° off course by rotational diffusion (1, 19), setting a maximum useful run duration. Neither of these limits depends on c. Bacteria should be sensitive to gradients by maintaining a large α but must not allow their run durations to wander outside these bounds in widely varying concentrations. Run duration depends on a 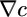term as derived in the text and on c ∫ R(t)dt. The integral of R should be zero to allow for sensitivity to 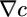while keeping 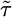within the limits above, thus creating a large dynamic range for the response (19). This argument leads us to set A = 1/2 so that ∫ R = 0. Experimentally, Alon et al. (20) have shown that this robustness of run duration to changes in absolute concentration is a property of the E. coli chemotactic network when cells respond to aspartate (see, however, ref. 1).

The optimized response function is shown in Fig. 4a, where we have required ∫ R = 0. It predicts a sharp, immediate, positive response with a drawn-out negative response peaking near 2.5τ. It was obtained here by developing a response function that (i) maximizes the transient velocity of bacteria up gradients when they are not in steady state and (ii) creates a steady state where bacteria aggregate in high concentration regions. 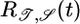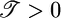The initial, short, positive lobe in makes and serves to move the bacteria up gradients when not in steady state, whereas the second, longer, negative lobe makes 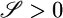and serves to produce the advantageous steady-state distribution.

The functional form of Eq. 16 fits the actual response function exhibited by individual flagellar motors in Segall et al. (8) (see Fig. 4b). Our theory concerns the whole cell, not single flagellar motors; correlations between the activity of single flagella and the behavior of the whole bacterium are not well understood (21, 4). Nevertheless, we find a surprisingly good fit. We have left A and τ as fitting parameters, and the best fit yields A = 0.56, which matches our expectation that A ≃ 0.5.

Values of 𝒯 and 𝒮 for any response function can be easily found by calculating their overlap with the kernels in Eqs. 6 and 13; a summary of such calculations for our three optimizations is shown in Table 1. The top half of the table provides the qualitative picture independent of model details; the lower half provides the values of 𝒯 and 𝒮 given by our model.

Table 1. Behavioral performance of different response functions.

Response function	Equation	𝒯	𝒮
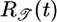	Positive lobe, weighted toward t = 0	+	−
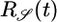	Negative lobe, weighted toward t ≃ τ	−	+
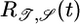	Initial brief positive lobe; negative lobe peaked beyond τ	+	+
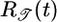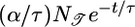		0.7	−0.5
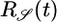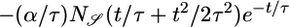		−0.4	0.9
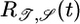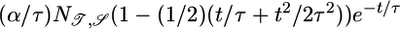		0.5	0.05

Transient velocity values (𝒯) and steady-state strength of aggregation (𝒮) for the various response functions R(t). The first three rows are heuristic, derived from qualitative arguments; rows 4-6 are derived from our particular model. The first and fourth rows are the response functions maximizing 𝒯; the second and fifth rows maximize 𝒮. The third and sixth rows maximize both 𝒯 and 𝒮, as described in the text. More positive values of 𝒯 and 𝒮 indicate more favorable behavioral performance; in the heuristic rows, favorable values are represented by + and unfavorable by −.

Discussion

The biphasic shape of the chemotactic response function has long been interpreted as a temporal comparator that automatically adapts to offsets in chemical concentration (8). Here, we have examined two aspects of bacterial chemotactic performance and found that neither aspect optimized alone produces a biphasic response. A composite response function, simultaneously optimizing both measures of performance, closely fits the shape of the experimental data, leading to an additional interpretation of R(t) as optimized with respect to these two behaviors, connecting each lobe to distinct behavioral performance.

Our theory makes predictions about the behavior of wild-type and mutant bacteria. The functional fit of 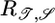to the wild-type data is quite good, so that we predict that experimental measures of wild-type 𝒯 and 𝒮 in the linear regime should roughly match those in Table 1. If L is the decay length of b(x) when bacteria are on a linear gradient, it is related to the expected transient velocity up the gradient, v̄, by the relation 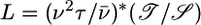. The first factor could be found on dimensional grounds, but we predict 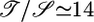for wild-type E. coli. For a gradient that elicits v̄ = 1 μm/s, this relation predicts L ≃ 5 mm. Response functions of mutant bacteria can be calculated (see ref. 22 or 23) or measured experimentally, as Segall et al. (8) have done for strains with mutant cheZ and for strains with mutant cheRcheB. Both of these mutant response functions are entirely positive, with durations of roughly 5 and 1 s, respectively. We predict that both mutants will have transient velocities up gradients but that both will reach an unfavorable steady-state distribution. Available data for both mutants does not rule out these predictions (24-27). Microscopic observations of t̄⁺ - t̄^- or measurements of b(x) in static spatial gradients could evaluate the validity and limits of this theory.