Abstract
Objective:
The paper aims to address the problem of massive unlabeled patients in electronic health records (EHR) who potentially have undiagnosed diabetic retinopathy (DR). It is desired to estimate the actual DR prevalence in EHR with 96 % missing labels.
Materials and methods:
The Cerner Health Facts data are used in the study, with 3749 labeled DR patients and 97,876 unlabeled diabetic patients. This extensive dataset spans the demographics of the United States over the past two decades. We implemented state-of-art positive-unlabeled learning methods, including ensemble-based support vector machine, ensemble-based random forest, and Bayesian finite mixture modeling.
Results:
The estimated DR prevalence in the population represented by Cerner EHR is approximately 25 % and the classification techniques generally achieve an AUC of around 87 %. As a by-product, a predictive inference on the risk of DR based on a patient’s personalized medical information is derived.
Discussion:
Missing labels is a common issue for EHR data quality. Ignoring these missing labels can lead to biased results in the analyses of EHR data. The problem is especially severe in the context of DR. It is thus important to use machine learning or statistical tools to identify the unlabeled patients. The tool in this paper helps both data analysts and clinicians in their practices.
Keywords: Diabetic retinopathy, Positive-unlabeled learning, Classification, Machine learning, Bayesian mixture models, Predictive inference
1. Introduction
Diabetic retinopathy (DR) is a vision-threatening microvascular complication of diabetes, and according to the 2002 American Diabetes Association Position Statement, nearly all patients with type 1 diabetes and over 60 % of patients with type 2 diabetes developed DR during the first 20 years of diabetes [1,2]. DR has no noticeable symptoms in the early stages, when current treatment methods can effectively halt the progression of the disease [3]. Treatment for late-stage DR is very expensive, and the vision loss is irreversible. Therefore, early detection of DR is vital for preventing disease progression and vision loss.
For the above reason, the American Diabetes Association recommends annual eye examinations for individuals with diabetes. However, compliance with the recommended examination is low due to the asymptomatic nature of DR and the lack of medical resources, especially in rural and medically underserved areas [4,5]. In the absence of imaging diagnosis, numerous studies in the literature have explored statistical and machine learning methods that utilize clinical information to identify risk factors and biomarkers for DR development [6–10]. As most diabetic patients have blood tests at least once per year, the data-driven statistical and machine learning approaches are timely and cost-effective and thus can be easily applied to clinical practices as decision-support tools.
Data-driven approaches without using imaging diagnosis typically rely on massive electronic health records (EHR), which contain rich information on routine laboratory tests and other clinical information. Thanks to the increasing computerization and digitization of health systems in the past two decades, EHR are digitally archived data from hospitals and clinics with massive patients’ medical records. Predictive models and algorithms become increasingly valuable given the rich information provided by EHR. These new data-analytical approaches utilizing EHR often generate novel insights and are more cost-effective compared with traditional methods. However, researchers and developers of statistical or machine learning algorithms often overlook the data quality of EHR, leaving a potential risk of invalidating their results. It is known that EHR data suffer from heavy missing and inaccurate inputs [11].
This paper focuses on the EHR data quality issue of large portion of unlabeled DR patients among diabetic patients. The ICD-9 or ICD-10 codes in EHR are typically used to determine the patient cohorts. For example, diabetic patients can be defined as subjects having at least one of 250.x, E10.x, and/or E11.x diagnosis codes, and further among diabetic patients, define DR patients as subjects with 362.0x, E10.31x-E10.35x or E11.31x-E11.35x diagnosis codes. An essential question arises: should diabetic patients lacking defined DR codes be automatically classified as non-DR? The answer hinges on the severity of the missing label problem and how many patients in the control group indeed possess DR but lack the appropriate labels (i.e., they remain undiagnosed). In the EHR database we used, only about 4 % of diabetic patients have the defined DR diagnosis codes, significantly underestimating the actual prevalence of DR among diabetics. In the literature, it is estimated that the DR prevalence among US adults with diabetes is 28.5 % (95 % CI 24.9 %–32.5 %) [12], and the global prevalence of DR in persons with diabetes is 34.6 % (95 % CI 34.5 %–34.8 %) [13]. Thus, machine learning models trained with a data set with 4 % DR and 96 % non-DR may be biased and unreliable.
There are two primary objectives in this paper: first, to estimate the prevalence of DR within EHR using positive-unlabeled learning approaches, and second, to provide personalized risk predictions based on a probabilistic model. We designate patients with the defined DR diagnosis codes as positively labeled, while patients without such codes as unlabeled. Positive-unlabeled learning aims to classify these unlabeled patients into either the positively labeled or the negatively labeled group. A unique challenge in our case is the extreme imbalance in labels, with only 4 % being positive, and a stark 96 % remaining unlabeled. We found that learning methods without proper splitting-and-combining strategy fail to work in such imbalanced scenarios, such as the general two-step approach [14,15] and the biased support vector machine (SVM) [16]. In contrast, methods that employ a splitting-and-combining strategy produce more reasonable results. For the second objective, conventional machine learning solutions, like the ensemble-based bagging-SVM [17,18] or bagging random forest often yield prevalence estimates without uncertainty quantification (confidence intervals etc.). Recently [19], developed a probabilistic approach using Bayesian finite mixture modeling to address the positive-unlabeled learning, which not only produces statistical estimates with uncertainties, but also outperforms existing machine learning algorithms.
In this paper, we use Cerner Health Facts EHR data and include over 100,000 diabetic patients in our study cohort. Following the pre-processing of the original data and feature selection, we apply both ensemble-based algorithms [17,18] and Bayesian finite mixture modeling [19] to our EHR data. This paper contributes in two key aspects of methodological implementation. Firstly, it is the first attempt to use EHR data with massive missing labels to estimate the actual DR prevalence in the United States. The tools described in this paper produce re-labeled EHR data with improved quality, laying a strong foundation for subsequent machine learning studies. Secondly, the proposed learning techniques allow us to perform statistical inference and to predict an individual’s risk of developing DR given the patient’s personalized medical information. This paper differs from Ref. [19] which uses a much smaller illustrative dataset and focuses on the statistical methodology. We leverage a more comprehensive dataset and a well-justified feature selection procedure to achieve the DR prevalence estimates. It is also worth noting that this paper presents statistical inference and personalized risk prediction which have not been discussed previously in Ref. [19].
As for practical contributions, our study provides insights for healthcare professionals, enhancing their understanding of the probability of DR development. This, in turn, bolsters the confidence of DR diagnosis. Our research has the potential to enhance healthcare management for diabetic patients and expedite the DR diagnosis process.
2. Materials and methods
2.1. Data source and pre-processing
Our data source is Cerner Health Facts EHR data warehouse (Cerner Corporation, Kansas City, MO) which contains clinical data from over 200 hospitals across the US in the past two decades. Cerner Health Facts data are de-identified and in compliance with Health Insurance Portability and Accountability Act (HIPAA). The data are mostly time-stamped patients’ clinical records including encounter, diagnosis, procedure, medication, vital signs, laboratory results, and other information. We identified diabetic patients as subjects having at least one of 250.x, E10.x, and/or E11.x diagnosis codes (ICD-9/10-CM) and DR patients as subjects with 362.0x, E10.31x-E10.35x or E11.31x-E11.35x diagnosis codes within diabetic patients. The study cohort includes 97,876 diabetic patients, among which 3749 are labeled with DR diagnosis.
We employed a window-based data aggregation approach described in Ref. [7] to extract laboratory results for the included patients. As shown in Fig. 1, laboratory data are averaged over a two-year window, ending six months prior to the onset of DR. For patients without DR diagnosis, the event of interest is chosen to be the last encounter in the EHR. It is noteworthy that, through this data aggregation approach, longitudinal effects and variation are not considered in this analysis.
Fig. 1.
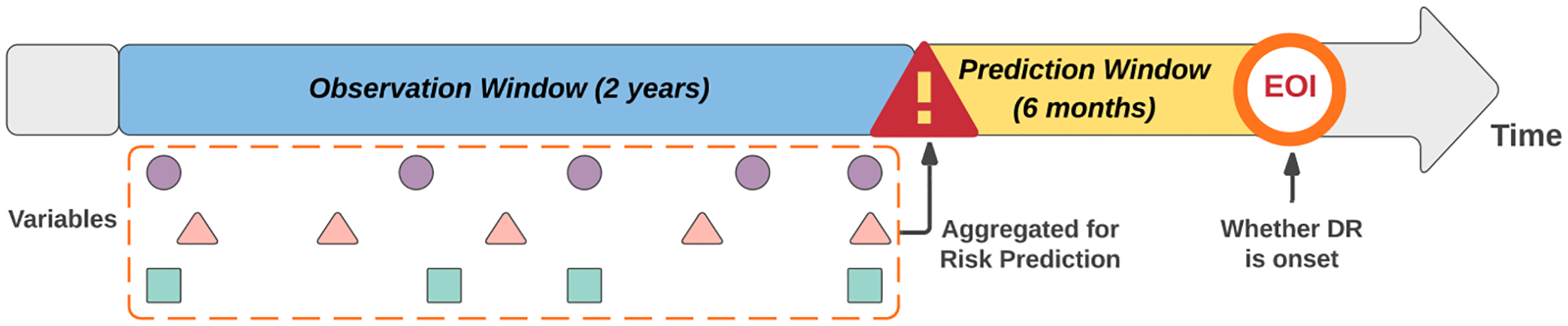
Data aggregation in the observation window. EOI represents event of interest [7].
2.2. Feature selection
To select features that will be used to classify unlabeled patients, we consider previous studies on the same dataset [7,8] which focused on feature selection [7]. used ensemble predictor selection with extreme gradient boosting (XGBoost) and selected the following eight essential predictors: creatinine, HbA1c, neuropathy, white blood count, nephropathy, glucose, hematocrit, sodium [8]. applied ablation feature selection, also with XGBoost, and highlighted features such as creatinine, neuropathy, hematocrit, blood urea nitrogen (BUN), nephropathy, albumin, calcium, sodium, anion gap. Based on the two studies, we understand that the two categorical features, specifically neuropathy and nephropathy, are important in terms of predicting retinopathy. This clinical correlation is not surprising, given that both are diabetic complications linked to DR [20]. For the continuous features, which are all lab results, we choose four top-ranked ones consistent across both studies for our classification task: creatinine, HbA1c, hematocrit and BUN.
While it is possible to include additional features for classification, doing so may reduce computational efficiency, offering only marginal gains. Generally, there is a well-established understanding of the biological relationship between these algorithm-selected biomarkers and DR. In-depth medical discussion on DR-related biomarkers can be found in Ref. [21], where HbA1c is notably emphasized.
Table 1 shows summary statistics for the selected variables and their bivariate associations with DR. For complications, we computed the odds ratio and its 95 % confidence interval. For lab results, we performed a two-sample -test comparing the DR group and the unlabeled group. Statistical significance in terms of -values is also reported for the selected features.
Table 1.
Summary statistics and association inference for selected variables.
| Complications | Total count (DR group count) | Odds ratio (95 % C·I.) | -value |
|---|---|---|---|
| Nephropathy | |||
| No | 92,153 (2711) | Reference | |
| Yes | 5723 (1038) | 7.3102 (6.6723–7.9032) | <0.001 |
| Neuropathy | |||
| No | 88,657 (2507) | Reference | |
| Yes | 9219 (1242) | 5.3541 | <0.001 |
| (4.9835–5.7527) | |||
| Lab results | DR average (S.D.) | Unlabeled average (S.D.) | -value |
| Creatinine | 1.9375 (1.8101) | 1.0674 (0.4551) | <0.001 |
| HbA1c | 8.3644 (2.0316) | 7.1374 (1.5094) | <0.001 |
| BUN | 27.4776 (14.6558) | 19.7311 (9.5616) | <0.001 |
| Hematocrit | 36.2432 (4.7178) | 38.9667 (4.7458) | <0.001 |
2.3. Extremely imbalanced missing labels
As aforementioned, the dataset contains 97,876 diabetic patients, among which 3,749, or about 4 %, have been diagnosed with DR. Such a low percentage of DR cases indicates a severe missing label problem as referenced in the medical literature. For instance, studies have reported substantially higher DR prevalence rates, such as 28.5 % (95 % CI 24.9 %–32.5 %) for the US [12] and 34.6 % (95 % CI 34.5 %–34.8 %) globally [13].
To estimate the actual DR prevalence in this EHR dataset and classify unlabeled patients lacking the ground truth or imaging data, we approach the challenge as a positive-unlabeled (PU) learning problem. Patients with DR diagnosis codes are confirmatory positive cases, while the unlabeled group is a mixture of positive and negative cases. We need to classify patients in the unlabeled group either deterministically or probabilistically based on their selected features. The fundamental assumption underlying this approach is that the features exhibit statistically significant differences between the positive group and the negative group.
Let us denote as the collection of positive cases and as the collection of negative cases. A feature vector is if it belongs to , or is if it belongs to . Let denote the unlabeled group and be an unlabeled feature vector. A PU-learning algorithm will assign each to either or by a classification rule and learn the probability , for . One significant technical challenge here is the extreme label imbalance (only 4 % positives), which makes some popular PU-learning algorithms, such as the general two-step approach [14,15] and the biased support vector machine (SVM) [16], perform inadequately. In this paper, we introduce two PU-learning methods specifically designed to effectively handle imbalanced data: the bagging ensemble algorithms [17] and Bayesian finite mixture modeling [19].
2.4. Bagging algorithms for positive-unlabeled learning
The bootstrap aggregation (bagging) ensemble algorithm was developed by Ref. [17] to solve the PU-learning problem. Specifically, the authors take a bootstrap sample from the unlabeled group and combine it with the positive group to train a classifier. Subsequently, the trained classifier is applied to out-of-bag samples to generate the probability of being positive. This procedure is repeated a certain number of times. At the end, each sample in the unlabeled group receives an aggregated score or probability of being positive. This score is derived from classifiers whose training sets exclude that specific sample.
The performance of the algorithm hinges on two critical parameters: the size of the bootstrap samples and the number of bootstrap samples . The experiments in Ref. [17] suggest that setting is a default choice, where is the size of the positive group . The preliminary results in Ref. [17] also show that the performance improves as increases, but it stabilizes at when . Therefore, in this paper, we implement the bagging algorithm with and .
A wide range of popular classification algorithms can be used to train the intermediate classifier for discriminating from a random subsample of . In this paper, we choose the support vector machine (SVM) and the random forest (RF) as intermediate classifiers, which lead to two algorithms for PU-learning, the bagging-SVM and the bagging-RF. The SVM is a supervised learning algorithm that identifies an optimal hyperplane in the high-dimensional feature space to maximally separate classes. The RF is an ensemble classification algorithm that builds multiple decision trees in the training step and combines predictions through voting. A pseudocode with training parameters is provided in Appendix A.
2.5. Bayesian mixture modeling for positive-unlabeled learning with uncertainty quantification
The bagging algorithm, while effective in PU-learning, lacks the capability to provide uncertainty quantification, such as error bounds or confidence intervals, for the prevalence estimate. Moreover, it doesn’t support inference on quantities of interest. Recently [19], developed a probabilistic model-based approach under the Bayesian framework for PU-learning with imbalanced data.
Let denote the feature vector for patient , which contains categorical variables and continuous variables . In our study, categorical variables are neuropathy and nephropathy, the two diabetic complications, and continuous variables are creatinine, HbA1c, hematocrit and BUN. Assume that the underlying distribution of for the positive group is and the underlying distribution for the negative group is . Then a patient without DR diagnosis codes has a probability of to be from the positive group and has a probability of to be from the negative group. Therefore, the parameter is interpreted as the proportion of true positive DR cases in the unlabeled group , or mathematically, . The finite mixture model assumes that the distribution for the unlabeled group is a mixture of and :
[19] considered a parametric model for and . Specifically, let conditionally follow a multivariate -distribution, which accommodates outliers that typically exist in laboratory measurements, and let follow a categorical distribution marginally. The specification leads to a conditional multivariate -distribution for the feature vector.
The finite mixture model is estimated by Bayesian inference, specifically employing a Markov Chain Monte Carlo algorithm as developed in Ref. [19]. The Bayesian inference allows us to obtain posterior distributions of the model parameters, including the mixing proportion . Technical details of Bayesian computations and posterior inference can be found in Ref. [19], and they are not the focus in this paper. A pseudocode of this inference procedure is provided in Appendix B.
The Bayesian inference also provides posterior probabilities for determining whether an unlabeled patient belongs to the positive group: . For instance, a patient has an estimated probability of 0.9 to be from the positive group and we may interpret that this patient is highly likely to be labeled as DR. If a binary classification is desired, a hard threshold of 0.5 may be used to classify unlabeled patients. Compared with the bagging-based machine learning algorithms, the Bayesian finite mixture model offers a twofold advantage: (1) the ability to estimate DR prevalence with a Bayesian confidence interval; (2) it supports statistical inference on parameters of interest (e.g., population mean, proportion), which is important in in the context of medical decision-making.
3. Results
3.1. Estimating the DR prevalence
The estimated DR prevalence is 25.07 % from Bagging-SVM and 26.38 % from Bagging-RF (uncertainty not available). The estimated DR prevalence is 24.37 % (95 % C.I. 23.89 %–24.84 %) from the Bayesian mixture model. The estimated DR prevalence reported in Ref. [12] is 28.5 % (95 % CI 24.9 %–32.5 %) for the U.S. from 2005 to 2008. These numbers are compared in Fig. 2. These estimates are consistent in general, suggesting that around one-quarter of the diabetic population likely have the underlying DR despite that diagnoses are not determined or missing for most of them. The result here also confirms that the original 4 % labeled DR cases severely underestimates the actual percentage in EHR. It is imperative for analysts working with EHR data not to blindly use the 4 % as positive cases and the remaining 96 % as negative cases. Such analyses will likely lead to biased conclusions.
Fig. 2.
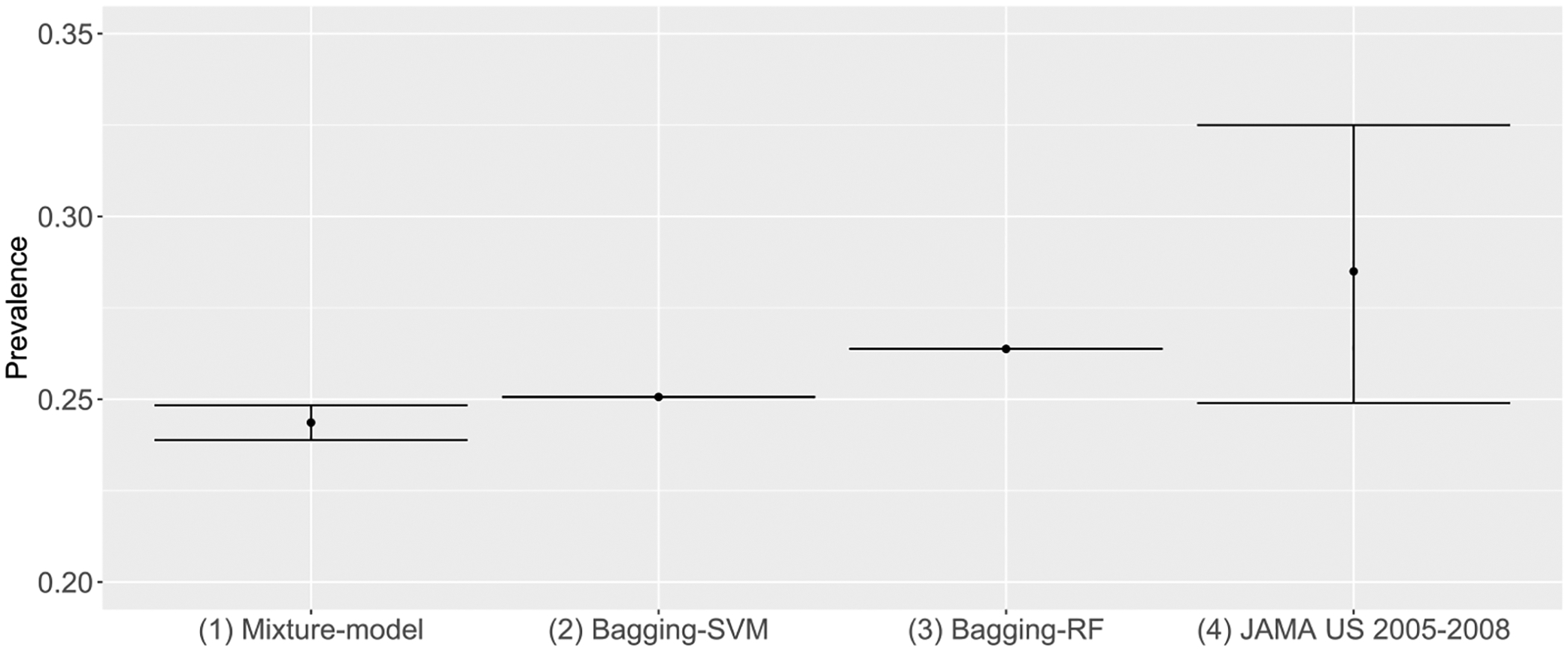
Comparing estimated DR prevalence.
The Bayesian mixture model not only provides estimates of population parameters but also furnishes valuable insights into the data. The posterior means (standard deviations) of lab variables under each categorial group are shown in Table 2, where DN denotes diabetic nephropathy and DNR denotes diabetic neuropathy. When comparing the proportions of patients with and without DR, a notable distinction emerges: 96.43 % of patients in the non-DR group have no additional complications, while only 53.85 % of patients in the DR group are free from other complications. Applying the Bayes rule and using Table 2, we immediately obtain
and
Table 2.
Posterior means (standard deviations) for parameters of interest in the mixture model. DN: diabetic nephropathy; DNR: diabetic neuropathy.
| DN, DNR | DN, Non-DNR | Non-DN, DNR | Non-DN, Non-DNR | ||
|---|---|---|---|---|---|
| DR | Proportion | 0.1280 (0.0010) | 0.1415 (0.0011) | 0.1920 (0.0012) | 0.5385 (0.0016) |
| Creatinine | 2.0728 (0.0117) | 2.0380 (0.0099) | 1.0967 (0.0031) | 1.1217 (0.0021) | |
| HbA1c | 8.0920 (0.0157) | 7.5310 (0.0148) | 8.4472 (0.0145) | 7.8591 (0.0096) | |
| BUN | 31.906 (0.1195) | 33.391 (0.1172) | 20.740 (0.0668) | 21.450 (0.0462) | |
| Hematocrit | 34.060 (0.0350) | 34.494 (0.0370) | 36.291 (0.0308) | 37.059 (0.0217) | |
| Non-DR | Proportion | 0.0003 (0.0001) | 0.0003 (0.0001) | 0.0351 (0.0009) | 0.9643 (0.0009) |
| Creatinine | 1.4175 (0.0071) | 1.2128 (0.0048) | 1.0740 (0.0088) | 1.1001 (0.0015) | |
| HbA1c | 6.8944 (0.0141) | 6.7263 (0.0017) | 6.9840 (0.0380) | 6.7305 (0.0049) | |
| BUN | 27.013 (0.2337) | 29.245 (0.0426) | 16.098 (0.1679) | 16.633 (0.0283) | |
| Hematocrit | 37.711 (0.0456) | 37.758 (0.0312) | 38.925 (0.1221) | 39.679 (0.0194) |
Given that the patient has DN, the probability that this patient also has DR is 0.9931, and given that the patient has DNR, the probability that this patient also has DR is 0.7444. These results underscore that these two complications (DN and DNR) are strongly indicative for DR. It is important to note that these probabilities are learned by the algorithm and cannot be used as a clinical fact.
The mean creatinine level is significantly higher in patients with DR and DN than other patients. The mean HbA1c level is significantly higher in DR patients than non-DR patients. The BUN level is significantly higher in DN patients than non-DN patients, and significantly higher in DR patients than non-DR patients. The hematocrit level is significantly lower in DN patients than non-DN patients, and significantly lower in DR patients than non-DR patients. Lab variables creatinine and HbA1c are clearly indicative for DR, while BUN and hematocrit show meaningful differences between DR and non-DR. It is noteworthy that, given a large sample size of EHR data, a marginal difference can be statistically significant and thus can still be selected to distinguish two groups by machine learning algorithms.
3.2. Classification of unlabeled patients
All three techniques (Bagging-SVM, Bagging-RF and mixture model) explored in this study are used to classify unlabeled patients into either the positive or negative group. We conduct a simulation study to assess their classification performance. Using the data classified by a PU-learning algorithm, we simulate artificial datasets by combining positively labeled patients from with a random sample of negatively labeled patients. We repeatedly simulate 30 datasets for assessment. In each dataset, we keep the positive cases and resample negative cases from the patients who have been negatively classified in the full data analysis. We acknowledge that the ground truth for those unlabeled patients is unknown so that this simulation combines confirmed positive cases with probably negative cases. Instead of simulating data from defined statistical distributions, which has been well studied in Ref. [19], the simulation here maintains the real data distribution by resampling. Then, for each dataset with known positives and negatives, we randomly mask 30 % of the positive cases and mix them with negative cases for later classification. The same algorithm is used for the full data analysis and the simulated classification under each scenario. We evaluate the classification performance by computing their accuracy, AUC, sensitivity, and specificity. The results are shown in Table 3. In terms of accuracy and AUC, all three techniques perform well. However, the mixture model approach achieves a much higher sensitivity than Bagging algorithms without losing much specificity.
Table 3.
Classification performance in simulations: mean metrics (standard deviations).
| Bagging SVM | Bagging RF | Mixture model | |
|---|---|---|---|
| Accuracy | 0.8038 (0.0082) | 0.8089 (0.0083) | 0.8897 (0.0102) |
| AUC | 0.8718 (0.0065) | 0.8700 (0.0056) | 0.8710 (0.0076) |
| Sensitivity | 0.5543 (0.0082) | 0.5643 (0.0159) | 0.9106 (0.0785) |
| Specificity | 0.9216 (0.0043) | 0.9198 (0.0052) | 0.8879 (0.0056) |
3.3. Personalized risk prediction
The Bayesian mixture model enables us to predict an individual’s risk of developing DR given the person’s complications and lab results. The probability is given by:
where is the estimated (posterior mean) mixing probability and is the set of estimated (posterior mean) distribution parameters. The input is the individual’s feature vector and the output is the probability that the patient has underlying DR. For instance, consider a patient diagnosed with DNR but not DN, with specific laboratory values: a creatinine level of 3.5, an HbA1c level of 10.5, a BUN level of 19.7 and a hematocrit level of 39.0. Utilizing the aforementioned formula, we calculate the probability of this patient having DR is 0.786. Then clinicians can leverage this probability as a risk assessment for individual patients and recommend timely eye examinations and proactive care measures.
We have demonstrated that the two complications DN and DNR are strongly indicative of DR, with and . Now, let us consider a patient who has neither of these complications, and we want to show how lab results can indicate the likelihood of DR. Since both creatinine and HbA1c are key biomarkers, Fig. 3 gives a comprehensive view of DR probabilities considering different combinations of creatinine and HbA1c levels, assuming BUN and hematocrit are held constant at their median levels for the population. Fig. 3 can be used to assist clinicians to assess the risk of DR for patients without any complications.
Fig. 3.
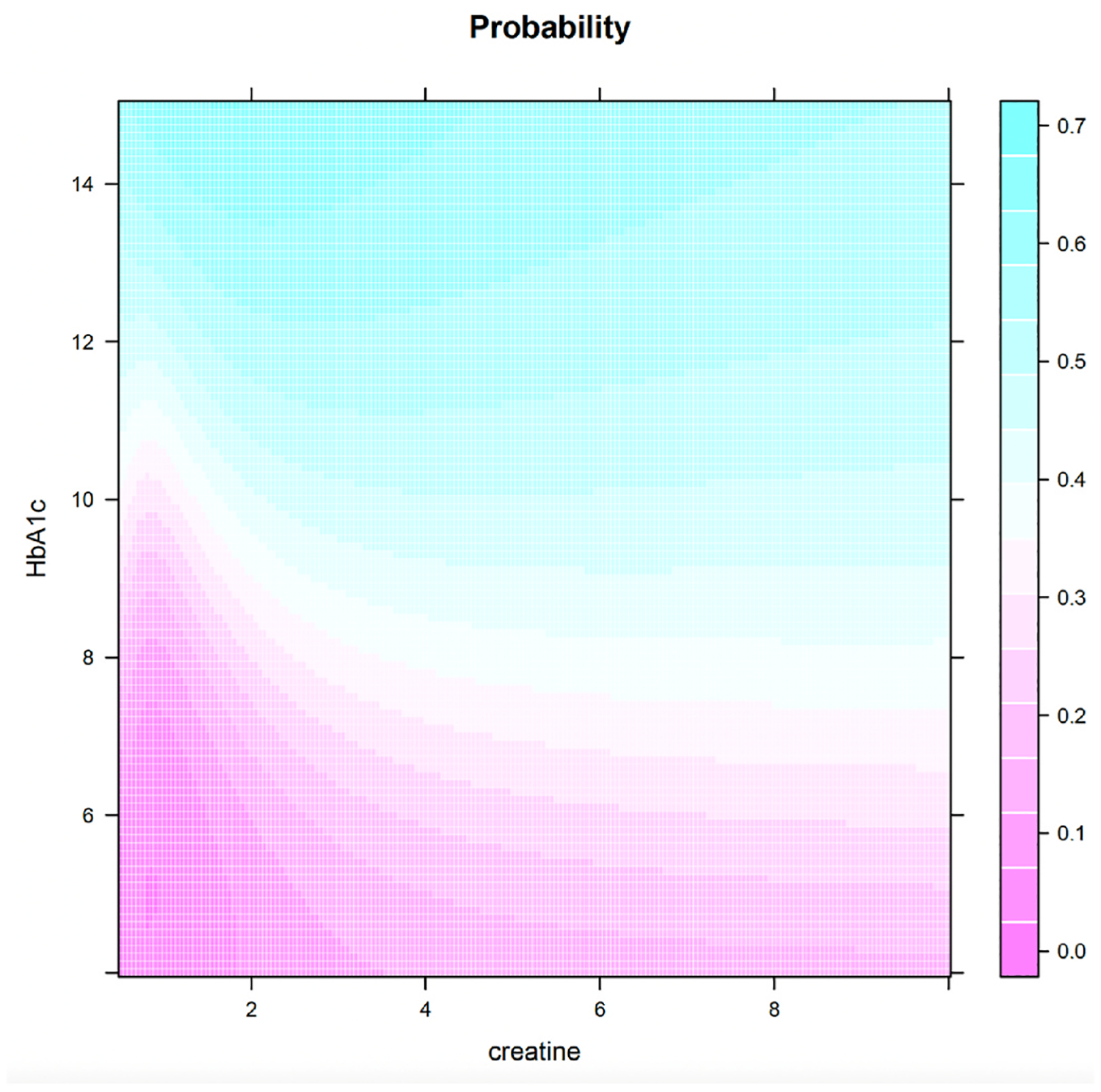
Probability of DR for a grid of creatinine and HbA1c values (Non-DN, Non-DNR).
In a similar vein, we plot Fig. 4 for patients with neither complication. Fig. 4 displays the probability of DR as a function of a single biomarker, while holding other biomarkers at the population median levels. The plot shows that BUN and hematocrit are less relevant, as they generally do not significantly alter the probability of DR. In contrast, the probability is, in general, an increasing function of creatinine and HbA1c. Although the link between DR and these biomarkers is well-documented in the literature, our research takes a step further by quantifying the associated risk. Furthermore, we have developed software that can precisely calculate the DR probability based on learning from the large EHR database. This contribution not only underscores the relevance of these biomarkers but also equips clinicians with a valuable tool for accurate risk assessment in DR management.
Fig. 4.
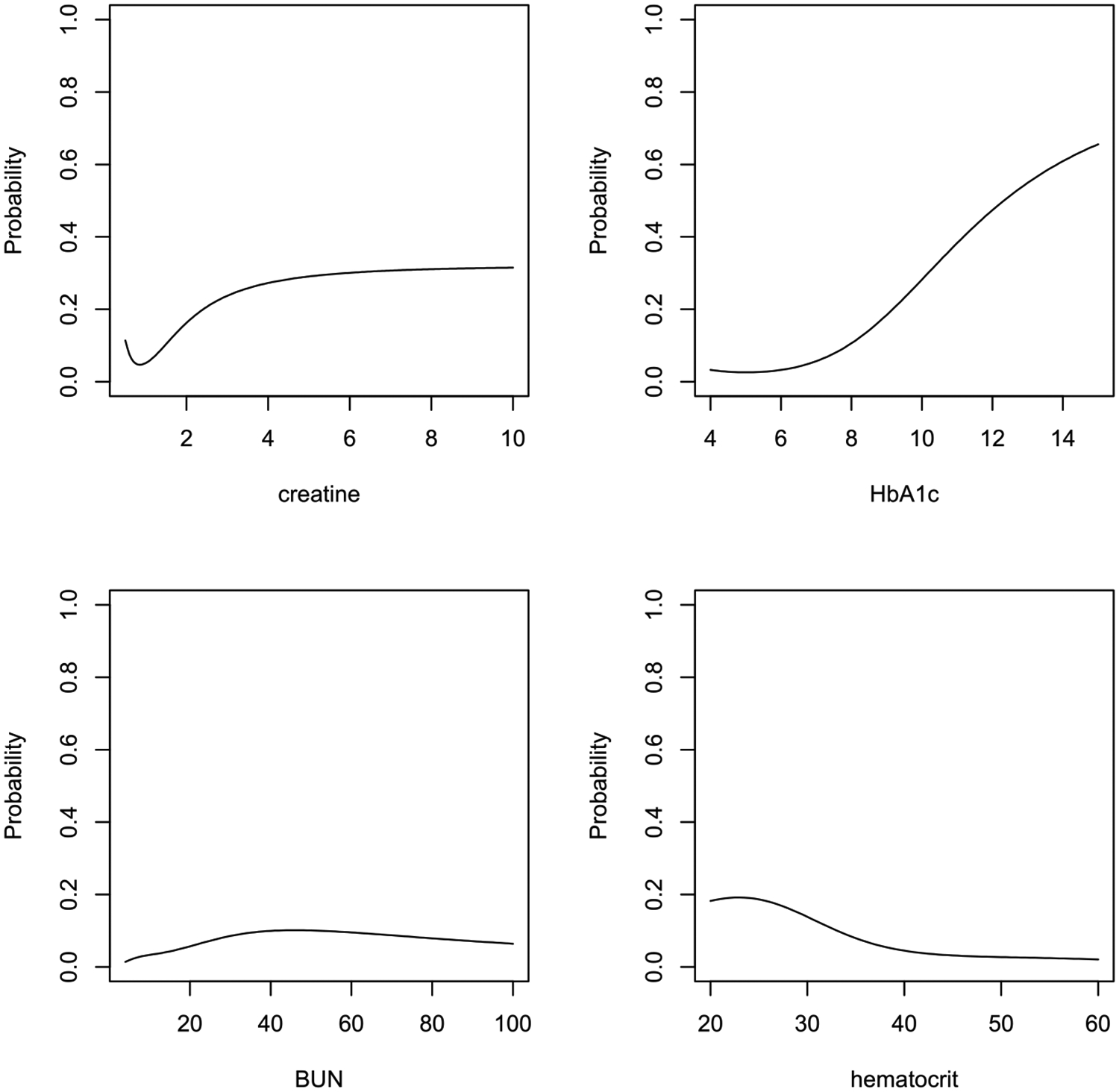
Probability of DR for each biomarker given other biomarkers are at population median levels (Non-DN, Non-DNR).
3.4. Clinical decision support
The research in this paper can provide clinical decision support in multiple ways. First, it validates the high prevalence of DR among diabetic patients and confirms that more than 20 % of diabetic patients already have pathology in their eyes although they may be asymptomatic. This result informs healthcare providers the urgent need to identify asymptomatic patients with ongoing DR pathology. The early detection and diagnosis of DR can help patients to receive effective treatments before the vision loss, thus mitigating the threat of a dramatic increase in late-stage DR patients. Second, the personalized risk prediction is a part of our non-image-based DR screening tool, which is a clinical decision support system. This tool can help primary care physicians to assess patients’ risk for DR and recommend ophthalmic exams for at-risk patients confidently. Third, for researchers and analysts who wish to develop clinical decision support tools using EHR, the methods in this paper can be used to pre-process their data with massive missing labels.
4. Discussion
This paper is the first attempt to estimate the actual DR prevalence using a large EHR dataset with over 100,000 patients nationally. By using machine learning and statistical models, we estimate the DR prevalence among the diabetic population to be around 25 %. This estimation is grounded in the recognition that only 4 % of cases are formally diagnosed in the dataset. Simultaneously, we re-classify the unlabeled patients based solely on their comorbidity and laboratory information and achieve an AUC of 87 %. Using the posterior inference from the Bayesian model, we developed a tool for calculating a patient’s DR risk based on the patient’s unique medical information. This research not only advances our understanding of DR prevalence but also equips healthcare professionals with valuable tools for enhanced risk assessment and patient care.
We point out previous relevant research using EHR data for studying DR. Recently [22], applied machine learning methods on an EHR dataset from the Los Angeles County Department of Health Services to identify undiagnosed DR patients. In their study, all patients had either teleretinal screening or in-person eye examinations, and hence the learning was supervised. The data in Ref. [22] contain 31 % DR patients and 69 % non-DR patients, and the authors concluded that machine learning methods could help clinicians in safety-net settings to identify unscreened diabetic patients who potentially have DR. While there have been other investigations into the application of machine learning for DR detection [23–25], they utilized significantly smaller sample sizes (fewer than 1000 participants). None of these studies above tackled the unique challenge of an extremely imbalanced positive-unlabeled learning problem.
The main limitation of our analysis is that the ground truth of the unlabeled patients in the Cerner EHR data is unknown, making the validation within the original data impossible. While we have done comprehensive simulation studies to evaluate our model’s performance as outlined in Ref. [19] and demonstrated in Table 3, we are constrained by resources from accessing EHR data with fully labeled patients for external validation. Although completely labeled DR data are hard to obtain, the learning methods we have illustrated may be applied to and validated with other disease datasets or even non-medical data.
It is well-known that EHR have been designed primarily for the purpose of medical billing instead of documenting clinical diagnoses so that the missingness of labels commonly exists. The proposed research in this paper is not limited to classifying DR cases but can be useful in phenotyping other diseases in EHR. For example [26], considered phenotyping positive-unlabeled EHR patients with primary aldosteronism, which is the most common cause of secondary hypertension. Our methods or algorithms may be applied to such positive-unlabeled scenarios. Besides the medical domain, the PU-learning problem arises from a broader spectrum of applications, including biological processes, drug discovery, ecological modeling, targeted marketing, remote sensing, recommender systems, etc. [27].
Using machine learning methods with non-imaging-based EHR to assess and predict DR risk remains an active and challenging research topic. The benefit of having accurate and reliable methods in this domain is tremendous in healthcare practices. Though the American Diabetes Association recommends annual eye examinations for individuals with diabetes, adherence to such guidelines remains low, especially within socio-economically disadvantaged groups, such as racial minority groups and the uninsured population [28,29]. Implementing an EHR-based risk assessment and prediction system holds the potential to significantly help clinicians and healthcare professionals in prioritizing and recommending targeted eye examinations to patients who exhibit a heightened risk of DR. This proactive approach can play a pivotal role in improving early detection, intervention, and ultimately, patient outcomes.
Acknowledgement
This work was conducted with data from the Cerner Corporation’s Health Facts database of electronic medical records provided by the Oklahoma State University Center for Health Systems Innovation (CHSI). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the Cerner Corporation.
Funding
Research reported in this publication was supported by the National Eye Institute of the National Institutes of Health under Award Number R01EY033861. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
APPENDIX
A. Pseudocode and Training Parameters for Bagging PU Learning
Algorithm 1:
Bagging PU learning
| Input: positive group , unlabeled group , size of the bootstrap samples , and number of bootstrap samples |
| Output: a function to assign a probability of being positive to each |
| //Initialize the accumulators |
| for to do: |
| Draw a bootstrap sample of size from |
| Treat as negative and train a classifier to discriminate from |
| Apply to generate a probability of being positive for all |
| Update: |
| end for |
| Return |
We use and for our training. For the intermediate classifiers SVM and RF, we use grid search and cross-validation to determine the optimal parameters within the predefined sets. In the SVM, the search range for the cost parameter is {10−12, 10−11, …, 101, 102}. For the RF model, the predefined search range for the number of trees is {50, 100, 300}. For the number of variables which are randomly sampled as candidates at each split in the RF, the default value of is used, where represents the total number of variables.
B. Pseudocode for Estimating the Bayesian Finite Mixture Model
Algorithm 2.
Consensus Monte Carlo and Markov Chain Monte Carlo
| Input: positive group , unlabeled group , number of splits in consensus Monte Carlo, number of iterations and burn-in size in MCMC, prior distributions for the set of all parameters in the model |
| Output: posterior distributions and classification probabilities |
| Split into subgroups with equal sizes |
| for to do: |
| Combine and as data |
| Perform MCMC on data to obtain posterior samples for in the loop: |
| for to |
| For the collection , where each represents a parameter in the model |
| Draw a sample from its full conditional distribution , denote |
| Let |
| end for |
| Discard burn-in samples and combine the rest posterior samples from all subgroups |
| according to certain weights for the subgroups |
| end for |
| Return approximated by posterior samples and computed using posterior samples |
The full conditional distributions in the MCMC can be found in Section 3 of [19], Equations 1 to 11. Weights are proportional to the inverse of posterior variance of each parameter. For [0, 1] bounded parameters, weights need to be adjusted to 1. The classification probabilities are computed by
Footnotes
Ethical Statement
The study does not involve humans or animals. The study does not contain any clinical trials. The electronic medical records data used in this paper are de-identified and HIPPA-compliant. The study was performed in compliance with the institutional guidelines for biomedical research.
CRediT authorship contribution statement
Ye Liang: Writing – review & editing, Writing – original draft, Methodology, Investigation, Funding acquisition, Conceptualization. Ru Wang: Writing – review & editing, Methodology, Formal analysis, Data curation. Yuchen Wang: Writing – review & editing, Methodology. Tieming Liu: Writing – review & editing, Investigation, Funding acquisition, Conceptualization.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- [1].American Diabetes Association. Diabetic retinopathy. Diabetes Care 2002;25 (suppl_1):s90–3. [Google Scholar]
- [2].National diabetes statistics Report. Atlanta, GA: Centers for Disease Control and Prevention, US Department of Health and Human Services; 2020. p. 12–5. [Google Scholar]
- [3].Solomon SD, Chew E, Duh EJ, Sobrin L, Sun JK, VanderBeek BL, Wykoff CC, Gardner TW. Diabetic retinopathy: a position statement by the American Diabetes Association. Diabetes Care 2017;40(3):412–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Ting DSW, Cheung GCM, Wong TY. Diabetic retinopathy: global prevalence, major risk factors, screening practices and public health challenges: a review. Clin Exp Ophthalmol 2016;44(4):260–77. [DOI] [PubMed] [Google Scholar]
- [5].Ciulla TA, Amador AG, Zinman B. Diabetic retinopathy and diabetic macular edema: pathophysiology, screening, and novel therapies. Diabetes Care 2003;26 (9):2653–64. [DOI] [PubMed] [Google Scholar]
- [6].Piri S, Delen D, Liu T, Zolbanin HM. A data analytics approach to building a clinical decision support system for diabetic retinopathy: developing and deploying a model ensemble. Decis Support Syst 2017;101:12–27. [Google Scholar]
- [7].Wang R, Miao Z, Liu T, Liu M, Grdinovac K, Song X, Liang Y, Delen D, Paiva W. Derivation and validation of essential predictors and risk Index for early detection of diabetic retinopathy using electronic health records. J Clin Med 2021;10(7): 1473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Homayouni A, Liu T, Thieu T. Diabetic retinopathy prediction using Progressive Ablation Feature Selection: a comprehensive classifier evaluation. Smart Health 2022;26:100343. [Google Scholar]
- [9].Sun Y, Zhang D. Diagnosis and analysis of diabetic retinopathy based on electronic health records. IEEE Access 2019;7:86115–20. [Google Scholar]
- [10].Lin WC, Chen JS, Chiang MF, Hribar MR. Applications of artificial intelligence to electronic health record data in ophthalmology. Translational vision science & technology 2020;9(2):13. 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Hripcsak G, Albers DJ. Next-generation phenotyping of electronic health records. J Am Med Inform Assoc 2013. Jan 1;20(1):117–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Zhang X, Saaddine JB, Chou CF, Cotch MF, Cheng YJ, Geiss LS, Gregg EW, Albright AL, Klein BE, Klein R. Prevalence of diabetic retinopathy in the United States, 2005–2008. JAMA 2010;304(6):649–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Yau JW, Rogers SL, Kawasaki R, Lamoureux EL, Kowalski JW, Bek T, Chen SJ, Dekker JM, Fletcher A, Grauslund J, Haffner S. Global prevalence and major risk factors of diabetic retinopathy. Diabetes Care 2012;35(3):556–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Li X, Liu B. Learning to classify texts using positive and unlabeled data. IJCAI 2003, August;3(2003):587–92. [Google Scholar]
- [15].Li XL, Yu PS, Liu B, Ng SK. Positive unlabeled learning for data stream classification. In: Proceedings of the 2009 SIAM international conference on data mining. Society for Industrial and Applied Mathematics; 2009, April. p. 259–70. [Google Scholar]
- [16].Liu B, Dai Y, Li X, Lee WS, Yu PS. Building text classifiers using positive and unlabeled examples. In: Third IEEE international conference on data mining. IEEE; 2003, November. p. 179–86. [Google Scholar]
- [17].Mordelet F, Vert JP. A bagging SVM to learn from positive and unlabeled examples. Pattern Recogn Lett 2014;37:201–9. [Google Scholar]
- [18].Claesen M, De Smet F, Suykens JA, De Moor B. A robust ensemble approach to learn from positive and unlabeled data using SVM base models. Neurocomputing 2015;160:73–84. [Google Scholar]
- [19].Wang R, Liang Y, Miao Z, Liu T. Bayesian analysis for imbalanced positive-unlabeled diagnosis codes in electronic health records. Ann Appl Stat 2023;17(2): 1220–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Jeng CJ, Hsieh YT, Yang CM, Yang CH, Lin CL, Wang IJ. Diabetic retinopathy in patients with diabetic nephropathy: development and progression. PLoS One 2016; 11(8):e0161897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Jenkins AJ, Joglekar MV, Hardikar AA, Keech AC, O’Neal DN, Januszewski AS. Biomarkers in diabetic retinopathy. Rev Diabet Stud: Reg Dev Stud 2015;12(1–2): 159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Ogunyemi OI, Gandhi M, Lee M, Teklehaimanot S, Daskivich LP, Hindman D, Lopez K, Taira RK. Detecting diabetic retinopathy through machine learning on electronic health record data from an urban, safety net healthcare system. JAMIA Open 2021;4(3):ooab066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Oh E, Yoo TK, Park EC. Diabetic retinopathy risk prediction for fundus examination using sparse learning: a cross-sectional study. BMC Med Inf Decis Making 2013;13: 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Tsao HY, Chan PY, Su ECY. Predicting diabetic retinopathy and identifying interpretable biomedical features using machine learning algorithms. BMC Bioinf 2018;19:111–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Cichosz SL, Johansen MD, Knudsen ST, Hansen TK, Hejlesen O. A classification model for predicting eye disease in newly diagnosed people with type 2 diabetes. Diabetes Res Clin Pract 2015;108(2):210–5. [DOI] [PubMed] [Google Scholar]
- [26].Zhang L, Ding X, Ma Y, Muthu N, Ajmal I, Moore JH, Herman DS, Chen J. A maximum likelihood approach to electronic health record phenotyping using positive and unlabeled patients. J Am Med Inf Assoc 2020;27(1):119–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Bekker J, Davis J. Learning from positive and unlabeled data: a survey. Mach Learn 2020;109:719–60. [Google Scholar]
- [28].Fisher MD, Rajput Y, Gu T, Singer JR, Marshall AR, Ryu S, Barron J, MacLean C. Evaluating adherence to dilated eye examination recommendations among patients with diabetes, combined with patient and provider perspectives. American Health & Drug Benefits 2016;9(7):385. [PMC free article] [PubMed] [Google Scholar]
- [29].Solomon SD, Shoge RY, Ervin AM, Contreras M, Harewood J, Aguwa UT, Olivier MM. Improving access to eye care: a systematic review of the literature. Ophthalmology 2022;129(10):114–26. [DOI] [PubMed] [Google Scholar]


