DUAL SELF-DISTILLATION OF U-SHAPED NETWORKS FOR 3D MEDICAL IMAGE SEGMENTATION

Abstract

U-shaped networks and its variants have demonstrated exceptional results for medical image segmentation. In this paper, we propose a novel dual self-distillation (DSD) framework for U-shaped networks for 3D medical image segmentation. DSD distills knowledge from the ground-truth segmentation labels to the decoder layers and also between the encoder and decoder layers of a single U-shaped network. DSD is a generalized training strategy that could be attached to the backbone architecture of any U-shaped network to further improve its segmentation performance. We attached DSD on two state-of-the-art U-shaped backbones, and extensive experiments on two public 3D medical image segmentation datasets demonstrated significant improvement over those backbones, with negligible increase in trainable parameters and training time. The source code is publicly available at https://github.com/soumbane/DualSelfDistillation.

1. INTRODUCTION

Deep learning algorithms such as Convolutional Neural Networks (CNNs) have proven to be extremely useful in performing medical image segmentation [1], which is a very important and challenging task in medical image analysis. One of the breakthrough algorithms which produced state-of-the-art results for end-to-end 2D and 3D medical image segmentation task is the U-Net [2] and the 3D U-Net [3], respectively. These U-shaped architectures consist of a CNN-based contracting encoder to capture the context of the input image and a CNN-based expanding decoder to localize the object in the image. Skip-connections between the encoder and decoder layers allow U-Nets to use the fine-grained details learned from the encoder blocks and construct a localized image in the decoder blocks. More recently, vision transformers (ViT) [4] have been used in the encoder of U-shaped networks [5].

Knowledge distillation is the process by which a large pre-trained model (teacher network) can transfer its knowledge to a smaller, lightweight model (student network) during its training [6, 7]. Recently, knowledge distillation has been used to improve the performance of lightweight networks for medical image segmentation [8]. The need of transferring knowledge from a large teacher network to a smaller student network was later eliminated by the process of self-distillation [9]. Self-distillation uses the deepest layer of a single model which acts as the teacher network to distill the knowledge to the shallower layers of the same model which acts as the student network [9]. Self-distillation has been applied for numerous computer vision tasks such as image classification [9].

In this paper, we propose a novel 3D dual self-distillation (DSD) framework that could be attached to any U-shaped image segmentation backbones. In DSD, the deepest encoder and decoder of the U-shaped backbones act as the teacher network for the shallower encoders and decoders which act as student networks. We found that the deepest encoder which is at the bottom of the contracting encoder path of the U-shaped network contains more contextual information compared to the shallower encoder layers. Similarly, the deepest decoder which is at the top of the expanding decoder path of the U-shaped network contains more semantic information than the shallower decoder layers. Thus, in our DSD framework, the information distills in a bottom-up manner on the encoder side and in a reverse top-down manner on the decoder side of an U-shaped backbone. Additionally, DSD also includes the distillation of the knowledge from the ground-truth labels to the decoder layers of the U-shaped network, which is a process known as deep supervision in medical image segmentation [10]. Thus, DSD leverages the benefits of deep supervision by overcoming optimization difficulties and achieving faster convergence [10].

Our major contributions are: (i) We incorporated the self-distillation process to U-shaped networks for medical image segmentation. Our novel design of DSD between encoders and decoders could be generalized to any U-shaped segmentation backbones. (ii) The self-distillation process in our DSD framework is a more general training approach than the deep supervision, which can be considered a special case of our framework. (iii) We performed extensive experiments on two public 3D medical image segmentation datasets, with DSD attached to two state-of-the-art U-shaped backbones (one ViT-based and the other CNN-based encoder) and demonstrated significant improvements over those backbones with negligible increase in trainable parameters and training time.

2. METHODOLOGY

In the following sections, we provide a detailed explanation of our proposed DSD framework as shown in Fig. 1.

Fig. 1:

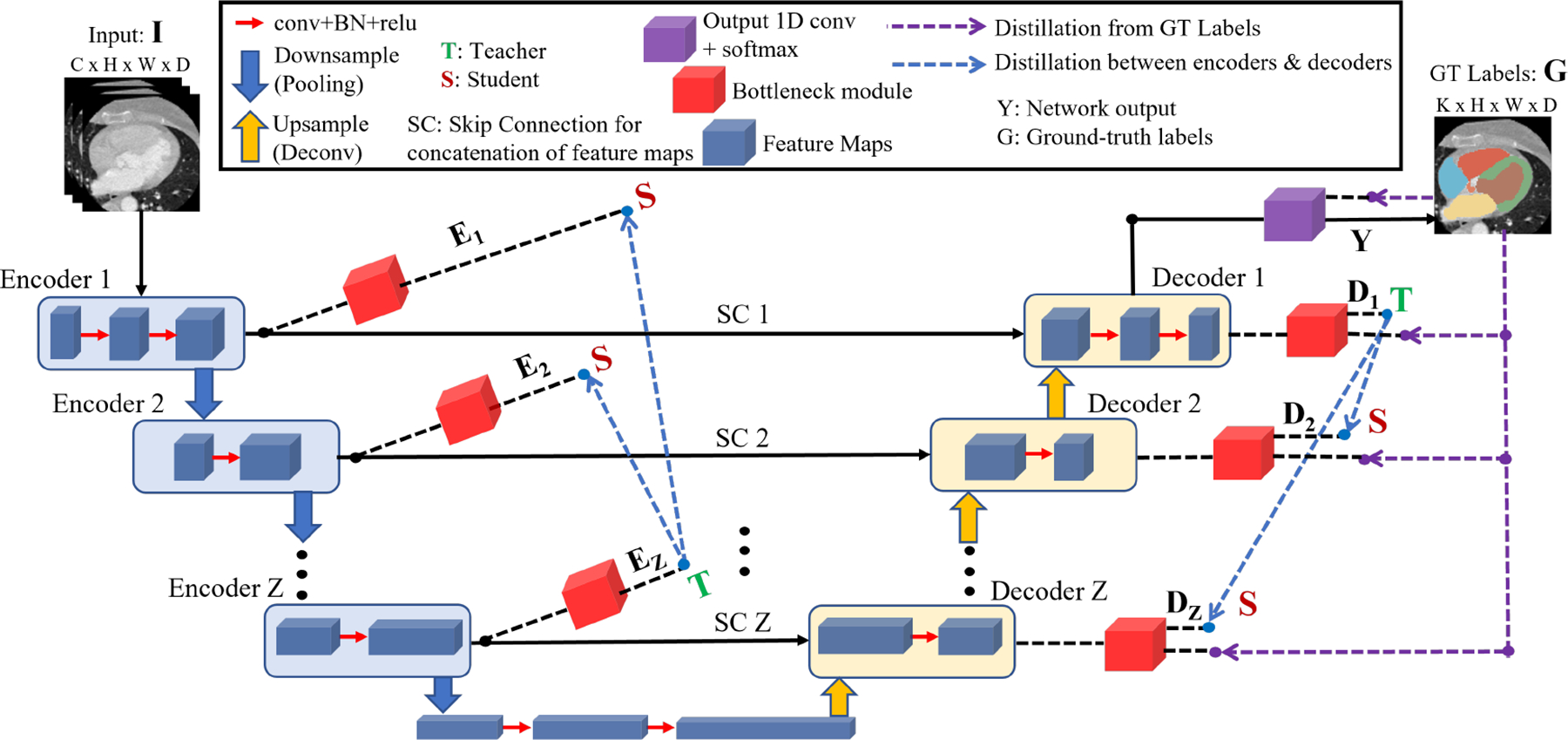
Self-distillation demonstrated with an U-shaped network for 3D medical image segmentation. All dashed lines shown are only used during training and removed during inference.

2.1. U-shaped backbone

The U-shaped backbone maps an input image I to the ground-truth (GT) labels G, where $I\in {\mathbb{R}}^{C\times H\times W\times D}$ is the image with H, W, D as the height, width and depth, respectively and C is the number of imaging modalities and $G\in {\mathbb{R}}^{K\times H\times W\times D}$ is the ground-truth labels with K classes.

The most common loss function used by a U-shaped network [11, 5] is the Dice Cross-Entropy (CE) loss (L_DCE), which is a compound loss function defined as follows:

$$L_{DCE}^Y=L_{\mathit{\text{dice}}}^Y+L_{CE}^Y$$ (1)

where, the Dice loss $L_{\mathit{\text{dice}}}^Y$ measures the pixel-wise similarity and the cross-entropy loss $L_{CE}^Y$ measures the pixel-wise difference in distributions between the network output Y and ground-truth labels G. This loss is back-propagated to the network to update the weights of the encoders and decoders.

2.2. Bottleneck Module

The bottleneck module shown by the red colored boxes in Fig. 1 constitutes an integral component of our proposed framework, which converts the feature maps $F(F\in {\mathbb{R}}^{K^{\prime }\times H^{\prime }\times W^{\prime }\times D^{\prime }})$ obtained from different encoder and decoder layers to a probability distribution $P\in {\mathbb{R}}^{K\times H\times W\times D}$ of the same shape as the network output Y. For the feature maps F, K′, H′, W′ and D′ denote the number of channels, height, width and depth respectively at a given layer, and they vary depending on the position of the encoder (Encoder ${\left.i\right|}_{i=1}^Z$) and decoder (Decoder ${\left.i\right|}_{i=1}^Z$ layers.

The bottleneck module consist of three layers: (i) 1D convolution layer: this layer changes the number of channels of feature maps obtained from the encoder and decoder layers to match the number of output classes K (from $F\in {\mathbb{R}}^{K^{\prime }\times H^{\prime }\times W^{\prime }\times D^{\prime }}$ to $F^{\prime }\in {\mathbb{R}}^{K\times H^{\prime }\times W^{\prime }\times D^{\prime }}$), (ii) Deconvolution layer: this layer upsamples the feature maps obtained from the 1D convolution layer to generate logits (L) that match the dimension of the output Y (from $F^{\prime }\in {\mathbb{R}}^{K\times H^{\prime }\times W^{\prime }\times D^{\prime }}$ to $L\in {\mathbb{R}}^{K\times H\times W\times D}$), (iii) Softmax layer: this layer converts the logits $L\left(L\in {\mathbb{R}}^{K\times H\times W\times D}\right)$ to soft labels which is a probability distribution P of the same shape as L, i.e. $P_{p,k}=\frac{{\mathrm{e}\mathrm{x}\mathrm{p}}^{L_{p,k}/\tau }}{{\sum }_{j=1}^K{\mathrm{e}\mathrm{x}\mathrm{p}}^{L_{p,j}/\tau }}$, where τ (τ > 1) denotes the temperature to generate the soft labels, and p ∈ N and k ∈ K are indices for pixels and classes, respectively, with N = H _* W _* D denoting the total number of pixels.

2.3. U-shaped backbone with Dual Self-distillation (DSD)

We propose a novel dual self-distillation (DSD) framework for U-shaped backbones as shown by the purple and blue dashed arrows in Fig. 1. Our DSD framework consists of two main components.

1. Distillation from ground-truth labels: the first part (purple dashed arrows in Fig. 1) is the distillation of knowledge from the ground-truth labels G to each decoder of the U-shaped network. This process is known as deep supervision in medical image segmentation [10]. For our DSD framework, we calculate the Dice Cross-Entropy (DCE) loss (Eq. 1) between each decoder layer’s softmax output ${\left.D_i\right|}_{i=1}^Z$ and the ground-truth labels G. This loss is defined as:

   $$L_{DS}=L_{DCE}^Y+\eta \sum _{i=1}^Z{L}_{DCE}^{D_i}$$ (2)

   where, L_DS denotes the deep supervision loss, Z denotes the number of decoders in the U-shaped architecture, $L_{DCE}^{D_i}$ denotes the Dice cross-entropy loss between i^th decoder and G, and η denotes the coefficient that controls the amount of supervision from G to ${\left.D_i\right|}_{i=1}^Z$.
2. Distillation between encoder and decoder layers: the second part (blue dashed arrows in Fig. 1) is the distillation of knowledge between encoder and decoder layers of the U-shaped network. On the encoder side, the deepest encoder (Encoder Z) forms the teacher network to the shallower encoders (Encoder 1, 2, …, (Z-1)) which form the student networks. We reverse the order of teacher and student on the decoder side due to the deconvolution operation. Hence, the deepest decoder (Decoder 1) forms the teacher network to the shallower decoders (Decoder 2, 3, …, Z) which form the student networks. For all the teacher-student pairs in the encoders and decoders of the U-shaped network, we compute the pixel-wise Kullback–Leibler (KL) divergence [12] between the output probability distributions (softmax) of teacher and student as follows:

   $$L_{KL}={\alpha }_1\sum _{i=1}^{Z-1}{D}_{KL}\left(E_i,E_Z\right)+{\alpha }_2\sum _{i=2}^Z{D}_{KL}\left(D_i,D_1\right)$$ (3)

   where D_KL(P^S, P^T) is the KL divergence between student (P^S) and teacher (P^T ) probability distributions, E_i and D_i are the i^th shallow encoder and decoder’s (student’s) softmax output (P^S) respectively, E_Z and D₁ are the deepest encoder and decoder’s (teacher’s) softmax output (P^T), respectively, Z is the number of encoders and decoders.
   We define our proposed dual self-distillation loss L_DSD as follows:

   $$\begin{gathered} L_{DSD}=L_{DCE}^Y+\eta \sum _{i=1}^Z{L}_{DCE}^{D_i} \\ +{\alpha }_1\sum _{i=1}^{Z-1}{D}_{KL}\left(E_i,E_Z\right)+{\alpha }_2\sum _{i=2}^Z{D}_{KL}\left(D_i,D_1\right) \end{gathered}$$ (4)

   where α₁ and α₂ denote the coefficients that controls the amount of self-distillation between the encoder and decoder layers, respectively. Note that our generalized DSD framework is reduced to deep supervision when α₁, α₂ = 0.

Therefore, our objective function is to minimize the L_DSD loss function in Eq. 4. Note that the training with our DSD framework (shown by dashed arrows in Fig. 1) uses very few extra parameters (brought by the bottleneck modules) and hence performs end-to-end training without increasing the training time when compared to the backbone architectures. During inference, the DSD framework is removed and hence it takes the same inference time as the U-shaped backbones.

3. EXPERIMENTS AND RESULTS

We attached our dual self-distillation (DSD) framework on two state-of-the-art U-shaped backbones and applied it on two benchmark datasets for medical image segmentation tasks, specifically whole heart and brain tumor segmentation.

3.1. Datasets

MMWHS dataset (Heart) –

High resolution 3D CT angiography datasets of 20 patients from the Multi-Modal Whole Heart Segmentation (MMWHS) dataset [13], with 7 classes of ground-truth labels of cardiac substructures was used. We split the data into a train and validation set of 16 and 4 patients respectively and then performed a 5-fold cross validation.

MSD dataset (Brain) –

The brain tumor segmentation task [14] was used from the Medical Segmentation Decathlon (MSD) dataset [15]. This task comprised of 484 patients having multi-modal multi-site MRI data with 3 classes of ground truth labels and 4-channel multi-modal input (FLAIR, T1w, T1gd, T2w). We split the data into a train/validation/test set of 388/72/24 patients following the split in [5].

3.2. Experimental setup and implementation details

In our experiments, we selected the UNETR [5] and nnU-Net [16] as our U-shaped backbones and attached the DSD framework to them. These backbones are selected because they have recently shown promising and state-of-the-art results for several medical image segmentation tasks. For all experiments, the training was performed including the background and evaluated only on the foreground classes. All DSD experiments were performed with η = 1, α₁, α₂ = 1 and temperature (τ = 3). These hyperparameters were empirically decided based on the performance on the validation set. The experiments were conducted with PyTorch v1.12, TorchManager v1.2 [17] and MONAI v0.9 [18] framework using a NVIDIA Quadro RTX 6000 GPU. Quantitative evaluations between predicted and ground truth segmentation regions were performed using the Dice similarity coefficient (Dice score) and 95^th percentile of the Hausdorff distance (HD95 in mm)[5].

3.3. Ablation study

Table 1 presents an ablation study comparing the following components of DSD framework: (i) Basic (η = 0 and α₁, α₂ = 0 in Eq. 4): This is the basic U-shaped backbone without any deep supervision and self-distillation. (ii) DS (η = 1 and α₁, α₂ = 0 in Eq. 4): DSD in this case is reduced to deep supervision (DS). (iii) SDD (η = 1, α₁ = 0, α₂ = 1): This shows the effect of self-distillation only between the decoder layers along with DS. (iv) SDE (η = 1, α₁ = 1, α₂ = 0): This shows the effect of self-distillation only between the encoder layers along with DS. (v) DSD (η = 1, α₁ = 1, α₂ = 1): This shows the effect of our proposed dual self-distillation which achieves the best performance. Lastly, we did not observe any noticeable improvement in performance with feature-map distillation [9] since it becomes redundant for pixel-level classification tasks.

Table 1:

Ablation study showing the mean Dice score of all 7 cardiac substructures of one fold of MMWHS validation set obtained by different components of our DSD framework.

Study settings	Basic	DS	SDD	SDE	DSD
Network	Dice↑	Dice↑	Dice↑	Dice↑	Dice↑
UNETR	76.12	78.29	80.13	79.90	80.93
nnU-Net	76.97	83.74	84.02	84.42	86.10

3.4. Prediction with MMWHS dataset

Tables 2 presents the 5-fold cross validation results and summarizes the mean dice score and HD95 of the 7 classes of cardiac substructures for the CT angiography (CTA) MMWHS dataset using UNETR and nnU-Net as the backbone along with the DSD framework. On average, across the 5-folds, when our proposed DSD framework is attached to the UNETR architecture, it outperforms the UNETR backbone with just 0.017% increase in the number of trainable parameters (and thus almost same training time) and when DSD is attached to the nnU-Net architecture, it outperforms the nnU-Net backbone with just 0.052% increase in the number of trainable parameters. A qualitative comparison (both on a 2D axial slice and 3D volume) between the predictions with UNETR, UNETR with DSD, nnU-Net and nnU-Net with DSD is shown in Fig. 2.

Table 2:

Quantitative comparison (5-fold mean and std of Dice score (%) and HD95 (mm)) on high-resolution cardiac CTA MMWHS dataset with UNETR and nnU-Net with and without the DSD framework.

Network	UNETR [5]		nnU-Net [16]		UNETR with DSD		nnU-Net with DSD
	Dice ↑	HD95 ↓	Dice ↑	HD95 ↓	Dice ↑	HD95 ↓	Dice ↑	HD95 ↓
mean ± std	78.24 ± 3.85	23.48 ± 9.00	83.55 ± 4.53	26.31 ± 6.98	80.94 ± 3.62	20.26 ± 8.23	86.49 ± 2.28	15.23 ± 5.11

Fig. 2:

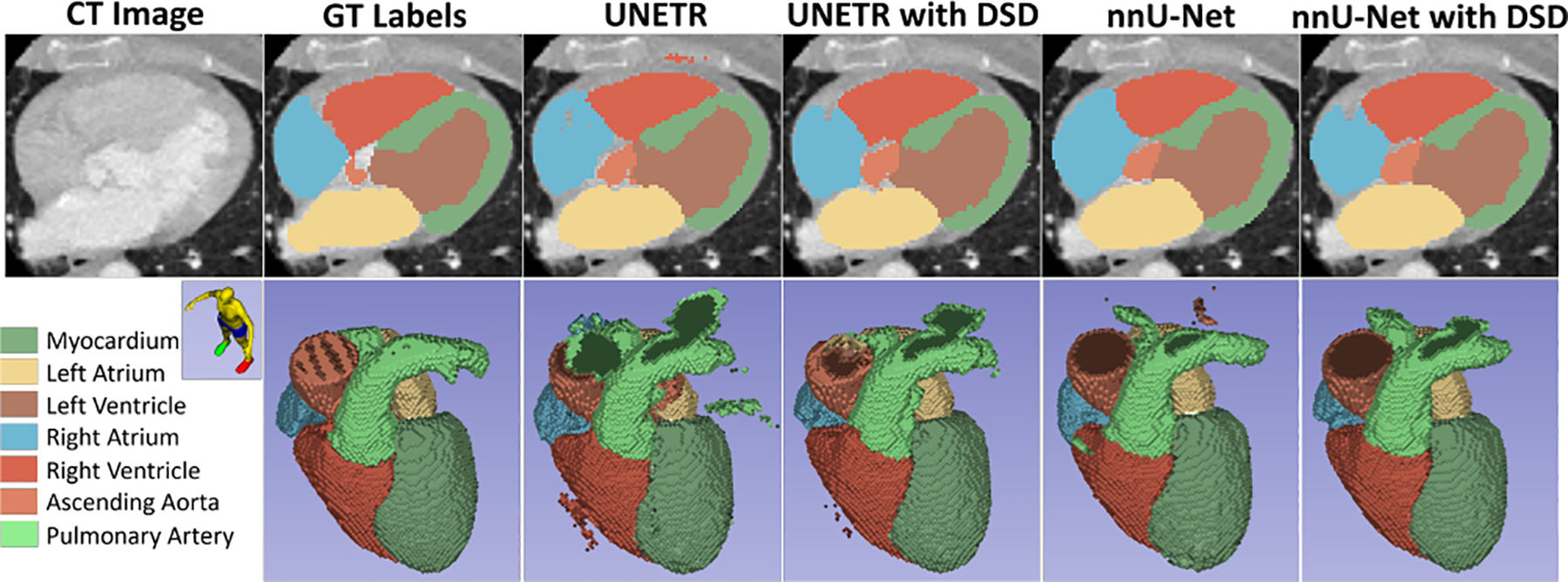
Qualitative comparison of an axial slice with ground-truth (GT) labels (on CTA) and predictions with UNETR and nnU-Net, highlighting the improvements with DSD.

3.5. Prediction with Brain Tumor dataset

Table 3 summarizes the prediction results for the MSD-BraTS dataset using UNETR and nnU-Net as the backbone. When the DSD framework is attached to a UNETR backbone, it significantly outperforms the UNETR backbone with a higher dice score and lower HD95, obtained with just 0.008% increase in the number of training parameters. When the DSD framework is attached to the nnU-Net, it outperforms the nnU-Net backbone with just 0.066% increase in the number of training parameters. Note that on this dataset, our method also outperformed the state-of-the-art segmentation methods with a big margin. Fig. 3 shows a qualitative comparison between the predictions with UNETR, UNETR with DSD, nnU-Net, and nnU-Net with DSD on a 2D slice.

Table 3:

Quantitative comparison (Dice score (%) and HD95 (mm)) for brain tumor segmentation task of MSD dataset with state-of-the-art methods. Our DSD framework is attached to the UNETR and nnU-Net backbones.

Network	UNet [2]		TransUNet [19]		CoTr [20]		UNETR [5]		nnU-Net [16]		UNETR with DSD		nnU-Net with DSD
Structure	Dice ↑	HD95 ↓	Dice ↑	HD95 ↓	Dice ↑	HD95 ↓	Dice ↑	HD95 ↓	Dice ↑	HD95 ↓	Dice ↑	HD95 ↓	Dice ↑	HD95 ↓
WT	76.6	9.2	70.6	14.0	74.6	9.2	75.2	22.6	75.7	25.7	80.4	9.8	78.5	19.0
ET	56.1	11.1	54.2	10.4	55.7	9.4	53.6	9.8	65.1	18.8	64.1	8.0	67.8	15.7
TC	66.5	10.2	68.4	14.5	74.8	10.4	78.1	14.8	81.8	10.9	85.2	3.6	84.4	9.6
mean	66.4	10.2	64.4	13.0	68.3	9.7	68.9	15.7	74.2	18.5	76.6	7.1	76.9	14.8

Fig. 3:

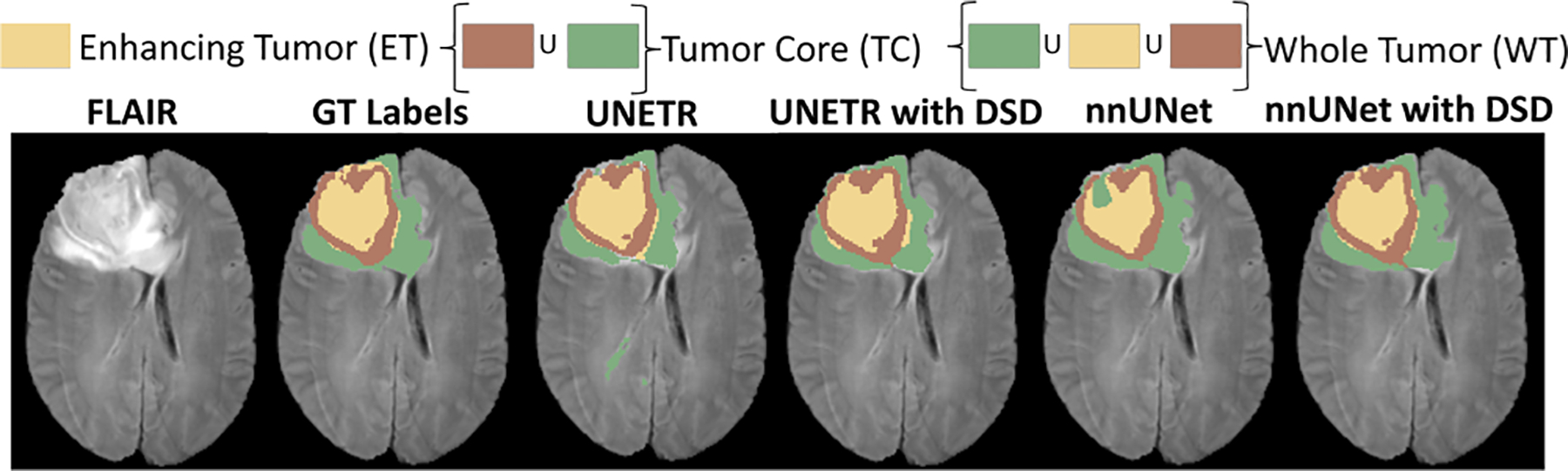
Qualitative comparison of an axial slice with ground-truth (GT) labels (on FLAIR MRI) and predictions from UNETR and nnU-Net, highlighting the improvements with DSD.

4. CONCLUSION

In this paper, we introduced a novel DSD framework that was attached to UNETR and nnU-Net backbones and evaluated on two benchmark datasets. Our results demonstrated that DSD could boost the segmentation performance of these U-shaped networks by a significant margin.

5. COMPLIANCE WITH ETHICAL STANDARDS

This research study was conducted retrospectively using human subject data made available in open access for MMWHS and MSD-BraTS datasets. Ethical approval was not required as confirmed by the license attached with the open access data.