CPARI: a novel approach combining cell partitioning with absolute and relative imputation to address dropout in single-cell RNA-seq data

Abstract

A key challenge in analyzing single-cell RNA sequencing data is the large number of false zeros, known as “dropout zeros”, which are caused by technical limitations such as shallow sequencing depth or inefficient mRNA capture. To address this challenge, we propose a novel imputation model called CPARI, which combines cell partitioning with our designed absolute and relative imputation methods. Initially, CPARI employs a new approach to select highly variable genes and constructs an average consensus matrix using C-mean fuzzy clustering-based blockchain technology to obtain results at different resolutions. Hierarchical clustering is then applied to further refine these blocks, resulting in well-defined cellular partitions. Subsequently, CPARI identifies dropout events and determines the imputation positions of these identified zeros. An autoencoder is trained within each cellular block to learn gene features and reconstruct data. Our uniquely defined absolute imputation technique is first applied to the identified positions, followed by our relative imputation technique to address remaining dropout zeros, ensuring that both global consistency and local variation are maintained. Through comprehensive analyses conducted on simulated and real scRNA-seq datasets, including quantitative assessment, differential expression analysis, cell clustering, cell trajectory inference, robustness evaluation, and large-scale data imputation, CPARI demonstrates superior performance compared to 12 other art-of-state imputation models. Additionally, ablation experiments further confirm the significance and necessity of both the cell partitioning and relative imputation components of CPARI. Notably, CPARI as a new denoising approach could distinguish between real biological zeros and dropout zeros and minimize false positives, and maximize the accuracy of imputation.

Introduction

Single-cell RNA sequencing (scRNA-seq) technology represents a powerful tool for researchers, offering a profound insight into the complexity of cell biology, disease occurrence, and developmental processes at the individual cell level. This technology overcomes the limitations inherent in traditional whole-tissue block RNA (bulk RNA) based sequencing, allowing for the resolution of cellular heterogeneity and facilitating the detection of gene expression patterns at single-cell resolution. This capability empowers researchers to discern tissue states with unprecedented precision, encompassing cell occupancy, cell-specific gene expression, and beyond. Despite the growing prominence of scRNA-seq technology in diverse biological fields, such as embryonic development and neuronal diversity [1, 2], the number of genes detected per cell remains constrained by technical constraints [3]. During sequencing experiments, the minute mRNA content within individual cells undergoes reverse transcription to cDNA, resulting in substantial mRNA loss and subsequent cDNA amplification. Consequently, technical factors, including amplification bias and a low RNA capture rate, result in the emergence of zero values within scRNA-seq data, commonly referred to as “dropout” events. These events signify the failure to detect the genuine expression of transcripts in certain cells during the sequencing process [4, 5]. And these zeros called “dropout zeros” can impact cell clustering, differential gene expression analysis, and inference of pseudo-temporal trajectories [6, 7]. Therefore, it is necessary to develop effective algorithms to identify dropout events within scRNA-seq data, thereby mitigating their adverse effects on downstream analyses.

In recent years, scholars have developed various algorithms aimed at addressing the dropout events in expression matrices within scRNA-seq data. These methods can be broadly categorized into four groups. The first category is based on modeling the expression value of each gene in each cell as a random variable, assumed to conform to a specific distribution model. Subsequently, the parameters of these distributions are estimated, often utilizing internal or external information, to facilitate imputation. For example, VIPER [8] assumes a zero-inflated Poisson distribution for gene expression levels, employing non-negative sparse regression and expectation-maximization (EM) algorithms for imputation. bayNorm [9] and SAVER [10] assume a Poisson-Gamma distribution for gene expression levels. While bayNorm employs an empirical Bayesian method for imputation, SAVER employs penalized Poisson LASSO regression. TsImpute [11] proposes a two-step imputation method to impute scRNA-seq data (ZINB imputation and IDW imputation). Despite their effectiveness, these model-based approaches lack consensus and may not be universally applicable to all datasets.

The second category comprises methods that utilize smoothing techniques by leveraging information from similar cells for imputation (smoothing model). For example, scImpute [12] utilizes cell similarity to impute values using non-negative least squares regression, sparse regression models, and EM algorithms. MAGIC [13] spreads data between similar cells using Markov transfer matrices for imputation. To distinguish dropout and real biological zeros, scRecover [14] employs the Zero-Inflated Negative Binomial (ZINB) model for dropout probability estimation of each gene and accumulation curves for prediction of dropout number in each cell. However, these smoothing-based methods typically require prior clustering of data, which can be challenging due to a lack of a priori information such as the number of clusters.

The third category involves methods based on the matrix factorization (matrix factorization model). These methods treat the imputation of dropout events as a low-rank matrix completion problem. For example, ALRA [15] obtains a low-rank approximation of the observed gene expression matrix through singular vector decomposition and imputes values by setting thresholds for gene expression entries. Nevertheless, these methods rely on the low-rank assumption of matrix, and many exhibit high computational complexity.

The fourth category encompasses methods based on deep learning to capture nonlinear relationships using nonlinear relationships for the imputation of dropout events (deep learning model). For example, DeepImpute [16] employs an autoencoder to compress expression matrices containing dropout events into a potentially low-dimensional space, corrects them in this space, and reconstructs the expression matrices using a decoder. DCA [17] extends this approach by incorporating a negative binomial distribution model for imputation. GE-Impute [18] utilizes graph embedding, specifically cellular graph, and biased random wandering for imputation. CL–Impute [19] proposes an approach (Contrastive Learning–based Impute) model for estimating missing genes without relying on preconstructed cell relationships.

Among the aforementioned methods, only scImpute, VIPER, scRecover, and TsImpute have the capability to distinguish between real biological zeros and dropout zeros [20]. However, none of these methods are based on deep learning models, which may limit their ability to fully capture data characteristics. In contrast, autoencoders, a fundamental component of deep learning, offer a promising solution for this challenge [21]. Their unsupervised feature learning and data reconstruction capabilities, combined with high computational efficiency, make them well-suited for scRNA-seq data imputation. Although TsImpute addresses the issue of insufficient imputation, it fails to account for local variations between cells. Consequently, it may struggle to capture subtle differences within cells, potentially compromising the accuracy of data analysis.

To overcome these limitations, we propose a novel imputation model, CPARI, which integrates cell partitioning with specifically designed absolute and relative imputation. CPARI not only leverages smoothing techniques and deep learning models but also accurately identifies dropout zeros. CPARI initially employs a refined approach to select highly variable genes and constructs an average consensus matrix using C-mean fuzzy clustering-based blockchain technology to obtain results at various resolutions. Hierarchical clustering is then used to identify distinct cellular blocks. Within each cellular block, CPARI trains an autoencoder to learn gene features and reconstruct data, focusing on local cell populations. Our uniquely defined absolute imputation technique is first applied to identified dropout positions, followed by relative imputation to address any remaining zeros. This approach ensures that both global consistency and local variation are preserved. Furthermore, by using cell relationship matrices to focus on local changes between cells, relative imputation captures subtle differences within cells, thereby improving the accuracy of predictions relative to the true values. Through comprehensive analyses on simulated and real scRNA-seq datasets, CPARI demonstrates superior performance compared to 12 other imputation models. It facilitates single-cell differential expression analysis, enhances unsupervised clustering performance, and improves the accuracy of inferred cell trajectories. Notably, CPARI effectively identifies dropout zeros and real biological zeros, recovers expression data, and preserves gene-to-gene and cell-to-cell consistency. Additionally, CPARI demonstrates strong robustness and is highly suitable for large-scale data imputation.

Materials and methods

Framework of CPARI

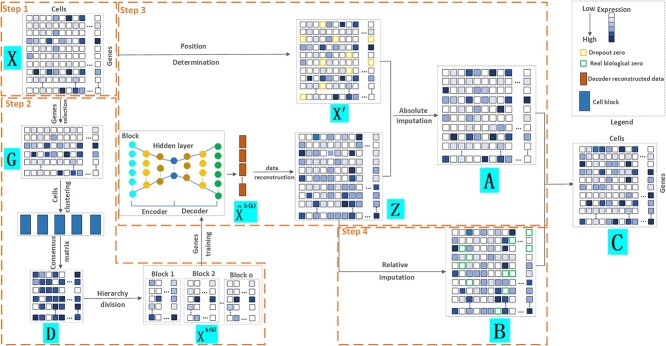
Our proposed model, CPARI, utilizes a block autoencoder architecture, integrating both cellular similarity metrics and gene-specific features to discern and address dropout events within scRNA-seq data (see Fig. 1). CPARI framework encompasses four primary steps: (i) data preprocessing and normalization, (ii) cell partitioning, (iii) absolute imputation, and (iv) relative imputation.

Figure 1.

Step-by-step workflow of CPARI. Step 1, the original count matrix is normalized to produce matrix 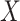. Step 2, cells are partitioned by selecting the highly variable gene matrix 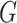, constructing a consensus matrix 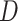from clustering results at various resolutions, and deriving the block matrix 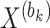. Step 3, absolute imputation is performed by identifying imputation locations to generate matrix 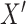. An autoencoder is trained within each block to obtain the reconstructed matrix 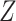, from which the imputed result 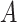is derived. Step 4, relative imputation is conducted by analyzing the correlation of the reconstructed matrix to produce matrix 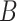. The final imputation matrix 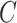is constructed by integrating the results from both relative and absolute imputation.

Preprocessing and normalization

Prior to imputation, the original scRNA-seq dataset undergoes rigorous preprocessing to ensure data quality and consistency. This preprocessing includes quality control, filtering, and normalization. As part of the preparation for the cell partitioning step, genes expressed in fewer than 3 cells and cells expressing fewer than 200 genes are excluded from further analysis. Subsequently, each gene’s expression level is normalized by dividing it by the total expression of the respective cell. The normalized expression values are then scaled by a factor of 1000 and logarithmically transformed, with the addition of a pseudo-count of 1. The “LogNormalize” method within the Seurat v4.3 software package [22] needs to be employed for the absolute imputation step, with a scale factor of 10000 to fine-tune the normalization process and results.

Cell partitioning

Highly variable gene matrix construction

Cell partitioning begins with the processing of original scRNA-seq data, which often contains missing values. Therefore, direct utilization of the original data for cell partitioning is not feasible. The initial step involves the identification of highly variable genes by computing the mean expression level of each gene across all cells:

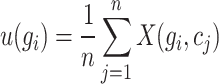(1)

where 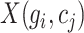represents the original expression value of gene 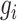in cell 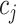within the original single-cell data matrix X (where 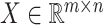, m represents the number of genes, and n represents the number of cells). The original single-cell data matrix is subsequently divided into 20 uniformly sized groups based on 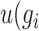). Furthermore, the Fano factor [23] of each gene within each group is standardized as follows:

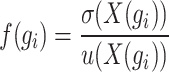(2)

where 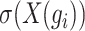represents the variance of the expression value of gene 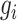across all cells, and 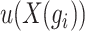represents the average expression level of gene 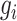across all cells. Highly variable genes are selected based on the criterion that 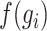is greater than 0.05 and 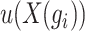within the range [0.01,3.5]. The resulting highly variable gene matrix is denoted as 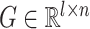, where 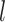represents the number of highly variable genes.

Average consensus matrix construction

The subsequent step in the partitioning process involves transforming the highly variable gene matrix G into an average consensus matrix. Specifically, due to a lack of a priori information such as the number of clusters, we applied C-mean fuzzy clustering based blockchain technology [24] to matrix G to obtain cell labels at various resolutions, with the optimal value set to 5.

To enhance the robustness and consistency of these cell labels across resolutions, a consistency consensus matrix, denoted by 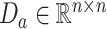, is constructed for each resolution level 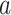, where 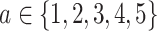. Each element 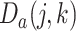within this matrix represents the number of times cell 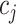and cell 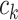are clustered into the same category. Specifically:

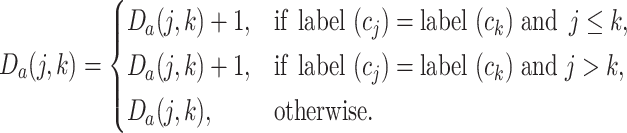(3)

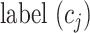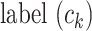where and represent the cluster assignments for cell 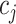and cell 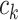at resolution level .

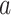Finally, to obtain a comprehensive view of cell co-clustering behavior across all resolutions, an average consensus matrix, denoted by 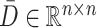, is calculated by averaging the corresponding entries across all consistency consensus matrices:

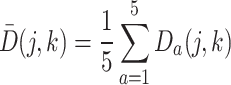(4)

Block count calculation

In the final step of partitioning, the original matrix 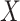is divided into 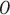subsets along the column direction, with each subset referred to as a block. To determine the optimal value of 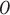, we first employed singular value decomposition (SVD) for :

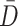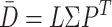(5)

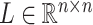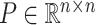where and represent orthogonal matrices capturing the spatial structure of the data, and 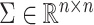represents a diagonal matrix whose elements on the diagonal represent the singular values of the matrix 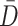. We retained the first 30 singular values for the cell partitioning, and the value of 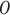is then identified as the smallest integer satisfying the following condition:

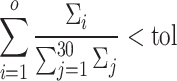(6)

where 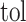represents a predefined threshold value. 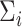represents the 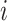th value of the diagonal elements of 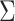, listed in descending order.

Similarity assessment

To assess the fidelity of the cell partitioning process, the cophenetic correlation coefficient [25, 26] is employed. As shown in Supplementary Table S1, the cophenetic correlation coefficients calculated on both the dropout and complete datasets closely approach 1. This finding suggests a high degree of similarity between the partitioned data and the original single-cell data, validating its suitability for imputation purposes.

Absolute imputation

Imputation position determination

A block obtained from cell partitioning is denoted as 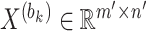( 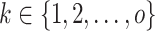), where 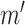denotes the number of genes within the block and 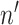denotes the number of cells within the block. The dropout rate 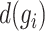and the coefficient of variation 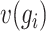of each gene within the block are calculated as follows:

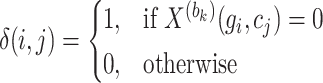(7)

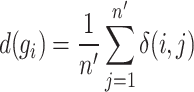(8)

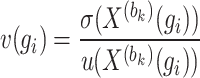(9)

where 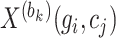represents the expression value of gene 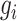in cell 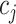within the 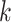th block 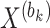. Vector 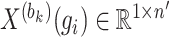represents the expression values of gene 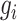across all cells within the 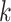th block.

Imputation process

Genes characterized by a greater 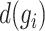and smaller 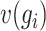are deemed more susceptible to the effects of dropout events. A curated indexed collection, denoted as 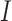, is formulated to encompass such genes as follows:

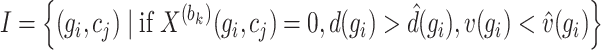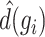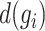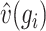where denotes the median of , and denotes the median of 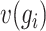. The expression value of 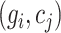in set 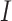is identified as the dropout zero. These dropout zeros in the original single-cell data matrix 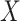are marked with -1. Consequently, a resulting matrix, denoted as 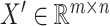, is constructed, with its elements defined as follows:

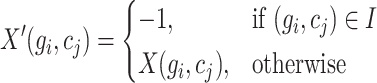(10)

where 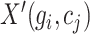represents any element within the matrix 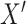. This strategy fully ensures the preservation of non-zero values in the original single-cell data matrix possible, thereby mitigating undue bias. An autoencoder, consisting of an encoder and a decoder, is employed to reconstruct gene features. The encoder comprises three fully connected layers and utilizes rectified linear units (ReLU) as activation functions to map the input data to a low-dimensional latent space. Specifically, the output 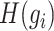of the encoder is computed as follows:

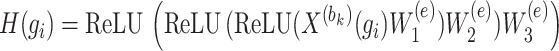(11)

where 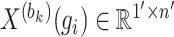represents the row vector within matrix 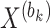relating to gene 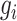, 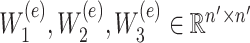denote the weight matrices of the three fully connected layers in the encoder. Subsequently, the decoder also consists of three fully connected layers to reconstruct the representation back to the original input space. The output 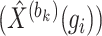of the decoder is calculated as follows:

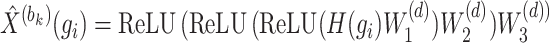(12)

where vector 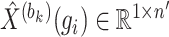represents the reconstructed expression values of gene 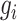across all cells within a block, 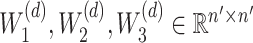represent the weight matrices of the three fully connected layers in the decoder.

Autoencoder model training

To train the autoencoder model, the backpropagation algorithm is employed. The training objective is to optimize a loss function which consists of two parts: a reconstruction error term and a regularization term. The reconstruction error term measures the difference between the data (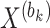) and the decoder-reconstructed data (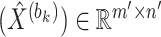), using the squared Euclidean distance as the metric. The regularization term controls the model complexity to prevent overfitting. The specific definition of the loss function is as follows:

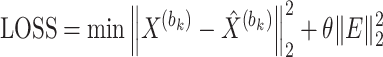(13)

where 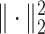denotes the squared Euclidean distance, 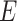is the regularization term, and 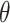is the regularization parameter used to balance the weight between the reconstruction error and the regularization term.

Throughout the training process, an Adam optimizer is employed to adjust the model parameters with a learning rate set at 0.0001, iterated until a predefined number of epochs is attained. Optimal model parameters are retained during training. Subsequently, upon training all blocks, the final reconstruction matrix 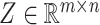is constructed as:

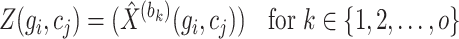(14)

where 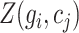represents an element in matrix 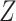corresponding to the reconstructed expression value of gene 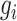in cell 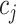within the relevant block 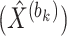. Finally, a matrix 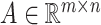is generated, wherein each element is defined as:

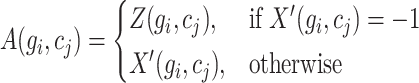(15)

Relative imputation

Absolute imputation alone cannot guarantee the identification of all dropout zero values. Therefore, relative imputation performs secondary imputation on dropout zero values that remain unrecognized after the initial process.

Correlation matrix construction

We conducted principal components analysis (PCA) to reduce dimensionality on the reconstruction matrix 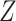, yielding the dimensionality reduction matrix 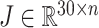, where 30 denotes the number of principal components. Subsequently, to compute the correlation coefficient for each cell, we derive the correlation matrix :

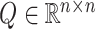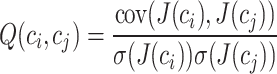(16)

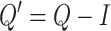(17)

where 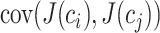represents the covariance between column 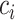and column 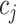in matrix 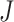. The diagonal elements of matrix 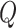are set to 1. 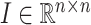represents the unit matrix.

To obtain the top 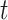correlated columns with the current column, each row in matrix 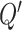retains only the 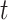largest values, where 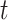is set to the optimal value of 4. The column index values of the 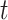largest values in each row form the matrix .

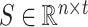Reconstructed matrix repair

By examining whether the elements corresponding to the top 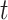correlated columns in matrix 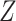are zero, the matrix 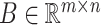was derived, with its elements defined as follows:

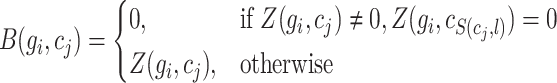(18)

where 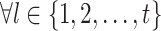, 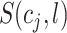denotes the index value of a particular cell within the top 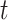correlated cells with cell .

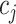Final imputation

The remaining dropout zeros after absolute imputation can be imputed according to matrix 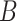to obtain the final imputation matrix :

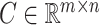(19)

In conclusion, accurate imputation position determination is crucial to avoid imputing non-zero or real zero values. Following the identification of imputation positions, data reconstruction is performed using an autoencoder within each block. To further enhance the reliability of the reconstructed data, relative imputation is employed. Relative imputation not only addresses the remaining dropout zeros from absolute imputation but also leverages correlation analysis to distinguish between real biological zeros and false positives, thereby minimizing the occurrence of false positives.

Datasets

The real dataset contains inherent missing values, rendering it incomplete and precluding a comprehensive evaluation of model performance. To address the limitations posed by the presence of missing values in the real dataset, we simulated complete datasets without any missing values. Therefore, the datasets used for our experiments contain two parts.

Simulated datasets

Inspired by Bubble [27], we utilized Splatter R package [28] to generate two distinct types of datasets using varied random seeds, as outlined in Table 1. Type 1 comprises Dataset1, Dataset2, and Dataset3, each consisting of 3000 cells and 1500 genes, segmented into 3 subtypes, and without any missing values. Subsequently, we identified differentially expressed genes within each subtype and introduced two constraints (mean offset and variance change) to the expressions of these genes [33]. After simulating the complete Datasets (Dataset1, Dataset2, and Dataset3), we proceeded to generate corresponding dropout datasets for each. These dropout datasets (Dataset1^*, Dataset2^*, and Dataset3^*) mimicked the effects of missing data by randomly removing entries at predefined rates. The dropout rates utilized were 30%, 40%, 50%, 65%, 80%, and 90%. Type 2 comprises dataset4, dataset5, dataset6, which closely resemble real datasets in terms of gene and cell counts. Each dataset contains 4000 cells and 10000 genes, categorized into 8 subtypes, is devoid of any missing values. For all complete datasets of type 2, we generated corresponding dropout datasets to simulate the effects of missing data by randomly removing entries at pre-defined rates of 80%.

Table 1.

Summary of the simulated scRNA-seq datasets

Dataset name	Cell type	Subtype number	Gene number	Cell number	Source
Dataset 1, Dataset 2, Dataset 3	Type1	3	1500	3000	Bubble [27]
Dataset 4, Dataset 5, Dataset 6	Type2	8	10000	4000	Splatter [28]

Real datasets

Four real datasets originating from four different sequencing platforms, with relevant information detailed in Table 2. These datasets encompass a diverse range of cell types and biological processes, having been generated using well-established and validated sequencing platforms. Such rigorous methodology ensures the accuracy and reliability of the data.

Table 2.

Summary of the real scRNA-seq datasets

Dataset name	Cell type	Subtype number	Gene number	Cell number	Sequencing platform
PBMC [29]	Peripheral blood mononuclear cells	8	16449	4271	10X Genomics
Worm neuron cells [30]	Worm neuronal cells	10	13488	4186	Sci-RNA-seq
Mouse bladder cells [31]	Mouse bladder cells	16	20670	2746	Microwell-seq
LPS [32]	Various cells	4	2047	306	Array

Results

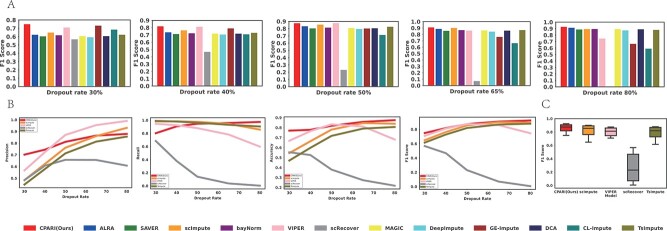
We conducted a comparative analysis of CPARI against 12 state-of-the-art imputation methods, which include ALRA [15], SAVER [10], scImpute [12], bayNorm [9], VIPER [8], scRecover [14], MAGIC [13], DeepImpute [16], GE-Impute [18], DCA [17], TsImpute [11], and CL-Impute [19]. SAVER, VIPER, bayNorm, and TsImpute belong to the category of distributional models, while ALRA operates as a matrix factorization model. MAGIC, scImpute, and scRecover are classified as smoothing models, and DCA, GE-Impute, DeepImpute, and CL-Impute are categorized as deep learning models. In the comparative analysis, a model denoted as “No-Imputation” is referenced, wherein diverse evaluation metrics are directly calculated on simulated datasets that include both complete and dropout datasets without using any imputation methods. Specific evaluation metrics include Standard F1 Score, Correlation (gene), Correlation (cell), Error, CMD (gene), CMD (cell), Modified F1 Score [34, 35], ARI [36, 37], NMI [38], POS [39–42]. For detailed metrics calculations, please refer to the Supplementary evaluation metrics.

CPARI effectively identifies dropout zeros and real biological zeros

As shown in Supplementary Table S2 and Fig. 2, CPARI consistently achieves the highest standard F1 scores across three simulated dropout datasets with identical dropout rates. As illustrated in Fig. 2A, for simulated dropout datasets (Dataset1^*, Dataset2^*, and Dataset3^*), CPARI consistently achieves the highest standard F1 scores, indicating superior efficacy in identifying both dropout zeros and real biological zeros. At the lowest dropout rate, CPARI, GE-impute, and VIPER significantly outperform other imputation models. As the rate of missing data increases, the performance of most imputation models gradually improves. However, scImpute, VIPER, GE-Impute, and scRecover exhibit a decline in performance, with scRecover’s performance approaching zero at the highest rate of missing data. Fig. 2B demonstrates that among models capable of identifying dropout zeros and real biological zeros (CPARI, ScImpute, VIPER, scRecover, and TsImpute), CPARI not only consistently improves but also outperforms other models across various dropout rates. Even at high dropout rates, CPARI maintains a clear advantage over other methods. Typically, as the missing rate increases, performance tends to decline due to reduced information. However, the F1 score, which focuses on the ratio of zeros and non-zeros, can improve at higher missing rates. This is because with more missing data, there are more opportunities to correctly impute “dropout events” (TP). Both CPARI and TsImpute address insufficient imputation, but CPARI’s superior performance stems from its selection of highly variable genes. This strategy effectively captures critical information, leading to improved F1 scores. In additional, the model’s accuracy and recall gradually increase with higher dropout rates, while precision remains relatively stable. This suggests that CPARI effectively captures crucial information by selecting highly variable genes, and its relative imputation method effectively addresses remaining dropout zeros and minimizes false positives, even under challenging conditions. As depicted in Fig. 2C, the robustness of CPARI to varying levels of missing data is further evident in the minimal fluctuation of its standard F1 score across different datasets. Supplementary Table S3 and Supplementary Fig. S1 confirm CPARI’s superior performance, even at 90% dropout rate for datasets (Dataset1^*, Dataset2^*, and Dataset3^*) and 80% dropout rate for larger datasets (Dataset4^*, Dataset5^*, and Dataset6^*).

Figure 2.

Evaluation of imputation methods for dropout zero identification. (A) Bar plots illustrating the imputation F1 score for various imputation methods across different dropout levels. (B) Line graphs depicting the trends of precision, recall, accuracy, and F1 score for different imputation methods under each dropout level. (C) Box plots representing the distribution of F1 scores for imputation methods across different dropout datasets.

These analytical results demonstrate that CPARI represents a robust and effective imputation model for scRNA-seq data, capable of handling high levels of missing data while accurately identifying dropout zeros and preserving the integrity of biological information.

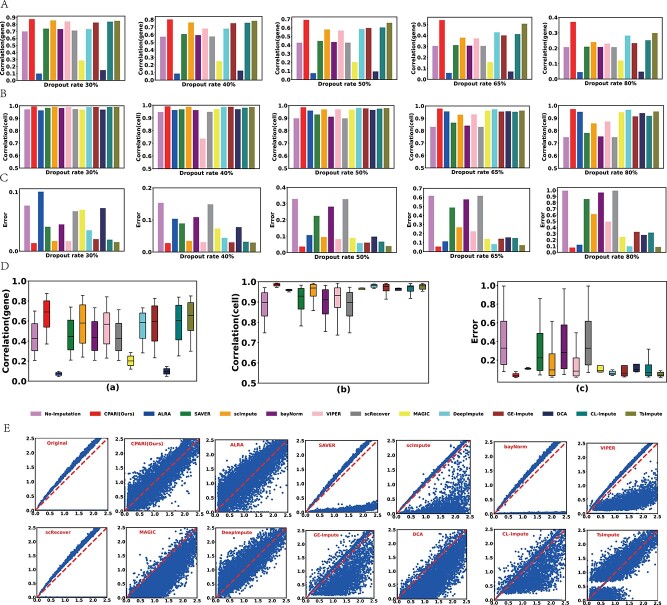
CPARI effectively recovers expression data

To assess the model’s ability to recover data, Correlation(gene), Correlation(cell), and Error were calculated on both simulated complete datasets and their corresponding dropout datasets. The average of each metric across dropout datasets with the same dropout rate was taken to obtain the final evaluation results.

CPARI effectively recovers gene expression data

As demonstrated in Fig. 3A and Supplementary Table S4, for simulated dropout datasets (Dataset1^*, Dataset2^*, and Dataset3^*), our CPARI consistently achieves the highest Correlation(gene) values compared to other models across different dropout rates. This indicates that CPARI performs best in recovering inter-gene correlation coefficients, possibly due to its effective reconstruction of genetic features during the imputation process. Compared to the No-Imputation model, CPARI exhibits performance improvements of 25%, 39%, 61%, 77%, and 79% at 30%, 40%, 50%, 65%, and 80% dropout rates, respectively. This suggests that CPARI’s data reconstruction capabilities effectively capture the underlying relationships between genes, even in the presence of extensive missing data. Conversely, ALRA, MAGIC, and DCA show Correlation(gene) values lower than the No-Imputation model, demonstrating their ineffectiveness in recovering inter-gene correlation coefficients. Supplementary Table S5 and Supplementary Fig. S2 further confirm CPARI’s superior performance, even at a 90% dropout rate for datasets (Dataset1^*, Dataset2^*, and Dataset3^*) and an 80% dropout rate for larger datasets (Dataset4^*, Dataset5^*, and Dataset6^*). These results underscore CPARI’s ability to accurately recover inter-gene correlation coefficients under high dropout rates and with relatively large datasets.

Figure 3.

Evaluation of imputation methods for data recovery. (A) Bar plots illustrating the mean correlation between the imputed and complete datasets for each gene, calculated using Pearson correlation coefficient (PCC). (B) Bar plots depicting the mean correlation between the imputed and complete datasets for each cell, calculated using PCC. (C) Bar plots representing the imputation error between the imputed and complete datasets. (D) Box plots showing the distribution of gene-level correlation, cell-level correlation, and imputation error for different imputation methods across various dropout datasets. (E) Scatter plots demonstrating the relationship between true and predicted values (log-transformed) for each gene and cell. The red baseline represents perfect alignment between the true and predicted values.

CPARI effectively recovers cell expression data

As shown in Fig. 3B and Supplementary Table S6, analysis of simulated dropout datasets (Dataset1^*, Dataset2^*, and Dataset3^*) reveals that nearly all imputation methods yield Correlation(cell) values exceeding those of the No-Imputation model. Notably, CPARI consistently achieves the highest Correlation(cell) values across various dropout rates, indicating its superior performance in recovering inter-cell correlation coefficients. This might be attributed to CPARI’s selection of highly variable gene pairs to partition cells, thereby effectively preserving inter-cellular correlations. Compared to the No-Imputation model, CPARI exhibits performance improvements of 2%, 4%, 9%, 17%, and 29% across different dropout rates. This indicates that CPARI’s ability to recover inter-cellular correlation coefficients strengthens as the dropout rate increases. At an 80% dropout rate, the advantages of imputation methods like SAVER, bayNorm, and scRecover over the No-Imputation model become less evident, while CPARI’s superiority remains pronounced. Supplementary Table S7 and Supplementary Fig. S3 further confirm CPARI’s exceptional ability to recover inter-cell correlation coefficients, even at a 90% dropout rate for datasets (Dataset1^*, Dataset2^*, and Dataset3^*) and an 80% dropout rate for larger datasets (Dataset4^*, Dataset5^*, and Dataset6^*). These results underscore CPARI’s robustness and effectiveness in preserving the integrity of cellular relationships in scRNA-seq data.

CPARI effectively reduces errors

Fig. 3C and Supplementary Table S8 demonstrate that for Dataset1^*, Dataset2^*, and Dataset3^*, almost all models consistently reduced the Error value compared to the No-Imputation model. However, as the dropout rate increased, CPARI’s Error value remained the lowest, indicating that CPARI can recover data with minimal error. This is likely because CPARI only impute dropout zeros while preserving non-zero values. Compared to the No-Imputation model, CPARI’s Error value decreased by 82%, 82%, 88%, 91%, and 92% at different dropout rates, respectively, indicating that higher dropout rates correspond to smaller errors in data recovery by CPARI. In Fig. 3D, across varying dropout rates in Dataset1^*, Dataset2^*, and Dataset3^*, CPARI consistently outperforms in terms of Correlation(gene), Correlation(cell), and Error metrics, with minimal fluctuations. This highlights CPARI’s robustness and ability to consistently maintain data integrity even under challenging conditions.

CPARI effectively improves imputation accuracy

Fig. 3E presents scatter plots comparing true values (x-axis) to imputed values (y-axis) under an 80% dropout rate. The optimal accuracy baseline is represented by a red dashed line. While no model perfectly aligns with this baseline, likely due to the inherent challenges of accurate recovery at high dropout rates, CPARI exhibits a notable improvement over other methods. The scatter plot for CPARI demonstrates a strong symmetry around the baseline, suggesting its stability and ability to accurately recover the original data distribution. In contrast, other imputation methods, such as bayNorm and scRecover, show limited effectiveness in improving accuracy, as evidenced by their scatter plots that closely resemble the Original (non-imputed) plot. These methods may struggle to restore the original data distribution, potentially leading to decreased accuracy. Among all the models evaluated, only CPARI, DeepImpute, and ALRA exhibit scatter plots that are relatively close to the baseline. This indicates their superior performance in recovering expression data, even under high dropout rates.

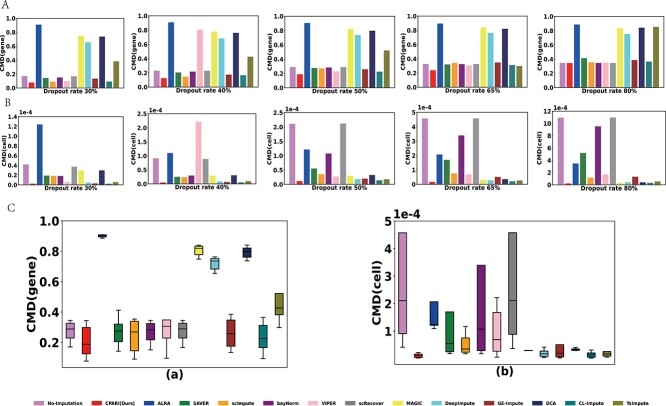
CPARI effectively preserves gene-to-gene and cell-to-cell consistency

Although Correlation (gene) and Correlation (cell) can measure correlations, they do not provide detailed information about the structure of gene–gene correlations and cell–cell correlations. Therefore, to comprehensively evaluate the consistency of gene and cell expressions across two datasets, we employed the CMD(gene) and CMD(cell). Fig. 4A and Fig. 4B demonstrates that across Datasets 1^*, Dataset 2^*, and Dataset 3^*, CPARI consistently achieves the lowest CMD (gene) and CMD (cell) values under varying dropout rates compared to other imputation methods. This indicates that CPARI effectively preserves both gene–gene and cell–cell consistency. Supplementary Table S9 further highlights CPARI’s superior performance in preserving cell-cell consistency. Compared to the No-Imputation model, CPARI’s CMD (cell) values decrease by 94%, 94%, 94%, 96%, and 97% at varying dropout rates, respectively. This trend suggests that CPARI’s ability to strengthen cell-level consistency becomes more pronounced as the dropout rate increases. Additionally, among the different dropout rates, CPARI, MAGIC, DeepImpute, CL-Impute, and TsImpute exhibit similar CMD (cell) values, indicating that their performance in preserving cell-level consistency is comparable. However, as demonstrated in Supplementary Table S10, CPARI uniquely achieves the lowest CMD(gene) values, suggesting its superior performance when considering both gene and cell expression consistency simultaneously. Fig. 4C further illustrates CPARI’s exceptional robustness in CMD (cell) and CMD (gene), with both medians reaching the lowest values. Additionally, Supplementary Tables S11 and S12, along with Supplementary Figs S4 and S5, demonstrate that even at a 90% dropout rate for datasets (Dataset1^*, Dataset2^*, and Dataset3^*) and an 80% dropout rate for larger datasets (Dataset4^*, Dataset5^*, and Dataset6^*), CPARI maintains the lowest CMD values. In summary, these results collectively demonstrate CPARI’s ability to maintain consistency between genes while simultaneously preserving consistency between cells, even under high dropout rates and across datasets of varying sizes.

Figure 4.

Evaluation of imputation methods for preserving consistency. (A) Bar plots illustrating the imputation CMD(gene) for different imputation methods under each dropout level. A lower CMD(gene) value indicates stronger gene-to-gene consistency. (B) Bar plots depicting the imputation CMD(cell) for different imputation methods under each dropout level. A lower CMD(cell) value indicates stronger cell-to-cell consistency. (C) Box plots showing the distribution of CMD(gene), CMD(cell), and imputation error for different imputation methods across various dropout datasets.

CPARI facilitates single-cell differential expression analysis

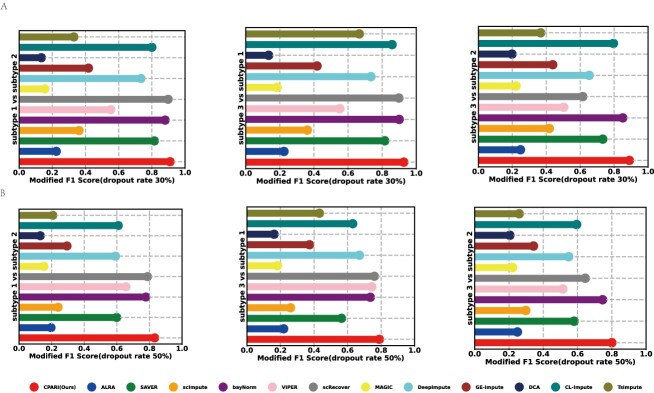
To accurately assess whether CPARI contributes to the differential expression analysis, we calculated the Modified F1 Score. As shown in Fig. 5A and Fig. 5B on the dropout datasets (Dataset1^*, Dataset2^*, and Dataset3^*) with 30% and 50% dropout rates, our CPARI achieves the highest Modified F1 Score for all three cell subtypes compared to other models. This indicates that CPARI is helpful for analyzing cellular differential expression. The Modified F1 Scores for other dropout rates in Dataset1^*, Dataset2^*, and Dataset3^* are presented in Supplementary Figs S6–S8.

Figure 5.

Evaluation of imputation methods for single-cell differential expression analysis. (A) Lollipop charts illustrating the modified F1 scores for the three cell types relative to each other at a 30% dropout rate. (B) Lollipop charts depicting the modified F1 scores for the three cell types relative to each other at a 50% dropout rate.

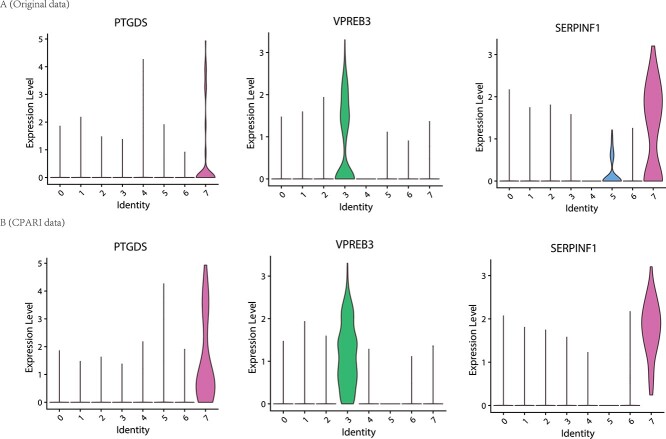
To investigate whether the CPARI model can enhance cell type annotation by augmenting the expression of cell type marker genes, we used the Seurat package to identify the expression of several key marker genes. As shown in Fig. 6A, in the original dataset (PBMC dataset [29]), PTGDS was identified as a marker gene in cluster CD19 and VPREB3 in cluster CD34, but their gene expression levels were not significant. However, after CPARI imputation, these genes were stably expressed in their respective clusters as shown in Fig. 6B. Additionally, due to missing data in the original dataset, SERPINF was minimally expressed in cluster 4T but highly expressed in cluster CD19 (Fig. 6A). After CPARI imputation, the SERPINF marker gene was stably and highly expressed in cluster CD19 (Fig. 6B).

Figure 6.

Evaluation of imputation methods for mark genes in specific subtypes. (A) Violin plots illustrating the distribution of expression levels for marked genes within each subtype in the original PBMC data. (B) Violin plots depicting the distribution of expression levels for marked genes within each subtype in the CPARI-imputed PBMC data.

CPARI effectively improves unsupervised clustering performance

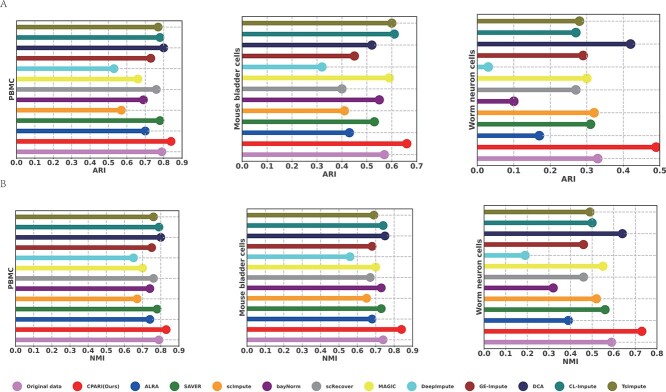
To evaluate the performance of different imputation methods, a set of datasets with large differences in clustering performance was selected, including the PBMC dataset (ARI=0.79), Mouse bladder cells dataset (ARI=0.57), and Worm neuron cells dataset (ARI=0.33).

CPARI effectively maintains clustering consistency

The clusters specified by scDSC [43] were clustered using k-means on these datasets, and the clustering results are shown in Fig. 7A and Fig. 7B and Supplementary Table S13. In the PBMC dataset, the ARI and NMI values for SAVER, scRecover, DCA, CL-Impute, and TsImpute are on par with those of the original data. This suggests that when the original data are of high quality, the impact of these imputation methods is minimal. However, our CPARI has the highest ARI and NMI values, which are 6% and 5% higher than those of the original data, respectively. This indicates that CPARI’s imputation results can further improve the quality of the data and the accuracy of the analysis. On the Mouse bladder cells dataset, although CL-Impute and TsImpute show some improvements in clustering performance over the original data, the gains are relatively small. In contrast, CPARI has a more pronounced advantage in imputation effectiveness. On the Worm neuron cells dataset, CPARI still maintains the highest ARI and NMI values, which are 24% and 42% higher than those of the No-Imputation model, respectively. Comprehensive results from these three datasets show that CPARI’s imputation ability can significantly improve the clustering performance of data regardless of the quality of the original data, demonstrating good robustness of CPARI.

Figure 7.

Evaluation of imputation methods for clustering consistency. To evaluate the performance of different imputation methods, a set of datasets with significant variations in clustering performance was selected, including the PBMC dataset (ARI = 0.79), the Mouse bladder cells dataset (ARI = 0.57), and the Worm neuron cells dataset (ARI = 0.33). (A) ARI for three types of widely varying datasets under different imputation methods. (B) NMI for three types of widely varying datasets under different imputation methods.

CPARI effectively enhances clustering visualization

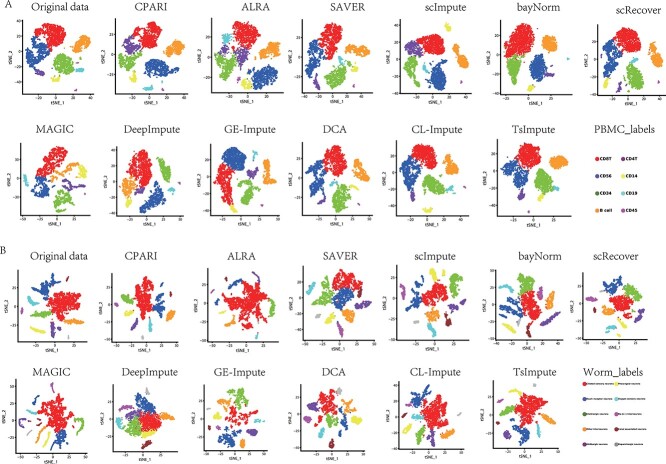
Fig. 8A shows t-SNE [44, 45] visualized clustering results on the PBMC dataset. Each subplot represents a different imputation model, with colors indicating different cell clusters. CPARI (ours), scImpute, and MAGIC models demonstrated clearer separation between clusters compared to the original data, where some clusters overlapped or were scattered. Fig. 8B shows t-SNE clustering results on the Worm neuron cells dataset. CPARI (ours), scImpute, and MAGIC models demonstrate superior performance, exhibiting high cluster separation and clear boundaries. In contrast, the original data show less distinct separation, with certain neuron types (such as red and orange) intermixed. Supplementary Fig. S9 demonstrates that even with an increase to 16 subtypes in the Mouse bladder cells dataset, CPARI (ours)remains the most effective in separating different neuron subtypes. These findings collectively suggest that CPARI is a valuable tool for improving the clustering and visualization of scRNA-seq data. By effectively imputing missing values, CPARI enables more accurate identification of cell subtypes and relationships.

Figure 8.

Visualization of cluster identification. Each point represents a cell, colored according to its assigned cluster label. This visualization provides insights into the grouping of cells and the separation between different clusters. (A) Visualization of the PBMC dataset. (B) Visualization of the Worm neuron cells dataset.

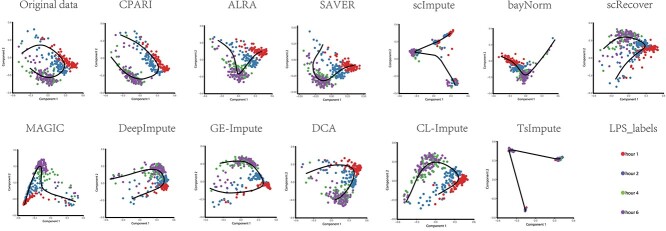
CPARI effectively improves cell trajectory inference

Fig. 9 shows the trajectory inference results using the SCORPIUS tool on imputed data from various imputation methods on the LPS dataset. Each subplot represents a different imputation model, with colored dots indicating different time points (red for hour 1, blue for hour 2, green for hour 4, and purple for hour 6). The inferred trajectories are depicted as lines connecting the cells. Detailed result analysis for each imputation model, as shown in the Supplementary Table S14. The original (non-imputed) data exhibit noisy clustering and less defined trajectories. Our CPARI model, along with DeepImpute and bayNorm, demonstrates superior performance in capturing the temporal progression of cells. The inferred trajectories are smooth, well-defined, and closely aligned with the known time points. In contrast, scImpute and TsImpute, despite producing seemingly plausible trajectories, exhibit inaccuracies in capturing the true temporal ordering.

Figure 9.

Evaluation of visualization of trajectory inference with SCORPIUS. This figure demonstrates the results of trajectory inference using the SCORPIUS tool on imputed data from various imputation methods applied to the LPS dataset. Each subplot represents a different imputation model, with colored dots indicating the time points (red for hour 1, blue for hour 2, green for hour 4, and purple for hour 6).

To assess CPARI’s efficacy in facilitating cell trajectory analysis, we employed the Pseudo-Time Ordering Score (POS) metric, which evaluates the consistency between inferred cell pseudo-time and actual time points. As shown in Supplementary Table S15 and Supplementary Fig. S10, CPARI (ours) achieved the highest POS index relative to other baseline methods. This indicates that the pseudo-temporal trajectories reconstructed by CPARI exhibit greater temporal consistency with the true cellular ordering. These findings underscore the importance of imputation in improving the quality of cell trajectory inference. By effectively addressing missing values, CPARI enables more accurate identification of cellular progression over time, providing valuable insights into dynamic biological processes.

Robustness evaluation

To rigorously evaluate the robustness of the CPARI model, we refrained from randomly converting non-zero values to zeros in an uncontrolled manner, as this approach could potentially disrupt inherent data patterns. Recognizing that the ZINB distribution has been widely effective in describing gene distribution across cells in scRNA-seq data [46–49], we conducted extensive simulations using the splatter tool which generates synthetic scRNA-seq data with realistic characteristics [50]. We performed 100 independent simulations and reported the mean and standard deviation of key performance metrics. The results, depicted in Supplementary Fig. S12, reveal minimal fluctuations in the gene correlation coefficient (Correlation(gene)), cell correlation coefficient (Correlation(cell)), and the ability to identify dropout zeros (F1 Score). These findings indicate that CPARI is not overly sensitive to variations in the simulated data and maintains consistent performance across different scenarios. This stability in performance suggests that CPARI can reliably handle the inherent variability and complexity of scRNA-seq data.

Scalability and performance in large-scale data imputation

The analysis of large-scale scRNA-seq data has emerged as a significant trend in single-cell genomics. This trend is exemplified by large-scale scRNA-seq clustering methodologies [51] and the development of foundational models for large-scale single-cell data analysis [52]. To evaluate CPARI’s performance on large-scale scRNA-seq data, we used a subset of the mouse visual cortex cell data from Hrvatin et al. [53], comprising between 10 000 and 50 000 cells, each characterized by 19 155 genes. We performed the imputations three times and measured the runtime and memory usage on a 16-core machine with 30 GB of memory. The results, depicted in Supplementary Fig. S14, we found that several competing imputation models, including TsImpute, scImpute, scRecover, VIPER, bayNorm, and CL-Impute, struggled with scalability. They either failed to return results within 24 hours for the 10 000-cell experiment or exceeded the memory limit. In contrast, CPARI, along with DeepImpute, MAGIC, and DCA, demonstrated excellent computational efficiency and scalability, with runtimes within the same order of magnitude. Notably, only CPARI was able to distinguish between real biological zeros and dropout zeros.

Additionally, for a comprehensive assessment, we employed the Splatter [28] simulated dataset, which contains 20 000 genes and 30 000 cells. Clustering visualization results (Supplementary Fig. S13) revealed that CPARI and DeepImpute effectively clustered the data while maintaining strong cluster separation, even in the presence of missing data. GE-Impute, on the other hand, exhibited poor performance in clustering. Correlation analysis (Supplementary Table S16) further confirmed CPARI’s superiority. CPARI demonstrated the highest correlation with the original data, both in terms of cell correlations (Correlation(cell)) and gene correlations (Correlation(gene)). This indicates its ability to accurately recover the underlying biological structure of the data.

Overall, these results highlight CPARI’s exceptional performance and scalability in handling large-scale scRNA-seq data, making it a valuable tool for researchers working with complex biological systems.

Ablation study

To validate a series of ablation studies were conducted while maintaining consistency in experimental conditions. To facilitate this investigation, several model variants were introduced, each representing a distinct configuration:

• NBNR (No Cell Partitioning, Relative Imputation): This variant lacks both cell partitioning and relative imputation.

• YBNR (Yes Cell Partitioning, No Relative Imputation): This variant incorporates cell partitioning but excludes relative imputation.

• NBYR (No Cell Partitioning, Yes Relative Imputation): This variant incorporates relative imputation but excludes cell partitioning.

When evaluated on simulated dropout datasets with an 80% dropout rate (Data1^*, Data2^*, Data3^*), CPARI consistently outperformed all three simplified variants across all metrics (Supplementary Fig. S11). This highlights the overall effectiveness of the complete CPARI model. Furthermore, the ablation study revealed the significance of each component:

• Importance of cell partitioning: Comparing NBYR and CPARI demonstrates the additional benefit of cell partitioning. CPARI consistently outperforms NBYR across all metrics, suggesting cell partitioning plays a crucial role in achieving optimal performance.

• Importance of relative imputation: Comparing NBNR and NBYR showcases the benefit of relative imputation. NBYR achieves better results than NBNR, indicating that relative imputation improves performance.

Furthermore, on real datasets, as shown in Supplementary Table S13, CPARI achieved the best NMI and ARI values on three real datasets compared to other methods and CPARI’s variants.

Conclusion

CPARI is a novel imputation model that effectively addresses the challenges posed by dropout events in scRNA-seq data. By combining cell partitioning with strategically designed absolute and relative imputation methods, CPARI preserves the original data’s distance structure, accurately distinguishes between real biological zeros and dropout zeros, and minimizes false positive signals. Before performing absolute imputation, cells are first partitioned, and imputation locations are determined based on the dropout rates and coefficient of variation for each gene, all derived from the global information of the original matrix. Thus, absolute imputation plays the role of handling global information. In contrast, relative imputation relies on the cell relationship matrix and focuses on the most relevant cells, thereby playing the role of handling local information. It is important to note that when applying these two imputation methods, absolute imputation is performed prior to relative imputation. This is because relative imputation specifically targets the remaining dropout zeros left by absolute imputation, without modifying non-zero values. Therefore, they follow a sequential relationship. The autoencoder-based architecture of CPARI not only ensures high computational efficiency but also contributes to the model’s reliability and robustness. Extensive evaluations on diverse simulated and real scRNA-seq datasets demonstrate the superior performance of CPARI compared to existing imputation methods. CPARI significantly improves downstream analyses, including differential expression analysis, clustering, visualization, and cellular trajectory inference. Its strong robustness and suitability for large-scale data imputation make it a valuable tool for researchers working with scRNA-seq data

Key Points

• CPARI is a novel imputation model that leverages cell partitioning and strategically designed absolute and relative imputation methods to address the challenges associated with dropout events in scRNA-seq data.

• CPARI effectively identifies highly variable genes and constructs an average consensus matrix using C-mean fuzzy block methodology. The resulting Cophenetic correlation coefficient approaches 1, indicating a strong preservation of the original data’s distance structure and facilitating the identification of distinct cellular subpopulations.

• CPARI’s absolute imputation method accurately differentiates between dropout zeros and real biological zeros, ensuring the integrity of the imputed data.

• CPARI’s relative imputation method effectively handles the remaining dropout zeros, further enhancing the accuracy and reliability of the imputation process.

Funding

This research was funded by National Natural Science Foundation of China (Grant No. 62166014) with funder of Y.Z., Natural Science Foundation of Guangxi Province (Grant No. 2020GXNSFAA297255) with funder of Y.Z.

Data availability

The 10X PBMC dataset comprises 4271 peripheral blood mononuclear cells from a healthy donor, obtained from the 10X scRNA-seq platform. This dataset was downloaded from the 10X Genomics website. The mouse bladder cells were obtained from the Microwell-seq platform, originating from the Mouse Cell Atlas project. We downloaded the count matrix of all 400 000 single cells sorted by tissues and selected approximately 2186 cells from the bladder tissue for our experimental data. The worm neuron cells were sourced from the sci-RNA-seq platform. We selected a subset of neural cells from the nematode Caenorhabditis elegans at the L2 larval stage and excluded cells labeled as “Unclassified neurons”. This resulted in a dataset of 4186 neural cells for our experiments. The authors used TLR ligands to stimulate mouse primary BMDCs and analyzed gene expression changes using Affymetrix arrays across nine time points (0.5, 1, 2, 4, 6, 8, 12, 16, 24 hours). Various TLR ligands (LPS, pIC, PAM, CpG, GRD) were used to stimulate BMDCs, leading to the LPS dataset consisting of scRNA-seq samples of mouse dendritic cells, with 306 cells collected at 1, 2, 4, and 6 hours. The true labels for these datasets were obtained from their respective references. The datasets were derived from publicly available sources: the PBMC datasets from https://support.10xgenomics.com/single-cell-gene-expression/datasets/2.1.0/pbmc4k, the worm neuron cells from https://cole-trapnell-lab.github.io/worm-rna/docs/, the LPS datasets from https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE17721, the mouse bladder cells from https://figshare.com/s/865e694ad06d5857db4b.

Code availability

Source codes used in our experiments have been deposited at the GitHub repository https://github.com/WyBioGroup/CPARI.