Validating the Influences of Methodological Decisions on Assessing the Spatiotemporal Stability of Speech Movement Sequences Using Children's Speech Data

Abstract

Purpose:

Prior research introduced quantifiable effects of three methodological parameters (number of repetitions, stimulus length, and parsing error) on the spatiotemporal index (STI) using simulated data. Critically, these parameters often vary across studies. In this study, we validate these effects, which were previously only demonstrated via simulation, using children's speech data.

Method:

Kinematic data were collected from 30 typically developing children and 15 children with developmental language disorder, all spanning the ages of 6–8 years. All children repeated the sentence “buy Bobby a puppy” multiple times. Using these data, experiments were designed to mirror the previous simulated experiments as closely as possible to assess the effects of analytic decisions on the STI. Experiment 1 manipulated number of repetitions, Experiment 2 manipulated stimulus length (or the number of movement units in the target phrase), and Experiment 3 manipulated precision of parsing of the articulatory trajectories.

Results:

The findings of all three experiments closely mirror those of the prior simulation. Experiment 1 showed consistent underestimation of STI values from smaller repetition counts consistent with the theoretical model for all three participant groups. Experiment 2 found speech segments containing fewer movements yield lower STI values than longer ones. Finally, Experiment 3 showed even small parsing errors are found to significantly increase measured STI values.

Conclusions:

The results of this study are consistent with the findings of prior simulations in showing that the number of repetitions, length of stimuli, and amount of parsing error can all strongly influence the STI independent of behavioral factors. These results further confirm the importance of closely considering the design of experiments, which employ the STI.

When speech is executed in a repetitive manner, natural and inherent variability becomes evident in the motion characteristics of articulatory movements (Lindblom, 1990). This variability is at least partially attributed to noise in the central nervous system and can be influenced by the ability of a motor action to adapt in response to environmental conditions (Maassen, 2004; van Beers et al., 2002). Understanding and quantifying articulatory stability is a necessary component for expanding current knowledge of typical and impaired speech motor control systems. A widely used method used to measure articulatory stability is the spatiotemporal index (STI; Chu et al., 2020; Kuruvilla-Dugdale & Mefferd, 2017; Smith et al., 1995, 2000; Wisler et al., 2022; Wohlert & Smith, 1998). The STI incorporates both spatial and temporal aspects of motor control over a multimovement trajectory, providing a single index representative of the overall stability of a speaker's articulatory movement sequences (Smith et al., 1995). Higher STI values reflect more variability in both the timing and amplitude of movement sequences, while lower STI values reflect greater consistency with a central motion pattern. Since its establishment, the STI has been utilized to investigate various aspects of speech motor control. Due to the widespread use of the STI as a stability metric, there is substantial variance in the methodologies used for its implementation. The implications of these methodological differences remain poorly understood due to the lack of systematic assessment of their effects on human speech data.

Research on articulator stability has shown that individual differences, including age, and the presence of speech disorders resulting from various etiologies can influence articulator stability. The maturation of speech and language abilities during childhood is associated with an increase in articulatory stability, with the STI decreasing across development in typical individuals (Goffman & Smith, 1999; Smith & Goffman, 1998; Smith & Zelaznik, 2004). Articulatory stability has been shown to decrease later in life (McHenry, 2003; Wohlert & Smith, 1998), with aging adults showing reduced stability, indicating challenges in generating well-controlled articulatory sequences. Reductions in spatiotemporal stability have been observed in disordered speech associated with Parkinson's disease (Anderson et al., 2008; Chu et al., 2020), traumatic brain injuries (McHenry, 2003), developmental language disorder (DLD; Goffman, 1999; Saletta et al., 2018), childhood apraxia of speech (Grigos et al., 2015; Moss & Grigos, 2012), and stuttering (Chu et al., 2020). This reduction in stability is not always the case, as individuals with amyotrophic lateral sclerosis (ALS) have shown increased articulator stability (Kuruvilla-Dugdale & Mefferd, 2017). This increased stability in ALS is thought to be related to either a compensatory response or stiffness from upper motor neuron involvement.

Performance factors such as speaking rate and linguistic and cognitive load have also been found to influence articulatory stability (Dromey et al., 2014; Dromey & Shim, 2008; Kleinow & Smith, 2000, 2006; MacPherson, 2019; Saletta et al., 2018). Furthermore, the influence of these factors has been observed to be greater in individuals with speech and language disorders, such as stuttering, relative to typical speakers (Smith & Kleinow, 2000). For typical adult speakers, articulatory movements are most stable at their habitual speaking rate and volitionally modifying their speaking rate results in less stable articulatory patterns, especially slowing rate (Smith et al., 1995). This is likely due to adapting neural systems to generate a new unpracticed speech pattern (Smith et al., 1995; Wohlert & Smith, 1998). Additionally, when producing speech that is more linguistically or cognitively complex, articulatory stability tends to decrease (MacPherson, 2019; Maner et al., 2000; Saletta et al., 2018). Furthermore, the stability of articulators diminishes when implementing new movement strategies, while it increases with practice (Walsh et al., 2006).

The widespread application of the STI by different research groups to investigate the speech motor control system in typical as well as in clinical populations has led to variation in methodological approaches used in implementing the STI. These methodological differences likely contribute to spurious variations in the STI values that emerge. This motivated our prior work on the effects of frequently occurring methodological decisions that may impact STI values. Using a synthetic framework, we focused on three commonly encountered methodological decisions that emerge when conducting speech research using the STI and offered insights for optimizing study designs to assess articulatory stability (Wisler et al., 2022). The synthetic data used were based on the design employed in the study of Lucero (2005). Individual productions are generated by applying random perturbations to the timing and amplitude of a synthetically generated template production of the phrase “buy Bobby a puppy” (BBAP). Specifically, we modified three characteristics: the number of repetitions, the length of the productions (which relates to the number of movement units), and the precision of the extraction of the articulatory trajectory from the speech stream. This simulation allowed us to investigate the influence of these parameters on the STI value under controlled, synthetic circumstances.

Using this simulation framework, we first examined the effect of the number of repetitions used to calculate the STI from synthetic trajectories. Our findings showed the importance of maintaining a consistent repetition count to mitigate bias when feasible. Because the STI is often applied to young children or to clinical populations where inclusion of a consistent number of productions may not be possible, we proposed a bias correction strategy. Next, we examined the effect of the length of a stimulus on the STI. Stimulus length here refers to the number of movement units in a target phrase. Consideration of stimulus length is important since timing deviations are cumulative and longer stimuli are anticipated to yield higher STI values in the absence of behavioral or performance-based effects. The results indicated that longer speech stimuli positively skewed STI values, highlighting the importance of using consistent stimulus lengths when comparing STI values across different conditions and participants. Finally, we examined the precision of selecting onset and offset points for segmenting speech stimuli, which could lead to temporal misalignment in the normalized waveform. As predicted, our findings demonstrated that even slight parsing errors result in increased STI values. Although the results of this study provided strong evidence for the influence of these methodological factors on the STI, the reliance of these experiments on synthetic data leaves some uncertainty as to the degree the reported observations will generalize to human speech production patterns.

Following from the findings from the synthetic data, the primary objective of the present study was to further investigate and validate the results, focusing on human speech data. We used a data set obtained from typically developing (TD) children and those diagnosed with DLD. These data were originally collected in the Goffman laboratory, with the aim of determining whether children with DLD show speech motor deficits that accompany their language difficulties. Children diagnosed with DLD exhibit impaired language development that is not explained by auditory, motor, or intellectual factors (Leonard, 2014). The present data set provides the opportunity to evaluate the properties of the STI examined in the previous study using synthetic data, but now relying on real data obtained from both populations with typical development and with language disorder. Although the selection of these data was partially based on its availability, we believe that the outcomes of this study will have broader implications and can be generalized to other populations of interest.

General Method

Using data from the kinematic motion trajectories of TD children and children with DLD, this article seeks to replicate three experiments conducted by Wisler et al. (2022). These experiments will be presented in the same order as in the previous article and were designed to mirror those as closely as possible, while adjusting to the constraints presented by the use of human data.

Data

The data analyzed for this study were drawn from previously collected cohorts (e.g., Zelaznik & Goffman, 2010). Institutional review board (IRB) approval was granted at Purdue University, where the data were collected and informed consent was completed, and The University of Texas at Dallas, where the data were analyzed. The IRB approval number for the data transferred from Purdue University and analyzed at The University of Texas at Dallas is IRB 17-134. Note that all data analyzed for this study consisted only of de-identified articulatory motion trajectories. Data were analyzed from 44 children. Sixteen of these were 8-year-olds with typical development, 14 were 6-year-olds with typical development, and 14 were between the ages of 6 and 8 years and either had DLD or had a history of DLD (identified when they were 4 years old). This set of children was selected for the validation study because both the range of ages and diagnosis (in the DLD group) were expected to show increased speech motor variability. All of the children were monolingual speakers of English, and all showed nonverbal cognitive skills that were within expected limits (all had a score great than 85 on the Columbia Mental Maturity Scale–Third Edition; Burgemeister et al., 1972). All also passed a hearing screening (20 dB responses at 500, 1000, 2000, and 4000 Hz). As expected for a diagnosis of DLD, all of the children assigned to this group performed below expected levels on the Structured Photographic Expressive Language Test–Second Edition (Werner & Kresheck, 1983) at the time of diagnosis. All children in the typical groups showed language skills within expected levels.

Stimuli

All children produced the sentence BBAP repeatedly. They first were introduced to this sentence via a brief story and imitated the sentence to assure that they understood the task. Children then were asked to produce the sentence each time the examiner held up a stuffed puppy. The target number of productions was 15, though at times fewer or more were elicited, as is often the case when testing young children. Productions with speech errors or disfluencies were excluded from analysis.

Instrumentation

Children were seated approximately 8 ft in front of an Optotrak motion capture camera (Northern Digital, Inc.), a commercially available system designed to record human movement in three dimensions. Eight infrared light-emitting diodes (IREDs) were placed on each child's face. Five of these IREDs were attached to modified sports goggles (two aligned on either side of the eyes, two on either side of the lips) or the forehead and were used as a frame of reference to subtract head movement. To track lip and jaw movement, IREDs were also placed on the upper lip, the lower lip, and on a splint attached to the jaw. All analyses presented in this article are based on the lip aperture, which measures the distance between the lower and upper lip markers. The kinematic signal was sampled at 250 Hz. A time-locked acoustic signal was used to verify the onsets and offsets of productions of BBAP. Motion trajectories were analyzed using custom MATLAB programs (MathWorks, 2019). Articulatory displacement data were low-pass filtered using a Butterworth filter with a cutoff frequency of 10 Hz (both forward and backward). The superior–inferior movements of the lower and upper lips were the focus of the kinematic analysis.

Parsing these phrases was accomplished using standard kinematic indices associated with peak velocity (for the full phrase BBAP) or zero-crossing in velocity (for the shorter segments). Figure 1 provides an illustration of the parsed segments in a sample production of BBAP. These points were initially selected visually, and then an algorithm selected the peak velocity (for the full phrase) or the zero-crossing (for the embedded shorter segments) within a 25-point (100-ms) analysis window. Notably, we also selected the motion dimensions that are dominant in the production of the phrase BBAP, including parsing from lower lip motion and completing the STI on lip aperture (Smith & Zelaznik, 2004). Note that although all three experiments use the kinematic trajectories of BBAP achieved by this process, the subsegments are only included in the stimulus length analysis presented in Experiment 2 (see Experiment 2: The Effects of Stimulus Length on STI section). The analysis of spatiotemporal stability and the influence of various factors on the reliability of this signal was the focus of the present investigation and will be described in the remainder of this article.

Figure 1.

Illustration of parsing for the three subcomponents of the phrase “buy Bobby a puppy” for a sample typically developing 6-year-old participant.

STI Calculation

In contrast to the previous simulation approach, for data from human participants, there is a need to undergo the standard preprocessing procedures (e.g., filtering, disfluency inspection) that are necessary before calculating the STI on speech data, as described above. Beginning with the kinematic data that have already undergone basic preprocessing procedures (e.g., filtering, disfluency inspection), as described in the Data section, the calculation of the STI follows the same standard procedure described in prior work (see Wisler et al., 2022) and by Smith et al. (1995, 2000). The initial step is to normalize the signals in both amplitude and time. To do this, the signals are amplitude-normalized by applying a z-score transformation (subtracting the average and dividing it by the standard deviation) and linearly time-normalized by setting each trajectory onto a 1,000-point time base using a spline interpolation. This resamples each token to a fixed length of 1,000 data points. The normalized signals are then overlaid across productions to calculate standard deviations at 2% time intervals throughout the duration of the signals. These 50 standard deviations are summed to generate the STI. It should be noted that the original time normalization procedure proposed by Smith et al. (1995) involved a Fourier resynthesis method; however, its effect on the STI was reported to be minimal in a follow-up study (Smith et al., 2000). Moreover, there is no formally reported formula for calculating the standard deviation used to derive the STI. It is generally assumed to use the standard sample standard deviation formula, with Bessel's correction:

$$\hat{\sigma }=\sqrt{\frac{1}{N-1}\sum _{i=1}^N{\left(x_i-\overline{x}\right)}^2}.$$ (1)

Generally, this formula is regarded as the default calculation method for the standard deviation and is widely used in programming environments such as MATLAB and R (MathWorks, 2019; R Core Team, 2017). Note that because the STI is typically applied to small samples (N ≤ 15), the difference between calculating the STI with and without Bessel's correction is nontrivial. Our prior work established that under normal conditions, STI values are strictly limited to the range of $0\le \mathrm{STI}\le 50\sqrt{2}\approx 70.7$ . However, this bound is only reached if you have two maximally different signals. In practice, even if productions are generated completely at random, they are likely to yield an STI value of less than 50. Thus, we believe 50 serves as a practical soft upper bound on the STI (Wisler et al., 2022).

Problem Statement and General Approach

Many studies that utilize the STI involve young children, or clinical populations are forced to reject a nontrivial percentage of the recorded repetitions due to disfluencies or other speech errors. These errors can also occur in typical participants, especially when studying complex behaviors such as incongruent stimuli or dual-task productions (e.g., Dromey & Shim, 2008). In these cases, it is likely that there will be varied, and often few, numbers of productions available for analysis. For this reason, it is of great value to determine the robustness of the STI in the face of varying numbers of tokens that are included in its calculation. When considering a measure such as the STI, it is best to think of that measure as an imperfect estimate of a true value. So, a person may have a “ground-truth” STI reflecting what we would measure their STI if we were able to collect an infinite number of repetitions, and any estimate of their STI based on a finite number of repetitions will be slightly above or below that true value. We know that the more repetitions we collect, the closer our estimate will become to the true value. Thus, the decision of how many repetitions to collect should be made to manage the trade-off between the accuracy of the measure and the logistic burden (and perhaps the impossibility) presented in collecting the additional data.

To better understand how this estimator error affects our analysis, it is necessary to decompose this error into two types: bias and variance. The bias in the STI refers to its tendency to systematically underestimate the true STI value. This underestimation can be over 20% when only two repetitions are used but shrink to around 3% for a standard 10 repetitions. Variance, on the other hand, refers to nonsystematic errors in the STI that could be positive or negative with equal likelihood. Although both bias and variance decrease for larger numbers of repetitions, the effect these two error types have on an analysis can be quite different.

Consider, for example, a comparison between two groups where all of the participants from one group produce five repetitions and all of the participants from the other group produce 10 repetitions. Although no study would be intentionally designed this way, it is possible for standard study designs to produce outcomes similar to this if one of the groups (e.g., from a clinical population or from young children) produces significantly more erroneous productions and thus the number of remaining error-free productions ends up being different across groups. In this scenario, based on the bias of the STI means, we would expect the STI values of the five-repetition group to be 6% lower than the true values whereas the bias for the 10-repetition group should only be 2.7% lower than the true value. Thus, if the two groups have the same “true” stability level, this difference in expected values will make it more likely to make a false discovery (reading the bias as a difference in motor control). If, however, the five-repetition group is less stable, then this bias will mute the difference between groups, making it less likely to measure a significant difference in the STI where a true difference exists. Note that this later case is the more likely scenario as more erroneous productions are likely a sign of decreased motor (and other types of) stability. Note that estimator variance plays a role in this analysis as well, but a far less complicated one. In a standard analysis, estimator variance (related to measurement error) is rolled into group variance (variation between participants in the same group); thus, fewer repetitions mean a smaller effect size and lower statistical power.

The goal of this experiment is to examine how closely the data from the children in this study mirror the bias characteristics described in the study of Wisler et al. (2022) and, as a result, how well the bias correction proposed there mitigates this bias. There it was noted that, like the sample standard deviation estimator, the STI when estimated on k repetitions (STI(k)) will systematically underestimate the true STI (STI(∞)) on average producing a value that is

$$E\left[\widehat{\mathrm{STI}}\left(k\right)\right]=\mathrm{STI}\left(\infty \right)\sqrt{\frac{2}{k-1}}\frac{\Gamma \left(\frac{k}{2}\right)}{\Gamma \left(\frac{k-1}{2}\right)}\mathrm{.}$$ (2)

Since this bias follows a known pattern that is fixed for a given number of repetitions, we can multiply by the inverse of this bias constant to calculate a bias-corrected STI estimator (BC-STI)

$$\begin{array}{c}{\widehat{\mathrm{STI}}}_c\left(k\right)=\widehat{\mathrm{STI}}\left(k\right)\sqrt{\frac{k-1}{2}}\frac{\Gamma \left(\frac{k-1}{2}\right)}{\Gamma \left(\frac{k}{2}\right)}\mathrm{.}\end{array}$$ (3)

It is worth noting that the question being investigated here is not whether or not the STI measure exhibits finite-sample bias in the data being analyzed. As the STI is based on the sample standard deviation, which is known to be a biased estimator, we can assume with relative certainty that the STI will exhibit some finite sample bias. Therefore, the key question to investigate is how well the observed bias characteristics align with those described in the study of Wisler et al. (2022), which relies on the additional assumption that the data are drawn from a normal distribution.

Experimental Method

To quantify the bias in the STI for a smaller number of repetitions, we select random subsamples from the set of repetitions available for each participant of sizes 2 through 10. For each number of repetitions, 100 different sets are selected from the total set of available repetitions for that participant. Sampling here is performed without replacement so that all repetitions in each set are unique (although the same repetition will necessarily be in more than one of the 100 sets). Once the STI has been measured across all subsamples, those values are averaged and compared against a ground-truth STI measure to characterize the bias of the STI for each number of repetitions. In the simulations in the study of Wisler et al. (2022), the ground-truth STI was calculated from an arbitrarily large number of repetitions (10,000). As repeating this process in real speech data is not feasible, we estimate the ground truth by calculating the bias-corrected STI from the maximum number of available repetitions for each participant. Although this ground truth is imperfect and may lead to minor inaccuracies in the bias calculation, it should not inhibit our ability to analyze changes in bias relative to the number of repetitions.

For a brief illustrative example of how this process works, suppose a participant has 25 total repetitions and we want to calculate the bias for k = 4 repetitions. We start by randomly selecting four of the 25 repetitions from this participant and calculating the STI. We then repeat this process with new random sets of four until we have 100 STI estimates in total. Next, we calculate the ground-truth STI by measuring the STI on the entire set of 25 repetitions. Finally, the 100 size-4 estimates are averaged, and the ground-truth STI is subtracted from this average to yield the k = 4 bias for the given participant.

After the bias has been calculated for all participants, the same bias characteristics are measured for the bias-corrected STI. Calculating bias for the bias-corrected STI follows the exact same procedure as for the traditional STI but uses Equation 3 to calculate both the estimated and ground-truth STI values. As this process gives a unique set of biases for each of the 45 participants, we then aggregate these values by calculating the mean and standard deviation of the bias values for each participant group. To determine whether a statistically significant bias exists, one-sample t tests are run for each k value in each of the three groups. To control for the familywise error rate, a Bonferroni correction is used to correct for the nine hypotheses tested in each experiment (different k values), setting the adjusted threshold to $\mathrm{\alpha }=\frac{.05}{9}=.0056$.

Results

Figure 2 displays the bias characteristics of the STI and BC-STI for each of the three participant groups. Visually, these results appear to very closely mirror the findings reported by Wisler et al. (2022). For the standard STI measure, we observe a negative bias that is large for small numbers of repetitions and decreases as the number of repetitions increases. Similarly, the bias-corrected measure exhibits a much smaller bias, which changes very little for different values of k.

Figure 2.

Plots of the bias of the spatiotemporal index (STI) versus number of repetitions for (a) typically developing 6-year-olds, (b) typically developing 8-year-olds, and (c) children with developmental language disorder (DLD). The bias is calculated at the participant level via random subsampling and then averaged across participants for each group to generate the displayed curves. The blue line depicts the bias of the standard STI, and the green line depicts the bias following bias correction.

Average bias values, along with the p values for the t-test results, are reported collectively in Table 1. For the traditional STI, statistically significant biases existed for all three groups and all k values. For the bias-corrected STI measure, only two of the 27 experiments found statistically significant biases after correction. Statistically significant p values are highlighted in bold. Note that these are noncorrected p values and, as a result, are evaluated for significance using the adjusted threshold α = .0056.

Table 1.

Summary of bias values for different numbers of repetitions and participant groups along with the p-value results of t tests to determine whether bias is statistically significant at the group level.

Group	STI	Variable	No. of repetitions
			2	3	4	5	6	7	8	9	10
6YO	STI	Bias	−4.722	−2.796	−1.813	−1.299	−1.018	−0.831	−0.679	−0.518	−0.432
		p	< .001	< .001	< .001	< .001	< .001	< .001	< .001	< .001	< .001
	BC-STI	Bias	−0.590	−0.602	−0.371	−0.264	−0.239	−0.225	−0.199	−0.132	−0.120
		p	.014	< .001	.008	.005	.013	.012	.012	.038	.086
8YO	STI	Bias	−4.392	−2.488	−1.573	−1.116	−0.810	−0.611	−0.533	−0.421	−0.348
		p	< .001	< .001	< .001	< .001	< .001	< .001	< .001	< .001	< .001
	BC-STI	Bias	−0.391	−0.379	−0.202	−0.145	−0.087	−0.057	−0.103	−0.084	−0.083
		p	.141	.015	.112	.126	.253	.333	.136	.111	.056
DLD	STI	Bias	−4.661	−2.315	−1.475	−1.032	−0.764	−0.574	−0.407	−0.297	−0.210
		p	< .001	< .001	< .001	< .001	< .001	< .001	< .001	< .001	.001
	BC-STI	Bias	−0.435	−0.107	−0.095	−0.094	−0.098	−0.093	−0.058	−0.049	−0.041
		p	.170	.533	.377	.381	.337	.337	.494	.442	.447

Note. Statistically significant p values falling below the Bonferroni-corrected α = .0056 threshold are highlighted in bold. BC-STI is the bias-corrected spatiotemporal index (defined in Equation 3). STI = spatiotemporal index; 6YO = 6-year-olds; 8YO = 8-year-olds; DLD = children with developmental language disorder.

Discussion

Overall, the results of this experiment provide strong support for the bias characteristics described in the study of Wisler et al. (2022), as well as for the validity of the bias-corrected STI measure proposed there, but now on real-world data. Although this study examined only a small population of TD children and children with DLD restricted to a relatively narrow age range (6–8 years) and we cannot say for certain these findings will generalize to other populations, the consistency of the bias characteristics across the participant groups and in relation to the simulation data engenders some confidence that these findings will be generalizable to other populations. It is also worth noting that, even in the rare cases, a statistically significant bias existed in the BC-STI measure; this bias was still negative, meaning that the bias correction failed to fully correct for the bias in that sample but did substantially mitigate it. While we cannot make the claim that the BC-STI is universally unbiased, it seems a safe conclusion that the BC-STI will provide a less biased estimate of the STI regardless of the population.

One critical question that neither the prior study nor this one can adequately address is how many repetitions should be used in calculating the STI. To address this question, we would need a thorough analysis of not only the bias properties of the STI but the variance as well. Analyzing the variance of the STI was intentionally omitted from these experiments as it cannot be accurately characterized using the subsampling approach that was employed. Since the same repetitions are included in different subsamples, the variance of the STI is underestimated, particularly as the size of the subsamples gets closer to the pool of repetitions they are drawn from. Thus, properly addressing this question would require either a data set specifically designed for it (and containing a much larger number of repetitions per participant) or reverting to a simulation framework that bypasses these limitations. Based on the current findings, we can only reassert the loose guidance outlined previously that (a) more repetitions will lead to more accurate measures of the STI, (b) 10–20 repetitions appear to provide a reasonable trade-off between measurement accuracy and data acquisition costs, and (c) measurement error can increase substantially for numbers of repetitions below 10. To better address this question, future work should examine how the number of repetitions precisely influences the actual outcomes of experiments using the STI. For example, it is important to address how much reducing the number of repetitions from 10 to five would reduce the statistical power of an experiment and how many additional participants would be necessary to compensate for this decrease. While there will be no universal answer for how many repetitions should be used, answering these questions would help researchers balance (and report on) the trade-off in designing their experiments.

Problem Statement and General Approach

In this section, we investigate the effect of stimulus length on the STI. Here, our use of the term “stimulus length” is meant to refer to the number of movement units in a target phrase. Although we consider measures such as duration in our results, duration is only a proxy, whereas the number of movement units is what is thought to be primarily driving this effect. It has long been known that the STI depends on the characteristics of the linguistic target (Smith et al., 2000). There are two types of linguistic factors that may affect the STI. The first relates to complexity; for example, a signal of the same length may show a higher STI when it is a nonword than when a meaningful referent is included (Heisler et al., 2010) or when it is an easier than a harder stress pattern (Goffman, 1999). However, importantly for the present discussion of the effects of length, much work has emphasized relationships between length and syntactic complexity (e.g., Kleinow & Smith, 2006; Maner et al., 2000).

There are both behavioral and mathematical reasons for influences of both length and linguistic complexity. From a behavioral perspective, the production of longer and more complex sequences presents challenges likely to yield less consistent articulatory motion patterns. From a mathematical perspective, the signal properties of the patterns being evaluated by the STI have long been known to influence its value. This was fist noted in the study of Smith et al. (2000), where it was observed that standard deviations tended to be higher in regions where the velocity in the record is higher. In our prior study, we analyzed the specific role of stimulus length in this signal effect to show that longer sequences tend to yield higher STI values. Thus, even without the previously described behavioral challenges, longer sequences are expected to yield higher STI values, as shown in the study of Wisler et al. (2022). This finding has been further supported by a recent investigation into articulatory stability of individuals with ALS across various stimuli (Teplansky et al., 2024). Although understanding how linguistic factors affect speech stability is an enduringly important research question, ambiguity between behavioral and signal-based influences present difficulties for directly answering it. One way studies have controlled for this is by using embedded stimuli, where a consistent linguistic target is embedded in several linguistic contexts of varying lengths and complexity (e.g., Kleinow & Smith, 2006; Maner et al., 2000). This approach isolates the behavioral (or linguistic complexity) component; however, it is uncertain how much information is being lost by not directly probing speech stability in the segments where the stimulus length and complexity are varied. Interpreting the degree to which differences in STI values can be attributed to behavioral effects outside of these embedded contexts requires a more complete understanding of the signal effect in real-world scenarios. Although Wisler et al. (2022) found that longer stimuli tended to yield higher STI values, the amount of increase in the STI was dependent on the level of temporal stability in the simulated speech production process. Also, in the absence of any temporal instability, no length effect was observed. The primary goal of this experiment is to understand the influence of signal properties on the STI in human speech.

To validate this in real-world data, we can look at different length segments embedded within the complete phrase BBAP. Note that this is an inversion of the experimental protocol that has been previously employed in some studies, which have investigated the effects of stimulus length and complexity on the STI. In those studies, the same phrase (i.e., BBAP) was embedded within longer linguistic frames (such as “He wants to buy Bobby a puppy at my store”) to examine the behavioral effects of stimulus length while controlling for signal properties (Kleinow & Smith, 2006; Maner et al., 2000). In contrast, in the present experiment, we seek to examine the effect of signal properties on the STI while controlling for behavioral differences. Thus, instead, we will be examining different subcomponents embedded within the same carrier phrase.

Experimental Method

To quantify the signal effects of stimulus length on the STI, we parse the phrase BBAP into three separate subcomponents “buy B,” “Bobby a p,” and “pupp.” Figure 1 displays an illustration of this segmentation for a sample production. Note that although more than 10 productions were available for many of the participants, only the first 10 were considered in this analysis. For all participants, both the STI and average duration are calculated for each of the four segments (the three subcomponents along with the whole phrase BBAP). It is important to note that duration does not directly measure stimulus length as defined in this article and is included only to show how the different stimuli vary in duration across participants. We first plot the relationship between STI and duration within each of the three participant groups to show how the duration and number of linguistic units in a phrase influence the STI. Then, we conduct a linear mixed-model analysis where group and segment are coded as categorical fixed effects and participant is coded as a random effect. Note that average duration is excluded from this model as it is expected to carry much of the same information as the segment variable.

Results

Figure 3 presents scatter plots illustrating the relationship between duration and STI for the three groups of participants. Within each population, there is a clear relationship between length of the stimuli and STI such that utterances with longer average durations (and correspondingly more movement units) tend to be associated with higher STI values. The results of the mixed-model analysis are presented in Table 2. In the model, the full phrase BBAP is coded as the base level, and the three subcomponents all have strongly significant (p < .0001) effects relative to it. The weakest effect is the largest subcomponent “Bobby a p,” which has a coefficient of 6.13 followed by “pupp” and “buy B,” with coefficients of 8.46 and 13.53, respectively. Note as the intercept for this model is 22.895, the magnitude of these effects is quite large. This means that the expected STI value in this data set for “buy B” is less than half that of the complete utterance. Relative to the magnitude of the stimuli effects, the group effects are much smaller; however, there is still a significant effect in the 8-year-old group relative to the baseline DLD group. Although the 6-year-old group does exhibit the expected negative effect, this effect was not found to be statistically significant.

Figure 3.

Plot of the spatiotemporal index (STI) values versus average duration for the phrase “buy Bobby a puppy” (BBAP) and each of the three subcomponents displayed for the (a) 6-year-olds, (b) 8-year-olds, and (c) children with developmental language disorder (DLD).

Table 2.

Results table for the regression model mapping the relationship between independent variables (participant group, phrase subcomponent) and the dependent variable (spatiotemporal index).

Term	Coefficient	SE	p
Intercept	22.895	0.79228	< .001
Group: 6YO	−1.3128	1.0022	.192
Group: 8YO	−2.5888	0.91838	.005
Stimuli: “Bobby a P”	−6.1352	0.64446	< .001
Stimuli: “buy B”	−13.527	0.64446	< .001
Stimuli: “pupp”	−8.4594	0.64446	< .001

Note. Both group and stimuli are coded as categorical variables with base categories of DLD and “buy Bobby a puppy,” respectively. Thus, coefficient magnitudes reflect the expected spatiotemporal index differences between the listed category and the base category. 6YO = 6-year-olds; 8YO = 8-year-olds; DLD = children with developmental language disorder.

Discussion

The results of this experiment appear to closely mirror the previous findings on simulated data. We observe that, when controlling for the utterance being produced (BBAP), calculating the STI on longer segments tends to yield higher STI values. This effect was found to be almost universal across the data set as the STI calculated on the whole phrase was higher than for any subcomponent in all but four participants. Although it is difficult to precisely characterize the nature of the relationship between stimulus length and STI from only a few different segments, it is interesting to note that the relationship between stimulus length and STI appears to be nonlinear. That is to say, as the length of stimuli increases, the amount the STI increases from each additional movement unit seems to decay. This should not be too surprising. As the STI is a bounded measure, increases in the STI with longer stimuli have to plateau at some point; however, the fact this nonlinearity is exhibited even in these short stimuli is worth noting. Particularly since such nonlinearities were not obvious in the corresponding simulation. Practically, this means that we might reasonably expect, from the perspective of signal and not behavioral effects, a greater increase in the STI between a consonant–vowel–consonant (such as [baIb] in “buy B”) and a short phrase (such as BBAP) than we would between a short phrase and a long phrase (“You buy Bobby a puppy and I buy Matt toys”).

Problem Statement and General Approach

The parsing of signals prior to calculation of the STI is generally recognized to be a critical step in the measure's calculation. Two identical repetitions that are parsed inconsistently will appear distinct, and the differences between them will contribute to a higher STI value. The errors created from inaccurate parsing are especially harmful due to the fact that linear temporal alignment means that a small parsing error at the beginning or end of the signal creates misalignment across the entire production. Although parsing errors can introduce significant errors to the measured STI, there remains no consensus on how signals should be parsed prior to STI analysis. Some laboratories rely on visual inspection to parse signals (Glotfelty & Katz, 2021; Kuruvilla-Dugdale & Mefferd, 2017). Others use a more algorithmic approach in which visual inspection is used to ascertain general onset and offset points, for example, associated with a peak or zero-crossing in velocity, and then an algorithm determines the local minimum, maximum, or zero value for more precise parsing (e.g., see Goffman & Smith, 1999, for a detailed description of an algorithmic approach used for parsing).

Prior examination of parsing errors in the study of Wisler et al. (2022) found that increasing parsing errors (a) increases the measured STI value and (b) reduces the measurable differences between productions of varying stability levels. Thus, it was found that productions coming from dramatically different stability levels yielded similar STI values when corrupted by large parsing errors. The goal of this experiment is primarily to examine the effects of controlled amounts of parsing error on the STI values calculated from children's speech productions and secondarily to examine how these changes in the STI value affect between-groups differences of 6- and 8-year-old TD children and children with DLD. Our expectation is that, similar to our observations for synthetic data, the injection of parsing errors will have a similar effect to those observed in simulation. Thus, it is expected that the injection of parsing errors will (a) increase the STI and (b) mute between-groups differences in the STI.

Experimental Method

To examine the effects of parsing errors on the STI, we start with the “true” parsings achieved via the procedure outlined in the Data section. We then insert random errors into the beginning and end points of each repetition of the phrase BBAP. These parsing errors are randomly generated according to a uniform distribution U(−∈, ∈), where ∈ is a parameter controlling the upper limit on the magnitude of parsing errors. Thus, by varying ∈, we can measure the effect of parsing errors on the STI. Note that this approach directly mirrors that used in the prior simulation (Wisler et al., 2022).

As a baseline condition, the STI is measured using the first 10 viable productions. From here, random parsing errors are injected to each repetition using a range of ∈ values spanning from 4 to 100 ms in increments of 4 ms. Note that the 4-ms value stems from the 250-Hz sampling rate of the data. Thus, for the ∈ = 4 ms condition, each beginning and end point will either be one sample early, one sample late, or unchanged with equal likelihood. After parsing errors have been inserted into all 10 productions, the STI is calculated. This process is repeated across a 100-iteration Monte Carlo simulation for each participant and each epsilon value to minimize the effects of randomness on the results, yielding a total of 112,500 (45 × 25 × 100) STI values.

For each iteration of the Monte Carlo simulation and each epsilon value, the Cohen's d between each pair of participant groups is calculated. The d values are then averaged across trials of the Monte Carlo simulation to examine how between-groups differences are affected by parsing error.

Results

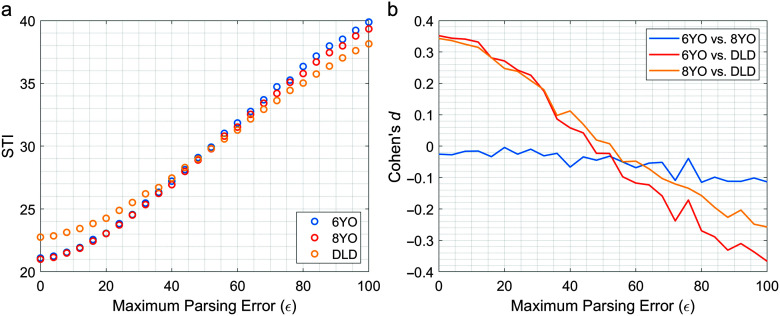
Figure 4a displays the average STI values for each group plotted against the magnitude of the parsing errors (∈), and Figure 4b displays the average Cohen's d for between-groups differences in these STI values. As was observed in the prior simulation study, STI values show a consistent increase across all three groups as the amount of parsing error increases. Interestingly, although parsing error increased across all the groups, how much the STI increased was not uniform across groups, as the STI values for the DLD group appeared to be noticeably less affected than the other two groups. As a result, despite exhibiting the highest STI values in the clean condition, the children with DLD exhibited lower STI values than the other two groups for ∈ > 50 m. Because of this, the Cohen's d values reverse over the course of the simulation with almost the same effect sizes occurring for the ∈ = 100 ms condition as for the baseline condition, just in the opposite direction.

Figure 4.

Plots displaying (a) the average spatiotemporal index (STI) for each participant group and (b) Cohen's d value for between-groups differences with reference to the maximum amount of injected parsing error (∈). 6YO = 6-year-olds; 8YO = 8-year-olds; DLD = children with developmental language disorder.

The differential effect of parsing error across the groups was not an expected result of this experiment and motivated further examination of what characteristics of the individual participants made their STI values more or less sensitive to parsing errors. Visual inspection of the productions of individuals least influenced by parsing errors showed that these participants also tended to produce longer duration sequences than their counterparts—in this case, not defined as number of movement units but as overall slower duration (i.e., slower speech rate). To examine this further, Figure 5 displays the relationship between average duration and sensitivity to parsing errors (measured as the average difference between the ∈ = 100 ms condition and the baseline condition). This plot shows a clear negative relationship between duration and parsing sensitivity, summarized by a Pearson correlation coefficient of −.7015, which is significant at the α = .001 level.

Figure 5.

Plot displaying the amount of increase in the spatiotemporal index (STI) value resulting from the insertion of ∈ = 100 ms of parsing error against the average duration for each participants productions of the phrase “buy Bobby a puppy.” 6YO = 6-year-olds; 8YO = 8-year-olds; DLD = children with developmental language disorder.

Discussion

Whereas the results of this experiment largely agree with the simulation findings presented in the study of Wisler et al. (2022), these results provide far more nuance. One difference in these results is that the higher sampling rate (250 Hz vs. 100 Hz) used here allows parsing error to be increased in smaller increments. As a result, we get a more specified picture of how the STI increases with the magnitude of the parsing errors. Across all three groups, this clearly shows a nonlinear increase, which rises slowly at first, then begins to speed up at around ∈ = 20 ms, and then slows down for ∈ > 80 ms as the STI values near the upper limit.

Perhaps the most interesting deviation in the results of this experiment from the prior simulation is the differences in how parsing errors affect the three groups. In the prior simulation, differences were observed in the effects of parsing errors across low and high stability levels; however, these differences appeared to relate simply to baseline differences. So, for more stable productions, the STI value is lower in the absence of parsing errors and thus has more room to grow when parsing errors are added. Thus, more stable conditions appear more sensitive to parsing errors, but only because they are converging to the same point from further away. In contrast, the results of this experiment show that differences in sensitivity exceed the differences in the baseline STI values, leading to consistently higher STI values in the TD children relative to the children with DLD once enough parsing error is added. Younger children or children with communication disorders often show slower speech rates; thus, it is important to understand how parsing error and slow speech rate may interact.

Although this finding seems counterintuitive, it makes sense when considering how parsing errors can be expected to affect different length productions. As was noted previously, the reason parsing errors affect the STI so strongly is that differences in the onset and offset points will create misalignment across the entire production. However, as the STI is calculated in normalized time, the significance of parsing errors is likely not based on their absolute magnitude, but rather on their magnitude relative to the absolute length of the utterance. Thus, it is reasonable to expect parsing errors to be less impactful in participants who speak more slowly and as a result produce longer duration utterances. Examining the relationship between average production duration and the increase in STI caused by 100 ms of parsing error appears to support this idea. The change in STI values resulting from parsing errors is strongly correlated with average duration, indicating that individuals who spoke more slowly tended to exhibit less sensitivity to parsing errors. Since the children with DLD tended to speak more slowly and produce longer duration utterances, they also tended to be less sensitive to parsing errors. Since experimenters have observed increased difficulty in the segmentation of children with DLD, another possible contributing factor could be that the reduced accuracy in the initial segmentation makes the effect of additional errors in the segmentation less impactful.

Conclusions

This study investigated, using a sample of children with typical development and with DLD, the effects of three methodological parameters: (a) number of repetitions, (b) length of stimuli, and (c) amount of parsing error on the value of the STI. The findings of these experiments closely mirrored previous findings obtained from synthetic data. Examining the effects of the number of repetitions used showed that calculating the STI from smaller numbers of repetitions yields results that are both more biased and more variable. Breaking the phrase BBAP into shorter segments and examining the STI values across different subcomponents showed that STI values tended to be higher when calculated on longer sequences with more movements. Finally, injecting parsing errors into the individual productions before calculating the STI led to a similar increase in STI values as observed in the synthetic data experiments. These findings were also largely consistent across all three groups: TD 6-year olds, TD 8-year-olds, and children (ages 6–8 years) with DLD. The exception to this was the results of the third experiment, which found that parsing error had a smaller effect on the children with DLD than the other two groups. This is likely because their slower speaking rate meant parsing errors made up a lower percentage of the production's total duration or that their onsets and offsets are less precise than those of their typical peers. In summary, these findings reinforce the importance of methodological consistency in the implementation of the STI and open up interesting new questions about how different factors affect this consistency.

Data Availability Statement

The data that support the findings of this study are available from Lisa Goffman (lisa.goffman@boystown.org) upon request.

Funding Statement

This research was supported by National Institute on Deafness and Other Communication Disorders Grants R01DC016621 awarded to Jun Wang and R01DC016813 awarded to Lisa Goffman and by the American Speech-Language-Hearing Foundation through a New Century Scholar Research Grant (PI: Wisler).