Evaluation of Machine Learning Based QSAR Models for the Classification of Lung Surfactant Inhibitors

Abstract

Inhaled chemicals can cause dysfunction in the lung surfactant, a protein–lipid complex with critical biophysical and biochemical functions. This inhibition has many structure-related and dose-dependent mechanisms, making hazard identification challenging. We developed quantitative structure–activity relationships for predicting lung surfactant inhibition using machine learning. Logistic regression, support vector machines, random forest, gradient-boosted trees, prior-data-fitted networks, and multilayer perceptron were evaluated as methods. Multilayer perceptron had the strongest performance with 96% accuracy and an F1 score of 0.97. Support vector machines and logistic regression also performed well with lower computation costs. This serves as a proof-of-concept for efficient hazard screening in the emerging area of lung surfactant inhibition.

Introduction

Inhaled chemicals and particles can affect lung health in multiple ways. In addition to biochemical effects on the cells, they can disrupt the lung surfactant (LS), a protein–lipid complex that forms a thin film at the gas exchange surface.¹ LS plays biophysical roles in breathing mechanics and particle clearance, as well as biochemical roles in particle transformation and immune regulation.² Some inhaled substances, including particles, that reach the alveoli can alter the properties or damage the components of LS. This mode of dysfunction is implicated in respiratory distress syndrome in infants and adults.³ Among the many chemicals humans are exposed to, identifying potential surfactant inhibitors is important for toxicologists and risk assessors.⁴⁻⁶

One way to accomplish this is using quantitative structure–activity relationships (QSARs), consisting of regression or classification models that attempt to relate molecular descriptors of chemicals to biological response.^7,8 Traditionally, QSAR models depend on theoretical or empirical frameworks and limit each task to a similar set of molecules. Theoretical knowledge in bioavailability, kinetics, and binding affinities between function groups and proteins would be combined to predict the effects on a receptor or whole organism.^9,10 These traditional methods fall short because of the burden of many complex considerations and the difficulty in translating results from one class of chemicals to another.¹¹ To remedy this, recent efforts have turned to approaches that start with a blank slate and discover the relationships between agnostic structural features and the desired output. Machine learning offers many tools for building these black-box models, for which it is unnecessary to predefine or fine-tune every interaction.¹²⁻¹⁴

This study used binary classification models to identify potential surfactant inhibitors. Multiple machine learning models were evaluated across low molecular weight chemicals through several cross-validation metrics. A set of 43 small-molecule chemicals were chosen, 19 from Liu et al. and 24 from Da Silva et al.^15,16 All chemicals were tested using a constrained drop surfactometer (CDS) and labeled as surfactant inhibitors if the average minimum surface tension from cycling was increased beyond 10 mN m^–1. This threshold is clinically associated with LS dysfunction and atelectasis. While there are other studies in this emerging field, they may use alternative methods or evaluate only a few chemicals, so these data were chosen to ensure consistency in determining surfactant inhibition. The results serve as a starting point for building predictive models that can be used to screen hundreds or thousands of other chemicals.¹⁷

Methods

Constrained Drop Surfactometer

The constrained drop surfactometer (CDS) was purchased from BioSurface Instruments, LLC (Manoa, HI) and operated using Axisymmetric Drop Shape Analysis v 2.0 (BioSurface Instruments, LLC). The details of chemical testing using the CDS are described in Liu et al.¹⁵ The data for an additional 24 chemicals using the same method were obtained from Da Silva et al.¹⁶ Collectively, the 43 chemicals were encoded by their structure using the simplified molecular input line entry system (SMILES) and a binary 0/1 label for whether the chemical was a surfactant inhibitor.

Molecular Descriptors

A set of 1826 molecular descriptors suitable for QSAR construction was calculated from the SMILES structures of chemicals using the open-source chemoinformatics library RDKit in conjunction with Mordred.¹⁸Mordred offers a large library of simplistic, 2D, and 3D descriptors as well as fast calculation speeds.

Data Processing

The molecular descriptors serve as input features for downstream machine learning models. Multiple data processing methods were investigated to determine their impact on model performance. Columns with missing values were either deleted or imputed (using SimpleImputer) with the column median using scikit-learn and then scaled using MinMaxScaler from scikit-learn.¹⁹ The effect of dimensionality reduction was also investigated by comparing unaltered data with a reduction to 43 components using principal component analysis (PCA) in scikit-learn.¹⁹ Furthermore, to investigate the effect of balance between the positive and negative classes, either data remained imbalanced or the positive class was oversampled to achieve balance using imblearn.²⁰

Classical Machine Learning

Four classical models were explored: logistic regression, support vector machines, random forest, and gradient-boosted trees. Logistic regression based classification was conducted using the LogisticRegression procedure from scikit-learn. All solver options (lbfgs, liblinear, newton-cg, newton-cholesky, sag, and saga) and three values of C (0.1, 1, and 10) were tested across data types. Classification using C-Support Vector Machines was conducted using the SVC routine from scikit-learn. All kernel options (linear, poly, rbf, and sigmoid) and three values of C (0.1, 1, and 10) were tested across data types. Random forest was conducted using the RandomForestClassifier, optimized by varying the hyperparameters n_estimators (50, 100, and 200) and max_depth (3 and 6). The XGBoost library was also used for a gradient-boosted tree approach, optimized with the hyperparameters max_depth (3 and 6) and min_child_weight (0.1, 1, and 10).²¹

Deep Learning

Deep learning models using artificial neural networks (ANNs) were generated using prior-data-fitted network (PFN) and multilayer perceptron (MLP) approaches. The library TabPFN provided a pretrained transformer specializing in small tabular data sets that can make fast predictions with no hyperparameter tuning.²² MLPs were built using the Pytorch and Lightning libraries.^23,24 The MLPs consisted of a dropout layer, two or thee hidden layers with rectified linear unit (ReLU) activation function, and an output layer. The presence of the additional hidden layer and the hidden layer width (number of intermediate neurons, 20 or 40) were varied as hyperparameters.

Model Evaluation

Cross-validation was conducted using 10 random seeds and fivefold cross-validation from scikit-learn. Four primary evaluation metrics were obtained from scikit-learn: accuracy, precision, recall, and F1 score. Runtime was also recorded using the time library. In classification, precision is defined as the fraction of positive labels among the retrieved positives, while recall is defined as the fraction of retrieved positives among the positive labels. Precision and recall can be considered measures of quality and quantity, respectively. F1 score is defined as the harmonic mean of precision and recall, which balances the two metrics.

Code Availability

This study’s data, code, and environments are publicly available on Github at [https://github.com/Jamesliu93/QSAR_BinCls_2024].

Results and Discussion

A panel of 43 low molecular weight chemicals was used to classify potential surfactant inhibition (Table 1). The simplified molecular input line entry system (SMILES) structures were used to calculate a set of 1826 molecular descriptors that served as input features. Logistic regression (LR), support vector machines (SVM), random forest (RF), gradient-boosted trees (GBT), prior-data fitted networks (PFN), and multilayer perceptron (MLP) were evaluated as potential classification models (Figure 1). Every model was subjected to fivefold cross-validation across 10 random seeds. Hyperparameters were varied for each model (except PFNs) to optimize for performance. Four evaluation metrics were recorded during each run: accuracy, precision, recall, and F1 score. The results for the top-ranked models of each type by F1 score are reported in Table 2. The full results for all models are available in Table S1, Figure S1, and Figure S2.

Table 1. Chemicals for the Training and Cross-Validation of QSAR Models^a.

name	CAS #	SMILES	label
(3-methoxy-2-methylpropyl)benzene	120811-92-9	CC(CC1=CC=CC=C1)COC	1
(vinyloxy)cyclohexane	2182-55-0	C=COC1CCCCC1	1
1-(5,6,7,8-tetrahydronaphthalen-2-yl)ethanone	774-55-0	CC(=O)C1=CC2=C(CCCC2)C=C1	1
1-aminoethanol	75-39-8	CC(N)O	1
1-butanol	71-36-3	CCCCO	0
1-ethyl-2-pyrrolidinone	2687-91-4	CCN1CCCC1=O	0
1-phenylethenyl acetate	2206-94-2	CC(=O)OC(=C)C1=CC=CC=C1	1
2-buten-1-one, 1-(2,2-dimethyl-6-methylenecyclohexyl)-	35087-49-1	CC=CC(=O)C1C(=C)CCCC1(C)C	1
2-butyne-1,4-diol	110-65-6	C(C#CCO)O	0
2-tridecenal	7069-41-2	CCCCCCCCCCC=CC=O	1
6-phenyl-1,3,5-triazine-2,4-diamine	91-76-9	C1=CC=C(C=C1)C2=NC(=NC(=N2)N)N	0
9-undecenal	143-14-6	CC=CCCCCCCCC=O	1
acrylamide	79-06-1	C=CC(=O)N	0
aniline	62-53-3	C1=CC=C(C=C1)N	0
α-thujone	546-80-5	CC1C2CC2(CC1=O)C(C)C	1
benzeneacetonitrile, alpha-butylidene-, (alphaZ)-	130786-09-3	CCCC=C(C#N)C1=CC=CC=C1	1
captan	133-06-2	C1C=CCC2C1C(=O)N(C2=O)SC(Cl)(Cl)Cl	0
decamethylcyclopentasiloxane	541-02-6	C[Si]1(O[Si](O[Si](O[Si](O[Si](O1)(C)C)(C)C)(C)C)(C)C)C	1
diethylene glycol	111-46-6	C(COCCO)O	0
diisopentyl ether	544-01-4	CC(C)CCOCCC(C)C	1
etaspirene	79893-63-3	CCC1=CCCC(C12C=CC(O2)C)(C)C	1
ethanol	64-17-5	CCO	0
ethyl acrylate	140-88-5	CCOC(=O)C=C	1
ethylene glycol	107-21-1	C(CO)O	0
glutaraldehyde	111-30-8	C(CC=O)CC=O	0
lactose	5965-66-2	C(C1C(C(C(C(O1)OC2C(OC(C(C2O)O)O)CO)O)O)O)O	0
maleic anhydride	108-31-6	C1=CC(=O)OC1=O	1
menthol	1490-04-6	CC1CCC(C(C1)O)C(C)C	0
methacrylic acid	79-41-4	CC(=C)C(=O)O	0
methyl acrylate	96-33-3	COC(=O)C=C	1
methyl dihydrojasmonate	24851-98-7	CCCCCC1C(CCC1=O)CC(=O)OC	0
methyl laurate	111-82-0	CCCCCCCCCCCC(=O)OC	1
methyl undec-10-enoate	111-81-9	COC(=O)CCCCCCCCC=C	1
m-xylylenediamine	1477-55-0	C1=CC(=CC(=C1)CN)CN	0
potassium nitrate	7757-79-1	[N+](=O)([O−])[O−][K+]	0
propionic acid	79-09-4	CCC(=O)O	0
propylene glycol	57-55-6	CC(CO)O	1
sodium glycocholate	863-57-0	CC(CCC(=O)NCC(=O)[O−])C1CCC2C1(C(CC3C2C(CC4C3(CCC(C4)O)C)O)O)C·[Na+]	1
sodium taurocholate	145-42-6	CC(CCC(=O)NCCS(=O)(=O)[O−])C1CCC2C1(C(CC3C2C(CC4C3(CCC(C4)O)C)O)O)C·[Na+]	1
sodium taurodeoxycholate	1180-95-6	CC(CCC(=O)NCCS(=O)(=O)[O−])C1CCC2C1(C(CC3C2CCC4C3(CCC(C4)O)C)O)C·[Na+]	1
tetrahydrofuran-3-carbaldehyde	79710-86-4	C1COCC1C=O	0
trimethoxyoctylsilane	3069-40-7	CCCCCCCC[Si](OC)(OC)OC	1
Triton X-100	2315-67-5	CC(C)(C)CC(C)(C)C1=CC=C(C=C1)OCCO	1

^aIn addition to the chemical name, the Chemical Abstracts Service (CAS) registry number, SMILES structure, and label (0/1 for non-inhibitor/inhibitor, respectively) are provided.

Figure 1.

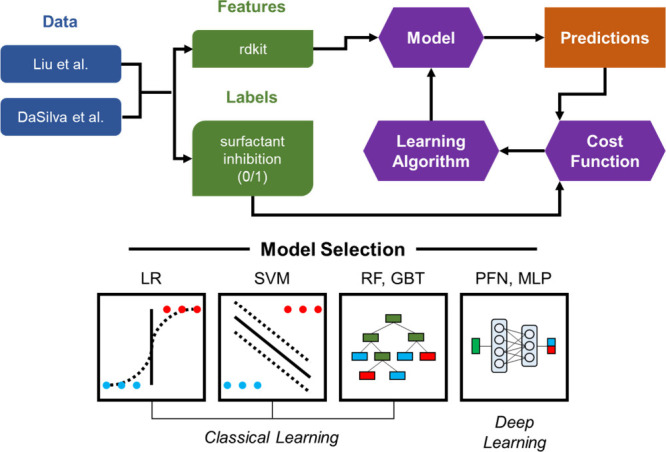
Study design and model selection. Features are extracted from the data and fed into a model architecture: logistic regression (LR), support vector machines (SVM), random forest (RF), gradient-boosted trees (GBT), prior-data-fitted networks (PFN), or multilayer perceptron (MLP). Iterations are performed to minimize the cost of the predictions compared to the original labels.

Table 2. Evaluation of Models by Accuracy, Precision, Recall, F1 Score, and Runtime^a.

data	model	hyperparameters	accuracy	precision	recall	F1 score	runtime (s)
ISO	LR	solver = newton-cg	0.76 ± 0.15	0.77 ± 0.20	0.81 ± 0.18	0.77 ± 0.16	1.6
		C = 0.1
SO	SVM	kernel = sigmoid	0.79 ± 0.13	0.84 ± 0.20	0.75 ± 0.21	0.78 ± 0.18	1.5
		C = 0.1
ISO	RF	n_estimators = 50	0.74 ± 0.17	0.77 ± 0.21	0.79 ± 0.19	0.75 ± 0.17	4.3
		max_depth = 6
SO	GBT	max_depth = 3	0.75 ± 0.16	0.76 ± 0.21	0.84 ± 0.19	0.77 ± 0.17	5.1
		min_child_weight = 0.1
SR	PFN	N/A	0.51 ± 0.13	0.56 ± 0.18	0.93 ± 0.16	0.66 ± 0.13	22.1
ISRO	MLP	depth = 2	0.96 ± 0.08	0.97 ± 0.08	0.97 ± 0.10	0.97 ± 0.08	372.3
		width = 40

^aThe models with the highest F1 scores are described by parameters and type: logistic regression (LR), support vector machines (SVM), random forest (RF), gradient-boosted trees (GBT), prior-data-fitted networks (PFN), and multilayer perceptron (MLP). Data processing: imputed (I); scaled (S); reduced (R); oversampled (O). Metrics are reported as mean and standard deviation for cross-validation across random seeds.

Logistic regression (LR) is a traditional method for attacking classification problems, where a linearized model is fed into a sigmoid function. The output is akin to a probability, which is then subjected to a threshold value to predict. Logistic regression is cost-effective but limited to linearly separable terms. The liblinear, lbfgs, newton-cg, and newton-cholesky logistic regression libraries were evaluated at different values of C across all data processing choices. Imputed, scaled, and oversampled data resulted in the best overall performance under fivefold cross-validation with an accuracy of 76% and an F1 score of 0.77 using the newton-cg solver and C = 0.1. Computation costs varied within an order of magnitude.

Support vector machines (SVMs) were also evaluated as a traditional method for classification. SVMs attempt to find a separating hyperplane in the data, which is very efficient for cleaner (i.e., low in noise) and smaller data sets. The linear, poly, rbf, and sigmoid kernels were evaluated at different values of C. The sigmoid kernel with C = 0.1 achieved the best overall performance on scaled and oversampled data with an accuracy of 79% and an F1 score of 0.78. Computation cost was comparable across the kernels.

Random forest (RF) was evaluated as a tree ensemble method. Random forest uses random sampling and random feature selection to build a bagged network of decision trees, each of which acts as an estimator contributing to the final prediction. The number of estimators (50/100/200) and the maximum tree depth (3/6) were chosen as hyperparameters for tuning. Performance varied widely by hyperparameters and data type. Models with 50 estimators and a maximum depth of 6 achieved the best performance on imputed, scaled, and oversampled data with an accuracy of 74% and an F1 score of 0.75. Computation cost was scaled roughly with the number of estimators.

Gradient-boosted trees (GBT) using XGBoost were also evaluated as a tree ensemble method. Gradient boosting differs from random forest in that it prunes structurally similar trees and prioritizes handling misclassified observations. Typically, this yields higher efficiency at the cost of some fine-tuning potential. The maximum depth (3/6) and minimum child weight (0.1/1/10) were selected as hyperparameters. Performance rarely varied with hyperparameters, but data type had an effect. The best performance was achieved with a maximum depth of 3 and a minimum child weight of 0.1 on scaled and oversampled data with an accuracy of 75% and an F1 score of 0.77.

Prior-data fitted networks (PFN) were evaluated as a deep learning method. The PFN used leverages a pretrained transformer to generate rapid predictions on small-scale tabular data, removing the need for hyperparameter tuning. The best performance was achieved on scaled and reduced data, with an accuracy of 51% and an F1 score of 0.66. Overall, the PFN method performed poorly, and it was close to a random classifier. This may be due to the bottleneck of a small data set, where closer to 1000 observations may have improved performance.

Multilayer perceptrons (MLP) were also evaluated as a deep learning method. Two or three hidden layers of variable width (20/40) were used to generate predictions. Models with only two hidden layers and a width of 40 neurons performed the best on imputed, scaled, reduced, and oversampled data with an accuracy of 96% and an F1 score of 0.97. The extra hidden layer typically reduced performance (likely due to overfitting or slower learning), while the layer width had a varied effect. Imputed missing values had a clear positive impact on performance.

The models from Table 2 are compared visually in Figure 2. Multilayer perceptrons (MLPs) provided the strongest performance among the model types. However, they also required the highest computation cost by a large margin. When considering efficiency, support vector machines (SVMs) and logistic regression (LR) emerge as viable options, with the next best performance and low computation time. The large gap between MLPs and the other methods may be due to intrinsic complexity in the relationship between chemical structure and lung surfactant inhibition, resulting in classes that are not linearly separable. As experimental data on surfactant inhibition grows, the best data treatments and model parameters will become clear. MLP performance will likely continue to scale well with increases in the number of observations, chemical diversity, and molecular descriptors. Additional comparisons of data processing treatments, hyperparameters, and performance vs computation cost are provided in the Supporting Information.

Figure 2.

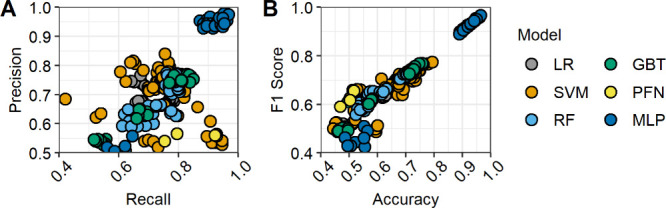
Comparison of classification models grouped by type: logistic regression (LR), support vector machines (SVM), random forest (RF), gradient-boosted trees (GBT), prior-data-fitted networks (PFN), and multilayer perceptron (MLP). (A) Precision (true positives out of retrieved positives) over recall (true positives out of labeled positives). (B) F1 score (harmonic mean of precision and recall) over accuracy (during validation).

There are some limitations to the work described here. First, the selection of molecular descriptors could be further expanded. Although Mordred provides one of the largest and most robust open-source libraries, other options, such as the proprietary Dragon software, may increase performance. In addition, the available data contained a small number of observations due to the novelty of lung surfactant as a toxicological model. This could limit the effectiveness of some algorithms and the available metrics for evaluation. As the field grows, more experimental data will be available to mitigate these factors.

Lung surfactant inhibition is still an emerging field of study, and the mechanisms for surfactant dysfunction are diverse. As our toxicological understanding of lung surfactant inhibition and other pathways leading to adverse health effects increases, capturing all the complex relationships between chemical structure and biological activity becomes prohibitively difficult. The machine learning models evaluated in this study present a promising approach for the rapid development of structure–activity prediction. Rather than resource-intensive systematic testing of large sets of chemicals, a smaller set can be leveraged for large-scale prediction, narrowing the scope for further screening.

Conclusions

In the dynamic landscape of environmental risk assessment, quantitative structure–activity relationship (QSAR) modeling has emerged as a pivotal tool for predicting the toxicological activities of chemical compounds based on their structural features. However, as the complexity of chemical data sets continues to grow, traditional QSAR models face challenges in capturing intricate relationships and exhibiting robust predictive performance. Machine learning techniques have brought about a paradigm shift, offering unparalleled opportunities to enhance the accuracy and efficiency of predictive modeling.

We have demonstrated the application of classification techniques to identify chemicals that may inhibit lung surfactant. Among six model types, the multilayer perceptron method provided the strongest performance and may scale well as the available experimental data increases. As little is known about the relationships between chemical structure and surfactant inhibition, this framework may aid hazard identification, particularly high-throughput screening. The synergy between machine learning and QSAR holds promise for addressing challenges related to nonlinearity, high dimensionality, and intricate interactions within chemical data sets.

Glossary

Abbreviations

LS

lung surfactant

QSARS

quantitative structure–activity relationships

CDS

constrained drop surfactometer

SMILES

simplified molecular input line entry system

PCA

principal component analysis

ANN

artificial neural network

PFN

prior-data-fitted network

MLP

multilayer perceptron

Relu

rectified linear unit

LR

logistic regression

SVM

support vector machines

RF

random forest

GBT

gradient-boosted trees

CAS

Chemical Abstracts Service

I

imputed

S

scaled

R

reduced

O

oversampled

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/envhealth.4c00118.

• Full results comparing data treatments and costs (Table S1 and Figures S1 and S2) (PDF)

The authors declare no competing financial interest.

Special Issue

Published as part of Environment & Healthspecial issue “Artificial Intelligence and Machine Learning for Environmental Health”.