Size effects of the tensile mechanical behavior of basalt containing hidden joints investigated by DFN–FDEM modeling

Abstract

Basalt, which is a geological medium used for engineering construction in Southwest China, contains defect structures at various scales. In particular, the widespread presence of mesoscale hidden joints significantly affects the mechanical properties of basalt and the stability of engineering structures. However, research in this specific subject has been limited. Hence, this study focused on basalt found in the Baihetan Hydropower Station and systematically explored the size effect of the tensile mechanical behavior of basalt with hidden joints. The investigation was based on a synthetic rock mass (SRM) model that combines the micro-discrete fracture network (μDFN) method and finite-discrete element method (FDEM), providing in-depth insights into the multiscale fracture mechanism of basalt. The results showed that: (1) the μDFN–FDEM model generated based on the statistical geometric parameters of hidden joints could accurately consider the real meso-structural characteristics of basalt, successfully replicating the mechanical behavior observed in laboratory tests and engineering sites. (2) The representative elementary volume (REV) size of basalt rock blocks containing hidden joints was approximately 0.5 m. With an increase in the sample size, the stress–strain curve characteristics under Brazilian disc splitting transitioned from a single-peak shape to a zigzag shape and then to a multi-peak shape, and the failure modes also shifted from single-center splitting failure to local structure-controlled failure and ultimately to a multicenter splitting failure.

(3) The failure mechanism of basalt containing hidden joints evolved with increasing sample size, progressing from high stress-induced tensile failure to local structure-controlled failure, and finally to tensile failure resulting from stress-structure coupling. These findings can help further enhance and refine fundamental theories and technical methods for multiscale analyses in geotechnical engineering, providing a robust scientific and technological support for the safe construction and operation of deep underground engineering projects.

Highlights

• •A DFN–FDEM model was used to characterize the basalt containing hidden cracks.
• •The REV size of the tensile strength of basalt rock blocks was determined.
• •The size effect of the tensile mechanical behaviors of basalt was analyzed.
• •The failure mechanism of basalt with increasing sample size was revealed.

1. Introduction

A rock mass is a complex heterogeneous geological body that forms over a long period through geological processes. It comprises rock blocks and structural planes and is found within a specific geological environment. Despite the apparent completeness of rock blocks, they contain mesoscale primary defects, such as grain boundaries, microcracks, and microvoids, which result in a significant size effect on their mechanical properties. These properties play a crucial role in the stability of engineering structures and the occurrence of various adverse geological disasters [[1], [2], [3], [4]]. An accurate understanding of the mechanical properties, including the deformation, strength, and failure characteristics, of rocks is vital for engineering design, construction, and disaster control. However, the existence of the rock size effect makes it challenging to obtain the mechanical properties of large rock masses found on-site from the test results of small rock blocks in the laboratory [[5], [6], [7], [8]]. Hence, it is crucial to explore the multiscale mechanical properties of brittle rocks.

Scholars have conducted systematic investigations into the size effect of different types of rocks, including sandstone, marble, and granite, under various stress conditions such as Brazilian disc splitting, uniaxial compression, and triaxial compression [[9], [10], [11], [12], [13], [14], [15], [16]]. The rock strength typically decreases with increasing sample size and tends to stabilize once the sample size reaches a critical value known as the representative element volume (REV). Currently, there is no unified understanding of the underlying causes of the rock size effect. Nevertheless, they can be generally classified into three categories: rock heterogeneity, rock end friction effect, and the combined effect of these factors. The size effect of rocks is a complex materials science problem influenced by both internal factors (e.g., particle size, mineral composition, defect type, and defect distribution) and external factors (e.g., loading rate, temperature, and saturation). To explain this size effect phenomenon and provide a theoretical basis for engineering applications, various size-effect models of rocks have been proposed and modified, including the fracture energy size effect, statistical size effect, multifractal size effect, unified size effect, and some empirical or semiempirical size-effect models.

Various methods have been employed to study the rock size effect, including tests, theoretical analyses, empirical estimation, and numerical simulations. In particular, the synthetic rock mass (SRM) method, which combines different numerical models representing the complete matrix with a discrete fracture network (DFN) model representing the structural planes, has been widely utilized for multiscale mechanical research in geotechnical engineering [17,18]. Numerical methods used in this research are typically categorized into continuous methods (such as the finite difference method (FDM), finite element method (FEM), and boundary element method (BEM)), discontinuous methods (such as the discontinuous deformation analysis (DDA) and discrete element method (DEM)), and hybrid methods (such as the finite-discrete element method (FDEM)). In particular, the FDEM, which integrates the strengths of both continuous and discontinuous methods, has become an important simulation technology for particle interaction, fragmentation, and fracture of brittle geotechnical materials [19,20]. By utilizing the SRM model, which incorporates a DFN model with multiple numerical software packages, such as the universal distinct element code (UDEC) and particle flow code (PFC), the size effect of fractured rocks has been systematically explored [[21], [22], [23], [24]].

Basalt, which is a typical volcanic extrusive rock, plays a crucial role as a geological environment medium in engineering construction in southwest China [25,26]. Zhang et al., Jiang et al., and Hu et al. examined the effects of different mesoscale defects, such as phenocrysts, amygdales, and hidden joints, on the macroscopic mechanical properties of basalt rock blocks. In these investigations, laboratory tests, numerical simulations, and statistical analyses were utilized to establish corresponding mechanical models and derive empirical formulae [[27], [28], [29]]. Liu et al., Meng et al., Jiang et al., and Dai et al. systematically analyzed the failure, deformation characteristics, and fracture evolution laws of basalt rock masses during the excavation process of underground caverns in the Baihetan Hydropower Station. These analyses were conducted through geological surveys, field monitoring, and numerical simulations, providing insights into the failure mechanisms of basalt rock masses [[30], [31], [32]]. Moreover, various methods have been used to systematically explore the size effect, anisotropy effect, unloading effect, and constitutive models of columnar jointed basalt, which has unique structural characteristics [[33], [34], [35], [36]].

The multiscale effect of brittle rocks with complex structures has been a fundamental scientific problem in the field of rock mechanics and engineering. However, on the one hand, existing research on the mechanical properties of basalt has mainly focused on conventional laboratory tests, theoretical analysis, or numerical simulations, and to some extent, the complex structural characteristics of such geotechnical materials have been overlooked. In particular, the influence of hidden joints on the size effect of the mechanical properties of basalt is often not considered. On the other hand, the conventional analysis of the rock size effect typically focuses on uniaxial compression conditions, with less emphasis on the size-dependent mechanical behavior under tensile loading. Moreover, commonly used numerical methods are predominantly continuous or discontinuous methods, with the FDEM being rarely introduced. Hence, a more thorough and systematic exploration is required to address the size-effect problem of rocks.

In this study, the size-dependent tensile mechanical behavior of basalt rock blocks containing hidden joints found in the Baihetan Hydropower Station was systematically explored based on an SRM model that combines the μDFN and FDEM models, providing a comprehensive understanding of the multiscale failure mechanism. The rest of this paper is organized as follows. First, the materials and methods are introduced, including the engineering background, distribution characteristics of hidden joints, basic principle of the FDEM, and establishment of an SRM model of basalt (Section 2). Subsequently, the results are presented, i.e., the size effect of the tensile mechanical behavior of basalt containing hidden joints, such as the tensile strength, stress–strain curve characteristics, failure mode, and crack evolution law (Section 3). Finally, the paper is concluded with a brief discussion and some conclusions (Sections 4, 5).

2. Materials and methods

2.1. Engineering background

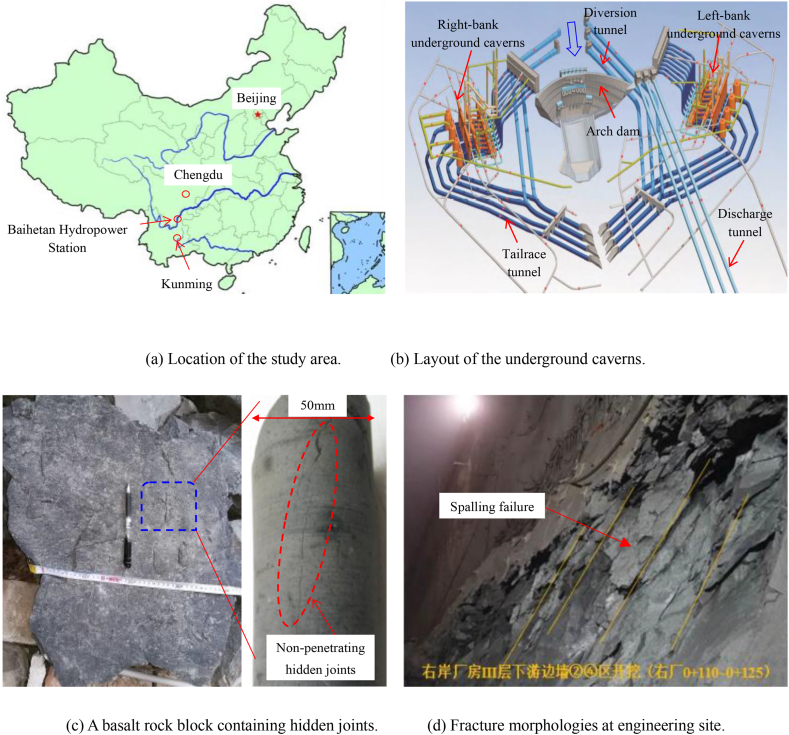
The Baihetan Hydropower Station, which is globally the largest hydropower project recently constructed, is located in the lower reaches of the Jinsha River between Sichuan Province and Yunnan Province in southwest China, with a total installed capacity of 16,000 MW [37]. The main body of the project includes dams, water diversion and power generation systems, and flood discharge and energy dissipation buildings, as shown in Fig. 1(a) and (b). The diversion and power generation systems on the left and right banks are located in the mountains on both sides of the upstream of the arch dam, where the four caverns, including the main powerhouse, the main transformer cavern, the tail water pipe maintenance gate chamber, and the tail water surge chamber, are arranged in parallel from the upstream to the downstream. The excavation size of the underground caverns on the left and right banks is the same, in which the main powerhouse is 438 m long, 31–34 m wide, and 88.7 m high. The rock wall thickness between the main transformer room (with length, width, and height of 368, 21, and 39.5 m, respectively) and the main powerhouse is approximately 61 m. The distance between the cylindrical tailrace surge chamber (with a diameter range of 43–48 m and a height range of 77–93 m) and the main transformer chamber is approximately 85 m. These attributes make the entire underground powerhouse cavern group the largest underground project in the world.

Fig. 1.

Layout of underground caverns and structural characteristics of basalt at Baihetan Hydropower Station [37] (It is noted that the permission to reprint Fig. 1 is obtained from the original publisher).

The Baihetan Hydropower Station belongs to a deep valley “V” type landform, with a very complicated geological condition. The engineering area is located in the Emeishan basalt stratum, and the lithology is mainly cryptocrystalline basalt, amygdaloidal basalt, and oblique basalt in the P₂β²–P₂β⁶ layer. The basalt in this area exhibits complex structural features owing to the special diagenesis and structural geology. Basalt rock masses commonly contain random hard structural planes, such as joints and cracks at the macroscale (meter-level to 10-m level), and local weak structural planes, such as faults and dislocation zones, at the engineering or geological body scale (above 10-m level). In addition, a large number of hidden joints at the mesoscale (centimeter-to-decimeter level) are typically found within basalt rock blocks, as illustrated in Fig. 1(c). Among the different types of basalts, the development degree of structural planes in cryptocrystalline basalt is the most significant. The rock mass is slightly weathered or fresh, dense and hard, with good integrity, which is dominated by the Class III surrounding rock mass. The underground cavern group of the Baihetan Hydropower Station belongs to a medium-deep buried condition, in which the ground stress is mainly a valley tectonic stress, and the horizontal stress is greater than the vertical stress, with the maximum principal stress values of the underground powerhouse on the left and right banks being in the ranges of 19–23 MPa and 22–26 MPa, respectively. In general, the underground cavern group is located in the middle and high ground stress area.

Results have shown that the average uniaxial compressive strength of basalt reaches 200 MPa, with a high strength stress ratio greater than 7, indicating that basalt is difficult to be destroyed under existing conditions. However, due to the large engineering scale, complex structural characteristics, and high in-situ stress, the fracture problem of surrounding rock masses during underground cavern excavation is significant. A series of failure modes, such as spalling, fracture relaxation, block shedding, collapse, and mild rock bursts, are widely revealed, among which spalling failure is the most significant, bringing great challenges to the stability control of surrounding rock masses, as shown in Fig. 1(d). This phenomenon highlights the inconsistency between the low rock mass strength encountered in engineering sites and the extremely high rock strength observed in laboratory tests. The essence of this issue lies in the multiscale fracture problem of hard brittle rocks, which is closely related to the presence of hidden joints in basalt rock blocks. Spalling failure is a typical failure mode observed in deep underground engineering and has been systematically explored; the most representative problems are the fracture problems of marble in the deep-buried diversion tunnel of Jinping II Hydropower Station and Lac du Bonnet (LdB) granite in Underground Research Laboratory (URL) of Atomic Energy of Canada Limited (AECL). For underground engineering, the excavation through hard rocks breaks the original stress balance state, resulting in a brittle failure of the surrounding rock mass near a tunnel face, mainly manifested as tensile fractures [38,39]. Hence, it is crucial to explore the size effect of the mechanical behavior of basalt containing hidden joints, to reveal its multiscale failure mechanism.

2.2. Statistical characteristics of hidden joints in basalt

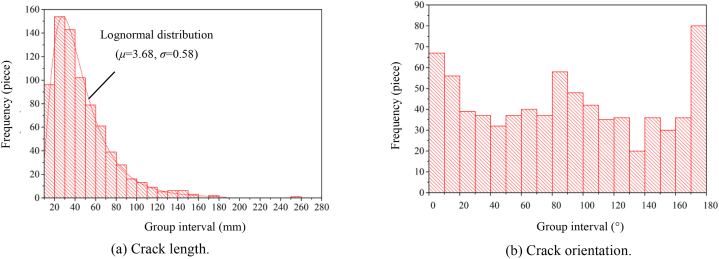
The CT scanning test conducted on some standard-sized basalt core samples with a diameter of 50 mm and a height of 100 mm provides valuable insights into the distribution characteristics of hidden joints in basalt. However, due to the high cost associated with CT scanning, it is not feasible to scan a large number of basalt core samples with standard sizes. As a result, there is limited availability of CT scanning data. Moreover, the limited penetration ability of CT scanning and the dense and hard nature of basalt restrict the scanning to only standard-sized samples. This makes it challenging to obtain more realistic and comprehensive data, particularly for large basalt rock blocks with sizes in the tens of centimeters. To accurately understand the structural characteristics of basalt rock blocks, a series of processing steps were undertaken on the surfaces of numerous basalt rock blocks, typically with sizes in the tens of centimeters, obtained from underground caverns. These steps included digital imaging, on-site sketching, image processing, and statistical analysis, as depicted in Fig. 2. Through this process, the distribution characteristics of the geometric parameters related to hidden joints were obtained. These parameters primarily included the crack length, crack orientation (defined as the angle between the length direction of the rock blocks and the crack direction), and crack density.

Fig. 2.

Physical forms and sketches of a basalt rock block containing hidden joints obtained from the underground caverns at Baihetan Hydropower Station.

In this study, approximately 800 hidden joints with a length of 10 mm or more, contained in approximately 30 basalt rock blocks, were selected and analyzed. Fig. 3 shows the distribution characteristics of the geometric parameters of these hidden joints. Clearly, the hidden joints in the basalt rock blocks exhibit irregular shapes, with a scattered distribution, short closures, intermittent extensions, and low penetration. The crack orientation does not display any noticeable regularity, indicating a uniform distribution without any dominant joint group. This observation may be closely related to the formation mechanism of the hidden joints. The crack length ranges from a few centimeters to tens of centimeters and follows a lognormal distribution, with a mean (μ) of 3.68 and a standard deviation (σ) of 0.58. Based on calculations, the areal density P₂₀, which is defined as the number of cracks per unit area, was found to be 0.00025 pieces/mm², and the areal density P₂₁, which represents the crack length per unit area, was found to be 0.012 mm/mm². Notably, hidden joints are primary tensile fracture structures formed by the rapid condensation and contraction of magma during the diagenesis of basalt. They belong to a V-level hard structural plane, which significantly influences the mechanical properties of basalt rock blocks. Consequently, these hidden joints have a certain impact on the stability of engineering structures.

Fig. 3.

Distribution characteristics of the geometric parameters of hidden joints in a basalt rock block.

2.3. Introduction to FDEM

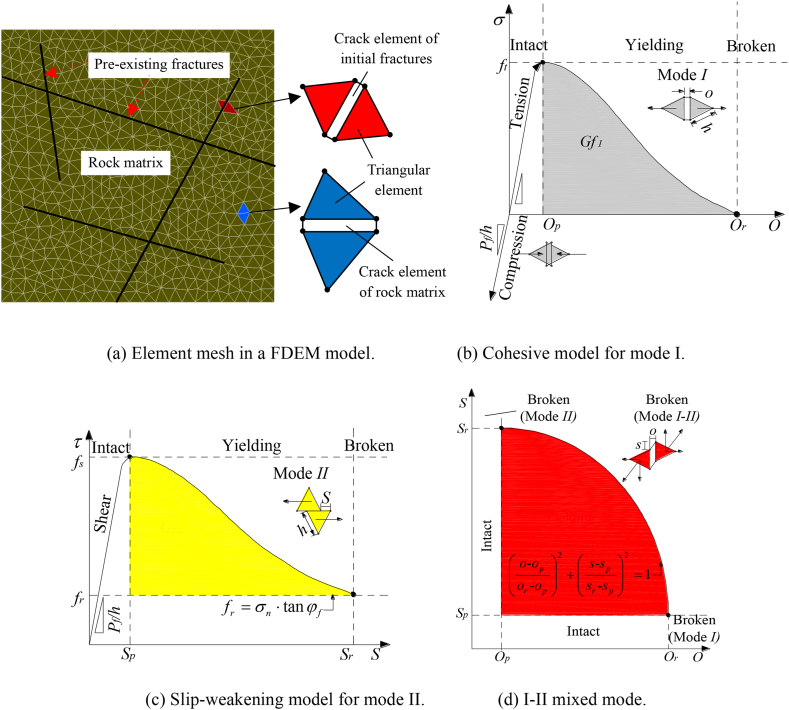
In this study, the Irazu code, which is based on the FDEM principle, was utilized for calculations. The model is composed of a three-node triangular finite element mesh, with four-node adhesive crack elements embedded between all the adjacent element edges, as illustrated in Fig. 4. The mechanical analysis of the triangular elements followed the linear elastic continuous medium theory. Contact forces were generated between all the contact pairs of the triangular elements, with the tangential friction force being calculated according to the Coulomb friction law, and the normal repulsive force was solved using the distributed contact-force penalty function method based on the potential function. By employing the maximum tensile stress failure criterion and the Mohr–Coulomb (MC) failure criterion, cohesive crack elements were used to simulate the progressive material failure, which may experience yielding and fracturing in Mode I (tensile failure), Mode II (shear failure), or mixed mode I–II (tensile–shear failure).

Fig. 4.

Mesh and constitutive behavior of crack elements in a FDEM model [40] (It is noted that the permission to reprint Fig. 4 is obtained from the original publisher).

The various defects present in rocks can be incorporated into the FDEM model by introducing a finite number of initial fractures distributed along the bedding planes. Moreover, this approach can be extended to encompass a broader range of scenarios involving arbitrary random discontinuities, known as the DFN–FDEM model. In the DFN–FDEM model, the DFN model representing the defect structures is combined with the FDEM model representing the intact rock matrix. A typical DFN model includes two sets of properties: (1) DFN geometric parameters, such as the orientation, length, spacing, and density of cracks; and (2) DFN mechanical properties, which corresponds to crack elements with distinct mechanical properties from the rock matrix. Based on the bonding force of the discontinuities, crack elements can be categorized into two types: cohesive and fractured. The mechanical behavior of cohesive crack elements mirrors that of the four-node cohesive crack element model mentioned earlier. On the other hand, for fractured crack elements, the elimination of these elements results in a purely frictional discontinuity surface, with its mechanical behavior solely governed by the contact model [40].

2.4. Generation of the SRM model of basalt

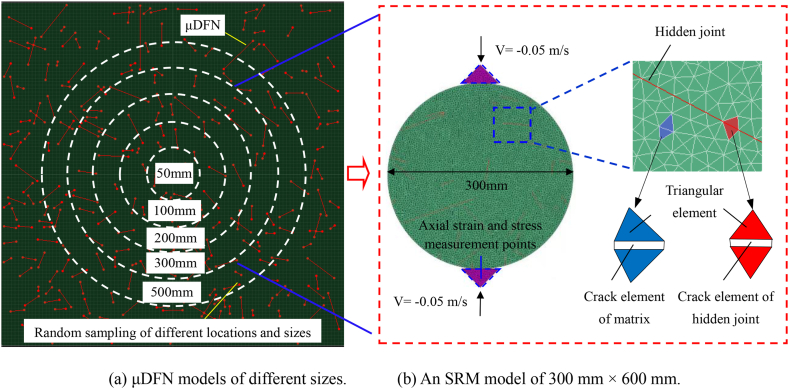
A comprehensive approach was adopted to investigate the impact of specimen size on the tensile mechanical properties of basalt containing hidden joints. Initially, a large DFN model measuring 5000 mm × 5000 mm was generated using the Monte Carlo method, based on the distribution characteristics of the geometric parameters of hidden joints. As the hidden joints are smaller than the macro-scale structural planes, they are referred to as μDFN. Subsequently, a series of Brazilian discs of varying locations and sizes were randomly selected within the model to create multiple small μDFN sub-models with diameters ranging from 25 mm to 600 mm, as shown in Fig. 5(a). These sub-models, representing hidden joints, were then integrated into the FDEM code Irazu, which represents the complete matrix, to establish an SRM model (μDFN–FDEM) that captures the true meso-structural characteristics of basalt, as shown in Fig. 5(b). Subsequent numerical tests involved conducting Brazilian disc splitting experiments on these SRM models using a range of meso-parameters obtained through verification, as shown in Table 1. The effects of the sample size on the macro-mechanical properties, such as the stress–strain behavior, tensile strength, and failure modes, of the basalt rock blocks with hidden joints, were analyzed, along with the micro-fracture evolution laws, including the stress, strain, and crack propagation. These analyses aim to reveal the multiscale fracture mechanism of basalt. To reduce this potential variability, uncertainty, and randomness, and considering the calculation time constraints, ten SRM models were created at each size level, and the average values of the calculation results from these samples were considered under the specified working conditions.

Fig. 5.

SRM (μDFN-FDEM) models of different-sized basalt rock blocks with hidden joints for Brazilian disc modelling.

Table 1.

Meso-mechanical parameters of standard-sized basalt samples used in FDEM models.

Mechanical parameters	Matrix	Hidden crack	Loading plate
Bulk density, ρ (kg/m3)	2900.00		8000
Poisson's ratio, ν	0.15		0.25
Young's modulus, E (GPa)	50.00		210
Internal friction angle, φ (°)	40.00	25.00	0.7
Cohesive strength, c (MPa)	75.00	15.00	200
Tensile strength, ft (MPa)	18.50	4.00	200
Mode-I fracture energy, Gf1 (N/m)	100.00	20.00	2400
Mode-II fracture energy, Gf2 (N/m)	1000.00	200.00	24000
Normal contact penalty, Pn (GPa·m)	500.00	100.00	2100
Tangential contact penalty, Pt (GPa/m)	500.00	100.00	2100
Fracture penalty, Pf (GPa)	500.00	100.00	2100

In the calibration process of the meso-parameters for the FDEM simulation, a systematic approach was adopted. Standard-sized random sampling was conducted under various loading conditions, including Brazilian disc splitting, uniaxial compression, and triaxial compression, within the previously generated large μDFN model. For each working condition, 10 numerical samples were selected, comprising three intact samples and seven cracked samples for uniaxial and triaxial compression, as well as four complete specimens and six cracked specimens for Brazilian disc splitting. Each specimen exhibited varying distribution characteristics in terms of the number, size, location, and angle of cracks, as depicted in Fig. 6. Subsequently, a series of FDEM simulations was performed on these samples, and the corresponding mechanical parameters were obtained. These parameters were then compared with the laboratory test results to validate and calibrate the meso-parameters of the SRM model. This calibration process was aimed at ensuring that the simulated mechanical behavior of the basalt samples closely aligned with the experimental observations, thereby enhancing the accuracy and reliability of the SRM model in capturing the true meso-structural characteristics of basalt [41].

Fig. 6.

Basalt FDEM specimens with a standard size for the meso-parameters calibration.

For uniaxial compression, the standard dimensions of the numerical basalt samples used for the meso-parameter verification were 50 mm × 100 mm (width × height), with triangular elements having a side length of 0.5 mm. Two slightly wider loading plates were positioned at the lower and upper ends. For axial loading, a vertical displacement rate of 0.05 m/s in opposite directions with the same value at both ends was employed. Although this value was higher than that used in laboratory tests, a sensitivity analysis of the loading rates indicated that a displacement rate ≤0.1 m/s can ensure that the model was in a quasi-static state and that the stability of the numerical result was maintained. The confining pressures corresponding to the laboratory tests were applied to the left and right boundaries, and a plane strain model was utilized with a time step of 1.5 × 10⁻⁶ ms. The axial strain and stress were determined using the node force and displacement of the lower and upper loading plates, while the lateral strain was calculated based on the node displacement of the middle local areas on the left and right sides.

The FDEM model of the basalt comprised hidden joints and a matrix, both of which were assumed to be homogeneous isotropic materials. In the selection of the initial meso-parameters, the matrix parameters were based on the test results of cryptocrystalline basalt. The values of the hidden joints, modeled as cohesive materials, were determined by referencing the shear test results of structural planes or by appropriately adjusting the matrix parameters. The parameters of the upper and lower plates were based on the properties of steel. An iterative calibration procedure was employed in this study. A series of numerical tests, including Brazilian disc splitting, uniaxial compression, and triaxial compression with standard sizes, were conducted to establish a set of meso-parameters. This iterative process was aimed to ensure that the obtained macro-mechanical properties by FDEM modeling aligned with the laboratory test results, as illustrated in Table 2 [42,43].

Table 2.

Macro-mechanical parameters of standard-sized basalt samples obtained through testing and FDEM modelling [42,43].

Type	E (GPa)	c (MPa)	φ (°)	UCS (MPa)	BTS (MPa)
Simulation	45.08	52.15	46.81	231.67	12.71
	49.88	82.63	39.78	318.46	21.66
	48.53	22.78	35.72	80.89	7.37
	43.23	37.8	46.55	161.09	22.51
	40.12	33.56	42.6	140.34	16.33
	47.68	25.33	40.57	64.23	26.05
	35.46	32.47	47.08	150.79	11.84
	49.88	82.63	39.78	320.21	26.05
	49.88	82.63	39.78	320.21	26.05
	49.88	82.63	39.78	320.21	26.05
Average	45.96	53.46	41.85	210.81	19.66
Test	45.82	57.44	41.16	197.01	18.50

3. Results

3.1. Size effect on tensile strength

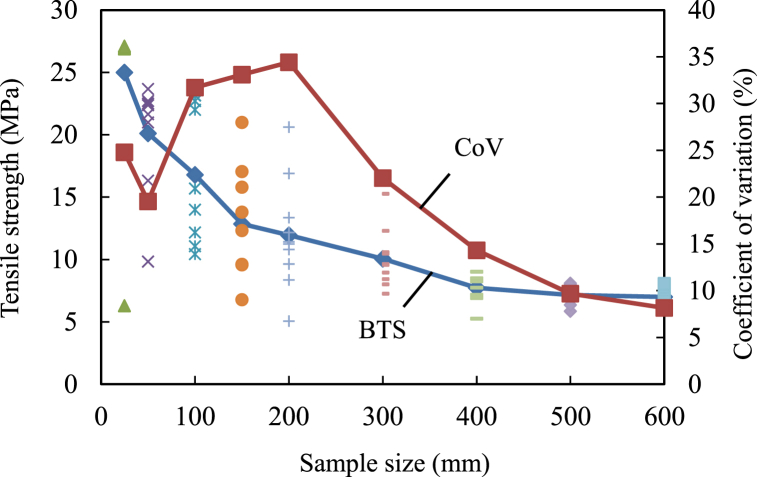
To understand the impact of sample size on the tensile strength of basalt containing hidden joints, the Brazilian tensile strength (BTS) and its coefficient of variation (CoV) for SRM models of various sizes were calculated. By analyzing the variation in the tensile strength with increasing sample size, the mechanical REV and the corresponding equivalent tensile strength were determined. Fig. 7 shows this analysis, where CoV is defined as the ratio of the standard deviation to the mean value. A CoV of less than 10 % was considered acceptable in this study.

Fig. 7.

Effect of sample sizes on the BTS of basalt samples with hidden joints.

With increasing sample size, the mean value of the BTS of basalt with hidden joints gradually decreased, with a more pronounced decreasing trend for smaller sizes. It eventually stabilized within a certain range after reaching a certain size threshold. With the increase in the sample size, the fluctuation range and dispersion degree in the BTS values between the different basalt samples of the same size decreased. The CoV initially showed a significant fluctuation, followed by a nonlinear reduction. Specifically, for sample sizes less than 200 mm, the variation in the BTS between different samples of the same size was wide, with significant CoV fluctuations exceeding 20 %, which was indicative of the non-representativeness of the model at this size. For sample sizes ranging from 200 to 400 mm, the variation in the BTS between different samples of the same size decreased significantly, with the CoV reducing but still remaining above 10 %. Once the sample size was ≥500 mm, the CoV fell below 10 %, and the BTS stabilized, suggesting that the numerical model at this size could represent the entire basalt rock blocks. The REV size of the basalt rock blocks containing hidden joints, determined by the dispersion and fluctuation in the BTS across different sample sizes, was 500 mm. At this size, the BTS was 7.15 MPa, which was approximately 30 % of that of the standard-sized basalt sample. Hence, these data can be considered as the equivalent continuum properties and utilized as input parameters in the numerical engineering analysis of complete rock masses or rock blocks in jointed rock masses.

In conclusion, because of the complexity of the characteristics of the natural rock structure, the mechanical parameters of standard-sized basalt obtained from laboratory tests significantly differ from those of larger basalt rock blocks. This implies that the mechanical parameters of large rock blocks cannot be accurately estimated based on the laboratory test results of small rock samples. Therefore, it is essential to conduct large in situ tests to obtain more accurate data for engineering applications. Although large in situ tests can partly characterize the mechanical properties of rock blocks or rock masses, they come with challenges, such as difficulty during testing, high cost, data dispersion, and poor reliability. This limits the feasibility of conducting in situ tests in a large number of engineering projects. The REV size of rock blocks obtained through a numerical simulation analysis typically falls in the range of 500–1000 mm, aligning with the size obtained from in situ tests. This size range can effectively characterize the structural characteristics and mechanical parameters of rock blocks. Therefore, it is crucial to conduct size-effect analysis by establishing a numerical model that accurately represents the real meso-structural characteristics of rock blocks. The research outcomes obtained from such analyses will be meaningful and valuable in understanding the behavior of rock masses in engineering applications.

3.2. Size effect on the characteristics of stress–strain curves

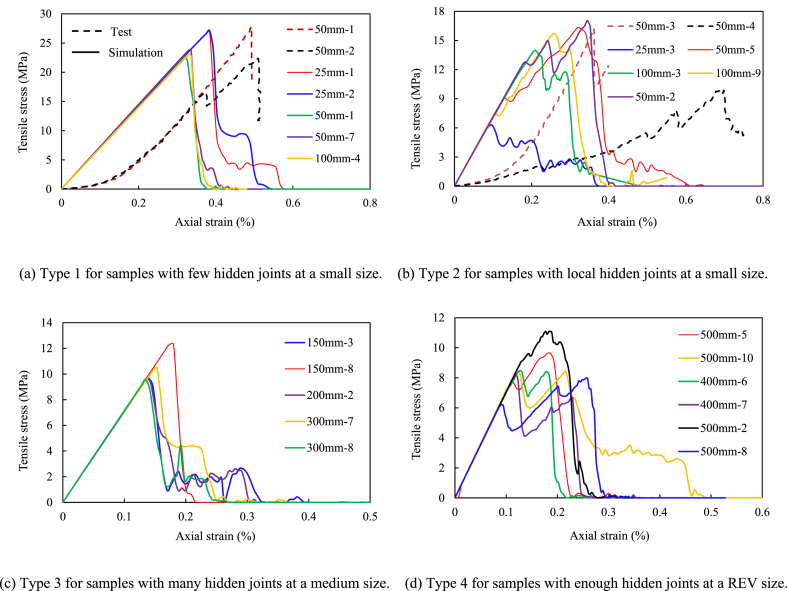
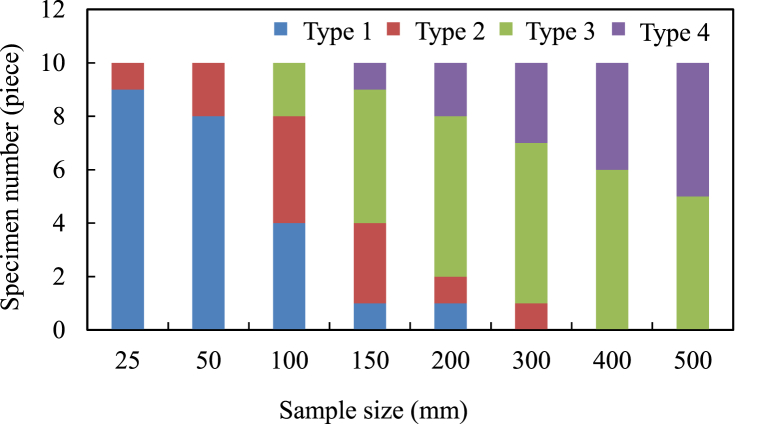
Fig. 8 shows the typical stress–strain curves of different-sized basalt samples containing hidden joints under Brazilian disc splitting, in which the real and imaginary lines represent the laboratory test and FDEM simulation results respectively, and different colored legends represent different sample numbers. Overall, the tensile stress–strain curves of basalt samples containing hidden joints can be categorized into four main types on the basis of their characteristics: high-strength unimodal shape (Type 1), serrated shape (Type 2), low-strength unimodal shape (Type 3), and multimodal shape (Type 4). Although basalt samples under each size condition contain two or more curve types, the dominant curve type is determined, one or two curve types, and it changes with the increase in the sample size. Generally, the dominant curve type of small-sized basalt samples is Type 1 or Type 2, that of medium-sized basalt samples is Type 3, and that of REV-sized basalt samples is Type 4, as shown in Fig. 9. It should be noted that, the “small size” generally refers to a size range of 25–100 mm, the “medium size” refers to a size range of 150–400 mm, and the “REV size” refers to sizes 500 mm and above. The specific details of each type are as follows.

Fig. 8.

Typical stress-strain curves of different-sized basalt samples containing hidden joints under Brazilian disc.

Fig. 9.

Stress-strain curve type variation in different-sized basalt specimens under Brazilian disc splitting.

In Fig. 8(a), the stress–strain curve of small-sized intact basalt samples appears to be smooth, with subtle pre-peak nonlinear characteristics and a predominantly linear elastic behavior. The peak strength is exceptionally high, followed by a rapid post-peak stress drop, indicating pronounced brittleness, which is characteristic of a high-strength unimodal shape (Type 1). In Fig. 8(b), the stress–strain curve of the small-sized basalt samples with local hidden joints exhibits a serrated pattern, with a noticeable stress fluctuation in the pre-peak stage. The peak strength decreases significantly, and the post-peak stress reduction is gradual, indicating a decrease in brittleness, representing a serrated shape (Type 2). Fig. 8(c) shows the stress–strain curve of the medium-sized basalt samples with numerous hidden joints, exhibiting a relatively smooth behavior with linear elasticity in the pre-peak stage. The peak strength is lower, and the post-peak stress reduction is gradual, suggesting a notable decrease in brittleness, which is characteristic of a low-strength unimodal shape (Type 3). In Fig. 8(d), the stress–strain curve of the REV-sized basalt samples with sufficient hidden joints has a linear elastic pre-peak stage. The peak stage exhibits a bimodal or multi-peak shape, with some samples even displaying a distinct yield plateau near the peak. The peak strength is the lowest, and the post-peak stress reduction is more gradual, indicating a significant decrease in brittleness, corresponding to a bimodal or multimodal shape (Type 4).

In summary, with the increase in the sample size, the internal defect structures within basalt also increased, leading to a gradual decrease in heterogeneity. This evolution is reflected in the tensile stress–strain curve under Brazilian disc splitting, which undergoes significant changes from the single-peak shape observed for small-sized intact samples to the serrated shape observed for medium-sized samples with local or more defects, and eventually to the double- or multi-peak shape exhibited by REV-sized samples with sufficient defects. This progression is accompanied by a continuous decrease in the brittleness degree of the material. The FDEM simulation results closely align with the laboratory test results, indicating a good agreement between the two methodologies.

3.3. Size effect on failure modes

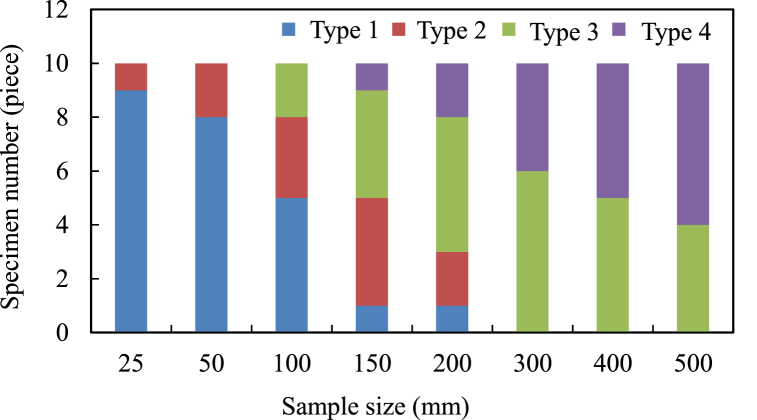
Fig. 10 shows the typical failure modes of different-sized basalt samples with hidden joints under Brazilian disc splitting, where the black, red, and cyan lines represent the initial hidden joints, shear failure cracks, and tensile failure cracks, respectively. Overall, the tensile failure modes of the basalt samples with hidden joints can be categorized into four main types based on their characteristics: single-center type (Type 1), noncentral type (Type 2), center-related type (Type 3), and multicenter type (Type 4). Although two or more failure mode types are observed in the basalt samples under each size category, the dominant failure type is determined, one or two failure types, and is closely related to the sample size. Generally, the dominant failure type of small-sized basalt samples is Type 1 or Type 2, that of medium-sized basalt samples is Type 3, and that of REV-sized basalt samples is Type 4, as shown in Fig. 11. The specific details of each type are as follows:

Fig. 10.

Typical failure modes of different-sized basalt samples with hidden joints under Brazilian disc splitting.

Fig. 11.

Failure mode variation in different-sized basalt specimens under Brazilian disc splitting.

In Fig. 10(a), the small intact basalt specimen exhibits a single-center splitting failure mode, characterized by a straight and smooth fracture surface located near the specimen center, parallel to the loading direction, predominantly comprising tensile cracks. Local crushing and shear failure can be observed at the lower and upper ends of the sample, representing a single-center type failure mode (Type 1). Fig. 10(b) shows the failure mode of the small-sized basalt samples with local hidden joints, exhibiting a noncentral failure mode. In this scenario, a main arc-shaped fracture extends from the outer part of the sample, with the rough fracture surface misaligned with the sample center, deviating from the original trajectory. The local initial hidden joints play a significant role, leading to shear failure, tensile failure, or a combination of both (i.e., a composite tension–shear failure), indicating a noncentral-type failure mode (Type 2). In Fig. 10(c), the medium-sized basalt samples with numerous hidden joints exhibit a center-related splitting failure mode. The relatively rough fracture surface was predominantly centered within the sample but deflected near the hidden joints. The local initial hidden joints in the middle of the sample influenced the failure pattern, leading to a composite tension–shear failure dominated by tensile failure, with shear failure occurring on the hidden joint surface and tensile failure at the crack tip, representing a center-related-type failure mode (Type 3). Fig. 10(d) shows the failure mode of the REV-sized basalt samples containing ample hidden joints, exhibiting a multicenter splitting failure mode. Multiple fracture surfaces extend from the upper end face to the lower end face, with the overall fracture trajectory being centralized in the sample but deflecting near the hidden joints. This mode combines the characteristics of multiple Type 3 failures. The composite tensile–shear failure was primarily governed by tensile failure, with shear failure occurring on the hidden joint surface and tensile cracks at the crack tip, representing a multicenter-type failure mode (Type 4).

In summary, with the increase in the sample size, more hidden joints occurred within the basalt, leading to a gradual decrease in its homogeneity. This evolution is reflected in the tensile failure modes observed under Brazilian disc splitting, which undergo significant changes from the single-center splitting failure observed in small-sized intact samples to the local structure-controlled failure seen in medium-sized samples with local or more defects, and eventually to the multicenter splitting failure exhibited by REV-sized samples with abundant defects. The FDEM simulation results are in good agreement with those obtained from laboratory tests or engineering sites, confirming the reliability and accuracy of the numerical modeling approach.

3.4. Size effect on crack evolution laws

The macroscopic failure of brittle rocks stems from the continuous closure, initiation, expansion, and penetration of the initial microcracks inside the sample, leading to a gradual fracture process from continuous to discontinuous. In this section, the meso-mechanical behaviors, such as the strain field, stress field, and crack propagation, of the FDEM samples of basalt of different sizes with hidden joints under Brazilian disc splitting are further examined. The analysis was aimed at revealing the multiscale failure mechanism, as shown in Fig. 12, Fig. 13, Fig. 14, Fig. 15, with marker points I–VI representing distinct failure stages. Given that the failure of brittle rocks during Brazilian disc splitting is primarily induced by tensile stresses, this study emphasized the horizontal stress σ_xx.

Fig. 12.

Fracture evolution processes of intact basalt FDEM samples at a small size under Brazilian disc splitting.

Fig. 13.

Fracture evolution process of basalt FDEM samples at a small size with local hidden joints under Brazilian disc splitting.

Fig. 14.

Fracture evolution process of basalt FDEM samples at a medium size with many hidden joints

under Brazilian disc splitting.

Fig. 15.

Fracture evolution process of basalt FDEM samples at a REV size with enough hidden joints

under Brazilian disc splitting.

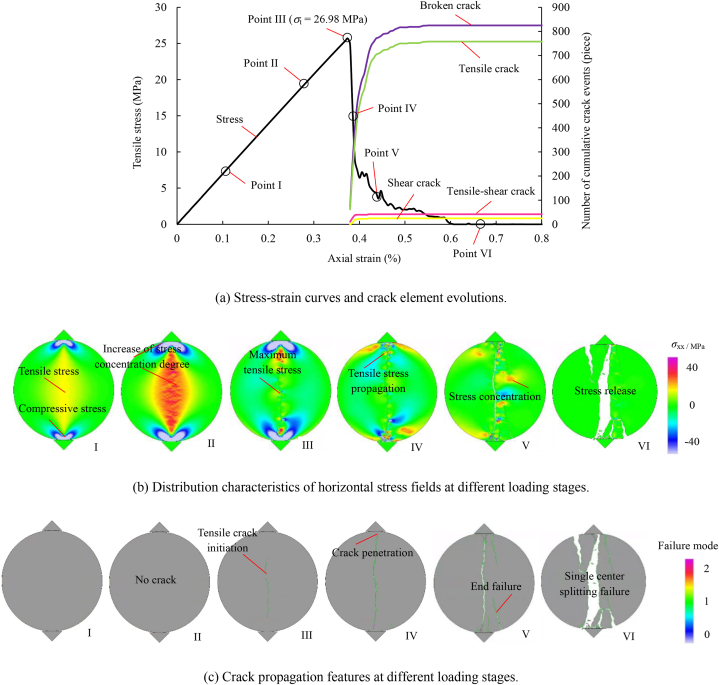
In Fig. 12, the fracture evolution process of small-sized intact basalt samples under Brazilian disc splitting reveals distinct stages of stress concentration and crack initiation. Initially, a slight stress concentration area can be observed in the local sample zone, with a tensile stress concentration along the loading diameter in the middle of the sample and a compressive stress concentration at the upper and lower ends. That is, the maximum tensile stress was generated at the center of the disc, and the stress field was symmetrical in the upper and lower ends and left and right directions (Point I). With increasing load, the stress concentration area of the sample in the pre-peak stage continued to expand from the upper and lower ends to the central region and the left and right sides, resulting in an increase in the degree and range of stress concentration. However, the overall stress level was low, and it failed to reach the local rock material strength required to form microfractures (Point II). As the peak strength was being approached, the stress concentration in the local sample area reached maximum, and the tensile stress concentration along the loading diameter in the middle of the sample exceeded the tensile strength of local rock materials, resulting in the initiation of tensile cracks along the loading diameter near the disc center (Point III). The post-peak load decreased rapidly, the number of cracks increased sharply, and the tensile-stress-concentration area at the formed crack tips continued to expand to the upper and lower ends of the specimen, forming more tensile cracks. In addition, the compressive stress concentration area at both ends exceeded the compressive strength of local rock materials, leading to the formation of shear cracks or composite tensile–shear cracks. These cracks continued to propagate, intersect, and extend throughout the entire specimen along the loading direction (Point IV). Subsequent to the post-peak loading, the significant tensile stress concentration at the upper and lower ends led to the formation of additional tensile cracks (Point V). In the residual stage, the stress field approached zero, and the existing cracks continued to open and propagate with further deformation, ultimately resulting in the overall failure of the sample (Point VI). Therefore, the entire failure process of the small intact basalt specimens was very short, exhibiting a single-center splitting failure mode dominated by tensile cracks, that is, a tensile failure mechanism driven by extremely high stresses.

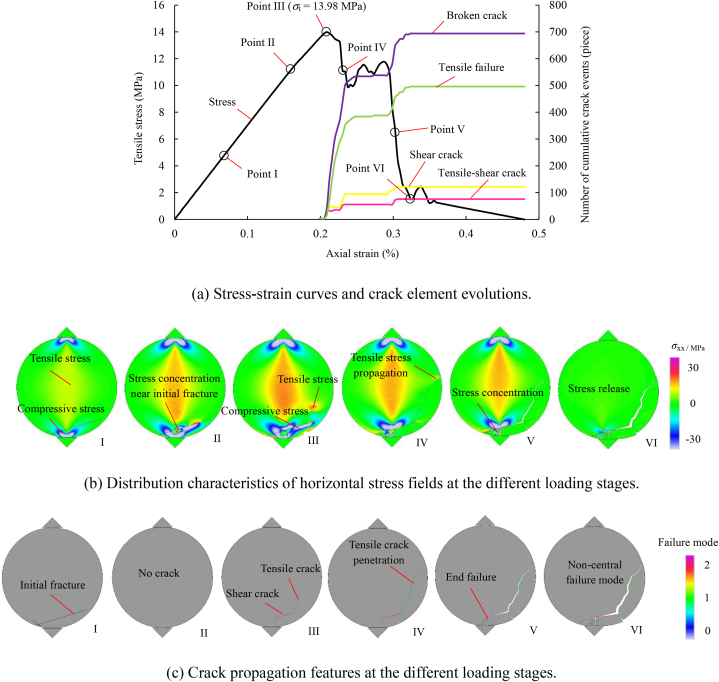
Fig. 13 shows the fracture evolution process of the small basalt samples containing a local hidden joint under Brazilian disc splitting. An initial hidden joint containing an inclination angle of approximately 20° was located at the lower end of the sample. Initially, the distribution of the horizontal stress fields in the sample in the initial loading stage mirrored that observed in the complete sample, with a tensile stress concentration in the middle zone and a compressive stress concentration at the upper and lower ends. The stress field exhibited low overall values, without visible fractures (Point I). As the loading progressed, the stress-concentration zones expanded, and the presence of a hidden joint introduced a heterogeneous stress field near the joint due to the difference in the elastic moduli between the matrix material and the joints. The superimposition of the stress-concentration areas due to the self-heterogeneity of the sample and loading-induced stress resulted in a significant stress concentration near the hidden joint, that is, the tensile stress concentration area was located at the upper and lower tips of the initial joint, and the compressive-stress-concentration area was located on the initial joint surfaces. However, the overall stress level was low, and there was no appearance of a fracture (Point II). As the peak strength was being approached, the heterogeneous stress field near the hidden joint intensified, leading to the initiation of shear cracks on the joint surface due to the low shear strength, followed by the formation of tensile cracks at the joint tips once the local tensile stress exceeded the tensile strength of the rock material (Point III). Post-peak loading triggered the expansion of a tensile crack at an angle of approximately 45° toward the loading direction until it traversed the sample, while the fracture did not penetrate the upper and lower ends, allowing the sample to retain some of its bearing capacity (Point IV). Subsequent loading exhibited a jagged stress profile with the intermittent stress increasing and decreasing, and the compressive-stress-concentration area was located at the lower end of the sample, resulting in the formation of shear cracks or composite tensile–shear cracks (Point V). In the residual stage, the stress field approached zero, and the existing cracks continued to open and propagate with further deformation, ultimately leading to sample failure (Point VI). In summary, compared with the intact basalt samples, small basalt samples containing local hidden joints exhibited a longer failure process, characterized by a noncentral failure mode dominated by composite tensile–shear cracks. The presence of initial local hidden joints played a significant role in structurally controlling the failure mechanism of the samples.

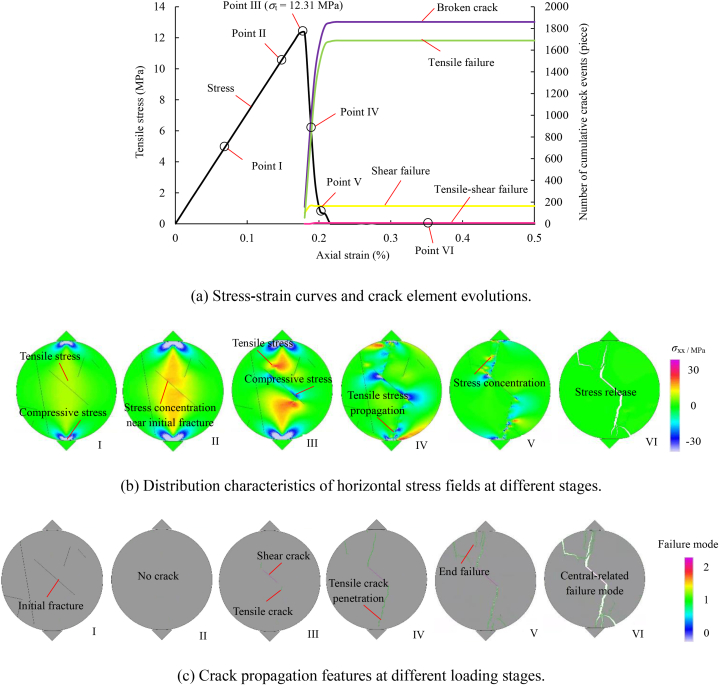
Fig. 14 shows the fracture evolution process of the medium-sized basalt samples containing numerous hidden joints under Brazilian disc splitting. An initial hidden joint with an inclination angle of approximately 45° was centrally located in the model, with additional hidden joints present in the other regions. Initially, the horizontal-stress-field distribution in the sample in the initial loading stage reflected that of the complete sample, with a tensile stress concentration at the center and a compressive stress concentration at the upper and lower ends. The overall stress field exhibited low values, without any visible fractures (Point I). Continuous loading resulted in an increase in the degree and range of the stress concentration, particularly near the hidden joints where significant stress concentrations occurred due to the superposition of the heterogeneity-induced and loading-induced stresses. However, these stress concentrations did not surpass the material strength required to initiate fracture (Point II). Upon reaching the peak strength, the local stress levels exceeded the strength of the rock material, leading to the formation of shear cracks on the hidden joint surfaces and tensile cracks at the tips of the hidden joints in the central area of the sample (Point III). Post-peak loading triggered rapid crack propagation, with tensile cracks expanding along the loading diameter until they penetrated through the upper and lower ends of the specimen, leading to a loss of bearing capacity (Point IV). Subsequent loading induced the formation of shear cracks or composite tensile–shear cracks at the ends of the specimen, where compressive stress concentrations were present (Point V). In the residual stage, the stress field approached zero, and existing cracks continued to propagate with further deformation, culminating in the overall failure of the sample (Point VI). Overall, the medium-sized basalt samples with multiple hidden joints exhibited a rapid failure process and a central-type failure mode characterized by composite tensile–shear cracking dominated by tensile cracks. The presence of initial hidden joints played a pivotal role in structurally controlling the failure mechanism of the samples.

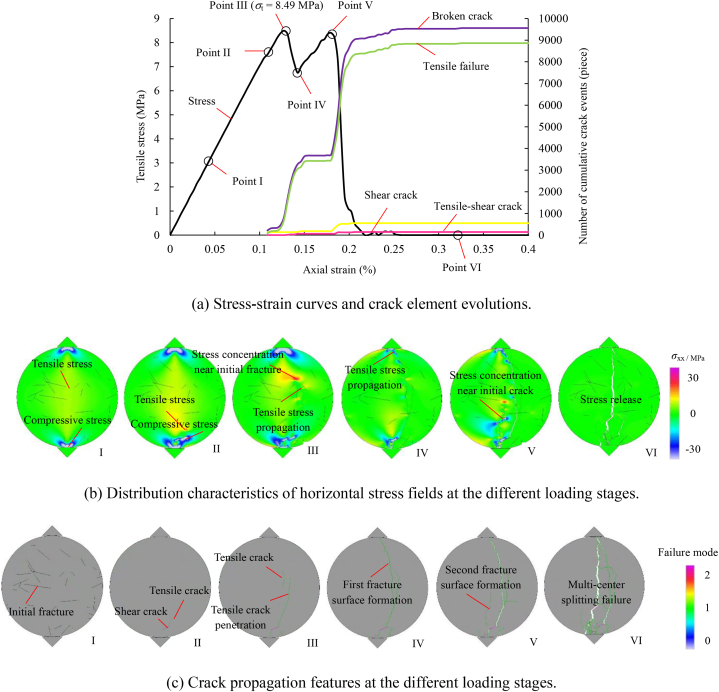
Fig. 15 shows the fracture evolution process of the REV-sized basalt samples with abundant hidden joints under Brazilian disc splitting. Initially, the stress-field distribution in the initial loading stage mirrored that of previous samples, with a tensile stress concentration at the center and a compressive stress concentration at the upper and lower ends. The overall stress field exhibited low values, without any visible fractures (Point I). With the increase in the loading, the degree and range of the stress concentration increased continuously. The superimposition of the stress-concentration zones due to rock heterogeneity and loading-induced stress led to significant local stress concentrations near the hidden joints. Once the material strength was exceeded, shear cracks were formed on the hidden joint surfaces, and tensile cracks appeared at the tips of the hidden joints in the lower part of the sample (Point II). As the first peak strength was being approached, the heterogeneous stress field near the hidden joints intensified, resulting in the expansion of tensile cracks along the loading direction. Moreover, local shear and tensile cracks initiated and propagated from some hidden joints in the central region, resulting in a local failure approximately parallel to the loading direction (Point III). Post-peak loading induced rapid crack propagation, with multiple shear and tensile cracks interacting and coalescing along the loading direction to form the first fracture surface that penetrated the upper and lower ends of the specimen (Point IV). Due to the large sample size, a single fracture surface did not lead to complete failure, allowing the specimen to retain some of its bearing capacity. Subsequent loading near the second peak strength triggered the initiation and expansion of a hidden joint in the middle and lower parts, forming a second fracture surface through the upper and lower ends of the sample (Point V). In the residual stage, the existing cracks continued to propagate, resulting in an overall failure accompanied by longitudinally spalling thin plates with a thickness range of 5–10 cm and a length in the tens-of-centimeter range (Point VI). In summary, compared with small intact basalt samples, the REV-sized basalt samples with sufficient hidden joints exhibited a longer fracture process, characterized by a multicenter splitting failure mode dominated by tensile–shear cracking dominated by tensile cracks, that is, a tensile failure mechanism caused by the stress-structure coupling.

In summary, for basalt samples of the same size containing hidden joints, the meso-mechanical behaviors, such as the stress, displacement, and crack fields, under loading underwent a gradual fracture evolution process, eventually leading to an overall macro-failure of the rock blocks, and these meso-mechanical behaviors were evidently consistent and collaborative with the macro-mechanical properties. For basalt samples of different sizes containing hidden joints, the number of hidden microcracks contained in the basalt increased continuously with increasing sample size, indicative of a gradual decrease in the homogeneity. This resulted in significant differences in their macroscopic mechanical properties. The failure mechanism also constantly varied, from the tensile failure mechanism caused by the purely high stresses to the failure controlled by local structures and then to the tensile failure mechanism caused by stress-structure coupling.

4. Discussion

4.1. Size effect on rock tensile strength

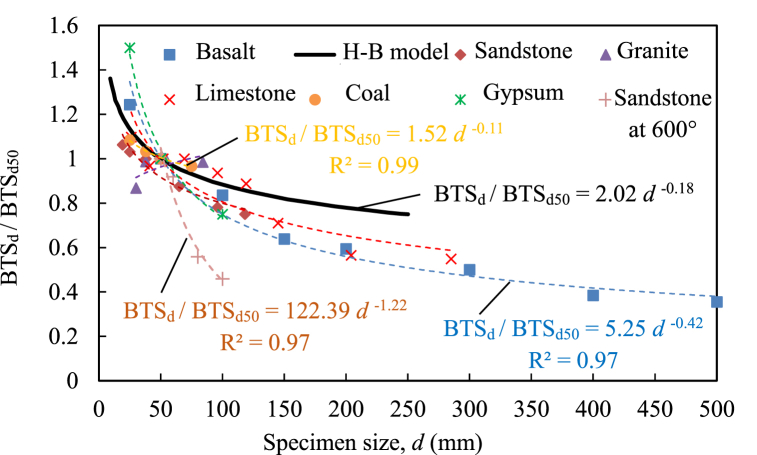
The tensile strength of hard and brittle rocks is significantly lower than their compressive strength. This can cause disasters driven by the tensile failure mechanism, such as spalling and rock bursts, which are predominant in deep underground engineering scenarios. Hence, the tensile strength is a crucial parameter for characterizing the mechanical properties of brittle rocks. The Brazilian disc splitting test is a widely used method in geotechnical engineering to measure the tensile strength of rocks, either through indirect or direct tensile tests [44]. A significant amount of research has been conducted on the size effect of rock mechanical properties, producing valuable insights and research outcomes. The results obtained in this study were compared with those obtained using conventional models of rock size effects, focusing on the H–B empirical formula and other relevant data from literature. The comparison, as depicted in Fig. 16, involved the normalized tensile strength (BTS_d50/BTS_d), where BTS_d50 and BTS_d represent the tensile strengths of rocks with a diameter of 50 mm and an arbitrary diameter, respectively [[45], [46], [47], [48], [49], [50], [51]]. This comparison was aimed at improving our understanding of the size effect on the tensile strength of the rock and provide insights into how the study results align with established models and literature findings on this topic.

Fig. 16.

Influence of specimen sizes on the tensile strength [[45], [46], [47], [48], [49], [50], [51]] (It is noted that the permission to reprint Fig. 16 is obtained from the original publisher).

Evidently, there exists a power function decay relationship between the BTS and the sample size for most rock materials, with the exception of granite. Typically, the BTS gradually decreases with increasing sample size, exhibiting a more pronounced decreasing trend in a smaller size range. Once the sample size reaches a critical value, the BTS may stabilize at a constant value. This critical sample size is known as the REV, where the corresponding mechanical properties are considered as equivalent continuum characteristics. The H–B empirical formula, expressed as σ_td50/σ_td = (50/d) ^0.18, is commonly used to represent rock types with good integrity or homogeneity. In this model, the BTS decreases gradually with increasing sample size and tends to stabilize quickly, leading to a lower REV. However, this formula may overestimate the strength of rocks with more microdefects or those influenced by factors such as temperature or weathering. For basalt containing hidden joints, the decreasing trend in the BTS with increasing sample size is in overall agreement with the H–B model results. However, in the case of basalt with hidden joints, this decreasing trend is more pronounced, leading to a higher power exponent and a higher REV. This indicates a more significant size effect on the tensile strength of rocks. Moreover, existing research on rock mechanical properties has often considered small sample sizes due to the shortcomings of the sample preparation and testing itself, with the size typically being less than 200 mm, which limits the ability to fully characterize the size effect characteristics of rocks. Therefore, studying the size effect of rock mechanical properties through a numerical simulation can provide more meaningful insights.

Apparently, there are no uniform laws or formulae governing the size effect of the mechanical properties of rocks. This variability is closely linked to internal factors such as the lithology, types of defects, distribution characteristics of defects, and external factors such as weathering, temperature, and loading rates. The size effect of the mechanical properties of a rock ultimately boils down to its structural intricacies. Therefore, it is imperative to gain a deeper understanding of the relationship between the rock structures and the REV or the corresponding mechanical parameters. Further research is required to establish a quantitative, intelligent prediction model that can comprehensively account for the various influencing factors including the lithology, defect type, and defect parameters. Such a model should aim to provide a more accurate and reliable representation of the mechanical properties of rocks. Essentially, by gaining a preliminary understanding of the geometric parameters of defect structures within a rock, such as the length, spacing, and density of structural planes, it will become feasible to rapidly determine the REV and the corresponding mechanical parameters. This knowledge can be useful in more effectively guiding engineering practices.

4.2. Fracture mechanism of different-sized brittle rocks

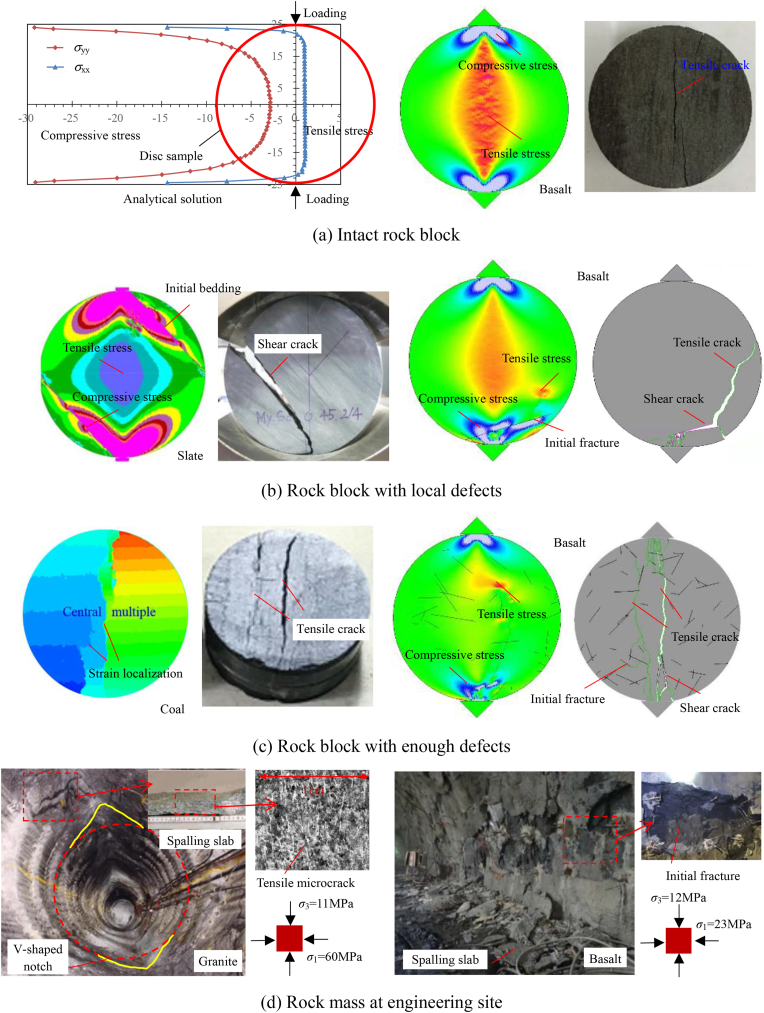
As a typical heterogeneous geological material, a rock contains structural planes at various levels, ranging from mesoscale primary defects, such as microcracks and pores, to random macroscale hard structural planes, such as joints and fissures, and even to local weak structural planes such as faults and dislocation zones at the engineering or geological body scale. These discontinuous structures contribute to a significant scale effect on the mechanical properties of rocks, impacting the occurrence of various adverse geological disasters. In this study, the obtained results were compared with other types of rock blocks containing native mesoscale defects. The size effects of the mechanical behavior, including the stress fields and failure modes, were explored to understand the multiscale failure mechanism of rocks, as depicted in Fig. 17, providing insights into the potential occurrence of geological disasters [38,39,[52], [53], [54], [55], [56]].

Fig. 17.

Structural characteristics, stress or strain distributions and failure modes of brittle geomaterials in different sizes under tensile action [38,39,[52], [53], [54], [55], [56]] (It is noted that the permission to reprint Fig. 17 is obtained from the original publisher).

In Fig. 17(a), small intact rock blocks, such as marble and granite, characterized by good homogeneity, exhibit a tensile strength under Brazilian disc splitting derived from 2D elastic mechanics theory. The analytical solution indicated that a compressive-stress-concentration area was found at the upper and lower ends, whereas a tensile-stress-concentration area was located in the middle of the sample loading diameter. This stress-field distribution pattern typically led to the initiation of microcracks at the center of the specimen, which then propagated toward the upper and lower ends until the specimen was fully penetrated. Hence, intact rock blocks subjected to tensile forces often demonstrate a single-center splitting failure mode dominated by tensile cracks. In the case of intact basalt, which has good homogeneity characterized by small particles, dense arrangement, and high strength, the stress-field distribution characteristics and failure modes under Brazilian disc splitting aligned closely with the theoretical solution. Therefore, it can be concluded that the tensile failure mechanism induced by high stresses plays a predominant role in the fracture behavior of intact basalt rock blocks.

As shown in Fig. 17(b), for small or medium-sized rock blocks, such as slates with local defects, the interaction between the stress-concentration zones generated under loading and those arising from inherent heterogeneity alters the original stress-field distribution. This modification resulted in a significant stress-concentration area near the initial defects, with a tensile stress concentration at the upper and lower tips of the defects and a compressive stress concentration on the defect surfaces. Initially, a shear failure occurred on the defect surface, followed by the formation of tensile cracks at the defect tip. These cracks continued to propagate, ultimately leading to sample failure. Consequently, small- or medium-sized rock blocks with local initial defects under a tensile stress typically exhibited a noncentral failure mode, characterized by shear failure, tensile failure, or a combination of both. In the context of basalt containing local hidden joints, which exhibited significant heterogeneity, the stress-field distribution characteristics and failure modes under Brazilian disc splitting were generally in line with the aforementioned research findings. Therefore, the initial local fractures, such as those from hidden joints, play a leading role in the failure mechanism, known as structural control failure.

In Fig. 17(c), large rock blocks, such as coal, containing ample initial defects and exhibiting poor homogeneity, present a complex fracture mechanism. In these cases, the defects in the local sample area may not play a leading role, whereas defects in the middle of the sample tend to have a more significant impact. The interaction between stress-concentration zones arising from sample heterogeneity and those induced by loading led to a pronounced stress concentration near the defects. This resulted in a shear failure on the defect surface, tensile failure at the defect tip, and continuous expansion of fractures, culminating in the formation of multiple fracture surfaces. For REV-sized rock blocks with sufficient initial defects under a tensile stress, a multicenter splitting failure mode could be observed, characterized by composite tensile–shear cracking dominated by tensile cracks. In the context of basalt rock blocks containing ample hidden joints, which exhibited significant heterogeneity, the stress-field distribution characteristics and failure modes under Brazilian disc splitting aligned with these findings. Consequently, the tensile failure mechanism driven by stress-structure coupling played a leading role in the fracture behavior of basalt rock blocks with hidden joints.

The Lac du Bonnet (LdB) granite found in the Underground Research Laboratory (URL) of Atomic Energy of Canada Limited (AECL), which is located at a depth of 420 m with an exceptionally high in situ stress (maximum principal stress of approximately 60 MPa), exhibits a UCS of approximately 200 MPa. This rock can be characterized by its dense and hard nature, with relatively undeveloped fractures, indicating good homogeneity, as shown in Fig. 17(d). Under such conditions, the issue of surrounding rock mass failure is significant, resulting in the formation of distinct V-shaped failure zones in the roof and floor of underground caverns, primarily manifested as layered spalling failure. The spalling thickness ranges from a few centimeters to several dozen centimeters; spalling typically occurs parallel to the maximum principal stress direction. The in situ failure behavior mirrors the axial splitting failure observed in laboratory tests under uniaxial compression, highlighting a tensile failure mechanism influenced by the extremely high in situ stresses. The hard and dense basalt at the underground caverns of the Baihetan Hydropower Station, which is at depths ranging from 260 to 330 m and experiences moderate-to-high in situ stress (maximum principal stress of 23 MPa), exhibits a UCS of approximately 220 MPa, indicating a relatively high strength-to-stress ratio (exceeding 7). This implies that the basalt is resistant to destruction under these conditions. However, the presence of widespread hidden joints in the basalt, which contributes to noticeable heterogeneity, poses a significant challenge in terms of surrounding rock mass failure, particularly through spalling failure. Spalling flakes vary in thickness from several centimeters to tens of centimeters, often revealing initial hidden joints along the sides of the spalling flakes. The in situ failure pattern differed markedly from the fragmentation failure of intact basalt observed in laboratory tests under uniaxial compression. The pattern resembled the splitting failure of REV-sized basalt rock blocks under similar conditions, emphasizing a tensile failure mechanism influenced by the combined effect of stresses and structures.

The complex mechanical response of a rock is the result of its structural characteristics under mechanical loading, with both the inherent defect structure and external loading contributing to rock failure. In the case of small intact basalt exhibiting overall homogeneity, its mechanical properties are primarily influenced by the applied loading, requiring high stresses to induce specimen failure, typically through a tensile failure mechanism driven by purely high stresses. Conversely, as the defect structure of basalt becomes more pronounced with increasing sample sizes (indicating greater heterogeneity), the mechanical properties are influenced by both the defect structure and applied loading. The stress concentration mechanism becomes more significant, leading to sample failure under low-load conditions, characterized by a tensile failure mechanism resulting from stress-structure coupling. Hence, it is crucial to consider the actual structural characteristics of a rock to comprehend its macroscopic and microscopic mechanical behaviors, ultimately to reveal its fracture mechanism.

5. Conclusions

In this study, the size effect of the tensile mechanical behavior of basalt containing hidden joints was systematically investigated using the SRM method, which combines μDFN and FDEM models, providing insights into the fracture mechanism of basalt. The key conclusions drawn from the study results are as follows:

• (1)The SRM model, which integrates an FDEM model representing the complete matrix and a μDFN model based on the statistical geometric parameters of hidden joints, could accurately capture the real meso-structural characteristics of basalt. It successfully replicated the mechanical behavior observed in laboratory tests and engineering sites. Thus, FDEM modeling can be useful in exploring the mechanical properties of hard rocks with complex structures.
• (2)An analysis of the tensile strength in relation to the sample size indicated that the REV size of basalt rock blocks containing hidden joints was approximately 0.5 m. With the increase in the sample size, resulting in a gradual increase in the heterogeneity, the stress–strain curve shifted from unimodal to serrated and eventually to multimodal patterns, and the failure mode progressed from single-center splitting failure to local structure-controlled failure and ultimately to multicenter splitting failure. The essence of the rock size effect is its own structural effect, indicating that it is crucial to consider the real structural features of a rock to understand its mechanical behavior.
• (3)With increasing sample size, the failure mechanism of basalt containing hidden joints under Brazilian disc splitting underwent continuous changes. Initially driven by purely high stresses leading to tensile failure, the mechanism evolved to failure controlled by local structures and ultimately to tensile failure under stress-structure coupling. The mechanical behavior of a rock is the comprehensive effect of its own structural characteristics under various complex conditions. The research findings provide reference for engineering design optimization, construction scheme formulation, and disaster prevention.
• (4)This study has some limitations. First, the analysis focused solely on the size effect of the rock mechanical properties with a specific distribution characteristic of the structural planes, without considering the impact of different structures on the REV and corresponding equivalent mechanical parameters. Second, the study primarily addressed basalt rock blocks containing mesoscale hidden joints, i.e., the size effect of rock blocks, overlooking the size effect of rock masses with macroscale hard structural planes such as joints and cracks. Future research should address these aspects to gain a more comprehensive understanding.

CRediT authorship contribution statement

Menghui Yang: Writing – original draft, Software, Investigation, Formal analysis, Data curation. Zhenjiang Liu: Writing – review & editing, Supervision, Resources, Project administration, Methodology, Funding acquisition, Conceptualization. Yu Zhou: Visualization, Validation, Software.

Data availability statement

The datasets generated within the scope of the current study are available from the corresponding author on reasonable request.

Ethical statement

This study did not involve human or animal subjects, and thus, no ethical approval was required.

Declaration of competing interest

The authors declare no known conflicts of interest associated with this publication nor any financial support that could have influenced its outcome.

Nomenclature

DFN

Discrete fracture network

FDEM

Finite-discrete element method

SRM

Synthetic rock mass

UCS

Unconfined compressive strength

BTS

Brazilian tensile strength

REV

Representative elementary volume

P₂₁

Areal fracture intensity

ρ

Bulk density

E

Young's modulus

ν

Poisson's ratio

φ

Internal friction angle

c

Cohesive strength

f_t

Tensile strength

K_Ic

Mode I fracture toughness

G_f1

Mode I fracture energy

G_f2

Mode II fracture energy

P_n

Normal contact penalty

P_t

Tangential contact penalty

P_f

Fracture penalty