Leveraging a Separation of States Method for Relative Binding Free Energy Calculations in Systems with Trapped Waters

Abstract

Methods for calculating the relative binding free energy (RBFE) between ligands to a target protein are gaining importance in the structure-based drug discovery domain, especially as methodological advances and automation improve accuracy and ease of use. In an RBFE calculation, the difference between the binding affinities of two ligands to a protein is calculated by transforming one ligand into another, in the protein–ligand complex, and in solvent. Alchemical binding free energy calculations are often used for such ligand transformations. Such calculations are not without challenges, however; for example, it can be challenging to handle interfacial waters when these play a crucial role in mediating protein–ligand binding. In some cases, the exchange of the interfacial waters with solvent water might be very infrequent in the course of typical molecular simulations, and such interfacial waters can be considered trapped on the simulation time scale. In these cases, RBFE calculation between two ligands, where one ligand binds with a trapped water while the other ligand displaces it, can result in inaccuracies if the surrounding water structure is not sampled adequately for both ligands. So far, a popular choice for treating the trapped waters in RBFE calculations is to combine free energy calculations with enhanced sampling methods that insert/delete waters in the binding site. Despite recent developments in the enhanced sampling methods, they can result in hysteresis in the RBFE estimate, depending on whether the simulations were started with or without the trapped waters. In this study, we introduce an alternative method, separation of states, to calculate the RBFE between ligand pairs where the ligands bind to the protein with different numbers/positions of trapped waters. The separation of states approach treats the sampling of the trapped waters separately from the free energy calculation of the ligand transformation. In our method, a trapped water in protein’s binding site is decoupled from the system first, and the cavity created by its decoupling is stabilized. We then grow a larger ligand into this cavity– a ligand that is known to displace the trapped water. In this study, we show that our method results in precise and accurate estimates of RBFEs for ligand pairs involving the rearrangement of trapped water via RBFE calculations for five such ligand pairs. We have optimized our simulation protocol to be suited for large distributed computational resources and have automated our RBFE calculation workflow.

1. Introduction

Computational methods for examining the binding of organic ligands to target proteins play a crucial role in structure-based drug design. While designing organic ligands that can potentially become drug molecules, a ligand’s selectivity and binding free energy upon its binding to the target protein are optimized. Upon ligand binding, water molecules and ions that were previously occupying the protein’s binding site are displaced from the binding site and are released to the solvent. The entropic contribution of the release of the water molecules to the solvent is a principal component in the binding free energy of the protein–ligand complex.

In some cases, some water molecules may not be released by the ligand’s binding, and these water molecules can localize in the binding site and can stabilize the protein–ligand complex by forming small water networks bridging protein residues and the ligand.¹⁻⁵ Modifications of chemical groups on a ligand to displace these water molecules may sometimes lead to an optimized and highly selective ligand for the target protein, if the modified ligand can make favorable interactions in the binding site while displacing the localized waters.^6,7

In molecular dynamics (MD) simulations, while the presence of such water molecules can strongly influence the binding free energies of protein–ligand complexes,^8,9 their movement can sometimes be too slow to be adequately sampled during the course of the simulations.¹⁰⁻¹² In a typical simulation, we can consider the movement of an interfacial water as slow if its unbinding and rebinding to its position in the protein’s binding site cannot be sampled during the time scale of the simulation. This lack of unbinding and rebinding of a water can sometimes be due to physical barriers imposed by the surroundings, e.g., if the water’s position is completely enclosed by protein and/or ligand atoms. However, even if a water is not restricted by its surroundings, but its exchange with the other solvent waters is very infrequent on the time scales of typical molecular simulations, it can be considered as a slow or “trapped” water, and its inadequate sampling can hamper the accuracy of the simulation.

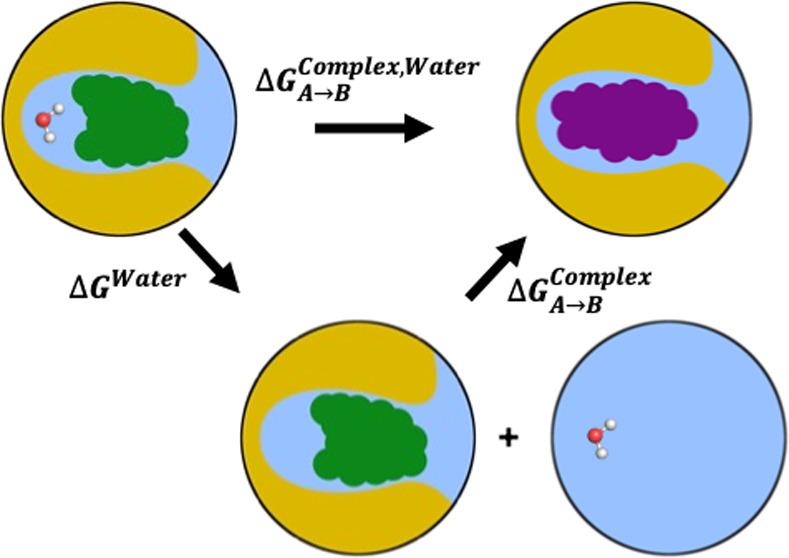
The problem of slow movement of such trapped waters persists in relative binding free energy (RBFE) calculations of ligands that bind to a protein with different numbers (and/or positions) of the trapped waters. In an RBFE calculation, the difference in the binding affinities of two ligands to a specific protein is calculated, as opposed to the binding affinities of the two ligands individually in the absolute binding free energy (ABFE) calculations (Figure 1). Typical MD simulation workflows treat such calculations by transforming one ligand to the other using alchemical methods.¹³⁻¹⁵ Effectively, this means that one ligand is replaced by the other while keeping the remaining system (i.e., the protein and all water molecules, including the trapped ones) essentially unchanged. If a water molecule is essential for the protein–ligand interactions of one ligand while the other ligand is known to displace it, such methods are likely to yield wrong results if the water molecule does not naturally rearrange itself in the time scale of the simulation. In these cases, the ligand transformation would yield either a binding mode for one ligand that is missing the water molecule essential for its interaction with the protein, or a system in which a water molecule is trapped in a cavity in which it interferes with the binding between the protein and the ligand that is known to displace it. Normally, simulation time scales used for such ligand transformations are not long enough to hope to either displace the trapped water or observe the water moving in to reach its binding site.

Figure 1.

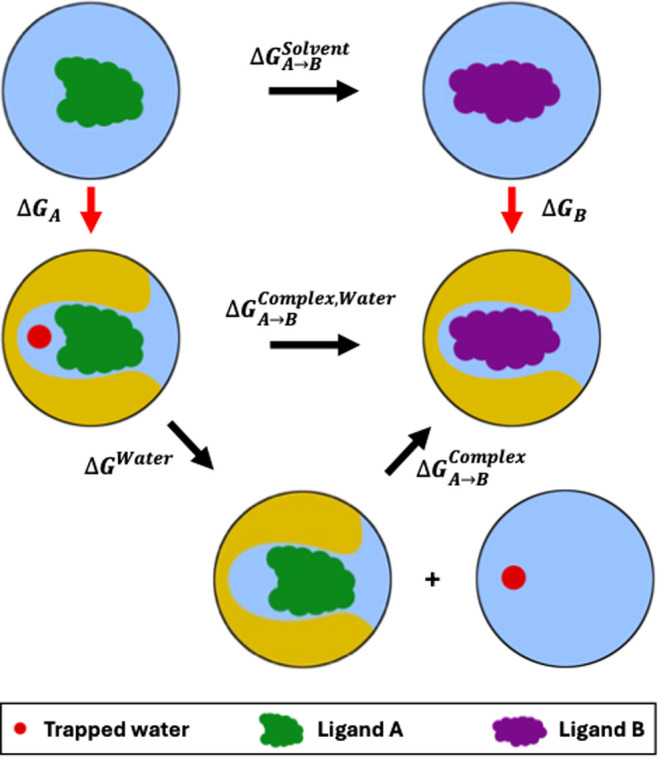
Relative binding free energy (RBFE) calculation between two ligands, where one ligand (ligand A) binds to the protein (yellow) with a trapped water, while the other ligand (ligand B) displaces it. The vertical transformations in red represent absolute binding free energy (ABFE) calculations for the individual ligands binding to the protein. The horizontal lines in black represent the transformations of the ligands in solvent (solvent leg of the RBFE calculation, ΔG^Solvent_A–>B) and in protein’s binding site (complex leg of the RBFE calculation, ΔG^{Complex,Water}_A–>B), the two components of the RBFE calculation. For the complex leg of the RBFE calculation, we use the separation of states approach where we first introduce a new state of the system (bottom) with a binding mode of the ligand A without the trapped water. In this state of the system, the trapped water is displaced from the binding site of the protein into the bulk solvent. From this binding mode of ligand A without the trapped water, we transform the ligand A into another ligand B that is known to displace the trapped water when it binds.

Some recent studies¹⁶⁻¹⁹ have addressed the challenge of sampling the trapped waters in the course of ligand transformations by inserting or deleting waters in the binding site using enhanced sampling methods, simultaneously with the ligand transformation. These methods normally require long simulation times to converge, and they can result in differences in RBFEs when the simulations are started with or without the known trapped waters.¹⁷⁻¹⁹ Such differences in the RBFEs are known as hysteresis. Recent studies on accessing the accuracies and efficiencies of these enhanced sampling methods in rehydrating trapped water sites showed that for several systems, the simulation time scale necessary to accurately predict the locations of the trapped waters might be well beyond that of typical free energy calculations.^12,20

Alternatively, if the positions and numbers of trapped waters are known for two ligands a priori, one might seek an efficient method to calculate the RBFE of the ligands with each in the context of its respective water structure or network, without relying on fully sampling potential water structures with each ligand present, i.e., without using the insertion and deletion attempts mentioned above to determine and sample the correct water structure, which is already known. Essentially, the choice may be between a combined approach of sampling all potentially relevant water structures along with the ligand transformation, i.e., mixing a challenging problem of the trapped waters’ sampling with a ligand RBFE calculation, or a separated approach of determining the respective positions of the trapped waters for each ligand first, and then holding them essentially fixed during the ligand RBFE calculation.

Recently, Ge et al.¹¹ proposed to treat the trapped water molecules in the RBFE calculation between two ligands using the latter approach, separation of states, which introduces an additional thermodynamic state to remove the trapped water, which needs displacing by one of the ligands, prior to performing the transformation of the ligands.

To the best of our knowledge, previously, only Michel et al.²¹ has performed ligand transformations by introducing intermediate states in free energy calculations that differ in the number of trapped waters. Specifically, Michel et al.’s work studied both ligands’ binding modes with and without trapped waters. This study examined ABFEs of trapped water molecules using the double-decoupling formalism employing Monte Carlo (MC) simulations. For convergence, the authors localized the trapped water at its putative location in the binding site using a spherical hard-wall potential. In their simulations, the hard-wall potential forbade the trapped water from escaping its binding site and also restricted solvent water molecules from diffusing near the trapped water. However, the study did not take into account the free energy to remove the spherical hard-wall potential when the trapped water was in a fully interacting state. Such a contribution would essentially represent free energy of decoupling the trapped water in a preexisting solvent cavity. Moreover, the hard-wall potential only restrained the solvent water from diffusing into the binding site of the trapped water, and no such restraint was applied to the surrounding environment, e.g., the protein’s side chains. This is important, because Ge et al.¹¹ have shown that unrestrained protein side chains in such simulations can occupy the binding site of the trapped water after its decoupling, severely hampering the convergence of the simulations. The study of Michel et al.²¹ thus has important connections to our present work, but we cannot apply the same approach here–not only due to the issues above, but also because a hard-wall potential cannot be implemented in typical MD simulations, as MD simulations require computation of a force, which is infinite at the boundary of a hard-wall potential. Despite these limitations, the prior study sets an important precedent for our work.

Here, our goal is to develop a stable MD-based protocol for the RBFE calculation (or the complex leg thereof, specifically; ΔG^{Complex,Water}_A–>B, Figure 1), which can efficiently handle displacement and/or insertion of water(s) on modifying a ligand. Specifically, we seek to handle the case of a transformation between a ligand A and a ligand B in a protein’s binding site, where ligand A binds with exactly one trapped water molecule and ligand B does not. Following the approach of Ge et al.,¹¹ we introduce an intermediate state in the alchemical transformation between the two ligands, where the intermediate state involves removal of the trapped water from the protein’s binding site (Figure 1). Our alchemical transformation, therefore, consists of three states: ligand A with the trapped water molecule (a favorable binding mode for ligand A), ligand A without the trapped water molecule (an unfavorable binding mode for ligand A), and ligand B without the trapped water molecule (favorable binding mode for ligand B). Ge et al.¹¹ demonstrated their method by calculating the ABFEs of trapped water molecules (ΔG^Water, Figure 1), i.e., calculating the binding affinities of water molecules to protein–ligand complexes. Their calculations presented a proof of concept for free energy calculations for water displacement–in this case, the transformation from the system with ligand A and a trapped water molecule to the system of ligand A without the trapped water molecule. The calculations showed promise that the method could be expanded to run RBFE calculations between ligands that bind to the protein with different numbers of trapped waters. However, the protocol used in this prior work¹¹ to perform these calculations was not without difficulties. For example, the authors encountered sampling problems with surrounding solvent water rehydrating the emptied trapped water site and with the protein undergoing significant conformational transformations upon removal of the trapped water, ultimately influencing their free energy estimates.

In this work, we have built on the MD-based ABFE protocol of Ge et al.¹¹ with a special focus on its potential pitfalls. Additionally, we have used harmonic and vdW restraints, both of which are practical for use in MD, unlike the hard-wall potential used in the previous study of Michel et al.²¹ (our approach probably mimics that potential to a significant extent). Moreover, we have designed this study to provide a clear and accurate definition of trapped water displacement. We will demonstrate how it can be adapted to be suitable for workflows involving minimal human interaction, avoiding the extensive analyses that were required to confirm correctness in the original work. We then further extended the ABFE protocol into an RBFE protocol, where the unfavorable binding mode of ligand A without the trapped water was transformed into a favorable binding mode of ligand B, and the ΔG^{Complex,Water}_A–>B was estimated by calculating the ΔG^Water and ΔG^Complex_A–>B (Figure 1). To the best of our knowledge, this is the first study of an MD-based separation of states approach being applied to RBFE calculations between ligands involving displacement of trapped waters.

2. Methods

2.1. Free Energy Calculation Methods

Free energy is a state function i.e., it is independent of the pathway that connects a starting state to a final state (also referred to as end states) of the system. In the present separation of states approach to binding free energy calculations, we connected the phase spaces of our end states by a pathway that implements physical restraints and alchemical transformations in our system, ultimately resulting in a thermodynamic cycle. While designing the thermodynamic cycle, we aimed at optimizing three aspects– first, the overall computational efficiency of the calculations, i.e., the total computational resources required (CPU/GPU time); second, the time to solution (wall clock time); and third, the automation of the simulation workflow (setup and analysis of the thermodynamic cycle). Optimizing these aspects is crucial, especially in drug discovery pipelines that often involve large numbers of protein–ligand pairs for affinity calculations. Therefore, our goal here is to develop a simulation protocol requiring minimal human intervention for its setup and analysis. In the following subsections, we have described the two types of free energy estimates we used in this study.

2.1.1. Equilibrium Free Energy Estimate

Estimating free energy differences at equilibrium requires that the simulations used be long enough that the sampled conformations represent the true underlying distribution of the states’ phase spaces. Equilibrium free energy calculations are performed by gradually transforming the system across the end states. To reliably estimate the free energy difference between the end states, the sampled phase spaces of the end states should have sufficient overlap.

For any alchemical or physical transformation, where the end states are distant in phase space, the path of transformation needs to be covered by intermediate (λ) states.²² These λ states ensure phase space overlap along the path of transformation, even if the end states themselves do not overlap.

To calculate the free energy difference between the end states along the path defined by the intermediate λ states, we used the Multistate Bennett Acceptance (MBAR) method^23,24 as the equilibrium free energy estimator. MBAR relies on equilibrium sampling of a single path between the end states through the intermediate λ states. For a reliable free energy estimate through MBAR, the simulations of the λ states need to be long enough (generally in the order of tens to hundreds of nanoseconds (ns)) to generate a representative sampling of the Hamiltonian, though exact time requirements depend on the characteristic time scales of the system.

2.1.2. Nonequilibrium Switching (NES) Free Energy Estimate

The NES free energy estimate relies on many independent and short simulations (“switches”) that bridge the end states by transitioning between them (out of equilibrium) in both directions.²² The Hamiltonian of the system is coupled to a parameter λ and is rapidly changed (usually within a few hundred picoseconds (ps) or less) from one end state to the other. The NES switches are started from configurations drawn from a representative equilibrium sampling of each of the end states. The NES switches result in a collection of sampled paths between the two end states. Because of the nonequilibrium nature of the short switches, there is work dissipation along the path of each of the switches, which needs to be accounted for.

Using the dissipated work along the NES switches, we can estimate the free energy difference between the end states by solving the Crooks fluctuation theorem^25,26 with the BAR estimator,²³ by numerically solving eq 1

1

where n_f and n_r are the number of switches in the forward and reverse directions, respectively, and ΔG is the free energy difference between the end states. The works along the forward and reverse pathways, W_f and W_r, are calculated by accumulating the energy changes as the coupling parameter λ is changed during the switches 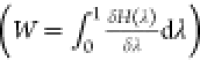, where H is the Hamiltonian of the system.

While the nonequilibrium switches are typically very short compared to the equilibrium simulations, the total computational effort can still be significant due to the number of switches that need to be run (usually around 50–100)²⁷ and the fact that they require an equilibrium simulation of the end states to generate the starting configurations. However, the separate switches are embarrassingly parallel and require only a short wall clock time, which allows efficient use of large distributed computational resources.

2.2. The Thermodynamic Cycle to Calculate the ABFE of a Trapped Water

In the first part of this study, we present a thermodynamic cycle for calculating the ABFE of a trapped water in a protein–ligand complex (Figure 2). Throughout this paper, we refer to this thermodynamic cycle as the “ABFE thermodynamic cycle”. The ABFE thermodynamic cycle presented here is an optimization of the thermodynamic cycle presented in the previous work of Ge et al.¹¹

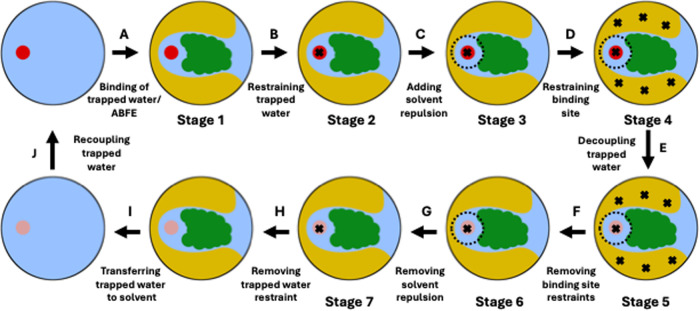
Figure 2.

Thermodynamic cycle to calculate the absolute binding free energy (ABFE) of a trapped water in a protein–ligand complex. The red circles in stages 1 through 4 and in the starting stage of edge A represent interacting trapped water, whereas the faded red/magenta circles in stages 5 through 7 and in the end stages of edge I represent noninteracting water. The dashed black circles around the trapped water in stages 3 through 6 represent solvent repulsion. The black crosses in stages 2 through 7 represent position restraints applied to different parts of the system– the trapped water and the protein’s binding site.

In the ABFE thermodynamic cycle, we restrain the interacting trapped water to its binding site (edge B), add a solvent repulsion term at the target position of the trapped water in the protein’s binding site to restrain the solvent from occupying the trapped water’s binding site (edge C), and restrain the binding site to avoid changes in its conformation (edge D). We apply these three restraints sequentially across stages 1 through 4 of our thermodynamic cycle.

From restrained stage 4, we decouple the trapped water, i.e., turn off its van der Waals (vdw) and Coulomb interactions simultaneously, in an NES simulation (edge E). Once the trapped water is decoupled, we remove the restraints in edges F through H in a reverse order to how they were applied. Finally, we transfer and recouple the noninteracting trapped water to bulk solvent in edges I and J, respectively. Edge A represents the ABFE of the trapped water, i.e., the free energy to bring a water from the solvent to the trapped water’s binding site in the complex, and is calculated by taking the negative of the summation of the free energies of all the other edges in the ABFE thermodynamic cycle.

The ABFE thermodynamic cycle is designed with the goal to keep the adjacent stages close in phase space. We applied the restraints serially to simplify the diagnosis of issues during the development of the thermodynamic cycle. We have found that stages 1 and 4 are close enough in phase space in our final workflow to apply all restraints in parallel, saving computation time. We have used this simplification when applying our methodology to RBFE calculations (see Section 2.4 for details). We found that it is not possible to use a similar simplification to release the binding site restraints (edges F), see Section 2.3.3.

We calculated the free energies of the edges B through D using an equilibrium free energy calculation and those of the edges F through G using a second equilibrium free energy calculation. We used an NES free energy calculation to estimate the free energy of decoupling the trapped water in edge E. The free energies of edges H, I and J depend on the restraint details and the water model, and not on the protein–ligand complex. We have described their calculations in the Supporting Document Section S1.2.

2.3. Rationale behind the Design of the ABFE Thermodynamic Cycle

We chose the restraints used in the ABFE thermodynamic cycle (Figure 2) keeping in mind various common sampling challenges that can arise in ABFE calculations of trapped water. We sought to ensure that our choice of restraints not only avoid the common sampling issues, but also result in a computationally inexpensive thermodynamic cycle. In the following sections, we have described the rationale behind using the restraints in our ABFE thermodynamic cycle, how we calculated the free energy contributions of those restraints, and how the restraints paved the way to extend the ABFE thermodynamic cycle into an RBFE thermodynamic cycle where ligand transformations can also be carried out, in addition to the decoupling of the trapped water.

2.3.1. Keeping the Trapped Water in the Binding Site

In our ABFE thermodynamic cycle, we apply a restraint on the trapped water (in edge B) to ensure that it stays near its putative location in the binding site, even after its interactions are turned off. The restraint is implemented as a harmonic potential with a minimum at the location of the trapped water in the crystal structure. The location is defined as a virtual site relative to two heavy atoms close to the pocket (see Section S1.3 of the Supporting Document for details). Without the restraint, the trapped water would wander off once its interactions with the protein are made sufficiently weak. The water would then need to find its way back into the binding site in the short NES switches of edge E, which is nearly impossible. As a second consideration, adding a restraint on the trapped water also prevents problems with slow, partially solvent-exposed water which may infrequently unbind and rebind in stages 2, 3, and 4.

From a physical perspective, all water molecules are indistinguishable in stage 1, however in stage 2 (and in all subsequent stages of the thermodynamic cycle), the trapped water is distinguishable from solvent waters because of the restraint on it. Because of this, the harmonic restraint in stages 2 to 4 needs to be treated carefully in the MBAR calculation for stages 1 through 4. An MBAR calculation requires the evaluation of the Hamiltonians of each of the states involved in the free energy calculation with the trajectories of each of these states. Hence, to calculate the correct restraint potential on the trapped water, we need to evaluate the Hamiltonian of stage 1 with the trajectory of stage 2, even though no water is restrained in stage 1. If the trapped water exchanges with a water from bulk solvent in stage 1, the Hamiltonian of stage 1 would not change because the trapped water is indistinguishable from the bulk solvent water that occupies the trapped water’s site. However, when we evaluate the Hamiltonian of stage 2 with the trajectory of stage 1, the restraint potential will be extremely high, because the Hamiltonian of stage 2 would consider the distinguishable trapped water, which is now in the bulk solvent in stage 1, to calculate the restraint potential. This would lead to extremely high restraint energies, making it difficult to converge the free energy calculation, but more importantly, also would not give us the free energy of interest. Specifically, we are interested in the free energy of restraining any (that is, indistinguishable) water to the target position, rather than the free energy of restraining this specific (distinguishable) water to the target position. Thus, we needed to change how our calculation handled the exchange of water. For indistinguishable water, upon water exchange, if the newly arrived bulk solvent water was considered as the new trapped water and was selected for the calculation of the restraint potential, the restraint potential will be correct for the case of indistinguishable waters, which is what we want.

Therefore, to calculate the correct restraint potential, we postprocessed the trajectory of stage 1, such that the water from the bulk solvent that is occupying the trapped water’s binding site, would be considered for the calculation of the restraint potential in the MBAR calculation. We did this by remapping/reindexing the trajectory waters to ensure the nearest water is always the one considered for restraint calculation. Without this reindexing, we would encounter challenges in systems where the trapped water is (partially) exposed to the bulk solvent and may periodically exchange with a water molecule from the bulk solvent in stage 1 (in later stages, the restraint prevents the exchange). Because water molecules are indistinguishable, such an exchange should not influence the restraint potential. When calculating the Hamiltonian of later stages with the trajectory of stage 1, we hence want to apply the harmonic restraint to the water molecule currently occupying the binding site in stage 1, and not track a molecule that has left the binding site and diffused into the solvent. Failure to treat the water molecules as indistinguishable in stage 1 could lead to very large free energies and poor overlap between stage 1 and its neighboring stage (stage 2). Thus, we here implemented proper treatment of indistinguishable water molecules through postprocessing.

In our ABFE thermodynamic cycle, we chose the harmonic restraint on the trapped water to be weak enough that the restraint does not significantly disturb the dynamics of the system when the water is interacting, but strong enough that the weakly interacting or noninteracting water does not stray too far from the binding site. For this reason, we restrained the trapped water at its target binding site using a harmonic restraint with a light force constant of 0.5 kcal mol^–1 Å^–2.

2.3.2. Avoiding Rehydration of the Binding Site

In our ABFE thermodynamic cycle, the trapped water is alchemically decoupled in edge E, i.e., its vdw and Coulomb interactions are turned off. This creates a cavity in the binding site. If the binding site has some level of solvent accessibility, it may rehydrate at different stages of the thermodynamic cycle, which would invalidate the thermodynamic cycle (e.g., by replacing the trapped water with a different water in some intermediate states but not others). To avoid the rehydration of the cavity, we added a repulsive potential for the solvent at the position of the trapped water in our ABFE thermodynamic cycle (edge C). This repulsive potential is only removed at the end of the thermodynamic cycle, in edge G, after the trapped water is decoupled.

Rehydration of the cavity can occur in different parts of the thermodynamic cycle. Without a solvent restraint, it could occur during the NES switching simulations (which would likely lead to poor convergence since the paths including rehydration may not reach the expected end states), or more likely, during the (longer) equilibrium simulation of the end state of the NES. If rehydration would occur in the end state, the switching NES simulations would be ill-defined, since some or all of the starting structures of the reverse NES (for coupling the trapped water) would now have a resident water present before trying to couple the noninteracting trapped water. A dry cavity is also paramount to create space for inserting a bigger ligand in the thermodynamic cycle for ligand transformation (Figures 1 and 3).

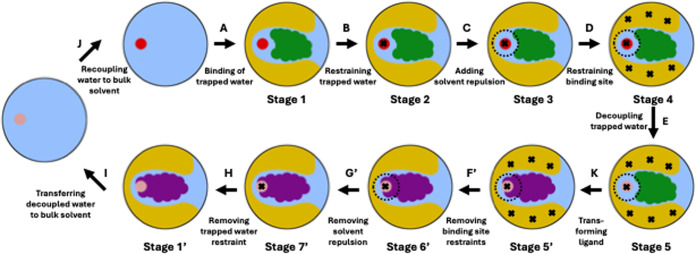
Figure 3.

Thermodynamic cycle to calculate the complex leg of the relative binding free energy (RBFE) between two ligands, where one ligand (green) binds to the protein with a trapped water while the other ligand (purple) displaces it. The red circles in stages 1 through 4 and in the starting stage of edge A represent interacting trapped water, whereas the faded red/magenta circles in stages 5, 5′, 6′, 7′, 1′, and in the end stage of edge I represent noninteracting water. The dashed black circles around the trapped water in stages 3 through 5 and in stages 5′ and 6’ represent solvent repulsion. The black crosses in stages 2 through 5 and in stages 5′ through 7’ represent position restraints applied to different parts of the system–the trapped water and the protein’s binding site. For an easy nomenclature, the stages and edges for the purple ligand are denoted with a ′ superscript for the corresponding stages and edges for the green ligand in the ABFE thermodynamic cycle (Figure 2). We have named the end state of edge H as stage 1′ because it represents the unrestrained binding mode of the purple ligand and its corresponding stage in the ABFE thermodynamic cycle is denoted by stage 1, i.e., the unrestrained binding mode of the green ligand.

Even after including the solvent restraint in our thermodynamic cycle, rehydration may still be observed along edge G, which turns off the solvent repulsion to correctly account for its effect. A rehydration along edge G would invalidate the ABFE thermodynamic cycle, since we are aiming to calculate the free energy of removing the trapped water. Releasing the position restraints along edge F allows the pocket to adapt to the absence of the trapped water, and might inhibit rehydration. If rehydration systematically occurs even after the system had time to rearrange, we consider the system to be unsuited for calculation of the ABFE of water using our method. One possible explanation of such behavior is that the water is less slow than initially assumed and that its binding and unbinding may be accessible to equilibrium simulations. In such cases, water sampling should be handled in conjunction with the free energy simulations themselves, rather than separated out as in the present work.

In this work, we observed rehydration of the binding cavity in stage 7 for one of the systems we studied (see Section 3.1.3 for details), but only when we started the simulation of stage 7 from a structure of the system that did not have time to adapt to the cavity created by the decoupling of the trapped water. For that one system, we tweaked our setup to use an equilibrated structure from stage 6 to provide starting coordinates for the simulation of stage 7, after which we did not observe any rehydration of the binding site in stage 7 anymore.

2.3.3. Avoiding Conformational Changes of the Binding Site

One of the key findings of the prior work¹¹ in this space is that, after a trapped water is removed, the cavity left behind by the trapped water can collapse, i.e., the protein can exhibit a conformational change upon decoupling of the trapped water as the protein’s side chains can now occupy the space previously occupied by the trapped water. Such a conformational change in the binding site can push the end states with the interacting and noninteracting trapped water far apart in phase space, which in turn can lead to problems in converging the free energy estimate. To ensure that the binding site’s conformation does not change upon decoupling of the trapped water, we applied harmonic Cartesian position restrains on the heavy atoms of the binding site of the trapped water (edge D). The Cartesian position restraints effectively make the stages 4 and 5 of our ABFE thermodynamic cycle origin-dependent, i.e., they are not invariant under translation or rotation.

The use of origin-dependent position restraints requires careful evaluation of the Hamiltonians of the origin-dependent stages (stages 4 and 5) with the trajectories of the origin-independent stages (stages 1 through 7, except stages 4 and 5) for correct MBAR calculations. Without special care, the Hamiltonian of an origin-dependent stage evaluated with the trajectory of an origin-independent stage will result in an incorrectly high potential of the restraints. This will be so even if the configuration of the binding site does not significantly change, because the absolute positions of the heavy atoms in the origin-independent trajectory will shift and/or rotate across the unrestrained simulation.

To calculate the correct potential of the binding site restraints, we exploited the translational and rotational invariance of the unrestrained stages to calculate the free energy associated with (only) the conformational rearrangement. We postprocessed the trajectories of the unrestrained stages by aligning every frame of the trajectories onto the reference positions of the restraints used for the restrained stages. We then used these realigned positions of the unrestrained frames to evaluate the Hamiltonians of the origin-dependent stages. The Python code for postprocessing the trajectories of the unrestrained stages, and for calculating the potentials of restraining the binding site can be found in the GitHub repository waterNES.²⁸

The postprocessing is necessary due to the choice of Cartesian position restraints over origin-independent restraints, such as, dihedral restraints or distance restraints between atoms. While we did experiment with origin-independent restraints, we were unable to find a setup that would consistently avoid pocket collapse across all target proteins included in our test set. For example, using dihedral restraints on the residues of a binding site to avoid collapse would pose challenges in systems where the binding site is formed by two separate chains of the protein (for example, HIV-1 Protease). In such cases, the binding site could still collapse by a translation motion of the two protein chains, while the dihedral restraints would be still in place. The Cartesian position restraints, on the other hand, are extremely straightforward to set up and very effective at keeping the binding pocket open. We therefore think that the postprocessing of the trajectories to calculate the correct potential of the origin-dependent restraints is a small price to pay for a simpler and more robust setup that favors automation.

We chose the positional restraints on the heavy atoms of the binding site to be weak enough that they do not impair the dynamics of the system significantly. We selected the heavy atoms for the position restraints according to the procedure described in Supporting Document Section S1.3, and restrained each of the selected heavy atoms with a light force constant of 0.5 kcal mol^–1 Å^–2.

After decoupling the trapped water from the system and removing the binding site restraints, the binding site may change its conformation in stage 6. This can result in the stages 6 and 5 being distant in phase space, and requires a free energy calculation routine that can adequately sample the conformational change. We therefore introduced 7 intermediate λ states between stages 5 (fully restrained) and 6 (fully unrestrained), and reduced the position restraint on the binding site across each subsequent λ state, using force constants amounting to 64, 32, 16, 8, 4, 2, and 1% of the force constant of the full position restraints in stage 5 (see Section S1.1 and Table S2 in the Supporting Document for details). Throughout the simulations of the intermediate λ states, the restraint on the trapped water and the solvent repulsion were kept in place.

2.4. The Thermodynamic Cycle to Calculate the RBFE between Ligands Involving Displacement of a Trapped Water

The RBFE between two ligands is the difference between the free energies to transform one ligand into the other in the complex (complex leg) and in the solvent (solvent leg) (Figure 1). For the complex leg of the RBFE calculation, we revised the ABFE thermodynamic cycle for the trapped water into an RBFE thermodynamic cycle that handles displacement of a trapped water upon modification of a ligand (Figure 3). In particular, we imagine this RBFE thermodynamic cycle will be used in cases where prior analysis has determined that modification of a particular initial ligand into another ligand will displace a relatively ordered (and especially a slow) water which requires separate handling in the free energy calculation.

Our restraining scheme resulted in excellent phase space overlap across stages 1 through 4 in our trapped water ABFE calculations, details of which are discussed in the Results Section 3.1.1, which prompted us to further optimize our RBFE thermodynamic cycle. Specifically, we combined the edges B, C and D into a single edge, i.e., edge M (Figure 4). Furthermore, we omitted the 7 intermediate λ states, which we introduced in the ABFE thermodynamic cycle to calculate the free energy of removing the restraints on the binding site. We also combined the edges F′ and G′ into a single edge L, because, after the (green) ligand is transformed into the bigger (purple) ligand, the binding site cavity created by the decoupling of the trapped water is filled by the bigger ligand and the solvent water or the protein residues cannot occupy the cavity. This way, combining the removal of the solvent repulsion and binding site restraints is an optimal choice.

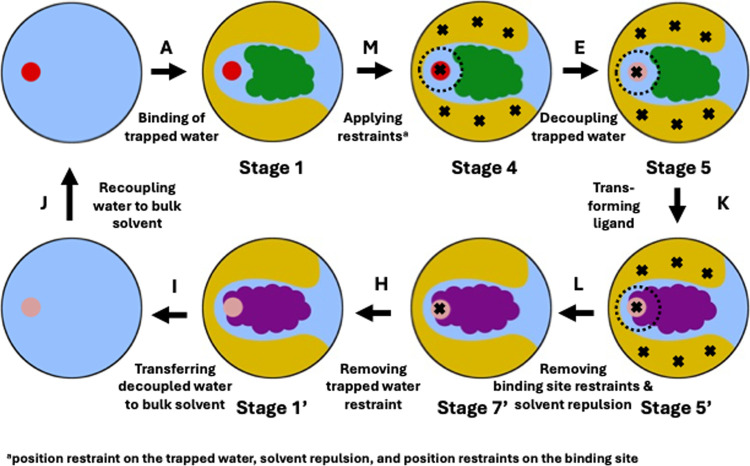
Figure 4.

Shortened thermodynamic cycle to calculate the complex leg of the relative binding free energy (RBFE) between two ligands, where one ligand (green) binds to the protein with a trapped water while the other ligand (purple) displaces it. The red circles in stages 1 and 4 represent interacting trapped water, whereas the faded red/magenta circles in stages 5, 5′, 7′, 1′ and in the end stage of edge I represent noninteracting water. The dashed black circle around the trapped water in stages 4, 5 and 5′ represents solvent repulsion. The black crosses in stages 4, 5, 5′ and 7′ represent position restraints applied to different parts of the system–the trapped water and the protein’s binding site. For an easy nomenclature, the stages and edges for the purple ligand are denoted with a ′ superscript for the corresponding stages and edges for the green ligand in the ABFE thermodynamic cycle (Figure 2). We have named the end state of edge H as stage 1′ because it represents the unrestrained binding mode of the purple ligand and its corresponding stage in the ABFE thermodynamic cycle is denoted by stage 1, i.e., the unrestrained binding mode of the green ligand.

Overall, in a shortened RBFE protocol (Figure 4), we simultaneously apply the harmonic restraint on the trapped water, solvent repulsion, and position restraints on the binding site (see Section 2.3 for details) in edge M. Thereafter, we decouple the trapped water using an NES simulation in edge E. After decoupling the trapped water, we perform a ligand transformation using a second NES simulation in edge K. After the ligand is transformed, we remove all the restraints, except the position restraint on the decoupled trapped water in edge L. Thereafter, we remove the restraint on the decoupled trapped water in edge H, and then transfer and recouple the water to bulk solvent, in edges I and J, respectively. Throughout this paper, we will refer to this shortened thermodynamic cycle for ligand transformation as the “RBFE thermodynamic cycle”, unless mentioned otherwise.

We calculated the free energy of edge M in an equilibrium free energy calculation, and the free energy of edge L in a second equilibrium free energy calculation. For calculating the free energies of decoupling the trapped water in edge E and of transforming the ligands in edge K, we ran two separate NES free energy calculations. We have described the calculation of the free energies of the edges H, I and J in the Supporting Document Section S1.2. We calculated the complex leg of the RBFE calculation between the two ligands by taking the summation of the free energies of edges M, E, K, L, H, I and J (Figure 4). For calculating the solvent leg of the RBFE calculation for the ligand transformation (Figure 1), we used an NES free energy calculation between equilibrium distributions of the two ligands in the solvent. For details of the equilibrium and the NES free energy calculations, for the complex and the solvent legs of the RBFE calculation, please refer to Sections 2.6.3 and 2.6.4, respectively.

Most of the observations made for the ABFE thermodynamic cycle are also important for RBFE calculations. The importance of restraining the trapped water remains, because edge E is identical in the ABFE and RBFE thermodynamic cycles. It is paramount that we prevent the rehydration of the binding site once the trapped water is decoupled because we want to grow the new ligand in a dry cavity. We also need to ensure that the binding cavity does not collapse upon removing the trapped water since that would make growing the new ligand more complicated. In contrast to the ABFE cycle, we are however expecting that the release of the binding site restraints will consist of a shorter path in phase space, since the larger ligand should fill out most of the space left behind by the removed trapped water.

2.5. Selected Systems

To test our ABFE protocol (Figure 2), we selected the 13 systems previously studied by Ge et al.,¹¹ because our efforts are directed toward optimizing the separation of states protocol originally introduced in that study. The 13 systems were originally taken from a previous study by Barillari et al.,²⁹ which focused on classifying conserved and displaceable water molecules across a large number of proteins/protein–ligand complexes. The 13 systems studied here consist of a Bovine Pancreatic Trypsin Inhibitor protein (BPTI; PDB ID: 5PTI(30)), and three protein–ligand complexes of each of Trypsin (PDB IDs: 1AZ8,³¹1C5T³² and 1GI1(33)), Factor Xa (PDB IDs: 1LPG,³⁴1F0S³⁵ and 1EZQ(35)), HIV-1 Protease (PDB IDs: 1EC0,³⁶1EBW³⁷ and 1HPX(38)), and Scytalone Dehydratase (PDB IDs: 3STD,³⁹7STD⁴⁰ and 4STD(40)) target proteins. For each target protein, the trapped water molecule of interest is located at the same location in the binding site of the protein across complexes.

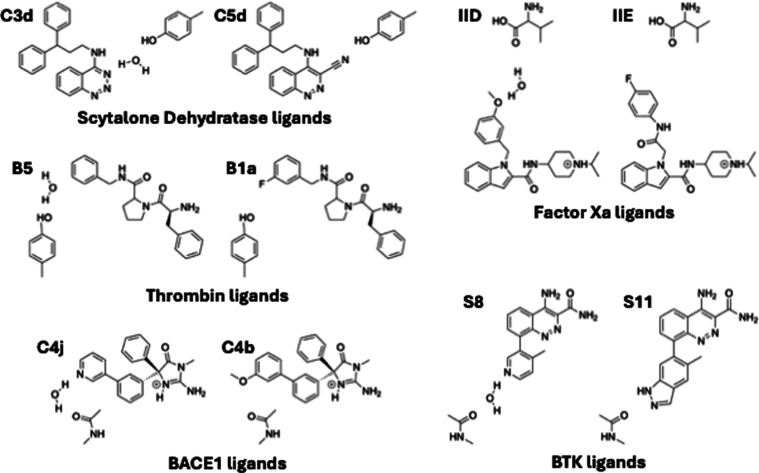
For our RBFE protocol for the transformation of ligands (Figure 4), we selected systems for which the binding affinities of two ligands for a target protein are experimentally known, and one of the two ligands binds to the target protein with exactly one trapped water while the other ligand displaces it. For testing our RBFE protocol, we identified five such ligand pairs (Figure 5), one for each of the five target proteins: Thrombin, Factor Xa, Scytalone Dehydratase, β-Secretase-1 (BACE1), and Bruton’s Tyrosine Kinase (BTK). The RBFEs for the ligand transformations for these protein–ligand systems have also been previously calculated by various computational studies.¹⁷⁻¹⁹

Figure 5.

Ligand pairs in the relative binding free energy calculations (RBFEs). In each pair, the ligand that binds with the trapped water is shown on the left and the ligand that displaces the trapped water is shown on the right. The trapped water molecule is also shown in each ligand pair.

2.6. Simulation Details

2.6.1. System Topology and Structure Preparation

For the ABFE calculations for the trapped waters, protein/protein–ligand complex structures were downloaded from the Protein Data Bank (PDB) for the respective PDB IDs listed in Section 2.5. Missing residues or heavy atoms were added using PDBFixer,^45,46 and the protonation states for the amino acid residues of the protein were determined according to the respective experimental pH reported on the PDB webpages of the complexes, using the PROPKA algorithm available on the PDB2PQR web server⁴⁷ to estimate the most likely protonation state of each residue at that pH. For the HIV-Protease system 1HPX, protonation states for the two aspartic acids (ASP-25 and ASP-125) in the binding site are known from a previous experimental study,⁴⁸ and the protonation states we obtained from the PDB2PQR web server agreed with those from the experimental study. The pK_a values for ligands were estimated using Chemicalize utility of ChemAxon, and we used the resulting predicted ligand protonation states, except when otherwise noted. We used OpenMM software package⁴⁹ to generate the force field parameters for the protein–ligand complexes. Protein structures were parametrized using the AMBER 14SB force field,⁵⁰ and ligands were parametrized using the OpenFF-2.0.0 force field (Sage)⁵¹ and the AM1-BCC charge model implemented in the OpenEye toolkit.⁵² We used TIP3P water model⁵³ to solvate our systems and added 0.2 molar Na⁺ and Cl^– to the simulation box.

We simulated the RBFE thermodynamic cycle for ligand transformation using a hybrid topology approach for the ligands. We prepared the structures of the individual protein–ligand complexes using the same procedure as that used for our ABFE calculations described above. The PDB structures of the complexes for the five ligand pairs with their target proteins are known experimentally, with the exception of the complex for ligand C 3d for the Scytalone Dehydratase system (Table 1). We generated the structure of this unknown Scytalone Dehydratase complex by aligning the common atoms of the ligand C 3d with those of a similar ligand in a known Scytalone Dehydratase complex structure (PDB ID: 5STD(40)).

Table 1. PDB IDs of Protein–Ligand Complexes Used in the RBFE Calculations for the Ligand Transformations.

protein	ligand	PDB ID
thrombin	B5	2ZFF(41)
	B1a	2ZDV(41)
scytalone	C 3d	5STDa(40)
dehydratase	C 5d	3STD(39)
factor Xa	IID	2BQ7(42)
	IIE	2BQW(42)
BACE1	C4j	4DJW(43)
	C4b	4DJV(43)
BTK	S8	4ZLZ(44)
	S11	4Z3V(44)

^aIndicates the PDB ID of the complex containing a closely related ligand.

After generating the parameters for the individual ligands of a ligand pair, we generated the hybrid topology and structure of the ligand pair using the PMX software package.⁵⁴ We concatenated the structure of the hybrid ligand to the structure of its respective protein taken from the complex that contained the trapped water molecule, as our calculations require the position of the trapped water to be known a priori. We solvated the structure of the protein with the hybrid ligand in a box of TIP3P water model⁵³ and added 0.2 molar Na⁺ and Cl^– to the simulation box.

For simulating the solvent leg of the ligand RBFE calculations, we solvated the structure of the hybrid ligand in a box of TIP3P water⁵³ and added 0.2 molar Na⁺ and Cl^– to the simulation box.

To implement the various restraints required to simulate both the ABFE and RBFE thermodynamic cycles, we modified the GROMACS topology files of the complexes, details of which are described in the Supporting Document Section S1.3. The topology files for all the ABFE and RBFE systems can be found in the GitHub repository associated with this paper, waterNES.²⁸

2.6.2. Energy Minimization and Equilibration

All MD simulations were run using GROMACS 2022.1 simulation package.⁵⁵ Water molecules in the system, except the trapped water, were constrained using SETTLE algorithm.⁵⁶ The atoms of the trapped water were constrained according to the procedure described in Supporting Document Section S1.3 (it could not be constrained with SETTLE because, in GROMACS, SETTLE cannot be applied to two different “molecule types”; in this case, the normal water and the (separately treated) trapped water). Coulomb and vdW interactions were calculated for a 10 Å cutoff radius and long-range Coulomb interactions were calculated using Particle Mesh Ewald (PME)⁵⁷ with a Fourier grid spacing of 1 Å. A time step of 2 fs was used in MD simulations.

For each of the ABFE and RBFE systems, starting from the solvated structure, we performed an energy minimization for 5000 steps using the steepest descent algorithm. Then, we equilibrated the system in an NVT ensemble for 10 ps, stabilizing the temperature of the system at 298.15 K using the stochastic dynamics integrator and an inverse friction constant of 2 ps. In the NVT equilibration, we restrained each of the heavy atoms of the protein and the ligand using a harmonic position restraint with a force constant of 1000 kJ mol^–1 nm^–2. Finally, we performed a 100 ps equilibration of the system in the NPT ensemble, by coupling the system to the Parrinello–Rahman barostat⁵⁸ in an isotropic pressure coupling of 1 bar using a time constant of 1 ps. During the NPT equilibration as well, each of the heavy atoms of the protein and the ligand were restrained using a harmonic position restraint with a force constant of 1000 kJ mol^–1 nm^–2. Full details of the input parameters for the simulations (GROMACS mdp files) can be found in the GitHub repository waterNES.²⁸

2.6.3. Equilibrium Free Energy Simulations

For simulation of the individual stages of the ABFE and RBFE thermodynamic cycles, three different λ schedules (Tables S1 and S2), scaling the harmonic restraint on the trapped water, the solvent repulsion term, and the position restraints on the binding site, were added to the GROMACS input parameters file for each stage (mdp files), details of which are described in Supporting Document Section S1.1. Simulations of all the stages of the thermodynamic cycles were run independently and were started from the structure obtained from the procedure described in Section 2.6.2. The stages were then simulated for a 6 ns production run in the NPT ensemble using the stochastic dynamics integrator and the Parrinello–Rahman barostat. The stages with Cartesian position restraints on the binding site used their respective starting structure (i.e., the final structure of the equilibration) as the reference structure for the position restraints.

The solvent legs of the RBFE calculations were run starting from the solvated structures of the hybrid ligands obtained from the procedure described in Section 2.6.1. Each of the solvated structures of the hybrid ligands was equilibrated using the equilibration procedure described in Section 2.6.2. For each of the two ligands in the hybrid structure, 6 ns of production run was generated in the NPT ensemble.

2.6.4. NES Simulations

In both the ABFE and RBFE thermodynamic cycles, NES simulations were performed for the alchemical transformations, i.e., trapped water decoupling and ligand transformation. The Gapsys soft-core potential⁵⁹ was used to turn on/off vdw interactions to avoid singularities in the alchemical transformations.

For the ABFE calculations, we generated 100 starting structures for the NES switches from the last 4 ns of the 6 ns production runs of stages 4 and 5. In each of the NES switches for water decoupling/coupling, the vdw and Coulomb interactions were turned off/on simultaneously over 250 ps by updating the λ value on every time step (Δλ = 0.000008).

In addition to the NES for the trapped water, ligand transformation was also simulated between stages 5 and 5′ in the RBFE thermodynamic cycle. For the ligand transformations, NES switches of 500 ps simulation time were run, transforming the vdw and Coulomb interactions of the ligands simultaneously by updating the λ value on every time step (Δλ = 0.000004).

The ligand transformation for the solvent leg of the RBFE calculation was also performed using NES simulation. We generated 100 starting structures from the last 4 ns of the 6 ns production runs of the two ligands in solvent (generated according to the procedure described in Section 2.6.3). From these starting structures of the two ligands, we ran NES switches of 500 ps simulation time (Δλ = 0.000004) transforming one ligand to the other.

2.6.5. Free Energy Calculation and Uncertainty Estimates

For both the ABFE and the RBFE thermodynamic cycles, the trajectories of the unrestrained stages needed to be postprocessed to obtain the correct values of the various restraint potentials implemented in the simulation protocols (see Sections 2.3 for details). After postprocessing the trajectories, we calculated the free energies of the equilibrium free energy simulations using the MBAR implementation in the Alchemlyb software package version 0.7.⁶⁰ For the free energy calculations of the NES simulations in the ABFE and RBFE thermodynamic cycles, and in the solvent leg of the RBFE calculations, we used the BAR implementation in the PMX software package.⁵⁴

We simulated three independent replicates of the ABFE and RBFE thermodynamic cycles for each of the systems studied here, as well as of the solvent leg of each of the ligand RBFE calculations. We calculated the uncertainties in our ABFE or RBFE estimates using the formula: 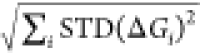, where the STD(ΔG_i) is the standard deviation in the free energy of edge i across the three replicates, and i runs over all the edges contributing to the ABFE or the RBFE estimate (see Sections 2.2 and 2.4 for details).

3. Results

We have calculated ABFEs of trapped waters in protein–ligand complexes using a separation of states approach. To calculate the ABFEs, we simulated a thermodynamic cycle that implemented a harmonic restraint on the trapped water, a solvent repulsion term, and position restraints on the protein’s binding site (Figure 2). Once the restraints were applied, we decoupled the trapped water using an NES simulation, and then removed the restraints.

We revised the ABFE thermodynamic cycle to calculate the RBFEs of ligand pairs, where in each ligand pair, one ligand binds to its target protein with a trapped water while the other ligand displaces it. In the RBFE thermodynamic cycle, we used the same restraints as used in the ABFE thermodynamic cycle. After applying the restraints, we decoupled the trapped water and transformed the ligand in two subsequent NES simulations, and then removed the relevant restraints.

To apply and remove the restraints in the thermodynamic cycles, we performed equilibrium free energy calculations.

3.1. ABFEs of Trapped Waters

3.1.1. Our Protocol Resulted in Precise Estimates of ABFEs of Trapped Waters in Protein–Ligand Complexes

We calculated ABFEs of trapped waters in 13 protein/protein–ligand complexes (Table 2) using the ABFE thermodynamic cycle (Figure 2). These 13 complexes are previously studied by Ge et al.,¹¹ and were originally introduced by Barillari et al.²⁹

Table 2. ABFEs (in Kcal Mol^–1) of Trapped Water Molecules in Protein–Ligand Complexes.

proteina	water identifierb	ABFEc
BPTI
5PTI	Wat:122	–3.59 ± 0.8
Trypsin
1AZ8	Wat:D:638	–2.83 ± 0.09
1C5T	Wat:D:325	–1.16 ± 0.1
1GI1	Wat:D: 268	–2.40 ± 0.2
FXad
1LPG	Wat:E:215	–2.14 ± 0.3
1F0S	Wat:E:68	–0.52 ± 0.4
1EZQ	Wat:E:100	–5.67 ± 0.1
HIV-1e
1EC0	Wat:A:627	–2.19 ± 0.8
1EBW	Wat:A:319	–2.76 ± 0.6
1HPX	Wat:A: 301	–5.67 ± 0.5
SDf
3STD	Wat:H:36	–1.32 ± 0.3
7STD	Wat:G:91	–1.79 ± 0.5
4STD	Wat:G:64	–0.09 ± 0.5

^aFor each protein, the PDB ID of the complex used in this study is provided.

^bThe water identifier refers to the ID of the trapped water in the PDB file, and is taken from Table 2 of the original study of Barillari et al.²⁹

^cUncertainities are calculated over three simulation repeats.

^dFXa = Factor Xa;

^eHIV-1 = HIV-1 Protease.

^fSD = Scytalone Dehydratase.

We simulated three replicates of the ABFE thermodynamic cycle for each of the 13 systems, and our calculations resulted in precise estimates of the trapped water ABFEs for all the systems. For each system, our equilibrium free energy calculation to restrain the system resulted in sufficient overlap among the sampled phase spaces of the different states (Figure S4). After decoupling the trapped water, we calculated the free energy to remove the restraints, using a second equilibrium free energy calculation. Here, we calculated the free energy to remove the binding site restraints using 7 intermediate λ states between the end states with and without the binding site restraints (see Section 3.1.3 for details). For each system, we obtained sufficient overlap among the sampled phase spaces in the simulations of the intermediate λ states bridging the path between the states with and without the binding site restraints (Figure S5). We also obtained sufficient overlap in our NES work distributions for decoupling and coupling the trapped water in all of our calculations.

The errors in our ABFE estimates were within 0.8 kcal mol^–1 (Table 2). Except for two HIV-1 Protease systems (1EC0and 1EBW) and the BPTI system (5PTI), all other systems resulted in errors within 0.5 kcal mol^–1. For all the systems, the application and removal of the binding site restraints resulted in the largest errors in our calculations, but each of these errors was generally below 0.4 kcal mol^–1. This relatively large statistical error could be expected because constraining the protein is a relatively difficult task. To constrain the orientation of the binding site to its orientation in an equilibrated starting structure of the simulation, we applied position restraints to a significant number of heavy atoms of the binding site, i.e., in the middle of the protein (see Section 2.3.3 for details). Across the three simulation replicates, variations in motion of the protein can result in different strains on the restrained heavy atoms, and hence, the free energy to restrain the binding site can exhibit relatively large statistical error.

3.1.2. We Compared our ABFEs of Trapped Waters with Literature Values

We compared our ABFE values with the prior literature^11,29 (Figure 6). Previously, Barillari et al.²⁹ studied the 13 systems under investigation here using the double decoupling method to decouple trapped waters from the proteins’ binding sites. They implemented replica exchange thermodynamic integration (TI) in MC simulations, and they used a hard-wall potential at the location of the trapped water to prevent solvent flooding- and a potential collapse- of the binding site during the water decoupling. Notably, our ABFEs for the BPTI, Trypsin, and Scytalone Dehydratase systems lie within 2 kcal mol^–1 of the corresponding ABFEs from the reference study (Figure 6). However, the reference study overestimates the binding affinities of the trapped waters in HIV-1 Protease systems and underestimates them in Factor Xa systems, compared to the binding affinities that we calculated for those two systems.

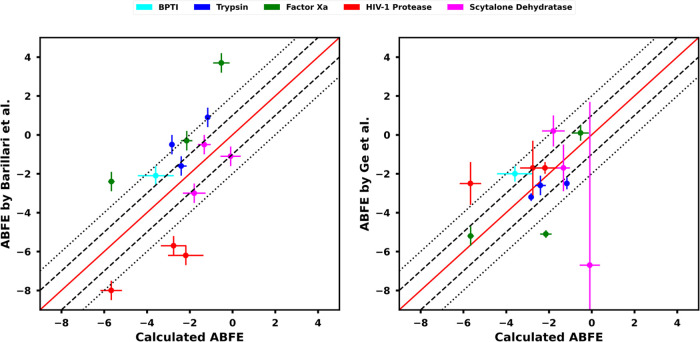
Figure 6.

Comparisons of the trapped water ABFEs calculated here with ABFEs from Barillari et al.²⁹ (left) and Ge et al.¹¹ (right). In both of the plots, error lines at 1 kcal mol^–1 (dashed) and 2 kcal mol^–1 (dotted) are also shown.

Because of differences in force fields and methods between the reference study and our present work (described below in this section) and the difficulties of validating these methods, we take the literature values only as reference and not as ‘ground truth’. The main goal of our ABFE calculations was to develop a robust protocol that ensures good phase space overlap in our equilibrium free energy calculations (see Section 2.2 for details), yields precise and well-converged ABFE estimates, and can readily be expanded to RBFE calculations, rather than to reproduce the reference values from the literature. The study by Barillari et al.²⁹ presented a good starting point to think about a correct sampling protocol for the decoupling of the trapped water, which is a precursor for a subsequent ligand transformation in our separation of states approach (Figure 1).

The differences in the ABFEs of the trapped water between our study and the reference study of Barillari et al.²⁹ can be attributed to a number of differences between the two studies. We have simulated water in our calculations using the TIP3P water model, whereas the reference study used the TIP4P water model. The reference study modeled the protonation states of the protein amino acids and ligands in their complex structures assuming a pH of 7, while we have taken the experimental pH for the respective complexes, as reported in the PDB database, to determine the protonation states. The reference study did not report the prepared structures of their simulated complexes, so comparison of the employed protonation states is not possible. Furthermore, the reference study used a hard-wall potential to restrain the trapped water at its approximate position in the binding site, as well as to prevent the surrounding (the solvent, the protein side chains, and the ligand) from occupying the binding site after the trapped water’s decoupling. In our study, we have used a Lennard-Jones repulsion term to prevent solvent flooding, and harmonic positional restraints to prevent a potential binding site collapse in our thermodynamic cycle. Additionally, the reference study’s use of the hard-wall potential for water means that the resulting free energy calculations are calculating a subtly different free energy. In particular, the prior study is essentially computing the binding free energy of a trapped water in a preexisting cavity, unlike our study, which computes the binding free energy of water to the target site in a protein including any contributions of displacing the surroundings.

The experimental ABFE of the trapped water for the BPTI system at 298 K is −4.7 ± 1.0 kcal mol^–1.⁶¹ To the best of our knowledge, this is the only reported experimental value of ABFE of the trapped water across the 13 systems studied here. Using our protocol, we calculated an ABFE of −3.59 ± 0.8 kcal mol^–1 for the trapped water in BPTI, which is somewhat different from the experimental value, but not outside statistical error. We did not find an explanation for this difference. The study by Barillari et al.²⁹ reported an ABFE of the trapped water of −4.1 ± 0.5 kcal mol^–1 for the BPTI system. However, Ge et al.¹¹ highlighted that the study of Barillari et al.²⁹ did not take into account the correct standard concentration of water in their calculations and also included an unnecessary symmetry correction term for water in their free energy estimate. After correcting for the standard concentration and symmetry correction in their calculations, their ABFE for the BPTI becomes −2.1 ± 0.5 kcal mol^–1. The lack of experimental measures of the ABFEs of trapped waters for the other 12 systems studied here made it a challenge to experimentally verify our results. Under these circumstances, we are satisfied to have a well converged estimate that lies within statistical error of the only experimental result.

The ABFE of trapped water for one of our HIV-1 Protease systems (PDB ID: 1HPX) was also calculated by the double decoupling method.^62,63 Two separate studies reported −3.1 ± 0.6 and −3.2 ± 0.4 kcal mol^–1 as the ABFE of the trapped water in 1HPX. With our protocol, we calculated an ABFE of −5.67 ± 0.5 kcal mol^–1 for this system, which remains in disagreement with the previous studies by more than 2 kcal mol^–1. The reason for this discrepancy might be the difference in the treatment of the trapped water between the reference studies and our study. In the reference studies, the trapped water was restrained in an interacting state with a harmonic constraint potential tuned to correspond to the range of motion of an interacting trapped water in the binding site. The contribution of the harmonic constraint potential was accounted for by an analytical correction term corresponding to the translational degrees of freedom of the trapped water. In our calculations, we have simulated a completely unrestrained state of water (stage 1, Figure 2) and have accounted for the harmonic position restraint on the trapped water (edge B, Figure 2) by explicitly calculating the free energy of the position restraint. Given this important difference in the trapped water treatment, our thermodynamic cycle potentially uses a more clear and well-defined definition of the trapped water’s displacement, which may explain the discrepancy in the ABFEs between ours and the reference studies. For the 1HPX system, the study by Barillari et al.²⁹ reported an ABFE of −10.0 ± 0.5 kcal mol^–1 for the trapped water (−8.0 ± 0.5 kcal mol^–1 after taking into account the correct standard concentration of water and neglecting the symmetry correction term, as previously described in this section), which reflects too strong binding of the trapped water compared to what we as well as the double decoupling studies observed.^62,63 The possible reason for this discrepancy might be the use of the hard-wall potential, to prevent solvent flooding and a binding site collapse, in the study of Barillari et al.²⁹ The hard-wall potential might estimate the binding affinity of the trapped water in the solvent-exposed binding site of the HIV-1 Protease system to be too potent because it reflects the binding free energy of the trapped water in a preexisting cavity.

3.1.3. Our ABFE Protocol Resolves Previously Reported Sampling Challenges Arising Due to the Cavity Left behind by the Decoupling of the Trapped Water

In our separation of states ABFE protocol, we applied a series of restraints to solve a major challenge in ABFE calculations of trapped waters, i.e., to stabilize the cavity left behind by the decoupling of the trapped water. Previously, Ge et al.¹¹ reported two major sampling challenges in simulating protein–ligand complexes with this cavity: solvent flooding of the cavity, and binding site collapse. Due to these sampling challenges, their calculations resulted in large errors in their free energy estimates (Figure 6). Our protocol resolves both of these sampling challenges by introducing a solvent repulsion term and protein binding site restraints in our thermodynamic cycle (Figure 2).

We prevented the solvent from flooding the binding site, once the trapped water was decoupled, by applying a solvent repulsion term before the trapped water decoupling (edge C, Figure 2). The solvent repulsion term is subsequently removed in our thermodynamic cycle, only after the trapped water is decoupled (edge G, Figure 2). Upon removal of the solvent repulsion term, the solvent could flood the binding site, which could have subsequently resulted in sampling issues in the simulation of an unrestrained state with a cavity in the binding site (stage 7, Figure 2). For one of the three replicates of the HIV-1 Protease system 1EC0, we did observe solvent flooding of the cavity in the simulation of the unrestrained state. However, our calculations resulted in a dry cavity in the unrestrained state, when we started the simulation of the unrestrained state from a structure that had time to adapt to the cavity in the binding site, i.e., the equilibrated structure of the system with a noninteracting water in the binding site, and the solvent repulsion in place (stage 6, Figure 2).

In our ABFE thermodynamic cycle, we calculated the free energy of restraining the binding site from a potential collapse. We implemented position restraints on the heavy atoms of the binding site to constrain its shape and postprocessed the trajectories of the unrestrained states to calculate the correct potential to restrain the binding site (see Section 2.3.3 for details). Previously, Ge et al.¹¹ observed the collapse of the binding site for the BPTI system in their simulations. To calculate the free energy of restraining the binding site from collapsing, they implemented position restraints on the binding site using 19 intermediate λ states between the unrestrained and the restrained states of the system, which made their calculation very lengthy and computationally very expensive. Despite a lengthy protocol, the phase space overlap among the intermediate λ states in their calculations remained low, making their free energy estimate unreliable. In our protocol, we captured the binding site collapse correctly by dividing the binding site restraint removal process using 7 intermediate λ states and reducing the strength of the restraints in each subsequent intermediate λ state. Because our binding site position restraints are origin-dependent (see Section 2.3.3 for details), we postprocessed the trajectories of the unrestrained states to calculate the correct free energy contribution for the removal of the position restraints. For the BPTI system, as well as for all the other systems in our study, the postprocessing of the trajectories resulted in sufficient phase space overlap among the intermediate λ states (Figures S3 and S5), which in turn resulted in reliable free energy estimates to remove the position restraints on the binding site.

3.2. RBFEs of Ligand Transformations Involving Trapped Waters

In the present separation of states approach (Figure 1), we are interested in deconvoluting the sampling challenges of trapped waters from the calculations of the free energies of ligand transformations. We are interested in calculating the RBFE between two ligands, one of which binds to the protein with a trapped water while the other ligand displaces it. For this, first, using our ABFE thermodynamic cycle (Figure 2), we created and stabilized a dry cavity in the binding site of the protein. Then, we revised our thermodynamic cycle to implement a ligand transformation step, in which a bigger ligand is grown in the cavity (Figure 4). In the following sections, we present the RBFE calculations for five such ligand transformations.

3.2.1. We Obtained Precise Estimates of the Ligand RBFEs

We calculated RBFEs (Table 3) for five ligand transformations with our RBFE thermodynamic cycle (Figure 4). In our calculations, we simultaneously applied the harmonic restraint on the trapped water, the solvent repulsion term, and the position restraints on the protein’s binding site (edge M), and calculated the free energy of applying these restraints using an equilibrium free energy calculation (see Section 2.6.3 for details). The equilibrium free energy calculation consisted of two states of the system: an unrestrained and a restrained state (stages 1 and 4, respectively). From the restrained state of the system, we decoupled the trapped water and transformed the ligand in two subsequent NES transformations (edges E and K, respectively). All the restraints, except the positional restraint on the trapped water, were removed simultaneously (edge L), and we calculated the free energy of removing the restraints using another equilibrium free energy calculation comprising of a restrained and an unrestrained state (stages 5′ and 7′, respectively), however with the transformed ligand.

Table 3. Relative Binding Free Energies (RBFEs) (in Kcal Mol^–1) for Ligand Pairs Studied Here.

system	ligands	RBFEcalc.a	RBFEexp.
thrombin	B5–B1a	–0.97 ± 0.4	–0.6141
scytalone dehydratase	C3d-C5d	–1.59 ± 0.5	–1.9839
factor Xa	IID-IIE	–2.46 ± 0.5	–1.9842
BACE1	C4j-C4b	0.32 ± 0.6	–0.6143
BTK	S8–S11	–4.08 ± 0.7	–1.9144

^aUncertainties are calculated over three simulation repeats.

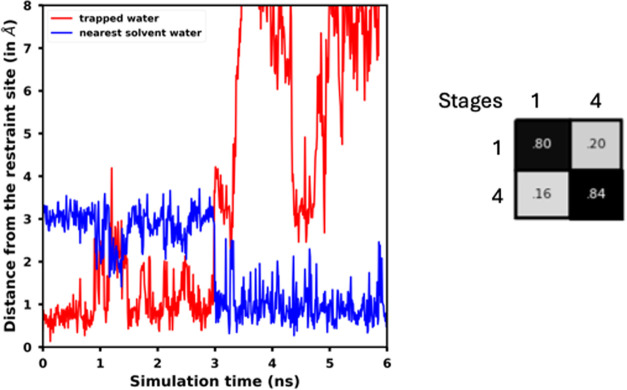
In our RBFE calculations, we obtained sufficient overlap between the sampled phase spaces by the unrestrained and restrained states, in both the equilibrium free energy calculations, as well as in the forward and reverse NES transformations for the trapped water decoupling and for the ligand transformation. This resulted in RBFEs for all the ligand pairs within a standard deviation of 0.7 kcal mol^–1 (Table 3). In our simulations for the BTK system, we observed an exchange between the trapped water and a solvent water in the simulation of the unrestrained stage, in all three replicates (Figure 7). We postprocessed the trajectory of the unrestrained stage to identify the exchanged solvent water as the new trapped water (see Section 2.3.1 for details). Our postprocessing efforts resulted in good phase space overlap between the restrained and unrestrained states of the system given the water exchange (Figure 7), and hence, in a correct estimate of the free energy to apply the restraints (edge M, Figure 4).

Figure 7.

(Left) Distances of the trapped water and nearest solvent water from the target binding site of the trapped water in BTK protein’s binding site, in the simulation of an unrestrained stage (stage 1, Figure 4) of the system. The nearest solvent water exchanges with the trapped water at around 3 ns during the simulation. (Right) Phase space overlap matrix for the equilibrium free energy calculation comprising of two states of the BTK system: an unrestrained stage, and a restrained stage (stages 1 and 4, respectively, in Figure 4). In the restrained state, the harmonic restraint on the trapped water, the solvent repulsion term, and the binding site position restraints are in place. The overlap matrix shows that we obtained good phase space overlap between the unrestrained and the restrained states, even though the trapped water was exchanged with a solvent water during the simulation of the unrestrained stage, because we remapped the trajectory of the unrestrained stage to identify the exchanged solvent water as the new trapped water upon exchange (see Section 2.3.1 for details).

We also calculated the RBFEs for the five ligand pairs with a larger thermodynamic cycle (Table S3), shown in Figure 3, where the restraints application and removal processes were divided across several different stages, same as in our ABFE thermodynamic cycle (Figure 2). Using the larger thermodynamic cycle, we calculated RBFEs within 0.7 kcal mol^–1 of the values we obtained from the shorter thermodynamic cycle (Table 3). Therefore, we conclude that the simultaneous application of the restraints, and their simultaneous removal, in our shorter RBFE thermodynamic cycle did not result in any significant loss in the accuracy of our RBFE calculations, compared to the incremental application, and removal, of the restraints across several different stages in the larger thermodynamic cycle.

3.2.2. We Compared our RBFEs for the Ligand Pairs with Literature Values

The systems considered here have previously been studied by other alchemical free energy approaches.^17−19,62 Ben-Shalom et al.¹⁹ studied the Thrombin, Scytalone Dehydratase and BTK systems using four different methods. They found that two of the four methods, where the trapped water was placed in the binding site using a hybrid Monte Carlo Molecular Dynamics (MC/MD), along with alchemical transformations of the ligands, resulted in more accurate RBFE calculations, compared to methods where water placement was not carried out along with the ligand transformations. Our RBFEs for the Thrombin and the BTK systems (Table 3) are in excellent agreement with the RBFEs reported in their study (−0.99 and −0.86 kcal mol^–1 for the Thrombin and −3.35 and −3.99 kcal mol^–1 for the BTK systems). Our RBFE value between the Thrombin ligand pair is also within the standard deviation from the experimentally reported RBFE of −0.61 kcal mol^–1.⁴¹ Though we found disagreement between our RBFE value between the Scytalone Dehydratase ligand pair (−1.59 ± 0.5 kcal mol^–1) and the values from Ben-Shalom et al.¹⁹ (−3.24 and −2.59 kcal mol^–1), our value is in a better agreement with the experimental value of −1.98 kcal mol^–139 than the values in the other study.

The Factor Xa system has previously been studied by Abel et al.,⁶⁴ using molecular dynamics simulations and a solvent analysis technique based on inhomogeneous solvation theory.⁶⁵ The previous study reported RBFE values of −1.73 and −1.95 kcal mol^–1 using two different solvent functionals. Our RBFE value of −2.46 ± 0.5 kcal mol^–1 between the Factor Xa ligand pair remains in line with the literature values, as well as with the experimental value of −1.98 kcal mol^–1.⁴²

Another study by Wahl et al.¹⁷ has reported RBFEs for three of the five systems studied here: the Scytalone Dehydratase, the BACE1, and the BTK systems. In their study, they calculated the RBFEs between ligands using Free Energy Perturbation (FEP) calculations and Replica Exchange Solute Tempering (REST) starting from different solvation states of the binding site, which resulted in large hysteresis. The hysteresis was reduced by introducing a Grand Canonical Monte Carlo (GCMC) step before the FEP calculations. Between the C 3d–C 5d ligand pair of Scytalone Dehydratase (Figure 5), they reported RBFEs of −0.91 and −1.33 kcal mol^–1 for two different initial solvation conditions, which are both in agreement with the RBFE we calculated. Ross et al.¹⁸ presented an advancement of the FEP method and reported the Scytalone Dehydratase ligand RBFEs of 0.37 and 1.04 kcal mol^–1 for two different initial solvation states. Our RBFE value (−1.59 ± 0.5 kcal mol^–1) disagrees with the values reported by Ross et al.,¹⁸ however, unlike the RBFEs reported by Ross et al., our RBFE agrees with the experimental RBFE of −1.98 kcal mol^–1.⁴²

Our RBFE value of 0.32 ± 0.6 kcal mol^–1 between the BACE1 ligand pair disagrees with the values reported by Wahl et al.¹⁷ (−2.15 and −1.78 kcal mol^–1) and Ross et al.¹⁸ (−1.69 and −2.35 kcal mol^–1). Neither we nor the previous studies could reproduce the experimental RBFE of −0.61 kcal mol^–1.⁴³

Between the BTK ligand pair, our RBFE value of −4.08 ± 0.7 kcal mol^–1 is in disagreement with the experimental RBFE of −1.91 kcal mol^–1,⁴⁴ as well as with the RBFE values reported by Wahl et al.¹⁷ (−1.76 and −3.32 kcal mol^–1), however it is in agreement with the values reported by Ross et al.¹⁸ (−4.21 and −3.68 kcal mol^–1).

Overall, we obtained RBFE values for our systems largely in agreement with the RBFE values reported by previous computational studies that implemented the MC/MD and GCMC methods, as well as with the experimental RBFE values. However, for the BACE1 system, we observe disagreements with the literature values. For the BTK system, even though our RBFE value agrees with a previous computational study,¹⁸ it remains in disagreement with the experimental estimate by around 2 kcal mol^–1. This prompted us to investigate the BACE1 and the BTK systems in greater detail, and our findings are described in the following sections.

3.2.3. Ligand Rotation and Lack of Conformational Sampling of the Protein Affected our RBFE Estimate between the BACE1 Ligand Pair

A sampling challenge we observed in our BACE1 simulations was the flexibility of the ligand. The BACE1 binding site can accommodate a rotation of the pyridine ring of the ligand C4j (Figure 5). In our simulations, upon decoupling of the trapped water, the hydrogen bond between the trapped water and the nitrogen of the pyridine ring vanished and this led to rotations of the pyridine ring. The rotations of the pyridine ring caused several of the NES switches for ligand transformation to start from the rotated conformations, which resulted in different degrees of overlap in the forward and reverse NES work distributions of the ligand transformation across our replicates. This resulted in a large error contribution (of 0.4 kcal mol^–1) of the ligand transformation edge in the thermodynamic cycle (edge K, Figure 4). The previous study by Wahl et al.¹⁷ has also reported the rotations of the pyridine ring of the ligand C4j in their simulations.

Between the BACE1 ligand pair, we calculated an RBFE of 0.32 ± 0.6 kcal mol^–1, which is within 1 kcal mol^–1 from the experimental value,⁴³ though, contrary to the experiment, our calculations estimate the binding free energy of the ligand C4j to be too favorable compared to that of the ligand C 4b. We found that our calculations were affected by some sampling challenges that could explain the difference between our RBFE estimate and the experimental value. These sampling challenges are also reported in previous studies of BACE1.⁶⁶⁻⁶⁸ Keränen et al.⁶⁶ studied BACE1 ligands structurally similar to the ligands in our study and reported that the sampling of opening and closing of the 10s loop and the motion of the binding site flap in the BACE1 receptor were crucial to the accuracy of their ligand RBFE calculations. They further showed that their simulations resulted in accurate results when both the open and closed states of the 10s loop were sampled, compared to when only one of the two states was sampled. Another study by Baumann et al.⁶⁷ made similar observations, calculating differences in ligand RBFEs up to 3.5 kcal mol^–1 depending on whether simulations were started from the open or the closed conformation of the 10s loop of the BACE1 protein. In our BACE1 simulations, we observed that all of our replicates sampled only the closed conformation of the 10s loop, which can be a probable cause for the inaccuracy of our RBFE estimate between the BACE1 ligand pair. The previous studies⁶⁶⁻⁶⁸ suggest that to truly converge our free energy calculations, we would need substantially longer simulations of all of the stages of our RBFE thermodynamic cycle to capture these loop motions.

3.2.4. Changes in the Binding Mode of the BTK Ligand Resulted in Nonoverlapping NES Work Distributions for the Ligand Transformation

In the simulation of the BTK complex, we observed a translation of ligand S8 (Figure 8) in the binding site. Similar to the BACE1 receptor’s binding site, the BTK receptor’s binding site can also accommodate a rotation of the ligand’s p-methyl-pyridine ring, as well as a small translation of the ligand S8. Upon decoupling of the trapped water, the hydrogen bond between the trapped water and the nitrogen atom of the p-methyl-pyridine ring of the ligand S8 vanished. Due to the absence of the hydrogen bond, we observed slight rotations of the p-methyl-pyridine ring and small translation motions of the ligand S8 in the binding site away from the ligand’s binding pose in the equilibrated starting structure of the simulations, in all three replicates of the BTK system.

Figure 8.

Comparison of the binding poses of the ligand S8 in two replicates of the BTK simulations for the state where the harmonic restraint on trapped water, solvent repulsion, and the position restraints on the binding site are in place (stage 5, Figure 4). On the left, two different poses for the ligand S8 are shown, and on the right, the corresponding NES work distributions plots for ligand transformation in the two replicates are shown. (Left) In the upper and lower images, the magenta pose corresponds to the ligand’s true binding pose in an equilibrated starting structure used for the simulations and is shown as the reference. The binding poses in yellow and cyan correspond to the binding poses in the two simulation replicates. The trapped water is shown in sticks and the restraint site of the trapped water is shown in gray spheres. In the cyan binding pose of the ligand, the ligand has unidirectionally translated away from its binding pose in the equilibrated starting structure of the simulation, which yields no overlap in the NES work distributions. In the yellow binding pose of the ligand, the ligand does not translate too far from its position in the equilibrated starting structure and yields a converged binding free energy calculation.

In one of the three replicates of the simulation of the restrained stage of the system (stage 5, Figure 4) with the ligand S8, the translation of the ligand was unidirectional (Figure 8). We measured this translation by calculating the distance of the nitrogen atom of the p-methyl-pyridine ring of ligand S8 from the restraint site of the trapped water. In the translated pose, this distance increased to more than 5 Å (as compared to 2.8 Å in the equilibrated starting structure of the simulation). Because of the ligand translation, we did not find any overlap in the NES work distributions of the ligand transformation (edge K, Figure 4) that started from the translated pose of the ligand. Because of the lack of overlap, the free energy calculation in that particular replicate was not reliable, and hence, we omitted that particular replicate (i.e., all the free energy values we obtained for the different edges in the simulation of that replicate) from the RBFE estimation and error calculation (see Section 2.6.5 for details) for the BTK system.

Additionally, the binding site in the remaining two replicates we considered for the RBFE estimation exhibited the largest fluctuations among any of our RBFE systems. This resulted in an error of 0.5 kcal mol^–1 for removing the restraints after the trapped water was decoupled and the ligand water transformed into the bigger ligand (ligand S11, Figure 5), ultimately resulting in an overall error of 0.7 kcal mol^–1 in the RBFE estimate for the BTK system. The previous study of Wahl et al.¹⁷ has also reported the large fluctuations in the binding site in their simulations of the BTK system.

4. Discussion

In this work, we successfully implemented a separation of states protocol to compute RBFEs for ligand pairs, where in each ligand pair, one ligand binds to the target protein with a trapped water while the other ligand displaces it. In our RBFE protocol, we implemented harmonic position restraint on the trapped water, a solvent repulsion term, and position restraints on the binding site. We calculated RBFEs for five ligand pairs and our calculations resulted in errors within 0.7 kcal mol^–1. Our calculated RBFE values are largely in agreement with literature values. Our RBFE protocol is an extension of a separation of states based ABFE protocol for trapped waters’ decoupling from proteins/protein–ligand complexes, first studied by Ge et al.¹¹ and further optimized in this study.

Our ABFE and RBFE protocols are optimized in such a way that they provide high efficiencies for the calculations by making use of large distributed computational resources. Specifically, the nonequilibrium (NES) free energy calculations implemented in our thermodynamic cycles are suited for parallelization over large distributed computing resources. We have calculated the RBFEs of ligand transformations and ABFEs of trapped waters in 105 ns (30 ns for equilibrium and 75 ns for the NES free energy calculations) and 109 ns (84 ns for equilibrium and 25 ns for the NES free energy calculations) simulation times per calculation, respectively. In principle, the RBFE protocol studied here can be made even more efficient by decoupling the trapped water and transforming the ligand simultaneously in a single NES free energy calculation. In our current protocol, we combine equilibrium simulations, to apply and remove the restraints, with NES simulations, to decouple the trapped water and transform the ligand. We do not necessarily see this particular combination of choices as critical for our protocol. All equilibrium simulations in our protocol are run in parallel, so they do not increase the time to solution. Moreover, NES simulations require drawing starting structures from the equilibrium simulations, making the equilibrium simulations necessary.

Here, we have studied systems with exactly one trapped water in focus. However, our separation of states protocol can be extended to study systems where a small network of trapped waters might play a role in ligand binding and different congeneric ligands might perturb this network differently. We believe that, with minor changes in our postprocessing techniques and with the general framework of our RBFE protocol, RBFE calculations involving small water networks can easily be performed. For example, multiple trapped waters can be restrained in the restraining edge of the RBFE thermodynamic cycle (edge M, Figure 4), and all of these trapped waters can be simultaneously decoupled/coupled in a single NES simulation (edge E, Figure 4) before transforming the ligand (edge K, Figure 4).

As our separation of states-based method requires prior knowledge of numbers and locations of the trapped water in contexts of each of the ligands, we are working on a separate study on how to best predict the water positions and occupancies in protein–ligand complexes. Enhanced sampling simulation methods, such as GCMC and its variants, can also be used to determine the locations of trapped waters, before performing the free energy calculation with our protocol. For example, a recent study¹⁸ combining GCMC with MD simulation for sampling the trapped waters in ligand RBFE calculations showed that most of the advantage offered by GCMC comes from better water sampling during the equilibration phase of simulations. While that study also tested GCMC during free energy calculations, most of the benefit came simply from better equilibration. Thus, better water equilibration (to access the numbers and locations of trapped water) – such as that offered by GCMC – will likely be sufficient in many cases, and may even be more efficient since it will not require mixing GCMC sampling in to binding free energy calculations. In our case, then, a GCMC equilibration of the initial structure, prior to water decoupling and ligand mutation with our protocol, should not add dramatically to the simulation time required for our protocol.

A limitation of our separation of states approach is related to the efficiency of the NES simulations. We have observed that the NES simulations are sensitive to the environment of the alchemical transformation. For a high overlap in the work distributions of the forward and reverse NES, the two end states must have a high phase space overlap stemming from the surrounding part of the alchemical transformation. In the short NES switches, a phase space gap stemming from the surroundings can not be bridged. We have observed that the ligands’ binding poses in the end states of the NES simulation is an important factor in this. Ligands that have a large conformational flexibility while bound to the protein can have different poses in the end states, which can significantly affect the NES work overlap. The phase space of a highly flexible ligand, however, can be greatly reduced to be close to its experimentally reported binding pose by weak dihedral restraints or orientational restraints on the ligand’s rotatable bonds.

5. Conclusions

Sampling the displacement of trapped water in binding free energy calculations is a challenging problem. In this work, we have introduced an MD-based separation of states method to calculate RBFEs between two ligands, focusing on the case where one ligand binds to the protein with a trapped water while the other ligand displaces that water. We have calculated precise estimates of the RBFEs between five such ligand pairs with our method, and our results are in good agreement with the literature RBFEs. Our separation of states protocol provides a fast and efficient method to precisely and accurately calculate the RBFE between ligands when a water displacement is involved. Our protocol is designed to efficiently use large distributed computational resources, to reduce the computational cost and the time to solution, and to automate the setup and analysis of the simulations. The Python scripts for running and analyzing the RBFE calculations can be downloaded from the GitHub repository waterNES(28)

In this separation of states study, we have proposed to deconvolute the challenging problem of sampling of the trapped waters from the free energy calculation of ligand transformation. Our method requires the determination of the respective positions of the trapped waters for the two ligands a priori, but then uses this information to make the binding free energy calculation significantly more efficient than it would be if the free energy calculations themselves had to adequately capture water rearrangement. We introduced an intermediate state in the ligand transformation process, where the trapped water is removed from the system and the cavity created by it is stabilized, such that a bigger ligand can be grown in the cavity. Our work on stabilizing the trapped water cavity was an optimization of previous efforts of Ge et al.,¹¹ in which the separation of states method was applied to calculate the ABFE of the trapped waters in protein–ligand complexes. Extending their protocol, we calculated and compared the ABFE of the trapped waters in test systems from the reference study, and developed it into a protocol for ligand transformation study, where a trapped water is involved in the ligand binding.

In this study, we calculated the RBFEs between ligand pairs where exactly one trapped water is involved in the binding of a ligand. However, our method is expected to result in precise and accurate RBFE estimates also for ligand transformations where small water networks need to be perturbed; we expect to study such cases in future work after identifying suitable test cases.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.4c01145.

• Details on preparing the GROMACS input files for running the thermodynamic cycles, and for calculating the free energies in Section S1. Overlap matrices and calculated free energies of the systems studied here are also provided in Section S2. GROMACS topology, coordinates and parameter files (MDP files) for our systems are provided in the GitHub repository waterNES (https://github.com/MobleyLab/waterNES) (PDF)

Author Present Address

^# D. E. Shaw Research, 120 W. 45th St., 39th Fl., New York, New York 10036, United States

Author Contributions

This work was conducted in the Mobley Lab at UC Irvine (S.W. and D.L.M.). Regular project check-ins were done with P.T.M. and C.B. Input files during the early stage development of the project were prepared by Y.G. Design of the ABFE thermodynamic cycle and initial test runs were performed by P.T.M., with suggestions from C.B. and D.L.M. Simulations for the ABFE systems and the RBFE calculations were performed by S.W. S.W. and P.T.M. wrote the manuscript. All authors reviewed the paper and many contributed to editing. S.W.: Conceptualization, data curation, formal analysis, investigation, methodology, software, visualization, validation, writing—original draft, and writing—review and editing, P.T.M.: Conceptualization, data curation, investigation, methodology, software, supervision, validation, visualization, and writing—original draft, Y.G.: data curation, C.B.: Conceptualization, formal analysis, funding acquisition, methodology, resources, and supervision, D.L.M.: Conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, resources, supervision, and writing—review and editing.

The authors declare the following competing financial interest(s): D.L.M. serves on the scientific advisory boards of OpenEye Scientific Software, Cadence Molecular Science and of Anagenex, and is an Open Science Fellow with Psivant Sciences.