Abstract
Background
Cancer classification has consistently been a challenging problem, with the main difficulties being high-dimensional data and the collection of patient samples. Concretely, obtaining patient samples is a costly and resource-intensive process, and imbalances often exist between samples. Moreover, expression data is characterized by high dimensionality, small samples and high noise, which could easily lead to struggles such as dimensionality catastrophe and overfitting. Thus, we incorporate prior knowledge from the pathway and combine AutoEncoder and Generative Adversarial Network (GAN) to solve these difficulties.
Results
In this study, we propose an effective and efficient deep learning method, named AEGAN, which combines the capabilities of AutoEncoder and GAN to generate synthetic samples of the minority class in imbalanced gene expression data. The proposed data balancing technique has been demonstrated to be useful for cancer classification and improving the performance of classifier models. Additionally, we integrate prior knowledge from the pathway and employ the pathifier algorithm to calculate pathway scores for each sample. This data augmentation approach, referred to as AEGAN-Pathifier, not only preserves the biological functionality of the data but also possesses dimensional reduction capabilities. Through validation with various classifiers, the experimental results show an improvement in classifier performance.
Conclusion
AEGAN-Pathifier shows improved performance on the imbalanced datasets GSE25066, GSE20194, BRCA and Liver24. Results from various classifiers indicate that AEGAN-Pathifier has good generalization capability.
Supplementary Information
The online version contains supplementary material available at 10.1186/s12859-024-06013-z.
Keywords: Pathway, Deep learning, Pathifier, Generative adversarial network, Imbalanced data
Background
Cancer is a complex disease caused by mutations in cellular DNA that may be due to a variety of factors such as genetic inheritance, environmental factors, lifestyle and health conditions [1, 2]. The danger of cancer lies not only in its deadly nature, but also in its physical and psychological effects on the patient [3]. Cancer treatment usually requires the use of rigorous treatment protocols such as chemotherapy, radiation and surgery, which can lead to physical side effects such as nausea, vomiting and fatigue and can have a serious impact on a patient’s life [4, 5]. Therefore, cancer prevention and early detection are crucial to reduce the harm of cancer [6, 7].
Cancer classification has become a challenging problem, and one of the major difficulties is the unbalanced gene expression data [8]. Moreover, Obtaining patient samples typically incurs significant costs, including medical equipment and technology, human resources, and data management [9]. The collection of patient samples may require substantial time and manpower, as well as specialized medical and laboratory facilities. These costs can potentially impact the budget and feasibility of the research project [10, 11]. And the unbalanced nature of these data may lead to degradation in the performance of classifiers, which may affect cancer diagnosis and treatment. It is widely recognized that gene expression data harbors characteristics encompassing high dimensionality, limited sample size, and pronounced noise. These characteristics often lead to challenges like the high of dimensionality and overfitting in data mining, causing many classical machine learning methods to lose their effectiveness. Following this direction, researchers have proposed a meta-analysis framework integrating data augmentation and elastic data shared lasso regularization to improve gene expression analysis [12]. In order to address the issue of excessively large data dimensions, feature selection has been widely employed to mitigate the high of dimensionality and related problems [13, 14]. Additionally, the Multi-Omics Meta-learning Algorithm (MUMA) focuses on multi-omics data analysis through sample weighting and interaction-based regularization for biomarker selection [15]. In recent years, various feature selection algorithms have been applied to tumor biomarker identification. For instance, methods such as Correlation-based Feature Selection (CFS), Mutual Information, Hypothesis Testing, Recursive Feature Elimination (RFE), Maximum Relevance Minimum Redundancy (mRMR), Random Forest, Lasso, 1-norm Support Vector Machine, SCAD, Elastic Net, and Elastic SCAD have been utilized [16–18]. Some feature extraction methods have been extensively employed for dimensional reduction in omics data, including Independent Component Analysis, Principal Component Analysis, Wavelet Transform, and Manifold Learning [19, 20]. Due to the highly spatial heterogeneity of cancer, which involves various fundamental cellular processes such as apoptosis, proliferation, differentiation, and migration, the reproducibility of gene-based tumor markers is poor among different populations of cancer patients [21]. As a result, the robustness of classifiers based on gene-based tumor markers has been widely questioned. The advancement of cancer treatment strategies requires better methods to identify robust biological tumor markers. To address the issue of gene marker instability, many approaches have proposed searching for more robust biological markers at the biological pathway level [22]. Consequently, the recent focus of research has been on cancer classification based on these robust markers, which fold gene-level data into compact and functional biological pathway-level data. This not only achieves more reliable classification performance but also provides better biological explanations for treatment strategy selection [23, 24]. Thus, we started to use deep learning techniques using AutoEncoder and GAN to deal with unbalanced data. The proposed methodology we present entails generating novel data by assimilating the underlying data distribution, thereby fostering enhanced equilibrium within the dataset. Furthermore, we leverage the pathifier algorithm to downscale gene expression data by incorporating pathway information, thereby facilitating notable enhancements in classifier efficacy. This approach offers a more precise and dependable instrument for cancer classification, with the potential to empower physicians in their diagnostic and therapeutic endeavors.
In this study, we propose an effective and deep learning method called AEGAN for addressing the issue of data imbalance in generating minority class samples in gene expression data. The proposed data balancing approach has been demonstrated to be useful for cancer classification and improving the performance of classifier models. Additionally, we incorporate prior knowledge from pathways and utilize the Pathifier algorithm to calculate the pathway scores of samples [25]. This combined approach, referred to as AEGAN-Pathifier, retains the biological functionality of the data while also possessing the ability to reduce data dimensionality. Experimental results show that when validated using classifiers, the performance of the classifiers improved significantly.
Methods
Datasets
The datasets are mainly from GEO and TCGA. GEO is a public repository for gene expression data. It is maintained by the National Center for Biotechnology Information (NCBI) and provides a platform for researchers to deposit, access, and analyze a wide range of high-throughput gene expression data [26]. TCGA is a landmark project that aimed to comprehensively characterize the genomic alterations in various types of cancer [27]. Moreover, TCGA collected and analyzed genomic, transcriptomic, and clinical data from thousands of cancer patients across multiple cancer types. Table 1 presents the sources of the dataset, number of genes, along with the quantities of the minority class () and majority class (), and the class imbalance ratio (). The formula for calculating the class imbalance ratio is given by the following equation.
| 1 |
Table 1.
The detailed information of Gene expression datasets
For dataset GSE25066, it includes 488 samples of breast cancer patients treated with NAC (antracyclines/taxanes) profiled with the U133A microarray. This dataset compared 99 pathologic complete response (pCR) samples and 389 residual disease (RD) samples. For dataset GSE20194, it is also a chemotherapy response data for breast cancer. This dataset compared 56 pathologic complete response (pCR) samples and 222 residual disease (RD) samples. For dataset Liver24, it is one RNA-Seq data set from TCGA. The Liver dataset consists of 421 samples obtained from comparing 371 liver cancer samples with 50 normal samples using the Agilent platform. The BRCA dataset comprises samples of breast cancer, derived from the TCGA platform. This dataset consists of 422 samples of the lumA subtype and 141 samples of the lumB subtype.
AEGAN
Due to the high dimensionality of gene expression data, which presents challenges in training GAN, we propose the AEGAN framework. In this framework, we leverage the power of AutoEncoder and GAN to address the limitations of traditional GAN in handling high-dimensional data.
AutoEncoder is a type of neural network architecture consisting of an encoder and a decoder [28]. The encoder, denoted as e, maps the input data to a lower-dimensional latent space representation. where X represents the input data and represents the encoded latent space representation. The decoder, denoted as d, reconstructs the original input data from the encoded representation. This architecture can be expressed as:
| 2 |
where L represents the loss function of the AutoEncoder, and the loss function used is MSELoss.
| 3 |
GAN is a type of generative machine learning model [29]. Due to the high cost of obtaining patient samples, we utilize this network to generate minority class sample data in order to achieve sample balance and improve classifier performance. GAN consist of a discriminator (D) and a generator (G). GAN model as shown in the following expressions.
| 4 |
| 5 |
The encoded gene expression data is subject to preprocessing using the function f(x), and subsequently utilized as the input for the discriminator. In addition, z represents the generated noise, which is used as the input for G(z). represents the Binary Cross Entropy loss function.
| 6 |
where y represents the real data, and represents the generated data. Furthermore, The discriminator uses ReLU and Tanh as activation functions. ReLU increases the nonlinearity of the network and prevents gradient vanishing, which is defined as follows:
| 7 |
Additionally, the generator also employs the Tanh activation function, given by:
| 8 |
These activation functions play a crucial role in enhancing the nonlinearity of neural networks and addressing the issue of gradient vanishing. This becomes particularly important when analyzing gene expression data, as it allows for capturing complex relationships and patterns within the data.
Analysis workflow
Data collection and preprocessing. In Fig. 1a, we initiate the process by gathering gene expression data and performing preprocessing. Probe information corresponding to gene names is obtained using platform information provided by Gene Expression Omnibu (GEO) and The Cancer Genome Atlas (TCGA). Both the GEO and TCGA datasets are utilized to validate our proposed algorithm for handling imbalanced data. The datasets from the GEO platform are acquired using the GEOquery library in the R language. Probes are then mapped to gene names based on the relevant platform information. As for the datasets from the TCGA platform, we collect them using the TCGAbiolinks library and retrieve gene names using the SummarizedExperiment library. The objective of obtaining gene names is to facilitate subsequent experiments in calculating pathway scores through the pathifier algorithm. Finally, we employ the Minmax approach for normalization, which allows us to unify the scales of features and enhance the efficiency of gradient descent as well as the stability of the model.
Fig. 1.
The proposed imbalanced data processing workflow (AEGAN-Pathifier). a gene expression data from GEO and TCGA. b AutoEncoder network architecture for encoding dimensional reduction of input data. c The encoded data is trained by a generative adversarial network to generate new sample data. d The generated data is first decoded and the Pathifier algorithm is used to calculate the pathway scores of the samples based on the KEGG pathway database and the gene expression data, and finally the scored dataset will be compared on different Classifiers for classification performance
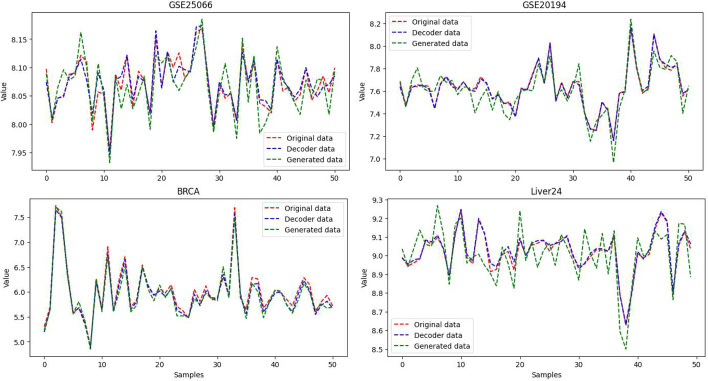
Data encoding. The problem of class imbalance not only affects the performance of classifiers but also increases the false negative rate in patient detection results. Therefore, we propose the AEGAN framework to address the issue of class imbalance in the sample data. In Fig. 1b, we present the AutoEncoder model that we developed. The encoder in the AutoEncoder is responsible for encoding high-dimensional gene expression data into low-dimensional latent variables, forcing the neural network to learn the most informative features. The decoder, on the other hand, aims to reconstruct the hidden variables back to the initial dimension. The ideal state is when the decoder’s output perfectly matches the input,resulting in an effectively self-encoded AutoEncoder. Figure 2 shows the similarity between the original data and the decoded data.
Fig. 2.
The similarity in Euclidean distance between the decoder data, generated data, and original data in AEGAN
Generate minority class samples. Due to the complexity of high-dimensional data as input to the GAN, it can adversely affect the performance of the model. Therefore, in the GAN, we leverage the characteristics of the AutoEncoder and use the gene-encoded data as input to enhance the performance of the network. In Fig. 1c, The generative adversarial network comprises a generator and a discriminator. The generator, a neural network model, aims to synthesize data that resembles real data by taking in a random noise vector as input and progressively generating output data through a series of transformation layers. Its objective is to deceive the discriminator as much as possible, rendering it unable to distinguish between the generated and real data. On the other hand, the discriminator, also a neural network model, aims to differentiate the generated data from the real data. It takes both the generated and real data as input and outputs a probability value that represents the likelihood of the input being real data. The discriminator’s goal is to accurately discern between the generated and real data. Ultimately, the well-trained generator is used to generate the needed samples of minority class data.
Calculate pathway scores. As shown in Fig. 1d, we introduce prior knowledge from the KEGG pathway database and the pathifier algorithm to calculate scores for samples in the pathway. This approach not only retains gene biological characteristics but also significantly reduces the sample dimension, further improving the classification performance of the classifier. Firstly, we use the generator to generate additional samples for the minority class to achieve sample balance. Then, we utilize the decoder to decode the gene expression data. By combining the KEGG pathway and the pathifier algorithm, we calculate the pathway scores for each sample. Finally, we compare the pathway scores of each sample using different data balancing methods and our proposed AEGAN algorithm across various machine learning classifiers to evaluate their performance.
KEGG pathway database and pathifier algorithm
In our research on cancer classification of samples, we introduce the KEGG pathway database (https://www.genome.jp/kegg/) and the Pathifier algorithm to calculate pathway scores for the samples. KEGG is a collection of databases and related software used to understand and simulate the higher-order functional behaviors of cells or organisms based on genomic information. KEGG computerizes data and knowledge on protein-protein interaction networks and chemical reactions that are involved in various cellular processes. Additionally, KEGG can be utilized as a reference knowledge for functional genomics and proteomics experiments [30].
Pathifier is an algorithm that infers a pathway score for each tumour sample based on gene expression data, which translates gene-level information into pathway-level information to generate compact and biologically relevant representations for each sample [31]. By combining this algorithm with the KEGG pathway database, we calculate the scores of samples on pathways. This approach not only retains the biologically relevant characteristics of genes but also achieves dimensional reduction. Furthermore, it enhances the performance of the classifier.
We provide a detailed description of the underlying principles of the Pathifier algorithm. Assuming a given list of pathway genes, denoted as K (), the gene expression data is constructed into a |K|-dimensional space, where each gene represents a dimension and each point represents a sample. All the sample points form a point cloud in the |K|-dimensional space, with the number of sample points being n. Subsequently, the Hastie and Stuetzle algorithm is employed to identify the principal curve within the point cloud, where represents points along the principal curve [32]. Assuming x is a point in the space, the corresponding is obtained using the following equations.
| 9 |
| 10 |
Once the principal curve is obtained, the point on the curve that is closest to the projected sample point x represents the position of the sample on the principal curve. The centroid formed by a subset of normal samples serves as the starting point of the principal curve. Thus, the pathway score for each sample is determined by the distance along the curve from its position on the curve to the starting point. After obtaining the pathway scores for each sample, we trained machine learning classification algorithms using this reduced-dimensional data and obtained classification metrics.
Results
Evaluation of AEGAN
We use Euclidean distance (d) to measure similarity in AutoEncoder’s decoder data (x) and original data (y), as well as generated data from Generative Adversarial Networks.
| 11 |
In the context of AutoEncoder, the Euclidean distance serves as a valuable metric for assessing the similarity between the decoder data and the original data. This distance measure allows us to quantify the resemblance between the reconstructed data produced by the decoder and the original input data.
Furthermore, when incorporating Generative Adversarial Networks, we can extend the use of Euclidean distance to evaluate the similarity between the decoded data and the original data. GAN consist of a generator network that generates synthetic data and a discriminator network that distinguishes between the generated data and the original data. By utilizing the Euclidean distance, we can measure the similarity between the generated data and the original data, providing insights into the GAN’s ability to produce data that closely resembles the original samples. From Fig. 2, it can be observed that the similarity between the original GSE25066 dataset and the datasets processed by AutoEncoder and GAN is d = 0.02 and 0.19, respectively. For the GSE20194 dataset, the similarity is d = 0.12 and 0.67. As for the BRCA dataset, the similarity is d = 0.52 and 0.88, while for the Liver24 dataset, the similarity is d = 0.11 and 0.65. Therefore, the data processed by our constructed network is highly similar to the original data. Therefore, the Euclidean distance is a valuable tool for quantifying the similarity between the decoder data and the original data in AutoEncoder models. Additionally, it can be extended to measure the similarity between the generated data from GAN networks and the original data. This approach allows for a comprehensive evaluation of both the AutoEncoder and GAN networks in terms of their ability to produce data that closely resembles the original samples.
Evaluation of AEGAN-Pathifier
The performance of different classifiers is significantly influenced by dimensional reduction, resampling, and other data preprocessing techniques. Additionally, imbalanced data can also lead to a decrease in classifier performance. Therefore, several classifiers are employed to evaluate the effectiveness and performance of our constructed AEGAN-Pathifier. These classifiers include the Random Forest Classifier (RF), Extra Trees Classifier (ET), Light Gradient Boosting Machine (LGBM) and Gradient Boosting Classifier (GBC). These classifiers are chosen based on their strong performance across various datasets [33]. Each classifier is evaluated using the same data preprocessing methods and the K-Fold Cross Validation technique with a fold number of 8. Furthermore, all evaluation experiments are conducted on a machine running the Ubuntu 20.04.6 LTS operating system with 64GB of memory, an Intel E5-2680v4 processor, and a 3090ti GPU.
The performance of data balancing methods is evaluated by comparing the performance of each classifier in three different scenarios. The first scenario involved training the classifiers using the original data without any balancing or feature reduction. The second scenario involves training the classifier using balanced data preprocessed by Smote, Edited Nearest Neighbours (ENN), and All K-Nearest Neighbors (AllKNN) algorithms. The third scenario involves training the classifiers using the balanced data preprocessed by AEGAN. Lastly, the fourth scenario involves training the classifiers using the gene pathway scores obtained from AEGAN-Pathifier. All classifiers are trained on the same training set and evaluated on the same test set in each scenario to ensure a fair evaluation of the classifiers. The performance of each classifier is measured based on all the metrics listed in Table 2.
Table 2.
Classification metrics
| Metric | Expression |
|---|---|
| Accuracy | |
| AUC | Area under ROC curve |
| Precision | |
| F1-Score | |
| Kappa | |
| Time (Sec) | Time taken for classification |
Results for GSE25066 dataset
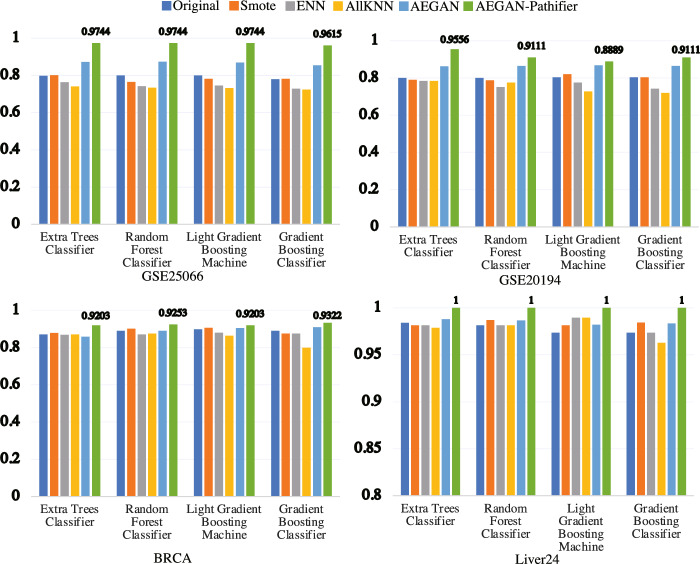
This section discusses the classification results after applying balancing methods to the GSE25066 dataset. Table 3 presents all the classifiers that show improved performance in terms of any metric on the GSE25066 dataset. The results indicate that ET, RF, LGBM and GBC achieve performance improvement when combined with AEGAN and AEGAN-Pathifier.
Table 3.
Results summary for the GSE25066 dataset
| Dataset: | GSE25066 | ||||||
|---|---|---|---|---|---|---|---|
| Classifier | Data balancing methods | Metrics | |||||
| Accuracy | AUC | Precision | F1-Score | Kappa | Time | ||
| ET | Original | 0.7974 | 0.7579 | 0.8014 | 0.8854 | 0.0370 | 0.4725 |
| Smote | 0.8020 | 0.7727 | 0.8231 | 0.8840 | 0.2036 | 1.4525 | |
| ENN | 0.7633 | 0.7694 | 0.8768 | 0.8419 | 0.3352 | 0.9200 | |
| AllKNN | 0.7406 | 0.7628 | 0.8902 | 0.8227 | 0.3231 | 0.8112 | |
| AEGAN | 0.8714 | 0.9319 | 0.7941 | 0.8834 | 0.7363 | 0.4162 | |
| AEGAN-Pathifier | 0.9744 | 1.0000 | 1.0000 | 0.9737 | 0.9487 | 0.0300 | |
| RF | Original | 0.7997 | 0.7330 | 0.8043 | 0.8862 | 0.0531 | 0.6362 |
| Smote | 0.7656 | 0.7637 | 0.8227 | 0.8581 | 0.1739 | 1.5538 | |
| ENN | 0.7428 | 0.7554 | 0.8740 | 0.8266 | 0.3039 | 0.8112 | |
| AllKNN | 0.7338 | 0.7486 | 0.8911 | 0.8164 | 0.3187 | 0.7062 | |
| AEGAN | 0.8743 | 0.9263 | 0.8013 | 0.8856 | 0.7428 | 0.5400 | |
| AEGAN-Pathifier | 0.9744 | 0.9980 | 1.0000 | 0.9737 | 0.9487 | 0.0700 | |
| LGBM | Original | 0.7997 | 0.7281 | 0.8105 | 0.8853 | 0.0997 | 0.3375 |
| Smote | 0.7816 | 0.7485 | 0.8240 | 0.8690 | 0.1695 | 16.3125 | |
| ENN | 0.7452 | 0.7709 | 0.8833 | 0.8277 | 0.3205 | 5.8900 | |
| AllKNN | 0.7315 | 0.7673 | 0.8874 | 0.8159 | 0.3135 | 6.4288 | |
| AEGAN | 0.8685 | 0.9255 | 0.8115 | 0.8783 | 0.7309 | 0.3113 | |
| AEGAN-Pathifier | 0.9744 | 0.9934 | 1.0000 | 0.9737 | 0.9487 | 0.0500 | |
| GBC | Original | 0.7792 | 0.7147 | 0.8109 | 0.8710 | 0.0760 | 0.3300 |
| Smote | 0.7815 | 0.7380 | 0.8329 | 0.8665 | 0.2367 | 30.2550 | |
| ENN | 0.7291 | 0.7694 | 0.8761 | 0.8175 | 0.2812 | 24.6562 | |
| AllKNN | 0.7246 | 0.7619 | 0.8901 | 0.8100 | 0.3060 | 13.9162 | |
| AEGAN | 0.8542 | 0.9302 | 0.7968 | 0.8646 | 0.7008 | 0.6075 | |
| AEGAN-Pathifier | 0.9615 | 0.9961 | 0.9500 | 0.9620 | 0.9231 | 0.0400 | |
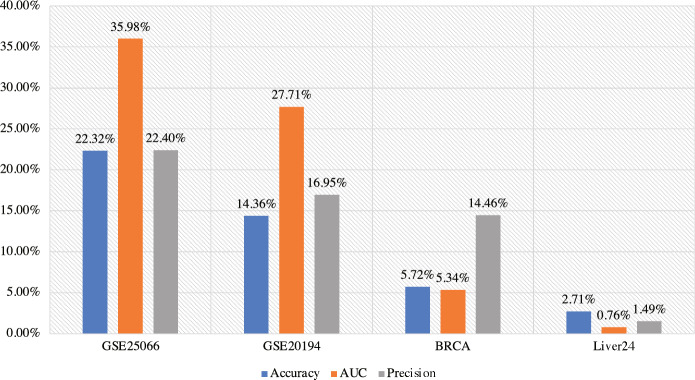
When the ET is combined with AEGAN, it shows significant improvements in performance compared to using the original data. Currently, it is noticeably increasing by 9.28% in Accuracy, 22.96% in AUC score, and exhibiting substantial improvement in Kappa and Time metrics. Additionally, when combined with AEGAN-Pathifier, it is outperforming the original data in terms of Accuracy, AUC, and Precision scores, with increases of 22.2%, 31.94%, and 24.78% respectively. Moreover, it demonstrates significant improvements in F1-Score, Kappa, and Time metrics.
When the RF is combined with AEGAN, it shows significant improvements in performance compared to using the original data. Specifically, there is a noticeable increase of 9.33% in Accuracy, 27.22% in AUC score, and substantial improvements in Kappa and Time metrics. Furthermore, when the RF is combined with AEGAN-Pathifier, it exhibits even greater improvements compared to the original data. There is an increase of 21.85% in Accuracy, 36.15% in AUC score, and 24.33% in Precision. Additionally, there were significant improvements in F1-Score, Kappa, and Time metrics.
When combining the LGBM with AEGAN, it is currently showing significant improvements in performance compared to using only the original data. Specifically, there is a noticeable increase of 8.6% in Accuracy and 27.11% in AUC score, along with substantial improvement in Kappa metric. Additionally, when combined with AEGAN-Pathifier, it outperforms the original data in terms of Accuracy, AUC, and Precision scores, with increases of 21.85%, 36.44%, and 23.38% respectively. Moreover, it demonstrates significant improvements in F1-Score, Kappa, and Time metrics.
When the GBC is combined with AEGAN, it shows significant improvements in performance compared to using the original data. Currently, it is noticeably increasing by 9.63% in Accuracy, 30.15% in AUC score, and exhibiting substantial improvement in Kappa metric. Additionally, when combined with AEGAN-Pathifier, it is outperforming the original data in terms of Accuracy, AUC, and Precision scores, with increases of 23.4%, 39.37%, and 17.15% respectively. Moreover, it demonstrates significant improvements in F1-Score, Kappa, and Time metrics.
Finally, we applied the Smote, ENN, and AllKNN techniques for data balancing on the original GSE25066 dataset and compared the results using four classifiers - ET, RF, LGBM, and GBC. However, we observed that employing these data balancing methods yielded significantly lower classification metrics compared to our proposed AEGAN and AEGAN-Pathifier methods.
Results for GSE20194 dataset
This section discusses the classification results of the GSE20194 dataset after applying balancing methods. Table 4 presents all the classifiers that have shown improved performance in various metrics on the GSE20194 dataset. The results indicate that ET, RF, LGBM and GBC have achieved performance enhancements when combined with AEGAN and AEGAN-Pathifier.
Table 4.
Results summary for the GSE20194 dataset
| Dataset: | GSE20194 | ||||||
|---|---|---|---|---|---|---|---|
| Classifier | Data balancing methods | Metrics | |||||
| Accuracy | AUC | Precision | F1-Score | Kappa | Time | ||
| ET | Original | 0.7995 | 0.7822 | 0.8043 | 0.8861 | 0.0283 | 0.7088 |
| Smote | 0.7911 | 0.7894 | 0.8139 | 0.8784 | 0.1567 | 1.7038 | |
| ENN | 0.7835 | 0.7812 | 0.8579 | 0.8630 | 0.3095 | 0.7262 | |
| AllKNN | 0.7835 | 0.7985 | 0.8890 | 0.8589 | 0.3784 | 0.8588 | |
| AEGAN | 0.8621 | 0.9449 | 0.7946 | 0.8749 | 0.7209 | 0.6875 | |
| AEGAN-Pathifier | 0.9556 | 0.9575 | 0.9545 | 0.9545 | 0.9111 | 0.5800 | |
| RF | Original | 0.7996 | 0.7918 | 0.8039 | 0.8857 | 0.0329 | 0.6362 |
| Smote | 0.7873 | 0.8181 | 0.8303 | 0.8727 | 0.2165 | 1.9038 | |
| ENN | 0.7516 | 0.7763 | 0.8307 | 0.8449 | 0.1883 | 0.7025 | |
| AllKNN | 0.7752 | 0.7919 | 0.8831 | 0.8535 | 0.3566 | 1.0163 | |
| AEGAN | 0.8646 | 0.9336 | 0.7959 | 0.8764 | 0.7267 | 0.7738 | |
| AEGAN-Pathifier | 0.9111 | 0.9654 | 0.9500 | 0.9048 | 0.8218 | 0.6600 | |
| LGBM | Original | 0.8034 | 0.7218 | 0.8163 | 0.8865 | 0.1531 | 5.2175 |
| Smote | 0.8193 | 0.7520 | 0.8521 | 0.8919 | 0.3311 | 13.5200 | |
| ENN | 0.7757 | 0.7954 | 0.8826 | 0.8538 | 0.3469 | 1.0238 | |
| AllKNN | 0.7272 | 0.7930 | 0.8742 | 0.8165 | 0.2678 | 4.1112 | |
| AEGAN | 0.8672 | 0.9425 | 0.8172 | 0.8758 | 0.7310 | 10.7238 | |
| AEGAN-Pathifier | 0.8889 | 0.9664 | 0.9474 | 0.8780 | 0.7770 | 0.4200 | |
| GBC | Original | 0.8037 | 0.7392 | 0.8267 | 0.8844 | 0.2160 | 15.4850 |
| Smote | 0.8033 | 0.7591 | 0.8323 | 0.8830 | 0.2350 | 2.0250 | |
| ENN | 0.7431 | 0.7284 | 0.8494 | 0.8328 | 0.2639 | 0.8925 | |
| AllKNN | 0.7194 | 0.7293 | 0.8687 | 0.8128 | 0.2579 | 11.6250 | |
| AEGAN | 0.8647 | 0.9336 | 0.8137 | 0.8743 | 0.7256 | 26.6250 | |
| AEGAN-Pathifier | 0.9111 | 0.9802 | 0.9500 | 0.9048 | 0.8218 | 2.7500 | |
When combined with AEGAN, the performance of the ET in terms of classification metrics, such as Accuracy and AUC, is significantly improved by 7.83% and 20.8%, respectively, compared to using only the original data. Additionally, there are substantial improvements in Kappa and Time metrics. Furthermore, when combined with AEGAN-Pathifier, it outperforms the original data with a remarkable increase of 19.52%, 22.41%, and 18.67% in Accuracy, AUC, and Precision scores, respectively. Moreover, there are significant improvements in F1-Score, Kappa and Time metrics.
When AEGAN is combined with the RF, there is a noticeable improvement in the classification metrics of Accuracy and AUC, with an increase of 8.13% and 17.91% respectively, compared to using only the original data. Additionally, significant enhancements are observed in the Kappa and Time metrics. Furthermore, when AEGAN-Pathifier is employed in conjunction with the classifier, there is a remarkable boost in performance. Specifically, there is a substantial increase of 13.94%, 21.92%, and 18.17% in Accuracy, AUC, and Precision scores respectively, compared to the original data. Moreover, significant improvements are observed in the F1-Score, Kappa and Time metrics.
When combined with AEGAN, the performance of the LGBM in terms of classification metrics, such as Accuracy and AUC, is significantly improved by 7.94% and 30.58%, respectively, compared to using only the original data. Additionally, there are substantial improvements in Kappa and Time metrics. Furthermore, when combined with AEGAN-Pathifier, it outperforms the original data with a remarkable increase of 10.64%, 33.89%, and 16.06% in Accuracy, AUC, and Precision scores, respectively. Moreover, there are significant improvements in F1-Score, Kappa, and Time metrics.
When combined with AEGAN, GBC demonstrates significant improvements in classification metrics such as Accuracy and AUC, with performance increases of 7.59% and 26.3%, respectively, compared to using the original data. Additionally, there are substantial enhancements in metrics like Kappa and Time. Furthermore, when combined with AEGAN-Pathifier, it shows even greater improvements. Specifically, there is a notable increase of 13.36%, 32.60%, and 14.91% in Accuracy, AUC, and F1-Score scores, respectively, compared to the original data. Moreover, there are significant advancements in metrics such as Kappa and Time.
In conclusion, the Smote, ENN, and AllKNN data balancing techniques are applied to the original GSE25066 dataset, and a comparison is made with the ET, RF, LGBM, and GBC classifiers. It is observed that these data balancing methods yield significantly lower classification metrics compared to our proposed AEGAN and AEGAN-Pathifier methods.
Results for the BRCA dataset
This section delves into the classification outcomes of the BRCA dataset after the implementation of balancing methods. Table 5 showcases all classifiers that exhibit enhanced performance across various metrics on the BRCA dataset. The findings demonstrate that the ET, RF, LGBM, and GBC all show improved performance when combined with AEGAN and AEGAN-Pathifier.
Table 5.
Results summary for the BRCA dataset
| Dataset: | BRCA | ||||||
|---|---|---|---|---|---|---|---|
| Classifier | Data balancing methods | Metrics | |||||
| Accuracy | AUC | Precision | F1-Score | Kappa | Time | ||
| ET | Original | 0.8704 | 0.9372 | 0.8487 | 0.6711 | 0.5957 | 0.4638 |
| Smote | 0.8781 | 0.9412 | 0.8064 | 0.7191 | 0.6412 | 1.9562 | |
| ENN | 0.8681 | 0.9335 | 0.6905 | 0.7415 | 0.6523 | 0.7500 | |
| AllKNN | 0.8706 | 0.9369 | 0.6821 | 0.7585 | 0.6707 | 0.5675 | |
| AEGAN | 0.8583 | 0.9643 | 0.9596 | 0.8407 | 0.7165 | 0.6075 | |
| AEGAN-Pathifier | 0.9203 | 0.9779 | 0.9714 | 0.9145 | 0.8388 | 0.0800 | |
| RF | Original | 0.8908 | 0.9330 | 0.8970 | 0.7277 | 0.6610 | 0.4475 |
| Smote | 0.9010 | 0.9370 | 0.8028 | 0.7714 | 0.7065 | 2.5938 | |
| ENN | 0.8706 | 0.9399 | 0.6995 | 0.7507 | 0.6631 | 0.7138 | |
| AllKNN | 0.8757 | 0.9390 | 0.7027 | 0.7633 | 0.6790 | 0.7488 | |
| AEGAN | 0.8898 | 0.9655 | 0.9714 | 0.8793 | 0.7795 | 0.5888 | |
| AEGAN-Pathifier | 0.9253 | 0.9828 | 0.9739 | 0.9215 | 0.8496 | 0.0700 | |
| LGBM | Original | 0.8985 | 0.9454 | 0.8407 | 0.7531 | 0.6889 | 0.4200 |
| Smote | 0.9060 | 0.9500 | 0.8254 | 0.7762 | 0.7159 | 22.5763 | |
| ENN | 0.8807 | 0.9419 | 0.6874 | 0.7586 | 0.6795 | 1.2237 | |
| AllKNN | 0.8631 | 0.9411 | 0.6523 | 0.7386 | 0.6463 | 0.7500 | |
| AEGAN | 0.9055 | 0.9681 | 0.9402 | 0.9016 | 0.8110 | 1.0688 | |
| AEGAN-Pathifier | 0.9203 | 0.9829 | 0.9483 | 0.9172 | 0.8390 | 0.0700 | |
| GBC | Original | 0.8908 | 0.9347 | 0.8255 | 0.7275 | 0.6587 | 0.6238 |
| Smote | 0.8833 | 0.9357 | 0.7735 | 0.7192 | 0.6448 | 34.5700 | |
| ENN | 0.8755 | 0.9344 | 0.6974 | 0.7506 | 0.6676 | 0.6775 | |
| AllKNN | 0.7995 | 0.8837 | 0.5672 | 0.6586 | 0.5242 | 0.7050 | |
| AEGAN | 0.9094 | 0.9717 | 0.9506 | 0.9046 | 0.8189 | 0.5725 | |
| AEGAN-Pathifier | 0.9322 | 0.9789 | 0.9511 | 0.9308 | 0.8630 | 0.0400 | |
When combined with AEGAN-Pathifier, ET demonstrates a noteworthy improvement of 5.72% and 4.34% in terms of Accuracy and AUC, respectively, compared to using the original data alone. Moreover, the F1-Score, Kappa, and Time metrics also exhibit substantial improvements.
When combined with AEGAN-Pathifier, the utilization of RF showcases a considerable enhancement of 3.86% and 5.34% in terms of classification performance, specifically Accuracy and AUC, compared to solely utilizing the original data. Additionally, significant enhancements are also observed in the F1-Score, Kappa, and Time metrics.
When employed in conjunction with AEGAN-Pathifier, the utilization of LGBM demonstrates a noteworthy enhancement of 2.42% and 3.96% in terms of classification metrics, specifically Accuracy and AUC, compared to solely utilizing the original data. Furthermore, notable improvements are observed in the F1-Score, Kappa, and Time metrics.
When employed in conjunction with AEGAN-Pathifier, the utilization of GBC showcases a notable improvement of 4.65% and 4.73% in terms of classification metrics, specifically Accuracy and AUC, compared to solely utilizing the original data. Furthermore, notable enhancements are observed in the F1-Score, Kappa, and Time metrics.
In conclusion, we apply SMOTE, ENN, and AllKNN data balancing methods on the BRCA original dataset and compare the results with the ET, RF, LGBM, and GBC classifiers. We observe that when utilizing these data balancing methods, the classification metrics exhibit slightly lower performance compared to our proposed AEGAN method and significantly lower performance compared to the AEGAN-Pathifier method.
Results for the Liver24 dataset
This section discusses the classification results of the Liver24 dataset after applying balancing techniques. Table 6 presents all the classifiers that have shown improved performance in terms of any metric on the Liver24 dataset. The results indicate that the GBC, Ada Boost Classifier, and Logistic Regression Classifier have achieved performance improvements when combined with AEGAN and AEGAN-Pathifier.
Table 6.
Results summary for the Liver24 dataset
| Dataset: | Liver24 | ||||||
|---|---|---|---|---|---|---|---|
| Classifier | Data balancing methods | Metrics | |||||
| Accuracy | AUC | Precision | F1-Score | Kappa | Time | ||
| ET | Original | 0.9841 | 0.9981 | 0.9911 | 0.9910 | 0.9189 | 0.4938 |
| Smote | 0.9815 | 0.9963 | 0.9908 | 0.9894 | 0.9120 | 1.3487 | |
| ENN | 0.9815 | 0.9980 | 0.9969 | 0.9894 | 0.9127 | 0.7300 | |
| AllKNN | 0.9788 | 0.9978 | 0.9939 | 0.9879 | 0.8976 | 0.5825 | |
| AEGAN | 0.9880 | 0.9998 | 0.9878 | 0.9878 | 0.9757 | 0.4888 | |
| AEGAN-Pathifier | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.0600 | |
| RF | Original | 0.9814 | 0.9985 | 0.9850 | 0.9895 | 0.9048 | 0.6762 |
| Smote | 0.9868 | 0.9992 | 0.9940 | 0.9925 | 0.9342 | 1.8700 | |
| ENN | 0.9814 | 0.9980 | 0.9908 | 0.9894 | 0.9128 | 0.6050 | |
| AllKNN | 0.9815 | 0.9968 | 0.9969 | 0.9894 | 0.9127 | 0.7138 | |
| AEGAN | 0.9865 | 0.9997 | 0.9853 | 0.9865 | 0.9726 | 0.5362 | |
| AEGAN-Pathifier | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.0600 | |
| LGBM | Original | 0.9735 | 0.9971 | 0.9822 | 0.9850 | 0.8586 | 5.9462 |
| Smote | 0.9815 | 0.9948 | 0.9910 | 0.9895 | 0.9104 | 30.1375 | |
| ENN | 0.9895 | 0.9967 | 1.0000 | 0.9940 | 0.9483 | 5.9812 | |
| AllKNN | 0.9895 | 0.9969 | 1.0000 | 0.9940 | 0.9483 | 5.5612 | |
| AEGAN | 0.9820 | 0.9992 | 0.9818 | 0.9823 | 0.9637 | 14.3412 | |
| AEGAN-Pathifier | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.0500 | |
| GBC | Original | 0.9736 | 0.9941 | 0.9853 | 0.9851 | 0.8640 | 9.9825 |
| Smote | 0.9842 | 0.9795 | 0.9941 | 0.9911 | 0.9167 | 18.2200 | |
| ENN | 0.9736 | 0.9806 | 0.9940 | 0.9849 | 0.8733 | 9.1812 | |
| AllKNN | 0.9629 | 0.9791 | 0.9879 | 0.9789 | 0.8214 | 8.9188 | |
| AEGAN | 0.9835 | 0.9979 | 0.9848 | 0.9834 | 0.9666 | 21.5088 | |
| AEGAN-Pathifier | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.0400 | |
From Table 6, it can be observed that the classifiers achieve good results on the original dataset, but there is still room for improvement. After incorporating our proposed AEGAN-Pathifier method for handling imbalanced data, all metrics reached 100%. Additionally, the time required for classification by the classifiers is significantly reduced. Therefore, our proposed method effectively enhances the performance of the classifiers and provides valuable assistance in accurately classifying cancer.
In conclusion, we apply the Smote, ENN, and AllKNN data balancing techniques to the original Liver24 dataset and compare them with the ET, RF, LGBM, and GBC classifiers. It is observed that these data balancing methods yield significantly lower classification metrics compared to our proposed AEGAN and AEGAN-Pathifier methods.
Results for pathway scores
This section discusses the pathway scores of the GSE25066, GSE20194, BRCA and Liver24 datasets and investigates whether these pathways are associated with cancer. According to Table 7, we select the top five pathways with the highest pathway scores. We conduct a literature search and find evidence linking these pathways to the cancer. Therefore, our proposed AEGAN-Pathifier method can provide better assistance for targeted therapies.
Table 7.
Top 5 pathways identified from AEGAN-Pathifier
| Datasets | Rank | Pathway ID | Pathway Name | Score | Proof |
|---|---|---|---|---|---|
| GSE25066 | 1 | hsa05211 | Renal cell carcinoma | 0.7869 | [34, 35] |
| 2 | hsa05132 | Salmonella infection | 0.7199 | [36] | |
| 3 | hsa03010 | Ribosome | 0.7100 | [37, 38] | |
| 4 | hsa00561 | Glycerolipid metabolism | 0.7026 | [39, 40] | |
| 5 | hsa04723 | Retrograde endocannabinoid signaling | 0.7003 | [41] | |
| GSE20194 | 1 | hsa00750 | Vitamin B6 metabolism | 0.7534 | [42] |
| 2 | hsa05332 | Graft-versus-host disease | 0.7206 | [43] | |
| 3 | hsa04211 | Longevity regulating pathway | 0.6828 | [44] | |
| 4 | hsa00591 | Linoleic acid metabolism | 0.6820 | [45] | |
| 5 | hsa05330 | Allograft rejection | 0.6819 | [46] | |
| BRCA | 1 | hsa00232 | Caffeine metabolism | 0.9653 | [47] |
| 2 | hsa03015 | mRNA surveillance pathway | 0.9198 | [48] | |
| 3 | hsa03040 | Spliceosome | 0.9197 | [49] | |
| 4 | hsa05212 | Pancreatic cancer | 0.9194 | [50] | |
| 5 | hsa05220 | Chronic myeloid leukemia | 0.9191 | [51] | |
| Liver24 | 1 | hsa04950 | Maturity onset diabetes of the young | 0.8350 | [52] |
| 2 | hsa00982 | Drug metabolism | 0.8150 | [53] | |
| 3 | hsa00360 | Phenylalanine metabolism | 0.7864 | [54] | |
| 4 | hsa00350 | Tyrosine metabolism | 0.7672 | [55] | |
| 5 | hsa00830 | Retinol metabolism | 0.7657 | [56] |
Discussion and conclusion
Accurate cancer classification underpins effective diagnosis and treatment planning. However, the limited availability of patient samples and class imbalance often affect classifier performance. To address these challenges, we developed AEGAN, a deep learning framework that combines AutoEncoder and GAN to generate synthetic samples for the minority class. By incorporating the KEGG pathway database and Pathifier algorithm, we calculated pathway scores for each sample. Our analysis reveals correlation between pathway genes and sample genes, suggesting the preservation of biological relationships while achieving dimension reduction. Overall, from Fig. 3 and 4, our experimental results demonstrate that the proposed method exhibits outstanding classification performance after handling imbalanced data samples. Additionally, our approach could potentially serve as a supportive tool for clinicians in cancer diagnosis and may contribute to personalized medicine by providing more accurate cancer classification.
Fig. 3.
Compare the accuracy metric among the Original data, Smote, ENN, AllKNN, AEGAN, and AEGAN-Pathifier methods in the scenarios of GSE25066, GSE20194, BRCA, and Liver24 datasets
Fig. 4.
The improvement of classifier metrics using AEGAN-Pathifier on each dataset
Improving cancer classification accuracy holds significant clinical value as it can assist physicians in better understanding individual patient conditions. Through continuous refinement of classification methods, we hope this research can provide valuable insights toward achieving precision medicine. In clinical practice, accurate classification information can help develop more targeted treatment strategies, which may have potential value in improving patient outcomes and quality of life. While our experimental results are promising, several limitations should be noted. Our validation is currently restricted to a limited number of cancer types with relatively small sample sizes. The computational complexity of our approach may also pose challenges in clinical settings. Future work should focus on extending the validation to more cancer types, incorporating additional biological prior knowledge to enhance interpretability, exploring model simplification strategies to reduce computational costs, and integrating multi-omics data for more comprehensive feature representation.
Supplementary Information
Acknowledgements
We would like to express our gratitude to the anonymous reviewers for their valuable and constructive comments on the original manuscript.
Abbreviations
- GAN
Generative adversarial network
- MUMA
Multi-omics meta-learning algorithm
- CFS
Correlation-based feature selectio
- RFE
Recursive feature elimination
- mRMR
Maximum relevance minimum redundancy
- GEO
Gene expression omnibu
- TCGA
The cancer genome atla
- NCBI
National Center for Biotechnology Information
- RF
Random forest
- ET
Extra trees
- LGBM
Light gradient boosting machine
- GBC
Gradient boosting classifier
- ENN
Edited nearest neighbours
- AllKNN
All K-nearest neighbors
Author Contributions
The idea and study design were conceived by QSZ. The experimental work was conducted by YLW. YLW drafted the manuscript, which was subsequently revised by QSZ with support from JH, HPL and ZMZ. All authors participated in discussions regarding the results and made contributions to the final manuscript. All authors have read and approved the published version of the manuscript.
Funding
This work was funded by the Postgraduate Research of Lianyungang (Grant No. LYG20210010), the Lianyungang Science and Technology Projects (Grant No. CG2223) and the National Natural Science Foundation of China (Grant No. 72174079).
Availability of data and materials
The code and datasets related to the paper can be found at https://github.com/dragon-wyl/AEGAN-Pathifier.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Jackson AL, Loeb LA. The contribution of endogenous sources of DNA damage to the multiple mutations in cancer. Mutat Res Fundam Mol Mech Mutagen. 2001;477(1–2):7–21. [DOI] [PubMed] [Google Scholar]
- 2.Friedberg EC, Wagner R, Radman M. Specialized DNA polymerases, cellular survival, and the genesis of mutations. Science. 2002;296(5573):1627–30. [DOI] [PubMed] [Google Scholar]
- 3.Stein KD, Syrjala KL, Andrykowski MA. Physical and psychological long-term and late effects of cancer. Cancer. 2008;112(S11):2577–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cianfrocca M, Goldstein LJ. Prognostic and predictive factors in early-stage breast cancer. Oncologist. 2004;9(6):606–16. [DOI] [PubMed] [Google Scholar]
- 5.Montazeri A. Health-related quality of life in breast cancer patients: a bibliographic review of the literature from 1974 to 2007. J Exp Clin Cancer Res. 2008;27(1):1–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Forbes LJ, Warburton F, Richards M, Ramirez A. Risk factors for delay in symptomatic presentation: a survey of cancer patients. Br J Cancer. 2014;111(3):581–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sun Y, Zhao Z, Yang Z, Xu F, Lu H, Zhu Z, Shi W, Jiang J, Yao P, Zhu HP. Risk factors and preventions of breast cancer. Int J Biol Sci. 2017;13(11):1387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Devarriya D, Gulati C, Mansharamani V, Sakalle A, Bhardwaj A. Unbalanced breast cancer data classification using novel fitness functions in genetic programming. Exp Syst Appl. 2020;140:112866. [Google Scholar]
- 9.Bohmer R. The hard work of health care transformation. N Engl J Med. 2016;375(8):709–11. [DOI] [PubMed] [Google Scholar]
- 10.Marshall DA, Hux M. Design and analysis issues for economic analysis alongside clinical trials. Med Care. 2009;47:14–20. [DOI] [PubMed] [Google Scholar]
- 11.Flight L, Arshad F, Barnsley R, Patel K, Julious S, Brennan A, Todd S. A review of clinical trials with an adaptive design and health economic analysis. Value Health. 2019;22(4):391–8. [DOI] [PubMed] [Google Scholar]
- 12.Huang HH, Rao H, Miao R, Liang Y. A novel meta-analysis based on data augmentation and elastic data shared lasso regularization for gene expression. BMC Bioinform. 2022;23(Suppl 10):353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Patil AR, Chang J, Leung M-Y, Kim S. Analyzing high dimensional correlated data using feature ranking and classifiers. Comput Math Biophys. 2019;7(1):98–120. 10.1515/cmb-2019-0008. [Google Scholar]
- 14.Remeseiro B, Bolon-Canedo V. A review of feature selection methods in medical applications. Comput Biol Med. 2019;112:103375. [DOI] [PubMed] [Google Scholar]
- 15.Huang H-H, Shu J, Liang Y. Muma: A multi-omics meta-learning algorithm for data interpretation and classification. IEEE J Biomed Health Inform. 2024;28(4):2428. [DOI] [PubMed] [Google Scholar]
- 16.Patil AR, Kim S. Combination of ensembles of regularized regression models with resampling-based lasso feature selection in high dimensional data. Mathematics. 2020. 10.3390/math8010110. [Google Scholar]
- 17.Abdulrauf Sharifai G, Zainol Z. Feature selection for high-dimensional and imbalanced biomedical data based on robust correlation based redundancy and binary grasshopper optimization algorithm. Genes. 2020;11(7):717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Patil AR, Park B-K, Kim S. Adaptive lasso with weights based on normalized filtering scores in molecular big data. J Theor Comput Chem. 2020;19(04):2040010. 10.1142/S0219633620400106. [Google Scholar]
- 19.Chandrashekar G, Sahin F. A survey on feature selection methods. Comput Electr Eng. 2014;40(1):16–28. [Google Scholar]
- 20.Jović A, Brkić K, Bogunović N. A review of feature selection methods with applications. In: 2015 38th international convention on information and communication technology, electronics and microelectronics (MIPRO),IEEE 2015. pp. 1200–1205
- 21.Galbraith SM, Lodge MA, Taylor NJ, Rustin GJ, Bentzen S, Stirling JJ, Padhani AR. Reproducibility of dynamic contrast-enhanced MRI in human muscle and tumours: comparison of quantitative and semi-quantitative analysis. NMR Biomed Int J Devot Dev Appl Magn Reson In Vivo. 2002;15(2):132–42. [DOI] [PubMed] [Google Scholar]
- 22.Ramanan VK, Shen L, Moore JH, Saykin AJ. Pathway analysis of genomic data: concepts, methods, and prospects for future development. TRENDS Genetics. 2012;28(7):323–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gao F, Wang W, Tan M, Zhu L, Zhang Y, Fessler E, Vermeulen L, Wang X. Deepcc: a novel deep learning-based framework for cancer molecular subtype classification. Oncogenesis. 2019;8(9):44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.De Palma FDE, D’argenio V, Pol J, Kroemer G, Maiuri MC, Salvatore F. The molecular hallmarks of the serrated pathway in colorectal cancer. Cancers. 2019;11(7):1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang JD, Wiemann S. Kegggraph: a graph approach to KEGG pathway in R and bioconductor. Bioinformatics. 2009;25(11):1470–1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Barrett T, Wilhite SE, Ledoux P, Evangelista C, Kim IF, Tomashevsky M, Marshall KA, Phillippy KH, Sherman PM, Holko M, et al. Ncbi geo: archive for functional genomics data sets-update. Nucleic Acids Res. 2012;41(D1):991–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tomczak K, Czerwińska P, Wiznerowicz M. Review the cancer genome atlas (TCGA): an immeasurable source of knowledge. Contemp Oncol /Współczesna Onkol. 2015;2015(1):68–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ng A. et al. Sparse autoencoder. CS294A Lecture notes. 2011. vol. 72(2011), pp. 1–19.
- 29.Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y. Generative adversarial networks. Commun ACM. 2020;63(11):139–44. [Google Scholar]
- 30.Kanehisa, M. The kegg database. In: ‘In silico’simulation of biological processes: Novartis Foundation Symposium 2002. Wiley Online Library, vol. 247, pp. 91–103. [PubMed]
- 31.Drier Y, Sheffer M, Domany E. Pathway-based personalized analysis of cancer. Proc Natl Acad Sci. 2013;110(16):6388–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hastie T, Stuetzle W. Principal curves. J Am Statis Assoc. 1989;84(406):502–16. [Google Scholar]
- 33.Maxwell AE, Warner TA, Fang F. Implementation of machine-learning classification in remote sensing: An applied review. Int J Remote Sens. 2018;39(9):2784–817. [Google Scholar]
- 34.Mascena Costa L, Debnath D, Harmon AC, Sousa Araujo S, Silva Souza H, Athayde Filho P, Wischral A, Gomes Filho A, Mathis JM, et al. Mechanistic studies of cytotoxic activity of the mesoionic compound mih 2.4 bl in mcf-7 breast cancer cells. Oncol Lett. 2020;20:2291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Huo Z, Gao Y, Yu Z, Zuo W, Zhang Y. Metastasis of breast cancer to renal cancer: report of a rare case. Int J Clin Exp Pathol. 2015;8(11):15417. [PMC free article] [PubMed] [Google Scholar]
- 36.Patel KD, Vora HH, Patel PS. Transcriptional biomarkers in oral cancer: an integrative analysis and the cancer genome atlas validation. Asian Pac J Cancer Prev APJCP. 2021;22(2):371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bohlen J, McLaughlin SL, Hazard-Jenkins H, Infante AM, Montgomery C, Davis M, Pistilli EE. Dysregulation of metabolic-associated pathways in muscle of breast cancer patients: preclinical evaluation of interleukin-15 targeting fatigue. J Cachexia Sarcopenia Muscle. 2018;9(4):701–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gallegos KM, Patel JR, Llopis SD, Walker RR, Davidson AM, Zhang W, Zhang K, Tilghman SL. Quantitative proteomic profiling identifies a potential novel chaperone marker in resistant breast cancer. Front Oncol. 2021;11:540134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Song L, Liu Z, Hu H, Yang Y, Li TY, Lin Z, Ye J, Chen J, Huang X, Liu DT, Zhou J, Shi Y, Zhao H, Xie C, Chen L, Song E, Lin S, Lin S. Proto-oncogene SRC links lipogenesis via lipin-1 to breast cancer malignancy. Nat Commun. 2020;11(1):5842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cala MP, Aldana J, Medina J, Sánchez J, Guio J, Wist J, Meesters RJ. Multiplatform plasma metabolic and lipid fingerprinting of breast cancer: a pilot control-case study in Colombian Hispanic women. PloS One. 2018;13(2):0190958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kisková T, Mungenast F, Suváková M, Jäger W, Thalhammer T. Future aspects for cannabinoids in breast cancer therapy. Int J Mol Sci. 2019;20(7):1673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wu X, Lu L. Vitamin b6 deficiency, genome instability and cancer. Asian Pac J Cancer Prev. 2012;13(11):5333–8. [DOI] [PubMed] [Google Scholar]
- 43.Holmberg L, Kikuchi K, Gooley TA, Adams KM, Hockenbery DM, Flowers ME, Schoch HG, Bensinger W, McDonald GB. Gastrointestinal graft-versus-host disease in recipients of autologous hematopoietic stem cells: incidence, risk factors, and outcome. Biol Blood Marrow Transpl. 2006;12(2):226–34. [DOI] [PubMed] [Google Scholar]
- 44.Zheng Y, Liu P, Wang N, Wang S, Yang B, Li M, Chen J, Situ H, Xie M, Lin Y, Wang Z. Betulinic acid suppresses breast cancer metastasis by targeting GRP78-mediated glycolysis and ER stress apoptotic pathway. Oxid Med Cell Longev. 2019;2019:8781690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Camarda R, Zhou AY, Kohnz RA, Balakrishnan S, Mahieu C, Anderton B, Eyob H, Kajimura S, Tward A, Krings G, et al. Inhibition of fatty acid oxidation as a therapy for MYC-overexpressing triple-negative breast cancer. Nat Med. 2016;22(4):427–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Steelman LS, Martelli AM, Cocco L, Libra M, Nicoletti F, Abrams SL, McCubrey JA. The therapeutic potential of MTOR inhibitors in breast cancer. Br J Clin Pharmacol. 2016;82(5):1189–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Cui W-Q, Wang S-T, Pan D, Chang B, Sang L-X. Caffeine and its main targets of colorectal cancer. World J Gastrointest Oncol. 2020;12(2):149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Popp MW, Maquat LE. Nonsense-mediated mRNA decay and cancer. Curr Opin Genet Dev. 2018;48:44–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bowling EA, Wang JH, Gong F, Wu W, Neill NJ, Kim IS, Tyagi S, Orellana M, Kurley SJ, Dominguez-Vidaña R, et al. Spliceosome-targeted therapies trigger an antiviral immune response in triple-negative breast cancer. Cell. 2021;184(2):384–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kleeff J, Korc M, Apte M, La Vecchia C, Johnson CD, Biankin AV, Neale RE, Tempero M, Tuveson DA, Hruban RH, et al. Pancreatic cancer. Nat rev Dis Prim. 2016;2(1):1–22. [DOI] [PubMed] [Google Scholar]
- 51.Ureshino H, Shindo T, Kimura S. Role of cancer immunology in chronic myelogenous leukemia. Leuk Res. 2020;88:106273. [DOI] [PubMed] [Google Scholar]
- 52.Doria A, Yang Y, Malecki M, Scotti S, Dreyfus J, O’Keeffe C, Orban T, Warram JH, Krolewski AS. Phenotypic characteristics of early-onset autosomal-dominant type 2 diabetes unlinked to known maturity-onset diabetes of the young (mody) genes. Diabetes Care. 1999;22(2):253–61. [DOI] [PubMed] [Google Scholar]
- 53.Harrelson JP, Lee MW. Expanding the view of breast cancer metabolism: promising molecular targets and therapeutic opportunities. Pharmacol Ther. 2016;167:60–73. [DOI] [PubMed] [Google Scholar]
- 54.Chen J, Liu X, Shen L, Lin Y, Shen B. CMBD: a manually curated cancer metabolic biomarker knowledge database. Database. 2021;2021:094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Poliaková M, Aebersold DM, Zimmer Y, Medová M. The relevance of tyrosine kinase inhibitors for global metabolic pathways in cancer. Mol Cancer. 2018;17(1):1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Bushue N, Wan YJY. Retinoid pathway and cancer therapeutics. Adv Drug Deliv Rev. 2010;62(13):1285–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The code and datasets related to the paper can be found at https://github.com/dragon-wyl/AEGAN-Pathifier.