Unraveling EEG correlates of unimanual finger movements: insights from non-repetitive flexion and extension tasks

Abstract

Background

The loss of finger control in individuals with neuromuscular disorders significantly impacts their quality of life. Electroencephalography (EEG)-based brain-computer interfaces that actuate neuroprostheses directly via decoded motor intentions can help restore lost finger mobility. However, the extent to which finger movements exhibit distinct and decodable EEG correlates remains unresolved. This study aims to investigate the EEG correlates of unimanual, non-repetitive finger flexion and extension.

Methods

Sixteen healthy, right-handed participants completed multiple sessions of right-hand finger movement experiments. These included five individual (Thumb, Index, Middle, Ring, and Pinky) and four coordinated (Pinch, Point, ThumbsUp, and Fist) finger flexions and extensions, along with a rest condition (None). High-density EEG and finger trajectories were simultaneously recorded and analyzed. We examined low-frequency (0.3–3 Hz) time series and movement-related cortical potentials (MRCPs), and event-related desynchronization/synchronization (ERD/S) in the alpha- (8–13 Hz) and beta (13–30 Hz) bands. A clustering approach based on Riemannian distances was used to chart similarities between the broadband EEG responses (0.3–70 Hz) to the different finger scenarios. The contribution of different state-of-the-art features was identified across sub-bands, from low-frequency to low gamma (30–70 Hz), and an ensemble approach was used to pairwise classify single-trial finger movements and rest.

Results

A significant decrease in EEG amplitude in the low-frequency time series was observed in the contralateral frontal-central regions during finger flexion and extension. Distinct MRCP patterns were found in the pre-, ongoing-, and post-movement stages. Additionally, strong ERD was detected in the contralateral central brain regions in both alpha and beta bands during finger flexion and extension, with the beta band showing a stronger rebound (ERS) post-movement. Within the finger movement repertoire, the Thumb was most distinctive, followed by the Fist. Decoding results indicated that low-frequency time-domain amplitude better differentiates finger movements, while alpha and beta band power and Riemannian features better detect movement versus rest. Combining these features yielded over 80% finger movement detection accuracy, while pairwise classification accuracy exceeded 60% for the Thumb versus the other fingers.

Conclusion

Our findings confirm that non-repetitive finger movements, whether individual or coordinated, can be precisely detected from EEG. However, differentiating between specific movements is challenging due to highly overlapping neural correlates in time, spectral, and spatial domains. Nonetheless, certain finger movements, such as those involving the Thumb, exhibit distinct EEG responses, making them prime candidates for dexterous finger neuroprostheses.

Supplementary Information

The online version contains supplementary material available at 10.1186/s12984-024-01533-4.

Background

Individuals with neuromuscular disorders often experience significant losses in hand strength, tone, movement, dexterity, joint range, and sensation, severely impacting their quality of life [1]. One promising technology for addressing these challenges is a motor brain-computer interface (BCI), the purpose of which is to decode motor intentions from the brain to directly control end effectors [2, 3]. For example, Hotson et al. successfully decoded individual finger movements using electrocorticography (ECoG) to control a modular prosthetic limb in real-time [4]. Additionally, a tetraplegic patient was able to achieve upper-limb movements with eight degrees of freedom during various reach-and-touch tasks and wrist rotations using an epidural ECoG-BCI [5]. Another innovative approach involves a hybrid electroencephalography (EEG)/electrooculography-driven hand exoskeleton, which enables quadriplegics to restore intuitive control of hand movements necessary for activities of daily living (ADLs) [6].

Advances in BCI-based neuroprostheses hold the promise of helping individuals with hand paralysis regain dexterity in finger movements. While invasive solutions are nearing this goal [7–11], non-invasive approaches, such as those using EEG, remain less effective [6, 12, 13]. This disparity is primarily due to the superior spatial resolution, spectral bandwidth, and signal-to-noise ratio (SNR) offered by invasive recordings [14, 15]. Nevertheless, EEG systems offer significant advantages: they are non-invasive, even portable, and generally more affordable than other brain-recording systems, while providing acceptable time and spatial resolution. These qualities make EEG-BCI a promising tool for neurorehabilitation. However, functional magnetic resonance imaging has shown that, although there is a small distributed finger-specific somatotopy in the human motor cortex, each digit shares overlapping representations [16, 17]. This overlap makes decoding finger movements inherently challenging. Recent advances in machine learning have enabled high-performance decoding from invasive recordings [8, 9, 11], prompting renewed interest in EEG. Recognizing that ADLs heavily depend on unimanual finger movements, we identified the need to investigate the potential of EEG in decoding fine single- (individual) and multi- (coordinated) finger movements of the same hand.

Movement can lead to either a decrease or an increase in the synchrony of underlying neuronal populations, known respectively as event-related desynchronization (ERD) and event-related synchronization (ERS) [18]. With EEG recordings, finger movements induce alpha and beta ERD prior to movement onset over the contralateral Rolandic region, which become bilaterally symmetrical immediately before movement execution. Beta ERS occurs upon movement termination, while the Rolandic alpha rhythm remains desynchronized. For a comprehensive review, we refer to [18]. Previous research has shown that the strength and spatial distribution of ERD/ERS encode critical information about hand movements, including kinematics, kinetics [19, 20], and movement types [21]. Regarding finger movements, Pfurtscheller et al. found that pre-movement alpha (10–12 Hz) ERD is similar for the index finger, thumb, and hand movements, but differs for later stages [18, 22]. Additionally, the post-movement beta ERS for fingers is significantly smaller compared to the whole hand. Ultra-high-density EEG studies have demonstrated finger-specific ERD/ERS representations, suggesting EEG could provide discriminating information crucial for decoding finger movements [12, 23–25].

Unlike ERD/ERS, which reflect power changes, movement-related cortical potentials (MRCPs) are prominent in the low-frequency band (e.g., 0.3–3 Hz) and can be easily visualized when performing or attempting movements [26, 27]. MRCPs are characterized by Bereitschaftspotential (BP) or readiness potential, and reafferent potential [26]. For finger-related movements, MRCPs typically feature an early bilateral negativity (early BP) starting around 3 s before movement onset, followed by a steeper negative slope (late BP) over the contralateral hemisphere about 0.5 s before movement onset [28]. Different hand movements induce characteristic MRCP patterns, allowing for differentiation [27, 29, 30]. However, MRCPs for different finger movements, particularly unimanual ones, are less studied. Quandt et al. pioneered decoding individual unimanual finger movements (thumb, index, middle, and little finger) using EEG and magnetoencephalography (MEG) recordings [31]. They observed that amplitude variations in time series provided the best information for discriminating finger movements, outperforming frequency band oscillations. This suggests that the MRCP profile contains rich information on unimanual finger movements.

Our brain supports a diverse repertoire of finger movements, including both individual and coordinated actions. It is important to determine whether these movements exhibit distinct and decodable EEG correlates, such as ERD/ERS and MRCPs. To date, no EEG study has systematically reported these neural correlates, leaving their potential in decoding fine finger movements largely unexplored. This study aims to investigate the EEG correlates of various unimanual finger movements, ranging from individual to coordinated ones. We focus on non-repetitive finger flexion and extension, simulating real-world grasping scenarios. This straightforward task design allows us to assess the limitations of EEG decoding, as complex (repetitive or rhythmic) finger movements are typically associated with stronger brain activation [32, 33]. While we anticipate some overlap in EEG correlates within the repertoire of finger movements, we expect to discern distinct ones that can serve as discriminative features for decoding. Our findings yield significant implications for the design of dexterous EEG-actuated finger neuroprostheses, potentially enhancing the quality of life of individuals with neuromuscular disorders. By identifying and decoding these EEG correlates, we can advance the development of more effective and precise neuroprosthetic devices.

Materials and methods

Participants

We recruited 16 healthy participants (sub1–sub16, 25.9 ± 2.7 years old, 6 males, 10 females). All subjects are right-handed. Fourteen of them completed the Edinburgh Handedness Inventory (https://www.brainmapping.org/shared/Edinburgh.php) and obtained average scores of 91.9 ± 8.5 on the augmented index and 90.3 ± 10.5 on the laterality index. Before the experiment, all subjects were informed about the study details and gave their consent. Six of them (sub11–sub16, 4 females) underwent a multi-session experiment (Supplementary Table s1), with 3, 3, 3, 2, 2, and 5 sessions, respectively. Therefore, there are a total of 28 sessions of the experiment. Participants were remunerated per session. This study was approved by the Ethical Committee of the University Hospital of KU Leuven (UZ Leuven) under reference number S6254.

Experiment setup

During the experiment, subjects needed to follow the instructions shown on the screen (ViewPixx, Canada) in front of them, while their brain signals and finger trajectories from their right hand were simultaneously recorded. We used high-density EEG, 58 active electrodes covering frontal, central, and parietal areas with positions following the 5% electrode system [34], and a Neuroscan SynAmps RT device (Compumedics, Australia) for recording. The ground electrode was set at AFz, and the reference electrode was at FCz. All electrode impedances were kept below 5 kΩ before recording. The sampling rate was set to 1000 Hz. Right-hand finger flexions and extensions were tracked using a digital data glove (5 Ultra MRI, 5DT, Irvine CA, USA). We designed the experimental paradigm by relying on Psychtoolbox-3 (www.psychtoolbox.net) to synchronize the EEG and glove data per trial.

Finger flex-maintain-extend paradigm

We designed a finger flex-maintain-extend paradigm including both individual (5 fingers) and coordinated (4 gestures) finger movements, as shown in Fig. 1b. The ‘no movement’ class was designed as the baseline for comparison. A single-session experiment comprises 30 blocks, with each block consisting of a single round of the 10 finger movement scenarios, namely, 30 trials per scenario for each session. Before the experiment, the subjects were told to relax and keep their right hand naturally open with the palm facing upwards on the table (considered the rest position). Figure 1a shows the timing of an exemplary Thumb trial. At the beginning of the trial, a picture is displayed on the screen for 2 s indicating which movement the subjects need to perform in that trial. When this movement scenario cue disappears, a grey circle shows up and starts shrinking at a fixed speed. On top of the circle, there is a cross with scales. When the circle reaches the outer scale (3 s), the subjects must immediately flex their finger(s) and maintain the action for 4 s. Until the circle reaches the inner scale, the subjects need to immediately extend their finger(s) back to the rest position. They were given 2-s rest between trials. We opt for this shrinking-circle design as it diminishes the effect of visual cues [27]. When a trial was started, the subjects were required to only move the indicated finger(s) according to the scenario cue. For the None class, the subjects had to keep their hand at rest while the circle shrinks.

Fig. 1.

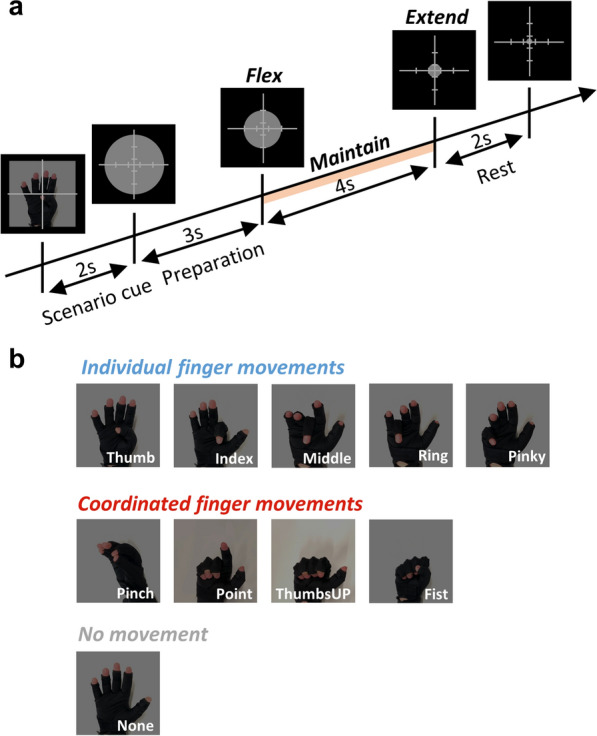
Paradigm details. a Timing of a trial. The cross is with scales that indicate when the subjects need to flex or extend the corresponding finger(s). b Different finger movement scenarios. During the experiment, the subject’s hand was positioned on the table with the palm facing upwards

Finger trajectory processing

The kinematic data from the data glove were used to precisely detect the onset of movement (finger flexion and extension). We first obtained the finger trajectories based on normalized bending sensor output. Then, we smoothed the trajectories and calculated the trajectory velocity for each movement’s representative finger. For individual finger movements, the representative one was the cued finger, and for coordinated finger movements, we selected the index finger for Pinch, ThumbsUP, and Fist, and the middle finger for Point. Next, the onset of movement was determined by the time when velocity exceeded a threshold of 0.2 times the maximal value (minimal value for finger extension). A graphical explanation is shown in Supplementary Fig. s1.

EEG data preprocessing

Data preprocessing was done by customized scripts and Fieldtrip functions [35]. Raw EEG data were first downsampled to 250 Hz for ease of computation. An antialiasing filtering was applied during this process. Then, the power line noise at 50 Hz was removed by a 3rd-order two-pass band-stop Butterworth IIR filter. Using the same type of band-pass filter, the EEG data were filtered between 0.1 and 70 Hz. We visually inspected faulty channels and excluded them for further preprocessing. Next, Independent Component Analysis was used, and components related to eye movements and abnormal artifacts were identified and removed. Last, the cleaned data went through common average referencing (CAR). We epoched the recordings according to trial markers once the continuous EEG data were preprocessed. We used 4 criteria to find bad channels in each trial. Specifically, a channel was considered bad when any of its kurtosis, mean value, and variance exceeded three times the standard deviation of the mean for all electrodes, or its peak-to-peak amplitude exceeded 200 microvolts. Bad trials, either noisy or containing undesired finger movements, were determined by visual inspection. The bad channel and trial information were kept. For later analysis, bad trials were excluded, and faulty channels and bad channels were interpolated with the average value of neighboring ones. We used the triangulation method in Fieldtrip to calculate each electrode’s neighbors. Ultimately, we obtained an average of 28.4 ± 2.0 clean trials per movement scenario across subjects and sessions.

EEG correlates

Each subject’s single-session data were analyzed to investigate EEG correlates, in which we focused on low-frequency band signals and ERD/ERS.

Low-frequency band signals

We obtained cleaned epochs in the low-frequency band (0.3–3 Hz). For each epoch, we looked into 2-s pre-movement and 2-s post-movement by indexing finger movement (flexion and extension) onset according to kinematic information. For the None case, we extracted epochs according to the corresponding trial marker. We averaged all epochs per finger movement which resulted in a low-frequency EEG template of dimensions 58 × 1000 × 10 (channels × time points × finger movements) for each subject. Two aspects of low-frequency EEG correlates were analyzed, i.e., their time series and MRCPs. The first aspect was examined by showing the temporal evolution of the amplitude topoplots between each movement and None. The second aspect was to analyze, for selected representative channels, their MRCPs.

ERD/ERS

We first segmented the cleaned data based on trial markers and then extracted the epochs. Then, we implemented the Morlet wavelet time–frequency transformation (ft_freqanalysis() function in Fieldtrip) on each epoch. The frequency of interest was set to 1–50 Hz with a resolution of 1 Hz. The time resolution was set to 0.01 s. The resulting power spectra of all trials from the same movement were averaged per subject. Finally, ERD/ERS for each movement was derived as:

$$ERD/ERS\left(f,,,t,,,c\right)=\frac{1}{N_s}\sum _{i=1}^{N_s}\frac{{\mathit{TFR}}_i\left(f,,,t,,,c\right)-{\mathit{TFR}}_i^{\mathit{baseline}}\left(f,,,c\right)}{{\mathit{TFR}}_i^{\mathit{baseline}}\left(f,,,c\right)}\times 100\%$$ 1

where ${\mathit{TFR}}_i\left(f,,,t,,,c\right)$ denotes the power spectrum of the i-th subject at frequency f, time t, and EEG channel c. ${\mathit{TFR}}_i^{\mathit{bseline}}(f,c)$ is the baseline, selected from the middle 1-s power spectra of the None movement, and N_s the total number of subjects. A negative value indicates ERD and vice-versa ERS.

Similarity analysis and clustering

We relied on Riemannian distance as the dissimilarity metric to assess the finger representations obtained from EEG [36, 37]. First, we obtained cleaned epochs during finger flexion and extension within the 0.3–70 Hz frequency band. One epoch contains 1-s pre-movement and 0.5-s post-movement. Then, each epoch was transformed into a covariance matrix that lies in the Riemannian manifold [38]. For finger flexion or extension, we obtained the centroids of each type of finger movement’s covariance matrices and calculated the pairwise Riemannian distance between them. A larger distance indicates a larger dissimilarity. Finally, we could get a symmetric representational dissimilarity matrix (RDM) that reflects the structure of the broadband EEG responses for different finger movements during flexion or extension. Hierarchical clustering was done based on this matrix. The resulting dendrogram was analyzed by looking into clustered finger movements.

Decoding models and implementation details

Feature extraction

We tested mainstream feature extraction methods in the literature related to hand and upper-limb movement classification tasks. First, we obtained the cleaned epochs from multiple frequency bands, including the low-frequency (0.3–3 Hz), delta (1–4 Hz), theta (4–8 Hz), alpha (8–13 Hz), beta (13–30 Hz), and low gamma (30–70 Hz) bands. Then, for the low-frequency band, feature extractors including time-domain amplitude [27, 29, 30, 39], discriminative spatial patterns (DSP) [40], and discriminative canonical pattern matching (DCPM) [41] were implemented. For the other frequency bands, we extracted band power, common spatial pattern (CSP) [42], and Riemannian geometry tangent space (RGT) [38] features.

Implementation

Denote the i-th EEG trial as $\mathit{X}\left(i\right)\in {\mathbb{R}}^{C\times P}$, where C and P indicate the number of channels and sampling points, respectively. In this study, we fixed the time window to be 1.5 s, and thus P = 375. The time-domain amplitude was taken every 0.12 s, resulting in a 754-dimensional feature vector for each trial with C = 58 channels. Considering the scarcity of training data, we removed redundant features using Lasso regularization with a regularization coefficient of 0.05 [43]. For DSP, we selected the top 10 eigenvectors as spatial filters, hence the trial channel dimension was reduced from 58 to 10. Then, the average value of each channel was extracted as a feature. For DCPM, the top 10 eigenvectors were selected as spatial filters during computation, and finally, the model outputs a 3-dimensional feature vector for each trial. To extract power features, we took the average square value of each trial’s channel, resulting in a 58-dimensional feature vector. For CSP, we selected the paired first and last 3 spatial filters and generated a 6-dimensional feature vector. Last, for RGT, the mapped features in Riemannian Tangent space have an original dimension of C × (C + 1)/2 but were reduced again using Lasso regularization. Note that the above description of feature dimensions is the theoretical value of a trial in one single frequency band. When multiple frequency bands’ information was fused, the dimensions changed accordingly.

Classification task

The shrinkage linear discriminant analysis (sLDA) model was used as the classifier for its excellent performance in single-trial EEG classification [27, 30, 39, 44]. The regularization parameter was set to 0.8 according to a trial–error test on one subject. Based on this model, we aim to investigate: (I) which feature extractor and frequency band contributes the most to finger movement detection and pairwise classification, and (II) whether we could build a model based on those contributing features and obtain an overall performance improvement. In order to address task I, we trained and tested several sLDA classifiers based on each feature type on the low-frequency, delta, theta, alpha, beta, and low gamma band, individually. The contribution of features and frequency bands was analyzed. For task II, we gathered all classifiers trained on the selected features and frequency bands and used majority voting for prediction. Based on this ensemble model, we also investigated the impact of data sizes, time window choices, and EEG electrode layouts on model performance. We tested the impact of data sizes on decoding performance with increasing sub11-sub16’s multi-session data. For time window choices, we considered three primary time windows [−1.6, −0.1]s, [−1, 0.5]s, and [0, 1.5]s to the movement onset (0 s). Likewise, different EEG electrode layouts (Supplementary Fig. s2) were selected from the 58 electrodes in total and compared based on the ensemble model. All data (28 sessions) were used for each task, except for the data size testing one. We performed tenfold cross-validation on all tasks. All trained models are subject-specific. The chance levels were estimated following [45], and we obtained 0.6225 for single-session and 0.5722 (estimated based on the averaged trial numbers across sub11–sub16) for multi-session pairwise classification (alpha = 0.05).

Statistical analyses

All statistical tests were conducted using MATLAB with a significance level of 0.05. For multiple within-factor conditions, such as finger movement scenarios, time windows, and electrode layouts, we relied on one-way repeated measures ANOVA. Then, a post hoc multiple comparisons test with Bonferroni correction was used to identify significant pairwise differences. For pairwise conditions, we relied on the Wilcoxon signed-rank test. We marked associated p-values using asterisks in figures (N.S.: not significant; *: p < 0.05, **: p < 0.01; *** p < 0.001).

Results

Low-frequency EEG signals correlate with non-repetitive finger flexion and extension

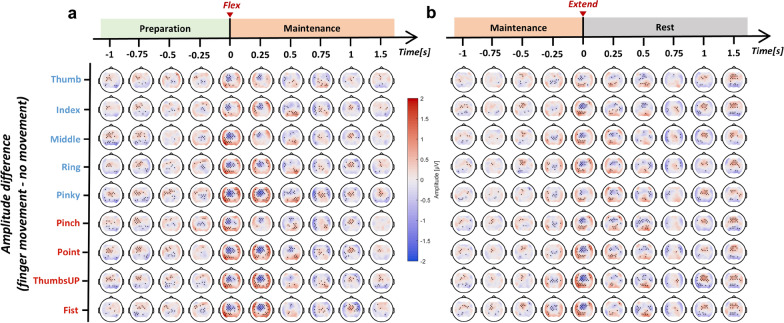
Figure 2 shows the evolution of amplitude difference between different finger movement scenarios and no movement (None). Overall, all finger movements induced significant changes in amplitude in the low-frequency band. Contralateral frontal-central brain regions were found to be the most active related to both finger flexion and extension. The EEG amplitude in those regions started decreasing 0.5-s before the onset of movement, reached the minimal at the moment of movement, and rebounded afterward. This phenomenon was consistent when the movement state transits from rest to flexed (flexion in Fig. 2a) or from flexed to rest (extension in Fig. 2b). An interesting finding was that brain regions surrounding the frontal-central showed a prominent short-term increase of amplitude during the movement, as shown in Fig. 2a, b when time equals 0 and 0.25 s. The MRCPs of a selection of channels are visualized in Fig. 3 and Supplementary Fig. s3. The temporal EEG waveform from FC1 indicated three significant features of finger movement-related MRCPs, including an early increase in amplitude 1-s preceding the movement, a strong negative potential around the movement onset, and followed by a clear positive rebound 1-s after. The MRCP morphologies were brain region-dependent. According to Supplementary Fig. s3, the ipsilateral and central-parietal channels (C2, CP1, and CP2) showed a more obvious positive rebound than a negative deflection. Besides, finger extension was found to have a smaller negative peak around movement onset compared to flexion. While non-repetitive finger flexion and extension could evoke clear MRCP patterns, they were highly overlapping.

Fig. 2.

Topographical EEG amplitude difference between different finger movements and no movement during a flexion and b extension in the low-frequency band (0.3–3 Hz). Time = 0 s corresponds to the movement onset, aligned by kinematic data. The channels with significant differences are marked in black

Fig. 3.

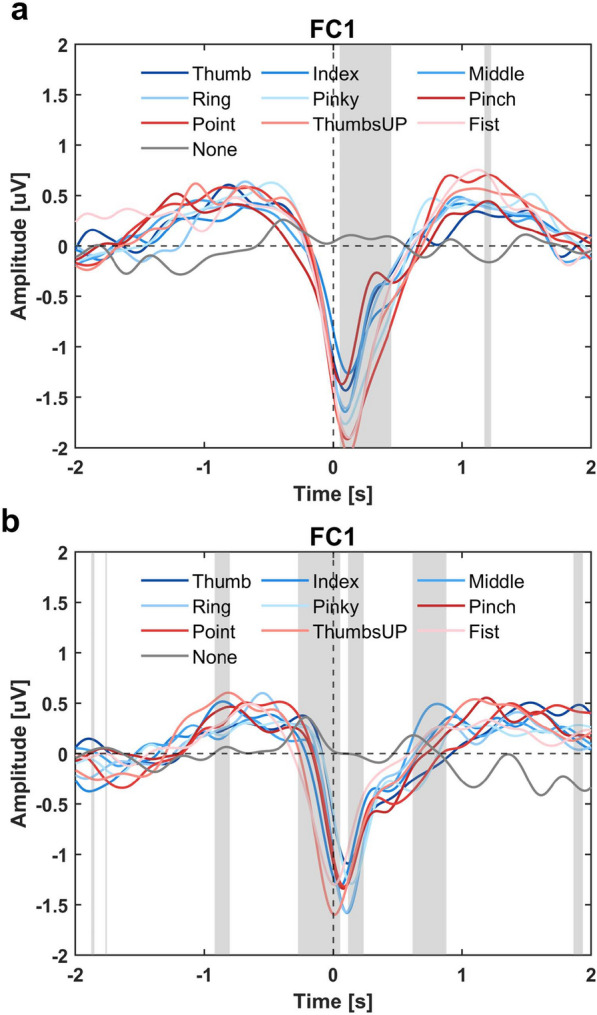
MRCPs of different finger movements during a flexion and b extension. Channel FC1 from the frontal-central brain regions was selected for visualization. Time = 0 s corresponds to the movement onset. The shaded area indicates a significant (p < 0.05) amplitude difference among those 9 movement scenarios

Finger flexion and extension induce prominent changes in ERD/ERS in the alpha and beta bands

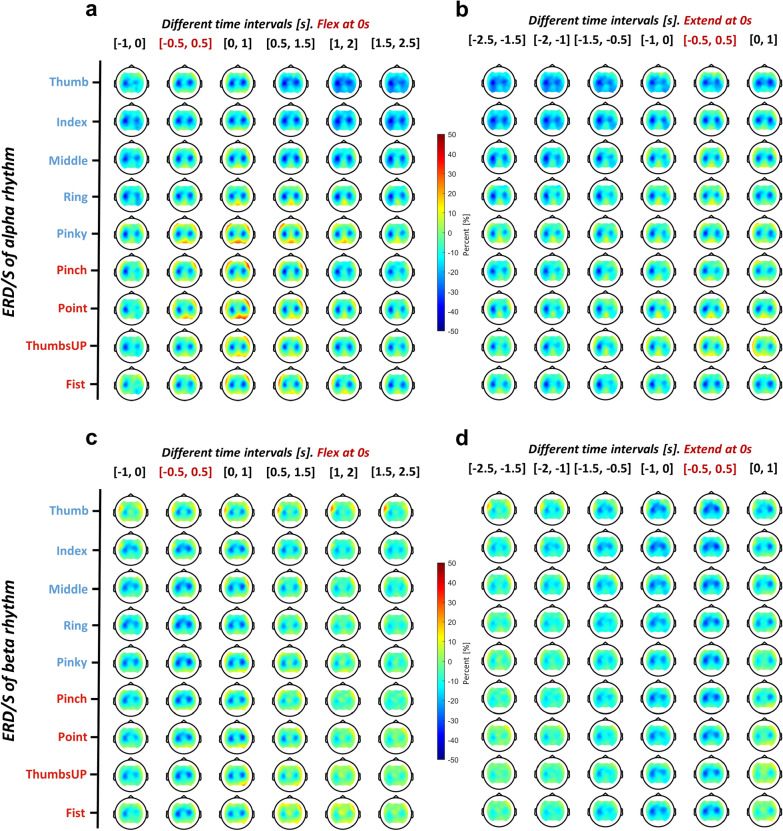
Figure 4 illustrates the progression of ERD/ERS changes during finger flexion, movement maintenance, and extension. Since finger flexion and extension onsets were detected separately using motion trajectories, we chose a time window of −1 to 2.5 s for flexion and −2.5 to 1 s for extension, ensuring that the movement maintenance period was fully captured. Prominent changes of ERD/ERS in the alpha and beta bands were found during different finger movement scenarios, and these changes were mainly located in central brain regions. For the alpha rhythm shown in Fig. 4a, b, a strong contralateral ERD was found before movement onset when referring to the time window [−1, 0] s for finger flexion and [−2, 0] s for finger extension. At movement onset, a stronger ERD was elicited on both sides, as depicted in the time window of [−0.5, 2.5] s for finger flexion and [−0.5, 1] s for finger extension. However, the beta band behaved differently in that a less strong ERD happened contralaterally before the flexion ([−1, 0] s), and a prominent rebound (ERS) occurred bilaterally for post-movement of finger flexion ([0.5, 2.5] s) and extension ([0, 1] s) (Fig. 4c, d). Statistical comparisons between the behavior of alpha and beta rhythms on channels C3 and C4 during different stages of the movement are reported in Table 1. There was a clear beta rebound in the movement maintenance (post-flexion) and relaxation (post-extension) stages, significantly different from the alpha rhythm on both C3 and C4 channels. Within the finger repertoire, individual finger movements activated more ipsilateral regions, which is evidenced by significantly stronger pre-flexion ([−1, 0] s) alpha ERD, and post-extension ([0, 1] s) beta ERD compared to the coordinated ones on the C4 channel (Supplementary Table s2).

Fig. 4.

Topographical EEG ERD/ERS of a, b alpha and c, d beta rhythm for different finger movements during (a, c) flexion and (b, d) extension. Each topoplot shows the averaged ERD/ERS value within the 1-s time window. Six windows were selected from −1 to 2.5 s for flexion and −2.5 to 1 s for extension with an interval of 0.5 s

Table 1.

Comparison between the ERD/ERS of alpha and beta rhythms during different stages of finger movement

Channel	Rhythm	ERD/ERS [%] during different stages of finger movement
		Pre-flexion	Ongoing-flexion	Maintenance (flexed)	Pre-extension	Ongoing-extension	Relaxation
C3	alpha	−35.4 ± 24.65	−35.87 ± 28.59	−37.53 ± 26.21	−36.84 ± 25.55	−35.75 ± 28.11	−32.63 ± 30.65
	beta	−27.83 ± 20.85	−31.89 ± 21.96	−17.99 ± 21.62	−30.95 ± 20.52	−32.90 ± 21.39	−19.54 ± 28.63
	p-value	0.0285	N.S	1.6651e−9	N.S	N.S	0.0016
C4	alpha	−21.51 ± 27.62	−29.98 ± 31.55	−31.66 ± 30.12	−22.77 ± 25.00	−28.14 ± 31.52	−31.21 ± 36.11
	beta	−19.37 ± 19.30	−29.58 ± 18.38	−14.70 ± 21.08	−23.57 ± 16.48	−30.43 ± 17.17	−24.45 ± 21.30
	p-value	N.S	N.S	1.3196e−7	N.S	N.S	0.0228

The ERD/ERS values are the grand averages across subjects and finger movement scenarios. The difference between alpha and beta rhythms was tested by Wilcoxon signed-rank test (alpha = 0.05), and the associated p-values were listed. Pre-flexion, ongoing-flexion, and maintenance correspond to time intervals of [−1, 0], [−0.5, 0.5], and [1, 2] s, respectively, in Fig. 4a, c, while pre-extension, ongoing-extension, and relaxation correspond to time intervals of [−1, 0], [−0.5, 0.5], and [0, 1] s, respectively, in Fig. 4b, d

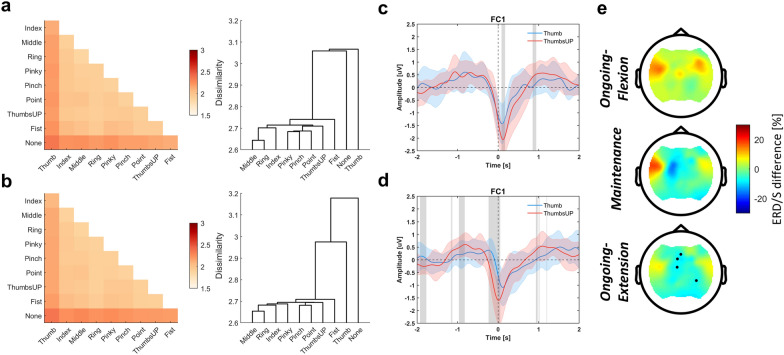
Similarity analysis reveals distinct EEG responses between finger movements

Similarity analysis results are presented in Fig. 5a, b for finger flexion and extension, respectively. None, as well as Thumb, exhibited a higher dissimilarity compared to the other movement scenarios, and this was also reflected in the dendrogram. Statistical test results showed that the cluster of None and Thumb was significantly distinct from the rest (p < 0.001 for both flexion and extension). However, for most of the finger movements, their neural representations were similar, especially for the individual finger group Middle-Ring. Figure 5c–e compares MRCPs and ERD/ERS between the Thumb and ThumbsUP movements. ThumbsUP was chosen for comparison as it represents the combination of the rest four fingers (Index-Middle-Ring-Pinky). We would like to know whether EEG supports at least two distinguishable finger groups and thus provides more degrees of freedom for control purposes. As seen in Fig. 5c, d, significant differences in MRCPs were found both in the pre-, ongoing-, and post-movement stages, where ThumbsUP showed stronger positive and negative deflections. Differences in beta band ERD/ERS were also found in contralateral brain regions, while only during finger extension did some channels show statistical differences.

Fig. 5.

Distinct EEG responses between finger movements. Similarity analysis results for a finger flexion and b extension. The left and right panels show the RDM (the lower triangular part of the symmetric matrix) and hierarchical clustering results, respectively. c, d show the MRCP of Thumb (blue) and ThumbsUP (red) movements in channel FC1 for finger flexion and extension, respectively. The variance and average values across subjects are plotted. The shaded gray area indicates a significant difference (p < 0.05) between the two finger movements. e Beta band ERD/ERS difference between Thumb and ThumbsUP movement (ERD/ERS_Thumb − ERD/ERS_ThumbsUP) at three movement states. Significant channels are marked

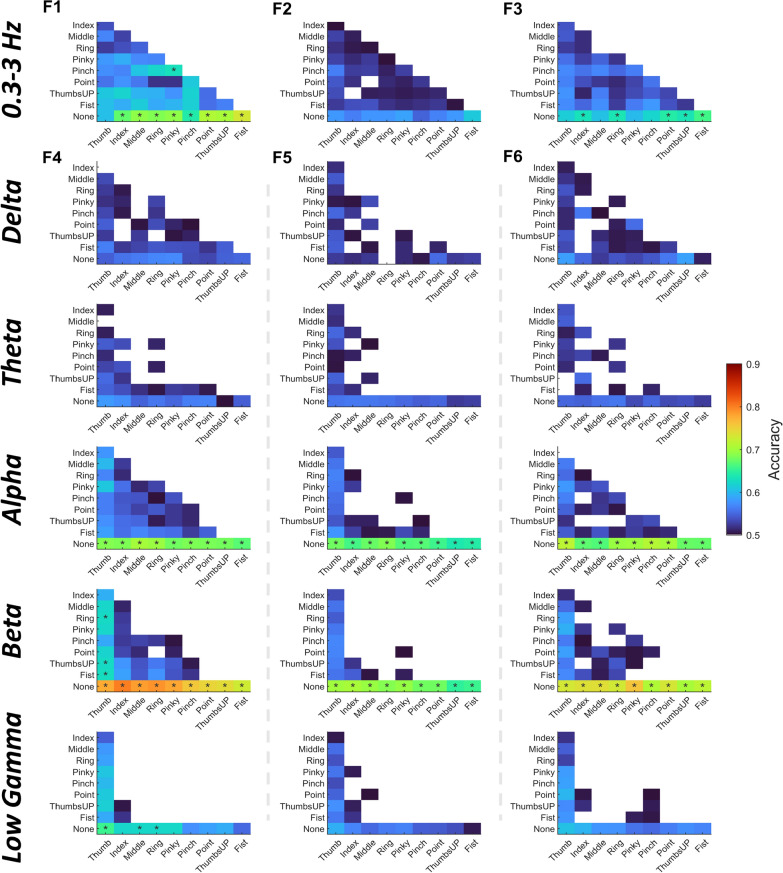
Features and frequency bands contribute differently to finger movement decoding

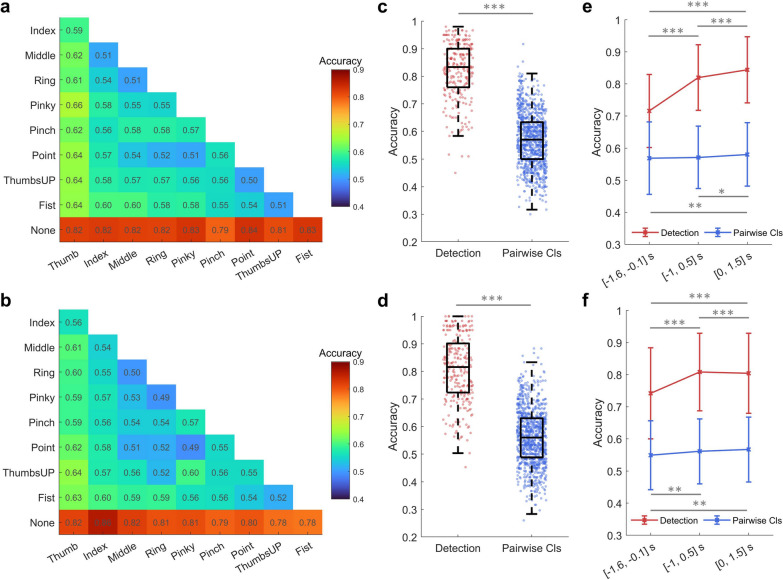
Figure 6 demonstrates different features and frequency bands’ contributions to decoding accuracy. First, the low-frequency band (0.3–3 Hz) performed better in differentiating finger movements than other frequency bands. On the other hand, alpha and beta bands performed well in detecting finger movements from the rest (None) condition. When referring to the amount and value of significant above-chance level accuracies, time-domain amplitude (F1) performed better than DSP (F2) and DCPM (F3) in the low-frequency band, while band power (F4) and RGT (F6) were comparable and relatively superior to CSP (F5) in other frequency bands. Taking each feature’s advantage together, an ensemble model was proposed, voting the results of three types of feature-trained sLDA: F1+sLDA, F4+sLDA, and F6+sLDA. The results are shown in Fig. 7. In Supplementary Fig. s5, we also tested three other types of ensemble models, and it turned out that the mentioned model performs best. The decoding performance markedly improved using the classifier ensemble. Specifically, for finger flexion, the highest detection accuracy reached 0.8352 ± 0.0962 (Point vs. None) and the pairwise classification accuracy reached 0.6550 ± 0.0974 (Thumb vs. Pinky). While for finger extension, the highest detection- and pairwise classification accuracies reached 0.8611 ± 0.0911 (Index vs. None) and 0.6364 ± 0.0890 (Thumb vs. ThumbsUP), respectively (Fig. 7a, b). What stands out in those accuracies was that the Thumb and Fist movements were easier to classify. When comparing the overall finger movement detection and pairwise classification performance, detection accuracy was significantly higher than classification accuracy (Flexion: 0.8198 ± 0.1023 vs. 0.5712 ± 0.0969, p < 0.001; Extension: 0.8081 ± 0.1210 vs. 0.5608 ± 0.1008, p < 0.001) (Fig. 7c, d). However, a quarter of the subjects and finger combinations still obtained significant above-chance level accuracies according to the boxplot of pairwise classification results. With more training data, the decoding performance increased from a group-level perspective (Supplementary Fig. s6c, d). The highest detection accuracy reached 0.8794 ± 0.0902 for Middle finger extension, and the highest pairwise classification accuracy reached 0.6650 ± 0.0607 for Thumb vs. Middle during flexion. However, from an individual-level perspective, the impact of data size on decoding performance differed within sub11-sub16 (Supplementary Fig. s6a, b, Table s3). Besides, there was a significant difference between time window choices, as can be seen in Fig. 7e, f. Movement detection was more sensitive to the time window choice compared to classification. Moreover, it is worth noting that decoding using the pre-movement period (time window of [−1.6, −0.1] s) is also feasible as we could observe above-chance level accuracies for certain finger combinations.

Fig. 6.

Feature contribution to the binary classification of finger flexion at different frequency bands. F1–F6 represents different feature extraction methods (F1: Time-domain amplitude, F2: DSP, F3: DCPM, F4: Band power, F5: CSP, F6: RGT). F1–F3 were tested on the low-frequency band, while F4–F6 were tested from delta to low gamma bands. The time window between −1 and 0.5 s was selected with 0 s indicating movement onset. sLDA serves as the classifier. Accuracies below 0.5 are not shown and the ones above the estimated chance level (0.6225, adjusted Wald interval, alpha = 0.05) are marked with stars. Similar phenomena can be observed when referring to finger extension results (Supplementary Fig. s4)

Fig. 7.

Binary classification results based on an ensemble model. The panels in the first row are for finger flexion, while those in the second row for finger extension. a, b provide the accuracy of each finger movement combination. c, d compare the detection and pairwise classification (abbreviated as Pairwise Cls) accuracy of finger movements. Each dot indicates a finger movement combination of one subject. e, f show the mean and standard deviation of detection and pairwise classification accuracy at different time windows ([−1.6, −0.1], [−1, 0.5], and [0, 1.5] s)

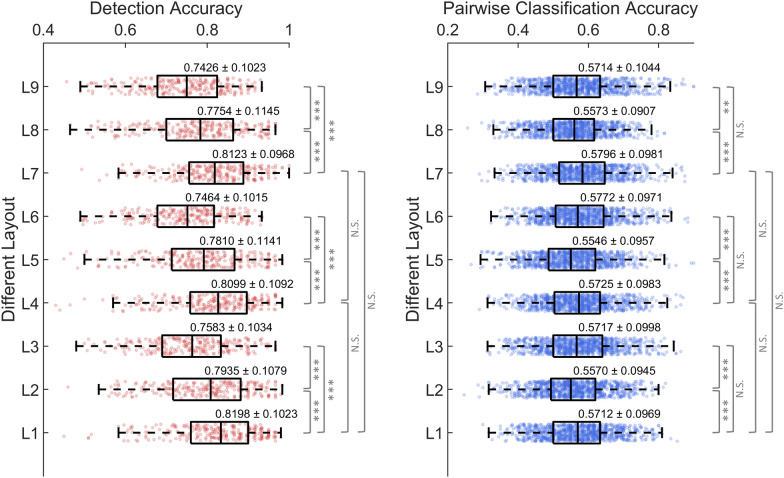
Bilateral electrode layout contributes to unimanual finger movement decoding

Figure 8 compares the finger flexion decoding performance at varying densities and brain region coverage electrode layouts. The choice of layout significantly impacted the decoding performance, as evidenced by the marked statistical results. First, bilateral layouts (L1, L4, and L7) obtained significantly higher accuracy than contralateral (L2, L5, and L8) and ipsilateral (L3, L6, and L9) ones, particularly for movement detection, where the ipsilateral layouts had the lowest accuracy. However, for pairwise classification, ipsilateral layouts were found to significantly outperform contralateral ones while exhibiting no significant difference from bilateral ones. Second, within the bilateral layouts, although the number of electrodes was substantially reduced from 58 (L1) to 14 (L7), the difference was not significant. Similar results were found for finger extension decoding (Supplementary Fig. s7), where bilateral layouts performed the best and the electrode density had no significant impact on performance.

Fig. 8.

Box plots of decoding accuracy of finger flexion for different EEG electrode layouts. L1 to L9 correspond to the layouts in Supplementary Fig. s2. Specifically, the layouts have three different densities (dense: L1, L2, L3; sparse: L4, L5, L6; sparse focal: L7, L8, L9), and cover three different brain regions (bilateral: L1, L4, L7; contralateral: L2, L5, L8; ipsilateral: L3, L6, L9). Each dot in the box corresponds to a finger movement combination of one subject. The grand average accuracy and standard deviation were noted above each box

Discussion

While studies have reported decodable EEG correlates of specific hand, upper limb, or lower limb movements, a systematic investigation on finger movements is lacking, albeit they are critical for supporting ADLs of a hand-disabled person. In our attempt to contribute to ADLs, we systematically compared EEG correlates of non-repetitive flexion and extension of individual and coordinated finger movements of the dominant hand. Our analysis showed that MRCPs and ERD/ERS from EEG could be discerned even for simple finger movements. Our feature and frequency band analysis identified low-frequency band time-domain amplitude, power and Riemannian features in alpha and beta bands as the most informative for single-trial finger movement decoding. Further combining those features we could precisely detect finger movements and obtain encouraging pairwise classification results on some finger combinations.

EEG correlates of unimanual non-repetitive finger flexion and extension

We looked into two aspects of EEG correlates: MRCPs and ERD/ERS, as they reflect different neuronal mechanisms of movement [26]. In general, we found clear MRCPs and ERD/ERS in response to our finger movement scenarios. Each movement scenario had a similar MRCP morphology in that a stronger negative deflection occurred before the movement, which we attributed to the late BP [26], and peaked around the movement onset. Later, the potential started to rebound and peaked at around 1 s after movement onset. We also noticed a small intermediate positive component 0.3 s after the movement onset, which likely corresponds to the reafferent potential P+300 [46]. A contradictory finding is that we didn’t see an early BP monotonously decreasing as reported in [26], but a positive component 1 s before the movement in concordance with previous studies working on hand and upper limb movements [29, 39, 47, 48]. We found this phenomenon to be brain region-dependent, as shown in Supplementary Fig. s3. The pre-movement positive component was observed in contralateral frontal-central channels, which were most responsive to finger movements (Fig. 2). Spatially, there was an interesting finding as contralateral frontal-central surrounding areas had a prominent short-term increase of amplitude during the movement, as also reflected in the study of [39]. This could result from the sequence activation within motor areas [26]. Regarding ERD/ERS, we found contralateral pre- and bilateral ongoing-movement alpha and beta ERD for all finger movements, with the contralateral side being more prominent (Fig. 4). However, a strong post-movement ERS was only found in the beta band for all finger movements around 1 s after the termination of flexion and extension, in line with the literature [18].

We found distinct EEG responses through similarity analysis when comparing EEG correlates of different finger movements, although their MRCP morphologies and ERD/ERS patterns are similar. According to Fig. 5a, b, the Thumb had a unique response compared to other movements, with the Fist being next. On the other hand, the EEG responses of other movements were clustered, particularly the Middle and Ring fingers. This neural basis partially explains why Thumb is easier to differentiate than others (Fig. 7a, b). From the neuromuscular control perspective, the activation of a larger muscle mass (like the case for coordinated finger movements) will involve a relatively larger population of cortical neurons [18]. As the Thumb shows higher individuation than other digits during self-paced movement [49], a unique neural response is expected, which is reflected by the clustering results. Besides, we attribute the tighter clustering of the Thumb and None conditions to the shorter displacement exhibited by Thumb movement. Moreover, this neuromuscular theory could also explain why a stronger positive/negative deflection of MRCP (Fig. 5c, d) was observed for coordinated finger movements compared to individual finger movements.

As for the comparison between finger flexion and extension, we found flexion-related MRCPs had a more pronounced negative peak around movement onset than extension (Fig. 3, Supplementary Fig. s3). However, our results contradict previous findings in that our MRCP was larger for the contralateral brain regions during muscle relaxation (extension) than for contraction (flexion) [50, 51]. The primary difference is our task design. We simulated a natural grasping scenario that requires the finger to first flex and maintain and then to release (extend). Thus, the extension task always came after flexion and movement maintenance, whereas wrist or finger relaxation and contraction are separate tasks in those studies [50, 51]. We assume the task design will cause this amplitude disparity, but it needs to be further studied.

The role of low-frequency EEG signals in differentiating finger movements

Low-frequency EEG signals encode upper and lower limb movements [27, 29, 52, 53], unimanual and bimanual reach-and-grasp [39, 48], and grasping types [21]. According to our study, we added that this signal is also informative in differentiating non-repetitive finger flexion and extension, a more subtle aspect of finger movement compared to repetitive movements. Moreover, referring to Fig. 6 (feature extraction methods F1–F3), we observe that low-frequency EEG signals, particularly the amplitudes, contain rich information about movement kinematics. Although low-frequency EEG is still informative in detecting finger movements, it is not comparable to the contribution of alpha and beta band signals (Fig. 6). Figure 3 suggests that discriminative amplitude information is present during pre-, ongoing-, and post-movement periods. However, as many finger movement scenarios were involved, their MRCP morphology is similar. Besides, we also found similarities between the MRCPs of our finger movements and that of other hand movements, such as palmar and lateral grasps [27, 29]. Therefore, there seems to be a limit to differentiating finger movements solely based on time-domain amplitude features. Spatial information could be added as compensation, as we saw topographical differences between different finger movements in low-frequency band signals in Fig. 2. We have tried two spatial-filter-based feature extractors DSP and DCPM using low-frequency EEG and obtained comparable results on some finger combinations to amplitude features, particularly for DCPM (Fig. 6, F1–F3).

The potential of EEG in decoding fine finger movements

We tested an extreme condition of single-trial finger movement decoding: unimanual, non-repetitive, simple flexion or extension in multiple finger movement scenarios. Our study returned a promising detection accuracy of over 80% on average for finger flexion and extension, and significant above-chance-level pairwise classification accuracy for Thumb versus other scenarios (Fig. 7a, b). The high detection accuracy could be attributed to our visual cue design (shrinking circle) and movement onset alignment, as also reported by Suwandjieff and Müller-Putz [54]. As to subject and finger combination variability, a quarter of them reached over 90% in movement detection and 64% in classification, which is quite encouraging (Fig. 7c, d). The decoding performance could be further improved by shifting the time window (Fig. 7e, f) and by incorporating more training data (Supplementary Fig. s5). Referring to the literature, Alsuradi et al. recently reported 60% 5-class decoding accuracy on a public dataset of imagined individual finger movements (similar but weaker cortical activations compared to attempted or performed movements) [55, 56], which is state-of-the-art as far as we know. During the imagery task, the participant imagined a flexion of the cued finger up or down for 1 s and completed a substantial number of trials [56]. Lee et al. achieved an average of 64.8% 5-finger pairwise classification accuracy using an ultra-high-density EEG system [12]. The participant extended the cued finger and maintained extension for 5 s. Overall, these cases show the feasibility of decoding specific finger movements. Although it is difficult to make a fair comparison, as each study differs in its experimental setup and paradigm design, our analysis of multiple finger movement scenarios and separate flexion and extension provided evidence in support of our decoding results, in the low-frequency time series, MRCPs, and ERD/ERS, extending the cited studies.

The challenge of EEG in decoding finger movements seems solvable by using advanced machine learning approaches, such as the Riemannian features extracted in this study, the neural networks used by Alsuradi et al. [55], or the customized ensemble model by Yang et al. [57]. However, EEG can only provide limited discriminative information when resolving fine finger movements, as in our case with the 9 finger movements shown in Figs. 2–5. Although the patch electrodes (placed on the scalp) used by Lee et al. have a better spatial resolution, and are claimed to provide a higher SNR, the resulting performance is still not ideal [12]. One encouraging fact is that we could discern a selection of finger movements with unique EEG responses out of a repertoire of them, as shown in Fig. 5. Therefore, for practical applications, we suggest focusing on decoding those movements with unique neural signatures and those that serve the user’s needs.

Implications for EEG-actuated finger neuroprostheses

Choosing appropriate electrode layouts is a critical issue when considering an out-of-the-lab application of BCIs. Our results show that the ipsilateral electrodes can also provide useful information for unimanual finger movement decoding (Fig. 8, Supplementary Fig. s7). As for the density of electrodes, we did see that higher density could result in better decoding performance, but as long as the electrodes cover the brain region of interest, the difference is minor, probably due to volume conduction. Another issue is the choice of the decoding time window as it determines the latency of neuroprostheses control. We tested three time windows as shown in Fig. 7e, f. There was a trade-off between performance and latency with a higher decoding performance at the cost of a longer latency. It is encouraging that we could obtain over 70% detection accuracy on average using purely pre-movement data (time window of [−1.6, −0.1] s), with finger movement classification also being feasible. Our EEG analysis supports these results as we noticed prominent MRCPs and ERD/ERS patterns 1-s before the movement onset. It has been suggested that the latency between the volitional movement onset and afferent feedback should be kept within 400–500 ms to promote cortical plasticity effectively [58, 59]. Our results indicate that designing low-latency neuroprostheses for use in finger neurorehabilitation is possible.

Limitations and future work

One limitation of this study comes from the scarcity of training data per finger movement, which potentially leads to the pairwise classification results being underestimated. Since we focused on ten scenarios of finger movement and looked into flexion- and extension-related EEG correlates, our study design inevitably resulted in limited trials for each scenario considering the subjects’ fatigue during recording. We assume the decoding performance has room for improvement as we noticed positive accuracy improvement for some subjects from the multi-session experiment results (Supplementary Fig. s6, Table s3). Theoretically, a higher decoding performance is expected when ample data is available from a single session, as combining multiple session data poses a transfer learning challenge [60]. We did not relate our analysis of the EEG representations to behavioral- (movement trajectories) or categorical model (individual vs. coordinated) representations [61]. Studies have shown characteristic representational similarities between EEG and grasping properties during different stages of movement [62, 63], and thus it would be interesting to investigate how neural patterns of various grasping differ from those of simple finger movements.

Conclusion

This study explored EEG correlates of unimanual, non-repetitive finger movements. We found significant decreases in low-frequency EEG amplitude in the contralateral frontal-central regions during finger flexion and extension, reflecting MRCPs. Strong ERD was observed in alpha and beta bands, with the beta band showing a notable post-movement rebound. The decoding results confirm that, while non-repetitive finger movements can be precisely detected, differentiating between them is challenging due to overlapping EEG correlates. Nevertheless, finger movements with distinct EEG responses and relatively superior decodability could be a primary focus for designing dexterous finger neuroprostheses, paving the way for improved BCI applications and a better quality of life for individuals with neuromuscular disorders.

Abbreviations

ADLs

Activities of daily living

ANOVA

Analysis of variance

BCI

Brain-computer interface

BP

Bereitschaftspotential

CSP

Common spatial patterns

DCPM

Discriminative canonical pattern matching

DSP

Discriminative spatial patterns

ECoG

Electrocorticography

EEG

Electroencephalography

ERD

Event-related desynchronization

ERS

Event-related synchronization

MRCPs

Movement-related cortical potentials

RDM

Representational dissimilarity matrix

RGT

Riemannian geometry tangent

sLDA

Shrinkage linear discriminant analysis

SNR

Signal-to-noise ratio

Author contributions

Q.S.: Conceptualization, Methodology, Software, Data collection, Formal analysis, Visualization, Writing—Original Draft. E.C.M.: Methodology, Data collection, Writing—Review & Editing. L.Y.: Software, Writing—Review & Editing. M.M.V.H.: Conceptualization, Methodology, Supervision, Funding Acquisition, Writing—Review & Editing. All authors read and approved the final manuscript.

Funding

This work was supported in part by Horizon Europe’s Marie Sklodowska-Curie Action (No. 101118964), Horizon 2020 research and innovation programme (No. 857375), the special research fund of the KU Leuven (C24/18/098), the Belgian Fund for Scientific Research—Flanders (G0A4118N, G0A4321N, G0C1522N), the Hercules Foundation (AKUL 043), and the China Scholarship Council (no. 202206050022).

Availability of data and materials

The datasets and analysis codes of the current study are available from the corresponding author upon reasonable request.

Declarations

Ethics approval and consent to participate

This study was approved by the Ethical Committee of the University Hospital of KU Leuven (UZ Leuven) under reference number S6254. All participants signed the informed consent form prior to their participation.

Consent for publication

Consent for publication of individual data has been obtained from all participants of the study.

Competing interests

The authors declare no competing interests.