ABSTRACT
Background
Robotic ultrasound visualises internal organs in real‐time for various medical applications without the harm of X‐rays. The ultrasound probe is attached to the robot's end effector using custom‐developed probe holders. This paper analyzes the impact of different probe holder geometries on the robot's base placement and reachability.
Methods
We propose a method to improve probe holder geometries and robot base placements to enhance reachability, validated using a 7‐DoF serial manipulator (KUKA iiwa 7) for ultrasound scans of multiple subcutaneous body parts.
Results
Without additional space restrictions, the number of robot base positions with high reachability could be strongly increased with an improved probe holder geometry. Under space constraints, previously unreachable target poses became accessible by adapting the probe holder geometry.
Conclusions
Our method provides an automated solution for determining improved probe holder geometries, enhancing reachability to target areas, especially when the robot's placing area is limited.
Keywords: reachability, robot base placement, robotic ultrasound, tool geometry, ultrasound liver examination
Abbreviations
- IRM
inverse reachability map
- RM
reachability map
- TCP
tool centre point
- US
ultrasound
1. Introduction
Ultrasound (US) imaging offers several advantages for diagnostic and interventional procedures. These include freedom from ionising radiation, good soft tissue contrast, high flexibility, and real‐time image acquisition. Furthermore, US can provide real‐time volumetric image data (4D US) [1]. In combination with a robotic system, precise and repeatable images can be acquired in an automated manner [2]. Robotic US thus represents a promising approach for automated diagnostic and interventional use.
An important factor for successful robotic US examinations is the positioning of the robot's base to the patient. The robot must be positioned in such a way that the target poses can be reached within the robot's working range. Furthermore, the corresponding joint configuration with which a defined target pose can be achieved determines the ability to alter the pose of the end effector, which is referred to as reachability. A higher reachability means a greater range of possible movements in this specific configuration, which is beneficial for the robot's motion planning.
The ability to calculate a quality index for defined poses of a robot offers a benefit for a number of applications in the field of robot manipulation. It is applied, for example, to support decision‐making processes such as the selection of appropriate grasping poses in humanoid robotics [3]. In this context, evaluation of the manipulability or reachability of a robot are well‐known methods to assess the ability to manoeuvre in a given workspace [3, 4]. Yoshikawa first introduced a manipulability index as a quality measure for redundant manipulators [5]. With this index the distance to singular configurations can be described. In other words, it can be quantified how easily the position and orientation of the end effector can be adjusted in a certain configuration [6]. This approach was extended to also take into account joint limits and obstacles [3]. Other methods described in the literature are based on the concept of filling a voxelised grid, either in 3D (only end effector positions) or 6D (end effector positions and orientations), with information on how well corresponding grid voxels can be reached by the robot. This can be, for example, the total number of all valid inverse kinematics solutions at the corresponding voxels [4, 7]. As a result, a reachability map (RM) is generated. Due to the discretised representation, the reachability entries can also be interpreted as a probability whether a pose in a corresponding voxel will lead to a valid inverse kinematics (IK) solution or not. For this reason, the term reachability distribution is sometimes used [3].
To find optimal robot base placements for defined TCP paths, reachability inversion can be used. For this purpose, RMs are inverted resulting in inverse reachability maps (IRMs) [7, 8, 9, 10]. IRMs characterise the reachability of a given TCP pose relative to the robot base pose as defined in the TCP's reference frame. These approaches often refer to mobile manipulators or humanoids allowing free base or stance placement. Orientation‐based reachability maps were introduced, which allow to incorporate of different tool geometries and task paths specified in the tool frame [11]. Other constraints, such as the surface geometry, can be included as shown in Birr et al. [9].
In addition to the placement of the robot base, the transformation from the robot flange to the tool centre point (TCP) influences the reachability of the defined TCP's target poses. This transformation can be designed according to the clinical setup to obtain an appropriate geometry of the probe holder. An approach for co‐optimisation of robot, environment, and tool design concerning motion planning is described in Toussaint et al. [12] Depending on the application, the robot geometry and the design of the tool can be adapted, thereby increasing the effectiveness of the execution of the corresponding task. However, the resulting robot geometries are currently only theoretically possible, as custom link shapes are required. In the context of robotic US, a kinematic optimisation for the design of a collaborative robotic end effector for tele‐echography is presented [13]. Here, the base position and the tool geometry of a robot concerning a manipulability measure are optimised for different poses on a patient.
Our research has a similar goal, but we take a different approach: instead of obtaining one optimal value for the base position and tool geometry [13], our approach consists of calculating the distributions of possible base positions for defined target poses in the context of robotic US. These distributions could be used to simplify the placement of a robot. Furthermore, we analyse how the reachability of the target poses can be increased by an improved geometry of the probe holder.
2. Methods
In this paper we consider a simulated robotic US scenario in which different areas on top and at the side of a patient are to be scanned. We propose a method to determine a tool geometry improving the reachability of the target poses while the robot base remains in an upright orientation.
This study did not involve any human participants, human data, or human tissue. As such, ethical approval was not required.
2.1. Experimental Setup
The experimental setup is shown in Figure 1 and involves a patient lying on a couch, while a 7 DoF redundant robot (KUKA iiwa 7) is moving an US probe attached to the end effector by a custom‐developed probe holder. Three different target poses to be scanned are defined. The target poses are located on the patient's semi‐cylindrical safety shell, with the target orientation being the surface normal, as shown in Figure 1B. A potential application is a robotic US examination of the liver, for which the probe is placed either centrally on the patient's abdomen (like target pose 3) or laterally on the rib cage (like target pose 1 and 2). In a more advanced scenario, robotic US could be used in radiotherapy of liver tumours [14, 15]. Due to the irradiation, no staff can be present in the treatment room, therefore a robot is ideal for holding the US probe. It is important that the correct positioning of the robot is planned in advance to avoid interrupting the treatment.
FIGURE 1.
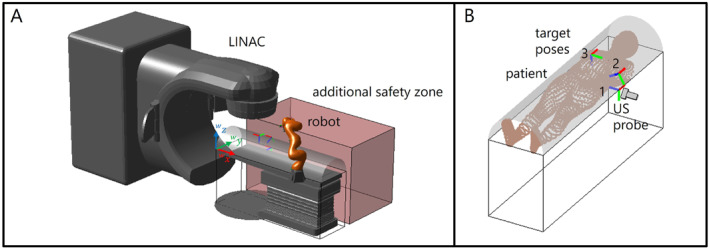
(A): Experimental setup consisting of a patient couch and a redundant robot (KUKA iiwa 7). For optimal robot base placement, we consider two scenarios, where in scenario 1 the robot can be positioned on both sides of the patient. In scenario 2, one patient side is restricted, for example by other medical equipment or staff, represented by the translucent red box. For example, the rotating irradiation unit of a LINAC could occupy one side of the patient to irradiate a certain target in the body, which is tracked using robotic US. (B): Target poses 1, 2 and 3 to be scanned by US probe.
The safety shell around the patient in Figure 1 represents the area in which no part of the robot, except for the US probe holder, must be located. We consider two scenarios for potential robot placements. In scenario 1 both sides of the patient are available for robot positioning. In scenario 2 the possible locations for the robot are reduced due to the consideration of a forbidden translucent red box as shown in Figure 1A which represents an area for other medical equipment (e.g., a linear accelerator (LINAC)) or medical staff on one patient's side. Thus, the target pose must be approached from the other side of the patient, which makes it more difficult to reach the pose.
The probe holder's geometry is defined by the transformation ee from the end effector to the TCP. We define the reference probe holder geometry as a pure translational extension of 0.1 m in the z‐direction of the end effector (see Figure 2A). The length of 0.1 m of the probe holder represents the minimum possible length for the straight attachment of our experimental US probe to the end effector. This setting allows us to use a small probe, but the cable must be bent for mounting. For the adapted tool geometries, the tool length is held constant, but it is attached to the end effector at a variable angle, represented by a rotation matrix (see Figure 2B). Thus, the probe holder geometry for a target pose is defined by the following transformation matrix:
| (1) |
FIGURE 2.
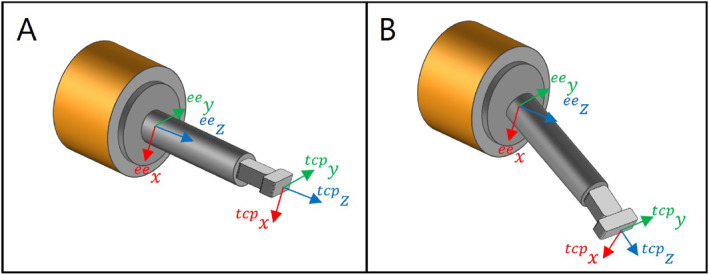
(A): Reference probe holder geometry, which is only a translational extension to the end effector by 0.1 m. (B): Example of an adapted probe holder geometry, where a rotation is applied to the reference tool geometry.
2.2. Generation of Reachability and Inverse Reachability Map
We use an inverse reachability map (IRM) to determine suitable robot base poses with high reachability for a defined target pose. The IRM is created from a reachability map, which is first explained below.
2.2.1. Workspace Sampling
The desired reachability map to be generated is a 6D map that represents the values for the reachability of every end effector pose in the workspace of the robot. First, a 3‐dimensional grid with a resolution of 0.1 m is created as visualised in Figure 3A, resulting in 2601 voxels. Every voxel is represented by a unit sphere whose centre is the end effector position. To achieve a uniform distribution of the end effector orientations, 50 points are evenly distributed on the surface of each unit sphere by minimising the electrostatic potential energy of a system of charged particles [16]. The direction from any point on the surface to the centre of the sphere represents the direction of the ee ‐axis, as shown in Figure 3B. The ee ‐ and ee ‐axes are tangential to the sphere surface. Each of these end effector orientations is additionally rotated around its ee ‐axis in a range from −180° to 150° in 30° steps, which results in a variation of the directions of the ee ‐ and ee ‐axes. For the sake of clarity, only three of these 12 rotated poses belonging to one ee ‐axis orientation are shown in Figure 3C. In summary, for each of the 2601 end effector positions, 600 different orientations are considered. This leads to a total number of 1,560,600 sampled poses, for which reachability values must be calculated and stored in the RM.
FIGURE 3.
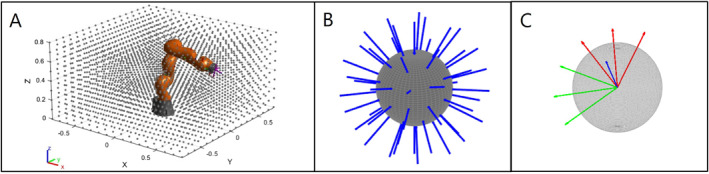
(A): Considered workspace of the robot, consisting out of 2601 positions represented by the centres of unit spheres. The dimensions of the workspace are , and , the resolution is 0.1 m. (B): 50 orientations of the ee ‐axis (shown in blue), defined by the direction from uniformly distributed points on the surface to the centre of the sphere. (C): Each of these 50 orientations is additionally rotated by 30° steps in a range from −180° to 150° to include all possible rotations around the ee ‐axis. To provide a better overview, only three rotations are shown. The ee ‐axes are red, while ee ‐axes are represented by green arrows.
2.2.2. Measure of Reachability
To calculate values for reachability corresponding to the sampled poses, all poses are searched for valid solutions for inverse kinematics. Since a redundant robot is used, the elbow angle is specified as an additional varying parameter to take the nullspace into account. The elbow angle is defined as the angle which describes the rotation of the elbow around the axis from the shoulder to the wrist. Thus, each of the 1,560,600 poses is checked for solutions of inverse kinematics, varying the angle of the elbow uniformly in 15 steps of 24° between 0° and 336°. The joint configurations resulting from the analytical inverse kinematics calculation [17] for all elbow configurations belonging to a sampled pose are checked for joint limits and self‐collisions and stored. The reachability value for each 6D entry of the RM is calculated as follows:
| (2) |
In Equation (2), represents the Jacobian of the configuration , where is the respective grid pose and the robot's elbow angle. We calculate the sum of Yoshikawa's manipulability indices for all possible configurations to reach a defined pose [5]. Yoshikawa's manipulability index represents a measure of how well an adjustment is possible in the respective configuration [3, 5]. Thus, high values of represent high reachability of the robot at the corresponding pose in the RM.
2.2.3. Reachability Inversion
The reachability of the robot flange from Section 2.2.2 is defined w.r.t a fixed robot base pose. The RM consists of tuples , where are base‐to‐flange transformations and are corresponding reachability values. Inverting the reachability data will lead to potential base poses for a fixed flange pose in the workspace. To generate an IRM, a second voxelised data grid is filled by tuples , where represents the inverted poses of the RM, that is the flange‐to‐base transformation [8].
2.3. Robot Base Placement
The procedure for finding safe and valid robot base poses is illustrated in Figure 4. First, the IRM is used to determine all potential robot base poses (see Section 2.3.1) which also include those with an oblique base. In a realistic use case, the orientation of the robot's base is fixed and upright, and hence, the poses with an upright base are extracted from the set of all potential poses. For the remaining inclined robot bases, we calculate the required rotation matrix of the tool transformation so that the robot base is aligned upright and the transformation from the base to the end effector remains the same (see Section 2.3.2). Finally, all robot configurations used to calculate the reachability values belonging to the upright base positions are checked for collisions with the safety zone (see Section 2.3.3). If collisions are detected, these joint configurations are not possible and corresponding reachability values must be reduced accordingly.
FIGURE 4.
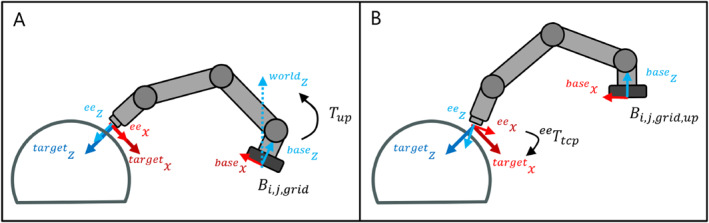
Base Placement Process. (A): Exemplary potential robot base pose , where the base ‐axis is aligned obliquely. (B): The oblique base was aligned upright by applying transformation and shifted accordingly so that the end effector position is retained. The resulting base position is referred to as .
2.3.1. Potential Robot Base Poses
The IRM was generated for end effector poses (see Section 2.2.3). This means that end effector poses must also be provided to use the IRM for determining potential robot base poses. For this purpose, the end effector target poses associated with the TCP target areas (target pose 1, 2, 3) are calculated by
| (3) |
where is the corresponding goal pose index and tcp represents the transformation from the TCP to the end effector for the reference probe holder geometry without any rotation at the end effector (see Figure 2A). All potential robot base poses for the end effector target pose can then be determined by multiplying the end effector target pose with the transformations of the IRM.
| (4) |
Each of the potential robot base poses is assigned the corresponding reachability value (see Equation 2) from the tuple of the IRM. The potential base poses are allocated to a 5D grid with a resolution of 0.1 m for the x‐,y‐ and z‐coordinates of the grid points. For each grid point, representing the positions of the base, 25 different orientations of the base ‐axis are possible, with a maximum inclination angle of 90°, so no robot bases hanging downwards are considered. Again, the base ‐axis orientations are defined by the direction from uniformly distributed points on the surface to the centre of a unit‐sphere. A nearest neighbour algorithm is used to assign each of the potential base poses to the nearest entry in this 5D grid, referred to as . The respective reachability values belonging to a grid entry are averaged. So far, no constraints have been applied to the potential robot base poses. This means that any position and inclination of the base ‐axis of the robot is possible, exemplarily shown in Figure 4A.
2.3.2. Compensation of Base Orientation Constraint by Tool Geometry
In our scenario, the robot base position can be varied in x‐,y‐ and z‐directions as long as it does not fall within the range of the safety zone. Moreover, we assume that the base is oriented in an upright position, with rotations around its base ‐axis possible. This assumption is made because it represents a realistic scenario, with a robot available in the treatment room, mounted upright on a mobile platform. Thus, the robot's base position can be varied in x‐ and y‐direction and rotated around its base ‐axis. Furthermore, the height of the patient couch can be adjusted, and thus the relative displacement between the robot base and the patient in ‐direction.
Out of all possible base poses of the robot, there are only a few for which the base ‐axis is already aligned in the direction of the world ‐axis. Many base poses with high reachability values are orientated obliquely. For this reason, our goal is to calculate a tool transformation to compensate for oblique orientations of the robot's base ‐axis and thus be able to improve the reachability of an upright‐oriented robot for specific target poses. For this purpose, the necessary rotation matrices are calculated to rotate the obliquely oriented robot bases to be upright. This is done by determining the axis and angle between the oblique base ‐axis and the upright world ‐axis :
| (5) |
| (6) |
The robot is rotated by the transformation matrix corresponding to the rotation by axis and angle , which results in the following robot's base pose:
| (7) |
The base of the robot is now aligned upright, but the pose of the end effector has changed to as a consequence of the rotation. The translational shift between the end effector pose before and after the rotation is calculated and expressed as a transformation matrix . Then, this shift is compensated for by relocating the base accordingly:
| (8) |
The corrected base pose ensures that the end effector is positioned as before (Figure 4B). However, there is still a difference in the desired end effector orientation. This difference is compensated for by a corresponding rotation applied to the tool geometry, as shown in Equation (1) and Figure 2B. The required tool rotation is calculated by:
| (9) |
represents the orientation of the end effector after the robot has been rotated by to ensure an upright base alignment and is the desired end effector orientation for the target pose . The number of compensating tool rotations calculated in this manner therefore corresponds to the number of possible different base orientations . The tool rotations are clustered with the corresponding base rotations to be compensated and the mean value is determined. This results in 25 different tool geometries tcp in our example, where is the index of the tool geometry and the target pose. Thus, we can reduce the 5‐dimensional distribution of all potential base poses to 25 different 3‐dimensional distributions of upright base poses with respective tool transformations.
2.3.3. Collision Check
The calculation of the reachability value associated with a pose in the IRM is based on the sum of Yoshikawa's manipulability indices of all possible configurations that can be used to approach this pose (see Equation (2)). The angle of the elbow is varied in discrete steps. The more positions of the robot's elbow are possible, the higher the reachability value. However, this does not take into account the fact that a robot configuration may not be possible due to obstacles, which would reduce the reachability value. For that reason, all robot configurations used to calculate the reachability values belonging to the upright base poses are checked for collisions with the safety zone. To do this, the positions of all robot joints are evaluated to determine whether they are located inside the patient safety zone. If collisions are detected, these joint configurations are not possible, and corresponding reachability values are reduced accordingly. We denote the corrected reachability values for the upright base poses as .
2.3.4. Base Poses Visualisation
The adapted base positions and their associated reachability values are finally assigned to the corresponding closest voxels of a 3‐dimensional grid. For each grid voxel, the reachability values of the closest base positions are averaged. Thus, a grid voxel with its associated reachability value describes the probability of how suitable this position is for placing the upright robot base to reach the TCP target poses. To facilitate comparability, the reachability values associated with base positions are normalised to the highest occurring value of the respective target in scenario 1. For visualisation purposes, the grid voxels are represented as coloured spheres (e.g., see Figure 5). The colours range from blue, through green and yellow to red, with blue representing low reachability and red representing high reachability.
FIGURE 5.
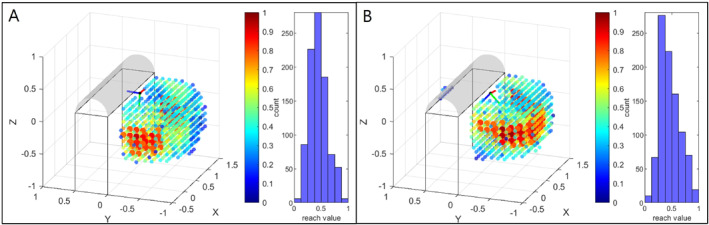
Visualisation of upright base positions for target pose 1 in scenario 1. (A) Shows the base positions without adapted tool geometry ( tcp ). The potential base positions are represented by coloured spheres, with the colour indicating the reachability value. The base positions with a value of more than 0.75 are shown as larger spheres. Moreover, histograms of the respective distributions are shown. The visualised coordinate systems consisting of a red x‐axis, green y‐axis, and blue z‐axis, represent the end effector target poses to be reached. In B, the distribution of base positions for the adapted tool geometry tcp , resulting in the maximum number of base positions with a reachability value > 0.75, is shown. Since an adapted tool geometry was used in B, the resulting flange target pose differs from A, where the reference geometry was applied without any rotation.
3. Results
We aim to automatically determine the selection of an adapted tool geometry and thus increase the number of potential base positions with high reachability of an upright‐orientated robot. Thus, we calculated distributions of upright base positions for respective tool transformations (see Section 2.3.2) for three defined target areas target pose 1, target pose 2 and target pose 3 in two different scenarios. For evaluation purposes, we count the number of base positions with a high reachability value that can be realised by applying a corresponding tool transformation. In our example, we therefore have 25 different distributions of upright base positions per target pose. In the following, we show the best distribution for each target pose and the scenario under consideration. The distributions of the base positions without adapted tool geometry ( tcp ) are used for comparison.
3.1. Scenario 1: No Additional Workspace Restriction
In scenario 1, the robot's base can be located on both sides of the patient as long as the safety box is not violated. The respective distributions with the largest number of base positions having a reachability value greater than 0.75 are shown in Table 1 and compared to the values derived from the base positions without corrected tool geometry ( tcp ). In addition, we visualise the base positions in Figures 5, 6 and 7. The resulting tool geometries are shown in Figure 8.
TABLE 1.
Maximum number of possible base positions with a reachability value > 0.75 for the appropriate tool transformation for scenario 1. In addition, the maximum and mean of the considered reachability values are specified for each target pose. The values for the reference tool geometry tcp are given for comparison.
| No. Of bases | Mean | Max | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Target area |
tcp
|
tcp
|
tcp
|
tcp
|
tcp
|
tcp
|
||||||
| Target pose 1 | 58 | 89 | 0.82 | 0.83 | 0.97 | 0.94 | ||||||
| Target pose 2 | 70 | 90 | 0.82 | 0.82 | 0.95 | 0.96 | ||||||
| Target pose 3 | 86 | 86 | 0.83 | 0.83 | 0.98 | 0.98 | ||||||
FIGURE 6.
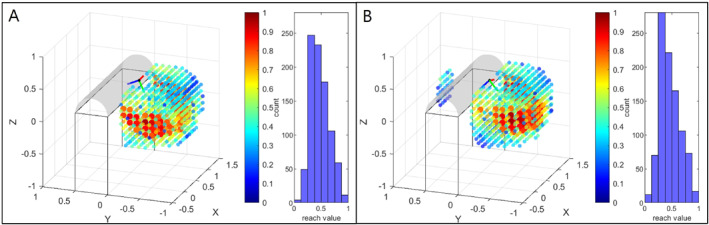
Visualisation of upright base positions for target pose 2 in scenario 1. In A, the base positions without adapted tool geometry ( tcp ) are shown for comparison. In B, the distribution of base positions for the adapted tool geometry tcp , resulting in the maximum number of base positions with a reachability value > 0.75, is shown.
FIGURE 7.
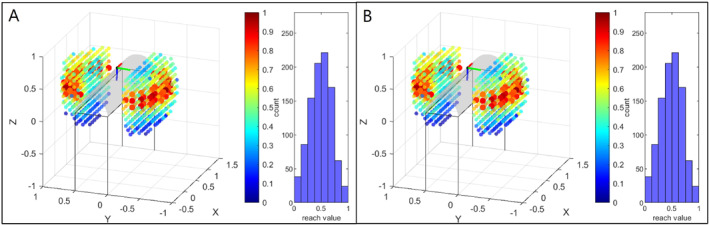
Visualisation of upright base positions for target pose 3 in scenario 1. In A, the distribution of base positions without adapted tool geometry ( tcp ) is presented. It can be seen that this is the same distribution as in B, where the distribution of base positions for the adapted tool geometry tcp , resulting in the maximum number of base positions with a reachability value > 0.75, is shown. Thus, for target pose 3, base positioning cannot be improved by an appropriate tool geometry.
FIGURE 8.
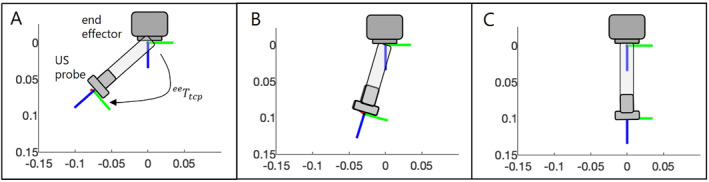
Visualisation of resulting tool geometries tcp in scenario 1. A: For target pose 1 the rotation angle of tcp is with a rotation axis of . B: The respective rotation angle of tcp for target pose 2 is with an axis of . C: For target pose 3, base positioning cannot be improved by an adaption of the reference tool geometry.
For target pose 1 we could increase the number of base positions with a reachability value higher than 0.75 from 58 to 89 by using an adapted tool geometry, which is an increase of about 52%. The respective base positions are visualised in Figure 5 as the larger reddish spheres. In Figure 5B, many more large reddish spheres can be seen, as an adapted tool geometry is used compared to Figure 5A, where the reference tool geometry is taken. This is confirmed by the histogram showing higher bars for high reachability values. Furthermore, it can be seen that reaching the target pose from the other side of the patient can now be achieved by using the adapted tool geometry (Figure 5B).
For target pose 2, 90 base positions of high reachability can be realised with an adapted tool geometry, as shown in Table 1 and Figure 6B. This is an improvement of 29% w.r.t the usage of the standard tool geometry, which only provides 70 positions, as shown in Figure 6A. The increase can also be seen in the histogram bars of high reachability values next to the base distributions, although not as clearly as for target pose 1. Target pose 2 can also only be achieved from the other side of the patient with an adapted tool transformation.
In contrast, for target pose 3 the tool transformation that leads to the largest number of base positions with a reachability value of more than 0.75 is the same as the reference tool geometry, which is why the same distributions can be seen in Figures 7A and 7B. In addition, it can be observed, that target pose 3 can easily be reached from both sides of the patient (see Figure 7).
3.2. Scenario 2: Additional Workspace Restriction
As can be seen from Figures 5A and 6A, target pose 1 and target pose 2 can only be reached from one side unless a customised tool geometry is used. To further investigate that problem, we now consider another scenario, where the preferred side is restricted and thus not available for placing the robot's base. For this scenario, we redetermine respective tool transformations to enable most base positions on the other side of the patient with a reachability value > 0.25 for target pose 1 and target pose 2. The limit value was reduced as almost no base placements with reachability values in the very high range as previously analysed ( > 0.75) are possible for these two target poses. The resulting distribution for target pose 1 is shown in Figure 9B and for target pose 2 in Figure 10B. The number of possible base positions has been greatly reduced compared to scenario 1, as a large part of the possible range has now been restricted, which is shown by the translucent red boxes. Nevertheless, using adapted tool geometries, new base placements are found which helps to reach the target poses from the other side of the patient. This was previously not possible for both target pose 1 and target pose 2 without an adapted tool geometry, which is shown in Figures 9A and 10A, where no coloured spheres can be recognised. By mounting the US probe with a customised probe holder geometry to the robot, four base positions for target pose 1 and 82 base positions for target pose 2 with reachability > 0.25 can be found, also represented by the larger spheres in Figures 9B and 10B. In addition, this is illustrated by Table 2. As expected, the average and maximum reachability values were lower for scenario 2 than in the unrestricted case of scenario 1. The resulting tool geometries are shown in Figure 12. It can be seen that the large angle (almost 90°) with which the probe is attached to the end effector increases the range of the robot. Thus, the target poses can be reached more easily, as the end effector no longer has to be tilted so much over the patient.
FIGURE 9.
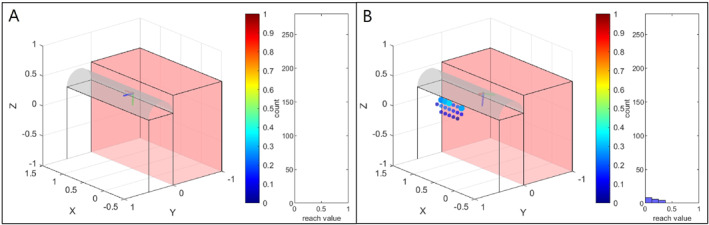
Visualisation of upright base positions for target pose 1 for scenario 2, where the area for potential base placements is strongly restricted, represented by the translucent red boxes. In A, no base positions can be found if no customised tool geometry is applied. The target flange pose cannot be reached from the other patient's side. However, this is possible if an adapted tool geometry is used. This can be seen in B, where the distribution of base positions for the adapted tool geometry, resulting in the maximum number of base positions with a reachability value > 0.25, is shown. The base positions with a value of more than 0.25 are shown as larger spheres.
FIGURE 10.
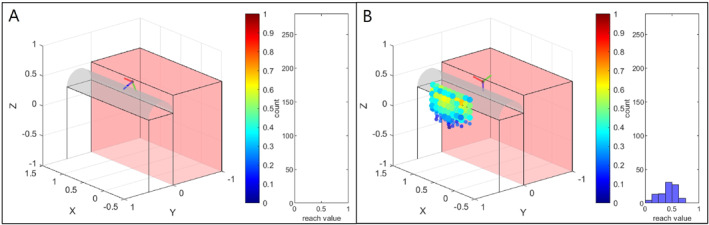
Visualisation of upright base positions for target pose 2 for scenario 2. In A, no base positions can be found if no adapted tool geometry is applied. In B, the distribution of base positions for the adapted tool geometry, resulting in the maximum number of base positions with a reachability value > 0.25, is shown. Due to the customised tool geometry, the target pose can now be reached from the other side of the patient.
TABLE 2.
Maximum number of possible base positions with a reachability value > 0.25 for target pose 1 and target pose 2) as well as > 0.75 for target pose 3 for the appropriate tool transformation for scenario 2. The area for the robot to be placed is additionally restricted. In addition, the maximum and mean of the considered reachability values are specified. The values for the reference tool geometry tcp are given for comparison.
| No. Of bases | Mean | Max | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Target area |
tcp
|
tcp
|
tcp
|
tcp
|
tcp
|
tcp
|
||||||
| Target pose 1 | — | 4 | — | 0.31 | — | 0.34 | ||||||
| Target pose 2 | — | 82 | — | 0.49 | — | 0.72 | ||||||
| Target pose 3 | 42 | 55 | 0.82 | 0.83 | 0.98 | 0.96 | ||||||
FIGURE 12.
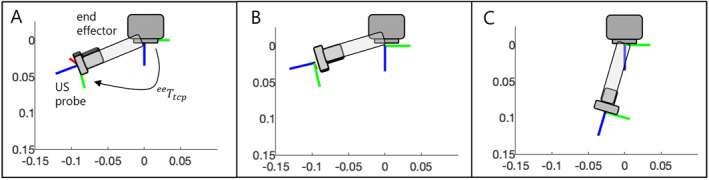
Visualisation of resulting tool geometries tcp in scenario 2 for target pose 1 (A), target pose 2 (B) and target pose 3 (C). For target pose 1 the rotation angle is with an axis of . For target pose 2 the rotation angle is with an axis of and for target pose 3 the rotation angle is with an axis of .
For target pose 3, there is a slight improvement from 42 to 55 potential base positions with a reachability value > 0.75 (see Table 2). Again, this can also be derived from the histograms in Figure 11. As the reachability of target pose 3 was already very good with the reference tool (see Figure 11A), only a slight angulation can be recognised for the geometry of an adapted tool, shown in Figure 12C. In addition, it can be seen from Table 2 that the mean and maximum reachability values remain on a similar level as without the adapted tool geometry.
FIGURE 11.
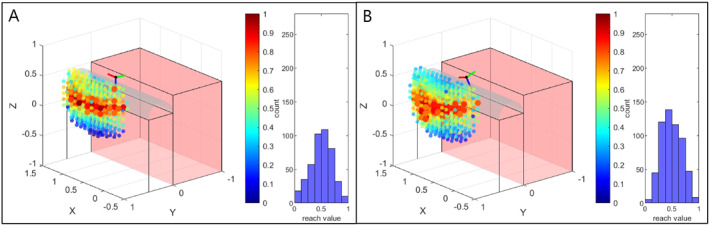
Visualisation of upright base positions for target pose 3 for scenario 2. A shows the base positions when no adapted tool geometry is applied. In B, the distribution of base positions for the adapted tool geometry, resulting in the maximum number of base positions with a reachability value > 0.75, is shown.
4. Discussion
4.1. Evaluation of Study Results
Based on the results shown, we can conclude that an adapted tool geometry can strongly increase the reachability of the US probe and the decrease depends on the target pose. The greatest improvements were achieved for target pose 1. For scenario 1, the number of possible base poses with reachability higher than 0.75 could be increased by around 52%. It must be noted that this percentage of improvement depends on the specific scenario and the reachability threshold chosen for the base position count, and is therefore not generally applicable. An even greater but also more difficult to quantify effect of using an appropriate tool geometry was observed in scenario 2, where it was not permitted to position the robot on one side of the patient. The target areas target pose 1 and target pose 2 could only be achieved by using an appropriate tool transformation. In contrast, no or only minor improvements were achieved with target pose 3. It should be noted that the results presented in Tables 1 and 2 depend on the threshold value used for the base position count. Choosing another threshold would lead to a different percentage of improvement. From this, it can be concluded that the desired inclination angle of the US probe strongly influences the possibility of improvement through a corresponding tool geometry. The more the end effector has to be tilted, the greater the potential to increase the reachability by selecting an adapted tool transformation. The reason for this is that it increases the workspace in which strongly inclined TCP target poses (i.e. pointing towards the robot base) can be reached. This means that poses can be approached for which the robot would otherwise have to be stretched out too far to reach them, as shown for target pose 1 and target pose 2 in scenario 2. In addition, once certain poses can be achieved, the limits of all joints except the fourth can restrict the possible rotation of the elbow, resulting in a lower reachability score. In general, the joint limits of joint 2 and joint 6 are most likely to be reached, as these are at 120°. In particular, if the end effector is pointing downwards and towards the base, as shown in Scenario 2, the sixth joint must be strongly bent to reach the target pose. As a result, the elbow may no longer be fully rotated as the sixth joint's limit is exceeded. If an appropriate tool transformation is used here, the sixth joint position is further away from its limit, and allows for more elbow rotation.
However, in addition to the promising results, it must also be said that the presented approach can only be applied if the orientations of the defined target area differ only slightly. This is due to the fact that different target orientations lead to different rotation matrices (see Equation 9). It follows that the resulting rotation matrices of the tool geometries depend not only on the base rotations to ensure an upright base, but also on . This means that can no longer be clustered according to the uprighting base rotations, which is the prerequisite for compensating for these base rotations by means of corresponding tool transformations. However, this does not affect the application. If the optimum tool geometry has to be calculated for a target area with different orientations, the mean value of the orientations can be calculated first. This orientation then represents the target orientation under consideration.
4.2. Practical Considerations
The results have shown that the optimal design of the tool geometry depends on the target pose and environment. This is a challenge in practice, as it is not possible to dynamically adjust the tool geometry during an intervention. Ideally, you would have a one‐size‐fits‐all solution in practice. For example, we mostly use a probe that is attached to the end effector at an angle of 45°. This geometry represents a compromise: Even though a pure extension provides the greatest possible general flexibility in the end effector orientations that can be achieved, the angulation increases the range of the US probe, and target poses on the patient with a large angle of inclination (e.g., target pose 1, Scenario 2) can be reached more easily. Moreover, the guidance of the cable of the US probe is simplified. However, during various volunteer studies in which robotised US scans were carried out, we found that this one‐size‐fits‐all solution can be unfavourable depending on the area to be reached on the patient and resulted in some volunteers having to be repositioned. An adapted probe holder geometry for US robots that always perform the same procedure (e.g., scan of the leg artery) could therefore be feasible and useful. Alternatively, a mechanism could be considered whereby the angle of attachment can be changed manually depending on the application, for example using a screw that can be tightened and loosened by hand. This would allow the tool geometry to be adjusted before the respective examination.
5. Conclusions
This work investigates how different probe holder geometries influence the placement of an upright robot base concerning reachability of the target poses. A redundant 7‐DoF serial manipulator was used to scan three different target poses on a patient with an US probe. First, reachability maps as well as inverse reachability maps were generated. These were used to determine potential placements for an upright robot base, while a respective tool transformation was applied and constraints such as patient safety and an additional restricted area were taken into account. It could be demonstrated, that the number of potential base placements with high reachability can be greatly increased by using an appropriate tool transformation, especially if the sixth joint of the robot has to function close to the joint's limit to reach the target position. This was particularly the case when the target pose had to be reached from the other side of the patient. Our proposed method offers an automated solution for finding such an adaptation of the tool transformation. It is beneficial if high reachability to the target area is required or the placing area of the robot is limited.
Author Contributions
Jonas Osburg: conceptualization, methodology, data curation, formal analysis, investigation, writing–original draft preparation. Ngoc Thinh Nguyen: methodology, writing–review & editing. Floris Ernst: supervision, funding acquisition, writing–review & editing.
Ethics Statement
This study did not involve any human participants, human data, or human tissue. As such, ethical approval was not required.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding: This project has received funding from the German Research Foundation (DFG) (ER 817/1‐2 and ER 817/4‐1).
Data Availability Statement
The datasets generated and analysed during the current study are available from the corresponding author upon reasonable request.
References
- 1. Ipsen S., Wulff D., Kuhlemann I., Schweikard A., and Ernst F., “Towards Automated Ultrasound Imaging – Robotic Image Acquisition in Liver and Prostate for Long‐Term Motion Monitoring,” Physics in Medicine and Biology 66, no. 9 (2021): 094002, 10.1088/1361-6560/abf277. [DOI] [PubMed] [Google Scholar]
- 2. Haxthausen V. F., Böttger S., Wulff D., Hagenah J., García‐Vázquez V., and Ipsen S., “Medical Robotics for Ultrasound Imaging: Current Systems and Future Trends,” Current Robotics Reports 2, no. 1 (2021): 55–71, 10.1007/s43154-020-00037-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Vahrenkamp N., Asfour T., Metta G., Sandini G., and Dillmann R., “Manipulability Analysis,” in 2012 12th IEEE‐RAS International Conference on Humanoid Robots (Humanoids 2012), 2012), 568–573, 10.1109/HUMANOIDS.2012.6651576. [DOI] [Google Scholar]
- 4. Kuhlemann I., Jauer P., Ernst F., and Schweikard A., “Robots With Seven Degrees of Freedom: Is the Additional DoF Worth it?,” in IEEE 2016 2nd International Conference on Control, Automation and Robotics (ICCAR), 2016), 10.1109/iccar.2016.7486703. [DOI] [Google Scholar]
- 5. Yoshikawa T., “Manipulability of Robotic Mechanisms,” International Journal of Robotics Research 4, no. 2 (1985): 3–9, 10.1177/027836498500400201. [DOI] [Google Scholar]
- 6. Zacharias F., Borst C., and Hirzinger G., “Capturing Robot Workspace Structure: Representing Robot Capabilities,” in 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2007), 10.1109/IROS.2007.4399105. [DOI] [Google Scholar]
- 7. Makhal A. and Goins A. K., “Reuleaux: Robot Base Placement by Reachability Analysis,” in 2018 Second IEEE International Conference on Robotic Computing (IRC), 2018), 10.1109/IRC.2018.00028. [DOI] [Google Scholar]
- 8. Vahrenkamp N., Asfour T., and Dillmann R., “Robot Placement Based on Reachability Inversion,” IEEE International Conference on Robotics and Automation (2013): 1970–1975, 10.1109/ICRA.2013.6630866. [DOI] [Google Scholar]
- 9. Birr T., Pohl C., and Asfour T., “Oriented Surface Reachability Maps for Robot Placement,” in 2022 International Conference on Robotics and Automation (ICRA), 2022), 3357–3363, 10.1109/ICRA46639.2022.9811600. [DOI] [Google Scholar]
- 10. Burget F. and Bennewitz M., “Stance Selection for Humanoid Grasping Tasks by Inverse Reachability Maps,” in 2015 IEEE International Conference on Robotics and Automation (ICRA), 2015), 10.1109/ICRA.2015.7139993. [DOI] [Google Scholar]
- 11. Dong J. and Trinkle J. C., “Orientation‐based Reachability Map for Robot Base Placement,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2015), 10.1109/IROS.2015.7353564. [DOI] [Google Scholar]
- 12. Toussaint M., Ha J. S., and Oguz O. S., “Co‐Optimizing Robot, Environment, and Tool Design via Joint Manipulation Planning,” in 2021 IEEE International Conference on Robotics and Automation (ICRA), 2021), 10.1109/ICRA48506.2021.9561256. [DOI] [Google Scholar]
- 13. Filippeschi A., Griffa P., and Avizzano C. A., “Kinematic Optimization for the Design of a Collaborative Robot End‐Effector for Tele‐Echography,” Robotics 10, no. 1 (2021): 8, 10.3390/robotics10010008. [DOI] [Google Scholar]
- 14. Gerlach S. and Schlaefer A., “Robotic Systems in Radiotherapy and Radiosurgery,” Current Robotics Reports 3, no. 1 (2022): 9–19, 10.1007/s43154-021-00072-3. [DOI] [Google Scholar]
- 15. Schlosser J., Gong R., Bruder R., et al., “Robotic Intrafractional US Guidance for Liver SABR: System Design, Beam Avoidance, and Clinical Imaging,” Medical Physics 43, no. 11 (2016): 5951–5963, 10.1118/1.4964454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Saff E. B. and Kuijlaars A. B. J., “Distributing Many Points on a Sphere,” Mathematical Intelligencer 19, no. 1 (1997): 5–11, 10.1007/BF03024331. [DOI] [Google Scholar]
- 17. Kuhlemann I., Schweikard A., Jauer P., and Ernst F., “Robust Inverse Kinematics by Configuration Control for Redundant Manipulators With Seven DoF,” in 2016 2nd International Conference on Control, Automation and Robotics (ICCAR), 2016), 10.1109/ICCAR.2016.7486697. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated and analysed during the current study are available from the corresponding author upon reasonable request.


