Abstract
Magnetoelectric (ME) devices combining piezoelectric and magnetostrictive materials have emerged as powerful tools to miniaturize and enhance sensing and communication technologies. This paper examines recent developments in bulk acoustic wave (BAW) and surface acoustic wave (SAW) ME devices, which demonstrate unique capabilities in ultra-sensitive magnetic sensing, compact antennas, and quantum applications. Leveraging the mechanical resonance of BAW and SAW modes, ME sensors achieve the femto- to pico-Tesla sensitivity ideal for biomedical applications, while ME antennas, operating at acoustic resonance, allow significant size reduction, with high radiation gain and efficiency, which is suited for bandwidth-restricted applications. In addition, ME non-reciprocal magnetoacoustic devices using hybrid magnetoacoustic waves present novel solutions for RF isolation, which have also shown potential for the efficient control of quantum defects, such as negatively charged nitrogen-vacancy (NV−) centers. Continued advancements in materials and device structures are expected to further enhance ME device performance, positioning them as key components in future bio-sensing, wireless communication, and quantum information technologies.
Keywords: magnetoelectric (ME) devices, bulk acoustic wave (BAW), surface acoustic wave (SAW), magnetic field sensors, antennas, isolators, bio-sensing, wireless communication, quantum technology
1. Introduction
Over the past few decades, magnetoelectric (ME) devices, which are based on a combination of both piezoelectric and magnetostrictive materials, have demonstrated their potential to miniaturize devices while enhancing functionality. In 2001, ME composites made of bi-layer laminates were demonstrated, marking a significant development in the field [1,2]. Since then, numerous ME composite materials and devices have been reported for various applications [3,4].
The efficiency of ME materials primarily depends on the magnetoelectric coefficient (α); a higher α indicates a greater response to stimuli [5]. This coefficient is constrained by the quality of the individual materials and the degree of connectedness between them. For a given composite material, α can be enhanced when measured at the mechanical resonance of the device, where it is amplified by the quality factor. Mechanical resonance is typically achieved by exciting the piezoelectric material, thereby generating a bulk acoustic wave (BAW) within the device. Numerous BAW-based ME devices, such as sensors and antennas, have been extensively investigated.
ME magnetic sensors capable of detecting bio-magnetic fields in the pico-Tesla to femto-Tesla range at room temperature have been demonstrated [6], offering an attractive alternative to other magnetic sensor techniques, such as magnetoencephalography (MEG), magnetocardiography (MCG), magnetomyography (MMG), and magnetoneurography (MNG) [7,8,9]. Their ultra-compact design makes them ideal for having higher spatial resolution. Cantilever-based magnetic field sensors towards biosensing using an inverse ME magnetoelectric effect are well investigated [10,11,12], with recent developments including an exchange bias-based magnetic multi-layer structure demonstrating a limit of detection (LOD) of 18 pT/Hz1/2 at 10 Hz [13]. More compact designs using nano-plate resonators capable of simultaneous magnetic field sensing and energy harvesting have also been demonstrated [14].
ME antennas based on BAW resonators, operating at their mechanical resonance, present a promising alternative to conventional electromagnetic antennas, which operate at electromagnetic resonance [15,16,17]. Operating at acoustic resonance and utilizing magnetic radiation allow these antennas to be significantly miniaturized without ground plane effects [18], making them highly useful for applications with strict size constraints, such as microwave devices and medical implants. Various ME antenna designs are discussed in the literature, each with its own advantages and limitations. Recent advancements include antenna arrays for increased gain [19] and solidly mounted resonators for improved power-handling capacity and stability [20].
Similarly, surface acoustic waves (SAW) can also be excited in piezoelectric substrates or layers, enabling a range of applications. SAW-based sensors employ various working principles, such as mass loading for bio-detection or the delta-E effect [21,22,23,24] for magnetic field detection. In these cases, a SAW generated at one end travels to the other, with an active layer between the delay line on the sensor substrate. The active layer changes the velocity of the traveling wave as a function of a particular stimulus (e.g., magnetic field), and this causes a phase shift in the traveling wave. Given the range of SAW devices, this review focuses on those using ME materials, including applications in magnetic field sensors, antennas, and isolators. SAW-based magnetic field sensors are well-studied in the literature, with an emphasis on detecting pico-Tesla-level magnetic fields [25]. Their high bandwidth makes them ideal candidates for bio-magnetic sensing [22]. An exchange-biased SAW magnetic field sensor with reduced magnetic noise achieves an improved LOD down to 28 pT/Hz1/2 at 10 Hz and 10 pT/Hz1/2 at 100 Hz [25], and novel SAW-based ME antennas have also been reported.
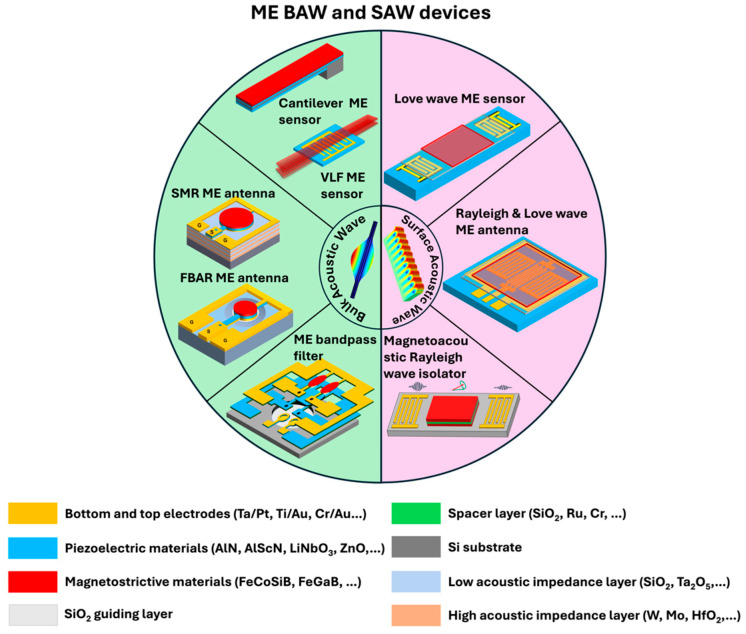
In this work, we start with a foundational overview of BAW and SAW concepts and a brief overview of the typical ME materials and their critical properties. After this, we present recent advancements in BAW and SAW technology in ME applications, including magnetic field sensors, ultra-high and low-frequency antennas, and isolators (Figure 1).
Figure 1.
Magnetoelectric (ME) device possibilities using BAW and SAW concepts. The ME devices include magnetic sensors, antennas, isolators, and filters.
2. Magnetoelectric Materials for BAW and SAW Devices
2.1. BAW and SAW
Bulk acoustic wave (BAW) and surface acoustic wave (SAW) devices have been widely used in sensors, actuators, filters, and oscillators, among others [26,27]. For instance, SAW actuators can repair or quarantine damage in mechanical systems for structural health monitoring [28] and transport material on microscales, and even nanoscales [29]. On the other hand, SAW sensors play a significant role in the chemical detection of explosives and vapors [30,31,32] and the biosensing of cancers, DNA, antigens–antibodies, biotoxins, etc. [33,34,35]. The performance of magnetoelectric devices highly depends on the mechanical quality factor of the acoustic resonators (the ratio of stored energy to energy loss in one resonant period), mechanical loss, and dielectric loss of wave modes. The parameters of the BAW and SAW modes used in ME devices are summarized in Table 1.
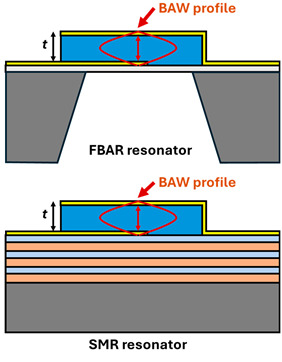
BAW is generated by applying an alternating AC voltage on the top and bottom of a piezoelectric layer. Due to the piezoelectric effect, a standing BAW can be built up in the thickness direction. Depending on the polarization of displacement, the BAW can be categorized into thickness-extensional mode with out-of-plane polarization and thickness-shear mode with in-plane polarization [36]. The resonance frequency is inversely proportional to the resonator thickness, where the wavelength equals twice the thickness. A thinner piezoelectric layer leads to a higher operation frequency. Typical BAW resonators include thin-film bulk acoustic resonators (FBAR) and solidly mounted resonators (SMR). FBAR is suspended in the air to reduce acoustic loss and enhance the mechanical quality factor. The suspension of the resonator can be realized by etching the backside of the Silicon on Insulator (SOI) wafer or etching the Si substrate with XeF2 vapor. Even though FBAR shows an extremely high mechanical quality factor and can be realized by releasing the resonator from a substrate [37], it is fragile and suffers from a low power-handling capability [20]. Compared to FBAR, SMR utilizes an acoustic Bragg reflector composed of several periods of low impedance (e.g., SiO2, Ta2O5) and high impedance layers (W, Mo, etc.) to confine the acoustic energy in the acoustic resonator [38]. SMR shows an advantage of strong power-handling capability [20] but typically has a degraded mechanical quality factor owing to additional acoustic energy leakage and loss brought about by the reflector [39]. In addition, the fabrication of such a resonator is complex, and the control of the surface roughness is crucial to reducing acoustic loss and maintaining the magnetic properties of the magnetostrictive film on top [40].
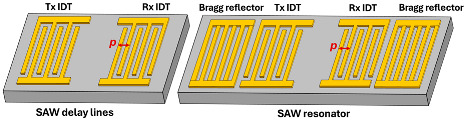
SAW devices are composed of two pairs of identical receiving and transmitting interdigital transducers (IDTs) on a piezoelectric film (e.g., AlN film on Si) or substrate (e.g., bulk single-crystal 128 Y-X cut LiNbO3). By applying a RF voltage on the transmission (Tx) IDTs, a surface acoustic wave can be generated to propagate towards the receiving (Rx) IDTs. The displacement magnitude decreases exponentially inside the piezoelectric materials, and most of the acoustic energy concentrates on the surface. Based on whether acoustic Bragg reflectors are used, SAW devices can be categorized into SAW delay lines and SAW resonators. Reflectors can be made of metal or dielectric stripes, grooves, and ion-implanted stripes [3]. SAW delay lines have a transmission behavior like a sinc function , where N, f0, and T refer to the number of finger pairs, center frequency, and acoustic travel time between the two IDTs, respectively. SAW delay lines have a relatively wide bandwidth but exhibit a high insertion loss due to acoustic energy leakage on the two sides of IDTs [41]. The bandwidth of the SAW delay lines is inversely proportional to the IDT finger numbers. With the depositions of additional Bragg reflectors, a standing wave can be formed inside the cavity of the SAW resonator, leading to a high mechanical quality factor with one sharp transmission peak. Typically, the pitch of Bragg reflectors is designed to be identical to that of the receiving and transmission IDTs [41]. Compared to BAW, the resonance frequency of the SAW devices was determined by the IDT design. The design formula of the resonance frequency, acoustic wavelength, and IDT pitch size (distance between the center of the two fingers) can be found in Table 1. One big challenge of SAW devices above 3 GHz is the increase in acoustic and electrical loses. In addition, the high frequency needs narrow IDTs that cannot be fabricated by industrial photolithography and require the use of laser or e-beam photolithography. The weak power handling of the narrow IDTs make their use challenging for practical applications.
Table 1.
BAW and SAW modes in ME devices.
| SAW/SAW Mode | BAW Thickness Extensional Mode | SAW Rayleigh Wave | SAW Love Wave |
|---|---|---|---|
| Resonator structure and acoustic wave profile |
|
|
|
|
|
||
| Wavelength |
|
|
|
| Resonance frequency | |||
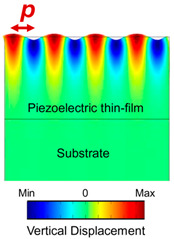
where p: pitch size; λ: wavelength; t: thickness of the BAW resonator, cR: Rayleigh wave velocity; cL: Love wave velocity; Eeq: equivalent Youngs modulus; ρeq: equivalent mass density. Here we assume the metallic ratio equals 0.5, which is used most commonly. The SAW Rayleigh wave profile is produced with permission from Ref. [3]. 2022 AIP Publishing. The SAW Love wave profile is produced with permission from [42].
2.2. Magnetoelectric Composites and Materials
2.2.1. ME Composites
Magnetoelectric (ME) materials are a special class of materials that can possess more than one ferroic property. Such materials can simultaneously exhibit ferroelectric and ferromagnetic properties. The direct ME effect corresponds to a change in electrical polarization in the material when it is subjected to a change in magnetic field, while the converse effects correspond to a change in magnetization upon changing the electrical field. The ferroelectric property of the materials is due to the relative shifts between the negative and positive charges in the materials, which usually require empty d orbitals. On the other hand, the ferromagnetic effect originates from the spins of the partially occupied d orbitals in the material. Due to these contradicting requirements, there are very limited naturally occurring single-phase magnetoelectric materials. Though such materials were postulated in 1894 [43], the first experimentally reported single-phase ME material was Cr2O3 in 1960 [44]. Other single-phase bulk ME materials include BiFeO3 [45,46,47], Aurivillius phases [48,49,50], Hexaferrite (Sr3Co2Fe24O41) [51], and layered perovskites (YBa1-xSrxCuFeO5) [52]. Though few of these materials demonstrate the room temperature bulk ME effect, only BiFeO3 is considered for actual applications [45,46,47].
Alternatively, multiferroic ME materials have a combination of inorganic ferroelectric (piezoelectric) and ferromagnetic (magnetostrictive) materials. This approach has an added advantage in that one could optimize/tailor the individual layer for the applications. Thus, it gives a higher degree of freedom for material selection. Direct piezoelectric materials produce an electrical charge when subjected to mechanical stress. The magnetostrictive materials produce a strain in the material when subjected to a magnetic field. When both these materials are coupled, then such a composite could exhibit a composite ME effect. In such materials, the ME coefficient depends on the following parameters.
In the above equation, is the ME coefficient, which gives the change in polarization due to the change in the magnetic field; is the piezoelectric coefficient, which maps the change in polarization (P) due to the strain (S) in the material. is the piezomagnetic coefficient, and it gives the change in strain (S) in the materials for a change in the magnetic field (H). is the coupling coefficient, which varies from zero to one and depends on the elastic connectivity between both materials.
In the case of bulk materials, the race to get composites with a high was initiated by combining particulate mixtures of piezoelectric materials (PbZrTiO3, BaTiO3, and PbTiO3, among others) and combining with ferrites (NiFe2O4 and CoFe2O4, among others). Such composites exhibit in the range of 1–500 mV/cm Oe [53,54,55,56,57]. The effect can be enhanced when it is measured at the mechanical resonance. This showed an increase in to 6–7 V/cm Oe [58,59,60,61]. Another well-explored bulk composites configuration is the 2-2 laminates, where laminates comprising ferromagnetic materials with giant magnetostriction, such as Terfenol-D [62,63] or amorphous Metglas [64,65], were used in combination with PZT. In such composites, a high ~5–6 V/cm Oe is demonstrated without exciting the composites at their resonance.
With the onset of advances in microsystem technology in the early 2000s, the field of ME composites not only invented novel composites with a high but also numerous real-world devices, such as magnetic field sensors, antennas [15], energy harvesters, isolators, and so on. The most well-researched connectivity explored is the 1-3 nanocomposites, where the 1D nanomagnetic pillars are embedded in a piezoelectric matrix, and 2-2 bilayer composites, where both are 2D films on a substrate. The former 1-3 connectivity is supposed to have a higher due to its increased surface area between the ferroelectric and magnetic phases [66,67]. However, leakage currents in the magnetic pillars limit their to between 20 and 80 mV/cm Oe [68,69,70]. On the other hand, the 2-2 laminar composites, initially thought to suffer from substrate clamping, have shown promising results, e.g., AlN/FeCoBSi [71] and BaTiO3/CoFe/BaTiO3 [72] have shown = 3–5 V/cm Oe due to perfect coupling. A further enhancement of in AlN/FeCoBSi composites to 9.7 kV/cm Oe at resonance in air and 19 kV/cm Oe at resonance under vacuum was demonstrated [73]. The 2-2 laminar configuration is most used in the BAW resonators.
2.2.2. Piezoelectric Materials
The piezoelectric materials were first discovered by Pierre and Jacques Curie in 1880 when they saw that certain crystals created an electrical charge when they were subjected to mechanical compression. Only a year later, in 1881, Gabriel Lippmann predicted the inverse piezoelectric effect based on the fundamental thermodynamic principle, which was experimentally demonstrated later by the Curie brothers. The piezo effect occurs in materials that do not have a center of symmetry. In such materials, without any external stress, the pseudo-positive and the pseudo-negative centers inside the materials coincide. However, upon deforming the material, the pseudo-positive and -negative centers are separated from each other, thus, resulting in creating a dipole movement in the crystal due to the application of mechanical stress. The fundamental equations that govern the direct and indirect piezo effect are as follows.
where is the electric field, is the dielectric displacement, is the stress, and is the strain field tensors. The is the dielectric permittivity, which is a (3 × 3) matrix, while the is the compliance matrix (6 × 6) (which is the inverse of the stiffness matrix). is the piezoelectric coefficient, and it is a (3 × 6) matrix. If , the equations for the direct effect transform into an equation describing electrical materials, while the indirect piezo effect transforms into Hooke’s law, which relates mechanical stress with strain. The piezoelectric matrix is further expanded as:
The most important parameters in the matrix are the and elements. The is the parameter of interest when the piezoelectric material is operated longitudinally while the are important during transverse operations.
With respect to the BAW and SAW devices, piezoelectric materials, whether single crystals or polycrystals, play a crucial role in acoustic wave excitation. In such devices, the piezoelectric materials are supplied with a RF voltage, which can excite an acoustic wave in the material. Shown in Table 2 is the list of commonly used piezoelectric materials for BAW and SAW devices. Though materials like PZT, PMN-PT, and PZN-PT possess high they have high losses and are not CMOS compatible. Alternatively, materials like quartz, LiNbO3, and LiTaO3 are well-used for realizing SAW/BAW devices, owing to their low losses and CMOS compatibility.
Table 2.
(a) Summarizing the important piezoelectric materials and their material properties used in SAW and BAW devices. (b) summarizing low-loss piezoelectric substrates for SAW and BAW devices.
| (a) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Material | Piezoelectric Coeff. (pC/N) | Relative Permittivity | Density (Kg/mm3) |
Elastic Modulus (GPa) |
|
Electromechanical Coupling Efficiency ) | Comments and Main Applications | ||
| PZT | −243 [74] | = 574 [74] | 2440 [74] | 2870 [74] | 7500 [3] | = 23.5 [3] | 1.6 [74] | 20–35% [74] | Highly used bulk and thin films (nano-rods) as sensors, actuators, energy harvesters, and antennas. |
| AlN | −2 [3] | =3.5–4.96 [3] | 9.2 [3] | 10.1 [3] | 3300 [3] |
= 130, = 99 [3] |
0.025 ± 0.011 [75] | Thin-film bulk acoustic resonator (FBAR): 7% [76]; contour mode resonator (CMR): 2% [77]; contour mode Lamb wave resonator (CMLR) resonator: 5.33%~7.1% [78,79,80] |
CMOS compatible, lead-free with very low loss. |
| Al1-xScxN | [81] | [81] | - | [82] | 3530 (x = 0.14), 3560 (x = 0.26) [81,83], [82] | [84] | 0.025~0.1 [85] | Lamb wave resonator: 7.83~10.28% [86,87]; contour mode resonator (CMR): 3.2%~5% [88]; Sezawa SAW mode: 3.8%∼ 4.5% [89]; Rayleigh SAW: 2%~2.2% [90]; Thin-film bulk acoustic resonator (FBAR): 5% ~14% [91] |
CMOS-compatible, lead-free, promising ferroelectric material [92,93,94,95,96]. |
| (PMN)0.7-(PT)0.3 | = −1395 | 4963 | 1386 | 7800~7820 [97]. | = 28 | <1 | 62% | Typically used in piezoelectric transducers, sonar systems, and energy harvesters. Material properties from [98]. | |
| (PZN)0.92–(PT)0.08 | = −1250 | = 2500 | 2900 | 7700 | 8315 | = 65 | 1–1.2 | 50% | Highest allows their use in ultrasonic devices in medical industry, actuators, and energy harvesters, among others. Material properties from [98] |
| ZnO | = −5 [99] | = 12.4 [99] | 9.2 [3] | 12.6 [3] | 5665~5680 [100,101] | = 44 [102] | 0.025~0.05 for RF sputtered thin films [103,104,105]. ALD film: 0.0001~0.002 [106] |
ZnO/SiC SAW resonator: 1.5%~3% [107]; FBAR ZnO resonator: 0.5%~3.4% [101]; Lamb wave resonator: 12.4%~14% [108,109] |
Lead free, bio-compatible, and non-toxic [110] |
| (b) | |||||||||
| Material | Piezoelectric Coeff. (pC/N) | Relative Permittivity |
Density
(Kg/m3) |
Elasticity
(GPa) |
|
Orientation | Electromechanical Coupling Efficiency ( ) | Comments | |
| = | |||||||||
| LiNbO3 | [3] | 84 [3] | 30 [3] | 4650 [26] |
= 74.8, [3] |
0.002–0.004 [111] | 41° Y cut-X propagating | Shear-horizontal SAW: 33.54% [112] | High electromechanical coupling, low dielectric and acoustic loss, used for SAW sensors, resonators, and filters [113] |
| X-cut Y propagating | coupled shear mode surface acoustic wave (CS-SAW) on LiNbO3/SiC: 34% [114] |
||||||||
| 128° Y cut-X propagating | Rayleigh SAW: 5.5% [113]; first-order antisymmetric (A1) Lamb mode: 46.4% [115] |
||||||||
| LiTaO3 | [3] | 51 [3] | 45 [3] | 7465 [26] |
= 93, [3] |
0.06 [116] | Z cut | Longitudinal BAW: 2.7% [117] | Used as a substrate material for BAW and SAW devices [118]; Used for shear horizontal wave based magnetoacoustic non-reciprocal RF devices |
| X cut, 112.2°–Y propagating | FBAR: 17.4% [117]; Fast shear BAW: 21.6% [117] | ||||||||
| 36 ° Y Cut–X propagating | Longitudinal BAW: 9.9% [117]; Leaky-SAW (L-SAW): 5.7% [119] |
||||||||
| 42° Y Cut X–propagating | Longitudinal BAW:9.0% [117]; shear-horizontal SAW (SH-SAW) on LiTaO3/SiC: 5.58% [120] | ||||||||
| Quartz |
= 2.31, = 0.727 [118] |
4.52 [118] | 4.68 [118] | 2560 [26] |
= 40.35, [121] |
0.01 [122,123] | ST-cut (42°75′ Y-cut, X-propagating) | Calculated for temperature sensor 0.14% [124] | Low acoustic loss, and high resonant frequency stability over a broad range of temperatures and pressures, used for BAW oscillators (typically AT-cut quartz with thickness shear mode) for frequency control in communication systems and clocks and SAW filters (ST-cut) [118] |
| AT-quartz (35°15′ Z-cut, X-propagating) | Bulk acoustic wave devices 8.8% [125] | ||||||||
2.2.3. Magnetostrictive Materials
The discovery of magnetostriction predates the piezoelectric effect. It was discovered by James Prescott Joule in 1842 [126], when he observed a change in the dimension of iron when he altering its magnetization. The opposite effect, the Villari effect, was discovered in 1864 and showed a change in magnetization when there is stress applied to the material [127]. The magnitude of the dimensional change is represented by lambda (), which is the ratio of change in length to the original length. is a dimensionless number and is typically reported in ppm. The origin of the effect is in the interaction of atomic magnetic moments with the elastic bond lengths of the crystal.
Above the Curie temperature, all the magnetic moments in a ferromagnetic material do not have any magnetic order, and the net magnetization is equal to zero. Upon cooling, spontaneous magnetization occurs in the material, and all of the magnetic moments align along the easy axis of the material (due to anisotropy). The sample either shrinks or expands depending on the sign of the magnetostriction constant, as the magnetic moments rotate towards or away from the external magnetic field direction. Now, if an external magnetic field is applied, such that the magnetic domains rotate 90 degrees, then one can get maximum magnetostriction. However, if the magnetic field is applied, such that the magnetic moments rotate by 180 degrees, then there is no effective change in the shape of the sample [128]. The change of magnetostriction as a function of the magnetic field, , is of interest and is termed the piezomagnetic coefficient. increases/decreases as a function of the external field and saturates when all of the magnetic moments point in the direction of the external magnetic field. This is termed saturation magnetostriction, . The equations that govern the magnetostriction are given by:
where is the magnetic induction, is the magnetic field, and is the stress field tensors. is the permeability at constant stress. is the compliance, and is the piezomagnetic coefficient of the material. In the above equations, if there is no magnetostriction (), the equations transform to describe classic magnetic materials and stress with strain (Hooke’s law) relation.
Rare earth-based bulk materials exhibit the highest magnetostriction. This is mainly due to the partially filled 4f orbitals, which have strong anisotropy [129]. Giant magnetostrictions of around 6000 ppm in Dysprosium [130] and 3000 ppm in Terbium [131] were reported in the 1960s, but the Curie temperature of these materials is well below room temperature (RT).
The highest RT magnetostriction achieved by far in either bulk or thin films is Terfenol-D (Tb0.27Dy0.73Fe2). It can demonstrate a of around 1840 ppm. It is obtained by combining two different Laves phase materials, TbFe2 and DyFe2, with opposite anisotropies, which have near-zero magnetic anisotropy [132,133]. Other materials that exhibit high magnetostriction are Galfenol (Fe81Ga19) [134] and FeSiBMn (Metglas) [135].
In thin films, giant magnetostriction was first reported by Quandt et al. in TbFe/FeCo multilayers with a saturation field of 20 mT [136,137]. Materials with such low saturation fields have high industrial relevance. In recent years, increasing studies has focused on actual devices, such as magnetic sensors, RF filters, and antennas, where materials with high piezomagnetic coefficients are particularly important. Thin film magnetostrictive materials have a high piezomagnetic coefficient, mainly originating from the absence of magnetocrystalline anisotropy. A few examples are FeGaB, FeCoBSi, CoFeC, and FeGaC. Table 3 below summarizes the bulk and thin film magnetostrictive materials and their parameters.
Table 3.
List of magnetostrictive materials in the literature. Also given are the saturation magnetostriction and the piezomagnetic coefficient.
| (ppm) | /d33, m (ppm/Oe) | Crystallography | Fabrication Method | Thermal Stability (°C) * | Comments/Ref. | |
|---|---|---|---|---|---|---|
| Terfenol-D Tb0.27Dy0.73Fe2 |
1840 | 2.4 | Single crystal, bulk | Casting | 650 | highest [133,138,139] |
| Galfenol (Fe81Ga19) | 395 | 3 | Single crystal, bulk | Casting | 700 | [134,140] |
| FeSiBMn (2605SA1 Metglas, Inc) | 27 | - | Amorphous, ribbons | Melt spinning | 395 | Low loss, high permeability [135,141] |
| (Fe90Co10)78Si12B10 | 30 | 6.3 | Amorphous, thin film | Magnetron sputtering | - | Amorphous thin film [10] |
| (Co50Fe50)95.2C4.8 | 60 | 10.3 | Amorphous, thin film | Magnetron sputtering | 500 | [142] |
| (Fe81Ga19)88B12 | 75 | 7 | Amorphous, thin film, as deposited |
Magnetron sputtering | - | [143,144] |
| (Fe81Ga19)88B12 | 75 | 12 | Amorphous, thin film, annealed @280°C for 120 min | Magnetron sputtering | - | Highest piezomagnetic coefficient [140] |
| (Fe80Ga20)89C11 | 81.2 | 9.71 | Amorphous, thin film | Magnetron sputtering | - | [145] |
* Thermal stability can either be Curie temperature or in the case of amorphous materials, the temperature the material forms nano-crystalline order, thus reducing its magnetostriction.
3. Magnetoelectric Sensors
Magnetic sensors are critical components in a wide range of technological applications due to their ability to detect and measure weak magnetic field signals with high sensitivity for high-precision measurements. They are crucial in industrial automation, navigation systems, medical diagnostics, and scientific research. For instance, in biomedical applications, magnetic sensors enable non-invasive, contactless, flexible, and fast detection of weak bio-magnetic signals from human organs and tissues, such as nerves, muscles, brains, and hearts, making them vital in health monitoring and medical diagnosis. Existing bio-magnetic sensing and diagnosis techniques, including magnetic resonance imaging (MRI) [146], magnetoencephalography (MEG), magnetocardiography (MCG) [7,147], magnetomyography (MMG), and magnetoneurography (MNG) [8,9], have provided real-time insight into physiological functions like neural and cardiac activities for invaluable data in both research and clinical environments. In industrial applications, magnetic sensors are employed for current sensing, position tracking, and detecting flaws in materials. They are essential for precision control and feedback systems in robotics and automated machinery, offering robustness in harsh environments like high temperatures and humidity [148]. Magnetic sensors are used for contactless current, angular position, and switch sensing in green energy power plants such as wind turbines and solar panel farms for optimal wind power generation. Their applications continue to expand as they become more integrated with emerging technologies like IoT and Industry 4.0 [149,150], further underscoring their importance.
Over the decades, various magnetic sensors have been intensively investigated and developed, aiming to improve sensitivity and reduce size, especially for bio-magnetic applications requiring stable fT-level magnetic sensing over a broad frequency range from 0.01 Hz to 1000 Hz [151,152,153,154]. Superconducting quantum interference devices (SQUID) are state-of-the-art magnetometers with a fT range magnetic signal sensing capability [155], which makes them capable of monitoring brain, nerve, skeletal muscle, and heart activities. However, the requirement for a cryogenic environment provided by liquid helium makes the operation of SQUID expensive, bulky, and energy intensive. Alternative systems, such as optically pumped magnetometers, also have similar issues of high complexity and cost owing to the need for a laser and a gas chamber, despite a superior equivalent magnetic noise level of below 100 fT/√Hz [156,157,158,159,160,161,162]. The miniaturization of magnetic sensors has been realized by advanced micro–nano fabrication techniques, leading to the demonstration of giant magnetoimpedance (GMI) sensors [163,164,165,166,167,168], giant magnetoresistance (GMR) [169,170,171] and tunnel magnetoresistance (TMR) sensors [172,173], etc. However, the notable thermal, flicker-, and spin–torque noise originating from high driving current limit the sensing performance of these compact magnetic sensors to the pT/Hz1/2 level [174,175,176,177]. The need for miniaturization, low noise, low power, and extremely high sensitivity has driven the development of the bulk acoustic wave (BAW) magnetoelectric (ME) sensors [11,147,178,179,180,181,182,183,184,185,186,187,188], which utilize high quality factor (Q) magnetoelectric coupling in a ME composite and realize strain-mediated power-efficient conversion from weak magnetic signals to voltage outputs. On the other hand, the surface acoustic wave (SAW) sensor can detect ultra-sensitive magnetic signals owing to the significant transmission change between SAW transducers in response to the modulus change of magnetostrictive film [22,23,24,25]. The state-of-the-art magnetoelectric magnetometers can enable the detection of single-digit fT magnetic fields at kHz at room temperature, greatly lowering the cost, power consumption, and form factor for biomedical magnetometry systems [4,189]. The following subsections will review the recent progress of BAW and SAW ME sensor fabrication, material synthesis, modulation scheme, and detection and noise performance improvement.
3.1. BAW ME Sensor
3.1.1. Bulk ME Sensors
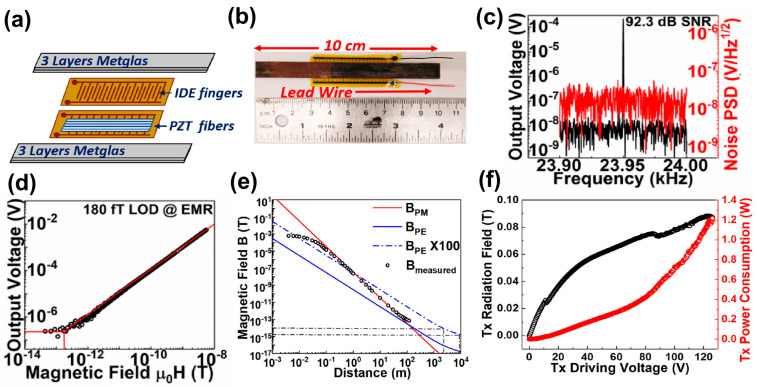
The BAW ME sensors utilize the direct ME effect to detect the voltage output in the piezoelectric layer induced by the strain of the magnetostrictive layer under an external magnetic field signal [4,190,191]. Depending on the sizes of the piezoelectric phase and the magnetostrictive phase, they can be categorized into bulk and thin-film BAW ME sensors. The bulk ME sensors are typically composed of ME laminates with one single-crystal piezoelectric substrate, such as PZT and PMN-PT, sandwiched by an epoxy-glued magnetic foil like Metglas [192]. Depending on the orientation of magnetization in the magnetostrictive layer and polarization in the piezoelectric layer, the bulk ME sensors can operate on different combined modes, including L-L, L-T, T-T, and T-L, where T refers to transverse and L stands for longitudinal. Since the thickness of the magnetostrictive is typically much smaller than the lateral dimension, the strong demagnetizing field forces the magnetostrictive to have in-plane magnetization. Therefore, most bulk ME sensors work on L-L or L-T modes so that they can exhibit a high ME coupling coefficient αME for high magnetic field sensitivity. Since αME can realize a 100 times improvement at electromechanical resonance (EMR) [193], the direct detection scheme of the ME voltage at EMR has been developed, with intensive efforts in boosting αME via geometry optimization [194,195,196,197,198], novel material development [199,200], and sensor fabrication improvement [201,202,203]. To reduce the hysteresis loss and enhance the mechanical quality factor of the ME resonator, Chu et al. utilized laser treatment on Metglas layers and epoxy-glued them to PMN-PZT fiber to form a ME sensor. The fiber can concentrate magnetic flux in the magnetic layer, leading to a high αME of 7000 V/cm Oe. By doping Mn into PMN-PZT, αME can be further boosted to 12,500 V/cm Oe owing to a more stabilized ferroelectric domain and pinned domain wall motion. However, the highest ME coefficient of bulk ME sensors is typically realized at tens of kHz or even higher. This frequency range is beyond the typical magnetic signal frequency from 0.01 Hz to 1 kHz.
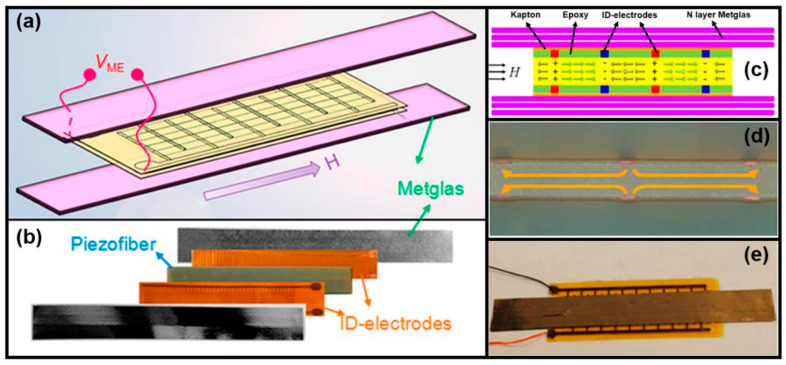
The highest off-resonant αME of 52 V/cm Oe was realized in PMN-PT single-crystal fiber laminated with six layers of magnetostrictive Metglas at 1 kHz in multiple L-L mode [192], as shown in Figure 2a,b. The multiple L-L acoustic mode leads to an alternative expansion and compression of the lattice in the piezoelectric layer, as shown in Figure 2c. The multi-push–pull modality in the ME composite was configured by a pair of Kapton interdigital (ID) electrodes, where the alternating electric field streamline is shown in Figure 2d. The final Metglas/ID electrodes/PMN-PT ME sensor is shown in Figure 2e. An extremely low equivalent magnetic noise of 5.1 pT/Hz1/2 @ 1 Hz was realized [64]. A similar performance of 8.2 pT/Hz1/2 @ 1 Hz was also realized in a 4 × 4 Metglas/Pb (Zr, Ti) O3 magnetoelectric (ME) sensor array unit in an open environment [188]. By magnetic frequency conversion (MFC), low limit of detections of 20 pT @1 Hz, 150 pT @ 0.1 Hz, and 200 pT @ 0.01 Hz were demonstrated owing to up-conversion of the frequency band near EMR for high sensitivity and rejection of low-frequency noise [204]. The details of this active detection scheme are elaborated upon in Section 3.1.2.
Figure 2.
(a) Schematic diagram of the Metglas/piezo fiber ME sensor configuration, featuring ID electrodes on the PMN-PT fiber core composite and symmetric three-layer Metglas actuators. (b) Exploded view of individual components. (c) Illustration of multiple alternating push–pull units for enhanced ME coupling. (d) Optical microscopy image of a longitudinally poled push–pull element within the core composite. (e) Photographs of the fully assembled Metglas/piezo fiber ME sensor. Reproduced with permission from Refs. [17,64]. Copyright 2021 IEEE; Copyright 2011 John Wiley and Sons.
Despite the success of the direct detection scheme in the realization of pT-level magnetic field sensing, a DC bias field typically needs to be applied by permanent magnets or solenoids on the ends of bulk ME sensors to realize maximum ME coupling and best sensitivity. The use of magnets makes the device bulky and adds additional magnetic noise sources and electromagnetic interference [17]. The mutual interference between each ME sensor also makes the integration of the sensor array challenging [205]. To realize non-zero ME coupling at a zero-bias field, self-biased ME composites (SMECs) have been developed in the last two decades. The self-biased ME effect was first discovered in co-fired LSMO-PZT laminates in 2002 [206], followed by another discovery in Fe–PZT–Fe in 2005 [207]. Existing self-biased ME composites can be classified as functionally graded FM-based SMECs [207,208,209,210,211], exchange bias-mediated SMECs [200,212], magnetostriction hysteresis-based SMECs [208,213,214], built-in stress-mediated SMECs [2,206,215,216], and non-linear SMECs [217,218,219]. The detailed development of SMECs can be found in [179].
3.1.2. Thin-Film ME Sensor
Compared to bulk ME sensors suffering from piezoelectric leakage and non-ideal glued mediated mechanical coupling, thin-film ME sensors realize atomic interfacial bonding between a magnetostrictive layer and a piezoelectric layer. The thin-film ME sensors show an ultra-compact size from mm to μm and show great potential for high spatial resolution magnetic sensing. The EMR of the compact thin-film ME sensors is in the kHz or MHz frequency range, which is far beyond the frequency band (0.01 Hz~1 kHz) of the magnetic signal to be detected. The ultra-low sensitivity at off-resonance mode and high 1/f noise levels make the direct passive detection scheme impractical. Indirect detection schemes have been developed for the operation of thin-film ME sensors, including magnetic frequency conversion (MFC), electrical frequency conversion (EFC), and the delta-E effect [190].
Magnetic frequency conversion relies on the quadratic magnetostriction effect versus a bias field and converts the low-frequency magnetic signal to the sidebands near EMR to ensure high magnetic sensitivity for practical magnetic sensing [217,218]. When a driving modulation AC field at a high-frequency fmod near EMR is applied to the ME sensors together with the magnetic signal at fsig, the output of the ME sensors includes the product of the two signals due to quadratic magnetostriction. The sensor output frequency spectrum contains fmod − fsig, fmod, and fmod + fsig, where the low-frequency noise is highly suppressed. However, the modulation magnetic field is typically generated by a modulation coil, which introduces additional high-frequency noise and high power consumption for driving it. The coil also limits the size miniaturization of the ME sensor system. To overcome these challenges, electrical frequency conversion has been developed, which exerts modulated voltage on the piezoelectric layer. The modulated voltage leads to periodic stress on the magnetostrictive layer and induces additional uniaxial magnetic anisotropy, affecting magnetization dynamics. Although a modulation coil is not required, the output electronics must have a large dynamic range to stay outside the saturation region and provide a strong modulation voltage for detecting very weak magnetic signals [11,17]. This can restrict the sensor’s ability to detect both very small and very large magnetic field variations. Electrical frequency conversion introduces noise from electronic components, like mixers, oscillators, and amplifiers [220]. These components, especially in low-power systems, are prone to phase noise and thermal noise, which degrade the sensor’s signal-to-noise ratio (SNR). As a result, the converted signal is often less pure and contaminated, making it harder to detect weak magnetic fields. The equivalent magnetic noise performance of the EFC-based ME sensor is limited to several nT/Hz1/2 [11].
For both MFC and EFC, the frequency up-conversion boosts the noise level while amplifying the magnetic signal. The optimal driving field or voltage is obtained by the balance between increasing the signal strength and maintaining a manageable noise level. The frequency up-conversion method often requires more complex circuitry and additional power to maintain the modulation and detection processes. This can limit its practical applications in low-power, portable devices or in scenarios where simplicity and energy efficiency are critical. While the resonance frequency is selected to enhance the detection capabilities, it also limits the sensor’s performance in a broad frequency range. Tuning to a specific frequency can make the sensor less effective for detecting magnetic fields that fall outside of this range. The output signal distortion and the introduction of additional spurious signals due to non-linear mixing are also problems that need to be addressed.
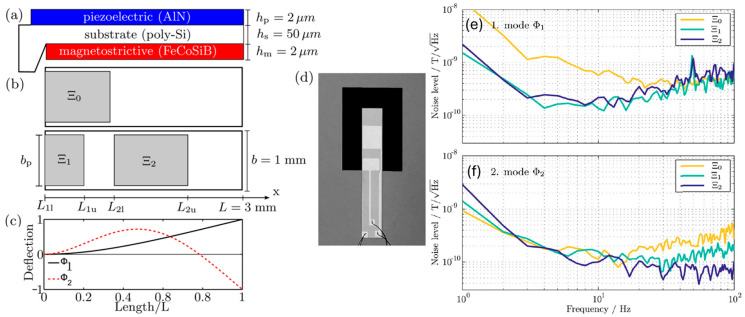
The delta-E effect is an alternative method that utilizes a resonance frequency shift in the ME resonator owing to the Young’s modulus change of the magnetostrictive material under a magnetic field excitation. This method can effectively enhance sensitivity, since the resonance frequency shift is more sensitive to external magnetic field signal change [221]. The dynamic range of ME sensors can also be enhanced because the sensors can operate on multiple mechanical resonance modes [221]. For instance, by applying different adapted electrode designs on a FeCoSiB (2 μm)/poly-Si (50 μm)/AlN cantilever beam (2 μm), the first and second transversal bending modes could be excited [221]. The sensitivity was boosted by a factor of six, and the dynamic range of the sensor output was reduced by 16 dB, which significantly eases the bandwidth requirements of readout electronics. The wide bandwidth of 100 Hz and an equivalent magnetic noise of 100 pT/Hz1/2 make the delta-E effect sensors promising for low-frequency magnetic field sensing [221].
Depending on the structure, size, and excitation configurations of the ME sensors, different bulk acoustic wave modes can be established for magnetic sensing under certain indirect detection schemes. Based on the structure of the ME sensors, they can be divided into cantilever-based ME sensors, nanoplate resonator (NPR) ME sensors, nanoplate resonator (NPR) array ME sensors, etc. The excited bulk acoustic wave modes and sensor performances were discussed.
Cantilever-Based ME Sensor
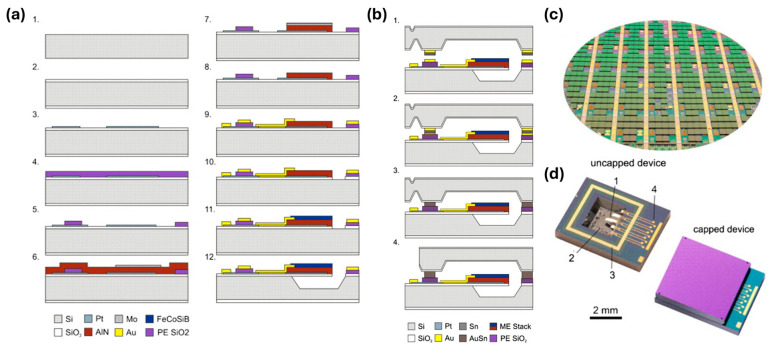
The cantilever-based ME sensors are typically composed of a surface-micromachined magnetostrictive layer and a piezoelectric layer on both sides of a poly-Si or thermal oxide Si substrate. The fabrication of cantilever-based magnetoelectric (ME) sensors involves a multi-step process that integrates both piezoelectric and magnetostrictive layers on the substrates to produce highly sensitive, miniaturized sensors [222], as shown in Figure 3a. The process typically initiates with the deposition of Ti/Pt layers to form the bottom electrode, followed by PECVD deposition of SiO2 for electrical isolation. Subsequently, piezoelectric layers, such as AlN, are deposited and structured using Mo hard masks and selective etching techniques. Following this, a Cr/Au layer is added to create conduction lines and electrical bond pads. For the magnetostrictive layer, materials like (Fe90Co10)78Si12B10 are deposited with Ta seed and capping layers, ensuring both adhesion and enhanced magnetic response. Finally, a selective silicon etching using XeF2 and TMAH releases the cantilever, resulting in a high-aspect-ratio structure that responds to magnetic fields with a measurable piezoelectric output.
Figure 3.
(a) Process flow of cantilever-based ME sensors. (b) Bonding process flow of capped wafer to effectively improve the mechanical quality factor and reduce the equivalent magnetic noise. (c) Photographs of ME sensor die on wafer (d) cantilever-based ME sensor with (1) ME cantilever, (2) etch groove, (3) bond frame, and (4) bond pads. Reprinted with permission from Ref. [222]. Copyright Elsevier 2013.
The first thin-film cantilever beam AlN/Si/FeCoSiB ME sensor was fabricated by Jahn et al. in 2011 [223], where a 20 mm × 3 mm silicon cantilever was covered with a 0.3 μm-thick molybdenum bottom electrode and a 1.8 μm-thick piezoelectric AlN on top. A 1.75 μm-thick magnetostrictive FeCoSiB top electrode with an area of 1.6 × 10−5 m2 acted as a third layer. A 7 mm broad trench was etched to reduce the mechanical resonance frequency to 330 Hz. The cantilever sensor was clamped onto an epoxy block. The maximum ME coefficient of 1200 V/cm Oe was realized at a 6 Oe bias field. The noise of the ME sensor system mainly comes from the intrinsic thermal noise of the ME sensor and the extrinsic noise of voltage and charge amplifiers. An equivalent magnetic noise of 5.4 pT/Hz1/2 was obtained at 330 Hz. Compared to the calculated noise spectrum, additional noise was found to come from magnetic coupling to ambient noise sources, such as transformers, switching power supplies, electric motors, and external mechanical vibrations at its bending resonance. A similar surface micromachined cantilever beam with a stack composed of SiO2/Ti/Pt/AlN/Cr/FeCoSiB was fabricated on a 150 mm Si (1 0 0) wafer [224], realizing a giant ME coefficient αME = 1000 (V m−1)/(A m−1) in resonance at 2.4 kHz. The resulting static ME coefficient is αME = 14 (V m−1)/(A m−1). In resonance operation, a sensitivity of 780 V/T and noise levels as low as 100 pT/Hz1/2 have been reached. The wafer bonding and encapsulation can effectively improve the mechanical quality factor and reduce the equivalent magnetic noise from 100 pT/Hz1/2 [224] for the non-encapsulated device to 27 pT/Hz1/2 [222]. Since commonly used glass frit and anodic bonding require temperatures beyond the 300 °C threshold for glass to crystallize and change properties, a transient liquid phase (TLP) bonding process was specially developed with a bonding temperature of 260 °C [225]. The bonding process is shown in Figure 3b. The cap wafer and sensor wafer are carefully aligned and loaded into a wafer bonder with a vacuum pressure of 5×10−5 mbar. By heating to 260 °C for 10 min, the melt and solid-liquid interdiffusion of the thin interlayer led to isothermal solidification, forming a robust bond between the wafers. The wafer-level packaged (WLP) magnetoelectric MEMS sensors after dicing were encapsulated [224], as shown in Figure 3c,d. In addition to encapsulation, PZT films with interdigital transducer electrodes were used as a piezoelectric phase for the Si cantilever ME sensors based on FeCoSiB films on the backside [186]. The limit of detection was improved to 2.6 pT/Hz1/2 at the mechanical resonance of ~975 Hz [186], which is only about 1/3 of the AlN-based ME sensor [147].
To improve magnetic sensitivity, a 1000 μm × 200 μm poly-silicon (5 μm)/Sc-doped AlN (Al0.73Sc0.27N, 1 μm)/FeCoSiB (2 μm) cantilever ME sensor was developed in 2020 [226]. The 1.38-fold increase in the piezoelectric coefficient and the relative permittivity ratio between AlScN and AlN [93] nearly doubles the magnetoelectric (ME) voltage coefficient, from 734 ± 38 V/cm/Oe for AlN ME sensors to 1334 ± 84 V/cm/Oe for AlScN ME sensors [226]. This enhancement is especially beneficial for applications that do not operate at the noise limit, such as current sensors, where higher sensitivity can reduce demands on the electronic system, thus lowering production costs [226]. However, the in-resonance detection limit remains nearly unchanged at 60 ± 2 pT/Hz1/2 for AlScN-based sensors compared to 62 ± 2 pT/Hz1/2 for AlN-based sensors, as the increased piezoelectric response boosts both thermomechanical noise and voltage output. Outside of resonance, however, the detection limit for AlScN-based devices shows a 1.85-fold improvement [226]. In addition to improving the properties of the piezoelectric layer, the magnetostrictive layer was improved by direct deposition on the smooth surface of the Si/SiO2 cantilever instead of on an AlN film [185]. The inverse bilayer ME sensor was enabled by reactive sputtering of an Al target powered by a 250 kHz pulsing unit in a N2 environment without intentional substrate heating. The room temperature deposition maintains the amorphous nature and superior magnetic properties of FeCoSiB, which cannot be realized in the process flow with high-temperature AlN deposition. A high-quality factor of 310 and ME coefficient of 5 kV/cm/Oe was realized at an EMR of 867.8 Hz, leading to the lowest equivalent magnetic noise of ~400 fT/Hz1/2.
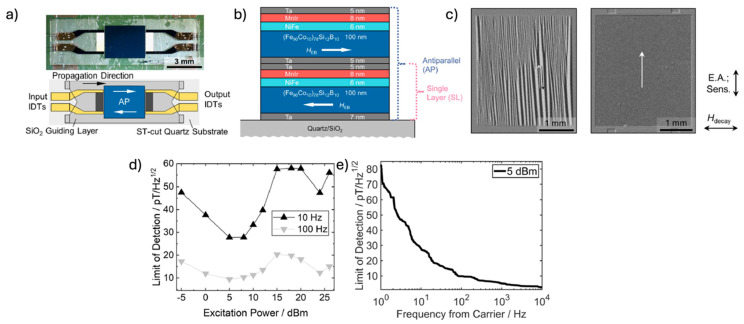
Starting from 2011, MFC has been used in both bulk ME sensors [227] and thin-film ME sensors [147]. In 2012, Jahn et al. utilized the MFC to realize a 1000-times sensitivity enhancement from unmodulated 1 μT/Hz1/2 @ 1 Hz to modulated 1 nT/Hz1/2@ 1 Hz. However, this equivalent magnetic noise is much worse than 7.1 pT/Hz1/2 in direct measurements due to the undesired additional noise under modulation from Barkhausen noise originating from magnetization jumps of pinned domain walls near defects. To reduce the magnetic noise, exchange bias stack 3 × (5 nm Ta/3 nm Cu/8 nm Mn-Ir/FeCoSiB) was first developed in 2013, which can realize a stable single domain state, indicating a well-defined magnetization reversal by coherent magnetization rotation for the FeCoSiB layer up to 100 nm with a ME coefficient of ~340 V/cm/Oe [212,228,229,230,231]. The structure of the stack was not altered up to 250 °C [229]. In 2015, the Ta 5 nm/Cu 3 nm/MnIr 8 nm/FeCoSiB 200 nm exchanged bias stack-based cantilever ME sensor was first demonstrated under MFC. Limits of detection of 180 pT/Hz1/2 @ 10 Hz and 300 pT/Hz1/2 @ 1 Hz using MFC were realized, which is 3 orders of magnitude better than 10 nT/Hz1/2 @10 Hz for a ~3 μm thick non-biased stack [230]. Using this exchange bias multilayer stack, a generalized numerical model was proposed to examine magnetic excess noise [232], which is the main noise source that arises with a pumping signal. It was found that the magnetic excess noise can be reduced by a DC-biased pump signal, thereby enhancing the signal-to-noise ratio (SNR) and improving LOD.
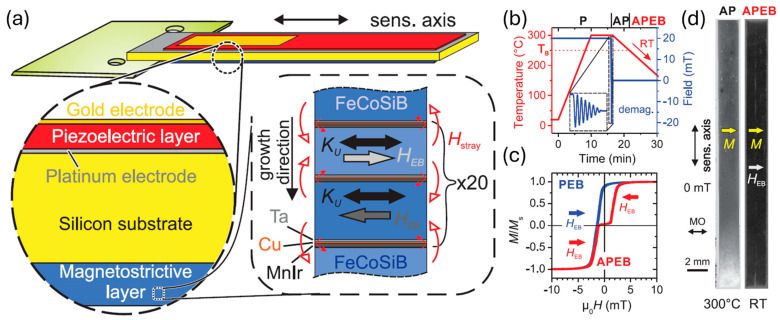
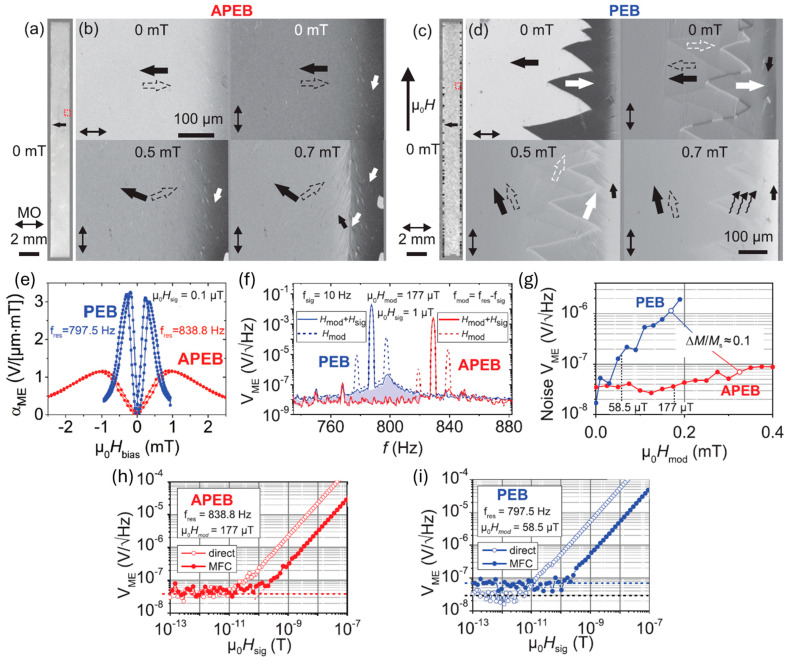
In the parallel exchange-biased (PEB) antiferromagnetic/ferromagnetic (AF/FM) stack demonstrated in 2012, limited magnetic domain control can only guarantee a single domain state for FeCoSiB thickness below 100 nm [212,228]. Due to the demagnetizing field, magnetic domains still form in a thick FeCoSiB layer, which limits the maximum achievable sensitivity and results in a poor LOD. In 2019, a cantilever ME sensor based on an antiparallel exchange bias (APEB) stack was developed, which can lead to single magnetic domain state formation without magnetic layer thickness restriction. The sensor structure and magnetic stack are shown in Figure 4a [181]. The Ta (25 nm)/Pt (150 nm)/AlN (2000 nm)/Cr (5 nm)/Au (100 nm) was sputtered on top of double-sided polished 350 μm-thick thermally oxidized Si, while the APEB stack was deposited on the bottom. The stack comprises 20 × [Ta(5 nm)/Cu(3 nm)/Mn3Ir(8 nm)/(Fe90Co10)78Si12B10(90 nm)/Ta(5 nm)/Cu(3 nm)/Mn3Ir(8 nm)/(Fe90Co10)78Si12B10 (110 nm)]. The imbalance of the adjacent FeCoSiB layer thickness leads to the difference in Zeemann energy and switching field of the two adjacent layers, easing the antiparallel alignment of magnetization and facilitating an antiparallel magnetostatic coupling of the two layers. The stack was first annealed at 300 °C with a 200 Oe field along the short axis of the cantilever to form PEB, as shown in Figure 4b. A decaying sinusoidal AC magnetic field followed by a linear cooling process was used to degauss the stack and transit PEB to APEB magnetization due to the magnetostatic interaction. The dominant bipolar APEB state was confirmed by the hysteresis in Figure 4c and field-dependent MOKE images in Figure 4d. The domain rotations in the APEB and PEB stack are shown in Figure 5a–d. In APEB, a single domain state was observed on the top surface, while magnetic domains were observed on the edge in PEB due to the demagnetizing effect. Applying a field along the long axis leads to a coherent magnetization rotation in the APEB stack without domain wall activity visible. However, in the PEB stack, immediate domain wall activity and compensated Néel wall structures are clearly visible. The invisible weak domain wall activity makes the APEB sensor show a significantly lower flat noise level than PEB (Figure 5f), even though the APEB stack has an operational frequency shift and a lower maximum magnetic sensitivity in the absence of the demagnetizing effect (Figure 5e). Under MFC, the noise performance of APEB is improved by more than one order of magnitude relative to the PEB sensor. In contrast to the PEB sensor, where the noise level increases steadily with a rising Hmod, the noise level of the APEB sensor remains stable (Figure 5g). This means the noise level of the APEB sensor is dictated solely by thermomechanical noise [178,223,233] independent of the detection scheme, while the PEB sensor still suffers from the dominant magnetic noise. The rejection of magnetic noise in the APEB sensor makes it have a LOD as low as 60 pT/Hz1/2 at 10 Hz, which is half that of the PEB sensor.
Figure 4.
Magnetically modulated cantilever ME sensor with antiparallel exchange bias (APEB) stack. (a) The sketch illustrates the ME cantilever design with the magnetic field sensing axis indicated. A cross-sectional view highlights the ME sensor’s structure, showing the Si substrate, a piezoelectric AlN layer, a Pt and Au electrode, and the magnetostrictive layer. The magnetostrictive layer consists of a repeated multilayer structure with Ta/Cu seed layers, an antiferromagnetic MnIr layer, and a magnetostrictive FeCoSiB phase. This structure includes a 20× repeated two-layer configuration. Key magnetic parameters are indicated, including the uniaxial anisotropy axis Ku, the exchange bias field Heb, and the magnetic stray field distribution Hstray. (b) A diagram shows the temporal application of temperature and magnetic field during the annealing process. (c) An inductive measurement shows the magnetization loop along the alternating EB axis, with a magnetization loop from a parallel exchange-biased (PEB) sample included for comparison. (d) Magnetic domain (MD) structures at 300 °C after demagnetizing the sensor and achieving a stabilized magnetization state at room temperature (RT) for the APEB sensor. The alignment of magnetization M, the EB field Heb in the top layer, the sensor’s magnetic field sensing axis, and the magneto-optical sensitivity (MO) axis are depicted. Reprinted with permission from Ref. [181]. Copyright 2019 AIP Publishing.
Figure 5.
Magnetic domain behavior and noise performance of magnetically modulated cantilever ME sensor with antiparallel exchange bias (APEB) stack and PEB stack. (a) A full-sensor view of the APEB’s magnetic domain structure, with magnetization directions marked by arrows. (c) A full-sensor view for the PEB sensor, highlighting differences in magnetic domain patterns compared to APEB. (b,d) Provide high-resolution domain images of specific regions at the right cantilever edge (indicated by red dashed boxes in (a,c)) for both APEB and PEB, respectively, illustrating domain behavior with and without an applied magnetic field. Dashed arrows denote the magnetization alignment in the second, non-visible FeCoSiB layer. (e) The magnetoelectric (ME) coefficient αME changes with bias field Hbias at the mechanical resonance frequency fres. (f) Frequency spectra of voltage noise density VME for both APEB and PEB sensors under the same modulation Hmod and signal fields Hsig. (g) Voltage noise dependency on Hmod, highlighting the sensitivity to modulation field strength. (h) and (i) show linearity plots of fres and magnetic frequency conversion (MFC) mode for a ME sensor with APEB and PEB phases, respectively. Noise floors and optimal Hbias and Hmod values for resonance and MFC modes are indicated, showing comparative sensor performance across configurations. Reproduced with permission from Ref. [181]. Copyright 2019 AIP Publishing.
In addition to magnetic excess noise, acoustic and vibrational noise is inherent in any acoustic mode and has a spectrum in the low-frequency region up to several kHz. Even though it can be suppressed by the shielded chamber during tests, vibrational noise cancellation is still necessary for practical applications. In 2016, a tuning fork consisting of two identical cantilever ME sensors on top and at the bottom of a mounting block was proposed to strongly reduce the acoustic and vibrational noise by canceling out vibrational couplings by means of analog signal processing [187,234]. The sensors, which utilize interdigital (ID) electrodes, comprise a multilayer stack of Ta (5 nm)/FeCoSiB (4 µm)/Si (300 µm)/ZrO2 (300 nm)/PZT (2 µm)/Cr (5 nm)/Au (100 nm) and work on the first bending mode at 958 Hz. A limit of detection of ~500 fT/Hz1/2 was realized for the tuning fork without an artificially added wideband piezoelectric loudspeaker, which is one order of magnitude better than 5 pT/Hz1/2 for a single cantilever ME sensor. With the acoustic-disturbing source, the single ME sensor shows two orders of voltage noise level and LOD decrease, while the turning fork ME sensor only degrades by a factor of four. To address the wide dynamic range requirement due to the large carrier signal leak to output under unbalanced magnetostriction characteristics, a carrier suppression technique was recommended [235]. This technique successfully reduced the carrier signal leakage by 60 dB and avoided oversteering the readout electronics, reducing the analog-to-digital conversion challenges [235].
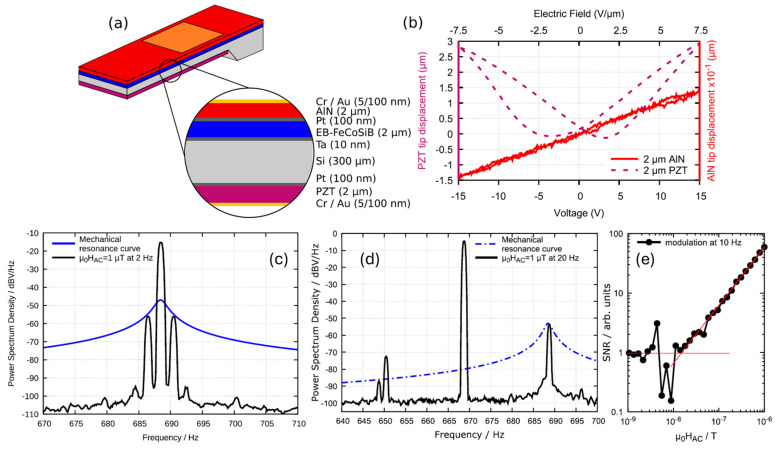
Electrically modulated cantilever ME sensors were first demonstrated in 2016 by Hayes et al. [11] to mitigate the challenges of MFC in size and energy consumption, potential crosstalk in sensor arrays and external interfering stray fields. In this method, the low-frequency magnetic signal is shifted to match the mechanical resonance of the sensor, while the electric modulation frequency is set to either the sum or difference of the resonance and signal frequencies. The sensor consists of an exchange-biased magnetostrictive multilayer, a non-linear piezoelectric actuation layer, and a linear piezoelectric sensing layer, as shown in Figure 6a. The electric modulation field is applied to the unpoled PZT layer showing a hysteretic, quadratic displacement with respect to applied DC voltage and a non-linear piezoelectric coefficient for EFC, while the linear AlN layer is used to detect the ME voltage, owing to its low loss tangent and high piezoelectric coefficient [236], as shown in Figure 6b. The instantaneous slope of the PZT displacement curve determines the piezoelectric conversion coefficients, which are reflected in the magnetostrictive layer’s response to small magnetic fields. Consequently, the AlN output voltage carries a signal resulting from the commutation between the high-amplitude carrier signal and the low-amplitude magnetic signal, akin to magnetic frequency conversion. Using two distinct piezoelectric layers provides the added advantage of natural electrical isolation between the actuation voltage and the readout signal, enabling the potential for operation without the need for compensation mechanisms. The high piezomagnetic coefficient of the exchange biased layer at a zero-bias field removes the need to apply a DC bias field to operate at the maximum magnetic sensitivity point. EFC was realized by applying a modulated voltage signal at mechanical resonance (fres = fmod = 689 Hz) on the PZT layer when the magnetic field signal (1 μT, fAC = 2 Hz) was applied in parallel. The output spectrum of the voltage signal at the AlN layer shows the maximum carrier signal peak at fres from electromechanical coupling to the PZT layer and two sidebands at fmod ± 2 Hz. A limit of detection of ~5 nT/Hz1/2 was obtained, as shown in Figure 6c. When the modulation frequency is set to fres − fAC = 669 Hz, the LOD slightly increases to ~10 nT/Hz1/2 due to thermal noise [237], as shown in Figure 6d,e. The advantage of EFC is that it allows the sensor to function at substantially higher resonance frequencies, which are difficult to reach with magnetic excitation due to the high magnetic field amplitudes needed. Higher resonance frequencies are beneficial for achieving wider bandwidths and reducing cross-sensitivity to acoustic noise and vibrations. A limitation of this approach arises from the resonator’s high-quality factor, which confines resonance amplification to a narrow frequency range of typically only a few Hz.
Figure 6.
Electrically modulated ME sensors with AlN layer for voltage output. (a) The schematic shows a magnetoelectric (ME) composite sample with three active layers: an exchange-biased FeCoSiB layer serving as the magnetostrictive phase, an AlN layer as the linear piezoelectric phase for readout, and an unpoled PZT layer as the nonlinear piezoelectric phase for excitation. (b) Displacement–voltage characteristic curve of the ME cantilever showing responses of both piezoelectric phases under a DC electric field. (c) The sensor output spectrum from the AlN layer when the PZT layer is excited at its mechanical resonance frequency of fmod = 689 Hz. (d) Sensor output spectrum from the AlN layer with the carrier signal frequency fres = fmod = 669 Hz, applied at 20 Hz below the mechanical resonance. (e) A linearity test under a 10 Hz magnetic field demonstrates that the noise floor reaches approximately 10 nT/√Hz. Reproduced with permission from Ref. [11]. Copyright 2016 AIP Publishing.
In addition to the AlN layer, the readout can also be performed by a pickup coil wound around the sensor [238,239,240]. In 2018, a mechanically decoupled pickup coil was used to detect the electrically modulated signal at quasi-DC frequencies from a 2 μm AlN/2 μm FeCoSiB cantilever [12]. The 15th flexural mode at 515.7 kHz and the 19th torsional mode (U mode) at 520.7 kHz were used to modulate the detected signal at 0.2 Hz, showing a LOD of 1.2 nT. Utilizing this U mode, a cantilevered mesoscopic ME structure was electrically excited [10], as shown in Figure 7a,b. The pickup coil senses the modulated magnetic field owing to the inverse ME effect under a modulated voltage on the piezoelectric layer, which was buffered by a low-noise, unity-gain buffer amplifier as the final voltage signal output. By tuning the capacitance, the voltage signal from the U-mode mechanical resonance can be boosted by about one order of magnitude, as shown in Figure 7c,d. As shown in Figure 7e, multiple magnetic domains form along the magnetic easy axis, leading to notable magnetic sensor due to the Bakhusen jump and degraded noise performance. Despite this, the U mode mechanical resonance (Figure 7f) exhibits a much sharper peak, with a quality factor (QUM) near 1000, which is about an order of magnitude higher than typical flexural modes. In flexural modes, oscillation losses are largely due to air damping [241,242], particularly in long cantilevers whose Q factor rarely exceed a few hundred in ambient conditions. In contrast, the U mode benefits from inherently reduced air damping, as fewer air molecules are displaced, allowing it to achieve a higher Q factor and, therefore, superior resonance sharpness and efficiency. The U mode demonstrates the highest sensitivity to small magnetic fields, particularly under moderate excitation levels [13]. The sensitivity and voltage noise spectrum are shown in Figure 7g,h respectively. The sensitivity at zero field shows a linear increase with a rising carrier voltage. At low frequencies (<20 Hz), two regimes are identified based on carrier amplitude. Below 200 mV, the noise increases only slightly, while above 200 mV, the noise surges by nearly seven times for an additional 100 mV of excitation. As shown in Figure 7i, a magnetic LOD of 210 pT/Hz1/2 @ DC was realized. Further increasing the signal frequency leads to the improvement of the LOD from 70 pT/Hz1/2 @ 10 Hz to 50 pT/Hz1/2 @ 53 Hz.
Figure 7.
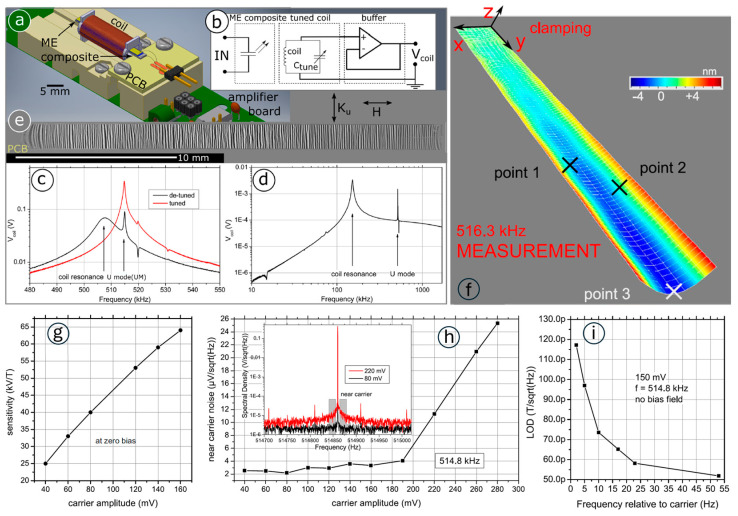
Electrically modulated U-mode ME sensors with a picking-up coil for voltage output. (a) Schematic setup: a composite, embedded in a pickup coil, is shown. The piezoelectric (PE) plate capacitor functions as the input, while the tuned pickup coil, coupled with an amplifier, provides the output signal. (b) Circuit representation: the ME composite is modeled as a radiative capacitor. The pickup coil generates a signal that is buffered by a low-noise, unity-gain buffer amplifier, enhancing signal integrity. (c) Frequency response analysis: the self-resonant frequency of the pickup coil (with quality factor Q∼150) and the mechanical resonance frequency (with quality factor Q∼1000, labeled as UM) are shown. Tuning the system maximizes voltage output at resonance, with de-tuning options also analyzed. (d) Wide frequency response: a broad response shows coil resonance effects and two distinct voltage peaks correspond to mechanical resonances of the system. (e) MOKE microscopy image: the full cantilever length is captured after magnetic field decay, showing magnetization along the thermally induced magnetic easy axis (Ku). Applied magnetic fields (H) align with the hard axis, while the left end of the cantilever is fixed to the PCB. (f) Vibrometry measurements showing the U-mode at 514.8 kHz. (g) Sensitivity at zero field showing a linear increase with rising carrier voltage amplitude. (h) Voltage noise characteristics versus carrier amplitude. At low frequencies (<20 Hz), two regimes are identified based on carrier amplitude. Below 200 mV, noise increases only slightly, while above 200 mV, noise surges by nearly seven times for an additional 100 mV of excitation. Inset shows the noise spectra for 80 mV and 220 mV cases; the 220 mV excitation exhibits a noticeable pedestal and increased broadband noise. (i) LOD is assessed across different test frequencies, showing an exponential noise increase towards the carrier, which limits sensor performance. Reproduced from Ref. [10].
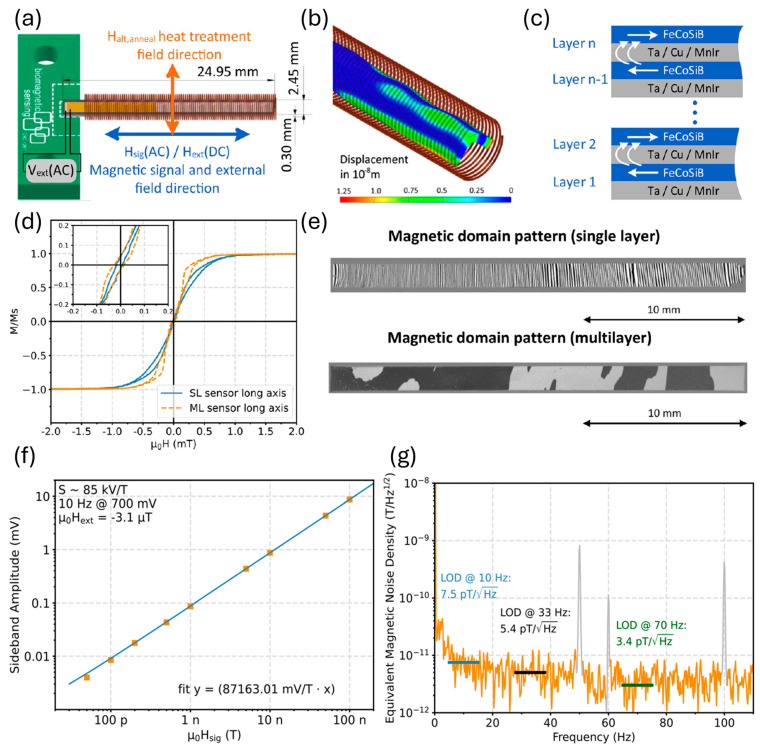
In 2024, a low noise exchange bias stack was first used to reduce magnetic noise in an EFC U-mode cantilever ME sensor with a pick-up coil for the voltage output [13], as shown in Figure 8a,b. The advanced layer stack design was performed for magnetic flux closure, where each Ta/Cu/MnIr layer was exchange-coupled to a FeCoSiB layer, as shown in Figure 8c. The B-H loop is shown in Figure 8d. Around zero magnetic field, a small hysteresis opening becomes visible due to individual local switching of magnetic domains at edges or individual switching of domains in the different layers with areas of different effective anisotropy in the multilayer. The observed nonlinear magnetization curve constrains the dynamic range of the sensor. In the multilayer exchange bias stack, no closure domains develop, indicating a dominant stray field coupling between the magnetic layers. This potentially leads to a reduction of magnetic noise by reducing the domain wall density, as shown in Figure 8e. Furthermore, the exchange bias pins the magnetic domain walls and, thus, reduces or eliminates domain wall mobility. As shown in Figure 8f, the sideband voltage amplitude increases linearly with the magnetic test signal from 50 pT to 100 nT, where a constant sensitivity of 85 kV/T across the test fields was demonstrated from 10 to 70 Hz. The detection limits are improved by an order of magnitude to less than 8 pT/Hz1/2 at 10 Hz and 18 pT/Hz1/2 at DC, as shown in Figure 8g.
Figure 8.
Low-noise inverse ME sensor based on electrically modulated U mode and exchange bias stack with a pickup coil. (a) Schematic of cantilever sensors in the inverse magnetoelectric configuration, featuring a simplified pickup coil covering the cantilever’s entire free length except where it connects to the circuit board. The measurement and bias field directions are shown by the blue arrow, while the orange arrow indicates the magnetic field direction applied during annealing. (b) Finite Element Method (FEM)-derived deflection of the cantilever in the U mode, depicted with amplified amplitude to illustrate bending. (c) Diagram of the advanced layer stack design for magnetic flux closure, showing Ta/Cu/MnIr layers, with each exchange-coupled to a FeCoSiB layer. The arrows represent potential magnetic flux closure and the preferred magnetization direction without cantilever excitation. (d) BH-Looper hysteresis curves for heat-treated single-layer (SL) and multi-layer (ML) samples (8 × 500 nm exchange bias layers) measured along the cantilever’s long axis, both with a total FeCoSiB thickness of 4 μm. (e) Magneto-optical Kerr micrographs of demagnetized domain patterns in SL and ML samples along the long axis, with sensitivity axis oriented along the cantilever’s short side. (f) Sideband amplitude response at several magnetic test signal amplitudes at 10 Hz, demonstrating extended linear behavior. (g) Equivalent magnetic noise density with limit of detection (LOD) calculated at 10 Hz (blue), 33 Hz (black), and 70 Hz (green), showing noise reduction and improved LOD at higher frequencies with a constant sensitivity of 85 kV/T across test fields from 10 to 70 Hz. Reproduced from Ref. [13].
In 2015, the delta-E effect was first used in a cantilever-based ME sensor [243]. The cantilever ME sensor is composed of 2 μm AlN and 2 μm FeCoSiB [243]. Operating in the first or second transversal bending mode at 7.6 kHz or 47.4 kHz, a limit of detection of 140 pT∙Hz−0.5 @ 20 Hz under a magnetic bias field and 1 nT∙Hz−0.5 @ 20 Hz without an external bias field was achieved [243]. Since the oscillation and vibration magnitude are small and linear, the interference between different modes can be rejected. In 2016, the adapted electrodes were developed to improve the sensitivity and reduce the dynamic range [221]. Different electrode designs of Ξ0, Ξ1 and Ξ2 were placed on top of the AlN (2 μm)/polySi (50 μm)/FeCoSiB (2 μm) cantilever ME sensor, as shown in Figure 9a,b. The first and second transverse bending modes can be excited, whose deflections are displayed in Figure 9c. The electrode design Ξ0 demonstrates high efficiency in the primary mode, Φ1, which is evident from its steep admittance change and significant phase shift, indicating robust energy coupling in this mode. However, its performance diminishes in the secondary mode, Φ2, where the response is less pronounced. In contrast, the adapted designs Ξ1 and Ξ2, which incorporate dedicated electrodes for each mode, provide enhanced operational efficiency across both modes. This design strategy ensures effective coupling for both Φ1 and Φ2, optimizing the sensor’s performance across a broader frequency range. The sensor was mounted on a silicon frame, as shown in Figure 9d. The dynamic range in the second mode shows a significant enhancement of 16 dB when transitioning from Ξ0 to Ξ2, indicating improved sensitivity and performance in this mode. The noise spectrums of different electrode designs at different modes are shown in Figure 9e,f. At low frequencies, noise levels increase due to resonance amplification, yet the second mode demonstrates superior performance above 20 Hz. This performance enhancement is especially pronounced with the optimized electrode design, Ξ2, which achieves a noise level below 100 pT/Hz1/2. This optimization makes Ξ2 highly effective for maintaining low noise levels in the second mode, enabling greater sensitivity and stability across a broader operational frequency range.
Figure 9.
Multimode delta-E effect magnetic field sensors with adapted electrodes. (a) Schematic cross-section of the cantilever beam, (b) top view of the cantilever showing the various electrode designs, (c) calculated deflection of the cantilever in the first and second transverse bending modes according to Euler–Bernoulli beam theory, and (d) photograph of the sensing cantilever mounted within a silicon frame. Effective noise level for the (e) first and (f) second modes. Reproduced with permission from Ref. [221]. Copyright 2016 AIP Publishing.
NPR ME Sensor
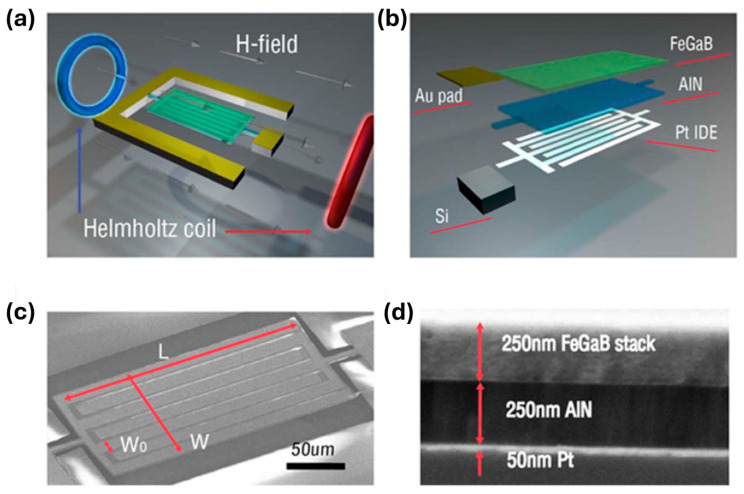
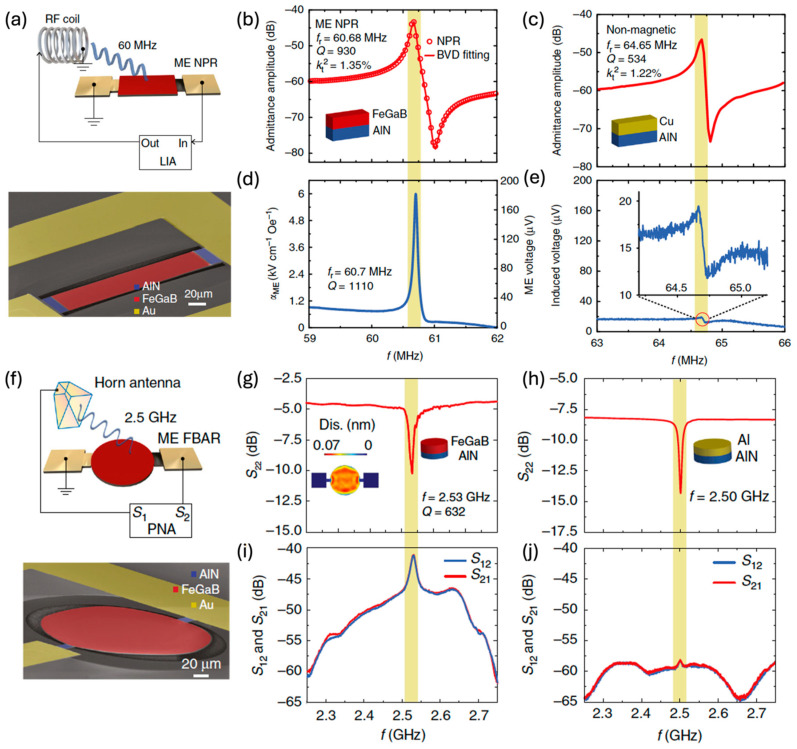
A 215 MHz self-biased ME MEMS magnetic sensor, based on a FeGaB/Al2O3 nano-plate resonator with precisely engineered inter-digital electrodes (IDEs), utilizes a high-quality ME MEMS resonator (quality factor, Q = 735) that is highly sensitive to DC magnetic fields near the electromechanical resonance (EMR), enabling an ultra-sensitive LOD of approximately 300 pT [180]. Upon applying a DC magnetic field to the ME heterostructure, the magnetostrictive strain in the FeGaB layer alters its Young’s modulus through the ΔE effect, resulting in shifts in EMR frequency and admittance of the MEMS ME resonator. This energy-efficient self-biased micro-scale MEMS magnetic sensor, based on a magnetostrictive/piezoelectric heterostructure, is compatible with CMOS fabrication and is promising for DC and low-frequency AC magnetic sensing applications.
As illustrated in Figure 10a, a DC magnetic field was generated by Helmholtz coils and applied along the length direction. Figure 10b reveals the sensor’s layered structure. The AlN piezoelectric layer is flanked by FeGaB/Al2O3 magnetostrictive layers and Pt IDEs. The active sensing area (100 μm × 200 μm) is fully covered by IDEs and magnetostrictive material, as shown in the SEM image in Figure 10c. In this configuration, the extensional vibration mode is excited in the AlN film, with the EMR frequency given by:
where W0 is the pitch width between IDEs, and Eeq and req represent the equivalent Young’s modulus and density, calculated as and , respectively, with Ei, ri, and vi being the Young’s modulus, density, and volume ratio of each layer in the sensor. A high EMR frequency of 215 MHz was achieved by optimizing the IDE pitch width, which facilitated strong ME coupling due to a flat magnetostrictive piezoelectric interface. Furthermore, the removal of the underlying Si substrate minimized the substrate clamping effects, enhancing both ME coupling and sensitivity.
Figure 10.
(a) Schematic and (b) layered structure of the ME sensor. Scanning electron microscopy images of the (c) fabricated MEMS ME sensor and the (d) cross-section. Reproduced from Ref. [180].
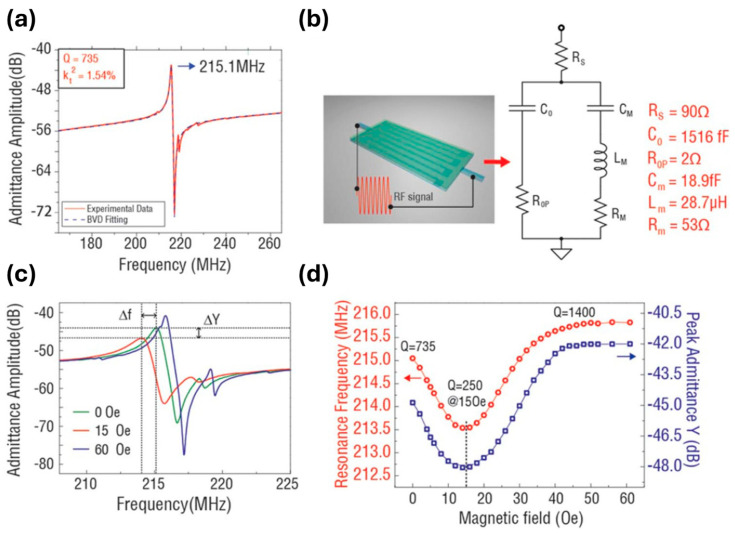
Figure 11a depicts the measured admittance and its modified Butterworth–van Dyke (MBVD) model fit for the ME magnetic sensor, revealing an EMR frequency of 215 MHz. From the MBVD fit, a quality factor Qm of 735 and an electromechanical coupling coefficient of 1.54% were extracted, with the being comparable to values for traditional AlN nano-plate resonators with similar electrode designs, while the Qm is substantially higher than those typically observed in low-frequency ME magnetic sensors. Figure 11b presents the MBVD equivalent circuit for the AlN/FeGaB MEMS magnetic sensor, where Rs, C0, and Rop represent the electrode resistance, ME resonator capacitance, and substrate parasitic resistance, respectively. Meanwhile, CM, LM, and RM correspond to motional capacitance, inductance, and resistance [180].
Figure 11.
(a) MBVD model fitting for admittance curve of the ME sensor. (b) The equivalent MBVD circuit of the ME resonator. (c) Admittance curves of the ME resonator under different DC bias magnetic fields. (d) EMR frequency and peak admittance amplitude at the resonance frequency versus DC magnetic fields. Reproduced from Ref. [180].
In Figure 11c, the admittance response to various DC magnetic fields indicates strong ME coupling, as both the EMR frequency and admittance amplitude are affected by the ΔE effect. Figure 11d shows the resonance frequency and peak admittance at varying DC bias fields, where both initially decrease before increasing, correlating with the magnetic loss associated with domain wall activity. A minimum Qm of 250 was reached at a transition field of 15 Oe.
NPR Array ME Sensor
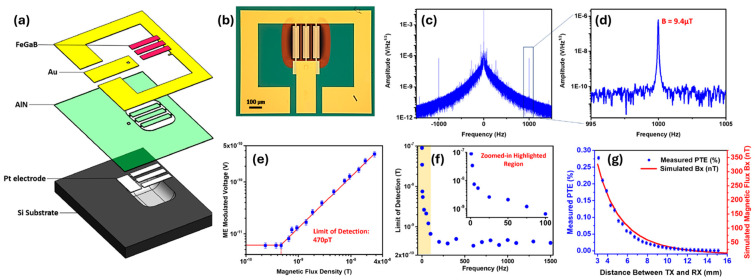
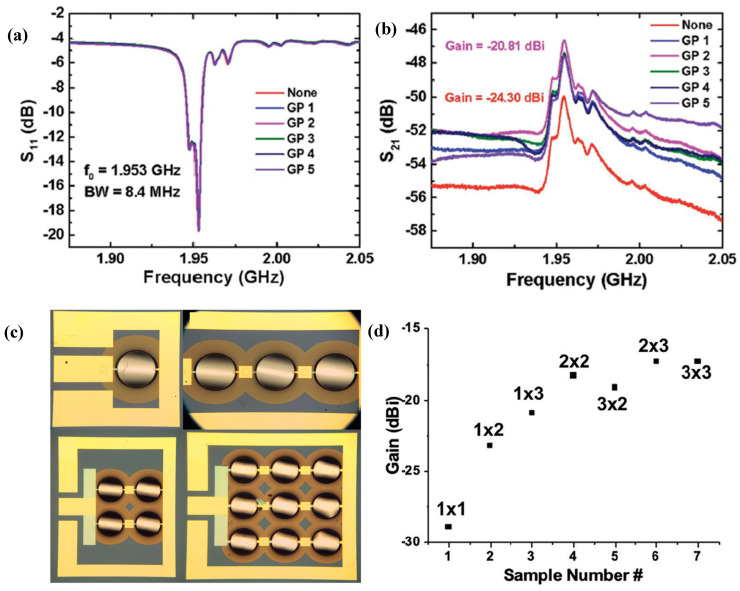
Bio-implanted ME sensors are crucial for the contactless monitoring of nerve activity and disorders in magnetomyography [8,9]. In addition to sensing and recording neural signals with high spatial resolution and superior LOD in a wide range, the ME sensors need to efficiently harvest wireless energy to power themselves without batteries and transmit recorded neutral activity data to outside receivers. In 2017, an ultracompact NPR ME antenna was demonstrated, showing a LOD of 40 pT at 60.7 MHz [15]. However, the off-resonance operation at 1 MHz shows a poor LOD above 0.1 μT. Increasing the number of sensor elements is an effective way to boost the magnetic sensing capability. In 2021, a smart dual-band NPR array ME sensor/antenna was fabricated, as shown in Figure 12a,b [14]. The ME sensor consists of three parallel 500 nm AlN/500 nm FeGaB NPR ME resonators and has a width mode of 63.6 MHz. Each resonator shows an ultracompact size of 250 μm × 50 μm. The total size of the ME sensor is 250 μm × 174 μm. To boost the magnetic sensitivity at low frequencies, a MFC technique was applied by a 9.4 μT modulation AC magnetic field at 1 kHz. As shown in Figure 12, a sideband modulation signal of 6.2 × 10−7 V/Hz1/2 was detected at 63.301 MHz, and a 470 pT LOD @ 1 kHz was demonstrated in Figure 12e. The LOD as a function of the modulation frequency is shown in Figure 12e. Sub-pico-Tesla LOD was maintained from 100 Hz to 1000 Hz, while the LOD degrades fast below 100 Hz due to the dominant 1/f noise. This performance allows the sense to sensor the hundreds of pT-level neutral magnetic field signals at the pial surface [205]. Moreover, the dual-band ME sensor has a thickness mode of 2.53 GHz, which can be used for wireless energy transfer. The high wireless power transfer efficiency with an overwhelming figure of merit (FOM) over other micro-coils make the self-biased and passive dual-band ME sensors/ultra-high frequency (UHF) antennas promising for implantable biomedical magnetic sensing applications [14].
Figure 12.
Self-biased NPR array dual-band ME sensor/antenna. (a) A 3D schematic of the ME sensor/antenna. (b) Optical image of a fabricated smart ME antenna. (c) Power spectrum of the reflected signal from the ME antenna after demodulation and lowpass filtering. (d) Zoom-in modulation signal at 1 kHz. (e) Modulated voltage as a function of modulated signal magnetic flux density, showing a 470 pT LOD. (f) LOD as a function of modulation signal frequency. (g) Power transfer efficiency as a function of distance between transmission and receiving antennas. Reproduced from Ref. [14].
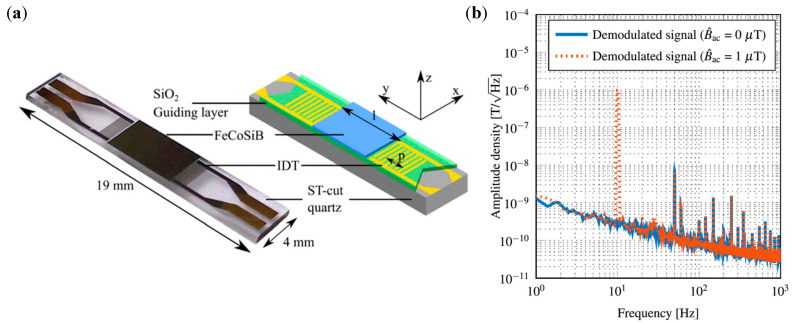
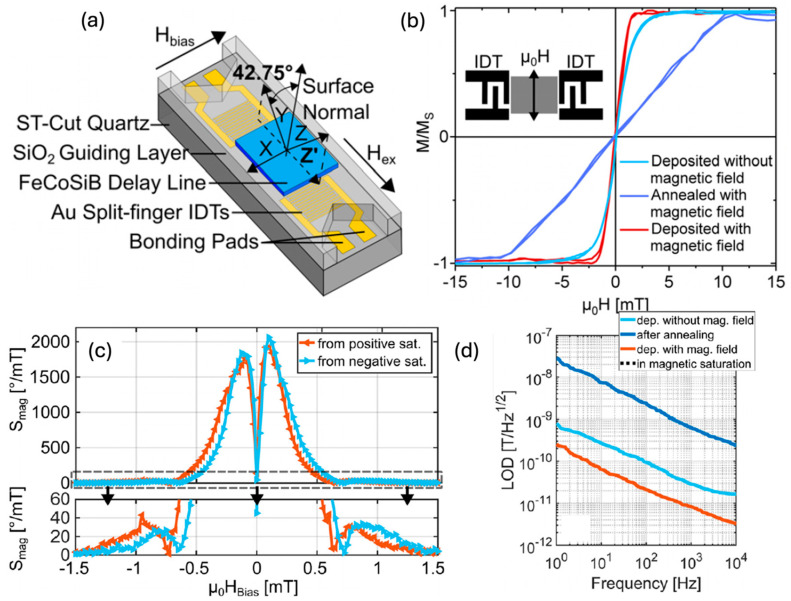
3.2. SAW Thin-Film ME Sensor
There are many SAW-based chemical, temperature, and biosensors available in the literature. In the current review, only SAW-based sensors that have both the piezoelectric and magnetostrictive layers are included. There are two types of SAW-based sensor concepts available, either a delay line [244] or a resonator [245]-type approach. Most of the demonstrated sensors work with the delay line configuration.
Such sensors consist of interdigital transducers (IDTs), typically made from Cr/Au, Al, or Ti/Au materials, on top of a piezoelectric layer/substrate (quartz, LiNbO3, and LiTaO3) and a magnetostrictive layer (for sensing). The basic physics behind the operation of SAW-based magnetic field sensors is the delta-E effect [21]. An electric signal on the IDTs produces an acoustic wave at one end of the sensor, and the acoustic wave travels along the delay line. A highly responsive magnetostrictive layer is present between two delay lines. The magnetostrictive layer changes Young’s modulus (ΔE) or shear modulus (ΔG) when an external sensing magnetic field (Hsense) is present. The change in modulus causes a change in the velocity with which the acoustic wave travels. Finally, at the other end of the device, the output IDTs convert this acoustic wave into electrical signals. The delta-E effect causes a phase shift of the acoustic waves, and this phase shift is a function of the Hsense. The sensitivity of the sensor is determined by the phase shift that can be caused by a magnetic field change and is reported with the unit of ‘°/mT’.
Though the initial SAW-based magnetic sensors were demonstrated in 1987 [244], only a few investigations followed up. This could be due to the availability and advancement in MEMS, piezoelectric, and magnetostrictive materials. Many different studies have been published in the last decade with a focus on SAW-based magnetic field sensing. Here, we report a few important ones.
An experimental study showed an increased sensitivity at low magnetic fields when the magnetic layer was changed from Ni to CoFeB (which exhibits increased magnetostriction) along the delay line of the sensor [245]. Zhou et. al. realized a SAW-based magnetic sensor using 200 nm TbCo2/FeCo on top of a LiNbO3 substrate. They use a Rayleigh wave that travels through the delay line. They report a change in the velocity of the wave as a function of the magnetic field. The discussed theoretical model agreed well with the experimental results [246].
Love waves, which are purely shear transverse-polarized waves, are widely utilized in magnetic field sensing, owing to ultra-sensitive response of the incorporated functional magnetic thin film to the target stimulus. A simulation for the structural sensitivity to the guiding layer (SiO2) thickness was investigated, and an optimal guiding layer thickness of 4.5 μm was determined and deposited on a ST-cut quartz substrate (Figure 13a) [22]. On top of this, a 200 nm FeCoSiB soft magnetic layer was deposited. The total sensitivity of the sensor depends on three different parameters, , where corresponds to the change in modulus for a change in magnetic field, limited by the magnetostriction of the material. The gives the change in the velocity for a change in modulus. It is limited by how well the acoustic wave is confined, and finally, gives the change in the phase shift of the acoustic wave for a change in velocity. For the device fabricated the authors report a sensitivity of 504°/mT. The magnetic noise floor was plotted as a function of frequency and the LOD is frequency-dependent (Figure 13b). At 10 Hz a LOD of 250 pT/Hz1/2 and at 100 Hz a LOD of 80 pT/Hz1/2 have been demonstrated with a bandwidth of 50 kHz [22]. The total sensitivity of the SAW sensor can be enhanceed by increasing one of the three sensitivity parameters. The authors investigated magnetic films with multiple thicknesses of 25–400 nm [247]. As anticipated, the increases with the thickness, but the insertion losses also increase at a higher thickness, which influences the LOD. Higher thickness leads to higher insertion losses, which in turn, increases noise and LOD [247]. They report that, for magnetic field sensing, it is best to keep the thickness between 50 and 250 nm.
Figure 13.
(a) Schematic of the wideband SAW-based magnetic sensor. The sensor is built on a ST–cut quartz substrate, with SiO2 guiding layer, and FeCoBSi as a sensing layer. (b) The image shows the frequency vs. amplitude density. The authors report a LOD of 80 pT/Hz1/2 at 100 Hz, a bandwidth of 50 kHz, and a dynamic range of 120 dB. Reprinted from Ref. [22].
To further enhance the LOD of the SAW-based sensor, a well-defined magnetic film orientation is essential. In a 2020 study, the authors investigate different configurations to enhance the magnetic orientation 1) by depositing the magnetic film under an in-situ magnetic field (180 Oe) or 2) by depositing film without any field and conducting a magnetic field (1300 Oe) annealing at 270 °C for 30 min after film deposition (Figure 14a,b) [23]. They analyzed the magnetic properties, sensitivity, and LOD of the different configurations. They report the highest sensitivity of 2000°/mT (at 0.1 mT bias field) for the magnetic field SAW sensor with the in-situ field for magnetic film deposition (Figure 14c). For the annealed film after deposition, a sensitivity of 17°/mT (at 10 mT bias field) was obtained for the corresponding magnetic field SAW sensor. The reason for this difference is that, by depositing the film under an in-situ field, the precise orientation of the magnetic domains with low total anisotropy can be realized, which leads to high sensitivity. They also investigate the corresponding phase noise from which they report different LODs for different configurations. Once again, the configuration deposited with an in-situ field gives the best LOD of 70 pT/Hz1/2 at 10 Hz and 25 pT/Hz1/2 at 100 Hz (Figure 14d). It is reported that the noise at low frequency is dominated by the magnetic noise, and a multi-layer approach is further proposed to reduce the noise.
Figure 14.
(a) The illustration of a Love-Wave-based magnetic sensor based on a ST–cut quartz substrate. (b) The magnetization loops of different configurations of stacks. Note that the one deposited under the in-situ field has low anisotropy (red) compared to the one with post annealing after film deposition (blue). (c) The measured sensitivity as a function of the applied DC bias field for the configuration deposited with in-situ magnetic field. (d) LOD as a function of frequency for different magnetic orientation configurations. The lowest LOD is from the device with the magnetic stack deposited with an in situ magnetic field. Reprinted with permission from Ref. [23]. Copyright 2020 AIP Publishing.
A 2023 study from Schell et al. showed an exchange bias-based SAW magnetic field sensor (Figure 15a) [25] to reduce the previously discussed magnetic noise at a low frequency. In the study, an anti-parallel alignment of an exchange-biased magnetostrictive layer is investigated on a ST–cut quartz substrate. The exchange bias stack with Ta (5 nm)/FeCoSiB (100 nm)/NiFe (6 nm)/MnIr (8 nm)/Ta (5 nm) layers was used to reduce the fluctuations that are caused by magnetic domain wall motion. A X-Ray Diffraction (XRD) pattern shows that the MnIr has a strong (111) texture, which is essential to achieve strong exchange bias. The (111) texture is realized by using a 6 nm NiFe seed layer. The anti-parallel alignment of the magnetic layer was obtained by depositing the film under an in-situ magnetic field. After the first layer deposition, the sample was rotated by 180°, and the second layer was deposited (Figure 15b). Such anti-parallel exchange-biased magnetic configuration showed a reduced magnetic domain wall density (Figure 15c) compared to a single layer, with the top of the magnetic layer showing a single domain state over the complete film. The sensor was characterized at different powers (0, 10, 15, and 24 dBm). Such anti-parallel exchange bias stacks lead to an increased sensitivity of up to ~2000°/mT from 0 to 15 dBm and achieved the highest sensitivity of 3250°/mT at 24 dBm. At a higher excitation power, the increase in sensitivity also increases the insertion losses, which further reduces the LOD. The LOD as a function of the excitation power is shown in Figure 15d for different excitation powers. For both 10 Hz and 100 Hz of the carrier frequency, the LOD first decreases and has a minimum between 5 and 10 dBm and then increases. The authors report a LOD of 28 pT/Hz1/2 at 10 Hz and 10 pT/Hz1/2 at 100 Hz (Figure 15e) at 5dBm, which is a factor of 2.5 lower compared to the single-layer stack. However, they point out that the mechanism of the influence of the excitation power on the phase noise needs further investigations for better understanding.
Figure 15.
(a) The SAW sensor design consisting of a ST–cut quartz substrate, a SiO2 guiding layer and an anti-parallel exchange biased magnetostrictive layer (for sensing). (b) The layer stack of the magnetostrictive layer; it consists of two layers (Ta/FeCoSiB/NiFe/MnIr/Ta) that are antiparallel to each other. The NiFe/MnIr induces the exchange bias in the FeCoSiB layers of. (c) The magneto-optical Kerr effect microscope images from the top on a single FeCoSiB layer and a two-layer anti-parallel exchange bias stack. The image clearly shows the significant reduction in the domain wall density. (d) LOD plotted as a function of excitation power at 10 Hz and 100 Hz. Note that the LOD has the lowest value at 5 dBm for both frequencies. (e) Frequency spectrum of LOD with 5 dBm power. The LOD decreases as frequency increases, and an impressive LOD below 5 pT/Hz1/2 is achieved at 1 kHz. Reprinted from Ref. [25].
The efforts above focus on SAW-based devices based on quartz substrates. A CMOS-compatible SAW-based magnetic field sensor was proposed by Meyer et al. [24]. The sensor used magnetron-sputtered AlScN as a piezoelectric material, showing a LOD of 72 pT/Hz1/2 above 10 kHz. Even though the LOD is higher than the SAW sensors based on quartz, the CMOS compatibility could make such a device more practical in industrial applications.
A multifunctional sensor that is operated both in Rayleigh and Love wave mode was demonstrated by Yang et al. The sensor consists of a ZnO and SiO2 guiding layer on top of a quartz substrate. The ZnO is used here for insulating and impedance-matching purposes. The Rayleigh mode, on the other hand, is sensitive to temperature change, with a sensitivity of −37.9 ppm/°C. The Love wave is insensitive to the temperature difference. The authors use the Love wave mode for the magnetic field sensing, which is different from the previous approaches. Here, the authors measure the shift in the resonant frequency caused by the sensing magnetic field. They demonstrate a sensitivity of −170.4 kHz/mT for magnetic field sensing. A wireless sensor read-out system for magnetic field measurement is also investigated. It works as the sensing magnetic field detunes the SAW resonator, which can be remotely measured using a reader [248]. More recently, Hu et al. have performed FEM modeling and demonstrated a SAW-based self-biased magnetic field sensor. The authors report a strong dependence of resonant frequency on AC magnetic field when the in-plane uni-axial anisotropy is at an optimal angle (8°) to the SAW propagation. A high sensitivity of 630.4 kHz/Oe was measured, showing a capability of detecting vector magnetic fields [249].
SAW-based magnetic field sensors are a very active research area with many developments in the last 15 years. Currently, an impressive LOD of 10 pT/Hz1/2 has been demonstrated at 100 Hz, with a bandwidth of up to 1 MHz [250]. The aim is to further reduce LOD into the femto-tesla range, which is pivotal to bio-medical applications. However, to achieve this, there are still some challenges to specifically reduce the 1/f noise at low frequencies. Going forward, this noise can be reduced by achieving precise control of the magnetic layer (by using materials with a high piezomagnetic coefficient (CoFeC [142] or FeGaC [145] or materials with low losses [251,252,253]) and using piezoelectric materials with high electromechanical coupling and low dielectric and mechanical damping (LiNbO3 and LiTaO3, which have large piezoelectric coefficients compared to quartz, Table 2).
4. Magnetoelectric Antennas
4.1. BAW ME Antenna
Antennas are an integral part of electrical circuits that enable the transfer of information. Conventionally, the antennas are made from conductors, have sizes that are comparable to the electromagnetic wavelength λ0 of the frequency signal they are transmitting and can be scaled down at maximum to λ0/10 [254]. This size is too large for certain applications, where the space is limited, e.g., in mobile phones and medical devices. Moreover, conventional antennas, when mounted parallel to the ground surface, suffer from the ground plane effect, which results in a reduced antenna gain. In such applications, magnetoelectric (ME) antennas are very attractive alternatives. As such, antennas operate at their acoustic resonance, which is determined by their physical size and acoustic velocity, rather than their electromagnetic resonance. The acoustic wavelength is five orders of magnitude smaller than the electromagnetic wavelength at a given frequency. Additionally, the ME antennas do not suffer from the ground plane effect, and the in-phase magnetic image current further enhances the antenna gain by 3 dB [19].
The active component of a bulk acoustic wave resonator is a ME composite, which consists of a piezoelectric and magnetostrictive material. The piezoelectric layer of a ME antenna is sandwiched between the top and bottom electrode, while a magnetostrictive layer is deposited on top of the sandwiched stack. The resonator can function as an antenna in the following way. As a transmitter, the RF signal is fed to the piezoelectric layer via top and bottom electrodes. The signal appropriately deforms the materials via piezoelectric effect, and the strain is transmitted to the magnetostrictive material through the coupling between the two materials. The magnetostrictive material oscillates accordingly due to inverse magnetostriction (Villari effect) and radiates electromagnetic waves. Alternatively, the resonator functions as a receiver as a high-frequency magnetic field is radiated on top of the magnetostrictive layer, which deforms due to the magnetostriction effect. The strain of the magnetostrictive layer is transferred to the piezoelectric layer and generates the proportional voltage due to the inverse piezoelectric effect. The BAW ME antennas can primarily be classified into two different types based on their operation configuration, namely (1) thin-film bulk acoustic resonators (FBARs) and (2) solidly mounted resonators (SMRs).
4.1.1. FBAR
Strain-mediated BAW-based ME antennas were first theoretically reported by Yao et al. [255] and Chen et al. [256]. The authors report a novel strain-mediated antenna that has a better radiation performance compared to conventional antennas. Experimentally, MEMS-based FBAR ME antennas were first reported by Nan et al. in 2017 [15]. Two different resonators were proposed, including a nanoplate resonator (NPR) which has a rectangular structure (oscillating along the width), and a FBAR (oscillating along the thickness). Both of the resonators consist of a piezoelectric AlN layer and a magnetostrictive FeGaB layer. Air cavities are formed below the resonators by etching substrates, in order to have excellent acoustic localization. Such a design, though challenging to fabricate, allows for better oscillation of the resonator. The resonance frequency of the NPR is 60.5 MHz, as determined by the width of the NPR. A RF coil was used to excite the antenna at its resonant frequency (Figure 16a). The NPR structure demonstrated α = 6 kV/cm Oe with an induced peak voltage of 180 μV. A control device was also demonstrated where the magnetostrictive FeGaB layer was replaced with Cu. This showed a peak-induced voltage of 18 μV, which is a factor of 10 below the ME NPR counterparts (Figure 16b–e).
Figure 16.
(a) The illustration of the NPR antenna and the measurement setup. The high-frequency magnetic field is generated by the RF coil. On the bottom, a SEM picture of the antenna is shown with different individual layers (AlN, FeGaB, and Au). (b) The admittance curve and the Butterworth–van Dyke mode, and the inset shows the various parameters. (c) Admittance curve of a control device, where the magnetic layer is replaced with Cu. (d) The ME coefficient (right) and ME-induced voltage in the piezoelectric layer as a function of frequency. (e) Analog-induced voltage in the piezoelectric layer of the control device; the inset shows a zoomed-in view of the red circle. (f) The set-up of a FBAR antenna that uses a horn antenna to excite the magnetostrictive layer. At the bottom, a SEM picture of the close-up of the FBAR antenna highlighting the individual layers (AlN, FeGaB, and Au). (g) Return loss curve (S22) of the ME FBAR antenna. The inset shows the simulated displacement of the ME FBAR device at resonance. (h) Return loss curve (S22) of the control FBAR device when the magnetic layer is replaced with a non-magnetic Al layer. (i) The transmission (S12) and receiving (S21) behavior of the FBAR antenna. (j) Transmission (S12) and receiving (S21) curves of the control FBAR device; note the sharp reduction of the peaks compared to the ME FBAR. Reprinted from Ref. [15].
The FBAR antenna demonstrated a clear resonance peak at 2.53 GHz (Figure 16f,g). The frequency is much higher compared to the NPR, as it is resonating along the thickness, which is one order of magnitude smaller compared to the width of the NPR. The ME FBAR antenna showed a gain of −18 dBi calculated by the gain transfer method. The authors compare the resonator performance with a control device, where the FeGaB layer is replaced with Al while keeping the rest the same. The control sample shows almost no transmission peaks, as is evident in the S21 and S12 peaks (Figure 16i,j). Thus, the transmission seen in the ME antenna directly results from the magnetic component (FeGaB).
Recent efforts to increase the gain of the FBAR antennas were demonstrated by using an antenna array [19]. This work also highlights ground plane immunity and a 3 dB gain enhancement when the ME FBAR antennas were mounted on top of ground planes of various sizes (GP1-GP5, Figure 17a,b). Typically, when conventional antennas are placed close to or in-plane with large conductive substrates, they suffer from the ground plane effect, leading to suboptimal antenna performance. This is primarily due to the generation of image currents in the ground plane that are out of phase, which greatly degrades the antenna’s radiation efficiency. In contrast, ME antennas rely on magnetic radiation and generate in-phase image currents instead of out-of-phase image currents, which results in a 3 dB gain enhancement, regardless of the ground plane size (GP1–GP5).
Figure 17.
(a) Return loss curve (S11) of the ME FBAR antenna with a resonant frequency of 1.95 GHz and an 8.4 MHz bandwidth mounted on different sizes of ground planes (GP1–GP5). (b) Transmission (S21) curves of the ME FBAR antennas along with a control device (mounted on top of a 2 cm × 2 cm plastic substrate). Note the 3 dB gain enhancement of the ME FBAR mounted on GP vs. control device. (c) Optical images of four ME FBAR antenna array configurations. (d) Gain enhancement of different antenna configurations, showing a non-linear increase in gain as a function of antenna number. Reprinted from Ref. [19].
The study investigated different ME antenna arrays that have different topologies including 1 × 1, 1 × 2, 1 × 3, 2 × 2, 3 × 2, 2 × 3, and 3 × 3 (Figure 17c). Increasing the number of antennas proportionally increases the volume of the magnetostrictive material and the total available magnetic moment for radiation. The authors expected that, as the number of antennas increased, the gain, radiation, and bandwidth would improve, since different structures have slightly varying thicknesses. The antennas consist of an AlN piezoelectric layer, with a multi-layer stack of FeGaB/SiO2 used as the magnetostrictive layer. The resonant frequency of the antennas in the array falls between 2.51 and 2.53 GHz, demonstrating excellent fabrication control.
The authors observed a non-linear increase in gain as a function of the antenna number (Figure 17d), mainly due to the mismatched input impedance as the resonator number increases. Nevertheless, the array with nine individual device elements showed the highest gain at −17.3 dBi, representing a 10 dBi enhancement compared to the single resonator. The radiation pattern of the ME antenna arrays follows that of a single ME antenna, with only the gain being enhanced while maintaining the same directionality. The increase in antenna size for the 3 × 3 array does not result in a proportional gain enhancement, indicating the need for further optimization. However, these efforts to realize such ME antenna arrays could enable multiband or wideband antennas for applications in wireless communication, power transfer, and implantable biomedical devices.
ME antenna bi-layer structures were also investigated for other applications. A NeuroRFID investigated by Zaeimbashi et al. consists of a compact ME antenna array with three NPRs that could simultaneously be used as energy harvesters and magnetic field sensors. The dual-band device has created a huge interest in the biomedical community [14]. The resonators have two resonating modes, one along the thickness and the other along the width of the oscillator. Like the previous FBAR antennas, an air gap between the substrate and the resonator is created to allow for strong acoustic wave excitation. As the thickness of the AlN is 500 nm, which is significantly lower than its width of 50 μm, it has a higher resonance frequency in the thickness mode at 2.5 GHz compared to the width mode at 63.6 MHz. The thickness mode was used for energy harvesting and showed a FOM of 3721, and the width mode was used for magnetic field sensing and allowed for a LOD of 470 pT/Hz1/2 (for details please check NPR array ME sensor section). Other devices such as a low-frequency MEMS-based ME magnetic sensor operating at 224 Hz were investigated. The resonating structure is a 70 μm diameter disk. The devices show a LOD of 800 pT at 1 μV at a resonance frequency of 224 kHz [257].
4.1.2. SMR
The SMR antennas differ from FBAR antennas by having no air gap between the resonator and the substrate. In the FBAR operation, acoustic localization is achieved by the air gap. However, in the case of the SMR, a so-called Bragg reflector is used to achieve the localization. The Bragg reflector consists of alternating layers of materials with high and low acoustic impendence and acts as an acoustic mirror. The antennas are fabricated on top of the Bragg reflector to isolate the resonator during excitation. The SMR has multiple advantages compared to the FBAR, such as no need to release the resonator in fabrication and increased device robustness.
The concept of SMR-based ME antennas was first proposed by Liang et al. in 2020 [16] and was more elaborately investigated in 2023 (Figure 18) [20]. The antennas were fabricated on top of a Bragg reflector (layered stack of W and SiO2). A SEM cross-section reveals the different layers of the antenna (Figure 18a,b). A highly textured ZnO with a Full Width Half Maximum (FWHM) of 2.29 was used as a piezoelectric material, while a 10-layer stack of (FeGaB (45 nm)/SiO2 (5 nm)) was used as a magnetostrictive layer. The antennas were excited with the help of a high-frequency magnetic field Hrf from a horn antenna along different directions. The maximum gain of −18.8 dBi is demonstrated when the Hrf is parallel to the easy axis direction, and it shows the lowest gain when the Hrf is parallel to the hard axis of the antenna. The authors also show an increased power-handling capability, with the 1 dB compression point at 30.4 dBm for the SMR, compared to 7.1 dBm for the FBAR counterpart (Figure 18c). Such high power-handling capabilities would allow SMR antennas to be supplied with higher input power, which could allow for the generation of stronger electromagnetic (EM) waves. A similar SMR-based antenna was reported by Ma et al., who demonstrated a SMR antenna working at 4.97 GHz with −25.1 dBi gain capable of 5G communication [258].
Figure 18.
(a) Cross-sectional view of the SMR ME antenna showing the different layers. The Bragg reflector (3 × W/SiO2), Pt (bottom electrode), ZnO, and FeGaB layers are evident. (b) Optical image of the SMR ME antenna. The GSG pads are used to feed the signal during transmission mode or read out the signal in the receiving mode of the antenna. (c) The power-handling capability of the SMR ME antenna compared to the FBAR ME antenna. The SMR has a 1 dB compression point at 30.4 dBm while the FBAR has it at 7.1 dBm. Reprinted from Ref. [20].
Over the last seven years, after the initial experimental evaluation of the BAW FBAR antennas, there have been significant breakthroughs in the field of ME antennas. The current research has been established for making antenna arrays with increased gain and SMR-based robust devices with high power-handling capability. However, for further enhancement of the antenna’s properties, two approaches can be considered. (1) A more detailed understanding of the micromagnetic dynamics driven by acoustic wave excitation must be realized, in particular, the correlation between the magnetic noise and the antenna’s properties during transmission and receiving modes. If the magnetic noise plays a major role, this can be reduced by incorporating exchange bias layers in the magnetic field layer. (2) Using materials with low losses can enhance the efficiency of the antennas. It is well demonstrated in the literature that AlN is a CMOS-compatible piezoelectric layer that has very low losses (tan δ: 0.025% ± 0.011, [75]). On the other hand, typical magnetostrictive materials have magnetic damping on the order of 10−4–10−3. Replacing them with yttrium iron garnets (which have a very low damping in the order of 10−5 [259]) would increase the radiation efficiency.
4.2. SAW ME Antenna
SAW-based ME antennas are a relatively new area of focus with only a couple of studies published to our knowledge [260,261]. A great advantage of using such SAW-based devices is that they can operate in the medical implant communication services (MICS) band (402–405 MHz), which is predominately used for implant communication. BAW-based NPR antennas that can operate in the MICS band were investigated previously, but the resulting structures are 8 μm wide, which are challenging to fabricate [262]. Realizing such 400 MHz FBAR antennas is challenging, as the thickness needed for a piezoelectric layer to excite is approximately 14 μm, which is challenging to achieve using physical vapor deposition techniques, such as sputtering or evaporation. Hence, SAW-based antennas provide an attractive alternative. In a recent 2024 study, Zhang et al. [261], showed a SAW-based antenna fabricated on top of a LiNbO3 substrate with FeGaB as the magnetostrictive component. As shown in Figure 19a–d, the antenna has (measured from the image 5 mm × 1.5 mm, [261]) increased in area by a factor of 16 compared to the bulk acoustic resonator (BAR) (SMR—0.67 mm × 0.67 mm, measured from [20]) counterparts. The proposed design showed an increased gain of −28 dBi at 430 MHz while using a FeGaB layer of 670 nm. Another new method was proposed to enhance the radiation of a SAW-based antenna operating at 1.87 GHz. The authors report an enhancement of efficiency by 70.95 ± 6.4% when a magnetic field was applied [260].
Figure 19.
(a) The illustration of the SAW-based ME antenna showing different layer configurations. (b) The optical image of the SAW-based ME antenna. (c,d) Device testing schematic and the associated radiation pattern of the SAW ME antenna. Reprinted with permission from Ref. [261]. Copyright 2024 IEEE.
SAW-based ME antennas are relatively new, and there have been limited investigations. Their large size in comparison with BAW ME antennas gives them a relative disadvantage. More considerations into device miniaturization and increased gain must be taken.
4.3. Very-Low-Frequency Antennas
Very-low-frequency (VLF: 3–30 kHz) electromagnetic (EM) waves can penetrate dense conductive media such as earth and water, which makes them ideal for applications such as underwater communications and navigation, subterranean mapping, underground communication, and ionospheric remote sensing [19]. However, the long wavelength (10 km~100 km) of VLF signals requires antennas to be large and have high power consumption. The development of magnetoelectric (ME) antennas based on bulk and surface acoustic wave resonators has significantly reduced VLF antenna size, scaling down from several square kilometers to just a few square centimeters [263,264,265].
The VLF ME antenna concept was first put forward by Sun and Li [266] in 2016, and a practical device was reported by Dong et al. in 2020 [263]. A communication system operating at very low frequency (VLF) that employs a magnetoelectric (ME) transmitter alongside a ME receiver was demonstrated, utilizing a pair of ME heterostructures functioning at their electromechanical resonance (EMR) frequency. The structure and image of the device are depicted in Figure 20a,b, respectively. This VLF antenna features Metglas as its ferromagnetic component and lead zirconate titanate (PZT-5) as the piezoelectric element. By applying an electric field to the PZT fibers’ surface, a surface acoustic wave (SAW) is generated, with the resonance frequency being determined by the pitch of the interdigitated electrode (IDE) fingers. The magnetic domain’s rotation, controlled by ME coupling, acts as the radiation source for the antenna. A notable peak at 23.95 kHz was observed, with a signal-to-noise ratio (SNR) of 92.3 dB measured, as illustrated in Figure 20c. The system attained a low limit of detection (LOD) of 180 fT, indicating a high electric field sensitivity suitable for long-range communication (Figure 20d,e). The expected magnetic field produced by the ME transmitter is shown in Figure 20e and modeled through a near-field electric and magnetic dipole approach for the piezoelectric and magnetostrictive phases. With a LOD of 260 fT/Hz1/2, a communication range reaching up to 120 m was accomplished [263]. It is anticipated that a range between 2.5 and 10 km could be achievable with a compact array consisting of 100 elements. Lastly, Figure 20f reveals that, as the driving voltage increased from 0.5 to 120 V, there was a rise in both the radiation intensity and the power consumption. The power consumption reached approximately 300 mW when the voltage reached 60 V. Despite this advancement in VLF communication, the bandwidth and efficiency of VLF ME antennas are still constrained by relatively low resonance frequencies at VLF. The authors also introduce a direct antenna modulation (DAM) by using a non-linear response. With a carrier signal at EMR frequency and a magnetic modulation signal frequency of 100 Hz, the antenna achieved 29 dB SNR at a 16 m communication distance [263].
Figure 20.
The VLF ME antenna: (a) A 3D model showing each layer. (b) An optical top view photograph with the antenna’s dimensions. (c) The measured received signal at the resonance frequency along with the noise floor. (d) The measured output voltage as the bias field decreases, showing the limit of detection. (e) Predicted and measured magnetic field distribution as a function of distance. (f) Radiation field and power consumption of the ME transmitter under varying driving voltages. Reprinted with permission from Ref. [263]. Copyright 2020 IEEE.
In 2022, Dong enhanced the magnetoelectric (ME) antenna by incorporating a higher Q-factor mechanical resonator using Metglas/PZT-8/Metglas, and by increasing the number of ME antennas in an array, he achieved a total radiation field of 200 nT at 1 m using 12 antenna array [264]. In the same year, Hu et al. developed a VLF antenna with a Metglas/PMN-PT structure, obtaining a giant converse magnetoelectric coefficient of 6 Oe·cm/V at 6.3 kHz [267]. In 2023, Du et al. demonstrated the feasibility of using ME antennas for portable underwater communication, reaching a maximum underwater propagation distance of 2.2 m [268]. Also in 2023, Fu et al. introduced a bias-free VLF ME antenna with the structure of annealed Metglas/Metglas/PZT/Metglas/annealed Metglas, which exhibited a high direct magnetoelectric coefficient (αDME = 107 V/cm·Oe) and a converse magnetoelectric coefficient (αCME = 9 G/V) without the need for biased magnetic field [269].
5. Magnetoelectric BAW/SAW Devices for Non-Reciprocity and NV− Center Excitation
5.1. Magnetoacoustic SAW Non-Reciprocal Isolators
Recent advances in integrated nonreciprocal components, such as isolators and circulators, have enabled a gamut of wireless communication/sensing modalities that are otherwise not possible [270,271,272,273,274,275,276,277]. For instance, isolators can be used to protect on-chip high-power amplifiers from back reflection. Integrated circulators in conjunction with self-interference (SI) cancellation technology can enable the feasibility of in-band full-duplex operation for future wireless systems and networks. Conventional circulators are based on the constructive or destructive interferences of electromagnetic signals under magneto-optical Faraday rotation in ferrite materials at different signal ports [278]. The constructive interference at the first port in one circuitry direction and the destructive interference at the second port enable the functionality of signal transmission along one circuitry direction and forbid the other direction [278]. The isolators can be easily realized by adding a perfectly matching load at one of the circulator ports. These ferrite-based isolators/circulators exhibit low insertion loss (<1 dB) and a high power-handling capability of up to tens of watts [279]. However, the operation requirement of a kOe-level bias field necessitates the setup of strong permanent magnets or electromagnets, which make the commercial isolators/circulators bulky and expensive, with high power consumption, manufacturing complexity, and potential electromagnetic interference. The extremely high growth temperature of thick ferrite material makes the fabrication of these isolators/circulators incompatible with semiconductor manufacturing techniques.
Emerging efforts in non-magnetic integrated CMOS isolators/circulators have shown great potential for full-duplex transceivers based on circulators and SI cancelers for wireless applications [278,279]. However, the non-magnetic integrated CMOS isolators/circulators exhibit high DC power consumption, ranging from tens to hundreds of milliwatts. For instance, recently proposed non-magnetic CMOS circulators [270,271,275,276] based on transistor modulation suffer from high power consumption (40–200 mW), making them non-amenable for low-power applications. Additionally, current integrated CMOS nonreciprocal components exhibit low bandwidths due to their reliance on resonant ring structures [270,271,275,276]. However, when bandwidth is prioritized, their power handling is compromised [276,280]. Therefore, integrated nonreciprocal technology targeting low-power applications while exhibiting integrated high-efficiency, high-linearity, and high-isolation does not exist today and is of great importance for the future IoT-driven world.
In recent years, magnetoacoustic isolators have been widely investigated, which exhibit substantial nonreciprocity with remarkable power efficiency and CMOS compatibility, showing great potential for low-power and wideband full-duplex wireless radio systems. Magnetoacoustic non-reciprocal isolators comprise a magnetic stack between two interdigital transducers on a piezoelectric substrate. By applying a RF voltage on the transmitting IDT, a surface acoustic wave can be generated and propagate toward the other IDT. When the surface acoustic wave passes through the magnetic stack, it can interact with the non-reciprocal spin wave (SW) in the magnetic stack via various mechanisms, including magnetoelastic coupling [281,282,283], magnetorotation coupling [284,285,286], spin-rotation coupling [287,288,289], and gyromagnetic coupling [290]. Among them, magnetoelastic coupling and magnetorotation coupling are strong and widely used for magnetoacoustic isolators. Magnetoelastic coupling refers to the change of magnetization precession under a strain or vice versa, while magnetorotation coupling arises from reorientating magnetic anisotropy and dipolar shape anisotropy during SAW-driven lattice rotational motion. The interaction between SAW and non-reciprocal SW generates magnetoacoustic waves that exhibit a much higher backward loss rate than the forward one or vice versa. The dramatic difference between the damping rate of the forward and backward magnetoacoustic waves allows the signal transmission in one direction and dampens that in the other direction, contributing to a magnetoacoustic isolator.
Ongoing research strives to enhance non-reciprocity strength and bandwidth while maintaining high transmission between device ports. Even though the SAW-SW coupling is inherently non-reciprocal due to helicity mismatch between fixed counterclockwise magnetization precession and reversible lattice rotational motion chirality [284,291,292], this non-reciprocity is typically weak and less than 3 dB/mm [291,292,293] in a magnetic stack with reciprocal spin wave dispersive relation, such as a single magnetic film.
Various magnetic stacks with non-reciprocal spin wave dispersion have been theoretically investigated and experimentally demonstrated, including interfacial Dzyaloshinskii–Moriya interaction (iDMI) stacks (e.g., CoFeB/Pt) [285], dipolar coupled stacks (e.g., FeGaB/SiO2/FeGaB) [294], and Ruderman–Kittel–Kasuya–Yosida (RKKY) synthetic antiferromagnets (e.g., CoFeB/Ru/CoFeB) [295], where the key parameters of the corresponding magnetoacoustic isolators are summarized in Table 4. The iDMI stack is typically composed of a magnetic layer and a heavy metal layer, such as a perpendicular magnetic anisotropy (PMA) Ta/CoFeB/MgO/Al2O3 stack [284]. The nonreciprocal behavior originates from iDMI and SAW-SW helicity mismatch (HM), the interaction between the chirality of rotational lattice distortions and the magnetization influenced by magnetic anisotropies. However, the bandwidth of such non-reciprocity is typically narrow (10~100 MHz) [296]. Non-reciprocity has also been demonstrated in interlayer dipolar coupling (IDC) stacks which are composed of two magnetic layers spaced by several nm thick insulating or conductive layers. As the spacer layer thickness decreases, the initially uncoupled reciprocal Damon–Eshbach spin wave (SW) modes in the two thin magnetic layers become coupled through the dipolar stray fields of the spin waves [297]. This coupling gives rise to symmetric (in-phase) modes and the antisymmetric (out-of-phase) modes [298,299]. The giant non-reciprocity of 48.4 dB/mm has been achieved at 1.435 GHz in the FeGaB (20 nm)/Al2O3 (5 nm)/FeGaB (20 nm) IDC stack with magnetization perpendicular to the non-collinear uniaxial anisotropy field directions (~60 degrees to the SAW propagation direction) [294], as shown in Figure 21. Phase non-reciprocity has also been realized at the same frequency and bias field condition [300].
Figure 21.
Experimental results on the giant nonreciprocity effect of hybridized SAW/SW in the FeGaB/Al2O3/FeGaB multilayer stack on the piezoelectric lithium niobate substrate at the frequency of 1435 MHz when a growth field (HG) was oriented at 60°. Acoustically Driven Ferromagnetic Resonance (ADFMR) plots were generated for hybridized SAW/SW traveling in the (A) +z direction and (B) −z direction. Resonance absorption, highlighted in blue on the color scale, was observed at the ADFMR frequency in directions orthogonal to the growth field, where strong magneto-acoustic interaction took place. (C) Field sweeps at ϕ = 150° for forward (blue) and reverse (orange) SAW propagation. (D) Field sweeps at ϕ = 330° for forward (blue) and reverse (orange) propagation. The isolation was determined by the difference between forward and reverse sweeps under identical static field conditions. The nonreciprocal power isolation of 48.4 dB was observed. Reprinted with permission from Ref. [294]. Copyright 2020 The American Association for the Advancement of Science.
For extremely thin (<1 nm) conductive spacer layers, it is necessary to account for interlayer RKKY exchange interactions [301,302]. RKKY antiferromagnetic exchange interaction has been theoretically proposed to have a wide non-reciprocal transmission band [296] and giant isolation strength suitable for wideband non-reciprocal RF isolators, circulators, and phase shifters [303]. Recently, this wide non-reciprocity has been experimentally demonstrated in a CoFeB/Ru/CoFeB RKKY stack [304], as shown in Figure 22a,b. A wideband non-reciprocity from 2 to 7 GHz was realized in the CoFeB (16 nm)/Ru (0.55 nm)/CoFeB (14 nm) stack, as shown in Figure 22c. The maximum non-reciprocity reached 10 dB for a 100 μm long magnetic stack at 4.86 GHz, corresponding to 100 dB/mm giant non-reciprocity. By optimizing the thickness of the CoFeB layer, 250 dB/mm giant non-reciprocity was achieved in the CoFeB (16 nm)/Ru (0.55 nm)/CoFeB (5 nm) stack [295], as shown in Figure 22d. Although synthetic antiferromagnetic (SAFM) structures have been quite successful, selecting a proper magnetic layer thickness is not trivial due to the trade-off between the IDC and RKKY requirements regarding the magnetic layer thickness. High IDC benefits from thicker magnetic layers or higher wavenumbers to enhance spin wave (SW) nonreciprocity. However, increasing the layer thickness weakens the RKKY antiferromagnetic coupling. Recently, the magnetoacoustic coupling between the shear horizontal waves in 36°-rotated or 42°-rotated Y-cut X-propagation LiTaO3 substrates and spin waves in ferromagnetic or anti-magnetostrictive bilayers has been investigated [305,306,307]. A giant non-reciprocity ranging from 60 dB/mm [305] to 82 dB/mm [307] has been realized when the bias field is applied perpendicular to the SAW propagation direction. The magnetoacoustic coupling in ferromagnetic bilayers [305] and anti-magnetostrictive bilayers [306,307] provides another practical and technologically simple system to realize transmission non-reciprocity for RF isolators/circulators.
Figure 22.
Wideband and giant nonreciprocity experimentally demonstrated in CoFeB/Ru/CoFeB RKKY stack. (a) Schematics of magnetoacoustic device. (b) SAW and SW dispersive relation near wide-band resonance region. (c) Wideband non-reciprocity from 2 to 7 GHz realized in CoFeB (20 nm)/Ru (0.46 nm)/CoFeB (20 nm) stack. (d) A 250 dB/mm giant non-reciprocity achieved in CoFeB (16 nm)/Ru (0.55 nm)/CoFeB (5 nm) stack. Image (a–c) is reprinted with permission from Ref. [304]. Copyright 2024 American Chemical Society; Image (d) is reprinted with permission from Ref. [295]. Copyright 2023 American Chemical Society.
As shown in Table 4, the demonstration of magnetoacoustic isolators typically yields a high insertion loss above 25 dB owing to high-order mode SAW harmonics, which is far from practical applications. Future work should be put into reducing insertion loss by utilizing fundamental mode IDT electrodes. In addition, a self-biased magnetic stack with a high magnetic anisotropy field should be developed to eliminate the need for a biased magnetic field, which necessitates the permanent magnet or electromagnet and makes the magnetoacoustic isolator bulky with high power consumption and electronic noise.
Table 4.
Summary of the experimentally demonstrated non-reciprocal magnetoacoustic isolators.
| Magnetic Stack | Piezoelectric Substrate | Mechanism | DC Bias Field (mT) | Operation Frequency f (GHz) | Magnetic Stack Length l (um) | Off Magnetoacoustic Resonance Insertion Loss (dB) | On Magnetoacoustic Resonance Insertion Loss (dB) | Non-Reciprocity | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| Ta/CoFeB(1.6 nm) | Y-cut Z-propagation LiNbO3 | SAW-SW HM, iDMI | 110 | 6.1 | - | - | - | - | [284] |
| CoFeB(5 nm)/Pt | Y-cut Z-propagation LiNbO3 | SAW-SW HM, iDMI | 21 | 6.77 | 750 | 71 | 87.5 | 28 | [285] |
| FeGaB(20 nm)/Al2O3(5 nm)/ FeGaB(20 nm) |
Y-cut Z-propagation LiNbO3 | IDC | 1 | 1.435 | 2200 | 60 | 65 | 22 | [294] |
| NiFe(20 nm)/Au(5 nm)/CoFeB(5 nm) | Y-cut Z-propagation LiNbO3 | IDC | 21 | 6.87 | 500 | 89 | 89.8 | 74 | [297] |
| CoFeB(20 nm)/Ru(0.46 nm)/ CoFeB(20 nm) |
128°-rotated Y-cut X-propagation LiNbO3 | IDC, RKKY | 5 | 1.4 | 1000 | 29 | 33 | 37 | [308] |
| Pt/Co(2 nm)/Ru(0.85 nm)/Co(4 nm)/ Pt |
Y-cut Z-propagation LiNbO3 | IDC, iDMI, RKKY | 60 | 6.77 | 750 | 81 | 81.75 | 3 | [309] |
| CoFeB(16 nm)/Ru(0.55 nm)/ CoFeB(5 nm) |
128°-rotated Y-cut X-propagation LiNbO3 | IDC, RKKY | 20 | 5.08 | 150 | 81 | 81.135 | 250 | [295] |
| Ta(2 nm)/Ru(2 nm)/CoFeB(16 nm)/Ru(0.55 nm)/CoFeB(14 nm)/Si3N4(3 nm) | Y-cut Z-propagation LiNbO3 | IDC, RKKY | 13.8 | 3 4.86 6.96 |
100 | 45.6 57.8 90.3 |
45.6 57.8 90.3 |
60 100 70 |
[304] |
| FeCoSi-B(10 nm)/NiFeCu(10 nm) | 36°-rotated Y-cut X-propagation LiTaO3 substrate | IDC | 9 | 2.33 | 500 | 54 | 69 | 60 | [305] |
| Ni (16 nm)/Ti (8 nm)/FeCoSiB(16 nm)/Ti (10 nm) | 42°-rotated Y-cut X-propagation LiTaO3 | IDC | 5.7 | 2.333 | 500 | 53 | 55 | 82 | [307] |
5.2. Magnetoacoustic BAW/SAW Devices for NV− Center Excitation
Negatively charged nitrogen-vacancy (NV−) centers in diamonds, comprising a nitrogen atom and a nearby lattice vacancy, are quantum spin defects with unique properties [310]. These centers exhibit extended coherence times exceeding 100 µs at room temperature [311], exceptional fidelity [312], and facile optical initialization and readout of quantum states [313]. Combined with their responsiveness to magnetic excitations over a wide temperature range, these features make NV− centers highly promising for quantum computing, communication, and information-processing applications [314,315,316], as well as for use as non-invasive nanoscale magnetic sensors [317,318,319].
The coherent manipulation of NV− centers can be achieved via alternating current (AC) magnetic fields, electric fields [320], and strain waves [321], enabling their function as hybrid quantum transducers and computational units. Unlike direct AC magnetic field excitation via microwave antennas, spin wave (magnon) excitations offer long-distance, coherent control of NV− centers over scales ranging from hundreds of microns to millimeters. Moreover, magnons can deliver 100 times stronger local driving fields with identical power inputs [322,323,324]. This power-efficient approach minimizes off-resonant spin wave noise at high power [325] while preserving the long coherence times required for magnon-mediated entanglement and communication between NV− center qubits. These properties facilitate the development of on-chip quantum processors and computational units. Furthermore, NV− centers can couple to terahertz optical photons, supporting their potential as microwave-to-optical quantum transducers that convert GHz qubit excitations into terahertz photons [326] for long-distance quantum information transfer. Together, the magnon–NV− and NV−–optic–photon couplings serve as foundational elements for hybrid quantum networks [327,328,329,330,331].
Phonons, with their extended lifetimes in solid-state systems, also represent excellent information carriers for quantum and coherent information processing. The small wavelengths of acoustic waves render phonons particularly suitable for on-chip quantum systems [332]. Strain wave-driven magnon excitations, which are more power-efficient than microwave-driven methods, can significantly reduce the size of NV−-center-based quantum transducers. In strong coupling regimes, magnon–phonon interactions lead to magnon–polaron hybrid states, enabling efficient information transduction between magnon and phonon systems. This process paves the way for phonon–magnon–NV–photon hybrid quantum transduction platforms.
Recent advancements have demonstrated the magnetoelectric control of NV− centers through magnetoelectric coupling in CoFeB/300 µm PMN-PT heterostructures [333], as depicted in Figure 23. The application of an external voltage (V) to the PMN-PT substrate induces changes in its electrical polarization, which generates lattice strain. This strain is transferred to the CoFeB film, altering its magnetic anisotropy, as illustrated in Figure 23a,d. When a fixed external magnetic field (Hext) is applied along the [100] x-axis, increasing the voltage from V = Voff to V = Von reverses the polarization (Pz), tuning the magnon band into resonance with the NV− electron spin resonance (ESR) transitions, as shown in Figure 23b,e. This magnon band shift arises from the coupling between electric, elastic, and magnetic orders within the multiferroic heterostructure. Specifically, as the voltage increases from 50 V to 200 V, the anisotropy field (Hk) decreases consistently from Hk = 30 Gauss to Hk = −22 Gauss, signifying a flipping of the magnetic easy axis from the x to the y direction, accompanied by the reversal of Pz (Figure 23c). Concurrently, the lowest spin relaxation rate (Γ1) increases significantly from 25.1 ± 2 [ms]−1 at V = Voff to 102.8 ± 9 [ms]−1 at V = Von, corresponding to a remarkable 400% tuning of Γ1. This pronounced tunability of Γ1 underscores the potential of magnetoelectric control to facilitate robust interactions between magnons and NV− centers in a highly energy-efficient manner.
Figure 23.
Magnetoelectric control of NV− center by CoFeB/PMN-PT BAW resonator. (a,d) Schematic illustration of the quantum spin defects (QSD)-magnon hybrid sample fabricated by dispersing nanodiamonds containing ensembles of NV− centers on a thin ferromagnetic film of CoFeB on a 300 μm thick PMN-PT ferroelectric substrate. (b,e) Maps of normalized B as a function of ω−k for both Von and Voff. The black lines enveloping the colormap are the calculated magnon dispersion lines for bulk modes (k∥M) and surface modes (k⊥M). The dashed colored lines represent the NV− ESR lines ωNV. (c) FMR frequency () (data in black lines) as a function of applied voltage extracted from the experimental results for a fixed external magnetic field Hext = 57 G along x-axis. The color map represents the calculated values of the magnetic noise spectral density Gm(ω, V) for an effective NV− height dNV = 77 nm. The dashed colored lines represent the maximum spread of the NV− ESR lines ωNV. The inset shows the detailed measurements of the magnetic anisotropy field as a function of applied voltage. (f) Measured relaxation rates Γ1 as a function of applied voltage for a fixed Hext = 57 G along the x-axis. The inset shows a schematic illustration of the magnetic anisotropy field for the two different voltages for a fixed Hext. The dashed line represents the theoretical fit of relaxation rates Γ1. These figures are reproduced from Ref. [333].
Surface acoustic wave (SAW) resonators are particularly advantageous for fostering strong magnon–phonon interactions, as they efficiently concentrate acoustic energy on the surface, facilitating robust coupling with spin waves. Furthermore, their planar structures simplify the fabrication process compared to bulk acoustic wave resonators. Recent advancements in SAW-driven magnon resonance have demonstrated highly localized and efficient control of NV− centers, achieving Rabi frequencies comparable to those induced by microwave excitation but with over 1000 times greater power efficiency [322,323]. In a key experiment, a 20 nm Ni or Co film was positioned between interdigital transducers (IDTs) operating at a fundamental frequency of 287 MHz [334]. The resulting power absorption exhibited a fourfold symmetry, peaking at ϕ = 45 degrees, as illustrated in Figure 24a. This absorption could be tuned using a biased magnetic field applied at 45 degrees, as shown in Figure 24b. At the fifth harmonic frequency of 1429 MHz, the power absorption exceeded that observed at both the fundamental and third harmonic frequencies. At this 1429 MHz frequency, a direct photoluminescence (PL) change in NV− centers was detected, aligning closely with their excited state resonance frequency (Figure 24c). The observed PL change is attributed to ferromagnetic resonance (FMR), as no PL signal was recorded at high fields near the IDT. The intensity of the NV− PL change diminished with the increasing distance from the leading edge of the magnetic film, which is consistent with signal absorption as the excitation propagates through the magnetic layer, as depicted in Figure 24d. To enhance the performance of magnetoelectric SAW (ME SAW) devices, it is imperative to utilize magnetic materials with low damping and strong magnetoelastic coupling. Additionally, the confinement and focus of surface acoustic wave energy are crucial for achieving efficient and localized control of NV− centers via SAW-driven magnetic resonance. Recent innovations include the application of Gaussian focusing techniques in SAW devices, which suppress acoustic diffraction loss and significantly enhance the quality factor (Q) to 22,400 at cryogenic temperatures (~30 K) [335]. Moreover, Bragg reflectors have been employed to enable strong magnon–phonon coupling, achieving a cooperativity of 1.2 [336]. Advancing the acoustic wave confinement and focusing strategies represents a promising research direction. Such efforts will support the development of strong magnon–phonon interactions and enable the coherent control of NV− centers, paving the way for hybrid quantum transducers that integrate magnons, phonons, NV− centers, and photons.
Figure 24.
Energy-efficient and local control of NV− centers by SAW-driven magnon resonance. (a) Plot of power absorption as a function of applied magnetic field for a 20 nm nickel ADFMR device at 1429 MHz. The x component of the field is taken to be parallel to the direction of SAW propagation, and the y component is in-plane and perpendicular to the direction of SAW propagation. The color bar indicates absorption in decibels per millimeter. (b) Line-cut along the angle of highest absorption (45°) showing a large field-dependent attenuation at 287, 861, and 229 MHz. The insets show the photograph of IDTs, magnetoelastic film, and clusters of nanodiamonds on the measured device. (c) Change in PL normalized to the DC level for NV− centers located off the ferromagnetic pad (red), and NV− centers on the pad with zero field (blue) and a high (35.8 mT) applied bias field (green) (d) NV− PL change in a 20 nm nickel sample as a function of longitudinal position from the edge of the ferromagnet closest to the excitation IDT at zero applied magnetic field. These figures are reproduced with permission from [334]. Copyright 2018 The American Association for the Advancement of Science.
6. Conclusions and Outlook
Based on a magnetostrictive/piezoelectric composite, BAW and SAW ME devices have revolutionized sensing, RF, and quantum technologies. BAW and SAW ME devices enable multiple functionalities, including ultra-sensitive magnetic sensing, high-gain wireless communications, extremely efficient wireless power transfer, non-reciprocal RF isolation and circulation, and energy-efficient excitation of quantum defects.
Over the past decade, ME sensors have garnered significant attention as promising tools for magnetic sensing applications. Utilizing magnetic/electrical frequency conversion and the delta-E effect, intensive efforts have been put into applying novel piezoelectric or magnetostrictive materials or stacks, improving piezoelectric or magnetostrictive material properties, electrode or sensor structure designs, and identifying and reducing thermal, magnetic [337], and acoustic noise [338]. Tens of pT magnetic noise performances have been realized in the low-frequency band for detecting bio-magnetic signals. Thin-film ME sensors offer low-profile, high spatial resolution, and contactless measurement options compared to electrode-based systems. Demos in magnetocardiography (MCG) and magnetic particle mapping (MPM), magnetoneurography (MNG), and magnetomyography (MMG) have been developing [7,8,14,15,339,340,341,342]. However, a sensitivity gap still exists between thin-film ME sensors and leading magnetometers, like SQUIDs and optically pumped magnetometers (OPMs). To narrow this gap, it is crucial to develop low-noise, soft magnetostrictive thin films with giant piezomagnetic coefficients and piezoelectric materials with a high mechanical quality factor [343], since the SNR of ME sensors in resonance mode increases by Qm1/2 and the SNR increases by Qm3/2 for the delta-E operation scheme [233,242,343]. In addition, acoustic mode optimization is also important. It has been demonstrated that second-order bending modes increase magnetic sensitivity compared to first-order modes due to the lesser impact of inhomogeneous internal stray fields and the weighting of local properties [344]. ME resonators with innovative structures and vibration modes at higher frequencies and high-quality factors can significantly boost signal-to-noise ratios (SNR). Controlling intrinsic noise in ME sensors also requires carefully managing magnetic domain activity, which can be achieved through engineering the magnetic layers and optimizing the excitation fields. Novel acoustic noise rejection and signal-processing techniques should be developed to reduce the need for bulky acoustic shielding chambers and reduce electronic noise, which is now limiting the performance of ME sensors. ME sensor array technology should also be investigated with effective crosstalk and interference rejection to increase screen time and ensure data accuracy and diagnosis reliability. Next-generation ME sensors should aim to reach detection limits in the femto-Tesla range across a wider frequency range (from 0.01 Hz to 1 kHz), which is achievable with innovative ME sensor designs and advanced noise-cancellation techniques.
Compared to conventional electrical antennas, whose sizes are limited by electromagnetic wavelength in meter-level at GHz frequencies, ME antennas exhibit an ultra-compact ,and ground plane immunity and 3 dB gain enhancement owing to magnetic dipole radiation. FBAR, SMR, and SAW ME antennas with different resonator structures and BAW/SAW acoustic modes have been demonstrated, with advancement in antenna gain, power-handling capability, radiation efficiency, and ground plane immunity. ME antennas with multiple functional bands for wireless communication, energy harvesting, and magnetic field sensing have been developed. Future work should be put into ME antenna array technologies to further increase the antenna gain and widen the bandwidth with ME resonator disks with different resonance frequencies. In addition, magnetic stacks with high self-biased resonance frequencies and piezoelectric materials with high electromechanical coupling should be integrated to realize strong magnon–phonon coupling at a zero-bias field, which has been theoretically demonstrated to boost antenna gain, radiation efficiency, and bandwidth [345]. To realize this, low-damping magnetic materials should be used in ME antennas with a CMOS-compatible integration method. For instance, integrating YIG films via ion implantation [346,347,348,349] onto piezoelectric layers should be explored for developing energy-efficient ME antennas.
Wideband and giant non-reciprocity have been demonstrated in magnetoacoustic devices where the Rayleigh surface acoustic wave interacts with non-reciprocal spin waves in magnetic stacks, including interfacial DMI stacks (e.g., CoFeB/Pt) [285], dipolar-coupled stacks (e.g., FeGaB/SiO2/FeGaB) [294], and RKKY synthetic antiferromagnets (e.g., CoFeB/Ru/CoFeB) [295]. Future efforts need to be put into the investigation of non-reciprocal spin waves with other SAW modes, like Sezawa mode [350], reducing the insertion loss by fundamental mode SAW, self-biased non-reciprocity without the need for external magnets, and system design of multiple magnetoacoustic devices, to realize wideband non-reciprocity from 2 to 16 GHz.
Efficient control of quantum defects such as NV− centers has been realized in BAW and SAW devices with 1000 times less power than microwave excitation. Future research should aim to achieve a heterogeneous integration of low-loss magnetic materials in ADFMR devices to facilitate NV− center manipulation within diamond crystals. This approach seeks to preserve the spin wave amplitude and propagation distance while enhancing the relaxation time (T1) and coherence time (T2) of the NV− centers and ensure that quantum information, initially transferred from acoustic phonons and stored in magnons, maintains sufficient longevity without significant decay or loss due to relaxation or decoherence. Extended T1 and T2 ensure the robust amplitude and extended propagation distance of spin waves and enable the long-distance transmission of quantum information across diverse storage and processing platforms through magnons. Fundamental mode SAW near 2.87 GHz should be utilized to excite spin waves in a magnetic stack for the excitation of NV− center ground states, which have a much longer lifetime than the excited states. A careful design should be conducted to ensure that magnetoacoustic devices have strong absorption at the frequency and magnetic field that align with the spin resonance of NV− centers.
Conflicts of Interest
The authors declare no conflict of interest.
Funding Statement
The financial support from the NSF TANMS ERC Award 1160504, NIH Award 1UF1NS107694, and the W.M. Keck Foundation is gratefully acknowledged. The authors Prasanth Velvaluri and Nian X. Sun would like to acknowledge the support from the Alexander von Humboldt Foundation for their support through the Feodor Lynen fellowship.
Footnotes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
References
- 1.Ryu J., Carazo A.V., Uchino K., Kim H.-E. Magnetoelectric properties in piezoelectric and magnetostrictive laminate composites. Jpn. J. Appl. Phys. 2001;40:4948. doi: 10.1143/JJAP.40.4948. [DOI] [Google Scholar]
- 2.Srinivasan G., Rasmussen E.T., Gallegos J., Srinivasan R., Bokhan Y.I., Laletin V.M. Magnetoelectric bilayer and multilayer structures of magnetostrictive and piezoelectric oxides. Phys. Rev. B. 2001;64:214408. doi: 10.1103/PhysRevB.64.214408. [DOI] [Google Scholar]
- 3.Will-Cole A.R., Hassanien A.E., Calisgan S.D., Jeong M.-G., Liang X., Kang S., Rajaram V., Martos-Repath I., Chen H., Risso A., et al. Tutorial: Piezoelectric and magnetoelectric N/MEMS—Materials, devices, and applications. J. Appl. Phys. 2022;131:241101. doi: 10.1063/5.0094364. [DOI] [Google Scholar]
- 4.Luo B., Will-Cole A.R., Dong C., He Y., Liu X., Lin H., Huang R., Shi X., McConney M., Page M. Magnetoelectric microelectromechanical and nanoelectromechanical systems for the IoT. Nat. Rev. Electr. Eng. 2024;1:317–334. doi: 10.1038/s44287-024-00044-7. [DOI] [Google Scholar]
- 5.Bichurin M.I., Filippov D.A., Petrov V.M., Laletsin V.M., Paddubnaya N., Srinivasan G. Resonance magnetoelectric effects in layered magnetostrictive-piezoelectric composites. Phys. Rev. B. 2003;68:132408. doi: 10.1103/PhysRevB.68.132408. [DOI] [Google Scholar]
- 6.Zhai J., Xing Z., Dong S., Li J., Viehland D. Detection of pico-Tesla magnetic fields using magneto-electric sensors at room temperature. Appl. Phys. Lett. 2006;88:062510. doi: 10.1063/1.2172706. [DOI] [Google Scholar]
- 7.Reermann J., Durdaut P., Salzer S., Demming T., Piorra A., Quandt E., Frey N., Höft M., Schmidt G. Evaluation of magnetoelectric sensor systems for cardiological applications. Measurement. 2018;116:230–238. doi: 10.1016/j.measurement.2017.09.047. [DOI] [Google Scholar]
- 8.Mackert B.-M. Magnetoneurography: Theory and application to peripheral nerve disorders. Clin. Neurophysiol. 2004;115:2667–2676. doi: 10.1016/j.clinph.2004.07.028. [DOI] [PubMed] [Google Scholar]
- 9.Elzenheimer E., Laufs H., Schulte-Mattler W., Schmidt G. Magnetic measurement of electrically evoked muscle responses with optically pumped magnetometers. IEEE Trans. Neural Syst. Rehabil. Eng. 2020;28:756–765. doi: 10.1109/TNSRE.2020.2968148. [DOI] [PubMed] [Google Scholar]
- 10.Hayes P., Jovičević Klug M., Toxværd S., Durdaut P., Schell V., Teplyuk A., Burdin D., Winkler A., Weser R., Fetisov Y., et al. Converse Magnetoelectric Composite Resonator for Sensing Small Magnetic Fields. Sci. Rep. 2019;9:16355. doi: 10.1038/s41598-019-52657-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hayes P., Salzer S., Reermann J., Yarar E., Röbisch V., Piorra A., Meyners D., Höft M., Knöchel R., Schmidt G., et al. Electrically modulated magnetoelectric sensors. Appl. Phys. Lett. 2016;108:182902. doi: 10.1063/1.4948470. [DOI] [Google Scholar]
- 12.Hayes P., Schell V., Salzer S., Burdin D., Yarar E., Piorra A., Knöchel R., Fetisov Y.K., Quandt E. Electrically modulated magnetoelectric AlN/FeCoSiB film composites for DC magnetic field sensing. J. Phys. D Appl. Phys. 2018;51:354002. doi: 10.1088/1361-6463/aad456. [DOI] [Google Scholar]
- 13.Thormählen L., Hayes P., Elzenheimer E., Spetzler E., Schmidt G., Höft M., McCord J., Meyners D., Quandt E. Low-noise inverse magnetoelectric magnetic field sensor. Appl. Phys. Lett. 2024;124:172402. doi: 10.1063/5.0196637. [DOI] [Google Scholar]
- 14.Zaeimbashi M., Nasrollahpour M., Khalifa A., Romano A., Liang X.F., Chen H.H., Sun N., Matyushov A., Lin H., Dong C.Z., et al. Ultra-compact dual-band smart NEMS magnetoelectric antennas for simultaneous wireless energy harvesting and magnetic field sensing. Nat. Commun. 2021;12:3141. doi: 10.1038/s41467-021-23256-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nan T.X., Lin H., Gao Y., Matyushov A., Yu G.L., Chen H.H., Sun N., Wei S.J., Wang Z.G., Li M.H., et al. Acoustically actuated ultra-compact NEMS magnetoelectric antennas. Nat. Commun. 2017;8:296. doi: 10.1038/s41467-017-00343-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Liang X., Chen H., Sun N., Gao Y., Lin H., Sun N.X. Mechanically driven SMR-based MEMS magnetoelectric antennas; Proceedings of the 2020 IEEE International Symposium on Antennas and Propagation and North American Radio Science Meeting; Toronto, ON, Canada. 5–10 July 2020; Piscataway, NJ, USA: IEEE; 2020. pp. 661–662. [Google Scholar]
- 17.Liang X., Matyushov A., Hayes P., Schell V., Dong C., Chen H., He Y., Will-Cole A., Quandt E., Martins P., et al. Roadmap on Magnetoelectric Materials and Devices. IEEE Trans. Magn. 2021;57:400157. doi: 10.1109/TMAG.2021.3086635. [DOI] [Google Scholar]
- 18.Liang X.F., Chen H.H., Hu Z.Q., Lin H., Huang H., Guo J.H., Ju D.F., Liu M., Sun N.X. Experimental Demonstration of Ground Plane Immunity for Magnetoelectric Antennas; Proceedings of the 2022 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP); Guangzhou, China. 27–29 November 2022; [DOI] [Google Scholar]
- 19.Luo B., Liang X., Chen H., Sun N., Lin H., Sun N. Gain Enhancement and Ground Plane Immunity of Mechanically Driven Thin-Film Bulk Acoustic Resonator Magnetoelectric Antenna Arrays. Adv. Funct. Mater. 2024;34:2403244. doi: 10.1002/adfm.202403244. [DOI] [Google Scholar]
- 20.Liang X., Chen H., Sun N., Luo B., Golubeva E., Müller C., Mahat S., Wei Y., Dong C., Zaeimbashi M., et al. Mechanically Driven Solidly Mounted Resonator-Based Nanoelectromechanical Systems Magnetoelectric Antennas. Adv. Eng. Mater. 2023;25:2300425. doi: 10.1002/adem.202300425. [DOI] [Google Scholar]
- 21.Lee E.W. Magnetostriction and magnetomechanical effects. Rep. Prog. Phys. 1955;18:184–229. doi: 10.1088/0034-4885/18/1/305. [DOI] [Google Scholar]
- 22.Kittmann A., Durdaut P., Zabel S., Reermann J., Schmalz J., Spetzler B., Meyners D., Sun N.X., McCord J., Gerken M., et al. Wide Band Low Noise Love Wave Magnetic Field Sensor System. Sci. Rep. 2018;8:278. doi: 10.1038/s41598-017-18441-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Schell V., Müller C., Durdaut P., Kittmann A., Thormählen L., Lofink F., Meyners D., Höft M., McCord J., Quandt E. Magnetic anisotropy controlled FeCoSiB thin films for surface acoustic wave magnetic field sensors. Appl. Phys. Lett. 2020;116:073503. doi: 10.1063/1.5140562. [DOI] [Google Scholar]
- 24.Meyer J.M., Schell V., Su J., Fichtner S., Yarar E., Niekiel F., Giese T., Kittmann A., Thormählen L., Lebedev V., et al. Thin-Film-Based SAW Magnetic Field Sensors. Sensors. 2021;21:8166. doi: 10.3390/s21248166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Schell V., Spetzler E., Wolff N., Bumke L., Kienle L., McCord J., Quandt E., Meyners D. Exchange biased surface acoustic wave magnetic field sensors. Sci. Rep. 2023;13:8446. doi: 10.1038/s41598-023-35525-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mandal D., Banerjee S. Surface Acoustic Wave (SAW) Sensors: Physics, Materials, and Applications. Sensors. 2022;22:820. doi: 10.3390/s22030820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yang Y., Dejous C., Hallil H. Trends and Applications of Surface and Bulk Acoustic Wave Devices: A Review. Micromachines. 2023;14:43. doi: 10.3390/mi14010043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dai X., Fang L., Zhang C., Sun H. Design of a Novel Passive Wireless Integrated SAW-Based Antenna Sensor for Structural Health Monitoring. J. Sens. 2020;2020:6121907. doi: 10.1155/2020/6121907. [DOI] [Google Scholar]
- 29.Bao X., Bar-Cohen Y., Sherrit S., Badescu M., Louyeh S. Transport powder and liquid samples by surface acoustic waves; Proceedings of the Nanosensors, Biosensors, and Info-Tech Sensors and Systems 2009; San Diego, CA, USA. 9–11 March 2009; p. 72910M. [Google Scholar]
- 30.Atashbar M.Z., Sadek A.Z., Wlodarski W., Sriram S., Bhaskaran M., Cheng C.J., Kaner R.B., Kalantar-zadeh K. Layered SAW gas sensor based on CSA synthesized polyaniline nanofiber on AlN on 64° YX LiNbO3 for H2 sensing. Sens. Actuators B Chem. 2009;138:85–89. doi: 10.1016/j.snb.2009.01.072. [DOI] [Google Scholar]
- 31.Sivaramakrishnan S., Rajamani R., Smith C.S., McGee K.A., Mann K.R., Yamashita N. Carbon nanotube-coated surface acoustic wave sensor for carbon dioxide sensing. Sens. Actuators B Chem. 2008;132:296–304. doi: 10.1016/j.snb.2008.01.041. [DOI] [Google Scholar]
- 32.Levit N., Pestov D., Tepper G. High surface area polymer coatings for SAW-based chemical sensor applications. Sens. Actuators B Chem. 2002;82:241–249. doi: 10.1016/S0925-4005(01)01018-8. [DOI] [Google Scholar]
- 33.Li D., Feng Y., Zhou L., Ye Z., Wang J., Ying Y., Ruan C., Wang R., Li Y. Label-free capacitive immunosensor based on quartz crystal Au electrode for rapid and sensitive detection of Escherichia coli O157:H7. Anal. Chim. Acta. 2011;687:89–96. doi: 10.1016/j.aca.2010.12.018. [DOI] [PubMed] [Google Scholar]
- 34.Chang K., Pi Y., Lu W., Wang F., Pan F., Li F., Jia S., Shi J., Deng S., Chen M. Label-free and high-sensitive detection of human breast cancer cells by aptamer-based leaky surface acoustic wave biosensor array. Biosens. Bioelectron. 2014;60:318–324. doi: 10.1016/j.bios.2014.04.027. [DOI] [PubMed] [Google Scholar]
- 35.Wang T., Green R., Nair R.R., Howell M., Mohapatra S., Guldiken R., Mohapatra S.S. Surface Acoustic Waves (SAW)-Based Biosensing for Quantification of Cell Growth in 2D and 3D Cultures. Sensors. 2015;15:32045–32055. doi: 10.3390/s151229909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Makkonen T., Pensala T., Vartiainen J., Knuuttila J.V., Kaitila J., Salomaa M.M. Estimating materials parameters in thin-film BAW resonators using measured dispersion curves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2004;51:42–51. doi: 10.1109/TUFFC.2004.1268466. [DOI] [PubMed] [Google Scholar]
- 37.Hashimoto K. RF Bulk Acoustic Wave Filters for Communications. Artech House; London, UK: 2009. [Google Scholar]
- 38.Ruby R. 11E-2 Review and Comparison of Bulk Acoustic Wave FBAR, SMR Technology; Proceedings of the 2007 IEEE Ultrasonics Symposium Proceedings; New York, NY, USA. 28–31 October 2007; pp. 1029–1040. [Google Scholar]
- 39.Thalhammer R., Aigner R. Energy loss mechanisms in SMR-type BAW devices; Proceedings of the IEEE MTT-S International Microwave Symposium Digest; Long Beach, CA, USA. 17 June 2005; pp. 225–228. [Google Scholar]
- 40.Liang X. RF Magnetoelectric Microsystems. Northeastern University; Boston, MA, USA: 2021. [Google Scholar]
- 41.Haydl W.H., Hiesinger P., Smith R.S., Dischler B., Heber K. Design of Quartz and Lithium Niobate SAW Resonators Using Aluminum Metallization; Proceedings of the 30th Annual Symposium on Frequency Control; Atlantic City, NJ, USA. 2–4 June 1976; pp. 346–357. [Google Scholar]
- 42.Yantchev V., Plessky V. COMSOL for Modelling of STW Devices; Proceedings of the 2015 COMSOL Conference; Grenoble, France. 14–16 October 2015. [Google Scholar]
- 43.Curie P. Sur la symétrie dans les phénomènes physiquessymétrie d’ un champ électrique et d’ un champ magnétique To cite this version. J. Phys. Theor. Appl. 1894;3:395–415. doi: 10.1051/jphystap:018940030039300. [DOI] [Google Scholar]
- 44.Astrov D.N. The magnetoelectric effect in antiferromagnetics. J. Exp. Theor. Phys. 1960;38:984–985. [Google Scholar]
- 45.Lebeugle D., Colson D., Forget A., Viret M. Very large spontaneous electric polarization in BiFeO3 single crystals at room temperature and its evolution under cycling fields. Appl. Phys. Lett. 2007;91:22907. doi: 10.1063/1.2753390. [DOI] [Google Scholar]
- 46.Eerenstein W., Mathur N.D., Scott J.F. Multiferroic and magnetoelectric materials. Nature. 2006;442:759–765. doi: 10.1038/nature05023. [DOI] [PubMed] [Google Scholar]
- 47.Catalan G., Scott J.F. Physics and Applications of Bismuth Ferrite. Adv. Mater. 2009;21:2463–2485. doi: 10.1002/adma.200802849. [DOI] [Google Scholar]
- 48.Mao X., Wang W., Chen X., Lu Y. Multiferroic properties of layer-structured Bi5Fe0.5Co0.5Ti3O15 ceramics. Appl. Phys. Lett. 2009;95:82901. doi: 10.1063/1.3213344. [DOI] [Google Scholar]
- 49.Mao X., Sun H., Wang W., Lu Y., Chen X. Effects of Co-substitutes on multiferroic properties of Bi5FeTi3O15 ceramics. Solid State Commun. 2012;152:483–487. doi: 10.1016/j.ssc.2012.01.001. [DOI] [Google Scholar]
- 50.Bai W., Gao Y.Q., Zhu J.Y., Meng X.J., Lin T., Yang J., Zhu Z.Q., Chu J.H. Electrical, magnetic, and optical properties in multiferroic Bi5Ti3FeO15 thin films prepared by a chemical solution deposition route. J. Appl. Phys. 2011;109:64901. doi: 10.1063/1.3553879. [DOI] [Google Scholar]
- 51.Kitagawa Y., Hiraoka Y., Honda T., Ishikura T., Nakamura H., Kimura T. Low-field magnetoelectric effect at room temperature. Nat. Mater. 2010;9:797–802. doi: 10.1038/nmat2826. [DOI] [PubMed] [Google Scholar]
- 52.Shang T., Canévet E., Morin M., Sheptyakov D., Fernández-Díaz M.T., Pomjakushina E., Medarde M. Design of magnetic spirals in layered perovskites: Extending the stability range far beyond room temperature. Sci. Adv. 2024;4:eaau6386. doi: 10.1126/sciadv.aau6386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Van Run A.M.J.G., Terrell D.R., Scholing J.H. An in situ grown eutectic magnetoelectric composite material. J. Mater. Sci. 1974;9:1710–1714. doi: 10.1007/BF00540771. [DOI] [Google Scholar]
- 54.Van Den Boomgaard J., Terrell D.R., Born R.A.J., Giller H.F.J.I. An in situ grown eutectic magnetoelectric composite material. J. Mater. Sci. 1974;9:1705–1709. doi: 10.1007/BF00540770. [DOI] [Google Scholar]
- 55.Zhai J., Cai N., Shi Z., Lin Y., Nan C.W. Junyi Zhai; Ning Cai; Zhan Shi; Yuanhua Lin; Ce-Wen Nan Magnetic-dielectric properties of NiFe2O4/PZT particulate composites. J. Phys. D Appl. Phys. 2004;37:823. doi: 10.1088/0022-3727/37/6/002. [DOI] [Google Scholar]
- 56.Islam R.A., Bedekar V., Poudyal N., Liu J.P., Priya S. Magnetoelectric properties of core-shell particulate nanocomposites. J. Appl. Phys. 2008;104:104111. doi: 10.1063/1.3013437. [DOI] [Google Scholar]
- 57.Islam R.A., Priya S. Effect of piezoelectric grain size on magnetoelectric coefficient of Pb(Zr0.52Ti0.48)O3–Ni0.8Zn0.2Fe2O4 particulate composites. J. Mater. Sci. 2008;43:3560–3568. doi: 10.1007/s10853-008-2562-9. [DOI] [Google Scholar]
- 58.Zeng M., Wan J.G., Wang Y., Yu H., Liu J.-M., Jiang X.P., Nan C.W. Resonance magnetoelectric effect in bulk composites of lead zirconate titanate and nickel ferrite. J. Appl. Phys. 2004;95:8069–8073. doi: 10.1063/1.1739531. [DOI] [Google Scholar]
- 59.Srinivasan G., DeVreugd C.P., Flattery C.S., Laletsin V.M., Paddubnaya N. Magnetoelectric interactions in hot-pressed nickel zinc ferrite and lead zirconante titanate composites. Appl. Phys. Lett. 2004;85:2550–2552. doi: 10.1063/1.1795365. [DOI] [Google Scholar]
- 60.Wu D., Gong W., Deng H., Li M. Magnetoelectric composite ceramics of nickel ferrite and lead zirconate titanate via in situ processing. J. Phys. D Appl. Phys. 2007;40:5002. doi: 10.1088/0022-3727/40/16/037. [DOI] [Google Scholar]
- 61.Venkata Ramanaa M., Ramamanohar Reddy N., Sreenivasulu G., Siva kumar K.V., Murty B.S., Murthy V.R.K. Enhanced mangnetoelectric voltage in multiferroic particulate Ni0.83Co0.15Cu0.02Fe1.9O4−δ/PbZr0.52Ti0.48O3 composites—Dielectric, piezoelectric and magnetic properties. Curr. Appl. Phys. 2009;9:1134–1139. doi: 10.1016/j.cap.2009.01.002. [DOI] [Google Scholar]
- 62.Ryu J., Priya S., Carazo A.V., Uchino K., Kim H.-E. Effect of the Magnetostrictive Layer on Magnetoelectric Properties in Lead Zirconate Titanate/Terfenol-D Laminate Composites. J. Am. Ceram. Soc. 2001;84:2905–2908. doi: 10.1111/j.1151-2916.2001.tb01113.x. [DOI] [Google Scholar]
- 63.Dong S., Zhai J., Bai F., Li J.F., Viehland D. Push-pull mode magnetostrictive/piezoelectric laminate composite with an enhanced magnetoelectric voltage coefficient. Appl. Phys. Lett. 2005;87:10–13. doi: 10.1063/1.2007868. [DOI] [Google Scholar]
- 64.Wang Y., Gray D., Berry D., Gao J., Li M., Li J., Viehland D. An extremely low equivalent magnetic noise magnetoelectric sensor. Adv. Mater. 2011;23:4111. doi: 10.1002/adma.201100773. [DOI] [PubMed] [Google Scholar]
- 65.Li M., Gao J., Wang Y., Gray D., Li J., Viehland D. Enhancement in magnetic field sensitivity and reduction in equivalent magnetic noise by magnetoelectric laminate stacks. J. Appl. Phys. 2012;111:104504. doi: 10.1063/1.4718441. [DOI] [Google Scholar]
- 66.Zhang J.X., Li Y.L., Schlom D.G., Chen L.Q., Zavaliche F., Ramesh R., Jia Q.X. Phase-field model for epitaxial ferroelectric and magnetic nanocomposite thin films. Appl. Phys. Lett. 2007;90:52909. doi: 10.1063/1.2431574. [DOI] [Google Scholar]
- 67.Wu H., Chai G., Zhou T., Zhang Z., Kitamura T., Zhou H. Adjustable magnetoelectric effect of self-assembled vertical multiferroic nanocomposite films by the in-plane misfit strain and ferromagnetic volume fraction. J. Appl. Phys. 2014;115:114105. doi: 10.1063/1.4868896. [DOI] [Google Scholar]
- 68.Amrillah T., Bitla Y., Shin K., Yang T., Hsieh Y.-H., Chiou Y.-Y., Liu H.-J., Do T.H., Su D., Chen Y.-C., et al. Flexible Multiferroic Bulk Heterojunction with Giant Magnetoelectric Coupling via van der Waals Epitaxy. ACS Nano. 2017;11:6122–6130. doi: 10.1021/acsnano.7b02102. [DOI] [PubMed] [Google Scholar]
- 69.Yan L., Xing Z., Wang Z., Wang T., Lei G., Li J., Viehland D. Direct measurement of magnetoelectric exchange in self-assembled epitaxial BiFeO3–CoFe2O4 nanocomposite thin films. Appl. Phys. Lett. 2009;94:192902. doi: 10.1063/1.3138138. [DOI] [Google Scholar]
- 70.Oh Y.S., Crane S., Zheng H., Chu Y.H., Ramesh R., Kim K.H. Quantitative determination of anisotropic magnetoelectric coupling in BiFeO3–CoFe2O4 nanostructures. Appl. Phys. Lett. 2010;97:52902. doi: 10.1063/1.3475420. [DOI] [Google Scholar]
- 71.Greve H., Woltermann E., Quenzer H.-J., Wagner B., Quandt E. Giant magnetoelectric coefficients in (Fe90Co10) 78Si12B10-AlN thin film composites. Appl. Phys. Lett. 2010;96:182501. doi: 10.1063/1.3377908. [DOI] [Google Scholar]
- 72.Nair S.S., Pookat G., Saravanan V., Anantharaman M.R. Lead free heterogeneous multilayers with giant magneto electric coupling for microelectronics/microelectromechanical systems applications. J. Appl. Phys. 2013;114:64309. doi: 10.1063/1.4818411. [DOI] [Google Scholar]
- 73.Jahns R., Piorra A., Lage E., Kirchhof C., Meyners D., Gugat J.L., Krantz M., Gerken M., Knöchel R., Quandt E. Giant Magnetoelectric Effect in Thin-Film Composites. J. Am. Ceram. Soc. 2013;96:1673–1681. doi: 10.1111/jace.12400. [DOI] [Google Scholar]
- 74.Erhart J., Půlpán P., Pustka M. Piezoelectric Ceramic Resonators. Springer; Berlin/Heidelberg, Germany: 2017. [DOI] [Google Scholar]
- 75.Yarar E., Hrkac V., Zamponi C., Piorra A., Kienle L., Quandt E. Low temperature aluminum nitride thin films for sensory applications. AIP Adv. 2016;6:75115. doi: 10.1063/1.4959895. [DOI] [Google Scholar]
- 76.Ruby R., Bradley P., Larson J., Oshmyansky Y., Figueredo D. Ultra-miniature high-Q filters and duplexers using FBAR technology; Proceedings of the 2001 IEEE International Solid-State Circuits Conference; San Francisco, CA, USA. 7 February 2001; pp. 120–121. Digest of Technical Papers. ISSCC (Cat. No.01CH37177) [Google Scholar]
- 77.Piazza G., Stephanou P.J., Pisano A.P. Piezoelectric Aluminum Nitride Vibrating Contour-Mode MEMS Resonators. J. Microelectromech. Syst. 2006;15:1406–1418. doi: 10.1109/JMEMS.2006.886012. [DOI] [Google Scholar]
- 78.Naik R.S., Lutsky J.J., Reif R., Sodini C.G., Becker A., Fetter L., Huggins H., Miller R., Pastalan J., Rittenhouse G., et al. Measurements of the bulk, C-axis electromechanical coupling constant as a function of AlN film quality. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2000;47:292–296. doi: 10.1109/58.818773. [DOI] [PubMed] [Google Scholar]
- 79.Bu G., Ciplys D., Shur M., Schowalter L.J., Schujman S., Gaska R. Electromechanical coupling coefficient for surface acoustic waves in single-crystal bulk aluminum nitride. Appl. Phys. Lett. 2004;84:4611–4613. doi: 10.1063/1.1755843. [DOI] [Google Scholar]
- 80.Cassella C., Hui Y., Qian Z., Hummel G., Rinaldi M. Aluminum nitride cross-sectional Lamé mode resonators. J. Microelectromech. Syst. 2016;25:275–285. doi: 10.1109/JMEMS.2015.2512379. [DOI] [Google Scholar]
- 81.Caro M., Zhang S., Riekkinen T., Ylilammi M., Moram M., Acevedo O.L., Molarius J., Laurila T. Piezoelectric coefficients and spontaneous polarization of ScAlN. J. Phys. Condens. Matter. 2015;27:245901. doi: 10.1088/0953-8984/27/24/245901. [DOI] [PubMed] [Google Scholar]
- 82.Ambacher O., Christian B., Feil N., Urban D.F., Elsässer C., Prescher M., Kirste L. Wurtzite ScAlN, InAlN, and GaAlN crystals, a comparison of structural, elastic, dielectric, and piezoelectric properties. J. Appl. Phys. 2021;130:45102. doi: 10.1063/5.0048647. [DOI] [Google Scholar]
- 83.Matloub R., Hadad M., Mazzalai A., Chidambaram N., Moulard G., Sandu C.S., Metzger T., Muralt P. Piezoelectric Al1−xScxN thin films: A semiconductor compatible solution for mechanical energy harvesting and sensors. Appl. Phys. Lett. 2013;102:152903. doi: 10.1063/1.4800231. [DOI] [Google Scholar]
- 84.Dubois M.-A., Muralt P. Properties of aluminum nitride thin films for piezoelectric transducers and microwave filter applications. Appl. Phys. Lett. 1999;74:3032–3034. doi: 10.1063/1.124055. [DOI] [Google Scholar]
- 85.Fichtner S., Reimer T., Chemnitz S., Lofink F., Wagner B. Stress controlled pulsed direct current co-sputtered Al1−xScxN as piezoelectric phase for micromechanical sensor applications. APL Mater. 2015;3:116102. doi: 10.1063/1.4934756. [DOI] [Google Scholar]
- 86.Zhou J., Liu Y., Xu Q., Xie Y., Cai Y., Liu J., Liu W., Tovstopyat A., Sun C. ScAlN/AlN Film-Based Lamé Mode Resonator With High Effective Electromechanical Coupling Coefficient. J. Microelectromech. Syst. 2021;30:677–679. doi: 10.1109/JMEMS.2021.3102145. [DOI] [Google Scholar]
- 87.Esteves G., Young T.R., Tang Z., Yen S., Bauer T.M., Henry M.D., Olsson R.H., III Al0.68Sc0.32N Lamb wave resonators with electromechanical coupling coefficients near 10.28% Appl. Phys. Lett. 2021;118:171902. doi: 10.1063/5.0047647. [DOI] [Google Scholar]
- 88.Lozzi A., Yen E.T.-T., Muralt P., Villanueva L.G. Al0.83Sc0.17N Contour-Mode Resonators With Electromechanical Coupling in Excess of 4.5% IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2019;66:146–153. doi: 10.1109/TUFFC.2018.2882073. [DOI] [PubMed] [Google Scholar]
- 89.Hashimoto K., Sato S., Teshigahara A., Nakamura T., Kano K. High-performance surface acoustic wave resonators in the 1 to 3 GHz range using a ScAlN/6H-SiC structure. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2013;60:637–642. doi: 10.1109/TUFFC.2013.2606. [DOI] [PubMed] [Google Scholar]
- 90.Wang W., Mayrhofer P.M., He X., Gillinger M., Ye Z., Wang X., Bittner A., Schmid U., Luo J.K. High performance AlScN thin film based surface acoustic wave devices with large electromechanical coupling coefficient. Appl. Phys. Lett. 2014;105:133502. doi: 10.1063/1.4896853. [DOI] [Google Scholar]
- 91.Yanagitani T., Suzuki M. Electromechanical coupling and gigahertz elastic properties of ScAlN films near phase boundary. Appl. Phys. Lett. 2014;105:122907. doi: 10.1063/1.4896262. [DOI] [Google Scholar]
- 92.Akiyama M., Kamohara T., Kano K., Teshigahara A., Takeuchi Y., Kawahara N. Enhancement of piezoelectric response in scandium aluminum nitride alloy thin films prepared by dual reactive cosputtering. Adv. Mater. 2009;21:593–596. doi: 10.1002/adma.200802611. [DOI] [PubMed] [Google Scholar]
- 93.Fichtner S., Wolff N., Lofink F., Kienle L., Wagner B. AlScN: A III-V semiconductor based ferroelectric. J. Appl. Phys. 2019;125:114103. doi: 10.1063/1.5084945. [DOI] [Google Scholar]
- 94.Parsapour F., Pashchenko V., Nicolay P., Murali P. Material constants extraction for AlScN thin films using a dual mode baw resonator; Proceedings of the 2018 IEEE Micro Electro Mechanical Systems (MEMS); Belfast, UK. 21–25 January 2018; Piscataway, NJ, USA: IEEE; 2018. pp. 763–766. [Google Scholar]
- 95.Parsapour F., Pashchenko V., Mertin S., Sandu C., Kurz N., Nicolay P., Muralt P. Ex-situ AlN seed layer for (0001)-textured Al 0.84 Sc 0.16 N thin films grown on SiO2 substrates; Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS); Washington, DC, USA. 6–9 September 2017; Piscataway, NJ, USA: IEEE; 2017. pp. 1–4. [Google Scholar]
- 96.Mayrhofer P.M., Persson P.O.Å., Bittner A., Schmid U. Properties of ScxAl1−xN (x = 0.27) thin films on sapphire and silicon substrates upon high temperature loading. Microsyst. Technol. 2016;22:1679–1689. doi: 10.1007/s00542-015-2798-7. [DOI] [Google Scholar]
- 97.Li C., Xu B., Lin D., Zhang S., Bellaiche L., Shrout T.R., Li F. Atomic-scale origin of ultrahigh piezoelectricity in samarium-doped PMN-PT ceramics. Phys. Rev. B. 2020;101:140102. doi: 10.1103/PhysRevB.101.140102. [DOI] [Google Scholar]
- 98.Luo L., Zhao X., Luo H. Single crystal PZN–PT, PMN–PT, PSN–PT and PIN–PT-based piezoelectric materials. In: Uchino K., editor. Advanced Piezoelectric Materials. Woodhead Publishing; Sawston, UK: 2010. pp. 239–286. (Woodhead Publishing Series in Electronic and Optical Materials). [Google Scholar]
- 99.Crisler D.F., Cupal J.J., Moore A.R. Dielectric, piezoelectric, and electromechanical coupling constants of zinc oxide crystals. Proc. IEEE. 1968;56:225–226. doi: 10.1109/PROC.1968.6246. [DOI] [Google Scholar]
- 100.Yanagitani T., Kiuchi M., Matsukawa M., Watanabe Y. Shear mode electromechanical coupling coefficient k15 and crystallites alignment of (112¯) textured ZnO films. J. Appl. Phys. 2007;102:24110. doi: 10.1063/1.2752133. [DOI] [Google Scholar]
- 101.Takeuchi M., Yamada H., Yoshino Y., Makino T., Arai S. Effective electromechanical coupling coefficient (kt2) for fundamental mode of thickness extensional mode thin film bulk acoustic wave resonator fabricated by ZnO thin film. Vacuum. 2002;66:463–466. doi: 10.1016/S0042-207X(02)00116-1. [DOI] [Google Scholar]
- 102.Gopal P., Spaldin N.A. Polarization, piezoelectric constants, and elastic constants of ZnO, MgO, and CdO. J. Electron. Mater. 2006;35:538–542. doi: 10.1007/s11664-006-0096-y. [DOI] [Google Scholar]
- 103.Kang D.J., Kim J.S., Jeong S.W., Roh Y., Jeong S.H., Boo J.H. Structural and electrical characteristics of R.F. magnetron sputtered ZnO films. Thin Solid Films. 2005;475:160–165. doi: 10.1016/j.tsf.2004.07.029. [DOI] [Google Scholar]
- 104.Rahimi N., Dalouji V., Rezaee S. Effect of annealing processing on morphology, spectroscopy studies, Urbach disordering energy, and WDD dispersion parameters in Cu-Al doped zinc oxide films. J. Dispers. Sci. Technol. 2022;43:990–999. doi: 10.1080/01932691.2020.1847657. [DOI] [Google Scholar]
- 105.Rahimi N., Dalouji V. Room temperature AC electrical, surface micro texture analysis, microwave permittivity and dielectric loss tangent in ZnO films doped by Cu, Al, and CuAl. Opt. Mater. 2024;148:114788. doi: 10.1016/j.optmat.2023.114788. [DOI] [Google Scholar]
- 106.Zaka H., Parditka B., Erdélyi Z., Atyia H.E., Sharma P., Fouad S.S. Investigation of dispersion parameters, dielectric properties and opto–electrical parameters of ZnO thin film grown by ALD. Optik. 2020;203:163933. doi: 10.1016/j.ijleo.2019.163933. [DOI] [Google Scholar]
- 107.Fu S., Wang W., Li Q., Lu Z., Chen Z., Luo J., Shen J., Wang R., Song C., Zeng F., et al. High-frequency V-doped ZnO/SiC surface acoustic wave devices with enhanced electromechanical coupling coefficient. Appl. Phys. Lett. 2019;114:113504. doi: 10.1063/1.5086445. [DOI] [Google Scholar]
- 108.Chen Y.-Y. Theoretical Analysis of Electromechanical Coupling Coefficient of Lamb Waves in ZnO/Si Multilayered Piezoelectric Plates. Jpn. J. Appl. Phys. 2010;49:07HD23. doi: 10.1143/JJAP.49.07HD23. [DOI] [Google Scholar]
- 109.Workie T.B., Tang P., Bao J., Hashimoto K. Analysis of high electromechanical coupling coefficient zinc oxide Lame’ mode resonators and a design technique for spurious mode mitigation. Chin. J. Phys. 2022;77:483–496. doi: 10.1016/j.cjph.2022.03.022. [DOI] [Google Scholar]
- 110.Bhadwal N., Ben Mrad R., Behdinan K. Review of Zinc Oxide Piezoelectric Nanogenerators: Piezoelectric Properties, Composite Structures and Power Output. Sensors. 2023;23:3859. doi: 10.3390/s23083859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Bouchy S., Zednik R.J., Bélanger P. Characterization of the Elastic, Piezoelectric, and Dielectric Properties of Lithium Niobate from 25 °C to 900 °C Using Electrochemical Impedance Spectroscopy Resonance Method. Materials. 2022;15:4716. doi: 10.3390/ma15134716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Huang S., Shuai Y., Lv L., Wei Z., Fan W., Wang Y., Zhu D., Pan X., Luo W., Wu C., et al. LiNbO3 Surface Acoustic Wave Resonators with Large Effective Electromechanical Coupling. Electronics. 2023;12:2964. doi: 10.3390/electronics12132964. [DOI] [Google Scholar]
- 113.Ma R., Liu W., Sun X., Zhou S., Lin D. FEM Simulation of a High-Performance 128° Y–X LiNbO3/SiO2/Si Functional Substrate for Surface Acoustic Wave Gyroscopes. Micromachines. 2022;13:202. doi: 10.3390/mi13020202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Dai Z., Cheng H., Xiao S., Sun H., Zuo C. Coupled Shear SAW Resonator With High Electromechanical Coupling Coefficient of 34% Using X-Cut LiNbO3-on-SiC Substrate. IEEE Electron Device Lett. 2024;45:720–723. doi: 10.1109/LED.2024.3368426. [DOI] [Google Scholar]
- 115.Lu R., Yang Y., Link S., Gong S. A1 Resonators in 128° Y-cut Lithium Niobate with Electromechanical Coupling of 46.4% J. Microelectromech. Syst. 2020;29:313–319. doi: 10.1109/JMEMS.2020.2982775. [DOI] [Google Scholar]
- 116.Jacob M.V., Hartnett J.G., Mazierska J., Giordano V., Krupka J., Tobar M.E. Temperature dependence of permittivity and loss tangent of lithium tantalate at microwave frequencies. IEEE Trans. Microw. Theory Tech. 2004;52:536–541. doi: 10.1109/TMTT.2003.821911. [DOI] [Google Scholar]
- 117.Bousquet M., Perreau P., Castellan G., Bertucchi M., Maeder-Pachurka C., Delaguillaumie F., Joulie A., Enyedi G., Sailler B., Mariolle D., et al. Potentialities of LiTaO3 for Bulk Acoustic Wave Filters; Proceedings of the 2020 IEEE International Ultrasonics Symposium (IUS); Las Vegas, NV, USA. 7–11 September 2020; pp. 1–4. [Google Scholar]
- 118.Saigusa Y. Quartz-Based Piezoelectric Materials. In: Uchino K., editor. Advanced Piezoelectric Materials. 2nd ed. Woodhead Publishing; Sawston, UK: 2017. pp. 197–233. [Google Scholar]
- 119.Hayashi J., Yamaya K., Suzuki M., Kakio S., Suzaki H., Yonai T., Kishida K., Mizuno J. High coupling and highly stable leaky surface acoustic waves on LiTaO3 thin plate bonded to quartz substrate. Jpn. J. Appl. Phys. 2018;57:07LD21. doi: 10.7567/JJAP.57.07LD21. [DOI] [Google Scholar]
- 120.Zhang L., Zhang S., Wu J., Zheng P., Zhou H., Yao H., Li Z., Huang K., Sun H., Ou X. High-Performance Acoustic Wave Devices on LiTaO3/SiC Hetero-Substrates. IEEE Trans. Microw. Theory Tech. 2023;71:4182–4192. doi: 10.1109/TMTT.2023.3267556. [DOI] [Google Scholar]
- 121.Heyliger P., Ledbetter H., Kim S. Elastic constants of natural quartz. J. Acoust. Soc. Am. 2003;114:644–650. doi: 10.1121/1.1593063. [DOI] [PubMed] [Google Scholar]
- 122.Mazierska J., Jacob M.V., Ledenyov D., Krupk J. Loss tangent measurements of dielectric substrates from 15 K to 300 K with two resonators: Investigation into accuracy issues; Proceedings of the 2005 Asia-Pacific Microwave Conference Proceedings; Suzhou, China. 4–7 December 2005; p. 4. [Google Scholar]
- 123.Fenske K., Misra D. Dielectric materials at microwave frequencies. Appl. Microw. Wirel. 2000;12:92–100. [Google Scholar]
- 124.Zhgoon S., Shvetsov A., Ancev I., Bogoslovsky S., Sapozhnikov G., Trokhimets K., Derkach M. SAW temperature sensor on Quartz. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2015;62:1066–1075. doi: 10.1109/TUFFC.2014.006840. [DOI] [PubMed] [Google Scholar]
- 125.Schmitt R.F., Allen J.W., Vetelino J.F., Parks J., Zhang C. Bulk acoustic wave modes in quartz for sensing measurand-induced mechanical and electrical property changes. Sens. Actuators B Chem. 2001;76:95–102. doi: 10.1016/S0925-4005(01)00591-3. [DOI] [Google Scholar]
- 126.Joule J.P. On a new class of magnetic forces. Ann. Electr. Magn. Chem. 1842;8:219–224. [Google Scholar]
- 127.Villari E. Intorno alle modificazioni del momento magnetico di una verga di ferro e di acciaio, prodotte per la trazione della medesima e pel passaggio di una corrente attraverso la stessa. Nuovo Cim. 1864;20:317–362. doi: 10.1007/BF02726917. [DOI] [Google Scholar]
- 128.Hristoforou E., Ktena A. Magnetostriction and magnetostrictive materials for sensing applications. J. Magn. Magn. Mater. 2007;316:372–378. doi: 10.1016/j.jmmm.2007.03.025. [DOI] [Google Scholar]
- 129.Cullen J.R., Clark A.E. Magnetostriction and structural distortion in rare-earth intermetallics. Phys. Rev. B. 1977;15:4510–4515. doi: 10.1103/PhysRevB.15.4510. [DOI] [Google Scholar]
- 130.Clark A.E., DeSavage B.F., Bozorth R. Anomalous Thermal Expansion and Magnetostriction of Single-Crystal Dysprosium. Phys. Rev. 1965;138:A216–A224. doi: 10.1103/PhysRev.138.A216. [DOI] [Google Scholar]
- 131.Rhyne J.J., Legvold S. Magnetostriction of Tb Single Crystals. Phys. Rev. 1965;138:A507–A514. doi: 10.1103/PhysRev.138.A507. [DOI] [Google Scholar]
- 132.Clark A., Abbundi R., Gillmor W. Magnetization and magnetic anisotropy of TbFe2, DyFe2, Tb0.27Dy0.73Fe2 and TmFe2. IEEE Trans. Magn. 1978;14:542–544. doi: 10.1109/TMAG.1978.1059879. [DOI] [Google Scholar]
- 133.Clark A.E. Handbook of Ferromagnetic Materials. Volume 1. Elsevier; Amsterdam, The Netherlands: 1980. Chapter 7 Magnetostrictive rare earth-Fe2 compounds; pp. 531–589. [Google Scholar]
- 134.Clark A.E., Wun-Fogle M., Restorff J.B., Lograsso T.A. Magnetostrictive properties of Galfenol alloys under compressive stress. Mater. Trans. 2002;43:881–886. doi: 10.2320/matertrans.43.881. [DOI] [Google Scholar]
- 135.Greer A.L. Metallic glasses. Science. 1995;267:1947–1953. doi: 10.1126/science.267.5206.1947. [DOI] [PubMed] [Google Scholar]
- 136.Quandt E., Ludwig A., Betz J., Mackay K., Givord D. Giant magnetostrictive spring magnet type multilayers. J. Appl. Phys. 1997;81:5420–5422. doi: 10.1063/1.364558. [DOI] [Google Scholar]
- 137.Quandt E., Ludwig A. Giant magnetostrictive multilayers (invited) J. Appl. Phys. 1999;85:6232–6237. doi: 10.1063/1.370231. [DOI] [Google Scholar]
- 138.Chu Y.W., Kharel P., Yoon T., Frunzio L., Rakich P.T., Schoelkopf R.J. Creation and control of multi-phonon Fock states in a bulk acoustic-wave resonator. Nature. 2018;563:666–670. doi: 10.1038/s41586-018-0717-7. [DOI] [PubMed] [Google Scholar]
- 139.Engdahl G., Mayergoyz I.D. Handbook of Giant Magnetostrictive Materials. Volume 107 Elsevier; Amsterdam, The Netherlands: 2000. [Google Scholar]
- 140.Dong C.Z., Li M.H., Liang X.F., Chen H.H., Zhou H.M., Wang X.J., Gao Y., McConney M.E., Jones J.G., Brown G.J., et al. Characterization of magnetomechanical properties in FeGaB thin films. Appl. Phys. Lett. 2018;113:262401. doi: 10.1063/1.5065486. [DOI] [Google Scholar]
- 141.Material properties Metglas, Inc. [(accessed on 4 October 2024)]. Available online: https://metglas.com/magnetic-materials/
- 142.Wang J., Dong C., Wei Y., Lin X., Athey B., Chen Y., Winter A., Stephen G.M., Heiman D., He Y., et al. Magnetostriction, Soft Magnetism, and Microwave Properties in Co−Fe−C Alloy Films. Phys. Rev. Appl. 2019;12:34011. doi: 10.1103/PhysRevApplied.12.034011. [DOI] [Google Scholar]
- 143.Lou J., Liu M., Reed D., Ren Y.H., Sun N.X. Giant Electric Field Tuning of Magnetism in Novel Multiferroic FeGaB/Lead Zinc Niobate-Lead Titanate (PZN-PT) Heterostructures. Adv. Mater. 2009;21:4711–4715. doi: 10.1002/adma.200901131. [DOI] [Google Scholar]
- 144.Lou J., Insignares R.E., Cai Z., Ziemer K.S., Liu M., Sun N.X. Soft magnetism, magnetostriction, and microwave properties of FeGaB thin films. Appl. Phys. Lett. 2007;91:182504. doi: 10.1063/1.2804123. [DOI] [Google Scholar]
- 145.Liang X., Dong C., Celestin S.J., Wang X., Chen H., Ziemer K.S., Page M., McConney M.E., Jones J.G., Howe B.M., et al. Soft Magnetism, Magnetostriction, and Microwave Properties of Fe-Ga-C Alloy Films. IEEE Magn. Lett. 2019;10:5500705. doi: 10.1109/LMAG.2018.2889630. [DOI] [Google Scholar]
- 146.Vijayalaxmi, Fatahi M., Speck O. Magnetic resonance imaging (MRI): A review of genetic damage investigations. Mutat. Res. Mutat. Res. 2015;764:51–63. doi: 10.1016/j.mrrev.2015.02.002. [DOI] [PubMed] [Google Scholar]
- 147.Jahns R., Greve H., Woltermann E., Quandt E., Knöchel R. Sensitivity enhancement of magnetoelectric sensors through frequency-conversion. Sens. Actuators A Phys. 2012;183:16–21. doi: 10.1016/j.sna.2012.05.049. [DOI] [Google Scholar]
- 148.Elzwawy A., Rasly M., Morsy M., Piskin H., Volmer M. Handbook of Nanosensors: Materials and Technological Applications. Springer; Berlin/Heidelberg, Germany: 2024. Magnetic Sensors: Principles, Methodologies, and Applications; pp. 891–928. [Google Scholar]
- 149.Pereira N., Lima A.C., Lanceros-Mendez S., Martins P. Magnetoelectrics: Three Centuries of Research Heading Towards the 4.0 Industrial Revolution. Materials. 2020;13:4033. doi: 10.3390/ma13184033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Lampropoulos G., Siakas K., Anastasiadis T. Internet of things in the context of industry 4.0: An overview. Int. J. Entrep. Knowl. 2019;7 doi: 10.37335/ijek.v7i1.84. [DOI] [Google Scholar]
- 151.Cohen D., Givler E. Magnetomyography: Magnetic fields around the human body produced by skeletal muscles. Appl. Phys. Lett. 2003;21:114–116. doi: 10.1063/1.1654294. [DOI] [Google Scholar]
- 152.Elzenheimer E., Laufs H., Sander-Thömmes T., Schmidt G. Magnetoneurograhy of an Electrically Stimulated Arm Nerve. Curr. Dir. Biomed. Eng. 2018;4:363–366. doi: 10.1515/cdbme-2018-0087. [DOI] [Google Scholar]
- 153.Zuo S., Heidari H., Farina D., Nazarpour K. Miniaturized Magnetic Sensors for Implantable Magnetomyography. Adv. Mater. Technol. 2020;5:2000185. doi: 10.1002/admt.202000185. [DOI] [Google Scholar]
- 154.Uchikawa Y., Kotani M. Measurement of Magnetic Field Produced from the Human Body. IEEE Transl. J. Magn. Jpn. 1992;7:600–607. doi: 10.1109/TJMJ.1992.4565462. [DOI] [Google Scholar]
- 155.Granata C., Vettoliere A., Russo M. An ultralow noise current amplifier based on superconducting quantum interference device for high sensitivity applications. Rev. Sci. Instrum. 2011;82:013901. doi: 10.1063/1.3521657. [DOI] [PubMed] [Google Scholar]
- 156.Nardelli N., Krzyzewski S., Korenko B., Romanov G., Hughes J., Alem O., Knappe S. Magnetic field imaging with microfabricated optically-pumped magnetometer arrays; Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC); San Diego, CA, USA. 3–7 March 2019; [Google Scholar]
- 157.Gerginov V., Pomponio M., Knappe S. Scalar magnetometry below 100 fT/Hz1/2 in a microfabricated cell. IEEE Sens. J. 2020;20:12684–12690. doi: 10.1109/JSEN.2020.3002193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Nardelli N.V., Krzyzewski S.P., Knappe S.A. Reducing crosstalk in optically-pumped magnetometer arrays. Phys. Med. Biol. 2019;64:21NT03. doi: 10.1088/1361-6560/ab4c06. [DOI] [PubMed] [Google Scholar]
- 159.Boto E., Meyer S.S., Shah V., Alem O., Knappe S., Kruger P., Fromhold T.M., Lim M., Glover P.M., Morris P.G., et al. A new generation of magnetoencephalography: Room temperature measurements using optically-pumped magnetometers. Neuroimage. 2017;149:404–414. doi: 10.1016/j.neuroimage.2017.01.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160.Alem O., Mhaskar R., Jiménez-Martínez R., Sheng D., LeBlanc J., Trahms L., Sander T., Kitching J., Knappe S. Magnetic field imaging with microfabricated optically-pumped magnetometers. Opt. Express. 2017;25:7849–7858. doi: 10.1364/OE.25.007849. [DOI] [PubMed] [Google Scholar]
- 161.Knappe S.A., Hughes J., Alem O. Microfabricated Optically-Pumped Magnetometers for Imaging Applications; Proceedings of the SPIE QUANTUM WEST; San Francisco, CA, USA. 28 January–3 February 2023; [DOI] [Google Scholar]
- 162.Knappe S., Alem O., Sheng D., Kitching J. Microfabricated Optically-Pumped Magnetometers for Biomagnetic Applications. Proc. J. Phys. Conf. Ser. 2016;723:012055. doi: 10.1088/1742-6596/723/1/012055. [DOI] [Google Scholar]
- 163.Dufay B., Saez S., Dolabdjian C.P., Yelon A., Ménard D. Characterization of an Optimized Off-Diagonal GMI-Based Magnetometer. IEEE Sens. J. 2013;13:379–388. doi: 10.1109/JSEN.2012.2216521. [DOI] [Google Scholar]
- 164.Portalier E., Dufay B., Saez S., Dolabdjian C. Noise Behavior of High Sensitive GMI-Based Magnetometer Relative to Conditioning Parameters. IEEE Trans. Magn. 2015;51:4002104. doi: 10.1109/TMAG.2014.2355414. [DOI] [Google Scholar]
- 165.Traore P.-S., Asfour A., Yonnet J.-P., Dolabdjian C.P. Noise performance of SDR-based off-diagonal GMI sensors. IEEE Sens. J. 2017;17:6175–6184. doi: 10.1109/JSEN.2017.2739480. [DOI] [Google Scholar]
- 166.Fernández E., García-Arribas A., Barandiarán J.M., Svalov A.V., Kurlyandskaya G.V., Dolabdjian C.P. Equivalent Magnetic Noise of Micro-Patterned Multilayer Thin Films Based GMI Microsensor. IEEE Sens. J. 2015;15:6707–6714. doi: 10.1109/JSEN.2015.2463254. [DOI] [Google Scholar]
- 167.Traoré P.S., Asfour A., Yonnet J.-P., Boudinet C. Digital electronic conditioning approach for the high-sensitivity off-diagonal GMI sensors. Sens. Actuators A Phys. 2018;271:290–302. doi: 10.1016/j.sna.2018.01.029. [DOI] [Google Scholar]
- 168.Kikuchi H., Kamata S., Nakai T., Hashi S., Ishiyama K. Influence of demagnetizing field on thin-film GMI magnetic sensor elements with uniaxial magnetic anisotropy. Sens. Actuators A Phys. 2015;230:142–149. doi: 10.1016/j.sna.2015.04.027. [DOI] [Google Scholar]
- 169.Wu K., Su D., Saha R., Wang J.-P. Spintronics. Wiley; Hoboken, NJ, USA: 2022. Giant Magnetoresistance (GMR) Materials and Devices for Biomedical and Industrial Applications; pp. 3–49. [Google Scholar]
- 170.Pannetier-Lecoeur M., Parkkonen L., Sergeeva-Chollet N., Polovy H., Fermon C., Fowley C. Magnetocardiography with sensors based on giant magnetoresistance. Appl. Phys. Lett. 2011;98:153705. doi: 10.1063/1.3575591. [DOI] [Google Scholar]
- 171.Shen H.-M., Hu L., Fu X. Integrated Giant Magnetoresistance Technology for Approachable Weak Biomagnetic Signal Detections. Sensors. 2018;18:148. doi: 10.3390/s18010148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Kurashima K., Kataoka M., Nakano T., Fujiwara K., Kato S., Nakamura T., Yuzawa M., Masuda M., Ichimura K., Okatake S., et al. Development of Magnetocardiograph without Magnetically Shielded Room Using High-Detectivity TMR Sensors. Sensors. 2023;23:646. doi: 10.3390/s23020646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Freitas P.P., Ferreira R., Cardoso S. Spintronic Sensors. Proc. IEEE. 2016;104:1894–1918. doi: 10.1109/JPROC.2016.2578303. [DOI] [Google Scholar]
- 174.Weitensfelder H., Brueckl H., Satz A., Pruegl K., Zimmer J., Luber S., Raberg W., Abert C., Bruckner F., Bachleitner-Hofmann A., et al. Comparison of Sensitivity and Low-Frequency Noise Contributions in Giant-Magnetoresistive and Tunneling-Magnetoresistive Spin-Valve Sensors with a Vortex-State Free Layer. Phys. Rev. Appl. 2018;10:054056. doi: 10.1103/PhysRevApplied.10.054056. [DOI] [Google Scholar]
- 175.Smith N., Katine J.A., Childress J.R., Carey M.J. Thermal and spin-torque noise in CPP (TMR and/or GMR) read sensors. IEEE Trans. Magn. 2006;42:114–119. doi: 10.1109/TMAG.2005.861783. [DOI] [Google Scholar]
- 176.Davies J.E., Watts J.D., Novotny J., Huang D., Eames P.G. Magnetoresistive sensor detectivity: A comparative analysis. Appl. Phys. Lett. 2021;118:062401. doi: 10.1063/5.0038187. [DOI] [Google Scholar]
- 177.Fermon C., Pannetier-Lecoeur M. Smart Sensors, Measurement and Instrumentation. Volume 6 Springer; Berlin/Heidelberg, Germany: 2013. Noise in GMR and TMR sensors. [Google Scholar]
- 178.Salzer S., Robisch V., Klug M., Durdaut P., McCord J., Meyners D., Reermann J., Hoft M., Knochel R. Noise Limits in Thin-Film Magnetoelectric Sensors With Magnetic Frequency Conversion. IEEE Sens. J. 2018;18:596–604. doi: 10.1109/JSEN.2017.2776039. [DOI] [Google Scholar]
- 179.Zhou Y., Maurya D., Yan Y., Srinivasan G., Quandt E., Priya S. Self-Biased Magnetoelectric Composites: An Overview and Future Perspectives. Energy Harvest. Syst. 2016;3:1–42. doi: 10.1515/ehs-2015-0003. [DOI] [Google Scholar]
- 180.Nan T.X., Hui Y., Rinaldi M., Sun N.X. Self-Biased 215MHz Magnetoelectric NEMS Resonator for Ultra-Sensitive DC Magnetic Field Detection. Sci. Rep. 2013;3:1985. doi: 10.1038/srep01985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181.Jovičević Klug M., Thormählen L., Röbisch V., Toxværd S.D., Höft M., Knöchel R., Quandt E., Meyners D., McCord J. Antiparallel exchange biased multilayers for low magnetic noise magnetic field sensors. Appl. Phys. Lett. 2019;114:192410. doi: 10.1063/1.5092942. [DOI] [Google Scholar]
- 182.Wang Y., Gao J., Li M., Hasanyan D., Shen Y., Li J., Viehland D., Luo H. Ultralow equivalent magnetic noise in a magnetoelectric Metglas/Mn-doped Pb(Mg1/3Nb2/3)O3-PbTiO3 heterostructure. Appl. Phys. Lett. 2012;101:022903. doi: 10.1063/1.4733963. [DOI] [Google Scholar]
- 183.Wang Y.J., Gao J.Q., Li M.H., Shen Y., Hasanyan D., Li J.F., Viehland D. A review on equivalent magnetic noise of magnetoelectric laminate sensors. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014;372:20120455. doi: 10.1098/rsta.2012.0455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 184.Wang Y., Li J., Viehland D. Magnetoelectrics for magnetic sensor applications: Status, challenges and perspectives. Mater. Today. 2014;17:269–275. doi: 10.1016/j.mattod.2014.05.004. [DOI] [Google Scholar]
- 185.Yarar E., Salzer S., Hrkac V., Piorra A., Höft M., Knöchel R., Kienle L., Quandt E. Inverse bilayer magnetoelectric thin film sensor. Appl. Phys. Lett. 2016;109:022901. doi: 10.1063/1.4958728. [DOI] [Google Scholar]
- 186.Piorra A., Jahns R., Teliban I., Gugat J.L., Gerken M., Knöchel R., Quandt E. Magnetoelectric thin film composites with interdigital electrodes. Appl. Phys. Lett. 2013;103:32902. doi: 10.1063/1.4812706. [DOI] [Google Scholar]
- 187.Salzer S., Jahns R., Piorra A., Teliban I., Reermann J., Höft M., Quandt E., Knöchel R. Tuning fork for noise suppression in magnetoelectric sensors. Sens. Actuators A Phys. 2016;237:91–95. doi: 10.1016/j.sna.2015.10.040. [DOI] [Google Scholar]
- 188.Shen Y., McLaughlin K.L., Gao J., Li M., Li J., Viehland D. Effective optimization of magnetic noise for a Metglas/Pb(Zr,Ti)O3 magnetoelectric sensor array in an open environment. Mater. Lett. 2013;91:307–310. doi: 10.1016/j.matlet.2012.10.003. [DOI] [Google Scholar]
- 189.Dong C., Sun C., Chen L., He Y., Liu Y., Luo B., Sun N.X. Ultra-Compact Magnetoelectric Sensors for Femto-Tesla Vlf Signal Reception. [(accessed on 20 November 2024)]. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5019077.
- 190.Viehland D., Wuttig M., McCord J., Quandt E. Magnetoelectric magnetic field sensors. MRS Bull. 2018;43:834–840. doi: 10.1557/mrs.2018.261. [DOI] [Google Scholar]
- 191.Carman G.P., Sun N. Strain-mediated magnetoelectrics: Turning science fiction into reality. MRS Bull. 2018;43:822–828. doi: 10.1557/mrs.2018.236. [DOI] [Google Scholar]
- 192.Chu Z., Shi H., Shi W., Liu G., Wu J., Yang J., Dong S. Enhanced Resonance Magnetoelectric Coupling in (1-1) Connectivity Composites. Adv. Mater. 2017;29:1606022. doi: 10.1002/adma.201606022. [DOI] [PubMed] [Google Scholar]
- 193.Dong S.X., Cheng J.R., Li J.F., Viehland D. Enhanced magnetoelectric effects in laminate composites of Terfenol-D/Pb(Zr,Ti)O-3 under resonant drive. Appl. Phys. Lett. 2003;83:4812–4814. doi: 10.1063/1.1631756. [DOI] [Google Scholar]
- 194.Wang Y., Hasanyan D., Li M., Gao J., Li J., Viehland D. Equivalent magnetic noise in multi-push-pull configuration magnetoelectric composites: Model and experiment. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2013;60:1227–1233. doi: 10.1109/TUFFC.2013.2686. [DOI] [PubMed] [Google Scholar]
- 195.Das J., Gao J., Xing Z., Li J.F., Viehland D. Enhancement in the field sensitivity of magnetoelectric laminate heterostructures. Appl. Phys. Lett. 2009;95:092501. doi: 10.1063/1.3222914. [DOI] [Google Scholar]
- 196.Wang Y., Gray D., Berry D., Li J., Viehland D. Self-amplified magnetoelectric properties in a dumbbell-shaped magnetostrictive/piezoelectric composite. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012;59:859–862. doi: 10.1109/TUFFC.2012.2270. [DOI] [PubMed] [Google Scholar]
- 197.Wang Y., Li M., Hasanyan D., Gao J., Li J., Viehland D. Geometry-induced magnetoelectric effect enhancement and noise floor reduction in Metglas/piezofiber sensors. Appl. Phys. Lett. 2012;101:092905. doi: 10.1063/1.4737906. [DOI] [Google Scholar]
- 198.Gao J., Gray D., Shen Y., Li J., Viehland D. Enhanced dc magnetic field sensitivity by improved flux concentration in magnetoelectric laminates. Appl. Phys. Lett. 2011;99:153502. doi: 10.1063/1.3650713. [DOI] [Google Scholar]
- 199.Gao J., Das J., Xing Z., Li J., Viehland D. Comparison of noise floor and sensitivity for different magnetoelectric laminates. J. Appl. Phys. 2010;108:084509. doi: 10.1063/1.3486483. [DOI] [Google Scholar]
- 200.Li M., Wang Z., Wang Y., Li J., Viehland D. Giant magnetoelectric effect in self-biased laminates under zero magnetic field. Appl. Phys. Lett. 2013;102:82404. doi: 10.1063/1.4794056. [DOI] [Google Scholar]
- 201.Wang Y., Gray D., Berry D., Li M., Gao J., Li J., Viehland D. Influence of interfacial bonding condition on magnetoelectric properties in piezofiber/Metglas heterostructures. J. Alloys Compd. 2012;513:242–244. doi: 10.1016/j.jallcom.2011.10.029. [DOI] [Google Scholar]
- 202.Li M., Berry D., Das J., Gray D., Li J., Viehland D. Enhanced sensitivity and reduced noise floor in magnetoelectric laminate sensors by an improved lamination process. J. Am. Ceram. Soc. 2011;94:3738–3741. doi: 10.1111/j.1551-2916.2011.04659.x. [DOI] [Google Scholar]
- 203.Wang Y., Gray D., Gao J., Berry D., Li M., Li J., Viehland D., Luo H. Improvement of magnetoelectric properties in Metglas/Pb (Mg1/3Nb2/3)O3–PbTiO3 laminates by poling optimization. J. Alloys Compd. 2012;519:1–3. doi: 10.1016/j.jallcom.2011.12.093. [DOI] [Google Scholar]
- 204.Liu Y., Jiao J., Ma J., Ren B., Li L., Zhao X., Luo H., Shi L. Frequency conversion in magnetoelectric composites for quasi-static magnetic field detection. Appl. Phys. Lett. 2013;103:212902. doi: 10.1063/1.4832861. [DOI] [Google Scholar]
- 205.Dong C., Liang X., Gao J., Chen H., He Y., Wei Y., Zaeimbashi M., Matyushov A., Sun C., Sun N.X. Thin film magnetoelectric sensors toward biomagnetism: Materials, devices, and applications. Adv. Electron. Mater. 2022;8:2200013. doi: 10.1002/aelm.202200013. [DOI] [Google Scholar]
- 206.Srinivasan G., Rasmussen E.T., Levin B.J., Hayes R. Magnetoelectric effects in bilayers and multilayers of magnetostrictive and piezoelectric perovskite oxides. Phys. Rev. B. 2002;65:134402. doi: 10.1103/PhysRevB.65.134402. [DOI] [Google Scholar]
- 207.Laletin V.M., Paddubnaya N., Srinivasan G., de Vreugd C.P., Bichurin M.I., Petrov V.M., Filippov D.A. Frequency and field dependence of magnetoelectric interactions in layered ferromagnetic transition metal-piezoelectric lead zirconate titanate. Appl. Phys. Lett. 2005;87:222507. doi: 10.1063/1.2137450. [DOI] [Google Scholar]
- 208.Zhang T., Yang X., Ouyang J., Chen S., Tong B., Zhu Y., Zhang Y. A New Magnetoelectric Composite with Enhanced Magnetoelectric Coefficient and Lower Resonance Frequency. Appl. Compos. Mater. 2014;21:579–590. doi: 10.1007/s10443-013-9344-5. [DOI] [Google Scholar]
- 209.Chen L., Li P., Wen Y., Wang P. Highly zero-biased magnetoelectric response in magnetostrictive/piezoelectric composite. J. Appl. Phys. 2012;112:24504. doi: 10.1063/1.4737404. [DOI] [Google Scholar]
- 210.Lu C., Li P., Wen Y., Yang A., Yang C., Wang D., He W., Zhang J. Zero-biased magnetoelectric composite Fe73.5Cu1Nb3Si13.5B9/Ni/Pb(Zr1−x,Tix)O3 for current sensing. J. Alloys Compd. 2014;589:498–501. doi: 10.1016/j.jallcom.2013.12.038. [DOI] [Google Scholar]
- 211.Lu C., Li P., Wen Y., Yang A., He W., Zhang J., Yang J., Wen J., Zhu Y., Yu M. Investigation of magnetostrictive/piezoelectric multilayer composite with a giant zero-biased magnetoelectric effect. Appl. Phys. A. 2013;113:413–421. doi: 10.1007/s00339-013-7557-y. [DOI] [Google Scholar]
- 212.Lage E., Kirchhof C., Hrkac V., Kienle L., Jahns R., Knöchel R., Quandt E., Meyners D. Exchange biasing of magnetoelectric composites. Nat. Mater. 2012;11:523–529. doi: 10.1038/nmat3306. [DOI] [PubMed] [Google Scholar]
- 213.Zhou Y., Chul Yang S., Apo D.J., Maurya D., Priya S. Tunable self-biased magnetoelectric response in homogenous laminates. Appl. Phys. Lett. 2012;101:232905. doi: 10.1063/1.4769365. [DOI] [Google Scholar]
- 214.Tong B., Yang X., Guo Z., Li K., Ouyang J., Lin G., Chen S. Preparation and characterization of AlN/FeCoSiB magnetoelectric thin film composites. Ceram. Int. 2013;39:6853–6859. doi: 10.1016/j.ceramint.2013.02.019. [DOI] [Google Scholar]
- 215.Yan Y., Zhou Y., Priya S. Enhanced magnetoelectric effect in longitudinal-longitudinal mode laminate with cofired interdigitated electrodes. Appl. Phys. Lett. 2014;104:32911. doi: 10.1063/1.4862183. [DOI] [Google Scholar]
- 216.Yan Y., Zhou Y., Priya S. Giant self-biased magnetoelectric coupling in co-fired textured layered composites. Appl. Phys. Lett. 2013;102:52907. doi: 10.1063/1.4791685. [DOI] [Google Scholar]
- 217.Shen L.G., Li M.H., Gao J.Q., Shen Y., Li J.F., Viehland D., Zhuang X., Sing M.L.C., Cordier C., Saez S., et al. Magnetoelectric nonlinearity in magnetoelectric laminate sensors. J. Appl. Phys. 2011;110:114510. doi: 10.1063/1.3665130. [DOI] [Google Scholar]
- 218.Shen Y., Gao J., Wang Y., Finkel P., Li J., Viehland D. Piezomagnetic strain-dependent non-linear magnetoelectric response enhancement by flux concentration effect. Appl. Phys. Lett. 2013;102:172904. doi: 10.1063/1.4803660. [DOI] [Google Scholar]
- 219.Shen Y., Gao J., Wang Y., Li J., Viehland D. High non-linear magnetoelectric coefficient in Metglas/PMN-PT laminate composites under zero direct current magnetic bias. J. Appl. Phys. 2014;115:94102. doi: 10.1063/1.4867516. [DOI] [Google Scholar]
- 220.Zhuang X., Sing M.L.C., Dolabdjian C., Wang Y., Finkel P., Li J., Viehland D. Mechanical Noise Limit of a Strain-Coupled Magneto(Elasto)electric Sensor Operating Under a Magnetic or an Electric Field Modulation. IEEE Sens. J. 2015;15:1575–1587. doi: 10.1109/JSEN.2014.2363880. [DOI] [Google Scholar]
- 221.Zabel S., Reermann J., Fichtner S., Kirchhof C., Quandt E., Wagner B., Schmidt G., Faupel F. Multimode delta-E effect magnetic field sensors with adapted electrodes. Appl. Phys. Lett. 2016;108:222401. doi: 10.1063/1.4952735. [DOI] [Google Scholar]
- 222.Marauska S., Jahns R., Kirchhof C., Claus M., Quandt E., Knöchel R., Wagner B. Highly sensitive wafer-level packaged MEMS magnetic field sensor based on magnetoelectric composites. Sens. Actuators A Phys. 2013;189:321–327. doi: 10.1016/j.sna.2012.10.015. [DOI] [Google Scholar]
- 223.Jahns R., Greve H., Woltermann E., Quandt E., Knochel R.H. Noise performance of magnetometers with resonant thin-film magnetoelectric sensors. IEEE Trans. Instrum. Meas. 2011;60:2995–3001. doi: 10.1109/TIM.2011.2122410. [DOI] [Google Scholar]
- 224.Marauska S., Jahns R., Greve H., Quandt E., Knöchel R., Wagner B. MEMS magnetic field sensor based on magnetoelectric composites. J. Micromech. Microeng. 2012;22:65024. doi: 10.1088/0960-1317/22/6/065024. [DOI] [Google Scholar]
- 225.Marauska S., Claus M., Lisec T., Wagner B. Low temperature transient liquid phase bonding of Au/Sn and Cu/Sn electroplated material systems for MEMS wafer-level packaging. Microsyst. Technol. 2013;19:1119–1130. doi: 10.1007/s00542-012-1708-5. [DOI] [Google Scholar]
- 226.Su J., Niekiel F., Fichtner S., Thormaehlen L., Kirchhof C., Meyners D., Quandt E., Wagner B., Lofink F. AlScN-based MEMS magnetoelectric sensor. Appl. Phys. Lett. 2020;117:132903. doi: 10.1063/5.0022636. [DOI] [Google Scholar]
- 227.Gillette S.M., Geiler A.L., Gray D., Viehland D., Vittoria C., Harris V.G. Improved Sensitivity and Noise in Magneto-Electric Magnetic Field Sensors by Use of Modulated AC Magnetostriction. IEEE Magn. Lett. 2011;2:2500104. doi: 10.1109/LMAG.2011.2151178. [DOI] [Google Scholar]
- 228.Lage E., Urs N.O., Röbisch V., Teliban I., Knöchel R., Meyners D., McCord J., Quandt E. Magnetic domain control and voltage response of exchange biased magnetoelectric composites. Appl. Phys. Lett. 2014;104:132405. doi: 10.1063/1.4870511. [DOI] [Google Scholar]
- 229.Hrkac V., Lage E., Köppel G., Strobel J., McCord J., Quandt E., Meyners D., Kienle L. Amorphous FeCoSiB for exchange bias coupled and decoupled magnetoelectric multilayer systems: Real-structure and magnetic properties. J. Appl. Phys. 2014;116:134302. doi: 10.1063/1.4896662. [DOI] [Google Scholar]
- 230.Röbisch V., Yarar E., Urs N.O., Teliban I., Knöchel R., McCord J., Quandt E., Meyners D. Exchange biased magnetoelectric composites for magnetic field sensor application by frequency conversion. J. Appl. Phys. 2015;117:17B513. doi: 10.1063/1.4913814. [DOI] [Google Scholar]
- 231.Lage E., Woltering F., Quandt E., Meyners D. Exchange biased magnetoelectric composites for vector field magnetometers. J. Appl. Phys. 2013;113:17C725. doi: 10.1063/1.4798791. [DOI] [Google Scholar]
- 232.Salzer S., Durdaut P., Röbisch V., Meyners D., Quandt E., Höft M., Knöchel R. Generalized magnetic frequency conversion for thin-film laminate magnetoelectric sensors. IEEE Sens. J. 2016;17:1373–1383. doi: 10.1109/JSEN.2016.2645707. [DOI] [Google Scholar]
- 233.Durdaut P., Salzer S., Reermann J., Robisch V., Hayes P., Piorra A., Meyners D., Quandt E., Schmidt G., Knochel R., et al. Thermal-Mechanical Noise in Resonant Thin-Film Magnetoelectric Sensors. IEEE Sens. J. 2017;17:2338–2348. doi: 10.1109/JSEN.2017.2671442. [DOI] [Google Scholar]
- 234.Röbisch V., Salzer S., Urs N.O., Reermann J., Yarar E., Piorra A., Kirchhof C., Lage E., Höft M., Schmidt G.U., et al. Pushing the detection limit of thin film magnetoelectric heterostructures. J. Mater. Res. 2017;32:1009–1019. doi: 10.1557/jmr.2017.58. [DOI] [Google Scholar]
- 235.Durdaut P., Salzer S., Reermann J., Rbisch V., McCord J., Meyners D., Quandt E., Schmidt G., Knchel R., Hft M. Improved magnetic frequency conversion approach for magnetoelectric sensors. IEEE Sens. Lett. 2017;1:1–4. doi: 10.1109/LSENS.2017.2699559. [DOI] [Google Scholar]
- 236.Trolier-McKinstry S., Muralt P. Thin film piezoelectrics for MEMS. J. Electroceram. 2004;12:7–17. doi: 10.1023/B:JECR.0000033998.72845.51. [DOI] [Google Scholar]
- 237.Zhuang X., Sing M.L.C., Dolabdjian C. Investigation of the near-carrier noise for strain-driven ME laminates by using cross-correlation techniques. IEEE Trans. Magn. 2012;49:120–123. doi: 10.1109/TMAG.2012.2220340. [DOI] [Google Scholar]
- 238.Zhuang X., Lam Chok Sing M., Dolabdjian C., Wang Y., Finkel P., Li J., Viehland D. Dynamic Sensitivity and Noise Floor of a Bonded Magneto(Elasto)Electric Laminate for Low Frequency Magnetic Field Sensing under Strain Modulations. Key Eng. Mater. 2015;644:236–239. doi: 10.4028/www.scientific.net/KEM.644.236. [DOI] [Google Scholar]
- 239.Fetisov Y.K., Petrov V.M., Srinivasan G. Inverse magnetoelectric effects in a ferromagnetic–piezoelectric layered structure. J. Mater. Res. 2007;22:2074–2080. doi: 10.1557/jmr.2007.0262. [DOI] [Google Scholar]
- 240.Hockel J.L., Wu T., Carman G.P. Voltage bias influence on the converse magnetoelectric effect of PZT/terfenol-D/PZT laminates. J. Appl. Phys. 2011;109:064106. doi: 10.1063/1.3553885. [DOI] [Google Scholar]
- 241.Naeli K., Brand O. Dimensional considerations in achieving large quality factors for resonant silicon cantilevers in air. J. Appl. Phys. 2009;105:014908. doi: 10.1063/1.3062204. [DOI] [Google Scholar]
- 242.Kirchhof C., Krantz M., Teliban I., Jahns R., Marauska S., Wagner B., Knöchel R., Gerken M., Meyners D., Quandt E. Giant magnetoelectric effect in vacuum. Appl. Phys. Lett. 2013;102:232905. doi: 10.1063/1.4810750. [DOI] [Google Scholar]
- 243.Zabel S., Kirchhof C., Yarar E., Meyners D., Quandt E., Faupel F. Phase modulated magnetoelectric delta-E effect sensor for sub-nano tesla magnetic fields. Appl. Phys. Lett. 2015;107:152402. doi: 10.1063/1.4932575. [DOI] [Google Scholar]
- 244.Hanna S.M. Magnetic Field Sensors Based on SAW Propagation in Magnetic Films. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1987;34:191–194. doi: 10.1109/T-UFFC.1987.26931. [DOI] [PubMed] [Google Scholar]
- 245.Elhosni M., Petit-Watelot S., Hehn M., Hage-Ali S., Aissa K.A., Lacour D., Talbi A., Elmazria O. Experimental study of multilayer piezo-magnetic SAW delay line for magnetic sensor. Procedia Eng. 2015;120:870–873. doi: 10.1016/j.proeng.2015.08.743. [DOI] [Google Scholar]
- 246.Zhou H., Talbi A., Tiercelin N., Bou Matar O. Theoretical and experimental study of multilayer piezo-magnetic structure based surface acoustic wave devices for high sensitivity magnetic sensor; Proceedings of the 2013 IEEE International Ultrasonics Symposium (IUS); Prague, Czech Republic. 21–25 July 2013; pp. 212–215. [DOI] [Google Scholar]
- 247.Kittmann A., Müller C., Durdaut P., Thormählen L., Schell V., Niekiel F., Lofink F., Meyners D., Knöchel R., Höft M., et al. Sensitivity and noise analysis of SAW magnetic field sensors with varied magnetostrictive layer thicknesses. Sens. Actuators A Phys. 2020;311:111998. doi: 10.1016/j.sna.2020.111998. [DOI] [Google Scholar]
- 248.Yang Y., Mengue P., Mishra H., Floer C., Hage-Ali S., Petit-Watelot S., Lacour D., Hehn M., Han T., Elmazria O. Wireless Multifunctional Surface Acoustic Wave Sensor for Magnetic Field and Temperature Monitoring. Adv. Mater. Technol. 2022;7:1–9. doi: 10.1002/admt.202100860. [DOI] [Google Scholar]
- 249.Hu W., Huang M., Xie H., Zhang H., Bai F. Self-Biased Magnetic Field Sensors Based on Surface Acoustic Waves through Angle-Dependent Magnetoacoustic Coupling. Phys. Rev. Appl. 2023;19:1. doi: 10.1103/PhysRevApplied.19.014010. [DOI] [Google Scholar]
- 250.Labrenz J., Bahr A., Durdaut P., Höft M., Kittmann A., Schell V., Quandt E. Frequency Response of SAW Delay Line Magnetic Field/Current Sensor. IEEE Sens. Lett. 2019;3:1–4. doi: 10.1109/LSENS.2019.2943129. [DOI] [Google Scholar]
- 251.Emori S., Gray B.A., Jeon H.-M., Peoples J., Schmitt M., Mahalingam K., Hill M., McConney M.E., Gray M.T., Alaan U.S., et al. Coexistence of Low Damping and Strong Magnetoelastic Coupling in Epitaxial Spinel Ferrite Thin Films. Adv. Mater. 2017;29:1701130. doi: 10.1002/adma.201701130. [DOI] [PubMed] [Google Scholar]
- 252.Li R.F., Li P., Yi D., Riddiford L.J., Chai Y.H., Suzuki Y., Ralph D.C., Nan T.X. Anisotropic Magnon Spin Transport in Ultrathin Spinel Ferrite Thin Films-Evidence for Anisotropy in Exchange Stiffness. Nano Lett. 2022;22:1167–1173. doi: 10.1021/acs.nanolett.1c04332. [DOI] [PubMed] [Google Scholar]
- 253.Geller S., Gilleo M.A. The crystal structure and ferrimagnetism of yttrium-iron garnet, Y3Fe2(FeO4)3. J. Phys. Chem. Solids. 1957;3:30–36. doi: 10.1016/0022-3697(57)90044-6. [DOI] [Google Scholar]
- 254.Volakis J.L., Chen C.-C., Fujimoto K. Small Antennas: Miniaturization Techniques & Applications. McGraw Hill; New York, NY, USA: 2010. [Google Scholar]
- 255.Yao Z., Wang Y.E., Keller S., Carman G.P. Bulk Acoustic Wave-Mediated Multiferroic Antennas: Architecture and Performance Bound. IEEE Trans. Antennas Propag. 2015;63:3335–3344. doi: 10.1109/TAP.2015.2431723. [DOI] [Google Scholar]
- 256.Domann J.P., Carman G.P. Strain powered antennas. J. Appl. Phys. 2017;121:44905. doi: 10.1063/1.4975030. [DOI] [Google Scholar]
- 257.Wang Y., Ma Z., Fu G., Wang J., Xi Q., Wang Y., Jia Z., Zi G. A Low-Frequency MEMS Magnetoelectric Antenna Based on Mechanical Resonance. Micromachines. 2022;13:864. doi: 10.3390/mi13060864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 258.Ma M., Chen C., Xu H., Liu P., Xiao B., Liang S., Fu S., Song C., Pan F. High-Frequency Magnetoelectric Antenna by Acoustic Excitation for 5G Communication. IEEE Antennas Wirel. Propag. Lett. 2024;23:1518–1522. doi: 10.1109/LAWP.2024.3360947. [DOI] [Google Scholar]
- 259.Chang H., Li P., Zhang W., Liu T., Hoffmann A., Deng L., Wu M. Nanometer-Thick Yttrium Iron Garnet Films With Extremely Low Damping. IEEE Magn. Lett. 2014;5:1–4. doi: 10.1109/LMAG.2014.2350958. [DOI] [Google Scholar]
- 260.Ma M., Chen C., Xu H., Cao Y., Han L., Xiao B., Liu P., Liang S., Zhu W., Fu S., et al. Enhanced Radiation Efficiency by Resonant Coupling in a Large Bandwidth Magnetoelectric Antenna. Adv. Funct. Mater. 2024;2408699:1–8. doi: 10.1002/adfm.202408699. [DOI] [Google Scholar]
- 261.Zhang C., Ji Y., Gu H., Zhang P., Liu J., Liang X., Yang F., Ren T., Nan T. Surface Acoustic Wave Actuated MEMS Magnetoelectric Antenna. IEEE Electron Device Lett. 2024;45:2009–2012. doi: 10.1109/LED.2024.3437157. [DOI] [Google Scholar]
- 262.Chen H., Liang X., Sun N., Sun N.-X., Lin H., Gao Y. An ultra-compact ME antenna design for implantable wireless communication; Proceedings of the 2020 IEEE International Symposium on Antennas and Propagation and North American Radio Science Meeting; Toronto, ON, Canada. 5–10 July 2020; Piscataway, NJ, USA: IEEE; 2020. pp. 655–656. [Google Scholar]
- 263.Dong C., Wang X., Lin H., Gao Y., Sun N.X., He Y., Li M., Tu C., Chu Z., Liang X., et al. A Portable Very Low Frequency (VLF) Communication System Based on Acoustically Actuated Magnetoelectric Antennas. IEEE Antennas Wirel. Propag. Lett. 2020;19:398–402. doi: 10.1109/LAWP.2020.2968604. [DOI] [Google Scholar]
- 264.Dong C., He Y., Liu X., Sun N.X. VLF Mechanical Antenna Arrays for Underwater Wireless Communications; Proceedings of the 16th International Conference on Underwater Networks & Systems; Boston, MA, USA. 14–16 November 2022; pp. 1–5. [Google Scholar]
- 265.He Y. Magnetic and Magnetoelectric Devices for Communication and Energy Harvesting Applications. Northeastern University; Boston, MA, USA: 2023. [Google Scholar]
- 266.Sun N.X., Li M. Magnetoelectric Very Low Frequency Communication System. 10,720,564. U.S. Patent. 2020 July 21;
- 267.Hu L., Zhang Q., Wu H., You H., Jiao J., Luo H., Wang Y., Duan C., Gao A. A very low frequency (VLF) antenna based on clamped bending-mode structure magnetoelectric laminates. J. Phys. Condens. Matter. 2022;34:414002. doi: 10.1088/1361-648X/ac8403. [DOI] [PubMed] [Google Scholar]
- 268.Du Y., Xu Y., Wu J., Qiao J., Wang Z., Hu Z., Jiang Z., Liu M. Very-Low-Frequency Magnetoelectric Antennas for Portable Underwater Communication: Theory and Experiment. IEEE Trans. Antennas Propag. 2023;71:2167–2181. doi: 10.1109/TAP.2022.3233665. [DOI] [Google Scholar]
- 269.Fu S., Cheng J., Jiang T., Wu H., Fang Z., Jiao J., Sokolov O., Ivanov S., Bichurin M., Wang Y. Bias-free very low frequency magnetoelectric antenna. Appl. Phys. Lett. 2023;122:262901. doi: 10.1063/5.0158020. [DOI] [Google Scholar]
- 270.Zhou J., Reiskarimian N., Krishnaswamy H. 9.8 Receiver with integrated magnetic-free N-path-filter-based non-reciprocal circulator and baseband self-interference cancellation for full-duplex wireless; Proceedings of the 2016 IEEE International Solid-State Circuits Conference (ISSCC); San Francisco, CA, USA. 31 January–4 February 2016; pp. 178–180. [Google Scholar]
- 271.Reiskarimian N., Dastjerdi M.B., Zhou J., Krishnaswamy H. 18.2 Highly-linear integrated magnetic-free circulator-receiver for full-duplex wireless; Proceedings of the 2017 IEEE International Solid-State Circuits Conference (ISSCC); San Francisco, CA, USA. 5–9 February 2017; Piscataway, NJ, USA: IEEE; 2017. [Google Scholar]
- 272.Dinc T., Nagulu A., Krishnaswamy H. A Millimeter-Wave Non-Magnetic Passive SOI CMOS Circulator Based on Spatio-Temporal Conductivity Modulation. IEEE J. Solid-State Circuits. 2017;52:3276–3292. doi: 10.1109/JSSC.2017.2759422. [DOI] [Google Scholar]
- 273.Kord A., Sounas D.L., Alu A. Magnet-Less Circulators Based on Spatiotemporal Modulation of Bandstop Filters in a Delta Topology. IEEE Trans. Microw. Theory Tech. 2018;66:911–926. doi: 10.1109/TMTT.2017.2757470. [DOI] [Google Scholar]
- 274.Kord A., Sounas D.L., Alù A. Achieving Full-Duplex Communication: Magnetless Parametric Circulators for Full-Duplex Communication Systems. IEEE Microw. Mag. 2018;19:84–90. doi: 10.1109/MMM.2017.2759638. [DOI] [Google Scholar]
- 275.Nagulu A., Krishnaswamy H. 28.5 Non-Magnetic 60GHz SOI CMOS Circulator Based on Loss/Dispersion-Engineered Switched Bandpass Filters; Proceedings of the 2019 IEEE International Solid- State Circuits Conference—(ISSCC); San Francisco, CA, USA. 17–21 February 2019; Piscataway, NJ, USA: IEEE; 2019. [Google Scholar]
- 276.Nagulu A., Krishnaswamy H. Non-Magnetic CMOS Switched-Transmission-Line Circulators With High Power Handling and Antenna Balancing: Theory and Implementation. IEEE J. Solid-State Circuits. 2019;54:1288–1303. doi: 10.1109/JSSC.2019.2905146. [DOI] [Google Scholar]
- 277.Nagulu A., Reiskarimian N., Krishnaswamy H. Non-reciprocal electronics based on temporal modulation. Nat. Electron. 2020;3:241–250. doi: 10.1038/s41928-020-0400-5. [DOI] [Google Scholar]
- 278.Yu Y. Microelectromechanical Magnet-Free Non-Reciprocal Devices for In-Band Full-Duplex Applications. Northeastern University; Boston, MA, USA: 2020. [Google Scholar]
- 279.Nagulu A., Krishnaswamy H. Non-Magnetic Non-Reciprocal Microwave Components—State of the Art and Future Directions. IEEE J. Microw. 2021;1:447–456. doi: 10.1109/JMW.2020.3034301. [DOI] [Google Scholar]
- 280.Nagulu A., Mekkawy A., Tymchenko M., Sounas D., Alu A., Krishnaswamy H. Ultra-Wideband Switched-Capacitor Delays and Circulators-Theory and Implementation. IEEE J. Solid-State Circuits. 2021;56:1412–1424. doi: 10.1109/JSSC.2021.3055230. [DOI] [Google Scholar]
- 281.Dreher L., Weiler M., Pernpeintner M., Huebl H., Gross R., Brandt M.S., Goennenwein S.T.B. Surface acoustic wave driven ferromagnetic resonance in nickel thin films: Theory and experiment. Phys. Rev. B. 2012;86:134415. doi: 10.1103/PhysRevB.86.134415. [DOI] [Google Scholar]
- 282.Bömmel H., Dransfeld K. Excitation of hypersonic waves by ferromagnetic resonance. Phys. Rev. Lett. 1959;3:83. doi: 10.1103/PhysRevLett.3.83. [DOI] [Google Scholar]
- 283.Weiler M., Dreher L., Heeg C., Huebl H., Gross R., Brandt M.S., Goennenwein S.T.B. Elastically Driven Ferromagnetic Resonance in Nickel Thin Films. Phys. Rev. Lett. 2011;106:117601. doi: 10.1103/PhysRevLett.106.117601. [DOI] [PubMed] [Google Scholar]
- 284.Xu M., Yamamoto K., Puebla J., Baumgaertl K., Rana B., Miura K., Takahashi H., Grundler D., Maekawa S., Otani Y. Nonreciprocal surface acoustic wave propagation via magneto-rotation coupling. Sci. Adv. 2020;6:eabb1724. doi: 10.1126/sciadv.abb1724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 285.Küß M., Heigl M., Flacke L., Hörner A., Weiler M., Albrecht M., Wixforth A. Nonreciprocal dzyaloshinskii–moriya magnetoacoustic waves. Phys. Rev. Lett. 2020;125:217203. doi: 10.1103/PhysRevLett.125.217203. [DOI] [PubMed] [Google Scholar]
- 286.Maekawa S., Tachiki M. Surface acoustic attenuation due to surface spin wave in ferro-and antiferromagnets. Proc. AIP Conf. Proc. Am. Inst. Phys. 1976;29:542–543. [Google Scholar]
- 287.Matsuo M., Ieda J., Saitoh E., Maekawa S. Effects of mechanical rotation on spin currents. Phys. Rev. Lett. 2011;106:76601. doi: 10.1103/PhysRevLett.106.076601. [DOI] [PubMed] [Google Scholar]
- 288.Matsuo M., Ieda J., Harii K., Saitoh E., Maekawa S. Mechanical generation of spin current by spin-rotation coupling. Phys. Rev. B—Condens. Matter Mater. Phys. 2013;87:180402. doi: 10.1103/PhysRevB.87.180402. [DOI] [Google Scholar]
- 289.Kobayashi D., Yoshikawa T., Matsuo M., Iguchi R., Maekawa S., Saitoh E., Nozaki Y. Spin current generation using a surface acoustic wave generated via spin-rotation coupling. Phys. Rev. Lett. 2017;119:77202. doi: 10.1103/PhysRevLett.119.077202. [DOI] [PubMed] [Google Scholar]
- 290.Kurimune Y., Matsuo M., Nozaki Y. Observation of gyromagnetic spin wave resonance in NiFe films. Phys. Rev. Lett. 2020;124:217205. doi: 10.1103/PhysRevLett.124.217205. [DOI] [PubMed] [Google Scholar]
- 291.Sasaki R., Nii Y., Iguchi Y., Onose Y. Nonreciprocal propagation of surface acoustic wave in Ni/LiNbO3. Phys. Rev. B. 2017;95:020407. doi: 10.1103/PhysRevB.95.020407. [DOI] [Google Scholar]
- 292.Tateno S., Nozaki Y. Highly nonreciprocal spin waves excited by magnetoelastic coupling in a Ni/Si bilayer. Phys. Rev. Appl. 2020;13:34074. doi: 10.1103/PhysRevApplied.13.034074. [DOI] [Google Scholar]
- 293.Hernández-Mínguez A., Macià F., Hernàndez J.M., Herfort J., Santos P. V Large nonreciprocal propagation of surface acoustic waves in epitaxial ferromagnetic/semiconductor hybrid structures. Phys. Rev. Appl. 2020;13:44018. doi: 10.1103/PhysRevApplied.13.044018. [DOI] [Google Scholar]
- 294.Shah P.J., Bas D.A., Lisenkov I., Matyushov A., Sun N.X., Page M.R. Giant nonreciprocity of surface acoustic waves enabled by the magnetoelastic interaction. Sci. Adv. 2020;6:eabc5648. doi: 10.1126/sciadv.abc5648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 295.Küß M., Glamsch S., Kunz Y., Hörner A., Weiler M., Albrecht M. Giant surface acoustic wave nonreciprocity with low magnetoacoustic insertion loss in CoFeB/Ru/CoFeB synthetic antiferromagnets. ACS Appl. Electron. Mater. 2023;5:5103–5110. doi: 10.1021/acsaelm.3c00844. [DOI] [Google Scholar]
- 296.Verba R., Tiberkevich V., Slavin A. Wide-Band Nonreciprocity of Surface Acoustic Waves Induced by Magnetoelastic Coupling with a Synthetic Antiferromagnet. Phys. Rev. Appl. 2019;12:054061. doi: 10.1103/PhysRevApplied.12.054061. [DOI] [Google Scholar]
- 297.Küß M., Heigl M., Flacke L., Hörner A., Weiler M., Wixforth A., Albrecht M. Nonreciprocal magnetoacoustic waves in dipolar-coupled ferromagnetic bilayers. Phys. Rev. Appl. 2021;15:34060. doi: 10.1103/PhysRevApplied.15.034060. [DOI] [Google Scholar]
- 298.Grunberg P. Magnetostatic Spin-Wave Modes of a Heterogeneous Ferromagnetic Double-Layer. J. Appl. Phys. 1981;52:6824–6829. doi: 10.1063/1.328636. [DOI] [Google Scholar]
- 299.Szulc K., Graczyk P., Mruczkiewicz M., Gubbiotti G., Krawczyk M. Spin-wave diode and circulator based on unidirectional coupling. Phys. Rev. Appl. 2020;14:34063. doi: 10.1103/PhysRevApplied.14.034063. [DOI] [Google Scholar]
- 300.Bas D.A., Verba R., Shah P.J., Leontsev S., Matyushov A., Newburger M.J., Sun N.X., Tyberkevich V., Slavin A., Page M.R. Nonreciprocity of Phase Accumulation and Propagation Losses of Surface Acoustic Waves in Hybrid Magnetoelastic Heterostructures. Phys. Rev. Appl. 2022;18:044003. doi: 10.1103/PhysRevApplied.18.044003. [DOI] [Google Scholar]
- 301.Grünberg P., Barnas J., Saurenbach F., Fuβ J.A., Wolf A., Vohl M. Layered magnetic structures: Antiferromagnetic type interlayer coupling and magnetoresistance due to antiparallel alignment. J. Magn. Magn. Mater. 1991;93:58–66. doi: 10.1016/0304-8853(91)90304-S. [DOI] [Google Scholar]
- 302.Fuss A., Demokritov S., Grünberg P., Zinn W. Short-and long period oscillations in the exchange coupling of Fe across epitaxially grown Al-and Au-interlayers. J. Magn. Magn. Mater. 1992;103:L221–L227. doi: 10.1016/0304-8853(92)90192-Q. [DOI] [Google Scholar]
- 303.Verba R., Bankowski E.N., Meitzler T.J., Tiberkevich V., Slavin A. Phase Nonreciprocity of Microwave-Frequency Surface Acoustic Waves in Hybrid Heterostructures with Magnetoelastic Coupling. Adv. Electron. Mater. 2021;7:2100263. doi: 10.1002/aelm.202100263. [DOI] [Google Scholar]
- 304.Küß M., Glamsch S., Hörner A., Albrecht M. Wide-Band Nonreciprocal Transmission of Surface Acoustic Waves in Synthetic Antiferromagnets. ACS Appl. Electron. Mater. 2024;6:1790–1796. doi: 10.1021/acsaelm.3c01709. [DOI] [Google Scholar]
- 305.Huang M., Liu Y., Hu W., Wu Y., Wang W., He W., Zhang H., Bai F. Large nonreciprocity of shear-horizontal surface acoustic waves induced by a magnetoelastic bilayer. Phys. Rev. Appl. 2024;21:14035. doi: 10.1103/PhysRevApplied.21.014035. [DOI] [Google Scholar]
- 306.Hu W., Huang M., Wu Y., Jia Y., Wang W., Bai F. Giant nonreciprocity of surface acoustic waves induced by an anti-magnetostrictive bilayer. Appl. Phys. Lett. 2024;124:182405. doi: 10.1063/5.0196523. [DOI] [Google Scholar]
- 307.Zhou Z., Hu W., Wu H., Huang M., Wu Y., Jia Y., Wang W., Bai F. Nonreciprocal transmission of surface acoustic waves induced by magneotoelastic coupling with an anti-magnetostrictive bilayer. J. Appl. Phys. 2024;136:163901. doi: 10.1063/5.0235303. [DOI] [Google Scholar]
- 308.Matsumoto H., Kawada T., Ishibashi M., Kawaguchi M., Hayashi M. Large surface acoustic wave nonreciprocity in synthetic antiferromagnets. Appl. Phys. Express. 2022;15:63003. doi: 10.35848/1882-0786/ac6da1. [DOI] [Google Scholar]
- 309.Küß M., Hassan M., Kunz Y., Hörner A., Weiler M., Albrecht M. Nonreciprocal magnetoacoustic waves in synthetic antiferromagnets with Dzyaloshinskii-Moriya interaction. Phys. Rev. B. 2023;107:24424. doi: 10.1103/PhysRevB.107.024424. [DOI] [Google Scholar]
- 310.Lenef A., Rand S.C. Electronic structure of the N-V center in diamond: Theory. Phys. Rev. B. 1996;53:13441–13455. doi: 10.1103/PhysRevB.53.13441. [DOI] [PubMed] [Google Scholar]
- 311.Ohno K., Heremans F.J., Bassett L.C., Myers B.A., Toyli D.M., Jayich A.C.B., Palmstrom C.J., Awschalom D.D. Engineering shallow spins in diamond with nitrogen delta-doping. Appl. Phys. Lett. 2012;101:082413. doi: 10.1063/1.4748280. [DOI] [Google Scholar]
- 312.Robledo L., Childress L., Bernien H., Hensen B., Alkemade P.F.A., Hanson R. High-fidelity projective read-out of a solid-state spin quantum register. Nature. 2011;477:574–578. doi: 10.1038/nature10401. [DOI] [PubMed] [Google Scholar]
- 313.Awschalom D.D., Hanson R., Wrachtrup J., Zhou B.B. Quantum technologies with optically interfaced solid-state spins. Nat. Photonics. 2018;12:516–527. doi: 10.1038/s41566-018-0232-2. [DOI] [Google Scholar]
- 314.Childress L., Hanson R. Diamond NV centers for quantum computing and quantum networks. MRS Bull. 2013;38:134–138. doi: 10.1557/mrs.2013.20. [DOI] [Google Scholar]
- 315.Taminiau T.H., Cramer J., van der Sar T., Dobrovitski V.V., Hanson R. Universal control and error correction in multi-qubit spin registers in diamond. Nat. Nanotechnol. 2014;9:171–176. doi: 10.1038/nnano.2014.2. [DOI] [PubMed] [Google Scholar]
- 316.Fuchs G.D., Burkard G., Klimov P.V., Awschalom D.D. A quantum memory intrinsic to single nitrogen-vacancy centres in diamond. Nat. Phys. 2011;7:789–793. doi: 10.1038/nphys2026. [DOI] [Google Scholar]
- 317.Taylor J.M., Cappellaro P., Childress L., Jiang L., Budker D., Hemmer P.R., Yacoby A., Walsworth R., Lukin M.D. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 2008;4:810–816. doi: 10.1038/nphys1075. [DOI] [Google Scholar]
- 318.de Lange G., Riste D., Dobrovitski V.V., Hanson R. Single-Spin Magnetometry with Multipulse Sensing Sequences. Phys. Rev. Lett. 2011;106:080802. doi: 10.1103/PhysRevLett.106.080802. [DOI] [PubMed] [Google Scholar]
- 319.Rondin L., Tetienne J.P., Hingant T., Roch J.F., Maletinsky P., Jacques V. Magnetometry with nitrogen-vacancy defects in diamond. Rep. Prog. Phys. 2014;77:056503. doi: 10.1088/0034-4885/77/5/056503. [DOI] [PubMed] [Google Scholar]
- 320.Whiteley S.J., Heremans F.J., Wolfowicz G., Awschalom D.D., Holt M. V Correlating dynamic strain and photoluminescence of solid-state defects with stroboscopic x-ray diffraction microscopy. Nat. Commun. 2019;10:3386. doi: 10.1038/s41467-019-11365-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 321.Miao K.C., Bourassa A., Anderson C.P., Whiteley S.J., Crook A.L., Bayliss S.L., Wolfowicz G., Thiering G., Udvarhelyi P., Ivady V., et al. Electrically driven optical interferometry with spins in silicon carbide. Sci. Adv. 2019;5:eaay0527. doi: 10.1126/sciadv.aay0527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 322.Andrich P., de las Casas C.F., Liu X.Y., Bretscher H.L., Berman J.R., Heremans F.J., Nealey P.F., Awschalom D.D. Long-range spin wave mediated control of defect qubits in nanodiamonds. npj Quantum Inf. 2017;3:28. doi: 10.1038/s41534-017-0029-z. [DOI] [Google Scholar]
- 323.Kikuchi D., Prananto D., Hayashi K., Laraoui A., Mizuochi N., Hatano M., Saitoh E., Kim Y., Meriles C.A., An T. Long-distance excitation of nitrogen-vacancy centers in diamond via surface spin waves. Appl. Phys. Express. 2017;10:103004. doi: 10.7567/APEX.10.103004. [DOI] [Google Scholar]
- 324.Muhlherr C., Shkolnikov V.O., Burkard G. Magnetic resonance in defect spins mediated by spin waves. Phys. Rev. B. 2019;99:195413. doi: 10.1103/PhysRevB.99.195413. [DOI] [Google Scholar]
- 325.Awschalom D.D., Du C.R., He R., Heremans F.J., Hoffmann A., Hou J., Kurebayashi H., Li Y., Liu L., Novosad V., et al. Quantum Engineering with Hybrid Magnonic Systems and Materials (Invited Paper) IEEE Trans. Quantum Eng. 2021;2:1–36. doi: 10.1109/TQE.2021.3057799. [DOI] [Google Scholar]
- 326.Hensen B., Bernien H., Dreau A.E., Reiserer A., Kalb N., Blok M.S., Ruitenberg J., Vermeulen R.F.L., Schouten R.N., Abellan C., et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature. 2015;526:682–686. doi: 10.1038/nature15759. [DOI] [PubMed] [Google Scholar]
- 327.MacQuarrie E.R., Gosavi T.A., Jungwirth N.R., Bhave S.A., Fuchs G.D. Mechanical Spin Control of Nitrogen-Vacancy Centers in Diamond. Phys. Rev. Lett. 2013;111:227602. doi: 10.1103/PhysRevLett.111.227602. [DOI] [PubMed] [Google Scholar]
- 328.Ovartchaiyapong P., Lee K.W., Myers B.A., Jayich A.C.B. Dynamic strain-mediated coupling of a single diamond spin to a mechanical resonator. Nat. Commun. 2014;5:4429. doi: 10.1038/ncomms5429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 329.Barfuss A., Teissier J., Neu E., Nunnenkamp A., Maletinsky P. Strong mechanical driving of a single electron spin. Nat. Phys. 2015;11:820–824. doi: 10.1038/nphys3411. [DOI] [Google Scholar]
- 330.Trifunovic L., Pedrocchi F.L., Loss D. Long-Distance Entanglement of Spin Qubits via Ferromagnet. Phys. Rev. X. 2013;3:041023. doi: 10.1103/PhysRevX.3.041023. [DOI] [Google Scholar]
- 331.Wang X.C., Xiao Y.X., Liu C.P., Lee-Wong E., McLaughlin N.J., Wang H.F., Wu M.Z., Wang H.L., Fullerton E.E., Du C.R. Electrical control of coherent spin rotation of a single-spin qubit. npj Quantum Inf. 2020;6:78. doi: 10.1038/s41534-020-00308-8. [DOI] [Google Scholar]
- 332.Li Y., Zhang W., Tyberkevych V., Kwok W.K., Hoffmann A., Novosad V. Hybrid magnonics: Physics, circuits, and applications for coherent information processing. J. Appl. Phys. 2020;128:130902. doi: 10.1063/5.0020277. [DOI] [Google Scholar]
- 333.Solanki A.B., Bogdanov S.I., Rahman M.M., Rustagi A., Dilley N.R., Shen T., Tong W., Debashis P., Chen Z., Appenzeller J. Electric field control of interaction between magnons and quantum spin defects. Phys. Rev. Res. 2022;4:L012025. doi: 10.1103/PhysRevResearch.4.L012025. [DOI] [Google Scholar]
- 334.Labanowski D., Bhallamudi V.P., Guo Q.C., Purser C.M., McCullian B.A., Hammel P.C., Salahuddin S. Voltage-driven, local, and efficient excitation of nitrogen-vacancy centers in diamond. Sci. Adv. 2018;4:eaat6574. doi: 10.1126/sciadv.aat6574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 335.Whiteley S.J., Wolfowicz G., Anderson C.P., Bourassa A., Ma H., Ye M., Koolstra G., Satzinger K.J., Holt M.V., Heremans F.J., et al. Spin-phonon interactions in silicon carbide addressed by Gaussian acoustics. Nat. Phys. 2019;15:490–495. doi: 10.1038/s41567-019-0420-0. [DOI] [Google Scholar]
- 336.Hatanaka D., Asano M., Okamoto H., Kunihashi Y., Sanada H., Yamaguchi H. On-Chip Coherent Transduction between Magnons and Acoustic Phonons in Cavity Magnomechanics. Phys. Rev. Appl. 2022;17:034024. doi: 10.1103/PhysRevApplied.17.034024. [DOI] [Google Scholar]
- 337.Durdaut P., Rubiola E., Friedt J.-M., Muller C., Spetzler B., Kirchhof C., Meyners D., Quandt E., Faupel F., McCord J., et al. Fundamental Noise Limits and Sensitivity of Piezoelectrically Driven Magnetoelastic Cantilevers. J. Microelectromech. Syst. 2020;29:1347–1361. doi: 10.1109/JMEMS.2020.3014402. [DOI] [Google Scholar]
- 338.Urs N.O., Golubeva E., Röbisch V., Toxvaerd S., Deldar S., Knöchel R., Höft M., Quandt E., Meyners D., McCord J. Direct Link between Specific Magnetic Domain Activities and Magnetic Noise in Modulated Magnetoelectric Sensors. Phys. Rev. Appl. 2020;13:24018. doi: 10.1103/PhysRevApplied.13.024018. [DOI] [Google Scholar]
- 339.Friedrich R.-M., Zabel S., Galka A., Lukat N., Wagner J.-M., Kirchhof C., Quandt E., McCord J., Selhuber-Unkel C., Siniatchkin M. Magnetic particle mapping using magnetoelectric sensors as an imaging modality. Sci. Rep. 2019;9:2086. doi: 10.1038/s41598-018-38451-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 340.Zaeimbashi M., Lin H., Dong C., Liang X., Nasrollahpour M., Chen H., Sun N., Matyushov A., He Y., Wang X., et al. NanoNeuroRFID: A Wireless Implantable Device Based on Magnetoelectric Antennas. IEEE J. Electromagn. RF Microw. Med. Biol. 2019;3:206–215. doi: 10.1109/JERM.2019.2903930. [DOI] [Google Scholar]
- 341.Hughes G.B., Josey A.F., Glasscock M.E., III, Jackson C.G., Ray W.A., Sismanis A. Clinical electroneurography: Statistical analysis of controlled measurements in twenty-two normal subjects. Laryngoscope. 1981;91:1834–1846. doi: 10.1288/00005537-198111000-00007. [DOI] [PubMed] [Google Scholar]
- 342.Zuo S., Schmalz J., Özden M.-Ö., Gerken M., Su J., Niekiel F., Lofink F., Nazarpour K., Heidari H. Ultrasensitive magnetoelectric sensing system for pico-tesla magnetomyography. IEEE Trans. Biomed. Circuits Syst. 2020;14:971–984. doi: 10.1109/TBCAS.2020.2998290. [DOI] [PubMed] [Google Scholar]
- 343.Spetzler B., Kirchhof C., Reermann J., Durdaut P., Höft M., Schmidt G., Quandt E., Faupel F. Influence of the quality factor on the signal to noise ratio of magnetoelectric sensors based on the delta-E effect. Appl. Phys. Lett. 2019;114:183504. doi: 10.1063/1.5096001. [DOI] [Google Scholar]
- 344.Spetzler B., Kirchhof C., Quandt E., McCord J., Faupel F. Magnetic Sensitivity of Bending-Mode Delta-E-Effect Sensors. Phys. Rev. Appl. 2019;12:64036. doi: 10.1103/PhysRevApplied.12.064036. [DOI] [Google Scholar]
- 345.Ji Y., Zhang C., Nan T. Magnon-Phonon-Interaction-Induced Electromagnetic Wave Radiation in the Strong-Coupling Region. Phys. Rev. Appl. 2022;18:64050. doi: 10.1103/PhysRevApplied.18.064050. [DOI] [Google Scholar]
- 346.Rabiei P., Steier W.H. Lithium niobate ridge waveguides and modulators fabricated using smart guide. Appl. Phys. Lett. 2005;86:161115. doi: 10.1063/1.1906311. [DOI] [Google Scholar]
- 347.Churaev M., Wang R.N., Riedhauser A., Snigirev V., Blésin T., Möhl C., Anderson M.H., Siddharth A., Popoff Y., Drechsler U., et al. A heterogeneously integrated lithium niobate-on-silicon nitride photonic platform. Nat. Commun. 2023;14:3499. doi: 10.1038/s41467-023-39047-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 348.Izuhara T., Gheorma I.L., Osgood R.M., Roy A.N.U., Bakhru H., Tesfu Y.M., Reeves M.E. Single-crystal barium titanate thin films by ion slicing. Appl. Phys. Lett. 2003;82:616–618. doi: 10.1063/1.1540727. [DOI] [Google Scholar]
- 349.Levy M., Osgood R.M., Kumar A., Bakhru H. Crystal ion slicing of single-crystal magnetic garnet films. J. Appl. Phys. 1998;83:6759–6761. doi: 10.1063/1.367673. [DOI] [Google Scholar]
- 350.Guida J., Giribaldi G., Colombo L., Rinaldi M., Ghosh S. Solidly Mounted Two-Dimensional Guided Modes in 30% Scandium Aluminum Nitride on Sapphire; Proceedings of the 2023 22nd International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers); Kyoto, Japan. 25–29 June 2023; pp. 2094–2097. [Google Scholar]