Abstract
The existing calculation method for the surrounding rock pressure of shallow buried bias tunnel fails to account for the impact of the progressive failure characteristics of the surrounding rock and slope creep, thereby neglecting the additional pressure arising from slope creep. Therefore, the progressive instability failure mode of the surrounding rock of shallow buried bias tunnel was obtained by numerical simulation. Based on this, the theoretical analysis model of the additional pressure of shallow buried bias tunnel was established, and the calculation formula of the additional pressure was derived. Further analysis revealed that the larger the deformation rate of the surrounding rock, the shorter the time it takes for the additional pressure to reach its maximum value. When the deformation rate of surrounding rock increases to a certain value, there will be no additional pressure on the liner, that is, the pressure will be released when the surrounding rock is excavated. In such scenarios, if the strength of the first lining is inadequate, cracking or even collapse of the first lining may occur during excavation.
Keywords: Shallow buried bias tunnel, Progressive failure mode, Slope creep, Additional surrounding rock pressure
Subject terms: Engineering, Civil engineering
Introduction
In recent years, cracking issues have become increasingly prevalent in shallow buried bias tunnel1–3, which many scholars currently attribute to biased load or landslide thrust4. However, it was found that the deformation cracking of shallow buried bias tunnel has obvious timeliness4,5. These time-dependent deformation phenomena cannot be adequately explained by biased loads or landslide thrusts alone. Therefore, it is necessary to further study the surrounding rock pressure of the shallow buried bias tunnel.
The primary reason for tunnel cracking often arises from an insufficient understanding of the mechanical characteristics involved6,7. A comprehensive comprehension of the deformation characteristics of the lining is essential as a prerequisite for tunnel design and addressing potential disaster of shallow buried bias tunnel8. Therefore, Liu et al.9 proposed an upper bound solution for assessing the surrounding rock pressure in shallow buried bias tunnel by using the principles of virtual work and the theoretical foundations of the limit upper bound method. Wang10, through extensive monitoring of shallow buried bias tunnel, obtained the deformation and crack distribution characteristics of the tunnel lining and proposed a novel approach to identify the possible causes of lining deformation and cracking. Over the course of a 5-year monitoring endeavor, Poisel et al.11 diligently tracked and observed a shallow buried bias tunnel. They observed that the width of lining cracks increased at an annual rate of 1.5 mm, while the convergence rate escalated at a rate of 3.5 mm/year. This observation strongly suggests that the deformation and cracking of tunnel linings within slope exhibit significant time-dependent behavior. Chiu et al.12 confirmed this view based on field monitoring data. Ruggeri et al.13 and Wei et al.14, drawing on their analyses of tunnel and slope deformation monitoring data, discerned the substantial influence of rainfall on time-dependent deformation. This underscores the critical role of environmental factors, particularly rainfall, in shaping the behavior of shallow buried bias tunnel. Based on model tests, Lei et al.15 found that the whole process of the instability of shallow buried bias tunnel in homogeneous layer can be described as follows: tunnel excavation causes collapse deformation, then induces surface tension on the deep buried side of the tunnel, and finally causes deep shear of the surrounding rock on the deep buried side to form a failure surface. It is proved that the instability process of shallow buried bias tunnel is a gradual cumulative failure process from local to whole. Schneider-Muntau and Cordes16 believed that the time-dependent deformation of shallow buried bias tunnels is caused by slope creep, and used numerical analysis methods to study the time-dependent deformation of tunnels. Causse class17established a numerical model of shallow buried bias tunnels using the creep model embedded in FLAC3D, and obtained the evolution law of tunnel deformation and stress under the action of slope creep. The above scholars called the creep constitutive model and parameters in the numerical software to analyze the tunnel deformation and stress, and did not establish additional pressure theoretical analysis models and calculation methods that consider the creep characteristics of slopes.
In summary, the current theory regarding surrounding rock pressure in shallow buried bias tunnels ails to consider the impact of progressive failure characteristics of the surrounding rock and slope creep on the surrounding rock pressure, thereby neglecting the additional pressure induced by slope creep. Therefore, based on the progressive failure mode of the surrounding rock of shallow buried bias tunnel, the creep constitutive model was introduced into the calculation model of surrounding rock pressure. Based on the analysis of the stress state of the surrounding rock in three stages, the analysis model of additional surrounding rock pressure of shallow buried bias tunnel was established, and the calculation formula of additional surrounding rock pressure was derived.
Progressive failure mode of surrounding rock and additional pressure of the tunnel
Progressive failure mode of surrounding rock
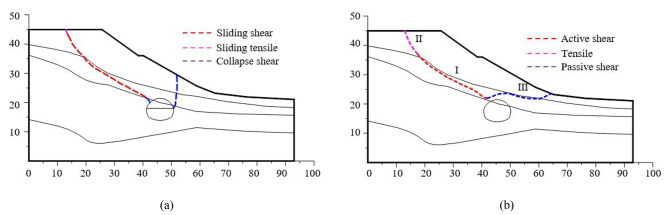
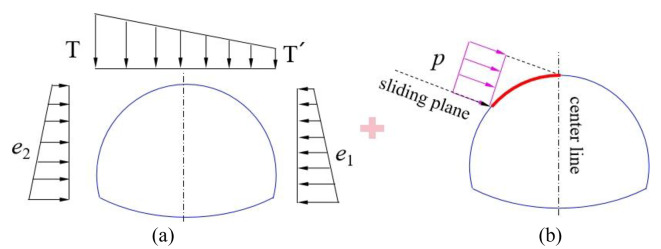
According to the model test results of Leiet al.15, the instability failure of the surrounding rock of shallow buried bias tunnel in homogeneous layer is essentially a progressive failure process from local to whole. Tian et al.18 used FLAC to simulate the progressive failure process of slope, and obtained the progressive failure mode of surrounding rock of shallow buried bias tunnel, as shown in Fig. 1. Under the condition of no support, the formation mechanism of failure plane of surrounding rock on both sides of shallow buried bias tunnel is different. The shallow buried side is the shear failure plane induced by the collapse of surrounding rock, while the deep buried side of the tunnel is the shear failure plane induced by the collapse of surrounding rock and slope sliding. The failure plane of the slope is divided into three parts according to the formation sequence and reasons. The Part I is the first failure plane formed by active shear due to the influence of tunnel excavation; The part II is the failure plane formed by tensile of slope top; The part III is the failure plane formed by passive shear under the push of the soil in the upper part of the slope. In the process of tunnel excavation, the tunnel is first subjected to the collapse load of rock and soil mass, and then subjected to the load caused by slope sliding. After the construction of the tunnel structure being completed, the load on the tunnel structure also includes the deformation effect from the slopes sliding, not just the soil collapse load.
Fig. 1.
Failure plane of surrounding rock20. (a) The failure plane of surrounding rock without support. (b) The failure plane of surrounding rock with support.
Additional pressure of the tunnel
After tunnel excavation, the rock and soil surrounding the excavation face initially experience collapse or compression deformation, which then gradually extends deeper into the surrounding rock mass. The installation of tunnel lining will effectively mitigate the deformation of surrounding rock. However, the deformation of the surrounding rock will persist even after the completion of lining, indicating a continuous process. Therefore, the load on the tunnel lining can be composed of two parts. One part is the surrounding rock pressure released once by tunnel excavation, and the other part is the additional pressure of lining to restrain the creep deformation of surrounding rock19. The late deformation in the soft rock tunnel is particularly conspicuous, leading to a substantial increase in the late load on the lining and posing a significant impact on its safety.
The deformation and cracking of shallow buried bias pressure tunnels typically occur following the completion of lining construction or during operation. In such instances, the slope experiences stable creep deformation, which can be effectively described using the generalized Kelvin model for rock and soil behavior.
It is posited that the stress state surrounding the tunnel is categorized into three distinct stages. The initial stage is illustrated in Fig. 2 (a). At this point, the tunnel has either just been excavated or the first lining has been applied, with the load 
released by the surrounding rock being supported by spring 1. The second stage is shown in Fig. 2 (b). The lining has just been applied, and the late additional pressure 
. The third stage is shown in Fig. 2 (c), after the lining being applied, the late additional pressure of the lining is p.
Fig. 2.
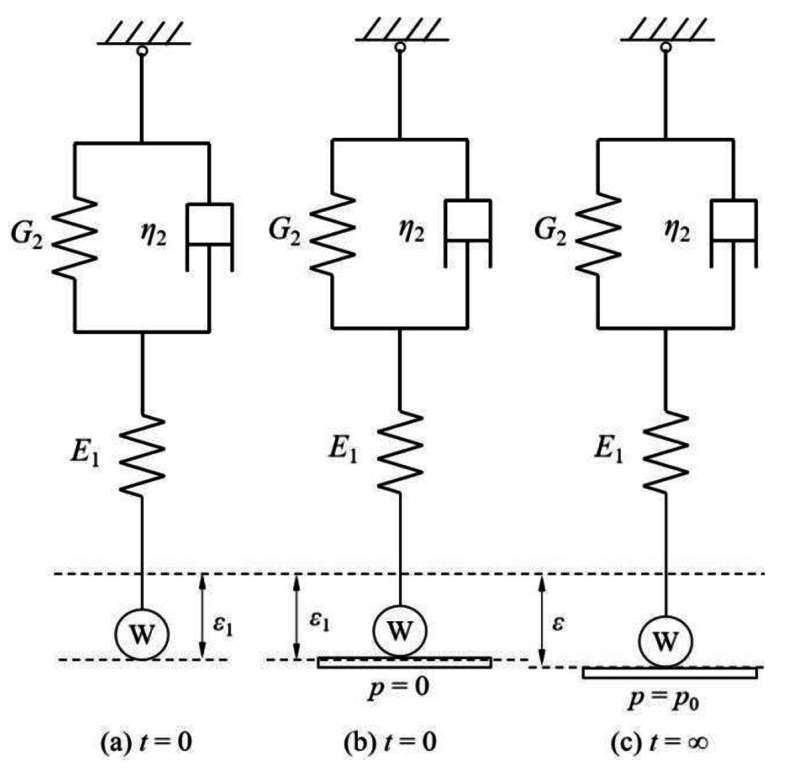
Calculation model of additional pressure on liner.
At time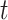 
, the total deformation is 
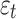, there are:
 |
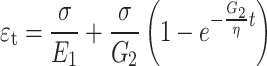1 |
According to (1):
 |
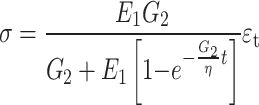2 |
At time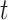 
, the late additional pressure is 
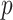, then:
 |
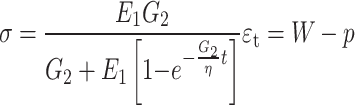3 |
The late additional pressure at time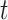 
in the above formula is 
:
 |
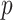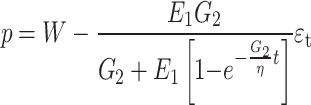4 |
Where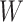 
is the load released by the surrounding rock just after the tunnel excavation, and the load is borne by spring 1. The deformation generated by the spring is 
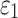. There are:
 |
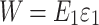5 |
Where 
is the shear modulus of the spring 1.
When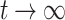 
, 
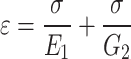, the final late additional pressure of the lining is:
 |
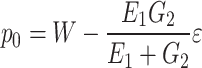6 |
Where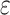 
is the total deformation at 
, 
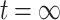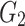is the shear modulus of the spring 2.
Because the elastic deformation of reinforced concrete lining is much smaller than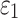 
, there is 
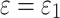. The additional pressure of the tunnel can be approximated by the following equation:
 |
7 |
Analysis model of additional pressure in shallow buried bias tunnel
Additional pressure analysis model
According to the formation mechanism of the failure plane, the sliding plane is divided into two parts. The Part I is the first failure plane formed by active shear due to the influence of tunnel excavation; The part II is the failure plane formed by tensile of slope top. The sliding plane is simplified as a folded line. The creep direction of the active shear part of the sliding body is regarded as the main sliding direction of the whole sliding body. The additional pressure calculation model is shown in Fig. 3. In Eq. (7),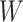 
is the load generated when elastic deformation occurs in the surrounding rock of tunnel excavation. According to the elastic pressure and elastic deformation obtained by the model, it can be considered that the load released and the deformation generated by the tunnel just excavated.
Fig. 3.
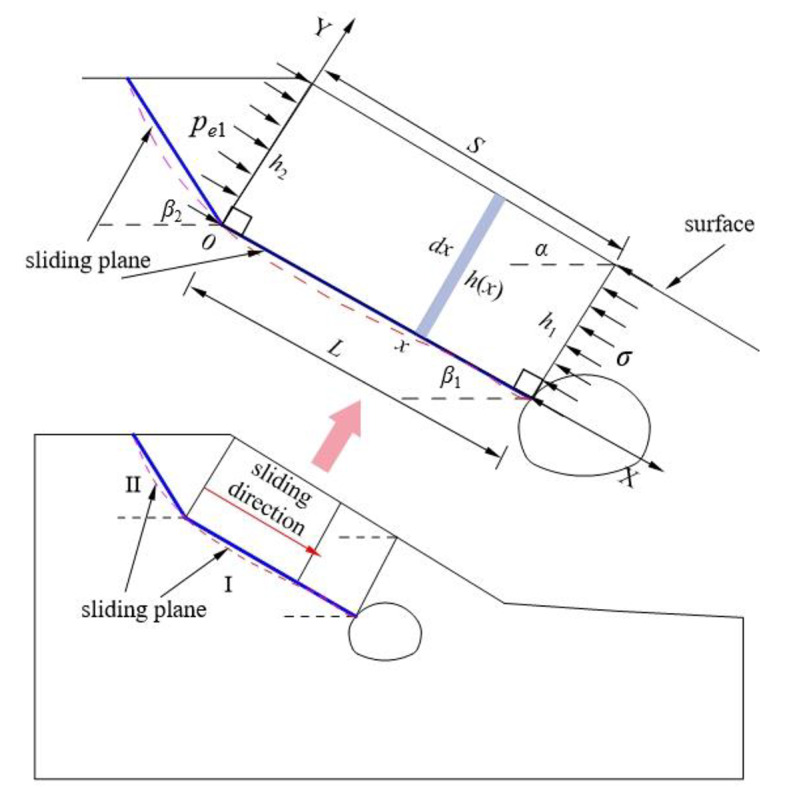
Calculation model of additional pressure for shallow buried bias tunnel.
Elastic pressure
The elastic pressure is the stress generated by the remaining sliding force on the slide after overcoming the sliding force. Take the micro unit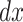 
at the position of 
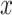, as shown in Fig. 4. The thickness of the corresponding slide is 
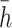, and the heavy weight of the rock and soil mass is 
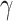, then the weight of the unit is:
Fig. 4.
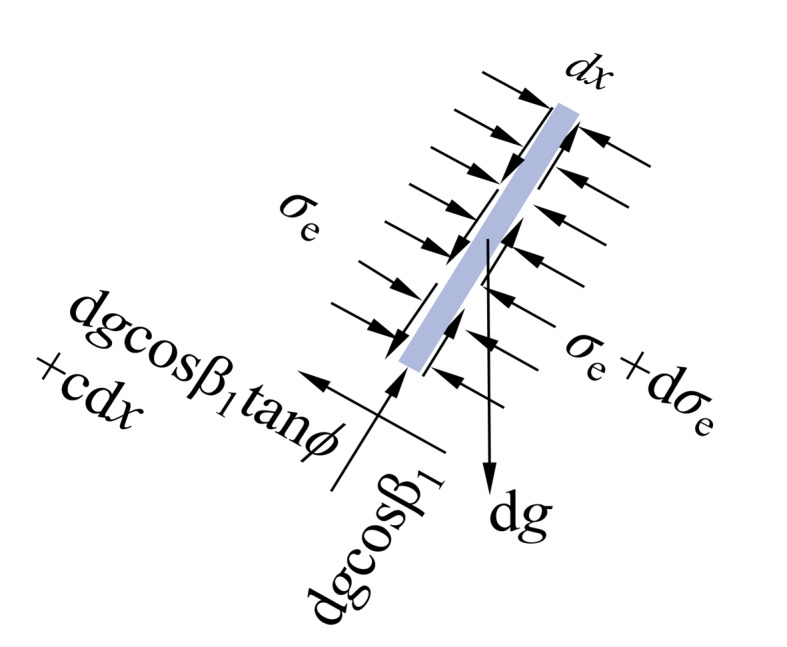
Schematic diagram of unit stress.
 |
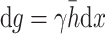8 |
The sliding force of the unit is:
 |
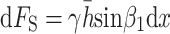9 |
The sliding resistance of the unit is:
 |
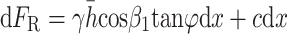10 |
Then the residual sliding force of the micro unit is the pressure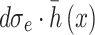 
acting on the slide section:
 |
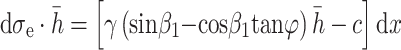11 |
Where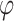 
is the friction angle, and 
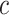is the cohesive force, according to the geometric relation: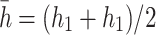 
When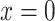 
, 
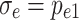, by integrating Eq. (11) from 
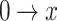, the compressive stress at any position of the slider can be obtained as follows:
 |
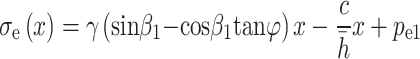12 |
When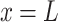 
, the elastic pressure of the slide on the deep buried side of the tunnel is:
 |
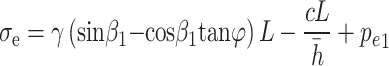13 |
Where,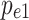 
is the pressure on the main sliding body along the main sliding direction.
Assuming that the sliding body follows the Hooke compression model. In unit width, the deformation in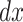 
length is Δ(x), the strain 
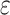can be expressed as:
 |
14 |
 |
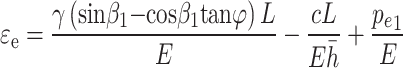15 |
Where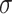 
and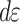 
are the compressive stress and micro strain; 
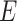is the elastic modulus.
Ignoring the elastic deformation at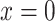 
, integrating Eq. (15) from 
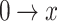, and the elastic deformation caused by compressive stress at any position of the main slider is:
 |
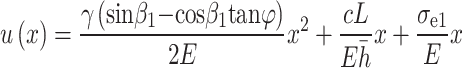16 |
When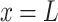 
, the elastic compression deformation of the slide on the deeply buried side of the tunnel is:
 |
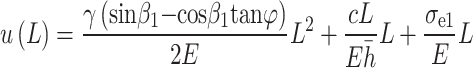17 |
Example verification
The prerequisite of the additional pressure analysis model of shallow buried bias tunnel is that the additional pressure acting on the lining comes from the slope creep. It is necessary to qualitatively verify the deformation of the slope as creep deformation, and then to quantitatively verify the reliability of the calculation formula.
Qualitative verification
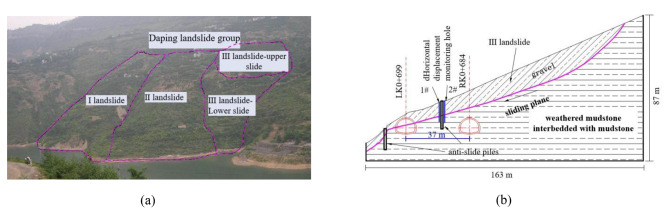
In order to qualitatively verify the rationality of the additional pressure analysis model of shallow buried bias tunnel, Sunjiaya tunnel was taken as an engineering example, and the deformation monitoring data and the theoretical data are compared. Sunjiaya tunnel is a separate two-line tunnel. The tunnel mileage of the left line is LK0 + 675-LK3 + 885, the length of the tunnel is 3210 m, the width of both tunnels is 13.0 m and the height of the tunnel is 7.0 m. The tunnel inlet section is located in the area of Daping Ancient landslide group, which consists of landslides No. I, II and III, as shown in Fig. 5 (a). The Sunjiya tunnel inlet pass through the Daping landslide, which is a typical shallow buried bias tunnel. The relative position between the tunnel and the III landslide and the layout of the horizontal displacement monitoring point of the landslide are shown in Fig. 5 (b).
Fig. 5.
Sunjiaya Tunnel. (a) Tunnel plan position. (b) Tunnel entrance section profile and horizontal displacement monitoring points.
The elastic deformation cannot be recorded in the field monitoring data, so the elastic deformation item represented in the formula (1) is omitted. The deformation of landslide should conform to the following change law.
 |
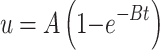18 |
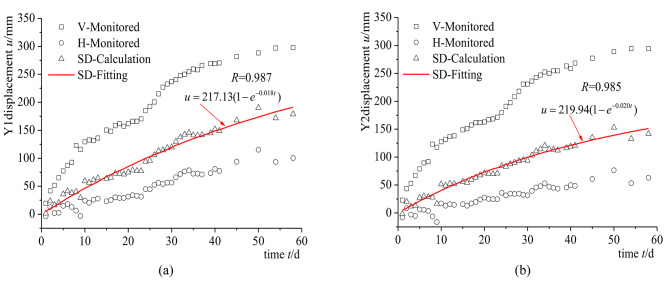
If the landslide conforms to the creep deformation characteristics, then the deformation of the surrounding rock on the deep buried side of the tunnel along the sliding surface direction should also conform to the change rule of Eq. (18). The vertical and horizontal displacements of two monitoring points on the deep buried side of the tunnel (Fig. 6, Y1 and Y2) were selected to synthesize the displacements along the landslide direction.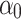 
is the angle between the slide plane and the horizontal plane.
Fig. 6.
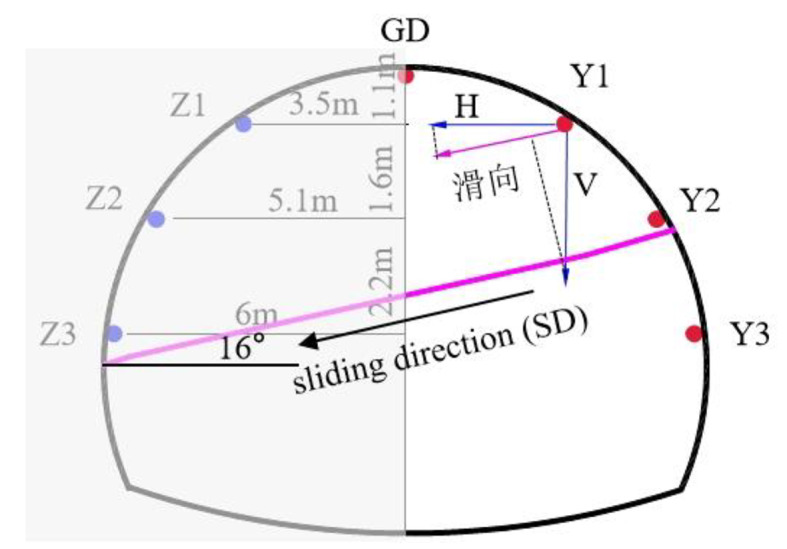
Layout of displacement monitoring points in tunnel surrounding rock.
 |
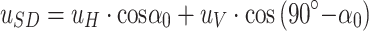19 |
The evolution of the displacement along the landslide direction over time is shown in Fig. 7. The displacement along the landslide direction was fitted well, with a higher correlation coefficient. This showed that the evolution of displacement along the landslide with time complies with the slope creep characteristics. It is proved laterally that the creep deformation of landslide mass is the external manifestation of the creep deformation of landslide rock and soil mass.
Fig. 7.
Evolution law of displacement along landslide direction with time. (a) Y1 monitoring point. (b) Y2 monitoring point.
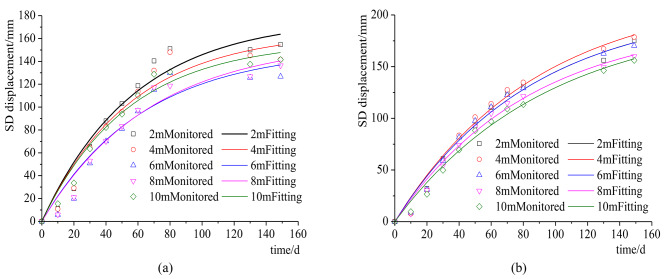
The displacement along the sliding direction was calculated from the displacement monitoring data of 1 # and 2 # at depths of 2,4,6,8 and 10, respectively. The monitoring data were drawn as a displacement curve over time, and Eq. (18) was adopted for fitting, as shown in Fig. 8. The displacement fitting of each point along the sliding direction is good, consistent with the slope creep characteristics.
Fig. 8.
Displacement along the direction of the landslide. (a) 1 # monitoring point. (b) 2 # monitoring point.
Quantitative validation
The reliability of the additional surrounding rock pressure calculation method was verified through an analysis of lining under slope creep conditions. The numerical calculation consists of two main steps: firstly, calculating the surrounding rock pressure generated by tunnel excavation and lining; secondly, conducting a creep calculation by clearing node displacement and unit state.
The additional pressure arises from the extrusion effect that occurs between the creep deformation of the slope and the tunnel. Therefore, for the numerical analysis, the tunnel lining was simulated by the Liner structural unit in FLAC3D. In addition to providing the mechanical characteristics of the shell structure, the Liner unit also considers the interaction between the lining shear direction friction force and the FLAC3D grid, and can apply the normal pressure. This Liner unit not only captures the mechanical characteristics of the shell structure but also accounts for the interplay between the lining’s shear-direction friction force and the FLAC3D grid. It is capable of applying both normal pressure and tensile forces, and allows for the lining structure to undergo failure within the surrounding rock grid. Hence, the Liner unit was employed to model both the upward extrusion effect and the tangential friction force between the lining and the surrounding rock medium. The the model upper surface is free, and the normal displacement constraints are applied to the left and right sides, and the bottom surface is fixed. The model consists of 3190 units and 25,260 nodes. The numerical model is depicted in Fig. 9.
Fig. 9.
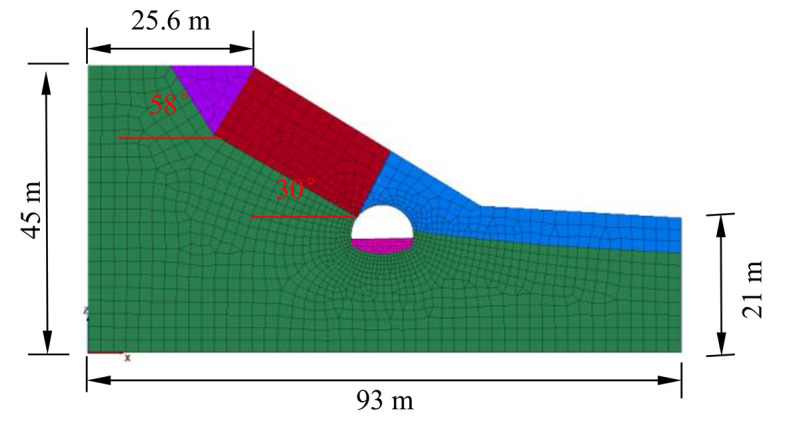
Numerical model.
The surrounding rock follows the Mohr-Coulomb constitutive model during tunnel excavation and support stages. In the calculation of the creep model, the rock formation parameters below the sliding surface remain unchanged, while the sliding body is simulated using a generalized Kelvin model. The mechanical parameters of the surrounding rock are presented in Table 1. Shear modulus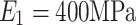 
, Kelvin shear modulus 
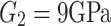, Kelvin viscosity 
.
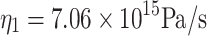Table 1.
Physical and mechanical parameters of materials18.
| Name | E/kPa | γ /kN/m3 | μ | Peak strength | Residual strength | ||
|---|---|---|---|---|---|---|---|
| c/kPa | φ /° | c /kPa | φ /° | ||||
| Backfill, gravels | 4.00E + 05 | 20 | 0.43 | 20 | 30 | 15 | 18 |
| Soft strata, clay | 3.00E + 05 | 18 | 0.35 | 30 | 18 | 25 | 15 |
| Greatly weathered shale rock | 3.00E + 06 | 25.9 | 0.3 | 200 | 30 | 200 | 30 |
| Slightly weathered limestone | 3.50E + 06 | 26.4 | 0.3 | 450 | 35 | 450 | 35 |
The tunnel in question adopts a full-section excavation method and undergoes subsequent lining. Following this, a creep time step of at least 1e-2 is computed, with the entire calculation period spanning 155,520,000 s( 5 years). After four years of calculation, the increase in pressure is almost zero. After 4 years of landslide creep, the distribution characteristics of normal pressure on tunnel lining are shown in Fig. 10. The normal pressure near the lining arch and invert is relatively small, and the pressure on the left and right side of the lining is larger. The maximum normal pressure is at the junction of the right wall foot and the invert. The normal pressure distribution of lining is asymmetrical. The pressure on the right side is greater than that on the left side.
Fig. 10.
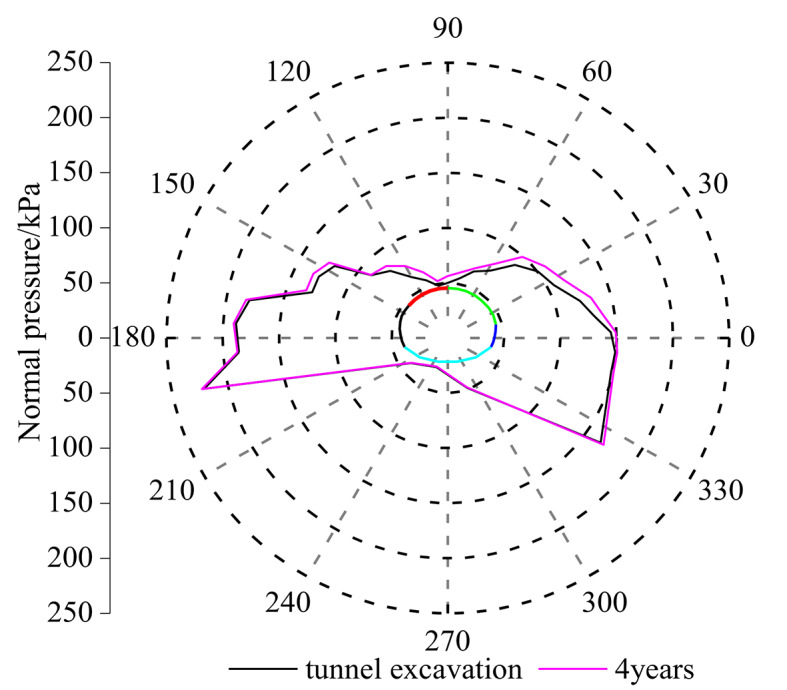
Radial pressure distribution characteristics of liner.
After 4 years of landslide creep, the percentage increase of normal pressure at each position of lining is shown in Fig. 11. The percentage increase of lining normal pressure gradually increases from the left wall foot, reaches the maximum in the area between the left lining and the sliding surface, and then gradually decreases. The area between the boundary between the lining and the sliding surface and the arch has the largest pressure increase, followed by the area between the lining arch and the right side and the sliding surface. However, the reason for the increase of normal pressure between the junction of the lining and the sliding surface and the vault is different from that between the vault and the right wall foot. The former is mainly due to the additional pressure produced by lining to prevent landslide deformation. The latter is the additional passive earth pressure caused by lining deformation and squeezing surrounding rock under the action of additional pressure on the left side. The invert normal pressure increase is negative, indicating that the invert normal pressure decreases after 4 years of landslide creep.
Fig. 11.
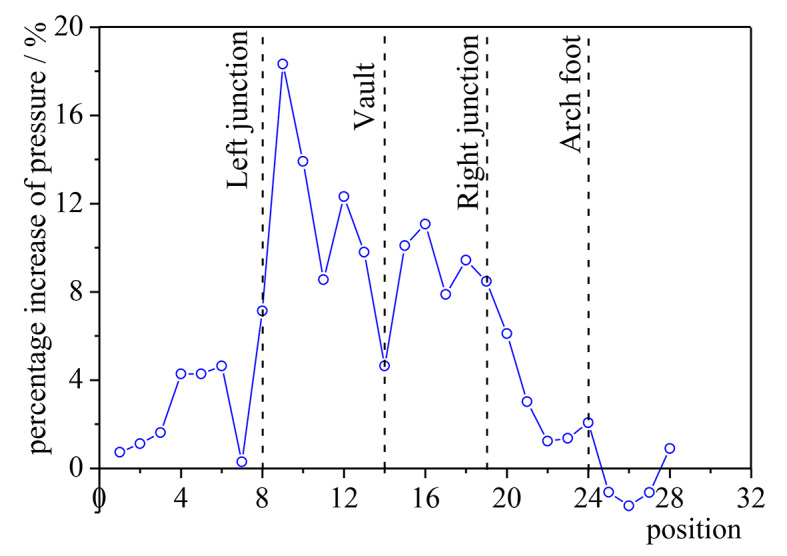
The increase of radial pressure at each position of liner.
The direction of the normal pressure at the intersection of the sliding surface and the tunnel lining is consistent with the direction of the sliding surface. This point was selected for numerical simulation and theoretical calculation for comparison. The curve of surrounding rock pressure with time is shown in Fig. 12.
Fig. 12.
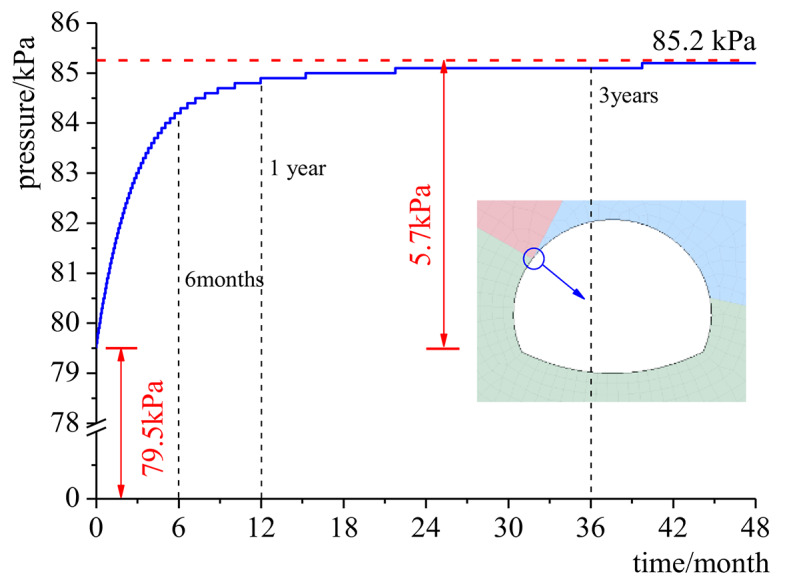
The curve of surrounding rock pressure with time.
When the slope creep time is 0, the surrounding rock pressure is 79.5 kPa. The surrounding rock pressure is the initial release pressure of tunnel excavation. When the slope excavation creep, the surrounding rock pressure increases with time. The overall pressure of surrounding rock has been stable for 4 years. At the end of year 4, the surrounding rock pressure was 85.2 kPa. The additional surrounding rock pressure caused by slope creep is 5.7 kPa. When the landslide creep lasted for 6 months, the additional surrounding rock pressure was 5.0 kPa, accounting for 87.7% of the total additional pressure. The remaining 12.3% of the additional pressure will be released in the next four years. The elastic pressure calculated according to Eq. (13) is 80.8 kPa, which is 1.3 kPa different from the initial release pressure of the numerical simulation, and 1.6% larger than that of the numerical simulation. Then, according to Eq. (6), the maximum lateral additional pressure caused by landslide creep is 6.24 kPa. The difference between the additional lateral wall rock pressure calculated according to Eq. (6) and the additional lateral pressure obtained by numerical simulation is 0.34 kPa, accounting for 9.5% of the numerical simulation. It showed that the additional lateral surrounding rock pressure calculated according to Eq. (6) has certain reliability, and the accuracy meets the engineering requirements.
Analysis and discussion
Assuming the deformation released by excavation is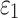 
. When 
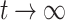, the total deformation is 
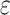. According to Eq. (6), the change of tunnel additional pressure with time is shown in Fig. 13. When 
, 
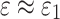, only the elastic deformation released by tunnel excavation, the surrounding rock does not produce creep deformation, and the additional pressure of lining is 
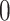. The lining additional pressure increases with the increase of time, and finally approaches 
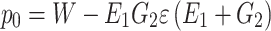. Let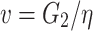 
to represent the deformation rate of surrounding rock. The greater the 
, the greater the deformation rate, and the surrounding rock can reach the total deformation 
in a shorter time.
Fig. 13.
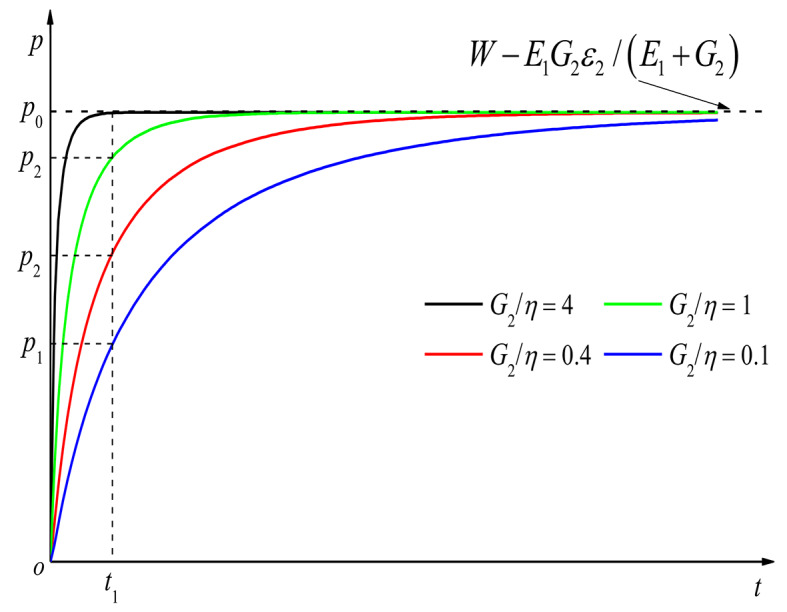
Additional pressure history curve of liner.
Assuming that the final deformation of surrounding rock after excavation is 
, the greater the deformation rate of surrounding rock, the additional pressure of lining can reach the maximum value in a shorter time. When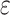 
is increased to a certain value, the surrounding rock will complete the deformation in a very short time after excavation. This situation is equivalent to the release of pressure after tunnel excavation, and the lining will not be subjected to additional pressure. This situation is equivalent to the release of pressure after the completion of tunnel excavation, and the lining will not be affected by additional pressure. However, if the strength of the initial branch is insufficient, the initial branch cracking and even collapse may occur during the excavation stage. However, if the strength of the first lining is insufficient, the first lining cracking and even collapse may occur during the excavation stage.
When the deformation rate of surrounding rock is different, the lining additional pressure applied at the same time is also different. When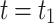 
, 
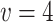, the pressure caused by creep deformation is close to 
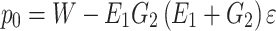. If the liner is applied at this time, the additional pressure on the liner is almost zero. However, when 
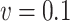, the pressure generated by the creep deformation is 
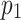. At this time, the liner will be subjected to 
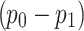In the late pressure.
The failure mode of the surrounding rock of the shallow buried bias tunnel changed before and after the lining being installed, which results in the change of the magnitude and direction of the additional pressure borne by the lining. In this case, the lining is highly likely to crack. Therefore, the influence of late additional pressure caused by slope creep should be considered in the design of shallow buried bias tunnel. The theoretical analysis model of surrounding rock pressure in shallow buried bias tunnel was established, as shown in Fig. 14. The direction of the additional pressure is consistent with the direction of the sliding plane. The action range of the additional pressure is the area between the interface of the sliding plane and the tunnel and the vault.
Fig. 14.
Theoretical analysis model of surrounding rock pressure in shallow buried bias tunnel. (a) Bias load for the soil collapse20. (b) Late additional pressure.
Conclusions
Based on the progressive failure mode of the surrounding rock of shallow buried bias tunnel, the creep constitutive model was introduced into the calculation model of surrounding rock pressure. Through a analysis of the stress state of the surrounding rock across three distinct stages, the analysis model of additional surrounding rock pressure of shallow buried bias tunnel was established, and the calculation formula of additional surrounding rock pressure was derived. The main conclusions are as follows:
The liner load is comprised of two main components: the surrounding rock pressure that is released during excavation and the additional pressure generated by the creep deformation of the liner-constrained surrounding rock. Importantly, the failure mode of the surrounding rock in shallow-buried biased tunnels undergoes a change before and after the application of the liner. Consequently, the additional pressure acting on the liner does not align uniformly with the pressure released during excavation in the same direction. Therefore, in the design of shallow buried bias tunnel, the influence of additional pressure should be considered.
The creep constitutive model was introduced into the analysis of tunnel additional pressure. The theoretical analysis model of tunnel additional pressure was established, and the calculation formula
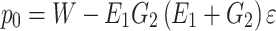of additional pressure was obtained. The difference of additional pressure between theoretical calculation and numerical simulation is 9.5%, which verified the rationality of the additional pressure analysis model and calculation formula.The greater the deformation rate of the surrounding rock is, the shorter the time when the additional pressure reaches the maximum value. When the deformation rate of surrounding rock increases to a certain value, there will be no additional pressure in the lining, that is, the surrounding rock is released after the excavation is completed; In this case, if the initial support strength is insufficient, the initial branch cracking or even collapse may occur in the excavation stage.
Acknowledgements
The present work is subsidised and supported by the National Natural Science Foundation of China (No. 52308375), the Shaanxi Province Postdoctoral Science Foundation (No. 2023BSHEDZZ273), the Science and Technology Innovation Team of Shaanxi Innovation Capability Support Plan (No. 2020TD005). The authors gratefully acknowledge the financial supports.
Symbols list
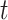
Time
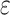
The total deformation
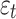
The deformation at time
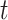
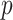
The late additional pressure
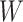
The load released by the surrounding rock just after the tunnel excavation
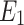
The shear modulus of the spring 1
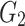
The shear modulus of the spring 2
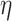
The coefficient of viscosity
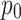
The final late additional pressure of the lining
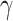
The heavy weight of the rock and soil mass
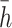
The thickness of the corresponding slide
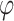
The friction angle
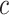
The cohesive force
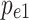
The pressure on the main sliding body along the main sliding direction
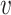
The deformation rate of surrounding rock
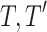
Loose earth pressure caused by tunnel excavation
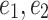
Lateral earth pressure on both sides
Author contributions
All authors contributed to the study conception and design. Dr.Tian Xiaoxu wrote the article. Prof. Zhanping Song provided the monitoring data; Dr.Wang Tong and Cheng Yun revised the language of the paper; Mr. Jiangsheng Xie and Mr. Zhi Liu provided the monitoring data.
Data availability
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
Declarations
Compliance with ethical standards
The authors confirm that they have no conflicts of interest for this work.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Fan, S. Y., Song, Z. P., Xu, T., Wang, K. M. & Zhang, Y. W. Tunnel deformation and stress response under the bilateral foundation pit construction - a case study. Arch. Civ. Mech. Eng.21 (3), 109 (2021). 10.1007/s43452-021-00259-7 [Google Scholar]
- 2.Cheng, Q. et al. Twin tunneling–induced deep-seated landslide in layered sedimentary rocks. B Eng. Geolo Environ.80 (12), 9071–9088 (2021). 10.1007/s10064-021-02482-1 [Google Scholar]
- 3.Wang, H. Z., Song, Z. P., Tian, X. X., Wen, B. & Zhang, Y. W. Investigation of the stress and strain distribution in the surrounding soil of a tunnel induced by the double-heading at bottom method. Int. J. Civ. Eng.22 (7), 1271–1289 (2024). 10.1007/s40999-024-00958-1 [Google Scholar]
- 4.Chen, H. et al. Failure mechanism and treatment measures of supporting structures at the portal for a shallow buried and asymmetrically loaded tunnel with small clear-distance. Nat. Hazards. 114, 2283–2310 (2022). 10.1007/s11069-022-05471-z [Google Scholar]
- 5.Tian, X. X., Song, Z. P. & Zhang, Y. W. Monitoring and reinforcement of landslide induced by tunnel excavation: a case study from Xiamaixi tunnel. Tunn. Undergr. Sp Tech.110, 1–14 (2021). 10.1016/j.tust.2020.103796 [Google Scholar]
- 6.Song, Z. P., Cheng, Y., Zhang, Z. K. & Yang, T. T. Tunnelling performance prediction of cantilever boring machine in sedimentary hard-rock tunnel using deep belief network. J. MT. Sci.20, 2029–2040 (2023). 10.1007/s11629-023-7931-y [Google Scholar]
- 7.Wu, K., Song, J. A., Zhao, N. N. & Shao, Z. S. Study on the time-dependent interaction between surrounding rock and yielding supports in deep soft rock tunnels. Int. J. Numer. Anal. Met.47, 1–20 (2023). 10.1002/nag.3650 [Google Scholar]
- 8.Qin, Y. W. et al. Failures in loess slope-tunnel system: an overview of trigging sources, acting mechanism and mitigation strategies. Eng. Fail. Anal.158, 107996 (2024). 10.1016/j.engfailanal.2024.107996 [Google Scholar]
- 9.Liu, Z. Z., Cao, P., Lin, H., Meng, J. J. & Wang, Y. X. Three-dimensional upper bound limit analysis of underground cavities using nonlinear Baker failure criterion. T Nonfer Metal Soc.30 (7), 1916–1927 (2020). 10.1016/S1003-6326(20)65350-X [Google Scholar]
- 10.Wang, T. T. Characterizing crack patterns on tunnel linings associated with shear deformation induced by instability of neighboring slopes. Eng. Geol.115 (2), 80–95 (2010). 10.1016/j.enggeo.2010.06.010 [Google Scholar]
- 11.Poisel, R., Mair am Tinkhof, K. & Preh, A. Landslide caused damages in a gallery. Rock. Mech. Rock. Eng.49 (6), 1–15 (2015). 10.1007/s00603-015-0765-3 [Google Scholar]
- 12.Chiu, Y. C., Lee, C. H. & Wang, T. T. Lining crack evolution of an operational tunnel influenced by slope instability. Tunn. Undergr. Sp Tech.65 (5), 167–178 (2017). 10.1016/j.tust.2017.03.004 [Google Scholar]
- 13.Ruggeri, P. et al. Deep-seated landslide triggered by tunnel excavation. ISL 2016-12th Int. Symp. Landslides. 12-19, (2016). 10.1201/b21520-219
- 14.Wei, H. et al. Coordinated evolution and mechanism characteristics of the tunnel-landslide system under rainfall conditions. Eng. Fail. Anal.146, 107118 (2023). 10.1016/j.engfailanal.2023.107118 [Google Scholar]
- 15.Lei, M. F., Peng, L. M. & Shi, C. H. Model test to investigate the failure mechanisms and lining stress characteristics of shallow buried tunnels under unsymmetrical loading. Tunn. Undergr. Sp Tech.46 (2), 64–75 (2015). 10.1016/j.tust.2014.11.003 [Google Scholar]
- 16.Schneider-Muntau, B. & Cordes, T. Comparison of measured and calculated interactions between slope creeping and tunnel structures. ce/papers. 2 (2), 505–510 (2018). 10.1002/cepa.722 [Google Scholar]
- 17.Causse, L., Cojean, R. & Fleurisson, J. A. Interaction between tunnel and unstable slope - influence of time-dependent behavior of a tunnel excavation in a deep-seated gravitational slope deformation. Tunn. Undergr. Sp Tech.50, 270–281 (2015). 10.1016/j.tust.2015.07.018 [Google Scholar]
- 18.Tian, X., Song, Z., Shen, X. & Xue, Q. S. Study on progressive failure mode of surrounding rock of shallow buried bias tunnel considering strain-softening characteristics. Sci. Rep-UK. 14, 9608 (2024). 10.1038/s41598-024-60324-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chu, Z. F., Wu, Z. J., Liu, B. G. & Liu, Q. S. Coupled analytical solutions for deep-buried circular lined tunnels considering tunnel face advancement and soft rock rheology effects. Tunn. Undergr. Sp Tech.94, 103111 (2019). 10.1016/j.tust.2019.103111 [Google Scholar]
- 20.XieJ, J. Stratigraphic pressure of shallow tunnel. China Civil Eng. J.10(6), 58–70 (1964). 10.15951/j.tmgcxb.1964.06.007. in Chinese. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.