Abstract
Talbot length, the distance between two consecutive self-image planes along the propagation axis for a periodic diffraction object (grating) illuminated by a plane wave, depends on the period of the object and the wavelength of illumination. This property makes the Talbot effect a straightforward technique for measuring the period of a periodic object (grating) by accurately determining the Talbot length for a given illumination wavelength. However, since the Talbot length scale is proportional to the square of the grating period, traditional Talbot techniques face challenges when dealing with smaller grating periods and minor changes in the grating period. Recently, we demonstrated a Fourier transform technique-based Talbot imaging method that allows for controlled Talbot lengths of a periodic object with a constant period and illumination wavelength. Using this method, we successfully measured periods as small as a few micrometers and detected sub-micrometer changes in the periodic object. Furthermore, by measuring the Talbot length of gratings with varying periods imaged through the combination of a thick lens of short focal length and a thin lens of long focal length and large aperture, we determined the effective focal length of the thick lens in close agreement with the theoretical effective focal length of a thick lens in the presence of spherical aberration. These findings establish the Talbot effect as an effective and simple technique for various sensing applications in optics and photonics through the measurement of any physical parameter influencing the Talbot length of a periodic object.
Subject terms: Optics and photonics, Physics
Introduction
In 1836, H. F. Talbot discovered a remarkable self-imaging phenomenon while studying periodic structures. A spatially coherent wave illuminating a periodic object produces an image of the object, without any imaging system, at regular intervals along the propagation direction. The image planes are known as Talbot planes1, and the distance between two consecutive Talbot planes is called Talbot length. The Talbot length, as derived by Lord Rayleigh2, is represented as
 |
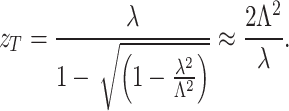1 |
Here,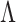 
is the grating period and 
is the wavelength of the incident radiation. At half of the Talbot length, the image has a lateral shift3 by an amount of 
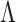/2.
However, the birth of the laser in 1960 has revitalized interest in the Talbot self-imaging effect. The elegance and simplicity of the Talbot effect have inspired a surge of studies in coherent optical signal processing, leading to a wide range of innovative applications that not only enrich our fundamental understanding of diffraction and its related optical phenomena but also extend to various other fields of science4. In recent times, the Talbot effect has been utilized to build measurement devices for various physical parameters, including spectrometry to measure the spectrum of an optical source in a compact footprint through the Fourier transform of Talbot lengths5–7, wavefront sensing8 and aberration measurement9, precise displacement, angle and tilt measurements10–12. Wavefront aberrations have been detected using the Talbot effect through various methods13,14. Additionally, aberration-like features have been observed in the post-paraxial Talbot effect15. Similarly, the X-ray Talbot interferometry has been employed to measure very small grating spacings and shapes for small-angle scattering16. In the strong imaging regime, where frequencies exceed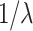 
, superoscillation enables subwavelength imaging with grating waves17, offering significant advantages over traditional imaging techniques. Over the past decade, numerous efforts have been made to develop super-oscillatory lenses and harness their capabilities for super-resolution or subwavelength imaging18,19. Since the Talbot length, as described by Eq. 1, is a function of the grating period, it can, in principle, be used as a measuring quantity to determine the unknown period of an object. In fact, efforts have been made to achieve high-precision grating period measurement using two-grating Talbot interferometers, successfully reaching a lower bound of 30 μm for the measured grating period20. However, when detecting an object period comparable to the wavelength, the non-paraxial Talbot effect requires the use of a more complex confocal microscope setup21, thereby diminishing the inherent simplicity of the Talbot effect. It is also important to note that the approximation used in calculating the Talbot length, as given by Eq. 1, does not hold in the non-paraxial Talbot effect, where the grating period is comparable to the incident wavelength3,22. Therefore, it is imperative to develop new experimental schemes that can detect subwavelength variations in periodicity through the direct measurement of Talbot lengths, all while preserving the simplicity of the experimental setup.
Here, we report on an experimental scheme, supported by a robust theoretical framework, to produce tunable Talbot lengths even for objects with small grating periods using standard optical components available in any optics laboratory and establish a Talbot-based sensor capable of measuring both small absolute grating periods and changes in periodicity within the subwavelength range. Additionally, we utilize the non-paraxial Talbot effect, observed for a grating period comparable to the wavelength of the illuminating light, to detect spherical aberration in a thick lens. This approach has enabled us to measure changes in the focal length of the thick lens of small focal length under non-paraxial illumination, both theoretically and experimentally.
Experimental architecture and theory
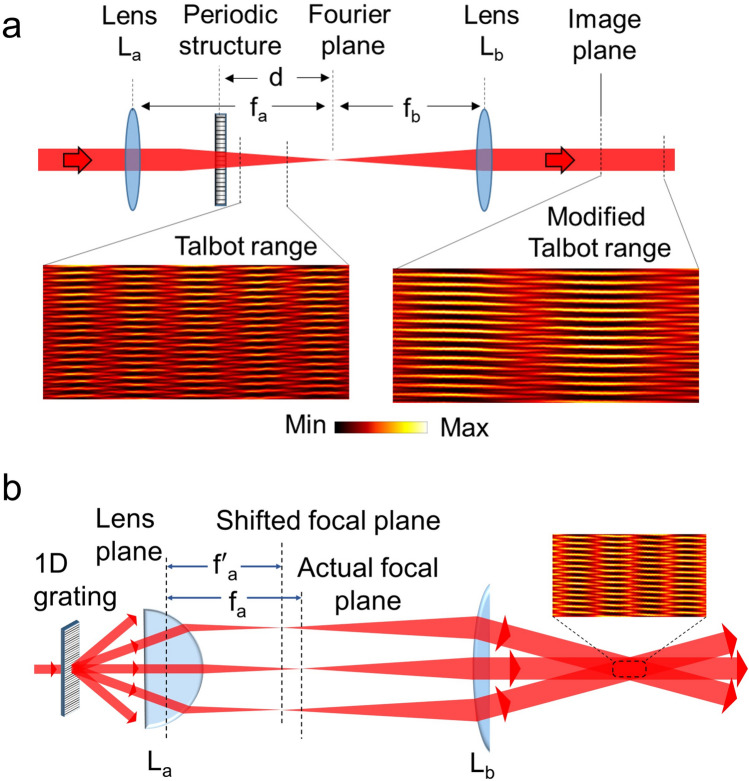
The concepts of the tunable Talbot length for sensing small variations in periodicity and the measurement of the effective focal length change or the spherical aberration of a thick lens are pictorially shown in Fig. 1a and Fig. 1b, respectively. In both cases, we have used a combination of lens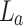 
of focal lengths, 
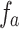, for Fourier transformation and 
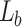of focal lengths, 
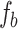, for inverse Fourier transformation to image23 the object (periodic structure of Fig. 1a and 1D grating of Fig. 1b) for the measurement of the Talbot images along propagation, avoiding the mechanical constraints of the experiment. The use of two lenses could appear to undermine the main advantage of lenseless imaging of the Talbot effect. However, recording of the Talbot images right after the image plane of the lens combination suggests an intentional adjustment to manage experimental constraints such as the size of setup, enhance resolution, or even allow for tunable Talbot distances, which would be difficult to achieve in a purely lenseless configuration. Since we are using lenses of long focal length and the object has a relatively large period, we remain within the paraxial Talbot effect regime. Experimentally, we have verified that lens aberrations do not affect our study, confirming the Talbot effect without distortions. Keeping the position of the lenses fixed, we have changed the object position depending on the need. To explore the tunable Talbot length as reported previously24, the periodic object (see Fig. 1a) is placed after the lens 
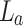, at a distance d from its back focal plane (Fourier plane), whereas for the measurement of the effective focal length of the thick lens, the object (see Fig. 1b) is placed at the front focal plane of the lens, 
.
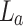Fig. 1.
Schematic representation of the experimental setup for a. verification of tunable Talbot length and measurement of small change in the grating period of the object using paraxial Talbot effect, and b. measurement of the effective focal length of thick less using the non-paraxial Talbot effect.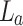 
and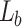 
are lenses of focal lengths, 
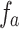and 
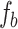, respectively. d is the position of the object away from the back focal plane of the lens, 
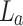. The objects are gratings. The collection of diffraction orders, − 1, 0, and +1, is due to the limited aperture of the lens, 
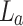at large diffraction angle of the small grating periods. Such collection limits the image resolution. Inset: light carpet measured in the experiments.
According to Fourier transform theory23, adjusting the position (distance, d) of the periodic object from the back focal plane of the lens,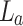 
, we can control the distribution of the spatial frequency of the object25 at the Fourier plane of lens 
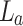due to the variation in the illuminated region of the object. In fact, it has been observed26 that any periodic object results in an array of spots at the Fourier plane, and the spatial distribution of the array depends on the position of the periodic object away from the back focal plane of the lens. Each spot of the array has an intensity profile26 the same as the input beam (here, Gaussian). Using the mathematical treatment of Fourier transform theory23, we can derive the modified pitch of the Gaussian beam array at the Fourier plane of the lens 
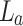due to the periodic object of pitch 
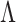placed at a distance d from the back focal plane as26,
 |
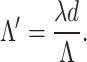2 |
Here,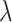 
is the wavelength of the beam illuminating the object. Similarly, the inverse Fourier transform of the Gaussian beam array using the lens 
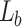results in the image of the periodic object at the image plane with effective pitch or period as
 |
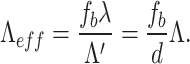3 |
As a result, the Talbot length,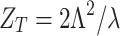 
, of the object of the period, 
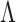, measured right after the object (see the inset Talbot range of Fig. 1a) will be modified for the measured Talbot length after the image plane (see the inset Modified Talbot range of Fig. 1a). Using Eqs. 2 and 3 we can find the modified Talbot length as,
 |
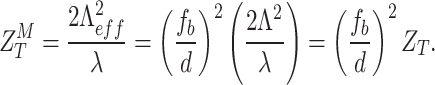4 |
Using Eq. 4, we can derive the change in modified Talbot length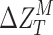 
due to the change of grating period (
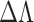) as
 |
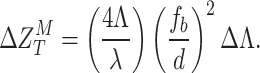5 |
It is evident from Eqs. 4 and 5, that the modified Talbot length,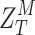 
and its change, 
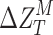, with the change in the periodicity, (
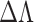), are modulated with a factor 
, square of the ratio of the focal length of the inverse Fourier transforming lens,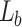 
, and the position of the periodic object away from the back focal plane of the Fourier transforming lens, 
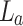. Therefore, for a fixed periodicity of the object (
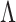), focal length of the lens (
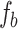), and illuminating wavelength (
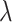), one can access variable Talbot length and determine the small variation of the grating period by simply adjusting the position of the object (i.e., the value of d). Again, from Eq. 5, it is evident that, for a fixed value of 
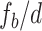, wavelength, 
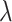, and change in Talbot length, 
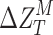, the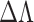 
is inversely proportional the period, 
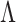, of the object. Therefore, one can achieve higher resolution (measure smaller value of 
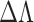) for longer grating periods, 
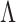. On the other hand, one has to select the value of d, such that the spot size of the beam illuminating the periodic object should be much larger than the period of the object to ensure the Talbot effect. Given these limitations, we had to limit the period of the grating to a certain value.
However, using the objects of smaller grating periods, we have studied the change of effective focal length of the thick lens due to the spherical aberration under non-paraxial illumination. Under paraxial approximation, a lens yields a multiplicative phase transformation factor given by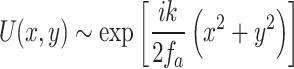 
, where x and y are the transverse position coordinate of the beam with wave-vector k on the lens plane and f is the focal length of the lens. This approximation holds under the condition of 
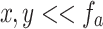. However, as evident from Fig. 1b, the thick lens of small focal length used to collect higher-order diffracted beams of the object of smaller period (less than 10 μm or so) needs modification to the phase transformation factor accounting non-paraxial condition. Without any approximation, the phase transfer function of the thick plano-convex lens with a radius of curvature R can be written as
 |
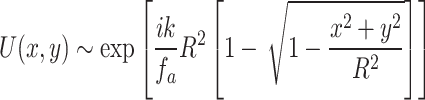6 |
It is known that the effective focal length,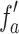 
, under the non-paraxial conditions, is smaller than the focal length 
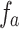at paraxial conditions. Thus, the multiplicative phase factor of the thick lens under non-paraxial conditions can be written as
 |
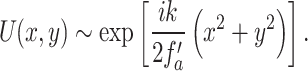7 |
Comparing Eqs. 6 and 7, we can write the modified focal length of the thick lens from the transition from paraxial to non-paraxial and associated spherical aberration as
 |
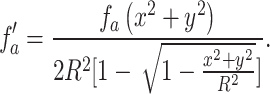8 |
In the presence of 1D periodic objects, all the above equations can be transformed to 1D dimension by making one coordinate zero (here, we consider y = 0). Again, using the diffraction equation of the grating of the period,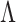 
, and illuminating wavelength, 
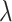, we can find the value of x as
 |
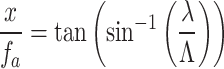9 |
Using the value of x in Eq. 8 and y = 0, we can numerically calculate the effective focal length of the thick lens as a function of period,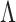 
, of the 1D grating. On the other hand, the Talbot length of the 1D grating for the schematic of Fig. 1b can be repeated as
 |
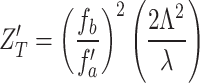10 |
due to the magnification of the 1D grating at the image plane by a factor,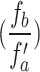 
, the ratio of focal length of lens, 
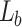, and effective focal length, 
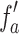, of lens, 
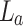, under non-paraxial condition. Using Eq. 10, we can represent the effective focal length of lens, 
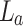, as
 |
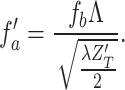11 |
It is evident from Eq. 11 that using a test target (1D grating) of known periods and measuring the corresponding Talbot length, we can find the change in the focal length of a thick lens under non-paraxial conditions or the spherical aberration.
Results and discussions
Verification of variable Talbot length
We first characterized the experimental setup shown in Fig. 1a to control the Talbot length by varying the object position, d, as described by Eq. 4, particularly for gratings with a lower period than previously reported24. While d can be adjusted continuously, we selected three discrete values to verify the tunable Talbot length for a fixed grating period and laser wavelength.
Using a He–Ne laser at 632.8 nm and lenses,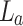 
and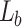 
of focal length 
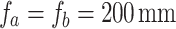, we placed a 1D periodic object, one-dimensional Ronchi grating (R1S1L1N Negative test target, Thorlabs) of period 25 μm at different positions satisfying the 4f imaging condition, d = 100 mm, 70 mm, and 40 mm. We recorded the intensity profiles using a CCD camera along the propagation direction with a distance step of 0.01, 0.05, 0.05, and 0.1 mm for 4f-imaging condition, d = 100 mm, 70 mm, and 40 mm, respectively. The light carpet was then constructed by concatenating the intensity line profiles from the CCD images along a 50 mm propagation distance from a fixed pixel line with a pixel width of 6.45 μm, consistent with Ref.24.
The results are presented in Fig. 2. The theoretical Talbot length for a period of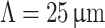 
, and the laser wavelength of 
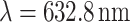is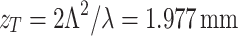 
. According to Eq. 4, the modified Talbot length for unit magnification remains 
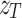. As shown in Fig. 2a, the experimentally measured light carpet for the 
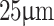grating period spans over a propagation distance of approximately 20 mm and clearly identifies multiple Talbot planes. The measured Talbot length was 
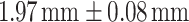, closely matching the theoretical value. For 
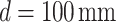(Fig. 2b), the light carpet extends over a longer propagation distance of 40 mm, with multiple Talbot planes and a magnified Talbot length of 
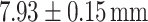. Similarly, as seen in Fig. 2c and d for 
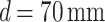and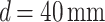 
, the light carpet extends over the entire 50 mm propagation distance, with three and one Talbot planes observed, corresponding to Talbot lengths of 
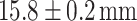and 
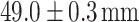, respectively. The Talbot length magnification factors were 
, 
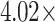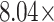, and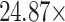 
, resulting from 
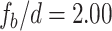, 2.83, and 4.99 for 
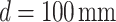, 70 mm, and 40 mm, respectively. This enhancement in Talbot length could significantly improve the measurement resolution of Talbot-based sensors, enabling the detection of small changes in the period or other physical parameters that influence the period of a periodic object.
Fig. 2.
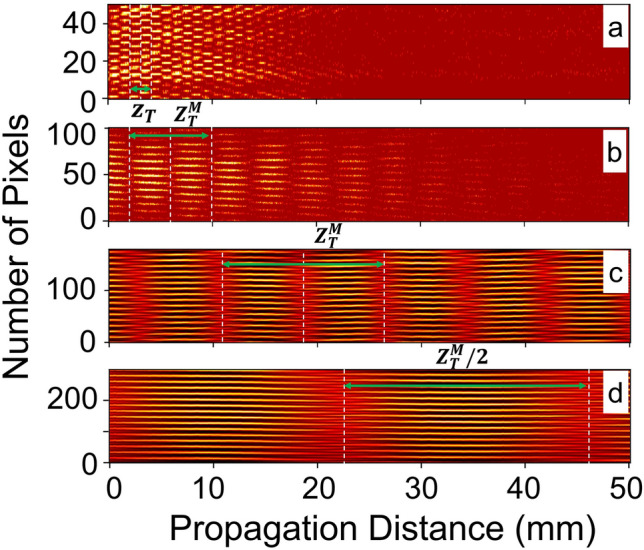
Observation of light carpet and subsequent Talbot length change for different positions of the periodic object, (a) 4f imaging, (b)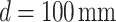 
, (c)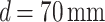 
, and (d) 
.
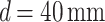According to Eq. 4, we can, in principle, further reduce the d value below 40 mm and produce longer Talbot lengths. However, in a separate experiment and numerical simulation, we observed the Talbot effect for an illumination spot size as small as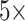 
the grating period. In such cases, only one Talbot length was observed, followed by strong beam divergence. Therefore, we limited our study to an illumination spot size of more than 
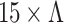, achieved with 
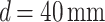. An alternative approach to further increase the Talbot length could involve selecting appropriate focal lengths for lenses 
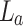and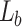 
to achieve a higher 
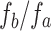ratio. However, this would result in a fixed Talbot length magnification for a given set of lenses, potentially undermining the goal of achieving a controlled Talbot length, which is the central focus of this study.
Measurement of small variation in periodicity
By establishing reliable control over the Talbot length of a periodic object with a fixed grating period (as small as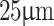 
) and a constant illumination wavelength, we demonstrate the capability of a Talbot-based sensor to measure small changes in the grating period. In the absence of a suitable periodic object, we used a 1D multi-grating periodically-poled lithium niobate (PPLN) crystal27 (HC Photonics) with the grating period varying from 
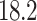to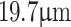 
(as specified by the vendor) with an increment of 300 nm. Placing the crystal at different positions satisfying the 4f imaging condition, 
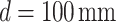, 70 mm, and 40 mm, we varied the grating period by moving the crystal in the transverse plane and measured the Talbot length from the intensity profiles recorded using the CCD camera along the propagation.
Experimentally, for the grating position of 4f condition,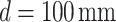 
, 70 mm, and 40 mm, we measured respective Talbot length variation of 1.07–1.25, 4.20–4.99, 8.71–10.04, and 26.15–30.87 mm for the grating period variation from 18.2 to 19.7 
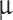m. As evident, we observe a large Talbot length variation (4.72 mm) for a grating period variation of 
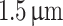while placing the object at 
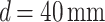, indicating the possibility of high measurement resolution for a Talbot-based sensor. Using Eq. 4 and the measured Talbot length, 
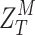, we have calculated the effective grating period (
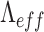) for the change of period, 
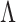, with the results shown in Fig. 3.
Fig. 3.
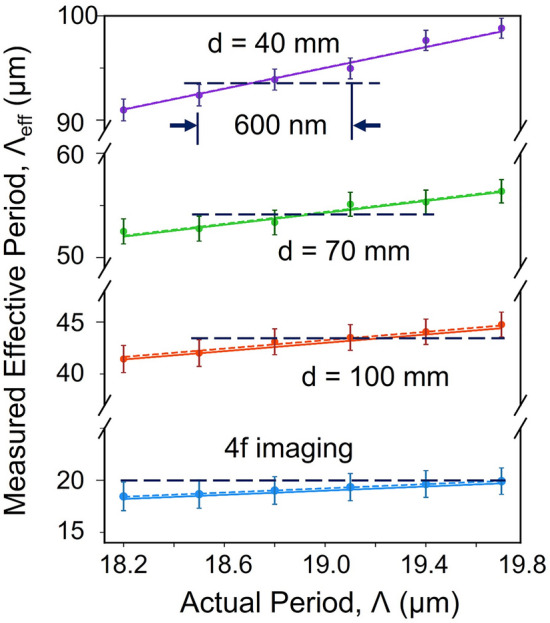
Variation of effective periodicity,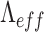 
, as a function of the actual periodicity, 
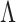, of the multi-grating crystal, for different position of the object satisfying 4f imaging condition, 
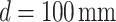, 70 mm and 40 mm. The solid lines are the theoretical results derived using the experimental parameters in Eq. 3. The black dash line and black arrows are used to identify the measurement resolution. The error bar is calculated using the measurement error of 
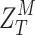in Eq. 5.
As shown in Fig. 3, the experimentally measured effective Talbot length,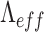 
, varies linearly with the actual grating period, 
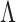, over ranges of 18.44–19.91, 36.44–39.75, 52.50–56.36, and 90.97–
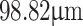. Using Eq. 4, the fit (solid line) to the measurement data (dots) demonstrates a close agreement between theory and experiment, with slopes of 1, 2, 2.85, and 5, precisely matching the values of (
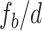) for changes in the grating period from 18.2 to 
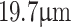, and the object positions satisfying the 4f imaging condition, 
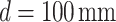, 70 mm, and 40 mm. It is also interesting to note that the measured effective grating period lies within the measurement error bar for all d values except 
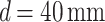. In fact, for 
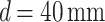, as evident from the purple line and dots in Fig. 3, one can clearly distinguish two grating periods (see the black dash and black arrows) with a difference of 600 nm.
However, to get a better perspective on the resolution of the Talbot-based sensor, we have summarized the measurement data in Table 1. As evident from the table, the measured grating period for the object position satisfying 4f-imaging condition has an error of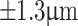 
. We have used the error propagation method in Eq. 5 to estimate the overall error in the grating period due to the measurement errors in all physical parameters such as, distance, d, the focal length, f, and the modified Talbot length. Since we have a single-frequency He–Ne laser at 632.8 nm with a linewidth of a few MHz, we did not include wavelength measurement error in the error calculation. On the other hand, the modified Talbot length was measured using a motorized stage with a resolution of 
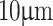, and the focal length of the lenses and the distance, d, were measured using a millimeter scale of resolution of 0.5 mm. Such a large error (±1.3 μm) can be attributed to the measurement inaccuracy resulting from the lower resolution (
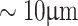) of the translation stage used to measure the relatively small Talbot length of the grating under the 4f-imaging condition. On the other hand, with the increase in Talbot length due to the use of shorter d values—100 mm, 70 mm, and 40 mm—we observe an improvement in measurement accuracy from 
, 
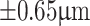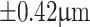to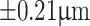 
, respectively.
Table 1.
Measured grating periods for different positions of the object.
Acutal grating period, 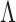 ( 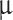m) |
Measured grating period from experiment,  ( ) |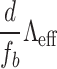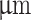
|||
|---|---|---|---|---|
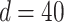 mm |
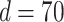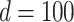 mm |
 mm |
4f imaging | |
| 18.2 | 18.2 ± 0.21 | 18.3 ± 0.42 | 18.1 ± 0.65 | 18.5 ± 1.37 |
| 18.5 | 18.5 ± 0.20 | 18.4 ± 0.42 | 18.4 ± 0.64 | 18.7 ± 1.35 |
| 18.8 | 18.8 ± 0.20 | 18.6 ± 0.41 | 18.9 ± 0.62 | 19.0 ± 1.33 |
| 19.1 | 19.0 ± 0.20 | 19.3 ± 0.40 | 19.1 ± 0.61 | 19.3 ± 1.31 |
| 19.4 | 19.5 ± 0.19 | 19.3 ± 0.40 | 19.4 ± 0.60 | 19.6 ± 1.29 |
| 19.7 | 19.8 ± 0.19 | 19.7 ± 0.39 | 19.7 ± 0.59 | 19.9 ± 1.27 |
In fact, for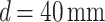 
, the Talbot-based sensor can measure a change in the grating period as small as 
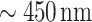for a grating period of 
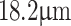. It is also evident from Table 1 that for a constant value, d, the measurement error or the resolution, as also evident from Eq. 5, improves with the increase in the grating period. For example, as evident from the second column of Table 1, the measurement error improves from 
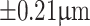to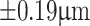 
for the increase of grating period from 
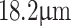to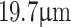 
. These results establish the reliability of the Talbot-based sensor in measuring changes in the grating period, or any physical parameter influencing the grating period of an object, by 450 nm, without requiring complex microscopic measurement systems. While large magnification factors in microscopic systems involving intricate lens designs and aberration control have traditionally been necessary for such precision, the current results demonstrate the potential for achieving similar measurements for a periodic object systematically placed between two long focal-length lenses.
Sensing of spherical aberration of a thick lens
We further use the Talbot effect to measure the effective focal length of a thick lens due to non-paraxial illumination or spherical aberration. To control the non-paraxial illumination to the lens,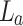 
, we used Ronchi gratings (R1S1L1N negative test target, Thorlabs) as the periodic object with known periods of 
, 
, 
, 
, 
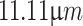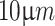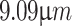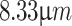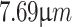and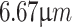 
. Due to the unavailability of suitable test grating with a shorter period, we have used a periodically-poled KTP (PPKTP) crystal of a known grating period of 
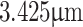. The experimental scheme is shown in Fig. 1b, where the periodic object is imaged using lenses, 
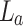and 
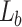in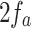 
-
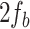combination. The thick lens, 
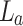, has a focal length, 
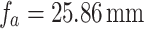(for 1064 nm wavelength, from Thorlabs data sheet) and an aperture size of 25.4 mm. We used lenses, 
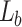, of two different focal lengths, 304.95 mm (at 1064 nm, Thorlabs) for grating periods 
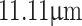to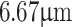 
and 507.86 mm (at 1064 nm, Thorlabs) for 
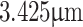grating, for appropriate magnification. Using the laser wavelength of 1064 nm, we recorded the light carpet of the object of different grating periods from the image plane of the lens, 
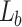, and calculated the Talbot lengths. Using the experimentally measured Talbot length for different grating periods, we have calculated the change in the effective focal length of the lens, 
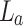, using Eq. 11. The results are shown in Fig. 4. As evident from the plot, the effective focal length of the thick lens, 
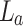, is lower than the vendor-specified focal length of 
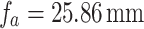(red dotted line) under paraxial illumination. In fact, with the decrease of the grating period from 
to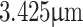 
, resulting in the increase of diffraction angle and non-paraxial illumination to the thick lens, the effective focal length, 
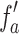, decreases from 25.58 to 23.01 mm. Using the experimental parameters in Eqs. 8 and 9, we numerically calculate the value of effective focal length, 
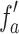as a function of the grating period, 
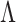, with the result shown by the solid line of Fig. 4 in close agreement with the experimental data (dots). From this study, it is evident that the Talbot effect can be effectively used to accurately measure changes in the focal length of a thick lens caused by spherical aberration under non-paraxial illumination. Additionally, the present study establishes the need for accurate focal lengths of the imaging systems used for the study of the non-paraxial Talbot effect.
Fig. 4.
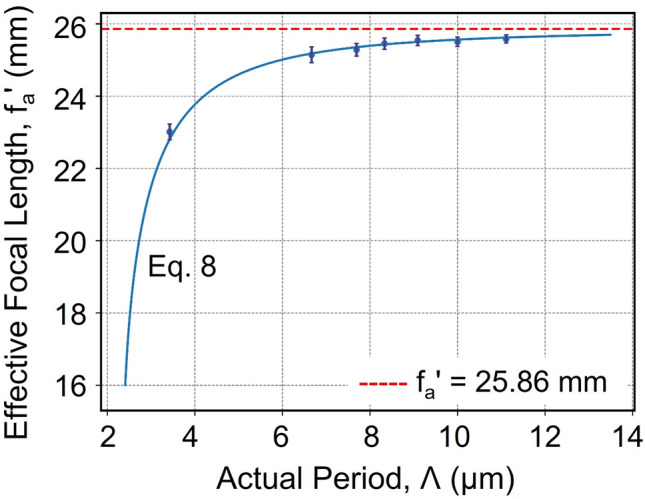
Variation of the effective focal length of the thick lens under non-paraxial illumination. The dotted line represents the actual focal length of the lens specified by the vendor. The solid line represents the numerically calculated effective focal length using experimental parameters in Eqs. 8 and 9.
Conclusion
In conclusion, we have developed a versatile experimental scheme for Talbot effect-based sensors using a suitable theoretical framework, enabling continuous control of Talbot lengths for periodic structures with micrometer-scale periods. By employing a grating with a period of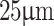 
, we achieved tunable Talbot lengths ranging from 1.97 to 49 mm, an enhancement of up to 25 times compared to the original range. This tunable Talbot length allowed the sensor to detect periodicity variations of 450 nm for a grating period as small as 
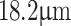with a 632.8 nm wavelength laser, demonstrating the capability to operate in the subwavelength regime without relying on microscopic systems. Furthermore, we derived and experimentally validated a mathematical expression for the effective focal length of a thick lens, accounting for spherical aberration in non-paraxial Talbot imaging. This advancement opens new possibilities for employing Talbot-based sensors to measure various physical parameters that influence the period of periodic objects in real-life applications.
Acknowledgements
S. J. S and G. K. S. acknowledge the support of the Department of Space, Govt. of India. M. E-Z acknowledges financial support from the Spanish Government through projects Nutech (PID2020-112700RB-I00); Ultrawave (EUR2022-134051), Alter (PID2023-150006NB-I00), Severo Ochoa Center of Excellence (CEX2019-000910-S); Generalitat de Catalunya (CERCA).
Author contributions
S. J. S. developed the experimental setup and performed measurements, data analysis, and numerical simulation. M. E. Z. participated in the analysis and data interpretation. G. K. S. developed the ideas and led the project. All authors participated in the discussion and contributed to the manuscript writing.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Declarations
Conflict of Interest
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Talbot, H. F. LXXVI. Facts relating to optical science No. IV. Lond. Edinb. Dublin Philos. Mag. J. Sci.9, 401–407 (1836). [Google Scholar]
- 2.Rayleigh, L. XXV. on copying diffraction-gratings, and on some phenomena connected therewith. Lond. Edinb. Dublin Philos. Mag. J. Sci.11, 196–205 (1881). [Google Scholar]
- 3.Berry, M. V. & Klein, S. Integer, fractional and fractal Talbot effects. J. Mod. Opt.43, 2139–2164 (1996). [Google Scholar]
- 4.Wen, J., Zhang, Y. & Xiao, M. The Talbot effect: Recent advances in classical optics, nonlinear optics, and quantum optics. Adv. Opt. Photonics5, 83–130 (2013). [Google Scholar]
- 5.Kung, H. L., Bhatnagar, A. & Miller, D. A. Transform spectrometer based on measuring the periodicity of Talbot self-images. Opt. Lett.26, 1645–1647 (2001). [DOI] [PubMed] [Google Scholar]
- 6.Ye, E., Atabaki, A. H., Han, N. & Ram, R. J. Miniature, sub-nanometer resolution Talbot spectrometer. Opt. Lett.41, 2434–2437 (2016). [DOI] [PubMed] [Google Scholar]
- 7.Taghi Tavassoly, M. & Abolhassani, M. Specification of spectral line shape and multiplex dispersion by self-imaging and Moiré technique. Opt. Lasers Eng.41, 743–753 (2004). [Google Scholar]
- 8.Podanchuk, D. V. et al. Adaptive wavefront sensor based on the Talbot phenomenon. Appl. Opt.55, B150–B157 (2016). [DOI] [PubMed] [Google Scholar]
- 9.Wang, A., Gill, P. & Molnar, A. Light field image sensors based on the Talbot effect. Appl. Opt.48, 5897–5905 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Spagnolo, G. S. & Ambrosini, D. Talbot effect application: Measurement of distance with a Fourier-transform method. Meas. Sci. Technol.11, 77 (2000). [Google Scholar]
- 11.Cao, B. et al. Out-of-plane displacement sensor based on the Talbot effect in angular-modulated double-layer optical gratings. Appl. Opt.61, 9873–9878 (2022). [DOI] [PubMed] [Google Scholar]
- 12.Testorf, M., Jahns, J., Khilo, N. A. & Goncharenko, A. M. Talbot effect for oblique angle of light propagation. Opt. Commun.129, 167–172 (1996). [Google Scholar]
- 13.Sekine, R. et al. Measurement of wavefront aberration of human eye using Talbot image of two-dimensional grating. Opt. Rev.13, 207–211 (2006). [Google Scholar]
- 14.Podanchuk, D. V. et al. Adaptive wavefront sensor based on the Talbot phenomenon. Appl. Opt.55, B150–B157 (2016). [DOI] [PubMed] [Google Scholar]
- 15.Ring, J. D., Lindberg, J., Howls, C. J. & Dennis, M. R. Aberration-like cusped focusing in the post-paraxial Talbot effect. J. Opt.14, 075702 (2012). [Google Scholar]
- 16.Sunday, D. F., List, S., Chawla, J. S. & Kline, R. J. Determining the shape and periodicity of nanostructures using small-angle x-ray scattering. J. Appl. Crystallogr.48, 1355–1363 (2015). [Google Scholar]
- 17.Deng, Z., Shapira, N., Remez, R., Li, Y. & Arie, A. Talbot effect in waveforms containing subwavelength multilobe superoscillations. Opt. Lett.45, 2538–2541 (2020). [DOI] [PubMed] [Google Scholar]
- 18.Rogers, E. T. et al. A super-oscillatory lens optical microscope for subwavelength imaging. Nat. Mater.11, 432–435 (2012). [DOI] [PubMed] [Google Scholar]
- 19.Huang, F. M., Zheludev, N., Chen, Y. & Javier Garcia de Abajo, F. Focusing of light by a nanohole array. Appl. Phys. Lett.90, 091119 (2007). [Google Scholar]
- 20.Photia, T. et al. High-precision grating period measurement. Appl. Opt.58, 270–273 (2019). [DOI] [PubMed] [Google Scholar]
-
21.Arrieta, E., Bolognini, N. & Torres, C. Talbot effect with a grating of period 1
m. Optik183, 988–993 (2019). [Google Scholar] - 22.Hua, Y., Suh, J. Y., Zhou, W., Huntington, M. D. & Odom, T. W. Talbot effect beyond the paraxial limit at optical frequencies. Opt. Express20, 14284–14291 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Goodman, J. W. Introduction to Fourier optics (Roberts and Company Publishers, 2005). [Google Scholar]
- 24.Bachimanchi, H., Sarkar, S. J., Ebrahim-Zadeh, M. & Samanta, G. K. Harnessing nonlinear frequency upconversion of Talbot effect with flexible Talbot lengths. Opt. Express32, 15967–15977 (2024). [DOI] [PubMed] [Google Scholar]
- 25.Jabir, M. V., Apurv Chaitanya, N., Aadhi, A. & Samanta, G. K. Generation of “perfect’’ vortex of variable size and its effect in angular spectrum of the down-converted photons. Sci. Rep.6, 21877 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Harshith, B. S. & Samanta, G. K. Controlled generation of array beams of higher order orbital angular momentum and study of their frequency-doubling characteristics. Sci. Rep.9, 10916 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Aadhi, A. et al. Airy beam optical parametric oscillator. Sci. Rep.6, 25245 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.