Time-series InSAR measurement using ICOPS and estimation of along-track surface deformation using MAI during the 2021 eruption of Fagradalsfjall Volcano, Iceland

Abstract

The eruption in Fagradalsfjall Volcano, located in Reykjanes Peninsula, Iceland, from several centuries’ dormant states, occurred for the first time on March 19, 2021. Observations of Fagradalsfjall Volcano were conducted in 2021, and the eruption period lasted for six months until 18 September 2021. Six days pair of interferograms were generated from ninety synthetic aperture radar (SAR) data. Thus, the SAR data will be acquired from the Sentinel-1 satellite from January until December 2021. Time-series measurements were conducted using a combination of persistent scatterer (PS) and distributed scatterer (DS) points to produce denser measurement points (MPs) in the study area. The improved combined scatterers interferometry with optimized point scatterers (ICOPS) algorithm is the time-series method that utilizes both PS and DS MPs and optimizes those combined MPs using a deep learning algorithm over different temporal intervals and using a statistical clustering approach to optimize the MPs spatially. Validation was conducted by comparing the ICOPS result with GPS measurement in Reykjavik. The comparison with the GPS measurement was performed to validate the line-of-sight (LOS) deformation from the ICOPS measurement, which resulted in an RMSE value of about 0.58 cm, which is considered a good correlation. Besides the time-series Interferometry SAR (InSAR) measurement, we used the integrated InSAR and multiple aperture interferometry (MAI) methods to estimate both LOS and along-track surface deformation, respectively, during the Fagradalsfjall, Iceland volcanic eruption. A pair of ALOS-2 data was used between 28 February 2021 and 23 May 2021. The result from the MAI method shows a deformation of approximately ± 2 mm in the azimuth direction around Fagradalsfjall Volcano. The deformation around Fagradalsfjall Volcano was suggested to be due to the activity of the magma reservoir beneath the Earth’s surface, which was formed by dike intrusion. The analysis of the seismicity in Fagradalsfjall was discussed by visualization of the distribution of earthquakes during the deformation occurrence. Further analysis can be conducted by applying multitrack analysis to find the 3D deformation pattern due to the eruption.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-79128-1.

Introduction

Fagradalsfjall Volcano, located in Reykjanes Peninsula in Iceland, had been dormant for several centuries before it started to erupt on March 19, 2021. The volcanic activity was monitored using the Global Navigation Satellite System (GNSS). The GNSS result shows slight inflation and deflation around Fagradalsfjall Volcano, which was found due to the extensive migration of magma at significant depths beneath the entirety of the western Reykjanes Peninsula¹. The eruption was initiated by a dike intrusion, which lasted six months and triggered the lava flow before finally stopping on September 18, 2021², . The Fagradalsfjall volcano was originally formed during the Last Glacial Age. It was once a tuya that stretched for 40 km. Following the eruption in 2021, the effusive nature of the explosion has transformed its geological features, making it a shield volcano³. Based on the tectonic settings, the Fagradalsfjall Volcano is located between the divergent boundaries of North American and Eurasian tectonic plates. This boundary drives significant volcanic and seismic activity along fissure swarms and transform faults. The region’s tectonic setting includes both extensional and strike-slip processes, with NE-SW-aligned fissure swarms causing volcanic eruptions and frequent microearthquake swarms related to strike-slip faults. Based on the geological settings, the Fagradalsfjall Volcano, characterized by young picrite and olivine tholeiite lava, exhibits early volcanic features like tuyas and tindars⁴.

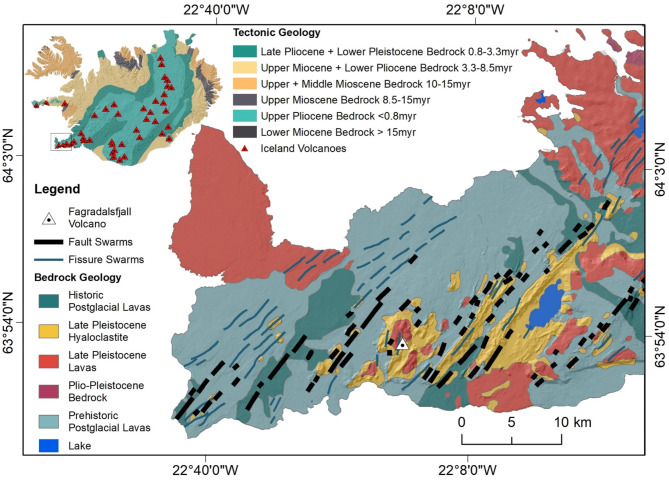
The geological map of Iceland in Fig. 1 shows the bedrock type in Reykjanes Peninsula with age distribution based on the tectonic zone around Iceland. The tectonic geology of the Iceland map indicates that the Reykjanes Peninsula consists of Upper Pliocene Bedrock with an age less than 0.8 million years old and includes rocks formed between the later part of the Pliocene epoch and right before the start of the Pleistocene epoch. Meanwhile, the bedrock geology type of the surrounding area of Fagradalsfjall Volcano consists of Hyaloclastite and Lavas that formed during the later stages of the Pleistocene epoch through volcanic eruptions in the glacial period^4,5. The geochemical analysis suggested that the magma originates from a near-Moho storage zone, which is located more than 15 km away⁶. Through a series of complex processes, magma flows from deeper layers of the mantle into shallower magma chambers, where it is then temporarily held. This phenomenon indicates the passage of magma through critical underground passages, demonstrating the complexity of geological processes involving changes in depth and magma reservoir⁷.

Fig. 1.

Geologic map of the study area in Reykjanes Peninsula, Iceland (this figure was modified from the geologic map of Iceland 1:500,000 by⁸). This map was processed using ArcMap version 10.4 (https://www.esri.com/).

Figure 1. Geologic map of the study area in Reykjanes Peninsula, Iceland (this figure was modified from the geologic map of Iceland 1:500,000 by⁸). This map was processed using ArcMap version 10.4 (https://www.esri.com/).

The six-month effusive eruption on Fagradalsfjall volcano resulted in a mean lava thickness of approximately 30 m with a total erupted volume of 0.15 km^37,9. Based on research from Pedersen et al., in 2022, The Fagradalsfjall eruption progressed through five distinct stages. Stage 1, from 19 March to 5 April, began with the opening of a 180 m fissure in the Geldingadalir valley, where lava concentrated around two main vents, ultimately covering 0.33 km² with a mean thickness of 22 m and a total volume of 7 million m³. In Stage 2, which lasted from 5 to 27 April, multiple new fissures appeared, causing the vent activity to shift and lava to spread into Meradalir and Syðri-Meradalur; during this stage, the lava covered 1.1 km² with a mean thickness of 16 m and a cumulative volume of 19.4 million m³. Stage 3, occurring from 27 April to 28 June, saw the eruption stabilize at a single vent, with a mean discharge rate rising from 9 to 13 m³/s, resulting in lava covering 3.82 km², with a mean thickness of 20.8 m and a total volume of 79.8 million m³. In Stage 4, from 28 June to 2 September, the eruption was characterized by episodic intense lava flows, achieving a mean discharge rate of 11.0 m³/s and increasing the total volume to 142.5 million m³, which led to significant thickening of the lava field. Finally, Stage 5, which lasted from 2 to 18 September, included a 9-day pause followed by renewed activity, with an average mean discharge rate of 5.6 m³/s and a peak of 12 m³/s; by the end of this stage, the lava volume reached 150.8 million m³, primarily deposited in Geldingadalir, including a substantial lava pond that drained into Nátthagi⁹.

Time-series interferometry synthetic aperture radar (InSAR) was known for its ability to monitor volcanic activity by exploiting the series of SAR images within the period of existing volcanic activity¹⁰. The volcanic activity in Fagradalsfjall Volcano caused deformation around the Reykjanes Peninsula overtime before the eruption⁷. Further analysis of the deformation around Fagradalsfjall Volcano could be conducted by generating a time-series InSAR method¹¹. There are three main reference methods for generating time-series InSAR: persistent scatterer interferometry (PSI), small baseline (SBAS), and combined PS and DS methods¹². The PSI method relies on persistent scatterer points that correspond to stable reflectors that are identified on the Earth’s surface, i.e., artificial objects. The SBAS method relies on distributed scatterers that are typically identified in areas with sparse stable reflectors¹³. On the other hand, the combined PS and DS process was motivated to improve MP density from the PS measurement and increase precise measurement from the DS measurements¹⁴. The combined PS and DS process was initiated by combining the measurements from PSI and SBAS, which utilized a single reference and small baseline interferogram network and used phase stability to select the pixel criteria. The result from the SBAS method was further inverted by singular value decomposition (SVD) in combination with the PS method¹⁵. The further development of the combined PS and DS process is introduced by SqueeSAR^™, which constructs a multi-reference network by selecting the pixel criteria using a statistical homogeneity test¹⁶. The main limitation of the previous methods used to combine PS and DS is that there is no further optimization of the measurement points resulting from combined scatter interferometry (CSI) results to produce more precise measurements¹⁷.

Thus, the improved combined scatterers interferometry with optimized point scatterers (ICOPS) was introduced to overcome this limitation¹⁴. The ICOPS process exploits a deep learning algorithm to optimize the measurement points (MPs) to increase the reliability of the time-series results and spatial optimization using the statistical cluster method^18,19. Despite the fact that the ICOPS algorithm has been developed in mountainous areas^20,21, the algorithm has never been tested to handle non-linear deformation caused by the pre-erupted inflation and post-erupted deflation from the volcanic eruption. Therefore, the purpose of this research is to investigate the ability of the ICOPS algorithm in Fagradalsfjall Volcano, Iceland. The volcanic eruption in 2021 in Fagradalsfjall is processed using Sentinel-1 data from January to December 2021. Further analysis was carried out by visualizing the deformation pattern that occurred around the Reykjanes Peninsula, which InSAR detected, and comparing it with the distribution of earthquakes that occurred within six days.

In addition, the integrated method was applied to calculate the along-track deformation, which was impossible to acquire from the conventional InSAR method. The conventional InSAR method has a limitation, which is that it can only obtain the LOS deformation and ignore the effect of deformation from multiple directions that can occur in earthquakes and volcanic eruptions. Therefore, the SAR processing method that is able to retrieve the along-track deformation is needed for further processing. The offset tracking method is one of the SAR techniques that can be used to retrieve the along-track deformation. However, some researchers prove that the offset tracking method to calculate along-track deformation was outperformed by the MAI method. Furthermore, the research on MAI continued to increase the coherence in the azimuth direction during MAI processing. The improved MAI method was then introduced from the residual interferograms that were produced from the hard filtering of InSAR processing. Thus, the improved MAI process utilized the integration of InSAR and MAI to create the final along-track deformation. The integrated InSAR and MAI methods could improve the coherence and filtering boundary during MAI processing²². Therefore, we also aimed to process the ALOS-2 data during the Fagradalsfjall eruption to retrieve both line-of-sight (LOS) and along-track (azimuth) deformation using integrated InSAR and multiple aperture interferometry (MAI) methods²³.

Previous studies analyzing surface deformation in Fagradalsfjall have only used a few pairs of interferograms to analyze volcanic activity in Fagradalsfjall⁷. Therefore, the analysis only shows spatial deformation changes. However, the use of more comprehensive SAR data can provide deeper insights into the volcanic activity process from a more detailed perspective in the form of time-series data. The InSAR time-series method can map deformation temporally, allowing the identification of deformation trends that may not be visible with only a few pairs of interferograms. In addition to the InSAR time series, this study also uses the Multi-Aperture Interferometry (MAI) technique to improve deformation analysis in three different aspects. First, deformation in the Line of Sight (LOS) direction provides vertical and horizontal information about ground motion. Second, deformation in the azimuth direction allows for the detection of lateral motion that conventional LOS approaches cannot detect. Third, deformation is measured over time, which provides an overview of the temporal dynamics of deformation and subsurface structural changes associated with volcanic activity. With this more comprehensive approach, the results of deformation analysis at Fagradalsfjall are expected to provide a more holistic understanding of the evolution of its volcanic activity.

Overall, the novelty of this study is that it investigates the ICOPS method to handle the non-linear deformation that is caused by volcanic eruptions. Because of that, the eruption of Fagradalsfjall volcano in 2021 will be used as the case study. The method’s performance will be assessed by comparing it with the GPS measurement and the conventional time-series InSAR method based on the SBAS. Further study that can be counted as a novelty is the measurement of azimuthal deformation from the 2021 Fagradalsfjall eruption, addressing the limited research on deformation in this direction. Finally, this analysis will contribute to a more robust understanding of the ICOPS method for addressing non-linear deformation in volcanic settings. At the same time, the integration of InSAR and MAI offers a comprehensive assessment of volcanic activity, capturing both line-of-sight and azimuthal deformation.

Data and methods

Datasets

The SAR datasets used in this study are described in Table 1. The ICOPS algorithm exploited a total of 90 C-band SAR datasets from Sentinel-1 A/1B. Both satellites have a wavelength of around 5.5 cm, which is sourced from the European Space Agency (ESA). Three different frames of Sentinel-1 with similar paths (path number 155) in descending flight direction were used to acquire interferograms over six days in 2021. The 90 data sets consisted of 30 data from Sentinel-1 A (frame number: 376), 30 data from Sentinel-1 A (frame number: 381), and 30 data from Sentinel-1B (frame number: 377). These data were radiometrically calibrated and corrected for thermal noise and orbital errors before the burst combination and selection for the coregistration process. The two different frames from Sentinel-1 A were merged to acquire broader information on the area of interest (black rectangle).

Table 1.

Description of SAR satellite used in this study.

Satellite	Sentinel-1 A/B	ALOS-2
Temporal Coverage	6 January 2021–26 December 2021	28 February 2021–23 May 2021
Temporal Resolution	6 days	84 days
Number of data	60 data	2 data
Flight Direction	Descending	Ascending
Band	C-band	L-band
Wavelength	5.6 cm	23.5 cm
Resolution	5 × 20 m	10 m
Mean Incidence Angle	37.03	36.32
Mean Heading Angle	199.78	-12.14
Polarization	VV	HH
Available Image Mode	VV/VH	HH/HV

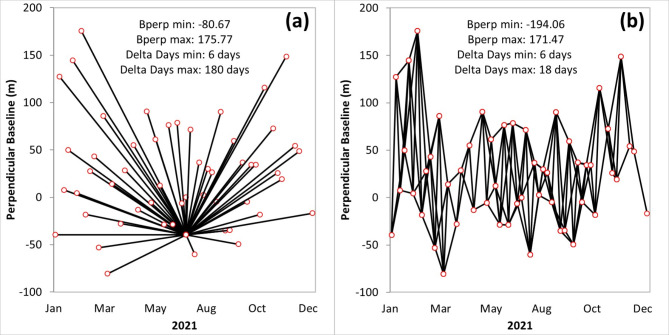
Additionally, the Sentinel-1B data could be burst-selected because the data frame covered the whole study area. Burst selection was conducted to match the Sentinel-1 data with the study area (black rectangle) and to minimize the time required during the coregistration process. The spatial resolution, incidence angle, and polarization used by the SAR data are about 5 × 20 m, 33.45°, and VV polarization. The perpendicular baseline (Bperp) between the reference and secondary images is described as a pair combination based on the single reference, as shown in Fig. 2a, and another pair combination based on the multi-reference, as shown in Fig. 2b. The single reference interferogram processing will generate 89 interferograms as input for PS processing. In contrast, the interferogram pairs with a temporal baseline of about 6, 12, and 18 days with a Bperp of about ± 200 m will be selected as the input of DS processing.

Fig. 2.

Sentinel-1 data coverage and the series of Sentinel-1 data are shown by perpendicular baseline graph for (a) single-reference and (b) multi-reference interferograms. The perpendicular baseline plot of Sentinel-1 data was created using Microsoft Excel 365 (https://www.microsoft.com/).

Figure 2. Sentinel-1 data coverage and the series of Sentinel-1 data shown by perpendicular baseline graph for (a) single-reference and (b) multi-reference interferograms. The perpendicular baseline plot of Sentinel-1 data was created using Microsoft Excel 365 (https://www.microsoft.com/).

Surface deformation in the azimuth direction in this study was also estimated along with the LOS direction using the ALOS-2 fine beam mode based on multiple aperture interferogram (MAI) methods. The ALOS-2 data is described in Table 1. The ALOS-2 data were in the ascending direction with HH polarization. The Bperp of the ALOS-2 data was approximately − 116.61 m with a range of days of roughly 84 days. The paired data of ALOS-2 were acquired between 28 February 2021 and 23 May 2021. Thus, both datasets contain deformation before and after the eruption of Fagradalsfjall.

Table 1. Description of SAR satellite used in this study.

ICOPS processing

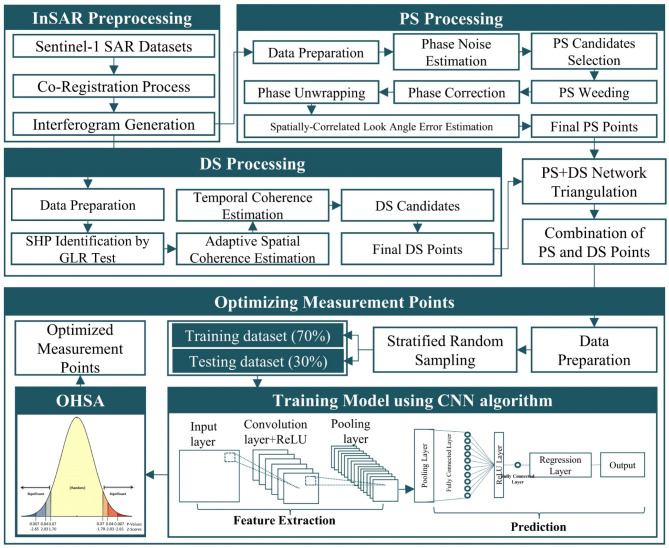
The workflow of the ICOPS time-series InSAR is shown in Fig. 3. The first step in our InSAR preprocessing was data preparation, which consists of the correction of several noises from the single-look complex (SLC) SAR data, such as thermal noise power, radiometric, and orbital phase. After that, we select a reference image for the coregistration process to adjust the other images to have data that is similar in extent and with subpixel accuracy. After the coregistration process is complete, all coregistered SLC images will be focused on a specific subset of the data that covers the study area. Then, the subset of SLC images will be used to generate differential InSAR (DInSAR) with the combination of SAR data pairs for PS processing using a single reference interferogram pair and DS processing using a multi-reference interferogram pair, as shown in Fig. 2a and b, respectively.

Fig. 3.

The methodology used to process the ICOPS method (this figure was a modified version from^18,19). This Figure was prepared using Microsoft PowerPoint 365 (https://www.microsoft.com/).

The PS process is initiated by selecting the pixel candidates based on the threshold for the amplitude dispersion index to be higher than 0.4, as suggested by the Stanford Methods for Persistent Scatterer (StaMPS) algorithm. We used the StaMPS approach for PS processing²⁴. The StaMPS algorithm is effective for detecting low-amplitude signals with consistent phases and for selecting PS points. It does not rely on a pre-defined deformation model to produce time-series deformation rates, making it well-suited for identifying non-linear deformation^24,25. The initial step in StaMPS processing involved estimating the phase noise value and selecting a subset of potential PS pixels from each interferogram. After that, the pixel candidates from each interferogram are analyzed to estimate their phase noise characteristics for PS selection. Then, the selected pixels are weeded for unnecessary pixel noise removal. After that, the selected pixels are DEM-corrected, and the corrected pixels will be phase unwrapped. Then, before generating the final PS points, the error from the spatially correlated DEM needs to be removed to reduce noise in the unwrapped pixels²⁴. Finally, the final results of PS measurement are generated and will be multi-looked to match the spatial resolution of multi-looked multi-reference interferograms. Meanwhile, for the DS candidates, spatial homogenous pixels (SHP) of the amplitude images need to be analyzed using the generalized likelihood ratio (GLR) test with the parameter window size of about 15 × 15 pixels. In addition to the amplitude data, the multi-reference interferogram pair images will be analyzed for their spatial and temporal coherence. Thus, the DS candidate with SHP values higher than 20, with spatial coherence higher than 0.2 and temporal coherence higher than 0.75, will be selected to produce the DS points. The next process will involve a combination of the PS and DS points to generate the combined scatterer (CS) points. The strategy for combining PS and DS points involves treating a DS point with an estimated optimal phase value as a quasi-PS point, which can be merged with its corresponding PS point for further analysis. To avoid redundancy, DS points that overlap with PS points are removed. After that, the unwrapped phase that is represented by the CS pixels will be used for time-series estimation. During the time-series estimation, inversion using singular value decomposition (SVD) will be carried out to retrieve the time-series result of CS MPs^14,18.

Then, the CS points will be optimized by a deep learning algorithm based on convolutional neural networks (CNN) algorithms, followed by a statistical cluster based on optimized hot spot analysis (OHSA). The Convolutional Neural Network (CNN) algorithm is a deep learning technique modeled after a neural network designed to mimic the functioning of the human brain’s cerebral cortex^26,27. The CNN consists of multiple layers, including convolutional, pooling, and fully connected layers^19,28. The first layer, known as the convolutional layer, is responsible for extracting features from the input using filters, producing feature maps that are then passed to subsequent layers²⁹. These filters serve as activation functions, processing the non-linear outputs from the convolution operation¹⁸. The ReLU activation function is commonly employed in this layer due to its effectiveness in activating all neurons involved in the process^30,31. Next is the pooling layer, which simplifies the convolutional layer’s output by reducing the size of the feature maps²⁹. The final stage is the fully connected layer, which links each pooling layer to refine the non-linear mapping of the data^27,32. Additionally, OHSA is a spatial statistical tool that detects significant clusters of high and low values known by hot and cold spot measurement points, respectively^33,34. The optimized terms referred to the automatization of finding the scale distance parameter to perform the spatial clustering analysis based on the Getis-Ord Gi* statistics model by analyzing incremental spatial autocorrelation^33,35. The usefulness of OHSA was applied in slow-moving landslide detection³³.

The initiation of optimization using a machine learning algorithm is data preparation, which produces “1” and “0” data. Previous research related to measurement point optimization has focused on land subsidence with mostly linear deformation patterns^14,18. Monitoring volcanic activity through the InSAR time series tends to produce varying data due to changes in volume before and after a volcanic eruption, which results in inflation and deflation processes associated with volcanic activity^36,37. For that reason, measurement point optimization was conducted by defining optimum time-series data by the Z score value for each time-series dataset. The Z-score represents the standard deviations between a specific data point and the means of the dataset. Thus, the z-score value that is farthest from the mean value is considered an outlier data^38,39. We assigned a value of “0” to Z score values greater than three and less than − 3. Additionally, we assigned a value of “1” to Z score values less than two and greater than − 2. We used machine learning to predict the optimum time-series data with Z score values between absolute values of 2–3. The next step after data preparation is randomly sampling the “1” and “0” data based on stratified random sampling with ratios of 70 and 30% data for training and testing data, respectively. After that, we developed the CNN architecture with several parameters such as batch size, epoch number, and learning rates assigned by the utilization of the gray wolf optimizer (GWO) algorithm^19,40.

The Grey Wolf Optimizer (GWO) algorithm is a metaheuristic method inspired by swarm intelligence (SI) that mimics the social structure and hunting strategies of grey wolves^40,41. In nature, grey wolves are apex predators that operate in packs with a well-defined hierarchy, where each wolf has a specific role based on its position in the group^40,42,43. Their hunting process begins by approaching and encircling prey, followed by coordinated pursuit and harassment. Once the prey is exhausted, the wolves move in for the final attack to complete the hunt. This behavior serves as the basis for the GWO algorithm’s optimization process^41,44.

The input data will be initiated to be processed on the first layer, which consists of convolutional layers of about 20 layers and a ReLU activation function that is suitable for the input data with non-linear properties. After that, the dimension of the input data needs to be reduced for effective processing by a down-sampling process using a two-dimensional average pooling layer. Then, the pooled data will result in 10 fully connected layers after the multiplication and weighting process by its matrix. Another process needs to be conducted to generate a final single fully connected layer to minimize the computational complexity by applying another activation ReLU layer to the ten fully connected layers. Thus, the single fully connected layer will be processed in the regression layer to make the prediction result suitable for further processing. After that, the prediction result from the CNN algorithm will be used to select the optimum point by removing the MPs with the lowest prediction value. Thus, the remaining MPs will be optimized once more using the OHSA method. The spatial clusterization of the deformation data from the result of CNN optimization will be identified as significant points based on their spatial reliability calculated by Getis-Ord Gi* statistics^18,19.

Overall, the process from interferometry pre-processing until interferogram formation for time-series analysis and MAI processing was conducted using GAMMA software. Meanwhile, the pixel selection process from PS, DS, and PS-DS processing was conducted using Matlab. The optimization process based on the CNN algorithm was also conducted using Matlab, and the optimization process based on the OHSA was conducted using ArcMap.

Figure 3. The methodology used to process the ICOPS method (this figure was a modified version from^18,19). This Figure was prepared using Microsoft PowerPoint 365 (https://www.microsoft.com/).

Integrated InSAR and MAI Processing

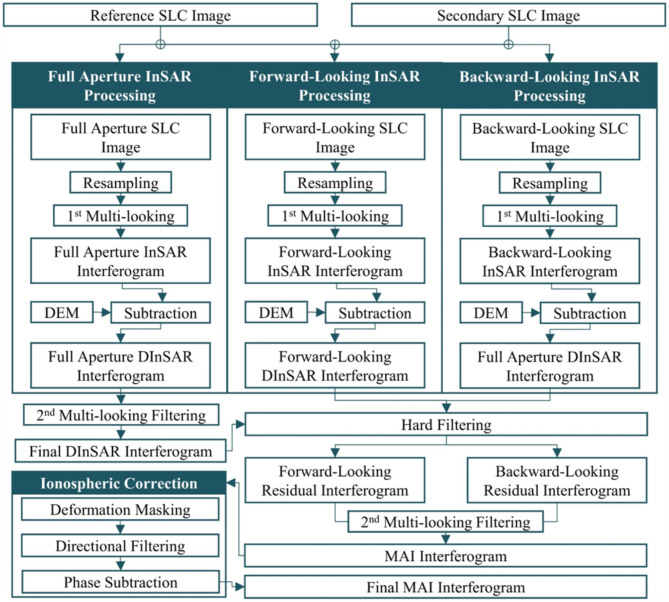
The surface deformation in Fagradalsfjall Volcano in this study was also processed using ALOS-2 data to generate the deformation for both azimuth and LOS direction. The integrated term, in this case, means the combination of the two methods in determining the MAI deformation map; during the MAI processing, the result from the final InSAR result was used to estimate forward and backward-looking residual interferogram^22,23. The generation of the along-track deformation in this study began with the preparation of the two SAR data that corresponded to the reference and secondary images. Both datasets were then prepared to be processed using the split beam InSAR method as the MAI SAR processor to generate three aperture modes: forward-looking, backward-looking, and full aperture SLC data⁴⁵. The workflow of the methodology of the integrated InSAR and MAI process is shown in Fig. 4. The DInSAR processing of the three aperture modes InSAR processing was mainly similar to that of conventional InSAR, with the final result generated by applying the multilook process to both reference and secondary SLC data by four in the range and by five in azimuth directions, respectively. The multi-look process was conducted to reduce noise and improve computational performance²³ The secondary image was then resampled based on the reference image to generate the topography InSAR image. The topo-phase interferogram from the DEM based on Copernicus data was then subtracted from the topography InSAR image. The subtraction process resulted in differential InSAR images for each set of aperture modes.

Fig. 4.

Workflow of MAI processing methods used in this study (this figure was modified from²²). This Figure was prepared using Microsoft PowerPoint 365 (https://www.microsoft.com/).

The first multilook DInSAR processing result was then filtered using adaptive filtering in the second multilook number of approximately twelve in the range and fifteen in the azimuth directions, respectively. The DInSAR results from the full-aperture InSAR processing that was filtered using adaptive filtering was the final DInSAR interferogram. The hard filtering method was then applied to the final DInSAR interferogram by applying an adaptive filter iteratively with large window sizes. The forward-looking and backward-looking DInSAR interferograms will be subtracted by the hard-filtered DInSAR interferogram, resulting in residual interferograms from both views. The multiple aperture interferogram will be generated from the residual interferograms of both forward-looking and backward-looking interferograms by multilook and adaptive filter processing. The multilook process was conducted on each of the two-looking interferograms to reduce the noise in each different-looking interferogram. Adaptive filtering was also performed on each of the different-looking interferograms with a 32-window size. This parameter will be applied to each look-direction interferogram and the full-aperture interferogram.

The result from the final MAI processing generated in the previous step needs to be further processed if ionospheric strikes are found in the final MAI result. In this study, directional median filtering was used to remove ionospheric artifacts by modeling the ionospheric strike using a directional median filter. The ionospheric strike model was then subtracted from the final MAI interferogram result contaminated by the ionospheric effect. This method was conducted iteratively with a kernel of approximately 251 in the along streak direction and 64 in the cross-ionospheric streak direction with a 340⁰ rotation angle. The information on the masked area was identified from the deformation area from the final DInSAR, the decorrelation data from the coherence map, and the pixel offset tracking data^22,46.

Figure 4. Workflow of MAI processing methods used in this study (this figure was modified from²²). This Figure was prepared using Microsoft PowerPoint 365 (https://www.microsoft.com/).

Results

ICOPS results

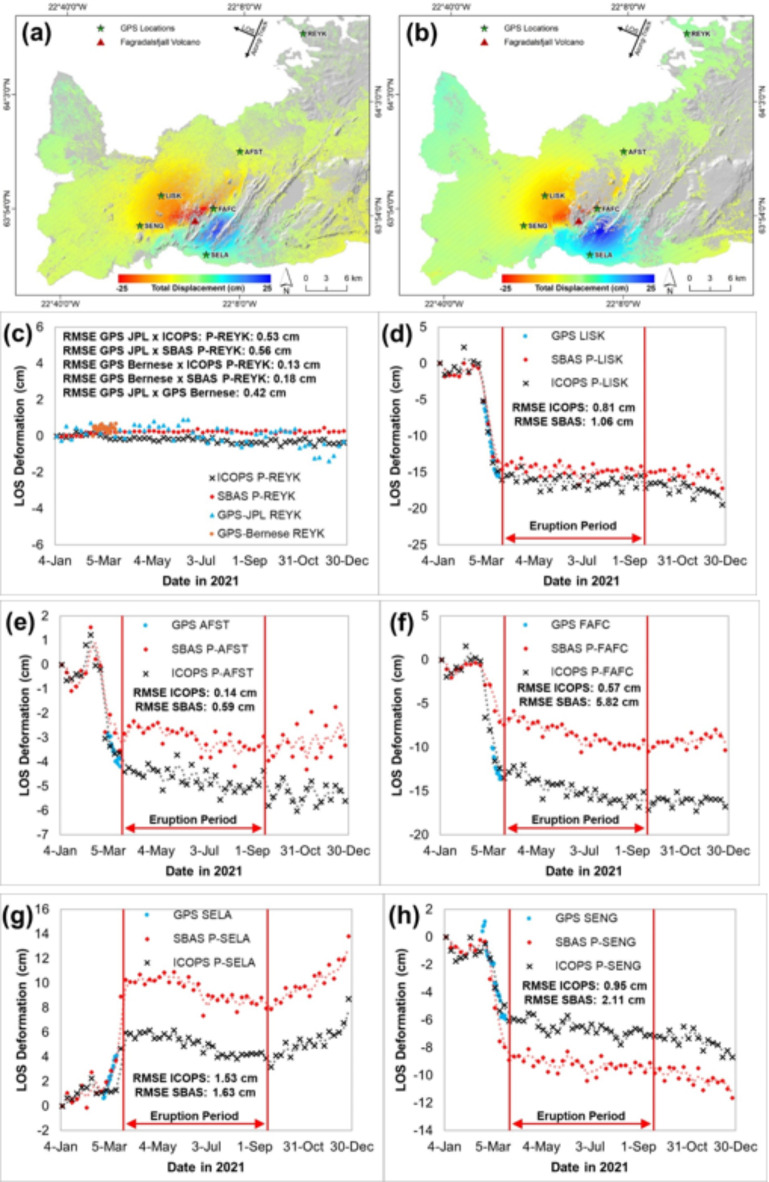
The result from the ICOPS (Fig. 5a) and the SBAS (Fig. 5b) shows the total LOS deformation in Reykjanes Peninsula overlaid with the hillshade imagery shows a pattern of displacement away from the satellite and displacement toward the satellite in the northwest and southeast of Fagradalsfjall volcano, respectively. The result from the ICOPS measurement shows a number of MPs of about 1,380,542, and for the SBAS, it is about 1,734,384. The number of MPs from SBAS is much higher than the ICOPS algorithm because the SBAS measurement did not carefully select the MPs from pixel selection such as PS and DS pixel selection. These discrepancies between the two methods were consistent with the result of ICOPS and SBAS measurements in Mount Melbourne, Antarctica²¹. After that, the results from both time-series methods were compared with GPS measurements in several areas, which are described by 6-star points shown in Fig. 5a and b. The GPS measurements used in this study were processed from the GNSS Rinex data^7,47 that had been processed using Bernese Software. Those GNSS data have varying availability, with the two data (REYK and SENG) containing complete one-month data, while the others consist of two to three weeks of data. Those data are within the date boundary between 20 February–21 March 2021. The result from the GNSS processing was compared with the result from NASA JPL on the REYK station, and the comparison shows a good result in RMSE of about 0.42 cm. Meanwhile, the comparison between the two methods with the GPS data shows that the range of RMSE value for ICOPS is about 0.13–1.53 cm, and the range of RMSE value for SBAS is about 0.18–5.82 cm. These results show that the ICOPS has better accuracy compared to the SBAS, shown by the smaller range of RMSE value, which is considered to be a good result demonstrated by the consistent deformation pattern compared to the GPS measurement, as shown in Fig. 5c–h. The time-series plot between the measurement points was measured around the deformation area, which is used for the GPS comparison. The time-series deformation results in Fig. 5b shows a stable deformation and the deformation in Fig. 5c–e and g show a negative direction of the LOS pattern before the eruption period. Meanwhile, for Fig. 5f, the displacement toward the satellite pattern was observed before the eruption occurred.

Fig. 5.

Total LOS deformation map of (a) ICOPS and (b) SBAS. The negative displacement shown by red toward the green color shows the displacement away from the satellite, and the positive displacement shown by green toward the blue color indicates the displacement toward the satellite. Comparison of the time series of GPS, ICOPS, and SBAS results in LOS direction in (c) REYK, (d) LISK, (e) AFST, (f) FAFC, (g) SELA, and (h) SENG stations. The total LOS deformation maps were processed using ArcMap version 10.4 (https://www.esri.com/). Additionally, the scatter plot of time-series deformation was created using Microsoft Excel 365 (https://www.microsoft.com/).

Figure 5. Total LOS deformation map of (a) ICOPS and (b) SBAS. The negative displacement shown by red toward the green color shows the displacement away from the satellite, and the positive displacement shown by green toward the blue color indicates the displacement toward the satellite. Comparison of the time series of GPS, ICOPS, and SBAS results in LOS direction in (c) REYK, (d) LISK, (e) AFST, (f) FAFC, (g) SELA, and (h) SENG stations. The total LOS deformation maps were processed using ArcMap version 10.4 (https://www.esri.com/). Additionally, the scatter plot of time-series deformation was created using Microsoft Excel 365 (https://www.microsoft.com/).

The validation results of both the SBAS and ICOPS methods against GPS measurements show a better comparison with ICOPS data, largely due to differences in the selection of MPs for data validation. MPs for both methods are selected by averaging the points available within a 100-meter radius of the GPS coordinates. Since SBAS typically has a higher density of MPs than ICOPS, the number of selected MPs for data plotting can vary based on this density. However, the quantity of MPs does not necessarily determine the quality of the final results. In fact, ICOPS, despite having fewer MPs, often provides better results after validation with GPS data. This is because ICOPS applies an optimization process to its MPs after obtaining time-series deformation data from CS points, reducing the impact of outliers caused by noise or phase jumps at certain dates and locations. Another factor contributing to discrepancies is that the comparison was made using line-of-sight (LOS) displacement, whereas GPS data is recorded in three-dimensional deformation. To align the GPS data with LOS, an average of the heading and incidence angles from SAR data was used rather than the specific incidence angle for each point. This approach assumes uniform angles across the area, but in reality, the heading and incidence angle for each point should vary, especially given the topographical differences in the study area.

Full-aperture InSAR and MAI interferogram

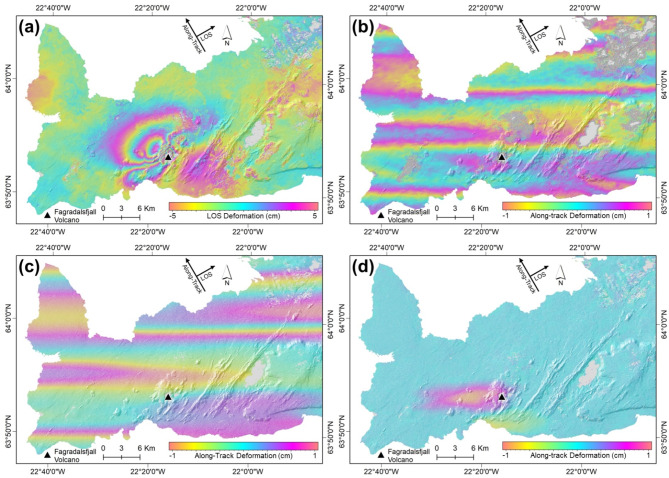
The outcomes derived from DInSAR and MAI processing of the ALOS-2 paired data yielded deformation in the cross-track (LOS) and along-track (azimuth) directions, as shown in Fig. 6a and b, respectively. The deformation results in the LOS direction show that displacement toward and away from the satellite patterns was found between 28 February 2021 and 23 May 2021. A displacement toward the satellite of approximately 20 cm was found in the northwestern area of Fagradalsfjall Volcano. Meanwhile, the area near the volcano to the southwest subsided up to 20 cm. The results from the MAI processing showed that the deformation was affected by the ionospheric effect. The streak-line pattern shows the ionospheric effect. Thus, the ionospheric effect in Fig. 6b needs to be mitigated, and the directional median filtering method was applied to the MAI interferogram to rectify the impact of the ionosphere^46,48.

Fig. 6.

SAR Interferogram from (a) DInSAR and (b) MAI processing. (c) Ionospheric streak pattern generated from directional filtering. (d) Ionosphere-corrected MAI interferogram. The direction of negative and positive LOS deformation is represented by the displacement away and displacement toward the satellite’s LOS. Meanwhile, the direction of negative and positive along-track deformation is represented by the displacement away and toward the satellite’s flight path direction. The maps in this figure were created using ArcMap version 10.4 (https://www.esri.com/).

After the MAI interferogram was masked in the possible deformation area from the LOS deformation, the iterative filter was applied with a window kernel of approximately 155 in the along streak direction and 31 in the across streak direction with a rotation angle parameter of approximately 160⁰. For the references, we used a 5 × 1 kernel size proportion in this study before the rotation of directional filtering as suggested that the effective bandwidths of the kernel size in the along and across direction were approximately 1–5. The ionospheric streak pattern from the directional median filtering is shown in Fig. 6c. The ionospheric streak pattern generated from the directional median filter was subtracted from the initial MAI interferogram (Fig. 6b), which was still affected by ionospheric effects. The result from the final subtraction resulted in the ionosphere-mitigated MAI interferogram, as shown in Fig. 6d, with the displacement in the azimuth track direction showing approximately − 2 mm in the area west of the volcano and 2 mm in the areas south and south of the volcano.

Figure 6. SAR Interferogram from (a) DInSAR and (b) MAI processing. (c) Ionospheric streak pattern generated from directional filtering. (d) Ionosphere-corrected MAI interferogram. The direction of negative and positive LOS deformation is represented by the displacement away and displacement toward the satellite’s LOS. Meanwhile, the direction of negative and positive along-track deformation is represented by the displacement away and toward the satellite’s flight path direction. The maps in this figure were created using ArcMap version 10.4 (https://www.esri.com/).

Discussion

InSAR and Earthquake Analysis

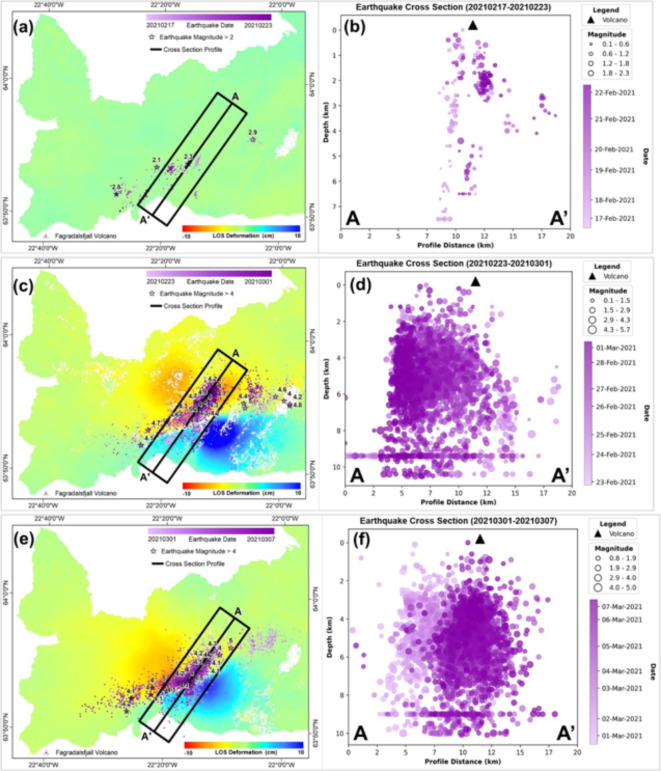
The analysis of the InSAR and seismic activity was shown by the cross-section analysis of the earthquake sequences near the Fagradalsfjall Volcano (Fig. 7). Most of the earthquake occurrence locations from the southwest to the northeast of Fagradalsfjall Volcano reflect the approximate location of dike intrusion. In this analysis, this approximate location was illustrated to analyze the cross-section of the earthquake. The DInSAR maps from 6 pair dates show the deformation activity from before the big earthquake occurred between 17 February 2021 and 23 February 2021 (Fig. 7. a, b) and during the increase of seismicity with deformation that occurred between 23 February 2021 and 19 March 2021 (Fig. 7. c–j) and the pair date after the eruption occurred on 19 March 2021 shown in Fig. 7. k and l. The areas around the dike intrusion show surface deformation characterized by a negative direction of the LOS pattern. Another possible cause of the deformation in this area was the strong magnitude earthquake on the northeastern flank of Fagradalsfjall Volcano. The seismic data extracted from the Icelandic Met Office (IMO) from January until December 2021 were selected within the interferogram pairs of Sentinel-1 data shown by the 2D cross-section from point A to A’ with a distance of about 20 km. The area of the cross-section profile was made for 2.5 km from both sides of the middle line profile. Thus, the analysis of the earthquake profile distance was only made within the 20 × 5 km areas of the cross-section.

Fig. 7.

The deformation map overlaid by earthquake distribution and cross-section of the earthquake sequences from A to A’: (a, b) 17 February 2021 and 23 February 2021, (c, d) 23 February 2021 and 1 March 2021, (e, f) 1 March 2021 and 7 March 2021, (g, h) 7 March 2021 and 13 March 2021, (i, j) 13 March 2021 and 19 March 2021, (k, l) 19 March 2021 and 25 March 2021. The positive displacement shown by green toward the blue color indicates the displacement toward the satellite, and the negative displacement shown by red toward the green color shows the displacement away from the satellite. The profile cross-section of the earthquake is made 5 km from the middle line profile. The earthquake distribution maps were processed using ArcMap version 10.4 (https://www.esri.com/). Additionally, the scatter plot cross-section of the earthquakes was generated using Matplotlib in Python (https://www.python.org/).

Figure 7. The deformation map overlaid by earthquake distribution and cross-section of the earthquake sequences from A to A’: (a, b) 17 February 2021 and 23 February 2021, (c, d) 23 February 2021 and 1 March 2021, (e, f) 1 March 2021 and 7 March 2021, (g, h) 7 March 2021 and 13 March 2021, (i, j) 13 March 2021 and 19 March 2021, (k, l) 19 March 2021 and 25 March 2021. The positive displacement shown by green toward the blue color indicates the displacement toward the satellite, and the negative displacement shown by red toward the green color shows the displacement away from the satellite. The profile cross-section of the earthquake is made 5 km from the middle line profile. The earthquake distribution maps were processed using ArcMap version 10.4 (https://www.esri.com/). Additionally, the scatter plot cross-section of the earthquakes was generated using Matplotlib in Python (https://www.python.org/).

The first earthquake occurred on 24 February 2021 with a magnitude of 5.7 at ± 1.1 km depth, and another earthquake ensued after the first seismic event with a magnitude of 5.2 at ± 4.8 km depth on 27 February 2021. After more than one week, there was another moderate magnitude (5.1 Mw) earthquake approximately 1.5 km to the southwest of Fagradalsfjall Volcano. This moderate-magnitude earthquake occurred subsequently four days later with a 5.4 magnitude at ± 3.1 km depth. In addition to moderate earthquakes, there were many micro- to low-magnitude earthquakes around Fagradalsfjall Volcano that are considered shallow earthquakes that could cause changes to the ground surface^49,50. Therefore, further analysis of the surface deformation and seismicity around Fagradalsfjall Volcano was performed using six days of Sentinel-1 paired data. The analysis of the six days of Sentinel-1 paired data focused on the six pairs of data (see Fig. 7b–g). Thus, in the selection of the dates for the seismicity analysis, the first pair of dates was used as a reference pair of dates with no prior significant deformation due to the lower seismicity occurrences. The last pair of dates, which is between 19 March and 25 March 2021, was suggested to have a deformation caused by the volcanic eruption that occurred on 19 March. Further analysis was also conducted to analyze the earthquake activities and the InSAR displacement through the dike model estimations. The model inversion will estimate the geometries and parameters from InSAR displacement from each period from 23 February until 25 March 2021. The single pair from 17 to 23 February is not modeled due to the inexistence of the deformation that occurred during that period. Finally, this additional analysis from the model inversion that is generated from Geodetic Bayesian Inversion Software (GBIS)⁵¹ is expected to aid the relationship between dike intrusion and earthquake activity.

The first week of the seismicity analysis between the paired dates of 17 February 2021 and 23 February 2021 showed 462 earthquakes distributed around the Reykjanes Peninsula (Fig. 7a). The strongest earthquakes that occurred during the first week were considered minor earthquakes, with magnitudes of approximately 2.9 and 2.1 that occurred on 18 February 2021, with additional earthquakes of 2.8 and 2.3 Mw occurring on 21 February 2021. The earthquake distribution map was compared with the surface deformation map shown in Fig. 7a. The surface deformation was acquired from the DInSAR map. The result indicates that no deformation occurred during the first week of the analysis, as evidenced by there is no existence of the non-existing deformation shown in Fig. 7a. The cumulative number of seismic events beneath the Reykjanes Peninsula is represented as a single dot with different colors defining the various times of earthquake occurrences to describe the magma movement beneath the Earth’s surface. The earthquake movement during the first week was toward the southwest and descended slightly to approximately 5 km beneath the Earth’s surface (Fig. 7b).

The second week of the seismic analysis shows an increase in earthquake occurrence (Fig. 7c) compared to the previous week. The increase in earthquake occurrence by 3987 events occurred during the second week is suggested to be the cause of the deformation between 23 February 2021 and 1 March 2021. The surface deformation during the second week was characterized by a pattern of displacement toward and away from the satellite (Figure S1). Supplementary Figure S1 shows that through model inversion, the deformation during the second week of analysis can be assumed using a single-segment dike with a uniform opening and a single-point source. Based on that assumption, the vertical dike with strike from northeast to southwest was spanning with a length of about ± 4 km. This assumption is limited to only a single segment of the dike that the GBIS software can produce. Thus, the previous research shows that the double segment dike has occurred during this period⁷. Those deformations were suggested to be caused by the low- and moderate-magnitude earthquakes during the second week with magnitudes greater than 4 M_w, as shown by the star points in Fig. 7c. The star points from the earthquake distribution show that the low-magnitude earthquakes between 4.0 and 4.9 occurred 28 times during the second week. Additionally, moderate earthquakes with magnitudes of 5.0 and 5.7 occurred three times on 24 February 2021, and an earthquake with a magnitude of 5.2 occurred on 27 February 2021. The increase in the number of earthquakes during the second week (20210223–20210301) was suggested to be due to the activity from the movement of magma beneath the Earth’s surface, and the magma movement during the second week was suggested to have a similar direction with the earthquake occurrence from yellow to red color. The high density of earthquakes was located within 1 km of the dike location between Fagradalsfjall Volcano and the northeast end of Keilir Volcano. The cross-section of the seismic events in Fig. 7d and the geometry visualization from Figure S1 describe the movement of magma in depth. The magma movement started as a dike intrusion from the southwest near the Fagradalsfjall Volcano. It moved toward the northeast as the depth of activity deepened between 2 and 6 km in depth, based on the earthquake depth locations and dike geometry model. The surface deformation during the second week, which began on 24 February 2021 after the 5.0 and 5.7 magnitude earthquakes, was suggested to begin the activity of the magma intrusion before the eruption of the Fagradalsfjall, which occurred on 19 March 2021.

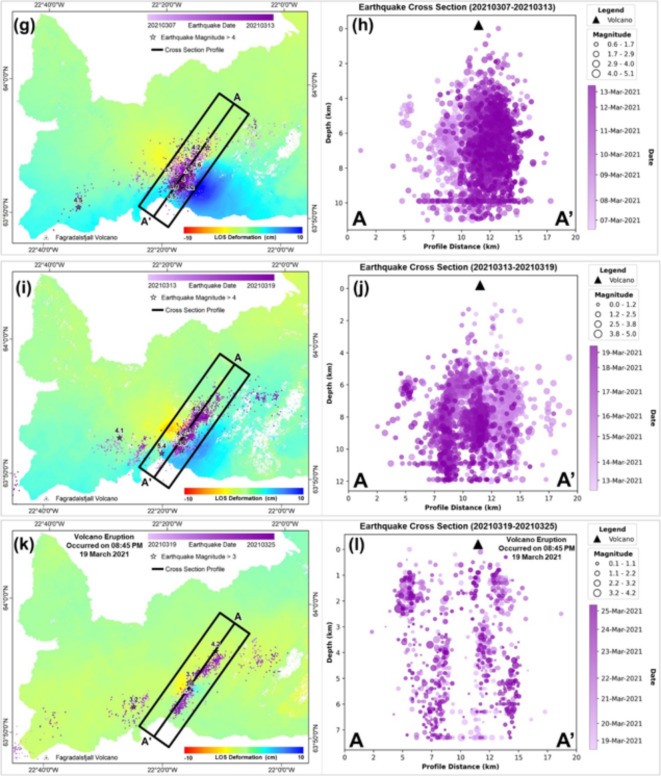
The third week of the analysis shows a distribution of earthquakes with lateral magma movement from northeast to southwest in the Reykjanes Peninsula starting on 1 March 2021 until 7 March 2021 (Fig. 7e). The deformation during the third week (Figure S2) is consistent with the increase in earthquake occurrences by 4161, with the strongest earthquakes of magnitude 5 on 1 March 2021 and 7 March 2021. The two moderate earthquakes with a magnitude of 5 were followed by low-magnitude earthquakes (4.0–4.9 M_w) that occurred 20 times during the third week. The earthquake occurrence described by the cross-section graph (Fig. 7f) shows the reverse pattern from the previous week (Fig. 7d). The earthquake pattern shows that the magma movement during the third week was initiated from the northeast toward the southwest of Fagradalsfjall Volcano. In this case, the magma movement from the earthquake hypocenter distribution shows an opposite movement based on the second-week earthquake distribution. Based on the earthquake depth analysis from the 2D view, the earthquake movement in depth was slightly descended to the earth’s surface. Despite the increase in total earthquake occurrences, the surface deformation during the third week decreased according to the number of fringe patterns and deformation areas. The third-week deformation area was smaller compared to the second-week result. The decrease in area deformation during the third week was suggested to be due to the decrease in earthquakes stronger than M_w 4 (22 earthquakes) compared to the earthquakes that occurred in the previous week (20210223–20210301) with 31 earthquakes. The higher magnitude of a moderate earthquake from the third week is also considered a smaller magnitude than the second week when the earthquake in the second week occurred up to 5.7 magnitude. Thus, a higher magnitude earthquake was suggested to be the cause of higher deformation occurrence in the second week. The result from the model inversion also shows a decrease dike’s length by about 1 km, leaving the dike length or about 3 km in the depth between 1 and 3 km. In this period, the dike model shows the location where the earthquake is not much distributed based on its hypocenter. This area was suggested to be the location of the magma movement that triggered the earthquake around during the dike intrusion.

The fourth week of the analysis, which is between 7 March 2021 and 13 March 2021, shows the deformation area during the fourth week (Fig. 7g) was smaller than that during the previous week (Fig. 7e) and consistent with the decrease in the number of earthquake occurrences by 3951. The strongest earthquakes during the fourth week were moderate earthquakes with magnitudes of 5 and 5.1 on 10 March 2021, and these earthquakes were followed by a M_w 5 earthquake on 12 March 2021. A total of 10 earthquakes with low magnitudes (4.0–4.9) are also displayed by the star points in Fig. 7g. The movement of the subsurface magma is described in the earthquake locations based on the cross-section graph (Fig. 7h). The locations of the earthquakes during the fourth week were close to the dike location, with movement from the northeast toward the southwest with descending movement, based on the earthquake depth locations. The smaller deformation areas during the fourth week were suggested to be caused by the low- to moderate-magnitude earthquake concentrated around the dike intrusion area. Thus, the dike location is shown in Supplementary Materials in Figure S3. The length of the dike model during this period is shorter than the previous week by showing the dike’s length of about 2 km with a depth between 1 and 3 km. The relation between the dike model and the earthquake activity shows that the location of the dike intrusion is located between the gap of the earthquake hypocenter distribution.

The fifth week of the analysis shows the distribution of earthquakes between 3 March 2021 and 19 March 2021 (Fig. 7i). The deformation area during the fifth week was smaller and consistent with the decrease in the number of earthquake occurrences by 3702. The decrease was also shown in the dike model inversion (Figure S4), with the dike striking from NNE to SSW only having a length of about 1 km in the depth between 1 and 3 km. The slight changes were only shown in the dike’s strike to 37° from the previous strike (50°). The relation between the earthquake activity and the dike model can be seen from the model geometry that the gap between the earthquake distribution was showing the location of dike intrusion. The strongest earthquake during the fifth week featured a magnitude of 5.4 at a depth of 3.1 km on 14 March 2021. The M_w 5.4 earthquake was located southwest of Fagradalsfjall Volcano. Another reason for the decrease in the deformation during the fifth week was the decrease in low- to moderate-magnitude earthquakes, which occurred only 6 times during the fifth week. The earthquakes that occurred during the fifth week reflected the magma movement before the eruption of Fagradalsfjall Volcano on 19 March 2021. The movement of the magma is described by the cross-section graph of the earthquake locations, as shown in Fig. 7j. The movement of magma during the fifth week was from the southwest toward the northeast and increased in depth. After that, the magma ascended to the surface of the earth, as shown by the earthquake’s rising movement locations. The ascending movement was suggested to be the initial process before the eruption occurred. The surface deformation that occurred in the fifth week was suggested to be shown by the result of the M_w 5.4 earthquake occurrence in a shallow depth approximately of about 3.1 km below the earth’s surface. Thus, the earthquake that occurred on 14 March 2021 was the last moderate earthquake that occurred prior to the initial eruption on 19 March 2021. The last moderate earthquake that occurred before the eruption at the Fagradalsfjall volcano described a decrease in seismic activity, as indicated by a decrease in the number of moderate earthquakes. Only one earthquake occurred during the fifth week. The moderate earthquake was also followed by only five low earthquakes with magnitudes between 4.0 and 4.9. Thus resulting in smaller deformation occurrence.

The last week of the analysis shows the distribution of earthquakes around the Reykjanes Peninsula between 19 March 2021 and 25 March 2021 (Fig. 7k). The deformation during the last week was found only around Fagradalsfjall Volcano, with a small displacement pattern toward and away from the satellite. This small deformation in the last week of the analysis is shown by the decrease of the dike’s width in model inversion (Figure S5). The relationship between the earthquake activity shows only a little earthquake activity around the dike model during the volcano eruption. The negative direction of the LOS pattern of the Fagradalsfjall Volcano was suggested to have occurred due to the deflation process after the volcanic eruption on 19 March 2021. Another possible cause of the displacement toward and away from the satellite pattern was the occurrence of low-magnitude earthquakes with magnitudes of 3.1 and 3.8 that occurred on 19 March 2021 at depths of 0.1 and 1.1 km, respectively. A 4.2 earthquake located near Keilir Volcano is considered to be a moderate-magnitude earthquake, but it did not create any deformation that DInSAR could record. A total number of 1325 earthquakes occurred around the dike intrusion between Fagradalsfjall Volcano and Keilir Volcano and are suggested to represent the approximate dike intrusion pattern. The earthquakes during the last week mainly occurred during the eruption event, as shown by the cross-section graph of the earthquake distribution in Fig. 7l.

Limitations and challenges of the study

This study tried to provide insight into the eruption of the Fagradalsfjall volcano by the utilization of multi-satellites based on Sentinel-1 and ALOS-2. Both satellites were processed differently, with Sentinel-1 data acquired in one year within 2021 to be used for performing multi-temporal InSAR analysis. Meanwhile, a pair of ALOS-2 data was acquired to analyze the deformation in the azimuth direction using the MAI method. Both methods used to process satellite data employ advanced techniques that are not commonly applied in research. As a result, the data processing stage may face limitations and challenges due to the complexity of these methods. The current ICOPS method has limitations in measuring non-linear time-series data. The reason behind this is that during the ICOPS development process, only the linear case assumption was used in the optimization stage of its measurement points. The use of only linear assumptions in the optimization stage gives significant weight to the correlation coefficient in identifying data affected by noise. As a result, non-linear data may be mistakenly classified as noisy and potentially removed. This can be problematic in cases like volcanic eruptions, where deformation time-series data often show non-linearity due to inflation before the eruption and deflation afterward. Therefore, this study modifies the parameters to identify outliers in non-linear time-series deformation data based on the previous approach, which used coefficient correlation²⁰ into the z-score statistical approach.

The z-score statistical method was chosen for detecting outliers because it offers several advantages, including its strong foundation in well-understood and validated statistical principles and its low time and computation complexity, which make it efficient for large datasets⁵². Its straightforward approach to identifying outliers by calculating how many standard deviations a data point is from the mean makes it a practical choice. However, this method does have limitations, particularly its reliance on the assumption that data follows a certain distribution⁵². This dependency means the method may not perform as effectively with data that significantly deviates from this distribution. To address these limitations and improve outlier detection, future research should explore alternative methods such as proximity-based and regression-based outlier detection method, which offers higher performance compared to the statistical method, and these methods offer robust solutions for both linear and non-linear data, providing a more comprehensive approach to identifying outliers and refining data analysis⁵². Despite the limitation of the z-score approach, the utilization of CNN to help predict the pattern of the data affected by outliers is expected to cover the shortcomings of the z-score method. Finally, the outliers detected from the z-score method that have low prediction values from CNN will be removed and considered noisy data⁵².

Another challenge of this study comes from the analysis of MAI in ALOS-2 data. The analysis of the azimuth direction measurement is very sensitive to the ionospheric effects, especially in low-frequency satellites such as the L-band satellite, which can produce the InSAR result to be affected by azimuth phase shift^53,54. The presence of noise in azimuth deformation data presents significant challenges, especially when there is no additional deformation data available for reference. While the directional filtering method used in this study is relatively straightforward, having noise-free data is crucial. If only one dataset is available and it is affected by ionospheric noise, it becomes more difficult to identify areas to preserve accurately. This increases the risk that the masking process could unintentionally remove true deformation areas. Ultimately, this complicates the validation of results obtained from ionospheric noise removal, potentially reducing the accuracy of the outcome. Therefore, it is recommended that before MAI processing, sufficient data is ensured, particularly from both ascending and descending tracks. Meeting these conditions allows for more comprehensive analysis, including 3D deformation retrieval using Line-of-Sight (LOS) and azimuth deformation data from both tracks.

In the analysis of InSAR and seismicity data, 6 pairs of InSAR data from 17 February until 25 March 2021 were analyzed with the earthquake occurrences distributed around the study area. Furthermore, the deformation generated from each pair of InSAR results is modeled inversely using GBIS. The purpose of the inverse model is to calculate the parameters of source deformation, and the geometry of the source deformation will be produced and analyzed with the earthquake hypocenter data. Because the main reason for volcanic activity is dike intrusion, the dike model based on uniform opening was used in this study. The inversion process can provide the geometry (length, width, location) and the number of openings for a uniform rectangular dipping dike model. This method determines the dike’s geometry and direction but has limitations in generating multiple patches to represent the distribution of opening around the dike model accurately. It is important to emphasize that this study does not discuss the opening distribution. The focus is solely on solving for the dike’s geometry through the inversion process, leaving the exploration of opening distribution and its representation for future research or alternative software solutions.

Conclusion

Monitoring Fagradalsfjall Volcano activity during 2021 was conducted using the ICOPS time-series method and Sentinel-1 data. The deformation around the volcano was characterized by displacement toward and away from the satellite. The reason for the deformation was suggested to be due to the activity of the magma reservoir that formed a dike intrusion between Fagradalsfjall and Keilir volcanoes. The comparison between time-series analysis using InSAR measurement was compared with GPS measurements in Reykjavik city, and the result shows that both measurements show a similar pattern and are comparable. Another measurement was conducted to estimate the along-track displacement using ALOS-2 data and the MAI method. The result from the MAI measurement shows a deformation of approximately ± 2 mm in the azimuth direction around Fagradalsfjall Volcano. The activity of the subsurface magma was analyzed using earthquake activity during the 6 days of the interferometric pairs. The six pairs show that there was an increase in earthquake activity with the deformation shown between the SAR images. Further analysis could be conducted by applying multitrack analysis to acquire the 3D deformation pattern due to the 2021 eruption of Fagradalsfjall Volcano.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author contributions

W.L.H.: writing—original draft, formal analysis, methodology, conceptualization, visualization. M. F. F: writing—review & editing, conceptualization, methodology. S. L.: writing—editing, funding acquisition, visualization. S. P.: resources, supervision, funding acquisition. W-K. B.: resources, methodology, supervision, investigation. C-K. H.: resources, methodology, supervision, data curation. H-C. K.: resources, supervision, funding acquisition. C-W. L.: writing—review & editing, conceptualization, funding acquisition, methodology, supervision.

Data availability

Sentinel-1 data used in this study are available at https://search.asf.alaska.edu/. The Copernicus GLO-30 digital elevation model (DEM) is available at https://portal.opentopography.org. The GNSS rinex files are openly available and were acquired from Open Science Framework at https://osf.io/n73cm/ 33.

Competing interests

The authors declare no competing interests.