Modeling and analysis of dengue transmission in fuzzy-fractional framework: a hybrid residual power series approach

Abstract

The current manuscript presents a mathematical model of dengue fever transmission with an asymptomatic compartment to capture infection dynamics in the presence of uncertainty. The model is fuzzified using triangular fuzzy numbers (TFNs) approach. The obtained fuzzy-fractional dengue model is then solved and analyzed through fuzzy extension of modified residual power series algorithm, which utilizes residual power series along with Laplace transform. Numerical analysis has also been performed in this study and obtained results are shown as solutions and residual errors for each compartment to ensure the validity. Graphical analysis depict the model’s behavior under varying parameters, illustrating contrasting trends for different values of and examining the impacts of transmission and recovery rates on dengue model in uncertain environment. The current findings highlighted the effectiveness of proposed uncertainty in epidemic system dynamics, offering new insights with potential applications in other areas of engineering, science and medicine.

Introduction

Dengue is one of the rapidly growing disease, transmitted by mosquitoes. Dengue cases have been increasing throughout the world. Approximately 3.9 billion people of 128 countries¹ are living in the dengue risk area. Globally, 390 million new cases of dengue infection are reported each year². Currently, there are 90 countries experiencing active dengue transmission in 2024. Still there is no approved vaccine or antiviral medication for this disease. According to world health organization, approximately 2.5 percent of dengue patients died each year¹. Dengue fever spread in an endemic area due to one of dengue viruses of different serotypes DENV-i, where i=1,2,3,4. Dengue viruses belongs to single-stranded RNA viruses and can spread through different type of mosquitoes including Asian Tiger mosquito, Aedes Albopictus, and day-feeding mosquito³.

Mathematical models are useful for understanding the dynamics of disease transmission to identify the variables that influence disease spread which ultimately helps in proposing disease control strategies^4,5. Mathematical modeling for investigating dynamics of infectious diseases has a long history. Kermack and McKendrick initially proposed SIR model for mathematical research on infectious diseases⁶. Esteva and Vargas reformulated this model in the dengue vector host dynamics for calculating variable and constant human populations^7,8. Since then, dengue disease transmission dynamics have been studied by many researchers. Gakkhar et al. studies dengue infection with and without awareness effect in Ref.⁹. Phaijoo and Gurung analyzed mobility effect on the spread of dengue in Ref.¹⁰. Agarwal and Verma have made significant contributions to epidemiological modeling by addressing various infectious diseases^11–13. Different scholars have studied various epidemic diseases for better control and prediction purposes^14–18.

It is observed that most of the work present in literature is analyzed using deterministic approach in modeling by considering fixed constant values of parameters. They assume that every individual could spread the disease and heal from it at a constant rate. However, such an assumption is in conflict with actual epidemic. There is always uncertainty in the parameters like transmission and recovery rates. In biological models, Zadeh was to first one to introduce uncertainty¹⁹ by developing fuzzy set theory. Mondal et al.²⁰ modified SIS epidemic model by considering disease transmission and treatment control parameters with uncertainties. De Barros et al. considered interactivity along with fuzziness in SI model of disease transmission^21–23.

A fractional derivative is generalization of integer order derivative. Fractional derivatives also play vital role in modeling and analysis of differential systems and provide better insights with memory effects²⁴. A fractional derivative approach is applied to many physical models, such as Fisher reaction-diffusion model²⁵, Lotka-Volterra population model²⁶, Schrodinger model²⁷, fuid flow model²⁸, cancer-tumor models^29,30, fuzzy fisher models^31,32 and Wu-Zhang model³³. Chatterjee and his co-authors have worked on developing epidemic models for measles and COVID-19 using fractional order derivatives^34–37. Ullah and his co-authors have explored innovative applications of fractional-order models to epidemic dynamics and policy interventions^38–42. Fuzzy-fractional differential equations (FFDEs) allow us to model and examine real-world problems including fractional order derivatives and uncertainty. Chellamani et al. applied fuzzy-fractional order approach to epidemic model for COVID-19⁴³. Qayyum and Tahir made a important contribution to the field by exploring a mathematical model for cancer tumor dynamics using multiple fuzzification approaches within a fractional environment⁴⁴. Qayyum et al. employed the extended He-Mohand algorithm within a fuzzy-Caputo framework to capture the dynamics of the system under uncertainty by modeling and analyzing a fuzzy-fractional chaotic financial system⁴⁵.

Motivated from above literature, a new model in fuzzy-fractional environment using triangular fuzzy numbers along with Caputo fractional derivative has been proposed for the analysis of epidemic dengue transmission. We apply this new idea to dengue transmission model and investigates some new insights into the dengue dynamics. According to the author’s knowledge, no one had previously used the concept of a fuzzy fractional to dengue dynamics, so this work is unique. For researchers working on epidemic models, the use of asymptomatic carriers and its analysis in fuzzy fractional environment will open up new doors of investigation. The remaining paper is structured as follows: in Section 2, the preliminaries are discussed. Section 3 focuses on the transmission dynamics of the dengue model. Section 4 provides a stability analysis for the reproduction number using the next-generation matrix method. Section 5 presents the fuzzy fractional modeling of the dengue virus. In Section 6, the application of the extended Residual Power Series Algorithm to fuzzy fractional dengue model is explored. Section 7 presents the numerical results and discussion of findings, and finally, Section 8 concludes the paper.

Preliminaries

Definition 1

Reference⁴⁵ The Caputo fractional derivative of a function is defined by:

1

Definition 2

Reference⁴⁵ Let be a piece-wise continuous function on the interval of exponential order , the Laplace transform of , is given by

2

and the inverse Laplace transform of is given by

3

The necessary properties of the Laplace transform and its inverse are summarize in the following Lemma.

Lemma 1

Reference⁴⁶ Let , be a piecewise continuous function on the interval . If

, and then

1. .

2. .

3. .

4. for .

5. , .

Definition 3

Reference⁴⁵ Let be a real set. Then, a fuzzy set in can be characterized by a membership function , where, : An r-level set of is = for

There are following conditions for a fuzzy set to be a fuzzy number:

1. is normal, that is, for we have .

2. is convex,that is min for all and

3. is semi-continuous.

4. Te set is compact.

Definition 4

Reference⁴⁵ A fuzzy number is categorized as a triangular fuzzy number (TFN) if it is defined by three distinct values where , forming a triangular shape. The membership function for this TFN is expressed as follows:

The interval form of TFN can be expressed as follows by using the r-Cut notation

4

where and represent the upper and lower bounds, respectively, for

Definition 5

Reference⁴⁵ A fuzzy number can also be expressed as , satisfying the following condition:

1. is a left continuous bounded monotonic increasing function.

2. is a left continuous bounded monotonic decreasing function.

3. for

Dengue model transmission

In an existing host-vector model for dengue transmission, human populations were traditionally divided into five compartments: exposed , susceptible , symptomatic (class of individuals who have a dengue fever and showing the symptoms), hospitalized , and recovered , and three mosquito populations including exposed , susceptible , and infectious . . The sum of total human individual population defined as:

However, in the present work, we have extended this model by adding a new compartment for asymptomatic individuals . This new compartment represents individuals who are infected with dengue but do not show symptoms. Despite being asymptomatic, these individuals contribute to the spread of the disease and can infect others.

By incorporating the asymptomatic class into the model, we aim to more accurately capture the dynamics of dengue transmission, as asymptomatic individuals play a significant role in the overall infection process. With the above discussion, we formulated a modified dengue model which is given as follows:

5

with

6

The biological description and values of parameters of model 5 are given in Table 1.

Table 1.

Biological description and values of parameters for dengue model.

Parameters	Description	Values	References
	Mosquito’s recruitment rate	3839.9	47
	Biting rate per mosquito per person	1.1971	47
	Transmission rate from infected human to susceptible mosquito	0.8541	47
	Mosquito’s natural death rate	0.0244	47
	Incubation rate of mosquito	0.7186	47
	Human’s recruitment rate	1525.1426	47
	Transmission rate from infected mosquito to susceptible human	0.6794	47
	Incubation rate of human	0.5550	47
	Human’s natural death rate		47
	Proportion of exposed to asymptomatic class	0.4450	Assumed
	Natural recovery rate of infected human	0.0154	47
	Recovery rate of hospitalized infected human	0.0840	47
	Recovery rate of asymptomatic humans	0.9846	Assumed
	Hospitalization rate of infected human	0.0904	47
	Death rate of human from disease	0.0969	47

Consider the feasible region

with

7

Lemma 2

Reference⁴⁷ The region given by is positively invariant for model (5) with the non-negative initial conditions (6).

Proof

The dengue model 5 leads to the following form:

and

Hence, , if and , if . So,

and

Thus, the region defined by is positively invariant. Furthermore, if and , then either the solutions will enter within a finite time, or will asymptotically approach and will asymptotically approach . Consequently, the regions defined by attract all solutions in .

Stability analysis

This section investigates the stability of dengue model for disease-free equilibrium (). By setting right side of (5) equal to zero, following expressions is obtained:

Reproduction number using the next generation matrix method we find reproduction number for dengue model (5). Considering the infected compartments in (5), specifically , , , , , and and following the guidelines outlined in Ref.⁴⁸, we derive the following matrices:

and

Let , , , and . The essential basic reproduction number for the model is determined through the spectral radius of the matrix , as defined by the following equation:

represents the average number of secondary infections occurring in both mosquitoes and human hosts due to one invective individual throughout their infectivity period. This parameter serves as an indicator of the potential spread of an emerging infectious disease within a community or population, and it helps determine the proportion of the population that should be vaccinated to achieve disease eradication. In biological models, , means infection will be uncontrollably spread in the population and hence will be more challenging to control epidemic. In the following lines, local stability of disease-free equilibrium (DFE) for the model (5).

Theorem 3

remains locally asymptotically stable for system (5) whenever .

Proof

The Jacobian matrix by evaluating the model (5) at the disease-free equilibrium , is:

From the matrix provided above, it can observed that the eigenvalues , , , and are clearly negative. The remaining four eigenvalues with negative real parts can be determined using the following equations:

where

The coefficients represented by for are positive for , , and , whereas may assume positive or negative depending on the value of . In the case of the disease-free equilibrium (DFE), where the value of the basic reproduction number should be less than 1, the last coefficient becomes positive when . Consequently, all coefficients for are positive, and they must conform the Routh-Hurwitz criteria. This criteria can be readily satisfied under the provided conditions , where for all . This condition ensures that .

Here

Therefore, the satisfaction of the Routh-Hurwitz criteria guarantees the local asymptotic stability of the dengue model described in (5) at the disease-free equilibrium .

Fuzzy-fractional modeling of dengue virus

This section focuses on modeling of fuzzy fractional dengue system. The specific modified dengue system (5-6) were examined.

The system (5) is modeled in fractional form by utilizing Definition 3, which is presented in the following equations. By using the definition 1, the given modified dengue system modeled in fractional form is given as

8

where is fractional parameter in a Caputo sense. By using Definitions 3-5, we have incorporated triangular fuzzy numbers (TFNs) approach in initia conditions to introduce uncertainty in the system. In parametric form, which can be written as:

9

Thus, the fuzzy-fractional modified dengue system as follows

10

with fuzzified conditions

11

Application of extended residual power series algorithm to fuzzy-fractional dengue model

In this section, we write in details the steps of applying the LRPS to solve fuzzy fractional modified dengue system (10,11)

where = . represents the upper bound solution and represents the lower bound solution.

After applying the Laplace transform the system (10) and (11) we get the following

12

Let we assume fractional truncated series of and as follows

13

Where are the unknown coefficients

Laplace residual functions are

14

To determine let we consider in (14) as follows

15

Since we obtain

16

Multiply (16) by . Then we solve the following system

17

to obtain the following outputs

18

In a same way unknown can be found.

with the fuzzified initial conditions

19

Results and discussion

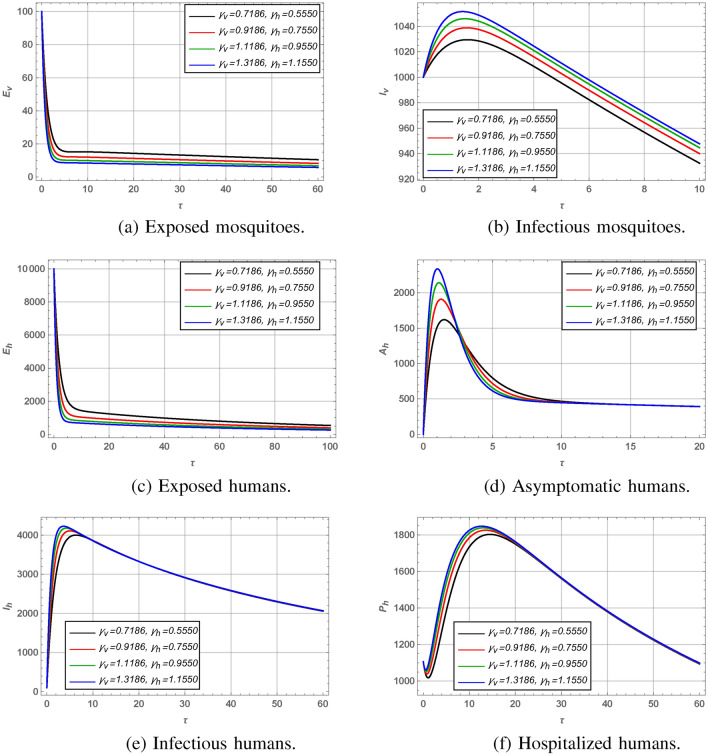
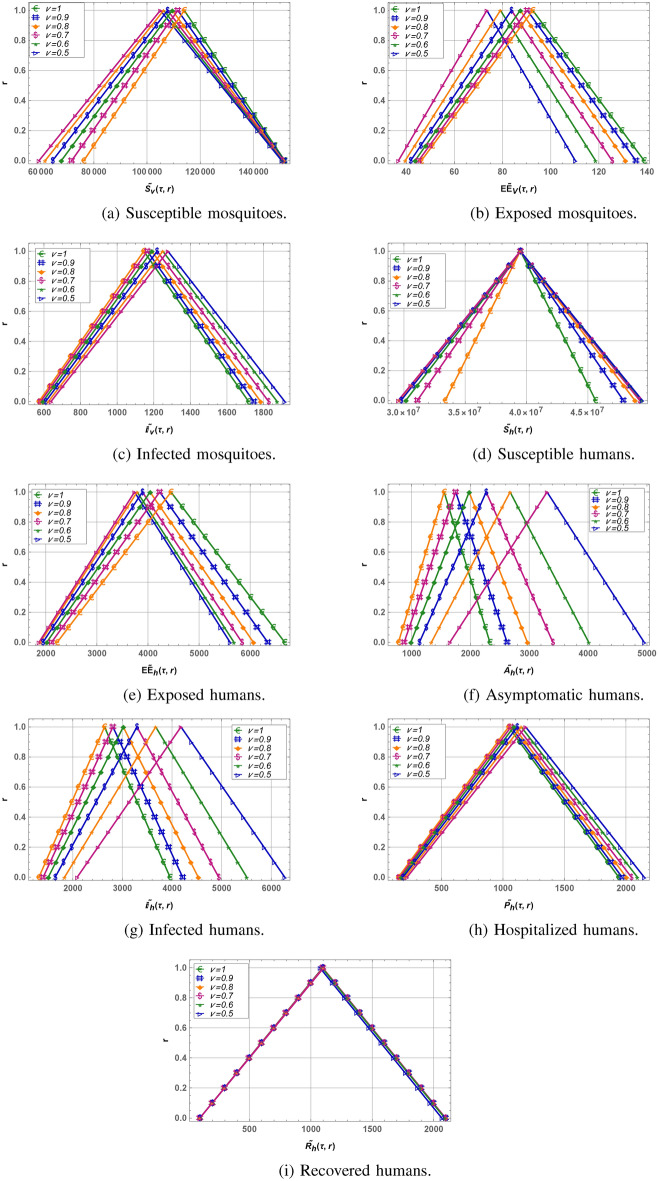
We modified an existing dengue model by adding an asymptomatic compartment to better represent individuals who are infected but do not show symptoms, yet still contribute to transmission. After this, we extended the model to a fuzzy-fractional framework to handle uncertainties and memory effects, using triangular fuzzy numbers to capture real-world variability. For the numerical analysis of the dengue fever model, we employed the Residual Power Series Method (RPSM) to derive approximate solutions and evaluate residual errors for various model compartments. Tables 2, 3 and 4 detail these approximate solutions and corresponding residual errors for the susceptible and infected classes of mosquitoes and humans, as well as for other compartments. Graphical analysis, presented in Figs. 1 and 2, explored the impacts of transmission and recovery rates on different model compartments, including exposed and infectious mosquito classes and exposed, infectious, asymptomatic, and hospitalized human classes. Figure 3 illustrates the lower and upper bounds of the fuzzy-fractional model for various values of the fractional parameter , showing the range of outcomes under uncertainty represented by triangular fuzzy numbers. These analyses provide valuable insights into dengue transmission dynamics and assess the robustness of model predictions under uncertain conditions.

Table 2.

RPS solution along with residual error for susceptible and infectious classes of mosquitoes and humans.

	RPS solution	Residual error	RPS solution	Residual error	RPS solution	Residual error	RPS solution	Residual error
0.	100000	0	1000	0		0	100	0
0.1	100140	0	1004.48				338.898	0
0.2	100279		1008.46			0	564.278	0
0.3	100418	0	1011.98				776.883
0.4	100557		1015.08				977.416
0.5	100695		1017.79				1166.54
0.6	100833		1020.15				1344.89
0.7	100970		1022.17				1513.04
0.8	101107		1023.9				1671.57
0.9	101244		1025.35				1821.01
1	101380		1026.54				1961.84

Table 3.

RPS solution along with residual error for Asymptomatic , Hospitalized and Recovered classes of humans.

	RPS solution	Residual error	RPS solution	Residual error	RPS solution	Residual error
0.	0		1106		1095	0
0.1	286.415		1088.15		1217.78
0.2	532.84		1072.69	0	1365.47
0.3	743.741		1059.48		1534.57
0.4	923.129		1048.35		1721.97
0.5	1074.6		1039.17		1924.93
0.6	1201.38		1031.79		2141.04
0.7	1306.35		1026.1		2368.15
0.8	1392.1		1021.98		2604.4
0.9	1460.93		1019.31		2848.15
1	1514.93		1017.98		3097.95

Table 4.

RPS solution along with residual error for Exposed classes of mosquitoes and humans.

	RPS solution	Residual error	RPS solution	Residual error
0	100	0	10000	0
0.1	92.8948	0	9539.36
0.2	86.3563		9103.92
0.3	80.3411		8692.29
0.4	74.8085		8303.14
0.5	69.7213		7935.23
0.6	65.0449		7587.39
0.7	60.7473		7258.5
0.8	56.7991		6947.51
0.9	53.173		6653.45
1	49.8438		6375.36

Fig. 1.

Effect of biting rate per person per mosquito on different classes of dengue model.

Fig. 2.

Effect of incubation rates of mosquitoes and humans on different classes of dengue model.

Fig. 3.

Fuzzy lower and upper bound solutions of fuzzy-fractional dengue model at different fractional points.

Conclusion

The objective of this research is modeling and simulation of fuzzy-fractional dengue virus by considering asymptomatic class of individuals. In current study, we combine fuzzy logic with fractional calculus to incorporate uncertainty along with memory effects in the dengue model. The Caputo sense of time-fractional derivative is employed for capturing memory effect while triangular fuzzy numbers (TFNs) approach is used for incorporating uncertainty in the dengue model. To solve and analyze obtained model, residual power series algorithm is hybridized with Laplace transform, and error analysis is illustrated through numerical tables. It is observed that errors are ranging from to , and to , for mosquito and human classes respectively. From this, it can be observed that the proposed methodology is providing convergent solutions for dengue model. The impact of fractional parameter on the dengue system profile concerning the r-cut are analyzed. As the r-cut approaches to 1, the system solution becomes less-fuzzified, and eventually transitioning into a crisp form at . Moreover, the behavior of transmission and recovery rates are examined across various classes of mosquitoes and humans in the study. In conclusion, the modeled fuzzy-fractional dengue system offers deeper insights for better understanding, predictions and control assessments of dengue transmission dynamics. Furthermore, proposed methodology holds promise for addressing various research areas in enhancing our understanding of infectious diseases, guiding public health responses, and ultimately saving lives by preventing and controlling outbreaks.

Author contributions

M. Q. Conceptualization; Methodology; Validation; Writing, Review and Editing; Supervision. Q.F. Code Writing; Visualization; Validation; Writing Original Draft. A.A. Analysis; validation; Writing, review and editing of manuscript; Software. M.K.H. Analysis; validation; Writing, review and editing of manuscript; Software.

Data availibility

The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.