CLARE-XR: explainable regression-based classification of chest radiographs with label embeddings

Abstract

An automatic system for pathology classification in chest X-ray scans needs more than predictive performance, since providing explanations is deemed essential for fostering end-user trust, improving decision-making, and regulatory compliance. CLARE-XR is a novel methodology that, when presented with an X-ray image, identifies the associated pathologies and provides explanations based on the presentation of similar cases. The diagnosis is achieved using a regression model that maps an image into a 2D latent space containing the reference coordinates of all findings. The references are generated once through label embedding, before the regression step, by converting the original binary ground-truth annotations to 2D coordinates. The classification is inferred minding the distance from the coordinates of an inference image to the reference coordinates. Furthermore, as the regressor is trained on a known set of images, the distance from the coordinates of an inference image to the coordinates of the training set images also allows retrieving similar instances, mimicking the common clinical practice of comparing scans to confirm diagnoses. This inherently interpretable framework discloses specific classification rules and visual explanations through automatic image retrieval methods, outperforming the multi-label ResNet50 classification baseline across multiple evaluation settings on the NIH ChestX-ray14 dataset.

Introduction

Chest X-Ray (CXR) scans play a vital role in the diagnosis of thoracic pathologies, being the most widely used imaging technique due to their affordability and convenience. Consequently, clinicians are asked to review an increasing number of scans during each shift¹. Given the complexity of the analysis, implementing a computer-aided diagnosis system as a preliminary screening tool can not only alleviate this burden but also help prevent misdiagnoses. Several studies have addressed this multi-label classification task, where multiple findings can be associated with a single image². These studies highlight the challenges posed by the increased number of labels and their interdependencies³. As the number of classes grows, their distinction becomes even more intricate, especially when acquiring sufficient training images for rare instances is not possible. State-of-the-art Deep Learning (DL) approaches are often model-centric, seeking to maximize the classification performance of off-the-shelf architectures on a given dataset. They typically embed images into high-dimensional features to extract relevant information, paired with their binary encoded ground truth (GT). Some authors argue that using binary vectors to designate the presence or absence of classes complicates the measurement of label correlation and encourages overfitting due to the extreme nature of the binary representation⁴. Furthermore, the high non-linearity of DL models results in opaque internal decision processes, making them less suitable for the clinical setting. This opacity prevents healthcare professionals from comprehending the reasoning behind specific diagnoses, hindering their validation of the model’s accuracy. Consequently, the lack of explanatory outputs fosters distrust among clinicians, discouraging the adoption of these models as a second opinion, while the current eXplainable Artificial Intelligence (XAI) methods remain insufficient for high-risk practical applications⁵.

The objective of this work is to provide a more data-centric approach to the problem, aiming to enhance the model’s learning capability and explainability by refining and reshaping the available dataset. In addition to image embedding, this study employs label embedding to encode the GT into a latent space, transforming initial binary vectors into a lower-dimensional Euclidean space. This enables the transition from a standard multi-label classification to a regression problem - a more transparent process where the model predicts continuous coordinates to further elucidate how and why decisions are made by positioning each image’s prediction in the reference space. This method provides physicians with instance-specific textual and visual justifications based on both the image and label features learned by the model. The contributions of the study are the following:

• Learning of a two-dimensional (2D) reference space capable of representing the image labels via embeddings.

• A data-centric regression-based approach for multi-label classification of CXR scans.

• An inherently interpretable set of rules to reach that multi-label classification.

• Visual explanations that exhibit similar cases, based on the image and GT labels’ positioning in the reference space.

Related work

In the field of computer vision, there is an extensive body of literature on image embedding (how to represent an image), but significantly less work has focused on label embedding (how to represent a class). Publications on label embedding for image classification are limited, using primarily natural image datasets paired with textual descriptions. Early work on this topic redefined original class labels into vectors, and then created two separate spaces: one for the image features and another for the label attributes⁶. By embedding each image in the feature space and each class in the attribute space, the “compatibility” between these embeddings can be estimated to make predictions, given that correct classes will ideally rank higher in compatibility than incorrect ones. The work in³ built upon this idea by ranking labels according to their relevance to the input image, in order to position semantically similar labels closer together in the continuous embedding space. Unlike the previous approach that compares two embedding spaces, this model transforms an image into the same space, positioning it near its associated labels. Another publication follows the same logic, jointly projecting features and labels into a latent space to model their interactions and learn label correlations⁷. Alternatively, one may also leverage label semantic information in spatial attention mechanisms that identify relevant image regions^8,9, allowing the model to focus on image feature regions with more pronounced label interdependencies. Some of the previous ideas have been combined into a novel approach¹⁰. Images and labels are fed into individual encoders, resulting in each image being described with a set of patch embeddings and a set of label embeddings. The method learns to associate image regions with labels by modeling their similarities, offering a tool to visualize the learned label concepts. The novelty of this publication lies in its interpretable outcome, for understanding the interaction between labels and patches. This opened the door for XAI-driven approaches using label embeddings, such as the proposed one. Prior to this, only one paper mentioned interpretability as an advantage of using label embeddings to identify meaningful similarities between classes⁴.

A more recent trend started using label embeddings for multi-label CXR classification, mostly as a way of learning pathology co-occurrence. The works in^11,12 explore the dependencies between findings to enhance classification performance. The image feature learning process is guided by the label correlation information derived from the label embeddings. Specifically, the relationship between pathologies is translated into a set of classifier scores that weight the extracted image features to produce the final prediction. The concept of using label embeddings for self-attention operations has also been extended to more complex classification architectures, Vision Transformers (ViTs), due to their promising results^13,14. Such studies introduce learnable label embeddings to detect and match class-specific image features. To the best of the authors’ knowledge, there is only publication addressing both label embeddings and XAI in CXR classification, though not in conjunction¹⁵. There, the proposed explanations are merely heatmaps highlighting the most relevant image regions for the predicted class, which is by far the most common XAI approach in this field^16–20. However, it is difficult to evaluate when there is no spatial GT available. An innovative alternative mimics clinical practice where radiologists look for cases with similar findings to support and explain their decisions^21,22. In this approach, image retrieval automatically finds similar cases within the dataset, allowing the end-user to compare these cases to validate the diagnosis. The present publication integrates label embedding and image retrieval concepts to build a more inherently interpretable framework. The objective is to avoid complex architectures while maintaining classification performance, and provide a 2D reference space for the GT that any user or developer can easily analyze. This is accomplished by favoring lower-dimensional label embeddings, as opposed to the state-of-the-art studies that increase label dimensions. The reference space, representing both the GT label embeddings and the predictions derived from image features, facilitates the understanding of the final decision-making process and the retrieval of similar images to further justify the model’s decisions.

Methodology

Dataset preprocessing

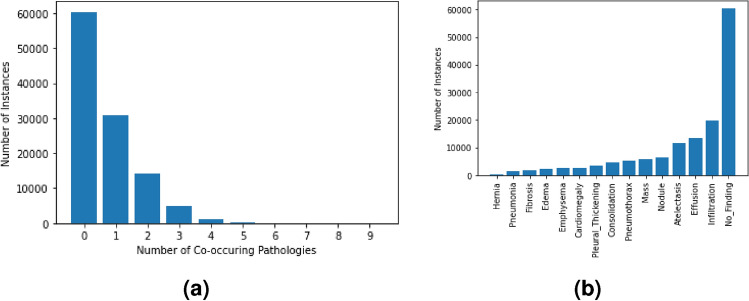
The NIH ChestX-ray14 (CXR14) is a large public dataset of 112,120 frontal CXR scans of 30,805 patients, annotated with one or more of 14 findings¹. The images have a maximum of 9 co-occurring pathologies, as shown in Fig.  1a. The total number of instances per pathology is represented in Fig. 1b, in which the No Finding observation is assigned if none of the pathologies are present. Both figures evidence the high imbalance of the annotations. Regarding preprocessing steps, this study considers a subset of the CXR14 data consisting of the 110,486 instances with up to 3 co-occurring pathologies, which is the most common scenario. In other words, all images annotated with 4 or more co-occurring findings were discarded due to severe under-representation. Following the same logic, and minding the reduced number of samples for the minority findings (e.g. hernia and pneumonia), the initial 14 pathologies were grouped into the 5 broader categories listed below, inspired by previous work²³. From here on, these 5 classes were considered in alternative to the 14 pathologies, meaning each original GT annotation was defined as a 5-class vector [Ca, Pa, Pn, Pl, Ot], where every element is assigned the value 1/0 if the corresponding pathology is present/absent. The available data was split into five folds, without patient overlap and preserving the original pathology proportions. Table 1 describes the resulting 26 annotation combinations.

• Cardiac pathologies (Ca): cardiomegaly.

• Parenchymal lesions (Pa): infiltration, fibrosis, atelectasis, mass, nodule, pneumonia, consolidation, and/or edema.

• Pneumothorax (Pn): pneumothorax.

• Pleural lesions (Pl): effusion, and/or pleural thickening.

• Other lesions (Ot): hernia, and/or emphysema.

Fig. 1.

Original distribution of the CXR14 dataset. Figure (a) shows the frequency of 0, 1 or of more co-occurring pathologies, while Figure (b) shows the frequency per pathology.

Table 1.

Number of instances per combination in the selected CXR14 subset.

Combination	Counts	Combination	Counts	Combination	Counts	Combination	Counts
No Finding	60,361	Ot	1,003	CaPaPl	289	CaPn	9
Pa	28,440	PaOt	576	PaPnOt	200	CaPaPn	6
PaPl	7,148	CaPl	532	PlOt	164	CaPnPl	3
Pl	5,332	CaPa	527	PaPlOt	100	CaPnOt	2
Pn	2,194	PnPl	516	PnPlOt	60	CaPaOt	2
PaPn	1,225	PnOt	339	CaOt	21
Ca	1,093	PaPnPl	333	CaPlOt	11

Framework

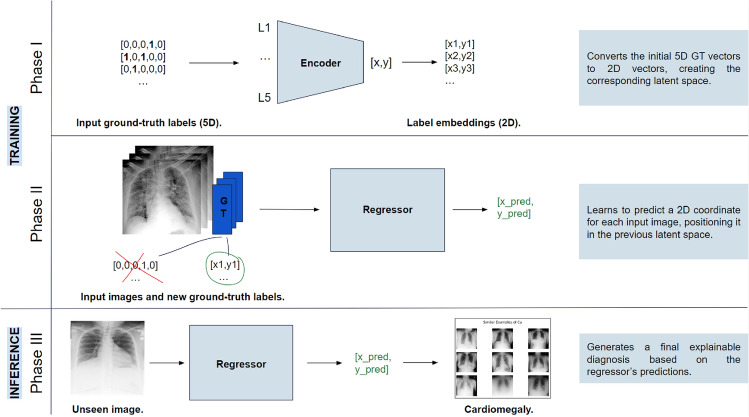
The CLARE-XR methodology intends to clarify CXR classification by providing explanations based on the presentation of similar cases along with the final decision. Each input image is passed to a regression model that predicts its corresponding [x, y] coordinates, positioning the scan within a latent space that contains the reference coordinates for all labels. The classification of each scan is determined by its relative position to these reference points, while the explanation strategy considers its relative position to a known set of training images in the same space to retrieve matching instances.

The latent space and the regressor model are obtained in Phase I and Phase II of the workflow, which correspond to the training phases. In Phase I, an autoencoder is trained and employed once, before the regression phase, to generate label embeddings that encapsulate the same information as the original GT vectors for the 5 classes (hereon, 5D GT). By transforming 5D GT vectors into 2D vectors, the autoencoder creates a latent space that contains the reference coordinates for all annotations. Note that this phase does not consider any images yet, and looks exclusively at the labels to produce their corresponding new coordinates. The regressor is trained in Phase II, where each image is associated with its new 2D GT resulting from the encoder in Phase I. This way, the regressor learns to map each image into a 2D coordinate in the same space as the references.

Phase III corresponds to the inference stage, which employs the trained regressor to predict the coordinate of an inference image and then attributes specific class(es) to that image by comparing and associating its coordinates to the label reference coordinates. This step combines distance measures and a set of classification rules to reach a final decision, which allow a deeper understanding of why an image is assigned to a certain class. The final decision and its positioning in the latent space are also crucial for the explainability component of the system to retrieve similar cases from a known set of training images. The framework is summarized in Fig. 2.

Fig. 2.

Framework of the CLARE-XR methodology.

Phase I—label autoencoder

The autoencoder phase seeks to create a new way of representing the 5D GT labels. This way, the GT vector of 5 binary elements will be represented as a vector with only 2 real-valued elements, and that will serve as a reference for the following phases. Firstly, a dummy training dataset is generated, containing all possible binary combinations of the 5 classes, except the No Finding annotation. As mentioned previously, only instances with 1, 2, or 3 co-occurring pathologies were considered to exclude rare cases and reduce the complexity of the approach, yielding a total of 25 annotation combinations (see Table 1). These 25 combinations were replicated 1000 times, resulting in a balanced training set of 25,000 instances. The validation and test sets used in this phase are composed of a single fold of the CXR14 data, keeping the original distribution of No Finding, single-class, and multi-label annotations.

This data was fed to an autoencoder architecture - a multi-layer perceptron whose encoder comprises 5 linear layers (each followed by ReLU activation), similar to the decoder. The encoder takes each vector with 5 positions (L) and encodes it to a latent size of 2, while the decoder reconstructs that representation back to 5 positions ($\widehat{L}$). Ideally, a proficient autoencoder is achieved if the reconstruction loss is nearly null, meaning that the input and output vectors are equal, and the model is capable of delivering accurate 2D encoded representations of the input vector. The Mean Squared Error (MSE) loss function $\frac{1}{N}{\sum }_{i=1}^N{(L_i-{\widehat{L}}_i)}^2$ was used to minimize the difference between the input and reconstructed label data (i.e. L and $\widehat{L}$). By the end of this phase, all possible labels are now translated by the encoder to a unique 2D vector, representing the present and absent pathologies, and used as a GT reference for the following regression phase.

Phase II—embedding-based regression

The regression phase pairs each available image with its new 2D GT representation resulting from the Phase I encoder. Note that those label embeddings are composed of [x,y] coordinates, which were min-max normalized to fit in a 0-1 scale. This aspect allows for a more efficient optimization routine of the Phase II regressor.

Previous work compared multiple DL models that could be used for transfer learning on CXR14, and concluded that ResNet demonstrated the greatest potential for fine-tuning in this domain²⁴. As such, a ResNet50 architecture was employed here to predict a pair of coordinates $[x_{\mathit{pred}},y_{\mathit{pred}}]$ per image, modifying the last fully-connected layer to consider these 2 real-valued output nodes. The model was pre-trained on ImageNet weights, so the input images were normalized initially to a 0-1 range and then standardized using ImageNet’s mean and standard deviation values. All available scans were resized to 256$\times$256 pixels to accelerate the training routine. The training data was also augmented to double the samples through soft random affine transformations (i.e. 5 degrees of rotation and 3 degrees of shear). Finally, a five-fold cross-validation scheme was implemented in all experiments. Note that each label combination has a specific reference embedding coordinate E, and so the goal of Phase II is to obtain a predicted embedding $\widehat{E}$ as close to that reference as possible. For example, an image labeled with cardiac and pleural lesions should be positioned in the reference embedding coordinates of that precise combination CaPl. The MSE loss function $\frac{1}{N}{\sum }_{i=1}^N{(E_i-{\widehat{E}}_i)}^2$ was used for such purpose.

Phase III—multi-label classification and explainability

The third phase addresses both the multi-label embedding-based classification and the XAI component in the inference stage of the process. Using the trained regressor from Phase II, each image is placed in the reference space using its predicted coordinates. Phase III then decides which pathology classes are present in an image to reach a diagnosis, based on its location and neighboring reference coordinates. This is achieved by measuring the Euclidean distance of each predicted coordinate to all 26 references obtained in Phase I. An instance-wise list of those distances in ascending order arranges the references from closest to farthest. Several sets of classification rules were proposed and evaluated to reach the most accurate diagnosis, minding that list. These rules can be split into two categories: rules based on the closest reference (top 1) and rules based on the three closest references (top 3). The latter assess if the neighboring references add further valuable insights that potentiate the method’s efficiency. The proposed sets of rules are as follows:

• Set of Rules 1 (top-1 approach): classifying an instance with the label(s) of its closest reference.

• Set of Rules 2 (top-3 approach): acts as a “control” experiment, assuming that all classes in all top-3 combinations are present in the image.

• Set of Rules 3 (top-3 approach): narrows down the results by considering only the recurrent classes (i.e. those that appear in at least 2 of the top-3 combinations).

• Set of Rules 4 (top-3 approach): refines these results by classifying an instance with the label(s) of its closest reference, plus adding the recurrent ones. This attributes a higher importance to the top-1 result (i.e. the most probable outcome), without discarding the surrounding information.

  Note that in all top-3 experiments, it is not logical to consider the No Finding reference if it is found in the second or third-closest references, as it cannot be a “recurrent pathology”. In these cases, that reference was not considered and replaced by the fourth-closest reference. Furthermore, any instance whose top-1 combination is No Finding is automatically attributed that decision, given the ease of the model in identifying normal scans.

Phase III identifies which set of rules maximizes classification performance, but it should also obtain coherent visual explanations that support the classification outcome. To fulfill this goal, the proposed XAI strategy takes advantage of the training set to retrieve similar instances with specific findings. By comparing the inference scan with others whose GT is known, the physicians can validate if the predicted pathologies are present in the case at hand.

By the end of Phase II, the regressor has positioned the training set images in the latent space, clustering those that share similar features in the same neighborhood. During inference, when presented with a new unseen image, CLARE-XR assigns the relevant class(es) to it. The XAI component then complements the decision by identifying the training set scans that most closely resemble the specific findings in the inference scan, given the predicted outcome. This approach retrieves e.g. the 9 images closest to the predicted coordinate, selecting the training set images that share the most features learned by the model. Consequently, these examples are expected to be similar to the inference scan, revealing the same anatomical cues and lesion types. For an easier understanding, this strategy will be further discussed with examples.

Results and discussion

This section analyses the results to evaluate the method’s ability to classify each scan in an explainable manner. The algorithms presented in this work were implemented using the PyTorch framework and an Nvidia GeForce GTX 1080 GPU (8 GB).

Baseline classifier

Before discussing the proposed methodology, it was crucial to establish a baseline that reflects the typical state-of-the-art approach^17,25. This baseline is a 5-class multi-label classifier, trained on the same images as the Phase II regressor and under identical conditions regarding data preprocessing/augmentation techniques, cross-validation scheme, etc., to ensure a fair comparison. The classifier is also composed of a ResNet50 pre-trained on ImageNet weights, whose last layer of the network is a fully-connected layer with 5 nodes, followed by sigmoid activation to get a probability prediction per class. A Binary Cross Entropy (BCE) loss function was used to approximate the predicted classes to the ground truth annotations.

The output probabilities were used to plot the Receiver Operating Characteristic (ROC) and Precision-Recall (PR) curves. These curves served as tools for determining class-specific optimal thresholds under two distinct evaluation criteria. The first aimed to maximize the true positive rate while minimizing the false positive one, whereas the second focused on maximizing the F1-score. Based on the selected class-specific thresholds, the predictions were binarized to evaluate several metrics, including accuracy, precision, recall, and F1-score. The performance of this baseline classifier is disclosed in Table 2. Note that the 26 possible combinations of labels are not considered in this analysis; instead, the evaluation follows the common multi-label approach, treating the 5 classes independently. As such, the class-wise values are obtained minding all instances predicted as positive for a given class, regardless of whether they are single-pathology or multi-label combinations.

Table 2.

Performance metrics of the multi-label baseline classifier.

Class	Accuracy		Precision		Recall		F1-score
	B_ROC	B_PR	B_ROC	B_PR	B_ROC	B_PR	B_ROC	B_PR
Ca	0.803	0.971	0.084	0.348	0.785	0.347	0.152	0.348
Pa	0.652	0.677	0.505	0.540	0.647	0.540	0.567	0.540
Pn	0.807	0.938	0.147	0.297	0.694	0.297	0.242	0.297
Pl	0.777	0.862	0.340	0.472	0.743	0.471	0.466	0.471
Ot	0.736	0.963	0.057	0.166	0.696	0.166	0.105	0.166
MEAN	0.755	0.882	0.226	0.365	0.713	0.364	0.307	0.364

Results obtained for all instances predicted as positive for a given class, regardless of whether they are single-pathology or multi-label. The precision, recall, and F1-score values were calculated using class-specific optimal thresholds, optimized based on the ROC curve (B_ROC) or the PR curve (B_PR).

The results obtained based on the ROC curve indicate a low precision and high recall scenario, leading to low F1-scores. This is typical in state-of-the-art classification approaches which favor false positive results over false negative ones²⁶. Examining the class-specific values reveals that the F1-score tends to reflect the dataset’s distribution. More prevalent classes (e.g. Pa, Pl) typically achieve higher F1-scores compared to underrepresented ones (e.g. Ot, Ca). In contrast, results derived from the PR curve demonstrate a more balanced trade-off between precision and recall, deviating from the F1-score’s dependence on class distribution. Overall, the optimization using the PR curve improved accuracy by 12.7% and F1-score by 5.7% compared to the ROC curve optimization, primarily by increasing precision at the expense of recall.

Label autoencoder

The dummy training set was used in this scenario due to the pathology correlation and imbalance verified in the original CXR14 distribution¹. Using the original set could cause the autoencoder to learn when two or more pathologies co-occur more often and shortcut the learning process based on that information, leading to biased reference embeddings. CLARE-XR prevents that by creating a fully-balanced dummy dataset with all possible combinations with up to 3 pathologies. The number of zeroes surpasses the number of ones given the binary nature of the 5-element vectors, and for this reason, it was not necessary to include the No Finding null vector during training. The remaining combinations were enough to learn that specific reconstruction.

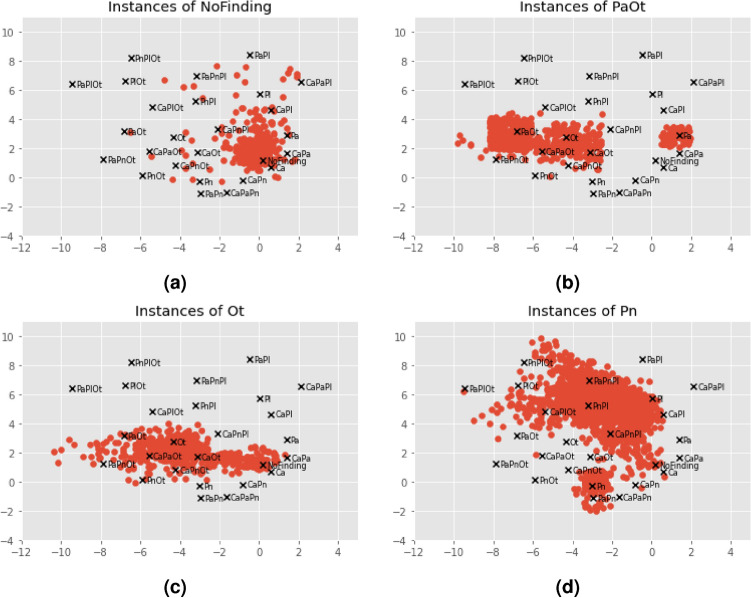
The best way to evaluate the quality of the encoder and its resulting 2D representations is to consider the decoder’s outputs. In other words, the embeddings are most likely a good representation of the original label vectors if the reconstructed vectors are similar to the input ones. The autoencoder presents low MSE values ($4.867\times {10}^{-7}\pm 0.021\times {10}^{-7}$), indicating that L and $\widehat{L}$ are similar. The previous metrics were also employed in this context to demonstrate the perfect reconstruction ability of the autoencoder: precision, recall and F1-score of $1.000\pm 0.000$. This was expected due to the limited number of combinations to reconstruct. It is now fundamental to inspect the resulting encoder’s representations and position them in their new latent space. Each of the 26 annotation combinations is handled independently by the encoder and assigned a distinct 2D coordinate shown in Fig. 3. The 5 single-class and No Finding embeddings are marked with a colored dot, while the remaining 20 multi-label embeddings are marked with black crosses. This plot serves as a guide for the following phases. While this cannot be generalized for all classes, certain findings are attributed to specific regions in the latent space. For instance, Pl findings occupy the top region of the plot, Ot findings occupy the left region, and Ca findings are concentrated in the lower right corner. In some cases, combinations of two pathologies are positioned in between the two corresponding single-class references (e.g. CaPa in between Ca and Pa). Note that a multi-label annotation is not guaranteed to be near its single-class references, and that this is not a requirement, since the autoencoder has no notion of what a pathology is or what are the common features across combinations (it merely encodes the vectors).

Fig. 3.

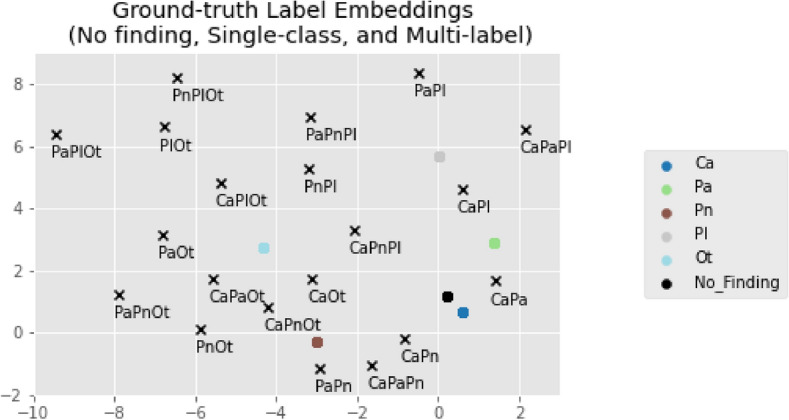
Reference label embeddings obtained by the Phase I encoder. The No Finding and single-class GT coordinates are plotted in colored dots, while the remaining multi-label combination coordinates are marked with black crosses.

Embedding-based regression

The regression model is optimized to decrease the distance between the predicted embedding coordinates and the GT coordinates, being initialized with the baseline classifier’s weights to be fine-tuned. It achieved an overall MSE of $2.015\pm 0.014$, and while the combination with the lowest MSE matches the most represented combination (No Finding), the opposite cannot be concluded. On the other hand, note that a high MSE value is indicative of a poor prediction, but a low MSE does not guarantee a perfect prediction - e.g. a Ca instance can be plotted on top of the No Finding reference and still obtain a low MSE.

Given the trained model, one may visualize the predicted coordinates per combination on top of the reference space. Figure 4 exemplifies the scattering of the predicted embeddings for the No Finding, PaOt, Ot and Pn combinations. In agreement with the MSE analysis, the 60 thousand No Finding instances form a dense cloud around the correct reference coordinate, meaning that the model easily identifies such cases. Note that the predictions do not need to match the reference coordinate exactly; they only need to fall within the area where the nearest coordinate remains the reference point. The remaining single-class and multi-label combinations maintain this tendency to group around the corresponding reference, but their predictions also spread out near other references that have at least one of their individual classes, or even to the No Finding one. A clear example of that is the PaOt dispersion in Fig. 4b, whose coordinates mostly gather around the PaOt, Ot and Pa references. These patterns are more defined when dealing with highly represented combinations, but even the under-represented ones are not randomly placed and present such predisposition.

Fig. 4.

Predicted embedding coordinates obtained by the Phase II regressor for different combinations. The GT references are marked with black crosses. All predicted coordinates whose GT matches the combination in the title are marked with red dots.

There are two single-class combinations worth discussing given their particularities - Ot and Pn in Figs. 4c and 4d, respectively. The Ot class aggregates lesions that do not fit any of the other classes, meaning that their associated pathologies (hernia and/or emphysema) do not share common characteristics. Such aspect makes it difficult for the model to learn their specific features and recognize their presence in an image. This is aggravated by the fact that Ot is the less represented single-class combination, resulting in a broader dispersion cloud. Even so, the predicted coordinates are located in areas whose closest reference combinations contain the Ot class. The Pn case is also interesting because even though it constitutes an independent class, pneumothorax can be interpreted as a pleural lesion (Pl class). That is reflected in the plot, where a significant percentage of the predictions is located in between the Pn and Pl references, i.e. in a region whose multi-label references contain both Pn and Pl. This is indicative of the partially shared features between the two classes. The same is not verified in the Pl scatter plot, perhaps due to a higher representation that facilitates learning the specific Pl features.

Multi-label classification

This phase of the methodology followed the same evaluation strategy as the multi-label baseline. Table 3 shows the results obtained for all classes, where the distance between each prediction and the closest references is taken into consideration to reach a final decision, depending on the considered set of rules. To identify the most suitable approach for this particular classification task, the authors prioritized evaluating the precision-recall trade-off using the F1-score. This choice stems from the limitations of the accuracy metric when applied to imbalanced datasets. Consequently, the F1-score served as the key metric for assessing and determining the efficiency of the proposed method.

Table 3.

Performance metrics of the CLARE-XR classification methodology.

Class	Accuracy		Precision		Recall		F1-score
	R1	R2	R1	R2	R1	R2	R1	R2
Ca	0.700	0.475	0.025	0.026	0.328	0.622	0.047	0.051
Pa	0.634	0.631	0.477	0.481	0.418	0.644	0.446	0.551
Pn	0.943	0.891	0.355	0.224	0.347	0.596	0.351	0.326
Pl	0.872	0.794	0.510	0.369	0.680	0.808	0.538	0.507
Ot	0.974	0.961	0.424	0.314	0.473	0.609	0.447	0.414
MEAN	0.825	0.750	0.358	0.283	0.449	0.656	0.375	0.370

Class	Accuracy		Precision		Recall		F1-score
	R3	R4	R3	R4	R3	R4	R3	R4
Ca	0.558	0.499	0.028	0.027	0.541	0.608	0.052	0.052
Pa	0.630	0.629	0.470	0.469	0.426	0.434	0.447	0.451
Pn	0.956	0.943	0.500	0.382	0.320	0.454	0.390	0.415
Pl	0.878	0.870	0.529	0.504	0.663	0.688	0.588	0.582
Ot	0.975	0.971	0.446	0.395	0.499	0.529	0.471	0.452
MEAN	0.799	0.782	0.394	0.355	0.490	0.543	0.390	0.390

Results obtained for all instances predicted as positive for a given class, regardless of whether they are single-pathology or multi-label. The precision, recall, and F1-score values were calculated based on the predictions obtained by each set of rules (R).

The set of rules 2 constitutes a “control” experiment in which all classes in the top-3 closest references are included in the final decision. As expected, it produces the most similar results to the multi-label baseline, achieving very low precision and higher recall, and thus privileging false positive results over false negative ones. Ideally, the remaining approaches should balance both metrics to fight this trade-off and increase the overall F1-score. All proposed sets of rules are successful at surpassing the precision and F1 values obtained by the multi-label classifier, partially compromising the recall. This is valid even for the straightforward top-1 approach in the set of rules 1. Both sets of rules 3 and 4 maximize the F1-score, revealing that the top-3 approaches are beneficial in this context. Considering the neighbor references adds useful information regarding recurrent pathologies and reduces the error when compared to the “hard” classification approaches of the baselines or top-1 rule. The set of rules 4 not only maximizes the F1 value, but also increases the recall by 5.3% in comparison to the set of rules 3, with a precision decrease of only 3.9%. For this reason, it was selected as the best approach for the task at hand.

Compared to the baseline, applying the set of rules 4 resulted in a 12.9% increase in precision and an 8.3% increase in F1-score with ROC-based optimization, or a 17.9% increase in recall and a 2.6% increase in F1-score with PR-based optimization. The CLARE-XR was the most efficient in classifying the presence of Pn, Pl and Ot lesions, consistently achieving higher F1-scores compared to the baseline.

While these results already highlight the superiority of the proposed method, additional experiments were conducted to enable a more thorough and equitable comparison with the baseline model, minding specifically the precision-recall trade-off. To compare the performance of both approaches at identical precision levels, the precision values achieved by the set of rules 4 were fixed, and the corresponding recall values for the baseline were obtained. This allows a direct comparison of the recall between the CLARE-XR method and the baseline under equivalent precision conditions. Similarly, the recall values achieved by the set of rules 4 were fixed, and the corresponding precision values for the baseline were measured, enabling a comparison of precision under identical recall conditions. These results are displayed in Table 4, and demonstrate that CLARE-XR consistently outperformed the baseline across these additional evaluation scenarios as well.

Table 4.

Performance metrics of the multi-label baseline, fixing the recall or precision obtained by the best setting of the CLARE-XR methodology (set of rules 4, R4).

Class	Recall (fixed by R4)	Precision	F1-score	Precision (fixed by R4)	Recall	F1-score
Ca	0.608	0.152	0.243	0.027	0.990	0.053
Pa	0.434	0.568	0.492	0.469	0.752	0.577
Pn	0.454	0.230	0.305	0.382	0.195	0.258
Pl	0.688	0.361	0.473	0.504	0.426	0.462
Ot	0.529	0.083	0.144	0.395	0.002	0.004
MEAN	0.543	0.279	0.332	0.355	0.473	0.271

In conclusion, the relative superiority of the proposed model leads to believe that CLARE-XR is effective in associating certain regions of the reference space to specific pathologies, and that this improvement is not simply due to the shift from the typical multi-label classification approach to an embedding-based multi-class one. Additionally, a typical multi-class approach would be limited to the already-existing combinations (i.e. its outcome will always select a combination previously seen in the training set), while the multi-label baseline and the proposed method are more flexible in that aspect (i.e. it is possible to get an output combination that was not present in the training set).

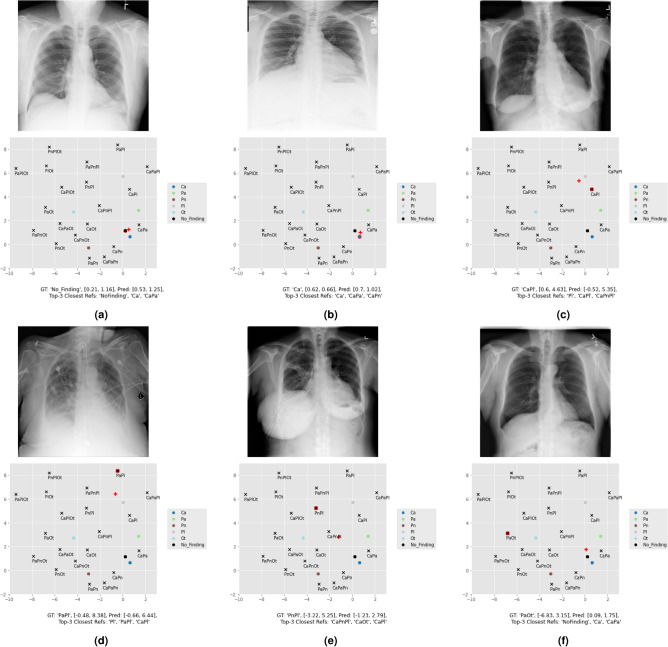
Figure 5 shows the predicted coordinates for multiple inference images, whose classification outcomes are discriminated in Table 5. In specific, Fig. 5a–c present a No Finding, a single-class, and a multi-label instance in which the proposed set of rules 4 correctly classified the images. These confirm that in general, the model tends to locate the prediction in the vicinity of the corresponding reference. Note that Fig. 5a was automatically classified as No Finding because it is the nearest reference, while in the following two examples of Ca and CaPl, the outcome weighted both the first position and the recurrent pathologies in the top 3. Fig. 5d–e are cases in which CLARE-XR is partially correct. Figure 5d corresponds to a PaPl instance classified as Pl (one true positive class and a false negative one). A possible justification for that is the Pl lesions being more evident in this image in comparison to the Pa ones. Figure 5e corresponds to a PnPl instance classified as CaPnPl (two true positive classes and a false positive one). This last example is essential to understand why the set of rules 4 is preferable to the set of rules 3, which would get a CaPl outcome instead and miss one of the ground-truth classes (Pn). In the medical context, a higher recall prevents false negative diagnoses such as this one. Finally, in Fig. 5f the model fails to diagnose a PaOt instance, classifying it as No Finding. The next section takes the same examples and explores the corresponding explanations to be presented to the clinicians along with the mentioned diagnoses.

Fig. 5.

Inference image examples and their respective predicted coordinates in the reference space (red plus sign). The No Finding and single-class references are plotted in colored dots, while the remaining multi-label combination coordinates are marked with black crosses. The corresponding GT reference is highlighted in red.

Table 5.

GT labels and final decision of the proposed sets of rules for multiple inference images.

Figure	GT	Set of Rules 1	Set of Rules 2	Set of Rules 3	Set of Rules 4
5a	No Finding	No Finding	No Finding	No Finding	No Finding
5b	Ca	Ca	CaPaPn	Ca	Ca
5c	CaPl	Pl	CaPnPl	CaPl	CaPl
5d	PaPl	Pl	CaPaPl	Pl	Pl
5e	PnPl	CaPnPl	CaPnPlOt	CaPl	CaPnPl
5f	PaOt	No Finding	No Finding	No Finding	No Finding

Explainability

It is important to discuss the information that will be disclosed to the clinicians, keeping in mind the goal of providing clear interpretable justifications along with the final decision. Suppose that the specialist inquires the system regarding a certain inference scan. The system will disclose the top-3 most likely combinations, letting them know that that image is attributed to a region in which those classes are predominant. The specialist is shown the final decision, with a brief textual explanation of how it was achieved based on the set of rules 4. E.g., the following text would be provided for the image in Fig. 5c: “This scan is likely to include findings associated with cardiac and pleural lesions, resulting in a CaPl diagnosis. The system has reached this decision because Pl is the most probable finding present in the image, and Ca is a recurrent finding in images with similar characteristics. Here is the complete list of possible lesions present: Pl, CaPl, CaPnPl .”

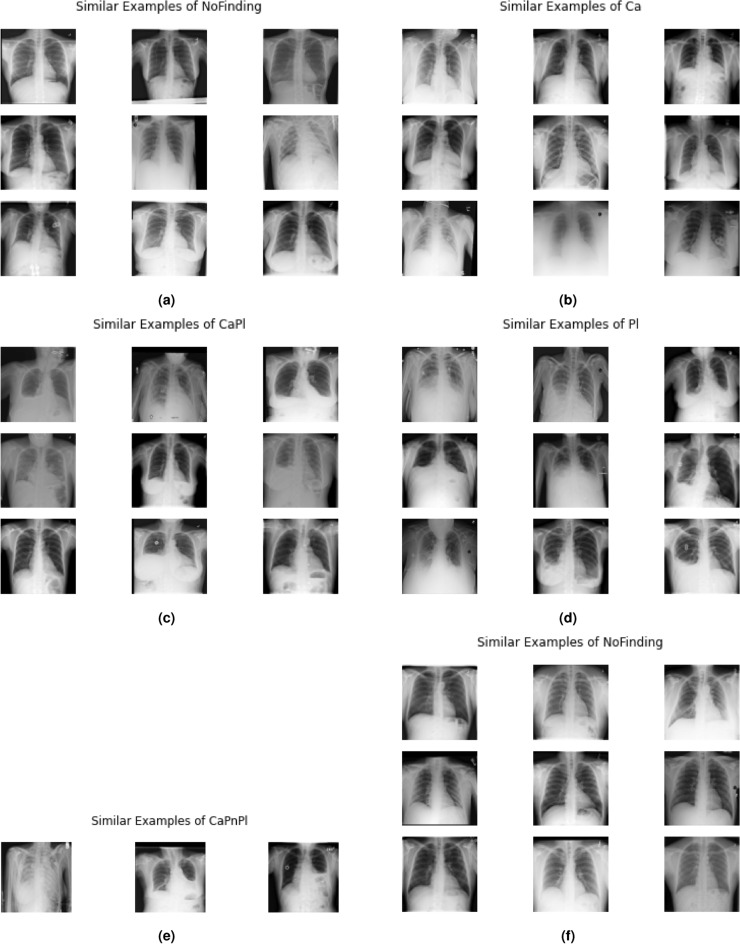
Additionally, a strategy was proposed to get complementary visual explanations based on the scatter plots, to validate the proposed diagnosis. Suppose that the model is provided the same inference scan in Fig. 5c with a CaPl prediction. The first step of the proposed XAI approach is to look at all the training set samples with that GT and position them in the reference space (red dots in Fig. 6). Then, images from the training set with coordinates closest to the predicted coordinate of the inference scan are selected and displayed as the most similar examples to that scan. The results are shown in Fig. 7, exhibiting comparable characteristics to the instances in Fig. 5, in the sense that they are represented by similar intensities and/or shapes (e.g. of the lesions, lungs, clavicles...).

Fig. 6.

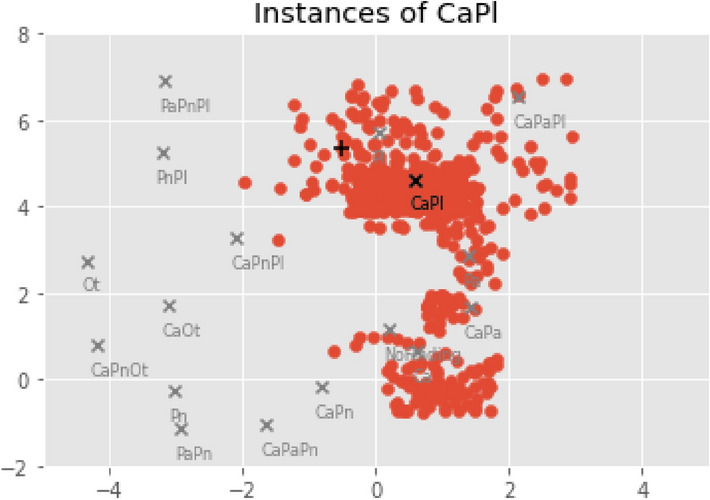
Embedding coordinates obtained by the Phase II regressor for the training instances annotated with CaPl (red dots). The GT reference is marked with the black cross, and the predicted coordinate for the current inference image is marked with a black plus sign.

Fig. 7.

Visual explanations for the inference image examples in Fig. 5, respectively.

In sum, the XAI approach generates a personalized explanation for each inference scan, providing examples that match that specific finding and patient. It is also possible to retrieve more than just 9 images if more examples are needed. Such functionality can be beneficial for non-specialist physicians, less experienced radiologists and/or educational purposes. Overall, the XAI stage of the work focused on justifying how that decision was achieved (using the set of rules to classify each case) and why the model decided so (showing similar examples that support the conclusion, based on the features learned by the model and the consequent positioning of the images in the reference space).

Limitations

This study initially applied the same concepts and methods to the original 14 classes of the CXR14 dataset, corresponding to a total of 470 possible label combinations with up to 3 co-occurring pathologies. However, only 369 of the 470 combinations were actually represented in the dataset, and 260 of those were represented by less than 30 images. For this reason, it was not possible to get statistically significant results, and it was necessary to reduce the complexity of the exercise by considering the 5 broader categories. In this scenario, all 26 possible combinations are represented in the dataset, with only 8 combinations being under-represented. This affects mostly the Ca class, present in 7 of those combinations. The class’s lowest precision values in Table 3, as well as the scarcity of examples for the explanations (e.g. Fig. 7e), are a consequence of such limitation. While this dataset is not ideal, the obtained results are justifiable and ensure the proof of concept of the CLARE-XR methodology. Additionally, note that the obtained results cannot be directly compared to any state-of-the-art publications because no other publication considered the same 5 broader categories and/or the same subset of the CXR14. The baseline was meticulously designed to address this aspect and was trained and evaluated under identical conditions as CLARE-XR, ensuring a fair and objective comparison.

Conclusions

Predictive performance cannot be the only requirement when developing an automatic system for pathology classification in CXRs. The importance of XAI in clinical applications cannot be overstated if the goal is to promote a system that supports regulatory compliance and improves clinical decision-making by complementing all its decisions with proper explanations that support the diagnosis. This promotes the trust of the end-user, who is now able to validate each outcome.

This work introduced the novel CLARE-XR approach that involves label embedding prior to the common image embedding, to enhance both predictive performance and model transparency. CLARE-XR automatically converts the original annotations into a continuous 2D embedded space, capturing the hidden structure of the labels. This transformation allows the multi-label classification to be framed as a regression task, where an image is mapped to a 2D coordinate instead of binary label vectors, positioning it within the embedded reference space. In this space, images with similar features are placed near each other, contextualizing neighboring information. The primary advantage of this method lies in its inherently interpretable framework, based on the lower-dimensional representation of the GT labels. This allows the definition of a clear set of classification rules and consequently provides physicians with justifications for the final diagnosis. Furthermore, visual explanations are offered through label embedding-based automatic image retrieval methods, showing tailored similar examples of the findings. This approach aligns perfectly with common clinical practices, where comparing scans is a standard method for confirming diagnoses. The results show that this framework outperforms the multi-label classification architecture across various evaluation settings on the CXR14 dataset. These two factors, predictive quality and XAI, collectively ensure that the system can be used effectively, safely, and responsibly in the healthcare setting.

The limited availability of high-quality, well-represented data, particularly in public datasets like CXR14, constrains the ability to conduct more in-depth studies encompassing a broader range of specific pathology classes. Moreover, the insufficient representation of rare pathology combinations directly affects the explainability component of the proposed method, as it depends on the available images for each combination to provide meaningful analogs for the inference case. A minimum amount of training images per combination should be defined to ensure a sufficient pool of examples is available to support meaningful explanations. Future work should aim to extend the experiments using a higher-quality dataset when available, with more images and classes to validate the previous conclusions. Given the modular nature of CLARE-XR, it could also be interesting to assess its performance when using alternative techniques in each phase. For example, substituting the autoencoder with a linear dimensionality-reduction approach such as Principal Components Analysis, or using a traditional machine learning regression model instead of a deep neural network. Additionally, more complex approaches could be explored for training the current autoencoder and/or regressor. For example, using contrastive learning to create an embedding space where similar samples are closer together and dissimilar samples are farther apart could further enhance the methodology.

Author contributions

J. Rocha conceived and conducted the experiments. J. Rocha, S.C. Pereira, A. Campilho, and A.M. Mendonça analyzed the results. P. Sousa validated the results from a medical standpoint. J.Rocha wrote the manuscript. All authors reviewed the manuscript.

Data availability

The dataset analyzed during the current study was made available by the NIH Clinical Center at https://nihcc.app.box.com/v/ChestXray-NIHCC.