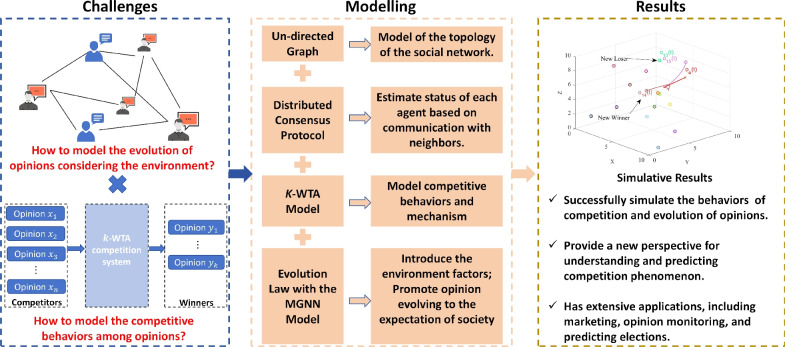
Abstract
In the context of social networks becoming primary platforms for information dissemination and public discourse, understanding how opinions compete and reach consensus has become increasingly vital. This paper introduces a novel distributed competition model designed to elucidate the dynamics of opinion competitive behavior in social networks. The proposed model captures the development mechanism of various opinions, their appeal to individuals, and the impact of the social environment on their evolution. The model reveals that a subset of opinions ultimately prevails and is adopted. Key elements of social networks are quantified as parameters, with parameter variations representing the dynamics of opinions. Furthermore, a modified gradient-based neural network is designed as the evolutional law of the opinion, whose stability and convergence are confirmed by theoretical analysis. Additionally, experiments simulate real-world competitive scenarios, demonstrating practical applications for the model. This model can be widely applied to various filed in social networks, offering a new perspective for understanding and predicting competition phenomenon in complex social systems. Overall, this work provides a structured and systematic approach to understanding opinion dynamics, which greatly enhances our ability to analyze competitive behaviors and anticipate the outcomes of diverse viewpoints in social networks.
Keywords: Opinion competition, k-winners-take-all (k-WTA), Social network, Recurrent neural network (RNN), Distributed scheme
Subject terms: Electrical and electronic engineering, Applied mathematics
Introduction
In recent years, the study of opinion dynamics in social networks has garnered significant attention. On the one hand, the development of new media technologies, such as social media platforms like TikTok and Little Red Book, has introduced numerous social factors that directly influence opinions1. On the other hand, these technologies are profoundly altering the structure of social networks, thereby changing the mechanisms of opinion evolution2. On the other hand, opinion dynamics has extensive applications in various domains, including marketing activities, political elections, etc3–5. To investigate and interpret the opinion dynamics on social networks, several models are presented to simulate the consensus problems, where consensus denotes the agreement on variables of interest among agents. Freeman et al. investigated the efficiency of two algorithms for average consensus problems, where each agent must estimate the average inputs of all agents6. Besides this, the joint influence of the dynamic property of individual agent and their interaction topology on opinion dynamics is studied, which may lead to polarity, consensus, or neutrality7. Moreover, regarding the consensus problem in the leader-follower cooperative interactions, a continuous-time model with the signed model is introduced, and its convergence and stability are analyzed under various leader’s states8. Furthermore, to capture the influential cognitive links, a multi-dimension learning model is designed for opinion dynamics, whose efficacy has been successfully verified through extensive subjective simulation9. The studies mentioned above examine opinion dynamics models under various conditions; however, they focus more on the collaboration between agents’ opinions.
In opinion dynamics, competition is also a common phenomenon, which refers to situations where multiple opinions or ideas coexist and compete for dominance within a social system10–12. More specifically, each individual (agent) in the social network may have a specific opinion regarding a certain topic/objective in the initial stage, such as the assessment of goods, support of the election candidate, and feeling about events12. Then, agents may communicate with their friends, families, and even strangers via social networks. After spread and interaction, those opinions that have advantaged status (being close to the social norm, having more communication channels, supported by opinion leaders) will be amplified and adopted by more and more agents. Finally, some opinions may win the competition and become consensus in social networks. Notably, investigating how opinions compete and evolve has real-world significance. For example, the evolution of opinion formulation on YouTube regarding COVID-19 has been investigated13. It is reported that the extent of polarization has increased as the pandemic unfolded, likely caused by echo chambers. The framework proposed in that study is helpful for regulatory agencies to take essential actions to mitigate social media-induced polarization. In addition, a conceptual model is designed to simulate the competitive behaviors of social networking firms, simulation synthesized with archival data illustrates that the firms emphasizing value cocreation actions and undertaking complex action repertoires can outperform others14. Similarly, regarding opinion dynamics, the strategies that make certain opinions popular can also be deduced by modeling the competitive behavior with real-world data. Furthermore, the opinion formation and evolution process are studied with an abundance of data from Twitter, revealing that public opinion often evolves into an ordered state, whose finding is beneficial for public opinion monitor15.
With the development of artificial intelligence technology and hardware circuits, utilizing neural network-related systems to simulate biological and even human behaviors and social phenomena has become a research hotspot. For instance, in16, a multi-input operant conditioning neural network incorporating blocking and competitive effects was proposed. The proposed model can realize blocking and overshadowing effects under multiple inputs and efficiently learn in complex environments. In another study, Sun et al. innovatively designed a memristor-based associative memory neural network circuit that establish a link between emotion and overshadowing17. Moreover, combining machine learning methods with causal regression methods, the influence of social bots on information diffusion in social networks was explored18. Regarding public opinion, a model combining edge computing with deep learning was proposed and applied to an emotion recognition model for network public opinion19. Additionally, using complex network theory, information dissemination theory, and disease spread theory, Zhao et al. constructed a model for disseminating emergency information20. Given this background, several models based on neural networks that describe competitive behavior have also been investigated. For example, a popular competitive model, the k-Winners-Take-All (k-WTA) model, is frequently used to simulate competitive mechanisms. k-WTA models can be classified into two types: centralized models and distributed models. For instance, the k-WTA model is transformed into a quadratic programming under certain condition, which enables the usage of schemes originally designed for solving quadratic programming to address k-WTA problems21. Similarly, Liu et al. converted the k-WTA model into a linear programming problem and proposed a neural network with a simple structure to estimate the outputs of the k-WTA model22. In addition, a novel k-WTA model has been designed, in which the coefficient k is implicitly determined by the initial state of the neuron rather than given directly22. Although these models have been proven to be effective, their centralized structure may suffer from poor scalability, uncertainty, and privacy disclosure23. To solve these limitations, a distributed k-WTA model was first introduced 24, whose global convergence was proved via Lyapunov theory. After that, Liu et al. employed a distributed k-WTA model in a location task, where the k robot closest to the target executes the tracking action25. Besides this, considering the perturbation in the system, a robust gradient-based differential k-WTA network is designed. This new model outperformed traditional models, and successfully solved the multi-robot coordination task26. In real life, each individual only interacts with its connected individuals (i.e., neighbors) in a social network, which inherently possesses a distributed structure. However, few existing works exploited the distributed k-WTA model to simulate the competitive behavior of opinions in the social network.
Therefore, this paper investigates the distributed opinion competition in social networks, whose schematic diagram is illustrated in Fig. 1. Firstly, the social networks and the links between agents are represented using an undirected graph and algebraic topology27. Furthermore, the graph is partially connected, with connections established based on the similarity of agents’ opinions. In comparison to a randomly connected topology28,29, this principle aligns more closely with real-world conditions, as individuals tend to communicate with those who share similar viewpoints. Then, a consensus model is exploited to model the interaction among neighbors. By integrating the distributed consensus model and the k-WTA model, the competitive mechanism is incorporated into the model. More specially, for those opinions in the k most favorable positions, as well as those have the top k largest input to k-WTA model, they continue to evolve and may converge to consensus. In contrast, the rest opinions may be deactivated and stop evolution. Within this mechanism, the positions of opinions are related to the social environment, making this model closer to the real-world scenarios. In addition, to guarantee the convergence of the proposed model, a modified gradient-based neural network (MGNN) is employed to drive opinion evolution, as well as solve time-varying problems. Unlike existing models30–32, the MGNN model enjoys a higher accuracy and low computing complexity. Up to this point, the distributed opinion competition scheme in social networks has been established. Theoretical analyses and simulation verification will also be provided in this paper. For clarity and ease of understanding, the definitions of symbols used throughout the article are provided in Table 1.
Fig. 1.
The schematic diagram of this paper.
Table 1.
symbols and definitions.
| Symbols | Definitions |
|---|---|
| G | Undirected graph of social network topology |
| n | Amount of agents in social network and the amount of inputs for k-WTA model |
|
|
Agents set and its elements |
| Edges set | |
|
|
Adjacent matrix and its elements |
| Weight of edge | |
| Neighbor set of ith agent | |
|
H and |
The Laplacian matrix and its elements |
|
|
The estimation of state of whole network and its derivative |
| Coefficients | |
| External input in consensus protocol and the output of the k-WTA model | |
|
|
Scalar state of ith agent and its derivative |
| Opinion of ith agent | |
| Expected state of target problem | |
| Function of fitness | |
| Input of the k-WTA model | |
| k | Amount of winners in social network |
| The kth largest input | |
| Auxiliary variable in the k-WTA model | |
| Output function of the k-WTA model | |
| Variable coefficient in MGNN model |
Preliminary
In this section, the preliminary and background are introduced to lay a basis for investigation. First, the mathematical model of the social network and the distributed communication protocol within the network are presented. Subsequently, the competition model (i.e., the k-WTA model) is introduced, detailing its definitions of inputs and outputs, as well as its mathematical model.
Description of social network
Without loss of generality, the social network topology is described with an undirected graph
| 1 |
where
Distributed consensus protocol
To study how each agent’s opinion competes and reaches consensus within a social network, the distributed consensus protocol proposed by Freeman et al. is adopted6, and the estimation of the consensus of the social network for ith agent can be formulated as
| 2 |
where
| 3 |
where
| 4 |
where
Fitness between opinions
The opinion held by an individual (i.e., the state of the agent) is associated with the social environment and opinion dynamics are significantly influenced by social factors such as social norms, communication channels, and other factors 35,36. Opinions that align with prevailing norms and gain support from influential figures or resonate with public sentiment are more likely to spread and gain acceptance, benefiting from positive feedback mechanisms. In contrast, opinions that deviate from norms, lack influential backing, or face resistance from social factors tend to struggle and may lose traction. Defining the expected opinion or status of a target social problem as
k-WTA model
The concept of winner-takes-all (WTA) has profound implications across various domains, stemming from its origins in electoral systems and social dynamics. Originally coined in the context of U.S. presidential elections, WTA dictates that the candidate with a relative majority in a state receives all of its electoral votes, regardless of the margin of victory37. This system highlights a stark reality: in competitive scenarios, the leading contender reaps disproportionate rewards, overshadowing competitors who may not differ significantly in support.
Beyond electoral systems, WTA extends into diverse arenas, including cell biology, coordination of robots, and opinion evolution38–40. In the realm of opinion evolution within social networks, these WTA manifest prominently. Social media platforms exemplify this by amplifying content that gains initial traction, thereby increasing its visibility and influence. Consider a scenario where many competing opinions on a controversial topic emerge. Due to algorithms favoring engagement and popularity, the opinion that gains an early edge perhaps due to timing, high emotional charge, resonance with a subset of users, or even strategic promotion—can quickly dominate the discourse41,42. As more users encounter and interact with this opinion, it garners additional attention, reinforcing its prominence through feedback loops of visibility and validation. For example, the phenomenon of WTA is observed in electronic word-of-mouth systems within the digital tourism domain, where a few influential microblogs dominate tourism discussions40. However, due to the complexity of competitive processes and environments, several winners will exist in many scenarios, leading to a k-WTA model. In a k-WTA model, the top k largest inputs out of total inputs output 1, while other inputs output 0.
To introduce influence from the social environment and competition in consensus protocol, u(t) in (4) is defined as the outputs of k-WTA model, where the k-winners are opinions with the top k highest fitness. Moreover, to make those opinions with the highest fitness has the largest inputs to the k-WTA model, the input
| 5 |
where
- State equation
where\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} \frac{\text {d}q(t)}{\text {d}t}=-\gamma \left( \sum \limits _{i=1}^N u_i(t)-k\right) , \end{aligned}$$\end{document} 6 \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\gamma >0$$\end{document} is scale factor, and q(t) is an auxiliary variable. - Output equation
where\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u_i(t)=-\Phi _{\Omega }\left( q(t)+\frac{v_i(t)}{2\lambda }\right) , \end{aligned}$$\end{document} 7 \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Omega =[0,1]$$\end{document} , and\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Phi _{\Omega }(\cdot )$$\end{document} is defined as\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} \Phi _{\Omega }(q(t)+\frac{v_i(t)}{2\lambda })=\left\{ \begin{aligned}&1, \,\,\,\,\,q(t)+\frac{v_i(t)}{2\lambda }>1\\&0, \,\,\,\,-1 \le q(t)+\frac{v_i(t)}{2\lambda } \ge 1\\&-1, \,q(t)+\frac{v_i(t)}{2\lambda }<-1. \end{aligned}\right. \end{aligned}$$\end{document} 8
In addition, to guarantee the solution of (6) and (7) equals to the solution of (5)
Modeling
In this section, the opinion dynamic problem is presented, and an MGNN is introduced to solve it. The convergence of the MGNN model is then proven theoretically. Finally, the entire distributed opinion competition model is derived.
Opinion evolution with MGNN model
According to the analyses presented in Preliminary, the opinion
Recently, massive neural networks have been investigated for their outstanding performance in solving time-varying problems, etc31,44,45. Among this class of neural networks, the zeroing neural network (ZNN) and gradient-based neural network (GNN) are two prevalent models. However, the ZNN model contains the inverse matrix, which leads to a high computing load and potential failures in solving. Thus, much effort has been devoted to designing GNN models46–48. By defining a non-negative scalar
| 9 |
where ρ > 0. To make
| 10 |
where
| 11 |
Compared with the traditional GNN model (9), the MGNN model (10) replaces the stationary coefficient
Convergence analysis
To demonstrate the convergence analysis of the MGNN model, the following theorem is provided.
Theorem 1
When update
Proof
Defining a positive definite Lyapunov candidate as
| 12 |
Inserting (10) into (12) leads to
| 13 |
Therefore, according to Lyapunov stability theorem48, the system is stable. In other words, the computed
The proposed model
First of all, as analyzed before, only those wined opinions can evolve. Thus, combining (6), (7), and (10), the opinion dynamic model should be rewritten as
| 14 |
In addition, term
| 15 |
Remark 1
According to the first equation in (15), the evolution of opinion is not only governed by the evolution rule (10) but also influenced by the output of the k-WTA model, where only the winners remain active and evolve. In addition, as depicted in the state equation (6) in the k-WTA model, solving the k-WTA model necessitates the status (i.e.,
Simulation results and discussion
Simulation setting
In this section, numerical simulations are performed to verify the availability of the proposed model, which also illustrates the process of opinion evolution. Firstly, the opinion of individual
Illustrative example
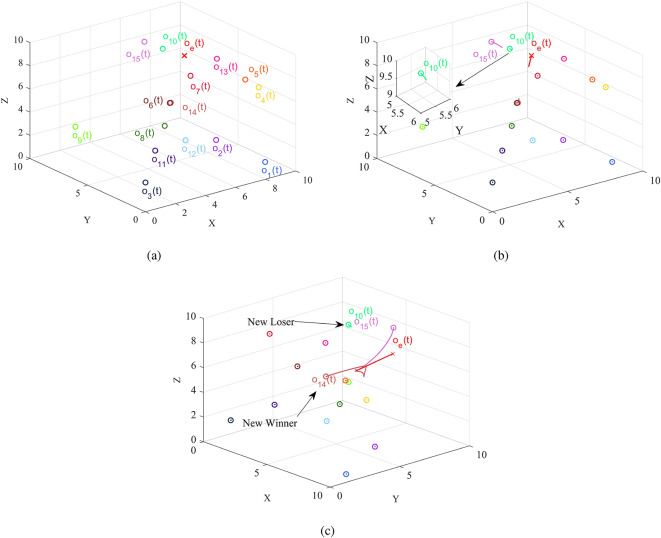
In Fig. 2, the distribution of opinions is displayed, where the circles denote the opinions of the individual and the cross denotes the social expectation. According to Fig. 2a, in the initial stage, opinions
Fig. 2.
Opinion dynamics in social network. (a) The randomly generated initial distribution of opinions in social network. (b) The opinions dynamics within
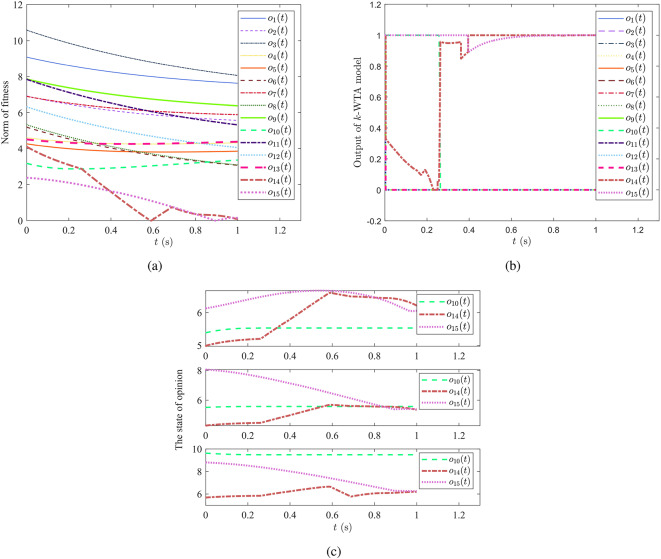
Figure 3 demonstrates detail and inner information about the opinion dynamic. As indicated in Fig. 3a,
Fig. 3.
Simulative trajectories of variables in the proposed model. (a) The norm of fitness between opinion
Discussion on topology
Regarding the topology of the social network, since the k-WTA model in this model only considers the situation with a certain number of competitors, these scale-free models (e.g., Barabasi–Albert model50) are not suitable for this work. Furthermore, the initial topology of this work is indeed the Erdős–Rényi model (i.e., nodes are connected with a certain probability)51. More specifically, the opinions held by each individual are generated randomly; those agents who have similar opinions (where the difference between opinions is smaller than a certain value) are connected. Otherwise, they are disconnected. Thus, individuals are connected with a certain probability at the initial stage. During the evolution of opinions, the topology of social networks is also constructed following the concept that individuals who hold similar opinions are connected. Compared with those randomly connected models (e.g., Erdős–Rényi model and stochastic block model29), this principle is more reasonable, as people tend to communicate with those who hold similar viewpoints.
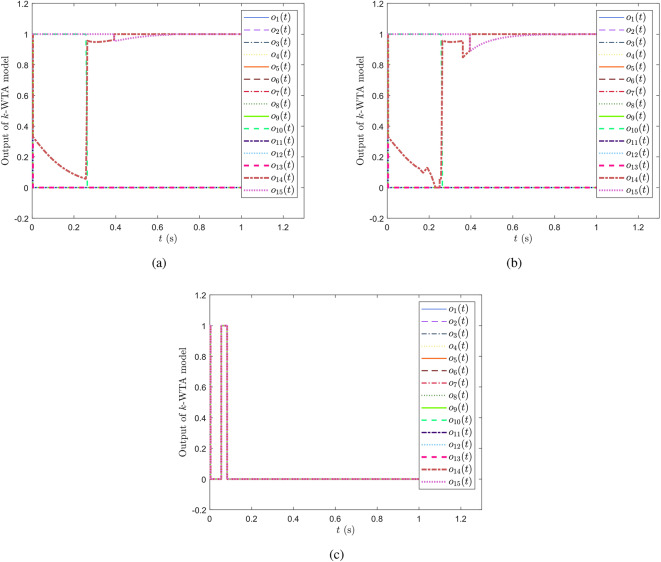
To demonstrate the effect of the topology, compared simulations are performed with a static topology that is the same as the initial topology of the proposed model in this work, the transitional topology proposed in this work, and the transitional model based on the Erdős–Rényi model, whose results are shown in Fig. 4a–c, respectively. According to Fig. 4, both the static and transitional models based on the conception proposed in this work can successfully generate the winners. Besides this, comparing with Fig. 4a,b, changes of the network structure have indeed occurred in the transitional model, making the figures of result different. Regarding to the Erdős–Rényi model, it fails to estimate the winners as shown in Fig. 4c. One potential reason is that the topology, as well as
Fig. 4.
The outputs of the proposed model with various typologies. (a) A static topology whose connections are based on the fitness between opinions. (b) The transitional model whose connections are based on the fitness between opinions. (c) The transitional Erdős–Rényi model.
Potential applications
According to the simulation results, the proposed model delves deep into the dynamics of opinion competition in social networks. It provides invaluable insights to better understand how various opinions form, develop and influence individual choices, extending its potential application scenarios. For example, the proposed model can be utilized to predict how different political opinions or ideologies may compete for the support of the major population, enabling those politicos to formulate effective communication strategies and finally win the election. Moreover, in the field of marketing, the company can leverage the model to simulate and forecast consumer perceptions towards various products or brands to craft available marketing strategies. Furthermore, the proposed model can also be employed in public opinion monitoring, entertainment promotion, and health information dissemination.
Conclusions
This paper has introduced an innovative distributed opinion competition model designed to simulate the evolution and competition of opinions within social networks. By integrating elements from the topology of social networks, distributed consensus protocols, and the k-WTA model, this approach captures the dynamics of opinion formation while accounting for interactions with neighbors and the broader influence of the social network. The competition and evolution of opinions result in a scenario where only a few opinions ultimately prevail. In addition, to drive the evolution of these opinions, an MGNN model has been developed, and its convergence has been rigorously proven through theoretical analysis. In the simulation section, an illustrative example of 15 opinions competing for 2 winners is displayed. The trajectories of opinions’ evolution and their competitive behaviors are demonstrated via visualization results. Simulations closely aligned with real-world conditions have validated the model’s effectiveness, highlighting its potential for application in various other social competitive behaviors. However, this study does not consider more complicated social network topology. Future research could explore how opinions compete and evolve within dynamically changing network structures, and how these changes affect the final distribution of opinions. In addition, the proposed model could integrate the real-time social media data to dynamically update the status of opinions and predict the final winners in some campaigns (e.g., the presidential election).
Acknowledgements
This work is supported by the program for scientific research start-up funds of Guangdong Ocean University (ID: 060302112401).
Author contributions
Z.F. and G.W. wrote the main manuscript text, concept, modeling, and Y.X. analyzing data. All authors reviewed the manuscript.
Data availability
Data and code are available upon request. Please contact the corresponding author by email to obtain the data and code used in the study.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Geng, L., Yang, S., Wang, K., Zhou, Q. & Geng, L. Modeling public opinion dissemination in a multilayer network with SEIR model based on real social networks. Eng. Appl. Artif. Intell.125, 106719 (2023). [Google Scholar]
- 2.Wei-Dong, H., Qian, W. & Jie, C. Tracing public opinion propagation and emotional evolution based on public emergencies in social networks. Int. J. Comput. Commun. Control13, 129–142 (2018). [Google Scholar]
- 3.Bimpikis, K., Ozdaglar, A. & Yildiz, E. Competitive targeted advertising over networks. Oper. Res.64, 705–720 (2016). [Google Scholar]
- 4.Lang, N., Wang, L. & Zha, Q. Targeted allocation of marketing resource in networks based on opinion dynamics. Mathematics10, 394 (2022). [Google Scholar]
- 5.Zhao, Y., Kou, G., Peng, Y. & Chen, Y. Understanding influence power of opinion leaders in e-commerce networks: An opinion dynamics theory perspective. Inf. Sci.426, 131–147 (2018). [Google Scholar]
- 6.Freeman, R. A., Yang, P. & Lynch, K. M. Stability and convergence properties of dynamic average consensus estimators. In Proceedings of the 45th IEEE Conference on Decision and Control, 338–343 (IEEE, 2006).
- 7.Liu, F., Xue, D., Hirche, S. & Buss, M. Polarizability, consensusability, and neutralizability of opinion dynamics on coopetitive networks. IEEE Trans. Autom. Control64, 3339–3346 (2018). [Google Scholar]
- 8.Liang, H., Yuan, F., Zhou, Z. & Su, H. Opinion separation in leader-follower coopetitive social networks. Neurocomputing434, 90–97 (2021). [Google Scholar]
- 9.Nematollahzadeh, S. M., Ozgoli, S., Haghighi, M. S. & Jolfaei, A. Learning influential cognitive links in social networks by a new hybrid model for opinion dynamics. IEEE Trans. Comput. Soc. Syst.8, 1262–1271 (2020). [Google Scholar]
- 10.Dhamal, S., Ben-Ameur, W., Chahed, T. & Altman, E. A two phase investment game for competitive opinion dynamics in social networks. Inf. Process. Manag.57, 102064 (2020). [Google Scholar]
- 11.He, G., Ruan, H., Wu, Y. & Liu, J. Opinion dynamics with competitive relationship and switching topologies. IEEE Access9, 3016–3025 (2020). [Google Scholar]
- 12.Hu, H. Competing opinion diffusion on social networks. R. Soc. Open Sci.4, 171160 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gupta, S., Jain, G. & Tiwari, A. A. Polarised social media discourse during COVID-19 pandemic: evidence from youtube. Behav. Inf. Technol.42, 227–248 (2023). [Google Scholar]
- 14.Gnyawali, D. R., Fan, W. & Penner, J. Competitive actions and dynamics in the digital age: An empirical investigation of social networking firms. Inf. Syst. Res.21, 594–613 (2010). [Google Scholar]
- 15.Xiong, F. & Liu, Y. Opinion formation on social media: an empirical approach. Chaos Interdiscip. J. Nonlinear Sci.24 (2014). [DOI] [PubMed]
- 16.Sun, J., Yue, Y., Wang, Y. & Wang, Y. Memristor-based operant conditioning neural network with blocking and competition effects. IEEE Trans. Ind. Inform. (2024).
- 17.Sun, J., Zhai, Y., Liu, P. & Wang, Y. Memristor-based neural network circuit of associative memory with overshadowing and emotion congruent effect. IEEE Trans. Neural Netw. Learn. Syst. (2024). [DOI] [PubMed]
- 18.Cai, M., Luo, H., Meng, X., Cui, Y. & Wang, W. Network distribution and sentiment interaction: Information diffusion mechanisms between social bots and human users on social media. Inf. Process. Manag.60, 103197 (2023). [Google Scholar]
- 19.Chen, M. & Zhang, L. Application of edge computing combined with deep learning model in the dynamic evolution of network public opinion in emergencies. J. Supercomput.79, 1526–1543 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhao, J.-H., Zeng, D.-L., Qin, J.-T., Si, H.-M. & Liu, X.-F. Simulation and modeling of microblog-based spread of public opinions on emergencies. Neural Comput. Appl.33, 547–564 (2021). [Google Scholar]
- 21.Liu, S. & Wang, J. A simplified dual neural network for quadratic programming with its kwta application. IEEE Trans. Neural Netw.17, 1500–1510 (2006). [DOI] [PubMed] [Google Scholar]
-
22.Liu, Q., Dang, C. & Cao, J. A novel recurrent neural network with one neuron and finite-time convergence for
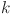 -winners-take-all operation. IEEE Trans. Neural Netw.21, 1140–1148 (2010).
[DOI] [PubMed] [Google Scholar]
-winners-take-all operation. IEEE Trans. Neural Netw.21, 1140–1148 (2010).
[DOI] [PubMed] [Google Scholar] -
23.Wang, X. et al. A distributed
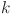 -winners-take-all model with binary consensus protocols. IEEE Trans. Cybern. (2023). [DOI] [PubMed]
-winners-take-all model with binary consensus protocols. IEEE Trans. Cybern. (2023). [DOI] [PubMed] - 24.Li, S., Zhou, M., Luo, X. & You, Z.-H. Distributed winner-take-all in dynamic networks. IEEE Trans. Autom. Control62, 577–589 (2016). [Google Scholar]
-
25.Liu, K. & Zhang, Y. Distributed dynamic task allocation for moving target tracking of networked mobile robots using
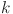 -wta network. IEEE Trans. Neural Netw. Learn. Syst. (2024). [DOI] [PubMed]
-wta network. IEEE Trans. Neural Netw. Learn. Syst. (2024). [DOI] [PubMed] -
26.Liu, M., Zhang, X., Shang, M. & Jin, L. Gradient-based differential
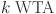 network with application to competitive coordination of multiple robots. IEEE/CAA J. Autom. Sin.9, 1452–1463 (2022). [Google Scholar]
network with application to competitive coordination of multiple robots. IEEE/CAA J. Autom. Sin.9, 1452–1463 (2022). [Google Scholar] - 27.Zhang, Y., Li, S. & Weng, J. Distributed estimation of algebraic connectivity. IEEE Trans. Cybern.52, 3047–3056 (2020). [DOI] [PubMed] [Google Scholar]
- 28.Tishby, I., Biham, O. & Katzav, E. Convergence towards an erdős-rényi graph structure in network contraction processes. Phys. Rev. E100, 032314 (2019). [DOI] [PubMed] [Google Scholar]
- 29.Lee, C. & Wilkinson, D. J. A review of stochastic block models and extensions for graph clustering. Appl. Netw. Sci.4 (2019).
- 30.Wang, G., Hao, Z., Huang, H. & Zhang, B. A proportional-integral iterative algorithm for time-variant equality-constrained quadratic programming problem with applications. Artif. Intell. Rev.56, 4535–4556 (2023). [Google Scholar]
- 31.Xiao, X., Jiang, C., Jin, L., Huang, H. & Wang, G. Nonlinear RNN with noise-immune: A robust and learning-free method for hyperspectral image target detection. Expert Syst. Appl.229, 120490 (2023). [Google Scholar]
- 32.Song, Z., Lu, Z., Wu, J., Xiao, X. & Wang, G. Improved ZND model for solving dynamic linear complex matrix equation and its application. Neural Comput. Appl.34, 21035–21048 (2022). [Google Scholar]
- 33.Knoke, D. & Yang, S. Social Network Analysis 154 (Sage, 2008).
- 34.Liu, M., Li, S. & Jin, L. Modeling and analysis of Matthew effect under switching social networks via distributed competition. IEEE/CAA J. Autom. Sin.9, 1311–1314 (2022). [Google Scholar]
- 35.Liu, M., Li, S. & Jin, L. Modeling and analysis of Matthew effect under switching social networks via distributed competition. IEEE/CAA J. Autom. Sin.9, 1311–1314 (2022). [Google Scholar]
- 36.Brady, W. J., McLoughlin, K., Doan, T. N. & Crockett, M. J. How social learning amplifies moral outrage expression in online social networks. Sci. Adv.7, eabe5641 (2021). [DOI] [PMC free article] [PubMed]
- 37.Belenky, A. S. A modified “winner-take-all’’ rule for awarding state electoral votes in US presidential elections and a game model for its analysis. Math. Comput. Model.48, 1308–1325 (2008). [Google Scholar]
- 38.Zhang, R. et al. Winner-takes-all resource competition redirects cascading cell fate transitions. Nat. Commun.12, 853 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Jin, L., Liang, S., Luo, X. & Zhou, M. Distributed and time-delayed-winner-take-all network for competitive coordination of multiple robots. IEEE Trans. Cybern.53, 641–652 (2022). [DOI] [PubMed] [Google Scholar]
- 40.Chen, W. Exploring the dynamics of electronic word-of-mouth in Chinese tourism: A social network perspective. J. Knowl. Econ. 1–23 (2024).
- 41.Wang, Z., Liu, H., Liu, W. & Wang, S. Understanding the power of opinion leaders’ influence on the diffusion process of popular mobile games: Travel frog on sina weibo. Comput. Hum. Behav.109, 106354 (2020). [Google Scholar]
- 42.Saquete, E., Zubcoff, J., Gutiérrez, Y., Martínez-Barco, P. & Fernández, J. Why are some social-media contents more popular than others? opinion and association rules mining applied to virality patterns discovery. Expert Syst. Appl.197, 116676 (2022). [Google Scholar]
-
43.Hu, X. & Wang, J. An improved dual neural network for solving a class of quadratic programming problems and its
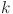 -winners-take-all application. IEEE Trans. Neural Netw.19, 2022–2031 (2008).
[DOI] [PubMed] [Google Scholar]
-winners-take-all application. IEEE Trans. Neural Netw.19, 2022–2031 (2008).
[DOI] [PubMed] [Google Scholar] - 44.Li, S. et al. A novel robustness-enhancing adversarial defense approach to AI-powered sea state estimation for autonomous marine vessels. IEEE Trans. Syst. Man Cybern. Syst. (2024).
- 45.Lin, C., Mao, X., Qiu, C. & Zou, L. DTCNet: Transformer-CNN distillation for super-resolution of remote sensing image. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. (2024).
- 46.Wang, G., Hao, Z., Li, H. & Zhang, B. An activated variable parameter gradient-based neural network for time-variant constrained quadratic programming and its applications. CAAI Trans. Intell. Technol.8, 670–679 (2023). [Google Scholar]
- 47.Zhang, Y., Li, S., Weng, J. & Liao, B. GNN model for time-varying matrix inversion with robust finite-time convergence. IEEE Trans. Neural Netw. Learn. Syst.35, 559–569 (2022). [DOI] [PubMed] [Google Scholar]
- 48.Ye, A., Xiao, X., Xiao, H., Jiang, C. & Lin, C. ACGND: towards lower complexity and fast solution for dynamic tensor inversion. Complex Intell. Syst. 1–15 (2024).
- 49.Li, S., Jin, L. & Li, S. Modeling and analysis of competitive behavior in social systems. IEEE Trans. Comput. Soc. Syst.10, 1347–1355 (2022). [Google Scholar]
- 50.Albert, R. & Barabasi, A. L. (2002): “statistical mechanics of complex networks. Rev. Mod. Phys.26, xii (2002). [Google Scholar]
- 51.Janson, S., Luczak, T. & Rucinski, A. Random Graphs (Wiley, 2011).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data and code are available upon request. Please contact the corresponding author by email to obtain the data and code used in the study.