Distinct network patterns emerge from Cartesian and XOR epistasis models: a comparative network science analysis

Abstract

Background

Epistasis, the phenomenon where the effect of one gene (or variant) is masked or modified by one or more other genes, significantly contributes to the phenotypic variance of complex traits. Traditionally, epistasis has been modeled using the Cartesian epistatic model, a multiplicative approach based on standard statistical regression. However, a recent study investigating epistasis in obesity-related traits has identified potential limitations of the Cartesian epistatic model, revealing that it likely only detects a fraction of the genetic interactions occurring in natural systems. In contrast, the exclusive-or (XOR) epistatic model has shown promise in detecting a broader range of epistatic interactions and revealing more biologically relevant functions associated with interacting variants. To investigate whether the XOR epistatic model also forms distinct network structures compared to the Cartesian model, we applied network science to examine genetic interactions underlying body mass index (BMI) in rats (Rattus norvegicus).

Results

Our comparative analysis of XOR and Cartesian epistatic models in rats reveals distinct topological characteristics. The XOR model exhibits enhanced sensitivity to epistatic interactions between the network communities found in the Cartesian epistatic network, facilitating the identification of novel trait-related biological functions via community-based enrichment analysis. Additionally, the XOR network features triangle network motifs, indicative of higher-order epistatic interactions. This research also evaluates the impact of linkage disequilibrium (LD)-based edge pruning on network-based epistasis analysis, finding that LD-based edge pruning may lead to increased network fragmentation, which may hinder the effectiveness of network analysis for the investigation of epistasis. We confirmed through network permutation analysis that most XOR and Cartesian epistatic networks derived from the data display distinct structural properties compared to randomly shuffled networks.

Conclusions

Collectively, these findings highlight the XOR model’s ability to uncover meaningful biological associations and higher-order epistasis derived from lower-order network topologies. The introduction of community-based enrichment analysis and motif-based epistatic discovery emphasize network science as a critical approach for advancing epistasis research and understanding complex genetic architectures.

Supplementary Information

The online version contains supplementary material available at 10.1186/s13040-024-00413-w.

Background

Epistasis, the interaction between two or more genes, is integral to the study of genetics and is ubiquitous in natural systems [1]. However, epistasis is challenging to detect and seldom explored experimentally due to the computational resources required to investigate all possible pairwise and higher-order interactions that can exist between genetic variants [2, 3]. Despite this, significant examples of statistical and biological epistasis have been detected in several systems [4–12]. Recently, and of primary interest for this work, results from Batista et al. 2024 [12] demonstrate that in two model systems, significant statistical epistatic interactions are not only present, but different interaction models yield distinct results.

Traditionally, methodologies for detecting epistasis in biological systems use the Cartesian (multiplicative) product of two or more SNPs to model interaction terms. While this approach originates from statistical practices due to its mathematical convenience, it has been shown to be limited in capturing the complexity of some systems [13]. Biological systems and genetic pathways are inherently complex, evolving in diverse ways to fulfill a range of biological functions [1, 14–16]. Many phenotypes arise from large, intricately connected biological networks [17], making it potentially limiting to assume that all biological interactions can be captured by Cartesian product-based models, which impose specific assumptions and characteristics on the interactions they detect. As a result, relying solely on Cartesian models may overlook more nuanced or non-linear interactions, potentially missing key aspects of how genes interact within these complex networks.

In the work of Batista et al. 2024, in addition to constructing interactions terms using the standard Cartesian interaction model, interaction terms using the exclusive-or (XOR) penetrance model were also constructed to investigate epistasis underlying body mass index (BMI) in rats and mice. In the pure and strict XOR model used in this study, the phenotype can only be explained by multi-locus genotypes (MLGs) (Supplementary File S1). Mathematically, this can be expressed as:

$$\begin{array}{c}\hfill \text{XOR}(A,B)=\left((,A,,\text{mod},,2,),+,(,B,,\text{mod},,2,)\right)\text{mod}2\end{array}$$ 1

Where A and B represent the genotype scores (0, 1, or 2) of two loci. The “modulo” operation, denoted mod, returns the remainder after division. In this case, since A and B can only take values 0, 1, or 2, A mod 2 and B mod 2 will return 0 when the genotype score is even (i.e., 0 or 2) and 1 when the score is odd (i.e., 1). The modulo operation reduces the multi-locus genotype scores to binary values (0 or 1), enabling us to apply the XOR logic. From this equation, it can be seen that the effect of one SNP alone does not provide sufficient information to detect significant associations with the phenotype. Thus, assuming full penetrance and equal allele frequencies in both loci under Hardy-Weinberg equilibrium assumptions, XOR is not linearly separable or detectable using any single-locus analyses like GWAS (Supplementary File S1; [18]). On the other hand, Cartesian multiplies the genotype score of each locus to construct the interaction term:

$$\begin{array}{c}\hfill \text{Cartesian}(A,B)=A\times B\end{array}$$ 2

In their work, the XOR interaction model was selected due to its extreme difference compared to the Cartesian model and its assumed lack of biological plausibility in living systems. Despite this, Batista and colleagues did detect significant statistical epistasis using the XOR model with it yielding more significant interactions in both species when compared to the Cartesian model [12]. Furthermore, XOR epistatic loci were significantly enriched for biologically relevant terms and pathways associated with metabolism and BMI, especially in rats, which were not detected with the Cartesian model. Here, we attempt to better understand the complex associations detected in the rat (Rattus norvegicus) system by Batista and colleagues under both interaction models using network analysis.

In light of these findings, it becomes evident that the complexity of biological systems is largely attributable to interconnected networks of genetic variants [19], extending beyond the scope of univariate effects typically seen in Mendelian traits and diseases [20–22]. This complexity highlights the need for network-based approaches to gain a comprehensive understanding of biological systems. By conceptualizing biological entities, such as genes, proteins, and metabolites, as nodes and representing the interactions between them as edges, network-based approaches offer a distinct and perhaps more complete perspective on the intricate interplay among these entities. Network based approaches assume that the intricacies of biological systems can be deciphered by analyzing the structures within biological networks. To this end, various biological networks, including protein-protein interaction networks [23–25], metabolic networks [26–29], gene regulatory networks [30, 31], and epistatic networks [32], have been proposed to describe the complex processes that drive traits and diseases.

Biological networks possess distinct properties that separate them from random networks, leading to various hypotheses on the mechanisms of biological systems. Firstly, these networks are scale-free [33], characterized by a few highly connected nodes known as hubs. This underpins the hypothesis concerning the role of hub nodes, suggesting that perturbations in these highly connected nodes are more likely to impact the outcome of the system than non-hub nodes [34, 35]. Secondly, high degrees of modularity [36] within these networks correspond to the division of the network into subgroups of closely interconnected nodes, where nodes within the same module are more likely to interact with each other than with nodes outside the module. This concept aligns with the hypothesis that biological entities, such as genes or proteins involved in the same biochemical process or disease, tend to interact more frequently with each other than other nodes, thus forming a localized cluster or module within the larger network [29, 37–39]. Thirdly, the small-world property [40] of biological networks ensures short paths between any pair of nodes, implying that perturbations in a node’s state can influence the activity of many nearby nodes and the network’s overall behavior [41]. Lastly, motifs [42], or subgraphs, that occur more frequently than expected, underscore the importance of certain structural patterns in carrying out biological functions, such as several regulatory motifs, have been identified [43].

Gene Set Enrichment Analysis (GSEA) [44] plays a crucial role in translating the structural insights of biological networks into a better understanding of their underlying biological functions. By identifying enriched gene sets, GSEA helps determine the specific biological processes, functions, or pathways that are over-represented in a given network or module. This allows us to link the structural properties of the network-such as hub nodes, network modules, small-world connections, and recurring motifs-to specific biological entities [44, 45]. Furthermore, GSEA can unravel the complex relationships between genetic variants and their synergistic roles in influencing traits, enhancing our ability to interpret epistatic interactions and gene-pathway interplay within these biological networks.

In the study by Batista and colleagues [12], the researchers explored epistasis utilizing two distinct models of interaction: Cartesian and XOR (Fig. 1). Building on their findings, our current work applies network science to analyze whether the networks constructed from these models exhibit distinct structural and topological features. By using the topology of lower-order epistasis interactions, we identify higher-order epistasis. Additionally, we aim to determine if the specific configurations within each network correlate with meaningful biological insights related to BMI, obesity, and metabolism in the R. norvegicus system. Overall, this approach seeks to clarify the genetic architecture of complex traits by interpreting SNP-SNP interactions through network-based representations.

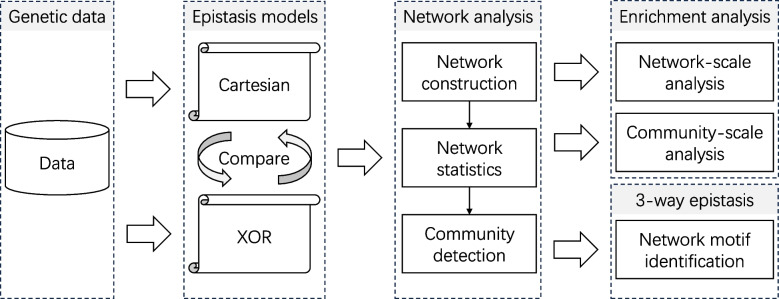
Fig. 1.

Epistatic network comparative analysis conceptual flowchart: This study evaluates genetic data using two distinct epistasis models to construct and compare epistatic networks. By employing edge thresholding to enhance network modularity, we construct and compare epistatic networks for the analysis of the complex trait of body mass index (BMI) in rats. Our comparative analysis emphasizes the unique insights gained from enrichment analysis at both network and community levels, alongside the identification of network motifs indicative of higher-order epistasis

Materials

Data source

Genetic and phenotypic data used in this analysis come from an openly available dataset of an outbred, related rat (Rattus norvegicus) population, consisting of both males and females, that is derived from eight inbred founders (Heterogenous Stock [46]). Specifically, the genotype and phenotype values used in our analysis, and by Batista et al., come from SNPs and phenotype scores utilized in a previously published GWAS [47, 48] investigating obesity-related traits in this population of (R. norvegicus).

Epistatic pairs

The methodology of Batista et al. 2024 [12] exhaustively tests the interaction terms of every possible pairwise interaction (n choose k). A total of 10,000 linkage disequilibrium (LD) pruned ($R^2$ cutoff = 0.95) SNPs with the largest main effects (lowest genome-wide corrected p-value) from the (R. norvegicus) GWAS [47, 48] were used in their analysis, resulting in 49,995,000 possible 2-way interactions for each epistatic model (Cartesian and XOR). Model specific p-values for each pairwise interaction were derived by performing a t-test on the interaction term (${\beta }_3$) assuming a null hypothesis where (${\beta }_3$) = 0. Given the large number of tests conducted, they applied the Benjamini-Hochberg procedure to control the false discovery rate (FDR). This method adjusts the p-values based on their rank and the total number of tests, ensuring that the proportion of false positives among the significant results remains low. To further validate the results, permutation testing was also performed (1,000 permutations). The phenotype of interest used in the epistasis analysis was body mass index (BMI) measured from the whole body, including the animal’s tail (BMI_TAIL). Pairs pruned for minor allele frequency (< 0.1 in either loci) and with FDR-corrected p-values < 0.05 (Cartesian: 3,438 pairs, XOR: 12,749 pairs) were used in all following analyses.

Construction of epistatic networks

Nodes and edges

In each epistatic network, a SNP is represented by a node. The interactions between these SNPs are represented by edges connecting these nodes. The strength of the interaction is represented by the edge weight, which is given by the statistical significance of the interaction (i.e., FDR-adjusted p-value).

Not all identified interactions are included in the final epistatic network. A cut-off value $\tau$ is determined and only interactions (edges) with their weights (FDR-adjusted p-value) less than or equal to this threshold are included. Once the significant epistatic interactions have been decided, these interactions are used to construct the network. The resulting epistatic network provides a representation of the most significant epistatic interactions between SNPs.

Quantifying the extent of community separation

SNPs do not work in isolation but in an interdependent manner to contribute towards phenotypic variation [20, 21, 32]. Hence, for our epistatic network, we expect the emergence of highly connected groups of nodes (communities) that represent biological pathways and/or functions [21].

Modularity is a measure used in network science to quantify the degree to which the network can be subdivided into clearly separated groups or communities. The modularity (Q) is calculated as follows:

$$\begin{array}{c}\hfill Q=\frac{1}{2m}\sum _{\mathit{ij}}\left[A_{\mathit{ij}},-,\gamma ,\frac{k_i{k}_j}{2m}\right]\delta (c_i,c_j).\end{array}$$ 3

In this equation, m represents the number of edges in the network. The summation term ${\sum }_{\mathit{ij}}$ runs over all pairs of nodes within the network. The adjacency matrix, represented by $A_{\mathit{ij}}$, contains elements that are equal to 1 if an edge connects nodes i and j, and 0 in the absence of a connection. The degree of a node, symbolized by $k_i$ and $k_j$ for nodes i and j respectively, corresponds to the count of edges connected to the node. The communities of nodes i and j are indicated by $c_i$ and $c_j$, respectively. The delta function, $\delta (c_i,c_j)$, gives a value of 1 if nodes i and j are within the same community (i.e., $c_i$ = $c_j$), and 0 if they are not. The resolution parameter, denoted by $\gamma$, establishes a trade-off between intra-group and inter-group edges. In the context of our experiment, the resolution parameter is set to 1.

The value of Q can be either positive or negative with values of high magnitude indicating a strong community structure [36]. A high modularity value (approaching 1) suggests a well-defined community structure within the network, while a modularity value close to 0 or negative indicates that the edges are distributed with no clear community organization.

Finding the optimal division of a network into communities that maximizes the modularity score is a challenging task, as there is an exponential number of potential divisions. Various heuristics and optimization algorithms have been developed to approximate optimal community division [49–51]. Based on the size and complexity of the networks in this study, we employ the Greedy community detection algorithm [49] for identifying communities within networks. This algorithm utilizes a greedy strategy to identify the community partition that yields the highest modularity. The process of greedy modularity maximization initially starts with every node existing in separate communities. It then merges pairs of communities to achieve the maximum increase in modularity. This process is iteratively repeated until the modularity cannot be improved further.

Determination of the epistatic network by tuning edge weight threshold

We introduce an edge weight cutoff, denoted as $\tau$, to select the most significant edges for inclusion in the network. This threshold defines which edges are retained, with the aim of maximizing the modularity of the resulting network.

We denote the network as $N=\{V,E,\tau \}$, where V represents the set of nodes (SNPs), E represents the set of edges (significant epistatic interactions), and $\tau$ represents the edge weight threshold. Each edge $e\in E$ that links two nodes $v_1,v_2\in V$ has an associated weight, denoted as $\omega (e)$. An edge e is included in the network if $\omega (e)\le \tau$.

To optimize network modularity, we gradually increase the edge weight threshold $\tau$ and track changes in modularity. We begin with $\tau$ set to 0. We then increase $\tau$ in increments of 0.0001. After each increase, we calculate the modularity, Q, of the resulting connected nodes along with other network metrics, such as the number of connected nodes, the number of edges, and the number of network-connected components. In order to gain a comprehensive understanding of the network’s evolution, we also monitor the number of undirected triangle network motifs. Network motifs are the basic building blocks of the network [42].

We select the $\tau$ value that yields the highest network modularity as the optimal edge weight threshold. This process ensures that the constructed network N not only captures the strongest genetic interactions but also exhibits a community structure that facilitates the identification of functionally relevant modules of SNPs.

Network comparison

We compare networks generated from XOR and Cartesian interaction models to identify common SNPs, epistatic interactions, and network communities. For the network with the highest network modularity, we perform comparisons at two different scales.

At the scale of nodes and edges of the epistatic network, we consider adjacent SNPs as identical due to linkage disequilibrium (LD). A SNP, n, is represented using a tuple $n=(c,p)$, where c stands for chromosome number and p stands for chromosome position. If the difference between a pair of SNPs is within a certain range $\delta$ and they are on the same chromosome, they are deemed identical. The way we determine identical SNPs can be formally expressed as follows. Given $n_1=(c_1,p_1)$ and $n_2=(c_2,p_2)$, we say $n_1$ and $n_2$ are the same (within the range $\delta$) if:

$$\begin{array}{c}\hfill n_1\approx n_2\iff \left(c_1,=,c_2\right)\wedge \left(|,p_1,-,p_2,|<\delta \right)\end{array}$$ 4

As for edge comparison, two interactions are considered identical if their SNPs are within the same base pair window. We represent an edge as a set of two SNPs $e=(n_1,n_2)$. Given two edges, $e_a=(n_1^a,n_2^a)$ and $e_b=(n_1^b,n_2^b)$. Edges $e_a$ and $e_b$ are considered identical if:

$$\begin{array}{c}\hfill e_a\approx e_b\iff \left(n_1^a,\approx ,n_1^b,\wedge ,n_2^a,\approx ,n_2^b\right)\vee \left(n_1^a,\approx ,n_2^b,\wedge ,n_2^a,\approx ,n_1^b\right)\end{array}$$ 5

As the range increases from 0 bases to 10 million base pairs (Mb) in 1 Mb increments, the number of common SNPs and epistatic interactions increase.

At the scale of network community, we identify the quantity of common nodes ${\mathrm{\Lambda }}_{(C_a\to C_b)}(\delta )$ from community $C_a$ to community $C_b$ with respect to the range parameter $\delta$. Let $C_a$ and $C_b$ be two network communities from two different epistatic networks. Each community is a set of nodes, i.e., $C_a=\{n_1^a,n_2^a,\cdots \}$ and $C_b=\{n_1^b,n_2^b,\cdots \}$. A node in the community $n_i^a\in C_a$ will be considered to have a common node in the other community $C_b$ if there exists at least one node that can be determined as similar. The number of such nodes in $C_a$ is used to quantify the similarity from $C_a$ to $C_b$. This similarity is directional, and its formal definition is as follows.

To determine if two nodes $n_1$ and $n_2$ is similar, we first define a function $f_{\delta }$ as:

$$\begin{array}{c}\hfill f_{\delta }(n_1,n_2)=\left\{\begin{array}{cc}1\hfill & \text{if}{n}_1\approx n_2\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\right)\end{array}$$ 6

Using the function $f_{\delta }$, we can define ${\mathrm{\Lambda }}_{(C_a\to C_b)}(\delta )$ as:

$$\begin{array}{c}\hfill {\mathrm{\Lambda }}_{(C_a\to C_b)}(\delta )=\sum _{n_i^a\in C_a}\underset{n_j^b\in C_b}{max}{f}_{\delta }\left(n_i^a,,,n_j^b\right)\end{array}$$ 7

We utilize ${\mathrm{\Lambda }}_{(C_a\to C_b)}(\delta )$ to compare each pair of network communities from the two epistatic networks with different interaction models. The comparison of nodes will also consider the range of their position. The number of common SNPs in $C_a$ will evolve as the change of the range parameter $\delta$.

We utilize the area under the curve (AUC) to quantify the similarity of community pair as a function of range ${\mathrm{\Lambda }}_{(C_a\to C_b)}(\delta )$. To compute the AUC, consider $\delta$ to have discrete values ranging from a minimum value ${\delta }_{\text{min}}$ to a maximum value ${\delta }_{\text{max}}$ with a step size s. The AUC can be approximated using the function shown as below:

$$\begin{array}{c}\hfill \text{AUC}=\sum _{k=0,s}^M\frac{{\mathrm{\Lambda }}_{(C_a\to C_b)}({\delta }_{\text{min}}+ks)+{\mathrm{\Lambda }}_{(C_a\to C_b)}({\delta }_{\text{min}}+(k+1)s)}{2\times (M+1)},\end{array}$$ 8

where $M=\lfloor \frac{{\delta }_{\text{max}}-{\delta }_{\text{min}}}{s}\rfloor -1$ represents the total number of steps between ${\delta }_{\text{min}}$ and ${\delta }_{\text{max}}$. To reflect the relative size between the number of common nodes and the overall number of nodes in community $C_a$, symbolized as $|C_a|$, the normalized $\text{AUC}$ is denoted as:

$$\begin{array}{c}\hfill {\text{AUC}}_{\text{norm}}=\sum _{k=0,s}^M\frac{{\mathrm{\Lambda }}_{(C_a\to C_b)}({\delta }_{\text{min}}+ks)+{\mathrm{\Lambda }}_{(C_a\to C_b)}({\delta }_{\text{min}}+(k+1)s)}{2\times (M+1)\times |C_a|}.\end{array}$$ 9

In our study, $\delta$ ranges from ${\delta }_{\text{min}}=0\text{Mb}$ to ${\delta }_{\text{max}}=10\text{Mb}$ with a step size of $s=1\text{Mb}$.

LD edge pruning for epistatic network

We implement a LD edge pruning process to investigate if refining significant SNP-SNP interactions identified through Cartesian and XOR models results in superior network topologies. This aims to highlight the most significant and independent interactions by reducing redundancy due to LD between nearby SNPs. Pruning is performed separately for each model using two genomic distance thresholds: 1 million base pairs (1 Mb) and 10 million base pairs (10 Mb).

All pruning procedures were conducted in R. For both the Cartesian and XOR models, we prune redundant interchromosomal pairs based on the following criteria when comparing two epistatic pairs: (1) The first SNPs (locus one) of both pairs are on the same chromosome. (2) The second SNPs (locus two) of both pairs are on the same chromosome. (3) The absolute difference in base pair positions between the first SNPs of both pairs is less than the threshold (1MB or 10Mb). (4) The absolute difference in base pair positions between the second SNPs of both pairs is less than the threshold. If all four conditions are met, we retain the pair with the lower FDR-corrected p-value from the original study [12] and omit the other. We also address mirror redundancies where two pairs meet the criteria but have reversed chromosomal combinations; in such cases, we retained the first identified pair and omit the duplicate.

For intrachromosomal pairs, we apply the same base pair criteria as above, focusing on pairs where both SNPs are on the same chromosome. Additionally, we implement an extra pruning step for intrachromosomal pairs where the absolute base pair difference between the two SNPs within a pair is less than the threshold. Pairs meeting this condition are omitted. We recognize that this severely limits the detection of close cis-acting epistatic events. However, this pruning strategy allows us to focus on epistatic interactions that are more likely to represent independent genetic effects, highlighting epistatic hubs in the genome. By considering only the most significant interactions, we aim to provide a clearer understanding of the genetic architecture underlying BMI.

Network permutation

Network permutation involves shuffling the edges of a given network while preserving its node degree distribution. This process allows for null hypothesis testing. In which, the network properties of the observed network are compared against random shuffled networks. The edge permutation process performs a number of swaps equal to 10 times the number of edges in the network. During each iteration, two edges are randomly chosen, and as long as the swap does not result in a self-loop or duplicate edges between the same nodes, the edges are swapped. This ensures that while the node degree distribution remains intact, the global connectivity pattern may change. After network permutation, network investigation is performed on the permuted networks (N = 1,000), and the resulting network statistics are compared to those from the original network.

Functional enrichment analysis

g:Profiler

Enrichment analysis discerns biological insights from a list of gene names by detecting statistically significant representation of biological functions, such as gene ontology (GO) terms and pathways. In our study, we utilize the R. norvegicus genome (Rnor version 6.0) as the reference. Our enrichment analysis starts with a list of SNPs, each identified by a unique ID consisting of chromosome number and chromosomal position in base pairs (for example 1:12345678). The list of SNPs are from the connected nodes of the epistatic network with the highest network modularity. For every SNP in the list, we include gene models 1 million base pairs upstream and downstream from the original position.

The prepared ranges (for example 1:11345678:13345678) are then directly used as inputs for g:Profiler [45]. Since g:Profiler works with the mRatBn7.2 assembly, the coordinates for SNPs for Rnor6.0 were converted to those of the mRatBn7.2 genome assembly. This was done using the liftover software developed by UCSC [52]. Our enrichment analysis is performed using g:Profiler’s R package to query gene models within these ranges. We use the default configuration for each query (Supplementary File S1-IV). All available data sources, including GO:Biological Process (GO:BP), GO:Cellular Component (GO:CC), GO:Molecular Function (GO:MF), REAC, KEGG pathways, miRNA and Transcription Factors (TFs), are considered for the analysis to provide a comprehensive understanding of potential biological implications. The biological terms returned by g:Profiler are filtered based on their g:SCS threshold. Only terms with an adjusted p-value less than 0.05 are retained.

The epistatic networks in this work are optimized for modularity to highlight distinct communities of interacting SNPs. To discern potential biological signals, we conduct enrichment analysis at two levels: the entire network scale and the community scale. For the network scale, all SNPs in the network are taken into account for enrichment analysis based on g:Profiler. Conversely, the community scale analysis focuses on each discrete community within the epistatic network. Given that the number of SNPs in each community is significantly lower than in the entire network, the enrichment analysis at this scale yields more targeted functional terms. This specificity provides a contrast to the broader perspective obtained at the network scale.

Comparative analysis of g:Profiler biological terms

To acquire a deeper understanding of the enriched biological terms for each interaction model, a comparative analysis is conducted. The table obtained from g:Profiler is organized according to the term sources (See Supplementary File S2). Venn diagrams are generated using the terms from both interaction models for each term source (using a custom R script).

In addition to analyzing enrichment at the lowest level of the ontological hierarchy, we wished to gain a broader perspective and facilitate the identification of biological differences between Cartesian and XOR networks in this exploratory network analysis. Thus, another layer of information is considered. To achieve this, we focus on the first child of the parent classification for each term. For instance, in the case of GO:BP, the parent is Biological Process, and the first child of interest is the term when going down one level in the GO hierarchy. This selection ensures an adequate level of variability can be captured, as the parent term alone offers no differentiation. This analysis is not conducted in the case of miRNA and TFs, where a hierarchical structure is absent. There are extremely few child terms for GO:CC and GO:MF, therefore not much variability exists at this level. Going down one level lower for both of these sources helps capture more variation. Thus, the second-order child is taken into consideration. The parent hierarchy information for each term is extracted using the R package “GOfuncR” (Supplementary File S4) [53]. Venn diagrams are generated for the five sources. At the community level, we conducted the same analysis and removed all terms related to immunity. After cross-referencing across both encodings and all communities, we retained only the terms unique to each community. This is because direct comparisons cannot be made because of the differing number of communities in each.

EnrichmentMap

Performing an enrichment analysis on a set of SNPs often yields a large volume of terms, which poses a significant challenge in interpreting the results. Thus, a proper summary of these terms is needed to simplify the process of interpreting and understanding the biological implications of our findings.

EnrichmentMap [54] visualizes functional terms as a network following the principle that terms sharing many genes suggest a higher degree of functional relatedness. In the generated network, each node represents a functional term, and the edges connecting them represent the overlap of genes associated with those terms. Nodes are sized relative to the total number of associated genes, and edges are weighted by the number of shared genes between the two connected terms. EnrichmentMap provides options to control the sparsity of edges in the network, and we configure this option to be sparse. The resulting clusters of related terms provide insight into the themes emerging from the enrichment analysis. EnrichmentMap can merge the results from different queries. In our analysis, node colors represent terms from different epistatic networks of varying interaction models and network communities.

AutoAnnotate [55], a Cytoscape plugin, is employed to further refine the output of EnrichmentMap. This plugin uses WordCloud [56] to generate a label for each cluster of nodes, serving as a theme for that community of terms. The use of AutoAnnotate enables a more intuitive interpretation of the clusters, facilitating our understanding of the functional enrichment results.

Results

This section presents a comprehensive analysis from three perspectives: First, it explores the unique network structures formed by the XOR and Cartesian interaction models, using edge weight thresholds to optimize network modularity and examine various network metrics. Second, it compares these networks, focusing on their similarities and differences in terms of nodes, edges, community structures, and their implications on identifying higher-order epistasis based on lower-order interactions. Third, we highlight the results of our enrichment analyses, which elucidate the functional terms and biological implications of the networks derived from each interaction model. Finally, we perform network permutation analysis to compare the observed network with null (random) networks.

XOR and Cartesian interaction models yield distinct network structures

Edge weight thresholding is employed to optimize network modularity. We also monitor several key metrics during this process: (1) the number of connected nodes, (2) the number of edges, (3) the number of network components, (4) the size of the largest network component, and (5) the number of triangles in the network. Network investigation is performed on the original epistatic networks as well as the networks filtered by the edge pruning process, which removes redundant edges within identical LD blocks.

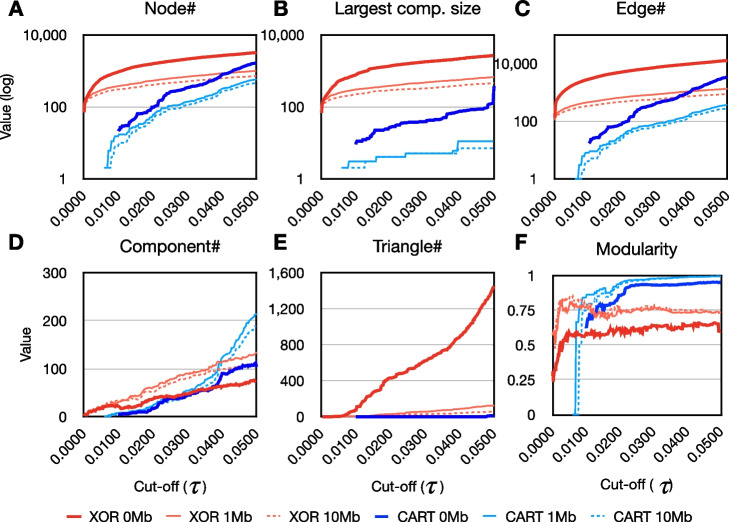
The evolution of network metrics with respect to edge weight cutoff $\tau$ for the three XOR-based epistatic networks are shown in Fig. 2. These networks are largely dominated by their largest connected component, where the ratio of nodes in the largest component to the total number of connected nodes consistently exceeds 80%. This ratio drops to 60% in LD-pruned networks. As $\tau$ increases beyond 0.0035, triangle motifs emerge in the non LD pruned network. At this point, the network consists of 440 connected nodes with 1,295 edges. A maximum modularity of $\sim 0.667$ is observed when $\tau$ reaches 0.0434. In contrast, the LD pruning process reduces the quantity of triangle network motifs and the highest network modularity occurs at a lower edge weight cutoff ($\tau =0.0029$) than the non LD pruned network.

Fig. 2.

Evolution of network metrics for Cartesian and XOR interaction models. A-F, These figures illustrate the evolution of network metrics in relation to the edge weight cut-off ($\tau$) within epistatic networks employing either Cartesian (blue) or XOR (red) interaction models. Solid bold lines represent networks without LD pruning (0Mb), while light blue and light red solid lines indicate networks with 1Mb LD pruning windows, respectively. Dashed lines correspond to the 10Mb LD pruning window

The evolution of network metrics in the Cartesian-based epistatic network is distinct compared to that of the XOR-based epistatic network. In the Cartesian network, the largest connected component does not dominate the network. This is evident as the ratio of the number of nodes in the largest component to the total number of connected nodes is always below 50%. Network fragmentation increases with the LD-based edge pruning process, as demonstrated by the greatly reduced size of the largest connected network component in LD pruned Cartesian networks (Fig. 2-B). Another distinction of the Cartesian network is its sparse occurrence of triangles (Fig. 2-E). Triangles begin to emerge when the edge weight cutoff surpasses 0.048, with 1,496 connected nodes and 2,852 edges. Even though the non LD pruned Cartesian network does develop triangles, the quantity is much lower than the XOR-based networks, highlighting the distinct network structures of the two interaction models. The Cartesian network reaches a maximum modularity of $\sim 0.951$ at a cutoff value of 0.0488. LD pruned Cartesian networks exhibit a similar pattern, with modularity approaching 1. However, this modularity is likely a consequence of the increased network fragmentation.

For non LD pruned networks, we employ the cut-off corresponding to the highest modularity edge threshold. We also explored the possibility of using the elbow point as the edge threshold (refer to Supplementary File S8-I). However, we ultimately opted not to utilize the elbow point in order to maximize the inclusion of as many SNPs as possible within the network. For LD pruned Cartesian networks, we employ a cutoff using the highest edge weight due to this retaining as many edges as possible. For LD pruned XOR networks, we instead use the highest network modularity. Given that the modularity evolution is distinct compared to Cartesian, we also adopt an edge cutoff of $\tau =0.05$ to capture all epistatic interactions with a significant adjusted p-value. The resulting epistatic networks are visualized in Fig. 3.

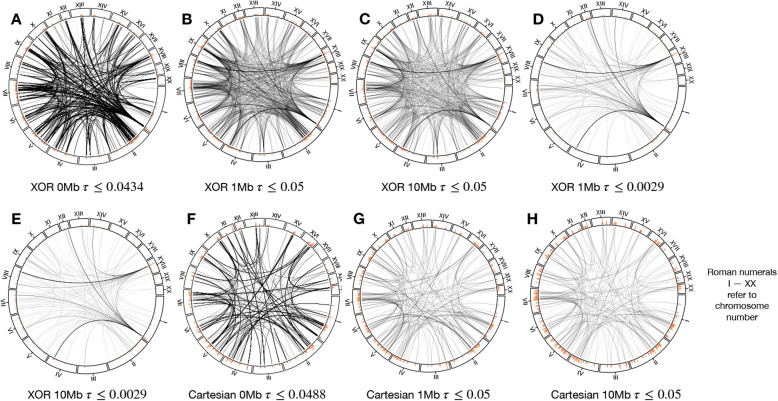
Fig. 3.

Visualization of High-Modularity epistatic networks. A For the XOR network without LD pruning (0Mb), a cutoff of $\tau =0.0434$ generates a network with 10,736 edges and 2,803 nodes. B For the XOR network with 1Mb LD pruning, $\tau =0.05$ generates a network with 993 nodes and 1,325 edges. C For the XOR network with 10Mb LD pruning, $\tau =0.05$ generates a network with 714 nodes and 872 edges. D For the XOR network with 1Mb LD pruning, $\tau =0.0029$ generates a network with 240 nodes and 271 edges. E For the XOR network with 10Mb LD pruning, $\tau =0.0029$ generates a network with 199 nodes and 215 edges. F For the Cartesian network without LD pruning (0Mb), $\tau =0.0488$ generates a network with 3,152 edges and 1,579 nodes. G For the Cartesian network with 1Mb LD pruning, $\tau =0.05$ generates a network with 584 nodes and 375 edges. H For Cartesian network with 10Mb LD pruning, $\tau =0.05$ generates a network with 468 nodes and 284 edges. Network visualizations created using Cytoscape [57] are available in Supplementary Files S8 II-VII and S9

XOR and Cartesian interaction models share similar SNPs but have distinct epistatic interactions

In addition to the metrics at the network scale, this section compares the node set, edge set, and network community allocation of the two epistatic networks with the highest network modularity. Since the node-level comparison takes into account the chromosome positions of the SNPs, we focus on comparing the two interaction models using networks without LD pruning.

Comparative analysis of node and edge overlap in XOR and Cartesian interaction models

This section explores the impact of the range parameter on the similarity assessment of nodes and edges in two distinct network models, focusing on how varying the positional range influences the identification of identical SNPs and their interactions.

As elucidated in Table 1, when comparing SNPs with their exact chromosome position (range = 0 base pairs), the two interaction models exhibit an overlap of 416 SNPs. The comparison of edges, illustrated in Table 2, shows that the two networks share 99 common edges (range = 0 base pairs), encompassing 51 SNPs. The majority of the SNPs connected by these common edges are situated within the chromosomal range of chr1.280924773 to chr1.282730801 which includes the putative quantitative trait locus (QTL) with the largest main effect signal for BMI_TAIL from the original GWAS (chr1.281788173) [47, 48].

Table 1.

Comparison of SNPs (nodes) in epistatic networks with different interaction models

Range	XOR in Cartesian		Cartesian in XOR
	Quantity	Percentage	Quantity	Percentage
0 Mb	416	14.84%	416	26.35%
1 Mb	1,979	70.60%	1,317	83.41%
2 Mb	2,209	78.81%	1,380	87.40%
3 Mb	2,354	83.98%	1,420	89.93%
4 Mb	2,416	86.19%	1,485	94.05%
5 Mb	2,467	88.01%	1,527	96.71%
6 Mb	2,530	90.26%	1,540	97.53%
7 Mb	2,559	91.30%	1,540	97.53%
8 Mb	2,571	91.72%	1,543	97.72%
9 Mb	2,614	93.26%	1,546	97.91%
10 Mb	2,656	94.76%	1,546	97.91%
All	2,803	100.00%	1,579	100.00%

Table 2.

Comparison of edges in epistatic networks with different interaction models

Range	XOR in Cartesian		Cartesian in XOR
	Quantity	Percentage	Quantity	Percentage
0 Mb	99	0.92%	99	3.14%
1 Mb	315	2.93%	682	21.64%
2 Mb	371	3.46%	834	26.46%
3 Mb	452	4.21%	1,070	33.95%
4 Mb	477	4.44%	1,217	38.61%
5 Mb	495	4.61%	1,261	40.01%
6 Mb	605	5.64%	1,302	41.31%
7 Mb	774	7.21%	1,337	42.42%
8 Mb	811	7.55%	1,691	53.65%
9 Mb	840	7.82%	2,014	63.90%
10 Mb	840	7.82%	2,312	73.35%
All	10,736	100.00%	3,152	100.00%

Further comparative investigation for the two epistatic networks considers the range parameter $\delta$ of chromosomal position. The results in Tables 1 and 2 illustrate that enlarging the base pair range $\delta$ is associated with an increase in identical SNPs and edges between XOR and Cartesian. Specifically, as the range extends from 0 to 10 Mb, 7.82% (or 840 epistatic interactions) of the interactions in the XOR model can be found in the Cartesian model. On the other direction, the fraction of identical edges in the Cartesian model is 73.35% (or 2,312 epistatic interactions), indicating that the majority of interactions in Cartesian are contained in the neighboring positions of the interactions in XOR (Table 2). Node comparison implies that the SNPs from both models are located close to each other. Table 1 demonstrates that for both models, an increase in range from 0 to 10 Mb allows for the detection of most SNPs in the other model (XOR in Cartesian: 94.76%, Cartesian in XOR: 97.91%). Overall, XOR identifies more epistatic interactions than Cartesian, but these additional interactions are located near the SNPs in Cartesian. This may result from interaction model affinity to certain loci within an LD block.

XOR exhibits more triangle network motifs than Cartesian

We also observe a remarkable distinction between the two epistatic networks in the number of triangular network motifs. In our comparison, the XOR model ($\tau =0.0434$) generates 1,033 triangles, significantly more than the nine triangles in the Cartesian model ($\tau =0.0488$). This considerable discrepancy suggests that the XOR model potentially captures more complex interactions among nodes within the network.

Another characteristic of the triangles in XOR lies in their chromosomal positions. This may suggest the XOR model has a greater potential for 3-way interactions. We observe that the SNPs of most triangles in XOR are located on different chromosomes. Whereas, the triangles in the Cartesian network are found to be on the same chromosome in close proximity, specifically within the chromosomal range of chr1.280924773 to chr1.282527574. This range overlaps with the position of the SNPs linked by the common edges (range = 0 base pairs) between the two epistatic networks (chr1.280924773 to chr1.282730801). These closely located triangles could be attributed to cis-regulatory epistatic interactions in association with the putative univariate QTL at chr1.281788173 [47, 48], or redundant false positives.

We further investigate the association between triangular motifs in epistatic networks and the presence of higher-order epistasis. To this end, we investigated the third-order epistatic p-values of all triangles in the network using the 3-way extension of the methodology presenting in Batista et al. 2024 [12], including 1,033 triangles coded in XOR and 9 triangles coded in Cartesian coordinates. Remarkably, none of the nine triangular motifs in the Cartesian model show significant 3-way epistasis (adjusted p-values less than 0.05). Conversely, approximately 13% of XOR triangles (132 out of 1,033) did result in significant 3-way epistasis (visualized in Fig. 4). The identical SNP names (N=88) involved in the 132 significant triangles in XOR result in 14 immunity-related terms (g:Profiler with a 1 Mb upstream and downstream range; File S7).

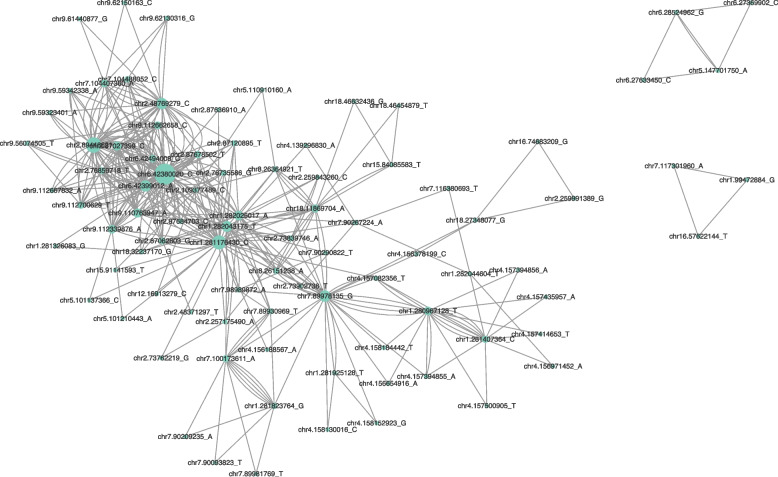
Fig. 4.

Visualization of epistatic network for XORtriangles with significant 3-way epistatic interactions. Each node represents a SNP, with the size of the node indicating the degree of interaction. The edges between nodes represent the pair-wise epistatic interactions with the XOR model. Note that pairs of nodes may be interconnected by multiple edges, stemming from our approach of incorporating edges based on triangular motifs. If an edge involves more than one triangle, then there will be more than one edge connected

XOR captures additional epistatic interactions that link to communities in Cartesian

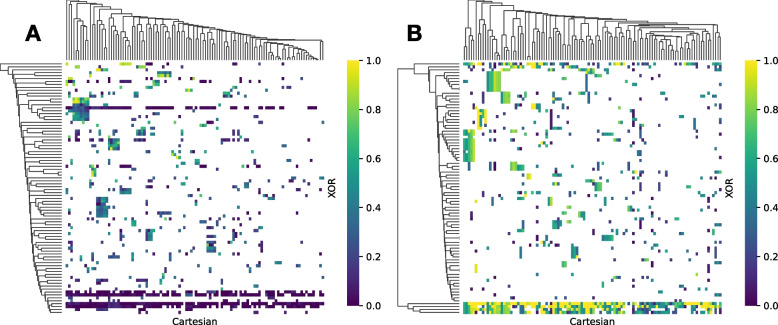
The comparative assessment of community assignments across both networks renders further insights about the common SNPs. The diagram, depicted in Fig. 5, describes the similarities of community assignments based on the normalized AUC defined in Eq. 9.

Fig. 5.

Cluster heat maps comparing the communities from different models based on normalized AUC, defined in Eq. 9. A visualization of the comparison from XOR to Cartesian. The comparison from Cartesian to XOR is shown in B)

The results elucidate the efficacy of the XOR model in identifying additional epistatic interactions, enriching our understanding of the genetic architecture by linking communities that are otherwise considered distinct in Cartesian. This is evidenced by the existence of five expansive network communities within the XOR epistatic network, which exhibit shared common SNPs with a majority of communities identified using the Cartesian model. Moreover, this pattern of SNP sharing is not restricted to the largest network communities. Smaller communities also demonstrate a consistent pattern of shared SNPs across both models. Hierarchically clustered heatmaps shown in Fig. 5 reinforce this observation, revealing a small fraction of communities that manifest congruent similarity patterns.

Enrichment analysis

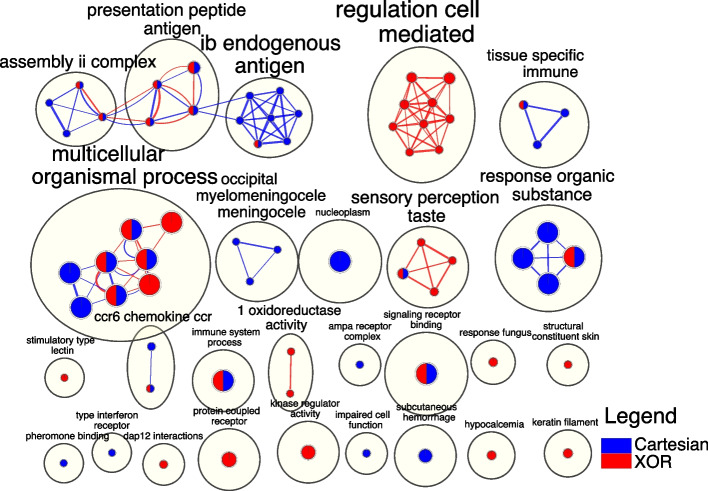
Network-scale enrichment analysis

The comparison of interaction models at the network level in R. norvegicus using g:Profiler reveals numerous functional categories for the lowest level in the hierarchy. For specific details for each category, refer to Supplementary File S2 and Fig. 6. This figure shows that most of the XOR and Cartesian terms are immunity-related. CCR6 chemokine receptor, response to organic substance, and signaling receptor binding are shared between the two epistatic networks. The XOR includes cell-mediated regulation, lectin response, DAP12 interactions, protein-coupled receptors, kinase regulator activity, hypocalcemia, skin structural constituent, and keratin filament. The Cartesian has terms for meningocele, nucleoplasm, pheromone binding, interferon receptor binding, impaired cell function and subcutaneous hemorrhage.

Fig. 6.

The EnrichmentMap depicts a network of terms extracted from SNPs within different epistatic networks (interaction models). Nodes correspond to biological terms generated from g:Profiler, while edges denote shared genes between terms. AutoAnnotate is employed to aggregate strongly interconnected nodes using cycles, with the theme of the enclosed terms delineated beside each cycle. The node size and edge thickness are proportionate to the gene count they represent. The origin of nodes and edges is indicated by a color coding scheme, where blue denotes origination from Cartesian and red from XOR

Referring to the detailed tables in Supplementary File S3, for GO:BP, most of the XOR terms highlight lectin response, sensory reception of bitter taste, and leukocyte mediated cytotoxicity while Cartesian terms primarily include immune responses, chemical stimuli, and developmental processes (seen in Fig. 6). Networks share terms associated with immunity and sensory perception of taste (visualized in Fig. 6. For GO:CC, the XOR network includes terms for cytoplasm and keratin filament (shown in Fig. 6), while the Cartesian network includes nucleoplasm terms. The shared terms include MHC protein complex. For GO:MF, the XOR network includes terms relating to skin epidermis structural constituent, ketosteroid monooxygenase activity, G-protein-coupled receptor binding, NADP+ oxidoreductase activity and kinase regulator activity, while the Cartesian network includes terms for pheromone binding, type I interferon receptor binding, and CCR chemokine receptor binding. Shared GO:MF terms include binding, signaling receptor binding, and CCR6 chemokine receptor binding.

For KEGG pathways, the Cartesian network includes terms related to diseases (immune system related), infections, phagosome, taste transduction, vitamin metabolism, and MAPK signaling pathway. In contrast, XOR includes gap junction and glutamatergic synapse. Shared terms between the two include one signaling pathway and terms associated with various diseases and immunity. For REAC, Cartesian pathways include the ER-phagosome pathway and the Endosomal/Vacuolor pathway while XOR includes DAP12 interactions. There are no shared REAC terms between the interaction models. For the other sources, such as “Transcription Factor” and “miRNA”, please refer to Supplementary File S2 in sheets TF-CartvsXOR and miRNA-CartvsXOR, respectively.

For the broad categorization (first child of the parent) analysis, almost all categories have shared terms relating to immunity. For the GO:BP category, Cartesian includes terms for cellular development, cellular differentiation, and cellular response to differentiation. The XOR has terms related to response to stimulus and regulation, while shared terms included sensory perception and immune response. Under GO:CC, Cartesian included intracellular membrane-bounded organelle and organelle lumen while XOR has terms such as cytoplasm, non membrane-bounded organelle, and supramolecular complex. The shared terms are plasma membrane, membrane protein complex and intracellular organelle. Under the GO:MF, Cartesian has terms for odorant binding, cytokine receptor binding, and protein-containing complex binding while XOR included terms for structural constituent of skin, oxidoreductase activity and kinase regulator activity. Shared terms are protein binding, receptor binding and binding. For KEGG, the Cartesian has terms for signaling molecules, transport and catabolism, sensory system, vitamin metabolism, and cancer. XOR includes cellular community and nervous system, while shared terms include immunity, cardiovascular system, and endocrine and metabolic disease. For REAC, there are no unique terms for XOR and Cartesian and only signal transduction is in the shared category. For specific details for each category, please refer to Supplementary File S4.

Community-specific enrichment analysis for different interaction models

The community-scale biological enrichment analysis unveils the distinct and shared functional roles of each SNP community.

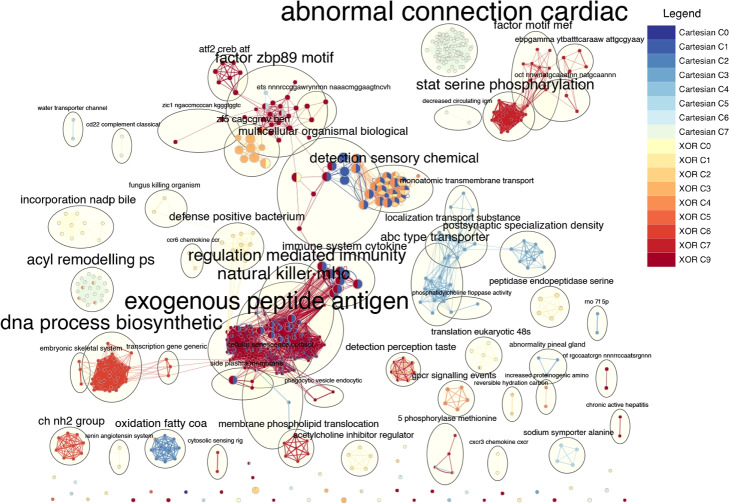
The largest term cluster within EnrichmentMap in Fig. 7 is named “exogenous peptide antigen”. Most of the large networks observed are related to immunity and defense responses. Most of the Cartesian communities contain terms related to transporters, signal transduction, chemical detection, organismal development, and fatty acid oxidation. The terms from XOR communities mostly include lipid transport and membrane dynamics, taste perception, amino acid synthesis, signaling, differentiation and development, DNA synthesis, and post-translational modifications. The comparison between interaction models reveals that the XOR model identifies a broader spectrum of biological terms that could be linked to BMI. A similar result was observed in the epistatic analysis our SNPs were derived from [12]. In particular, we observe clusters such as “detection perception taste”, “fatty acid oxidation”, “amino acid synthesis” which reflect terms related to rat visual and digestive systems.

Fig. 7.

The EnrichmentMap portrays a community-scale comparison of terms derived from SNP communities within distinct epistatic network models. Nodes symbolize biological terms generated from g:Profiler and edges signify the shared genes among these terms. AutoAnnotate clusters closely linked nodes into communities, with each cluster’s overarching theme inscribed beside the cycle. Node size and edge breadth are scaled to the quantity of genes they signify. The origin of nodes and edges is depicted with colors shown in the legend

We generated one table for the communities looking at unique terms across encodings and communities. We used the first child of parent to conduct this analysis. For Cartesian, community C0 has a solitary term, “digestive system” under KEGG, related to metabolism. No terms were unique to C0, C4, and C6 for Cartesian. For XOR, C0 contains “Metabolism of vitamins and cofactors” under REAC, C5 includes “Glycan biosynthesis and metabolism” under KEGG, C6 has terms related to organic compound biosynthetic and metabolic processes under GO:BP, and C7 includes “Metabolism of amino acids and derivatives” under REAC. For specific details with all communities and encodings, please refer to the Supplementary File S6. We also conducted the same analysis using the terms themselves. Under Cartesian, C0 has “Triglyceride lipase activity” under GO:MF and “Fat digestion and absorption” under KEGG. C2 includes terms such as “Fatty acid beta-oxidation multienzyme complex” under GO:CC, metabolic pathways involving fatty acid metabolism under REAC, and “Cortisol synthesis and secretion” under KEGG. Community C3 has terms exclusively for transporter activity. Community C7 includes “Long-term depression”, “Ether lipid metabolism” under KEGG, “Glycerophospholipid catabolic activity” under GO:BP, and terms relating to lipid metabolism under REAC. For XOR, community C0 comprises terms related to the metabolism of vitamins, minerals, and bile acids and salts under REAC. Community C2 has “Carbonate dehydratase activity” under GO:MF. C5 contains “Mannose type O-glycan biosynthesis” under KEGG, and “Serotonin and Anxiety” under WikiPathways (WP). C6 has terms related to amino acid metabolism under KEGG, and terms related to organic compound biosynthetic and metabolic processes under GO:BP. For C7, the terms include membrane lipid regulation under GO:BP, and amino acid metabolism under KEGG. Under C9, “Lipid and atherosclerosis” is under the KEGG source. Please refer to Supplementary File S5 for the complete table.

Network investigation for permuted networks

We conducted 1,000 network permutation to shuffle the observed epistatic network while preserving its node degree distribution (Supplementary File S8 VIII). In this section, we examine network properties, including the number of disconnected components, the size of the largest connected component, the number of triangle motifs, and modularity. The investigation compares epistatic network with and without the LD pruning process against permuted networks. Overall, the observed networks without LD pruning exhibit distinct properties compared to permuted networks, suggesting that the network patterns of the observed structure may arise from trait-relevant epistatic interactions.

For the epistatic networks without LD pruning, consistent network patterns were observed across both the XOR and Cartesian epistatic models. Quantifying the disparity using Z-score, the observed network displays a significantly higher number of connected components (XOR 0Mb: 48.77, Cartesian 0Mb: 13.49), a smaller largest connected component size (XOR 0Mb: −171.80, Cartesian 0Mb: −121.03), fewer triangle motifs (XOR 0Mb: −47.05, Cartesian 0Mb: −5.11), and greater modularity (XOR 0Mb: 141.90, Cartesian 0Mb: 146.12). These findings indicate that epistatic networks without LD edge pruning are more fragmented and contain fewer triangle motifs than expected under the null hypothesis, which could facilitate increased modularity.

On the other hand, most network properties of epistatic network with LD pruning also exhibit differences from the original network. Notably, in the XOR 1Mb network, the network has a greater modularity (Z-score: −5.43) than the null hypothesis at an edge weight cutoff of 0.05 (Supplementary File S8 VIII-C). This characteristic suggests less prominent community structure can be attributed to its more prominent triangle motifs (Z-score: 3.18). The Cartesian 1Mb network (Supplementary File S8 VIII-E), meanwhile, is more fragmented compared with null hypothesis model, as suggested by the number of connected network components (Z-score: 21.84) and the size of the largest connected component (Z-score: −1.19).

Discussion

Our comparative network analysis on epistatic networks reveals that distinct network structures emerge from different network models. This disparity arises from XOR’s improved sensitivity to epistatic interactions compared to the Cartesian model. We found that the XOR model can capture additional epistatic interactions between the same set of SNPs captured by Cartesian and the second-order XOR model presents a unique network motif that can be used to discover higher-order epistasis. Through functional enrichment analysis at the network community scale, we uncovered that the XOR model effectively identifies additional biologically relevant terms and functions, which the Cartesian model fails to detect. Our results underscore XOR’s capability to implicate important biological relationships between SNPs, but also highlight the critical role of network structure analysis in investigating epistasis. Our findings offer new evidence on the biological plausibility of the XOR model and the use of network-based investigation genetic interactions underlying complex traits.

Distinct epistatic networks evolve under each interaction model

We compare epistatic networks constructed from different interaction models. Each network is defined by the threshold $\tau$ that maximizes its modularity, ensuring that the resulting networks are optimally organized into distinct modules.

Figure 2 summarizes the network structure discrepancy between the two epistatic models. The XOR networks are characterized by a larger number of nodes and edges compared to the Cartesian networks. We further observe that most SNPs in both non LD pruned epistatic networks are closely located with each other in regards to genomic position (Table 1), and most edges in the Cartesian network are also present in the XOR network, but not the other way around (Table 2). This implies that the XOR model captures more epistatic interactions involving an adjacent set of SNPs.

A significant difference is also observed in the network community structure. The XOR network is dominated by its largest connected component, as additional edges in the XOR network link different components found in the Cartesian model. This leads to a more unified network community in the XOR network, while the Cartesian network is more fragmented.

We also observe that the XOR network contains a greater number of triangles (n = 1,033) than Cartesian (Fig. 2-E). We consider the triangle motifs in Cartesian (n = 9) are likely false-positives for higher-order epistasis as the positions of the corresponding SNPs are in close genomic proximity. Although close cis-acting epistasis is another possible explanation, the Cartesian triangles likely arise from high levels of LD with a locus with high main effect. When testing these triangle motifs for 3-way epistasis, we find that approximately 13% of the triangles in the XOR network have significant adjusted p-values. This result suggests that the XOR model, when combining network investigation, can discover higher-order epistatic interactions through the topology of second-order interactions. This finding is encouraging because if higher-order interactions can be discovered using the network structure of lower-order epistasis, the time and complexity of discovering higher-order interactions will be greatly reduced.

Last but not least, the XOR network has a lower modularity compared to the Cartesian network. This lower modularity in XOR can be attributed mainly to the additional epistatic interactions it captures, which tend to bridge distinct network communities found by the Cartesian model. These bridging edges often span across different network communities, thereby reducing modularity. Additionally, the presence of triangles in the XOR network, especially those that cross community boundaries, further contributes to the reduced modularity. In contrast, the near absence of triangles and the higher number of disconnected components in the Cartesian network contribute to its higher modularity, indicating a more segmented community structure than the XOR network.

Network level enrichment analysis reveals shared and unique biological signals between interaction models

Our enrichment results at the network level indicate both shared and unique biological signals in each model’s network. GO terms, KEGG and REAC pathways reveal that immunity-based enrichments are shared between Cartesian and XOR models at both high and low levels of biological organization that we assessed in our enrichment analysis (see Supplementary Files S2, S3 and S4). This is somewhat expected due to ubiquity of immunity-based enrichments regularly observed across systems and phenotypes [58–62] including in the results of the original epistasis analysis that this work is inspired by [12]. Immune functions are underlain by diverse gene networks that are integral to general stress responses observed in many systems [44, 59, 63]. High BMI likely induces stress response mechanisms that activate immunity-related genes and gene networks. Our results suggest that immunity-related signals are detectable and prevalent in our networks regardless of the epistatic model used.

Under GO:BP in both XOR and Cartesian networks, we observe terms for sensory perception of taste and taste transduction. Specific to the Cartesian network, we observe REAC pathways relating to taste transduction and reception. (see Supplementary File S3). These terms are clearly connected to ingestion and metabolism [64, 65] and are likely directly related to BMI. We also see terms for cell differentiation and development that could be related to adipogenesis, which has an important role in BMI [66]. In XOR network, we particularly observe terms relating to sensory perception of bitter taste. It has been studied that humans with obesity often have a decreased sensitivity to bitter taste [67]. Earlier studies have also linked bitter taste to G-protein coupled receptors [68–70], which was observed under the GO:MF terms for the XOR network. Under the XOR network, we also see GO:BP, GO:MF, and KEGG terms associated with cell-cell signaling and receptor binding. These are accompanied by enrichments associated with lectin receptor activity. But since these phrases are related to immunity, they probably also belong to the shared immunity-related terms in the Cartesian network. Furthermore, under XOR, we observe glutamatergic synapse, which has been shown to be associated with food intake and body weight [71]. One more interesting observation under XOR is the structural constituent of the skin epidermis which has also been linked to obesity [72].

Taken together, our network-level enrichment results indicate that broad biological systems can be implicated using either interaction model in regard to BMI in rats. Similar results were observed in the original epistatic analysis where terms shared by both interaction models were involved in immunity [12]. However, each model has the potential to highlight unique pathways that would have been missed if only one interaction model was utilized in this system. Moreover, our enrichment results align with findings from our network analysis in that each epistatic network’s unique topology likely highlights distinct genetic architectures associated with the phenotype. Our analysis here serves as evidence illustrating that the Cartesian interaction model (or any one model) alone is not adequate to explore all of the possible epistatic interactions that occur in living systems and should be supplemented by other models/penetrance functions, including non-linearly separable models, like XOR.

Community level enrichment analysis highlights the advantages of the XOR model and network investigation

The exploration of epistatic networks using community-based enrichment analysis reveals that the XOR model uncovers network structures containing a greater abundance of metabolic terms compared to the Cartesian model, particularly within this specific system and phenotype. For Cartesian, we observe GO and KEGG pathways in communities C0 and C2 that relate to lipase activity, mitochondrial fatty acid oxidation, and fat digestion and absorption. It has been shown that fatty acid oxidation is directly linked to metabolism and could have potential in therapies for obesity [73, 74]. In communities C5 and C6, we observe terms relating to ion and water channel activity. The roles of ion channels in the development of obesity in rats have been well documented and are involved in adipose cell proliferation, food intake, and gastric emptying (overeating) [75]. Specific to the XOR network, we observe that community C0 has terms for the metabolism of fat-soluble vitamins, bile acid, and bile salt synthesis. A recent study investigated the interaction between vitamin D and obesity and BMI and numerous studies have found an inverse association [76]. Communities C5, C6, and C7 have terms involving amino acid metabolism, and also serotonin and anxiety. A recent study demonstrated that obesity induced by a high-fat diet elevates neuroinflammation and heightens anxiety-related defensive behaviors. The serotonergic system, which plays a key role in emotional regulation, was found to be particularly significant in modulating these anxiety-like responses [77]. Metabolism of branched-chain amino acids was found to be involved in the pathogenesis of obesity and type-II diabetes [78]. At the first child of parent level, community C0 within the Cartesian has a digestive system term likely has broad implications regarding metabolism and BMI. Within the XOR network, communities C5, C6, and C7 have terms relating to amino acid metabolism, which was also seen at the term level as well.

In conclusion, our community-level enrichment analysis highlights the efficacy of XOR as a model of epistasis in this system and phenotype. The unique interactions and biological insights identified by XOR at the network level and via GSEA are pivotal in revealing a more profound understanding of the genetic architecture of BMI in rats. These results also highlight the need for network structure analysis and the unique advantages of XOR coding, and perhaps other interaction models, in epistasis studies by extracting more of the “hidden heritability” underlying important phenotypes and diseases.

LD network pruning reduces redundancy but may lead to network fragmentation

LD pruning eliminates redundant SNPs. When this approach is extended to network-based epistasis analysis, a significant number of edges are removed (Fig. 2-E). However, we found that removing redundant epistatic interactions may also result in network fragmentation. Due to this reason, the major analysis of this research is performed on non LD pruned networks to allow for a more comprehensive investigation of epistatic interactions.

The effects of network fragmentation vary between different epistasis models. As shown in Fig. 2-B, LD-pruned XOR networks maintain large connected components that span most of their nodes (Supplementary File S8 III-V). In contrast, LD-pruned Cartesian networks fail to form obvious connected components (Supplementary File S8 VII), with the largest component containing no more than 11 nodes. This difference is likely due to the XOR model detecting more epistatic interactions between existing network communities compared to the Cartesian model, which makes the XOR network more resistant to fragmentation from LD pruning.

LD-induced fragmentation can also reduce the size of hub nodes in epistatic networks, distributing their connections to multiple smaller hubs in LD pruned networks. In the 1 Mb LD pruned XOR network ($\tau =0.0029$), two of the three hub nodes (chr1.281176430_C and chr1.282025017_A) appear to be highly duplicated (Supplementary File S8 III and S9). These nodes are located close to each other on chromosome 1 and share 393 common neighbors in the unpruned network (chr1.281176430_C has 626 neighbors, and chr1.282025017_A has 639 neighbors). It is important to note that these hubs are in close genomic proximity of the SNP with the largest univariate signal in the original GWAS study our SNPs are derived from [47, 48]. Thus, this duplication is likely due to strong LD in this genomic region. However, duplicated hubs do not pose an issue in the network without edge pruning, as each forms its own hub. The LD pruning process forces edges of duplicated hubs to compete with each other, distributing the connections of hub nodes across multiple smaller hubs in the pruned network.

LD epistasis pruning also has a negative impact on the number of triangle motifs in the XOR network. As shown in Fig. 2, LD pruning drastically reduces the number of triangles, from 1,146 (in the 0Mb network at $\tau =0.05$) to 126 (in the 1Mb network at $\tau =0.05$). This suggests a reduced likelihood of detecting higher-order epistatic interactions. The loss of triangles may stem from a similar mechanism as hub shrinkage process, where the likelihood of retaining all three edges necessary to form a triangle diminishes due to LD pruning, causing these motifs to vanish in the pruned network.

Overall, LD pruning leads to greater network fragmentation, with the Cartesian network being notably more susceptible, resulting in a sparse and limited network. Although 1 Mb pruning is likely the most biologically relevant in this system, we focus on the non LD pruned networks to highlight the differences between the interaction encodings and showcase the potential of our network-based approach to investigate epistatic interactions.

Limitations and future work

The construction of the epistatic networks uses the precise chromosomal positions of SNP to discriminate individual nodes. Consequently, nodes and edges in close proximity are identified as separate entities. However, such over detailed representation could result in network fragmentation after LD pruning among edges. There is a clear need for advanced analytical methods that can account for the similarities among nodes and edges. To overcome this challenge, the adoption of network representation learning methods, especially graph neural networks [79], emerges as a promising solution. These techniques excel at generating embedding representations for the information associated with the nodes [80, 81]. In the context of our epistatic networks, these embeddings are capable of identifying nodes and edges with similar chromosomal positions, thereby substantially improving the efficiency of network analysis while avoiding the effects of network fragmentation from LD edge pruning. In addition to network fragmentation, asymmetric associations between loci pose another challenge in constructing reliable interaction networks. Asymmetric associations occur when one locus has a strong interaction with another, but the reverse interaction is weaker or absent. This can lead to false-positive detection of epistasis, as these interactions may appear dependent when they are not truly reciprocal. Although the original manuscript [12] applied stringent quality control measures, such as FDR correction and permutation testing, the current analysis may still be susceptible to these effects. Future work should explore more advanced models to better distinguish true interactions from asymmetric associations, potentially incorporating statistical tests that assess the bidirectionality of interactions or machine learning models designed to capture complex dependencies. Addressing this limitation is essential to ensure the robustness and interpretability of the constructed networks. Additionally, while our study identifies statistical epistasis using interaction models and significance testing, it is important to recognize that statistical epistasis does not necessarily imply biological epistasis. Therefore, future work should focus on validating statistically significant epistatic pairs through experimentation. Validation in systems like R. norvegicus through techniques such as gene editing or other approaches will help distinguish between genuine biological interactions and statistical associations.

Conclusions

This comparative network analysis illustrates that multiple interaction models help elucidate complex epistatic interactions in a model system. Although both models identify distinct network structures, the XOR model integrates network communities found in Cartesian, revealing novel biological functions through community-scale enrichment analysis. Specifically, the fifth community within the XOR network has revealed WP terms associated with serotonin and anxiety pathways that had not been previously implicated to be involved with BMI, obesity, or metabolism in our earlier study [12] Additionally, the XOR model identifies unique triangular motifs, with approximately 13% being significant for three-way epistasis after FDR correction, demonstrating a novel approach for identifying complex interactions through lower-order interaction topologies. These motifs may simplify the identification of high-order interactions in epistatic data, which is often computationally expensive. In summary, this comparative analysis highlights the importance of network analysis in epistasis studies. We illustrate that networks connect different entities, providing a more complete view of the complex associations underlying epistatic interactions. Using this approach, we identify novel biological insights and evidence of higher-order epistasis not found in the original study.

Abbreviations

AKT

AK strain Transforming

AUC

Area Under the Curve

BMI

Body Mass Index

BP

Biological Process

CC

Cellular Component

EGFR

Estimated Glomerular Filtration Rate

ERBB2

ERythroBlastic oncogene B receptor tyrosine kinase 2

FDR

False Discovery Rate

GO

Gene Ontology

GSEA

Gene Set Enrichment Analysis

GWAS

Genome-Wide Association Study

KEGG

Kyoto Encyclopedia of Genes and Genomes

LD

Linkage Disequilibrium

Mb

MegaBase(s) (1e6 base pairs)

MHC

Major Histocompatibility Complex

MLG

Multi-Locus Genotype

MF

Molecular Function

OSA

Over-Representation Analysis

QTL

Quantitative Trait Locus

REAC

REACtome pathway database

SNP

Single Nucleotide Polymorphism

TFs

Transcription Factors

WP

WikiPathways

XOR

eXclusive OR

Authors’ contributions

ZS, PJF, and PB contributed equally to this work. ZS, PJF, and PB wrote the original manuscript. ZS performed all network science analyses and network/community-based functional enrichment analysis using g:Profiler and EnrichmentMap. PF and PB performed hierarchical GSEA analyses and term comparisons. PF and PB implemented 3-way epistasis analysis for SNPs associated with Cartesian and XOR triangle motifs. AG and NM assisted in implementing this additional 3-way analysis and also with code troubleshooting. JHM and TH served as mentors, providing guidance and assistance, as well as editing the final manuscript. All authors read and approved the final manuscript.

Funding

The authors gratefully acknowledge support from the NIH under Grant R01 LM010098 awarded to Jason H. Moore.

Data availability

Rat phenotype data and GWAS summary statistics are available at https://library.ucsd.edu/dc/object/bb83725195. Rat genotype data are available at https://library.ucsd.edu/dc/object/bb15123938. The implementations of the algorithms for 2-way and 3-way epistasis detection given in Python are offered via GitHub at https://github.com/EpistasisLab/epistasis_detection. The implementations of the network investigation given in Python are offered via GitHub at https://github.com/shazhendong/Network_Epistasis. The scripts to perform GSEA and obtain the parents of interest and genes given a set of SNPs are available on the Open Science Framework (OSF): https://osf.io/qfnec/.

Declarations

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.