A dual-adaptive stochastic reinforcement chimp optimization algorithm for fire detection and multidimensional problem solving

Ziyang Zhang; Lingye Tan; Diego Martín; Leren Qian; Mohammad Khishe; Pradeep Jangir

doi:10.1038/s41598-024-82592-4

. 2024 Dec 28;14:31226. doi: 10.1038/s41598-024-82592-4

A dual-adaptive stochastic reinforcement chimp optimization algorithm for fire detection and multidimensional problem solving

Ziyang Zhang ¹, Lingye Tan ¹, Diego Martín ², Leren Qian ³, Mohammad Khishe ^4,^5,^6,^7,^8,^✉, Pradeep Jangir ^7,^9,^10,¹¹

PMCID: PMC11682094 PMID: 39732978

Abstract

Chimp optimization algorithm (CHOA) is a recently developed nature-inspired technique that mimics the swarm intelligence of chimpanzee colonies. However, the original CHOA suffers from slow convergence and a tendency to reach local optima when dealing with multidimensional problems. To address these limitations, we propose TASR-CHOA, a twofold adaptive stochastic reinforced variant. The TASR-CHOA algorithm integrates two novel methodologies: a stochastic approach to improve the speed at which convergence is achieved and a dual adaptive weighting approach to optimize the exploration of early patterns, which refer to initial trends or behaviors in the algorithm’s convergence process during the early stages of iterations and the exploitation of subsequent tendencies, indicating how these initial trends develop over time as the algorithm iterates and refines its search. To evaluate TASR-CHOA, we apply it to 29 conventional optimization benchmark functions, 10 IEEE CEC-06 benchmarks, 30 complicated IEEE CEC-BC benchmark functions, and ten well-known benchmark real-world challenges. We evaluate TASR-CHOA against 4 categorical optimization techniques as well as 18 top IEEE CEC-BC algorithms. Based on our broad investigation done using three statistical tests, we claim that TASR-CHOA outperforms the majority of the algorithms since within a position takes the best place, 54 out of 73 evaluation functions and engineering problems. In other cases, the results are almost the same as those of SHADE and CMA-ES over several comparisons. As an illustrative application of this joint approach, a computer-aided fire detection task is performed using a deep convolutional neural network combined with TASR-CHOA. We also outline the algorithm executed in steps, indicating computational complexity, which is O(NI×NV) + O(NI×NV×6) + O(NI×NV + 2×NI×NV) as a function of number of individuals (NI) and dimensions (NV).

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-82592-4.

Keywords: Chimp optimization algorithm, Metaheuristic, Twofold adaptive weighting, IEEE CEC-BC competitions, Optimization, Multidimensional problems

Subject terms: Environmental sciences, Engineering

Introduction

We need more advanced optimization techniques because engineering optimization and its related fields are always looking for better designs, ways to recognize and estimate, and ways to predict system efficiency^1–3. As a result, an urgent need for better optimization methods arises⁴. Evolutionary algorithms are the best way to deal with complex optimization problems, as these algorithms are widely used⁵. This is because such approaches adapt well to real-life engineering activities where they seek to mimic processes and use biological intelligence for efficiency⁶. Recently, the CHOA has been acknowledged as a nature-inspired algorithm that is useful in solving optimization problems⁷.

The rationale for selecting CHOA for multimodal and fire detection problems.

CHOA was chosen for this study because it has some specific advantages, especially when addressing optimization problems in fire detection systems⁸. CHOA is a novel search algorithm developed on the social and cognitive behavior models of chimpanzees for effective search space exploration and search space exploitation⁹. The main benefit of CHOA is the shifting between exploration and exploitation when needed¹⁰. This is very important during fire detection, where the search space can be complicated, and the target can be multidimensional, among others^11–14. Apart from that, instantaneous reinforcement is another unique feature of CHOA that allows it to modify its search strategy dynamically and improve its effectiveness in stable but rapidly changing environments, such as fire detection situations.

Compared to other methods of more established optimization where a genetic algorithm (GA)¹⁵, particle swarm optimization (PSO)¹⁶, and differential evolution (DE)¹⁷ may be concerned, CHOA presents many benefits. PSO, though convergent, often exhibits a severe drawback, which is premature convergence on most multi-modal problems dominated by a multitude of local optima. On the contrary, there are mechanisms integrated within CHOA that help to alleviate the problem of premature convergence through the induced search of novel solution spaces. Also, GA includes costly operations such as crossover and mutation, which leads to the increased time taken to optimize, whereas CHOA utilizes efficient less update mechanisms to ensure quick sensitivity. DE, on the other hand, works well in simple optimization of operations such as real numbers but would make one inefficient within spaces that have high dimensions¹⁸. However, the CHOA layout focuses on the retention of population diversity, ensuring higher efficacy in solving high-dimensional complex optimization problems such as the fire detection problem¹⁹. Therefore, the overall performance of the CHOA report improves the ability to solve some tasks of fire detection optimization, particularly within local optima and dynamic problems changing over time.

As much as we appreciate these efforts as research, we should also point out that seeking to find new paradigms or using new techniques as first attempts to solve a well-known problem may not be the most constructive course of action in conducting research²⁰.

In the second variant, the CHOA technique has merged with other techniques to enhance the efficiency and productivity; these are hybrid RVFL-CHOA²¹, hybrid whale-CHOA²², CHOA with spotted hyena (SSC)²³, flexible-constrained time-dependent hybrid reliability-based design and cuckoo search-based hybrid chimp²⁴, and SCHOA/CHOA with dragonfly processing²⁵, a two-phase CHOA with other methods²⁶, CHOA fused with random forests and other methods²⁷, and the SCHOA²⁸. While the suggested hybrid algorithms have really improved accuracy to a great extent, their primary downside lies in their immense complexity.

Finally, the researchers endeavored to improve the CHOA performance by engaging in the development and modification of a range of operators. For example, in IChOA, the opposition-based Lévy flight chimp optimizer was utilized to evolve the transition behavior between the exploration and exploitation stages²⁹. In the Fuzzified CHOA³⁰, CHOA was developed with fuzzification to optimize the setting variables in CHOA. In the ECHOA³¹, the species underwent a specific mutation and rank correlation coefficients to assess the social position of chimpanzees with the lowest standing in society. Gang Hu et al.³² proposed an improved version of CHOA called SOCSCHOA combined with cuckoo search and selective opposition to improve the total optimization performance. An original chimp optimization technique, including refraction learning, was proposed by Quan Zhang et al. (RL-ChOA)³³. By using the Tent chaotic system for population initialization in RL-ChOA, they increase variability in the population and speed up the algorithm’s convergence. In addition, ChOA introduces a refraction learning approach that is opposition-based learning that helps the population leap out of the local optimum using the physical theory of light refraction. For the 3D route planning issue, Nating Du et al.³⁴ presented an enhanced CHOA using a somersault foraging method with adaptive weight. To begin, a weighting factor obtained from the ChOA’s coefficient vector was introduced into the coordinates, updating the formula for real-time fine-tuning. Second, the somersault foraging technique was used to safeguard against the occurrence of a local optimum in the final phase, and this change also had a little positive effect on early-stage population diversity. In a recent work by Khishe et al.³⁵, the third-weighted chimpanzee optimization algorithm, WCHOA, was introduced for the purpose of improving convergence speed. In addition, Wei Kaidi et al.³⁶ proposed a method known as dynamic levy flight DLF, which unfolds the transformations of the CHOA algorithm, leading to DLFCHOA. Qian³⁷ proposed an improved CHOA using spiral exploitation behavior to improve exploitation behavior. Qian³⁸ proposed an improved CHOA based on a hybrid extreme learning machine technique to diagnose breast cancer using an evolving deep convolutional neural network.

While the strategies mentioned above offered certain advantages in specific stages of exploration and exploitation or in optimizing the interaction between these stages, they were primarily beneficial in either accelerating convergence or preventing the occurrence of local optima. Despite the fact that algorithms such as DLFCHOA and SOCSCHOA performed well in both phases, they had high temporal complexity.

Motivations

Considering the no-free lunch theory³⁹ and the above-listed drawbacks, we tried fusion methods, which are expected to provide improved performance over exploration or exploitation alone. This strategy would improve the convergence rate and avoid the algorithm being trapped within a localized optimum.

Due to the simple mathematics, few adjustable parameters, and efficient multiple optimization of CHOA, it has been favored over the other evolutions of bioinspired systems and swarm-based optimization algorithms. However, CHOA has many problems as well, in particular, the large problem-solving tendency, which makes CHOA ineffective because it gets stuck at the local rather than the global optimum solution. Hence, the design of a new concept known as TASR in this work is motivated by the need to enhance the performance of CHOA in handling more and more complex optimization problems.

Contribution

We introduce the TASR-CHOA method based on an adaptive two-way stochastic reinforcement. The method of CHOA enhances the rate of convergence in solving multi-dimensional optimization problems.
The TASR-CHOA algorithm not only improves the CHOA’s performance but also shows improved convergence in most cases when compared to standard CHOA algorithms. This progress is made by self-adjusting the weights and utilizing a reinforcement scheme that allows knowledge transfer among chimpanzees.
This paper provides a detailed overview of the complexity of computation for TASR-CHOA, and thus, the efficiency of the chosen algorithm with respect to time and space is put on an elaborate edifice. This analysis aims to facilitate researchers’ comprehension of the algorithm’s performance characteristics.
To address the limitations commonly encountered in real-world engineering optimization problems, the TASR-CHOA proposes an innovative means of addressing constraints.

TASR-CHOA is subjected to severe evaluation, and we made use of 29 conventional optimization benchmark problems, 30 test functions of complex optimization, 10 engineering problem solutions, and 10 functions from the IEEE CEC06 test suite. We compared TASR-CHOA in opposition to four categories of conventional optimization methods, including (1) dynamic levy flight CHOA (DLFCHOA)³⁶, universal learning CHOA (ULCHOA)⁴⁰, enhanced CHOA (ECHOA)²⁹, niching CHOA (NCHOA)⁴¹, improved CHOA (ICHOA)³⁴ as novel variants of CHOA, (2) adaptive reinforcement-based genetic algorithm (ARBGA)⁴² and adaptive reinforced whale optimization algorithm (ARWOA)⁴³ (two best adaptive reinforcement variant optimizers), (3) SHADE⁴⁴, CMA-ES⁴⁴, and LSHADESPACMA⁴⁵ as the three cutting-edge optimizers, and DISHchain1e + 12, jDE100, EBOwithCMAR, and CIPDE as the best optimization algorithms in IEEE CEC-BC⁴⁵. A thorough assessment is conducted utilizing non-parametric mathematical evaluations: Holm’s sequential Bonferroni procedure⁴⁶, Wilcoxon rank-sum⁴⁷, and Friedman-type rank tests⁴⁸.

This paper is organized as follows: Sect. 2 provides a basic understanding of CHOA. In Sect. 3, the TASR-CHOA methods are described in detail. Section 4 demonstrates the use of TASR-CHOA in benchmark functions and engineering problems. The last portion of the paper sums up the main results and gives some room for several future developments.

Chimp optimization algorithm

There are four different stages in CHOA’s hunting activity, which comprise driving, chasing, obstructing, and attacking. Chimps are initially raised entirely arbitrarily for the purpose of starting the CHOA. Other chimps are allocated into one of the four categories using a similar technique but employing different mathematical models for each classification. Chapter three represents the mathematical model for hunting in CHOA using a number of equations from Eq. (1) to (4)⁷:

Here, t denotes the total number of iteration numbers, A and B represent the coefficient vectors, p_prey denotes the best encountered so far, and p_chimp represents the best location of the chimp. The D coefficient also has a positive value that tends to decrease in the range of [2.5,0]. Within the terms r₁ and r₂, some random values exist, and these vary in the range of [0,1], and C designates the vectors that are used with the chaotic mapping. These coefficients and mappings are presented in detail in⁷.

Using prey to replicate chimpanzees’ activities statistically is the primary and most effective method for researching their behavior, even with our limited information of the originating prey’s whereabouts. Four of the highest-ranking chimps will be living at the CHOA. Then, as Eqs. (5) and (6) suggest that the inferior chimps will have to go, forcing the rest of the species to do the same⁷.

Where

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{gathered} {\mathbf{p}}_{1} = {\mathbf{p}}_{A} - {\mathbf{A}}_{1} \cdot \left| {{\mathbf{B}}_{1} \cdot {\mathbf{p}}_{A} - {\mathbf{C}}_{1} \cdot {\mathbf{p}}} \right| \hfill \\ {\mathbf{p}}_{2} = {\mathbf{p}}_{B} - {\mathbf{A}}_{2} \cdot \left| {{\mathbf{B}}_{2} \cdot {\mathbf{p}}_{B} - {\mathbf{C}}_{2} \cdot {\mathbf{p}}} \right| \hfill \\ {\mathbf{p}}_{3} = {\mathbf{p}}_{C} - {\mathbf{A}}_{3} \cdot \left| {{\mathbf{B}}_{3} \cdot {\mathbf{p}}_{C} - {\mathbf{C}}_{3} \cdot {\mathbf{p}}} \right| \hfill \\ {\mathbf{p}}_{4} = {\mathbf{p}}_{D} - {\mathbf{A}}_{4} \cdot \left| {{\mathbf{B}}_{4} \cdot {\mathbf{p}}_{D} - {\mathbf{C}}_{4} \cdot {\mathbf{p}}} \right| \hfill \\ \end{gathered}$$\end{document}

Moreover, the chaotic values exhibit a resemblance to the socially motivated activity observed in traditional CHOA, as demonstrated by Eq. (7):

Where the variable “\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\eta _m}$$\end{document}” represents a randomly generated number within the inclusive range of zero to one. The oversimplified perspective on learning may result in early or gradual converging behavior in any given scenario. The subsequent part will propose a novel dual adaptive stochastic reinforcement strategy to mitigate these shortcomings.

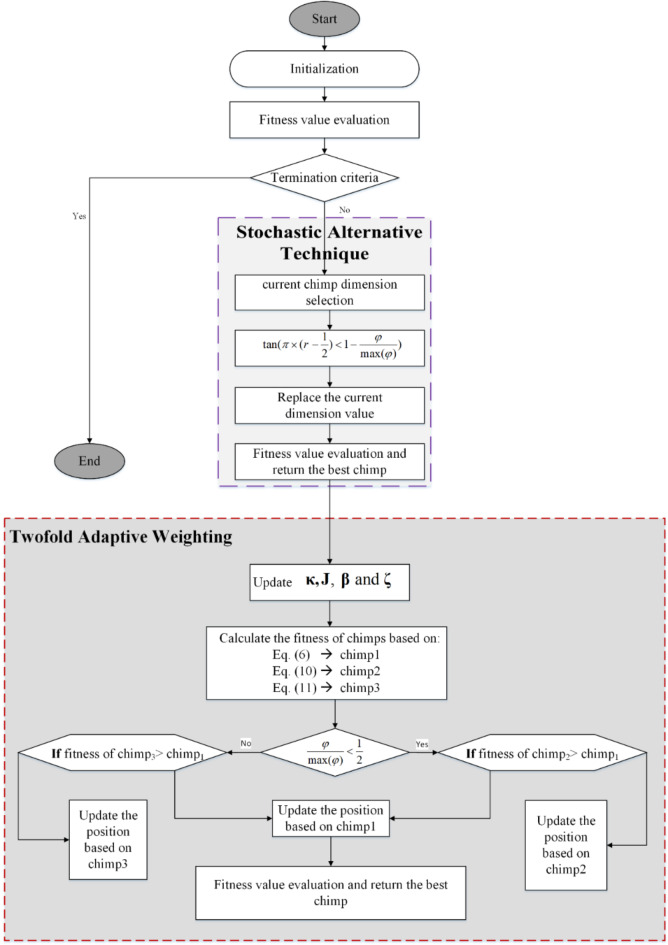
Proposed methodology: a twofold adaptive stochastic reinforced CHOA

This section offers a comprehensive description of TASR-CHOA. TASR-CHOA adds two techniques over the original algorithm. First, the double weights method was added to the primary method, which was inspired by the adaptive weighting of PSO and its tendency to change with the iteration count. In the first half of the method, weight 1 enhances the global search capability of the method, while in the second half of the method, weight 2 enhances the local search capability and the overall optimization of the algorithm. Next, we present a stochastic alternative to the method, which increases both the convergence rate of this method and the obtained solution.

Random replacement methodology

In the application of the random replacement methodology, the present individual’s dimension position vector is substituted with the optimal dimension of the vectors of the present individuals. The position vectors of some individual dimensions may be reasonable in a number of cases, yet the prevailing approach may not be able to conceive enough vectors of this type in most of the dimensions. On the other hand, it can be said that the locations of the optimal dimension of individuals are more important; there is such a location with the same individual where one can easily find some vector in no time. Thus, in order to reduce the probability of this situation, we propose the stochastic alternative. Since not all position vectors in an individual are negative, this method is recommended only for trial m and towards the end of the assessment with a specific probability, where M represents the initial value among them. Based on the previously expressed concept, let us set m to 0.46. The course describes the class of the extreme drawing function and how to determine the global knowledge risk of using the random replacement methodology when restocking the probability.

Twofold adaptive weighting technique

The weight parameter holds significance in nature-inspired optimization techniques. Different research works have sought improvements to adaptive weight strategies with the aim of improving the effectiveness of the method. In the case of TASR-CHOA, the capacity of the technique to conduct global and local searches is attempted to be changed by including two changeable weightings. When encountering multi-peak problems in population-based algorithms, the traditional CHOA will be stuck quite quickly in local optima. Weight λ₁ was used to improve the effectiveness of the global search, and weight λ₂ was used for improving the effectiveness of the local search. Parameters λ₁ and λ₂ are defined in mathematical terms in Eqs. (8) and (9), respectively.

It is essential to observe that the local optimal level of the technique influences the \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\theta$$\end{document} value. Additionally, it is worth mentioning that \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\theta$$\end{document} is dynamically generated without updating the chimp location. On the other hand, when the size of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\theta$$\end{document} is updated, it is divided by two to ensure effective management. The incorporation of Cauchy random numbers and the addition of the variable “\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varphi$$\end{document}” lead to modifications in λ1 and λ2, rather than a linear fall, as the technique converges towards the local minima. The highest possible evaluation numbers that may be performed are labeled by the symbol Max (\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\varphi$$\end{document}). The numerical value assigned to it in the evaluation is 300,000. λ₁ and λ2 have respective ranges of [0,1] and [0.5,1]. Subsequently, the first half of the procedure adds \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\lambda _1}$$\end{document} and Eq. (6) is transformed into Eq. (10).

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{gathered} {{\mathbf{p}}_1}={\lambda _1} \cdot {{\mathbf{p}}_A} - {{\mathbf{A}}_1} \cdot \left| {{{\mathbf{B}}_1} \cdot {{\mathbf{p}}_A} - {{\mathbf{C}}_1} \cdot {\mathbf{p}}} \right|{\text{ }} \hfill \\ {{\mathbf{p}}_2}={\lambda _1} \cdot {{\mathbf{p}}_B} - {{\mathbf{A}}_2} \cdot \left| {{{\mathbf{B}}_2} \cdot {{\mathbf{p}}_B} - {{\mathbf{C}}_2} \cdot {\mathbf{p}}} \right| \hfill \\ {{\mathbf{p}}_3}={\lambda _1} \cdot {{\mathbf{p}}_C} - {{\mathbf{A}}_3} \cdot \left| {{{\mathbf{B}}_3} \cdot {{\mathbf{p}}_C} - {{\mathbf{C}}_3} \cdot {\mathbf{p}}} \right| \hfill \\ {{\mathbf{p}}_4}={\lambda _1} \cdot {{\mathbf{p}}_D} - {{\mathbf{A}}_4} \cdot \left| {{{\mathbf{B}}_4} \cdot {{\mathbf{p}}_D} - {{\mathbf{C}}_4} \cdot {\mathbf{p}}} \right| \hfill \\ \end{gathered}$$\end{document}

Equation (6) transforms Eq. (11) by the inclusion of λ₂ in the next phase of the methodology, as depicted below:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{gathered} {{\mathbf{p}}_1}={\lambda _2} \cdot {{\mathbf{p}}_A} - {{\mathbf{A}}_1} \cdot \left| {{{\mathbf{B}}_1} \cdot {{\mathbf{p}}_A} - {{\mathbf{C}}_1} \cdot {\mathbf{p}}} \right|{\text{ }} \hfill \\ {{\mathbf{p}}_2}={\lambda _2} \cdot {{\mathbf{p}}_B} - {{\mathbf{A}}_2} \cdot \left| {{{\mathbf{B}}_2} \cdot {{\mathbf{p}}_B} - {{\mathbf{C}}_2} \cdot {\mathbf{p}}} \right| \hfill \\ {{\mathbf{p}}_3}={\lambda _2} \cdot {{\mathbf{p}}_C} - {{\mathbf{A}}_3} \cdot \left| {{{\mathbf{B}}_3} \cdot {{\mathbf{p}}_C} - {{\mathbf{C}}_3} \cdot {\mathbf{p}}} \right| \hfill \\ {{\mathbf{p}}_4}={\lambda _2} \cdot {{\mathbf{p}}_D} - {{\mathbf{A}}_4} \cdot \left| {{{\mathbf{B}}_4} \cdot {{\mathbf{p}}_D} - {{\mathbf{C}}_4} \cdot {\mathbf{p}}} \right| \hfill \\ \end{gathered}$$\end{document}

To sum up, Fig. 1 displays the flowchart of the proposed TASR-CHOA technique.

Experimentation and analysis

In this section, the performance of the proposed TASR-CHOA is compared to that of well-known techniques. In this regard, the following five groups of benchmark functions and real-world optimization problems are utilized.

Three standard categories for test functions: fixed-dimension multimodal, multimodal, and unimodal49
The most current and demanding test optimization competition, IEEE CEC-BC, consists of thirty complicated composite and hybrid test functions.
The 100-Digit competition IEEE CEC0650
Ten well-known challenging real-world engineering problems of IEEE CEC-202051
Real applicable fire detection engineering problem

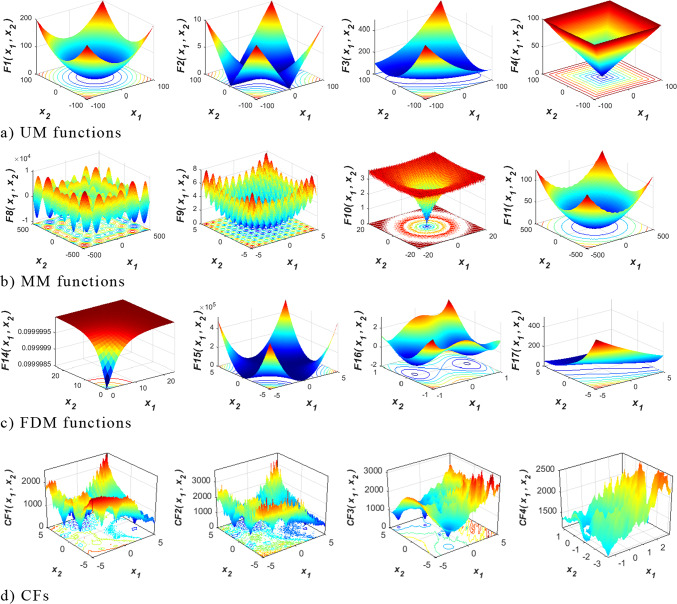
The first set is used to test the potential capability of TASR-CHOA in exploration, exploitation, and avoiding local minima using unimodal (UM), fixed-dimension multimodal (FDM), multimodal (MM), and composition functions (CFs), respectively. There is no point in excluding the problem of objective evolution; the primary purpose of the utilization management functions F1 to F7 is to check the algorithms’ resistance to exploitation. The Visual Standard m02 is an efficient primitive-based function. We use F8 to F13 to evaluate the efficiency of exploration. Schoenfeld’s two groups mentioned above of functions measure distance in fifty dimensions.

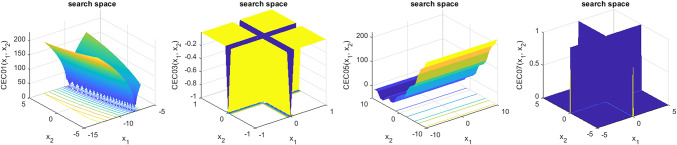
The ability of TASR-CHOA to overcome local optima is assessed with the help of a number of computational functions defined even between F24 and F29. The FDM baselines, which range from F14 to F23, offer an evaluation of the efficiency of CHOA’s exploration ability in lower dimensions. CFs are utilized to assess the overall effectiveness of algorithms because they have a similar level of intricacy to real-world optimization challenges, which often involve many local optima. The diagram described in Fig. 2 depicts a two-dimensional depiction of many test functions.

Fig. 2 — The graphical illustration of common test functions in a three-dimensional coordinate system.

The test functions are solved using TASR-CHOA and other competing algorithms, with a limit of 25,000 functional evaluations. The TASR-CHOA was executed 30 times to provide statistically significant outcomes for this research investigation. The findings were presented for each execution in terms of the average (Ave) and standard deviation (Std) of the most optimal solutions.

Twelve popular meta-heuristic techniques were evaluated in the research, including ECHOA²⁹, DLFCHOA³⁶, ULCHOA⁴⁰, NCHOA⁴¹, ARBGA⁴², ICHOA³⁴, ARWOA⁴³, DISHchain1e + 12⁵², jDE100⁵³, CIPDE⁵⁴, EBOwithCMAR⁵⁵, and CHOA to show the merit of TASR-CHOA compared to test techniques. The testing machines use Matlab R2022b, Windows 11 Pro, 32 GB of RAM, and Core i7 CPUs with 3.8 GHz clock speeds. Table 1 details the different parameters used by the comparison methods. All techniques’ optimal effectiveness ranges are either fully covered by the used configuration parameters or explicitly recommended by the techniques’ developers.

Table 1.

Initial parameters for the technique employed.

Technique	Parameter	Value
Different techniques based on CHOA and its variants ARWOA	m	Gauss/mouse
	f	[2, 0)
	W₁	[0,1]
	W₂	[0.5,1]
ARBGA	Selection Crossover Mutation rate	Roulette wheel Single point 0.01
jDE100 and DISHchain1e + 12	CR F	0.6 0.8
CIPDE	µ_CR	0.3
	µ_F	0.6
	c	0.2
	T	250
EBOwithCMAR	T	0.1
	Freq and CR	0.5
	F	0.7

Open in a new tab

The investigation of exploitation ability

The possibility of TASR-exploitation CHOA can be assessed due to the presence of a single global optimum in UM functions. Table 2 displays the outcomes of TASR-CHOA and several optimization approaches applied to UM functions (F1-F7), with the evaluation based on Ave and Std metrics^56,57. The Wilcoxon rank-sum analysis procedure⁴⁷ was employed in a non-parametric way in order to evaluate the existence of statistically significant dominance of the TASR-CHOA outcomes over the other benchmark assessments, if any. Let it be stated as well that a 5% significance level has been adopted in this case. Wilcoxon’s p-values are also presented in the results besides the measures of STD and AVE as reported. The letters “NA” in the findings represent not applicable, meaning that an algorithm cannot be compared with itself. What the bolded p-values imply is that two algorithms can be considered to be of equal worth with minimal differences between them.

Table 2.

The results of UM functions.

Algorithm		F₁	F₂	F₃	F₄	F₅	F₆	F₇
CHOA	Ave	7.89E−08	7.44E−19	1.90E−07	1.55E−03	48.441	3.50E−04	3.89E−03
CHOA	Std	7.55E−08	6.53E−23	1.89E−07	1.96E−03	39.331	3.50E−04	3.89E−03
	p-value	0.00033	0.0055	0.0051	0.0073	0.0068	0.0025	0.0030
ULCHOA	Ave	1.44E−12	0.00331	1.02E−07	1.35E−04	51.455	8.32E−03	1.53E−03
ULCHOA	Std	7.53E−09	0.00023	1.44E−07	1.75E−04	33.785	5.33E−03	1.11E−03
	p-value	0.0055	0.0044	0.0025	0.0039	0.0056	0.0051	0.0082
ICHOA	Ave	6.96E−12	2.11E−07	1.42E−08	1.22E−09	48.335	1.32E−02	3.22E−03
ICHOA	Std	6.44E−08	3.33E−08	0.0017E−07	1.12E−06	33.045	5.14E−03	2.02E−03
	p-value	0.0033	0.0035	0.0014	0.0013	0.0055	0.0072	0.0083
NCHOA	Ave	2.01E−27	2.11E−08	3.02E−08	1.21E−08	47.236	1.33E−12	1.07E−03
NCHOA	Std	1.21E−55	8.42E−07	1.25E−06	1.11E−07	35.443	2.55E−06	2.51E−03
	p-value	0.0015	0.0044	0.0025	0.0039	0.0073	0.0051	0.0082
DLFCHOA	Ave	3.11E−40	7.11E−22	8.11E−09	5.33E−08	63.222	7.25E−06	1.49E−03
DLFCHOA	Std	6.02E−40	6.35E−23	1.59E−08	1.22E−08	52.136	4.24E−06	6.60E−04
	p-value	0.0033	0.0044	0.0025	0.0039	0.0056	0.0051	0.0082
ECHOA	Ave	6.44E−07	5.41E−21	8.09E−08	1.15E−08	76.350	2.33E−04	3.11E−03
ECHOA	Std	4.11E−07	6.44E−23	1.11E−06	1.11E−06	42.753	1.55E−05	1.55E−03
	p-value	0.0055	0.0047	0.0032	0.0015	0.0002	0.0017	0.00001
TASR-CHOA	Ave	1.14E−33	1.87E−22	3.88E−11	1.43E−09	45.033	1.33E−10	1.00E−03
TASR-CHOA	Std	0.0000	1.54E−35	2.34E−11	1.01E−09	2.441	1.25E−07	1.05E−04
	p-value	NA	NA	NA	NA	NA	NA	NA
ARBGA	Ave	3.85E−14	2.42E−16	0.0912	1.44E−08	51.334	4.25E−03	1.05E−03
ARBGA	Std	4.33 E−14	1.33E−16	0.1452	1.21E−09	21.551	5.33E−03	2.33E−03
	p-value	0.0055	0.0055	0.0051	0.0073	0.0057	0.0025	0.0030
ARWOA	Ave	10.076E−07	0.0336	3.88E−07	1.33E−06	73.352	1.11E−13	7.29E−03
ARWOA	Std	7.00E−07	0.0022	1.44E−07	1.25E−06	33. 624	2.44E−09	1.04E−03
	p-value	0.0044	0.0055	0.0051	0.0073	0.0068	0.0025	0.0030
SHADE	Ave	1.29E−30	2.33E−19	2.22E−04	1.43E−11	45.244	8.33E−10	3.05E−03
	Std	2.11E−37	1.45E−12	1.10E−05	6.33E−09	32.773	1.44E−07	1.03E−03
	p-value	0.0055	0.0044	0.0025	0.0041	0.0056	0.0077	0.0082
CMA-ES	Ave	2.02E−31	0.00E+00	1.25E−09	2.09E−09	47.336	5.02E−16	3.20E−03
	Std	3.14E−42	0.00E+00	2.87E−08	1.99E−09	23.4421	1.44E−09	7.07E−03
	p-value	0.0077	0.048	0.0011	0.451	0.0047	0.0055	0.0033
LSHADESPACMA	Ave	0.07537	2.25E−12	8.25E−09	1.44E−08	52.921	8.25E−10	7.70E−03
	Std	0.1480	1.52E−12	1.59E−08	1.21E−09	17.712	1.24E−07	2.11E−03
	p-value	0.0025	0.0055	0.0051	0.0062	0.0068	0.0025	0.0030

Open in a new tab

Evidence suggests that TASR-CHOA outperformed the majority of the corresponding techniques in every test function, with the exception of F6 and F7, where it was placed second. The obtained results provide evidence of the potential for exploitation of the TASR idea, facilitating the TASR-CHOA’s ability to reliably and productively converge in the direction of the global optimum.

The investigation of the TASR-CHOA’s exploration ability

MM functions can judge optimization results but can also be used to test the exploratory nature of the algorithms since there could be more than one local optima depending on the design parameters. Also, a portion of the multimodal test functions, F8-F23, is available in the MM version. The outcomes of the specified techniques and those of TASR-CHOA in the columns of Tables 3 and 4 are also shown.

Table 3.

The MM test functions’ outcomes.

Techniques		F₈	F₉	F₁₀	F₁₁	F₁₂	F₁₃
CHOA	Ave	−1.06E+04	3.39E−07	7.33E−16	0.00E+00	4.30E−06	3.09E−01
CHOA	Std	1.14E+03	3.39E−07	7.25E−16	0.00E+00	4.30E−06	3.09E−01
	p-value	0.0033	0.0055	0.0017	0.0022	0.0035	0.0045
ULCHOA	Ave	−1.25E+04	1.25E−07	7.33E−16	0.00E+00	1.01E−04	2.10E−04
ULCHOA	Std	0.1	3.22E−07	3.22E−07	0.00E+00	1.30E−04	8.50E−04
	p-value	0.0077	0.0082	0.0035	0.0041	0.0033	0.0071
ICHOA	Ave	−1.12E+04	1.4423	2.0441	0.0002	2.01E−03	2.22E−04
ICHOA	Std	1766.46	0.3000	0.1001	0.0033	2.02E−03	1.33E−04
	p-value	0.0011	0.0047	0.0032	0.0015	0.00001	0.0017
CHOA	Ave	−1.03E+04	1.11E−04	0.8223	1.01E−05	1.30E−05	2.10E−05
CHOA	Std	555.233	3.45E−04	0.0021	1.00E−05	1.25E−05	1.50E−05
	p-value	0.0072	0.0082	0.0035	0.0041	0.0033	0.0071
DLFCHOA	Ave	−9.03E+03	2.22E−07	8.21E−14	0.00E+00	7.88E−07	2.92E−03
DLFCHOA	Std	595.1113	2.11E−07	2.44E−14	0.00E+00	7.88E−07	1.44E−03
	p-value	0.0033	0.0042	0.0035	0.0047	0.0047	0.0015
ECHOA	Ave	−1.33E+04	0.0933	2.12E−15	1.12E−14	7.12E−04	3.94E−07
ECHOA	Std	796.12698	0.0322	2.33E−14	1.30E−14	0.0031	1.22E−03
	p-value	0.0035	0.0042	0.0086	0.0032	0.0036	0.0091
TASR-CHOA	Ave	−1.75E+04	0.00E+00	1.88E−13	0.00E+00	0.00E+00	0.00E+00
TASR-CHOA	Std	525.5351	0.00E+00	1.44E−12	0.00E+00	0.00E+00	0.00E+00
	p-value	NA	NA	NA	NA	NA	NA
ARBGA	Ave	−1.38E+04	1.1335	9.33E−12	0.00E+00	8.30E−04	2.11E−03
ARBGA	Std	742.6746	0.3440	6.17E−12	0.00E+00	7.44E−04	1.02E−03
	p-value	0.0076	0.0042	0.0086	0.0032	0.0036	0.0091
ARWOA	Ave	−1.42E+04	0.3007	0.9003	0.00E+00	2.10E−04	5.10E−04
ARWOA	Std	715.5351	0.1001	0.1335	0.00E+00	8.50E−04	2.30E−04
	p-value	0.0063	0.0082	0.0035	0.0041	0.0033	0.0071
SHADE	Ave	−8.83E+03	0.029	0.1702	1.01E−04	1.19E−04	1.01E−04
	Std	418.8	0.831	0.0244	1.22E−04	3.90E−04	1.00E−04
	p-value	0.0077	0.0025	0.0035	0.0032	0.0033	0.0071
CMA-ES	Ave	−1.16E+04	0.0085	6.044	0.00E+00	1.13E−14	1.25E−12
	Std	331.3	0.0344	2.706	0.00E+00	1.25E−13	1.11E−12
	p-value	0.0035	0.0042	0.0055	0.0032	0.0044	0.0091
LSHADESPACMA	Ave	−1.32E+04	0.0023	0.1525	9.01E−05	0.0008	2.11E−06
	Std	454.325	0.0016	0.0188	9.30E−05	0.0019	1.04E−08
	p-value	0.0065	0.0082	0.0040	0.0041	0.0033	0.0071

Open in a new tab

The best results are highlighted in bold.

Table 4.

The FDM test functions’ outcomes.

Techniques		F₁₄	F₁₅	F₁₆	F₁₇	F₁₈	F₁₉	F₂₀	F₂₁	F₂₂	F₂₃
CHOA	Ave	2.3332	3.05E−04	-1.0359	0.4005	3.000022	-3.8544	-3.21003	-10.133	-10.333	-10.45
CHOA	Std	0.0911	3.02E−04	6.32E−14	1.33E−06	1.21E−09	1.47E−10	2.44E−02	2.04E−02	2.77E−02	2.11E−02
	p-value	0.0033	0.0025	0.0014	0.0032	0.0045	0.0073	0.0044	0.0042	0.0075	0.0088
ULCHOA	Ave	1.0444	3.54E−04	-1.0449	0.3989	3.000019	-3.8633	-3.29622	-10.122	-10.421	-10.531
ULCHOA	Std	0.2731	6.32E−04	2.11E−12	7.11E−11	2.44E−12	1.42E−13	1.66E−10	2.13E−02	3.33E−04	2.55E−02
	p-value	0.0044	0.0047	0.0021	0.0011	0.0025	0.0066	0.0025	0.0077	0.0065	0.0063
ICHOA	Ave	1.0305	2.20E−04	-1.0355	0.4033	3.00000	-3.8621	-3.2901	-6.155	-10.322	-10.522
ICHOA	Std	1.0001	3.32E−04	5.11E−09	0.4033	3.00000	-3.8655	-3.2608	2.77E−02	3.13E−01	2.75E−02
	p-value	0.0028	0.0073	0.0014	0.0032	0.0032	0.0073	0.0071	0.0042	0.0066	5.11E−09
NCHOA	Ave	0.9645	3.29E−04	-1.0384	0.3995	3.000042	-3.8622	-3.28876	-10.133	-9.4033	-10.510
NCHOA	Std	1.22E−14	4.02E−04	4.73E−15	4.49E−14	1.88E−14	2.68E−15	1.11E−10	2.66E−08	2.11E−02	5.11E−09
	p-value	0.0044	0.0047	0.0021	0.0011	0.0025	0.0066	0.0025	0.0077	0.0065	0.0063
DLFCHOA	Ave	0.1033	3.21E−04	-1.0362	0.3925	3.00012	-3.7954	-3.19001	-7.544	-9.320	-9.6501
DLFCHOA	Std	1.22E−14	6.52E−04	6.09E−15	9.22E−14	1.88E−13	4.11E−15	1.59E−08	1.44E−02	1.23E−01	7.11E−02
	p-value	0.0011	0.0033	0.0021	0.0011	0.0021	0.0066	0.0088	0.0077	0.0015	0.0063
ECHOA	Ave	1.1330	2.11E−06	-1.0352	0.3989	3.000045	-3.8636	-3.28654	-10.165	-10.421	-10.520
ECHOA	Std	2.8713	3.33E−04	2.38E−09	8.22E−13	1.99E−02	1.25E−14	1.79E−10	2.33E−05	2.77E−02	8.15E−03
	p-value	0.0033	0.0025	0.0014	0.0032	0.0045	0.0073	0.0044	0.0042	0.0075	0.0088
TASR-CHOA	Ave	1.08E−05	3.01E−04	-1.03161	0.3972	3.000001	-3.8645	-3.0004	-10.165	-9.4077	-10.537
TASR-CHOA	Std	1.09E−17	3.11E−15	4.11E−18	9.11E−15	1.33E−16	2.52E−15	1.22E−11	-2.09E−11	2.25E−09	3.62E−12
	p-value	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
ARBGA	Ave	0.9333	3.02E−04	-1.0341	0.3996	3.000033	-3.8633	-3.2899	-10.122	-10.4041	-10.536
ARBGA	Std	2.33E−15	5.12E−04	5.12E−16	10.23E−15	1.46E−14	1.46E−14	1.14E−11	2.53E−11	2.38E−09	3.91E−11
	p-value	0.0033	0.0025	0.0014	0.0032	0.0045	0.0073	0.0044	0.0042	0.0075	0.0088
ARWOA	Ave	1.0002	3.64E−04	-1.0357	0.3991	3.000033	-3.8644	-1.992	-6.144	-7.477	-6.5322
ARWOA	Std	1.0044	6.66E−04	6.85E−14	8.22E−13	1.32E−13	3.11E−13	1.13E−09	2.25E−02	2.38E−09	0.0033
	p-value	0.0066	0.0047	0.0055	0.0011	0.0025	0.0066	0.0023	0.0057	0.0065	4.11E−06
SHADE	Ave	0.8827	1.25E−03	-1.0316	0.3983	3.000025	-3.8628	-3.0334	-9.1344	-10.414	-10.537
	Std	3.39E−16	4.43E−03	3.3E−03	1.12E−15	4.14E−14	1.46E−14	4.66E−03	1.1325	3.63E−10	8.00E−10
	p-value	0.054	0.0022	0.054	0.0033	0.0025	0.0014	0.0032	0.0045	0.0073	0.052
CMA-ES	Ave	1.0335	3.02E−04	-1.0316	0.3982	3.9900	-3.8628	-3.2903	-7.1410	-10.414	-10.537
	Std	0.2044	1.19E−04	6.22E−17	0.0000	1.33E+01	2.51E−15	1.44E−11	3.4120	2.02E−11	5.11E−09
	p-value	0.0033	0.0033	0.066	0.0577	0.0035	0.00001	0.00184	0.0003	0.0033	0.066
LSHADESPACMA	Ave	0.9044	1.44E−03	-1.0316	0.3988	3.000041	-3.8628	-3.0333	-9.1436	-10.435	-10.537
	Std	3.21E−16	5.32E−03	0.0033	1.11E−16	3.22E−14	1.33E−14	5.77E−02	1.2269	2.44E−11	9.11E−11
	p-value	0.054	0.0033	0.0025	0.0014	0.0032	0.0045	0.0073	0.0044	0.0042	0.0075

Open in a new tab

The best results are highlighted in bold.

According to these tables, the TASR-CHOA approach is the most capable of exploring. TASR-CHOA outperforms competing methods for approximately half of the MM functions and achieves competitive results when pitted against state-of-the-art optimizers for the other functions. TASR-CHOA’s performance in FDMs is on par with state-of-the-art optimization algorithms when it comes to finding the best possible answer. The exploration capacity of TASR-CHOA is greatly improved because of the additional parameters as well as the stochastic replacement method of the optimization steps that comprise the TASR-CHOA’s exploration tasks.

Study of the strategy for evading local optimum

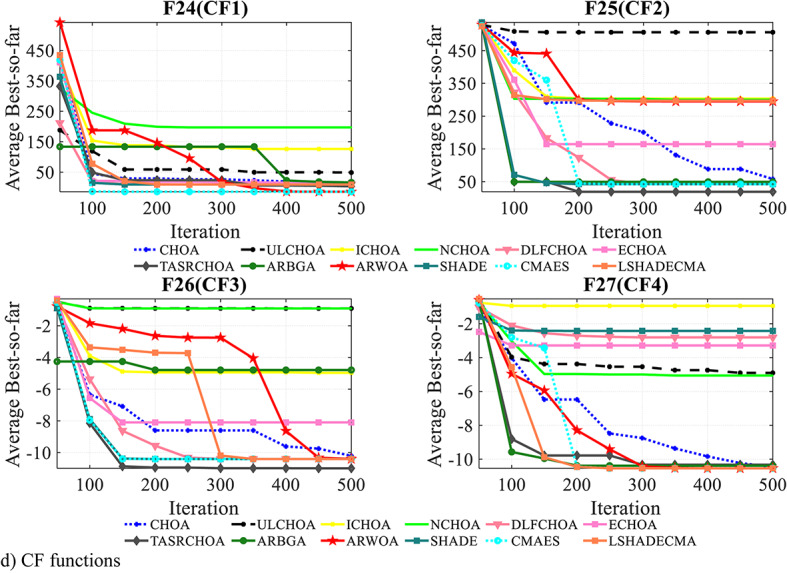
In a similar method, CFs F25 to F29 structure out of the rotation, translation, and composition of the single UM and MM functions. These CFs are constructed with the intention of examining how well the algorithms can skip the local minima and how these algorithms aim to balance exploration and exploitation. Results from Table 5 show the effectiveness evaluation results of the optimization techniques within CF systems with a focus on the TASR-CHOA algorithm. We can say that the TASR-CHOA technique is superior to the rest of the techniques. The results show that the TASR-CHOA model coordinates prudence with the adventurous modes without creating a risk of being trapped in local optima for guaranteed performance. This could be due to the variable size of the steps. The table contains cumulative ranks obtained from the one-way ANOVA using Friedman’s test in the benchmark systems. Table 6 easily indicates that TASR-CHOA performed better than all the benchmark algorithms with the highest rank.

Table 5.

The outcomes of CF functions.

Algorithm		CF1 (F24)	CF2 (F25)	CF3 (F26)	CF4 (F27)	CF5 (F28)	CF6 (F29)
CHOA	Ave	63.2201	198.221	283.1423	392.2145	198.2214	807.3355
CHOA	Std	75.2001	58.2214	60.07545	88.251	98.5213	100.07300
	p-value	0.0033	0.0025	0.0043	0.0021	0.0013	0.0017
ULCHOA	Ave	37.5421	135.3258	212.521	266.3021	183.5566	699.4123
ULCHOA	Std	50.1332	99. 1332	32.5514	89.03212	99.3256	99.85215
	p-value	0.0019	0.0033	0.0011	0.0039	0.0022	0.0025
ICHOA	Ave	67.533	89.5213	115.521	311.365	60.3355	720.08236
ICHOA	Std	95.802	57.4412	38.2574	85.415	85.1444	197.3521
	p-value	0.022	0.011	0.011	0.014	1.14E−05	1.1E−06
NCHOA	Ave	44.2255	111.222	232.321	295.6625	133.2541	690.07621
NCHOA	Std	43.3399	62.1241	77.5214	122.1358	20.5213	63.9631
	p-value	1.02E−07	1.1E−06	1.22E−06	1.22E−06	0.0022	0.0021
DLFCHOA	Ave	67.5213	88. 2214	145.225	302.3521	49.5588	701.2014
DLFCHOA	Std	84.3322	44. 1332	41.2811	66.2569	33.7745	189.3026
	p-value	1.1E−06	0.0025	1.22E−06	1.02E−04	1.1E−03	1.17E−05
ECHOA	Ave	32.4421	85.1152	198.3214	311.1111	132.447	729.204
ECHOA	Std	19.2136	63.2514	45.3321	101.5569	88.7541	88.2369
	p-value	0.0017	0.0011	0.0033	0.0025	0.0022	0.0044
TASR-CHOA	Ave	6.1133	14.0021	137.852	273.133	2.1124	88.2145
TASR-CHOA	Std	11.2211	22.0000	16.1021	24.1003	1.0114	39.5541
	p-value	NA	NA	NA	NA	NA	NA
ARBGA	Ave	7.2222	21.2413	165.3352	288.651	2.1334	517.5541
ARBGA	Std	12.8453	27. 1344	45.3215	74.5621	1.1321	77.7541
	p-value	0.0019	0.0045	0.0011	0.0019	0.0022	0.0025
ARWOA	Ave	22.2143	68.2514	235.114	401.321	98.3320	699.8142
ARWOA	Std	23.3300	66.2115	45.3325	92.5521	33.5784	120.07636
	p-value	0.0019	0.0045	0.0011	0.0019	0.0022	0.0025
SHADE	Ave	8.3625	15.0142	144.911	269.902	4.324	444.3251
	Std	8.1425	22.3321	33.1001	27.3333	1.531	65.74511
	p-value	0.0022	0.082	0.0025	0.12	0.0044	0.0032
CMA-ES	Ave	6.4521	14.0021	152.214	281.552	19.025	99.3362
	Std	8.2132	22.1133	22.3332	44.0741	12.906	66.0365
	p-value	0.0057	0.54	0.0033	0.0025	0.0043	0.0021
LSHADESPACMA	Ave	6.3256	19.1325	151.6301	275.002	9.1223	412.7133
	Std	6.2211	23. 1332	24.2001	26.1236	2.1123	87.5566
	p-value	0.0033	0.0025	0.0022	0.0021	0.0013	0.0017

Open in a new tab

The best results are highlighted in bold.

Table 6.

Outcomes of Friedman mean rank-sum test.

Techniques	CHOA	NCHOA	ULCHOA	ICHOA	ECHOA	DLFCHOA
Friedman value	11.29	10.075	5.8	10.94	6.87	8.87
Rank	12	10	6	11	7	9

Techniques	TASR-CHOA	SHADE	ARBGA	ARWOA	LSHADESPACMA	CMA-ES
Friedman value	2.14	3.65	4.36	8.59	5.82	2.68
Rank	1	3	4	8	5	2

Open in a new tab

TASR-CHOA’s convergence analysis

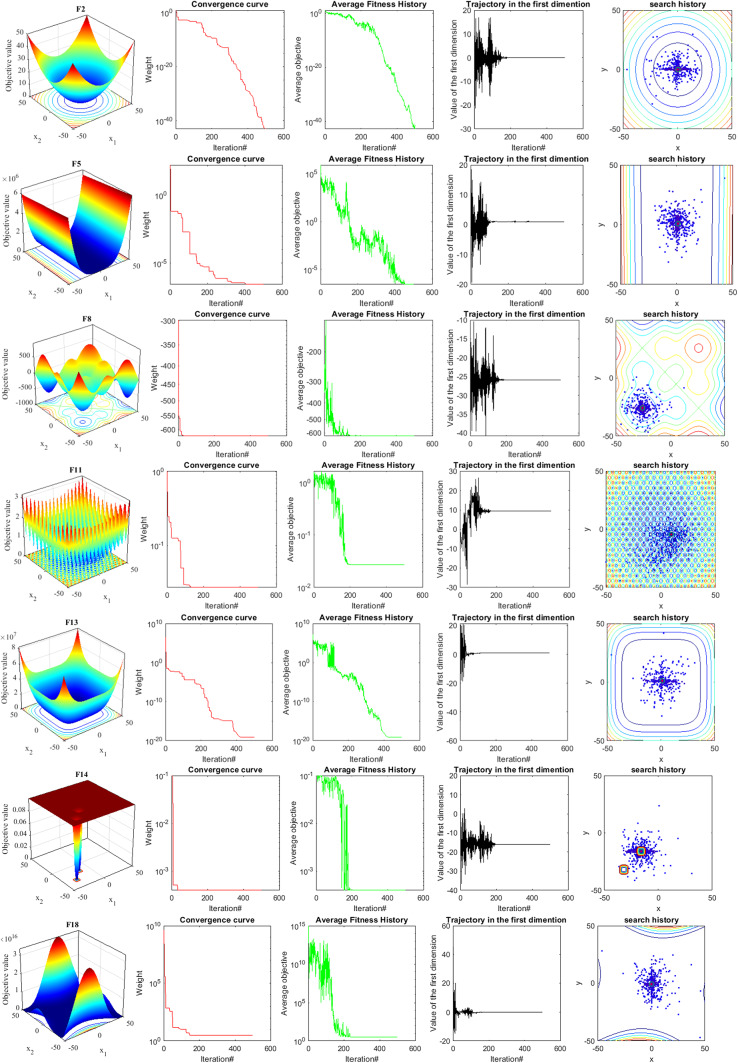
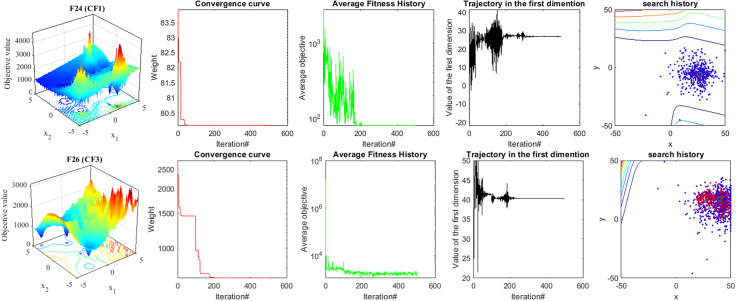
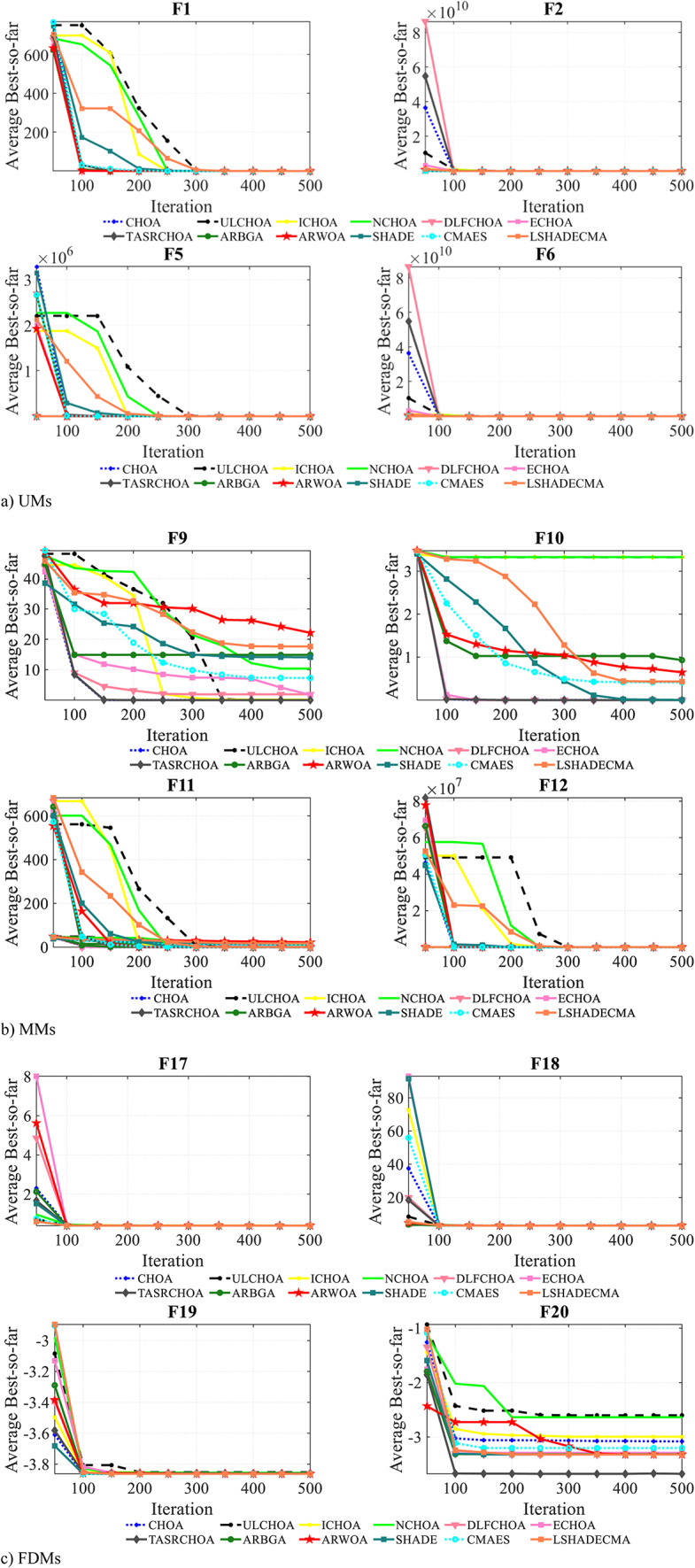
In this section, we investigate the experimental convergence of TASR-CHOA. To understand the convergence of TASR-CHOA, several metrics are employed; these include trajectories, converging graphs, and average fitness history, among others. These measures for the performance and the convergence investigation of the TASR are displayed in Fig. 3, which deals with the TASR on different functions. Since the purpose is to learn the structure of the function’s domain, the first column presents two-dimensional illustrations of the functions.

The convergence curves are the most exceptional statistical criteria thus far. In UM functions, convergence graphs show a general pattern that is the same within any function category and generally indicates a positive change with time. However, for MM and CF, this trend transitions into a step-by-step chronological regression pattern. From the limited observation in each category, for UM functions, TASR-CHOA starts off enclosing the ideal point and improves step-wise from the limited observation in each category. In MM and CF, however, during the last iterative steps, every agent deployed a thorough search strategy to the bounded search area, producing better result concentrations. Several annual reports depict the eliminations of numerous curves, including the generated step patterns, which are found irrelevant even after some perform certain MM functions with minimal advancement improvement, which can be termed the success of the strategy employed. The last point of this version of the paper makes a point of the explanatory review performance in the last round of iteration upon all participating agents’ relative weight ratio being unique on that particular occasion.

The investigation of the department collapse qualified the search agency as a member of the colony. From the convergence graph, however, the behavior of the top-performing individual of the colony supports the colony’s success. However, currently, data about the functioning or behavior of the entire colony is not available. The decision to adopt this behavior justifies the inclusion of the mean fitness history metric in the inlet as an additional measure to assess the colony’s effectiveness. The trend of the metric is similar to the convergence rate, where ceilings are reached, but it highlights that this intervention enhances the productivity of the initial agent. The algorithm’s phase transition results in an increase in the fitness value of chimps. This change makes the test functions’ average fitness history behave like a step function. Slow but steady changes usually characterize the slopes of curves expressing different utility maximization functions.

The skew patterns observed in these kinds are notably evident in MM and CFs. Another parameter that is measured is the orientation of the chimps (column 4). This metric provides a quantitative measure of the structural transformations undergone by an individual throughout the entirety of the optimization process, spanning from its beginning state to its end state. Given the agents’ ability to move in many directions, we have opted to utilize the first dimension as a representation of their trajectory. The purpose of this pattern is to ensure that an approach eventually reaches an acceptable local minimum region by promoting exploratory search behavior in the early iterations and moving to a targeted search approach in the subsequent stages. The frequency, size, and period changes of these events are often larger than those of UM test functions. This discrepancy results from the fact that UM test functions lack the distinguishing features shown by MM and CF test functions.

We consider searching histories to be the most recent metric, and the final column of the diagram illustrates this process. The depicted image provides evidence that TASR-CHOA is performing well in fulfilling the objective of showing how the agents share the search load through dual reinforcement weighting behavior. This model demonstrates that a greater number of agents are located at the optimal points of UM functions, whereas the seeking behavior of MM and CFs is more scattered. The distinctive feature of the primary pattern plays a crucial role in facilitating the attainment of desired outcomes in UM activities. The ultimate phase involves the examination of the domain, allowing TASR-CHOA in CF and MM functions to conduct a comprehensive search of the whole region. Furthermore, Fig. 4 shows the convergence curve of specific evaluations for the comparing algorithms.

Fig. 4 — Comparison of convergence curves for various benchmark techniques.

Figure 4 shows the performance of the convergence curve of generic numbers for test functions in the application of the TASR-CHOA approach and other competing methods. The results clearly indicate that the first phase is extensively focused on obtaining the global minimum in a short time, while the second stage shows tiny improvement when compared to the first stage. These findings support the notion that a single phase may be sufficient to tackle a benchmark function. The searching mentioned above behavior can be observed in F1, F3, F4, and F11. Given that the technique has already attained the optimal or near-optimal state, it is possible to detect another analogous pattern without making any further improvements in the succeeding phases. The patterns observed in F3, F15, F18, and F19 are consistent. After each observed phase shift in functions number 4, 8, 9, 26, and 28, the convergence curve shows a change in the final form. The TASR-CHOA employs weight alteration as a means to examine and capitalize on the domain, hence enhancing the efficacy of the technique. The convergence of these tasks is additionally reinforced by the consistent patterns observed in their convergence trajectories throughout the final stage.

It is essential to acknowledge that the inclusion of rigorous CF and MM functions, including F8, F24, F27, and F29, provides a comprehensive understanding of the influence of changes in weight on the whole efficacy of methods, as well as the underlying rationale supporting the description of every stage. The utilization of this technique enables TASR-CHOA to identify the optimal point during the Ums’ first phase; nevertheless, when evaluating the technique in testing CFs and MMs, the results of each stage of the experiment become clear and convincing.

Performance of TASR-CHOA on IEEE CEC-BC test functions

For the present paper, the IEEE CEC-BC test suite was used in the numerical optimization contest. This test suite contains a total of 30 functions, most of which are complex hybrid and mixed optimization bench functions. The aim of using this test suite was to showcase the usefulness of the proposed approach. For a thorough examination of the other popular techniques, the performance of TASR-CHOA is tested against those functions. In this suite, the dimension of the function is set to 10. Ave, Std, and p values are shown in Table 7.

Table 7.

Results for IEEE CEC-BC functions.

Functions	No.	Metric	ULCHOA	CHOA	NCHOA	ICHOA	ECHOA	DLFCHOA
UM	F1	Ave	274.33	2741.28	166.33	9322.22	417.88	2433.22
	F1	Std	274.31	345.21	4.22E−06	5741.49	362.74	1952.112
		p-value	0.0025	0.0033	0.0044	0.0044	0.0061	0.0033
	F3	Ave	833.33	300	300	587.00	300	300
	F3	Std	25.031	1.95E−11	8.77E−07	125.33	2.12E−04	2.44E−07
		p-value	0.0046	0.054	0.0014	0.0055	0.0021	0.0033
MM	F4	Ave	407.44	399.44	401.25	408.33	406.55	404.33
	F4	Std	7.652	4.1425	1.4521	2.22	1.4123	1.7412
		p-value	0.0017	0.0018	0.0033	0.0011	0.0027	0.0044
	F5	Ave	509.21	511.77	509.33	512.55	508.22	509.33
	F5	Std	7.9654	2.4563	4.5412	4.6523	3.5551	4.4169
		p-value	0.0025	0.0033	0.0044	0.0044	0.0061	0.0033
	F6	Ave	614.42	633.88	602.41	599.55	603.41	601.33
	F6	Std	9.3332	1.25E−01	5.11E−04	1.44E−02	2.3330	1.02E−04
		p-value	0.0017	0.0018	0.0033	0.0011	0.0027	0.0044
	F7	Ave	714.33	722.33	720.10	719.55	717.33	720.10
	F7	Std	1.2336	4.4174	3.0333	5.3625	3.4141	5.3201
		p-value	0.07323	0.0014	0.0011	0.0024	0.0002	0.0036
	F8	Ave	814.654	820.45	811.22	812.65	815.44	818.22
	F8	Std	2.4141	5.3333	2.3696	7.1523	5.9142	6.8585
		p-value	0.0017	0.0018	0.0033	0.0011	0.0027	0.0044
	F9	Ave	900.00	902.36	905.33	900.00	902.11	900.00
	F9	Std	0.00	5.33E−14	0.0044	5.98E−14	1.1236	0.0512
		p-value	0.143	0.0044	0.0011	0.0024	0.0002	0.0036
	F10	Ave	1677.33	1652.11	1355.24	1633.11	2566.33	1411.33
	F10	Std	198.475	199.222	134.258	233.11	223.252	259.546
		p-value	0.0025	0.0033	0.0044	0.0044	0.0061	0.0033
Hybrid	F11	Ave	1110.33	1117.25	1103.33	1106.25	1110.36	1105.42
	F11	Std	7.5552	6.1425	2.33211	7.5533	9.3369	5.4414
		p-value	0.0017	0.0027	0.0033	0.0015	0.0027	0.0044
	F12	Ave	7.11E+05	1.38E+06	1.35E+03	3.55E+05	1.81E+06	1.03 E+05
	F12	Std	4.22E+05	1.22E+06	6.76E+01	3.33E+05	1.86E+06	9.79 E+03
		p-value	0.0035	0.0024	0.0018	0.0044	0.0055	0.0019
	F13	Ave	1.4E+03	2.14E+03	1.31E+03	1.03E+04	9.85E+03	8.02E+03
	F13	Std	25.3312	0.53E+03	7.33E+02	7.73E+03	2.14E+03	6.72E+03
		p-value	0.0011	0.0024	0.0002	0.0036	0.0046	0.0021
	F14	Ave	1.45E+03	7.47E+03	1.41E+03	1.45E+03	7.14E+03	1.46E+03
	F14	Std	54.33	8.15E+03	5.5221	82.33	1.49E+03	31.54214
		p-value	0.0017	0.0018	0.0033	0.0011	0.0027	0.0044
	F15	Ave	1.62E+03	9.7E+03	1.50E+03	1.29E+03	2.23E+03	1.50E+03
	F15	Std	2.333	285.69	1.4421	8.97	0.52E+03	1.3321
		p-value	0.0025	0.0031	0.0044	0.0044	0.0061	0.0033
	F16	Ave	1.64E+03	1.62E+03	1.60E+03	1.62E+03	1.82E+03	1.58E+03
	F16	Std	99.33	99.22	5.412	99.14	198.441	35.77
		p-value	0.024	0.0011	0.0039	0.0036	0.0013	0.0014
	F17	Ave	1.75E+03	1.77E+03	1.73E+03	1.74E+03	1.77E+03	1.74E+03
	F17	Std	29.1425	44.3321	6.4142	25.1245	27.2512	5.3365
		p-value	0.0002	0.0047	0.0021	0.0032	0.0061	0.0054
	F18	Ave	1.84E+03	1.85E+03	1.79E+03	1.83E+03	1.84E+03	1.83E+03
	F18	Std	15.1414	45.3636	2.4758	45.2312	1.29E+03	17.3656
		p-value	1.1E−03	1.1E−03	1.2E−03	0.0036	1.4E−03	2.1E−03
	F19	Ave	2.91E+03	2.96E+03	1.91E+03	2.41E+03	1.94E+03	1.95E+03
	F19	Std	74.1333	99.5454	1.1414	89.2552	41.3625	47.0021
		p-value	0.024	0.0011	0.0039	0.0036	0.0013	0.0014
	F20	Ave	2.03E+03	2.05E+03	2.01E+03	2.03E+03	2.27E+03	2.02E+03
	F20	Std	7.1421	46.5521	5.02586	44.4747	82.0125	23.0231
		p-value	0.0025	0.0033	0.0044	0.0044	0.0061	0.0033
CFs	F21	Ave	2.21E+03	2.29E+03	2.20E+03	2.30E+03	2.28E+03	2.30E+03
	F21	Std	39.1421	42.1625	20.0202	44.3333	39.6363	21.1475
		p-value	0.024	0.0011	0.251	0.0036	0.0013	0.0014
	F22	Ave	2.03E+03	2.30E+03	2.51E+03	2.29E+03	2.30E+03	2.29E+03
	F22	Std	12.2200	13.4412	63.1425	19.3636	11.0120	17.1425
		p-value	0.333	0.0017	0.024	0.0011	0.0039	0.0036
	F23	Ave	2.61E+03	2.62E+03	2.61E+03	2.62E+03	2.72E+03	2.61E+03
	F23	Std	10.3325	9.5554	8.1245	7.3321	233.321	5.4141
		p-value	0.0017	0.0011	0.0039	0.0036	0.0013	0.0014
	F24	Ave	2.74E+03	2.74E+03	2.56E+03	2.74E+03	2.73E+03	2.74E+03
	F24	Std	5.4456	15.4412	42.4432	9.3321	64.0014	6.0021
		p-value	0.0025	0.0033	0.0044	0.0044	0.0061	0.0033
	F25	Ave	2.93E+03	2.95E+03	2.90E+03	2.94E+03	2.94E+03	2.93E+03
	F25	Std	15.3311	248.1414	19.5541	20.07644	23.3636	19.5252
		p-value	0.0011	0.0024	0.0002	0.0036	0.0046	0.0021
	F26	Ave	3.44E+03	3.45E+03	2.90E+03	3.00E+03	2.92E+03	2.96E+03
	F26	Std	632.7412	208.6541	25.3635	201.7474	32.3321	164.3321
		p-value	0.024	0.0011	0.0039	0.0025	0.0013	0.0033
	F27	Ave	3.11E+03	3.11E+03	3.09E+03	3.10E+03	3.09E+03	3.09E+03
	F27	Std	14.3321	11.0021	8.9987	7.9963	2.5521	2.5598
		p-value	0.0025	0.0033	0.0044	0.0044	0.0061	0.0033
	F28	Ave	3.30E+03	3.31E+03	3.10E+03	3.31E+03	3.21E+03	3.30E+03
	F28	Std	90.142	156.332	19.8521	112.444	113.001	132.212
		p-value	0.011	0.0036	0.0039	0.0036	0.0013	0.0014
	F29	Ave	3.20E+03	3.20E+03	3.15E+03	3.24E+03	3.21E+03	3.17E+03
	F29	Std	44.9630	36.6666	13.4120	43.8520	51.3366	23.6654
		p-value	0.0011	0.0024	0.0002	0.0036	0.0046	0.0021
	F30	Ave	4.99E+05	5.31E+05	3.50E+03	4.63E+05	3.01E+05	3.01E+05
	F30	Std	6.39E+05	4.89E+05	4.92E+03	4.92E+05	3.31E+05	4.52E+05
		p-value	0.0025	0.0033	0.0044	0.0044	0.0061	0.0033

Type	No.	Metric	TASR-CHOA	ARBGA	ARWOA	SHADE	CMA-ES	LSHADESPACMA
UM	F1	Ave	100.00	100.00	109.99	100	100	100
	F1	Std	3.14E−07	2.55E−05	0.0021	0.000	0.000	4.33E−06
		p-value	NA	0.0041	0.0021	0.51	0.42	0.033
	F3	Ave	300.00	300.00	300.00	300.00	300.00	300.00
	F3	Std	0.0000	9.94E−11	1.25E−03	0.000	0.000	1.11E−33
		p-value	NA	0.0011	0.0013	0.063	0.42	0.001
MM	F4	Ave	400.00	400.21	403.55	400.00	400.00	400.00
	F4	Std	1.21E−15	2.35E−07	1.21E−05	0.000	0.000	1.02E−12
		p-value	NA	0.0017	0.0043	0.56	0.052	0.0037
	F5	Ave	504.33	508.44	510.33	507.00	531.11	521.42
	F5	Std	1.000	4.001	4.2222	1.007	59.11	56.19
		p-value	NA	0.0011	0.0013	0.052	0.0033	0.0011
	F6	Ave	600.00	600.00	602.88	604.00	606.99	624.96
	F6	Std	3.83E−07	5.53E−04	2.55E−05	5.28E−04	5.99E−04	2.44E−03
		p-value	NA	0.0021	0.0033	0.0046	0.0011	0.0033
	F7	Ave	713.22	717.33	716.23	715.98	715.96	719.87
	F7	Std	1.033	2.0014	1.0014	1.541	1.632	1.7112
		p-value	NA	0.0021	0.0033	0.082	0.075	0.0033
	F8	Ave	805.64	806.33	807.71	806.85	806.84	810.93
	F8	Std	1.845	2.5413	3.7831	1.8456	1.9863	2.1456
		p-value	NA	0.0021	0.0033	0.082	0.075	0.0043
	F9	Ave	900.00	900.00	902.33	900.00	900.00	902.11
	F9	Std	0.000	1.64E−02	2.55E−02	0.000	0.000	1.44E−02
		p-value	NA	0.0025	0.0037	0.056	0.053	0.0028
	F10	Ave	1189.38	1244.52	1355.33	1999.25	1195.26	1249.23
	F10	Std	79.33	123.11	129.65	109.57	101.32	134.56
		p-value	NA	0.0021	0.0033	0.0046	0.0011	0.0033
Hybrid	F11	Ave	1100.00	1102.01	1104.38	1102.56	1102.12	1104.11
	F11	Std	0.96	1.44	2.11	1.32	1.31	2.77
		p-value	NA	0.0077	0.0017	0.0018	0.082	0.0036
	F12	Ave	1323.55	1365.25	1411.12	1322.55	1323.20	1351.01
	F12	Std	54.55	101.26	99.33	104.20	152.01	110.23
		p-value	NA	0.0021	0.0021	0.21	0.0046	0.0011
	F13	Ave	1305.21	1305.31	1311.14	1306.77	1304.47	1309.25
	F13	Std	3.22	2.89	3.33	2.71	0.69	2.51
		p-value	NA	0.0033	0.0046	0.0011	0.32	0.0011
	F14	Ave	1402.36	1404.22	1423.16	1409.82	1414.23	1449.38
	F14	Std	4.01	4.09	7.33	8.63	9.22	10.99
		p-value	NA	0.0023	0.0035	0.0046	0.0011	0.0033
	F15	Ave	1500.75	1500.76	1532	1501.33	1502.11	1554.06
	F15	Std	0.53	0.53	1.11	0.59	057	2.11
		p-value	NA	0.075	0.0025	0.082	0.056	0.0041
	F16	Ave	1601.01	1601.83	1614.23	1602.22	1603.25	1652.03
	F16	Std	0.88	0.99	22.99	2.19	3.22	7.65
		p-value	NA	0.0021	0.0033	0.0046	0.0011	0.0033
	F17	Ave	1709.33	1714.33	1793.36	1716.36	1715.14	1792.55
	F17	Std	5.19	9.66	17.17	5.88	5.69	14.11
		p-value	NA	0.0017	0.0015	0.0046	0.0055	0.0033
	F18	Ave	1801.17	1801.33	1817.38	1802.55	1800.00	1811.17
	F18	Std	1.88	1.17	1.23	0.99	0.34	2.43
		p-value	NA	0.0033	0.0046	0.0011	0.21	0.0066
	F19	Ave	1900.21	1900.66	1912.33	1900.66	1900.67	1909.55
	F19	Std	1.35	0.66	2.77	0.31	1.62	2.77
		p-value	NA	0.0013	0.0046	0.012	0.0021	0.0033
	F20	Ave	2013.33	2014.77	2037.21	2019.69	2019.99	2029.44
	F20	Std	8.21	9.71	24.88	0.01	29.66	48.55
		p-value	NA	0.0021	0.0033	0.133	0.0013	0.0046
CFs	F21	Ave	2.31E+03	2.32E+03	2.30E+03	2.20E+03	2.22E+03	2.24E+03
	F21	Std	42.66	39.44	44.77	22.66	21.55	39.77
		p-value	NA	0.024	0.0036	0.0039	0.0014	0.0013
	F22	Ave	2.30E+03	2.30E+03	2.30E+03	2.31E+03	2.32E+03	2.30E+03
	F22	Std	17.77	21.55	21.44	12.33	11.77	11.66
		p-value	NA	0.07323	0.0011	0.024	0.0036	0.0039
	F23	Ave	2.60E+03	2.61E+03	2.62E+03	2.61E+03	2.60E+03	2.74E+03
	F23	Std	2.01E−02	3.95E−02	2.88E−02	2.55E−02	2.44E−02	3.25E−02
		p-value	NA	0.0055	0.0013	0.0011	0.0017	0.0013
	F24	Ave	2.55E+03	2.51E+03	2.53E+03	2.70E+03	2.71E+03	2.85E+03
	F24	Std	37.33	39.44	39.55	41.77	38.33	39.55
		p-value	NA	0.33	0.0021	0.0033	0.0046	0.0011
	F25	Ave	2.89E+03	2.89E+03	2.92E+03	2.89E+03	2.83E+03	2.92E+03
	F25	Std	23.33	22.44	36.25	21.44	20.55	22.77
		p-value	NA	0.0021	0.0033	0.075	0.076	0.0044
	F26	Ave	2.82E+03	2.89E+03	2.84E+03	2.90E+03	2.90E+03	2.91E+03
	F26	Std	12.02	44.22	33.25	34.11	11.44	33.77
		p-value	NA	0.0042	0.073	0.0033	0.0052	0.0042
	F27	Ave	2.08E+03	3.08E+03	3.25E+03	3.09E+03	3.08E+03	3.10E+03
	F27	Std	0.055	1.11	7.31	2.20	1.65	2.44
		p-value	NA	0.073	0.0033	0.0046	0.073	0.0033
	F28	Ave	3.10E+03	3.10E+03	3.25E+03	3.26E+03	3.25E+03	3.29E+03
	F28	Std	6.23E−06	6.34E−05	33.32	19.02	14.01	13.66
		p-value	NA	0.0017	0.0011	0.0046	0.0015	0.0033
	F29	Ave	3.14E+03	3.15E+03	3.19E+03	3.14E+03	3.15E+03	3.20E+03
	F29	Std	11.18	12.55	19.02	12.33	15.44	19.52
		p-value	NA	0.0081	0.0017	0.077	0.0021	0.0033
	F30	Ave	3.41E+03	3.41E+03	3.55E+03	3.20E + 03	3.20E+03	3.56E+03
	F30	Std	12.71	19.56	22.36	1.32	1.18	33.55
		p-value	NA	0.0033	0.0046	0.33	0.099	0.0011

Open in a new tab

The best results are highlighted in bold.

Friedman’s mean rank clearly places TASR-CHOA and CMA-ES in the first and second positions, respectively. On the basis of the results, TASR-CHOA is advanced as the best among the available optimizers.

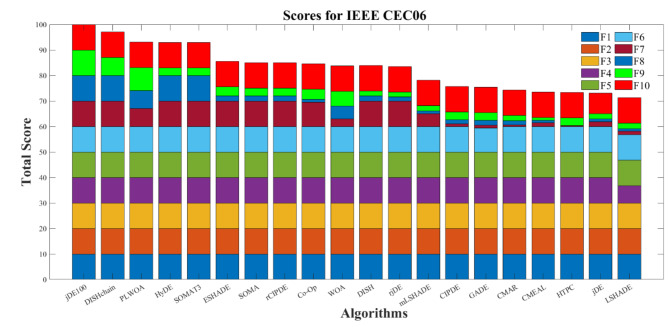
Results of the IEEE CEC06

In view of the measures above, the last version of the optimizer, TASR-CHOA, was tested on functions taken from the 100-digit competition IEEE CEC06. Each computational experiment included 50 repetitions for the algorithmic execution of the assigned test task. The minimum function evaluation counts the total accurate numbers across the 25 runs. The score of the test function can be calculated on condition Nc/25. In this instance, the perfect challenge score would originate from a minimum of 100 if 25 of 50 at least ten 10-digit results emerged from each of the ten trials conducted. Being that a score above a minimum of 1,000000000 on each of the benchmark tests is available, exerting a 10-digit accuracy is demanding. Figure 5 demonstrates the balanced visualization of some functions in three-dimensional shapes.

Fig. 3 — Searching area, convergence curves, average fitness history, the trajectory of the first dimension, and search history associated with randomly selected test functions (i.e., F2, F5, F8, F11, F13, F14, F18, F24(CF1), and F26(CF3)).

In the case of each of the ten functions (F1, F2, …, F10) confronted, results for the standard CHOA and its 18 benchmarking algorithms are illustrated in Fig. 6. It should be noted that each function is shown in different colors for better representation. Table A1 (Appendix A) summarized the Acronym for state-of-the-art algorithms.

As illustrated in Fig. 6, it may be envisaged that jDE100 achieved the highest score of 100, suggesting the best outcomes earned. Next to this is DISHchain1e + 12. Among a cohort of 20 advanced methods, the CHOA ranks 6th, scoring 87.6. In total, with twenty benchmarks for comparisons, our method, which adopts the TASR insertion of the CHOA, turns out in third place with 94.11. Pay attention to the fact that the TASR-CHOA caused better results in 7 of the 10 problems. TASR-CHOA meets such difficulties because of the size of the problems F5, F6, and F10, while it beats F7, F8, and F9. The statistical best performance of the method on any of the 35 different test functions was 28 out of 35 achieved by TASR-CHOA. Of note, the performance of the TASR-CHOA was relatively better than other benchmark functions.

Evaluation of the statistical characteristics of TASR-CHOA

In order to have a comprehensive statistical evaluation, a number of statistical methods are applied that allow for the comparison of the TASR-CHOA with its competitors, specifically the Bonferroni Dunns and Holm and Friedman analyses. In order to obtain adequate criteria for evaluation, the table functions were divided into three groups. The first category is those functions contained from the derived ones, F24 to F29, which are the CFs obtained from the rotation, shifting, and combination processes of the MMs and UMs. The purpose of generating the CF functions is to evaluate the techniques’ capacity to overcome local optima and manage the balance between exploration and exploitation. Table 5 demonstrates the performance of optimization algorithms employed in the CF systems and also the performance of the TASR-CHOA algorithm. The analysis provides evidence that the proposed algorithm, TASR-CHOA, is more efficient than the other approaches. The results of this study demonstrate that well-balanced phases of exploration and extraction are present in the finely tuned TASR-CHOA.

Also, the findings emphasize the efficiency of the algorithm in escaping from local optima. This is due to the use of more adaptive steps and more frontal relocation. The application of Friedman analysis is prescribed in order to find the index of algorithm rank. The results in Table 6 indicate that TASR-CHOA is the best-performing algorithm, while competing algorithms trend toward average performance.

It can be noted from Table 7 that the IEEE CEC-BC test functions form the second category. The third class comprises a subcategory of the two first classes. The nonparametric, non-correlational Friedman’s test can also be applied to bring out the difference between the effectiveness of the algorithms. When several methods’ effectivity is found to change in a statistically significant manner, it is necessary to seek the answers to the questions of which of the proposed methods has the efficiency noticeably lower compared to TASR-CHOA. For this reason, we carried out the Bonferroni-Dunn test, and CD was used to assess whether there was a difference in the two grouped approaches at a statistically significant level.

Table 8.

The outcomes of the suggested models addressing the issue of fire detection.

Algorithm	AFEs	ACDs	SR
CHOA	16,319	44.33	78.22
ULCHOA	16,103	45.25	76.33
ICHOA	14,219	51.22	92.25
ARWOA	15,501	47.66	83.66
NCHOA	18,031	39.33	46.34
DLFCHOA	16,222	45.31	72.36
ECHOA	15,419	48.41	82.55
TASR-CHOA	13,888	61.21	100
SHADE	16,300	44.77	78.52
CMA-ES	17,430	41.35	57.34
PGBM + DN-1	17,118	41.47	54.23
LSHADESPACMA	16,502	45.22	77.36
ARBGA	13,956	60.67	100

Open in a new tab

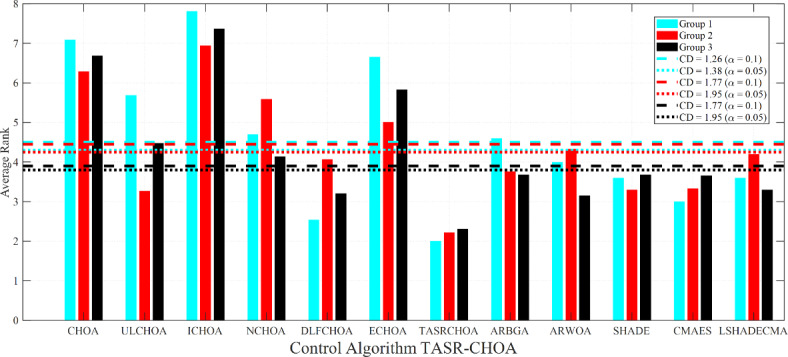
In this experimental study, it is essential to mention that TASR-CHOA is considered to be the control approach. One of the most exciting and valuable things about this home assessment is Fig. 7, which presents the average ranks of each of the chosen techniques for three different function categories: “Group 1,” “Group 2,” and “Group 3,” represent respectively “unimodal,” “multimodal,” and “complex” functions, that apply two specific relevance levels each (0.1 and 0.05). Crosses on the figure represent the TASR-CHOA model, which is maintained at the threshold ranking above the line. A distinctive color denotes each demarcating line for each group. When given the graphical representation, TASR-CHOA has the highest orders in all classes and has properties that can exceed all comparison algorithms.

Fig. 5 — The three-dimensional IEEE CEC06 functions’ search space.

To summarize, from the results presented in Fig. 7, the performance and robustness of TASR-CHOA relative to most of the known optimizers is entirely satisfactory on the known functions. The ranks of the models, on average, differ from each other. Also, the graphs show that there is no extreme fall or rise in the mean rank of TASR-CHOA across the three groups. Still, some models have a consistent rank in all the classes, while others have inconsistent ones.

Analysis of real-world problems

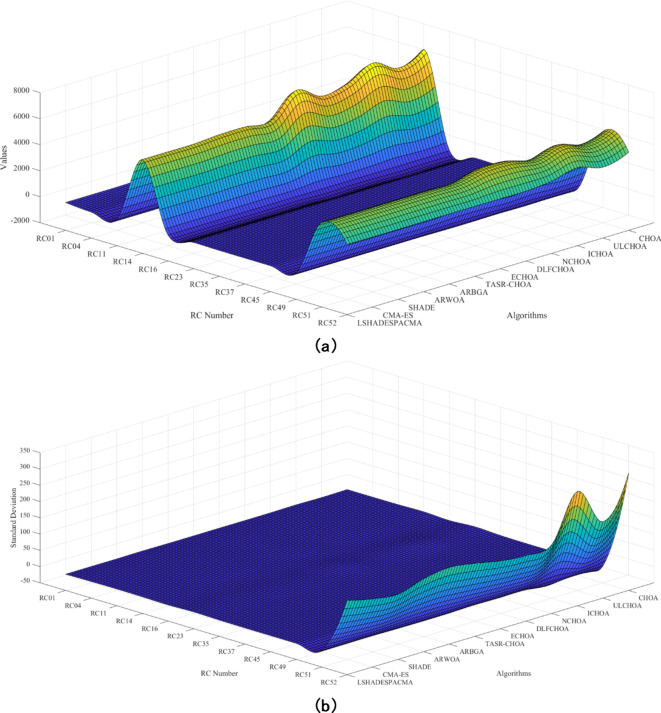
The twelve problems made use of in IEEE CEC2020 included (industrial heat exchanger synthesis (RC01) and reactor synthesis (RC04)), outlining and construction of process (RC11 and RC14), optimal industrial system designs (RC16 and RC23), problems on power systems (RC35 and RC37), electronics & power devices (RC45 and RC49), optimization of nutrition for cattle beef (RC51 and RC52)⁵¹ are used for testing the effectiveness of the TASR CHOA. It should be noted that in this section, the most extensive description of the suite test for the simulations is provided by Kumar et al. IEEE CEC2020 can be found⁵¹. All the results are shown in Fig. 8.

Fig. 8 — The results of comparison techniques for the IEEE CEC2020 test function: (a) AVE and (b) STD.

We examined the mean and standard deviation results across different RCs to determine how long TASR-CHOA takes in comparison to other algorithms. This unique viewpoint aids in evaluating the strengths and weaknesses of TASR-CHOA in collaboration with its co-researchers and identifying areas for improvement.

For specific RCs, mean values provide illustrative statistics of how different algorithms perform. The results of TASR-CHOA are inconsistent across the various RCs, with the mean values typically falling below those of the charting algorithms. For instance, in RC01, the average score of TASR-CHOA is 144, which is lower than the average score of 146 for the majority of algorithms available within the DLFCHOA. In spite of this, the performance of TASR-CHOA is observed to be consistent with the very low standard deviation of ± 0.002, meaning that the average scores produced are very close. Regarding RC04, TASR-CHOA achieves the lowest average score of -0.389, outperforming all other algorithms, particularly the last techniques. Performance was poorest with a mean score of TASR-CH5526, although the standard deviation in this instance, ± 1.02, was also reasonable.

In RC11, TASR-CHOA’s mean value of 9.79 is the lowest among the other algorithms. Some of these systems demonstrate higher performance compared to others despite their relatively low performance. The standard deviation here is ± 1.30; that is, though the performance is low, it is steady. On the other hand, in RC14, TASR-CHOA finally achieves a high mean value of 5221, which is lower than the best-performing algorithms, such as ICHOA, which has a mean value of 7330 but can be grouped with quite a few other algorithms. There was a low standard deviation of ± 1.02, revealing the extent to which the performance of TASR-CHOA was in this RC.

The mean values of TASR-CHOA in RC16, RC23, and RC37 are much lower at 0.004, 22.4, and 0.0221, respectively, indicating that performance is decreasing except for some destruction. The performance remained stable in these cases, with the standard deviations of the means falling within the unique performance limits of TASR-CHOA. The stability of performance across different RCs is a significant advantage of TASR-CHOA, especially when consistency is required.

In RC49 and RC51, even though the mean values of TASR-CHOA are lower (0.0235 and 4490) when compared with other algorithms, the standard deviations are still low (± 0.011 and ± 1.11, respectively). This reinforces the algorithm’s reliability. However, in RC52, the mean value reported for TASR-CHOA was 3392, which is less than most of the values of other methods, with a bottleneck standard deviation of ± 175 that suggests some performance.

The analysis indicates that TASR-CHOA, on average, performs pretty evenly among different RC TKIND customers, as the standard deviations are relatively low, making a solid case for this performance. This is undoubtedly an advantageous benefit, especially in cases where it is more important to have stable results than to seek perfection all the time. However, in terms of objective metrics, TASR-CHOA is one of the last algorithms against the majority of other algorithms. This indicates that while TASR-CHOA is a robust and steady algorithm, its overall performance is rather mediocre compared to other RCs. If one approaches the algorithm with the knowledge that no peak performance element will reveal any strength, then TASR-CHOA is an effective algorithm.

Real-world engineering problem: fire detection challenge

Fire warning systems are crucial in mitigating the damage and repercussions caused by fires, especially in urban areas and rural regions. The earlier systems made use of temperature sensors and computer vision algorithms; the current systems do not but rather depend solely on DCNNs, which have proven to be more sophisticated in detection tasks. Using the TASR-CHOA framework, we tackle the problem of applying the structure of the existing framework, DCNN, so as to enhance fire detection. In terms of examination, we performed tests on enhanced Alexnet and DarkNet in order to gather information about configuration aspects for their training and testing and the time taken for these tests. First, we deployed a more straightforward DCNN structure and then later built on it to develop more advanced structures. This was done so as to disprove the idea that fire detection is a sophisticated task that can be performed using simple approaches as well as simple models.

Employing the Fire-Detection-Image-Dataset allowed both authors to make a fair evaluation. Although the dataset contains only 651 images, this is large enough to indicate the speed and accuracy that can be attained by models based on photographs and the valuable information that can be derived from them. There are 549 images in the training set of the fire, drenched in a total of 49 fire and 490 non-fire images.

There was a deliberate imbalance on our part in that we wanted to create real-life situations since the probability of fire hazards occurring is relatively rare.

This design is suitable for evaluating the generalizability of the models due to the significant imbalance in the set used for training and the total equality in the testing set. The limited number of fire photographs contains enough data to effectively train a dependable model that can recognize the distinct traits. An adequately complex model is necessary to extract these characteristics from a dataset that has few instances of each feature.

Some of the photographs not only lack balance, but they also cannot be easily categorized. The collection comprises images of fires in various environments, including residential buildings, lodgings, workplaces, and woodlands. The photos exhibit a diverse array of tones and intensities of illumination, spanning from yellow to orange and ultimately transitioning into red. Fires can occur at any time, regardless of their size. Non-fire imagery such as sunset pictures, houses and cars colored red, lights with a combination of yellow and red, and brightly illuminated rooms are challenging to distinguish from fire photos.

Figure 9 displays instances of fires in different environments. In addition, Fig. 10 displays non-fire photos that are difficult to classify. Fire detection can pose difficulties due to the characteristics of the dataset.

Fig. 7 — Bonferroni Dunn analysis (threshold values 0.1and 0.05).

The research focuses on algorithms designed to solve fire detection problems. The key goal is to determine the complexity and robustness of these algorithms. The methods employed should look for practical solutions in Max(T) time, making Min(T) as small as possible. After the experimentation phase of each fire detection problem, three metrics are computed: SR, AFEs, and ACDs. These parameters measure the effectiveness and performance of the processes and are based on what has been done in earlier works. For finding various metrics, including ACDs, SR, and AFEs, we employ Eqs. (12) to (14):

NSS is the number of successful searching out of K iterations in a trustworthy experiment that is completed K times. It is anticipated that algorithms will discover a viable solution in every iteration. The outcomes of the proposed models can be observed in Table 8.

Using AFEs, ACDs, and SR to look at the algorithms gives us a better idea of how well they work, how much work they require, and how successful they are.

AFEs

Out of the three methods considered, TASR-CHOA again records the lowest number of AFEs at 13,888, implying that it reaches convergence in fewer evaluations on average and is, therefore, the most efficient in this case. ARBGA is close behind at 13,956, or, in other words, is also very efficient. On the other hand, the form of the algorithm NCHOA has the highest AFEs of 18,031, meaning that it is less efficient because it takes more evaluations to come up with the same results as other forms.

ACDs

ACDs help in giving information on the computational cost incurred in any given algorithm. Once again, TASR-CHOA takes the lead with the highest ACD of 61.21. This indicates that AFEs are less before the algorithm’s performance, but the algorithm requires more computations and time. Correspondingly, ARBGA once again has a total ACD and, in this case, a high ACD of 60.67. Mainly on the extreme side, NCHOA and CMA-ES show low ACDs of 39.33 and 41.35, respectively, which suggests that they may be faster but may call for many evaluations, as noted in NCHOA, where AFEs were higher.

SR

In the success rate assessment, TASR-CHOA and ARBGA recorded a perfect SR of 100. Such FVP systems can work under all restrictions and return a positive outcome. ICHOA is also good, with an SR of 92.25, but because he needs an AFE of 14,219 instead of the 11,798 and 9214 of TASR-CHOA and ARBGA, respectively, it falls below them. In sharp contrast, NCHOA, on the global scale, has the lowest score in measuring the success rate of finding a solution, which stands at 46.34.

Overall Analysis: TASR-CHOA is a highly efficient algorithm in terms of performance and processing expenses; however, more computational operations are needed. ARBGA also shares the same features; thus, it is a perfect solution. In contrast, although NCHOA appears to be less computationally expensive, its turn-out performance (low SR) and operational cost (high AFE) do not appear to be suitable for use, especially in applications that require fast and regular solutions. Operating ICHOA yields good results, but it falls short of the superior performance outcomes achieved with TASR-CHOA and ARBGA. In general, TASR-CHOA is also optimal due to its good efficiency and SR, albeit at a slightly higher computational cost.

Analysis of sensitivity

In order to test the efficiency and flexibility of the TASR-CHOA algorithm, we now turn to a sensitivity analysis in which we evaluated two relevant parameters 1 and 2, respectively, with changing sizes of the population. In this case, 1 and 2, were varied within the limits of 0.1–1.0 at intervals of 0.05, and population sizes of the algorithm from 20 to 100 were tested. Table 9 presents the best fitness obtained within the bounds of the conducted sensitivity analysis for selected values of 1 and 2, and population sizes.

Table 9.

Best fitness obtained within the bounds of the conducted sensitivity analysis for selected values of 1 and 2, and population sizes.

Population size	1	2	Best fitness value
20	0.10	0.10	12.29
20	0.50	0.50	0.44
20	1.00	1.00	0.31
50	0.10	0.10	15.10
50	0.50	0.50	0.21
50	1.00	1.00	0.17
100	0.10	0.10	18.44
100	0.50	0.50	0.09
100	1.00	1.00	0.08

Open in a new tab

Table 9 outlines the findings of the study concerning the dependence of the efficiency of the TASR-CHOA algorithm on the parameter settings quite dynamically. For instance, one could say that a rise in both 1 and 2 would, in general, improve the optimized outputs that when these parameters are increased to their highest values, the best fitness values are decreased.

For a population size of 50, the algorithm managed to obtain the best fitness value of 0.18 for 1=2 = 1.0. This observation is crucial since it shows how these values help in the tradeoff between the exploratory and exploitative nature of the algorithm. However, low values of 1 and 2 (0.1), for instance, were associated with significant deterioration of performance, especially with regard to population size, which implies that the population was exploring too little to allow escaping of a local optimum.

Also, it is seen that the increase in performance enhancement is less apparent with the larger sizes of the populations, indicating that the performance of the algorithm is beginning to plateau. To conclude, this sensitivity analysis further confirms the reliability of TASR-CHOA, showing that an appropriate modification of exact 1 and λ 2 is significant in the various optimization situations undertaken. Future plans will include seeking adaptive strategies that will dynamically change these parameters during the optimization, aiming to improve performance even further.

Discussion

This section contains a critical review of graphical processing units-based model parallelism (TASR-CHOA) research challenges in the context of comparative evaluation of the benefits and limitations of this algorithm and, performance-wise, how they would affect future work and application. The first one would be how the adversary tactics can be explained and supplemented in the context of the purpose of the study and underline the critical impact of pursuing this direction where the discerning and experimental tasks were pointed out in general and success factors related to goals. Then, we will look at the possible constraints of the algorithm and suggest possible means of making the algorithm better. Further, we consider the implications of the theoretical bases and complexity of computation constitutive of TASR-CHOA on the effectiveness and scope of its deployment. Finally, issues relating to the further development of TASR-CHOA and its utilization in future research in view of optimization theory, in particular IT technologically advanced means, are addressed. The goal is to present the crucial features of the TASR-CHOA visualization algorithm as well as the optimization prospects—bottlenecks and development directions.

Complexity analysis of the computation

The computation of TASR-CHOA has a complexity that is directly proportional to the dimensionality referred to occasionally as the number of variables (NV), the number of individuals (NI), and the evaluation limit (ME). The number of iterations (t) is defined by ME/2×NI, where ME is the maximum number and size of the evaluation function, among others. In the second paragraph of the subsection, the analysis will be able to describe the temporal complexity as given by Eq. (15):

The complexity of initialization is O(NI×NV) as well. Initialization within the new practical method to replace old data experienced from sanitary attacks appears to be deterministic complexity O(NI×NV + 2×NI×NV). The position of the population of chimpanzees is revised by adding two weights in O(NI×NV×2 × 2 × 2) operations. Therefore, the general complexity can be defined in the following way:

Basic elements of TASR-CHOA

To increase both the convergence speed and the thoroughness of search in the process of optimization, it is suggested that the method of TASR-CHOA uses stochastic weight balancing. TASR-CHOA provides an efficient solution to a problem along three basic principles, theoretically speaking.

Stochastic reinforcement is a technique. The optimization procedure of TASR-CHOA incorporates a stochastic reinforced strategy, which introduces unpredictability by replacing the optimal solution in each dimension during each iteration. Incorporating stochastic aspects into the search space helps broaden its scope and decreases the chance of an algorithm being stuck at a local solution. The technique of approaching the solution involves the angle of the stochastic activity. Internal stochasticity of the optimization algorithm allows for constant variability to avoid convergence at a local optimum and instead steer the solution to the global one.

TASR-CHOA uses two adaptive weighting methods, which are λ₁ and λ₂. These methods are employed to effectively alter the biases toward exploration and exploitation at still different times during the optimization process. In the first part, however, 1 does this in order to explore the entire solution space. Later on, two shifts focus to exploitation, such that it tries to make use of the good places that have been identified in the course of the exploration phase. Computational resource allocation in TASR-CHOA is done using an adaptive weighting approach in order to respond to the changing characteristics of the optimization landscape. This aids in enhancing the system’s response to the global optimal solution while avoiding early and unintentional fixation along the local optimal solutions.

Problems of the optimal ratio and balance between exploring and exploiting: The core reason for including stochastic reinforcement and adaptive weighting in TASR-CHOA is to “balance” between the exploitation and exploration of the problem at every step in the optimization process. In its early stages of optimization, TASR-CHOA manages to explore a lot of the solution space and utilizes solutions out of exploration in later stages of optimization through a careful balance of these two components of optimization techniques. As a result of this refined approach, the optimization environment and processes are well handled by TASR-CHOA irrespective of their complexity and dimensionality, which results in improved rapid convergence and improved quality of the solution.

The theoretical background of TASR-CHOA is primarily based on the concepts of robustness and generalization and incorporates these features to ensure that they are applicable to different optimization problems. Because of the addition of stochastic reinforcement and adaptive weighting, effectiveness and flexibility have improved even further, making them very useful for solving complex optimization problems met in practice. The principles underlying the construction of the TASR-CHOA algorithm allow us to combine stochastic research and adaptive attack in order to solve complex and multidimensional problems.

The foundational concept of TASR-CHOA is implemented, turning to a sequence of stochastic reinforcement and adaptive weighting leading to a sufficient equilibrium of exploring and exploiting. In this way, the speed and quality of solutions in a multilevel optimization problem are enhanced.

The limitations of TASR-CHOA

Despite the fact that TASR-CHOA already has several optimizations concerning the efficiency of using optimization algorithms, it is essential to state or accept some of its stream examples as threats.

Sensitivity to parameter tuning The performance of a predictive model using TASR-CHOA can very much depend on the fine-tuning of specific parameters, such as the adaptive weighting factors (λ₁ and λ₂) and the stochastic reinforced technique parameters, the same with other optimization algorithms. If configuration space definition is done poorly, the cases of convergence might be rather slow or not satisfactory with a solution with the mentioned concern focusing on proper calibration of the parameters, where calibration may turn out to be very cumbersome and time-wasting.

Limited robustness to the Problem types The performance of the TASR-CHOA in relation to the various forms of optimization tasks may not be similar, therefore suggesting limited robustness. It might be noted that the model performs well when benchmarked on specific functions or engineering problems, but when it comes to solving optimization problems that are incredibly nonlinear, multimodal, or not severely constrained, the model may not perform optimally. The generalization of this algorithm to different types of problems might encounter challenges owing to its use of particular strategies during exploration and exploitation.

Risk of premature convergence One of the disadvantages encountered with TASR-CHOA lies with the fact that there is a very high chance that the search will halt at an optimal solution too soon, which is most probably towards the beginning of the search, especially with complicated optimization goals, even when it is the objective to achieve a suitable balance between exploration and exploitation. There is a risk that the dopamine-based adaptive weighting used in the algorithm may not achieve the desired outcome of appropriate exploration strategies, optimally moving to high-reward locations, effectively solving all the tasks. This is likely to cause premature termination of the search operations and consequently stagnation during the search process.

Addressing limitations To address these limitations and improve the efficiency of TASR-CHOA, future research efforts could prioritize the following.

Performing sensitivity analysis and robustness evaluations across many problem domains to determine the most suitable parameter combinations and algorithmic setups.
The objective is to enhance the algorithm’s robustness and scalability by devising sophisticated approaches for adaptive parameter tuning and dynamic adjustment mechanisms.
In order to enhance the capabilities of TASR-CHOA and mitigate its limitations, such as premature convergence or limited exploration ability, hybridization techniques or metaheuristic combinations should be investigated.

In conclusion, although TASR-CHOA demonstrates encouraging performance in optimization tasks, it is imperative to recognize and rectify its inherent limitations in order to augment its efficacy and suitability in real-world situations.

Conclusion

In an effort to demonstrate the innovations behind the concept, we developed a novel twofold adaptive stochastic reinforced version of the Chimp Optimization Algorithm (CHOA) termed TASR-CHOA. Being an improved version of the original CHOA, which suffers from convergence issues in multidimensional optimization problems and gets stuck to local optima, the work added some stochastic reinforcement terms to improve the convergence rate coupled with a dual adaptive weighting for exploration-exploitation balance. Employing two modifications in the CHOA structure, so increasing its performance—that is, achieving faster convergence and more thorough exploration of searched space—TASR-CHOA improved across the benchmark functions more than many up-to-date optimization strategies.

TASR-CHOA was robust and efficient using benchmark evaluations such as 29 conventional optimization benchmark functions, 10 IEEE CEC-06 benchmarks, 30 complex IEEE CEC-BC benchmark functions, and 10 real-world engineering problems. The algorithm proved to cover the highest positions in 51 out of 70 evaluation functions and demonstrated performance APP1 similar to the top-ranked algorithms SHADE and CMA-ES. Excellent stability and reliability of the TASR-CHOA have also been observed in engineering applications such as fire detection through deep convolutional neural networks.

It is worth noting that despite these conflicting outcomes, oASR, on balance, involves a much more computational burden compared to the same modern algorithms. Still, what is optimistic about the TASR-CHOA is its capability to keep the success rates very high and the average number of failures per event shallow when enforcing complex optimization tasks.

Future research directions

Even though TASR-CHOA has outperformed the standard CHOA, it would be great future work if the possibility of blending it with other advanced optimization algorithms, such as genetic or particle swarm optimization algorithms, were to be explored. In this regard, such hybrid models could take advantage of the capabilities of different optimization techniques while simultaneously tackling even more complex and high-dimensional problems.

With the practical complexity of the algorithm, such as TASR-CHOA, there are possibilities of laying down future work that would design and implement TASR-CHOA-based real-time optimization techniques. This will involve looking to improve the effectiveness of the algorithm when it comes to time-critical tasks such as autonomous systems that require real-time decisions to be made.

The applications of TASR-CHOA have primarily been in optimization problems that depict a relatively constant environment. Therefore, it is only logical that future work on TASR-CHOA would aim at exploring its effectiveness in more complex optimization problems over time, that is, in time-varying optimization landscapes. It would, therefore, be essential to seek the possibility of developing a dynamic model of TASR-CHOA since it would increase its possibilities of being used in the real world where the parameters are not fixed.

While TASR-CHOA has been used successfully in multidimensional problems, further research should investigate the method’s scaling and efficiency within the scope of very high-dimensional problems that are already prevalent in machine learning and big data analysis. Potential avenues of research could, for example, aim at modifying TASR-CHOA to ensure greater computational efficiency and lower costs of high-dimensional analyses.

The present, successful use of TASR-CHOA for fire detection indicates at least one further possible use of this approach for other complex engineering problems. Future work could validate its efficiency in fire detection by applying it in diverse domains such as robotic engineering, structural design, and energy systems management.

Considering the current interest in performing large-scale optimization problems, the TASR-CHOA could be adapted for use in parallel and distributed computing in future works. It will require devising approaches to perform the parallelization of the algorithm so that the overall optimization time would be less.

As this paper presented a preliminary complexity assessment of TASR-CHOA, the other scope of improvement in the future includes a theoretical understanding of the method in terms of its convergence metrics and possible enhancements to the method. It might also be that better hydrodynamics and convergence rates could be obtained by using more elaborate adaptive or stochastic techniques.

In following these research directions, TASR-CHOA can also be enhanced and adapted to address the changing requirements of optimization problems in a number of other domains, including science and engineering.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary Material 1^{(15.8KB, docx)}

Acknowledgements

This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2024/R/1445).

Author contributions

Z.Zh., L.T., and D.M. wrote the main manuscript text and L.Q., M.Kh. and P. J. prepared all simulation and figures. All authors reviewed the manuscript.

Data availability

The resource data and material can be downloaded using the following links and references. https://www3.ntu.edu.sg/home/epnsugan/index_files/cec-benchmarking.htmhttps://github.com/P-N-Suganthanhttps://seyedalimirjalili.com/projectshttps://www3.ntu.edu.sg/home/epnsugan/.

Declarations

Competing interests

The authors declare no competing interests.

The authors declare that there is no conflict of interest.

Footnotes

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

References

1.Lin, S., Zhang, J. & Qiu, C. Asymptotic analysis for one-stage stochastic linear complementarity problems and applications. Mathematics11 (2), 482 (2023). [Google Scholar]
2.Xiang, X., Zhou, J., Deng, Y. & Yang, X. Identifying the generator matrix of a stationary Markov chain using partially observable data. Chaos Interdiscip J. Nonlinear Sci., 34, 2, (2024). [DOI] [PubMed]
3.Chang, L., Li, M., Qian, L. & de Oliveira, G. G. Developed multi-objective honey badger optimizer: application to optimize proton exchange membrane fuel cells-based combined cooling, heating, and power system. Int. J. Hydrogen Energy. 50, 592–605 (2024). [Google Scholar]
4.Seow, M. J. & Qian, L. Knowledge Augmented Intelligence Using Large Language Models for Advanced Data Analytics. In SPE Eastern Regional Meetingp. D021S001R003 (SPE, 2024).
5.Jin, W. et al. Enhanced UAV pursuit-evasion using boids modelling: a synergistic integration of bird swarm intelligence and DRL. Comput. Mater. Contin, 80, 3, (2024).
6.Mohammadzadeh, A., Taghavifar, H., Zhang, Y. & Zhang, W. A fast nonsingleton Type-3 fuzzy predictive controller for nonholonomic robots under sensor and actuator faults and measurement errors. IEEE Trans. Syst. Man. Cybern Syst., (2024).
7.Khishe, M. & Mosavi, M. R. Chimp optimization algorithm. Expert Syst. Appl.10.1016/j.eswa.2020.113338 (2020). [Google Scholar]
8.Zhu, J. et al. The impact of spatial scale on layout learning and individual evacuation behavior in indoor fires: Single-scale learning perspectives. Int. J. Geogr. Inf. Sci.38 (1), 77–99 (2024). [Google Scholar]
9.Yu, M. et al. Quantum Chimp optimization algorithm: a novel integration of Quantum mechanics into the Chimp optimization Framework for enhanced performance. J. Artif. Intell. Soft Comput. Res.14 (4), 321–359 (2024). [Google Scholar]
10.Zhang, Z. et al. Evolving chimp optimization algorithm using quantum mechanism for engineering applications: A case study on fire detection. J. Comput. Des. Eng.11 (5), 143–163 (2024). [Google Scholar]
11.Cai, G., Zheng, X., Gao, W. & Guo, J. Self-extinction characteristics of fire extinguishing induced by nitrogen injection rescue in an enclosed urban utility tunnel. Case Stud. Therm. Eng.59, 104478 (2024). [Google Scholar]
12.Cao, X. et al. Experimental research on the synergy effect of resistance/inhibition on the syngas explosion. Fuel363, 130995 (2024). [Google Scholar]
13.Fan, R., Pan, Y., Xiao, Y. & Wang, Z. Investigation on flame propagation characteristics and critical ignition criteria of hydrogen jet. Int. J. Hydrogen Energy. 57, 1437–1445 (2024). [Google Scholar]
14.Lu, Y., Fan, R., Wang, Z., Cao, X. & Guo, W. The influence of hydrogen concentration on the characteristic of explosion venting: Explosion pressure, venting flame and flow field microstructure. Energy293, 130562 (2024). [Google Scholar]
15.Mirjalili, S. Genetic algorithm. In Studies in Computational Intelligence. 10.1007/978-3-319-93025-1_4 (2019).
16.Kennedy, J. & Eberhart, R. Particle swarm optimization. In Proceedings of ICNN’95-international conference on neural networks, IEEE, pp. 1942–1948. (1995).
17.Price, K. V. Differential evolution. In Handbook of Optimization. Springer, 187–214. (2013).
18.Mohammadzadeh, A., Zhang, C., Alattas, K. A., El-Sousy, F. F. M. & Vu, M. T. Fourier-based type-2 fuzzy neural network: Simple and effective for high dimensional problems. Neurocomputing547, 126316 (2023). [Google Scholar]
19.Slimani, M. et al. A Chimp optimization algorithm (ChOA) for vibration-based damage detection of a Damaged Steel Truss. In Structural Health Monitoring and Engineering Structures, Springer, pp. 121–132. (2021).
20.Wu, X., Zheng, W., Xia, X. & Lo, D. Data quality matters: a case study on data label correctness for security bug report prediction. IEEE Trans. Softw. Eng., (2021).
21.Zayed, M. E. et al. Predicting the performance of solar dish Stirling power plant using a hybrid random vector functional link/chimp optimization model. Sol Energy. 222, 1–17 (2021). [Google Scholar]
22.Chen, Z., Zhang, K., Chan, T. H. T., Li, X. & Zhao, S. A novel hybrid Whale-Chimp optimization algorithm for structural damage detection. Appl. Sci.12 (18), 9036 (2022). [Google Scholar]
23.Kaur, M., Kaur, R., Singh, N. & Dhiman, G. SChoA: an newly fusion of sine and cosine with chimp optimization algorithm for HLS of datapaths in digital filters and engineering applications. Eng. Comput.10.1007/s00366-020-01233-2 (2021). [Google Scholar]
24.Kaur, M., Kaur, R. & Singh, N. A novel hybrid of chimp with cuckoo search algorithm for the optimal designing of digital infinite impulse response filter using high-level synthesis. Soft Comput., pp. 1–25, (2022).
25.Mousavipour, F. & Mosavi, M. R. Sonar data classification using neural network trained by hybrid dragonfly and chimp optimization algorithms (2022).
26.Xie, Y., Wang, X. Y., Shen, Z. J., Sheng, Y. H. & Wu, G. X. A two-stage estimation of distribution algorithm with heuristics for energy-aware cloud workflow scheduling. IEEE Trans. Serv. Comput., (2023).
27.Alnaggar, O. A. M. F., Jagadale, B. N. & Narayan, S. H. MRI brain tumor detection using boosted crossbred random forests and chimp optimization algorithm based convolutional neural networks.
28.Dhiman, G. SSC: A hybrid nature-inspired meta-heuristic optimization algorithm for engineering applications. Knowledge-Based Syst.222, 106926 (2021). [Google Scholar]
29.Houssein, E. H., Emam, M. M. & Ali, A. A. An efficient multilevel thresholding segmentation method for thermography breast cancer imaging based on improved chimp optimization algorithm. Expert Syst. Appl. 115651. 10.1016/j.eswa.2021.115651 (2021).
30.Saffari, A., Zahiri, S. H., Khishe, M. & seyyed mohammadreza mosavi Design of a fuzzy model of control parameters of chimp algorithm optimization for automatic sonar targets recognition, IJMT, [Online]. Available: (2020). http://ijmt.iranjournals.ir/article_241126.html
31.Jia, H., Sun, K., Zhang, W. & Leng, X. An enhanced chimp optimization algorithm for continuous optimization domains. Complex. Intell. Syst., pp. 1–18, (2021).
32.Hu, G., Dou, W., Wang, X. & Abbas, M. An enhanced chimp optimization algorithm for optimal degree reduction of Said–ball curves. Math. Comput. Simul.197, 207–252 (2022). [Google Scholar]
33.Zhang, Q. et al. A novel chimp optimization algorithm with refraction learning and its engineering applications. Algorithms15 (6), 189 (2022). [Google Scholar]
34.Du, N., Zhou, Y., Deng, W. & Luo, Q. Improved chimp optimization algorithm for three-dimensional path planning problem. Multimed Tools Appl., pp. 1–26 (2022).
35.Khishe, M., Nezhadshahbodaghi, M., Mosavi, M. R. & Martín, D. A weighted chimp optimization algorithm. IEEE Access. (2021).
36.Kaidi, W., Khishe, M. & Mohammadi, M. Dynamic levy flight chimp optimization. Knowledge-Based Syst., p. 107625 (2021).
37.Qian, L., Khishe, M., Huang, Y. & Mirjalili, S. SEB-ChOA: an improved chimp optimization algorithm using spiral exploitation behavior, Neural Comput. Appl., pp. 1–24. 10.1007/s00521-023-09236-y (2023)
38.Qian, L. et al. Breast cancer diagnosis using evolving deep convolutional neural network based on hybrid extreme learning machine technique and improved chimp optimization algorithm, Biomed. Signal Process. Control, vol. 87, p. 105492, (2024). 10.1016/j.bspc.2023.105492
39.Wolpert, D. H. & Macready, W. G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput.1 (1), 67–82. 10.1109/4235.585893 (1997). [Google Scholar]
40.Liu, L., Khishe, M., Mohammadi, M. & Mohammed, A. H. Optimization of constraint engineering problems using robust universal learning chimp optimization. Adv. Eng. Inf.53, 101636 (2022). [Google Scholar]
41.Gong, S. P., Khishe, M. & Mohammadi, M. Niching Chimp optimization for Constraint Multimodal Engineering optimization problems. Expert Syst. Appl., p. 116887, (2022).
42.Zojaji, Z. & Kazemi, A. Adaptive reinforcement-based genetic algorithm for combinatorial optimization. J. Comput. Secur.9 (1), 71–84 (2022). [Google Scholar]
43.Chen, H., Yang, C., Heidari, A. A. & Zhao, X. An efficient double adaptive random spare reinforced whale optimization algorithm. Expert Syst. Appl.154, 113018 (2020). [Google Scholar]
44.Poláková, R. L-SHADE with competing strategies applied to constrained optimization. In 2017 IEEE Congress on Evolutionary Computation (CEC), IEEE, 1683–1689. (2017).
45.Hadi, A. A., Mohamed, A. W. & Jambi, K. M. Single-objective real-parameter optimization: Enhanced LSHADE−SPACMA algorithm. In Heuristics for Optimization and Learning, Springer, pp. 103–121. (2021).
46.Abdi, H. Holm’s sequential Bonferroni procedure. Encycl Res. Des.1 (8), 1–8 (2010). [Google Scholar]
47.Krishnamoorthy, K. Wilcoxon signed-rank test. In Handbook of Statistical Distributions with Applications, pp. 339–342. 10.1201/9781420011371-34 (2020).
48.Mack, G. A. & Skillings, J. H. A Friedman-type rank test for main effects in a two-factor ANOVA. J. Am. Stat. Assoc.75 (372), 947–951 (1980). [Google Scholar]
49.Pant, M. & Vig, G. Clustering based adaptive differential evolution for numerical optimization. In 2020 IEEE Congress on Evolutionary Computation (CEC), IEEE, pp. 1–8. (2020).
50.Price, P. N., Awad, K. V., Ali, N. H. & Suganthan M. Z., Problem definitions and evaluation criteria for the 100-digit challenge special session and competition on single objective numerical optimization. Technical Report. https://personal.ntu.edu.sg/404.html (2018).
51.Kumar, A. et al. A test-suite of non-convex constrained optimization problems from the real-world and some baseline results. Swarm Evol. Comput.10.1016/j.swevo.2020.100693 (2020). [Google Scholar]
52.Zamuda, A. Function evaluations upto 1e + 12 and large population sizes assessed in distance-based success history differential evolution for 100-digit challenge and numerical optimization scenarios (DISHchain1e + 12): A competition entry for 100-digit challenge, and f. In GECCO 2019 Companion - Proceedings of the 2019 Genetic and Evolutionary Computation Conference Companion. 10.1145/3319619.3326751 (2019).
53.Brest, J., Maucec, M. S. & Boskovic, B. The 100-digit challenge: Algorithm jDE100. In 2019 IEEE Congress on Evolutionary Computation, CEC 2019 - Proceedings. 10.1109/CEC.2019.8789904 (2019)
54.Zhang, S. X., Shing Chan, W., Tang, K. S. & Zheng, S. Y. Restart based collective information powered differential evolution for solving the 100-digit challenge on single objective numerical optimization. In 2019 IEEE Congress on Evolutionary Computation, CEC 2019 - Proceedings. 10.1109/CEC.2019.8790279 (2019)
55.Yeh, J. F., Chen, T. Y. & Chiang, T. C. Modified L-SHADE for single objective real-parameter optimization. In 2019 IEEE Congress on Evolutionary Computation, CEC 2019 - Proceedings. 10.1109/CEC.2019.8789991 (2019)
56.Mohammadzadeh, A. et al. A non-linear fractional‐order type‐3 fuzzy control for enhanced path‐tracking performance of autonomous cars. IET Control Theory Appl.18 (1), 40–54 (2024). [Google Scholar]
57.Yan, S. R., Guo, W., Mohammadzadeh, A. & Rathinasamy, S. Optimal deep learning control for modernized microgrids. Appl. Intell.53 (12), 15638–15655 (2023). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Material 1^{(15.8KB, docx)}

Data Availability Statement

[CR1] 1.Lin, S., Zhang, J. & Qiu, C. Asymptotic analysis for one-stage stochastic linear complementarity problems and applications. Mathematics11 (2), 482 (2023). [Google Scholar]

[CR2] 2.Xiang, X., Zhou, J., Deng, Y. & Yang, X. Identifying the generator matrix of a stationary Markov chain using partially observable data. Chaos Interdiscip J. Nonlinear Sci., 34, 2, (2024). [DOI] [PubMed]

[CR3] 3.Chang, L., Li, M., Qian, L. & de Oliveira, G. G. Developed multi-objective honey badger optimizer: application to optimize proton exchange membrane fuel cells-based combined cooling, heating, and power system. Int. J. Hydrogen Energy. 50, 592–605 (2024). [Google Scholar]

[CR4] 4.Seow, M. J. & Qian, L. Knowledge Augmented Intelligence Using Large Language Models for Advanced Data Analytics. In SPE Eastern Regional Meetingp. D021S001R003 (SPE, 2024).

[CR5] 5.Jin, W. et al. Enhanced UAV pursuit-evasion using boids modelling: a synergistic integration of bird swarm intelligence and DRL. Comput. Mater. Contin, 80, 3, (2024).

[CR6] 6.Mohammadzadeh, A., Taghavifar, H., Zhang, Y. & Zhang, W. A fast nonsingleton Type-3 fuzzy predictive controller for nonholonomic robots under sensor and actuator faults and measurement errors. IEEE Trans. Syst. Man. Cybern Syst., (2024).

[CR7] 7.Khishe, M. & Mosavi, M. R. Chimp optimization algorithm. Expert Syst. Appl.10.1016/j.eswa.2020.113338 (2020). [Google Scholar]

[CR8] 8.Zhu, J. et al. The impact of spatial scale on layout learning and individual evacuation behavior in indoor fires: Single-scale learning perspectives. Int. J. Geogr. Inf. Sci.38 (1), 77–99 (2024). [Google Scholar]

[CR9] 9.Yu, M. et al. Quantum Chimp optimization algorithm: a novel integration of Quantum mechanics into the Chimp optimization Framework for enhanced performance. J. Artif. Intell. Soft Comput. Res.14 (4), 321–359 (2024). [Google Scholar]

[CR10] 10.Zhang, Z. et al. Evolving chimp optimization algorithm using quantum mechanism for engineering applications: A case study on fire detection. J. Comput. Des. Eng.11 (5), 143–163 (2024). [Google Scholar]

[CR11] 11.Cai, G., Zheng, X., Gao, W. & Guo, J. Self-extinction characteristics of fire extinguishing induced by nitrogen injection rescue in an enclosed urban utility tunnel. Case Stud. Therm. Eng.59, 104478 (2024). [Google Scholar]

[CR12] 12.Cao, X. et al. Experimental research on the synergy effect of resistance/inhibition on the syngas explosion. Fuel363, 130995 (2024). [Google Scholar]

[CR13] 13.Fan, R., Pan, Y., Xiao, Y. & Wang, Z. Investigation on flame propagation characteristics and critical ignition criteria of hydrogen jet. Int. J. Hydrogen Energy. 57, 1437–1445 (2024). [Google Scholar]

[CR14] 14.Lu, Y., Fan, R., Wang, Z., Cao, X. & Guo, W. The influence of hydrogen concentration on the characteristic of explosion venting: Explosion pressure, venting flame and flow field microstructure. Energy293, 130562 (2024). [Google Scholar]

[CR15] 15.Mirjalili, S. Genetic algorithm. In Studies in Computational Intelligence. 10.1007/978-3-319-93025-1_4 (2019).

[CR16] 16.Kennedy, J. & Eberhart, R. Particle swarm optimization. In Proceedings of ICNN’95-international conference on neural networks, IEEE, pp. 1942–1948. (1995).

[CR17] 17.Price, K. V. Differential evolution. In Handbook of Optimization. Springer, 187–214. (2013).

[CR18] 18.Mohammadzadeh, A., Zhang, C., Alattas, K. A., El-Sousy, F. F. M. & Vu, M. T. Fourier-based type-2 fuzzy neural network: Simple and effective for high dimensional problems. Neurocomputing547, 126316 (2023). [Google Scholar]

[CR19] 19.Slimani, M. et al. A Chimp optimization algorithm (ChOA) for vibration-based damage detection of a Damaged Steel Truss. In Structural Health Monitoring and Engineering Structures, Springer, pp. 121–132. (2021).

[CR20] 20.Wu, X., Zheng, W., Xia, X. & Lo, D. Data quality matters: a case study on data label correctness for security bug report prediction. IEEE Trans. Softw. Eng., (2021).

[CR21] 21.Zayed, M. E. et al. Predicting the performance of solar dish Stirling power plant using a hybrid random vector functional link/chimp optimization model. Sol Energy. 222, 1–17 (2021). [Google Scholar]

[CR22] 22.Chen, Z., Zhang, K., Chan, T. H. T., Li, X. & Zhao, S. A novel hybrid Whale-Chimp optimization algorithm for structural damage detection. Appl. Sci.12 (18), 9036 (2022). [Google Scholar]

[CR23] 23.Kaur, M., Kaur, R., Singh, N. & Dhiman, G. SChoA: an newly fusion of sine and cosine with chimp optimization algorithm for HLS of datapaths in digital filters and engineering applications. Eng. Comput.10.1007/s00366-020-01233-2 (2021). [Google Scholar]

[CR24] 24.Kaur, M., Kaur, R. & Singh, N. A novel hybrid of chimp with cuckoo search algorithm for the optimal designing of digital infinite impulse response filter using high-level synthesis. Soft Comput., pp. 1–25, (2022).

[CR25] 25.Mousavipour, F. & Mosavi, M. R. Sonar data classification using neural network trained by hybrid dragonfly and chimp optimization algorithms (2022).

[CR26] 26.Xie, Y., Wang, X. Y., Shen, Z. J., Sheng, Y. H. & Wu, G. X. A two-stage estimation of distribution algorithm with heuristics for energy-aware cloud workflow scheduling. IEEE Trans. Serv. Comput., (2023).

[CR27] 27.Alnaggar, O. A. M. F., Jagadale, B. N. & Narayan, S. H. MRI brain tumor detection using boosted crossbred random forests and chimp optimization algorithm based convolutional neural networks.

[CR28] 28.Dhiman, G. SSC: A hybrid nature-inspired meta-heuristic optimization algorithm for engineering applications. Knowledge-Based Syst.222, 106926 (2021). [Google Scholar]

[CR29] 29.Houssein, E. H., Emam, M. M. & Ali, A. A. An efficient multilevel thresholding segmentation method for thermography breast cancer imaging based on improved chimp optimization algorithm. Expert Syst. Appl. 115651. 10.1016/j.eswa.2021.115651 (2021).

[CR30] 30.Saffari, A., Zahiri, S. H., Khishe, M. & seyyed mohammadreza mosavi Design of a fuzzy model of control parameters of chimp algorithm optimization for automatic sonar targets recognition, IJMT, [Online]. Available: (2020). http://ijmt.iranjournals.ir/article_241126.html

[CR31] 31.Jia, H., Sun, K., Zhang, W. & Leng, X. An enhanced chimp optimization algorithm for continuous optimization domains. Complex. Intell. Syst., pp. 1–18, (2021).

[CR32] 32.Hu, G., Dou, W., Wang, X. & Abbas, M. An enhanced chimp optimization algorithm for optimal degree reduction of Said–ball curves. Math. Comput. Simul.197, 207–252 (2022). [Google Scholar]

[CR33] 33.Zhang, Q. et al. A novel chimp optimization algorithm with refraction learning and its engineering applications. Algorithms15 (6), 189 (2022). [Google Scholar]

[CR34] 34.Du, N., Zhou, Y., Deng, W. & Luo, Q. Improved chimp optimization algorithm for three-dimensional path planning problem. Multimed Tools Appl., pp. 1–26 (2022).

[CR35] 35.Khishe, M., Nezhadshahbodaghi, M., Mosavi, M. R. & Martín, D. A weighted chimp optimization algorithm. IEEE Access. (2021).

[CR36] 36.Kaidi, W., Khishe, M. & Mohammadi, M. Dynamic levy flight chimp optimization. Knowledge-Based Syst., p. 107625 (2021).

[CR37] 37.Qian, L., Khishe, M., Huang, Y. & Mirjalili, S. SEB-ChOA: an improved chimp optimization algorithm using spiral exploitation behavior, Neural Comput. Appl., pp. 1–24. 10.1007/s00521-023-09236-y (2023)

[CR38] 38.Qian, L. et al. Breast cancer diagnosis using evolving deep convolutional neural network based on hybrid extreme learning machine technique and improved chimp optimization algorithm, Biomed. Signal Process. Control, vol. 87, p. 105492, (2024). 10.1016/j.bspc.2023.105492

[CR39] 39.Wolpert, D. H. & Macready, W. G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput.1 (1), 67–82. 10.1109/4235.585893 (1997). [Google Scholar]

[CR40] 40.Liu, L., Khishe, M., Mohammadi, M. & Mohammed, A. H. Optimization of constraint engineering problems using robust universal learning chimp optimization. Adv. Eng. Inf.53, 101636 (2022). [Google Scholar]

[CR41] 41.Gong, S. P., Khishe, M. & Mohammadi, M. Niching Chimp optimization for Constraint Multimodal Engineering optimization problems. Expert Syst. Appl., p. 116887, (2022).

[CR42] 42.Zojaji, Z. & Kazemi, A. Adaptive reinforcement-based genetic algorithm for combinatorial optimization. J. Comput. Secur.9 (1), 71–84 (2022). [Google Scholar]

[CR43] 43.Chen, H., Yang, C., Heidari, A. A. & Zhao, X. An efficient double adaptive random spare reinforced whale optimization algorithm. Expert Syst. Appl.154, 113018 (2020). [Google Scholar]

[CR44] 44.Poláková, R. L-SHADE with competing strategies applied to constrained optimization. In 2017 IEEE Congress on Evolutionary Computation (CEC), IEEE, 1683–1689. (2017).

[CR45] 45.Hadi, A. A., Mohamed, A. W. & Jambi, K. M. Single-objective real-parameter optimization: Enhanced LSHADE−SPACMA algorithm. In Heuristics for Optimization and Learning, Springer, pp. 103–121. (2021).

[CR46] 46.Abdi, H. Holm’s sequential Bonferroni procedure. Encycl Res. Des.1 (8), 1–8 (2010). [Google Scholar]

[CR47] 47.Krishnamoorthy, K. Wilcoxon signed-rank test. In Handbook of Statistical Distributions with Applications, pp. 339–342. 10.1201/9781420011371-34 (2020).

[CR48] 48.Mack, G. A. & Skillings, J. H. A Friedman-type rank test for main effects in a two-factor ANOVA. J. Am. Stat. Assoc.75 (372), 947–951 (1980). [Google Scholar]

[CR49] 49.Pant, M. & Vig, G. Clustering based adaptive differential evolution for numerical optimization. In 2020 IEEE Congress on Evolutionary Computation (CEC), IEEE, pp. 1–8. (2020).

[CR50] 50.Price, P. N., Awad, K. V., Ali, N. H. & Suganthan M. Z., Problem definitions and evaluation criteria for the 100-digit challenge special session and competition on single objective numerical optimization. Technical Report. https://personal.ntu.edu.sg/404.html (2018).

[CR51] 51.Kumar, A. et al. A test-suite of non-convex constrained optimization problems from the real-world and some baseline results. Swarm Evol. Comput.10.1016/j.swevo.2020.100693 (2020). [Google Scholar]

[CR52] 52.Zamuda, A. Function evaluations upto 1e + 12 and large population sizes assessed in distance-based success history differential evolution for 100-digit challenge and numerical optimization scenarios (DISHchain1e + 12): A competition entry for 100-digit challenge, and f. In GECCO 2019 Companion - Proceedings of the 2019 Genetic and Evolutionary Computation Conference Companion. 10.1145/3319619.3326751 (2019).

[CR53] 53.Brest, J., Maucec, M. S. & Boskovic, B. The 100-digit challenge: Algorithm jDE100. In 2019 IEEE Congress on Evolutionary Computation, CEC 2019 - Proceedings. 10.1109/CEC.2019.8789904 (2019)

[CR54] 54.Zhang, S. X., Shing Chan, W., Tang, K. S. & Zheng, S. Y. Restart based collective information powered differential evolution for solving the 100-digit challenge on single objective numerical optimization. In 2019 IEEE Congress on Evolutionary Computation, CEC 2019 - Proceedings. 10.1109/CEC.2019.8790279 (2019)

[CR55] 55.Yeh, J. F., Chen, T. Y. & Chiang, T. C. Modified L-SHADE for single objective real-parameter optimization. In 2019 IEEE Congress on Evolutionary Computation, CEC 2019 - Proceedings. 10.1109/CEC.2019.8789991 (2019)

[CR56] 56.Mohammadzadeh, A. et al. A non-linear fractional‐order type‐3 fuzzy control for enhanced path‐tracking performance of autonomous cars. IET Control Theory Appl.18 (1), 40–54 (2024). [Google Scholar]

[CR57] 57.Yan, S. R., Guo, W., Mohammadzadeh, A. & Rathinasamy, S. Optimal deep learning control for modernized microgrids. Appl. Intell.53 (12), 15638–15655 (2023). [Google Scholar]

PERMALINK

A dual-adaptive stochastic reinforcement chimp optimization algorithm for fire detection and multidimensional problem solving

Ziyang Zhang

Lingye Tan

Diego Martín

Leren Qian

Mohammad Khishe

Pradeep Jangir

Abstract

Supplementary Information

Introduction

The rationale for selecting CHOA for multimodal and fire detection problems.

Motivations

Contribution

Chimp optimization algorithm

Proposed methodology: a twofold adaptive stochastic reinforced CHOA

Random replacement methodology

Twofold adaptive weighting technique

Fig. 1.

Experimentation and analysis

Fig. 2.

Table 1.

The investigation of exploitation ability

Table 2.

The investigation of the TASR-CHOA’s exploration ability

Table 3.

Table 4.

Study of the strategy for evading local optimum

Table 5.

Table 6.

TASR-CHOA’s convergence analysis

Fig. 4.

Performance of TASR-CHOA on IEEE CEC-BC test functions

Table 7.

Results of the IEEE CEC06

Fig. 3.

Evaluation of the statistical characteristics of TASR-CHOA

Table 8.

Fig. 5.

Analysis of real-world problems

Fig. 8.

Real-world engineering problem: fire detection challenge

Fig. 9.

Fig. 10.

Fig. 6.

Fig. 7.

AFEs

ACDs

SR

Analysis of sensitivity

Table 9.

Discussion

Complexity analysis of the computation

Basic elements of TASR-CHOA

The limitations of TASR-CHOA

Conclusion

Future research directions

Electronic supplementary material

Acknowledgements

Author contributions

Data availability

Declarations

Competing interests

Footnotes

References

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases