Synergizing quantum techniques with machine learning for advancing drug discovery challenge

Abstract

The Quantum Computing for Drug Discovery Challenge, held at the 42nd International Conference on Computer-Aided Design (ICCAD) in 2023, was a multi-month, research-intensive competition. Over 70 teams from more than 65 organizations from 12 different countries registered, focusing on the use of quantum computing for drug discovery. The challenge centered on designing algorithms to accurately estimate the ground state energy of molecules, specifically OH+, using quantum computing techniques. Participants utilized the IBM Qiskit platform within the constraints of the Noisy Intermediate Scale Quantum (NISQ) era, characterized by noise and limited quantum computing resources. The contest emphasized the importance of accurate estimation, efficient use of quantum resources, and the integration of machine learning techniques. This competition highlighted the potential of hybrid classical-quantum frameworks and machine learning in advancing quantum computing for practical applications, particularly in drug discovery.

Introduction

The first ACM/IEEE Quantum Computing for Drug Discovery Challenge (QCDDC’23) at the 42nd ICCAD in 2023 presented a pioneering platform for participants to design quantum computing algorithms. The contest, with a focus on estimating molecular energy for drug discovery, specifically targeted the ground state energy estimation of the OH+ molecule. Teams, leveraging the IBM Qiskit platform in the NISQ era, faced the challenge of achieving accurate results under noisy and resource-limited conditions^1,2. This competition highlighted the significance of integrating quantum computing with machine learning techniques and underscored the potential of hybrid classical-quantum frameworks in solving complex, real-world problems in the pharmaceutical domain.

The aim of QCDDC’23 is to propel quantum computing solutions to meet critical real-world challenges, with this year’s focus on drug discovery. By integrating with classical AI/ML/optimization techniques, the challenge aims to make significant contributions to the field of drug discovery. A key aspect of this endeavor is the estimation of the ground state energy of molecules^3,4, a crucial but extremely challenging task for classical computers⁵. Current NISQ machines also face numerous factors affecting the outcomes of quantum algorithms. However, a scalable hybrid classical-quantum framework could greatly enhance both the reliability and efficiency of this process, potentially revolutionizing the approach to drug development and design. This challenge represents a significant stride in merging quantum computing with pharmaceutical research, opening new avenues for medical breakthroughs.

QCDDC’23 is the first competition related to quantum computing held at a top venue conference in computer science. The initiative received robust support from the Association for Computing Machinery Special Interest Group on Design Automation, the Institute of Electrical and Electronics Engineers Council on Electronic Design Automation, Dorahacks, and JPMorgan Chase & Co. Over 70 spirited teams from more than 65 esteemed organizations converged to take part in this cutting-edge challenge. Contestants are tasked with designing and implementing an open-source quantum algorithm focused on calculating the ground state energy of the OH+ molecule. Unlike other challenges that solely emphasize accuracy, the proposed quantum algorithm in QCDDC’23 must be deployable and executable on IBM Qiskit’s platform, with special consideration of the noise model calibrated from real quantum computers. Entries will be evaluated based on accuracy, and quantum resource consumption, including the number of shots and circuit duration. Therefore, QCDDC’23 was to design algorithms to accurately estimate molecular energy using quantum computing^6,7consider the real machine noisy environment and implement on the IBM Qiskit platform⁸. Participants in this challenge are encouraged to innovate at the intersection of machine learning and quantum computing, specifically targeting the unique challenges of the NISQ era. A promising approach is the development of hybrid classical-quantum frameworks, which utilize a limited number of qubits more effectively by sacrificing affordable classical computational costs⁹. Additionally, exploring machine learning-based ansatz (architecture) search schemes could lead to the discovery of optimal quantum circuits with minimized circuit depths, tailored to the constraints of limited decoherence time^10–12. Another significant area is the creation of error mitigation techniques aimed at bolstering the reliability of quantum circuits in noisy environments^13,14. These efforts are essential for advancing the practicality and applicability of quantum computing technologies. The key ingredients to the success of the contest task include preprocessing (problem dimension reduction), circuit design and optimization, and post-error mitigation. The successful submissions considered these three steps reflected comprehensively in the scoring of the shot, circuit duration, and accuracy. In the recently concluded rankings based on final scores shown in Fig. 1. The top eight teams, along with the innovation award recipient, were invited to the 42nd International Conference on Computer-Aided Design to receive their awards.

Fig. 1.

(a) The top part shows an overview of the cross-study of quantum computing and classical machine learning techniques. (b) The bottom part shows the comprehensive performance metrics and the performance of the top eight teams in this year’s challenge.

This paper comprehensively discusses QCDDC’23 from various perspectives. Initially, it delves into the motivations and objectives behind organizing the competition, followed by a detailed introduction to the contest’s setup, including the chemistry-oriented contest problem, data, and evaluation methods. Furthermore, the paper discusses the outcomes of the winning teams, provides an in-depth analysis of innovative designs, and projects future directions for improvements in quantum computing challenges. Particularly, it elaborately describes the efficient and accurate co-design of classical-quantum computing on superconducting quantum computing platforms, highlighting the advancements and potential in this burgeoning field.

The Hamiltonian of the molecule, the source code of the top-eight teams and innovation award team, together with the unified evaluation method, and all other additional information about the contest can be accessed at https://qccontest.github.io/QC-Contest/index.html.

Results

In this section, we examine the outcomes using various performance indicators. We delve into the final scores of the teams, offering insights into their achievements. This is followed by an in-depth analysis of overall performances, focusing on how different algorithms and frameworks impact detection accuracy, the total shot count, and the circuit’s operational duration, the detailed scores of teams in terms of each metric are shown in Fig. 3.

Fig. 3.

Comprehensive performance analysis of 20 teams, showcasing overall scores, accuracy percentages, quantum computational resource cost, and grading scores for algorithm design. The detailed scores and performances can be accessed at https://qccontest.github.io/QC-Contest/Winners.html.

Top 3 designs

1st place team

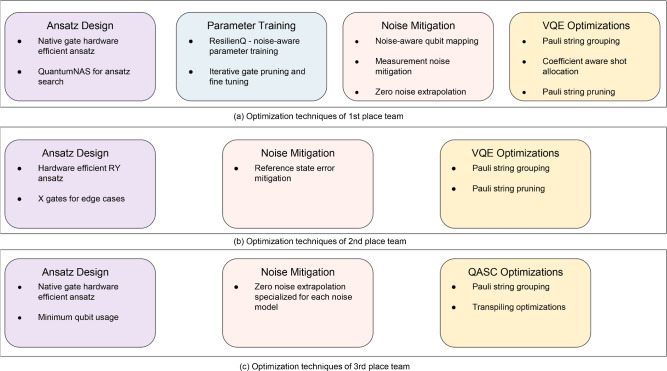
The first team leverages variational quantum eigensolve and provides innovative optimizations in ansatz design, parameter training, noise mitigation, as well as VQE-specific optimizations, as shown in Fig. 2 (a).

Fig. 2.

The figure summarizes innovative optimization techniques utilized by the top 3 teams.

Specifically, to search for hardware-efficient ansatz with native gates, QuantumNAS¹¹ SuperCircuit is trained and utilized. QuantumNAS reduces quantum resource usage by leveraging a SuperCircuit to efficiently evaluate potential quantum circuits using classical simulations. This allows for noise-adaptive evolutionary searches and iterative pruning. This technique minimizes quantum computation resource usage without compromising circuit robustness, which is pivotal for NISQ devices. With classical modeling and optimization, QuantumNAS trades affordable classical resources for more efficient and scalable quantum circuit design. The team optimizes the circuit depth and number of parameters by setting a threshold for the expectation value (−76) and selecting the shallowest circuit that achieves the threshold. After selecting the ansatz, the team proposes a novel noise-aware parameter training technique - ResilienQ, which leverages a differentiable classical simulator to acquire intermediate results and enables back-propagation with noisy final outputs from quantum circuits. This methodology synergistically combines the noise awareness of real quantum machines with the differentiability of classical simulators, enhancing the robustness and efficiency of training. To further reduce circuit depth and complexity, the team adopts an iterative gate pruning process, which involves removing gates with near-zero rotation angles and replacing gates with angles close to 180 degrees with their non-parameterized counterparts, such as replacing RX($\pi$) with X. As a result of the pruning process, the ansatz primarily consists of X gates.

To make the algorithm viable and practical on noisy NISQ quantum hardware, the team adopts three error mitigation techniques in post-processing: noise-aware qubit mapping, measurement noise mitigation, and Zero-noise Extrapolation (ZNE). Noise-aware qubit mapping determines the best qubit set based on the noise calibration information. Measurement noise mitigation with the 0–1 measurement error matrix obtained from noise calibration is used to reduce measurement errors. Zero-noise extrapolation is applied to further reduce the incoherence errors. These techniques collectively improve detection accuracy. Additionally, the team employs VQE-specific optimizations such as Pauli string grouping, novel coefficient-aware shot allocation, and Pauli string pruning. These optimizations reduce the number of required measurements and variance in results by up to 77%. The first-place team achieves an accuracy of 99.893% with 1800000 shots in 138.667 seconds.

2nd place team

The second team proposes a novel ansatz construction, an efficient Pauli grouping method, and reference state error mitigation¹⁵, as shown in Fig. 2 (b).

The team employs an innovative RY hardware-efficient circuit featuring linear qubit connections and parallel CNOTs to shorten the quantum circuit duration and thus achieve lower error rate on noisy hardware. Specifically, the circuit consists of interleving RY and CNOT gates as illustrated in the team’s report

$$\begin{array}{c}\hfill |\mathrm{\Psi }(\theta )⟩=\prod _{l=k}^1\left[L_{R_y}^{(l)},(\theta ),L_{\text{CNOT}}^{(l)}\right]L_{R_y}^{(0)}(\theta )|\varphi ⟩\end{array}$$ 1

where k is the total number of layers, and the layers are defined by the team as

$$\begin{array}{cc}\hfill L_{\text{CNOT}}^{(l)}=& \prod _{j=\frac{N}{2}-1}^1{\text{CNOT}}_{2j,2j+1}\prod _{j=\frac{N}{2}}^1{\text{CNOT}}_{2j-1,2j}\hfill \end{array}$$ 2

$$\begin{array}{cc}\hfill L_{\mathit{Ry}}^{(l)}(\theta )=& \prod _{j=N}^{1}R{Y}_j({\theta }_j)\hfill \end{array}$$ 3

Moreover, X gates are appended to specific qubits to handle edge cases.

Then, based on the observation that the ground state wavefunction of chemical systems is typically dominated by the HF state, the team performs Pauli grouping by combining terms such as XX and YY and reasons that these terms might have the same expectation value. This approach effectively reduces non-commutable terms and results in a total of 20 measurement groups, as opposed to 631 terms in the original Hamiltonian. Although the grouping and simplification of Pauli operators are not exact, they save quantum resources without compromising accuracy. The team further adopts reference state error mitigation to improve detection accuracy with minimal computational overhead. The second-place team achieves an accuracy of 99.93% with 240000 shots in 5024 seconds.

3rd place team

The third team adopts QASC (Quantum Architecture Search for Chemistry), a technique based on Monte Carlo Tree Search (MCTS) to efficiently determine the structure of variational quantum circuits for a specific task, as shown in Fig. 2 (c).

The iterative QASC process contains two phases: the learning phase, where a partition tree is built recursively to group the architectures with similar performance, and the search phase, where architectures are sampled, evaluated, and utilized to refine the boundaries in the learning phase in the next iteration. An important prerequisite of the QASC process is defining the search space and structure encoding. The team provides key insights into selecting hardware-efficient ansatz and structure encoding to improve the overall efficiency of finding a high-performance model. Specifically, the team determines the minimum number of trainable parameters (12) to achieve satisfactory performance. Additionally, the team notices the significance of the first qubit on detection accuracy, therefore always placing quantum gates on the first qubit. Moreover, the ansatz employs two primary building blocks consisting of basic gate operations: SX, RZ, and CNOT to ensure hardware efficiency. The single-qubit block combines two SX gates with an RZ gate, all operating on the same qubit. The two-qubit block is structured with a CNOT gate followed by an RZ rotation on the target qubit. In the iterative QASC process, classical statistical methods are integrated with quantum circuit structure search to improve performance under constrained quantum resources.

Following the searched circuit, post-optimization techniques are leveraged to further reduce resource usage and improve detection accuracy. Pauli grouping are used to reduce shrink the list of Pauli strings down to 39, and the total number of shots are reduced to 39$\times$shots. Given the limited complexity of searched circuit, the teams uses Qiskit’s default transpilation option with the heaviest optimization level (3) for transpilation optimization. The team further improves detection accuracy by adopting Zero-noise Extrapolation (ZNE). By conducting experiments, the team chooses appropriate noise scaling methods and extrapolation methods for each noise model. For FakeKolkata, FakeMontreal, and FakeCairo, the team sets scaling factors (1, 3, 5), (1, 3, 5, 7, 9) and (3, 5, 7), respectively. The team proposes average slope (AvS), a modified linear extrapolation, for FakeKolkata and FakeCairo, and the team uses Richadson extrapolation (Rich) for FakeMontreal. The third-place team achieves an accuracy of 99.732% with 858000 shots in 2080 seconds.

Innovation award design

To encourage innovative solutions for the ground state energy estimation challenge, we established an Innovation Award. The winning team utilized the CAFQA⁹ method to achieve high-accuracy initializations for variational quantum algorithms. Traditional VQA methods often initialize parameters directly on a quantum machine or use HF initialization, both of which are prone to noise and tend to have lower initialization accuracy on NISQ hardware. In contrast, CAFQA initializes VQA parameters by searching in an efficient and scalable way through the classically simulable portion of quantum space, known as the Clifford space, using discrete search optimization. This noise-free starting state is closer to the optimal solution, so the VQA converges much faster. Even without additional post-processing techniques, the team achieved a high accuracy of 98.07% with minimal resource utilization. CAFQA serves as an important example of synergy between quantum and classical computing to boost quantum capability in the NISQ era and beyond.

Overall comprehensive performances

The champion team, Team MIT-EPiQC-CMU-Duke, excelled with an impressive accuracy score of 99.893. In terms of quantum resource cost, they utilized 1, 800, 000 shots, with an average circuit duration of 138.667dt. Their approach borrowed the idea of neural architecture search, one of the most widely studied machine learning tasks, enabling automatic optimization of quantum circuit structures. They also implemented noise-aware parameter training using feedback from a noisy simulator, effective noise-aware qubit mapping, and measurement noise mitigation using a 0-1 error matrix from noise calibration. The Zero Noise Extrapolation (ZNE) technique they employed significantly reduced the impact of severe noise in the quantum environment, enhancing the reliability of quantum algorithms. Similar to neural network pruning, they further introduced quantum gate pruning to remove gates with negligible rotation angles and substituted gates with angles close to 180 degrees with corresponding non-parameterized gates, like replacing a $\text{RX}(\pi )$ gate with X gate, to reduce circuit depth. This strategy was pivotal in achieving the shortest circuit duration among the teams. Moreover, they incorporated Pauli grouping and Pauli string pruning into their framework to reduce the number of shots needed. The runner-up, Team TQL, finished with an accuracy score of 99.93, using 240, 000 shots and a circuit duration of 5024dt. They also applied Pauli grouping to minimize the number of shots, and for error mitigation, they employed state error mitigation with an HF state as the reference. Their approach involved manual and iterative adjustments based on a hardware-efficient ansatz, which, although effective, was not as comprehensive and generic as the machine learning and genetic algorithm-based approach of Team MIT-EPiQC-CMU-Duke. The third-place team, Team QuantumLoop, introduced an iterative algorithm for circuit architecture search, divided into a learning phase and a search phase. The learning phase involved building a partition tree for sampling in the search phase, which then used the trained samples from the learning phase. This method resulted in a final circuit duration of 2080dt. They also utilized ZNE and Pauli grouping methods, along with a machine learning-based technique for measurement error mitigation, to further reduce noise introduced during measurement.

Details in quantum resource cost

One of the key metrics, the quantum resource cost, has been the focus of intense efforts, particularly in the aspect of reducing the number of shots and the circuit duration required for quantum computations. Teams have employed various strategies to achieve this goal, the detailed score in terms of the number of shots and the circuit duration are shown in Fig. 4.

Fig. 4.

This figure details the quantum resource costs associated with the top 20 participating teams in a recent quantum computing challenge. The data is meticulously divided into two primary categories for each team: the number of quantum shots executed, which indicates the total count of quantum circuit executions, and the circuit duration, reflecting the time complexity of the quantum operations. This breakdown provides a comprehensive view of the efficiency and computational demands of each team’s approach to tackling quantum computational tasks.

To reduce the number of shots, teams implemented technologies including the tapering method, which reduces the number of Pauli strings in the quantum circuit¹⁶. This technique involves identifying symmetries in the quantum system that can be exploited to simplify the circuit without losing computational accuracy. Another popular approach is the use of Pauli grouping strategies¹⁷. By cleverly grouping Pauli operators, teams have been able to significantly reduce the number of measurements needed, thereby lowering the shot count. This not only saves computational resources but also enhances the efficiency of quantum algorithms. The contextual subspace method represents another innovative approach, where classical computers are used to assist in the computation of certain parts of the problem^18–20. This hybrid quantum-classical technique leverages the strengths of both computing paradigms, optimizing the use of quantum resources while relying on classical systems for more manageable computations.

When it comes to minimizing the duration of quantum circuits, most teams have turned to machine learning-based methods for circuit structure search. These algorithms utilize classical computation power to efficiently explore the vast space of possible circuit configurations, identifying those that offer the best trade-offs between accuracy and execution time. The effective collaboration between quantum and classical systems enables promising result with limited quantum resources. Some teams have further enhanced their approaches by incorporating advanced state initialization methods, such as the Hartree-Fock technique. This method provides a good starting point for quantum computations, reducing the overall circuit depth and, consequently, the duration. Given the short coherence time of NISQ devices, shorter circuit durations allow for the execution of deeper circuits. Therefore, the algorithms proposed in the challenge have the potential to address more complex molecules on NISQ hardware.

The team that achieved the best overall performance went a step further by analyzing the characteristics of quantum pulses at a granular level. They proposed an approximation method for basic gates, which allowed them to optimize the pulse sequences used in the quantum circuits. This innovation led to significant improvements in the duration metric, setting a new standard for efficiency in quantum computing.

Discussion

In this paper, we introduce the first ACM/IEEE Quantum Computing for Drug Discovery Challenge, which focuses on the fundamental problem of molecular energy estimation within drug development issues. Specifically, we discuss the challenge problem, the chemical background, and the significance of applying quantum computing in this application. We further elaborate on how the molecular Hamiltonians, which serve as the dataset, were obtained, the metrics for comprehensive performance evaluation, and the settings for the platforms and noise models used. We also showcase the designs of the participating teams and analyze the frameworks proposed by the teams. The analysis of the results obtained by the participating teams is presented along with an in-depth discussion, aimed at further contributing to research and engineering efforts in the application of quantum computing in drug development.

The ACM/IEEE Quantum Computing Challenge marked the first quantum computing themed contest held at a top international computer science conference. This event provided a platform for teams to showcase their research and advancements in the intersection of machine learning and quantum computing technologies. Looking ahead, the integration of quantum computing technologies and machine learning, including but not limited to applications in drug discovery, aims to enable quantum computing to aid classical machine learning or for classical machine learning to benefit quantum computing. It is important to note that the goal is not to replace classical computing and machine learning with their quantum counterparts. Instead, the focus is on designing hybrid frameworks that complement each other^21–24, addressing problems that are previously challenging or impossible for classical computing to solve independently.

Methods

Contest problem

In this subsection, we first provide a comprehensive background of the contest, setting the stage for a deeper understanding of its relevance and significance. Following this, we delve into the objectives of the contest, detailing the specific goals and aspirations that it aims to achieve. This part of the discussion will focus on the intended impact of the competition, the challenges it seeks to address in the field, and how it aligns with broader trends and needs in the industry. By establishing this context, we lay a foundational understanding that enriches the reader’s appreciation of the contest’s significance and the innovations it fosters.

The landscape of drug discovery has been dynamically evolving, powered persistently by state-of-the-art innovations^25,26. The key to these advancements is the quest to decipher complex molecular interactions that stand at the heart of transformative medical treatments²⁷. Within the plethora of tools that have risen to prominence, computational methodologies hold a distinctive place, acting as the linchpin in understanding and navigating the labyrinthine world of molecules. Particularly, machine learning, with its prowess in unearthing deep-seated patterns and refining solutions, has emerged as an indispensable asset^28,29. Yet, the real game-changer beckons at the confluence of quantum computing and machine learning³⁰. This connection, while nascent, is bursting with potential and promises to overhaul the very essence of drug discovery. Not only does it unlock doors to challenges once believed to be insurmountable for traditional computing paradigms, but it also augments our capacities in predicting and fathoming molecular behaviors with a so far unimagined precision.

A critical molecule in the pharmacological landscape is the hydroxyl cation ($·$OH+)³¹. This cation is more than just a molecular entity; it’s a central axis for numerous drug interactions. Its high reactivity is linked to oxidative stress, resulting in a range of health conditions, from neurodegenerative disorders and cardiovascular diseases to cancer^31,32. Beyond its pathogenic roles, the hydroxyl cation is also integral to the efficacy of many drugs. With the development of quantum computing, we can potentially achieve a deeper understanding of the interactions and effects of molecules like the hydroxyl cation, accelerating breakthroughs in therapeutic developments^33,34. Understanding the quantum mechanics of the hydroxyl cation deeply impacts drug discovery. The key is determining its ground state energy, a foundational element for modeling complex drug interactions. The quantum domain, constrained by qubit numbers and error rates, poses challenges, particularly for larger molecules¹⁸. The hydroxyl cation, with its smaller size, fits within current quantum computing capabilities, making it an ideal focus for quantum simulations. Moreover, the hydroxyl cation is selected to ensure that the competition target presents sufficient difficulty and complexity, while allowing us to evaluate accuracy, resource efficiency, and innovation in a clear and consistent manner. We believe that innovations on the simpler hydroxyl molecule not only address immediate research needs but also lay the groundwork for future exploration of larger molecular structures, which are crucial for advancing drug development.

In the realm of quantum chemistry and drug discovery, the significance of accurately estimating the ground state energy of molecules like OH+ cannot be overstated. The ground state energy is a critical indicator of a molecule’s chemical properties, including its stability and potential reactivity. For drug discovery, understanding these properties at the quantum level allows for the design of molecules with desired therapeutic effects and minimal side effects. Particularly for complex molecules, traditional computational methods may fall short, making quantum computations a promising alternative. This accurate quantum mechanical characterization of molecular systems opens new avenues in rational drug design, potentially leading to more effective and targeted therapies.

This approach is pivotal for the evolution of drug discovery in the quantum age. The drug discovery pipeline is a multi-step process and each task is critical to developing new therapeutics efficiently and effectively. Quantum computing has the potential to enhance not only the ground state energy estimation but also other stages such as molecular design³⁵. Even under the limitations of current NISQ devices, hybrid classical-quantum models effectively leverage affordable classical computational resource and harness quantum advantages to tackle challenges with unprecedented computational power. This synergy between quantum and classical approaches hold the potential to advance the drug discovery pipeline in a practical and scalable way.

Contest objective

The ACM/IEEE Quantum Computing Challenge marked the first quantum computing themed contest held at a top international computer science conference. This event provided a platform for teams to showcase their research and advancements in the intersection of machine learning and quantum computing technologies. Looking ahead, the integration of quantum computing technologies and machine learning, including but not limited to applications in drug discovery, aims to enable quantum computing to aid classical machine learning or for classical machine learning to benefit quantum computing. It is important to note that the goal is not to replace classical computing and machine learning with their quantum counterparts. Instead, the focus is on designing hybrid frameworks that complement each other, addressing problems that were previously challenging or impossible for classical computing to solve independently.

The objective of the Quantum Computing for Drug Discovery Challenge (QCDDC’23) is to advance the application of quantum computing in the field of pharmaceutical research. Contestants are tasked with developing an innovative quantum algorithm capable of accurately calculating the ground state energy of the molecule, and the hydroxyl cation is selected in the contest as an example. This challenge not only focuses on achieving precision in quantum computations but also emphasizes the practical implementation of these algorithms, considering the noise models of real quantum computers. Successful algorithms should demonstrate efficiency in quantum resource usage, including optimizing the number of shots and circuit duration, essential for feasible quantum simulations in drug discovery. This challenge aims to bridge the gap between theoretical quantum computing and practical applications in medicinal chemistry, potentially revolutionizing the approach to pharmaceutical development.

Evaluation

In this subsection, we first introduce the designated platform and the noise model derived from an actual quantum system. Following that, the evaluation metrics used to assess the overall performance of each team’s design will be discussed. Additionally, the evaluation method, which allows teams considerable flexibility in designing their methods based on the platform, will also be presented.

Platform, system and noise model from real quantum processor backend

We acknowledge the use of IBM Quantum services in this competition. Qiskit⁸, primarily developed by IBM, is an open-source quantum computing framework. It offers tools for creating and manipulating quantum programs and running them on prototype quantum devices and simulators. Designed with modularity in mind, Qiskit provides components that span all aspects of quantum computing, from foundational elements to advanced quantum algorithms. Noise presents a significant challenge in the field of contemporary quantum computing^36–38. Therefore, we urge all participants to consider inherent noise when designing their quantum algorithms or circuits. Qiskit⁸offers tools for simulating quantum algorithms or circuits as they would be executed on actual quantum devices, including the associated noise. Since not everyone has access to real machines, for fairness, we require all participants to train their models on a given noise model, which will be released on the registration deadline date. Simulating a quantum system with an integrated noise model is crucial for understanding the potential performance of quantum algorithms on current NISQ devices^36,39. We recognize that while participants might be inclined to optimize basis gates at the pulse level to shorten the duration of the quantum circuit and conserve quantum resources⁴⁰, characterizing a time-dependent noise model from a real quantum machine poses unsolved challenges in preparation for this quantum computing drug discovery challenge. Regrettably, we must resort to using the standard gate-based noise model for evaluating circuits. The noise models from ibmq_cairo, ibmq_kolkata, and ibmq_montreal were integrated into the testing process, giving participants a genuine feel of practical hardware conditions.

Evaluation metrics

Accuracy of ground state energy estimation In quantum computing, accuracy in estimating the ground state energy of quantum systems is paramount. This is a key problem in quantum mechanics and quantum chemistry, with implications in material science, pharmaceuticals, and beyond. Accurate estimations are essential for understanding the properties and behaviors of complex quantum systems.

The precision of ground state energy estimation is measured using the following formula:

$$\begin{array}{c}\hfill E_{\text{score}}=\left(1,-,\left|\frac{E_{\text{estimated}}-E_{\text{ideal}}}{E_{\text{ideal}}}\right|\right)\times 100\%\end{array}$$ 4

where $E_{\text{estimated}}$ represents the average result from the participant’s framework across ten different computational seeds, and $E_{\text{ideal}}$ is the objective value determined using classical computational methods.

This scoring mechanism allows participants to earn up to 100 points, with a higher score indicating greater accuracy. The score is a percentage that reflects the closeness of the estimated energy to the ideal value. This component challenges participants to optimize their algorithms and enhances understanding of the quantum systems being studied. It emphasizes the need for rigorous testing against classical benchmarks, promoting accuracy and reliability in quantum research.

Efficient utilization of quantum resources The competition also evaluates participants on their efficient use of quantum resources, which is divided into two critical aspects: the total number of quantum circuit shots and circuit size.

Total Number of Shots of Quantum Circuits: The total number of shots for quantum circuits is a pivotal metric for assessing resource efficiency. The maximum allowable number of shots is 3,786,000, correlating to the unoptimized problem Hamiltonian consisting of 631 Pauli strings, with a default setting of 6,000 shots per measurement prior to optimization. This constraint encourages participants to optimize their quantum measurements efficiently. The scoring for quantum circuit shots is as follows:

• Under 1,800,000 shots: Participants achieving this threshold will be awarded 25 points, incentivizing the reduction of quantum resources used.

• Between 1,800,000 and 3,786,000 shots: Points are allocated on a sliding scale, starting from 15 points for 3,786,000 shots and increasing up to 25 points for 1,800,000 shots, calculated using the formula:

  $$\begin{array}{c}\hfill 15+\frac{(3,786,000-n)}{(3,786,000-1,800,000)}\times 10\end{array}$$ 5

  where $n$ is the total number of shots utilized. This formula encourages participants to minimize the number of shots used, rewarding efficiency with higher scores.

Circuit Size (Duration): Circuit size, or duration, is another vital metric, reflecting the complexity and efficiency of the quantum circuits developed. The competition ranks participants based on the compactness and execution speed of their circuits, with the top rank earning 15 points. Subsequent ranks are awarded points with a decreasing scale, highlighting the importance of optimizing circuit design for both performance and resource conservation.

Efficient resource utilization is vital not just technically, but also economically and ecologically, encouraging sustainable development in quantum computing technology.

Technical reflection and description In addition to the quantitative evaluation of participants’ submissions in the quantum computing competition, a significant emphasis is placed on a qualitative assessment. This assessment revolves around a comprehensive introspection and articulate presentation of the methodologies employed by the participants. It’s not just about what was achieved, but also about how it was achieved and the thought process behind it.

The qualitative evaluation is segmented into several key areas:

• Innovation and Pre-processing Techniques: Participants are expected to clearly describe any innovative approaches or pre-processing techniques they have implemented. This could include unique methods of optimizing quantum circuits, novel approaches to problem decomposition, or creative algorithms that enhance the efficiency of the computation. The novelty and effectiveness of these techniques are of prime interest.

• Utilization of Classical Resources: Alongside quantum resource optimization, how participants have leveraged classical computing resources forms a critical part of their technical strategy. This includes, but is not limited to, the use of classical algorithms for preprocessing, data analysis, or hybrid quantum-classical computation approaches. A well-thought-out balance between quantum and classical resources can be indicative of a more sophisticated and practical approach to problem-solving in the realm of quantum computing.

• Technical Novelty: The degree of technical innovation will be a key factor. This includes the development of new methods or the novel application of existing techniques to the challenges presented in the competition. Originality and creativity in problem-solving are highly valued.

• Logical Coherence: The clarity and logic of the technical narrative are paramount. Participants should strive to present their methodologies and thought processes in a manner that is both coherent and comprehensible. This includes a clear articulation of the steps taken, logical progression of ideas, and a well-structured presentation of their work.

This reflective and descriptive component is allocated a total of 10 points. The allocation of these points will be judiciously carried out by a panel of three expert graders. The graders will evaluate submissions based on the depth of self-reflection, technical novelty, logical coherence, and other salient factors. The aim is to reward not only technical proficiency but also innovation, thoughtful analysis, and clarity of expression. This aspect of the evaluation underscores the significance of not only achieving results but also understanding the journey to those results. It encourages participants to think critically about their methodologies, fostering a culture of continuous learning and improvement.

Evaluation method

We delineate a comprehensive framework designed to ensure participants effectively navigate the complexities of quantum computing, particularly focusing on the integration of noise models and system models reflective of real-world quantum systems. To facilitate a standardized yet flexible approach in the competition, the following components are detailed:

Upon commencement, participants are provided with a detailed noise model and system model, meticulously crafted to mimic the intricacies of a real quantum environment. These models serve as the foundation upon which teams will build and evaluate their quantum computing solutions. A crucial requirement for participants is adherence to the topology map of FakeMontreal. This topology, representative of a quantum computing architecture, sets the stage for realistic simulation and testing of quantum algorithms, ensuring that designs are not only innovative but also applicable within the constraints of actual quantum hardware. To accommodate a diverse range of strategies and to reflect the variability in real quantum systems, we offer participants the choice among three distinct noise models extracted from FakeCairo, FakeMontreal, and FakeKolkata. Each model presents unique challenges and characteristics, allowing teams to tailor their approaches based on the specific nuances of these simulated environments. In the spirit of promoting robustness and adaptability in algorithmic design, we recommend participants utilize specific seeds for algorithmic processes, transpiling, and measurement within Qiskit. This guidance is aimed at fostering consistency and fairness in the evaluation process. The final scoring will be derived from the average outcomes across 10 distinct seeds: five from a provided list of seeds and the other five from a concealed set of test seeds. This methodology ensures that assessments are comprehensive, accounting for variability and promoting strategies that are resilient across a spectrum of conditions.

The overarching objective of this evaluation method is to challenge teams to devise quantum computing solutions that are not only theoretically sound but also practically viable within the constraints of current quantum technology. By navigating the specified topology, choosing among the provided noise models, and adhering to a structured approach for seed selection and result averaging, participants demonstrate their capacity to develop strategies that balance innovation with practical applicability. This detailed approach to evaluation underscores the competition’s commitment to advancing the field of quantum computing by fostering an environment where theoretical knowledge and practical skills converge, ultimately leading to the development of solutions that push the boundaries of what is currently achievable in quantum computing.

Dataset

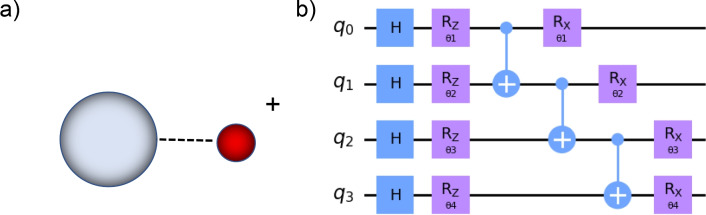
The data provided for this challenge revolves around the central theme of drug discovery, focusing on the fundamental quantum mechanics of the hydroxyl cation ($·$OH), as shown in Fig. 5. As a pivotal entity in numerous drug interactions and physiological processes, an intricate understanding of the hydroxyl cation is crucial. To aid participants in this endeavor, we’ve curated a specialized dataset tailored to encapsulate the hydroxyl cation’s Hamiltonian.

Fig. 5.

(a) Illustrates a molecular model of the OH+ ion, showcasing its atomic structure and bonding configuration. (b) Presents an example of a Variational Quantum Eigensolver (VQE) circuit, demonstrating the quantum computational approach to solving molecular energy states.

The process for obtaining the Hamiltonian begins with a high-precision quantum chemical calculation of the molecule’s electronic structure. Sophisticated computational methods, such as Hartree-Fock or more advanced post-Hartree-Fock techniques, are utilized. These methods are crucial for providing an accurate and detailed representation of the electronic orbitals. In the Hartree-Fock method, the many-electron wave function of the molecule is approximated by a single Slater determinant, which simplifies the complex many-body problem. However, to capture electron correlation effects more accurately, post-Hartree-Fock methods such as Configuration Interaction (CI), Møller-Plesset perturbation theory (MP2), or Coupled Cluster Theory are often employed. These approaches involve sophisticated calculations to model the interactions and correlations between electrons, providing a more comprehensive understanding of the electronic structure. Once the electronic structure is accurately determined, the electron orbitals are then mathematically represented using fermionic operators. The transformation from fermionic operators to Pauli strings is achieved through techniques like the Jordan-Wigner or Bravyi-Kitaev transformations, which map the fermionic algebra onto the algebra of Pauli matrices. This mapping is essential for quantum simulations, as quantum computers natively understand operations in terms of Pauli matrices.

Author contributions

Z.L., Z.H., M.P., D.W., Y.S., W.J., and X.X. contributed to the overall idea of this paper. Z.L. and Z.H. wrote the main manuscript. Y.S., and D.H. contribute to figures. Y.Z., and Q.J. analyses the data.

Data availability

The datasets generated and analyzed during the current study are available in the [https://github.com/qccontest/QC-Contest-Demo/tree/main], and full contest information with top performance teams results could be accessed at [https://qccontest.github.io/QC-Contest/Winners.html].

Declarations

Competing Interest

The authors declare no competing interests.