Endograft-specific hemodynamics after endovascular aneurysm repair: a CFD analysis

Abstract

Intraluminal prosthetic graft thrombus (IPT) has been described in case of endovascular aortic pathology repair. This study aimed to assess hemodynamic indicators associated with various anatomical morphologies following endovascular aortic repair (EVAR), aiming to offer further references for the choice of clinical therapy. Six model models (normal, iliac compression, aortic compression, aortoiliac compression, iliac distortion, and long-leg stent) were established based on common anatomical morphologies following EVAR. Hemodynamic indicators, such as flow velocity, time-average wall shear stress (TAWSS), oscillatory shear stress index (OSI), and relative residence time (RRT), were captured using computational fluid dynamics (CFD), and the differences between the six models were examined. The peak blood flow velocity at the compressed side iliac artery and the uncompressed side iliac artery corresponding to the aortoiliac artery compression model and the aortic compression model decreased by 30.63% to 48.62%, compared with that in the normal model. Compared with that in the normal model, the peak blood flow velocity at the aorta and the distorted side iliac artery in the iliac distortion model decreased by 7.89% and 41.13%, respectively. The length of the iliac artery stent has little effect on the blood flow velocity. The TAWSS at Iliac grafts showed varying degrees of decline in the other three compression models, particularly in the aortic compression model compared to the normal model. The TAWSS increases at the corner of the artery showing distortion but exhibited a significant decrease toward the distal end of the corner. The areas with higher OSI, and longer RRT were concentrated in the aortoiliac compression model and the iliac distortion model. We found that endograft compression and distortion may be risk factors for IPT. Moreover, the influence of longer stents on the hemodynamics inside stent-grafts is negligible. However, future real-world studies should be conducted to test and verify this speculation.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-83148-2.

Introduction

Abdominal aortic aneurysm (AAA), characterized by elastin degradation and subsequent aortic dilation at the inferior segment, can be surgically addressed via endovascular repair (EVAR) ¹. This novel procedure offers a decreased perioperative mortality and morbidity compared with conventional open surgery. As a standard therapy, EVAR is preferred for AAA extending below the renal arteries². Intraluminal stent grafts relieve systemic pressure within the aneurysmal sacs while preventing sac enlargement and rupture. Following endograft incorporation into an AAA, the aortic wall’s mechanics, vessel luminal configuration, and local hemodynamics undergo change. Moreover, the stent-graft (SG) experiences continual mechanical pressure from countless heartbeat cycles and repetitive pulsatile blood flow, influencing its modification overtime. In particular, altered hemodynamics forming within the endograft are likely to contribute to the development of an intraluminal prosthetic graft thrombus (IPT) soon after implantation or months later, raising the risk of distal ischemia³. A prior study reports an IPT emergence rate following EVAR ranging between 10.7 and 33%^4,5.

IPT with critical or acute limb ischemia has a serious impact on patients’ quality of life⁶. The study of IPT was recently identified as an issue requiring further investigation by the Society for Vascular Surgery practice guidelines on the management of AAA patients⁷. Previous studies have indicated that factors such as the aorta-iliac stent graft configuration, compression, or distortion leading to changes in cross-sectional area, and other hemodynamic alterations within the graft contribute to the formation of IPT^4,8. Morphological analysis alone may not be sufficient for a comprehensive assessment of IPT. A critical role in the development and progression of IPT is attributed to hemodynamics⁹. As blood flow is influenced by geometric shape, a hemodynamic study incorporates the geometric characteristics of how EVAR affects the remodeling of the infrarenal portion of the abdominal aorta. This is done to better understand how different implant design features impact local arterial morphology.

In this study, we established a series of ideal anatomical models based on CTA scan data. Through CFD analysis, we observed and assessed the morphological and hemodynamic changes in the vessels after EVAR, including flow velocity, time-averaged wall shear stress, oscillatory shear index, and relative residence time, providing further reference for the clinical treatment methods.

Methodology

Aortic model reconstruction

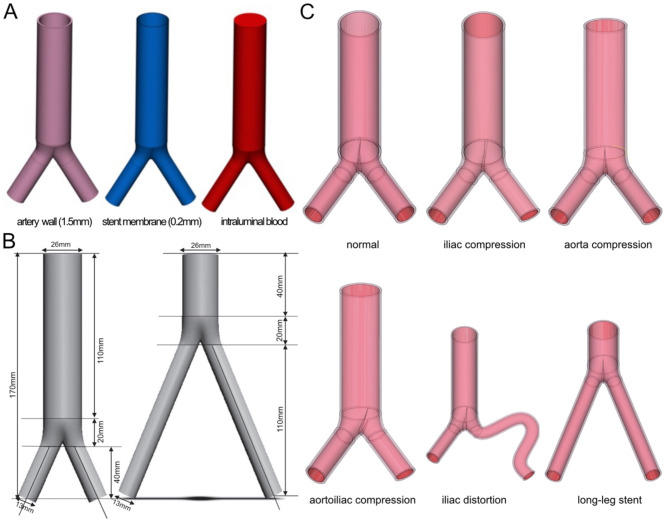
Figure 1 encapsulates the complete technical process. The aortoiliac model was reconstructed using Mimics 21.0, which is software developed by the Materialise Company based in Belgium. The model was generated from Computed Tomography Angiography (CTA) data obtained from the Shanghai Ninth People’s Hospital. The CTA dataset had a resolution of 512 × 512 pixels and a layer interval of 0.625 mm. The aortic structure (Fig. 2A) comprised a 1.5 mm arterial wall, a 0.2 mm stent membrane, and intraluminal blood. Based on relevant literature^10–12, Materialise Company’s 3-Material Medical 13.0 software from Belgium was utilized to convert the iliac aorta model into six distinct models: normal, iliac compression, iliac distortion, aortoiliac compression, aorta compression, and long-leg stent (as illustrated in Fig. 2B,C). In the arterial compression group, the degree of oppression was 50%. In the iliac compression group, the right iliac artery was compressed by 50%. In the iliac distortion group, the distortion angles of the iliac artery are 120° and 320°, respectively. In the long leg stent group, the length of stent was 110 mm compared with the normal group 40 mm. Additional patching, noise reduction, and surface fitting were performed at Geomagic Studio 2014 (Raindrop Company, America) to produce a geometric solid model of the aortoiliac stent, vascular wall, and intraarterial blood flow with a relatively smooth surface. Finally, the six categories of aortoiliac stent models were imported into ANSYS Fluent 2020 (ANSYS Company, America) for finite element mesh delineation, attribute sets, material parameter definition, load application, boundary condition constraint setting, and simulation calculation analysis.

Fig. 1.

Flow chart of finite element technique. CT: computed tomography, FEM: finite element model.

Fig. 2.

Ideally constructed three-dimensional models of specific geometries. (A) Structural parameters of aortoiliac stents. (B) Modeled dimensions of normal and long-leg models. (C) Schematic diagram of the establishment of ideal models.

Numerical approaches.

Governing equations

The Quemada model was used to simulate blood as a non-Newtonian, incompressible fluid with laminar flow characteristics^10–12. The following is a description of the governing equations:

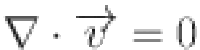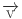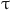: the fluid velocity vector, : the density of blood, : the stress tensor, 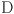: the deformation tensor, 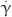: the shear rate, : the infinite shear rate viscosity, 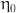: the zero shear rate, t: time in this simulation.

The blood parameter values in the equation are = 1050 kg/cm³, 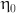= 0.607 Pa, =3.45*10^–3 Pa, = 0.3568, and 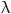= 3.313 s. In this study, the structural material of the aneurysm model was assumed to be homogeneous and isotropic, with a Poisson’s ratio of 0.27, an elastic modulus of 10 MPa, and a density of 6000 kg/m³. The density, Poisson’s ratio, and elastic modulus of the aneurysm wall were selected as 1120 kg/m³, 0.49, and 1.2 MPa, respectively^13,14.

Boundary conditions

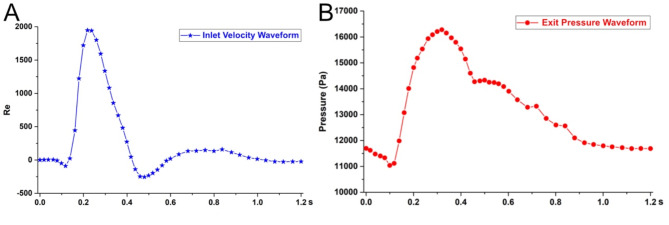
The inlet and outlet of the aortoiliac artery stent model are controlled by the velocity and pressure boundary conditions (Fig. 3). The flow velocity is used as the inlet boundary condition in this test, while the pressure waveform is used as the outlet boundary condition. The overall computation time is based on the heart cycle time of the main iliac artery (0~1.2 s)¹⁵. The nodes in the aortic wall of the vessel and the stents in the inlet and outlet sections are fixed and constrained, constraining the six degrees of freedom to keep the end faces stationary.

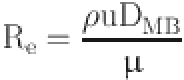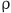: the density of blood, 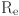: Reynolds number, 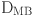: diameter, : inlet mean velocity, : blood viscosity.

Fig. 3.

Boundary conditions. (A) Aortic inlet velocity boundary curve, (B) Iliac artery outlet pressure boundary curve.

Evaluation parameters

Based on the investigation of transient non-Newtonian pulsatile flow, the resulting hemodynamic wall stresses, and flow patterns in six distinct SG geometries were examined to predict and compare their IPT risks. For each simulation, a time step of 0.001 s was used consistently. In each simulation process, four cardiac cycles were run for each model to remove any initialization effects, and the results of the fourth cycle were extracted for hemodynamic analysis¹⁶.

The mathematical expressions described in the following paragraphs were used to calculate evaluation parameters such as velocity, wall shear stress (WSS), oscillating shear index (OSI), and relative residence time (RRT) at 4 relatively typical moments (0.22 s, 0.32 s, 0.40 s, 0.84 s). The WSS, OSI, and RRT are critical in evaluating the changes in the SG hemodynamic environment after EVAR¹⁷. This study focused on the numerous near-wall hemodynamic characteristics that have been proven to influence thrombus development. As a result, the pulsatile cycle time-averaged wall shear stress (TAWSS), which is used to define the general characteristics of WSS, was investigated. These parameters identified in previous studies to correlate with IPT, and we selected OSI ≥ 0.4, TAWSS ≥ 1.5 Pa, and RRT ≥ 2 (1/Pa) as the critical values for result analysis^18–20. The TAWSS was established as follows:

where represents the period of the cardiac cycle and represents the instantaneous WSS vector.

OSI values were calculated using the following formula²¹.

where denotes the mean value of WSS throughout a cardiac cycle.

The relative residence time (RRT) is calculated from the wall shear stress, and has been used as an additional predictor of a higher risk of thrombus development²².

The RRT is defined as follows:

Results

Flow velocity

Figure 4 illustrates the flow velocity in the six ideal models at four consecutive time points (0.22 s, 0.32 s, 0.40 s, 0.84 s) during the cardiac cycle. The streamlines depict the velocity level for each SG type, represented by different colors. The peak blood flow velocity changes at point 3, corresponding to different compression positions, are minor, ranging from 0.292 to 0.304 m/s. However, the peak blood flow velocity changes at point 1 and point 2 are significantly affected, particularly in the iliac artery compression, ranging from 0.778 to 0.843 m/s. Comparatively, the peak blood flow velocity at point 1 and point 2, corresponding to the iliac artery compression, was increased significantly by 36.63% and 32.99%, respectively, when compared with that in the noncompression model. Furthermore, the peak blood flow velocity at point 1 and point 2, corresponding to the aortoiliac artery compression model and the aortic compression model, decreased by 30.63% to 48.62%, compared to that in the normal model (Fig. 5).

Fig. 4.

The velocity streamlines at four consecutive points in a cardiac cycle of the six ideal models and different colors indicate different velocities. (A) normal, (B) iliac compression, (C) aorta compression, (D) aortoiliac compression, (E) iliac distortion, (F) long-leg stent.

Fig. 5.

Line plot of velocity with artery compression. (A) Point 1: center of the compressed side iliac artery, (B) Point 2: center of the non-compressed side iliac artery, (C) Point 3: center of the aorta, (D) show the locations of the sections in the artery.

Figure 6 illustrates the peak blood flow velocity at three points: point 3, point 2, and point 1 in the iliac distortion model, which measured 0.304 m/s, 0.843 m/s, and 0.778 m/s, respectively. In contrast, the normal model exhibited peak blood flow velocities of 0.280 m/s, 1.003 m/s, and 0.458 m/s at the same positions. Compared with that in the normal model, the peak blood flow velocity in the iliac distortion model decreased by 7.89% and 41.13% at point 3 and point 1, respectively. However, a dissimilar result appeared at point 2, as the peak blood flow velocity increased by 18.98%.

Fig. 6.

Line plot of velocity with iliac distortion groups. (A) Point 1: center of the distorted side iliac artery, (B) Point 2: center of the non-distorted side iliac artery, (C) Point 3: center of the aorta, (D) show the locations of the sections in the artery.

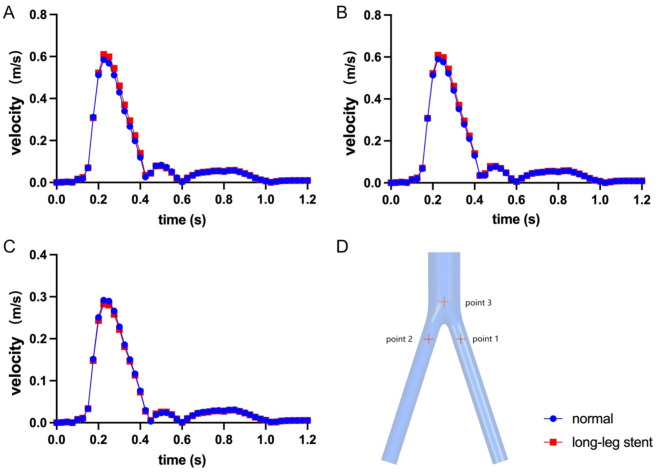
Figure 7 illustrates that the peak blood flow velocities at point 3, point 2, and point 1 in the normal model were 0.292 m/s, 0.617 m/s, and 0.585 m/s, respectively. Similarly, the peak blood flow velocities at the same position in the long-leg stent model were 0.280 m/s, 0.612 m/s, and 0.609 m/s, respectively. The difference in the peak blood flow velocities between the two models was less than 5%. In short, the length of the iliac artery stent has a negligible impact on the peak blood flow velocities in the SG. The use of a long leg stent may slightly decrease the blood flow velocities of the bilateral iliac arteries by approximately 5% within 0.15 ~ 0.45 s, which is not significant in other periods. Furthermore, the peak blood flow velocity of the aortic lumbar region will increase by 3% within 0.2 ~ 0.3 s. The peak blood flow velocity of the six different models is shown in Table 1. Overall, the length of the iliac artery stent has a minimal effect on the blood flow velocities.

Fig. 7.

Line plot of velocity with long-leg stent group. (A) Point 1: center of the right-side iliac artery, (B) Point 2: center of the left-side iliac artery, (C) Point 3: center of the aorta, (D) show the locations of the sections in the artery.

Table 1.

Peak velocity in the six ideal models.

	Peak Velocity(m/s)
	Point1	Point2	Point3
Normal	0.585	0.617	0.292
Iliac compression	0.778	0.843	0.304
Aorta compression	0.306	0.317	0.285
Aortoiliac compression	0.396	0.428	0.293
Iliac distortion	0.458	1.003	0.280
Long-leg stent	0.609	0.612	0.280

Point 1: center of the right-side iliac artery (compression or distortion) , (B) Point 2: center of the left-side iliac artery, (C) Point 3: center of the aorta.

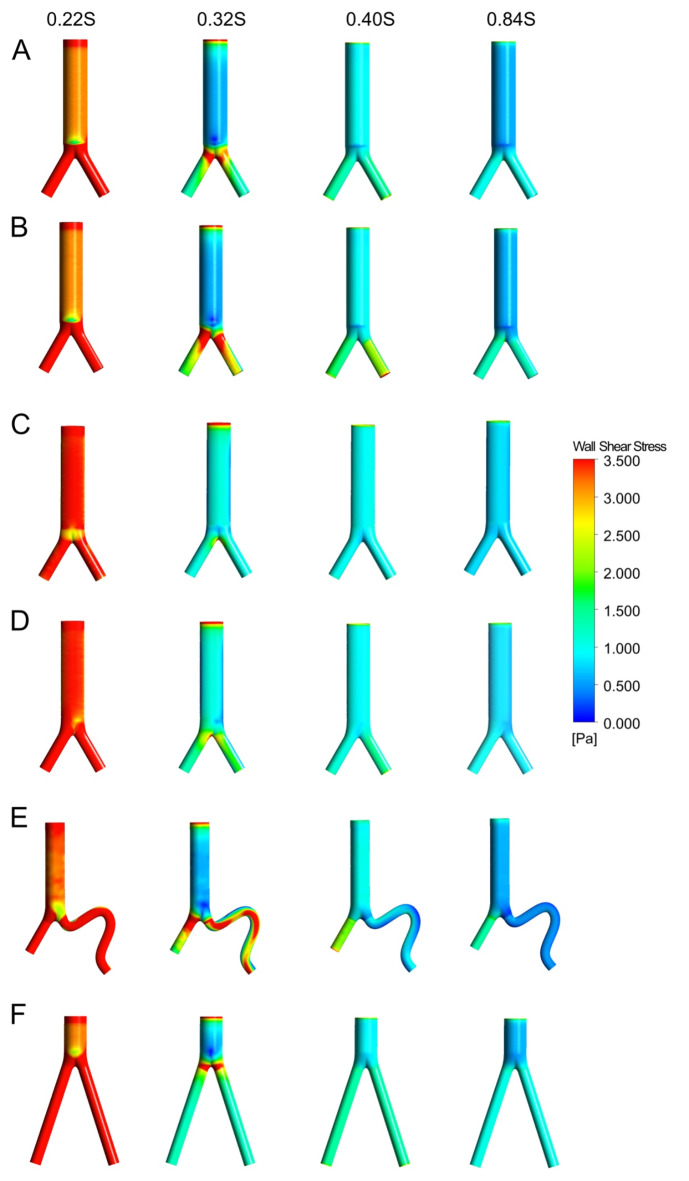
WSS, OSI, and RRT distributions

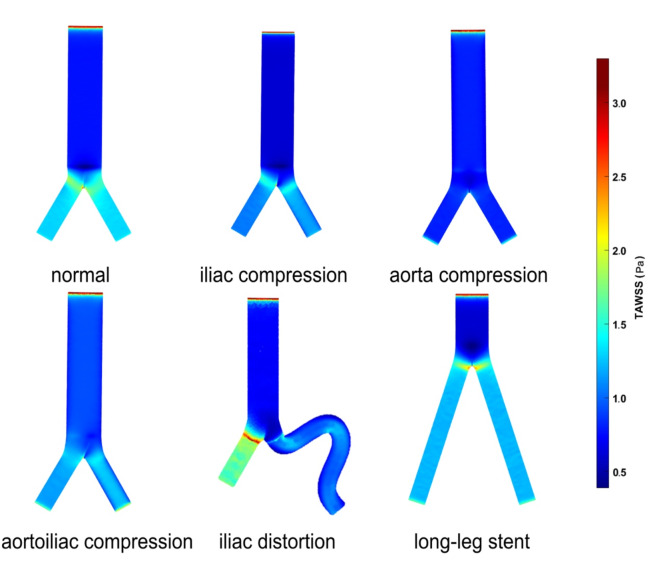
Figure 8 depicts the WSS distribution at four different points in the cardiac cycle in each of the six models. As shown in Fig. 9, the TAWSS is less than 1.5 Pa in most areas of all six models. Relatively high TAWSS regions are localized mostly in the bifurcated SG limb portion, proximal to the iliac limb SGs, and the twisted section. TAWSS is influenced to varying degrees by different stent compression locations. The TAWSS at iliac grafts showed varying degrees of decline in the other three compression models compared to the normal model. This difference was more pronounced in the model with aortic compression. In the iliac distortion model, it has been observed that the fluctuation range of TAWSS on the torsion side of the artery was relatively large. Specifically, there is an increase in TAWSS at the corner where the artery twists, followed by a significant decrease in TAWSS toward the distal end of the corner. However, in patients with nontwisted iliac artery stents, the TAWSS increased. Additionally, TAWSS values were found to be somewhat lower in the long-leg stent model.

Fig. 8.

The wall shear stress (WSS) distributions of the six ideal models. (A) normal, (B) iliac compression, (C) aorta compression, (D) aortoiliac compression, (E) iliac distortion, (F) long-leg stent.

Fig. 9.

The time-average wall shear stress (TAWSS) distributions of the six ideal models.

Figure 10A shows the OSI cloud image of the models. The distal end of the main body component of bifurcated SGs, the proximal end of the iliac limb SGs, and the twisted section of SGs have very high OSI (above 0.4)²³. Comparing the OSI between the different compression positions of the stents, it can be found that the oscillation of blood flow at the constriction side of the iliac artery and the aortic bifurcation area is more intense. The effect of aortic compression on OSI was smaller than that of the iliac artery compression and aortoiliac compression models. The distortion of the iliac artery aggravates the oscillation of blood flow, especially near each curve. The use of longer stents resulted in a slight decrease in the oscillation of blood flow in the aorta and iliac arteries. As shown in Fig. 10B, the areas with longer RRT (above 2) were concentrated in the aortoiliac compression model and the iliac twisted side. We further calculated the high OSI, TAWSS, and RRT areas for the six models as shown in Table 2.

Fig. 10.

The oscillatory shear index (OSI), and relative residence time (RRT) distributions of the six ideal models. (A) OSI distributions, (B) RRT distributions.

Table 2.

Areas with an OSI ≥ 0.4, TAWSS ≥ 1.5 Pa, and RRT ≥ 2(1/Pa) in six models.

Area(mm2) Model	TAWSS ≥ 1.5 (Pa)	OSI ≥ 0.4	RRT ≥ 2 (1/ pa)
Normal	252.65	163.81	92.32
Iliac compression	186.18	726.86	78.41
Aorta compression	57.73	191.90	115.52
Aortoiliac compression	111.25	809.57	135.20
Iliac distortion	755.49	389.34	216.53
Long-leg stent	271.63	157.06	81.55

Discussion

Although the enhanced technological properties of EVAR devices overcome previous shortcomings, several obstacles remain²⁴. The post-EVAR morphology varies anatomically and is related to a varying frequency of post-operative adverse effects²⁵. Despite EVAR’s high technical success rate, IPT remains one of the leading complications after SG implantation²⁶.

Computational fluid dynamics has been shown to be an efficient method of investigating the influence of endograft implantation on blood flow, with several advantages including noninvasiveness, low-cost, high-resolution analysis, and greater model customization. These flow disturbances were accurately quantified in our simulations using specific models and should be analyzed separately to assess the effects of each endograft configuration on hemodynamics.

First, this study revealed that SG compression leads to a decrease in blood flow velocity, and the aortic compression model exhibited the most noticeable comparable drop, approximately 48.62% (Fig. 5A). Similarly, there were comparable results when comparing different iliac distortion models. However, there was no discernible difference between the long and short-leg models (Fig. 7). Thrombosis, also known as blood clotting, is a phenomenon that is closely associated with low-velocity blood flow. In theory, low velocity causes a low TAWSS distribution²⁷. Low TAWSS is associated with unstable flow conditions such as turbulence, blood recirculation areas, and blood “stagnation” regions, which increase the risk of thrombosis and intimal hyperplasia^27–29.

Second, our findings indicated that sites with low TAWSS corresponded to regions with low flow velocity. Next, we compared the TAWSS, OSI, and RRT to identify the parameters’ consistent patterns. TAWSS is an important hemodynamic parameter that has a direct effect on the endothelium layer. The simulation findings demonstrate that the proportion of low TAWSS areas is mostly affected by compression and distortion, while the length of the SG has minimal effect, indicating that increasing the length does not increase the risk of thrombosis (Table 1). The study conducted by Liu et al. analyzed patients with IPT and revealed that compared to individuals without IPT, they exhibited lower flow velocity, lower tortuosity, and lower WSS. ³⁰.

In addition, the high OSI area was mostly located in the proximal end and the twisted section of SGs. These findings from previous studies show that hemodynamic disturbances cause drastic changes in hemodynamic parameters, which may predispose individuals to IPT^17,31. Changes in hemodynamic parameters may be able to predict IPT in proximal distorting iliac limb SGs. Our data have shown that the lower TAWSS (Fig. 9) locations corresponded to higher OSI (Fig. 10A) and longer RRT areas (Fig. 10B). In addition, our analysis indicates that the long-leg stent model did not experience significant alterations in OSI or RRT. These findings suggest that the use of a long-leg stent may not greatly impact the hemodynamic factors within the SGs, compared to other types of models. This information can help inform decisions about stent selection and treatment planning for patients with similar vascular conditions.

To date, TAWSS, OSI, RRT, and a few other features that are thought to be linked to the onset and progression of thrombosis have been reported in some studies. The hemodynamic environment underlying various modalities is unknown due to the disparities in settings, and it should be of significant use to examine the differences in hemodynamic features. Both the curvature of the device and the change in diameter may be responsible for these hemodynamic modifications. Therefore, we advocate that: (1) preoperative planning to prevent steep curves at endograft bends, (2) appropriately increasing the length of the iliac artery stent to avoid twisting³², (3) balloon dilation during the operation to improve compression as necessary, and (4) appropriate antithrombotic therapy for patients with arterial distortion. Short and intermediate stent graft patency may be more dependent on changes in endograft flow. Endograft compression and distortion have been identified as risk factors for IPT. We believe that more CFD research is needed to elucidate the link between flow patterns and vascular disease.

Limitations

Our study has some limitations. First, the anatomy after EVAR in the real world is more complex than our models. The models used in subsequent research should be generated from clinical cases, enhancing findings with information from "real-world" situations. Second, in both the elective and acute clinical outcomes for the treatment of complicated aortic aneurysms, off-the-shelf or doctor-modified fenestrated and branching endografts appear to be effective and safe³³. Further understanding of the relationship between the hemodynamic environment and clinical outcomes may require future studies that consider these specialized technologies. Third, previous research has suggested that the hemodynamics close to the arterial wall will be impacted by the folds brought about by stent graft bending^34,35. However, our future study will concentrate on the effect of folds, which has not been taken into account by the current models.

Conclusion

The present study addresses with the hemodynamic changes in SGs under different anatomic structures. Our research revealed that endograft compression and distortion are identified as potential risk factors for IPT. Furthermore, longer stent length yields marginal alterations in SG hemodynamics. This finding suggests that when the impact of the morphology of SG on hemodynamics is examined, the hemodynamic changes brought on by arterial compression and distortion of the iliac artery cannot be disregarded.

Electronic Supplementary Material

Below is the link to the electronic supplementary material.

Author contributions

Conceptualization: Y.Z., P.Q., X.Y.; Methodology: Y.Z., D.Z., X.S., X.Y., J.C.; Investigation: D.Z., X.Y., P.Q.; Data analysis: Y.Z., P.Q., X.S.; Supervision: Y.L., X.L., X.Y.; Writing—original draft: Y.Z.; Writing—review & editing: Y.Z., P.Q., X.Y. All authors reviewed the manuscript.

Funding

This work was supported by these funding as follows: the National Natural Science Foundation of China (82300540, 82170509, 82370494, 82170411), Clinical Research Program of 9th People’s Hospital (JYLJ202204), Shanghai Science and Technology Innovation Action Plan (21S31904300, 21Y11909500), Shanghai Municipal Health Bureau Project (20224Y0170, 202240145), and Original Exploration Project of Shanghai Ninth People’s Hospital (No.JYYC004).

Data availability

The data sets engendered and/or evaluated within the present study canalso be procured from the corresponding author upon reasonable request.

Declarations

Competing interests

The authors declare no competing interests.