The analysis of urban collaborative governance in public health emergencies with fuzzy theory based on BP algorithm

Abstract

This study seeks to improve urban supply chain management and collaborative governance in the context of public health emergencies (PHEs) by integrating fuzzy theory with the Back Propagation Neural Network (BPNN) algorithm. By combining these two approaches, an early warning mechanism for supply chain risks during PHEs is developed. The study employs Matlab software to simulate supply chain risks, incorporating fuzzy inference techniques with the adaptive data modeling capabilities of neural networks for both training and testing. The results demonstrate that the proposed model effectively identifies factors contributing to supply chain deterioration, with a warning error as low as 0.001, significantly enhancing the accuracy and timeliness of demand forecasting. The BPNN algorithm, through its self-learning and adaptive features, facilitates dynamic optimization and precise scheduling across various stages of the supply chain. This capability is particularly valuable in addressing challenges associated with sudden demand spikes and resource allocation. As a result, the mechanism is able to accurately and promptly identify adverse trends in the supply chain, thereby enhancing the efficiency and flexibility of urban emergency responses, mitigating risks, and offering both theoretical and practical contributions to urban collaborative governance.

Introduction

The prevalence of public health emergencies (PHEs) today significantly impacts global economic and social development¹. Establishing a robust PHE management system that effectively minimizes risk through early warning, rapid response, and comprehensive post-event evaluation is a critical challenge for nations worldwide². A key element of such an emergency management system is the emergency supply chain, which plays a vital role during PHEs. Effective emergency supply chain management (SCM) during these events requires collaboration among all supply chain members to ensure the timely delivery of essential supplies to disaster-affected areas through scientific organization and comprehensive planning³.

General Secretary Xi has stated, “Only the strongest system and the strongest rule of law can provide a reliable guarantee for the construction of ecological civilization”⁴. Urban and regional collaborative governance requires not only the advancement of ecological civilization but also a comprehensive legal framework and rigorous enforcement of the rule of law. There is a need to study and develop laws and regulations concerning emergency expropriation, tax relief, emergency medical services, assistance to vulnerable populations, and regional resource allocation and cooperation during emergencies. It is also necessary to clearly define the responsibilities and obligations of various governance entities during PHEs to achieve objectives such as optimal supply and demand matching, reduced operational cycles, cost-effective operations, appropriate inventory reserves, and the provision of high-quality assurance materials⁵.

The inherent dynamics and complexity of the supply chain introduce numerous uncertainties that can hinder collaboration among supply chain nodes and impact overall effectiveness. To ensure resilient and sustainable supply chain operations, it is essential to employ advanced and preventive approaches in supply chain risk management to promptly and effectively monitor early warning signals⁶. Integrating Back Propagation Neural Network (BPNN) with fuzzy theory offers a promising method for training data to provide timely warnings and corrections for adverse trends. This approach represents a stable research direction within the current SCM system, with the increasing application of risk early warning theory in supply chain risk management to mitigate risk occurrences⁷.

In the face of frequent global public health events, effectively managing emergency supply chains to address sudden PHEs has become a significant challenge for countries worldwide. Existing emergency management systems often face several issues, including inefficient emergency response that leads to delays in resource allocation and supply chain operations; inadequate coordination mechanisms that hinder collaboration among stakeholders; and insufficient accuracy in information processing, which fails to address uncertainties and ambiguous information during emergencies. These problems not only affect the effectiveness of emergency responses but also result in suboptimal resource allocation, thereby impairing the overall management of public health events. This study aims to explore how improving emergency SCM can enhance responses to PHEs. The core issue of the study is how to leverage advanced forecasting and risk management methods to address uncertainties and ambiguous information in the supply chain, thereby improving the efficiency and accuracy of emergency responses. To this end, this study proposes an innovative emergency SCM model that integrates fuzzy theory with the BPNN algorithm to address the shortcomings identified in current research. Specifically, the objectives of this study include: (1) using fuzzy theory to effectively handle uncertainties and ambiguous information in public health events, thereby enhancing the flexibility and accuracy of the supply chain; (2) employing the BPNN algorithm to adaptively optimize supply chain strategies, improving the flexibility and effectiveness of emergency responses; and (3) proposing a new integrated model to resolve issues such as inadequate coordination mechanisms and inaccurate information processing in existing emergency management systems, thus enhancing the overall efficiency of urban collaborative governance. By achieving these objectives, this study aims to provide both theoretical support and practical guidance for managing emergency supply chains in public health events.

The contributions of this study are as follows:

• Integration of Fuzzy Theory and BPNN Algorithm: This study introduces a method that integrates fuzzy theory with the BPNN algorithm. The goal of this integration is to improve the accuracy and response speed of early warning mechanisms for supply chain risks, particularly in the context of PHEs.

• Development of a Supply Chain Risk Early Warning Mechanism: An early warning mechanism is developed that can promptly and accurately detect adverse trends in the supply chain. This mechanism also provides management recommendations to mitigate associated risks, thereby enhancing supply chain resilience during PHEs.

• Application of Matlab Software: Matlab software is employed to simulate supply chain risks, combining fuzzy inference techniques with the adaptive data modeling capabilities of neural networks for both training and testing. This approach improves the model’s practical applicability and effectiveness.

• Enhancement of Urban Emergency Response Efficiency and Flexibility: This study offers a method to enhance the efficiency and flexibility of urban emergency responses, thereby strengthening urban collaborative governance, which is critical for managing PHEs. Additionally, the study provides not only new theoretical insights but also practical guidance for the application of urban collaborative governance and SCM in the context of public health crises.

Literature review

In recent years, global research has extensively explored supply chain risks and mitigation strategies, underscoring the importance of early warning systems for potential hazards. Browning et al. investigated how to rebuild supply chains post-COVID-19 through innovation to enhance resilience. They focused on the evolution of forecasting, risk management, and product design, and identified research opportunities for addressing systemic disruptions. Scholars have emphasized the necessity of integrating these three areas to strengthen overall supply chain resilience⁸. Zimon and Madzík proposed four principles for developing early warning indicators for supply chain risks: sensitivity, flexibility, comprehensiveness, and the integration of both qualitative and quantitative indicators⁹. Ghadge et al. employed rough set and grey theory within the framework of early warning models for supply chain knowledge-sharing risks. They utilized the fuzzy comprehensive assessment method to effectively evaluate supply chain risks and establish risk warning levels¹⁰. Aljohani introduced an innovative supply chain risk management strategy that leverages machine learning and predictive analytics to enhance agility and real-time risk prevention capabilities. By applying predictive analytics methods such as time series analysis, anomaly detection, and natural language processing to real-time monitoring systems, businesses can promptly identify and mitigate risks as they arise¹¹.

Traditional methods of supply chain risk management often rely on statistical models or rule-based decision support systems, which have limitations in addressing the complexities and uncertainties of modern supply chain environments. In contrast, fuzzy theory is adept at managing ambiguity and incomplete data in supply chains. By utilizing fuzzy sets and fuzzy reasoning, it provides more flexible and accurate risk assessments¹². The BPNN algorithm, a machine learning technique, enhances the accuracy and adaptability of predictive models by learning from extensive datasets and recognizing patterns. This makes it particularly advantageous in dynamic supply chain environments¹³. Researchers have integrated fuzzy theory with the BPNN algorithm to create composite models, such as fuzzy neural networks. These models incorporate multidimensional information from various data sources, enabling more effective identification and prediction of potential risks in the supply chain¹⁴. Compared to traditional methods, these composite models better capture nonlinear relationships and stochastic variations within the supply chain, thereby enhancing the precision and practicality of risk warnings. Specifically, a risk early warning system combining fuzzy theory with the BPNN algorithm can detect potential risk signals early, allowing enterprises and government agencies to implement timely preventive or corrective actions. This approach helps minimize the risk of supply chain disruptions and losses, leading to greater cost-effectiveness and resource optimization¹⁵.

In the context of SCM during PHEs, Ahlqvist et al. examined how policymakers addressed shortages of generic drugs through supply chain risk management strategies. Although the strategies implemented by policymakers during the pandemic were limited, most shortages were mitigated due to prior measures taken to address routine disruptions. They also highlighted both the direct and indirect roles of policymakers in supply chain risk management¹⁶. Tukamuhabwa et al. noted that internal social capital and supply chain risk management capabilities significantly predicted supplier performance. Logistics capabilities partially mediated the relationship between internal social capital and supply chain risk management capabilities, while supply chain risk management capabilities fully mediated the relationship between logistics capabilities and supplier performance¹⁷. This provided new empirical evidence for improving supplier performance in the public healthcare sector of developing countries. Xu et al. explored the impact of the pandemic on global SCM and proposed a framework to address challenges at various stages of a pandemic. This framework included key areas such as government policies, supply chain redesign, economic financing strategies, operational adjustments, and technology adoption, aiming to enhance responsiveness, resilience, and recovery for businesses¹⁸. These studies provide crucial theoretical and empirical support for understanding and improving SCM during PHEs, highlighting the key roles of policymakers, internal social capital, and SCM capabilities in enhancing supply chain resilience and performance.

In real-world decision-making, multiple factors such as cost, time, quality, and risk often need to be considered. Multi-criteria decision-making (MCDM) is a methodology and set of techniques designed to support decisions under multiple, conflicting criteria. By utilizing mathematical modeling and analytical techniques, MCDM helps decision-makers make rational, scientifically grounded choices in complex, multidimensional environments¹⁹. In supply chain management, particularly during public health emergencies, MCDM techniques can be used to evaluate and optimize various decision paths. For example, Chatterjee and Kar applied an interval-valued fuzzy TOPSIS method to address multi-criteria decision problems in supply chain risk management. Their model provides an effective approach for handling complex, uncertain scenarios, thus offering scientific support for supply chain management decisions²⁰. In another study, Chatterjee et al. used the fuzzy analytic hierarchy process (AHP) method to prioritize project proposals in portfolio management, highlighting the significant role of MCDM in resource allocation and project management²¹. Additionally, Chatterjee and Kar developed an AHP-VIKOR multi-criteria decision framework based on unified granular numbers, integrating both subjective and objective weights to enhance decision robustness and applicability, providing optimization tools for complex systems²². Moreover, Chatterjee and Kar optimized supplier selection in telecom supply chain management by combining a fuzzy Rasch model with the COPRAS-G method, demonstrating the advantages of MCDM techniques in addressing complex supply chain challenges²³.

In summary, a review of the existing literature reveals several limitations in previous research on SCM during PHEs, particularly in addressing complexity and uncertainty. Many studies rely on traditional statistical models or rule-based decision support systems, which are ill-equipped to handle the dynamic changes characteristic of modern supply chain environments. Additionally, much of the existing research remains at a static analysis level, failing to effectively capture the complexities and dynamics introduced by PHEs, leading to inaccurate risk identification and forecasting. This study proposes a novel supply chain risk early warning model that integrates fuzzy theory with the BPNN algorithm to address these limitations. Fuzzy theory is well-suited for managing ambiguity and incomplete data within the supply chain, offering more flexible and accurate risk assessments. Meanwhile, the BPNN algorithm enhances prediction accuracy and adaptability by learning from large datasets and recognizing patterns. By combining these two approaches, the model not only improves adaptability and robustness in complex, dynamic environments but also optimizes the efficiency of supply chain operations. This provides a more reliable solution for urban collaborative governance, particularly during PHEs.

Methods and materials

The model development process for this study involves several key steps to ensure the scientific validity and effectiveness of the supply chain risk early warning system. Firstly, problem identification and needs analysis are conducted to gain a deep understanding of the SCM requirements during PHEs. This phase identifies critical issues, such as the operational status of various nodes in the supply chain, potential risks, and their impacts, laying the groundwork for model design. Next, historical data related to PHEs are collected, including material demand, supply conditions, and records of logistics disruptions. This data is then cleaned and standardized to ensure accuracy and consistency. Following this, the model design and development phase utilizes fuzzy theory to address uncertainties within the supply chain. The results from fuzzy reasoning are fed into the BPNN, which is trained and optimized to adjust network weights, thereby enhancing the model’s predictive capability and stability. After model development, Matlab software is used for model validation and testing. This involves simulating various PHE scenarios to assess the model’s performance and reliability. The subsequent sections provides a detailed description of the actual construction steps of the model.

SCM and collaborative governance of PHEs

A PHE is characterized as an event that “emerges abruptly, causes or has the potential to cause significant social harm, and requires the implementation of specialized emergency response plans.” Such events include natural disasters, accidents, public health crises, and social security incidents²⁴. PHEs are distinguished by four key characteristics, as illustrated in Fig. 1.

Fig. 1.

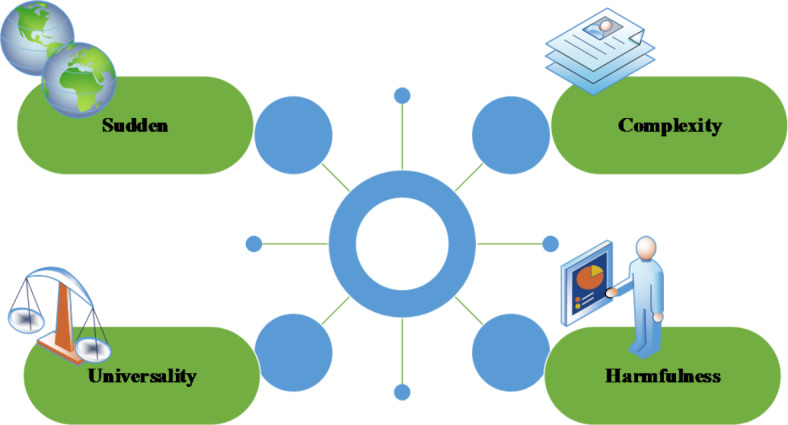
Characteristics of PHE.

In Fig. 1, PHEs are characterized by their sudden onset, widespread impact, complexity, and potential for significant harm. If not controlled effectively and promptly following their emergence, PHEs can cause extensive damage to lives, property, and the environment. Such situations may lead to issues such as disorganized management, inefficient resource allocation, inadequate professional oversight, and insufficient information support. Therefore, the development and management of an effective emergency supply chain are crucial²⁵.

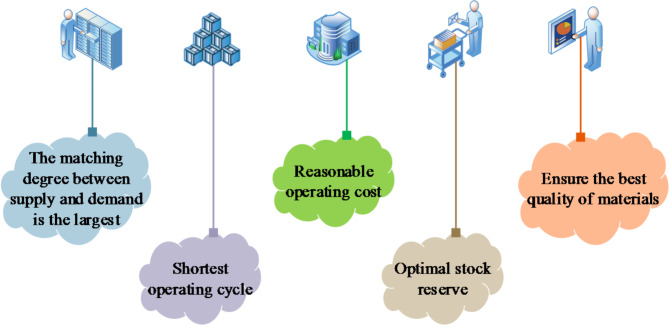
The emergency supply chain is structured with government emergency management departments serving as the central command and control hub. It is established through collaboration with other government agencies, social enterprises, public organizations, and various stakeholders²⁶. This collective effort forms the emergency supply chain, which operates as a “virtual organization” with unified emergency objectives. Figure 2 outlines the primary management goals of this structure.

Fig. 2.

Objectives of emergency SCM.

In Fig. 2, the primary objectives of emergency SCM are outlined across five key areas: maximizing supply-demand alignment, reducing operational cycles, controlling operational costs, optimizing inventory reserves, and ensuring the highest quality of materials. These objectives are interconnected and collectively aimed at enhancing the efficiency and effectiveness of emergency management. They provide specific guidance for the design and validation of the model. By optimizing these objectives, this study seeks to improve the responsiveness and flexibility of the emergency supply chain, ensuring the rapid and effective fulfillment of needs during PHEs, while reducing costs and maintaining material quality. Optimizing emergency SCM for PHEs requires collaboration in urban governance to achieve optimal supply-demand matching, the shortest operational cycles, reasonable operational costs, optimal inventory reserves, and the highest quality material support²⁷. Additionally, strong cooperation and support between federal and local government leaders are essential. Enhancing coordination, communication, and responsiveness is crucial. In health emergency management, timely expert consultation, technical support, rescue teams, emergency medicine, and equipment are critical for strengthening urban and regional collaborative governance capacities²⁸. Figure 3 provides optimization recommendations for urban and regional collaborative governance during significant PHEs.

Fig. 3.

Optimization suggestions for urban collaborative governance of public health events.

Figure 3illustrates the optimization recommendations for urban and regional collaborative governance during major PHEs. It emphasizes the central role of government agencies in emergency management. To effectively respond to PHEs, it is essential to fully mobilize and coordinate all sectors of society—including government agencies, social organizations, businesses, and the media—to foster synergy²⁹. These recommendations provide a practical framework for the study, ensuring that the model’s application aligns with real-world governance needs. By implementing systematic collaborative governance, the model aims to enhance emergency response capabilities and improve resource allocation efficiency.

Fuzzy theory and BPNN

In recent years, with the increasing complexity of urban governance, traditional SCM methods have revealed limitations in addressing uncertainties and dynamic environments during PHEs. Information in emergency management often exhibits high levels of ambiguity and uncertainty, making it difficult to describe using precise mathematical models. Fuzzy theory effectively handles the vagueness and incompleteness in data through fuzzy sets, membership functions, and fuzzy reasoning, particularly excelling in demand forecasting and uncertainty management. Meanwhile, the BPNN algorithm, with its powerful self-learning and adaptive capabilities, plays a crucial role in recognizing and learning complex data patterns, especially in optimizing and precisely scheduling various stages of the supply chain within dynamic environments. By combining fuzzy theory with BPNN, the advantages of both approaches can be fully leveraged, demonstrating unique superiority in managing the complexity and uncertainty of supply chain risk early warning. Fuzzy theory excels at capturing and describing vague information, while BPNN achieves precise pattern recognition and forecasting through data training. The integration of these methods provides a solid theoretical foundation and technical support for establishing a robust supply chain risk early warning mechanism. Therefore, this study selects fuzzy theory and BPNN to develop a supply chain risk early warning mechanism that can better address the complexity and uncertainty of PHEs.

Fuzzy Theory

Fuzzy theory adeptly manages the ambiguity and incompleteness inherent in supply chain data through the use of fuzzy sets, membership functions, and fuzzy reasoning. For instance, it effectively addresses various uncertainties encountered in demand forecasting. During model construction, selecting appropriate membership functions and rule settings is critical, as these decisions significantly impact the model’s ability to accurately respond to complex real-world scenarios³⁰. The representation of fuzzy concepts through membership functions plays a pivotal role in this process. The membership function is expressed as Eq. (1).

1

In Eq. (1), 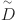represents a fuzzy set, and .

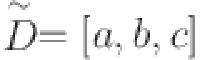In the SCM model, the objective function is often represented as a fuzzy concept within the decision-making process. It can be expressed using fuzzy numbers and is typically classified into cost-based and benefit-based objectives³¹. This study employs a seven-level classification system for dividing fuzzy semantic intervals, which is considered from both theoretical and practical perspectives. From a theoretical standpoint, a seven-level classification provides sufficient granularity to accurately describe varying degrees of fuzzy uncertainty in SCM. Compared to a classification with too few levels, a seven-level system is better able to capture the gradual nature of risk and return, especially during PHEs, when the supply chain’s risk profile often changes in varying degrees. Therefore, the seven-level semantic intervals offer a more flexible framework to describe these complex variations.From a practical perspective, the seven-level fuzzy semantic intervals are characterized by good operability and ease of understanding in the decision-making process. The refinement of these intervals helps decision-makers more intuitively conduct risk assessments and resource allocations. By subdividing fuzzy intervals, decision-makers can more clearly identify risk levels at different stages and segments of the supply chain, thereby formulating more precise response measures. Furthermore, the hierarchical nature of the seven-level system ensures computational efficiency, especially when data is limited, while effectively balancing complexity and predictive accuracy. This avoids issues related to information overload or excessive model complexity. Thus, the seven-level fuzzy semantic intervals represent an optimal balance between theoretical rigor and practical applicability. The details are presented in Table 1.

Table 1.

Interval division corresponding to fuzzy semantics.

Level code	Fuzzy interval	Fuzzy semantics
N1	1 ≤ n < 0.92	Quite high
N2	0.92 ≤ n < 0.76	High
N3	0.76 ≤ n < 0.59	Slightly higher
N4	0.59 ≤ n < 0.42	Middle
N5	0.42 ≤ n < 0.25	Slightly lower
N6	0.25 ≤ n < 0.08	Low
L	0.08 ≤ n < 0	Quite low

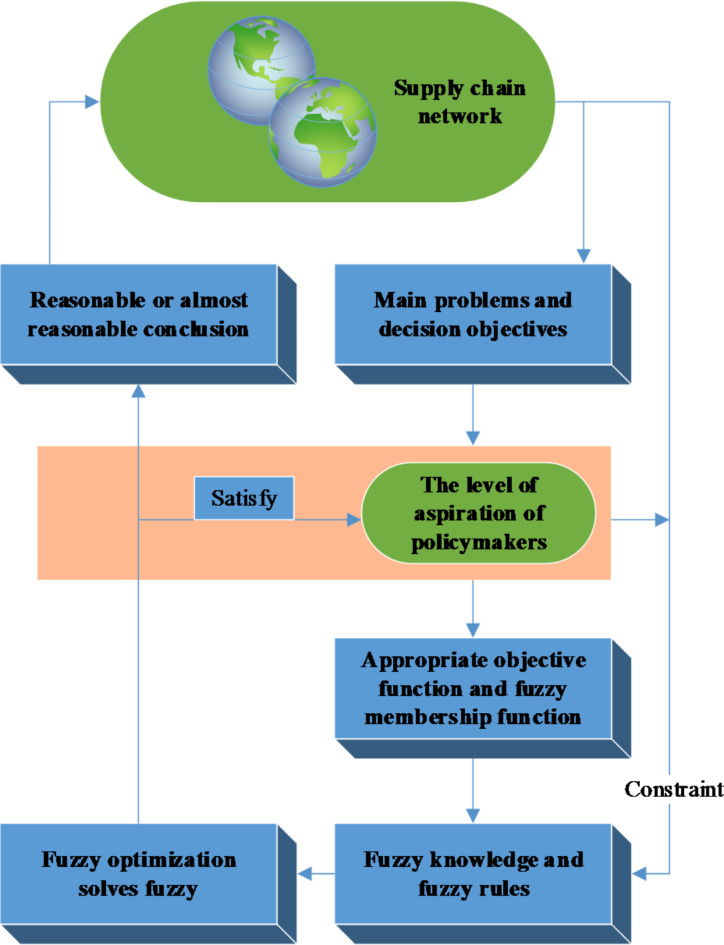
Fuzzy uncertainty in the supply chain refers to the inherent ambiguity or partial lack of clarity that decision-makers may encounter regarding information about individuals, entities, and environmental conditions. This uncertainty often leads decision-makers to rely on their own subjective judgments. In essence, decision-makers begin by recognizing fuzzy uncertainty, using fuzzy representations of uncertain parameters and objectives. They then apply fuzzy rules or knowledge to derive conclusions that are reasonable, or nearly reasonable, but still subject to some degree of fuzzy uncertainty³². Figure 4 illustrates this decision-making process.

Fig. 4.

Decision-making process of supply chain fuzzy uncertainty.

Figure 4 illustrates the enhanced capability of this study to address fuzzy uncertainty within the supply chain. This improves the accuracy of early warning mechanisms and the effectiveness of emergency responses, thereby optimizing the decision-making process in SCM.

In the application of fuzzy theory, selecting appropriate membership functions and rule settings is critical for the accuracy and reliability of the model. Commonly used membership functions, such as triangular and trapezoidal functions, effectively handle fuzzy data and uncertain information. For instance, in supply chain demand forecasting, triangular membership functions can represent varying levels of demand, such as high, medium, or low. The creation of fuzzy rules—such as “if demand increases and a supply chain disruption occurs, then the risk level rises”—helps translate expert knowledge into the model’s rule system. This enables the model to make reasonable decisions when faced with complex real-world scenarios. The parameter settings for membership functions, including the partitioning of fuzzy intervals, are based on the seven-level classification outlined in Table 1. This method accurately reflects various fuzzy semantics, enhancing the model’s adaptability to real-world data. Furthermore, the core of fuzzy theory lies in its ability to manage information uncertainty. Decision-makers apply fuzzy rules and knowledge to make reasonable inferences about uncertain parameters and objectives, resulting in near-reasonable conclusions. This approach not only strengthens the model’s capacity to handle fuzzy information but also improves decision support within SCM.

BPNN

The BPNN algorithm is a neural network training method based on gradient descent. It optimizes the network’s weights and biases through backpropagation, enabling the learning and recognition of complex data patterns. In the context of supply chain fuzzy decision-making, it is essential to thoroughly consider the characteristics of the problem and accurately capture the fuzzy uncertainties to effectively address real-world needs. This consideration is particularly important for facilitating the computation of uncertainties during the reasoning process³³.

Early warning in supply chain risk management involves the systematic identification, monitoring, and analysis of potential hazards throughout the supply chain’s operation. This approach helps supply chain managers understand the risks associated with various departmental activities. As a result, practical measures can be implemented to prevent and control risks, ensuring smooth operations while safeguarding the economic interests of supply chain entities.

This study evaluates the “three benefits” of the PHE supply chain using a three-layer BPNN model. The “three benefits” indicators include economic, social, and environmental benefits. In summary, a review of the existing literature reveals several limitations in previous research on SCM during PHEs, particularly in addressing complexity and uncertainty. Many studies rely on traditional statistical models or rule-based decision support systems, which are ill-suited to handle the dynamic changes inherent in modern supply chain environments. Additionally, much of the existing research remains at the level of static analysis, failing to effectively capture the complexities and dynamics introduced by PHEs. As a result, this leads to inaccurate risk identification and forecasting. This study proposes a novel supply chain risk early warning model that integrates fuzzy theory with the BPNN algorithm to overcome these limitations. Fuzzy theory is well-suited for managing ambiguity and incomplete data within the supply chain, offering more flexible and accurate risk assessments. Meanwhile, the BPNN algorithm improves prediction accuracy and adaptability by learning from large data patterns. By combining these two approaches, the model enhances both adaptability and robustness in complex, dynamic environments, while also optimizing the efficiency of supply chain operations. This provides a more reliable solution for urban collaborative governance, particularly during PHEs.

Additionally, economic, social, and environmental benefits serve as comprehensive measures of supply chain performance, reflecting the multidimensional impact of the supply chain during PHEs. The number of neurons in the hidden layer can be calculated using Eq. (2):

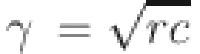2

Here, 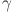, r and c represent the number of neurons in the hidden layer, input layer, and output layer, respectively.

When the BPNN algorithm is used to train the data, the forward propagation output of the neural network is calculated first. The output value of each neuron in the hidden layer is given by Eq. (3):

3

In Eq. (3), 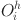represents the output value of the i-th neuron in the hidden layer; represents the activation function of the hidden layer neuron. is the connection weight from the j-th neuron of the input layer to the i-th neuron of the hidden layer; 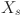represents the input vector of the input layer; s represents the number of input samples; 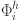indicates the hidden layer threshold.

The output value of the k-th neuron in the output layer is expressed as shown in Eq. (4):

4

In Eq. (4), 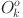represents the output value of the k-th neuron in the output layer; 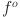is the activation function of the output layer neuron; 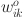indicates the connection weight from the i-th neuron of the hidden layer to the k-th neuron of the output layer; 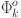represents the threshold value of the output layer.

The error of the BPNN model is given by Eq. (5):

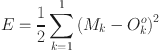5

In Eq. (5), is the error of the BPNN model, and 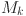is the expected output value of the k-th neuron in the output layer.

Next, the BPNN’s backpropagation algorithm adjusts the weights, and the modified weight from the hidden layer to the output layer neuron is given by Eq. (6):

6

In Eq. (5), represents the change in the weight between the neurons in the hidden layer and the output layer, 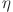represents the learning efficiency of the model, and is the error term, defined as 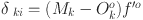, where 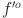is the derivative of the output layer’s activation function.

The corrected weight from the input layer to the hidden layer is given by Eqs. (7) and (8):

7

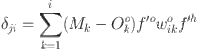8

Here, is the corrected weight change between the input layer and the hidden layer neurons, 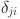is the error term, and 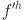is the derivative of the hidden layer’s activation function. This process continues until the model’s network error reaches the desired accuracy, at which point the correction process is stopped.

Finally, the input indicators for the BPNN are processed, and the five integrated indicators are fed into the model. To account for magnitude differences, the normalized equation, as specified in Eq. (9), is used for calculation:

9

In Eq. (9), is the normalized result of the j-th component in the input vector, and is the j-th component of the s-th vector.

The output layer of the BPNN model comprises three units: economic benefits, social benefits, and environmental benefits of the supply chain. Once the network model’s error meets the specified accuracy requirements, the model can be employed to guide the selection of the PHEs supply chain. The structure of the model is illustrated in Fig. 5.

Fig. 5.

Structure of BPNN model.

Utilizing this model structure, supply chain units can evaluate the “three benefits” indicators based on expected metrics for procurement, production, collection, distribution, and delivery. This allows for the assessment of the operational effectiveness of the supply chain³⁴. In summary, the BPNN model architecture consists of three layers: the input layer, the hidden layer, and the output layer. The input layer contains five nodes, each corresponding to a core operational indicator of the supply chain: procurement, production, collection, distribution, and delivery. These five indicators comprehensively represent the main operational components of the supply chain, each of which has a significant impact on overall supply chain functioning, particularly during PHEs, where coordination among these components is essential. By selecting these five indicators as input nodes, the model ensures strong representativeness and comprehensiveness in capturing the operational state of the supply chain. The output layer consists of three nodes, which are dedicated to predicting the economic, social, and environmental benefits of the supply chain. These three indicators represent the comprehensive performance of SCM in response to PHEs, reflecting not only the economic efficiency of the supply chain but also its capacity to support society and its impact on environmental sustainability. Furthermore, as shown in Eq. (2), the number of neurons in the hidden layer is determined. With five neurons in the input layer and three in the output layer, the hidden layer is set to contain four neurons. This configuration ensures that the model has enough complexity to capture the nonlinear relationships between inputs and outputs while avoiding overfitting due to an excessive number of hidden layer neurons. This arrangement allows the model to maintain a high level of generalization when handling complex data, while also reducing computational costs, ensuring its effectiveness and operability in practical applications within SCM.

Supply chain risk early warning for PHEs based on fuzzy theory and the BPNN algorithm

By integrating fuzzy theory with the BPNN algorithm, this study offers distinct advantages and significant improvements over existing models in the context of urban collaborative governance. Traditional SCM models typically rely on linear programming and static optimization methods, which often struggle to address the high complexity and uncertainty associated with PHEs. In contrast, the proposed model incorporates fuzzy theory to effectively manage the ambiguity and uncertainty inherent in emergencies, enhancing flexibility and adaptability in real-world applications. The application of the BPNN algorithm significantly improves the model’s predictive accuracy and response speed, overcoming the inefficiencies and inaccuracies of traditional methods in addressing complex, nonlinear problems. BPNN’s self-learning and adaptive capabilities allow it to uncover intricate nonlinear relationships within large datasets, thereby facilitating accurate predictions and optimized supply chain operations. This advancement results in improved efficiency in emergency responses and greater accuracy in resource allocation and risk management. Furthermore, the proposed model integrates diverse theories and algorithms to perform multi-level, multi-dimensional analysis and optimization. Within the urban collaborative governance framework, it synthesizes information and resources across various departments and levels, creating an efficient collaborative response mechanism. In contrast, traditional models often lack this comprehensive perspective and coordination capability, presenting challenges for cross-departmental cooperation and resource optimization. Thus, the developed model offers substantial benefits for managing SCM and urban collaborative governance during PHEs. By combining fuzzy theory with the BPNN algorithm, the model enhances predictive accuracy, response efficiency, adaptability, and robustness in complex, dynamic environments, providing more reliable and effective solutions for urban collaborative governance.

The primary objective of developing an emergency supply chain system for PHE events is to respond promptly to emergency needs and to allocate and distribute materials efficiently to disaster-affected areas. This demands swift, high-quality, and cost-effective cooperation among all units involved in the emergency supply chain³⁵. Figure 6 illustrates the structure of the emergency supply chain for PHE events.

Fig. 6.

Emergency supply chain structure of PHEs.

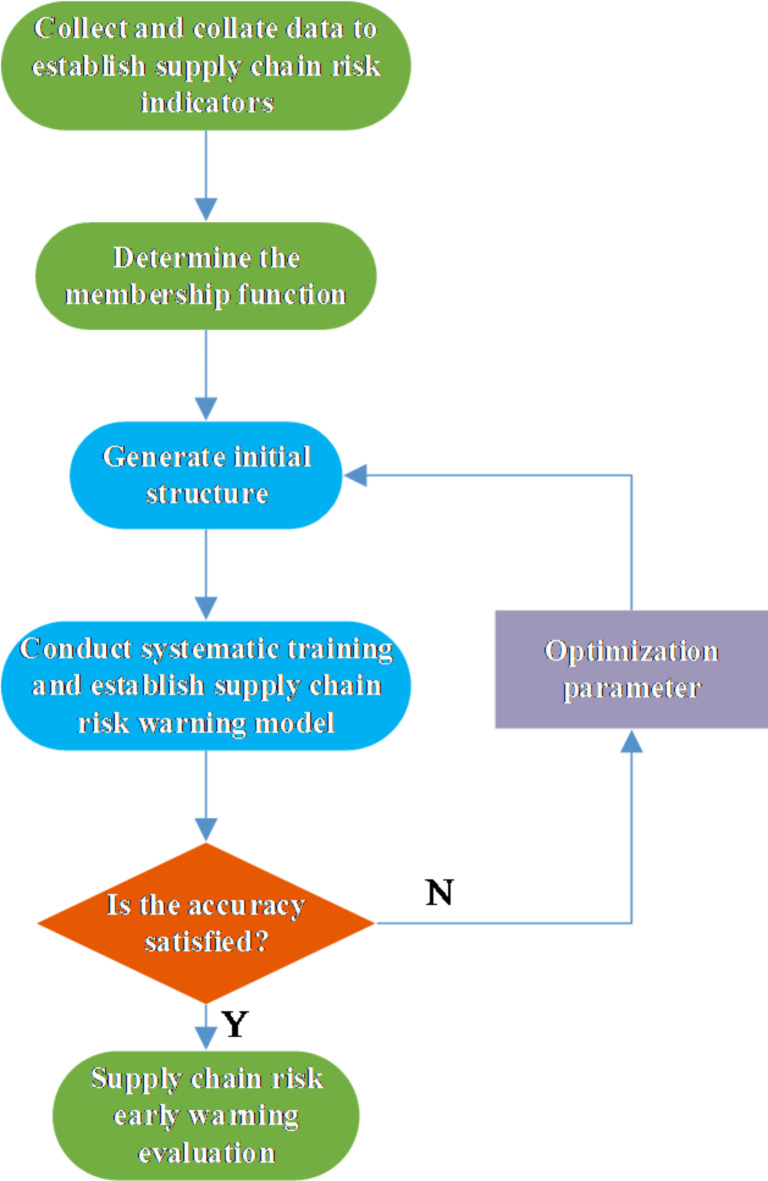
Figure 6 illustrates the collaboration methods and resource allocation processes among member units in response to emergency demands. This structure facilitates the identification of collaborative requirements and optimization goals at each stage, effectively integrating fuzzy theory and the BPNN algorithm to enhance the efficiency and effectiveness of the supply chain’s emergency response. In the integration of fuzzy theory with the BPNN algorithm, the output from fuzzy theory serves as the input for the BPNN. This combination enables the neural network to further refine and enhance the model’s predictive capabilities through fuzzy reasoning. During the construction of the early warning mechanism, fuzzy logic initially processes a large volume of risk data. The neural network algorithm then utilizes its ability to approximate nonlinear functions with high precision to implement risk warning functions. Figure 7 outlines the steps involved in constructing the early warning mechanism for the PHEs emergency supply chain.

Fig. 7.

Steps for establishing the early warning mechanism of the PHEs emergency supply chain.

Figure 7 illustrates that in the initial phase of model construction, it is essential to collect data related to supply chain risks. This data may include material demands during past epidemics, operational statuses of various supply chain components, and records of logistics disruptions. Next, membership functions for each risk indicator need to be defined. These membership functions quantify the definitions of fuzzy sets. For instance, different membership functions can be established for risk levels (such as “low,” “medium,” and “high”) to map actual data into fuzzy sets. This process involves selecting appropriate mathematical functions (such as triangular, trapezoidal, or Gaussian functions) to define each fuzzy set. Once the membership functions are determined, the initial structure of the model is constructed based on the input indicators and output results. Typically, the number of nodes in the input layer corresponds to the number of collected risk indicators, while the number of nodes in the output layer is determined by the number of warning result categories. After establishing the preliminary structure, systematic training is conducted to build the supply chain risk warning model. Through BPNN, the model continuously adjusts weights based on prediction errors during the training process. Several key parameters, such as the learning rate (commonly set at 0.01) and the momentum factor (e.g., 0.9), must be configured to ensure the model’s convergence and effectiveness. At the end of each training iteration, the model’s accuracy is evaluated by calculating the error between predicted and actual results. If the accuracy does not meet preset standards, the parameter optimization phase begins. This phase primarily adjusts parameters like the learning rate and the number of hidden layer nodes to enhance model performance. Once the model’s accuracy requirements are satisfied, final supply chain risk warning assessments can proceed. At this stage, the risk data processed through fuzzy logic is input into the BPNN model, generating the final risk warning results. These results assist decision-makers in formulating effective emergency response measures, thereby improving the efficiency of SCM during public health events. The combination of fuzzy theory and BPNN leverages fuzzy reasoning’s uncertainty-handling capabilities and the neural network’s learning abilities, offering an efficient solution for emergency supply chain risk management during public health events. This process provides a comprehensive guide for implementing the early warning mechanism proposed in the study, ensuring the model’s effectiveness and accuracy in practical applications.

To ensure the robustness of the model, Matlab software is employed to integrate fuzzy reasoning with neural network adaptive modeling, enabling the testing of the fuzzy neural network implementation algorithm. To validate the model’s practical efficacy, a testing approach based on real-world data is applied. Specifically, historical data from public health events—including material demand and supply data during past epidemics, records of logistical disruptions, and operational conditions across various supply chain stages—are utilized for model validation. Multiple experiments involving fuzzy reasoning training are conducted, with the system’s initial accuracy set to zero and the number of training iterations configured to 50. The early warning errors before optimization are compared with the final optimized data to evaluate the model’s performance.

During the model validation process, a sensitivity analysis is first conducted to assess the model’s responsiveness to key risk factors. This analysis involves adjusting for variables such as demand fluctuations, data quality, and critical neural network parameters to test the model’s stability and adaptability under different conditions. The responsiveness to each risk factor is evaluated, and combined with expert assessments, areas of weakness within the model are identified. Subsequently, a comparative analysis is performed between the results of the BPNN algorithm alone and those of the hybrid model integrating fuzzy theory. This comparison allows for precise identification of error differences within the model and helps evaluate the improvements achieved. These validation steps not only enhance the model’s applicability in real-world scenarios but also further demonstrate its potential for effective risk warning in PHE supply chains.

The proposed early warning mechanism based on fuzzy theory and the BPNN algorithm is illustrated in Fig. 8.

Fig. 8.

Workflow of the early warning mechanism based on fuzzy theory and BPNN algorithm.

As depicted in Fig. 8, a structured methodology integrates fuzzy theory with the BPNN algorithm to establish an early warning mechanism for supply chain risks. The process commences with data collection, where historical data related to PHEs—such as material demand, supply chain disruptions, and logistics constraints—are sourced from diverse channels. This data is then meticulously cleaned and standardized to ensure precision and uniformity. In the fuzzy theory processing stage, membership functions are defined for critical risk indicators, translating real-world data into fuzzy sets. To address uncertainty, a comprehensive set of fuzzy rules is developed, enabling nuanced risk assessments. The subsequent phase involves constructing a BPNN model, where the architecture, including input, hidden, and output layers, is designed. The model is trained and optimized using historical datasets, with iterative adjustments to network weights to improve predictive accuracy. The final step validates and tests the model using MATLAB software, simulating various PHE scenarios to assess its performance and robustness. This integrated workflow ensures the mechanism effectively identifies and evaluates supply chain risks, providing accurate and dependable early warnings to support proactive decision-making.

Results

Sensitivity analysis and robustness evaluation

Sensitivity analysis and robustness evaluation are conducted to validate the model’s reliability and effectiveness in managing various scenarios and data fluctuations. Sensitivity analysis examines the extent to which changes in critical input parameters affect the model’s output, providing insights into how variations influence predictions. For instance, in a supply chain context, it evaluates the impact of a 10% increase or decrease in demand on inventory levels or delivery speeds. By systematically adjusting key parameters, sensitivity analysis identifies the factors with the most significant influence, enabling targeted improvements to enhance model accuracy. Robustness evaluation, by contrast, assesses whether the model maintains stable and reliable performance under uncertain or extreme conditions. It determines the model’s resilience to imperfect data, such as noisy or incomplete inputs, and its adaptability to unexpected external disruptions. For example, in SCM, robustness evaluation may simulate sudden disruptions or abrupt market demand shifts to test the model’s predictive and responsive capabilities. This analysis ensures that the model remains reliable and functional despite variability in data or environmental conditions. Together, these evaluations strengthen the scientific foundation of the model while highlighting its practical applicability. They underscore the innovative design and robustness of the PHE supply chain risk early warning model based on fuzzy theory and the BPNN algorithm, particularly in addressing the complexities of modern supply chain environments.

(1) Sensitivity Analysis.

Sensitivity to Demand Fluctuations: Two tests assess the model’s sensitivity to fluctuations in demand. Initially, the range of demand variation is increased from the standard ± 10% to ± 20%. The results reveal that with an expanded fluctuation range of ± 20%, the model’s early warning accuracy slightly decreases, with the error increasing from 0.005 to 0.008. This outcome highlights that higher demand fluctuations introduce greater uncertainty into the supply chain, thereby increasing data complexity. While the BPNN effectively handles smaller fluctuation ranges, larger variations challenge its predictive capabilities, leading to higher warning errors.

Sensitivity to Data Quality: The effect of data quality on the model’s performance is evaluated using historical datasets with varying levels of completeness, including data sets with less than 80% completeness. The findings indicate that when data completeness falls below 80%, the early warning error significantly increases from 0.004 to 0.009. This demonstrates that diminished data quality adversely affects the model’s predictive capacity, as neural networks heavily rely on accurate and comprehensive historical data for effective learning. Consequently, reduced data quality limits the model’s ability to fit and process input information, emphasizing the necessity of maintaining high data integrity in practical applications to optimize predictive accuracy.

Sensitivity to Parameter Adjustments: The model’s sensitivity to adjustments in key neural network parameters is also examined. This includes modifying the learning rate from 0.01 to 0.001 and increasing the number of hidden layer nodes from 50 to 100. A reduced learning rate of 0.001 slows the model’s convergence but marginally lowers the error from 0.006 to 0.005, indicating improved stability when processing complex data. Additionally, increasing the number of hidden layer nodes enhances the model’s predictive accuracy, reducing the error from 0.006 to 0.004. These findings demonstrate the significant impact of parameter adjustments on the model’s fitting ability, particularly highlighting the importance of optimizing hidden layer configurations to improve prediction precision.

The results of the sensitivity analysis are summarized in Table 2.

Table 2.

Results of sensitivity analysis.

Sensitivity dimension	Test scenario		Warning error
Demand fluctuation sensitivity	Demand fluctuation range		Initial	After adjustment
	± 10%		0.005	0.005
	± 20%		0.005	0.008
Data quality sensitivity	Data Integrity		Initial data	Low quality
	≥ 80%		0.004	0.004
	< 80%		0.004	0.009
Parameter adjustment sensitivity	Learning rate	Number of hidden layer nodes	Initial	After adjustment
	0.01	50	0.006	0.006
	0.001	50	0.006	0.005
	0.01	100	0.006	0.004

These findings highlight the model’s performance variations across different conditions, offering valuable insights into its stability and adaptability. By conducting these detailed tests, critical parameters can be refined, thereby enhancing the model’s reliability and effectiveness in practical applications.

(2) Robustness Evaluation.

External Environmental Changes: The model’s response capabilities are evaluated by simulating various public health events, including influenza outbreaks, COVID-19 pandemics, and endemic infectious disease outbreaks. These scenarios cover epidemics of different scales to evaluate the model’s adaptability in managing diverse public health crises. The results show that the model demonstrates strong adaptability across different types of epidemics. Specifically, the early warning errors are 0.004 for influenza outbreaks and 0.005 for endemic infectious diseases. For the COVID-19 pandemic, however, the early warning error is slightly higher at 0.006 due to its greater complexity and extensive data requirements. This suggests that although the model’s performance is marginally less robust when addressing more complex public health events, it still provides effective early warning information. The complexity of the COVID-19 pandemic—characterized by rapid transmission, large scale, and heightened resource demands—exceeds that of typical infectious diseases. Consequently, the model faces greater challenges in processing diverse and uncertain data, resulting in a minor increase in prediction error.

Noise Data Evaluation: Simulated or real-world noise data, such as sudden supply chain disruptions or abnormal fluctuations, are introduced to evaluate the model’s performance under unexpected conditions. The results indicate that while noise data increases the early warning error, the error remains within an acceptable range. For instance, under normal conditions, the early warning error is 0.004. When simulating supply chain disruptions, this error rises to 0.007, and for abnormal fluctuations, it increases to 0.008. Noise data can interfere with the model’s training process, complicating the accurate identification of effective risk signals. Despite this, the model demonstrates resilience, as the errors remain manageable. However, in extreme scenarios, such as large-scale supply chain disruptions or severe fluctuations, the model’s predictive capability may face more significant challenges.

Strategy Adjustment Robustness: The model’s stability and effectiveness under various response strategies are evaluated by testing different approaches, such as adjusting resource allocation schemes or modifying emergency response strategies. The results reveal substantial improvements in the model’s performance when employing optimized strategies. For example, reallocating resources reduces the early warning error from 0.006 to 0.005, and implementing optimized emergency response strategies further lowers it to 0.004. These findings highlight that well-designed response strategies can significantly enhance the model’s early warning accuracy. Resource reallocation improves coordination among supply chain components, preventing bottlenecks caused by resource shortages or over-allocation. During public health emergencies, effective resource scheduling significantly boosts the supply chain’s responsiveness, reducing prediction errors. Optimized strategies also improve the supply chain’s flexibility and ability to manage uncertainty, enabling the model to capture its operational state more accurately and further reduce warning errors. The results of the robustness evaluation are summarized in Table 3.

Table 3.

Results of robustness evaluation.

Robustness analysis dimension	Test scenarios	Warning error
External environment changes	Influenza outbreak	0.004
	COVID-19 pandemic	0.006
	Endemic infectious disease	0.005
Noise data evaluation	Normal conditions	0.004
	Supply chain disruption	0.007
	Abnormal fluctuations	0.008
Strategy adjustment robustness	Original strategy	0.006
	Resource reallocation	0.005
	Optimized emergency response	0.004

In addition, the model’s accuracy, recall, and F1 score are compared across different scenarios, with the results shown in Fig. 9.

Fig. 9.

Accuracy Results of the Model in Different Scenarios.

Figure 9 illustrates the model’s performance across various scenarios. The results show that the model performs exceptionally well in cases involving influenza outbreaks and endemic diseases, achieving accuracy rates of 0.95 and 0.94, respectively, with F1 scores close to 0.93. These findings highlight the model’s ability to effectively identify and predict risks associated with these relatively familiar public health events, demonstrating strong adaptability and stability. For the COVID-19 pandemic, the accuracy and recall rates are slightly lower at 0.92 and 0.90, respectively. However, an F1 score of 0.91 indicates that the model remains reliable in managing complex public health events. The slight decline in performance is likely due to the higher data requirements and complexity associated with the COVID-19 pandemic. When evaluating the impact of noise data, such as supply chain disruptions and abnormal fluctuations, the model achieves accuracy rates of 0.90 and 0.88, with recall rates of 0.88 and 0.85, respectively. F1 scores, however, drop below 0.86 in these scenarios. While this suggests that the model retains a reasonable level of predictive capability under uncertainty and emergencies, its performance is relatively weaker when faced with substantial noise. In scenarios involving strategic adjustments, the model demonstrates consistent performance. Notably, after implementing optimized emergency response strategies, both accuracy and F1 scores improve significantly, reaching 0.95 and 0.94, respectively. These results indicate that optimized strategies enhance the model’s effectiveness in predicting and managing risks during public health emergencies.

Table 4 compares the performance of the proposed model, which integrates fuzzy theory with the BPNN algorithm, against other algorithms (LSTM, standalone BPNN, and the model by Aljohani (2023)) in terms of accuracy, recall, F1 score, and prediction time.

Table 4.

Comparison of Accuracy and Efficiency of this Model Algorithm and other Model algorithms.

Model type	Accuracy	Recall	F1 score	Prediction time (s)
Proposed model (Fuzzy Theory + BPNN)	0.95	0.92	0.93	3
Aljohani (2023)	0.9	0.85	0.88	12
LSTM	0.88	0.8	0.84	15
BPNN	0.85	0.78	0.81	10

As shown in Table 4, the proposed model delivers superior performance across all evaluation metrics. With an accuracy of 0.95, recall of 0.92, and an F1 score of 0.93, the model outperforms its counterparts in predicting supply chain risks. Furthermore, its prediction time of just 3 s significantly outpaces the other models, demonstrating exceptional efficiency. The model by Aljohani (2023), while achieving commendable results with an accuracy of 0.90, recall of 0.85, and F1 score of 0.88, is hindered by a longer prediction time of 12 s. Similarly, the LSTM and standalone BPNN models display comparatively lower accuracy and recall, coupled with prediction times of 15 s and 10 s, respectively. In summary, the proposed model stands out as the most effective solution for predicting supply chain risks, offering a superior combination of accuracy, recall, and efficiency. Its significantly faster prediction speed is particularly advantageous for supply chain management scenarios that demand rapid responses, such as those occurring during public health emergencies. This demonstrates the practicality and robustness of the proposed approach in real-world applications.

Validation of model effectiveness

The data used for model validation primarily originate from historical records of past PHEs, including material demand and supply data during epidemic outbreaks, records of logistics disruptions, and operational conditions of various supply chain components. Overall, the model demonstrates strong stability and adaptability across multiple public health crises and varying data conditions, highlighting its high practical value. Specifically, the data on material demands and supply during epidemic outbreaks are sourced from reports by national public health departments and the WHO. These datasets include medical supply needs, supply chain conditions, and logistics flow information from events such as the SARS outbreak in 2003, the H1N1 flu pandemic in 2009, and the COVID-19 pandemic in 2020. Records of logistics disruptions are obtained from logistics service providers and local governments, covering transport delays, supply interruptions, and distribution obstacles observed during these emergencies. Data on the operational conditions of supply chain components are primarily derived from industry reports and academic studies conducted in collaboration with various supply chain enterprises. These reports provide insights into supplier management practices, inventory levels, and demand forecasting processes. In terms of data handling, privacy and confidentiality are prioritized. The datasets used for validation have been anonymized to ensure the confidentiality of participants and communities. Personal identifiable information (PII) has been removed or encrypted, and access to raw data is restricted to authorized personnel only. Data analysis and presentation follow the principle of minimizing identification risks, ensuring that no participant’s privacy is compromised in any way. This dataset plays a crucial role in evaluating the performance of the PHEs supply chain risk warning system, which integrates fuzzy theory and the BPNN algorithm, under similar circumstances. The study aims to improve public health emergency response systems without causing any harm or inconvenience to participants.

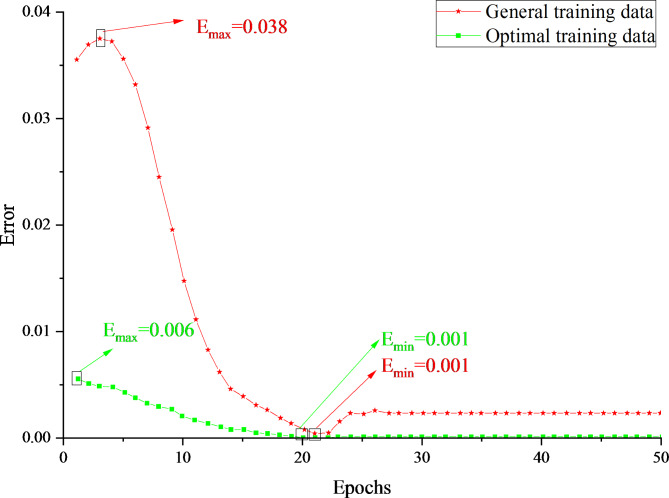
Through multiple experiments involving fuzzy reasoning training, the initial early warning errors are compared with the optimized data obtained after training. The results of these comparisons are presented in Fig. 10.

Fig. 10.

Comparison of fuzzy reasoning training.

Figure 10 illustrates the significant fluctuations observed in the early warning training data before stabilization. Initially, after reaching a minimum error value, the error trend rises and becomes unstable. However, with extensive training and optimization, the error value in the optimal training scenario is minimized to 0.001. Once this minimum is achieved, the error curve stabilizes and remains steady, indicating effective early warning performance. These results demonstrate the model’s potential to significantly enhance the efficiency of urban collaborative governance and emergency SCM in practical applications. For instance, during the initial stages of an epidemic, the model can analyze historical and real-time data to predict potential risks of supply chain disruptions, providing accurate and timely warnings. This predictive capability allows relevant departments to optimize resource allocation and manage emergency response schedules effectively, ensuring the timely supply and distribution of essential materials.

A practical implementation of this method is demonstrated in a city that successfully allocated medical supplies during an epidemic, effectively preventing shortages. During the early stages of the pandemic, the model is employed to predict demand for medical supplies by analyzing historical epidemic data, real-time demand forecasts, and current inventory levels. The model’s input layer processed demand data for items such as masks, protective clothing, and disinfectants—resources that typically show significant fluctuations during peak flu seasons. Through fuzzy reasoning training, the model identified key factors affecting material demand and optimized the early warning system. The hidden layer’s four neurons captured the complex nonlinear relationships in the data, while the output layer provided predictions of economic, social, and environmental benefits. The implementation of the model resulted in significant improvements in the accuracy of warnings, as summarized in Table 5.

Table 5.

Model validation results in the case study.

Key indicators	Predicted value	Actual value	Error value	Accuracy
Mask demand	10,000	9558	558	95.6%
Protective clothing demand	5000	4822	178	96.4%
Disinfectant demand	2000	2081	81	95.95%
Number of shipping delays	3	4	1	66.7%
Number of distribution bottlenecks	2	3	1	50%

According to the results in Table 5, the model achieves high accuracy rates in predicting the demand for masks, protective suits, and disinfectants, with rates of 95.6%, 96.4%, and 95.95%, respectively. These results demonstrate the model’s ability to effectively identify and predict actual demand for medical supplies, significantly reducing prediction errors. This case underscores the effectiveness of integrating fuzzy theory with the BPNN algorithm in emergency management, enhancing urban emergency capabilities and optimizing SCM efficiency. The model’s predictive and responsive capabilities highlight the critical role of data-driven decision support systems in ensuring the timeliness and accuracy of resource allocation during PHEs. Implementing the proposed model presents several challenges, such as ensuring data completeness and timeliness and addressing regional variations in material demands. To address these challenges, the model must integrate multi-source data and employ advanced data preprocessing techniques to ensure the quality and consistency of input data. Additionally, parameter adjustments tailored to specific regional needs and cultural contexts are crucial for enhancing the model’s adaptability. In terms of scalability, research indicates that while the model performs well within certain regions or cultural contexts, its effectiveness across diverse geographical or cultural settings may be limited. To enhance its universality, future iterations could incorporate a broader range of data sources and predictive methodologies, such as AI and big data analytics, to improve overall performance and applicability. The model’s design should prioritize flexibility and adaptability, allowing for dynamic modifications to align with the unique requirements of various regions. By adopting this approach, the model can effectively address localized supply chain risks while providing comprehensive risk warning and management capabilities on a global scale. This dual focus ensures both targeted efficiency and broader applicability, enhancing the model’s utility in managing complex and dynamic supply chain environments.

PHE events are classified into four levels based on their nature, severity, and scope: Level A (particularly significant), Level B (significant), Level C (large), and Level D (general). The emergency supply chain response level aligns with these classifications and corresponds to national emergency management response levels. Table 6 outlines the specific operational protocols for each level.

Table 6.

Operational protocols for different response levels in emergency supply chains.

Response level	Level A	Level B	Level C	Level D
Scope	Nationwide	Provincial	Municipal	Municipal
People mobilized	All	Part	Part	Part
Reserve strength	Central enterprises	Local enterprises	General enterprises	General enterprises
Mobilization budget	Large	Relatively large	General	Less

The operational protocols for the emergency supply chain at different response levels include several key aspects: (1) the scope of response, which can range from nationwide to provincial or municipal levels; (2) the participants involved in the response, which may include all members or only selected ones; (3) the classification of reserves, such as central, local, or enterprise reserves; and (4) the emergency budget, which is adjusted according to the response level. To effectively address the classification of events at different levels, the following steps and methods are proposed to ensure the response mechanism’s effectiveness and practicality. First, clear criteria should be established for event categorization and scale assessment. These criteria should be based on multiple dimensions, including the nature of the event, transmission speed, impact range, and potential risks. For instance, the nature of the event can be classified by evaluating the pathogenicity of the pathogen, modes of transmission, and the number of infections. Transmission speed can be measured by the number of new cases per unit of time. The impact range can be assessed through data on case distribution and the consumption of medical resources. The specific indicators for each dimension should be developed in collaboration with professional public health institutions to ensure the standards are scientific and authoritative. Second, emergency response agencies should establish a multi-channel data collection mechanism, which should include, but not be limited to, reports from medical institutions, government data, social media, and public feedback. During the data analysis phase, modern tools and techniques, such as machine learning and data mining, should be employed to extract key trends and patterns from large datasets to support decision-making. Real-time analysis of emergency supply chain responses can provide dynamic updates for event classification, allowing the response mechanism to react quickly based on the latest developments in the epidemic. During the emergency response process, all participants at various levels should adhere to pre-established emergency plans. Resource allocation strategies should be promptly adjusted based on classification results and data analysis. For example, in a Level A event, the immediate mobilization of central enterprise reserves is necessary, along with nationwide coordination of medical personnel and supplies as required. In contrast, in a Level D event, local enterprises can self-coordinate with smaller-scale volunteer involvement. By following these steps, the efficiency and flexibility of the emergency supply chain in responding to public health events can be ensured. Adhering to these response-level action plans allows each supply chain member to act promptly and accurately, thereby optimizing emergency outcomes through the most efficient allocation and utilization of resources.

Following the integration of fuzzy theory with the BPNN algorithm, a comparison is made between the results of the BPNN operation and those of the hybrid model to assess any differences in error. Figure 11 illustrates these comparative results:

Fig. 11.

Comparison of error analysis.

Figure 11 demonstrates that when the BPNN model operates independently, significant fluctuations in error values occur. However, after integrating the fuzzy clustering algorithm, the error values decrease substantially and show only minor fluctuations around zero, indicating improved performance. The hybrid model uses the fuzzy clustering algorithm to segment the input data, after which the enhanced BPNN is trained through classification. Due to the increased similarity of data within each cluster, the hybrid model achieves higher accuracy compared to the traditional BPNN model. Additionally, the reduced number of training samples per class, along with their heightened similarity, significantly reduces both training time and complexity. Furthermore, the model effectively detects outliers, which enhances its capability to predict and mitigate risks. In the context of urban collaborative governance and emergency SCM, this model demonstrates the ability to proactively identify potential supply chain disruption risks and accurately predict risk levels. This capability enables relevant departments to optimize resource allocation and dispatch plans, thereby improving the speed and efficiency of emergency responses. For example, during an outbreak, a city can avoid shortages of medical supplies through real-time analysis and early warnings provided by the model, ensuring the timely supply of essential epidemic prevention materials. This significantly improves the overall efficiency and effectiveness of emergency management. These practical applications underscore the value of the early warning model, which integrates fuzzy theory with the BPNN algorithm, in enhancing urban emergency governance and SCM efficiency.

The findings of this study have significant implications for SCM and urban collaborative governance. By integrating fuzzy theory with the BPNN algorithm in the early warning model, this innovative approach enhances the ability to respond to PHEs. In SCM, the model can analyze both historical and real-time data to accurately predict potential risks within the supply chain, greatly improving resource allocation precision and emergency response efficiency. For example, during an epidemic outbreak, the model can quickly adjust material distribution plans based on real-time data, preventing resource shortages and ensuring the timely supply of medical materials. This ability for dynamic optimization and precise scheduling makes SCM more flexible and efficient in responding to sudden public health events. Empirical research demonstrates that the model’s low error rate confirms its effectiveness in practical applications. A lower error rate indicates that the model can provide timely and accurate risk warnings in emergencies, complementing existing theoretical frameworks on supply chain risk management. Specifically, existing literature emphasizes the importance of real-time data analysis and dynamic decision-making, while this study validates the feasibility and effectiveness of this approach through practical cases, demonstrating how to optimize resource allocation in complex and uncertain environments.

In terms of urban collaborative governance, the model’s effectiveness fosters cooperation among various levels of government and related departments. By providing accurate risk warnings and data support, all parties involved can take timely and effective actions, enhancing overall collaborative efficiency in responding to PHEs. Specifically, the model helps relevant departments develop scientifically grounded emergency plans, improving organizational capabilities and response speed during crises. Moreover, it promotes standardization in PHE management and data-driven decision-making, further optimizing urban governance structures and resource allocation strategies.Overall, this study strengthens both the scientific and practical aspects of PHE response and offers robust theoretical support and practical guidance for urban collaborative governance.

Discussion

This study advances research by integrating fuzzy theory with the BPNN algorithm to develop a risk early warning model for PHEs in SCM. The goal is to leverage urban collaborative governance to effectively mobilize social resources during PHE outbreaks, thereby facilitating the resolution of public health challenges. This model provides theoretical guidance for the development and management of emergency supply chain systems during PHE events. The significant fluctuations in training data and the stabilization of the final optimal training error demonstrate that through multiple rounds of training and optimization, the model can achieve effective early warning performance when handling uncertainty and complex data. Specifically, in emergency SCM, the model is capable of accurately identifying potential supply chain disruption risks in the early stages of an epidemic. It provides effective warnings that optimize resource allocation and emergency dispatch, ensuring the timely supply of critical materials. This addresses the central question of the study: how to improve the efficiency and accuracy of emergency supply chain responses. An analysis of the results in Figs. 9 and 10 validates the advantages of the model, which combines fuzzy theory with the BPNN algorithm, in enhancing prediction accuracy and reducing error fluctuations. In Fig. 9, the training error stabilizes at a minimum value of 0.001 after sufficient optimization, demonstrating the model’s robust early warning capabilities in managing complex and dynamic supply chain environments. Figure 10 further shows that by integrating the fuzzy clustering algorithm with the BPNN model, error values are significantly reduced. This indicates that the hybrid model is more accurate than the traditional BPNN model when processing data with similar characteristics, and it also reduces training time and complexity. These results confirm the hypothesis of this study: combining fuzzy theory with the BPNN algorithm can effectively enhance the risk early warning capability and management efficiency of emergency supply chains. Additionally, the study categorizes emergency supply chain responses into four levels and establishes specific operational rules for each level. These rules address response scope, mobilization of personnel, reserve forces, and budgets, providing clear strategies for different levels of emergency situations. This graded response mechanism ensures optimal resource allocation and rapid reactions, aligning with the study’s objective of addressing PHE challenges by optimizing SCM and improving urban collaborative governance efficiency.

Overall, the findings of this study provide robust theoretical support and practical guidance for enhancing emergency management and supply chain operation efficiency. In practical applications, the optimized early warning model offers substantial tools for various stakeholders. For example, government agencies can utilize the model’s real-time risk assessment capabilities to formulate and adjust emergency response plans to tackle the complex challenges posed by PHEs. The government can quickly mobilize national or local resources, optimize the distribution of relief supplies, and ensure that the urgent needs of critical areas and populations are met promptly. For businesses, supply chain operators can use the model to predict potential supply chain disruption risks, adjust production and logistics strategies, and mitigate losses caused by demand fluctuations or supply interruptions. For instance, at the onset of an epidemic, companies can predict material shortages and proactively adjust inventory and supply chains, mitigating the impact of unexpected situations on production operations. Social organizations and non-governmental organizations can use the precise data provided by the model to optimize the efficiency of their relief efforts, ensuring that aid resources are delivered quickly and accurately to where they are most needed. In summary, this study provides effective guidance and tools to enhance emergency response efficiency, ensure stable supply chain operations during PHEs, and support effective urban collaborative governance.

To ensure that the model provides accurate warnings and effective decision support for various PHE scenarios, the following steps should be considered for adjustment and implementation: ① Event Classification and Scale Assessment: Start by categorizing the PHE and assessing its scale and impact. This involves determining the event’s scope (local, regional, or national), severity (e.g., flu outbreak, novel coronavirus pandemic), and its potential impact on the supply chain. ② Data Collection and Analysis: Gather relevant data based on the event’s scale and type, including historical epidemic data, current supply chain information, and resource distribution. This data is crucial for adjusting the model’s input parameters and prediction metrics. ③ Model Parameter Adjustment: Modify the fuzzy theory parameters and the BPNN configuration according to the event’s specific characteristics. For example, in cases with significant demand fluctuations, adjust the fuzzy semantic intervals to enhance prediction accuracy. For events with a broader impact, consider increasing the number of hidden layer nodes in the BPNN model to better handle complex data. ④ Scenario Simulation and Testing: Run simulations of various scenarios to evaluate the model’s performance under different emergency conditions. This includes simulating different types of public health events (e.g., flu outbreaks, coronavirus pandemics) and varying scales of events (e.g., local, national) to assess their impact on the supply chain. ⑤ Result Optimization and Validation: Optimize the model based on the simulation results, focusing on its stability and adaptability to different types and scales of events. Perform multiple validations to ensure that the model can effectively recognize and respond to PHEs in practice. ⑥ Implementation Strategies and Adjustments: Develop specific implementation strategies, including resource allocation and emergency response measures, and adjust them based on real-time conditions. For large-scale epidemics, optimize resource distribution and emergency response strategies to improve efficiency. ⑦ Continuous Monitoring and Feedback: Continuously monitor the model’s prediction performance during the event and provide feedback and adjustments as needed. This ensures that the model can adapt to new changes and challenges, maintaining its effectiveness and accuracy. By following these steps, the model can be better adapted to various scales and types of PHEs, thereby enhancing the responsiveness and efficiency of SCM. These guidelines optimize the model’s practical application, enabling it to provide accurate warnings and decision support during different public health events.

The findings of this study indicate that the proposed model algorithm offers substantial advantages in terms of robustness and adaptability. When applied to various public health events, such as influenza outbreaks and the COVID-19 pandemic, the model demonstrated varying levels of predictive accuracy and responsiveness. For well-understood public health events, such as influenza outbreaks, the model achieved high accuracy, recall, and F1 scores, reflecting its efficiency and reliability in scenarios with established patterns. However, when applied to the more complex and dynamic conditions of a global pandemic like COVID-19, characterized by rapid transmission, widespread impact, and unpredictable resource demands, the model’s predictive accuracy slightly decreased, though it remained high. This variation suggests that while the model performs excellently in both routine and complex events, further optimization may be needed to enhance its performance in extreme or unknown scenarios. These findings highlight the model’s adaptability across different emergency response levels and its ability to manage complex scenarios. Additionally, the model demonstrated robustness in handling public health emergencies, successfully adjusting to data fluctuations and environmental changes. Even when confronted with compromised data integrity or significant demand fluctuations, the model maintained a reasonable level of predictive capability. This combination of adaptability and robustness not only contributes to the theoretical innovation of the model but also affirms its practical applicability in real-world situations.

Although this study provides innovative solutions for SCM during PHEs and urban collaborative governance, several limitations present potential directions for future research. Firstly, the model validation in this study relies on historical data and simulation, which, while demonstrating the model’s effectiveness, may encounter issues such as insufficient or mismatched real-world data, potentially affecting prediction accuracy. Historical data may suffer from selection bias, such as certain key data not being recorded or inadequately reflected. In particular, performance and demand fluctuations in different public health events may not fully capture the complexities and dynamic changes of various scenarios. Therefore, future research should focus on collecting more real-time data through case studies and verifying the model’s effectiveness under dynamically changing environmental conditions to enhance the generalizability of the findings. Secondly, the choice of parameters significantly impacts the model’s optimization and training outcomes. Optimal settings for these parameters may vary depending on the type of event and data characteristics. Future studies could explore more automated and adaptive parameter adjustment methods to enhance the model’s adaptability and stability across diverse scenarios. Additionally, while the model performs reasonably well when handling extreme situations or outliers, there is still room for improvement. In particular, the accuracy and stability of the model may be significantly affected in cases of insufficient data integrity or highly complex demand fluctuations. The risks of overfitting in neural networks and the associated computational costs are also concerns in practical applications, which may limit the model’s general applicability, especially in scenarios with high-frequency data changes. Additionally, the complexity and computational cost of the model present challenges, particularly with the BPNN algorithm when handling large-scale data. The model’s real-time performance and processing capabilities may be constrained in actual applications. Future research should investigate more efficient algorithms and computational techniques to improve the model’s real-time performance and processing capabilities. Finally, given the diversity and complexity of PHEs, future research should explore the integration of additional data sources and predictive methods, such as artificial intelligence and big data analytics, to further enhance the model’s overall performance and applicability. These directions will contribute to improving both the scientific and practical aspects of PHE management, providing more comprehensive and effective support for addressing future public health crises.

Conclusion

This study presents an innovative supply chain risk early warning model that integrates fuzzy theory with the BPNN algorithm, aimed at enhancing emergency management and urban collaborative governance during PHEs. Key findings indicate that the model effectively reduces early warning errors to 0.001, demonstrating superior performance in addressing complex and emergent events. The application of this model not only improves the precision of predicting potential supply chain disruptions but also facilitates the optimal allocation and scheduling of resources during PHEs. These results highlight the model’s high efficacy and practicality in real-world applications, providing robust data support for relevant authorities and optimizing emergency response strategies. To address the increasingly diverse and complex PHE events, it is crucial for governments and social organizations to collaborate on measures that strengthen grassroots response capabilities and leverage social forces in PHE governance. Guiding public engagement, enhancing scientific response attitudes, improving self-protection awareness, reducing panic, and encouraging active participation in PHE responses are essential steps.

While the model proposed in this study offers several advantages, it also presents certain limitations. First, the model’s performance is contingent on the quality and completeness of historical data. Any bias or incompleteness in the data may compromise the accuracy of its predictions. Second, the selection of model parameters may introduce potential biases, particularly in the choice of membership functions and rule settings within fuzzy theory, which could be influenced by subjective judgment. Additionally, the model’s generalizability may be limited by specific geographical, cultural, or economic contexts, potentially restricting its applicability across different regions or cultural backgrounds. Lastly, the model may require further optimization to improve its robustness when handling extreme conditions or outliers.

To address these limitations, future research could explore several avenues. First, to reduce reliance on historical data and enhance real-time response capabilities, methods for integrating real-time data streams—such as social media data and Internet of Things (IoT) sensor data—could be investigated to provide more timely inputs. Second, automated and adaptive parameter adjustment methods could be developed to minimize the model’s dependence on subjective researcher judgment, thereby improving its adaptability across various scenarios. Furthermore, to enhance the model’s generalizability, strategies for cross-regional and cross-cultural validation could be implemented to evaluate and optimize its performance in diverse contexts. Finally, alternative algorithms, such as deep learning or other machine learning techniques, could be explored to improve the model’s ability to handle complex and anomalous data. These research directions will contribute to advancing the scientific rigor and practical applicability of the model, offering more comprehensive and effective support for managing potential public health crises in the future.

Data availability

The datasets used and/or analyzed during the current study are available from the corresponding author Ting Yu on reasonable request via e-mail 13,588@sdjzu.edu.cn.

Author contributions

Ting Yu: Conceptualization, methodology, software, validation, formal analysis, writing—original draft preparation, project administration, funding acquisitionPeidong Sang: investigation, resources, data curation, writing—review and editing, visualization, supervision.

Declarations

Competing interests

The authors declare no competing interests.

Ethics statement

The studies involving human participants were reviewed and approved by School of Management Science and Engineering, Shandong Jianzhu University Ethics Committee (Approval Number: 2022.684421). The participants provided their written informed consent to participate in this study. All methods were performed in accordance with relevant guidelines and regulations.