Abstract
A novel adaptive model-based motion control method for multi-UAV communication relay is proposed, which aims at improving the networks connectivity and the communications performance among a fleet of ground unmanned vehicles. The method addresses the challenge of relay UAVs motion control through joint consideration with unknown multi-user mobility, environmental effects on channel characteristics, unavailable angle-of-arrival data of received signals, and coordination among multiple UAVs. The method consists of two parts: (1) Network connectivity is constructed and communication performance index is defined using the minimum spanning tree in graph theory, which considers both the communication link between ground node and UAV, and the communication link between ground nodes. (2) A multi-UAV motion control strategy is proposed that combines Improved Particle Swarm Optimization (IPSO) and Distributed Nonlinear Model Predictive Control (DNMPC), where the Kalman filter is utilised to estimate future positions of the mobile nodes. Simulation results in both single and complex environments show that the presented method can drive the UAVs to reach or track the optimal relay positions and improve network performance, while demonstrating the benefits of considering the impact of environments on channel characteristics.
Keywords: Relay, Cooperative motion control, Multiple unmanned aerial vehicles, Global message connectivity, Wireless networks, Intelligent optimization
Subject terms: Aerospace engineering, Electrical and electronic engineering
Introduction
Over the past few decades, utilizing collaborative multi-agent to achieve a goal has proven huge advantages in a variety of missions, including disaster response and rescue1, environmental perception and monitoring2, reconnaissance and surveillance3, forest fire prevention4, and more scientific research. A key requirement of multi-agents system is to implement and optimize the of quality communication for information exchange. However, the increasing distance and obstacles such as surrounding terrain and buildings can seriously affect the quality of wireless communication, making it difficult for users to achieve this requirement5.
To resolve this issue, communications relay can be deployed to enhance the transfer of information in the system6. Unmanned Aerial Vehicles (UAVs) which are equipped with wireless communication devices have been considered ideal for achieving this purpose, and the advantages of using UAVs as communication relays include: (1) better relay performance compared with terrestrial or satellite relays7. For example, in contrast with ground-to-ground communication affected by obstacles such as buildings, trees or terrain, power attenuation of the signal in ground-to-air channel can be much smaller; (2) using UAVs as communication relays requires no human intervention and has the advantages of excellent adaptation and robust survivability, particularly in severe conditions8; (3) UAVs can be quickly deployed on demand due to its fast speed and flexible maneuverability.
However, the problem of relay UAVs motion control is closely related to the properties of wireless signal transmission, which is influenced by the environment, and the UAVs themselves have motion constraints, making controlling the motion of multiple UAVs acting as relays very challenging.
There are growing interests in utilising UAVs as relays, and various methods have been proposed to optimize the communication quality of UAVs relay network. Pasandideh et al.9 proposed an improved particle swarm optimization algorithm for the deployment of UAV base stations under natural disasters, aiming to find the minimum number and optimal location for UAV deployment, and achieved good results. Ono et al.10 proposed a changeable-rate relay method so as to establish communication links among multiple ground users when a disaster happened, in which the flight atitude and minimum turning radius of the UAV were analyzed and provided. Oriented to efficiently collecting data from the ground sensors, Mozaffari et al.7developed a framework to optimize the deployments and motion control of relay UAVs. Krijestorac and Hanna11 utilised an approach of deep reinforcement learning to study the deployment problem of connecting the relay UAV to users with unknown locations.
Other researchers have concentrated on utilising UAVs as mobile users’ relays. Zeng et al.12 proposed an iterative algorithm which jointly optimizes transmission power and trajectories of the relay UAVs to maximize throughput in mobile relay systems. Chamseddine et al.13 developed a guidance law for mobile ground units, which uses angle of arrival(AoA) data and received signal strength(RSS) to drive the relay UAVs to the optimal positions without knowing the location of the ground units. Wu et al.14 proposed an adaptive model-based motion control approach for UAV communication relay, aiming at enhancing the communication quality of aerial multi-user systems. Seungkeun and Lun et al.15,16 proposed a relay UAVs motion control method for mobile nodes, aiming at improving the networks connectivity and communications performance among multiple naval vessels. Bor-Yaliniz et al.17 presented a mixed integer nonlinear optimization method for solving three-dimensional positioning problem of relay UAV oriented to ground cellular nodes, and provided a computationally efficient numerical solution to this issue. Ladosz et al.18presented a mixed channel prediction method based on models and learning for trajectory planning of relay UAV under dynamic urban conditions and achieved better performance. Wu and Gao19 proposed a relay UAV motion control framework combining gradient method and least squares estimation, aiming to improve the communication quality of ground multi-user system. El-Emary et al.20 proposed a task scheduling and allocation algorithm for UAV-based MEC systems, which reduced the energy consumption of user equipment during task offloading. Ranjha et al.21 proposed an altered genetic algorithm for UAV-enabled relays in MEC Systems, which can minimize the task completion time and empower ultrareliable and low latency communications. In order to implement URLLC in UAV-enabled MEC Systems, Ranjha et al.22 proposed a fair and efficient trajectory design problem and used an iterative sub-optimal joint fairness and trajectory design algorithm to solve it, reducing the energy consumption of ground IoT devices.
However, the above work either assumes that the user is static, which is unable to be met in majority of UAV-assisted relay applications, as the movement of the agents are usually determined by their tasks; or the channel model is too simplified, which will result in poor network performance after optimization; or the impact of complex environmental areas on wireless channels, such as building density in urban environments, is not considered; or only the communications link between relay UAVs and ground nodes is considered, without considering the communication link between ground nodes.
Particle Swarm Optimization (PSO) algorithm is a swarm intelligence algorithm that simulates the predation behavior of bird flocks. Each particle in the algorithm is a potential solution to the problem, and the optimal solution to the problem is obtained by sharing individual information in the population and iterative search of the particle swarm. However, traditional particle swarm optimization algorithm has the disadvantages of slow overall convergence speed and susceptibility to falling into local optima. To address this issue, Ye et al.23 proposed an improved multi-objective constrained particle swarm optimization algorithm, which improved the fitness function to include multiple constraints and penalty terms, and accelerated the convergence by optimizing the fitness function. Before updating the particle position in each iteration, the Levy flight strategy was integrated, which significantly reduces the risk of falling into local optima without increasing the computational complexity. Prakash et al.24 introduced the sigmoid function to convert the position vector of particles into binary variables, and made corresponding modifications to the update formula for particle positions. They also combined the improved PSO algorithm with the Ant Colony Optimization Algorithm to form a Hybrid Heuristic algorithm, which is used to solve the optimal relay nodes in wireless sensor networks, further accelerating the efficiency of the solution. Bhardwaj et al.25 proposed an improved integer particle swarm optimization algorithm by rounding the position and velocity values of particles, and used this algorithm to iteratively search for the optimal allocation of power values between D2D source node and relay node to maximize the transmission rate of the D2D link.
With this background, this paper proposes a novel relay UAVs motion control method, which drives multiple UAVs to their expected relay positions while considering the motion constraints of the UAVs, in order to maintain network connectivity and achieve optimal communication performance. The main innovations of this article are: (1) Jointly considering unknown multiple users’ mobility, environmental complexity, and the unavailable angle-of-arrival data of received signals. Moreover, simultaneously considering the communication link between relay UAV and ground unmanned vehicle as well as the communication link between ground unmanned vehicles when optimizing the network performance. (2)A novel motion control strategy for multiple relay UAVs serving a fleet of ground unmanned vehicles communication is proposed that combines minimum spanning tree(MST), improved particle swarm optimization (IPSO), and decentralised nonlinear model predictive control(DNMPC). By utilizing the motion estimation of ground unmanned vehicles, the current states of UAVs, and the environmental channel states, the algorithm finds control input sequences within a specific time range, thereby optimizing network connectivity.
This article uses a motion control strategy that combines IPSO and DMNPC to plan relay trajectories for multiple UAVs to enhance the communication connectivity between ground unmanned vehicles in urban environments. DMNPC mainly predicts the states of each UAV in the next few steps under the current control input based on the UAV’s motion equation and the channel model, so as to decide the optimal MST communication topology based on the predicted UAV states, ground node states, and environmental channel states in the next few steps, and it is carried out in a distributed rather than centralized manner; IPSO is responsible for quickly searching for the optimal relay position for the next step near its current position based on the states of each UAV predicted by DMNPC and other information. IPSO is responsible for determining the optimal relay position, while DMNPC provides real-time path tracking control in a dynamic environments, and the combination of the two can quickly adjust the path when the environment changes. The advantage of this combination is that it can not only take advantage of the NMPC algorithm in dealing with complex models and constrained multivariable nonlinear optimization problems, but also take advantage of the parallel processing and fast optimization speed of the IPSO algorithm, and the entire system is optimized and controlled in a distributed manner, which further reduces the calculation time of the overall optimization control of the system, and has strong survivability.
The rest of this article is structured as follows: Sect. 2 explains UAV and ground node model used in this study, as well as some assumptions. Section 3 introduces the realistic channel model and the modeling of global message connectivity(GMC) based on the concept of minimum spanning tree. Section 4 proposes an online deployment and motion control algorithm for multiple relay UAVs based on estimated information to maximize network connectivity. Numerical simulation results under different relay scenarios are presented in Sect. 5, and the results are analyzed. Subsequently, concluding remarks are given in Sect. 6.
System model
The motivation for this work is to utilize the communication relay capabilities of multiple UAVs to expand communications links and improve network performance, mainly for a fleet of ground unmanned vehicles. When ground unmanned vehicles perform tasks in harsh environments lacking satellite communications and are far apart from each other, relay UAVs can provide them with effective communication connections.
Scenario of air-ground relay
Consider an air-to-ground relay network composed of 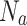 UAVs
UAVs 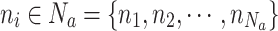 and
and 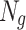 ground unmanned vehicles
ground unmanned vehicles 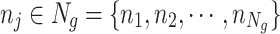 in an urban environment, with ground unmanned vehicles carrying out tasks in the region
in an urban environment, with ground unmanned vehicles carrying out tasks in the region 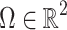 , such as search and rescue. Since the communication between ground unmanned vehicles is easily affected by the surrounding terrain, obstacles, tall buildings, etc., fixed-wing multi-UAVs equipped with higher-performance communication equipment act as relays in the air to provide higher quality communication links between ground unmanned vehicles. It is worth noting that most previous works on UAVs acting as communication relays only considered the communications link between relay UAV and user node. The difference in this work is that it also considers the communication link between user nodes. In other words, this work is to find the best communication network among all available communication links that can maintain all nodes connected.
, such as search and rescue. Since the communication between ground unmanned vehicles is easily affected by the surrounding terrain, obstacles, tall buildings, etc., fixed-wing multi-UAVs equipped with higher-performance communication equipment act as relays in the air to provide higher quality communication links between ground unmanned vehicles. It is worth noting that most previous works on UAVs acting as communication relays only considered the communications link between relay UAV and user node. The difference in this work is that it also considers the communication link between user nodes. In other words, this work is to find the best communication network among all available communication links that can maintain all nodes connected.
The scenario of air-to-ground relay corresponding to this work is illustrated in Fig. 126. The yellow circular dots indicate ground unmanned vehicles, and it is assumed that they are carrying out their own tasks. The cuboid represents buildings of different heights in a city. The red solid line indicates the communication link between relay UAV and ground unmanned vehicle, and the blue solid line represents the communication link between ground unmanned vehicles. The purple solid line indicates the communication link between relay UAVs, while the cyan dashed line indicates the flight trajectories of relay UAVs.
Fig. 1.
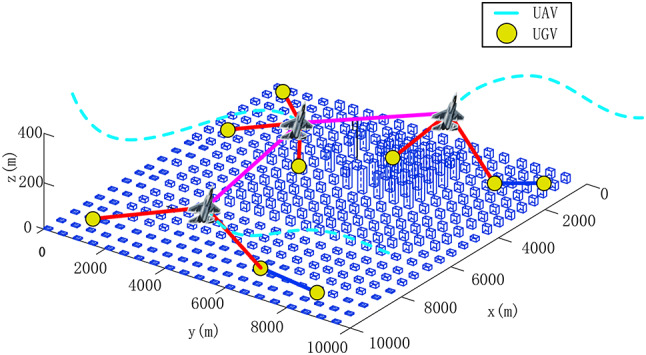
Illustration of air-to-ground relay communication scenario in urban environment.
In addition, compared to rotorcraft, the fixed-wing UAV has a faster speed and wider operating range. However, it has motion constraints such as minimum flight speed and minimum turning radius, etc. This work uses multiple fixed-wing UAVs as communication relays, and these constraints have been considered in subsequent designs.
Relay UAV kinematic model
Assuming that the relay UAVs have a flight controller for heading and speed maintenance function, and this work concentrate on designing guidance inputs for this controller to achieve efficient communication relay. Considering the speed control and turn rate control of the relay UAV, the following kinematic model is used27:
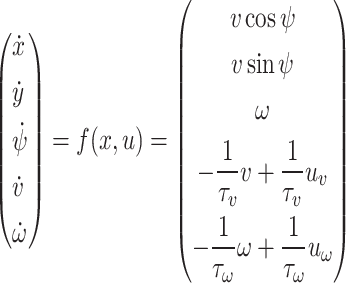 |
1 |
where 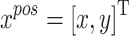 represents the position of the relay UAV,
represents the position of the relay UAV, 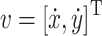 represents the velocity of the relay UAV,
represents the velocity of the relay UAV, 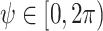 represents the heading angle of the relay UAV,
represents the heading angle of the relay UAV, 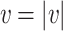 represents the speed, and
represents the speed, and 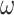 represents the turn rate. Due to the limited dynamic performance of the UAV, for a given flight speed
represents the turn rate. Due to the limited dynamic performance of the UAV, for a given flight speed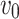 , the maximum turn rate is14:
, the maximum turn rate is14:
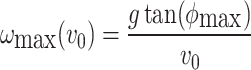 |
2 |
where g represents gravitational acceleration, 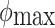 is the maximum bank angle of the relay UAV.
is the maximum bank angle of the relay UAV.
In addition,  and
and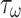 are constants that consider the time delay of the actuator, and can be obtained by analyzing characteristic of the autopilot. The control inputs
are constants that consider the time delay of the actuator, and can be obtained by analyzing characteristic of the autopilot. The control inputs 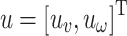 are speed control commands and turn rate control commands respectively, and their values comply with the following constraints15:
are speed control commands and turn rate control commands respectively, and their values comply with the following constraints15:
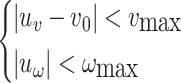 |
3 |
here 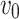 represents the relay UAV’s nominal speed. We can use Euler integration to discretize the UAV continuous kinematic equation represented by Eq. (1) into:
represents the relay UAV’s nominal speed. We can use Euler integration to discretize the UAV continuous kinematic equation represented by Eq. (1) into:
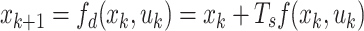 |
4 |
here 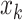 represents the state of relay UAV at time k,
represents the state of relay UAV at time k, 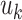 is the control inputs applied to the UAV at time k, and
is the control inputs applied to the UAV at time k, and 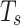 represents the unit step time.
represents the unit step time.
Ground node kinematic model
Referring to [30], a smooth-turning random mobility model is used to characterize the movement of the ground unmanned vehicle. Let 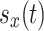 ,
,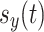 ,
,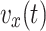 ,
,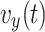 ,
,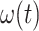 ,
,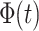 respectively describe the x coordinate, y coordinate, x direction velocity, y direction velocity, turn rate, and heading angle of the ground unmanned vehicle at moment t, and the corresponding mathematical model can be expressed as:
respectively describe the x coordinate, y coordinate, x direction velocity, y direction velocity, turn rate, and heading angle of the ground unmanned vehicle at moment t, and the corresponding mathematical model can be expressed as:
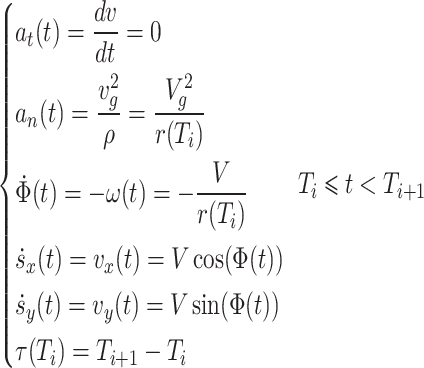 |
5 |
where 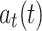 denotes the tangential acceleration of the ground unmanned vehicle,
denotes the tangential acceleration of the ground unmanned vehicle, 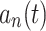 denotes the normal acceleration of the ground unmanned vehicle,
denotes the normal acceleration of the ground unmanned vehicle, 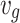 is the speed of the ground unmanned vehicle, and in the smooth-turn random mobility model, it is assumed to be constant, namely
is the speed of the ground unmanned vehicle, and in the smooth-turn random mobility model, it is assumed to be constant, namely 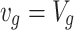 ,
,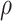 denotes the radius of curvature for curved motion, and
denotes the radius of curvature for curved motion, and 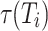 is the interval time.
is the interval time.
Assumptions
(1)The fixed-wing UAVs are assumed to carry out relay missions with a constant speed and fixed altitude, therefore, the control inputs of the relay UAVs is simplified from 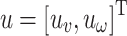 to
to 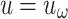 .
.
(2)The movement of ground unmanned vehicles are determined by their own tasks and are neither affected by the network nor by the relay UAVs.
(3)The relay UAVs are assumed to fly at relatively high altitudes without having to consider obstacle avoidance in the air.
Communication network connectivity
In this work, the quality of communication networks is established on the basis of global message connectivity(GMC), which are determined by the cost of information transmission to all nodes. This section first introduces realistic wireless communication models, including air-to-ground channel modelling, ground-to-ground channel modelling, and air-to-air channel modelling. Then, based on the concept of minimum spanning tree, efficient communication network connections are implemented.
Air-to-ground channel model
Most previous studies using UAVs as communication relays have used wireless communication models that only consider communication distance, which are actually oversimplified because using controllers that only consider geographical range will result in degraded communication performance. This work refers to the work of Al-Hourani et al.28,29 and adopts a more realistic wireless communications model between the ground unmanned vehicle nodes and the relay UAVs, in which the impacts of the environments on the probability of Line-of-Sight are reflected.
The radio signal emitted by the relay UAVs is first propagated in free space and then reached the low altitude environment, as shown in Fig. 2. Owing to the impact of terrain, buildings, trees, etc., signals undergoes shadowing and scattering phenomena, leading to extra losses in air-to-ground channel. Thus, the path losses of air-to-ground signal transmission can be modeled as28,29:
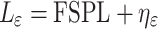 |
6 |
Fig. 2.
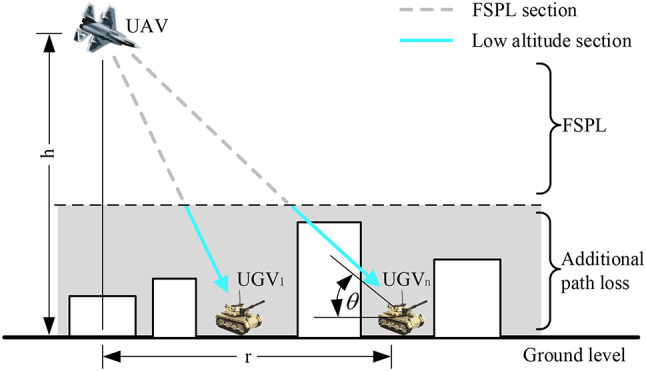
Illustration of relay UAV-ground unmanned vehicle signal transmission.
where 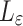 is the propagation losses in air-to-ground channel, in dB,
is the propagation losses in air-to-ground channel, in dB, 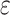 is the propagation group,
is the propagation group, 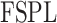 is the free space propagation loss between relay UAV and ground unmanned vehicle, and
is the free space propagation loss between relay UAV and ground unmanned vehicle, and 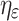 represents the additional loss caused by shadowing, scattering, etc., generally expressed by a Gaussian distribution, and the value of
represents the additional loss caused by shadowing, scattering, etc., generally expressed by a Gaussian distribution, and the value of 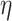 largely depends on the signal propagation group
largely depends on the signal propagation group 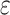 to which it belongs.
to which it belongs.
In order to find the expected value of path losses between relay UAV and ground unmanned vehicle node with an elevation angle of 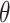 , the following formula can be applied28,29:
, the following formula can be applied28,29:
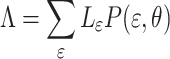 |
7 |
where 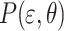 is the probability that the
is the probability that the 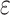 signal propagation group with an elevation angle of
signal propagation group with an elevation angle of 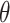 appears,
appears, 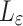 represents the path loss of the
represents the path loss of the 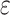 propagation group. This work follows the supposition of two transmission groups28, which in a strict manner corresponds to the Line-of-Sight(LoS) propagation conditions and Non-Line-of-Sight(NLoS) propagation conditions, namely
propagation group. This work follows the supposition of two transmission groups28, which in a strict manner corresponds to the Line-of-Sight(LoS) propagation conditions and Non-Line-of-Sight(NLoS) propagation conditions, namely 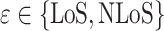 , then
, then
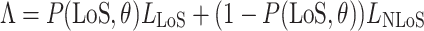 |
8 |
For air-to-ground communication, the 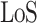 and
and 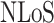 components exist in the following form28,29:
components exist in the following form28,29:
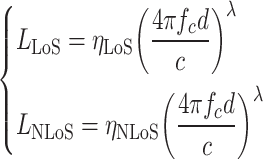 |
9 |
here d represents the distance between relay UAV and ground unmanned vehicle node, 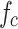 represents the carrier frequency of radio wave, c represents the speed of light wave,
represents the carrier frequency of radio wave, c represents the speed of light wave, 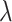 represents the path attenuation factor with a value range of 2–6,
represents the path attenuation factor with a value range of 2–6, 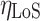 and
and 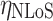 respectively represent the extra path loss of
respectively represent the extra path loss of 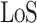 propagation link and
propagation link and 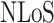 propagation link.
propagation link.
The 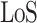 probability is affected by the environment and is a function of the transmitting antenna height
probability is affected by the environment and is a function of the transmitting antenna height 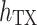 and the receiving antenna height
and the receiving antenna height 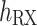 , and is related to the statistical parameters of the environment. In conformity with recommended document of the International Telecommunications Union29, it might be expressed as:
, and is related to the statistical parameters of the environment. In conformity with recommended document of the International Telecommunications Union29, it might be expressed as:
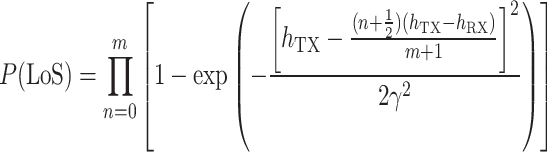 |
10 |
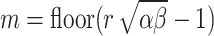 |
11 |
where 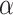 represents the percentage of building land areas to total land areas,
represents the percentage of building land areas to total land areas, 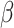 represents the number of buildings per square kilometer,
represents the number of buildings per square kilometer, 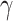 is a proportional parameter describing the height distribution of buildings based on the Rayleigh probability density function, r denotes the ground distance between transmitting antenna and receiving antenna, as illustrated in Fig. 2. Since the receiving antenna height
is a proportional parameter describing the height distribution of buildings based on the Rayleigh probability density function, r denotes the ground distance between transmitting antenna and receiving antenna, as illustrated in Fig. 2. Since the receiving antenna height 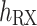 is far lower than height of the buildings and the relay UAVs, it can be ignored, so the ground distance r between relay UAV and ground unmanned vehicle can be formulated as:
is far lower than height of the buildings and the relay UAVs, it can be ignored, so the ground distance r between relay UAV and ground unmanned vehicle can be formulated as:
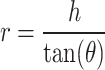 |
12 |
here h represents the altitude of the relay UAV. By fitting the channel attenuation of Eq. (10) in different environments, it can be found that Eq. (10) can be expressed by the Sigmoid function (S-Curve) as29:
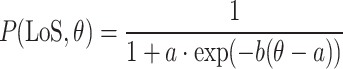 |
13 |
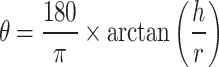 |
14 |
where 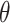 represents the elevation angle between ground unmanned vehicle and relay UAV, as illustrated in Fig. 2; a and b represent the S-Curve parameters. Therefore, the average channel gain g between relay UAV and ground unmanned vehicle can be expressed as:
represents the elevation angle between ground unmanned vehicle and relay UAV, as illustrated in Fig. 2; a and b represent the S-Curve parameters. Therefore, the average channel gain g between relay UAV and ground unmanned vehicle can be expressed as:
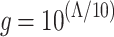 |
15 |
The quality of wireless communications, such as bit error rate, throughput, delay, capacity, etc., are tightly associated with the received signal strength(RSS). This study uses it as a measure of channel performance, which can be given as follows:
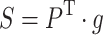 |
16 |
where S is the value of the received signal strength, and 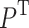 is the transmitting power.
is the transmitting power.
Ground-to-ground channel model
Previous studies on using UAVs as communication relays only considered the single communication link between relay UAV and user node. However, in practical applications, if the communication link quality between two user nodes is good, such as being close and without serious communication obstacles, the UAV only needs to relay and connect one of the two user nodes with other user nodes to form a network, and then connect the adjacent user node. From the above analysis, it can be seen that in the study of only considering a single communication link between relay UAV and user node, the communication topology structure of the relay network remains unchanged; while in the study of simultaneously considering the communication link between relay UAV and user node, as well as the communication link between user nodes, the communication topology of the relay networks is in dynamic changes, and there are essential differences between the two different studies.
The complexity of ground-to-ground signal transmission makes it difficult to accurately model it. This work utilises the following model to characterize the ground-to-ground channel30,31:
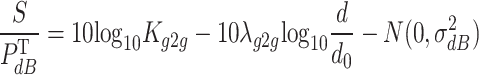 |
17 |
where S represents the received signal strength, 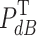 represents the transmitting power, in
represents the transmitting power, in 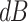 ,
, 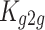 represents the ground-to-ground channel gain, which is a dimensionless constant and is related to the antenna characteristics and the average attenuation characteristics of the channel,
represents the ground-to-ground channel gain, which is a dimensionless constant and is related to the antenna characteristics and the average attenuation characteristics of the channel, 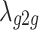 is the path attenuation factor, which is affected by terrain, buildings, etc. in the environments, and typically varies from 2 to 6, d represents the geometric distance between transmitting node and receiving node, and
is the path attenuation factor, which is affected by terrain, buildings, etc. in the environments, and typically varies from 2 to 6, d represents the geometric distance between transmitting node and receiving node, and 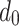 represents the far-field reference distance of the antenna.
represents the far-field reference distance of the antenna.
Observing Eq. (17), we can find that if 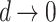 , then
, then 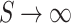 , which is obviously unrealistic, so this model can only be used at large-scale distances, and the minimum value of this distance is called the Fraunhofer distance, denoted as
, which is obviously unrealistic, so this model can only be used at large-scale distances, and the minimum value of this distance is called the Fraunhofer distance, denoted as 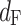 :
:
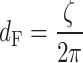 |
18 |
where 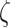 is the wavelength of the signal. When applying Eq. (17), the condition
is the wavelength of the signal. When applying Eq. (17), the condition 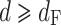 needs to be satisfied.
needs to be satisfied.
It is worth noting that when S is less than a specific threshold, the two users may be considered disconnected, but the entire relay networks in our work are assumed to be linked to each other with a rather robust transmitting power, and concentrates on how to utilize the signal strength S to improve global message connectivity(GMC) as the network evolves.
Air-to-air channel model
Since this article studies multi-UAV relay, there exist air-to-air communication channels in the system. Refering to [33] and [34], the following model is utilised for characterizing the air-to-air channel:
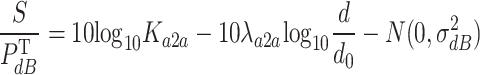 |
19 |
where 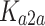 represents the air-to-air channel gain, which is a dimensionless constant and is related to the antenna characteristics and the average attenuation characteristics of the channel,
represents the air-to-air channel gain, which is a dimensionless constant and is related to the antenna characteristics and the average attenuation characteristics of the channel, 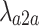 is the path attenuation factor, which is affected by terrain, buildings, etc. in the environment, and generally ranges from 2 to 6, and the remaining parameters are the same as in the ground-to-ground channel model. It is worth noting that the line of sight propagation path usually appears more frequently in the air-to-air channel, therefore, the value of
is the path attenuation factor, which is affected by terrain, buildings, etc. in the environment, and generally ranges from 2 to 6, and the remaining parameters are the same as in the ground-to-ground channel model. It is worth noting that the line of sight propagation path usually appears more frequently in the air-to-air channel, therefore, the value of 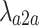 is usually smaller than
is usually smaller than 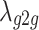 in the ground-to-ground channel model.
in the ground-to-ground channel model.
MST-based network connectivity
As the number of vehicles in the ground unmanned vehicle fleet grows, communication complexity of the relay networks climbs significantly. Therefore, maintaining network connectivity to efficiently transmit information among the fleet can be a difficult problem. Under this circumstances, it is necessary to decide which link ought to be employed to transmit data across the network so as to: (1)make sure all nodes are connected; (2)the communication performance index of the entire network based on global message connectivity(GMC) have been optimized.
In the concept of minimum spanning tree in graph theory, each edge has a different weight, and the different weights of the edges can be used to reflect the signal strength of different communication links. Therefore, from the perspective of edge definition and weight, the minimum spanning tree can be used to construct the communication topology relationship, and the nodes in the graph are also defined as ground nodes and UAV nodes in this article. In addition, the minimum spanning tree is to find the path with the lowest transmission cost from all possible information transmission paths. The purpose of constructing the entire air-to-ground relay system in this article is also to ensure that all nodes in the system can be included in the communication topology and that information can be transmitted among all nodes in the system with the lowest transmission cost. Therefore, the use of the minimum spanning tree in graph theory can enhance the construction of network connectivity for UAVs and ground nodes. An example of the corresponding minimum spanning tree communication topology in this article is shown in Fig. 3.
Fig. 3.
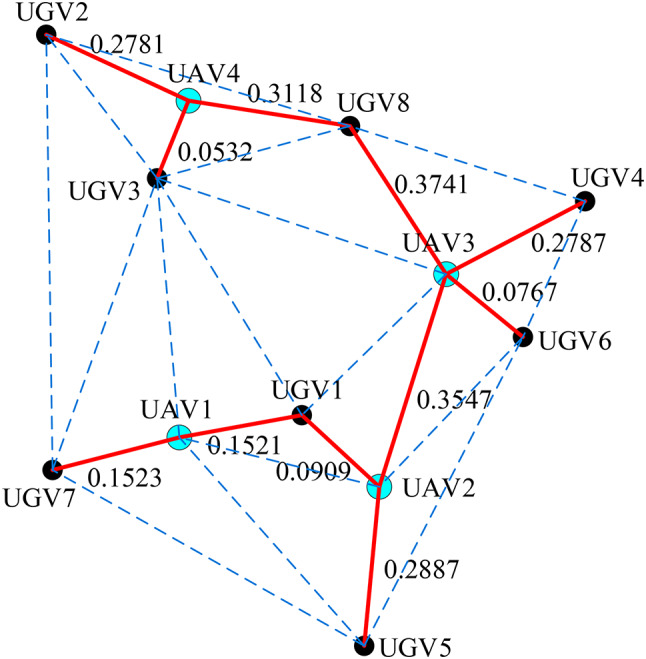
Communication network topology based on minimum spanning tree.
There can be various spanning trees in each graph, which are subgraphs that connect all vertices of the graph. We can calculate the total cost of a specific spanning tree by assigning an appropriate weight to each edge and summing up the weights of all edges. kFinally, MST is determined to be the spanning tree having the the lowest cost32. The edge weight in our work is set as a function of RSS, that is, the weight coefficient of the communication topology graph is designed as:
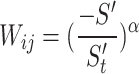 |
20 |
where 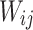 represents the edge weight,
represents the edge weight, 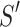 is the
is the 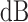 format of the received signal strength S in the above Eq. (16) and Eq. (17), namely
format of the received signal strength S in the above Eq. (16) and Eq. (17), namely 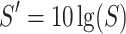 ,
,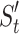 is the baseline received signal strength, which can be determined based on experience and actual needs, and
is the baseline received signal strength, which can be determined based on experience and actual needs, and  is the scaling factor.
is the scaling factor.
From Eq. (20), it can be seen that the weight of an edge is relevant to the received signal strength. The smaller the weight of an edge, the greater signal strength between two nodes, and the more likely information is to be transmitted to all users within the network. In order to discover the MST solution of a graph, multiple polynomial-time algorithm can be used, and the Kruskal algorithm is used in our work.
Motion control of relay UAVs
This work optimizes the communication connectivity and performance of the air-ground relay networks by controlling the motion of multiple relay UAVs. When the fixed-wing UAV equipped with wireless transceivers is flying in the air, it communicates with ground unmanned vehicle nodes and other relay UAVs through a wireless ad-hoc manner. Therefore, the work studied in this article may also involve ad-hoc networks or the domain of Internet of Things(IoT). This section first introduces the optimal deployment strategy of relay UAVs under stationary communication nodes, and then analyzes and designs the optimal motion control strategy of relay UAVs in detail in the scenario of mobile communication nodes.
Optimal deployment for stationary nodes
This work drives the UAVs to their desired relay positions by controlling the motion of multiple relay UAVs, thereby maintaining the communication connectivity of the network and achieving optimal communication performance. Assuming that the relay UAVs maintain a constant altitude and speed, leaving the control inputs of the UAVs as turn rate 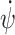 . Therefore, the optimization problem of relay UAVs motion control can be expressed as:
. Therefore, the optimization problem of relay UAVs motion control can be expressed as:
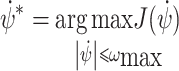 |
21 |
where J represents the objective function of networks performance which reflects the communication quality of data links.
To achieve the aim of finding optimal positions for multi-UAV acting as aerial communications relays among a fleet of stationary ground unmanned vehicles, it is essential to first construct the performance index of the networks connectivity. This work utilises the definition of global message connectivity(GMC), which denotes the cost of successfully transmitting information to all nodes through minimum spanning tree. The lower the cost, the better the quality of relay communication. If the position of relay UAVs and ground unmanned vehicles are known, the minimum spanning tree can be established using 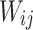 in the above Eq. (20). Let matrix
in the above Eq. (20). Let matrix 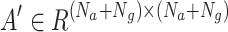 represents the adjacency matrix of the minimum spanning tree under a specific case. If the communication link from node i to node j is part of the minimum spanning tree, then
represents the adjacency matrix of the minimum spanning tree under a specific case. If the communication link from node i to node j is part of the minimum spanning tree, then 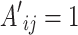 , otherwise,
, otherwise, 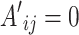 . Since the sum of edge weight in a minimum spanning tree correspond to the total cost of successfully transmitting information to all nodes through this minimum spanning tree(MST), this work defines the performance index of GMC as:
. Since the sum of edge weight in a minimum spanning tree correspond to the total cost of successfully transmitting information to all nodes through this minimum spanning tree(MST), this work defines the performance index of GMC as:
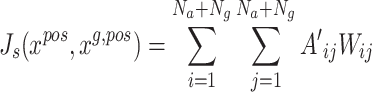 |
22 |
where 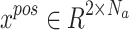 represents the positions of relay UAVs,
represents the positions of relay UAVs, 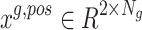 represents the positions of ground unmanned vehicle nodes. The adjacency matrix
represents the positions of ground unmanned vehicle nodes. The adjacency matrix 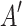 and the edge weight
and the edge weight 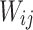 are jointly determined by the positions of relay UAVs, the positions of ground unmanned vehicles, and the channel conditions of the environment. Therefore, the deployment problem of relay UAVs can be expressed as: optimizing the positions
are jointly determined by the positions of relay UAVs, the positions of ground unmanned vehicles, and the channel conditions of the environment. Therefore, the deployment problem of relay UAVs can be expressed as: optimizing the positions 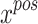 of UAVs to minimize the performance index of GMC, that is:
of UAVs to minimize the performance index of GMC, that is:
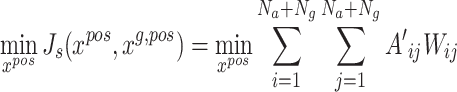 |
23 |
Once the optimal positions are acquired, the UAVs will be deployed to these locations for relaying. Since they are fixed-wing, the UAVs will hover around these points rather than hovering at the optimal relay points33.
Optimal motion control for mobile nodes
Driving multiple relay UAVs to optimal positions so as to continuously provide the best possible communication quality among a fleet of ground unmanned vehicles is a critical and challenging issue that requires excellent motion control of relay UAV. Compared with the deployment of multiple UAVs under stationary nodes, the relay control of UAVs in dynamic environments requires prediction of the motion of ground unmanned vehicle nodes. Therefore, this section first introduces the estimation algorithm for the future positions of ground unmanned vehicle nodes, and then designs an online motion control strategy for relay UAVs under mobile nodes by combining distributed nonlinear model predictive control (DNMPC) and improved particle swarm optimization (IPSO) algorithms.
Kf-based position prediction
The optimal positions of relay UAVs are related to the positions of ground unmanned vehicle nodes, and this section predicts the future positions of ground unmanned vehicle nodes based on Kalman filtering34. The discrete system equation of the ground unmanned vehicle node from time k to time 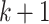 can be formulated as:
can be formulated as:
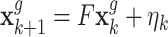 |
24 |
where 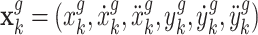 is the states vector of the ground unmanned vehicle node at time k,
is the states vector of the ground unmanned vehicle node at time k, 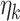 is the process noise, expressed by a Gaussian variable with a mean value of 0 and a covariance matrix of
is the process noise, expressed by a Gaussian variable with a mean value of 0 and a covariance matrix of 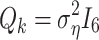 ,
, 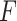 is the state transition matrix:
is the state transition matrix:
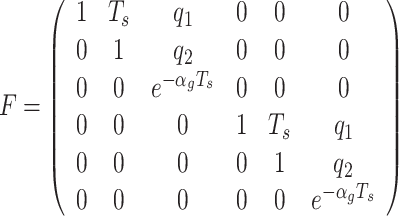 |
25 |
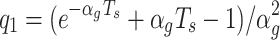 |
26 |
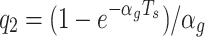 |
27 |
where 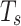 is the time length from time k to time
is the time length from time k to time 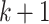 ,
, 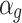 is a parameter used to simulate different types of maneuvering targets, and its value is related to the speed of the mobile object. When the speed is slow,
is a parameter used to simulate different types of maneuvering targets, and its value is related to the speed of the mobile object. When the speed is slow, 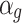 is smaller, and when the speed is fast,
is smaller, and when the speed is fast, 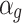 is larger.
is larger.
Assuming that the ground unmanned vehicle can use GPS or other types of sensors to measure its own position, and only requires a small bandwidth to transmit the position information to the UAV, then the noisy position observation of the ground unmanned vehicle node at time k can be given as:
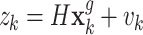 |
28 |
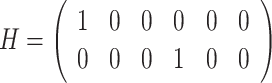 |
29 |
where 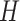 represents the observation matrix,
represents the observation matrix, 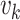 represents the observation noise, expressed by a Gaussian variable with its mean value of 0 and the covariance matrix of
represents the observation noise, expressed by a Gaussian variable with its mean value of 0 and the covariance matrix of 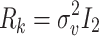 .
.
Prediction
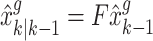 |
30 |
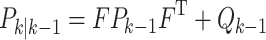 |
31 |
Kalman gains
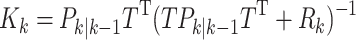 |
32 |
State measurement and covariance matrix
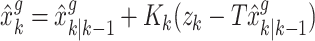 |
33 |
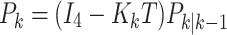 |
34 |
Distributed NMPC and the mechanism of consistency
Offline optimization strategies often have better global optimization performance, but are not flexible or fast enough35. An important feature of nonlinear model predictive control (NMPC) is the implicit determination of control laws by solving constrained optimization problems online. This flexibility and the explicit use of models are the main advantages of NMPC. In view of the multi-variable, multi-constraint, and nonlinear characteristics of UAVs relay communication, the use of nonlinear model predictive control is an effective method for online optimization of the trajectories of relay UAVs in dynamic environments. In addition, since it would be almost impossible to simultaneously optimize the control input sequence for the entire multiple relay UAVs in a centralized manner35, this work uses a completely distributed nonlinear model predictive control strategy.
NMPC usually adopts a receding horizon process to handle dynamic situations, that is, within a certain time horizon, the local optimum is used to replace the global optimum. Suppose the number of receding optimization steps is 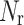 , the current moment is
, the current moment is 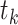 , the sampling period is
, the sampling period is 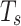 , thus we can express the control input sequence as
, thus we can express the control input sequence as 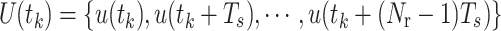 , abbreviated as
, abbreviated as 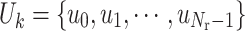 , and the corresponding prediction state sequence is
, and the corresponding prediction state sequence is 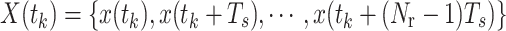 , abbreviated as
, abbreviated as 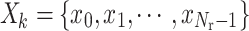 . The optimized communication performance index for the motion control of relay UAVs under mobile communication nodes is:
. The optimized communication performance index for the motion control of relay UAVs under mobile communication nodes is:
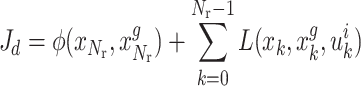 |
35 |
s.t.
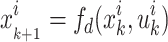 |
36 |
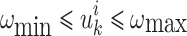 |
37 |
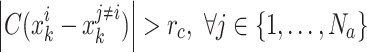 |
38 |
where
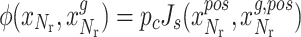 |
39 |
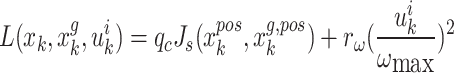 |
40 |
here i represents the i-th relay UAV, 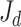 is the performance index of GMC under dynamic environments,
is the performance index of GMC under dynamic environments, 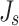 is the performance index of GMC under a stationary environment, as shown in Eq. (22),
is the performance index of GMC under a stationary environment, as shown in Eq. (22), 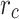 represents the safe distance between relay UAVs for preventing collisions,
represents the safe distance between relay UAVs for preventing collisions, 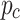 ,
,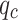 , and
, and 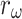 are constant weight coefficients,
are constant weight coefficients, 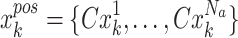 represents the current positions of the relay UAVs,
represents the current positions of the relay UAVs, 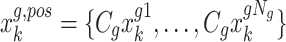 represents the positions of ground unmanned vehicles, which are obtained from the position estimation based on Kalman filtering,
represents the positions of ground unmanned vehicles, which are obtained from the position estimation based on Kalman filtering, 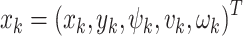 represents the states vector of relay UAV at moment k,
represents the states vector of relay UAV at moment k, 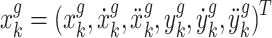 represents the states vector of ground unmanned vehicle node at moment k, C and
represents the states vector of ground unmanned vehicle node at moment k, C and 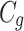 are determined by
are determined by 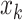 and
and 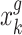 respectively, and the specific values are:
respectively, and the specific values are:
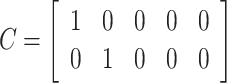 |
41 |
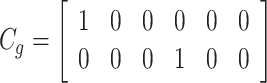 |
42 |
Each relay UAV determines the minimum spanning tree and optimizes its controller in an independent manner based on future states prediction of other relay UAVs, positions estimate of ground unmanned vehicles, and environmental channel conditions. Assuming that the required data is able to be distributed between relay UAVs through communications during one sampling period, depending on the capabilities of the onboard communication devices and the number of relay UAV, the above assumption might be loosened by scaling up the sampling period.
Distributed optimizations are carried out after obtaining control input from prior sampling and shared states of other relay UAVs. If the relay UAVs exchange identical positional data at every time step, the MST solutions obtained by relay UAVs to maintain the entire network connected would be the same36. However, due to communication delays and corruption, the MST of every individual relay UAV can be intermittently different from each other.
The method to address this issue in this work is to communicate the minimum spanning tree structures with each relay UAV’s ID tag within the relay UAVs group, with detailed process shown in Fig. 4, and then selecting the minimum spanning tree with the lowest cost in cases that differences exist between the relay UAVs.
Fig. 4.
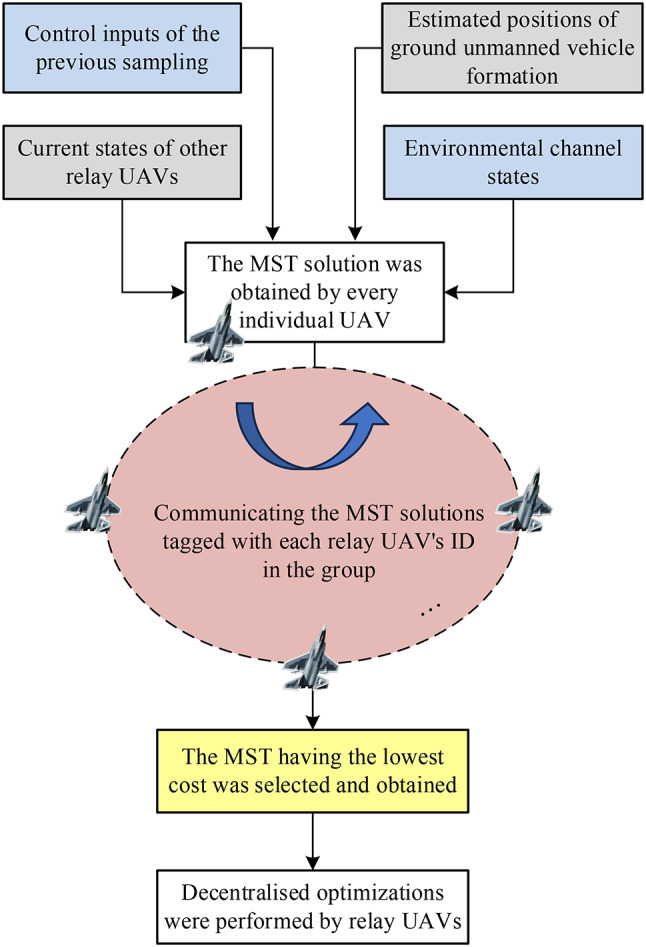
Consistency mechanism in distributed optimizations.
The proposed distributed structure is beneficial compared to a centralized structure, as it not only greatly reduces the computational burden, but also can be seen as more robust in consideration of achiving a successful mission, as even in the event of several relay UAVs failing during the mission, the remaining relay UAVs can continue to perform the communications relay mission.
Improved-PSO
The Particle Swarm Optimization (PSO) algorithm originates from the study of birds foraging behavior. Each particle in this algorithm is a potential solution for the problem, and it utilizes the sharing of individual information in the population and the iterative search of the particle swarm to acquire the optimal solution for the problem. Introducing the particle swarm optimization algorithm into distributed nonlinear model predictive control can further speed up the acquisition of optimal output prediction values for air-ground relay networks.
Suppose the number of particles in the population is q, the dimension of each particle is D, the position of the i-th particle is 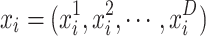 , the speed of the i-th particle is
, the speed of the i-th particle is 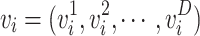 ,
, , the historical optimal positions that the i-th particle passes through are
, the historical optimal positions that the i-th particle passes through are 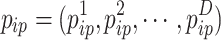 , and the historical optimal positions of the population are
, and the historical optimal positions of the population are 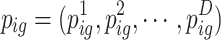 . The update equation of particle position in this work can be expressed as:
. The update equation of particle position in this work can be expressed as:
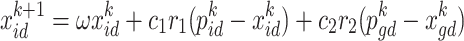 |
43 |
where 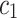 and
and 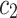 are termed as learning factor,
are termed as learning factor,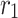 and
and 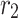 are both random number with their value ranges from 0 to 1,
are both random number with their value ranges from 0 to 1,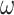 denotes the inertia weight, k denotes the number of iteration,
denotes the inertia weight, k denotes the number of iteration, 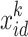 denotes the position of the i-th particle in the d-th dimension at the k-th iteration,
denotes the position of the i-th particle in the d-th dimension at the k-th iteration, 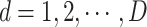 .
.
According to the iterative optimization principle of PSO algorithm in Eq. (43), it can be observed that when the inertia weight 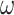 increases, the global optimization ability of the particles will be enhanced, but the search accuracy and local optimization ability will be worse; on the contrary, when the value of inertia weight
increases, the global optimization ability of the particles will be enhanced, but the search accuracy and local optimization ability will be worse; on the contrary, when the value of inertia weight 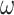 is small, the search accuracy and local optimization ability will be enhanced, but the global optimization ability of the particles will be weakened37. To make the entire algorithm converge faster, the global optimization ability of particles should be strengthened at the beginning of the algorithm iteration, and the local optimization ability and search accuracy of particles should be strengthened in the subsequent stages37. Based on this, this work first adopts the method of nonlinear decreasing inertia weight
is small, the search accuracy and local optimization ability will be enhanced, but the global optimization ability of the particles will be weakened37. To make the entire algorithm converge faster, the global optimization ability of particles should be strengthened at the beginning of the algorithm iteration, and the local optimization ability and search accuracy of particles should be strengthened in the subsequent stages37. Based on this, this work first adopts the method of nonlinear decreasing inertia weight 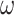 to improve the classic PSO algorithm, specifically:
to improve the classic PSO algorithm, specifically:
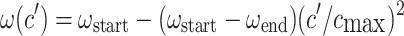 |
44 |
where 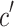 represents the current number of iteration, when
represents the current number of iteration, when 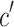 is small, the inertia weight
is small, the inertia weight 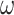 is larger, and when
is larger, and when 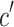 is large, the inertia weight
is large, the inertia weight 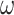 is smaller, and
is smaller, and 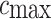 represents the maximum number of iteration.
represents the maximum number of iteration.
Moreover, in view of the gradual convergence of particle positions in later stage of iterative evolution of the PSO method, which leads to slow convergence of the optimization and falling into local extremum at such time, this work introduces the extremum perturbation operators38 and adjusts the individual extremum 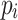 and population extremum
and population extremum 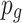 in the population through the random perturbation generated by them, thereby generating a new search direction. The extremum perturbation operators are:
in the population through the random perturbation generated by them, thereby generating a new search direction. The extremum perturbation operators are:
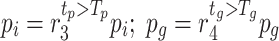 |
45 |
where 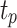 and
and 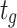 are the number of evolutionary steps at which
are the number of evolutionary steps at which 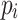 and
and 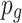 have stalled, respectively,
have stalled, respectively, 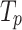 and
and 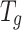 are the step thresholds for
are the step thresholds for 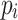 and
and 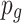 to generate disturbances, respectively,
to generate disturbances, respectively, 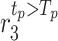 and
and 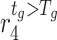 are uniform random functions with conditions and their specific values are:
are uniform random functions with conditions and their specific values are:
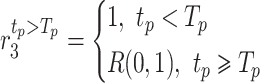 |
46 |
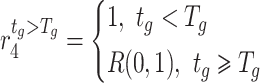 |
47 |
where 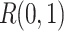 is a random number with its value from 0 ~ 1. Based on the above improvements to the inertia weight
is a random number with its value from 0 ~ 1. Based on the above improvements to the inertia weight 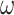 and the introduction of extremum perturbation operators, the update equation of particle positions in the improved-PSO algorithm is transformed into:
and the introduction of extremum perturbation operators, the update equation of particle positions in the improved-PSO algorithm is transformed into:
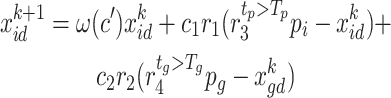 |
48 |
IPSO-DNMPC-based motion control for multiple UAVs
The NMPC algorithm is effective in processing constrained, multi-variable, nonlinear optimization control with complex models, at the cost of a relatively high computation, while the PSO algorithm has the characteristic of parallel processing and fast optimization speed, and, in order to make the PSO algorithm more powerful and further enhance its optimization ability, this work improved the value of the inertia weight 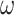 in the previous section, further accelerating the speed of PSO algorithm in optimization, and together introduced the extremum perturbation operators to improve the situation of falling into local extremum.
in the previous section, further accelerating the speed of PSO algorithm in optimization, and together introduced the extremum perturbation operators to improve the situation of falling into local extremum.
Therefore, in the scenario of using multiple relay UAVs to support the communications among a fleet of mobile ground unmanned vehicles, considering the motion of ground unmanned vehicles and the constraints of fixed-wing UAVs, this work proposes an IPSO-DNMPC-based motion control strategy for relay UAVs under dynamic environments. 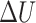 is used as the optimization variable of the IPSO algorithm, and dimension D of each particle in the population is equal to the predicted horizon
is used as the optimization variable of the IPSO algorithm, and dimension D of each particle in the population is equal to the predicted horizon 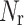 , and Eq. (35) ~ (40) are selected as objective functions for calculating each particle’s fitness. The specific implementation procedures are as follows:
, and Eq. (35) ~ (40) are selected as objective functions for calculating each particle’s fitness. The specific implementation procedures are as follows:
Step1 Obtaining motion state estimations of ground unmanned vehicle nodes by utilizing sensor data and filtering techniques;
Step 2 Based on the predicted positions of ground unmanned vehicles, the current states of other relay UAVs, the control input from previous sampling, and the environmental channel states, each individual UAV obtains an MST solution;
Step 3 Communicating the MST solutions tagged with every relay UAV’s ID within the group, and selecting the minimum spanning tree which has the lowest cost;
Step 4 Based on the lowest-cost MST, each individual UAV iteratively optimizes the objective function using the IPSO algorithm in a completely distributed manner and obtains the optimal control input sequence 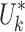 ;
;
Step 5 Executeing the first item of each relay UAV’s optimal control input sequence and updating their respective states;
Step 6 Repeating the above steps until the mission is completed.
The pseudocodes corresponding to the entire optimization process is shown in Table 1, and the motion control flowchart of multiple relay UAVs based on the IPSO-DNMPC algorithm is illustrated in Fig. 5.
Table 1.
Pseudocodes for motion control of relay UAVs.
| Algorithm for motion control of multiple relay UAVs | |
|---|---|
| 1. | Predicting the future position of UGVs 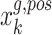 based on KF. based on KF. |
| 2. | Obtaining current states of relay UAVs 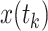 and environmental channel state information and environmental channel state information 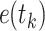 . . |
| 3. | Each individual UAV calculates its own MST solution 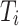 . . |
| 4. | Communicating the MST solutions within the group, so that the MST having the lowest cost is selected, namely 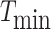 . . |
| 5. | Initializing the parameters, i.e.,the current iteration  . . |
| 6. | Initializing each particle’s position . . |
| 7. | Choose the current optimal input 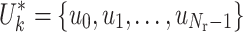 and calculate the corresponding objective function and calculate the corresponding objective function 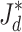 . . |
| 8. |
While
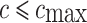
|
| 9. | Update each particle’s position by Eq. (48). |
| 10. | Calculate the corresponding objective function 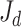 . . |
| 11. |
If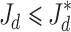 ,then ,then |
| 12. |
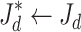 ,and ,and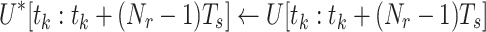
|
| 13. | End if |
| 14. |
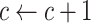
|
| 15. | End while |
| 16. | Return and execute the first item of 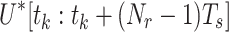 . . |
Fig. 5.
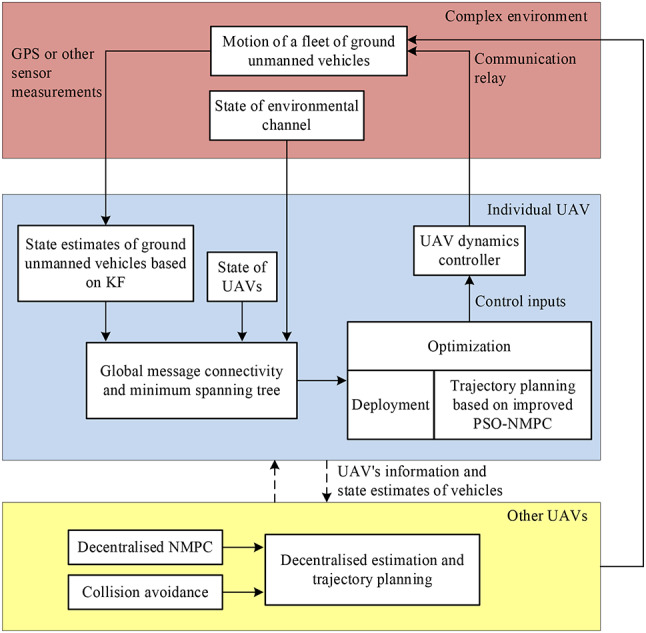
A flowchart of optimal deployment and motion control for multiple UAVs acting as communication relays among a fleet of ground unmanned vehicles.
Simulation and results
Parameters
This section verifies the feasibility of the proposed optimal deployment and motion control method for multiple relay UAVs supporting communications among a fleet of ground unmanned vehicles through simulation experiments. The smooth-turning random motion model39is used to represent the motion of ground unmanned vehicle nodes, and the relay UAVs cannot know the speed and direction of the movement of mobile users, but can only know their positions. The task environments are sorted into four typical types, namely suburban, urban, dense-urban and high-rise-urban areas, with the corresponding channel parameters28,29 shown in Table 2 and coverage range shown in Table 3.
Table 2.
Channel parameter for different areas.
| Channel parameter | Suburban | Urban | DenseUrban | HighRiseUrban |
|---|---|---|---|---|
|
0.1 | 0.3 | 0.5 | 0.5 |
|
750 | 500 | 300 | 300 |
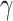
|
8 | 5 | 20 | 50 |
| a | 5.0188 | 9.6101 | 11.9480 | 27.1562 |
| b | 0.3511 | 0.1592 | 0.1359 | 0.1228 |
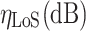
|
0.1 | 1.0 | 1.6 | 2.3 |
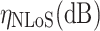
|
21 | 22 | 23 | 34 |
Table 3.
Coverage of various types of areas.
| Environmental areas | Coverage center | Coverage radius (m) | |
|---|---|---|---|
| X(m) | Y(m) | ||
| Suburban | 6000 | 7000 | 9000 |
| Urban | 6490 | 4480 | 3600 |
| DenseUrban | 7000 | 3150 | 2000 |
| HighRiseUrban | 7340 | 2300 | 600 |
The relay UAVs are fixed-wing and have motion constraints, and other parameters used for simulation are shown in Table 4. It should be noted that as the number of ground unmanned vehicles grows, the time it takes to seek the MST solution in the entire relay network increases, thereby increasing the time of the entire optimization process. Meanwhile, the relay UAVs will need higher communications bandwidth to acquire information from all ground unmanned vehicles. Therefore, the maximum number of ground unmanned vehicles that can be covered by the presented approach needs to be determined based on actual computing and communication resources. For situations where there are too many ground unmanned vehicles, clustering can be used to classify them into multiple different clusters, with each cluster assigning several UAVs for relay.
Table 4.
Other simulation parameters.
| Parameter | Value | Unit |
|---|---|---|
Nominal speed of the UAV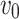
|
40 | m/s |
| Flight altitude h | 400 | m |
Turn rate constraint 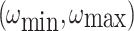
|
(−0.3,0.3) | rad/s |
Minimum turning radius 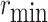
|
133.3 | m |
Safe distance between relay UAV 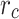
|
50 | m |
Nominal speed of the UGV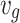
|
10 | m/s |
Scaling factor 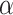
|
10 | N/A |
Baseline received signal strength 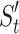
|
−110 | dBm |
Weighting factor 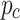
|
1e1 | N/A |
Weighting factor 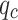
|
2 | N/A |
Weighting factor 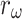
|
1e5 | N/A |
Learning coefficient 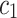
|
3 | N/A |
Learning coefficient 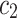
|
3 | N/A |
Sampling time 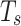
|
0.5 | s |
Receding horizon step 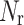
|
5 | N/A |
Air-to-air channel gain 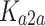
|
1e-6 | N/A |
Path attenuation factor 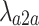
|
3 | N/A |
Ground-to-ground channel gain 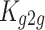
|
1e-6 | N/A |
Path attenuation factor 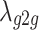
|
5 | N/A |
Far-field reference distance 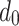
|
200 | m |
Fraunhofer distance 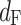
|
500 | m |
In addition, there is a trade-off between the sampling time and the network performance. If the sampling frequency is faster, the communication performance of the relay network will be better. However, NMPC requires a heavier computational load because within a given cycle, number of the receding optimization steps becomes more. Due to the lower movement speed of ground unmanned vehicles compared to aerial relay UAVs, the frequency of guidance commands generated for communication relay is lower than the frequency of relay UAVs’ flight control commands. Based on this, the sampling time used in this work is 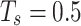 s. However, when the ground unmanned vehicle nodes are moving rapidly, more frequent sampling is needed to ensure the coverage of air-ground relays. In practical applications, the sampling time
s. However, when the ground unmanned vehicle nodes are moving rapidly, more frequent sampling is needed to ensure the coverage of air-ground relays. In practical applications, the sampling time 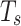 for predictive control ought to be determined according to the number of ground unmanned vehicles and the onboard computing capability of the relay UAVs.
for predictive control ought to be determined according to the number of ground unmanned vehicles and the onboard computing capability of the relay UAVs.
Stationary users
Using relay UAVs to support the communications among stationary ground unmanned vehicles is a simple and common scenario. In Experiment 1, UAVs are used as relays to support the communications among eight stationary ground unmanned vehicles. The positions of ground unmanned vehicles are (6540,4000), (2660,9800), (4340,7600), (10800,7260), (7460,500), (9860,5200), (2760,3300), and (7260,8400), with the unit in m, the transmitting power are 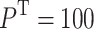 mW, and the signal frequency are
mW, and the signal frequency are 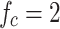 GHz.
GHz.
As shown in Fig. 6(a), eight ground unmanned vehicles are distributed in an area of 12 km x 14 km. The black dashed line in Fig. 6(a) represents all available communication links between ground unmanned vehicle nodes, and the numbers on the line show the cost of each communication link transmitting messages. The lower the cost, the greater the signal strength, and the better the communication quality. The solid blue line in Fig. 6(a) shows the MST structure representing the communication networks topology between eight ground unmanned vehicles when there are no relay UAV. In this example, the cost of GMC is 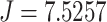 .
.
Fig. 6.
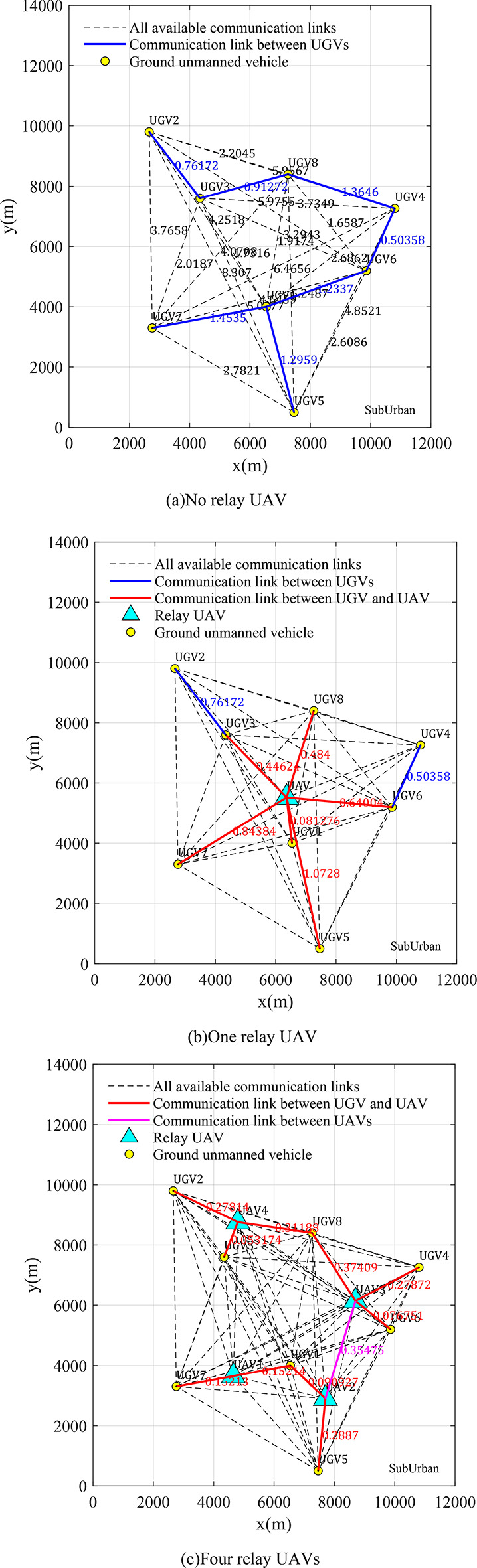
Optimal UAVs deployment results and the minimum spanning tree connections for a fleet of static ground unmanned vehicles. (a) No relay UAV, (b) One relay UAV, (c) Four relay UAVs.
Figure 6(b) illustrates the optimized MST connections and communication cost of using one single realy UAV to serve communications among a fleet of ground unmanned vehicles in the same suburban environment. Among them, the red solid lines represent the air-ground communication links between the relay UAV and the ground unmanned vehicle node, and the blue solid lines represent the ground-ground communication links between the ground unmanned vehicle and the ground unmanned vehicle. By optimizing the optimal relay positions, the cost of GMC becomes 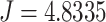 .
.
Comparing Fig. 6(a) and (b), we can see that after deploying one single relay UAV to serve the communications among ground unmanned vehicles, the cost of global message connectivity for the entire network is significantly reduced from 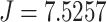 that without relay to
that without relay to 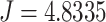 that with one relay. This means that deploying only one single UAV to relay for a fleet of ground unmanned vehicles can improve the communication quality by 56%.
that with one relay. This means that deploying only one single UAV to relay for a fleet of ground unmanned vehicles can improve the communication quality by 56%.
It can be expected that the more UAVs used for relay, the lower the cost of GMC and the better the communication quality of the entire network, as given in Fig. 6(c) and Fig. 7. Nevertheless, as the number of relay UAV grows, the rate of improving global message connectivity cost gradually decreases, as shown in Fig. 7. Further observation of Fig. 7 reveals that the rate of change in global message connectivity cost is related to the transmitting power 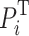 of the nodes. The smaller the transmitting power
of the nodes. The smaller the transmitting power 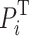 of the communications node, the greater the improvement is able to be achieved by deploying UAVs as communication relays to serve the communications among a fleet of ground unmanned vehicles.
of the communications node, the greater the improvement is able to be achieved by deploying UAVs as communication relays to serve the communications among a fleet of ground unmanned vehicles.
Fig. 7.
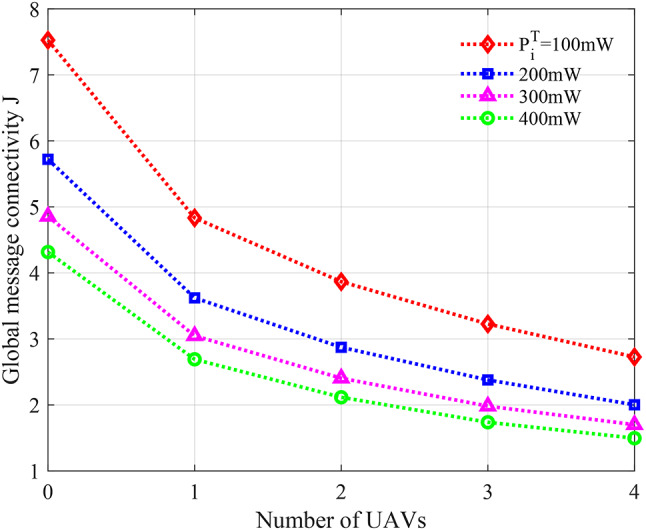
Relationship between the cost of GMC and the number of UAVs.
The comparative experiments in experiment 1 verifies the feasibility and efficiency of the presented optimal deployment and motion control method for relay UAVs under stationary nodes. Next, we will discuss the actual performance of our method under mobile nodes and conduct comparative experimental analysis.
Mobile users
In experiment 2, three UAVs are used as relays to serve the communications among eight mobile ground unmanned vehicles. The motion trajectories of the ground unmanned vehicles are randomly generated based on the smooth turn random mobility model39, with a motion speed of 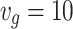 m/s and a transmitting power of
m/s and a transmitting power of 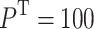 mW for each ground unmanned vehicle. The initial positions of the relay UAVs are (1000,9000), (2000,1000), (11200,6400) respectively, with the unit in m, and a flight speed of
mW for each ground unmanned vehicle. The initial positions of the relay UAVs are (1000,9000), (2000,1000), (11200,6400) respectively, with the unit in m, and a flight speed of 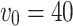 m/s, a expected flying radius of 300 m. The simulation time is set to 1320 s.
m/s, a expected flying radius of 300 m. The simulation time is set to 1320 s.
In order to highlight the relay motion control effect of the approach presented in this work under mobile nodes, the relay UAV motion control strategy based on IPSO-DNMPC algorithm, the relay strategy of UAVs circling around fixed points, and the relay strategy of UAVs’ random motion are separately simulated under the same conditions. The random motion of the UAVs are given by the smooth-turn random mobility model39. The simulation results under different relay strategies are shown in Fig. 8, and the corresponding cost curves of global message connectivity are shown in Fig. 9.
Fig. 8.
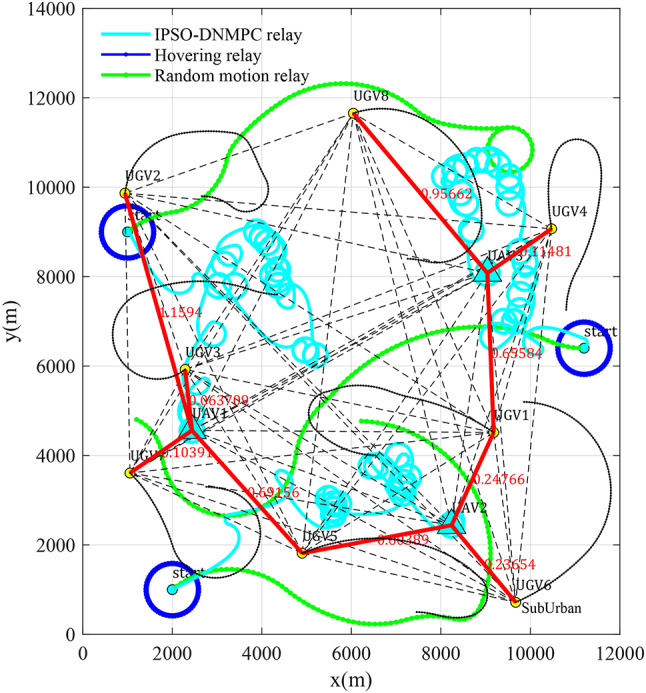
Optimal UAV motion control result and the minimum spanning tree connections using three UAVs for a fleet of mobile ground unmanned vehicles.
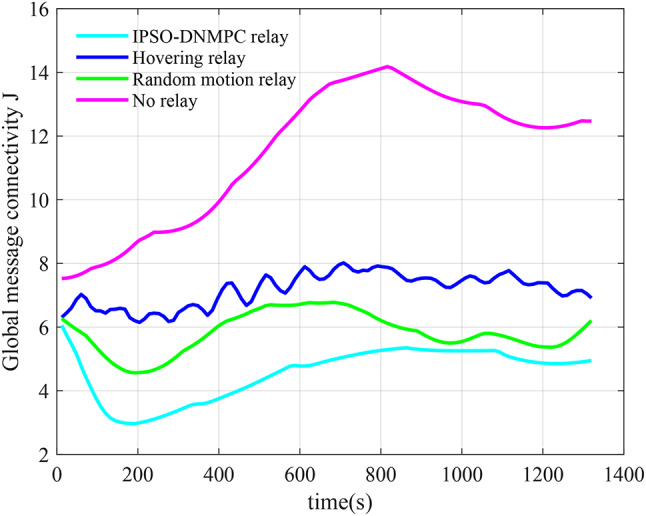
Fig. 9.
Comparison of communication performance under different relay strategies.
Observing the four curves in Fig. 9, we can find that the communication cost in the case of no relay is always at the highest position among the four. Compared with the case of no relay, the global message connectivity cost of the entire network has been significantly reduced in the case of hovering relay and random motion relay. However, for relays based on the IPSO-DNMPC algorithm in this article, the cost of GMC is always at the lowest position, and the control effect of relay communication is the best. For example, at the time of 190s, the global message connectivity cost corresponding to the relay strategy based on the IPSO-DNMPC algorithm is 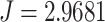 , while at the same time, the global message connectivity costs corresponding to the random motion relay strategy and the hovering relay strategy are
, while at the same time, the global message connectivity costs corresponding to the random motion relay strategy and the hovering relay strategy are 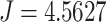 and
and 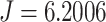 , respectively. Compared to the random motion relay strategy, the communication performance of our algorithm has improved by 53.72%, and compared to the hovering relay strategy, the communication performance of our algorithm has improved by 108.91%.
, respectively. Compared to the random motion relay strategy, the communication performance of our algorithm has improved by 53.72%, and compared to the hovering relay strategy, the communication performance of our algorithm has improved by 108.91%.
In addition, observing the purple curve corresponding to the no-relay case in Fig. 9, we can find that the communication cost among ground unmanned vehicles has experienced a process of first increasing and then declining, indicating that as the ground unmanned vehicle nodes move, the distance between them becomes farther and farther in early stage, and gradually approaches in later stage; Observing the cyan curve corresponding to the relay strategy based on the IPSO-DNMPC algorithm in Fig. 9, we can find that except for 0 ~ 190s, the changing trends of the curve are basically consistent with the changing trends of the curve in the case of no relay. This indicates that the motion control method of relay UAVs proposed in this work can adaptively adjust the positions of relay UAVs according to the motion of ground unmanned vehicle nodes, so as to keep the communication performance of the entire network optimized. And the reason why there is a decline in the 0 ~ 190s stage is that all three relay UAVs start the relay mission from the edge of the mission area, which means that the communication cost of the entire relay network is already relatively high at the initial moment; Finally, observing the green and blue curves corresponding to the random motion relay strategy and the hovering relay strategy in Fig. 9, we can find that the changing trends of the two curves do not follow the changing trends of the curve in the case of no relay, and the fluctuations generated by the two curves are irregular. This is because neither the random motion relay nor the hovering relay adaptively adjusts the motion of the relay UAVs according to the motion of the ground unmanned vehicle nodes.
The comparative results in the above experiment 2 show that the relay UAV motion control approach based on the IPSO-DNMPC algorithm presented in this work can effectively support the communications among a fleet of mobile ground unmanned vehicles. Next, we will discuss the actual effect of our method in controlling relay UAVs to support the communications among a fleet of ground unmanned vehicles under complex and dynamic environments, verify the impact of environments on the channel and relay communication, and focus on the real-time changes in the communication topology of the entire air-ground relay network as vehicles in the fleet enter different types of urban areas.
Real-time changes in communication topology under complex environments
On the basis of experiment 2, in experiment 3, to highlight the effectiveness of the relay UAV motion control method proposed in this work in supporting the communications among a fleet of ground unmanned vehicles under complex and ever-changing urban environments, the task environments are sorted into four typical types, namely suburban, urban, dense-urban and high-rise-urban areas, with the corresponding channel parameters28,29 shown in Table 2 of Sect. 5.1 and coverage range shown in Table 3 of Sect. 5.1. Other experimental parameters remain unchanged compared to experiment 2.
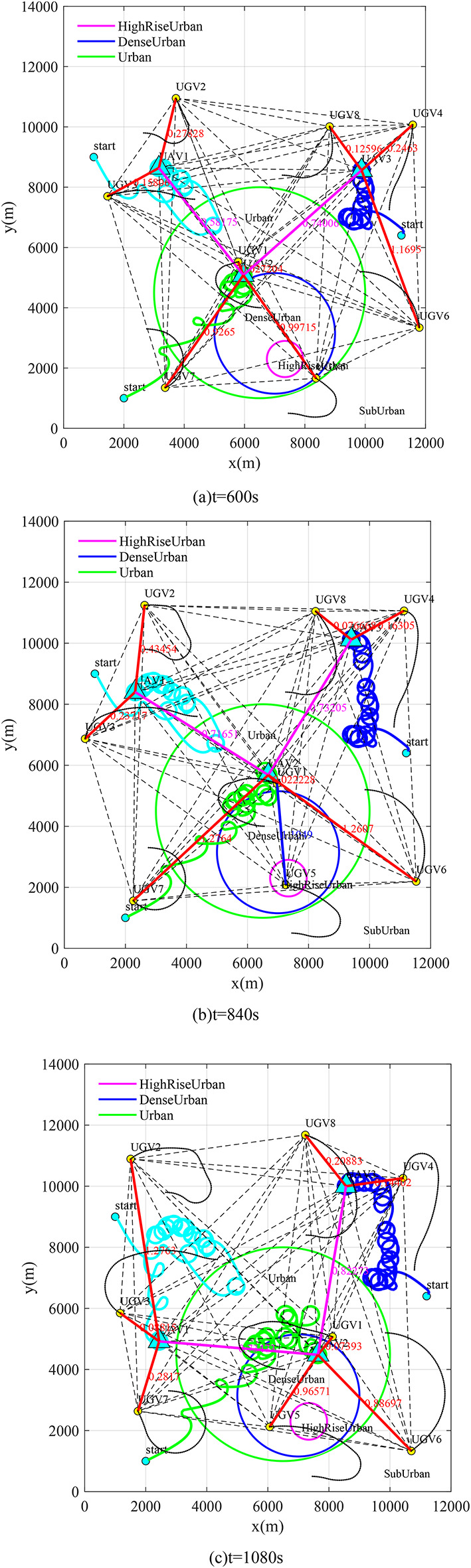
The simulation results of three time moments during the experiment are selected, as given in Fig. 10(a)~(c). In Fig. 10, circles of different colors represent the coverage range for different types of environmental areas. High-rise-urban areas are marked with purple circles, dense-urban areas with blue circles, urban areas with green circles, and the remaining areas classified as suburban.
Fig. 10.
Real-time changes in communication topology under complex environments. (a) t = 600s, (b) t = 840s, (c) t = 1080s.
Observing Fig. 10(a)~(c), it can be seen that as the ground unmanned vehicles moves, they will enter different urban areas at various moments. In Fig. 10(a), the ground unmanned vehicle 5 has not yet entered the high-rise-urban area which has the worst communication conditions. It is noted that there exits a direct communication link between the ground unmanned vehicle 5 and the relay UAV at this moment. However, in Fig. 10(b), the ground unmanned vehicle 5 has already moved to the high-rise-urban area. According to the empirical channel parameter given in Table 2 and the air-to-ground channel models in Eq. (9) and Eq. (13), the communication environment in this area has a low probability of 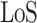 in the channel due to high-density and high-altitude buildings, resulting in a harsh communication environment for users in this area. If it directly establishes a communication link with the relay UAV, the communication quality will be very poor. In Fig. 10(b), the relay UAV has indeed disconnected the direct communication link with the ground unmanned vehicle 5, and instead communicates with the ground unmanned vehicle 5 through the ground unmanned vehicle 1. In Fig. 10(c), the ground unmanned vehicle 5 has left the high-rise-urban area, and the relay UAV has resumed its direct communication link with the ground unmanned vehicle 5.
in the channel due to high-density and high-altitude buildings, resulting in a harsh communication environment for users in this area. If it directly establishes a communication link with the relay UAV, the communication quality will be very poor. In Fig. 10(b), the relay UAV has indeed disconnected the direct communication link with the ground unmanned vehicle 5, and instead communicates with the ground unmanned vehicle 5 through the ground unmanned vehicle 1. In Fig. 10(c), the ground unmanned vehicle 5 has left the high-rise-urban area, and the relay UAV has resumed its direct communication link with the ground unmanned vehicle 5.
This is in line with the above theoretical analysis, which verifies the feasibility of the relay UAV motion control method proposed in this work under complex urban environments, that is, the air-ground relay network can dynamically adjust the communication topology of the network according to changes in environmental channels, and control the UAVs to fly to the relay positions with optimal communication performance while maintaining connectivity throughout the entire network. It also verifies the significance of considering the impact of environments on channel characteristics when designing the motion control method for relay UAVs, which are crucial in practical communication relay missions.
Comparison of relay communication performance under different channel models
Most previous studies using UAVs as communication relays used wireless communication models that only considered communication distance or other oversimplified channel models, resulting in a decrease in communication performance. To reflect the impacts of channel models on relay control results and highlight that the realistic channel model used in this work can achieve better relay communication performance, this experiment 4, based on experiment 3, conducts simulation experiments on three scenarios: relay UAV motion control based on the channel model in this work, relay UAV motion control based on the distance channel model, and no relay. The comparative curves of the cost of global message connectivity are given in Fig. 11.
Fig. 11.
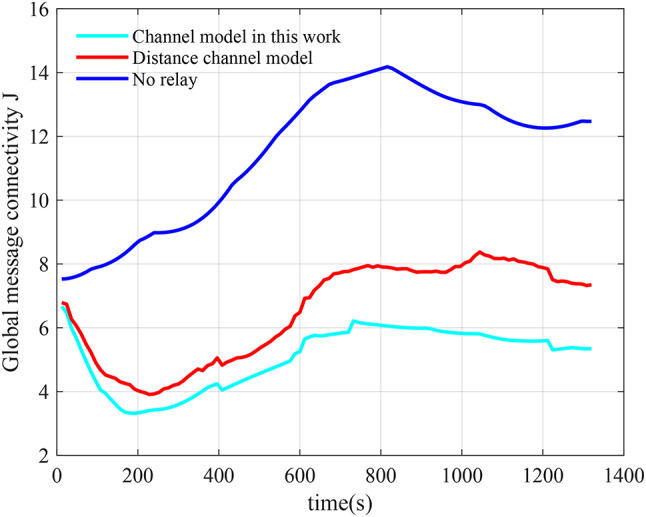
Comparisons of relay communication performance under different channel models.
Observing the three curves in Fig. 11, we can see that the communication cost in the case of no relay is always at the highest position among the three. Compared with the case of no relay, the cost of GMC for the entire network has been significantly reduced in the relay based on the distance channel model. However, the cost of GMC in the air-ground relay communication based on the channel model in this work is always at the lowest position, and the control effect of relay communication is the best.
Comparison of relay communication performance under different motion control algorithms
In order to further verify the feasibility and superiority of the DNNPC-IPSO algorithm proposed in this paper in multi-UAV relay motion control, the improved PSO algorithm proposed by Pasandideh et al.9 is combined with the DNNPC method in this paper and denoted as the DNNPC-IPSO-Pasandideh algorithm; at the same time, the gradient-based relay UAV motion control method proposed by Wu et al.14 is applied to the simulation scenario of this paper and denoted as the gradient-based algorithm. In Experiment 5, based on Experiment 3, simulation experiments are conducted on the three algorithms: gradient-based relay UAV motion control, DMNPC-IPSO-Pasandideh algorithm-based relay UAV motion control, and DMNPC-IPSO algorithm-based relay UAV motion control. The comparison curves of the global message connectivity cost over time are shown in Fig. 12. At the same time, in order to compare the computational time cost of different motion control algorithms, Matlab is used to record and average the calculation time of each optimal relay position during one simulation, and the corresponding table is shown in Table 5.
Fig. 12.
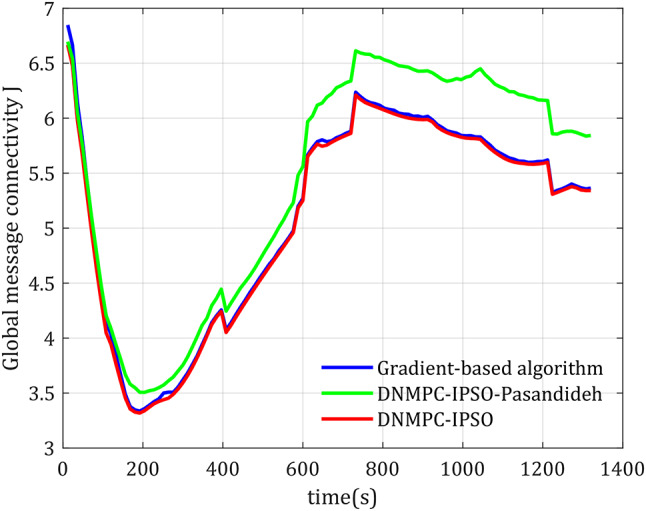
Comparisons of relay communication performance under different motion control algorithms.
Table 5.
Average calculation time for optimal relay position.
| Different algorithms | Average calculation time | Unit |
|---|---|---|
| Gradient-based algorithm | 15.134 | ms |
| DNMPC-IPSO-Pasandideh | 8.795 | ms |
| DNMPC-IPSO | 9.326 | ms |
From Fig. 12; Table 5, it can be seen that the relay UAV motion control algorithm proposed in this paper achieves the best performance; although the relay UAV motion control algorithm based on DMNPC-IPSO-Pasandideh achieves similar communication performance to the method proposed in this paper, its calculation time for the optimal relay position is much higher than that of the method proposed in this paper; and although the gradient-based relay UAV motion control algorithm is slightly better than the method proposed in this paper in terms of calculation time, its realized relay communication performance is poor.
Conclusions
(1) In order to improve the communication connectivity and communication performance of air-ground relay networks, a motion control method for multiple relay UAVs that combines improved particle swarm optimization and distributed nonlinear model predictive control is proposed. Numerical simulation results demonstrate that the proposed motion control method can drive the UAVs to reach or track the motion of the optimal relay positions, and significantly improves the communication quality and connectivity of the networks in both static and dynamic environments.
(2) The cost of global message connectivity is constructed based on the concept of minimum spanning tree in graph theory, which can conveniently and accurately evaluate the communication performance of the relay network. In addition, the network connectivity not only considers the communication link between the UAV and the ground node, but also considers the communication link between the ground node and the ground node, which has more practical application value.
(3) The results of comparative simulation experiments under complex and dynamic environments show that considering the impact of environments on channel characteristics is beneficial and can achieve better network performance under complex urban environments.
Author contributions
Tao. designed the research, processed the data and drafted the manuscript; Liu. helped organize the manuscript and processed the data.
Data availability
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.ALJEHANI, M. INOUE M. Communication and autonomous control of multi-UAV system in disaster response tasks[C]//Agent and Multi-Agent Systems: Technology and Applications: 11th KES International Conference, KES-AMSTA 2017 Vilamoura, Algarve, Portugal, June 2017 Proceedings 11. Springer International Publishing, : 123–132. (2017).
- 2.XU, G. et al. Internet of things in marine environment monitoring: A review[J]. Sensors19 (7), 1711 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.PARK, J. H. et al. Multiple UAVs-based surveillance and reconnaissance system utilizing IoT platform[C]//2019 International conference on electronics, information, and communication (ICEIC). IEEE, : 1–3. (2019).
- 4.HU, J. et al. Fault-tolerant cooperative navigation of networked UAV swarms for forest fire monitoring[J]. Aerosp. Sci. Technol.123, 107494 (2022). [Google Scholar]
- 5.FU, X. & BI, H. GAO X. Multi-UAVs cooperative localization algorithms with communication constraints[J]. Math. Probl. Eng., : 1–8. (2017).
- 6.LI, B. et al. A survey on unmanned aerial vehicle relaying networks[J]. IET Commun.15 (10), 1262–1272 (2021). [Google Scholar]
- 7.MOZAFFARI, M. et al. Mobile unmanned aerial vehicles (UAVs) for energy-efficient Internet of Things communications[J]. IEEE Trans. Wireless Commun.16 (11), 7574–7589 (2017). [Google Scholar]
- 8.WON, J. et al. A survey on UAV placement and trajectory optimization in communication networks: From the perspective of air-to-ground channel models[J] (ICT Ex, 2022). [Google Scholar]
- 9.Pasandideh, F., Rodriguez Cesen, E. & Henrique Morgan Pereira, F. An improved particle swarm optimization algorithm for UAV base station placement[J]. Wireless Pers. Commun.130 (2), 1343–1370 (2023). [Google Scholar]
- 10.ONO, F. & OCHIAI, H. A wireless relay network based on unmanned aircraft system with rate optimization[J]. IEEE Trans. Wireless Commun.15 (11), 7699–7708 (2016). [Google Scholar]
- 11.KRIJESTORAC, E. & HANNA, S. CABRIC D. Uav access point placement for connectivity to a user with unknown location using deep rl[C]//2019 IEEE Globecom Workshops (GC Wkshps). IEEE, : 1–6. (2019).
- 12.ZENG, Y., ZHANG, R. & LIM T, J. Throughput maximization for UAV-enabled mobile relaying systems[J]. IEEE Trans. Commun.64 (12), 4983–4996 (2016). [Google Scholar]
- 13.CHAMSEDDINE, A. et al. Communication relay for multiground units with unmanned aerial vehicle using only signal strength and angle of arrival[J]. IEEE Trans. Control Syst. Technol.25 (1), 286–293 (2017). [Google Scholar]
- 14.WU, G. et al. Mobility control of unmanned aerial vehicle as communication relay in airborne multi-user systems[J]. Chin. J. Aeronaut.32 (6), 1520–1529 (2019). [Google Scholar]
- 15.KIM, S. et al. Coordinated trajectory planning for efficient communication relay using multiple UAVs[J]. Control Eng. Pract.29, 42–49 (2014). [Google Scholar]
- 16.LUN, Y., YAO, P. & WANG, Y. Trajectory optimization of SUAV for marine vessels communication relay mission[J]. IEEE Syst. J.14 (4), 5014–5024 (2020). [Google Scholar]
- 17.BOR-YALINIZ R I, EL-KEYI A, Y. A. N. I. K. O. M. E. R. O. G. L. U. H. Efficient 3-D placement of an aerial base station in next generation cellular networks[C]//2016 IEEE international conference on communications (ICC). IEEE, : 1–5. (2016).
- 18.LADOSZ, P. et al. A hybrid approach of learning and model-based channel prediction for communication relay UAVs in dynamic urban environments[J]. IEEE Rob. Autom. Lett.4 (3), 2370–2377 (2019). [Google Scholar]
- 19.WU, G. & GAO, X. Mobility control of unmanned aerial vehicle as communication relay to optimize ground-to-air uplinks[J]. Sensors20 (8), 2332 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.El-Emary, M. et al. Energy-efficient task offloading and trajectory design for UAV-based MEC systems[C]//2023 19th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob). IEEE, : 274–279. (2023).
- 21.Ranjha, A. et al. Facilitating URLLC vis-á-vis UAV-enabled relaying for MEC systems in 6-G networks[J]. IEEE Trans. Reliab., (2024).
- 22.Ranjha, A., Naboulsi, D. & El-Emary, M. Towards facilitating URLLC in UAV-enabled MEC systems for 6G networks[C]//International Symposium on Ubiquitous Networking. Cham: Springer International Publishing, : 55–67. (2022).
- 23.Ye, F. et al. QoS-Optimized Deployment of Mobile Relay AUVs in Underwater Acoustic Sensor Networks[C]//2024 IEEE 99th Vehicular Technology Conference (VTC2024-Spring). IEEE, : 1–6. (2024).
- 24.Prakash, P. S., Kavitha, D. & Reddy, P. C. Delay-aware relay node selection for cluster-based wireless sensor networks[J]. Measurement: Sens.24, 100403 (2022). [Google Scholar]
- 25.Bhardwaj, P. & VC A R, Prema, C. Performance Analysis of Combined Relay Selection and Power Allocation in Relay Assisted D2D Communications[C]//2023 IEEE 20th India Council International Conference (INDICON). IEEE, : 457–461. (2023).
- 26.LADOSZ, P., OH, H. & CHEN W, H. Optimal positioning of communication relay unmanned aerial vehicles in urban environments[C]//2016 International Conference on Unmanned Aircraft Systems (ICUAS). IEEE, : 1140–1147. (2016).
- 27.WU, J. et al. Distributed trajectory optimization for multiple solar-powered UAVs target tracking in urban environment by Adaptive Grasshopper Optimization Algorithm[J]. Aerosp. Sci. Technol.70, 497–510 (2017). [Google Scholar]
- 28.AL-HOURANI A, KANDEEPAN, S. JAMALIPOUR A. Modeling air-to-ground path loss for low altitude platforms in urban environments[C]//2014 IEEE global communications conference. IEEE, : 2898–2904. (2014).
- 29.AL-HOURANI A, KANDEEPAN, S. Optimal LAP altitude for maximum coverage[J]. IEEE Wirel. Commun. Lett.3 (6), 569–572 (2014). [Google Scholar]
- 30.CHENG, X. & HUANG, Z. Vehicular communication channel measurement, modelling, and application for beyond 5G and 6G[J]. IET Commun.14 (19), 3303–3311 (2020). [Google Scholar]
- 31.BITHAS, P. S. et al. UAV-to-ground communications: Channel modeling and UAV selection[J]. IEEE Trans. Commun.68 (8), 5135–5144 (2020). [Google Scholar]
- 32.POP P C. The generalized minimum spanning tree problem: An overview of formulations, solution procedures and latest advances[J]. Eur. J. Oper. Res.283 (1), 1–15 (2020). [Google Scholar]
- 33.MUSLIMOV T Z & MUNASYPOV R A Multi-UAV cooperative target tracking via consensus-based guidance vector fields and fuzzy MRAC[J]. Aircr. Eng. Aerosp. Technol.93 (7), 1204–1212 (2021). [Google Scholar]
- 34.GUANG, Z. et al. Non-cooperative maneuvering spacecraft tracking via a variable structure estimator[J]. Aerosp. Sci. Technol.79, 352–363 (2018). [Google Scholar]
- 35.Ferranti, L. et al. Distributed nonlinear trajectory optimization for multi-robot motion planning[J]. IEEE Trans. Control Syst. Technol.31 (2), 809–824 (2022). [Google Scholar]
- 36.Jiang, Z. et al. Distributed coordinated control scheme of UAV swarm based on heterogeneous roles[J]. Chin. J. Aeronaut.35 (1), 81–97 (2022). [Google Scholar]
- 37.Liu, W. et al. A novel sigmoid-function-based adaptive weighted particle swarm optimizer[J]. IEEE Trans. cybernetics. 51 (2), 1085–1093 (2019). [DOI] [PubMed] [Google Scholar]
- 38.Liu, H., Zhang, X. W. & Tu, L. P. A modified particle swarm optimization using adaptive strategy[J]. Expert Syst. Appl.152, 113353 (2020). [Google Scholar]
- 39.WAN, Y. et al. A smooth-turn mobility model for airborne networks[J]. IEEE Trans. Veh. Technol.62 (7), 3359–3370 (2013). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.


