Abstract
Collapsible loess soils, known for their significant volume reduction upon the wetting, pose critical challenges in the geotechnical engineering. The estimation of the wetting-induced settlement is crucial for the foundation design and the determination of the negative skin friction on the pile. In this paper, a new method is proposed to estimate the wetting induced collapse from the wetting soil-water characteristic curve (SWCC) and the index properties of the loess soils. In the proposed model, both the water-entry value (WEV) and constant water content suction (ψwc) were adopted for the quantification of the volume change with respect to the reduction in soil suction. The proposed method is verified against the experimental data from published literature. Subsequently, the ground settlement of the loess soil in the inundated condition was calculated by adopting the proposed method and comparing the results with the field measurement data. The results of study indicated that the performance of the proposed method is better than the conventional method in predicting the ground settlement by using the local code in China.
Keywords: Collapsible loess, wetting-induced collapse, soil-water characteristic curve, settlement prediction
Subject terms: Civil engineering, Geology, Sedimentology
Introduction
Loess soils, characterized by their silt-sized particles, are formed through the accumulation of wind-blown dust and are predominantly found in arid and semi-arid regions (Chen et al.1, Sheeler2). Li et al.3 introduced that the loess soils cover approximately 10% of the Earth’s land surface, showcasing a widespread global distribution. Zhao et al.4 indicated that one of the most notable regions with extensive loess deposits is the Loess Plateau in China, which hosts the largest and thickest accumulation of loess in the world. Li et al.5 stated that the unique structure of loess soils, which includes a loose, honeycomb-like metastable configuration, contributed to their high susceptibility to collapse upon wetting, a property that defines their geotechnical significance.
Wang et al.6 and Weng et al.7 indicated that the loess soils presented significant challenges to the geotechnical engineers because of the collapsible nature upon wetting. This characteristic is particularly problematic in construction and urban development, as the sudden and significant volume reduction of loess soils can lead to the failure of foundations and other structures built upon them. In engineering practice, it is important for the geotechnical engineer to have comprehensive understanding of identification, characterization, and mitigation strategies to ensure the stability and integrity of structures in regions with the collapsible loess deposits. Houston et al.8,9and Shao et al.10 explained that the primary mechanism for the volume reduction in loess soils was the breakdown of the soil’s structure upon wetting. Moreover, the moisture-sensitive nature of loess and loess-like soils, with their high porosity, results in a large settlement once the soil becomes saturated. This presents a challenge for the practical engineering such as road construction, shallow foundation, pile foundation in those areas with loess soils. Nguyen et al.11 introduced different methods to improve the mechanical parameters of the soil and minimize the effect of wetting induce collapse of loess soils in engineering practice.
Fredlund and Gan12, Fredlund and Rahardjo13 and Fredlund et al.14 concluded that the the collapsibility of the loess soil could be explained using the principles of unsaturated soil mechanics. Fredlund et al.15 explained that the unsaturated soil structure was strengthened by the suction in soil, which provided apparent cohesion to the soil. However, when these soils were wetted, either naturally or due to human activities, the reduction in matric suction leaded to a decrease of capillary bonding between the soil particles. This process could result in a sudden and significant reduction in the soil volume, commonly referred to as the collapse. Pereira and Fredlund16 explained that the phenomenon of wetting induced could be further understood through the soil-water characteristic curve (SWCC). Zhai and Rahardjo17, Zhai et al.18–20 indicated that the SWCC was pivotal in predicting the hydraulic and mechanical behavior of unsaturated soils. In the context of loess collapsibility, the SWCC helps in understanding how the changes in matric suction influence the water content in soil, which in turn, result in the instability of soil structure.
Despite the advancements in understanding the behaviors of loess soils, there is a research gap persists in accurately predicting the collapse of loess by using the SWCC. The empirical models may not fully capture the exact behaviors of loess soils under different wetting conditions. In addition, the parameters in those empirical models have no physical meaning and different users might adopt different model parameters. It is noted that high variability of determined results might be obtained associated with the empirical models.
The objective of this study is to examine the volume change of loess soils in response to wetting. A new model was proposed to estimate the soil volume change of loess by using wetting SWCC. Subsequently, the ground settlement of loess in inundated condition was estimated by using both proposed method and the method from local code in China. The estimated results from both methods were compared with field measurement data.
Volume change behavior of collapsible loess
Pereira and Fredlund16 developed a comprehensive model to predict the volume change behavior of compacted metastable-structured residual soil during wetting induced collapse. They indicated the three distinct phases of the soil in the wetting process, such as the pre-collapse, collapse, and post-collapse phases. Kato and Kawai21 utilized a modified triaxial test to investigate the deformation characteristics of compacted clay under isotropic and triaxial stress states. The work from Sun et al.22,23 provide significant insights into the collapse behavior of unsaturated compacted soils, particularly focusing on the factors such as the initial densities, stress conditions, and hydraulic conductivity during the wetting induced collapse.
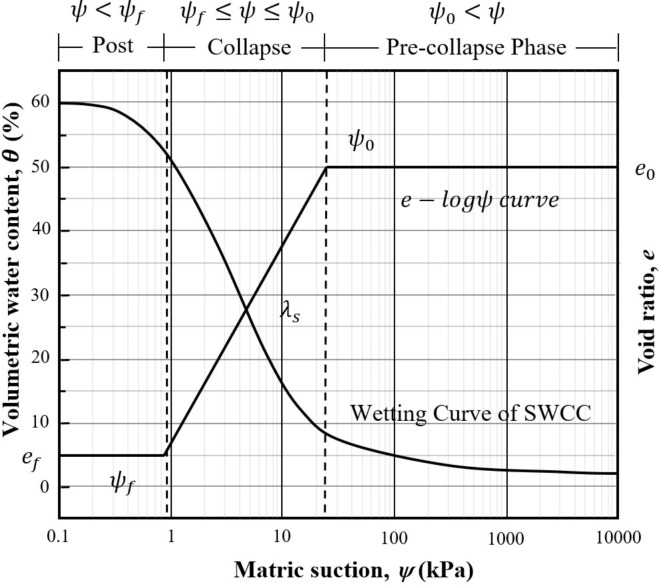
Pereira and Fredlund16 introduced the relationship between matric suction and both the volumetric water content and the void ratio (e) of loess, describing the three phases of soil behavior upon wetting, as illustrated in Fig. 1. On the left side, the wetting SWCC demonstrates transitioning through the pre-collapse, collapse, and post-collapse phases. Meanwhile, the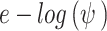 
curve representing the change in void ratio e as matric suction decreases is also illustrated in Fig. 1. In the pre-collapse phase, the soil retains a stable void ratio despite decreasing matric suction, indicating a slight change in the volume. When the matric suction continues to decrease, a significant soil volume changes can be observed which indicates the collapse phase occurs.
Fig. 1.
The phases of loess collapsing and SWCC (modified from Li et al.5)
Hou et al.24 explained that the long-term wetting induced collapse of loess could be estimated by using Eq. (1) as follows:
 |
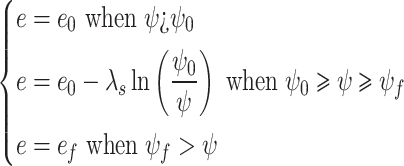1 |
where, ψf denotes the final suction which separates the post and collapse phases; ψ0 denotes the critical suction which separates the collapse and pre-collapse phases;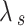 
denotes the rate of volume decrease with decrease in the matric suction; e0 denotes the initial void ratio of the loess before the collapse; and ef denotes the final void ratio after the collapse, as shown in Fig. 1.
It is worthy to note that all those parameters can be determined from the oedometer test and the wetting SWCC. Equation (1) describes the variation of the void ratio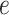 
during the collapse process. As illustrated in both Eq. (1) and Fig. 1, it is important to determine the ψf, and ψ0 for the evaluation of the collapse of soil during the wetting process.
Estimation of critical suction (ψ0)
The estimation of critical suction (ψ0) is a pivotal aspect of understanding the collapse behavior of loess upon wetting. Accurately determining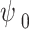 
is essential for predicting collapse potential. Xie et al.25 proposed a method for the estimation of the critical suction value from the water entry value (WEV) of wetting SWCC. Zhang et al.26 measured the SWCCs and 
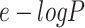curves of compacted loess with various initial void ratios (or initial water contents). They observed that SWCCs were affected by the initial void ratio, suggesting that critical suction would also be influenced by the initial states of soil. Zhai and Rahardjo27 and Zhai et al.28 introduced mathematical method for determination of the residual suction and the air-entry value by replacing the conventional graphical method. It seems that similar approach can be adopted for the estimation of the WEV and constant water content suction (ψwc) of wetting SWCC.
In this paper, Fredlund and Xing29 model, as shown in Eq. (2) is adopted for the representation of the SWCC. The correction factor is set to be equal to 1, as suggested by Leong and Rahardjo30.
 |
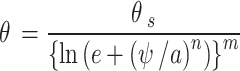2 |
where,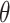 
is the volumetric water content; 
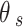is the saturated volumetric water content; 
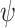is the matric suction; a, n, and m are fitting parameters which are commonly determined from the best fitting the SWCC equation with the experimental data.
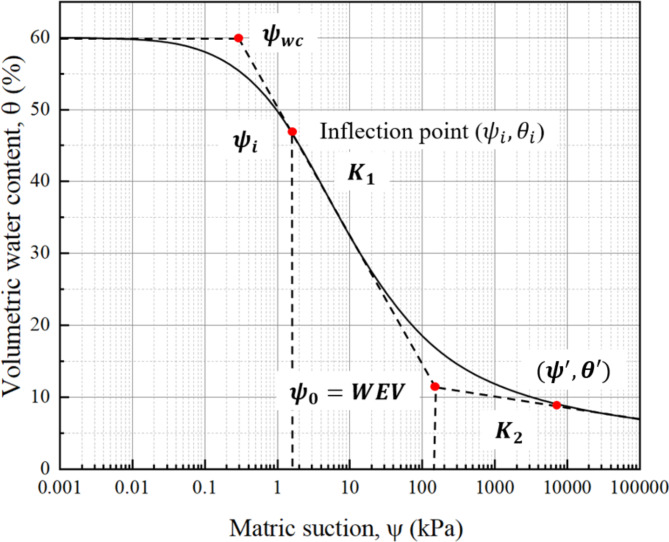
A typical wetting SWCC and the definition of the WEV and ψwc associated with the wetting SWCC was illustrated in Fig. 2. The intersection of the tangent line from the inflection point and a horizontal line from the initial point of wetting SWCC defines the ψwc. Meanwhile, the intersection of the tangent line from the inflection point and the tangent line at the point the curve drops linearly defines the WEV.
Fig. 2.
Variables of wetting SWCC.
The inflection point can be obtained by defining the second derivative,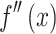 
, to be equaling zero, as illustrated in Eq. (3).
 |
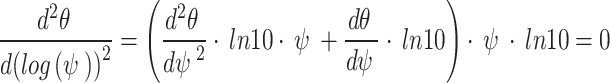3 |
Equation (3) can be simplified as Eq. (4) as follows:
 |
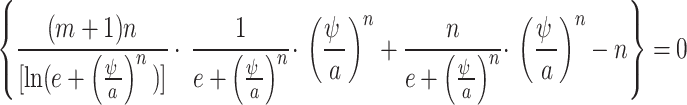4 |
The suction corresponding to the inflection point (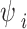
) can be obtained by solving Eq. (4). When 
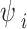is known, the volumetric water content corresponding to the inflection point can be obtained by using Eq. (2).
The slope at any point on the wetting SWCC can be obtained by differentiating Eq. (2) in the log scale as shown in Eq. (5). The slope at the inflection point (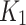
) can be obtained by substituting ψ = ψi into Eq. (5) as shown in Eq. (6).
 |
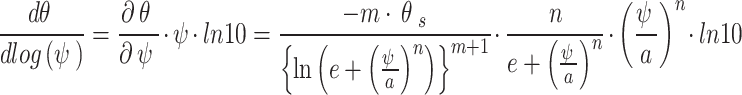5 |
 |
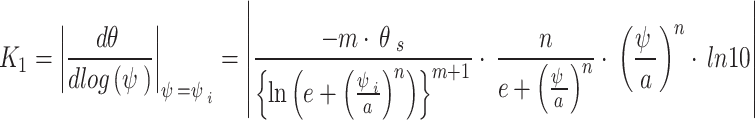6 |
Based on the geometrical relationship as shown in Fig. 2,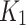 
can also be expressed as follows:
 |
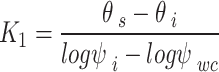7 |
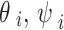is the volumetric water content and matric suction at inflection point respectively. Since 
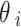can be determined by using Eq. (2) and 
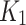can be calculated by using Eq. (7), 
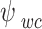can be obtained by using Eq. (8) as follows:
 |
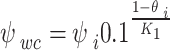8 |
Similar to the determination of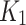 
, the slope at the point which the curve starts to drop linearly (
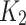) can be obtained by substituting 
into Eq. (5) as shown in Eq. (9) as follows:
 |
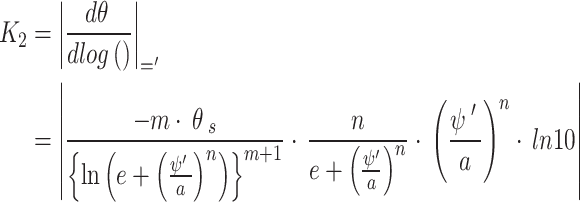9 |
The volumetric water content at the point which the curve starts to drop linearly (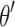
) can be obtained by substituting 
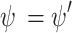into Eq. (2) as follows:
 |
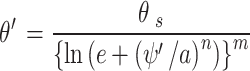10 |
Based on the geometric relationship as shown in Fig. 2, K2 can also be defined by using Eq. (11) as follows,
 |
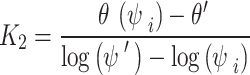11 |
As a result, the WEV can be obtained by using Eq. (12) as follows:
 |
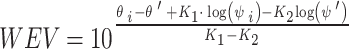12 |
Estimation of the collapse rate (λ)
The collapse rate is an important parameter in understanding the decrease in soil volume in the wetting induced collapse. As shown in Fig. 1, the collapse rate is defined by Eq. (13) as follows:
 |
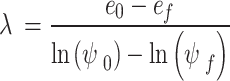13 |
where,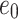 
is the initial void ratio; 
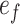is the final void ratio after collapse; 
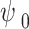is the critical suction (ψ0 = WEV is adopted in this paper), 
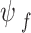is the final suction (ψf = ψwc is adopted in this paper).
The parameter ef, denotes the final void ratio after collapse and can be estimated from the collapse coefficient as shown in Eq. (14).
 |
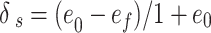14 |
where, δs is the collapse coefficient and e0 is the initial void ratio.
Consequently, the collapse rate λ can be obtained by substituting Eq. (14) into Eq. (13) as follows:
 |
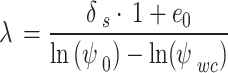15 |
In most the soil investigation report, both the collapse coefficient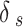 
and the initial void ratio 
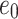were recorded. As a result, the collapse rate can be obtained easily by using Eq. (15) and the experimental data from the soil investigation report.
Validation of the proposed method
There were total nine sets of experimental data, including the compacted clays from Kato and Kawai21, residual soils from Pereira and Fredlund16, and natural loess from Garakani et al.31, collected to verify the WEV determined from Eq. (12). Table 1 illustrates the Fredlund and Xing29’s fitting parameters (a, n and m) for the wetting SWCCs under different net normal stresses (P) and the determined WEVs for the soils from different literature. The calculated WEVs were also compared with the critical suction, ψ0, as interpreted from Xie et al.25.
Table 1.
indicated that the calculated WEV from the method proposed in this paper agreed well with the interpreted ψ0 from Xie et al.25.
| Soil type | P (kPa) | a | n | m |  |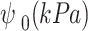
 |
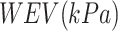References |
|---|---|---|---|---|---|---|---|
| Compacted clay | 20 | 4.02 | 2.47 | 0.284 | 33 | 35.4 | Kato and Kawai21 |
| 98 | 11.77 | 2.24 | 0.312 | 73 | 72.5 | ||
| 196 | 19.71 | 2.84 | 0.26 | 91 | 105.8 | ||
| Residual soil | 50 | 0.99 | 1.33 | 0.48 | 29 | 28.9 | Pereira and Fredlund16 |
| 100 | 2.583 | 2.295 | 0.401 | 33 | 33.0 | ||
| 200 | 2.45 | 1.26 | 0.54 | 92 | 56.8 | ||
| Natural loess | 50 | 24.238 | 1.259 | 0.910 | 100 | 110.6 | Garakani et al.31 |
| 200 | 46.154 | 11.404 | 0.271 | 216 | 86.2 | ||
| 400 | 19.962 | 1.709 | 0.642 | 368 | 348.7 |
Table 1. The fitting parameters of wetting SWCC and the critical suction for the soils.
To verify the reliability of the proposed method for the estimation of the soil volume change due to the wetting induced collapse, the natural loess from Garakani et al.31 was used for the verification. The calculated parameters and SWCC fitting parameters of undisturbed natural loess were shown in Table 2.
Table 2.
The fitting parameters of wetting SWCC and critical suction for the natural loess.
| Soil type |  |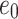
 |
 |
 |
 |
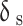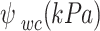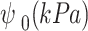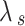fitting parameters in Fredlund and Xing [30] model | ||
|---|---|---|---|---|---|---|---|---|
 |
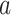n |  |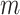
||||||
| Natural Loess | 0.77 | 0.04 | 8.10 | 110 | 0.027 | 1.26 | 0.91 | 0.77 |
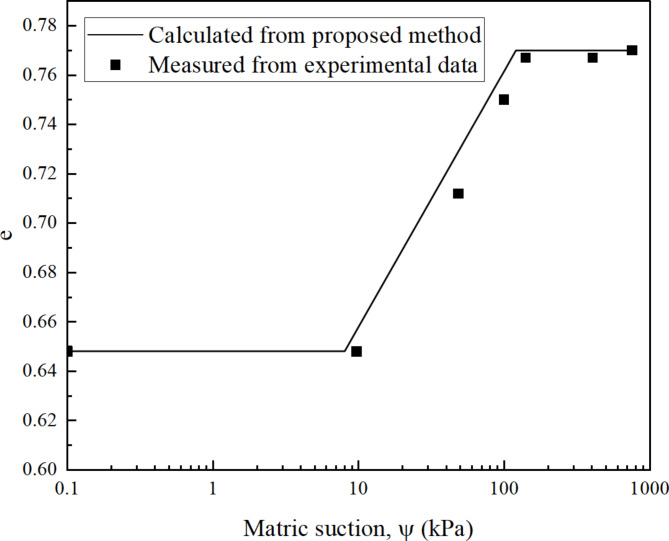
By using the SWCC data from Garakani et al.31, both the critical suction and collapse rate could be determined by using Eqs. (12) and (15), respectively. The computed critical suction equals 110 kPa, and the collapse rate is 0.027. The comparison between the soil volume change from the proposed method and the experimental data was illustrated in Fig. 3. The black line represents the estimated results from the proposed model while the black squares denote the measured data. It shows that estimated results from the proposed model agree well with the experimental data as presented by Garakani et al.31.
Fig. 3.
Validation of the model.
Estimation of ground settlement due to the wetting-induced collapse
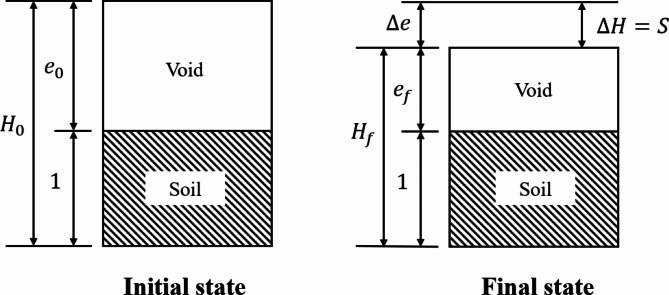
The schematic diagram of soil solid and the void in the soil element at the initial and final state were illustrated in Fig. 4. Upon wetting, the soil layer experiences a change in void ratio, resulting in a final thickness of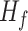 
and a final void ratio of 
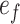. Dealing with a soil profile consisting of multiple layers, the total settlement can be calculated by summation of the settlements of different individual layers. Consider a soil profile with 
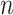layers, each having an initial thickness of 
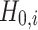, an initial void ratio of 
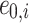, and a final void ratio of 
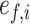(where 
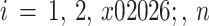). The settlement of each layer can be calculated by using the Eq. (16) as follows:
 |
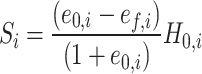16 |
where, e0,i is the initial void ratio of the soil layer i; ef, i is the final void ratio of the soil layer i, which can be determined by using the proposed method in this paper.
Fig. 4.
Illustration of the deformation of the soil element.
As result, the total ground settlement (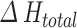
), can be obtained by summation of the compressions of all the soil layers, as shown in Eq. (17):
 |
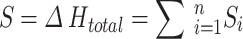17 |
Wang et al.32 excavated a 4 m x 4 m x 30 m test pit and installing monitoring instruments such as an inclinometer tube, settlement plate, and soil moisture sensor at the bottom of the pit. Both the suction profile and the ground settlement during the inundation were monitored in the whole wetting process. To analyze ground settlement of the loess as mentioned in Wang et al.32, the 25 m thick collapsible soil is divided into five sub-layers. The index properties of the soil in each sub-layers are illustrated in Table 3.
Table 3.
The index properties of loess in 5 layers.
| Soil layer | Depth,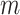 
|
Collapse coefficient | Void ratio | Liquid limit (%) | Plastic limit (%) |
|---|---|---|---|---|---|
| L1 | 5 | 0.126 | 1.061 | 30.0 | 19.8 |
| L2 | 10 | 0.101 | 1.040 | 26.3 | 16.9 |
| L3 | 15 | 0.088 | 1.004 | 29.7 | 18.1 |
| L4 | 20 | 0.036 | 0.924 | 29.5 | 17.6 |
| L5 | 25 | 0.013 | 0.814 | 28.8 | 18.5 |
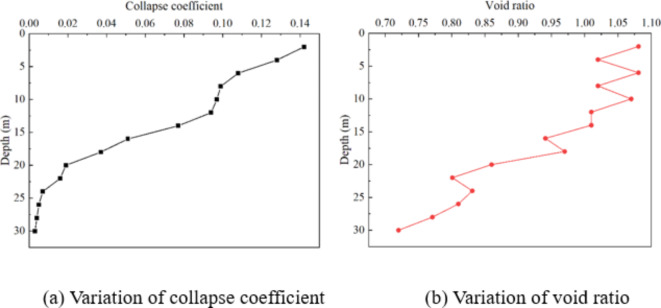
The variations of the collapse coefficient and void ratio with respect to depths were obtained from the soil investigation report and illustrated in Fig. 5 (a) and (b), respectively. It can be observed that both the collapse coefficient and void ratio decrease with increase in depth. When the depth exceeds 22 m, the collapse coefficient is less than 0.015. According to the Chinese standards for building construction in collapsible loess regions: GB50025-2018 (MOHURD33), , the soil could be classified as non-collapsable soil because the value of δs for those soil is less than 0.015.
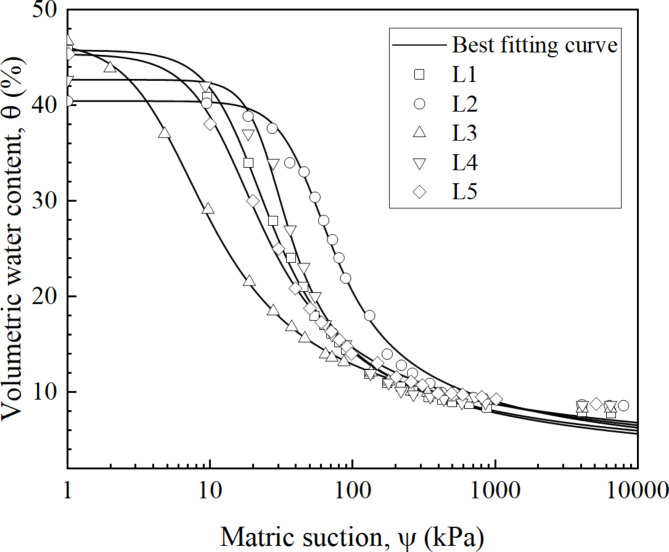
The wetting soil-water characteristic curves (SWCCs) derived from Kang et al.34 for the five soil layers at different depths were illustrated in Fig. 6. These SWCCs were used to obtain the critical suction value and constant water content suction for each layer. Based on the proposed method in this paper, the critical suction values of soil at depths of 5 m, 10 m, 15 m, 20 m, and 25 m, were obtained as 60 kPa, 70 kPa, 78 kPa, 92 kPa, and 124 kPa, respectively. The collapse settlements for each layer and total ground settlement are illustrated in Table 4. Considering the simplified assumptions in model calculations and the spatial variability of soil parameters, it is necessary to make appropriate corrections to the calculation results. According to the code GB50025-2018, a correction factor of 1.5 was adopted in the estimation of the ground settlement in the method following the local code (MOHURD33). After the correction, the cumulative settlement by using the method following the local code was about 1.416 m.
Fig. 6.
Wetting SWCCs of loess from five layers.
Fig. 5.
Collapse coefficient and void ratio variation to depth..
Table 4.
Proposed method for calculating final settlement.
Depth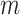
|
Collapse coefficient | Constant water suction (kPa) | Critical suction (kPa) |
Void ratio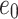
|
Collapse rate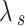
|
Suction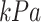
|
Calculated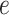
|
 
|
 
|
|---|---|---|---|---|---|---|---|---|---|
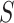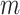
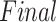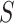
| 2 | 0.142 | 8.1 | 60 | 1.081 | 0.072 | 2 | 0.836 | 0.236 | 0.354 |
| 4 | 0.128 | 8.1 | 60 | 1.02 | 0.063 | 4 | 0.849 | 0.169 | 0.254 |
| 6 | 0.108 | 8.1 | 60 | 1.081 | 0.055 | 4 | 0.932 | 0.143 | 0.214 |
| 8 | 0.099 | 9.5 | 70 | 1.02 | 0.047 | 6 | 0.904 | 0.114 | 0.172 |
| 10 | 0.097 | 9.5 | 70 | 1.07 | 0.047 | 10 | 0.978 | 0.089 | 0.133 |
| 12 | 0.094 | 9.8 | 78 | 1.01 | 0.043 | 13 | 0.932 | 0.077 | 0.116 |
| 14 | 0.077 | 9.8 | 78 | 1.01 | 0.036 | 19 | 0.960 | 0.050 | 0.075 |
| 16 | 0.051 | 9.8 | 78 | 0.941 | 0.023 | 25 | 0.915 | 0.027 | 0.040 |
| 18 | 0.037 | 11 | 92 | 0.97 | 0.016 | 31 | 0.952 | 0.018 | 0.027 |
| 20 | 0.019 | 11 | 92 | 0.86 | 0.008 | 40 | 0.853 | 0.007 | 0.010 |
| 22 | 0.016 | 11 | 92 | 0.801 | 0.006 | 44 | 0.796 | 0.005 | 0.008 |
| 24 | 0.007 | 14 | 124 | 0.831 | 0.003 | 44 | 0.828 | 0.003 | 0.005 |
| 26 | 0.005 | 14 | 124 | 0.81 | 0.002 | 44 | 0.808 | 0.002 | 0.003 |
| 28 | 0.004 | 14 | 124 | 0.771 | 0.001 | 52 | 0.770 | 0.001 | 0.002 |
| Total | 0.944 | 1.416 |
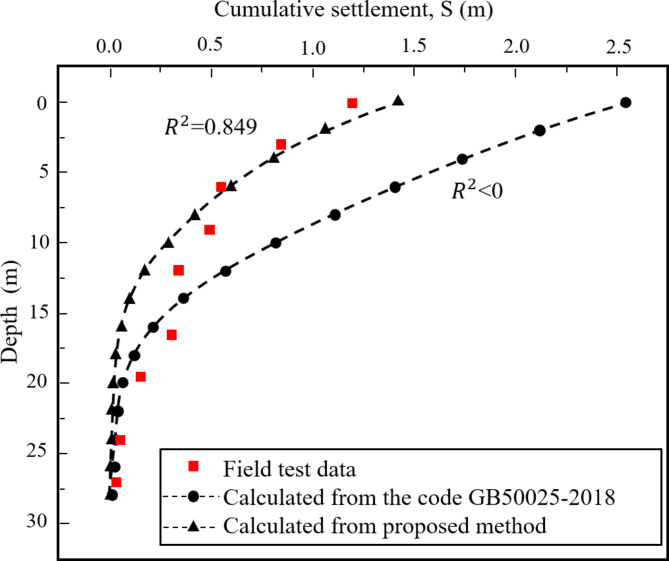
Both the calculated settlement from the proposed method and that from the code GB50025-2018 were compared with the field measured data and illustrated in Fig. 7. The estimated results from the proposed method agree well with the field test data, with a coefficient of determination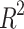 
of 0.849 while the results from the code GB50025-2018 have a R2 less than 0.
Fig. 7.
Cumulative settlements from both method as compared with field measurement data.
Figure 7 indicated that the estimation of the wetting induced ground settlement based on local code GB50025-2018 overestimated the ground settlement. It should be noted that the method from GB50025-2018 is based on the principles of saturated soil mechanics while the method proposed in this paper is based on the principles of unsaturated soil mechanics. The wetting SWCC was incorporated in the estimation of the wetting induced ground settlement in the proposed method. As a result, the principles of unsaturated soil mechanics are crucial for the evaluation of the wetting induced ground settlement. Both the wetting SWCC and variation of the void ratio before and after collapse should be measured for the evaluation.
Conclusions and Recommendations
In this paper, mathematical equations were proposed for the determination of the water entry value (WEV) and constant water content suction (ψwc). The determined results from the proposed equation agreed well with the values reported in the published literatures. Subsequently, both determined WEV and ψwc from the proposed method were adopted to compute the ground settlement of loess in the inundated condition. The estimated results from proposed method had a better performance than that computed from the local code GB50025-2018 as compared with the field measurements. The proposed method provides an alternative method for the estimation of the ground settlement of loess soils due to the wetting-induced collapse. Therefore, based on the study in this paper following conclusive points and recommendations can be obtained.
New mathematical equations were proposed and verified for the determination of the WEV and ψwc
A new method which incorporating the wetting SWCC was proposed to estimate the wetting induced ground settlement.
In order to estimate the wetting induced settlement, the wetting SWCC rather than the drying SWCC of soil should be measured.
The effect of the stress level on the variation of SWCC should be considered for the estimation of the wetting induced ground settlement.
Acknowledgements
The authors would like to acknowledge the financial supports they received from the National Natural Science Foundation of China (No. 52078128, 52178317), China Huaneng Group Co. Ltd. (No. HNKJ19-H17), Enterprise Development Grant (Co-Innovation Program): BZ2023016 (Jiangsu) and CIP-2207-CN1064 (Singapore)，the Research Fund for Advanced Ocean Institute of Southeast University (Key Program KP202404).
Author contributions
Li C, Chen YH, Xiang K, Dai GL, Gong WM, Yang SJ prepared the original mansucript, Satyanaga A, Chua YS, Gao P, Zhai Q review and revised the mansucript, Chen YH and Xiang K preapred all the figures, Gong WM produced the concept, Dai GL, Satayanaga and Zhai do the superivsion works.
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Chen, K., Shao, D., Liu, Z., Chen, L. & He, G. Experimental study on basic engineering properties of loess improved by burnt rock. Sci. Rep.13 (1), 11023. 10.1038/s41598-023-38083-z (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sheeler, J. B., Of engineering properties & of loess in the United States. Summarization and comparison. Highway Res. Rec., 212. (1968). https://trid.trb.org/View/126929
- 3.Li, Y., Shi, W., Aydin, A., Beroya-Eitner, M. A. & Gao, G. Loess genesis and worldwide distribution. Earth Sci. Rev.201, 102947. 10.1016/j.earscirev.2019.102947 (2020). [Google Scholar]
- 4.Zhao, J., Luo, X., Ma, Y., Shao, T. & Yue, Y. Soil characteristics and new formation model of loess on the Chinese Loess Plateau. Geosci. J.21 (4), 607–616. 10.1007/s12303-016-0069-y (2017). [Google Scholar]
- 5.Li, P., Vanapalli, S. & Li, T. Review of collapse triggering mechanism of collapsible soils due to wetting. J. Rock Mech. Geotech. Eng.8 (2), 256–274. 10.1016/j.jrmge.2015.12.002 (2016). [Google Scholar]
- 6.Wang, J., Zhang, D., Wang, N. & Gu, T. Mechanisms of wetting-induced loess slope failures. Landslides16(5), 937–953. 10.1007/s10346-019-01144-4 (2019). [Google Scholar]
- 7.Weng, X. et al. Physical modeling of wetting-induced collapse of shield tunneling in loess strata. Tunn. Undergr. Space Technol.90, 208–219. 10.1016/j.tust.2019.05.004 (2019). [Google Scholar]
- 8.Houston, S. L., Houston, W. N. & Spadola, D. J. Prediction of field collapse of soils due to wetting. J. Geotech. Eng.114 (1), 40–58 (1988). [Google Scholar]
- 9.Houston, S. L., Houston, W. N., Zapata, C. E. & Lawrence, C. Geotechnical engineering practice for collapsible soils. In D. G. Toll (Ed.), Unsaturated Soil Concepts and Their Application in Geotechnical Practice (pp. 333–355). Springer Netherlands. (2001). 10.1007/978-94-015-9775-3_6
- 10.Shao, X., Zhang, H. & Tan, Y. Collapse behavior and microstructural alteration of remolded loess under graded wetting tests. Eng. Geol.233, 11–22. 10.1016/j.enggeo.2017.11.025 (2018). [Google Scholar]
- 11.Nguyen, C. D., Burlacu, C. & Boti, I. Loessoid Soils Improvement – Laboratory Tests and Road Engineering Applications. Romanian J. Transp. Infrastructure. 8 (1), 53–64 (2019). [Google Scholar]
- 12.Fredlund, D. G. & Gan, J. K. M. The Collapse Mechanism of a Soil Subjected to One-Dimensional Loading and Wetting. In E. Derbyshire, T. Dijkstra, & I. J. Smalley (Eds.), Genesis and Properties of Collapsible Soils (pp. 173–205). Springer Netherlands. (1995). 10.1007/978-94-011-0097-7_9
- 13.Fredlund, D. G. & Rahardjo, H. Soil Mechanics for Unsaturated Soils (Wiley, 1993).
- 14.Fredlund, D. G., Rahardjo, H. & Fredlund, M. D. Unsaturated Soil Mechanics in Engineering Practice (John Wiley and Sons Inc., 2012).
- 15.Fredlund, D. G., Morgenstern, N. R. & Widger, R. A. The shear strength of unsaturated soils. Can. Geotech. J.15 (3), 313–321. 10.1139/t78-029 (1978). [Google Scholar]
- 16.Pereira, J. H. F. & Fredlund, D. G. Volume Change Behavior of Collapsible Compacted Gneiss Soil. J. Geotech. GeoEnviron. Eng.126 (10), 907–916. 10.1061/(ASCE)1090-0241(2000)126:10(907) (2000). [Google Scholar]
- 17.Zhai, Q. & Rahardjo, H. Estimation of permeability function from the Soil-Water Characteristic Curve. Eng. Geol.199, 148–156 (2015). [Google Scholar]
- 18.Zhai, Q., Rahardjo, H., Satyanaga, A. & Dai, G. L. Estimation of unsaturated shear strength from soil-water characteristic curve. Acta Geotech.14 (6), 1977–1990 (2019). [Google Scholar]
- 19.Zhai, Q., Rahardjo, H., Satyanaga, A. & Dai, G. L. Estimation of tensile strength of sandy soil from soil–water characteristic curve. Acta Geotech.15, 3371–3381 (2020). [Google Scholar]
- 20.Zhai, Q. et al. and Chua YS A new mathematical model for the estimation of shear modulus for unsaturated compacted soils. Can. Geotech. J.61 (10), 2124–2137 (2024). [Google Scholar]
- 21.Kato, S. & Kawai, K. Deformation Characteristics of a Compacted Clay in Collapse Under Isotropic and Triaxial Stress State. Soils Found.40 (5), 75–90. 10.3208/sandf.40.5_75 (2000). [Google Scholar]
- 22.Sun, D. A., Sheng, D. C., Cui, H. B. & Sloan, S. W. A density-dependent elastoplastic hydro-mechanical model for unsaturated compacted soils. Int. J. Numer. Anal. Meth. Geomech.31 (11), 1257–1279. 10.1002/nag.579 (2007). [Google Scholar]
- 23.Sun, D., Sheng, D. & Xu, Y. Collapse behaviour of unsaturated compacted soil with different initial densities. Can. Geotech. J.44 (6), 673–686. 10.1139/t07-023 (2007). [Google Scholar]
- 24.Hou, X., Vanapalli, S. K. & Li, T. Wetting-induced collapse behavior associated with infiltration: A case study. Eng. Geol.258, 105146. 10.1016/j.enggeo.2019.105146 (2019). [Google Scholar]
- 25.Xie, W. L., Li, P., Vanapalli, S. K. & Wang, J. D. Prediction of the wetting-induced collapse behaviour using the soil-water characteristic curve. J. Asian Earth Sci.151, 259–268. 10.1016/j.jseaes.2017.11.009 (2018). [Google Scholar]
- 26.Zhang, L., Li, T. & Zhang, Y. A simple method for predicting wetting-induced collapse behavior of compacted loess with various initial void ratios and moisture contents. Environ. Earth Sci.82 (1), 24. 10.1007/s12665-022-10674-5 (2022). [Google Scholar]
- 27.Zhai, Q. & Rahardjo, H. Determination of soil–water characteristic curve variables. Comput. Geotech.42, 37–43. 10.1016/j.compgeo.2011.11.010 (2012). [Google Scholar]
- 28.Zhai, Q., Rahardjo, H. & Satyanaga, A. Effects of residual suction and residual water content on the estimation of permeability function. Geoderma303, 165–177. 10.1016/j.geoderma.2017.05.019 (2017). [Google Scholar]
- 29.Fredlund, D. & Xing, A. Equations for the soil–water characteristic curve. Can. Geotech. J. - CAN. GEOTECH. J.31 (4), 521–532 (1994). [Google Scholar]
- 30.Leong, E. C. & Rahardjo, H. Review of Soil-Water Characteristic Curve Equations. Journal of Geotechnical and Geoenvironmental Engineering, 123(12), 1106–1117. (1997). 10.1061/(ASCE)1090-0241(1997)123:12(1106).
- 31.Garakani, A. A., Haeri, S. M., Khosravi, A. & Habibagahi, G. Hydro-mechanical behavior of undisturbed collapsible loessal soils under different stress state conditions. Eng. Geol.195, 28–41. 10.1016/j.enggeo.2015.05.026 (2015). [Google Scholar]
- 32.Wang, F. et al. Immersion test and collapsibility evaluation of deep loess site. Hydro Sci. Eng.5, 131–138 (2023). (In Chinese). [Google Scholar]
- 33.Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB50025-2018: Standard for building construction in collapsible loess regions. (2018).
- 34.Kang, H. et al. A study of hysteresis of soil and water characteristics of intact loess. Hydrogeol. Eng. Geol.47(2), 76–83 (2020). (In Chinese). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.