Evaluating sampling techniques for quantifying Asiatic garden beetle (Maladera formosae) (Coleoptera: Scarabaeidae) infestations in commercial mint

Abstract

The Asiatic garden beetle, Maladera formosae Brenske (AGB), has become a significant pest of commercial mint fields in northern Indiana. Larval feeding on mint roots can cause stunted growth and plant death when densities are high. Sampling approaches that provide reliable estimates of larval densities in mint have not been established, leaving farmers without the knowledge necessary to implement integrated pest management (IPM) strategies. To address this knowledge gap, we evaluated strategies for estimating AGB larval densities and plant performance in commercial mint systems. We used 2 sampling methods to collect larval density and plant performance data from 3 mint fields and conducted simulations to optimize sampling intensity (accuracy and precision) and sampling scheme (random vs. systematic) using these data. Additionally, we examined the sensitivity and efficiency of each sampling method. Compared to the cup-cutter method, the quadrat method provided the most accurate and precise estimates of larval density and plant performance, with ≤ 7 samples required per 0.2 ha. Quadrat excavation was also more sensitive, increasing the probability of detecting AGB larvae within a 32 m² plot by 76.7%, and requiring significantly less time to survey an equivalent volume of soil for AGB larvae. When the quadrat method was employed, random sampling schemes provided below-ground biomass estimates that were significantly closer to the true mean of the sampling area. The results of this research will facilitate the development of IPM decision-making tools for farmers and support future research for AGB and other soil insect pests affecting mint production.

Introduction

A diversity of insect pests reside beneath the soil surface during one life stage or more. Scarab larvae (Coleoptera: Scarabaeidae), wireworms (Coleoptera: Elateridae), weevils (Coleoptera: Curculionidae), cutworms, and armyworms (Lepidoptera: Noctuidae) are well-known soil-dwelling pests that inflict damage to plants during the larval stage, either by feeding on roots, or by moving from the soil to the surface to feed on above-ground plant tissues (Capinera 2001). Damage attributed to this suite of pests varies across cropping systems and can result in reductions in plant growth, performance, or even plant death when pest pressure is severe (Potter et al. 1996, Roda et al. 1996, Saussure et al. 2015). Given their subterranean nature, detecting and quantifying soil-insect populations in the field can be challenging and often requires unique and labor-intensive sampling methods to estimate population densities and corresponding plant damage (Mankin et al. 2000).

In the case of scarab larvae, sampling techniques vary across systems, but typically involve excavating and sorting through a predetermined volume of soil, using either square quadrat frames ranging in size from 10 cm × 10 cm to 30 cm × 30 cm, or cylindrical, golf course cup-cutters with a 10 cm diameter (Forschleri and Gardner 1991, Dalthorp et al. 2000a, Redmond and Potter 2010, Jordan et al. 2012, Pekarcik et al. 2023). In turfgrass systems, the removal of sod to search for scarab larvae has been a standard method to quantify population densities for decades (Potter and Potter 1999). However, the aggregated distribution of scarab larvae, like those of the well-studied Japanese beetle (Popillia japonica Newman), presents additional challenges in detection because a higher number of large-volume samples are required to gain reliable estimates of population density (Dalthorp et al. 2000b). Furthermore, soil-dwelling insects, like scarab larvae, have received less attention than above-ground insect pests, resulting in a paucity of scientific information necessary to support the development of data-driven integrated pest management (IPM) programs for soil-insect pests (Hunter 2001, Zvereva and Kozlov 2012). Currently, there is no clear consensus on either the intensity (number of samples per unit area) required to gain accurate and precise estimates of soil-insect populations, or the relative sensitivity (ability to detect pests) of certain sampling methods, and it is unclear if random or systematic sampling schemes provide the best estimates of scarab larval densities (Jordan et al. 2012, Shah et al. 2012, McGarvey et al. 2016, Pekarcik et al. 2023). As a result, the development of decision-making tools needed to implement successful IPM strategies for subterranean insects has been hindered (Nyamwasa et al. 2017).

The development of field sampling protocols to reliably estimate soil-insect populations sometimes relies on the use of simulated data, drawn from predetermined distributions, putatively representative of the target organism. While the use of simulated data can provide obvious benefits by simplifying and hastening the development of sampling guidelines, simulations can only approximate the actual distribution of an organism and may not reflect its real-world distribution in the same way as physical sampling (Willers et al. 1990, Shah et al. 2012, McGarvey et al. 2016). Although surprisingly uncommon, conducting simulations with data collected during physical sampling events can prove useful for this purpose because the data are drawn directly from a representative sample (Hewitt et al. 1993, O’Rourke and Jones 2011). The ability to leverage pilot data collected from the field as the basis for simulations to develop optimal sampling protocols may be particularly useful for estimating populations of soil-dwelling scarab larvae, which are known to be aggregated in their distribution across the landscape and require substantial effort to collect and process individual samples. Such an approach could also prove useful in situations where reliable sampling protocols have yet to be developed, or when novel pest–crop associations appear.

The Asiatic garden beetle (Maladera formosae Brenske) (Coleoptera: Scarabaeidae) (hereafter, AGB), is an invasive scarab species and an economically important pest in several agricultural systems. Scarab larvae, like AGB, are univoltine and comprise a species complex comprising many well-known pests of multiple plant species in the United States, including turfgrass, ornamentals, vegetables, and field crops, like corn and soybean, although they are sporadic pests of the latter (Tashiro 1987, Youngman et al. 1993, Capinera 2001, Hesler et al. 2018). In the Midwestern United States, AGB larvae actively feed from late July through October, overwintering during the colder months and becoming active again the following year, from April to mid-June, prior to pupation (Hallock 1936a, Tiwari et al. 2019). These insects develop through 3 larval instars and complete their life cycle in one year (Capinera 2001). As such, fall and spring larval populations represent the same developmental cohort even though crop status and developmental phenology usually differ across these two seasons.

In Indiana, AGB was first reported in 2006 as a pest of turf, corn, and ornamental plants (Krupke et al. 2007). However, in the last decade, farmers have reported AGB as a serious pest of commercial spearmint and peppermint grown for oil in north-central Indiana. Commercial mint is grown as a short-term perennial crop that is cultivated for 3–5 yr in rotation with corn and soybean (Weller et al. 2000). Thus, the size of mint fields in northern Indiana range widely, between 12–60 ha, in line with the typical scale of corn and soybean fields in the region. New fields are started by planting stolons in early spring and harvest takes place once or twice each year, from late June to mid-August, depending on mint species (peppermint vs. spearmint). Harvesting foliage annually from the same field as mint becomes established over the 3- to 5-yr production cycle allows farmers to maximize mint oil yield, but also presents the opportunity for AGB larvae to inflict root damage repeatedly to the same crop for consecutive years. Moreover, the temporal coincidence of harvest with AGB oviposition and the beginning of larval development results in plants experiencing the combined stress of regrowth and root feeding. The accumulation of root-feeding damage by AGB larvae during the late summer, fall, and spring can cause wilting, discoloration, and death of mint plants (Fig. 1). Additionally, moist, loose-textured soils are preferred by ovipositing AGB adults, and because mint plants thrive in these conditions, mint grown on sandy, irrigated soils is likely more vulnerable to AGB infestation (Hallock 1936b, Weller et al. 2000). The continued occurrence of AGB larval infestations and their associated damage in commercial mint production raises novel questions about the most reliable approach for estimating larval density in the field, as well as the relationship between larval density and plant performance, so an associated damage threshold can be identified. A reliable, but practical protocol for sampling and estimating AGB larval density and plant performance parameters in the field is a foundational step toward the development of a damage threshold and economic injury level to support grower IPM decision-making in this system. Work reported herein represents the first step towards this goal.

Fig. 1.

Root damage to mint caused by Asiatic garden beetle, Maladera formosae Brenske, larvae. Severity of root damage increases from left to right. The nominal scale to assess root health ranged from 1-5 with 1 = no visible root damage, rhizomes present and healthy; 2 = some feeding on tertiary and secondary roots discernable, rhizomes mostly intact and healthy; 3 = tertiary and secondary roots clearly damaged, rhizomes obviously stunted; 4 = tertiary roots absent along with most secondary roots, rhizomes missing; 5 = no tertiary or secondary roots present, primary roots heavily damaged, no rhizomes present.

The objective of this study was to optimize a sampling protocol for AGB larval populations in commercial mint fields. In support of this objective, we used field-collected data to conduct a series of simulations designed to (i) characterize the accuracy and precision of AGB larval density and plant performance estimates provided by cup-cutter vs. quadrat excavation sampling techniques across a range of sampling intensities, (ii) quantify the time required to process samples using each method, (iii) directly compare the sensitivity of cup-cutter vs. quadrat excavation methods for detecting AGB larvae, and (iv) compare the relative utility of random vs. systematic sampling schemes for estimating AGB larval densities and plant performance parameters within the sampled area. We hypothesized that sampling intensity could be significantly reduced relative to the maximum sampling intensity deployed in previous studies without concomitant decreases in accuracy and precision (Dalthorp et al. 2000b). Because of the relatively large difference in the volume of soil evaluated by the 2 different sampling methods (0.0009 m³ vs. 0.009 m³), we hypothesized that the quadrat method would provide improved sensitivity, increasing our ability to detect AGB larvae, which tend to be distributed in an aggregated pattern in soils across the landscape. Lastly, because of the aggregated distribution of most scarab species, we hypothesized that simple random sampling would provide more accurate estimates of mean larval densities compared to systematic sampling schemes (Worner et al. 1999, Shah et al. 2012).

Materials and Methods

Field Sites and Sampling Approach

Data for the current study were collected during the spring of 2021 and fall 2022 from 3 commercial mint fields with a history of larval AGB infestation. All fields were located in Starke County, IN, and the GPS coordinates, size, and soil characteristics of each field are specified in Table 1. We evaluated soil characteristics within a 0.2 ha sampling area within each field (described below) by collecting 20 soil cores with an Oakfield 36 soil sampler with foot step (Forestry Suppliers, Inc, Jackson, MS) and sending them to A&L Great Lakes Laboratories (Fort Wayne, IN, USA) for analysis.

Table 1.

The location, size, mint species, crop age, and soil characteristics of 3 mint fields used to assess Asiatic garden beetle, Maladera formosae Brenske, larval density, and plant performance parameters. Soil texture was determined via particle size analysis.

Field	Year	Season (Sampling Method)	NE Corner	Field Size (ha)	Mint Species*	Crop Age (years)	Organic Matter (%)	Sand (%)	Silt (%)	Clay (%)	USDA Soil Classification
1	2021	Spring (Cup-cutter)/Fall (Quadrat)	41°12ʹ49ʹʹ N 86°53ʹ40ʹʹ W	30.25	Spearmint	3	2.6	84	10	6	Loamy Sand
	2022	Spring & Fall (Quadrat)
2	2021	Spring & Fall (Quadrat)	41°13ʹ13ʹʹ N 86°52ʹ16ʹʹ W	50.59	Peppermint	1 & 2	9.1	83	13	4	Loamy Sand
	2022	Spring & Fall (Quadrat)
3	2021	Spring & Fall (Quadrat)	41°12ʹ48ʹʹ N 86°39ʹ20ʹʹ W	56.78	Peppermint	2	2.6	87	9	4	Sand
	2022	Spring & Fall (Quadrat)

^*Spearmint = Mentha × spicata, Peppermint = Mentha × piperata.

A spatial sampling grid was established in each mint field based on a method modified from Dalthorp et al. (2000a) and Zvereva and Kozlov (2012). Briefly, an 8 × 8 grid consisting of sixty-four, 32 m² cells (5.66 × 5.66 m) (total area = 0.2 ha) was established in each field, and the GPS coordinates of each corner of the sampling grid were recorded for future reference. These 0.2 ha areas were chosen based on the grower’s previous experience with AGB infestation, pre-sampling efforts indicating AGB presence, and ease of access from nearby roadways. The grid in each field was sampled using either a golf course cup-cutter method, quadrat excavation method, or both (detailed below). All 64 cells within each field grid were sampled in late May or early June of 2021, with the exception of Field 3, where only 48 contiguous cells (total area = 0.15 ha) were sampled. Field 2 was sampled twice during October of 2022 to provide a direct comparison between mean estimates of AGB larval density gained from each sampling method. We conducted all simulations and comparisons using these data.

For both sampling methods, the number, species, and instar of all scarab larvae collected from each field were recorded to estimate the density and species composition of the scarab larval complex (including Japanese beetle and masked chafer, Cyclocephala spp.). Because other scarab species were sporadically detected and represented only a small fraction of the scarab species present during any sampling event (< 10% non-AGB), only AGB larval numbers were used for our analyses. The first soil sampling method utilized a lever-action golf course cup-cutter (Golf Griffin, Cedar Falls, IA) to assess AGB larval density, while plant height and root rating were used to assess plant performance. This approach was implemented in Fields 1 and 2 by extracting a round soil core (10.8 cm diameter × 10 cm depth = 0.0009 m³ volume) from the center of each cell, then breaking the soil apart into a plastic dishpan (Sterilite Corporation, Townsend, MA, USA) to search for larvae. The height of the mint plant closest to the soil core was measured to the nearest 0.1 cm using a ruler, then collected using the same cup-cutter device to extract the entire plant and its roots from the soil. The condition of the roots was assessed on an ordinal rating scale of 1–5, where 1 represented healthy roots without any apparent damage, and 5 represented extensive damage with only primary roots remaining (Fig. 1). Above- and below-ground plant biomass was not measured for the cup cutter sampling method.

The second soil sampling method utilized a square quadrat frame and excavation of soil with a shovel to assess AGB larval density, while above- and below-ground plant biomass were used to assess plant performance. For this approach, each response variable described above was assessed within the footprint of the same quadrat. The quadrat excavation method was implemented in Fields 2 and 3 using a quadrat frame constructed from 2.54 cm PVC pipe (25.0 cm width × 25.0 cm length). The PVC frame was placed in the center of each cell and all living, above-ground plant biomass within the frame was harvested using electric shears (Craftsman, Towson, MD). The soil within each frame was then excavated using a flat spade to a depth of 10.0 cm (0.006 m³ volume) and sifted through a 0.32 cm (1/8-inch) hardware cloth box sieve (60.96 cm length × 30.48 cm width × 10.16 cm depth) to extricate the larvae and below-ground plant biomass. All above- and below-ground plant biomass were placed separately into labeled plastic bags inside an insulated cooler and transported to the lab where it was weighed fresh the same day it was collected.

Optimizing Sampling Intensity

Analyses were performed in RStudio (Version 2023.03.0 + 386) using the base R, tidyverse, cowplot, readxl, and car packages unless otherwise specified (Fox 2019, Wickham et al. 2019, Wilke 2020, Wickham 2023, RStudio). To optimize sampling intensity, we modeled the relationship between the number of samples collected and the accuracy and precision of AGB larval density estimates at each level of sampling intensity using piecewise regression. In the present study, accuracy refers to how close an estimate comes to the true mean (i.e., mean value of field-collected data using all cells in the sampling grid located in each field), while precision refers to the relative variability of an estimate around that mean. Fifty sets of random draws (iterations) were taken from the field-collected data, encompassing the entire continuum of possible sample sizes based on the 64-cell grid in each field (n = 1, 2, … 63). Due to the reduced number of cells from which data was collected in Field 3 (n = 48), maximum sample size estimates for that field did not exceed 47. This procedure was repeated for each field using each of the response variables associated with the 2 sampling methods (Quadrat method = AGB larval density and above- and below-ground biomass; Cup cutter method = AGB larval density, plant height, and root rating).

To characterize the relationship between sampling intensity and accuracy, we adapted the method developed by Pérez-Llorca et al. (2018), where the absolute difference between the estimated mean (provided by each iteration within a given sample size) and the true mean was calculated, converted to percent difference ((| $\overline{x}$_field - $\overline{x}$_subsample|) / $\overline{x}$_field × 100), and averaged across all 50 iterations for that sample size. We also determined the number of samples required to fall within 20% of the true mean. To characterize the relationship between sampling intensity and precision, we calculated the total variance among all means estimated from the 50 iterations for each sample size. Piecewise regressions were performed using the SEGMENTED package in RStudio, as described in Muggeo (2008) to determine the breakpoint, or inflection point, where increases in sampling intensity are not accompanied by concomitant gains in accuracy or precision to the same degree as lower sample sizes (· = 0.05). These analyses were performed for each variable in each field individually to provide a representative range of breakpoints that might reasonably be expected to vary based on field conditions.

Evaluating the Sensitivity of Different Sampling Methods

Future efforts to identify the relationship between AGB larval density, plant performance, and economic injury levels in commercial mint are contingent on knowledge of reliable sampling strategies for this pest in mint fields. Therefore, we directly compared the sensitivity (i.e., the ability to detect AGB larvae when present) of the golf course cup-cutter and quadrat excavation method by sampling one field (Field 2) in October of 2022 using both methods. Based on the results that a sample size of 30 provided robust estimates of AGB larval density, we randomly selected 30 cells from within the 64-cell grid and employed both sampling methods, side-by-side. AGB larval densities were converted to a binary outcome reflecting the presence or absence of larvae in each cell. The binary data were then used to represent the frequency of larval detection, serving as a proxy for the sensitivity for each method. To assess the relationship between the sampling method used and the frequency of AGB larval detection, we employed a chi-square test of independence (· = 0.05) with a 2 × 2 contingency table.

Evaluating Sampling Efficiency

To estimate the relative efficiency of the 2 different sampling methods examined, we recorded the time required to collect AGB larval density and plant performance data using each method. Six different individuals were timed, using a stopwatch, to quantify the amount of time (in seconds) required to sample one cell within a sampling grid. These data were then averaged to provide an estimate of the time required to sample an equivalent volume of soil (0.006 m³) using each method and a t-test was performed to compare the time required to sample this volume of soil, with each of the 6 individuals serving as independent replicates (n = 6).

Comparing Sampling Schemes

Using a sampling intensity of 30 cells per grid, we compared the accuracy of 3 systematic sampling schemes to 3, independently generated iterations of a simple random sampling scheme. The systematic sampling schemes (Fig. 2) were designed using artificial patterns that provided relatively even, full-field coverage: (i) checkered scheme, (ii) X scheme, and (iii) reverse X scheme. Data from all 3 systematic sampling schemes were pooled for analysis. For Field 3, modified versions of the 3 systematic sampling schemes were employed to account for the reduced number of cells (48 instead of 64) included in the original dataset during the spring of 2021. The random sampling schemes were created by randomly selecting 30 cells from all available cells (48 or 64) a total of 3 times from each field using RStudio.

Fig. 2.

Three systematic sampling schemes used to estimate Asiatic garden beetle larval densities in commercial mint: A) Checkered Scheme, B) X Scheme, and C) Reverse X Scheme. Each scheme is overlaid on a 8 × 8, 64-cell grid.

We examined how the sampling scheme influenced estimated means for each of the 3 variables associated with the cup-cutter and quadrat methods, resulting in a total of 6 response variables (AGB larval density for each sampling method, plant height, root rating, above-ground biomass, and below-ground biomass). Mean values for each response variable were calculated using the data collected from plots designated by each sampling scheme. Because plant biomass was not measured in Field 1 during the spring of 2021, only Fields 2 and 3 were used for those comparisons. The estimated means provided by the random and systematic sampling schemes were compared by calculating the mean absolute difference between the estimated means gained from each of the 30-sample schemes and the estimated means gained from the original 64 or 48 sample schemes for each response variable and field. The absolute differences from each field were pooled by response variable, and estimated means were calculated for each type of sampling scheme (random or systematic). The mean absolute differences for the cup-cutter and quadrat methods were compared separately, using multivariate analysis of variance (MANOVA) (· = 0.05), with “field” as a blocking variable to determine if the accuracy of the estimated means varied between sampling schemes.

Results

Optimizing Sampling Intensity

To optimize sampling intensity, we examined the relationship between accuracy, precision, and sample size to identify the breakpoint at which gains in accuracy or precision declined as sampling effort increased. We used the average absolute percent difference from the true mean of the sampling area among the 50 iterations as a measure of accuracy at each level of sampling intensity. Results from the accuracy regressions are compiled in Table 2.

Table 2.

Statistical outputs and performance parameters for segmented regression analysis modelling relationships between the accuracy of estimated means and sampling intensity (number of random samples/sampling grid). Response variables include Asiatic garden beetle, Maladera formosae Brenske, larvae/0.25 m² (larval density), plant height (cm), root rating (1–5 nominal scale), above-ground biomass (g), and below-ground biomass (g). Breakpoints estimates represent the sampling intensity where diminishing returns in accuracy accrue with additional sampling effort. Accuracy was calculated as the mean absolute difference (%) between estimates provided by 50 random draws at each level of sampling intensity (n = 1–63 or 1–47) and the mean estimated by sampling all cells in a 64- or 48-cell sampling grid (i.e., True Mean). Total area = 0.2 or 0.15 ha. N ≤ 20% = the number of samples required to fall within 20% of the true mean.

Field	Sampling Method	Response Variable	True Mean (± SE)	Accuracy Breakpoint (± SE)	df	t	P	R 2	N ≤ 20% True Mean
1	Cup-cutter	Larval Density	13.0 ± 2.7	6.7 ± 0.3	59	−11.8	<0.001	0.95	26.6
2	Cup-cutter	Larval Density	5.5 ± 1.8	7.2 ± 0.4	59	−12.4	<0.001	0.95	42.8
1	Cup-cutter	Plant Height	14.0 ± 0.5	7.2 ± 0.3	59	−14.2	<0.001	0.96	1.0
2	Cup-cutter	Plant Height	16.3 ± 0.4	9.8 ± 0.5	59	−14.0	<0.001	0.96	1.0
1	Cup-cutter	Root Rating	1.3 ± 0.1	7.0 ± 0.4	59	−11.7	<0.001	0.96	1.0
2	Cup-cutter	Root Rating	1.0 ± 0.0	27.9 ± 1.9	59	−16.6	<0.001	0.96	1.0
2	Quadrat	Larval Density	0.8 ± 0.2	16.6 ± 1.3	59	−10.7	<0.001	0.95	44.7
3	Quadrat	Larval Density	3.6 ± 0.3	5.5 ± 0.3	43	−10.2	<0.001	0.95	4.9
2	Quadrat	Above-ground Biomass	29.0 ± 2.7	6.7 ± 0.3	59	−13.7	<0.001	0.97	6.1
3	Quadrat	Above-ground Biomass	51.7 ± 3.4	4.5 ± 0.3	43	−8.4	<0.001	0.96	3.3
2	Quadrat	Below-ground Biomass	26.3 ± 3.0	5.3 ± 0.2	59	−12.2	<0.001	0.95	5.3
3	Quadrat	Below-ground Biomass	84.1 ± 7.6	5.4 ± 0.6	43	−9.3	<0.001	0.96	5.0

When using the cup-cutter, we found that breakpoint estimates for AGB larval density ranged from 6.68 ± 0.33 to 7.23 ± 0.35 samples per grid, and the sampling intensity required to fall within 20% of the true mean ranged from 26.55 to 42.81 samples (Supplementary Fig. 1). Higher mean larval densities within the sampled area of each mint field coincided with a lower breakpoint estimate in the regression and a lower level of sampling intensity required to fall within 20% of the true mean. The breakpoint estimates for plant height ranged from 7.21 ± 0.30 to 9.75 ± 0.45 samples per grid, with all estimates falling within 20% of true means, regardless of sampling intensity (Supplementary Fig. 2). Finally, the breakpoint estimates for root rating ranged from 7.00 ± 0.36 to 27.85 ± 1.86 samples per grid, and similar to plant height, all breakpoint estimates fell within 20% of the true mean, regardless of sampling intensity (Supplementary Fig. 3).

When using the quadrat method, breakpoint estimates for AGB larval density ranged from 5.47 ± 0.31 to 16.59 ± 1.34 samples per grid, and the sampling intensity required to fall within 20% of the true mean ranged from 4.94 to 44.73 samples (Supplementary Fig. 1). Similar to estimates of AGB larval density gained using the cup-cutter method, higher mean larval densities were associated with lower breakpoint estimates and a reduction in the sampling intensity required to fall within 20% of the true mean. For above-ground biomass, breakpoint estimates ranged from 4.52 ± 0.31 to 6.68 ± 0.29 samples per grid, with a relatively low level of sampling intensity (n ≤ 6.08 samples) required to fall within 20% of the true mean (Supplementary Fig. 2). For below-ground biomass, breakpoint estimates ranged from 3.30 ± 0.89 to 5.30 ± 0.24 samples per grid, with the sampling intensity required to fall within 20% of the true mean ranging from 5.31 to 13.39 samples per grid (Supplementary Fig. 3).

We calculated the variance among the means of the 50 iterations for each sample size (n = 63 or 47) and leveraged this variance as a measure of precision relative to sampling intensity. When evaluating the precision of estimates gained from the 2 sampling methods, breakpoint estimates for AGB larval density gained from the cup-cutter ranged from 4.10 ± 0.18 to 5.17 ± 0.22 samples per grid, 5.25 ± 0.20 to 5.67 ± 0.28 samples per grid for plant height, and 4.10 ± 0.28 to 6.39 ± 0.24 samples per grid for root rating (Supplementary Figs. 4–6). Precision breakpoint estimates for AGB larval density gained from the quadrat method ranged from 3.59 ± 0.12 to 11.52 ± 1.56 samples per grid, 4.28 ± 0.17 to 4.92 ± 0.14 samples per grid for above-ground biomass, and 4.10 ± 0.15 to 5.23 ± 0.23 samples per grid for below-ground biomass (Supplementary Figs. 4–6). All results from the precision analyses are compiled in Table 3.

Table 3.

Statistical outputs and performance parameters for segmented regression analysis modelling relationships between the precision of estimated means and sampling intensity (number of random samples/sampling grid). Response variables include Asiatic Garden beetle, Maladera formosae Brenske, larvae/0.25 m² (larval density), plant height (cm), root rating (1-5 nominal scale), above-ground biomass (g), and below-ground biomass (g). Breakpoint estimates represent the sampling intensity where diminishing returns in precision accrue with additional sampling effort. Precision was calculated as the average variance among the means estimated by 50 random draws at each level of sampling intensity (n = 1–63 or 1–47). True means represent estimates provided by sampling all cells in the 64- or 48-cell grid. Total area = 0.2 or 0.15 ha.

Field	Sampling Method	Response Variable	True Mean (± SE)	Precision Breakpoint (± SE)	df	t	P	R 2
1	Cup-cutter	Larval Density	13.0 ± 2.7	5.2 ± 0.2	59	−12.4	<0.001	0.91
2	Cup-cutter	Larval Density	5.5 ± 1.8	4.1 ± 0.2	59	−11.7	<0.001	0.89
1	Cup-cutter	Plant Height	14.0 ± 0.5	5.3 ± 0.2	59	−14.3	<0.001	0.94
2	Cup-cutter	Plant Height	16.3 ± 0.4	5.7 ± 0.3	59	−11.4	<0.001	0.93
1	Cup-cutter	Root Rating	1.3 ± 0.1	6.4 ± 0.2	59	−14.9	<0.001	0.94
2	Cup-cutter	Root Rating	1.0 ± 0.0	4.1 ± 0.3	59	−7.4	<0.001	0.76
2	Quadrat	Larval Density	0.8 ± 0.2	11.5 ± 1.6	59	−4.7	<0.001	0.63
3	Quadrat	Larval Density	3.6 ± 0.3	3.6 ± 0.1	43	−15.2	<0.001	0.97
2	Quadrat	Above-ground Biomass	29.0 ± 2.7	4.3 ± 0.2	59	−13.3	<0.001	0.93
3	Quadrat	Above-ground Biomass	51.7 ± 3.4	4.9 ± 0.1	43	−16.6	<0.001	0.97
2	Quadrat	Below-ground Biomass	26.3 ± 3.0	4.1 ± 0.2	59	−13.9	<0.001	0.92
3	Quadrat	Below-ground Biomass	84.1 ± 7.6	5.2 ± 0.2	43	−12.6	<0.001	0.94

Evaluating the Sensitivity of Different Sampling Methods

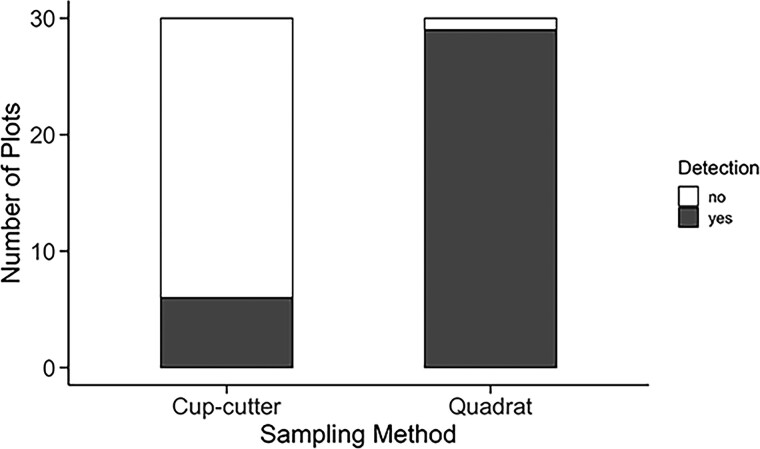
When the 2 sampling methods (cup-cutter vs. quadrat) were performed side-by-side in the field, the quadrat method was more sensitive (χ² = 33.19, df = 1, P < 0.001) (Fig. 3). When adjusted for sampling area, the cup-cutter method estimated mean larval densities of 8.2 ± 3.2 larvae/0.25 m², whereas the quadrat method provided a slightly higher estimate of 9.5 ± 2.0 larvae/0.25 m². While mean larval density estimates provided by each sampling method fell within the standard error of the other, the detection frequency of the cup-cutter method was much lower than that of the quadrat method. The cup-cutter method resulted in a 79.3% decrease in detection frequency compared to the quadrat method, such that the cup-cutter detected larvae in only 6 of 30 cells compared to the quadrat method, which detected larvae in 29 of 30 cells.

Fig. 3.

The number of plots, out of 30, where at least 1 Asiatic garden beetle larva was detected using either the cup-cutter or quadrat excavation method. Each method was performed within the same 30 plots, in the same field, on the same day during fall 2022.

Evaluating Sampling Efficiency

Using the cup-cutter method, sampling larval density and plant performance parameters in one cell within a sampling grid required 107 ± 8 s whereas 1,320 ± 76 s was required using the quadrat method. However, using the cup cutter method to sample an area equivalent to that of a single quadrat (0.25 m²) would require ~25 cup-cutter samples, translating to a sampling time of 2,670 ± 196 s The quadrat method required significantly less time than the cup-cutter to sample the same volume of soil (0.006 m²) within a single cell (t = 6.66, P = 0.001).

Comparing Sampling Schemes

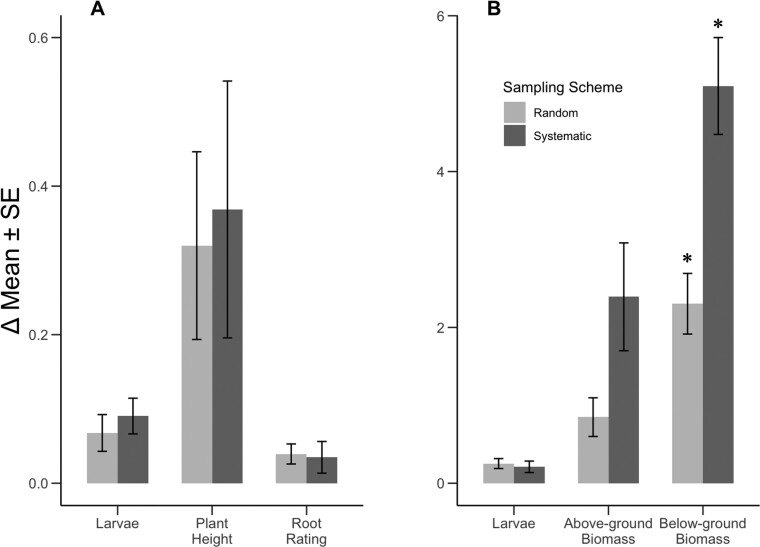
Using the cup-cutter approach at a sample size of 30, there was no significant difference in the accuracy of estimates provided by random vs. systematic sampling schemes (F_{1, 9} = 0.17, P = 0.91) (Fig. 4). However, the random sampling scheme provided AGB larval density and plant height estimates that were numerically more similar to the true mean, while the opposite was true for root rating. In contrast, estimated means resulting from the quadrat method were significantly more accurate when a random sampling scheme was employed (F_{1, 9} = 5.79, P = 0.03). In particular, more accurate estimates of below-ground biomass were gained using a random sampling scheme (F_{1, 9} = 20.27, P = 0.001) and estimates of above-ground biomass were numerically more similar to the true mean using this approach.

Fig. 4.

Comparisons of mean absolute differences (Δ Mean ± SE) between the true mean and estimated means provided by 30-samples taken using a random vs. systematic sampling scheme (n = 6). (A) Asiatic garden beetle, Maladera formosae Brenske, larval density estimated using a golf course cup-cutter (10 cm depth), plant height (cm), and root rating (1-5 nominal scale). (B) Asiatic garden beetle larval density estimated by excavating a 0.25m² quadrat of soil (10 cm depth), above-ground biomass (g), and below-ground biomass (g). Asterisks denote estimated means for a particular variable differ significantly between random and systematic sampling schemes (α = 0.05). True means represent estimates provided by sampling each cell in a 64- or 48-cell grid. Total area = 0.2 or 0.15 ha.

Discussion

There are currently no established sampling methods for estimating AGB larval densities and their effects on the performance of commercial mint. Moreover, there is no established economic injury level or action threshold to guide farmer’s management decisions for this pest. Our study lays the groundwork for addressing these knowledge gaps and suggests that random sampling of mint fields at an intensity of 5–7 samples/0.2 ha using a 0.25 m² quadrat is sufficient to gain accurate and precise estimates of AGB larval density. These results provide a baseline for future studies to evaluate the relationship between AGB larval density and mint damage, as well as mint oil yield.

Within the areas we sampled, the ability to reliably estimate AGB larval populations in mint fields varied with the intensity of infestation. Fields with relatively low mean larval densities required more intense sampling to gain stable population estimates. For example, the highest breakpoint estimate for AGB larval density, and the highest number of samples required to fall within 20% of the true mean, came from the mint field with the lowest AGB larval density (Field 2), and this trend appeared to be consistent regardless of sampling method (cup-cutter or quadrat excavation). These breakpoint estimates for sampling accuracy are congruent with findings from a previous study, which used a comparable quadrat method to estimate scarab larval populations in corn (Jordan et al., 2012). However, results herein additionally indicate that the sampling method (cup-cutter vs. quadrat) may influence the accuracy of AGB larval density estimates, and that accurate estimates can be obtained with a relatively low number of samples (5–7 samples/0.2 ha) when population densities are high (Field 1). Greater sampling intensity may be required to maintain accuracy when AGB larval densities in the field are low (Table 2, Supplementary Fig. S1).

While sample accuracy describes how close a sample estimate is to the true mean, precision reflects the relative variability of estimates around that mean. In this sense, evaluating sampling precision allowed us to determine the sampling intensity required to gain stable estimates of AGB larval density. Similar to the pattern observed for sample accuracy, when AGB larval densities were low in the field (< 1) (Table 3, Supplementary Fig. S4), greater sampling intensity was required to gain precise estimates. However, the breakpoint estimates for sample precision were always lower than corresponding breakpoint estimates for sample accuracy suggesting that accurate AGB larval density estimates will likely be precise under most circumstances.

Improved detection is a common goal in integrated pest management because it allows for timely detections that can potentially reduce yield losses (Banga et al. 2018, Lima et al. 2020). The quadrat excavation method displayed superior sensitivity for detecting AGB larvae, likely due to the larger volume of soil that is sampled using this method. Of the 30 plots sampled, the quadrat excavation method detected larvae in 29 plots, while the cup-cutter method detected larvae in only 6 plots. A recent study compared mean numbers of AGB larvae collected in corn and soybean fields using both a standard, golf course cup-cutter and a compact soil-cutter (20.3 cm × 20.3 cm) and found that the standard cup-cutter was more sensitive in detecting AGB larvae per soil volume sampled, but this varied with larval AGB density in the field (Pekarcik et al. 2023). However, the accuracy and precision of these sampling methods were not evaluated. Our results suggest that cup-cutters are likely to underestimate the presence of larval AGB infestations in the field, due to the lower volume of soil that is excavated. In fact, 25 cup-cutter samples would be required to evaluate the same soil volume sampled with a single 0.25 m² quadrat. We measured the time required for 6 individuals to complete the sampling of a single cell using both the quadrat and cup-cutter method. Based on statistical comparison of the time required to sample using each method, we expect that roughly twice the amount of time would be required to survey the same amount of soil using the cup-cutter method.

We examined 4 different plant response parameters, plant height, root rating, and above- and below-ground biomass, to identify a reliable and efficient method to quantify plant damage caused by AGB larvae. In comparison to breakpoint estimates of AGB larval density, the breakpoint estimates for plant performance were generally lower (less than 10 samples required per 0.2 ha). One notable exception to this trend was the breakpoint estimate for root rating (cup cutter method), where as many as 28 samples/0.2 ha were required to provide accurate estimates. This observation likely stems from the relatively high proportion of undamaged root masses sampled during our study, leading to a disproportionate influence of a relatively small number of severely damaged roots at smaller sample sizes (Table 1, Supplementary Fig. S3).

Variation in plant morphology is likely to influence the accuracy of sampling methods used to estimate damage by soil-dwelling insects. Unlike other row crops, such as corn or soybean, mint plants have large fibrous root systems that include rhizomes and stolons that expand horizontally to create a dense mat-like structure (Taneja and Chandra 2012). This high root density is typical of perennial plants, like mint, that store carbohydrates in these underground structures (Roumet et al. 2006). Although ordinal scale root ratings are used successfully in crops with uniform root structure, like corn, to evaluate feeding damage by soil-insect pests, implementing this approach accurately in mint was challenging given its dense, non-uniform root morphology (Oleson et al. 2005). The aggressive growth habit of mint may also make it difficult to assess root conditions for individual plants, especially once plants spread beyond planted rows and into a solid stand (Green and Erickson 1960). As a result, root biomass estimates provided a more efficient and accurate measure of below-ground plant performance than root rating in the present study.

The accuracy of plant height estimates (cup-cutter method only) never varied by more than 20% from the actual mean regardless of sampling intensity. Estimates of above-ground biomass (quadrat method) were similarly accurate, remaining within 20% of the actual mean, but the number of samples required to obtain accurate above-ground biomass estimates was marginally and consistently lower. This result suggests that above-ground plant biomass may provide more accurate and precise estimates of mint performance than plant height, and ultimately the quadrat method may provide marginal reductions in sampling intensity compared to the cup-cutter for plant performance variables.

The spatial distribution of insects and their damage can influence the relative utility of different sampling schemes when implemented at scale. For most variables evaluated in our study, a random sampling scheme was only marginally more accurate than a systematic sampling scheme (Fig. 4), with one exception: estimates of below-ground plant biomass gained from random sampling schemes were significantly more accurate than those gained from systematic sampling at an intensity of 30 samples/grid. While systematic sampling schemes are often deployed due to the speed and ease of implementation, random sampling schemes can sometimes provide less-biased population estimates (McGarvey et al. 2016). Previous studies comparing sampling schemes have reported mixed results, but in situations where insect populations are aggregated or rare, the benefits of random vs. systematic schemes may be marginal (Bourdeau 1953, Willers et al. 1990, Shah et al. 2012). For example, McGarvey et al. (2016) demonstrated that systematic sampling schemes increased precision when sampling aggregated populations, while random sampling schemes reduced sampling bias, often at the cost of precision. In contrast, simulations performed by Worner et al. (1999) and Shah et al. (2012), demonstrated that random sampling increased the probability of detecting target individuals occurring in aggregated distributions, providing evidence that systematic sampling may not always be more sensitive. We addressed this ambiguity directly by comparing the accuracy of random vs. systematic sampling schemes for estimating AGB larval density and plant performance parameters at a sampling intensity of thirty, which was above the breakpoint estimates for all response variables.

The ability to make sound IPM decisions relies heavily on the capacity of scientists and farmers to reliably estimate pest populations and their associated impacts on plant productivity. This is the first study to assess the impact of sampling intensity, method, and scheme on the accuracy and precision of larval AGB density and plant performance estimates in commercial mint. While the results of our study are limited to the context of mint fields with irrigated, sandy soils in Indiana, the literature strongly suggests that AGB is most problematic under exactly these circumstances, not just in mint but in corn as well (Hallock 1936b, MacKellar and DiFonzo 2018, Tiwari et al. 2019). Based on our knowledge of the distribution of scarab larvae, our findings indicate that mint farmers may be able to limit sampling efforts to AGB “hot spots” in the field, or to fields with a history of infestation, and focus on these areas to make management decisions (Potter et al. 1996, Dalthorp et al. 2000a). This remains to be tested and further work is needed to validate the utility of this sampling protocol to make predictions at larger spatial scales (field level). Regardless, results reported herein may be leveraged in the near term to support the development of a damage threshold and economic injury level for AGB larvae in commercial mint.

Supplementary data

Supplementary data are available at Journal of Economic Entomology online.

Author contributions

Connor Sturr (Conceptualization [equal], Data curation [lead], Formal analysis [lead], Investigation [equal], Methodology [equal], Visualization [lead], Writing—original draft [lead]), Douglas Richmond (Conceptualization [equal], Funding acquisition [lead], Investigation [equal], Methodology [equal], Project administration [lead], Resources [lead], Supervision [lead], Writing—review & editing [lead]), and Elizabeth Long (Conceptualization [equal], Funding acquisition [lead], Investigation [equal], Methodology [equal], Project administration [lead], Resources [lead], Supervision [lead], Writing—review & editing [lead])