Comprehensive Review of CO₂ Adsorption on Shale Formations: Exploring Widely Adopted Isothermal Models and Calculation Techniques

Abstract

The continuous use of fossil fuels has a huge impact on climate change because they release CO₂, which is a major greenhouse gas that causes 70–75% of global warming. Shale reserves could be used to store CO₂ to lower greenhouse gas emissions. This could happen mostly through adsorbed gas, which can make up about 85% of all shale gas. It is important to fully understand the CO₂ adsorption processes in shale, especially when using isothermal models, to get accurate estimates of storage capacity and predictions of how shale will behave. This work examines the application of several isothermal models, including Langmuir, Freundlich, Brunauer–Emmett–Teller, Dubinin–Radushkevich, Dubinin–Astakhov, Sips, Toth, and Ono-Kondo lattice models, to explore the adsorption of CO₂ on shale formations. The aim of this research work is to assess the efficiency of these models in forecasting CO₂ adsorption in different shale samples with specific mineral compositions, total organic content (TOC), surface areas, and pore geometry at 298 K and up to 2 MPa. This review provides a state-of-the-art knowledge on the constraints of existing models and proposes adaptations, such as integrating density-dependent correction factors and hybrid modeling techniques, to enhance precision during numerical simulation work. Furthermore, the possible incorporation of molecular dynamic (MD) simulations with experimental data is suggested to improve the understanding of the CO₂ adsorption in the geological rock at the molecular scale. The results emphasize the need for future studies to concentrate on the improvement of models and empirical validation to more accurately forecast the storage behavior of CO₂ in shale formations at resevoir conditions.

1. Introduction

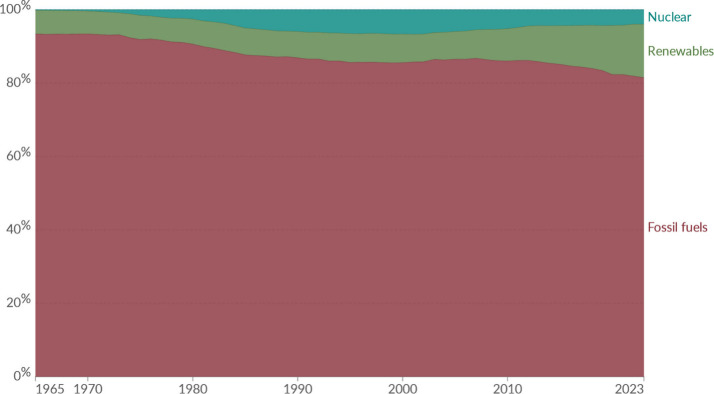
Fossil fuels remain a significant source of energy generation, fulfilling 84% of the energy needed until 2030 and the remaining will be fulfilled by renewable resources as illustrated in Figure 1.¹ Climate change is greatly impacted by the continued use of fossil fuels that emit CO₂. It is a key greenhouse gas (GHG) and accounts for 70–75% of emissions causing global warming; in that regard immediate environmental action is required to slow down it.² CO₂ emissions from burning of fossil fuels make up around two-thirds of the present GHG emissions. Numerous data sets indicate that the primary cause of the total increase in GHG emissions in 2023 was the growth in fossil CO₂ emissions, which increased by 0.8–1.5%.³⁻⁶

Figure 1.

Global trends of primary energy consumption. Reproduced from ref (17). Copyright 2024 Energy Institute. Licensed under CC BY 4.0.

Shale reservoirs have become a viable means of storing CO₂ to reduce GHG emissions.⁷⁻¹¹ The vast surface area, low porosity, and substantial organic content of these reservoirs increase their capacity to store CO₂.¹²⁻¹⁶ Gas stored in shale can be found in three different forms, (a) dissolved, (b) free, and (c) adsorbed gas, shown in Figure 2.¹⁸ Pores and natural or induced fractures usually store free gas, while adsorbed gas is stored by organic as well as inorganic material like clay, kerogen and dissolved gas in oil and water.¹⁹ Gas in adsorbed phase accounts for about 85% of the total volume of gas in shale.²⁰ For this reason, knowing how CO₂ adsorbs in shale is essential to accurately estimating storage capacity and forecasting shale behavior. Shale formations typically lie at 1000 to 3000 m depth having pressure up to 27 MPa. So, high pressure and temperature adsorption experiments are essential for understanding adsorption behavior in these formations. However, challenges, such as the lack of high-pressure equipment and insufficient high-pressure data for CO₂ adsorption in shale hinder comprehensive exploration and characterization.²¹

Figure 2.

Schematic representation of gas distribution in shale formations showing the natural fractures and matrix structure. Reproduced with permission from ref (22). Copyright 2013 Elsevier.

For understanding and calculating CO₂ adsorption on shale, isothermal models play a critical role. These models give the relation between the amount of gas adsorbed and the pressure while keeping temperature constant. Studies to characterize CO₂ adsorption on shale have used a variety of isotherms, notably Langmuir, Dubinin–Radushkevich (D-R), Freundlich, Dubinin-Astakhov (D-A), and Brunauer–Emmett–Teller (BET), each with certain assumptions and applicability.²³⁻²⁶ These models have varying degrees of success based on the characteristics of shale samples chosen and the methods of experiments adopted.

Recent research has greatly enhanced our comprehension of the process by which shale formations adsorb CO₂. Scientists analyzed the characteristics of CO₂ on shale at subcritical conditions by employing Langmuir, Ono-Kondo lattice (OK), D-A, and D-R models. Research findings of these studies revealed that the OK model had the highest level of accuracy, as evidenced by coefficient of determination (R²) values ranging from 0.95 to 0.99.²⁷ A separate study highlighted the significance of selecting the appropriate adsorption models for the analysis of experimental findings. The two models Langmuir and OK were determined to be suitable for representing CO₂ adsorption on Dadas formation samples at temperatures of 25, 50, and 75 °C.²⁸ Another researcher utilized multiple isotherm models at a temperature of 24.85 °C and pressure range of 0.1 to 2 MPa to examine the CO₂ adsorption capacity on shale samples CM03, CM07, SM05, and US03. Their investigation demonstrated a strong correlation between the desorption data and the adsorption results. The Langmuir, Freundlich, Sips, and Toth models provided a good fit for the data, with all models having R² values exceeding 0.95.²⁹

However, there are still notable deficiencies despite this progress. The majority of experiments have been carried out under subcritical conditions, indicating that the isothermal models developed are mainly derived from data obtained at low pressure and temperature. As a result, these models frequently fall short in precisely forecasting results in supercritical conditions. The behavior of CO₂ in supercritical states, which occur at elevated pressures and temperatures commonly found in deep shale formations, is not well understood and necessitates thorough investigation. The unavailability of high-pressure equipment and insufficient high-pressure data exacerbate this gap, impeding the thorough investigation and understanding of the CO₂ adsorption mechanisms under such settings.

Recent technological breakthroughs have started to tackle some of these deficiencies. Recent advancements in high-pressure adsorption apparatuses and sophisticated characterization techniques, such as micro-CT scanning and advanced spectroscopic approaches, have significantly improved the CO₂ adsorption investigation methods in shale at high pressures and temperatures. These technologies provide more precise measurements and provide enhanced understanding of the adsorption processes at the molecular level.^30,31

The objective of this research study is to fill the research gap mentioned by reporting a comprehensive review of the prevalent isothermal models used for calculating the adsorption of CO₂ on shale. The aim of this work is to improve the understanding of the CO₂ adsorption mechanisms in shale formations by examining their theoretical foundations and evaluating their effectiveness in different geological settings. The primary objective is to offer valuable insights and recommendations for future research to enhance the precision of storage capacity estimations and deepen our understanding of shale behavior during CO₂ adsorption.

2. Shale Gas Storage Mechanisms

Shale reservoirs store gas in different forms like free gas stored in pores and fractures, adsorbed gas stored in organic and inorganic minerals, and dissolved gas stored in oil and water.^32,33 This diversity in gas storage forms is crucial to understanding the adsorption capacity of shales, particularly for CO₂ sequestration applications. Accurately evaluating shale gas resources requires knowledge of the quantities and behaviors of gases stored in different forms, which can directly influence adsorption measurements and model accuracy. Several studies have emphasized the importance of understanding these gas storage mechanisms to improve the precision of adsorption capacity evaluations in shale formations.³⁴⁻³⁶

Adsorption in shale is influenced by the composition of percentage of organic matter, minerals, moisture content, amount of pore volume, and pressure and temperature conditions.^20,37,38 The ability of shale to adsorb is particularly altered by the percentage of organic matter and the amount of specific surface area. For instance, clays like illite and montmorillonite exhibit higher gas sorption capacities compared to kaolinite, which is particularly relevant for CO₂ adsorption studies in shale formations.^36,39 However, the presence of moisture can significantly reduce the adsorption of clay minerals due to water occupying adsorption sites, emphasizing the need for moisture-controlled experimental conditions.^39,40

The porosity of shale rock considerably significantly influence the gas adsorption process. It is divided into micropores (less than 2 nm), mesopores (between 2 and 50 nm), and macropores (greater than 50 nm). Among all pores, micropores having organic matter and clay minerals are intensely important for CO₂ adsorption due to their high surface area and affinity for gas molecules.⁴⁰⁻⁴³ While fractures can contribute to the overall surface area, their impact on gas adsorption is less understood but could potentially provide substantial adsorption sites especially under supercritical conditions relevant to CO₂ storage.

Furthermore, the shale adsorption capacity has a positive correlation with the total organic carbon (TOC) content. This relationship is influenced by variations in organic matter type, mineral composition, thermal maturity, and pore distribution. In formations with high maturity levels, such as the Upper Devonian Muskwa and Middle Devonian Besa River Formations high gas adsorption is attributed to significant kerogen aromatization and the presence of micropores.^36,39

3. Adsorption

The adherence of gases on the adsorbent surface is defined as adsorption.³⁰ The adsorption process has two primary components, (i ) the adsorbate that adsorbs onto the surface and (ii ) the adsorbent where adsorption occurs.^31,44,45 Adsorption occurs when the absorbent has a bond defect that facilitates the adsorbent capacity to thermodynamically adsorb the adsorbate.⁴⁶ Desorption happens when the adsorbate has sufficient energy to separate off the adsorbent surface and displace the force keeping it there. Equation 1 is the general mechanism of adsorption.^23,47

1

3.1. Types of Adsorption

Adsorption can be categorized into two primary categories: physisorption and chemisorption. In order to assess the adsorption capacity of various adsorbents and adsorbates, there are several adsorption isotherms available. The main adsorption types and adsorption isotherms are shown in Figure 5. A detailed explanation of the two types is provided below.

Figure 5.

Types of adsorption and isotherms with descriptions.

3.1.1. Physisorption

Physical adsorption also known as physisorption involves attachment of CO₂ molecules on the shale surface through weak van der Waals forces without the formation of chemical bonds.^48,49 This type of adsorption typically occurs at low adsorption enthalpies (20 to 40 kJ/mol), making it a reversible process.⁵⁰ Physisorption is characterized by formation of multiple layers of CO₂ on the shale surface; it is temperature-sensitive and tends to decrease as temperature rises.^47,51 This mechanism is particularly relevant in the context of CO₂ adsorption in shale, as it is commonly assumed by models such as BET and Freundlich, which predict adsorption based on multilayer formation on heterogeneous surfaces.⁵²Figure 3 illustrates the primary features of physisorption during CO₂ interaction with shale.

Figure 3.

Illustration of CO₂ adsorption (physisorption) mechanisms in shale. Reproduced from ref (23). Copyright 2020 Springer Nature.

3.1.2. Chemisorption

Chemisorption involves a stronger interaction where chemical bonds are formed between the CO₂ molecules and the shale surface. This process occurs at higher adsorption enthalpies (30 to 400 kJ/mol) and typically involves the formation of a single molecular layer on the adsorbent surface.^47,53 Chemisorption is considered irreversible due to the requirement for high activation energy to break these bonds. In the context of CO₂ storage in shale reservoirs, chemisorption may play a secondary role to physisorption but understanding its mechanisms can help in accurately predicting the total adsorption capacity in shale formations. Models that take into account the surface chemistry and specific interactions of CO₂ with shale minerals, such as the modified Langmuir or hybrid models could better predict adsorption behavior when chemisorption is significant.⁵⁴⁻⁵⁶Figure 4 outlines the primary features of chemisorption.

Figure 4.

Illustration of CO₂ adsorption (chemisorption) mechanisms in shale. Reproduced from ref (23). Copyright 2020 Springer Nature.

3.2. Molecular Simulation

MDs can significantly enhance the understanding of adsorption in shales at the molecular level, as they provide detailed insights for adsorption mechanisms. Recent studies employing simulations like MDs and Grand Canonical Monte Carlo (GCMC) have elucidated the interactions between gas molecules and the heterogeneous surfaces of shale formations. These simulations offer valuable data on the adsorption capacity, selectivity, and influence of pore size distribution and surface chemistry on adsorption behavior. For instance, Zeng et al. demonstrated through MD simulations that CO₂ and CH₄ exhibit different adsorption behaviors in organic nanopores highlighting the impact of pore structure on gas storage capacity.³¹ Similarly, Thomas reviewed the perspectives of gas adsorption and storage in kerogens and shales using advanced simulation techniques, providing a comprehensive understanding of the molecular-level interactions and their implications for CO₂ sequestration strategies.⁴⁵ Incorporating these simulation insights can bridge the gap between experimental observations and theoretical predictions, thereby optimizing the CO₂ storage and enhanced gas recovery processes in shale formations.

3.3. Isotherms of Adsorption

Adsorption isotherms are sorted into six types by the International Union of Pure and Applied Chemistry (IUPAC) based on the isotherm form due to relation between adsorbate and adsorbent, can be seen in Figure 5.⁵⁷ Many IUPAC categorized isotherms feature hysteresis loops, which suggest the presence of mesoporous material where capillary condensation adsorption takes place.⁵⁸ It is believed that the independent domain hypothesis, which states that the relative vapor pressure should be higher when the pores are filled than when they empty, is the primary factor in hysteresis.⁵⁹ The pore-blocking effect has the potential to enhance hysteresis as per the network theory.⁶⁰

3.4. Governing Equations for Adsorption

Adsorption can be broadly defined as adsorption of absorbent onto adsorbate as a result of a deficiency in bonds between the adsorbent and the adsorbate.⁵⁸Equation 2 displays the general equation for adsorption.

2

where V_ads is CO₂ adsorbed volume, V_gas is bulk phase volume, V_solid is shale volume in sample cell, and V_total is system volume as a whole.⁵⁶

There will be spaces between the shale grains when it is loaded in the sample cell, preventing the grains from filling the entire cell. Measuring these vacuum areas is essential, since failing to do so will result in an inaccurate adsorbent and adsorbate total volume. Equation 3 is used to calculate the void space volume.

3

where V_void is the void space volume.

Prior to the adsorption experiment, the empty space is often determined using helium (He) with very low adsorption potential. The temperature, pressure, volume, and compressibility of the gas in both the cell and pump are used to compute the void space volume. Equation 4 can be used to calculate the volume of void spaces.

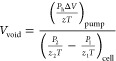4

where P₁ and P₂ represent pressure, and z with subscripts 1 and 2 represent compressibility of He before and after expansion, respectively. T is the cell temperature, and P_h is He pressure in pump.

Once the empty space has been determined, Equation 5 may be used to compute the number of moles of CO₂ absorbed.

5

where n_inj is CO₂ injected volume, n_unads is unadsorbed CO₂ volume, and n_ads is the adsorbed CO₂ volume.

Equation 6 is used to determine the number of CO₂ moles injected, which is the same for both the Gibbs and absolute calculation approaches.

6

where R is the universal gas constant and equals 8.314 J/(mol K).

3.4.1. Absolute Adsorption

When the unadsorbed volume is determined, absolute adsorption takes the adsorbed phase volume into account. As a result the value is higher than it would be with Gibbs adsorption. Equation 7 depicts that relation.¹⁶

7

where, V_gs is the cell total gas volume.

3.4.2. Gibbs Adsorption

This method is used to calculate the amount of CO₂ that has not been adsorbed. When calculating unabsorbed volume the Gibbs adsorption method does not calculate the adsorbed phase volume. Otherwise, the adsorption value will be lower than the absolute value because Gibbs calculation underestimates the amount of CO₂ that has been adsorbed. Equation 8 is used for calculating the Gibbs volume.⁶¹

8

In Equation eq 8, V_void takes the place of the V_gas. Due to its exclusive focus on the vacuum area within cells, this approach underestimates the anticipated adsorption value and fails to take into consideration the unadsorbed phase.

Equation 9 can be used to determine the unadsorbed volume of CO₂ in the context of Gibbs adsorption.⁵⁶

9

where P_af represents the pressure while z_af represents the compressibility.

Equation 5 can be used to compute the Gibbs adsorption, if the Gibbs unadsorbed CO₂ volume is known. The Gibbs adsorption value can be utilized to calculate the absolute adsorption by connecting the two values using Equation eq 10.⁵⁶

10

where ρ represents the variable for density. The determination of the adsorbed gas density (ρ_ads) is a challenging task, but it can be obtained by calculating the volume using the liquid density at its boiling point.⁶⁰

3.5. Impact of Supercritical CO₂

The transition of CO₂ to a supercritical state significantly impacts the pore structure, geomechanical properties, and wettability of the shale. Supercritical CO₂ (scCO₂) exhibits unique properties, such as higher diffusivity and lower viscosity compared to those of its liquid and gaseous states, which enhance its ability to penetrate and interact with shale formations. Studies have shown that scCO₂ can alter the pore structure by swelling organic matter and dissolving certain minerals leading to changes in porosity and permeability.^26,62 Geomechanically the injection of scCO₂ can induce stress changes in the reservoir, potentially affecting its stability and mechanical properties.^28,63 Additionally, scCO₂ can alter the wettability of shale surfaces which influences the adsorption capacity and fluid flow behavior.^64,65 These changes are crucial for optimizing CO₂ sequestration strategies and ensuring the long-term stability of the storage sites. It is crucial to include these factors in our understanding of CO₂ adsorption in shale in order to create precise models and forecasts of storage capacity.

3.6. Methods of Quantification

The amount of gas adsorbed in shale is often measured in the laboratory using volumetric or gravimetric adsorption experiments.^66,67 Because of its strong representativeness, the ability to achieve the necessary testing conditions of pressure and temperature, and other characteristics the volumetric method is widely used in industry.⁶⁸ The experimental arrangement for measuring the volumetric adsorption is depicted in Figure 6. This approach estimates gas adsorption by measuring the pressure between sample and reference volumes before and after gas expansion.

Figure 6.

Schematic diagram of the volumetric method. Reproduced from ref (70). Copyright 2023 Frontiers Media. Licensed under CC BY 4.0.

The volumetric adsorption equipment consists of a reference cell in which the CO₂ is heated to the predefined conditions, and then the desired pressure is applied. The reference and sample cells are linked by a high-pressure valve and the sample cell contains shale. To see enough gas expansion, the reference cell volume should be lower than that of the sample cell. This will make it easier to observe equilibrium pressure. The valve is opened to permit gas expansion after both cells are ready and the reference cell CO₂ has been heated and compressed. The adsorption value can be computed once the equilibrium pressure has been attained. Although the volumetric approach is extensively employed because of its many benefits, there are certain significant drawbacks that should be considered to prevent errors in the adsorption value.

Because of its precise estimating features, ease of operation, and shorter equilibrium time, the gravimetric method is also widely utilized in industry. This technique quantifies gas adsorption by measuring the quantity of gas adsorbed in relation to the applied pressure.²⁷ Magnetic suspension balance apparatus is frequently used to carry out gravimetric method of weighing measurements. The gravimetric technique measures adsorption using mass rather than pressure. By employing a microbalance to measure the mass differential, it is possible to calculate amount of gas that the shale has adsorbed.⁶⁹ The microbalance is used in place of the pressure transducers, which is the only setup variation from the volumetric setup. A schematic of the gravimetric adsorption measurement setup is shown in Figure 7.

Figure 7.

Schematic diagram of the gravimetric method. Reproduced from ref (65). Copyright 2021 American Chemical Society.

Both measurement techniques have a number of important benefits and drawbacks, and these should be understood before starting the experiment to prevent mistakes. Table 1 lists the advantages and disadvantages.^23,71,72

Table 1. Advantages and Disadvantages of Gravimetric and Volumetric Methods.

Volumetric Method	Gravimetric Method
Simpler setup, no complex tools needed	Extremely accurate microbalances
Larger volume of adsorbent required	More complex usage
Streamlined measurement with calibrated transducers	Only milligrams of adsorbent needed
Challenging equilibrium tracking	No wall adsorption issues in single-component measurements
Cell wall adsorption can be adjusted in calculations	Requires monitoring of multiple parameters and calibrations
Low frequency recording	High-frequency kinetics recording

4. Modeling Approaches

4.1. Isothermal Models

Isothermal adsorption models provide a mathematical framework to describe the interaction between adsorbates and adsorbents. These models are essential for calculating the amount of CO₂ stored in shale strata. The common models used for CO₂ adsorption on shale include Langmuir, Freundlich, D-A, D-R, Sip, Toth, BET, and OK models.^73,74 The Langmuir model is a popular model used to determine the amount of CO₂ adsorbed on the shale surface. The BET model represents multimolecular layer adsorption and is mostly applied to low-temperature nitrogen adsorption. Many researchers have applied Langmuir, D-R, and D-A models to investigate CO₂ adsorption on shale at pressures less than 12 MPa.²⁷Table 2 shows the summary of isothermal models with their linear and nonlinear equations, applicability, and limitations.

Table 2. Isothermal Models Used for Modeling of CO₂ Adsorption on Shale^{57,60,75,76,80,92,93}.

isotherm model	description	linear	nonlinear	limitations
Langmuir	Describes adsorption of gas molecules on solid surfaces. It assumes that adsorption takes place at homogeneous sites.			Presupposes monolayer adsorption with no interactions between adsorbed molecules on a homogeneous surface. It is not applicable to heterogeneous surfaces or multilayer adsorption. At high pressures, where multilayer adsorption becomes substantial, the model breaks down.
Freundlich	Describes solutes interacting with a solid surface, particularly the adsorption process. It is one of the oldest and simplest models to explain the adsorption characteristics. The model assumes that the surface is heterogeneous and heat of adsorption is distributed unevenly.			A theoretically unfounded empirical model that suggests it is unable to forecast the adsorption mechanism. It is less useful at larger concentrations since it does not explain saturation, just suggesting adsorption on heterogeneous surfaces.
D-R	Utilized in the investigation of vapor and gas adsorption on uneven surfaces. In contrast to more basic models such as Freundlich or Langmuir isotherms, the D-R model takes into consideration both the porosity and heterogeneity of the adsorbent material.			Assumes a heterogeneous surface with a Gaussian energy distribution, which is more appropriate for subcritical vapor adsorption. Particularly at higher pressures, it might not be able to forecast the adsorption process with complete accuracy for all types of adsorbates.
D-A	Describes an adsorption process where a substance adheres to the surface of a solid. The D-A model is especially relevant for microporous materials, where it can accurately predict the adsorption behavior within the pores.			Expansion of the D-R isotherm that adds a new parameter in an effort to overcome some of its shortcomings. Still, it makes an assumption about a certain kind of energy distribution, thus it might not apply to other adsorbent–adsorbate systems, especially those with intricate interactions.
Sip	Hybrid of Freundlich and Langmuir models that is intended to accurately represent adsorption processes across a broad concentration range. It assumes that the surface is energetically heterogeneous and the adsorption process is localized (i.e., there is no adsorbate transmigration in the plane of the surface).			Hybrid of the Freundlich and Langmuir isotherms that is intended to forecast heterogeneous adsorption at both high and low concentrations. For some systems, its complexity and requirement for several parameters may make it less useful.
Toth	An extension of the Langmuir that assumes a surface with identical sites, and each can hold only one adsorbate molecule. The Toth model, however, modifies this by incorporating a distribution function for the energy of adsorption sites, which accounts for the heterogeneity of real surfaces.			Specially designed to provide a more flexible fit than the Langmuir model for adsorption on heterogeneous surfaces. Its presumption that the adsorption energy will drop smoothly and continuously might not apply to all heterogeneous surfaces, though.
BET	Extends the Langmuir theory to multilayer adsorption with the assumption that the adsorbate molecules form a multilayer on the adsorbent surface. In this first layer of adsorbate it behaves similarly to the Langmuir model, adhering directly to the solid surface. Additional adsorbate layers can then form on top of the first. This model is applied where the adsorption process is physisorption, involving relatively weak van der Waals forces.			Presumes multilayer adsorption, mostly useful in a narrow range of relative pressures. At very low or high relative pressures, where monolayer or capillary condensation events predominate, respectively, it is unable to anticipate adsorption with any degree of accuracy.
OK	Based on a well-developed lattice theory, the Ono-Kondo model describes adsorption behavior in both monolayer and multilayer formats. It describes adsorption behavior based on the physical properties and accessible characterization of the adsorbent and makes predictions under a variety of circumstances			Less useful for heterogeneous surfaces and complicated interaction situations due to its assumptions about homogeneous adsorption sites and simpler interactions. Its practicality in real-world scenarios is further impacted by the difficulty of parameter estimation.

4.1.1. Langmuir Isotherm

The purpose of the Langmuir model is to determine the adsorption behavior between gaseous and solid phases. It is also used to compare and quantify the adsorptive capabilities of various adsorbents.⁷⁵ By maintaining balance between adsorption and desorption rates (dynamic equilibrium), the Langmuir isotherm explains the surface coverage. Adsorption is directly proportional to the fraction of adsorbent surface that is exposed while desorption is inversely proportional.⁷⁶Equation 11 presents the Langmuir linear form:

11

where C_e is the equilibrium concentration in (mg/g), K_L is the Langmuir constant in (mg/g), q_m is maximum adsopriton and q_e is adsoprtion capacity.

Zhou et al. used the Langmuir model to examine CO₂ adsorption on shale which shows strong correlation in the fitting curves reflecting the effectiveness of the model at subcritical pressures.²⁷ In contrast another study indicated varying degrees of fit for PAK and SLP shales with R² value 0.994, highlighting the model representational effectiveness.⁷⁷ Chi et al. found that the Langmuir + k model aligns well with CO₂ experimental adsorption data with Average Absolute Deviation (AADs) ranging from 2.12% to 3.10%.⁷⁸ However, the Langmuir model effectiveness decreased at high temperatures and pressures, particularly in the supercritical/liquid region failing to capture the unique adsorption characteristics of CO₂.^28,65 This limitation is attributed to the surface heterogeneity of shale at 150 °C, where the Langmuir application is not applicable.⁷⁹

High R² values in the Langmuir model, which matches CO₂ adsorption on shale quite well indicate strong model alignment especially at higher temperatures of 80 °C as shown in Figure 8. The results show that while overall adsorption volume and adsorption stability decrease with increasing temperature, the Langmuir model fits better at higher temperatures more in line with theories of monolayer adsorption.⁶⁵

Figure 8.

Fitting results of the Langmuir model for CO₂ adsorption on shale. Data extracted from ref (29). Copyright 2020 Elsevier.

4.1.2. Freundlich Isotherm

Based on experimental findings, Herber Freundlich proposed the Freundlich isotherm model. Studies of adsorption for heterogeneous and rough surfaces can benefit from the application of this model.⁷⁵Equation 12, which is not limited to the creation of monolayers, is the oldest known description of nonideal and reversible adsorption.⁸⁰ The following is the Freundlich isotherm.⁸¹

12

where 1/n and K_F represent the adsorption intensity and adsorption capacity, respectively.

The Freundlich model superior fit to experimental data on shale samples is attributed to its ability to better account for surface heterogeneity, characterized by diverse minerals and organic matter. This adaptability makes the Freundlich model more aligned with the complex nature of shale as opposed to other models that may oversimplify these characteristics.⁷⁹

In order to emphasize various TOC levels and maturities, the study investigated the adsorption of CO₂ on shale samples at varying temperatures (50, 100, and 150 °C). It demonstrated that CO₂ has a high capacity for adsorption, which makes storage in shale appropriate for CO₂. Temperature has a major effect on adsorption because different gases absorb different amounts of heat. Clay in shale may prevent CO₂ from adhering because of its swelling properties. The adsorption of shale is more accurately represented by the Freundlich and BET isotherms, as shown in Figure 9; rather than the Langmuir isotherm.⁷⁹

Figure 9.

Fitting results of the Freundlich model of CO₂ adsorption on shale. Data extracted from ref (79). Copyright 2020 Elsevier.

4.1.3. Dubinin–Radushkevich Isotherm

D-R is an empirical model that uses Gaussian energy distribution for representing the adsorption mechanism on heterogeneous surfaces.⁷⁵ This isotherm, models adsorption as a pore filling mechanism in a semiempirical equation and is only suitable for an intermediate range of adsorbate concentrations since it exhibits implausible asymptotic behavior and cannot predict Henry’s laws at low pressure.⁸⁰ This basic equation applies to physical adsorption processes, assumes a multilayer character involving van der Waal’s forces, and qualitatively characterizes the adsorption of gases and vapors on microporous sorbents.⁷⁶Equation 13 is the mathematical representation of the D-R isotherm.⁸²

13

where B is activity coefficient or adsorption energy constant and n is hetrogenity parameter. The study fitted the CO₂ adsorption data on shale using Langmuir, Freundlich, BET, D-A, D-R, and OK models. Freundlich and D-A models proved to be the most successful at a pressure range of 1–4 MPa as shown in Figure 10. While the performance of BET was less than desirable within the range of 0–5 MPa, the Langmuir, D-R, and OK models accurately predicted adsorption. This comparison research helps to clarify the adsorption behavior of shale especially under near-critical conditions.⁸³

Figure 10.

Fitting results of the D-R model of CO₂ adsorption on shale. Data extracted from ref (83). Copyright 2022 Elsevier.

4.1.4. Dubinin–Astakhov Isotherm

When examining the adsorption of gases onto microporous material, the D-A model Equation eq 14 is frequently used. The D-A equation is represented by the following expression:⁷⁵

14

where n_DA is a heterogeneity parameter, q_m represents the maximal adsorption capacity, measured in milligrams per gram (mg/g), ε_DA is the adsorption potential (kJ/mol), and E_DA is the system’s characteristic energy (kJ/mol). The adsorption potential where C_s,DA is measured, given by Equation eq 15, is the highest degree of adsorbate solubility.

15

The D-A model demonstrated better overall fitting performance for CO₂ adsorption on shales compared to the D-R model, particularly at high pressures. The D-A model parameter n varied for CO₂ (0.698–1.452), reflecting the structural heterogeneity of different shales. This adaptability contributed to the model accuracy. In contrast the D-R model fixed n value of 2 lead to less accurate fits especially for CO₂ adsorption data. The D-A model flexibility in accounting for shale variability resulted in more accurate adsorption isotherms.²⁷ D-A had moderate to good fit, with R² values of 0.953 for PAK shale and 0.993 for SLP shale from Damodar Valley basin, India. indicating a slightly less consistent performance compared to other models.⁷⁷ The study by Xie et al. employed experimental setups and theoretical models to understand gas adsorption behaviors. The methodology included high-pressure isothermal adsorption experiments using shale samples from the Longmaxi Formation, assessing adsorption under various pressures (0–25 MPa) and temperatures (30–100 °C). Models such as Langmuir, BET and D-A were fitted to the experimental data evaluating their applicability through R² values. Key results revealed distinct adsorption behaviors for CO₂, with CO₂ showing higher adsorption affinity influenced by pressure and temperature. The D-A model has significant flexibility under a variety of settings, according to the study which evaluated the fitting effectiveness of several models. Figure 11 illustrates how well the D-A model fits the data for CO₂ adsorption in shales after being skillfully modified for high-temperature CO₂ adsorption. Its R² values for CO₂ were from 0.9864 to 0.9964 illustrating the model reliability and broad applicability. Notably, the model efficacy remains unaffected by temperature variations, reinforcing its suitability across a range of conditions and aligning well with the micropore filling theory in shale adsorption studies.⁶⁵

Figure 11.

Fitting results of the D-A model of CO₂ adsorption on shale. Data extracted from ref (27). Copyright 2019 Elsevier.

4.1.5. Sips Isotherm

The Freundlich and Langmuir isotherms are combined to generate the hybrid Sips isotherm model.^75,80 It is a suitable isotherm to forecast how heterogeneous structures would adsorb substances without encountering the rising adsorbate concentration limitation that the Freundlich isotherm does. The Sips isotherm can be a reliable predictor of a monolayer adsorption system since at low and high concentrations, it changes into the Freundlich and Langmuir isotherms, respectively.⁷⁵ The generic Equation eq 16 below represents the mathematical form of the Sips model.⁸⁴

16

where a_s is the Sips constant. Equation 17 is the linearized form of Sips model.⁸²

17

As can be shown by a good fit across a pressure range of 0 to 2 MPa, the Sips model in Figure 12 closely matches the experimental data, suggesting it accurately describes the material adsorption behavior with CO₂. It appears that the material has a significant capacity for CO₂ or may need higher pressures to attain saturation, because it shows a growing adsorption capacity with rising pressure and does not approach saturation within the measured range. This behavior points to possible useful application in fields where effective gas adsorption is crucial. It also shows a significant initial affinity for CO₂ that progressively levels off.

Figure 12.

Fitting results of the Sips model of CO₂ adsorption on shale. Data extracted from ref (29). Copyright 2020 Elsevier.

4.1.6. Toth Isotherm

József Tóth presented the Toth isotherm model based on a quasi-Gaussian energy distribution theory in 1995.⁸⁰ The Toth model is an additional empirical equation that was created to enhance the fitting of the Langmuir model based on experimental data. It is helpful in characterizing heterogeneous adsorption systems that meet both high and low concentration boundaries.⁸⁵ The expression for the Toth isotherm model is as follows shown in Equation 18:

18

where the Toth constants, K_L and n, are expressed in terms of mg/g.

It is clear that this equation reduces to the Langmuir model when n = 1. Thus, the heterogeneity of the adsorption system is characterized by the parameter n, and the system is considered heterogeneous if it deviates farther from 1. The Toth isotherm can be rearranged in the following Equation 19 to produce a linear form.⁷¹

19

The graph shown in Figure 13, with a persistent strong connection between the Toth model fit and the experimental data for CO₂ adsorption on a material from 0 to 2 MPa indicates that the Toth model is a reliable description of the adsorption properties of the material. The increasing adsorption capacity with pressure is suggestive of a fast uptake at first because of the high-energy sites. However, this uptake eventually tapers off suggesting that maximum capacity may be approached without reaching a clear saturation point within the pressure settings examined.

Figure 13.

Fitting results of the Toth model of CO₂ adsorption on shale. Data extracted from ref (29). Copyright 2020 Elsevier.

4.1.7. BET Isotherm

The BET isotherm, which is used to describe the adsorption of gaseous substances was developed based on the multimolecular adsorption hypothesis in 1938 by Brunauer, Emmet, and Teller.⁸⁶ Brunauer et al. established a classification of five isotherms to describe physical adsorption systems. They took into account two pressure zones for adsorbing gas components into the adsorbents. At temperatures around the point of condensation, the isotherms exhibited a concave shape at low pressures and a convex shape at high pressures. On a molecular size scale the convex shape of the isotherms at high pressures can be linked to the liquid state of components that are condensed in adsorbent capillaries.⁷⁵ Systems made up of ionic adsorbent and a nonpolar molecule adsorbate experience a multimolecular adsorption layer due to the capillary condensation action. The first layer of adsorption is polarized by the surface layer of the adsorbent leading to the polarization of subsequent layers of adsorption. The BET model in its most general version can be seen in Equation 20.⁸⁷

20

The values q_m, C_e, and C₀ represent the maximal adsorption capacity, monolayer concentration, and BET adsorption constant, respectively. The BET model encompasses relative pressures (P/P₀) ranging from 0.05 to 0.3.

One of the primary applications of the BET isotherm is to determine specific surface area, pore size, and shape of porous adsorbent. In a low temperature device the measurement of partial pressures is conducted by manipulating the pressure of a gas (often nitrogen gas at 77 K) by an adsorption/desorption process. The morphology and characteristics of pores can be elucidated by comparing the resulting adsorption/desorption isotherm with the five standard BET isotherm curves.⁷⁵

The BET model performance in fitting CO₂ adsorption data exhibits noteworthy effectiveness, especially in scenarios involving multilayer adsorption. For CO₂ adsorption on PAK and SLP shales this model achieved exceptional R² values of 0.995 and 0.997.⁷⁷ This adaptability suggests a propensity for multilayer adsorption at lower temperatures, underlined by the model’s consistent high performance in CO₂ adsorption fitting, where R² values varied from 0.9840 to 0.9967.⁶⁵ This analysis underscores the versatility and precision of the BET model in capturing diverse adsorption behaviors.

In order to emphasize various TOC levels and maturities, the study investigated CO₂ adsorption on shale samples at varying temperatures of 50, 100, and 150 °C. It was found that CO₂ has a high affinity for adsorption which makes shale suitable for CO₂ sequestration and increased gas recovery. Temperature has a major effect on adsorption, because different gases absorb different amounts of heat. Shale clays may prevent CO₂ from adhering, because of their swelling properties. Shale adsorption is found to be better described by the BET isotherm shown in Figure 14; than by the Langmuir isotherm.⁷⁹

Figure 14.

Fitting results of the BET model of CO₂ adsorption on shale. Data extracted from ref (88). Copyright 2016 American Chemical Society.

4.1.8. Ono-Kondo model

Density changes in a gas–liquid interface were first described by the OK lattice theory. Aranovich et al. used the OK model to investigate gas adsorption on microporous materials.⁸⁹ Derived from a comprehensive lattice theory, the OK model describes adsorption behavior in both monolayer and multilayer formats. It describes adsorption behavior based on the physical properties and accessible characterization of the adsorbent and makes predictions under a variety of circumstances. Equation 21 displays the OK model.²⁷

21

The variables T, k, n_abs, n₀, ρ_f, and ρ_a represent the absolute temperature in Kelvin, molar density of free gas, maximum monolayer saturation adsorption, and molar density of fluid adsorption in mol/L, respectively.

Gas adsorption may be simulated using the OK model; however, model parameters need to be carefully considered. The high-precision state equation can be utilized to calculate ρ_f. The OK hypothesis states that ρ_a is analogous to the density of the adsorption phase in the critical state of a gas. Nevertheless, under a specific crucial situation the CO₂ adsorption phase density cannot be ascertained through the use of gas state equations. The van der Waals equation shown in Equationeq 22 can be used to get ρ_a for the CO₂ gas.⁹⁰

22

where P_c and T_c denote the critical pressure and temperature, respectively. In the critical state, the computed phase density of CO₂ is 23.34 mol/L. The least squares approach can be used to determine the two unknown parameters, n₀ and ε_s, as the parameters were acquired accurately.⁹¹

CO₂ adsorption on shales was examined using the OK model, which has two important parameters, n₀, the saturated adsorption density of a monolayer, which indicates maximal monolayer adsorption capacity, and an interaction energy parameter connected to the adsorbed gas and shale micropores. Models that fit the experimental data demonstrated a strong correlation. The R² values ranged from 0.9516 to 0.9992, suggesting that this model provides an effective fit.²⁷ The model’s somewhat higher AADs for CO₂ (2.70–3.79%) suggested that there was a greater affinity and interaction energy between CO₂ and shale, which affected the behavior and rate of adsorption shown in Figure 15.⁷⁸ The CO₂ adsorption data on Dadas formation samples at various temperatures were well-fitted by this model. They offered a more realistic depiction of the behavior of CO₂ in various circumstances, particularly at greater pressures.²⁸

Figure 15.

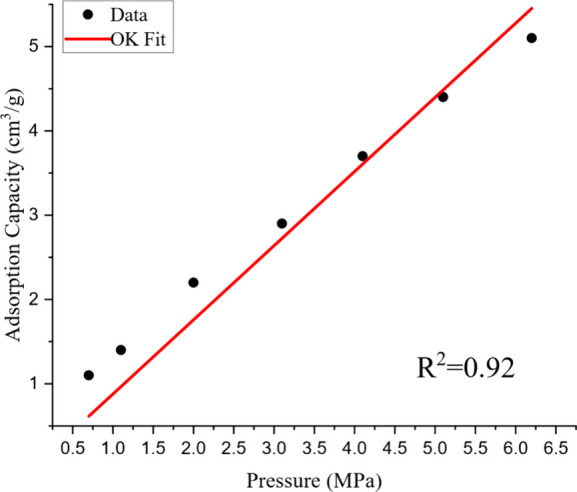
Fitting results of the OK model of CO₂ adsorption on shale. Data extracted from ref (27). Copyright 2019 Elsevier

4.2. Evaluation of the Isothermal Adsorption Models

The CO₂ adsorption capabilities of shale samples from the Marcellus and Le-Roy formations in the United States were examined in our study. The TOC content, mineral composition, surface area, pore volume, and average pore size of these samples and adsorption capacity graph against pressure were drawn at a constant temperature of 298 K. The samples showed a wide range of mineral concentrations and TOC variations, ranging from 3.28% to 16.2%; Table 3, highlighting the variety of geological settings from which they were taken.

Table 3. Origin, TOC Content, and Physical Characteristics of the Shale Samples.

sample	TOC (wt %)	pick up location	origin	feldspar	calcite	illite	kaolinite	smectite	surface area (m2/g)	pore volume (cm3/g)	average pore size (nm)
CM03	3.6	Le-Roy Formation	USA	12		43	5	25	17.5637	0.020818	4.74114
CM07	3.28			26	5	48	11		14.4316	0.016796	4.69346
SM05	13.8	Union springs Formation		40	24	9		12	21.076	0.017206	3.26549
US03	16.2			4	10	50	2		41.5686	0.029139	2.80398

Data adapted from ref (29). Copyright 2020 Elsevier.

In order to assess these samples ability to absorb CO₂ their physical properties are essential. As an illustration, sample CM03 has a TOC of 3.6%, a large surface area of 17.5637 m²/g and a considerable amount of illite. On the other hand sample US03 had the lowest average pore size of 2.80398 nm among the samples examined and the largest surface area of 41.5686 m²/g with the highest TOC of 16.2%.

All samples had an increase in adsorption capacity with pressure, according to the empirical data shown in Figure 16, with capacities ranging from 13 to 20 cm³/g. The straight relationship between pressure and the increase in CO₂ adsorption shows how highly suitable these shales are for sequestering CO₂ under the investigated circumstances. Because of its large surface area and high illite concentration, CM03 demonstrated a noteworthy ability for CO₂ adsorption. Because of its high feldspar and illite contents, CM07 showed enhanced adsorption capabilities at higher pressures. With a high TOC and a mineralogy that included both feldspar and calcite, SM05 showed a clear adsorption tendency. The highest surface area and pore volume were found in US03, which most likely had a major impact on its adsorption behavior. The tendency of adsorption to increase with pressure indicates that the storage capability of hydrocarbons is not only determined by TOC. As an alternative our results demonstrate how important a range of properties are for CO₂ adsorption such as surface area, pore structure, and mineral composition.

Figure 16.

Adsorption of CO₂ on CM03, CM07, SM05, and US03 Marcellus samples at 25 °C and up to 2 MPa pressure. Data extracted from ref (29). Copyright 2020 Elsevier.

4.3. Nonlinear Isotherm Fitting and Analysis

A suite of eight isotherm models including Langmuir, Freundlich, Sips, Toth, D-A, D-R, BET, and OK was utilized in order to successfully carry out the examination of the CO₂ adsorption behavior for a variety of shale samples. This was accomplished through the use of nonlinear fittings. The purpose of this fitting was to determine whether or not each model was compatible with the actual data that was gathered from the Marcellus shale deposits, which were maintained at a constant temperature of 298 K.

The adsorption data of shale sample CM03 was analyzed using several isotherm models shown in Figure 17. The results indicate that the BET and Sips models had the greatest R² values suggesting a good match with the experimental data. Given the sample intricate pore structure and varied adsorption site affinities, it appears that models that take into consideration heterogeneous adsorption processes and maybe multilayer adsorption adequately capture CM03 adsorption behavior. Although the R² values of the Langmuir and Toth models are marginally lower, they nevertheless demonstrate a high association. Nonetheless, the adsorption features of CM03 may not be entirely captured by their simple assumptions. Furthermore, the D-A, D-R, and OK models also match well suggesting that their hypotheses regarding the distribution of adsorption energy and the properties of the pore structure agree with the CM03 behavior to some extent.

Figure 17.

Isotherm modeling of CO₂ adsorption on CM03. Data extracted from ref (29). Copyright 2020 Elsevier.

The CM07 shale sample adsorption data was analyzed using a variety of isotherm models. The results in Figure 18 showed that the Freundlich and Sips models had the highest R² values 0.99 and 0.9971, respectively, suggesting a very good match to the data. This implies that models that consider heterogeneous surfaces and pressure-dependent adsorption properties properly predict the adsorption behavior of CM07. With R² values of 0.98, the D-R and BET models also show strong fits, indicating a large microporous percentage and possible multilayer adsorption, respectively. In contrast, the Langmuir, Toth, and OK models show somewhat lower but still good fit with R² values of 0.90. But the D-A model has the lowest R² value of 0.85, suggesting a poor fit that could be brought about by inconsistencies between the model presumptions and the physical characteristics of the CM07 sample. The heterogeneity of adsorption sites and possible multilayer adsorption are highlighted by the best-fit models for CM07 overall, reflecting the sample porous structure and surface characteristics. Conversely, less accurate models might miss some subtleties, like the presence of meso- and macropores or nonuniform energy distributions. Comprehending these differences is essential for enhancing CO₂ sequestration tactics and accurately forecasting the adsorption behavior.

Figure 18.

Isotherm modeling of CO₂ adsorption on CM07. Data extracted from ref (29). Copyright 2020 Elsevier.

The adsorption data of shale sample SM05 was analyzed using isotherm models and the results are shown in Figure 19; the Freundlich and D-R models had the greatest R² values 0.99 and 0.98, respectively, suggesting a good match. These models, which are optimized for microporous materials and heterogeneous surfaces successfully represent the variety of adsorption sites and possible microporous nature of SM05. Furthermore, the R² values of 0.90 for the BET, Langmuir, Toth, and OK models show decent fits indicating that these models can describe the adsorption behavior but not as well as the D-R and Freundlich models. In contrast the R² values of the Sips and D-A models are lower at 0.85 and 0.88, respectively. This suggests that the models match the data less well and that the assumptions made may not adequately account for the unique features of SM05 adsorption behavior. Overall, the analysis indicates that models that consider heterogeneous surface energies and possibly varying pore sizes best describe SM05 adsorption capacity. These models reflect complex interactions between CO₂ molecules and the sample surface, providing information that can be used to optimize CO₂ sequestration techniques for shale formations that are similar to those of SM05.

Figure 19.

Isotherm modeling of CO₂ adsorption on SM05. Data extracted from ref (29). Copyright 2020 Elsevier.

The US03 shale sample CO₂ adsorption data was analyzed using isotherm models. The results showed that the Freundlich, Sips, and D-R models had the best R² values of 0.99, 0.9971, and 0.98, respectively, indicating excellent fits as shown in Figure 20. These models accurately represent the intricate adsorption behavior of US03 taking into consideration surface heterogeneity and microporous structures. With R² values of 0.90, the Langmuir and Toth models likewise offer decent fits; nevertheless, they are marginally less accurate than the previously discussed models, maybe because of their simplifying assumptions. Likewise, the R² value of 0.90 indicates that the BET and OK models fit well pointing to multilayer adsorption mechanisms on US03. On the other hand, D-A model has a lower R² value of 0.88, which highlights discrepancies between its assumptions and the adsorption properties of the sample and indicates a less effective fit. All things considered, the models that suit US03 best highlight the significance of taking into account surface heterogeneity and the possibility of both monolayer and multilayer adsorption, offering valuable information that is essential for maximizing CO₂ collection and storage tactics in shale formations such as US03.

Figure 20.

Isotherm modeling of CO₂ adsorption on US03. Data extracted from ref (29). Copyright 2020 Elsevier.

These findings provide insight into the complex nature of adsorption processes in shale formations and demonstrate that there is no one model that can fully represent the adsorption process across all samples. Different adsorption capacities and behaviors are caused by the distinct mineralogy and TOC of each formation. Because of this, it is necessary to employ a variety of analytical methods to obtain a comprehensive understanding of the gas adsorption potential.

4.4. Comparative Analysis of Model Fitting

Shale samples have unique attributes in terms of the TOC, mineral composition, surface area, pore volume, and average pore radius. These variations impact the adsorption characteristics and the accuracy of model fitting.^23,36,54

The Sips and Freundlich models are the most suitable for CM03, as they accurately represent both high and low concentration adsorption situations and appropriately consider surface heterogeneity as shown by their high R² values in Figure 17.²⁶ This heterogeneous surface is likely influenced by the presence of smectite, which enhances the applicability of the Freundlich model.¹⁹ The Sips model excels in its capacity to smoothly switch between Langmuir and Freundlich behavior, thereby accurately representing the subtle dynamics of adsorption at various pressures.

As for CM03, Freundlich and Sips models offer the most suitable match for CM07, as they accurately represent the diverse surface characteristics of the sample caused by the substantial presence of illite. The D-R model good fit is most likely attributed to the microporous structure impacted by illite and kaolinite, which impact the pore-filling mechanism.⁷⁸ The reduced surface area and pore volume in comparison to those of CM03 may somewhat decrease the adsorption capacity, factors that are accurately accounted for by the Freundlich and Sips models.

Due to its capacity to support both monolayer and multilayer adsorption the Sips model is well-suited for SM05, particularly for organic-rich shales with large surface areas and intricate pore architectures.³⁶ The BET model is particularly suitable for accurately representing multilayer adsorption on uniform surfaces, which corresponds to the occurrence of non-clay minerals such as feldspar and calcite.²³ The moderate fits of the Toth model, which accounts for surface heterogeneity are probably attributed to the relatively smaller fraction of clays.

The excellent performance of the Sips and D-R models for US03 can be credited to its high surface area and microporous structure which promote heterogeneous adsorption. The small pore size and TOC indicate significant microporosity making the D-R model, which assumes a Gaussian energy distribution in microporous material very suitable.³⁶ Due to its flexibility in simulating both monolayer and multilayer adsorption, the Sips model also demonstrates a strong fit. Nevertheless, the OK model, which was specifically developed for microporous materials, has a suboptimal performance, sometimes attributed to certain interactions that are not completely accounted for in the model.

The comparison analysis shows that the selection of the isothermal model should be closely consistent with the particular attributes of the shale sample, including TOC, mineral composition, surface area, and pore size distribution.⁸¹ The Sips and Freundlich models consistently yield the most accurate predictions for most samples, demonstrating their adaptability to represent both high and low concentration adsorption situations and accommodate variations in surface properties.³⁵ The D-R model is more efficient for samples with greater microporosity and TOC, where adsorption occurs mostly in microporous geometries. Accurate predictions of the CO₂ adsorption behavior in shale formations can be achieved by selecting a suitable model according to the characteristics of the sample.

4.5. Sensitivity Analysis

To gain a deeper understanding of how particular features of shale samples impact the accuracy of the isothermal model fitting, a sensitivity analysis was performed. The present study investigates the impact of several parameters, including TOC, mineral content, surface area, pore volume, and average pore size, on the precision and appropriateness of several isothermal models in forecasting CO₂ adsorption.

4.5.1. Total Organic Carbon

The high TOC observed in samples SM05 (13.8 wt %) and US03 (16.2 wt %) increases the ability to adsorb substances because of the greater abundance of organic material which offers a greater number of adsorption binding sites.^23,36 Increased TOC results in improved fitting accuracy for the Freundlich and D-R models.¹⁹ These models are capable of handling the intricacies related to heterogeneous adsorption sites and changing the energy distributions. The Sips approach maintains its effectiveness by virtue of its adaptability in managing concentrations ranging from low to high. Conversely, the Langmuir model that assumes uniform adsorption exhibits slightly decreased precision with increasing TOC values. This is because this model fails to consider the increasing surface heterogeneity that is observed at higher TOC levels.

4.5.2. Mineral Content

The adsorption behavior is extensively influenced by the presence of particular minerals, such as illite and smectite.³⁶ Samples CM03 and CM07, which contain significant amounts of illite and smectite, demonstrate strong compatibility with the Freundlich and Sips models, which are robust in addressing surface heterogeneity. Conversely SM05, which contains a significant amount of feldspar and calcite is more compatible with the BET model, which is more appropriate for multilayer adsorption on surfaces that are more uniform. Shale samples containing significantly high clay mineral content, such as illite and smectite exhibit improved compatibility with models that consider the presence of diverse surfaces and the distribution of adsorption energy, such as Freundlich, Sips, and D-R.^19,78

4.5.3. Surface Area

The surface area is measured in the number of adsorption sites. Higher surface areas, as seen in sample US03 (41.57 m²/g), support models that may explain significant adsorption including multilayer adsorption, which is effectively represented by the BET model.⁸¹ As a result of its capacity to simulate both monolayer and multilayer adsorption, the Sips model also benefits from large surface areas. Typically, an increase in surface area enhances the performance of models that take into account several adsorption layers or diverse adsorption sites such as BET and Sips. By contrast, models such as Langmuir that posit a solitary layer of adsorption exhibit less sensitivity or accuracy as the surface area increases owing to their restricted scope.

4.5.4. Pore Volume and Pore Size

Pore volume and pore size distribution have a substantial impact on adsorption capacity and accuracy of isothermal model implementation.¹⁹ Samples exhibiting lower pore sizes, such as US03 (2.80 nm) demonstrate compatibility with the D-R model which is well tailored for materials with microporous structures. The suitability of the Freundlich model is attributed to its capacity to encompass a broad spectrum of adsorption energies linked to different grain sizes. Shales characterized by larger pore volumes and smaller pore sizes have greater sensitivity to models that consider microporosity and adsorption energy distributions, such as the D-R and Freundlich models. In contrast, the efficacy of these models is diminished by larger pores and smaller pore volumes as documented in samples with a higher mineral content and larger pore shapes, such as SM05.

Sensitivity analysis shows that the accuracy of fitting isothermal models to adsorption data is greatly influenced by shale properties, such as TOC, mineral content, surface area, pore volume, and pore size. Models such as Freundlich, Sips, and D-R, which consider surface heterogeneity adjustable adsorption energies, and microporosity, exhibit greater responsiveness to variations in TOC and mineral content, resulting in improved accuracy in fitting heterogeneous samples.¹⁹ By contrast, models like Langmuir and BET, which make the assumption of more homogeneous adsorption conditions, exhibit reduced sensitivity to these factors and demonstrate superior performance in samples with more consistent properties.^36,81 In order to obtain precise predictions of the CO₂ adsorption behavior, it is necessary to customize the selection of the isothermal model according to the particular characteristics of the shale.

5. Conclusion

This review presents a thorough examination of the process of CO₂ adsorption on shale formations by employing several isothermal models such as the Langmuir, Freundlich, BET, D-R, D-A, Sips, Toth, and OK models. The results indicate that although certain models such as Sips, Freundlich, and D-R achieve good performance in specific circumstances, they have constraints in forecasting CO₂ adsorption in all shale samples because of differences in mineral composition, TOC, surface area, and pore properties. The work emphasizes the necessity of modifying models by introducing density-dependent correction factors and the integration of micropore filling and multilayer adsorption mechanisms in hybrid modeling methodologies. Furthermore, the work highlights the value of combining MD simulations with experimental data to improve our comprehension of CO₂ adsorption processes at the molecular scale.

5.1. Novel Perspectives

Analyzing isothermal model fittings at 298 K and pressures ranging from 0 to 2 MPa on four different shale samples can provide fresh insights that enhance the knowledge and prediction of CO₂ adsorption in shale formations.

• (1)While models like Sips, Freundlich, and D-R achieve effectiveness in certain situations, they face challenges in precisely forecasting CO₂ adsorption in all shale samples because of differences in mineral composition, TOC, surface area, and pore characteristics. Implementing density-dependent correction factors in models like Langmuir, Freundlich, and BET can enhance the accuracy of simulating CO₂ behavior at different pressures by considering compressibility and fluid-like characteristics. A hybrid model that integrates the micropore-filling notion of D-R with the multilayer adsorption framework of BET has the potential to provide a more precise depiction of shales containing both micropores and mesopores, such as CM03 and US03. Furthermore, the utilization of dynamic models that adapt parameters in real-time according to experimental variables, such as pressure, temperature, and shale composition, could enhance the accuracy of adsorption predictions.
• (2)Integration of MD simulations with experimental data has the potential to greatly improve the comprehension of CO₂ adsorption processes at the molecular scale in shale formations. These simulations offer valuable understanding of the atomic-level interactions between CO₂ molecules and a range of minerals and organic compounds, including illite, smectite, calcite and kerogen. Incorporating these interactions into current isothermal models should enhance their precision, thereby enabling more precise predictions of adsorption behavior. Molecular dynamics simulations can also provide guidance for the creation of novel models that consider intricate interactions, such as the competing adsorption between carbon dioxide and methane or alterations in pore structure caused by pressure.
• (3)Measurements of sensitivity show that the adsorption of CO₂ in shale is greatly affected by the distribution of pore sizes and the chemistry of the surface. Samples containing smaller holes, such as US03, exhibit increased adsorption because of confinement effects. This phenomenon is well described by models like D-R, which assume that micropores are filled with a Gaussian energy distribution. Conversely, the BET model provides a more precise description of multilayer adsorption in samples containing bigger holes, such as mesopores and macropores, such as SM05. Implementing a pore-size-dependent parameter could enhance the precision of the model by considering the unique contributions of each pore size to overall adsorption capacity. The inclusion of factors for specific chemical interactions and chemisorption effects, especially for minerals such as illite, smectite, and calcite can improve the accuracy of forecasts for samples containing high levels of TOC or reactive minerals.

5.2. Research Prospects

Important study directions are identified to further our knowledge of CO₂ adsorption in shale formations based on comparison and sensitivity studies performed.

• (1)Existing models can be optimized for better representation of surface heterogeneity, microporosity, and the characteristics of supercritical CO₂. Further investigation should be prioritized for the development of sophisticated isothermal models specifically designed for shale deposits. These models should incorporate both monolayer and multilayer adsorption properties and be capable of dynamically adapting to supercritical conditions.
• (2)Analyzing shales that have not been extensively studied but include distinct mineral and organic compositions can aid in the identification of novel prospective locations for CO₂ storage. Cross-sectional investigations of different shale formations can reveal geological characteristics that either promote or hinder the adsorption of CO₂.
• (3)Future research is recommended for the long-term geochemical interactions between CO₂ and shale minerals under different settings to examine the impact on CO₂ retention, mineral dissolution, and alterations in shale characteristics, to maintain the integrity of storage throughout time.
• (4)Research can be aimed to investigate possible routes for CO₂ leakage and conduct life cycle assessments to determine the environmental consequences of CO₂ sequestration in shale, considering variables such as energy consumption, emissions, and impacts on ecosystems and groundwater.

The authors declare no competing financial interest.