Phononic modulation of spin-lattice relaxation in molecular qubit frameworks

Abstract

The solid-state integration of molecular electron spin qubits could promote the advancement of molecular quantum information science. With highly ordered structures and rational designability, microporous framework materials offer ideal matrices to host qubits. They exhibit tunable phonon dispersion relations and spin distributions, enabling optimization of essential qubit properties including the spin-lattice relaxation time (T₁) and decoherence time. In this study, through spin dynamic and vibrational spectroscopic characterizations of two radical-embedded framework materials, we show that hydrogen-bonded networks give rise to a low Debye temperature of acoustic phonons and generates sub-terahertz optical phonons, both of which facilitate spin-lattice relaxation. Whereas deuterating hydrogen-bonded networks reduces both phonon frequencies and T₁, eliminating such flexible structural motifs raises phonon dispersions and improves the T₁ by one to two orders of magnitude. The phononic tunability of spin-lattice relaxation in molecular qubit frameworks would facilitate the development of solid-state qubits operating at elevated temperatures.

Recently, metal-organic framework materials have emerged as a promising platform for realizing molecular qubits. Here the authors study the role of phonons in spin relaxation within molecular qubit frameworks and show that hydrogen-bonded networks and their deuteration facilitate spin relaxation.

Introduction

Molecular electron spin qubits empower unique quantum technologies including multi-level quantum error correction¹ and chemical-specific quantum sensing^2,3 thanks to their atomic scale designability, versatile tunability, and high-temperature quantum coherence^4–6. In order to maintain the quantum information during quantum operations, the qubit should display a long spin decoherence time (T₂), which is upper bounded by twice of another key metric, the spin-lattice relaxation time (T₁)^7,8. As T₁ is determined by spin-phonon coupling, its optimization demands fine-tuning of phonon dispersions. Typically, molecular electron spin qubits are integrated into condensed matter matrices through dissolution in liquid^9,10, dispersion in polymers^11,12, or co-crystallization with diamagnetic analogs^13,14. These systems lack either well-defined phonon dispersion relations due to amorphousness or fine phononic tunability due to the limitation of co-crystallization. They do not allow sophisticated phonon engineering thereby hindering rational improvement of T₁.

Ordered and microporous materials, e.g., metal−organic frameworks^2,3,15–17, covalent organic frameworks¹⁸, and ion-paired frameworks^19,20, offer alternative matrices to host molecular electron spin qubits by using them as building blocks. The corresponding materials, molecular qubit frameworks (MQFs), provide a great platform to optimize qubit metrics and implement quantum information science (QIS) applications. Their bottom-up synthesis and high spatial ordering impart well-defined phonon dispersion relations, which may be tailor-designed through reticular chemistry to suppress spin-lattice relaxation^17,21,22. In addition, MQFs feature nanoscale pores capable of incorporating guest molecules/ions, which could alter crystal structures as well as local chemical and magnetic environments. Accordingly, the guest molecules might controllably tune phonon dispersions and in turn spin-lattice relaxation, which is hardly achievable in densely packed inorganic solids and other diluted molecular systems. Such phononic tunability may be harnessed for relaxometric sensing of adsorbents²³, rendering MQFs as promising candidates for quantum sensing of chemical analytes.

A viable strategy to improve the T₁ of MQFs is to tune phonon dispersions via structural design. Previous studies on MQFs have attempted to modulate the spin-lattice relaxation by modifying node masses²², linker lengths²², side chains²⁴, and guest molecules^23,25. Nonetheless, they did not characterize phonon dispersions nor achieve salient T₁ variation, so a conclusive experimental demonstration of this strategy has remained elusive so far. Herein, we report hundred-fold modulation of T₁ of MQFs via incorporation of hydrogen-bonded networks and their deuteration (Fig. 1a). Both structural variations generate low-frequency phonon dispersions and significantly reduce the T₁, demonstrating effective phononic modulation of spin-lattice relaxation in MQFs.

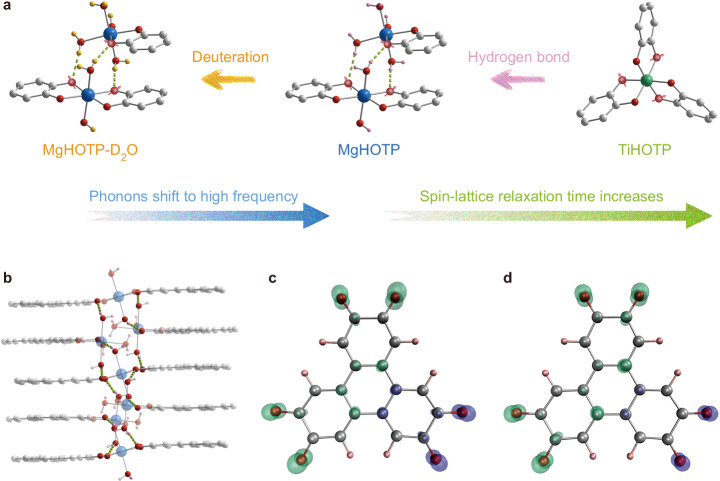
Fig. 1. Crystal structures and spin density distributions of MQFs.

a Phononic modulation of spin-lattice relaxation in MQFs via hydrogen-bonded networks and their deuteration. Green dash lines represent hydrogen bonds. Grey, pink, yellow, red, blue, and green spheres represent C, H, D, O, Mg, and Ti, respectively. Red spheres with arrows represent possible oxygen sites where electron spins mainly reside. H atoms of HOTP ligands, solvent molecules, and (CH₃)₂NH₂⁺ cations are omitted for clarity. b A portion of MgHOTP structure viewed perpendicular to the crystallographic c axis, highlighting hydrogen-bonded networks. c, d Spin density distribution of HOTP under c, 1-electron and d 3-electron oxidation (isosurface = 0.01). Green and purple clouds represent positive and negative spin densities, respectively.

Results

Structures and qubit characteristics

We synthesized two metal−organic frameworks embedding semiquinone-like HOTP radicals (HOTP = 2,3,6,7,10,11-hexaoxytriphenylene), namely {[Mg(H₂O)₂]₃HOTP₂}{[Mg(H₂O)₄]₃HOTP}₂ (MgHOTP) and [(CH₃)₂NH₂]₂TiHOTP (TiHOTP), according to the literature^3,26. Powder X-ray diffraction (PXRD) confirmed their structures and crystallinity (Supplementary Fig. 1). MgHOTP displays a layered structure with two alternating structural motifs: a layer of extended two-dimensional honeycomb-like sheet, [Mg(H₂O)₂]₃HOTP₂, and a layer comprising isolated trinuclear clusters, [Mg(H₂O)₄]₃HOTP³. These connect to each other through π−π stacking and hydrogen bonds, the latter of which consists of an oxygen atom from the HOTP ligand in one layer and a coordinating H₂O bound to Mg²⁺ in the adjacent layer (Fig. 1a). Together, they form quasi-one-dimensional hydrogen-bonded networks in the out-of-plane direction (Fig. 1b). In contrast, TiHOTP shows an interpenetrated three-dimensional structure with (CH₃)₂NH₂⁺ cations in the pores²⁶. The Ti⁴⁺ is coordinated by three orthogonal HOTP ligands, so this material does not possess π−stacked HOTP motifs nor coordinating H₂O molecules (Fig. 1a).

X-band (9.6 GHz) continuous-wave electron paramagnetic resonance (CW-EPR) spectroscopy revealed single resonance peaks with g_// = 2.00292 and $g_{\perp }=$2.00335 for MgHOTP and g_// = 2.00193 and $g_{\perp }=2.00227$ for TiHOTP (Supplementary Fig. 2). W-band (94 GHz) CW-EPR spectroscopy further confirmed the g-anisotropy (Supplementary Fig. 3). These g-factors are close to the free-electron value (g_e = 2.00232) with small g-shifts indicating weak spin-orbit coupling (Supplementary Table 1), so the EPR features are attributed to HOTP radicals. The HOTP ligand could transform into a semiquinone-like radical under 1, 3, or 5-electron oxidation (Supplementary Fig. 4). In a previous study about MgHOTP, the oxidation states of HOTP ligands were assigned as −6 and −3 in the extended sheets and isolated clusters, respectively, based on their average C−O bond lengths (1.39(5) Å and 1.32(5) Å)³. The antiferromagnetic coupling between adjacent HOTP³⁻ mediated by the HOTP⁶⁻ gives rise to singlet π-dimers, which may be broken by stacking faults to generate radicals. Meanwhile, the spontaneous oxidation of HOTP ligands could also lead to radicals. In TiHOTP, the charge balance and the average C−O bond length (1.399 Å) indicates an oxidation state of −6 for the HOTP ligand²⁶, which may form a radical upon spontaneous oxidation as well. As HOTP radicals act as defects in these materials, we could not resolve their exact oxidation states. Density functional theory (DFT) calculations on the 1, 3, and 5-electron-oxidized forms of HOTP revealed their mono-radicaloid characteristics (Fig. 1c, d; Supplementary Fig. 5 and Supplementary Table 2). The electron spin predominantly resides on oxygen atoms and slightly distributes to the aromatic rings because of conjugation. Hence, interactions with oxygen atoms of the HOTP radical, e.g. coordinating or hydrogen bonding interactions, might alter its spin dynamics.

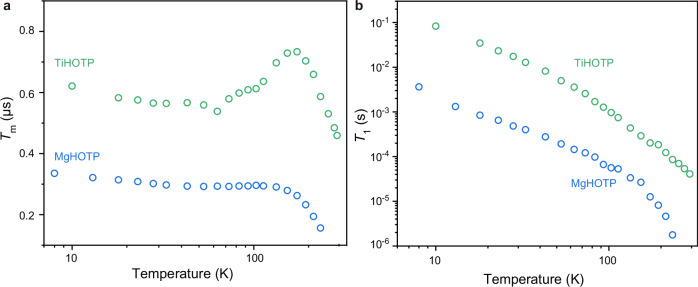
Both MgHOTP and TiHOTP display Rabi oscillations in nutation experiments as revealed by our previous and current studies (Supplementary Fig. 6)³, so they behave as MQFs. Their quantum coherence was investigated by the Hahn echo decay pulse sequence using X-band pulse EPR spectroscopy at various temperatures (Supplementary Figs. 7b and 8b, and Supplementary Tables 3, 4). Temperature dependencies of the phase memory time (T_m), which resembles the T₂ while encompassing all decoherence sources, of both MQFs can be divided into three regions (Fig. 2a). In the low- and high-temperature regions, the T_m decreases gradually and sharply with rising temperatures, respectively. In the medium-temperature region, the T_m of MgHOTP almost remains a constant between 43 K and 113 K, whereas that of TiHOTP increases with rising temperature between 63 K and 173 K. Mechanistic analysis revealed that in the high-temperature region, the decoherence of both MQFs is caused by a temperature-dependent relaxation-induced electron spin diffusion (also called electronic spectral diffusion) and a temperature-independent term that may include nuclear spin diffusion, electron spin flip-flop, and instantaneous diffusion (Supplementary Fig. 9 and Supplementary Note 6)^27,28. Notably, both MQFs sustain quantum coherence at temperatures much higher than most metal-based molecular electron spin qubits^4,21,29,30. This is attributed to the negligible spin-orbit coupling strengths of Mg²⁺, Ti⁴⁺, and the HOTP radical that help suppress the spin-lattice relaxation (vide infra) and in turn the electronic spectral diffusion that scales with the square root of T₁^6,28.

Fig. 2. Spin dynamics of MgHOTP and TiHOTP.

a T_m acquired at various temperatures. b T₁ acquired at various temperatures.

Extrapolation of these decoherence processes to the low- and medium-temperature regions showed the presence of a thermally activated process, whose contribution to the decoherence reaches the maximum at 28 K for both MQFs (Supplementary Fig. 9). This behavior is similar to what was observed for the motion-induced decoherence process, where a slow motion at low temperature expedites the decoherence but a fast motion at high temperature improves the coherence, the latter of which is called motional narrowing³¹. Such motion may involve methyl tunneling within (CH₃)₂NH₂⁺ in TiHOTP and proton tunneling within hydrogen bonds in both MQFs (the O−H···O bond between coordinating H₂O and HOTP in MgHOTP and the N−H···O bond between (CH₃)₂NH₂⁺ and HOTP in TiHOTP)^32–35.

Upon confirming the qubit nature of both MgHOTP and TiHOTP, we examined their spin-lattice relaxation by conducting variable-temperature T₁ measurements with the inversion recovery pulse sequence using X-band pulse EPR spectroscopy (Supplementary Figs. 7a and 8a, and Supplementary Tables 3, 4). Their T₁ values decrease monotonically with rising temperature (Fig. 2b). The T₁ of MgHOTP decreases from 3.96 ms at 8 K to 1.7 μs at 233 K. TiHOTP displays much slower spin-lattice relaxation—its T₁ gradually declines from 83 ms at 10 K to 41 μs at 294 K, rendering it as a MQF with room-temperature quantum coherence. The T₁ value of TiHOTP exceeds those of most metal-based coordination complexes (Supplementary Table 5)^4,21,29,30, demonstrating the importance of weakening the spin-orbit coupling for improving the T₁. Notably, although MgHOTP and TiHOTP share the same spin center, the T₁ of the former is 1–2 orders of magnitude shorter across a wide range of temperature, which likely stems from differences in their phonon dispersion relations.

Ultralow-frequency optical phonons in MgHOTP

Phonon dispersion relations of MgHOTP and TiHOTP were characterized by Fourier-transform infrared (FT-IR), Raman, and Brillouin light scattering (BLS) spectroscopy. The first two techniques probe optical phonons at relatively high frequencies³⁶, whereas the last accesses lower frequencies and measures both optical and acoustic phonons³⁷. Together, these techniques reveal phonons close to the Γ-point (zero momentum) of the Brillouin zone.

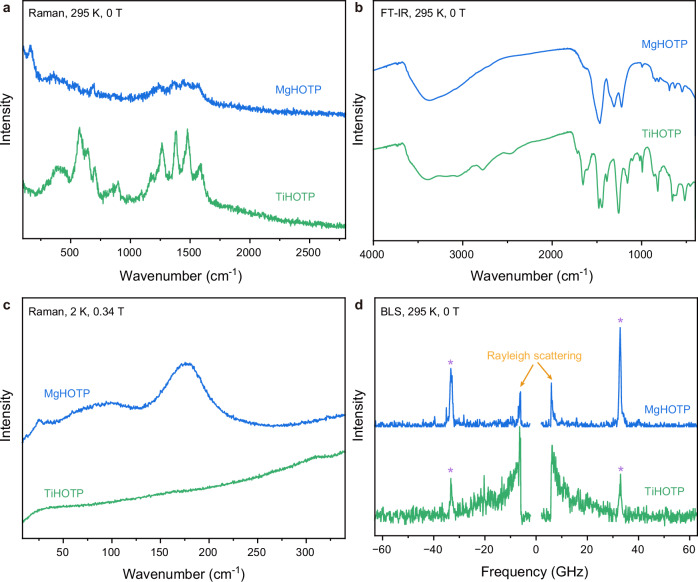
We first performed FT-IR and Raman spectroscopy in the wavenumber ranges of 400 cm⁻¹–4000 cm⁻¹ and 100 cm⁻¹–2800 cm⁻¹, respectively, at 295 K without applied magnetic field. The FT-IR spectrum of each MQF displays a broad peak centered at 3350 cm⁻¹, a group of relatively strong peaks between 1150 cm⁻¹ and 1700 cm⁻¹, and a group of relatively weak peaks between 500 cm⁻¹ and 1050 cm⁻¹ (Fig. 3b). The first two sets of peaks are attributed to vibrational modes of protic functional groups (O–H stretch in MgHOTP or N–H stretch in TiHOTP) and HOTP ligands (C=O, C–O, and aromatic C–C stretches, etc.), respectively^38,39. The last set of peaks may be attributed to a combination of the fingerprint region of HOTP ligands and vibrational modes of coordination spheres^26,40. The latter two sets of peaks are present in Raman spectra of both MQFs as well (Fig. 3a). The Raman spectrum of MgHOTP displays a weak peak at 355 cm⁻¹ and a strong peak at 165 cm⁻¹, and that of TiHOTP shows a broad peak centered at 400 cm⁻¹. These peaks point out the necessity to conduct precise Raman spectroscopic characterization at low frequency.

Fig. 3. Optical phonons in MgHOTP and TiHOTP.

a Raman spectra collected at 295 K and under 0 T with 633 nm excitation. b FT-IR spectra collected at 295 K and under 0 T. c Raman spectra collected at 2 K and under 0.34 T with 633 nm excitation. The downturn below 25 cm⁻¹ of the spectrum of TiHOTP stems from Rayleigh scattering. d BLS spectra collected at 295 K and under 0 T with 532 nm excitation. Peaks marked with asteroids are background signals from the substrate. Signal rises marked with arrows stem from Rayleigh scattering.

Low-frequency optical phonons play significant roles in the spin-lattice relaxation of molecular qubits as recently revealed by theoretical analysis, ab initio computations, and vibrational spectroscopic studies^41–45. To simulate the experimental conditions of pulse EPR spectroscopy, we acquired Raman spectra at 2 K, under 0.34 T, and with a wavenumber range of 8 cm⁻¹–2000 cm⁻¹ (Fig. 3c and Supplementary Fig. 11). The laser wavelength and power were optimized to improve the precision and signal-to-noise ratio in the low-frequency region (Supplementary Fig. 10). Below 350 cm⁻¹, TiHOTP displays only a weak peak at 310 cm⁻¹. In contrast, MgHOTP exhibits a relatively narrow peak at 24 cm⁻¹ and two broad peaks centered at ~90 cm⁻¹ and 175 cm⁻¹. Further Raman spectroscopic characterization of these two MQFs at 2 K and under 0 T or 3.5 T revealed the same features (Supplementary Figs. 12 and 13). In addition, BLS spectroscopy showed that neither MgHOTP nor TiHOTP displays phononic features in the frequency range of 3 GHz − 300 GHz (0.1 cm⁻¹–10 cm^-1) (Fig. 3d; Supplementary Figs. 14−16), indicating the absence of optical phonons. The acoustic phonons were not observed possibly because of their relatively low density of states (DOS) and accordingly low BLS intensity⁴⁶.

We conducted DFT calculations to assign the low-frequency optical phonons in MgHOTP and TiHOTP. The complexities of frameworks make the ab initio calculation of their phonon dispersion relations unfeasible, so we focused on representative portions of structures (Supplementary Fig. 17). The former consists of a [Mg(H₂O)₄]₃HOTP cluster and part of the adjacent honeycomb layer to include interlayer hydrogen bonds; the latter is [Ti(2,3-dioxytriphenylene)₃]²⁻. The calculation results closely match with the abovementioned low-frequency Raman spectra (Supplementary Figs. 18 and 19 and Supplementary Tables 6−8). The portion of TiHOTP shows three vibrations at 231 cm⁻¹, 301 cm⁻¹, and 334 cm⁻¹, which are attributed to torsional, wag, and stretch modes of Ti−O bonds coupled with the scissoring mode of triphenylene, respectively. The vibrations below 200 cm⁻¹ display negligible intensities. In contrast, numerous and significant vibrations below 200 cm⁻¹ are present in the portion of MgHOTP, most of which are related to the coordinating H₂O molecules that form hydrogen bonds with oxygen atoms of HOTP ligands. There are three clusters of vibrations peaked at 82 cm⁻¹, 121 cm⁻¹, and 166 cm⁻¹, all of which involve the rock mode of H₂O coupled with trampoline-like vibrations of benzene rings^47–50. Notably, the experimentally observed phonon at 24 cm⁻¹ is missed in the calculation results that show negligible vibrations below 70 cm⁻¹. Thus, this optical phonon should involve multiple unit cells of MgHOTP that cannot be captured by the calculation on a small portion of the structure. Considering structural differences between MgHOTP and TiHOTP, we tentatively assign the phonon at 24 cm⁻¹ in the former to the extended hydrogen-bonded networks.

As the frequency ranges of BLS and Raman spectroscopy overlap, they show that the lowest-frequency optical phonons in MgHOTP and TiHOTP are at 24 cm⁻¹ and 310 cm⁻¹, respectively. These provide upper limits to the Debye cutoff frequencies of acoustic phonons (ω_D) and in turn the Debye temperature (T_D) as $T_D=\hslash {\omega }_D/k_B$ (ℏ represents the reduced Planck constant and k_B the Boltzmann constant)⁵¹. Thus, the T_D values of these two MQFs are upper bounded by 35 K and 446 K, respectively. For solid-state materials, T_D is typically used as a proxy of structural rigidity⁵¹, so TiHOTP is more rigid than MgHOTP. Although the small size of crystallites prevents us from quantifying the hardness of these MQFs, the difference of rigidity is consistent with their different structures—the Ti–O bond is stronger than the Mg–O bond due to the higher valence state of Ti⁴⁺, and the relatively weak interlayer interactions through π−π stacking and hydrogen bonding in MgHOTP may further reduce its rigidity. Because the high T_D of TiHOTP indicates a low acoustic phonon DOS⁵¹, the higher structural rigidity of this MQF should suppress spin-lattice relaxation processes that involve acoustic phonons.

Spin-lattice relaxation mechanisms

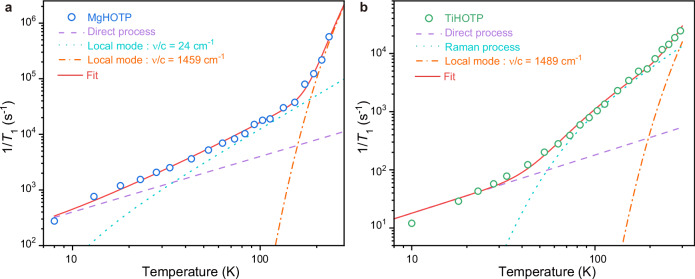
The above vibrational spectroscopic studies revealed optical phonons that may participate in the spin-lattice relaxation. To further articulate spin-lattice relaxation mechanisms in MgHOTP and TiHOTP, we characterized their T₁ in the temperature range of 10 K−93 K by W-band (94 GHz) pulse EPR spectroscopy. The T₁ values acquired at X-band and W-band almost overlap above 53 K for MgHOTP and 73 K for TiHOTP (Supplementary Fig. 20 and Supplementary Tables 9, 10). Below these temperatures, the T₁ is significantly shorter at W-band. This comparison indicates that field-dependent one-phonon relaxation is salient at lower temperatures, and that field-independent two-phonon relaxation dominates at higher temperatures^6,44. The former is also called the direct process, which describes the relaxation of excited spin via resonant emission of a phonon, typically an acoustic phonon at X-band. The latter describes a process where the excited spin absorbs a phonon to transition to a virtual state and consecutively emits another phonon to relax to the ground state. Either acoustic or optical phonons could participate in the two-phonon relaxation, which are conventionally called Raman or local-mode processes, respectively^41,42,44. The relaxation rates of these processes are positively correlated to the spin-phonon coupling strength and the DOS of corresponding phonons^52,53.

Accordingly, we analyzed spin-lattice relaxation mechanisms of the two MQFs with the following equation:

$$\frac{1}{T_1}=A_{Dir}T+A_{Ram}{\left(\frac{T}{T_D}\right)}^9{\int }_0^{\frac{T_D}{T}}{x}^8\frac{e^x}{{\left(e^x-1\right)}^2}dx+{\sum }_i{A}_{Loc,i}\frac{e^{h{\nu }_i/k_{B}T}}{{\left(e^{h{\nu }_i/k_{B}T}-1\right)}^2}$$ 1

where ν represents the linear frequency of optical phonon participating in the local-mode process, T represents the experimental temperature, and A_Dir, A_Ram, and A_Loc are pre-factors⁶. The first two terms describe the direct and Raman processes, respectively. The last term is the sum of multiple local-mode processes where the phonon frequencies were extracted from the abovementioned vibrational spectra. The lowest-frequency optical phonons and vibrational modes corresponding to C−O and metal−oxygen stretches were considered because they involve oxygen atoms of HOTP and should exert largest contributions to the spin-lattice relaxation.

We tried various combinations of these processes to simulate the temperature dependencies of T₁ acquired at X-band for MgHOTP and TiHOTP (Supplementary Note 11). The simulation revealed that the spin-lattice relaxation of TiHOTP involves direct and Raman processes as well as a local-mode process with ν/c = 1489 cm⁻¹ (c represents the speed of light) that is assigned to the C−O stretch in the semiquinone moiety (Supplementary Figs. 23b and 24, and Supplementary Table 11)^38,39. These processes were used to fit the temperature dependence of 1/T₁ for TiHOTP (Fig. 4b and Supplementary Fig. 26b). The fitting revealed A_Dir = 1.8 K⁻¹·s⁻¹ for the direct process, which dominates below 50 K. This is consistent with the divergence temperature between the T₁ values acquired at X-band and W-band. The Raman process dominates above 50 K with A_Ram = 1.0 × 10⁵s⁻¹ and T_D = 302 K, the latter of which is lower than its upper limit derived from vibrational spectroscopy (446 K). This process is salient likely because optical phonons remain inactive when T < < T_D. Above 213 K, the C−O stretch becomes sufficiently active such that its corresponding local-mode process is discernable with A_Loc = 2.0 × 10⁷s⁻¹. Notably, TiHOTP exhibits significantly smaller A_Dir, A_Ram, and A_Loc as well as higher T_D and ν than the values obtained for some Cu(II)- and V(IV)-based molecular qubits, together giving rise to longer T₁ (Supplementary Tables 5, 11 and 12)^25,52,54. In addition, the three pre-factors of TiHOTP are larger than those of semiquinone radicals, indicating that incorporating these molecules into TiHOTP facilitates their spin-lattice relaxation (Supplementary Tables 11 and 12).

Fig. 4. Spin-lattice relaxation mechanisms of MgHOTP and TiHOTP.

Spin-lattice relaxation rates (1/T₁) of a MgHOTP and b TiHOTP acquired at various temperatures and their fitting results based on Eq. 1. Circles represent experimental data. Red solid lines represent overall fits. Purple dash lines represent contributions from direct processes. Light blue dot lines represent contributions from the local-mode process driven by the 24 cm⁻¹ optical phonon for MgHOTP or the Raman process for TiHOTP. Orange dash-dot lines represent contributions from local-mode processes driven by C−O stretches in semiquinone moieties.

Based on the simulation for MgHOTP, both direct and C−O stretch-induced local-mode processes (ν/c = 1459 cm⁻¹) contribute to the spin-lattice relaxation (Supplementary Figs. 23a and 25, and Supplementary Table 11). Fitting the temperature dependence of T₁ showed that the former is preeminent below 40 K with A_Dir = 40 K⁻¹·s⁻¹ (Fig. 4a and Supplementary Fig. 26a). The latter dominates above 180 K with A_Loc = 3.7 × 10⁹s⁻¹, causing the upturn of relaxation rate. Between 40 K and 180 K, the relaxation is dictated by another process whose rate is proportional to T². Given a low T_D (T_D < 35 K) and a low optical phonon frequency (ν/c = 24 cm⁻¹), both Raman and local-mode processes obey such thermal behavior in this temperature range (Supplementary Figs. 22, 23a and 25). Therefore, both processes may contribute to the spin-lattice relaxation and their contributions are indistinguishable. Although the exact value of T_D cannot be determined for MgHOTP, it is much lower than the T_D of TiHOTP.

This analysis rationalizes the faster spin-lattice relaxation in MgHOTP compared to that in TiHOTP. First, the direct process in MgHOTP is faster by 22 times, consistent with its higher acoustic phonon DOS indicated by the lower T_D. Second, the Raman process (or the local-mode process driven by the lowest-frequency optical phonon) is faster by 6 orders of magnitude at 10 K and 1–2 orders of magnitude above 40 K. This is attributed to the lower T_D and/or the lower frequency of optical phonon. Third, the local-mode process induced by C−O stretches in semiquinone moieties is faster by 2 orders of magnitude, whose origin is unclear but may be related to the adjacent hydrogen bonds (vide infra). Overall, the first two processes enhance the relaxation rate by 1–2 orders of magnitude between 10 K and 153 K, and the third process further facilitates the spin-lattice relaxation at higher temperatures. Therefore, in order to achieve long T₁ in an MQF, it is critical to improve its T_D and eliminate low-frequency optical phonons, both of which highlight the rigid structure as a critical target for the material design.

Influence of hydrogen-bonded networks on spin-lattice relaxation

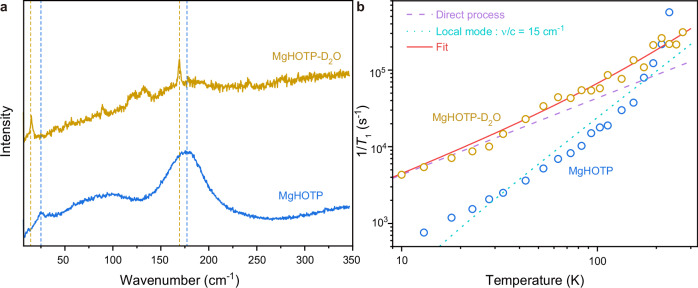
To verify the assignment of the lowest optical phonons to extended hydrogen-bonded networks in MgHOTP and to demonstrate the phononic tunability of its spin-lattice relaxation, we prepared this MQF with coordinating D₂O. PXRD and CW-EPR characterization of the product, MgHOTP-D₂O, confirmed the same crystal structure and radical characteristics with MgHOTP (Supplementary Figs. 27 and 28). Combination-peak electron spin echo envelope modulation characterization with X-band pulse EPR spectroscopy revealed a peak at 4.52 MHz, which is twice the nuclear Larmor frequency of ²H and confirms the presence of coordinating D₂O (Supplementary Fig. 29)⁵⁵. The Raman spectrum of MgHOTP-D₂O collected at 2 K and under 0.34 T shows three sharp peaks at 15 cm⁻¹, 89 cm⁻¹, and 169 cm⁻¹ (Fig. 5a and Supplementary Fig. 11). Compared with corresponding Raman peaks of MgHOTP, the first and third peaks red-shift by 9 cm⁻¹ and 6 cm⁻¹, respectively. In addition, MgHOTP-D₂O shows two broad peaks at ~120 cm⁻¹ and 132 cm⁻¹, which are absent in the Raman spectrum of MgHOTP. Therefore, these two new peaks, as well as the peaks at 15 cm⁻¹ and 169 cm⁻¹ are assigned to optical phonons involving hydrogen bonds in MgHOTP-D₂O. As this material exhibits no feature in BLS spectra (Supplementary Figs. 14−16), its T_D is upper-bounded by 22 K. Indeed, because deuterium is twice as heavy as hydrogen, the deuteration should also shift acoustic phonons towards lower frequencies, so the T_D of MgHOTP-D₂O is likely much lower than that of MgHOTP⁵⁶.

Fig. 5. Isotope effects of spin-lattice relaxation in MgHOTP.

a Raman spectra of MgHOTP and MgHOTP-D₂O collected at 2 K and under 0.34 T with 633 nm excitation. Blue dash lines mark the maxima of peaks at 24 cm⁻¹ and 177 cm⁻¹ for MgHOTP. Yellow dash lines mark the maxima of peaks at 15 cm⁻¹ and 169 cm⁻¹ for MgHOTP-D₂O. b. Spin-lattice relaxation rates of MgHOTP and MgHOTP-D₂O. Circles represent experimental 1/T₁ data acquired at various temperatures. Fitting results are only shown for MgHOTP-D₂O. The red line presents the overall fit. The purple dash line and light blue dot line represent contributions from the direct process and the local-mode process driven by the 15 cm⁻¹ optical phonon for MgHOTP-D₂O, respectively.

The deuteration of MgHOTP reduces its T₁ by an order of magnitude below 100 K, which is 0.23 ms at 10 K (Fig. 5b; Supplementary Figs. 31 and 32, and Supplementary Table 13). Simulating and fitting the temperature dependence of T₁ with Eq. 1 reveals that the deuteration alters spin-lattice relaxation processes (Supplementary Table 12 and Supplementary Note 12). It facilitates the direct process by 10 times and the Raman process (or local-mode process driven by the lowest-frequency optical phonon) by an order of magnitude, both of which combined lead to a shorter T₁ at low temperatures. These are in line with the lower T_D and the red shift of the lowest optical phonon in MgHOTP-D₂O. In contrast, the C−O stretch-induced local-mode process becomes negligible upon deuteration, which helps MgHOTP-D₂O retain longer T₁ than MgHOTP above 233 K. Thus, hydrogen bonds likely regulate this process by affecting the C−O stretch in the semiquinone moiety.

Based on these isotope effects, we attribute the lowest-frequency optical phonon at 24 cm⁻¹ in MgHOTP to the extended hydrogen-bonded networks. Traditionally, hydrogen bonds are believed to improve structural rigidity that should suppress spin-lattice relaxation⁵⁷. Nonetheless, the comparison between TiHOTP and MgHOTP reveals that hydrogen-bonded networks give rise to low T_D and sub-terahertz optical phonons that reduce T₁. These structural motifs inherit long-range ordering from the crystalline structure, so they could accommodate phonons with long wavelengths and accordingly low frequencies. In contrast, although hydrogen bonds between HOTP and (CH₃)₂NH₂⁺ may be present in TiHOTP, they do not form extended networks and hence do not generate low-frequency optical phonons. Indeed, the vibrational mode of localized N−H···O hydrogen bond is typically above 3300 cm⁻¹⁵⁸, so it should be inactive and should not contribute to the spin-lattice relaxation at relatively low temperature. Thus, for MQFs, it is critical to avoid hydrogen-bonded networks that involve spin centers to achieve long T₁.

The comparison between MgHOTP and MgHOTP-D₂O shows that deuterating hydrogen-bonded networks in MQFs facilitates the spin-lattice relaxation by red-shifting both acoustic and optical phonons. The coordinating H₂O may be perceived as onsite solvent that interacts with the HOTP radical. Solvent deuteration is a widely used approach for improving the T_m of molecular electron spin qubits by taking advantage of the low gyromagnetic ratio of ²H^33,59. However, its influence on the spin-lattice relaxation remains underexplored. Previous studies revealed that for vanadium-based coordination complexes dissolved in a mixture of N,N-dimethylformamide and toluene, the solvent deuteration barely alters their T₁ values⁶⁰. For trityl⁶¹, nitroxide⁵⁷, and semiquinone radicals⁶² dissolved in protic solvents (e.g. water, glycerol, ethanol), the solvent deuteration tends to improve their T₁ values. Our observation differs from these phenomena, highlighting the distinct phononic environment in MQFs and its rational tunability provided by the ordered structures.

Discussion

In conclusion, our studies reveal that extended hydrogen-bonded networks in MgHOTP give rise to a low Debye temperature (T_D < 35 K) and ultralow-frequency optical phonons down to 24 cm⁻¹, both of which significantly facilitate spin-lattice relaxation. Deuteration further reduces frequencies of acoustic and optical phonons, shortening the T₁ by an order of magnitude below 100 K. In contrast, free of such flexible structural motifs, TiHOTP displays a much higher Debye temperature (T_D = 302 K) and exhibits no optical phonon below 310 cm⁻¹, so it sustains much longer T₁ across 10 K–294 K. Hence, the rational structural design of MQFs enables fine phononic modulation to suppress spin-lattice relaxation. This presents opportunities for the solid-state integration of molecular electron spin qubits that is essential for their QIS applications. In addition, guest molecules could also form hydrogen bonds with spin centers in MQFs. Harnessing such interactions may enable guest-tunable spin-lattice relaxation and quantum sensing of guest molecules.

Methods

Synthesis

MgHOTP

Mg(acetate)₂·4H₂O (1.27 mmol) was dissolved in 3.6 mL of de-ionized water in a 20 mL scintillation vial. Separately, 0.03 mmol of 2,3,6,7,10,11-hexahydroxytriphenylene (HHTP) was dissolved in 0.4 mL of dimethyl sulfoxide (DMSO), and this solution was added to the Mg(acetate)₂ solution. The reaction mixture was heated on a hotplate at 80 °C for 24 h in the air. It was then cooled down to room temperature. The solids were washed sequentially with de-ionized water, ethanol, and acetone three times, respectively³. MgHOTP-D₂O was synthesized with the same procedure by using D₂O and deuterated DMSO as the solvent.

TiHOTP

HHTP (0.093 mmol) and tetrabutylammonium bromide (0.093 mmol) were weighed into a Teflon liner in a N₂-filled glovebox. N,N-Dimethylformamide (4 mL), titanium (IV) isopropoxide (0.12 mmol) and triethylamine (0.22 mmol) were added to the Teflon liner. The reaction mixture was stirred for 1 h. The Teflon liner was then sealed in a stainless-steel autoclave, which was heated in an oven at 180 °C for 48 h in the air. The reaction mixture was cooled down to room temperature, and the solids were collected by centrifugation and washed by N,N-dimethylformamide, ethanol, and acetone three times, respectively²⁶.

CW-EPR spectroscopy

X-band (9.6 GHz) CW and pulse EPR spectroscopy was performed on a CIQTEK EPR100 spectrometer equipped with EPR-VTS-L-D1-PWC closed-loop helium cryostat and Lakeshore336 temperature controller at the Instrumentation and Service Center for Molecular Sciences, Westlake University. A standard DPPH radical sample was used to calibrated magnetic field, which revealed −0.351 mT correction. The modulation amplitude, microwave power, and temperature were set to 0.1 mT, 0.2 mW, and 296 K, respectively.

W-band (94 GHz) CW and pulse EPR spectroscopy was conducted on a CIQTEK EPR-W900 spectrometer at CIQTEK Co., Ltd. The magnetic field was calibrated by a standard Mn(II):CaO sample. The modulation amplitude, microwave power, and temperature were set to 0.1 mT, 0.04 mW, and 296 K, respectively.

Pulse EPR spectroscopy

Hahn echo decay pulse sequence (π/2 ‒ τ ‒ π ‒ τ ‒ echo) was used to measure T_m with 256 points, where the length of π pulse is 32 ns. The background noise was canceled by two-step phase cycling with pulse phases of (+x, +x) and (-x, +x). The Hahn echo was monitored under various τ. The resulting Hahn echo decay curve was fitted by the following exponential decay function to extract T_m:

$$I=A{e}^{\frac{2\tau }{T_m}}+I_0$$ 2

where I is echo intensity, A is a pre-factor, and I₀ accounts for the baseline drift.

Inversion recovery pulse sequence (π ‒ t ‒ π/2 ‒ τ ‒ π ‒ τ ‒ echo) with 512 data points was used to acquire T₁. The length of t started at 400 ns with different step increments that vary with temperature. τ was fixed at 200 ns. The background noise and unwanted echoes were canceled by four-step phase cycling with pulse phases of (+x, -x, +x) (+x, +x, +x) (-x, -x, +x) and (-x, +x, +x). For variable-temperature pulse EPR measurements, samples were cooled below 10 K for at least 2 hours before conducting spin dynamics experiments. Temperature was controlled by a closed-loop liquid-helium-free cooling system. The temperature of sample was monitored by comparing T₁ values obtained from consecutive inversion recovery experiments—the thermal equilibrium was assumed to be reached when the change of T₁ value was less than 1%. It typically took 20 to 30 minutes to reach the thermal equilibrium. Inversion recovery curves were fitted by the following biexponential decay function to extract T₁:

$$I=A_1{e}^{\frac{-t}{T_1}}+A_2{e}^{\frac{-t}{T_s}}+I_0$$ 3

where I is echo intensity, A₁ and A₂ are pre-factors, T_s describes a fast relaxation process, and I₀ accounts for the baseline drift.

Vibrational spectroscopy

FT-IR spectroscopy was conducted on a Nicolet iS50 spectrometer (Thermo Fisher Scientific) at the Instrumentation and Service Center for Molecular Sciences, Westlake University. MQFs were dispersed into potassium bromide powder and pressed into pellets by a hydraulic press.

Room-temperature Raman spectra were acquired with 633 nm laser excitation by WITec Alpha300RAS spectrometer at Instrumentation and Service Center for Molecular Sciences, Westlake University.

Raman spectroscopy at low temperature and under applied magnetic field was conducted with 633 nm laser excitation at the Synergetic Extreme Condition User Facility (SECUF) on HR-evolution spectroscopy equipped with attocube2100 cryostat utilizing He as the exchange gas, allowing the sample to be cooled to 1.6 K and application of magnetic fields up to 9 T.

Brillouin light scattering spectroscopy in the backscattering geometry was conducted by a confocal microscope system. The system is composed of high contrast (~10¹⁵) (3 + 3)-pass tandem Fabry Pérot interferometers and a confocal microscope with a ×50 bright field objective lens (numerical aperture NA = 0.35) both from JRS Scientific Instruments in Switzerland. The detector is a Hamamatsu C11202-050. The incident light was emitted from a single longitudinal mode laser source at 532 nm and focused on the top surface of the sample. The confocal setup assures that the collected scattering information was from as near to the surface as possible. The laser power was about 1 mW. No laser heating effect on the sample was observed. In our experiments, the polarization configurations were circular polarization (σ + σ−) that could collect all potentially polarized BLS signals in principle⁶³.

DFT calculation

All DFT calculations were performed using the ORCA software (version 5.0.4)⁶⁴. The data post-processing was carried out with Multiwfn⁶⁵. Grimme’s atom-pairwise dispersion correction with the Becke-Johnson damping scheme (D3BJ) method was included to account for long-range dispersion interaction^66,67. The def2/J auxiliary basis set⁶⁸ and RIJCOSX approximation⁶⁹ were utilized to accelerate the calculations. The structures of HOTP radicals were optimized using B3LYP functional^70,71 with the def2-TZVPD basis set⁷². The structures were confirmed as local minimums according to the frequency analysis. The geometry of MgHOTP and TiHOTP fragments were optimized at the B3LYP^70,71 level with def2-TZVP(-f) basis set⁷². The absence of imaginary frequency confirmed that the optimized structures represent local minima.

Author contributions

L.S. and A.Z. conceived the idea, designed experiments, and oversaw the project. A.Z. conducted material synthesis, EPR characterization, and vibrational spectroscopy. D.L. and S.L. performed DFT calculation. M.T. and F.J. assisted with Raman spectroscopy. Y.L., S.P., and J.Z. assisted with BLS spectroscopy. X.Z. and Z.S. assisted with W-band EPR spectroscopy. L.S. and A.Z. co-wrote the manuscript. All authors have given approval to the final version of the manuscript.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data supporting our findings are included in the article and supplementary files. Additional data generated during the study are available from the corresponding author upon request. Source data are provided with this paper.

Competing interests

The authors declare no competing interest.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-54989-2.