Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2024 Dec 30;14:31595. doi: 10.1038/s41598-024-78901-6

Impacts of lateral conductive heat flow on ground temperature and implications for permafrost modeling

Yu Zhang 1,✉, Gang Hong 1, Mitchell T Bonney 1
PMCID: PMC11685618  PMID: 39738234

Abstract

Permafrost ground temperature and its spatial distribution are usually calculated using one-dimensional models based on heat flow in the vertical direction. Here, we theoretically calculated the impacts of lateral conductive heat flow on ground temperature under equilibrium and transient conditions. The results show that lateral heat flow has strong impacts on ground temperature, especially in deep ground. The different patterns of ground temperature with depth observed at 191 boreholes in a small mining area in northeastern Canada can generally be explained by the effects of lateral heat flow. Lateral effects are widespread in permafrost regions due to the large spatial variation in near surface ground temperature. Our analysis shows that one-dimensional permafrost models may have errors of 5 °C when the size of the grid cell is small. We estimated the horizontal extents and depths of the effects of lateral heat flow under typical conditions. These results can be used as a guide for modeling and mapping permafrost and selecting observation sites in the field.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-78901-6.

Keywords: Lateral conductive heat flow, Ground temperature, Permafrost, Modeling, Mapping

Subject terms: Cryospheric science, Climate and Earth system modelling, Climate-change impacts

Introduction

Climate warming is causing permafrost thaw1,2, which has significant impacts on infrastructure, ecosystems, hydrology, and greenhouse gas emissions3–5. One-dimensional (1D) models are usually used to quantify the impacts of climate warming on permafrost and associated eco-environmental changes6–10. Annual mean near-surface ground temperature (Tnsg) in permafrost regions can vary 5 to 10 °C at landscape scales due to variations in topography, snow cover, vegetation, water, and soil conditions, particularly the effects of water bodies and redistribution of snow by wind11–14. This large spatial variation in Tnsg affects permafrost condition and its response to climate change.

Permafrost distributions have been modeled and mapped at increasingly high spatial resolutions to capture these spatial variations and the associated eco-environmental effects. The grid cell size of permafrost maps has decreased from tens of kilometers9,15 to around one kilometer6,16–19, to tens of meters7,8,20–22, and even less than ten meters12,23,24. Other than a few studies covering small areas25–30, most permafrost maps were developed using 1D modeling approaches, which explicitly or implicitly assumed that the ground temperature (Tg) is determined by heat flow in the vertical direction. The effects of lateral heat flow from surrounding areas are not considered. This assumption is reasonable for Tg near the ground surface or when the grid cell size is large. However, the impacts of nearby grid cells become significant and cannot be ignored when grid cell size is small, as indicated by three-dimensional (3D) modeling studies28–30 and other analyses25,26,31–35.

In addition, Tnsg varies with time due to climate change and land surface disturbance36,37, such as wildfire, lake drainage, formation of thermokarst ponds and lakes, and land use change. Climate change can cause variations in Tnsg at different rates for different land cover types, while disturbances can cause step-changes in Tnsg for the impacted area. Both types of changes affect Tg through vertical and lateral heat flows.

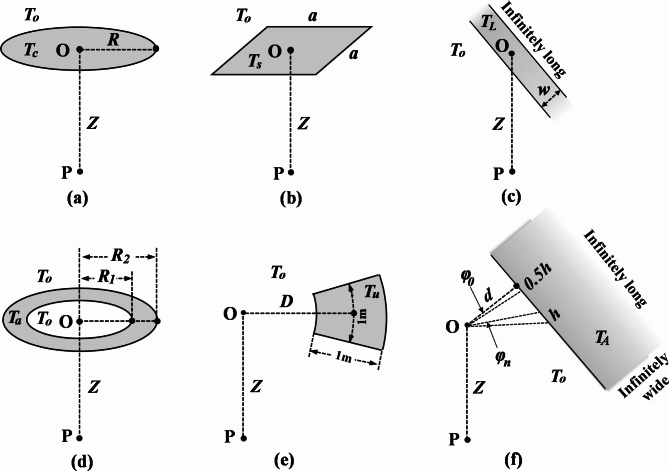
We theoretically calculated the effects of lateral conductive heat flow on Tg for six cases (Fig. 1) considering their simplicity in calculation and practical application. The effects of a circular area can be calculated analytically for both equilibrium and transient conditions. The effects of an annulus can also be calculated analytically, and the method can be used for calculating the effects of a unit area on Tg at any distance. The method can also be used to estimate the impacts on the Tg near a very large area, such as large water bodies or lands with a different Tnsg. An infinitely long strip-shaped area can represent rivers, roads, pipelines, and powerline corridors, and a square can represent a grid cell commonly used in spatial modeling. The calculation was based on the basic equations developed by Lachenbruch34, which assumes that the ground has a uniform thermal diffusivity and no latent heat is involved. We used a step-increase in Tnsg by 10 °C and a gradual warming rate of 0.1 °C yr− 1 to show the transient impacts on Tg.

Fig. 1.

Fig. 1

Open in a new tab

Diagrams for the impacts of Tnsg on Tg at point P which is directly below the point O on the ground surface. (a) a circular area centered at point O. (b) a square centered at point O. (c) an infinitely long strip. (d) a circular annulus centered at point O. (e) a fraction of an annulus which has a ring width of 1 m and an average arc length of 1 m. (f) a very large area beside point O. Tc, TS, TL, Ta, Tu and TA are the Tnsg of the shaded areas, and To is the Tnsg of other areas. The meanings of other variables are shown in the figure and described in the method section.

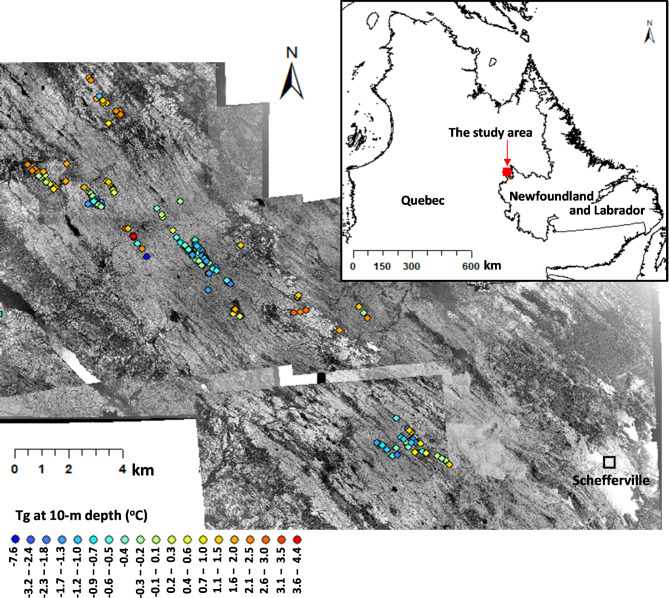
Ground temperature up to 100-m depth was observed at 191 boreholes in a 20-km by 4-km area about 8 km northwest of Schefferville (54°48’ N, 66°49’ W) in northeastern Canada between 1957 and 1982 (Fig. 2 and Figure S1). This area lies within the sporadic discontinuous permafrost zone38 and is transitional from boreal forest to tundra in a subarctic climate39. The observed Tg temperature profiles show different variation patterns with depth (Supplementary Figure S2), which are very different from the expected linear increases with depth under equilibrium conditions. More details on the area and data collection are included in Supplementary Text S1 and Table S1.

Fig. 2.

Fig. 2

Open in a new tab

Locations of the 191 borehole sites in a mining area near Schefferville (54°48′ N, 66°49′ W) in northeastern Canada. The Tg data are from Smith et al.40. The colors of the circles are for the mean Tg at about 10-m depth. The background is a mosaic of 1948 air photographs underlain by 1975 air photographs to fill some gaps. We used these air photographs to represent the land conditions before the disturbance of mining operations. A satellite image for the present condition was shown in Supplementary Figure S1. The historical air photographs were from the National Air Photo Library at Natural Resources Canada.

Results

Theoretically calculated lateral effects on Tg under equilibrium and transient conditions

Under equilibrium conditions, the impacts of the local grid cells with side-lengths of 2z, 4z, 6z, and 10z (Fig. 1b) account for only 33%, 59%, 71%, and 82% of the total effects of the entire ground surface on Tg at depth z. The impact of the local grid cell decreases with depth, decreasing to 10% and 1% of the surface impact at depths of ~ 1.2a and ~ 4.0a, respectively (a is the side-length of the grid cell). Below these depths, 90% and 99% of the Tg are determined by the surrounding area, respectively. For an infinitely long strip with a width w (Fig. 1c), its impact on Tg is similar to the impact of a square with a side-length of 1.5w in shallow depths (z < 0.5w), but the impact of the strip becomes larger than that of a square at deep depths. The impact of the strip on Tg decreases to 10% and 1% of the entire surface impact at the depths of ~ 3.2w and ~ 31.8w, respectively. For a site beside a very large area (Fig. 1f), the impact of the large area on the Tg of the site decreases with the distance but increases with depth and approaches a maximum value, which is half of the difference in Tnsg between the large area and the other area. If the Tnsg of the large area differs by 10 °C from the other area, the minimum distance from the large area is ~ 32z to keep the impact on the Tg at depth z less than 0.1 °C (or less than 1% of the difference in Tnsg). The impacts of different shapes of the ground surface can be estimated by dividing the area into unit areas (Fig. 1e). The impact of a unit area on Tg decreases rapidly with the distance to the unit area, and there is a maximum impact depth, which is ~ 0.71 times of the distance from the site to the unit area. These values do not depend on the diffusivity of the ground under equilibrium conditions.

Under transient conditions, lateral conductive heat flow affects relatively small areas and shallow depths for timescales of one or two centuries. If the Tnsg of a circular area has a 10 °C step-increase, its impact on Tg increases with both time and the size of the circular area, but the impact has a limit for a given time and a limit for a given size of the circular area. When time is infinitely long, the impact depth (using a criterion of 0.1 °C or 1% of the step-change in Tnsg) is ~ 7.0R (R is the radius of the circular area). If the circular area is infinitely large, its impact on Tg reaches 175 and 245 m deep, respectively, in 100 and 200 yrs. The impact on the Tg is < 0.1 °C by the entire area beyond radii of ~ 140 and 196 m of the site, respectively, in 100 and 200 yrs. In other words, these radii are the minimum sizes of a local area to keep the impacts of surrounding areas less than 0.1 °C in these two timescales. If the Tnsg of the entire area has a gradual increase rate of 0.1 °C yr− 1, its impact on Tg (> 0.1 °C) reaches 140 and 218 m deep, respectively, in 100 and 200 years. To keep the impacts of surrounding areas less than 0.1 °C, the required minimum radii of the local areas are 120 m and 180 m for timescales of 100 and 200 yrs, respectively. If a site is near a very large area (Fig. 1f), the impact of the large area on the Tg of the site decreases rapidly with distance. If the Tnsg of the large area has a 10 °C step-increase, the impacts of the large area are < 0.1 °C when the distances are greater than 96 and 134 m in 100 and 200 yrs, respectively. If the Tnsg of the large area has an increase rate of 0.1 °C yr− 1, the impacts of the large area are < 0.1 °C when the site is 70 and 120 m away from the large area in 100 and 200 yrs, respectively. These estimates are based on a typical ground thermal diffusivity (7.27×10-7 m2s-1), and the impacts increase with the increase in diffusivity. A 50% increase in diffusivity increases the transient impact depth or extent by ~ 21%, and a 50% decrease in diffusivity decreases the impact depth or extent by ~ 30%. The impact depth or extent is independent of ground thermal properties under equilibrium conditions. Supplementary Text S2 provides more detailed calculation results and analysis.

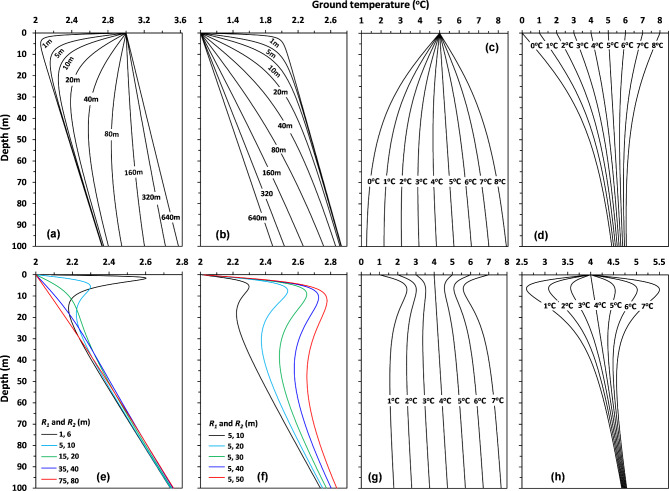
Lateral heat flow causes non-linear patterns in the distribution of Tg with depth. Figure 3a-d shows the distributions of Tg profiles under equilibrium conditions due to the impacts of local circular areas with different Tnsg from the other area. Figure 3e-h shows the impacts of annuli on the Tg profiles. There is a depth where the annulus has a maximum impact on the Tg. The impact of an annulus also depends on the Tnsg of the annuli and the other area (Fig. 3g and h). These results indicate that different size of circular area or annulus and their Tnsg can produce very different patterns of Tg profiles. Transient changes in Tnsg can also cause non-linear patterns in Tg profiles, and the patterns depend on time, location and size of impact areas (Supplementary Figures S3(c-e), S4(a-c), S5(a-c), and S7).

Fig. 3.

Fig. 3

Open in a new tab

Distributions of Tg with depth due to the impacts of (a–d) circular areas and (e–h) annuli with different Tnsg from other areas under equilibrium conditions. (a) the effects of circular areas of different radii (shown for each curve). The Tnsg of the circular areas (Tc) are 3 °C, and the Tnsg of the other area (To) is 2 °C. (b) same as panel ‘a’ but using Tc = 1 °C. (c) the effects of a circular area with different To (shown for each curve). Tc = 5 °C and the radius (R) is 50 m. (d) the effects of a circular area with different Tc (shown for each curve). To = 5 °C and R = 50 m. (e) the effects of annuli with different sizes but the same ring width of 5 m. The Tnsg of the annuli (Ta) is 1 °C, and the Tnsg of the other area (To) is 2 °C. The radii of the inner and outer circles  (R1 and R2) are shown in the legends. (f) the effects of annuli with different radii for outer circles but the same radius for the inner circle (R1 = 5 m). Ta = 3 °C, and To = 2 °C. (g) the effects of an annulus with different To (shown for each curve). Ta = 4 °C, R1 = 5 m, and R2 = 20 m. (h) the effects of an annulus with different Ta (shown for each curve). To = 4 °C, R1 = 5 m, and R2 = 20 m. The definitions of the variables are shown in Fig. 1 and described in the method section. In all cases, the geothermal heat flux is 0.022 W m− 2, and the thermal conductivity is 3 W m− 1 °C− 1.

Comparisons between theoretically calculated and observed Tg profiles near Schefferville

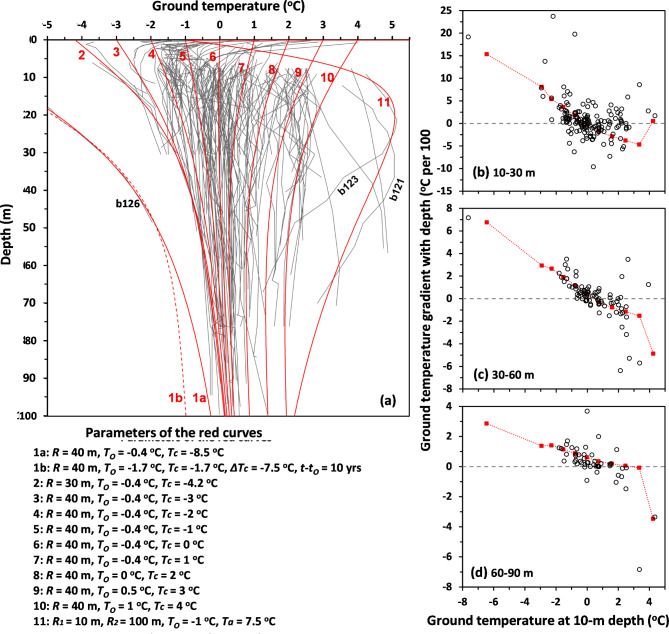
Observed Tg at the 191 boreholes show different non-linear variations with depth (Supplementary Figure S2 or the grey curves in Fig. 4a). The variation range of Tg became smaller with depth, although there were less observations at deeper depths. Except for the very cold site b126, Tg ranged from about − 3 °C to 4 °C at 10 m, from − 1.7 to 5.1 °C at 30 m, from − 0.5 to 3.5 °C at 60 m, and from − 0.7 to 1.4 C at 90 m.

Fig. 4.

Fig. 4

Open in a new tab

Comparisons between theoretically calculated and observed Tg near Schefferville. (a) comparisons between observed Tg profiles (grey curves) and theoretically calculated Tg profiles (red curves). (b–d) comparisons between the observed Tg-depth gradients (black circles) and theoretically calculated Tg-depth gradients (red dashed curve with squares, which were calculated based on the red solid curves in panel ‘a’) in 10–30 m, 30–60 m and 60–90 m depth ranges, respectively. In panel ‘a’, the solid red curves 1a, and 2–10 were calculated based on the impacts of circular areas under equilibrium conditions (R is the radius, Tc the Tnsg of the circular area, and To the Tnsg of the other area); the dashed red curve 1b was the calculated Tg after 10 yrs of a -7.5 °C step-changes in Tnsg of a circular area (Tg was in equilibrium condition before the step-change); and the red curve 11 was based on the impact of an annulus under equilibrium conditions (R1 and R2 are radii of the inner and outer circles, respectively, and Ta is the Tnsg of the annulus). The thermal conductivity was 3 W m− 1 °C− 1 and the geothermal heat flux was 0.022 W m− 2 according to the observations in this area41,42.

The general patterns of observed Tg profiles are similar to that of the impacts of local areas with different Tnsg from other areas (Fig. 3d). The Tg variation pattern of the site b126 can also be explained by transient changes in Tnsg in a local area (the red dashed curve 1b in Fig. 4a). The calculated and observed Tg gradients are comparable, especially at 30–60 m and 60–90 m depths (Fig. 4b-d). These results indicate that the observed patterns of Tg profiles can generally be explained by the effects of lateral conductive heat flow due to differences in Tnsg in local areas. The observed Tg profiles at shallow depths (less than ~ 7 m) are different from the theoretically calculated ones probably because of the effects of thawing and freezing and the observed Tg at shallow depths might not represent seasonal variations of Tg well.

Implications for permafrost modeling and mapping

One-dimensional permafrost models assume that Tg is determined by conditions in the local area. The initial conditions of 1D models are usually estimated by running the model iteratively (spinning up) assuming the Tg is in equilibrium. Our theoretical calculation indicates that the impact of a local grid cell under equilibrium conditions is related to the ratio between the size of the grid cell and depth of Tg (Supplementary Figure S3(a)). To include 59% of the impacts of the entire ground surface, the side-length of the grid cell should be four times of the depth at which the Tg is considered. Permafrost thickness in Canada ranges from less than 10 m to nearly a kilometer43,44. The required side-lengths of the grid cells are 40 m, 400 m, and 2 km for calculating Tg at 10 m, 100 m, and 500 m depths, respectively. These are the grid cells sizes to include only 59% of the impact of the entire ground surface on the Tg at these depths. To include a higher percentage, the grid cell needs to be larger.

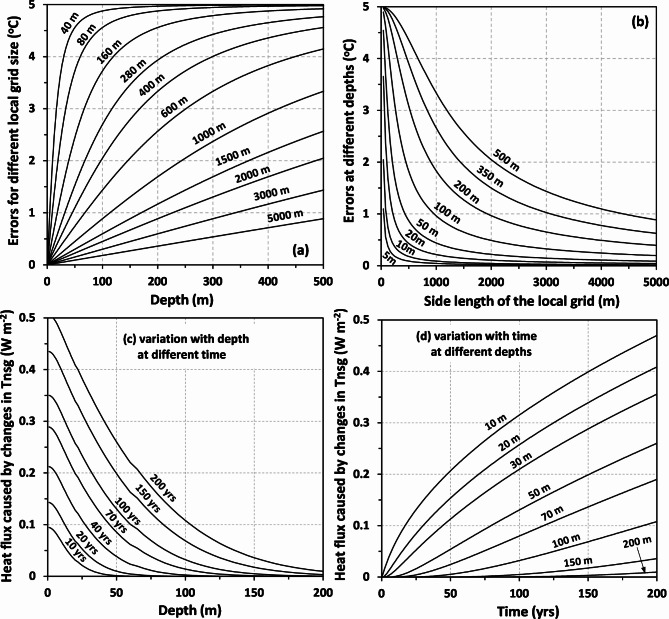
The required grid cell size for 1D modeling can also be estimated based on calculated errors. Figures 5a and b show the errors of Tg calculated based on the local grid cell at equilibrium conditions without considering lateral effects from the surrounding area, which is assumed 5 °C lower than the local grid cell in Tnsg, a difference frequently observed in permafrost regions11–14. The error increases with depth (Fig. 5a). When the local grid cell is small, the error increases rapidly with depth approaching the maximum value because Tg in deep ground is dominated by the effects of the surrounding area. When the local grid cell is large, the error increases gradually with depth (Fig. 5a). Figure 5b shows how the error decreases with the size of the local grid cell at different depths at equilibrium conditions. To keep the errors < 1 °C at 10 m, 100 m, and 500 m depths, the side-lengths of the local grid cells must be > 88 m, > 880 m, and > 4.4 km, respectively. These are the grid cell sizes required to keep the errors < 1 °C at these depths if the difference in Tnsg between the grid cell and the surrounding area is 5 °C. Although this is an extreme spatial pattern, it indicates that initializing 1D models needs to use a large grid cell.

Fig. 5.

Fig. 5

Open in a new tab

Potential errors for modeling Tg based on a local grid cell under equilibrium conditions (a,b) and downward heat fluxes caused by increasing Tnsg by 0.1 °C yr− 1 (c,d). (a) variation of the errors with depth for different grid cell sizes (shown for each curve) without considering lateral effects from the surrounding area under equilibrium conditions. (b) the same as panel ‘a’ but for variation of the errors with grid cell size at different depths (shown for each curve). The Tnsg of the local grid cell was set as 5 °C warmer than the surrounding area, and the Tg was in equilibrium. (c) variation of downward heat flux with depth in different years (shown each curve) caused by increasing Tnsg by 0.1 °C yr− 1. (d) the same as panel ‘c’ but for variation with time at different depths (shown for each curve). The thermal conductivity and heat capacity were assumed as 1.6 W m− 1 °C− 1 and 2.2 × 106 J m− 3 °C− 1, respectively.

The required grid cell size for transient change is smaller than that required at equilibrium conditions. For time scales of 100 and 200 years with an increasing rate of 0.1 °C yr− 1 for Tnsg, the required radii of the local areas are 120 and 180 m, respectively, to keep the impacts of surrounding areas less than 0.1 °C.

The impact depth due to changes in Tnsg also depends on time. If the Tnsg of the entire ground surface increases at a rate of 0.1 °C yr− 1, its impact (using a criterion of 0.1 °C) reaches 87 m, 140 m, and 218 m in 50, 100, and 200 years, respectively. These are the minimum depths if we want to use a relatively constant Tg (varies < 0.1 °C) or a constant heat flux (varies < 0.01 W m− 2) as the lower boundary condition in a model. Warming of the ground surface causes a heat transfer from the surface to deeper depths, and the heat flux is increasing with time (Fig. 5c and d). Thus, using a constant geothermal heat flux as the lower boundary condition can overestimate the increase in Tg with climate warming if the lower boundary is shallow. Therefore, permafrost models need to use a deep ground profile9,45,46, which allows us to define the lower boundary conditions using a constant geothermal heat flux. On the other hand, using a deeper ground profile requires considering a larger surface area for model initialization. Therefore, the grid cell size for 1D modeling cannot be small and the lateral heat flow has to be considered for fine resolution modeling.

Accurately quantifying Tg profiles is important for determining the presence or absence of permafrost, depth of permafrost, and their changes with climate and land surface disturbances. Current permafrost monitoring, modeling and mapping approaches focus on thawing and freezing conditions near the ground surface12,17,18,20, where the effects of lateral conductive heat flow are small. The effects of lateral conductive heat flow become larger in deeper ground, which can significantly affect the Tg and the thawing and freezing conditions in deep depths. These conditions are important for infrastructure stability, engineering operations, groundwater, geohazards, and for assessing the responses of permafrost to climate change and disturbances of the land surface occurred locally and in surrounding areas.

Discussion

The effects of lateral heat flow on Tg and permafrost have been recognized in early permafrost studies25–27,33,34,41,47 and in recent 3D modeling studies28–30. Furthermore, the effects of different shapes of water bodies on Tg were also recognized25,26,31,35. However, all permafrost maps for large areas were developed based on 1D approaches without considering lateral effects from surrounding areas. The 1D process-based models are initialized assuming that Tg is in equilibrium with the Tnsg and that Tg almost linearly increases with depth48. Our theoretical calculation and observations near Schefferville show that lateral heat flow can cause large variations in Tg distribution with depth. Errors in initial conditions directly affect the accuracy of the modeled Tg and associated permafrost conditions, especially when grid cells are small, i.e., spatial resolutions are high.

The multiple-site observations across different landscapes near Schefferville suggest that laterally affected Tg profiles are probably widespread in permafrost regions considering the large variations in Tnsg across landscapes11–14. Kanigan et al.32 estimate that almost all terrestrial sites in the Mackenzie Delta experience some effects of lateral heat flow from water bodies. The spatial distributions of the permafrost base are usually much smoother than expected based on the spatial variations in Tnsg41,49. Thus, Tg profiles must be variable from place to place. Spatially detailed permafrost information is required for engineering operations and environmental assessments. Therefore, it is necessary to include the effect of lateral heat flow when modeling and mapping Tg and permafrost conditions at high spatial resolutions.

Most Tg profiles observed and reported in recent decades were influenced by climate warming50,51. The non-linear Tg profile can be caused by both lateral heat flow under equilibrium conditions (Fig. 3) and by transient changes in Tnsg (Supplementary Figures S4(a-c), S5(a-c), and S7). Therefore, not all non-linear patterns of observed Tg profiles are due to climate warming. Long-term observations are important to discriminate the effects of climate warming from that of lateral heat flow, as the former changes with time while the latter is relatively stable. Long-term ground surface temperature history has been reconstructed based on observed Tg profiles assuming the non-linear patterns of the Tg profiles are caused by changes in Tnsg of the local area52,53. Therefore, one should be cautious when selecting observation sites for such inversion estimation of climate history.

The ubiquitous conductive heat flow calculated in this study is only a baseline condition for the effects of lateral heat flows. The results of this study can be used as a general guide for modeling and mapping permafrost and selecting observation sites in the field. However, the calculated transient effects did not include latent heat and water flow effects. Seasonal thawing and freezing and thawing of ground ice have significant impacts on Tg2. Latent heat processes occur mainly in top ground layers and lateral conductive heat effects on Tg is small at shallow depths. Therefore, we can use a 1D model to calculate Tg dynamics, including thawing and freezing processes, and then use the simulated annual mean Tg several meters below ground surface as the Tnsg to calculate the lateral conductive heat effects. Water flows can significantly increase lateral heat flow and cause variation in Tg and permafrost thaw28,29,54. Water flow strongly depends on local topography, hydrology, ground materials, thawing and freezing conditions, and 3D models are usually needed to quantify these complex processes.

Methods

Calculating lateral conductive heat flow effects on Tg

We calculated the effects of lateral conductive heat flow on Tg for six cases considering their simplicity in calculation and practical applications (Fig. 1).

If the land surface has a uniform Tnsg except an area S that has a different Tnsg, the difference of Tnsg in S will cause a disturbance in Tg under and near this area due to heat conduction. If S is a circular area centered directly above the ground point P (Fig. 1a), its impact on Tg at point P can be calculated based on Lachenbruch34 (Eq. 30)

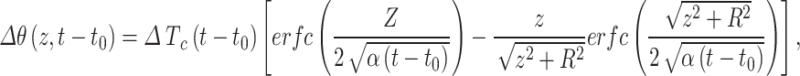graphic file with name M1.gif 1

where R is the radius of the circular area. ΔTc(t-t0) is a step-change of Tnsg in the circular area from time t0. The Tnsg inside and outside of the circle are the same before time t0 and Tg is assumed in equilibrium at time t0. Δθ(z, t-t0) is the changes in Tg at depth z at point P at time t due to disturbance of ΔTc(t-t0). erfc() is the complementary error function and its calculation is described later in the text. α is the thermal diffusivity of the ground (m2 s− 1), which is assumed uniform and constant. Equation 1 and the following equations also assume no thawing and freezing in the ground. Under equilibrium conditions (t is infinitely large), Eq. 1 reduces to

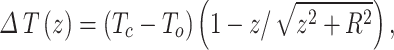graphic file with name M2.gif 2

where ΔT(z) is the changes in Tg at depth z at point P. Tc and To are the Tnsg of the circular area and the other area (°C), respectively.

For simplicity, Eq. 1 can be expressed as

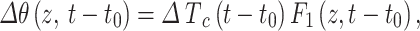graphic file with name M3.gif 3

where

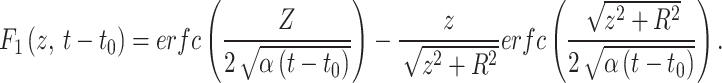graphic file with name M4.gif 4

If ΔTc varies from year to year, the transient change of the Tg can be expressed as the cumulative effects of the net changes from year to year

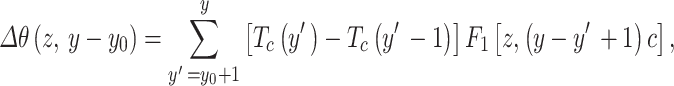graphic file with name M5.gif 5

where y0 is the first year in which the Tnsg of the circular area equals the Tnsg outside of the circular area (Tc(yo) = To) and Tg is in equilibrium. y is a year after y0. y´ is a mid variable for the years from y0 + 1 to y. Tc(y´) and Tc(y´-1) are the Tnsg of the circular area in years y´ and y´-1, respectively. c is a constant converting the time from year to seconds (365.25 × 24 × 60 × 60). F1[z,(y- y´+1)c] can be calculated using Eq. 4 by replacing t-t0 with (y- y´+1)c.

If the circular area is infinitely large, Eq. 1 becomes

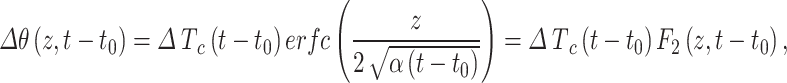graphic file with name M6.gif 6

where

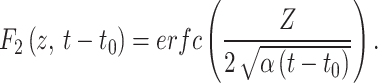graphic file with name M7.gif 7

If ΔTc varies from year to year, its impact on Tg can be calculated in a similar way as Eq. 5 but using F2.

If the area S is a square centered directly above the ground point P (Figure S1(b)), its impact on Tg at point P under equilibrium conditions can be calculated based on Lachenbruch34 (Eq. 32 and set x = 0, y = 0, a = b):

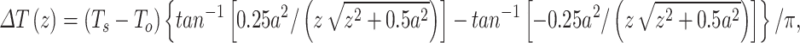graphic file with name M8.gif 8

where a is the side-length of the square (m), and Ts is the Tnsg of the square (°C).

If the area S is an infinitely long strip above the ground point P (Fig. 1c), its impact on Tg at point P under equilibrium conditions can be calculated based on Lachenbruch34 (Eq. 32 and set x = 0, y = 0, a = 0.5w, b infinitely large):

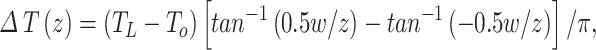graphic file with name M9.gif 9

where TL is the Tnsg of the strip (°C), and w is the width of the strip (m). The point O is at the center of the strip.

If the area S is an annulus (Fig. 1d) which has a step-change in Tnsg, its impact on the Tg under the center of the annulus can be calculated based on Lachenbruch34 (Eq. 33)

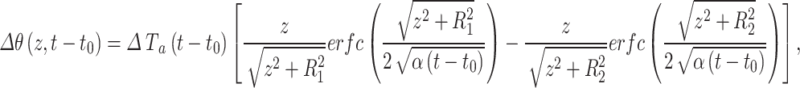graphic file with name M10.gif 10

where R1 and R2 are the radii of the inner and outer circles of the annulus. ΔTa(t-t0) is a step-change of Tnsg in the annulus from time t0. The Tnsg inside and outside of the annulus are the same before time t0 and Tg is assumed in equilibrium at time t0. Under equilibrium conditions (t is infinitely large), Eq. 10 reduces to

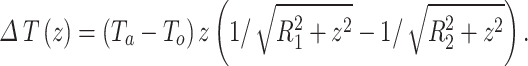graphic file with name M11.gif 11

Equation 10 can be simplified as

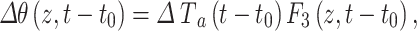graphic file with name M12.gif 12

where

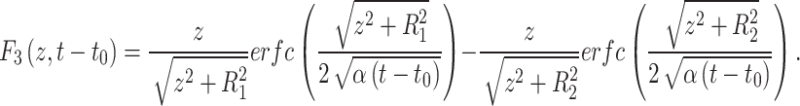graphic file with name M13.gif 13

If ΔTa varies from year to year since y0, its transient impact on Tg can be expressed as the cumulative effects of the net changes from year to year

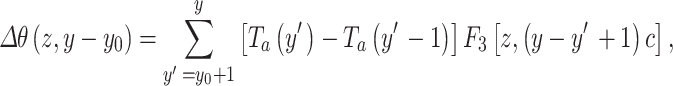graphic file with name M14.gif 14

where F3[z,(y- y´+1)c] can be calculated using Eq. 13 by replacing t-t0 with (y- y´+1)c.

Equation 10 can also be used to calculate the effect of a section of an annulus. If the ring width of an annulus is 1 m (R2- R1 = 1 m) and the average arc length is 1 m, the area of this section of annulus is 1 m2 (Fig. 1(e)). For such a unit area of annulus, Eq. 10 becomes

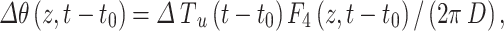graphic file with name M15.gif 15

where

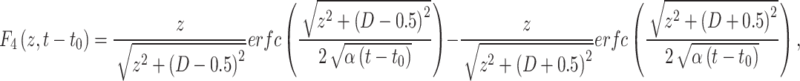graphic file with name M16.gif 16

where D is the distance from point O to the center of the unit area of annulus. ΔTu(t-t0) is a step-change of Tnsg in the unit area from time t0. Such a unit area of annulus is very similar to a unit square. Therefore, this equation can be used to estimate the effects of any land area shapes by dividing the areas into various unit areas. Similar to Eq. 14, Eq. 15 can also be used to calculate the transient effect if ΔTu varies from year to year

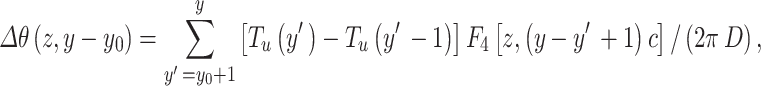graphic file with name M17.gif 17

where F4[z,(y- y´+1)c] can be calculated using Eq. 16 by replacing t-t0 with (y- y´+1)c.

If the point O is beside an infinitely long and wide area (Fig. 1f), the impact of this large area with a step-change in Tnsg on the Tg at point P can be calculated numerically using Eq. 10 (the large area can be approximated using a large number of tiny fractions of annulus with different R1 and an infinitely large R2)

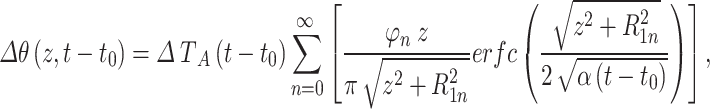graphic file with name M18.gif 18

where

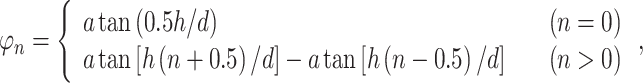graphic file with name M19.gif 19
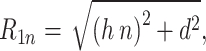graphic file with name M20.gif 20

where d is the distance of the point O to the edge of the large area. ΔTA(t-t0) is a step-change of Tnsg of the large area from time t0. n is an integer from 0 to infinite for numerical calculation using a step h (Fig. 1f). It assumes that the Tnsg in and outside of the large area are the same before time t0 and Tg is in equilibrium at time t0. Under equilibrium condition (t-t0 is infinitely large), Eq. 18 becomes

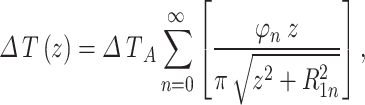graphic file with name M21.gif 21

where ΔT(z) is the impact of the area under equilibrium conditions on the Tg under the point O.

Equation 18 can be simplified as

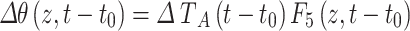graphic file with name M22.gif 22

where

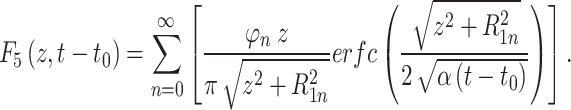graphic file with name M23.gif 23

If ΔTA varies from year to year since y0, the transient variation of the Tg can be expressed as the cumulative effects of the net changes from year to year

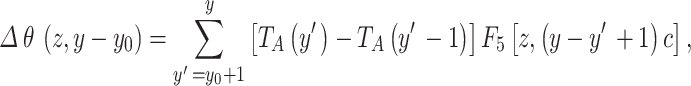graphic file with name M24.gif 24

where F5[z, (y- y´+1)c] can be calculated using Eq. 23 by replacing t-t0 with (y- y´+1)c.

Abramowitz and Stegun55 provide several approximations for the error function with varying accuracy (Eq. 7.1.25-28). We select the following one which has a maximum error of 2.5 × 10− 5

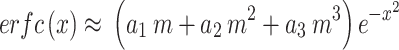graphic file with name M25.gif 25

where m = 1/(1 + p x). p, a1, a2, and a3 are constants (p = 0.47047, a1 = 0.3480242, a2 = − 0.0958798, a3 = 0.7478556).

The variation of Tg with depth and time can be expressed as

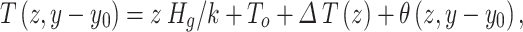graphic file with name M26.gif 26

where T(z, y-y0) is the Tg at depth z in year y. ΔT(z) is the impacts of area S on Tg at depth z under equilibrium conditions as calculated by Eqs. 2, 8, 9, 11 and 21. θ(z, y-y0) is transient changes calculated by Eqs. 5, 14, and 24. Hg is the geothermal heat flux (W m− 2), which is assumed to be constant across the area. k is the thermal conductivity (W m− 1 °C− 1), which is assumed uniform across the area and depth as well. All these equations are only for conductive heat flow. They do not include the effects of convective heat flow and the latent heat (thawing and freezing of the ground).

Thermal conductivity of the ground generally ranges from 0.5 to 5 W m− 1 °C− 1 based on observations across northern North America above 45° N latitude56,57. The median value of these observations is 1.6 W m− 1 °C− 1. Volumetric heat capacity of the ground generally ranges from 1.3 to 2.8 MJ m− 3 °C− 1 for unconsolidated ground materials, and from 1.8 to 3 MJ m− 3 °C− 1 for solid rock58. We used a value of 2.2 MJ m− 3 °C− 1 in the analysis. Using the selected values for thermal conductivity and heat capacity, the thermal diffusivity would be 7.27 × 10− 7 m2 s− 1. We also tested the sensitivity of the transient impacts on Tg by increasing and decreasing the diffusivity by 50%. For the Schefferville area, the thermal conductivity and the geothermal heat flux were set as 3 W m− 1 °C− 1 and 0.022 W m− 2 according to the conditions of this area40,41.

To show the transient impacts on Tg, we used a step-increase in Tnsg by 10 °C as this value is comparable to the temperature differences between large water bodies and land in the Arctic13,31,59 and the Tnsg variations caused by snow redistribution in the Arctic11,12. For gradual change in Tnsg, we used a warming rate of 0.1 °C yr− 1, which is comparable to or slightly higher than the increase rate of annual mean air temperature in the Arctic in the past four decades60. We used 0.1 °C as a criterion to determine the depth or extent affected by changes in Tnsg. This criterion is equivalent to 1% of the step-change in Tnsg change, and it is the same amount (but in °C) as the constant gradual change rate in Tnsg (°C).

Comparisons between the calculated and observed Tg profiles near Schefferville

We calculated the average Tg profile for each observed site and put all the sites together to show the general patterns of the Tg profiles in this area (Supplementary Figure S2). For each site, the average Tg at each depth was calculated using all available Tg observations at that depth. Some obvious abnormal values were manually excluded. The average Tg at shallow layers (< 7 m) was not calculated when the number of observations were less than 30 days and the observations did not include both summer and winter. Due to lack of detailed site information about the Tg observations, we analyzed their variation patterns collectively to highlight their general characteristics and the effects of lateral heat flow on the Tg profiles.

Except two boreholes (b121 and b123 in Fig. 4a) with very high Tg at 20 to 40 m depths, the general patterns of the Tg profiles observed near Schefferville are similar to the impact of local areas with different Tnsg as shown in Fig. 3d. Therefore, we calculated Tg profiles based on Eqs. 2 and 26 using different parameters. Except three cases (the red curves 8 to 10 in Fig. 4a), Tnsg outside of the circular areas was set as -0.4 °C based on the average of the observed Tg at all sites. The radii of the local areas and their Tnsg were tuned to fit the general patterns of the observed Tg profiles. The theoretically calculated Tg profiles (the red curves in Fig. 4a) are comparable to the general patterns of the observed ones although each site is unique and can be fit better using a unique set of parameters. The observed two warmest sites (boreholes b121 and b123) are similar to the impacts of annuli as shown in Fig. 3h. These two sites were in or near a valley with a river according to 1948 air photographs. They probably were measured at relatively high areas within the valley with less snow accumulation locally and outside of the valley. Therefore, we calculated the Tg profile based on the effects of an annulus (the red curve 11 in Fig. 4a). Site b126 was near a tailing pond based on 1975 air photographs and high-resolution Google Earth imagery. Therefore, we calculated its Tg assuming the local area was much colder than the surroundings and was in equilibrium (the red solid curve 1a in Fig. 4a). It is also possible that the Tg was not in equilibrium. We calculated the Tg profile again (the red dashed curve 1b in Fig. 4a) assuming a step-change in Tnsg of a circular area centered at the site (Its Tnsg decreased 7.5 °C from − 1.7. The radius of the area is 40 m, and the time is 10 yrs after a step-change in Tnsg. These values are tuned by comparing with the observed Tg profile of site b126. The thermal conductivity and the geothermal heat flux are the same as for the other red curves). The calculated Tg at 100 m depth is colder than other sites. It is very likely that the observed Tg variation pattern of b126 was due to the combination effects of both equilibrium and transient processes.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary Material 1 (5.6MB, docx)

Acknowledgements

The authors thank Sharon Smith for providing help to access the ground temperature data which she and others compiled previously. Robert Way and Alexandra Lewis also provided related information and archives about the permafrost studies near Schefferville. Brendan O’Neill and Chris Burn carefully reviewed the earlier versions of the manuscript. Two anonymous reviewers also reviewed the paper. Their comments and suggestions greatly improved the quality of the paper. This study was funded by Earth Observation Baseline Data for Cumulative Effects project and Modelling and Mapping Permafrost in Hudson Bay Lowlands project. This work also contributes to NSERC PermafrostNet and a project affiliated to the Arctic-Boreal Vulnerability Experiment (ABoVE), a NASA Terrestrial Ecology program.

Author contributions

Y.Z. designed the study and prepared the initial manuscript. G.H. processed air photographs and satellite data. G.H and M.T.B. supported calculations, results analysis, and contributed to the writing of the manuscript.

Data availability

The ground temperature data used in the analysis are from Smith et al. (2003), and the data are available at https://nsidc.org/data/GGD605/versions/1. The air photographs are from the National Air Photo Library (NAPL) in Natural Resources Canada. The calculated results are available from the corresponding author on request.

Declarations

Competing interests

The authors declare no competing interests.

Footnotes

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

References

  • 1.O’Neill, H. B., Smith, S. L., Burn, C. R., Duchesne, C. & Zhang, Y. Widespread permafrost degradation and thaw subsidence in northwest Canada. J. Geophys. Res. Earth Surf.128, e2023JF007262. 10.1029/2023JF007262 (2023). [Google Scholar]
  • 2.Smith, S. L., O’Neill, H. B., Isaksen, K., Noetzli, J. & Romanovsky, V. E. The changing thermal state of permafrost. Nat. Rev. Earth Environ.3(1), 10–23. 10.1038/s43017-021-00240-1 (2022). [Google Scholar]
  • 3.Hjort, J. et al. Impacts of permafrost degradation on infrastructure. Nat. Rev. Earth Environ.3, 24–38. 10.1038/s43017-021-00247-8 (2022). [Google Scholar]
  • 4.Meredith, M. et al. Polar regions. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate (eds Pörtner, H. O. et al.) 203–320, 10.1017/9781009157964.005 (Cambridge University Press, 2019). [Google Scholar]
  • 5.Romanovsky, V. E. et al. Changing permafrost and its impacts. In Snow, Water, Ice and Permafrost in the Arctic (SWIPA). Ch. 4, 65–102 (2017). (AMAP, 2017). [Google Scholar]
  • 6.Nicolsky, D. J., Romanovsky, V. E., Panda, S. K., Marchenko, S. S. & Muskett, R. R. Applicability of the ecosystem type approach to model permafrost dynamics across the Alaska North Slope. J. Geophys. Res. Earth Surf.122, 50–75. 10.1002/2016JF003852 (2017). [Google Scholar]
  • 7.Zhang, Y. Spatio-temporal features of permafrost thaw projected from long-term high-resolution modeling for a region in the Hudson Bay Lowlands in Canada. J. Geophys. Res. Earth Surf.118, 542–552. 10.1002/jgrf.20045 (2013). [Google Scholar]
  • 8.Zhang, Y. et al. Modelling and mapping permafrost at high spatial resolution in Wapusk National Park, Hudson Bay Lowlands. Can. J. Earth Sci.49, 925–937. 10.1139/E2012-031 (2012). [Google Scholar]
  • 9.Zhang, Y., Chen, W. & Riseborough, D. W. Disequilibrium response of permafrost thaw to climate warming in Canada over 1850–2100. Geophys. Res. Lett.35, L02502. 10.1029/2007GL032117 (2008). [Google Scholar]
  • 10.Marchenko, S., Romanovsky, V. & Tipenko, G. Numerical modeling of spatial permafrost dynamics in Alaska, In Proceedings of the Eighth Int. Conference on Permafrost, 190-204 (Willey, Institute of Northern Engineering, University of Alaska, 2008).
  • 11.Cao, B. et al. GlobSim (v1.0): deriving meteorological time series for point locations from multiple global reanalyses. Geosci. Model. Dev.12(11), 4661–4679. 10.5194/gmd-12-4661-2019 (2019). [Google Scholar]
  • 12.Garibaldi, M. C., Bonnaventure, P. P. & Lamoureux, S. F. Utilizing the TTOP model to understand spatial permafrost temperature variability in a high Arctic landscape, Cape Bounty, Nunavut, Canada. Permafr. Periglac. Process.32(1), 19–34. 10.1002/ppp.2086 (2021). [Google Scholar]
  • 13.Jorgenson, M. T. et al. Resilience and vulnerability of permafrost to climate change. Can. J. Res.40(7), 1219–1236. 10.1139/X10-060 (2010). [Google Scholar]
  • 14.Zhang, Y. et al. Landscape-scale variations in near surface soil temperature and active-layer thickness: implications for high-resolution permafrost mapping. Permafr. Periglac. Process.32(4), 627–640. 10.1002/ppp.2104 (2021). [Google Scholar]
  • 15.Burke, B., Zhang, Y. & Krinner, G. Evaluating permafrost physics in the CMIP6 models and their sensitivity to climate change. Cryosphere. 14, 3155–3174. 10.5194/tc-14-3155-2020 (2020). [Google Scholar]
  • 16.Jafarov, E. E., Marchenko, S. S. & Romanovsky, V. E. Numerical modeling of permafrost dynamics in Alaska using a high spatial resolution dataset. Cryosphere. 6, 613–624. 10.5194/tc-6-613-2012 (2012). [Google Scholar]
  • 17.Gisnås, K., Etzelmüller, B., Farbrot, H., Schuler, T. V. & Westermann, S. CryoGRID 1.0: Permafrost distribution in Norway estimated by a spatial numerical model. Permafr. Periglac. Process.24, 2–19. 10.1002/ppp.1765 (2013). [Google Scholar]
  • 18.Obu, J. et al. Northern Hemisphere permafrost map based on TTOP modelling for 2000–2016 at 1 km2 scale. Earth-Sci. Rev.193, 299–316. 10.1016/j.earscirev.2019.04.023 (2019). [Google Scholar]
  • 19.Gruber, S. Derivation and analysis of a high-resolution estimate of global permafrost zonation. Cryosphere. 6, 221–233. 10.5194/tc-6-221-2012 (2012). [Google Scholar]
  • 20.Bonnaventure, P. P., Lewkowicz, A. G., Kremer, M. & Sawada, M. C. A permafrost probability model for the southern Yukon and northern British Columbia, Canada. Permafr. Periglac. Process.23, 52–68. 10.1002/ppp.1733 (2012). [Google Scholar]
  • 21.Duchesne, C., Wright, J. F. & Ednie, M. High-resolution numerical modeling of climate change impacts to permafrost in the vicinities of Inuvik, Norman Wells, and Fort Simpson, NT, Canada. In Proceedings of Ninth Int. Conference on Permafrost, Vol. 1 (eds Kane, D. L., & Hinkel, K. M. ), 385–390 (2008).
  • 22.Pastick, N. J. et al. Distribution of near-surface permafrost in Alaska: estimates of present and future conditions. Remote Sens. Environ.168, 301–315. 10.1016/j.rse.2015.07.019 (2015). [Google Scholar]
  • 23.Panda, S. K., Prakash, A., Solie, D. N., Romanovsky, V. E. & Jorgenson, M. T. Remote sensing and field-based mapping of permafrost distribution along the Alaska Highway Corridor, Interior Alaska. Permafr. Periglac. Process.21, 271–281. 10.1002/ppp.686 (2010). [Google Scholar]
  • 24.Thaler, E. A. et al. High-resolution maps of near‐surface permafrost for three watersheds on the Seward Peninsula, Alaska derived from machine learning. Earth Space Sci.10, 12. 10.1029/2023EA003015 (2023). [Google Scholar]
  • 25.Brown, W. G., Johnston, G. H. & Brown, R. J. E. Comparison of observed and calculated ground temperatures with permafrost distribution under a northern lake. Can. Geotech. J.1, 147–154 (1964). [Google Scholar]
  • 26.Smith, M. W. Permafrost in the Mackenzie delta, Northwest Territories. Geological Survey Paper 75– 28, Geological Survey of Canada, Energy Mines and Resources Canada, Ottawa, Canada (1976).
  • 27.Smith, M. W. & Hwang, C. T. Thermal disturbance due to channel shifting, Mackenzie delta, N.W.T. Canada. In Proc. 2nd Int. Conference on Permafrost, North American Contribution, 51–60 (1973).
  • 28.Liu, W., Fortier, R., Molson, J. & Lemieux, J-M. Three-dimensional numerical modeling of cryo-hydrogeological processes in a river-talik system in a continuous permafrost environment. Water Resour. Res.58, e2021WR031630. 10.1029/2021WR031630 (2022). [Google Scholar]
  • 29.Kurylyk, B. L., Hayashi, M., Quinton, W. L., McKenzie, J. M. & Voss, C. I. Influence of vertical and lateral heat transfer on permafrost thaw, peatland landscape transition, and groundwater flow. Water Resour. Res.52, 1286–1305. 10.1002/2015WR018057 (2016). [Google Scholar]
  • 30.Zhou, F., Zhang, A., Li, R. & Hoeve, E. Spatio-temporal simulation of permafrost geothermal response to climate change scenarios in a building environment. Cold Reg. Sci. Technol.56, 141–151. 10.1016/j.coldregions.2008.12.004 (2009). [Google Scholar]
  • 31.Burn, C. R. Tundra lakes and permafrost, Richards Island, western Arctic coast, Canada. Can. J. Earth Sci.39(8), 1281–1298. 10.1139/e02-035 (2002). [Google Scholar]
  • 32.Kanigan, J. C. N., Burn, C. R. & Kokelj, S. V. Permafrost response to climate warming south of treeline, Mackenzie delta, Northwest Territories, Canada. In Proceedings of 9th Int. Conference on Permafrost, Vol. 1 (eds Kane, D. L., & Hinkel, K. M.), 901–906. (Institute of Northern Engineering, University of Alaska Fairbanks, 2008).
  • 33.Lachenbruch, A. H. Thermal effects of the ocean on permafrost. Geol. Soc. Am. Bull.68(11), 1515–1530 (1957). [Google Scholar]
  • 34.Lachenbruch, A. H. Three-dimensional heat conduction in permafrost beneath heated buildings. U.S. Geol. Surv. Bull.1052-B, 51–69 (1957). [Google Scholar]
  • 35.Mackay, J. R. Pingos of the Pleistocene Mackenzie River Delta Area. Geographical Bulletin 18, 21–63 Geographical Branch, Department of Mines and Technical Surveys, Ottawa, Canada. (1962).
  • 36.Li, X. Y. et al. Influences of forest fires on the permafrost environment: a review. Adv. Clim. Chang. Res.12, 48–65. 10.1016/j.accre.2021.01.001 (2021). [Google Scholar]
  • 37.Nitze, I., Grosse, G., Jones, B. M., Romanovsky, V. E. & Boike, J. Remote sensing quantifies widespread abundance of permafrost region disturbances across the Arctic and Subarctic. Nat. Commun.9, 5423. 10.1038/s41467-018-07663-3 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Heginbottom, J. A., Dubreuil, M. A. & Harker, P. A. Canada Permafrost, in National Atlas of Canada, 5th ed. (Natural Resources Canada, 1995). [Google Scholar]
  • 39.Granberg, H. B. Permafrost mapping at Schefferville, Quebéc. Phys. Geogr.10, 249–269. 10.1080/02723646.1989.10642381 (1989). [Google Scholar]
  • 40.Smith, S., Granberg, H. B. & Burgess, M. Schefferville permafrost temperature database, Version 1. Geological Survey of Canada, Natural Resources Canada, Data https://nsidc.org/data/GGD605/versions/1 (Accessed July 2021) (2003).
  • 41.Jones, I. G. An attempt to quantify permafrost distribution near Schefferville, Quebec. A thesis for the degree of Master of Science, Department of Geography, McGill University, Montreal, QC. (1976).
  • 42.Granberg, H. B., Lewis, J. E., Moore, T. R., Steer, P. & Wright, R. K. Schefferville Permafrost Research. Volume I, Parts 1a and 1b: Summary, Review and Recommendations, and Catalogue of Available Materials. Earth Physics Branch Open File Number 84– 7 10.4095/293687 (1984).
  • 43.Smith, S. L. & Burgess, M. M. A digital database of permafrost thickness in Canada. Open. File4173 (2002).
  • 44.Zhang, Y., Chen, W. & Riseborough, D. W. Temporal and spatial changes of permafrost in Canada since the end of the little ice age. J. Geophys. Res.111, D22103. 10.1029/2006JD007284 (2006). [Google Scholar]
  • 45.Alexeev, V., Nicolsky, D., Romanovsky, V. & Lawrence, D. An evaluation of deep soil configurations in the CLM3 for improved representation of permafrost. Geophys. Res. Lett.34, L09502. 10.1029/2007GL029536 (2007). [Google Scholar]
  • 46.Delisle, G. Near-surface permafrost degradation: how severe during the 21st century? Geophys. Res. Lett.34 (L09503). 0.1029/2007GL029323 (2007).
  • 47.Nicholson, F. H. & Granberg, H. B. Permafrost and snow cover relationships near Schefferville, Quebec. In Permafrost: North American contribution to the Second International Conference on Permafrost. 151–158. (1973).
  • 48.Ross, C., Siemens, G. & Beddoe, R. Initialization of thermal models in cold and warm permafrost. Arct. Sci.8, 362–394. 10.1139/as-2021-0013 (2022). [Google Scholar]
  • 49.Minsley et al. Airborne electromagnetic imaging of discontinuous permafrost. Geophys. Res. Lett.39, L02503. 10.1029/2011GL050079 (2012). [Google Scholar]
  • 50.Burn, C. R. & Zhang, Y. Permafrost and climate change at Herschel Island (Qikiqtaruq), Yukon Territory, Canada. J. Geophys. Res.114, F02001. 10.1029/2008JF001087 (2009). [Google Scholar]
  • 51.Clow, G. D. Temperature data acquired from the DOI/GTNP Deep Borehole Array on the Arctic Slope of Alaska, 1973–2013. Earth Syst. Sci. Data 6, 201–218 10.5194/essd-6-201-2014 (2014).
  • 52.Lachenbruch, A. H. & Marshall, B. V. Changing climate: geothermal evidence from permafrost in Alaska. Science. 234(4777), 689–696. 10.1126/science.234.4777.689 (1986). [DOI] [PubMed] [Google Scholar]
  • 53.Beltrami, H., Gosselin, C. & Mareschal, J. C. Ground surface temperatures in Canada: spatial and temporal variability. Geophys. Res. Lett.30(10), 1499. 10.1029/2003GL017144 (2003). [Google Scholar]
  • 54.Dong, L., Fu, C., Liu, J. & Wang, Y. Disturbances of temperature-depth profiles by surface warming and groundwater flow convection in Kumamoto Plain, Japan. Geofluids2018, 8451276 (2018).
  • 55.Abramowitz, M. & Stegun, I. A. (eds) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55, 297. (United States Department of Commerce, National Bureau of Standards, 1983). [Google Scholar]
  • 56.Pollack, H. N., Hurter, S. J. & Johnson, J. R. Heat flow from the earth’s interior: analysis of the global data set. Rev. Geophys.31(3), 267–280 (1993). [Google Scholar]
  • 57.Majorowicz, J. A., Skinner, W. R. & Safanda, J. Large ground warming in the Canadian Arctic inferred from inversions of temperature logs. Earth Planet. Sci. Lett.221, 15–25 (2004). [Google Scholar]
  • 58.Pahud, D. Geothermal Energy and Heat Storage. Laboratorio di Energia, Ecologia ed Economia, CH-6952, Canobbio, 133 (2002).
  • 59.Brewer, M. C. The thermal regime of an Arctic lake. EOS Trans. AGU. 39, 278–284. 10.1029/TR039i002p00278 (1958). [Google Scholar]
  • 60.Rantanen, M. et al. The Arctic has warmed nearly four times faster than the globe since 1979. Commun. Earth Environ.3, 168. 10.1038/s43247-022-00498-3 (2022). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Material 1 (5.6MB, docx)

Data Availability Statement

The ground temperature data used in the analysis are from Smith et al. (2003), and the data are available at https://nsidc.org/data/GGD605/versions/1. The air photographs are from the National Air Photo Library (NAPL) in Natural Resources Canada. The calculated results are available from the corresponding author on request.

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES