Abstract
Plastic damage of REBCO (REBa2Cu3O7-x, where RE=rare earth) coated conductors by screening current stress (SCS) is a significant concern for ultra-high-field superconducting magnets. Indeed, the third Little Big Coil (LBC3), a REBCO magnet that generated a record, high field of 45.5 T, showed wavy plastic damage produced by excess SCS in all pancakes except two made with single-slit conductors having their slit edges pointing inward towards the magnet center. Reasons for this slit edge orientation-dependent damage mitigation having not yet been presented, we made it the central issue of this new Little Big Coil (LBC4). Accordingly, we constructed and tested LBC4 by replicating LBC3, except that only single-slit tapes were used and every slit edge pointed inward towards the magnet center. LBC4 reached 44.0 T without quench but with some dissipation. After a small lowering of the current without disappearance of the dissipation, the current was charged again, resulting in a quench at 43.5 T due to excess heating in one pancake-to-pancake joint. Indeed, LBC4 exhibited much less wavy conductor damage than LBC3, demonstrating significant SCS mitigation. Detailed post mortem showed a transverse variation of critical current density ( ) across the LBC4 conductor,
) across the LBC4 conductor, 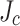 being highest at the slit edge and lowest at the not-slit edge. Our computed screening current stresses were markedly lowered by this
being highest at the slit edge and lowest at the not-slit edge. Our computed screening current stresses were markedly lowered by this 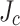 gradient. This paper shows the importance of considering such transverse
gradient. This paper shows the importance of considering such transverse 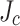 variability, which has not previously been considered, in the precise stress analysis of ultra-high-field REBCO magnets.
variability, which has not previously been considered, in the precise stress analysis of ultra-high-field REBCO magnets.
Subject terms: Superconducting properties and materials, Electrical and electronic engineering, Mechanical engineering, Superconducting properties and materials
Introduction
Superconducting magnets using REBCO (REBa2Cu3O7-x, where RE = rare earth) coated conductors have enabled high fields above 30 T1–3 and even 40 T4,5. One key achievement is a record-high direct current magnetic field of 45.5 T explored through the ‘Little Big Coil (LBC)’ framework utilizing a superconducting REBCO magnet operating in the extremely high background field of 31.1 T5. However, the first LBC test campaign (LBC1–3) concluded that a critical challenge in achieving fields above 40 T is to mitigate screening current stress (SCS) amplification of Lorentz forces and its resulting plastic conductor damage. One intriguing sign of SCS mitigation was revealed by an extensive post mortem of LBC3. It showed only two undamaged single pancakes in the stack of twelve single pancakes, both of which were wound with single-slit conductors having their slit edges pointing inward towards the magnet center, unlike other damaged pancakes with opposite orientation or with two slit edges. Interestingly, the computed peak stresses of these two undamaged pancakes exceeded 1 GPa, as did those of other damaged pancakes, incompatible with the absence of wavy plastic damage to the two.
The obvious next step was to make a new REBCO magnet, LBC4, using only single-slit conductors with all slit edges pointing inward towards the magnet center while replicating LBC3 in all other important respects. Interestingly, the test outcomes were remarkably different. LBC4 attained its peak field of 44.0 T without quench despite some dissipation, different from LBC3 that showed quench right after reaching its peak field of 45.5 T. Reducing the current of LBC4 slightly did not remove the dissipation, and ramping was then resumed with quench occurring at a lower field of 43.5 T. LBC4 post mortem showed much less conductor damage than in LBC3, thus confirming that correct conductor slit orientation can significantly mitigate SCS damage.
An important part of our LBC4 post mortem was to understand this curious slit edge orientation effect that so far has not been considered in any SCS simulation models. Since the SCS magnitude is determined by the local critical current density (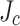 ), we decided to investigate the variation of
), we decided to investigate the variation of 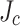 across the conductor width. Local transport current measurement, local magnetization scanning, and magneto-optical imaging (MOI) all confirmed a significant transverse
across the conductor width. Local transport current measurement, local magnetization scanning, and magneto-optical imaging (MOI) all confirmed a significant transverse 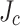 variability of the SuperPower conductors used in LBC1–4 with the highest
variability of the SuperPower conductors used in LBC1–4 with the highest 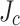 being found at the slit edge and the lowest
being found at the slit edge and the lowest 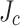 at the not-slit edge. Redoing our SCS calculations with the
at the not-slit edge. Redoing our SCS calculations with the 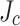 gradient derived from our post mortem significantly reduced the peak stress to 800 MPa (previously >1 GPa) due to the substantially lower
gradient derived from our post mortem significantly reduced the peak stress to 800 MPa (previously >1 GPa) due to the substantially lower 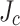 values at the not-slit edges located on the outward edge of each pancake. The first part of this paper describes the design, fabrication, and test results obtained in achieving 44.0 T with the REBCO insert coil, providing detailed information on the coil quench and conductor degradation. The second part focuses on LBC4 post mortem and its SCS simulation results, especially on the conductor degradation caused by wavy plastic deformation induced by screening current overstress. Lastly, we discuss the results in the context of the present, still imperfect REBCO coated conductor technology whose variability is still significant.
values at the not-slit edges located on the outward edge of each pancake. The first part of this paper describes the design, fabrication, and test results obtained in achieving 44.0 T with the REBCO insert coil, providing detailed information on the coil quench and conductor degradation. The second part focuses on LBC4 post mortem and its SCS simulation results, especially on the conductor degradation caused by wavy plastic deformation induced by screening current overstress. Lastly, we discuss the results in the context of the present, still imperfect REBCO coated conductor technology whose variability is still significant.
Results
Design, construction, and experimental setup of LBC4
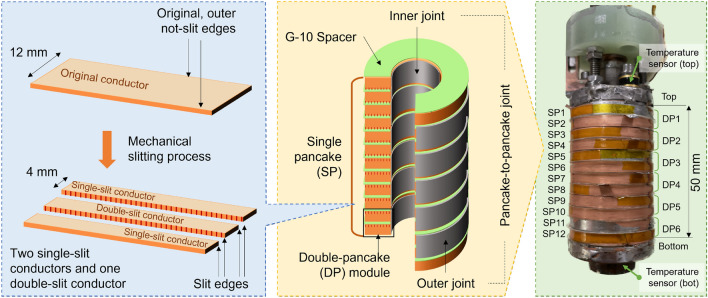
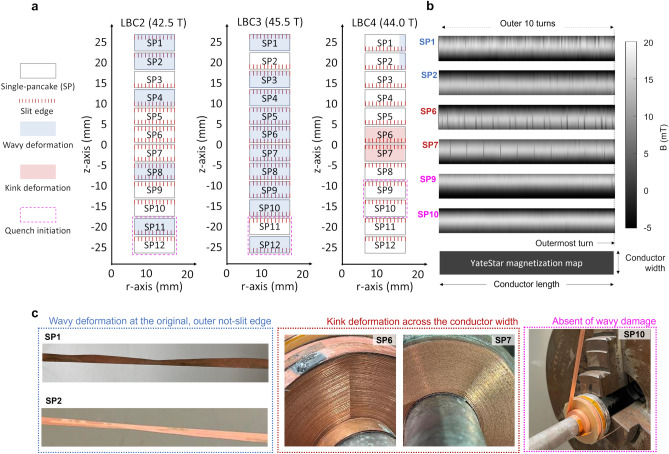
LBC4 consists of six double-pancake (DP) modules, each consisting of two single pancakes (SP). Outer joints connected adjacent DP modules, while inner joints connected the two adjacent single pancakes in a DP module. Voltage taps were attached to the outermost turns of each DP module to compare dissipation DP to DP. A calibrated Hall sensor was inserted at the LBC4 center to measure the central field. Two cryogenic temperature sensors were installed at the top and bottom copper flanges to measure the temperatures in regions where trapped helium gas bubbles were expected. Figure 1 illustrates the single-slit conductor production process, the magnet construction, and the final assembly. Table 1 summarizes the key conductor and magnet specifications.
Figure 1.
Construction of LBC4 replicated LBC3 (45.5 T) except in using only single-slit conductors with all slit edges pointing inward towards the magnet center. The left box illustrates the production of 4-mm wide conductors by mechanically slitting the original 12-mm wide conductor into single-slit and double-slit conductors.
Table 1.
LBC4 key parameters.
| Parameters | Values |
|---|---|
| REBCO-coated conductor | |
| Manufacturer and ID | SuperPower SCS4030-AP |
| Slitting profile | Single-slit |
| Tape width; thickness | 4.02 mm; 0.043 mm |
| Substrate (Hastelloy C-276); each side cooper thickness | 30 µm; 5 µm (10 µm total) |
| LBC4 | |
| Winding inner diameter; outer diameter | 14.0 mm; 33.8–34.0 mm |
| Overall height | 50.0 mm |
| Number of SPs; turns per SP | 12; 220.2 (average) |
| Internal resistance; outer joint resistance | 0.2–2.0 µ ; 75–200 n ; 75–200 n
|
| Magnet constant | 60.3 mTA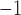
|
| Total inductance | 48.5 mH |
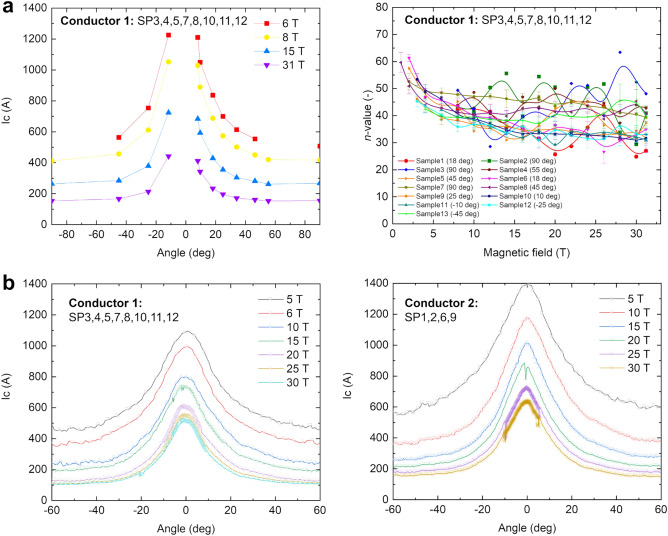
We used two different REBCO tape batches in the winding. The measured critical current (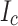 ) performance of each batch in high fields at 4.2 K is summarized in Fig. 2. Figure 2a presents high-field transport current
) performance of each batch in high fields at 4.2 K is summarized in Fig. 2. Figure 2a presents high-field transport current 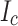 for Conductor 1 used in SP3–5, 7, 8, and 10–12 at various discrete angles and fields up to 31 T from which index numbers n used for the power-law E-J law modeling the REBCO tape V-I characteristic were derived. Such data are hard to get, especially near the ab-planes most relevant to the SCS of LBC4 because of the very high
for Conductor 1 used in SP3–5, 7, 8, and 10–12 at various discrete angles and fields up to 31 T from which index numbers n used for the power-law E-J law modeling the REBCO tape V-I characteristic were derived. Such data are hard to get, especially near the ab-planes most relevant to the SCS of LBC4 because of the very high 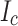 values. Accordingly, Fig. 2b presents torque-magnetometry6 over a continuous angular range around the ab-planes for both the lower (Conductor 1) and the higher
values. Accordingly, Fig. 2b presents torque-magnetometry6 over a continuous angular range around the ab-planes for both the lower (Conductor 1) and the higher 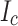 tapes (Conductor 2 used in SP1, 2, 6 and 9). These torque data show that Conductor 2 has a consistently 20–25% higher
tapes (Conductor 2 used in SP1, 2, 6 and 9). These torque data show that Conductor 2 has a consistently 20–25% higher 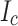 than Conductor 1. Conductor
than Conductor 1. Conductor 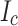 measurement details are described in the Methods section.
measurement details are described in the Methods section.
Figure 2.
Measurements of (a) the field- and angle-dependent transport critical current at 4.2 K, 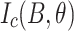 , and the resistive transition index n and (b) continuous
, and the resistive transition index n and (b) continuous 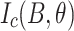 moments by torque magnetometry from which
moments by torque magnetometry from which 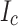 has been derived at 4.2 K.
has been derived at 4.2 K.
Magnet characteristics during its operation up to 44.0 T
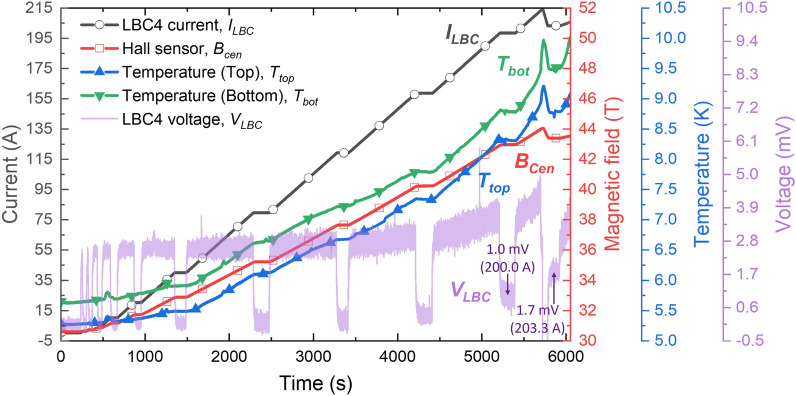
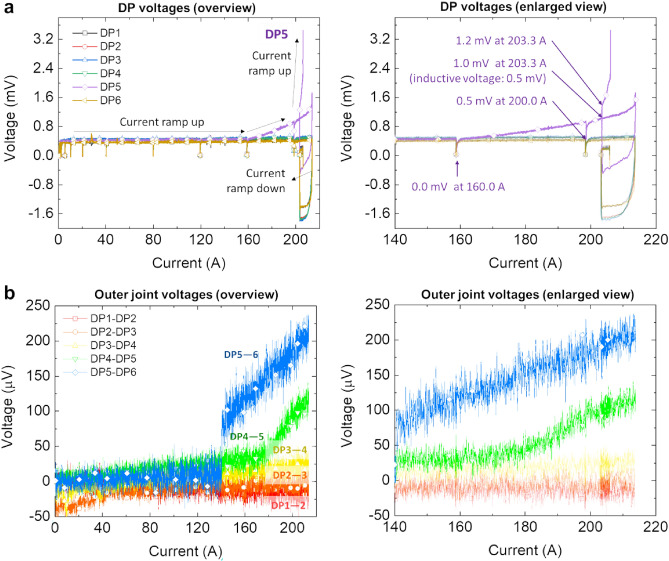
Figure 3 shows the measured current, voltage, magnetic field, and temperatures during the 31.1 T background field test, while Fig. 4 provides detailed voltages for every DP module and each outer joint.
Figure 3.
Temperatures, voltages and magnetic fields observed during testing of LBC4 in the 31.1 T background magnetic field. LBC4 first attained 44.0 T at 213.5 A without quench but with some dissipation. The current was reduced to 203.3 A and then increased again with greater dissipation, resulting in a quench at 206.0 A and 43.5 T.
Figure 4.
Voltages across (a) all DPs and (b) DP-to-DP outer joints during the test. Each provides an overview and an enlarged view after the dissipation initiation (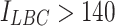 A). The right plot of (a) shows that the first damage occurred in joints neighboring DP5 where excessive screening current overstress was expected. The right plot of (b) shows that the initial dissipation started in the DP5–DP6 outer joint at 140 A with a voltage jump7, this then generating dissipation in the DP4–DP5 joint at about 180 A. Note that all other joints behaved normally. This dissipation caused a local temperature increase in DP5 and its neighbors, initiating flux flow in DP5 and subsequent LBC4 quench.
A). The right plot of (a) shows that the first damage occurred in joints neighboring DP5 where excessive screening current overstress was expected. The right plot of (b) shows that the initial dissipation started in the DP5–DP6 outer joint at 140 A with a voltage jump7, this then generating dissipation in the DP4–DP5 joint at about 180 A. Note that all other joints behaved normally. This dissipation caused a local temperature increase in DP5 and its neighbors, initiating flux flow in DP5 and subsequent LBC4 quench.
At the 213.5 A peak current and 44.0 T field, the DP5 voltage reached 1.6 mV (corresponding to the critical electric field, 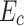 , of 1 µV/cm). Here, the heat generated at this pancake-to-pancake joint was not well dissipated due to the presence of trapped He bubbles8, leading to a temperature increase up to 10.0 K. We stopped charging for a few seconds to scrutinize this dissipation, finding that it continuously increased, unlike the decay of the inductive charging voltage seen in all other DPs. Accordingly, we discharged LBC4 down to 203.3 A. Sadly, a steady voltage of 0.7 mV was observed that we took as a sign of outer joint
, of 1 µV/cm). Here, the heat generated at this pancake-to-pancake joint was not well dissipated due to the presence of trapped He bubbles8, leading to a temperature increase up to 10.0 K. We stopped charging for a few seconds to scrutinize this dissipation, finding that it continuously increased, unlike the decay of the inductive charging voltage seen in all other DPs. Accordingly, we discharged LBC4 down to 203.3 A. Sadly, a steady voltage of 0.7 mV was observed that we took as a sign of outer joint 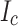 degradation. We resumed ramping and found the DP5 voltage and top and bottom temperatures all increased non-linearly, indicating dissipation that was not present on the first ramp to 44.0 T. This new dissipation then led to quench at 206.0A and 43.5 T.
degradation. We resumed ramping and found the DP5 voltage and top and bottom temperatures all increased non-linearly, indicating dissipation that was not present on the first ramp to 44.0 T. This new dissipation then led to quench at 206.0A and 43.5 T.
After the magnet quench, we evaluated the resistances of every DP and every outer joint of LBC4 at 77 K. Most showed only marginal changes compared to their pre-test 77 K resistances. Only the DP1–DP2 outer joint, DP3, and DP4 exhibited notable changes. Before the high-field test, the values were 200 n , 300 n
, 300 n , and 200 n
, and 200 n , but after test, they increased to 1.3 µ
, but after test, they increased to 1.3 µ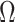 , 750 µ
, 750 µ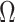 , and 250 µ
, and 250 µ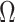 . Since only DP5 and its neighboring joints exhibited dissipation during the high-field test, we conclude that these resistance changes occurred during quench, not during the high-field test.
. Since only DP5 and its neighboring joints exhibited dissipation during the high-field test, we conclude that these resistance changes occurred during quench, not during the high-field test.
Post mortem damage assessment
Figure 5 summarizes the key findings needed to explain the properties of each pancake in LBC4: (a) conductor damage comparison between LBC2 (42.5 T), LBC3 (45.5 T), and LBC4 (44.0 T)9; (b) YateStar magnetization map of the outer ten turns in key pancakes of LBC4, and (c) representative conductor deformation images of selected pancakes. During LBC4 pancake unwinding, two types of damage were observed. One was major kink damage in SP6 and SP7, while the second was wavy plastic rippling damage, earlier found quite widely in LBC1–3 but here in only a few outer turns of a few SP. The impact of this plastic conductor damage within each SP was assessed with our continuous  measuring tool, YateStar, which gave us a longitudinal and some transverse positional record of damage in terms of its local 77 K
measuring tool, YateStar, which gave us a longitudinal and some transverse positional record of damage in terms of its local 77 K 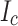 performance. The black vertical stripes in the YateStar magnetization map of the outer ten turns of each pancake illustrate that local degradation starts at the outer edge and that this position correlates to the plastic damage generated by the rippling.
performance. The black vertical stripes in the YateStar magnetization map of the outer ten turns of each pancake illustrate that local degradation starts at the outer edge and that this position correlates to the plastic damage generated by the rippling.
Figure 5.
Summary of post mortem results. (a) Shows damage-pattern maps that indicate much less conductor damage to LBC4 than to LBC2 and LBC3 conductors. (b) YateStar scans of outer 10 turns in selected SP of LBC4. Marginal wavy plastic damage was observed in the ten outer turns of SP1 and SP2 but none in SP3–5. Significant correlated plastic kinking was observed in SP6 and SP7 that initiated at a step discontinuity in the inner winding joint: this was not a result of screening current overstress. The scan of SP8–12 showed no signs of wavy damage that could cause local 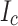 drops.
drops.
An important observation of the LBC4 post mortem performed after reaching 44.0 T is that it showed much less damage than did LBC2 (42.5 T) and LBC3 (45.5 T). Because LBC2–4 all used the same winding design and the same SuperPower AP conductor, we consider the only major variable between them to be the slit edge orientation in each SP. Unlike the widespread plastic, wavy damage observed in LBC2 and LBC3, LBC4 showed wavy plastic damage only in ten outer turns of SP1 and SP2. No damage was seen in SP7–12, even though, by symmetry, some damage might have been expected for SP11 and 12. However, as Fig. 2 shows, SP11 and 12 were wound with a tape with about 20% lower 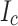 than SP1 and SP2. By contrast, the central pancakes, SP6 and SP7, showed kinks without outward or inward edge concentration, but with uniform severe damage spread across the whole conductor width without any waviness seen in SP1 and SP2. These kinks were aligned radially at the same azimuthal angle located outward of a small inner lead step, where the inner 4-mm wide turn was soldered to the 8-mm wide tape for the inner joint10,11. Intriguingly, SP1–2, SP6, and SP7, which showed plastic damage, correlate well with the outer joint and DP modules that exhibited significant 77 K resistance increases after the quench: DP1–DP2 outer joint, DP3 (containing SP5 and SP6), and DP4 (containing SP7 and SP8).
than SP1 and SP2. By contrast, the central pancakes, SP6 and SP7, showed kinks without outward or inward edge concentration, but with uniform severe damage spread across the whole conductor width without any waviness seen in SP1 and SP2. These kinks were aligned radially at the same azimuthal angle located outward of a small inner lead step, where the inner 4-mm wide turn was soldered to the 8-mm wide tape for the inner joint10,11. Intriguingly, SP1–2, SP6, and SP7, which showed plastic damage, correlate well with the outer joint and DP modules that exhibited significant 77 K resistance increases after the quench: DP1–DP2 outer joint, DP3 (containing SP5 and SP6), and DP4 (containing SP7 and SP8).
As the LBC1–3 test campaign proved, conductor waviness originated in excessive tensile hoop stress induced by screening current overstress. Such damage would have been attributed to crack propagation and subsequent local 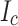 degradation as shown in Fig. 5b and LBC3 post mortem. Indeed, waviness of SP1 and SP2 always occurred preferentially where the largest SCS was predicted. However, we conclude that the radially aligned kinks of SP6 and SP7 were not a result of any excess SCS but resulted from a rebound impact induced by rapid tensile hoop stress relaxation during the quench. This conclusion is consistent with the lack of any voltage increase in these pancakes before quench. The radial alignment seen in Fig. 5c points back to a step solder-joint discontinuity where two pancakes were joined to the 8 mm wide inner joint12. A key microscopic observation was that neither wavy nor kinked regions exhibited Hastelloy-substrate fracture, only substrate yield. This finding indicates that the peak stress in wavy regions exceeded the Hastelloy yield stress but was lower than its fracture stress.
degradation as shown in Fig. 5b and LBC3 post mortem. Indeed, waviness of SP1 and SP2 always occurred preferentially where the largest SCS was predicted. However, we conclude that the radially aligned kinks of SP6 and SP7 were not a result of any excess SCS but resulted from a rebound impact induced by rapid tensile hoop stress relaxation during the quench. This conclusion is consistent with the lack of any voltage increase in these pancakes before quench. The radial alignment seen in Fig. 5c points back to a step solder-joint discontinuity where two pancakes were joined to the 8 mm wide inner joint12. A key microscopic observation was that neither wavy nor kinked regions exhibited Hastelloy-substrate fracture, only substrate yield. This finding indicates that the peak stress in wavy regions exceeded the Hastelloy yield stress but was lower than its fracture stress.
Transverse critical current density investigation
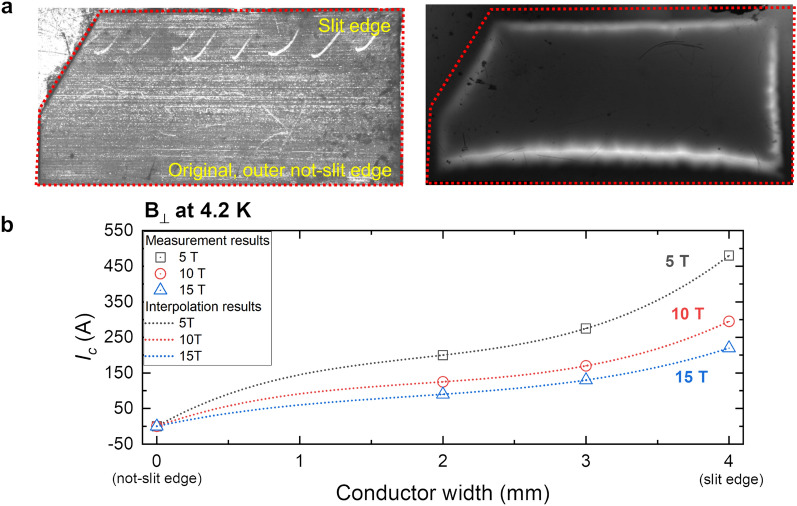
The intriguing local 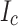 variability revealed by the YateStar scans led us to perform local MOI inspection of an as-delivered, unused and undamaged sample. After zero-field cooling to 10 K, a 160 mT perpendicular field was applied to observe flux penetration into the original outside edges of the tape. Instead of this penetration being symmetric, penetration was deeper at the outer not-slit edge compared to the slit edge (Fig. 6a), thus signaling lower
variability revealed by the YateStar scans led us to perform local MOI inspection of an as-delivered, unused and undamaged sample. After zero-field cooling to 10 K, a 160 mT perpendicular field was applied to observe flux penetration into the original outside edges of the tape. Instead of this penetration being symmetric, penetration was deeper at the outer not-slit edge compared to the slit edge (Fig. 6a), thus signaling lower 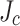 at this not-slit edge, despite it having obstructive edge microcracks. This counterintuitive finding is direct evidence for transverse
at this not-slit edge, despite it having obstructive edge microcracks. This counterintuitive finding is direct evidence for transverse 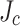 variability across the conductor with
variability across the conductor with 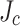 being lower at the not-slit edge.
being lower at the not-slit edge.
Figure 6.
Magneto optical image (MOI) and transport current measurement results on sectioned LBC4 conductor samples. (a) Superficial light microscope and MOI map (ZFC, then 160 mT perpendicular field at 10 K) shows deeper field penetration at the original, not-slit edge, indicating that this edge has lower 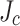 than the central, slit edge. (b) Transport current measurement of residual
than the central, slit edge. (b) Transport current measurement of residual 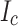 after first cutting away 1 mm, then 2 mm slices from the width, starting at the higher
after first cutting away 1 mm, then 2 mm slices from the width, starting at the higher 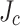 slit edge. Based on these measurements, the
slit edge. Based on these measurements, the 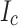 distribution across the conductor was formulated by a cubic function. The non-linear transverse
distribution across the conductor was formulated by a cubic function. The non-linear transverse 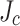 variability across the LBC4 conductor is obvious. Measurements were made in perpendicular fields at 4.2 K.
variability across the LBC4 conductor is obvious. Measurements were made in perpendicular fields at 4.2 K.
To be more specific, we then measured the local transport 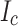 by cutting 1 mm pieces away from the slit side, finding that the first 1 mm removed caused a 40% drop, not a 25%
by cutting 1 mm pieces away from the slit side, finding that the first 1 mm removed caused a 40% drop, not a 25% 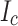 drop, while the second 1 mm removed gave a 30% drop (Fig. 6b). This result was formulated into a transverse
drop, while the second 1 mm removed gave a 30% drop (Fig. 6b). This result was formulated into a transverse 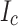 distribution with a cubic function considering the measured
distribution with a cubic function considering the measured 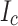 values and the number of data points. Then, the relative
values and the number of data points. Then, the relative 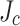 gradient (
gradient (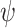 ) across the conductor width was obtained through transverse differentiation and normalization. The result was a best-fit quadratic function
) across the conductor width was obtained through transverse differentiation and normalization. The result was a best-fit quadratic function 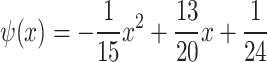 , where
, where 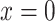 at the not-slit edge, and
at the not-slit edge, and 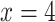 at the slit edge. The derived gradient was used to define non-uniform
at the slit edge. The derived gradient was used to define non-uniform 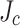 distribution across the conductor width (
distribution across the conductor width (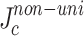 ):
):
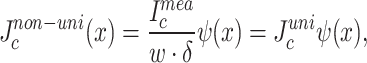 |
1 |
where 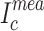 , w, and
, w, and 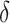 stand for measured
stand for measured 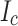 , width of a tape, and thickness of a tape.
, width of a tape, and thickness of a tape.
Simulations of the impact of transverse 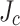 variability on the local screening current stress enhancements
variability on the local screening current stress enhancements
Figure 7 shows the measured uniaxial stress-strain curve of an LBC4 conductor sample at 77 K. On raising the stress, the deformation is initially (1) purely elastic without any expected 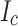 damage, then (2) elastic-plastic (elastic Hastelloy-plastic copper), and finally (3) plastic both for the Hastelloy and the copper. Region 3 is characteristic of the plastic deformation that degrades
damage, then (2) elastic-plastic (elastic Hastelloy-plastic copper), and finally (3) plastic both for the Hastelloy and the copper. Region 3 is characteristic of the plastic deformation that degrades 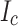 in both wavy and kinked regions. Based on prior studies, a 95%
in both wavy and kinked regions. Based on prior studies, a 95% 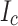 retention stress limit of 700 MPa can be assumed that would correspond to a strain of 0.4%13.
retention stress limit of 700 MPa can be assumed that would correspond to a strain of 0.4%13.
Figure 7.
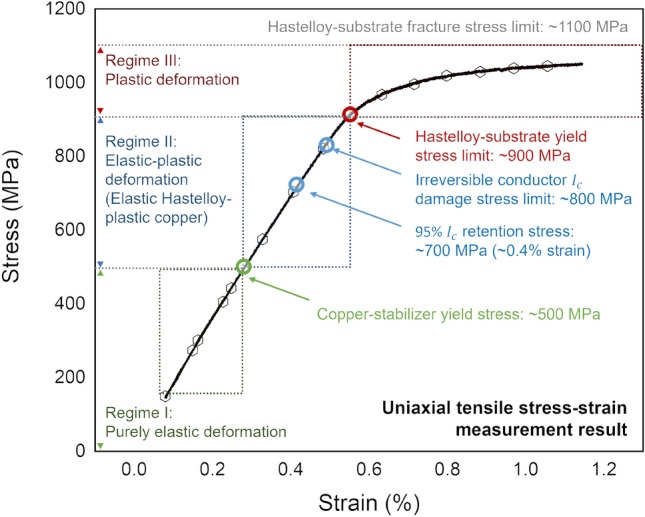
The measured uniaxial stress-strain curve of the LBC4 conductor at 77 K.
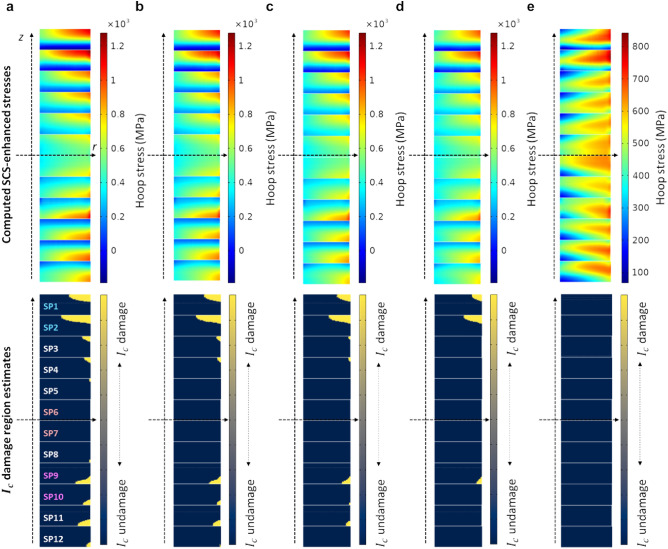
Figure 8 shows the computed SCS-enhanced hoop stresses 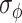 and the estimated
and the estimated 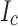 damage regions (bending stress considered) using the Fig. 7 data for all turns of LBC4 at the peak current and field of 213.5 A and 44.0 T. These simulations considered five different assumptions of the relative
damage regions (bending stress considered) using the Fig. 7 data for all turns of LBC4 at the peak current and field of 213.5 A and 44.0 T. These simulations considered five different assumptions of the relative 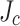 gradient across the conductor: (a) uniform
gradient across the conductor: (a) uniform 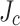 (
(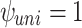 ); (b–d) linear
); (b–d) linear 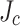 gradients with
gradients with 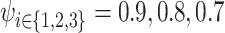 at the not-slit edge and
at the not-slit edge and 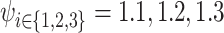 at the slit edge; and finally with (e) the measured
at the slit edge; and finally with (e) the measured 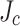 gradient (
gradient (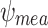 ). Figure 9 shows further details of each gradient used in each SCS simulation. Simulation details are described in Methods.
). Figure 9 shows further details of each gradient used in each SCS simulation. Simulation details are described in Methods.
Figure 8.
Summary of computed SCS-enhanced hoop stresses and estimated 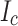 damage regions where
damage regions where 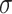 exceeds 700 MPa (bending stress considered) in the cross-sectional view of LBC4 at the peak current and field of 213.5 A and 44.0 T, considering: (a) uniform
exceeds 700 MPa (bending stress considered) in the cross-sectional view of LBC4 at the peak current and field of 213.5 A and 44.0 T, considering: (a) uniform 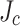 (
(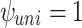 ); (b–d) linear
); (b–d) linear 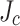 gradient with
gradient with 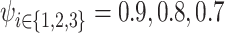 at the not-slit edge and
at the not-slit edge and 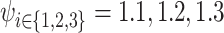 at the slit edge; and (e) the measured
at the slit edge; and (e) the measured 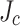 gradient (
gradient (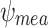 ). From (a) to (d), the same color range was used to evaluate local SCS enhancements according to various cases of the transverse
). From (a) to (d), the same color range was used to evaluate local SCS enhancements according to various cases of the transverse 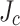 variation. In (e) the scale maximum is lower due the mitigating effect of the real transverse
variation. In (e) the scale maximum is lower due the mitigating effect of the real transverse  variation.
variation.
Figure 9.
The relative  gradient for each simulation in Fig. 8.
gradient for each simulation in Fig. 8.
A first comment is that the peak hoop stresses at the outer turns in SP1 and SP2 are larger than in the symmetrically placed SP11 and SP12 in every simulation case since SP1 and SP2 have 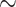 20% higher
20% higher 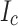 than the SP11 and SP12 conductors. This finding explains the observed asymmetry in finding wavy plastic damage for SP1 and 2 but not for SP11 and 12. A second finding of the simulations is that the larger the relative
than the SP11 and SP12 conductors. This finding explains the observed asymmetry in finding wavy plastic damage for SP1 and 2 but not for SP11 and 12. A second finding of the simulations is that the larger the relative 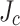 gradient, the more significant is the SCS mitigation and the damage reduction. Figure 8a–d indicate the implications of transverse
gradient, the more significant is the SCS mitigation and the damage reduction. Figure 8a–d indicate the implications of transverse 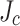 variation for the SCS more explicitly. Comparing the simulations of Figure 8a (no gradient) and d (high gradient
variation for the SCS more explicitly. Comparing the simulations of Figure 8a (no gradient) and d (high gradient 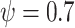 at the not-slit edge and 1.3 at the slit edge), we observe that there are (1) a 40% reduction in SP1 and SP2 and (2) a 60% reduction in LBC4 on average. The simulations for the measured
at the not-slit edge and 1.3 at the slit edge), we observe that there are (1) a 40% reduction in SP1 and SP2 and (2) a 60% reduction in LBC4 on average. The simulations for the measured 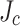 gradient in Fig. 8e are even more different, with the peak stress on the inner windings retreating from the outer edge of lower
gradient in Fig. 8e are even more different, with the peak stress on the inner windings retreating from the outer edge of lower 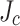 to the tape center. These local simulations show that the impact of the real variation of
to the tape center. These local simulations show that the impact of the real variation of 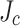 is present throughout the whole coil and provides an important and markedly different stress distribution.
is present throughout the whole coil and provides an important and markedly different stress distribution.
A key finding is that simulations with the measured 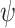 predict mostly undamaged
predict mostly undamaged 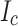 regions in LBC4, entirely consistent with our post mortem. In contrast, simulations with a uniform
regions in LBC4, entirely consistent with our post mortem. In contrast, simulations with a uniform 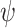 (conventionally assumed in many reports on SCS simulations) still predict the peak SCS-enhanced stresses of over 1.1 GPa at outer turns in SP1 and SP2, which is incompatible with that absence of Hastelloy substrate fracture in these pancakes. In addition, the predicted stresses of other pancakes are mostly about 1 GPa, which is also incompatible with the absence of plastic Hastelloy yield. However,
(conventionally assumed in many reports on SCS simulations) still predict the peak SCS-enhanced stresses of over 1.1 GPa at outer turns in SP1 and SP2, which is incompatible with that absence of Hastelloy substrate fracture in these pancakes. In addition, the predicted stresses of other pancakes are mostly about 1 GPa, which is also incompatible with the absence of plastic Hastelloy yield. However, 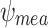 might suggest too large gradient across the conductor width. Presumably, the “real” gradient is expected to be between
might suggest too large gradient across the conductor width. Presumably, the “real” gradient is expected to be between 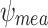 and
and 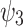 . This concern results from the use of the cubic function for
. This concern results from the use of the cubic function for 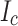 distribution and the quadratic function for
distribution and the quadratic function for 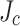 gradient, which was inevitable considering the measured local
gradient, which was inevitable considering the measured local 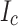 data, leading to a conclusion that further measurements are required to find a truly realistic
data, leading to a conclusion that further measurements are required to find a truly realistic
 considering the conductor manufacturing process and other specifications such as micro-crack and misoriented grain distributions.
considering the conductor manufacturing process and other specifications such as micro-crack and misoriented grain distributions.
Peak stress evaluation with the measured uniaxial stress-strain curve and comparison to the SCS simulations
We estimated the peak stress range of each pancake with the measured stress-strain curve (Fig. 7) as summarized below:
SP1–2: wavy regions in outer turns indicate that a peak stress of 900–1100 MPa was reached at 44.0 T.
SP6–7: these central pancakes have a peak stress of <800 MPa at 44.0 T, but do achieve 900–1100 MPa at kinked regions during quench. We recall that we do not believe that the kinked regions are due to excess SCS but to a discontinuity in the inner joint on this DP.
We conclude that all other pancakes without observable wavy damage were subject to stress <800 MPa.
Table2 summarizes the computed peak hoop stress at 44.0 T of every pancake presented in Fig. 8a–e and compares it to the stress-strain curve estimation.
Table 2.
Comparisons between the computed and the post mortem estimated peak hoop stress of every pancake in LBC4 at 44.0 T [unit: MPa].
| Computation | Estimation | |||||
|---|---|---|---|---|---|---|
| Figure 8a | Figure 8b | Figure 8c | Figure 8d | Figure 8e | Figure 7 | |
| SP1 | 1160 | 1120 | 1070 | 1020 | 790 | 900–1000 |
| SP2 | 1270 | 1230 | 1170 | 1120 | 840 | 900–1000 |
| SP3 | 970 | 930 | 890 | 840 | 670 | <800 |
| SP4 | 970 | 940 | 900 | 850 | 680 | <800 |
| SP5 | 900 | 880 | 840 | 810 | 660 | <800 |
| SP6 | 820 | 800 | 790 | 770 | 660 | <800 |
| SP7 | 810 | 790 | 780 | 750 | 650 | <800 |
| SP8 | 900 | 870 | 830 | 790 | 640 | <800 |
| SP9 | 1160 | 1120 | 1080 | 1020 | 740 | <800 |
| SP10 | 970 | 920 | 870 | 820 | 670 | <800 |
| SP11 | 1000 | 950 | 890 | 840 | 670 | <800 |
| SP12 | 910 | 860 | 810 | 770 | 690 | <800 |
Despite discrepancies in SP1 and SP2, this comparison shows much better agreement between the computed and estimated peak stresses when the measured 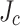 gradient is used, thus emphasizing the importance of considering such transverse
gradient is used, thus emphasizing the importance of considering such transverse 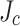 variability in a realistic SCS simulation and conductor damage analysis. In addition, we validate the deficiency of the conventional assumption of uniform
variability in a realistic SCS simulation and conductor damage analysis. In addition, we validate the deficiency of the conventional assumption of uniform 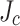 across the conductor to explain local stresses by SCS and real SCS damage but confirm the
across the conductor to explain local stresses by SCS and real SCS damage but confirm the 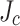 gradient effect on peak stress mitigation.
gradient effect on peak stress mitigation.
Discussion
Damage in LBC4, unlike that in LBC1–3, was rare and not well predicted by SCS calculations performed with the usual assumption of uniform transverse 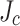 . Under the uniform
. Under the uniform 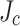 scenario LBC2, 3 and 4 would all have had the similar damage patterns. The much lower damage seen in LBC4 incited this broader evaluation of the impact of critical current density non-uniformities on the screening current stresses of high-field magnets like LBC.
scenario LBC2, 3 and 4 would all have had the similar damage patterns. The much lower damage seen in LBC4 incited this broader evaluation of the impact of critical current density non-uniformities on the screening current stresses of high-field magnets like LBC.
Longitudinal non-uniformity of REBCO coated conductors is well-known as is bath-to-batch variation of conductors made to the same specifications14. Longitudinal evaluation of conductors using the commercial 77 K self-field evaluation tool TapeStar15 is used by virtually all commercial vendors to show local variations  so as to cut out imperfections. However, being a very weak field device it is not very sensitive to variations of vortex pinning strength. In this case, as Fig. 2 shows, there were two lots of conductor used for the 12 pancakes (Conductor 1 versus Conductor 2 with 20–25% higher
so as to cut out imperfections. However, being a very weak field device it is not very sensitive to variations of vortex pinning strength. In this case, as Fig. 2 shows, there were two lots of conductor used for the 12 pancakes (Conductor 1 versus Conductor 2 with 20–25% higher 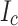 ) that had significant
) that had significant 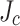 variations of the type studied earlier by Francis14. These variations made the expected symmetrical SCS damage predictions (SP1/2 versus SP11/12) invalid. This variability of
variations of the type studied earlier by Francis14. These variations made the expected symmetrical SCS damage predictions (SP1/2 versus SP11/12) invalid. This variability of 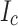 is well known for metal-organic chemical vapor deposition (MOCVD) conductors14, although the large amount of work needed to get accurate
is well known for metal-organic chemical vapor deposition (MOCVD) conductors14, although the large amount of work needed to get accurate 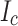 measurements at high fields and many angles generally makes it impractical to do SCS predictions taking account of such longitudinal variations except by using short samples cut from each end of the tape used in the pancakes.
measurements at high fields and many angles generally makes it impractical to do SCS predictions taking account of such longitudinal variations except by using short samples cut from each end of the tape used in the pancakes.
In order to rationalize the observed wavy, plastic damage generated by SCS overstress with the SCS predictions, we additionally considered the possibility that there was a transverse variation of 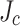 too. We and many others16–18 have previously considered that the edge cracks characteristic of all mechanically slit coated conductor locally reduce the effective width of the tape and thus
too. We and many others16–18 have previously considered that the edge cracks characteristic of all mechanically slit coated conductor locally reduce the effective width of the tape and thus 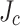 in the vicinity of the slit. Indeed, mechanical slitting does do this but what the magneto-optical-imaging shows is the overall
in the vicinity of the slit. Indeed, mechanical slitting does do this but what the magneto-optical-imaging shows is the overall 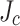 is actually lower well away from the the not-slit edge too, a result that we explore further in a second paper concentrating on a more detailed post mortem. This observation inspired us to measure the variation of transport
is actually lower well away from the the not-slit edge too, a result that we explore further in a second paper concentrating on a more detailed post mortem. This observation inspired us to measure the variation of transport 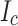 across the conductor and then to use this variation to modify our SCS calculations based on the high field variation of
across the conductor and then to use this variation to modify our SCS calculations based on the high field variation of 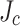 shown in Fig. 6b. The origin of this variation lies in a generally overlooked feature of SuperPower MOCVD conductor arising from the fact that the conditions of REBCO growth are not uniform across the 12 mm tape—in particular the outer edges of the tape develop a much higher concentration of a-axis grains and CuO precipitates that tend to block current and lower the local
shown in Fig. 6b. The origin of this variation lies in a generally overlooked feature of SuperPower MOCVD conductor arising from the fact that the conditions of REBCO growth are not uniform across the 12 mm tape—in particular the outer edges of the tape develop a much higher concentration of a-axis grains and CuO precipitates that tend to block current and lower the local 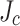 averaged over the scale of a few µm2 seen by the MO image. The density of these defects falls towards the center of the tapes such that near the slit edges at the 4 and 8 mm width, the
averaged over the scale of a few µm2 seen by the MO image. The density of these defects falls towards the center of the tapes such that near the slit edges at the 4 and 8 mm width, the 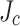 is much higher, even though slitting cracks that typically penetrate 20–40 µm into the tape are present at these edges.
is much higher, even though slitting cracks that typically penetrate 20–40 µm into the tape are present at these edges.
When the LBC coils are tested, they are immersed in the full 31 T background field before being charged such that the 31 T field penetrates the pancakes and generates positive and negative screening currents within each pancake. As the transport current is raised, it penetrates at the outer pancake edges and displaces the electric center of the tape towards the magnet center as the opposite-sign magnetization screening current is replaced by transport current. The net effect of these currents is to generate tensile stresses on the outer tape edges and compressive stresses on the inner edges, the tensile stresses being much larger in the case of our LBC test where the peak LBC field reached 12.9 T in its 31.1 T background.
We observed two forms of irreversible degradation to the 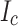 resulting from the tests. One was the line of radial kinking generated—we believe—by the sudden collapse at quench of the outward Lorentz force on the winding against a step in the solder joints connecting the 4 mm wide tapes of SP6 and 7 to the 8 mm wide tape connecting the two single pancakes. This is essentially a design fault in our construction without general application or connection to the SCS calculations. The broader issue of importance for the SCS simulations is the plastic waviness observed widely in LBC2 and LBC3 but only in a few turns of LBC4. Waviness is a direct result of the enhanced SCS at the outer edge of the end pancakes (SP1 and SP2).
resulting from the tests. One was the line of radial kinking generated—we believe—by the sudden collapse at quench of the outward Lorentz force on the winding against a step in the solder joints connecting the 4 mm wide tapes of SP6 and 7 to the 8 mm wide tape connecting the two single pancakes. This is essentially a design fault in our construction without general application or connection to the SCS calculations. The broader issue of importance for the SCS simulations is the plastic waviness observed widely in LBC2 and LBC3 but only in a few turns of LBC4. Waviness is a direct result of the enhanced SCS at the outer edge of the end pancakes (SP1 and SP2).
Although we made a qualitative description of the damage in terms of the measured stress-strain curve of our conductor, we know that permanent wavy damage is only possible when the Hastelloy becomes plastic. The question of 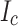 damage is tied directly to what happens to the REBCO layer. In principle the complex oxide buffer stack, all elastic solids, is well anchored to the Hastelloy so that fracture of the REBCO should only occur when the Hastelloy becomes plastic. Consistent with this, outer edge damage is indeed evident in the YateStar scans of the outside, wavy turns of SP 1 and 2. Such YateStar damage to
damage is tied directly to what happens to the REBCO layer. In principle the complex oxide buffer stack, all elastic solids, is well anchored to the Hastelloy so that fracture of the REBCO should only occur when the Hastelloy becomes plastic. Consistent with this, outer edge damage is indeed evident in the YateStar scans of the outside, wavy turns of SP 1 and 2. Such YateStar damage to 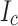 is not seen where there is no wavy damage, as was the case for all turns of SP11 and 12, made with lower
is not seen where there is no wavy damage, as was the case for all turns of SP11 and 12, made with lower 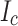 conductor that did not achieve the critical stress needed for plastic deformation of the Hastelloy.
conductor that did not achieve the critical stress needed for plastic deformation of the Hastelloy.
The simulations that we made of the SCS in Fig. 8 are interpreted in the context of the observed damage and the measured uniaxial stress-strain curve for the tape. Although we cannot measure the exact stresses generated in LBC4 at 44.0 T, our variable 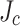 simulations are quite predictive of the observed wavy damage seen in our post mortem with respect to where the damage occurs in individual pancakes, where it occurs in the pancake stack and why there is no symmetry of behavior between DP1 and DP6.
simulations are quite predictive of the observed wavy damage seen in our post mortem with respect to where the damage occurs in individual pancakes, where it occurs in the pancake stack and why there is no symmetry of behavior between DP1 and DP6.
An important lesson that we take away from LBC4 is that quench was actually initiated not by excess SCS but by overheating at the joints between pancakes. The extremely high 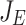 of the coils—>1200 A/mm2—makes avoidance of high joint resistance essential. In fact we were very pleased that only DP5 had R >1 µ
of the coils—>1200 A/mm2—makes avoidance of high joint resistance essential. In fact we were very pleased that only DP5 had R >1 µ as made and it was indeed this joint that initiated quench. Like the negative effect of the step for SP6 and SP7, there are many details of construction that must be perfected in order to enable damage-free, ultra-high-field coils.
as made and it was indeed this joint that initiated quench. Like the negative effect of the step for SP6 and SP7, there are many details of construction that must be perfected in order to enable damage-free, ultra-high-field coils.
Lastly, we should comment that the LBC magnets were constructed only with MOCVD conductors made by SuperPower. The central finding of this study is that a hitherto generally overlooked feature of the SuperPower MOCVD conductor19, its transverse structural and 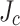 inhomogeneity20–22, needs to be considered. However, many coated conductors are now made by pulsed laser deposition (PLD), where REBCO growth conditions are more uniform and presumably
inhomogeneity20–22, needs to be considered. However, many coated conductors are now made by pulsed laser deposition (PLD), where REBCO growth conditions are more uniform and presumably 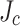 too. Moreover, unlike the mechanical slitting process to produce 4 mm wide conductors from a 12 mm wide original conductor, multiple manufacturers are experimenting with or selling laser-slit tapes. We are not yet aware of the effect of different growth and slitting conditions on the transverse
too. Moreover, unlike the mechanical slitting process to produce 4 mm wide conductors from a 12 mm wide original conductor, multiple manufacturers are experimenting with or selling laser-slit tapes. We are not yet aware of the effect of different growth and slitting conditions on the transverse 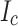 so for now remain open as to whether the change of slitting type is beneficial to the conductor properties. The Shanghai Superconductor group have reported that the fatigue strength of laser slit tapes is better than mechanically slit tapes, although the difference is not huge23. How the particular lessons of using MOCVD tape for LBC1–4 play out more generally will be tested soon on the LBC test bed with PLD and laser-slit conductors from other manufacturers24.
so for now remain open as to whether the change of slitting type is beneficial to the conductor properties. The Shanghai Superconductor group have reported that the fatigue strength of laser slit tapes is better than mechanically slit tapes, although the difference is not huge23. How the particular lessons of using MOCVD tape for LBC1–4 play out more generally will be tested soon on the LBC test bed with PLD and laser-slit conductors from other manufacturers24.
A final conclusion is that many, perhaps most, high field REBCO coils will enter dangerous SCS conditions unless the conductors are effectively supported. Although many SCS simulations are being made today, the important predictive outputs of Fig. 8 depend vitally on not just the local 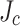 values of the tape but also of a good understanding of the stress-strain properties of the particular conductor used for the coil. There are at least two important variables that need attention: one is the amount of Cu on the conductor, while the second is the degree of anneal that the cold-worked Hastelloy may have received during the REBCO growth process, both of which could significantly affect the performance of any LBC. The influence of the Cu content in SuperPower conductors of the same type used here is reported in25 for Cu substrates of 20, 40 and 100 µm thickness, as compared to our tape with 5 µm thickness on either side. If we accept that the critical parameter for REBCO damage is its strain and that permanent damage starts to occur at 0.4% strain, we see that our safe working stress of
values of the tape but also of a good understanding of the stress-strain properties of the particular conductor used for the coil. There are at least two important variables that need attention: one is the amount of Cu on the conductor, while the second is the degree of anneal that the cold-worked Hastelloy may have received during the REBCO growth process, both of which could significantly affect the performance of any LBC. The influence of the Cu content in SuperPower conductors of the same type used here is reported in25 for Cu substrates of 20, 40 and 100 µm thickness, as compared to our tape with 5 µm thickness on either side. If we accept that the critical parameter for REBCO damage is its strain and that permanent damage starts to occur at 0.4% strain, we see that our safe working stress of 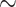 720 MPa is reduced to 620, 515 and 400 MPa when Cu thicknesses of 20, 40 and 100 µm are used. Clearly any increase in the Cu content of the conductor would have increased the propensity for damage.
720 MPa is reduced to 620, 515 and 400 MPa when Cu thicknesses of 20, 40 and 100 µm are used. Clearly any increase in the Cu content of the conductor would have increased the propensity for damage.
We finally note the potential for the REBCO growth conditions to modify the properties of the cold-rolled Hastelloy (or 310 Stainless steel) as discussed in26. There it is shown that simulated anneals of 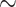 15 minutes at 700, 750 and 800
15 minutes at 700, 750 and 800  C can change the initial 0.2% proof stress of cold-rolled Hastelloy C276 (1464 MPa as manufactured but before use) supplied by SuperPower to 1524, 1477 and 1224 MPa. Clearly higher REBCO growth temperatures may pose challenges for use of REBCO coated conductors where the primary support comes only from the conductor itself. Detailed knowledge of both the transverse
C can change the initial 0.2% proof stress of cold-rolled Hastelloy C276 (1464 MPa as manufactured but before use) supplied by SuperPower to 1524, 1477 and 1224 MPa. Clearly higher REBCO growth temperatures may pose challenges for use of REBCO coated conductors where the primary support comes only from the conductor itself. Detailed knowledge of both the transverse 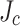 variation and the exact mechanical properties of the conductor used for the magnet will be vital for realistic SCS simulations.
variation and the exact mechanical properties of the conductor used for the magnet will be vital for realistic SCS simulations.
Methods
Critical current measurements
The selected single-slit REBCO-coated conductors for LBC4 were parameterized at 4.2 K by measuring their magnetic field-dependent critical current 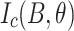 at various field magnitudes and angles, using two different methods. First, torque magnetometry6 was used to measure continuous angle dependency information at selected high fields. A sinusoidal-square function extrapolates the field and angle dependency from the measurement data to a reasonable extent:
at various field magnitudes and angles, using two different methods. First, torque magnetometry6 was used to measure continuous angle dependency information at selected high fields. A sinusoidal-square function extrapolates the field and angle dependency from the measurement data to a reasonable extent:
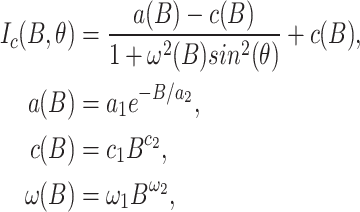 |
2 |
where B and 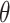 are the magnetic field magnitude and angle, while
are the magnetic field magnitude and angle, while 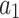 ,
, 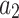 ,
, 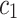 ,
, 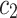 ,
, 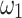 , and
, and 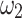 are coefficients for the extrapolation. Here, transport current measurement14 was used to find the coefficient as well as provide reference
are coefficients for the extrapolation. Here, transport current measurement14 was used to find the coefficient as well as provide reference 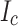 data points at various fields and angles.
data points at various fields and angles.
For the transport current measurement, several sample holders that are tilted to an external magnetic field with certain angles were used where samples were exposed to external magnetic fields. As flowing transport current from a power supply, 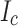 and n-value were measured considering the critical electric field of 1 µV/cm. For the torque magnetometry, a rotating sample holder clamping a REBCO tape was exposed to various background fields. Torque was measured using a load cell as the sample holder rotated in the external fields. Measured torque data was transformed into
and n-value were measured considering the critical electric field of 1 µV/cm. For the torque magnetometry, a rotating sample holder clamping a REBCO tape was exposed to various background fields. Torque was measured using a load cell as the sample holder rotated in the external fields. Measured torque data was transformed into 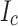 using a standard Bean model calculation27.
using a standard Bean model calculation27.
Post mortem examinations
All pancakes were unwound carefully at low speed to allow subsequent YateStar28 measurement at 77 K. YateStar has 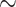 1 mm lengthwise resolution in its induced current map generated by passing the tape through a 0.5 T electromagnet. Its 21 Hall probe array has significant transverse resolution too as is apparent from the maps in Fig. 5. These gray-colored screening current magnetization maps indicate great lengthwise and transverse uniformity for SP9 and SP10, but periodic upper-edge non-uniformity in wavy regions for SP1 and SP2.
1 mm lengthwise resolution in its induced current map generated by passing the tape through a 0.5 T electromagnet. Its 21 Hall probe array has significant transverse resolution too as is apparent from the maps in Fig. 5. These gray-colored screening current magnetization maps indicate great lengthwise and transverse uniformity for SP9 and SP10, but periodic upper-edge non-uniformity in wavy regions for SP1 and SP2.
Magneto-optical-imaging29 was used to visualize the magnetic flux density within tapes cooled to the superconducting state without field applied and then imaged while a perpendicular field up 160 mT was then applied. Inversion of the measured field enabled calculation of the current distributions from 7 to 80 K. The MOI maps are very sensitive to any obstructions to current flow in the REBCO layer on a scale of 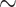 0.1 mm.
0.1 mm.
Screening current stress simulation
Screening current calculations were performed with an in-house electromagnetic simulation model30–39 that uses H-formulation with edge elements40, homogenized superconductivity domain41, and the power-law  constitutive law42 as the superconductor material property. The measured
constitutive law42 as the superconductor material property. The measured 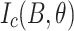 at 4.2 K shown in Fig. 2 is parameterized for this calculation. A ‘cosine squared’ function6 was used to formulate the measured
at 4.2 K shown in Fig. 2 is parameterized for this calculation. A ‘cosine squared’ function6 was used to formulate the measured 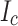 and extrapolate unmeasured
and extrapolate unmeasured 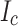 in various field angles and magnitudes. An index value n of 30 was used. The relative
in various field angles and magnitudes. An index value n of 30 was used. The relative 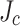 gradient (
gradient (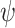 ) across the conductor width determines the local
) across the conductor width determines the local 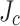 for this calculation by multiplying the measured
for this calculation by multiplying the measured 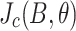 and
and 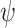 . Lastly, this electromagnetic simulation was completed using the Dirichlet boundary condition of zero fields at a closed boundary far from the current source (so-called the “air” boundary).
. Lastly, this electromagnetic simulation was completed using the Dirichlet boundary condition of zero fields at a closed boundary far from the current source (so-called the “air” boundary).
Calculated current densities and magnetic fields from the electromagnetic simulation were used to calculate SCS-enhanced stresses and strains43, where the Lorentz force was set to be a body load. The double-sided roller conditions (i.e., zero axial deformation) of every pancake were applied. This condition is probably valid since a pre-load force was applied after each pancake winding and after stacking all pancakes. Compressive bending stress was considered due to the REBCO layers all facing inward toward the winding mandrel. The turn-to-turn contact boundary condition considers the self-supporting properties of our dry-winding44 of our LBC magnet. We calculate the effective Young’s moduli  GPa) of the LBC4 conductor and set them as the primary mechanical material properties. However, we did not consider the transition from elastic to elastic-plastic deformation transition at 900 MPa of the Hastelloy-substrate37 and the subsequent drop in effective modulus that drives the waviness that we observed for the highest computed SCS values.
GPa) of the LBC4 conductor and set them as the primary mechanical material properties. However, we did not consider the transition from elastic to elastic-plastic deformation transition at 900 MPa of the Hastelloy-substrate37 and the subsequent drop in effective modulus that drives the waviness that we observed for the highest computed SCS values.
Acknowledgements
A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement No. DMR-2128556 and the State of Florida. This work was primarily supported by the DOE Office of Fusion Energy Sciences Grant DE-SC0022011. The authors would like to note that after completion of this manuscript, we learned of work done by Yufan Yan and co-authors that also discusses the influence of transverse current density on screening-current-induced stress.
Author contributions
J.B. and D.C.L. conceived the idea and supervised the work and the writing; K.K. and J.B. contributed to the coil construction and the coil unwinding process; K.K. and G.B. handled the instrumentation; J.B., S.N., and S.H. performed SCS simulations; D.A. and J.J. measured LBC4 conductors critical current during long night shifts; X.H. and A.P. measured local critical currents with transport current measurement and magneto-optical imaging approaches respectively; and G.B. and J.L. inspected conductor damage.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Fazilleau, P., Chaud, X., Debray, F., Lecrevisse, T. & Song, J.-B. 38 mm diameter cold bore metal-as-insulation HTS insert reached 32.5 T in a background magnetic field generated by resistive magnet. Cryogenics106, 103053 (2020). [Google Scholar]
- 2.Liu, J. et al. World record 32.35 tesla direct-current magnetic field generated with an all-superconducting magnet. Supercond. Sci. Technol.33, 03LT01 (2020). [Google Scholar]
- 3.Weijers, H. W. et al. Progress in the development and construction of a 32-T superconducting magnet. IEEE Trans. Appl. Supercond.26, 4300807 (2016). [Google Scholar]
- 4.Bai, H. et al. The 40 T superconducting magnet project at the national high magnetic field laboratory. IEEE Trans. Appl. Supercond.30, 4300405 (2020). [Google Scholar]
- 5.Hahn, S. et al. 45.5-Tesla direct-current magnetic field generated with a high-temperature superconducting magnet. Nature570, 496–499 (2019). [DOI] [PubMed] [Google Scholar]
-
6.Jaroszynski, J. et al. Rapid assessment of REBCO CC angular critical current density J c (B, T= 4.2 K,
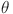 ) using torque magnetometry up to at least 30 tesla. Supercond. Sci. Technol.35, 095009 (2022).
) using torque magnetometry up to at least 30 tesla. Supercond. Sci. Technol.35, 095009 (2022).
- 7.Matsuda, T. et al. Degradation of the performance of an epoxy-impregnated REBCO solenoid due to electromagnetic forces. Cryogenics90, 47–51 (2018). [Google Scholar]
- 8.Bai, H., Hannahs, S., Markiewicz, W. & Weijers, H. Helium gas bubble trapped in liquid helium in high magnetic field. Appl. Phys. Lett.104 (2014).
- 9.Hu, X. et al. Analyses of the plastic deformation of coated conductors deconstructed from ultra-high field test coils. Supercond. Sci. Technol.33, 095012 (2020). [Google Scholar]
- 10.Song, J.-B. et al. Metal-as-insulation HTS insert for very-high-field magnet: A test report after repair. IEEE Trans. Appl. Supercond.32, 4300206 (2022). [Google Scholar]
- 11.Takahashi, S. et al. Hoop stress modification, stress hysteresis and degradation of a REBCO coil due to the screening current under external magnetic field cycling. IEEE Trans. Appl. Supercond.30, 4602607 (2020). [Google Scholar]
- 12.Kajita, K., Takao, T., Maeda, H. & Yanagisawa, Y. Degradation of a REBCO conductor due to an axial tensile stress under edgewise bending: A major stress mode of deterioration in a high field REBCO coil’s performance. Supercond. Sci. Technol.30, 074002 (2017). [Google Scholar]
- 13.Barth, C., Mondonico, G. & Senatore, C. Electro-mechanical properties of REBCO coated conductors from various industrial manufacturers at 77 K, self-field and 4.2 K, 19 T. Supercond. Sci. Technol. 28, 045011 (2015).
- 14.Francis, A. et al. Development of general expressions for the temperature and magnetic field dependence of the critical current density in coated conductors with variable properties. Supercond. Sci. Technol.33, 044011 (2020). [Google Scholar]
- 15.Furtner, S., Nemetschek, R., Semerad, R., Sigl, G. & Prusseit, W. Reel-to-reel critical current measurement of coated conductors. Supercond. Sci. Technol.17, S281 (2004). [Google Scholar]
-
16.van der Laan, D. C. & Ekin, J. Dependence of the critical current of YBa2Cu3O7-
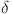 coated conductors on in-plane bending. Supercond. Sci. Technol.21, 115002 (2008). [Google Scholar]
coated conductors on in-plane bending. Supercond. Sci. Technol.21, 115002 (2008). [Google Scholar] -
17.van der Laan, D. C. et al. The effect of strain on grains and grain boundaries in YBa2Cu3O7-
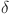 coated conductors. Supercond. Sci. Technol.23, 014004 (2009). [Google Scholar]
coated conductors. Supercond. Sci. Technol.23, 014004 (2009). [Google Scholar] -
18.van der Laan, D. C., Haugan, T. J. & Barnes, P. N. Effect of a Compressive Uniaxial Strain on the Critical Current Density of Grain Boundaries in Superconducting YBa
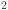 Cu
Cu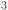 O
O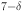 Films. Phys. Rev. Lett.103, 027005 (2009). [DOI] [PubMed]
Films. Phys. Rev. Lett.103, 027005 (2009). [DOI] [PubMed] - 19.Chang, C. . C. . et al. Origin of surface roughness for c-axis oriented Y-Ba-Cu-O superconducting films. Appl. Phys. Lett.57(17), 1814–1816. 10.1063/1.104143 (1990).
- 20.Solovyov, Mykola et al. Non-uniformity of coated conductor tapes. Superconductor Science and Technology26(11), 115013. 10.1088/0953-2048/26/11/115013 (2013). [Google Scholar]
- 21.Gömöry, F. et al. AC loss in pancake coil made from 12 mm wide REBCO tape. IEEE Trans. Appl. Supercond.23, 5900406 (2013). [Google Scholar]
- 22.Hu, D., Ainslie, M. D., Zou, J. & Cardwell, D. A. Numerical analysis of non-uniformities and anisotropy in high-temperature superconducting coils. IEEE Trans. Appl. Supercond.25, 4900605 (2014). [Google Scholar]
- 23.Guo, C. et al. Enhancement of electro-mechanical behaviors in RE-Ba-Cu-O composite superconducting tapes with laser slit edges. Supercond. Sci. Technol.35, 115009 (2022). [Google Scholar]
- 24.Bradford, G. et al. Property variations in modern REBCO coated conductors from multiple manufacturers. In IOP Conf. Ser.: Mater. Sci. Eng., vol. 1302, 012011 (IOP Publishing, 2024).
- 25.Zhang, Y. et al. Stress-strain relationship, critical strain (stress) and irreversible strain (stress) of IBAD-MOCVD-based 2G HTS wires under uniaxial tension. IEEE Trans. Appl. Supercond.26, 8400406 (2016). [Google Scholar]
- 26.Radcliff, K., Walsh, R., Larbalestier, D. & Hahn, S. The effect of reinforcement substrate alloy selection on mechanical properties of REBCO coated conductors. In IOP Conf. Ser.: Mater. Sci. Eng., vol. 756, 012023 (IOP Publishing, 2020).
- 27.Tarantini, C. & Larbalestier, D. C. Procedures for proper validation of record critical current density claims2410, 22195 (2024). [Google Scholar]
- 28.Coulter, J., Ugurlu, O., Willis, J., Holesinger, T. & Xie, Y.-Y. Identifying and Investigating Jc Variations in Coated Conductors Fabricated by Mocvd/ibad. In AIP Conf. Proc., vol. 1219, 347–354 (American Institute of Physics, 2010).
- 29.Polyanskii, A. A. & Larbalestier, D. C. Magneto-optical characterization techniques. In Handbook of Superconductivity, 371–382 (CRC Press, 2022).
- 30.Bang, J. et al. Field measurement and analysis of a 3 T 66 mm no-insulation HTS NMR magnet with screening current and manufacturing uncertainty considered. IEEE Trans. Appl. Supercond.29, 4601305 (2019). [Google Scholar]
- 31.Bang, J. et al. A numerical method to calculate spatial harmonic coefficients of magnetic fields generated by screening currents in an HTS magnet. IEEE Trans. Appl. Supercond.30, 4901405 (2020). [Google Scholar]
- 32.Bang, J. et al. A customized electric heater to mitigate screening current by optimal control on temperature distribution in a high-temperature superconductor coil. J. Appl. Phys.132, 183911 (2022). [Google Scholar]
- 33.Bang, J. et al. A real-time monitoring system for investigating electromagnetic behaviors of an HTS coil. IEEE Trans. Appl. Supercond.32, 9001505 (2022). [Google Scholar]
- 34.Bang, J., Park, J., Choi, K., Kim, G. & Hahn, S. A numerical method to calculate screening current-dependent self and mutual inductances of REBCO coils. Supercond. Sci. Technol.36, 085003 (2023). [Google Scholar]
- 35.Bang, J. et al. The effect of field-dependent n-value on screening current, voltage, and magnetic field of REBCO coil. IEEE Trans. Appl. Supercond.34, 4902105 (2024). [Google Scholar]
- 36.Bang, J. A FEM simulation model to calculate local currents and voltages of NI REBCO coil with both screening current and transverse current considered. IEEE Trans. Appl. Supercond.34, 4904907 (2024). [Google Scholar]
- 37.Bang, J., Bradford, G., Lee, J., Kim, K. & Larbalestier, D. Elastic-plastic conductor damage evaluation at over 0.4% strain using a high-stress REBCO coil. Supercond. Sci. Technol.37, 095011 (2024).
- 38.Bang, J. et al. Harmonic errors of a 9.4 T all-REBCO NMR magnet affected by screening current and geometric inconsistency of coated conductors. Sci. Rep.14, 19146 (2024). [DOI] [PMC free article] [PubMed]
- 39.Lee, J. et al. Lengthwise characterizations of crystallographic tilt in contemporary REBCO coated conductors. IEEE Trans. Appl. Supercond. Early Access. 10.1109/TASC.2024.3505115 (2024).
- 40.Brambilla, R., Grilli, F. & Martini, L. Development of an edge-element model for AC loss computation of high-temperature superconductors. Supercond. Sci. Technol.20, 16–24 (2006). [Google Scholar]
- 41.Zermeno, V. M., Abrahamsen, A. B., Mijatovic, N., Jensen, B. B. & Sørensen, M. P. Calculation of alternating current losses in stacks and coils made of second generation high temperature superconducting tapes for large scale applications. J. Appl. Phys.114, 173901 (2013). [Google Scholar]
- 42.Rhyner, J. Magnetic properties and AC-losses of superconductors with power law current—voltage characteristics. Physica C212, 292–300 (1993). [Google Scholar]
- 43.Park, J. et al. Parametric study on effect of friction and overbanding in screening current stress of LBC magnet. IEEE Trans. Appl. Supercond.31, 4603205 (2021). [Google Scholar]
- 44.Hahn, S., Park, D. K., Bascunan, J. & Iwasa, Y. HTS pancake coils without turn-to-turn insulation. IEEE Trans. Appl. Supercond.21, 1592–1595 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.