Simulation and experiment of leakage and diffusion of natural gas pipelines with different burial depths under different pressures

Abstract

In this paper, we studied the diffusion characteristics and distribution patterns of gas leakage in soil from buried natural gas pipelines. The three-dimensional simulation model of buried natural gas pipeline leakage was established using Fluent software. Monitoring points of gas leakage mole fraction were set up at different locations, and the influence of buried depth and pressure factors on the mole fraction and diffusion of leaked gas was analyzed. Additionally, a leakage pressure drop test of the buried natural gas pipeline was carried out. The results show that the CH₄ gas mole fraction curve at 0.03 m and 0.05 m below the leakage point fluctuates sharply during the second to third second of leakage, with the CH₄ gas mole fraction fluctuating by about 7%. The buried depth has the greatest influence on CH₄ in the leakage point range of 0.05 m, with the CH₄ gas mole fraction above and below the leakage hole differing by nearly 10 times in numerical value. As the buried pipeline depth increases, the pressure drop of the monitoring points at 0.1 m, 0.2 m, 0.3 m, 0.4 m, and 0.5 m is 27.64%, 24.02%, 21.52%, 17.65%, and 17.11%, respectively. In the x-axis direction, CH₄ gas presents a U-shaped diffusion in the soil, and after leaking for 200 s, CH₄ gas diffused to the top of the pipeline. The errors of the finite element numerical solution and the experimental values of the leakage pressure drop curve of the buried natural gas pipeline under four working conditions are 5.9%, 5.5%, 5.2%, and 5.0%, which are all within the allowable range. The accuracy of the finite element calculation results and the reliability of the test are verified.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-82794-w.

Introduction

Natural gas is indeed a clean energy source, and its development and utilization are due to the tense energy situation¹. In the context of the proposed national dual carbon (carbon neutral, carbon peak) strategic goals, the realization of long-distance transportation of natural gas energy is to meet the strategic needs of energy development². At present, China’s long-distance natural gas energy transportation mainly relies on pipeline transportation. After years of continuous construction and development, a mature natural gas energy pipeline network system has been formed nationwide^3,4. Buried natural gas pipelines are an important part of the pipeline transportation system, and their safety, reliability, and economy directly affect the operational efficiency and stability of the entire gas supply system⁵. In the service process of buried pipelines, local leakage will occur due to factors such as corrosion, environmental impact, material aging, and third-party damage^6–8. Meanwhile, the higher permeability of natural gas will accelerate the corrosion rate of pipelines. Once natural gas leakage occurs, the corrosion rate of pipelines will be accelerated. This could result in explosions, casualties, inadequate energy supplies, and huge economic losses and environmental impacts^9,10. Therefore, it is necessary to study the gas leakage characteristics and diffusion laws of buried natural gas pipelines.

Aiming at the gas leakage characteristics and diffusion laws of buried natural gas pipelines, domestic and foreign researchers have carried out a large number of theoretical and experimental studies. Jianlu et al.¹¹ studied the gas leakage diffusion behavior and concentration distribution characteristics, and analyzed the influence of different leakage directions of buried natural gas pipelines on gas diffusion. The diffusion characteristics of natural gas in soil under different concentrations, release pressures, and leakage directions were investigated. On the other hand, Sun et al.¹² conducted a quantitative analysis of the leakage of in-service natural gas pipelines and studied the relationship between the leakage amount and the danger range of leakage. Xu et al.¹³ studied the diffusion characteristics of hydrogen-doped natural gas (HBNG) in pipelines, simulated and analyzed the influence of hydrogen-doped natural gas on pore diffusion characteristics, and revealed the ventilation strategies of high-pressure pipelines under different leakage conditions. Hamid et al.¹⁴ analyzed the influence of soil on pipeline friction by means of simulation and experiments to solve the problem of the inner materials of buried pipeline responding to discontinuous internal Replacement Pipe (IRP) systems in different seasons. The research results have great value for the application of buried natural gas pipelines in industry. Yihuan et al.¹⁵ studied the failure forms of natural gas pipelines and used a fuzzy Bayesian Network (BN) to predict the failure risk of pipelines. Gao et al.¹⁶ discussed the safety risk factors of buried natural gas pipelines, analyzed the changes of pipeline materials caused by natural gas physical properties, and summarized the shortcomings of natural gas pipelines in terms of failure mechanisms, leakage and explosion mechanisms, and mixing ratios. Hu et al.¹⁷ studied the diffusion characteristics of pure hydrogen/hydrogen-doped natural gas in the soil environment and analyzed the influence of buried depth, soil particles, pressure, hydrogen doping ratio, and other factors on the leakage and diffusion characteristics of buried pure hydrogen/hydrogen-doped natural gas pipelines. Beyond this, Liu et al.¹⁸ established an integrated leakage model for natural gas pipelines, analyzed the characteristics of small hole leakage and gas diffusion in pipelines above ground and in free space, and studied the influence of different natural gas concentrations on gas diffusion. Liu et al.¹⁹ reviewed the research progress and existing problems in the integrity of natural gas pipelines at home and abroad, and they found that the failure damage mechanism and deterioration law of pipeline metal materials were not clear at present. Wang et al.²⁰ analyzed the problem of surface corrosion of natural gas pipelines and applied barrier coatings on the inner surface of pipelines to reduce the gas penetration of gas media, extend the service life of buried pipelines, and avoid the risk of pipeline leakage. Qi et al.²¹ analyzed the influence on the gas leakage and diffusion rule under hydrogen-doped conditions, established a half-closed plane leakage model, and studied the diffusion and mole fraction change of the rule under hydrogen-doped gas under different wind speed conditions. Xing et al.²² sorted out the relevant requirements and applicability evaluation methods of pipeline performance in domestic and foreign natural gas transport environments, analyzed the performance indicators of pipelines under the influence of different factors, and pointed out the shortcomings of the development of natural gas pipelines. Moreover, Li et al.²³ conducted a comprehensive study on several problems of hydrogen-doped pipelines, compared and analyzed the differences in hydrogen-doped pipeline transportation at home and abroad, and systematically evaluated the current situation of hydrogen-doped natural gas pipelines in terms of leakage. Shanbi et al.²⁴ established a leakage model for underground hydrogen-doped natural gas pipelines in cities, and analyzed leakage characteristics and gas diffusion rules under different hydrogen mixing ratios, different burial depths, different pressures, and different soil particle conditions. Lin et al.²⁵ studied the characteristics of small hole leakage in the buried natural gas pipeline, calculated the relationship, modeled the expression between the diameter of the small hole and the leakage rate, simulated and analyzed the diffusion law of natural gas in the soil after the leakage of the buried pipeline, and gave the dynamic diffusion pattern of natural gas in the soil.

Existing studies mainly focus on the leakage characteristics and diffusion patterns of buried natural gas pipelines in a limited space, but do not consider the pressure drop characteristics, gas mole fraction and distribution patterns near the leakage point^26,27. Therefore, the finite element software Fluent was used in this paper to establish a buried natural gas pipeline leakage model, explore the effects of buried depth and pipeline pressure on gas at different monitoring points in the leak area, and reveal the pressure drop change rule and gas mole fraction change at various points in the local area of the buried natural gas pipeline leak hole, as well as the gas distribution cloud map in the x-axis direction. Thus, we provided a reference study for the leakage prevention, diffusion, and safe transportation of buried natural gas pipelines.

Simulation and experiments envolving buried natural gas pipeline leakage

Physical models and mesh

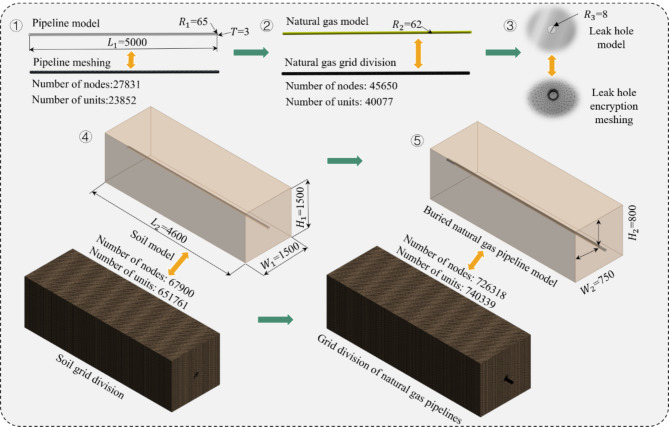
A buried natural gas pipeline leakage model is established by using the define DM module in Fluent, which consists of four parts: ① pipeline model, ② natural gas model, ③ leakage hole model, and ④ soil model. Take the burial depth of 0.8 m, leakage hole diameter of 0.8 mm, and pipeline pressure of 0.6 MPa as examples (as shown in Fig. 1), pipeline model length L₁ = 5000 mm, pipe wall thickness T = 3 mm, and pipe diameter R₁ = 65 mm. Hexahedral mesh was used to divide the pipeline model. The mesh size was 5 mm, and the grid was divided into 27,831 nodes and 23,852 units. The length of the natural gas model is the same as that of the pipeline, and the diameter of the model is R₂ = 62 mm. A hexahedral grid is selected to divide the natural gas model. The grid size is 5 mm, and the grid is divided into 45,650 nodes and 40,077 units. Considering the small size of the leak hole, the grid around the leak hole is encrypted, and the grid division is gradually sparse. The diameter of the leak hole R₃ = 8 mm, and the mesh size is set to 0.2 mm. For soil model lengths, we have L₂ = 4600 mm, width W₁ = 1500 mm, height H₁ = 1500 mm. Because the soil model is relatively regular, hexahedral mesh is used to divide the soil grid, and the mesh size is 15 mm. The grid is encrypted near the pipeline, the mesh size is 3 mm, and the grid is divided into 67,900 nodes and 651,761 units. The grid of the buried natural gas pipeline leakage model is divided into 726,318 nodes and 740,339 units^28,29.

Fig. 1.

Leakage model of buried natural gas pipeline.

Boundary conditions

On the basis of establishing the leakage model of the buried natural gas pipeline, the left end of the pipeline model was set as the inlet, the flow direction vector of the gas was set to 0 in the x direction and 1 in the y direction, the flow velocity was set to 2 m/s, and the molar fraction of methane at the inlet was set to 0.95. The right end is set as the outlet. Considering the influence of pipeline leakage pressure drop, the pressure value at the outlet of the pipeline is slightly lower than the pressure value at the entrance, and the standard atmospheric pressure at the soil outlet is 101,325 Pa. The leakage hole in the middle of the pipeline is defined as the internal surface interface, and gas can flow into the soil from the pipeline. The top surface of the soil model is set as the free outlet outlet1, and other soil surfaces are set as the wall surface. The soil model is set as a porous medium with a porosity of 0.68 and a soil temperature of 300 K. The viscosity resistance coefficient and inertia resistance coefficient of the soil are 5.27 × 10⁹ and 8.2 × 10⁴, respectively, and the thermal conductivity is 1.8 W/(m·K). The RNG (Renormalization Group) k-ε model is used for the calculation and analysis of complex fluid flows. Considering that the buried gas pipeline model is long, the leakage point is small, and the gas diffusion is local, the diffusion form and distribution of the buried gas pipeline in the soil at the initial leakage stage are studied. Considering the limitation of computing hardware simulation and analysis computing power, the soil models of 5000 mm natural gas pipeline and 4600 mm are selected for research. Assuming that the ratio of Reynolds stress to the average deformation rate of the k-ε model is the same in all directions, the variables and unmeasurable factors in the model are simplified, and the unknowns of buried natural gas pipeline leakage are minimized to the greatest extent. The equation of turbulent kinetic energy k of the model is shown in Eq. (1). The equation of turbulent kinetic energy dissipation ε is shown in Eq. (2).

1

2

3

Formula: 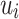Represents the upward velocity component of each side, 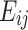Represents the component of the deformation rate, 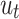Represents turbulence model viscosity, among , , , , .

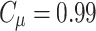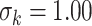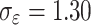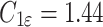Simulated condition

According to the operation characteristics and design specifications of buried natural gas pipelines^30–32, we selected the depth and pressure level of buried natural gas pipelines that are relatively common at present, and set five pipeline pressures of 0.8 MPa, 1.6 MPa, 2.0 MPa, 4.0 MPa, and 6.0 MPa, and four burial depths of 0.8 m, 1.0 m, 1.5 m, and 2.0 m, respectively. The influence of different burial depths and pressure levels on the law of natural gas leakage and diffusion is studied. The above conditions for setting burial depths are set as simulated working condition 1, and the conditions for setting pressure levels as simulated working condition 2. The simulated working conditions for buried natural gas pipeline leakage are shown in Table 1.

Table 1.

Simulation conditions of buried natural gas pipeline leakage.

Simulated condition	Buried depth /m	Pressure rating/MPa	Simulated condition	Pressure rating/MPa	Buried depth /m
Working condition one	1.0	0.8	Working condition two	1.6	0.8
		1.6			1.0
		2.0			1.5
		4.0			2.0
		6.0

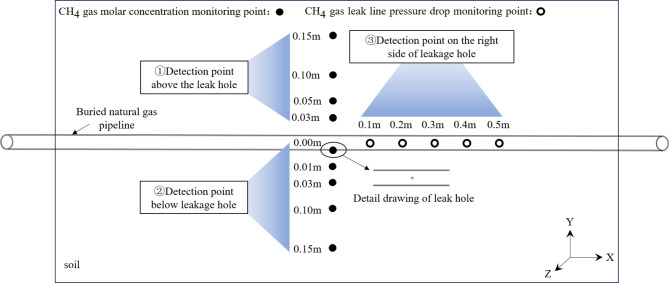
According to the simulation and analysis conditions in Table 1, considering that the buried natural gas pipeline leakage model is a left-right symmetrical structure, the monitoring points on the right side of the model are selected for research and analysis. Multiple monitoring points are set directly above and below the buried natural gas pipeline leakage hole and on the right side of the leak hole, respectively. The total calculation time is set at 200 s, and the time step is set at 0.05 s. The monitoring points are mainly used to detect the changes in pressure drop and gas diffusion mole fraction at each position over time, and to extract the cloud map of gas diffusion mole fraction in the x-axis plane, with extraction intervals set at 2 s, 40 s, 120 s, and 200 s, to observe the dynamic diffusion law and distribution pattern of gas leakage from buried natural gas pipelines in soil within 200 s. The layout of specific buried natural gas pipeline leakage monitoring points is shown in Fig. 2.

Fig. 2.

Schematic diagram of leakage monitoring points of buried natural gas pipelines.

Experimental design

The CH₄ gas leakage and pressure drop test of a buried natural gas pipeline was carried out. The DN = 65 mm steel pipeline, commonly used for buried natural gas, was selected as the test object^32,34. Pressure sensors and flow sensors were installed on the leak hole of the buried natural gas pipeline, and the natural gas pipeline was placed in the test soil box, as shown in Fig. 3a. The soil mass is placed in the test chamber, and three glass plates are placed on the side of the soil chamber to facilitate the observation of the soil mass’s morphological changes during gas leakage, as shown in Fig. 3b. The pressure test sensor is installed on the leak hole of the natural gas pipeline to facilitate the test of the change in pressure drop during the leakage of the natural gas pipeline, as shown in Fig. 3c. The gas flow tester tests the gas flow of natural gas leakage and obtains the data of natural gas leakage at different buried depths, as shown in Fig. 3d. The data recorder is used to record and store the data of the data display instrument, as shown in Fig. 3e. The hydraulic device is used to apply external load on the soil to simulate the soil static pressure under different buried depths of the buried pipeline, and the CH₄ gas leakage at the leak point of the buried natural gas pipeline and the pressure drop parameter on the right side of the pipeline are monitored³⁵. The test condition is consistent with the finite element simulation analysis condition, and the test results can verify the correctness of the finite element simulation results. The models and specifications of the experimental equipment are shown in Table 2. The leakage test of the buried natural gas pipeline is shown in Fig. 3.

Fig. 3.

Leakage test diagram of buried natural gas pipeline: (a) Natural gas pipeline; (b) test soil tank; (c) pressure sensor; (d) gas flow sensor; (e) data logger.

Table 2.

Model and specification of experimental equipment.

Equipment and instrument	Specification and model	Equipment and instrument	Specification and model
Data recorder	12 Data Receiving channel	Pressure transmitter	Pressure range 0–10 MPa
	32-bit ARM chip		Precision class 0.25
	Input voltage signal 0–10 V or current signal 0-100 mA		Threaded connection M20*1.5
	Memory 64 MB		Output signal current 4–20 mA
	Sampling period 1 s		Monitoring media gas, liquid, water
	Maximum power consumption 10 W		Operating temperature − 20–85 °C
	Modbus communication protocol		Power supply 4–20 mA
	Operating temperature 0–50 °C		Response time 10 ms
Gas flowmeter	Pressure range 0–10 MPa	Gas flowmeter	Accuracy ± 1.5 FS
	Flow range 0.005–1500 slpm		Overall material SUS304
	Operating temperature − 20–60 °C		Modbus communication, RTU communication

Result analysis

Different pressure simulations

Analysis of CH4 molar concentration at the monitoring point below the pipeline

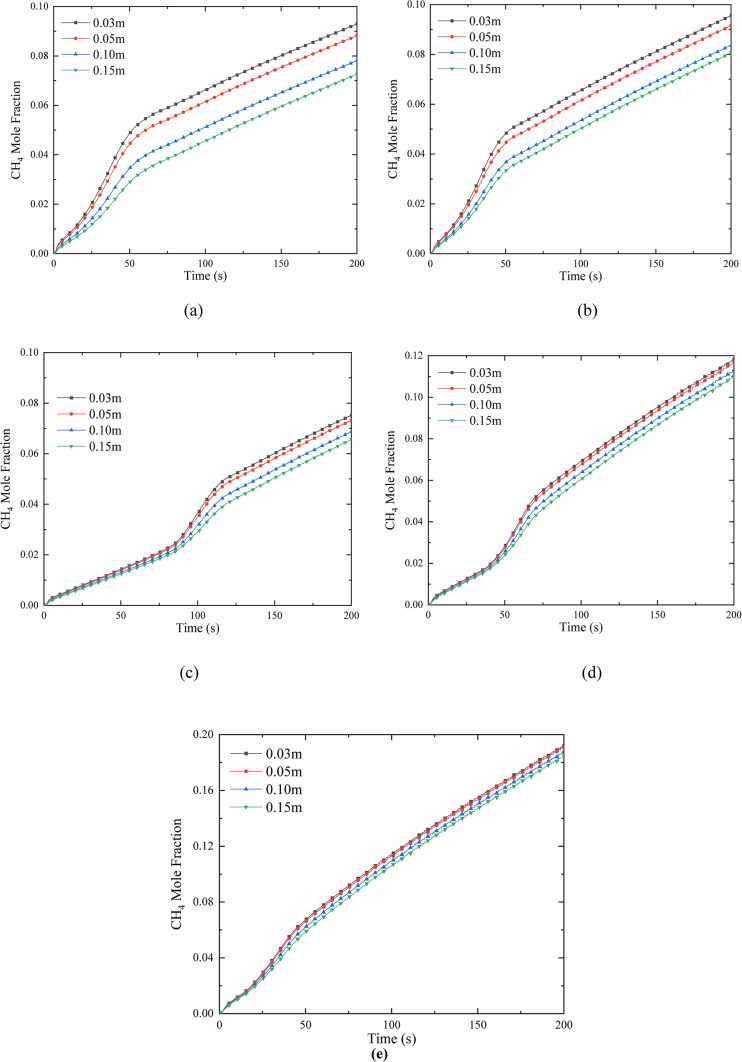
The gas leakage and diffusion characteristics of the buried natural gas pipeline under the conditions of 1 m burial depth, 0.8 MPa, 1.6 MPa, 2.0 MPa, 4.0 MPa, and 6.0 MPa were simulated, and the change of CH₄ gas mole fraction at the monitoring point directly below the leak hole of the buried natural gas pipeline under different pressure conditions at 1 m burial depth was analyzed. The CH₄ gas mole fraction curve at the monitoring point below the buried natural gas pipeline is shown in Fig. 4.

Fig. 4.

Mole fraction diagram of CH₄ gas at monitoring point under buried natural gas pipeline: (a) 0.8 MPa pressure 1 m burial depth; (b) 1.6 MPa pressure 1 m burial depth; (c) 2.0 MPa pressure 1 m burial depth; (d) 4.0 MPa pressure 1 m buried depth; (e) 6.0 MPa pressure 1 m buried depth.

It can be seen from Fig. 4 that the CH₄ gas mole fraction curve changes at the monitoring point below the buried natural gas pipeline under 1 m buried depth and different pressure conditions. In Fig. 4a, the CH₄ gas mole fraction curve in front of the leak hole presents a rapid increase and then a steady change trend, while the CH₄ gas mole fraction curve at the monitoring points 0.03 m and 0.05 m below the leak hole presents a steady change trend after first increasing (segments 0 ~ A), then decreasing (segments A ~ B), and then increasing (the end of B). The monitoring points at 0.00 m, 0.03 m, 0.5 m, 0.10 m, and 0.15 m need 2 s, 23 s, 25 s, 27 s, and 54 s to reach the stable value, respectively. Under the condition of 0.8 MPa buried depth 1 m, the maximum CH₄ gas mole fraction monitored at 0.15 m away from the leak hole is about 0.85. If it does not reach the maximum value of 0.9, the time required for CH₄ gas mole fraction to reach the maximum value also increases with the increase of the monitoring point distance. The CH₄ gas mole fraction curves of monitoring points in Fig. 4b–e are basically the same as those in Fig. 4a. With the increase of buried pipeline pressure, the CH₄ gas mole fraction curves of monitoring points at 0.03 m and 0.05 m have a large fluctuation. The CH₄ gas mole fraction curve at the monitoring points at 0.10 m and 0.15 m did not fluctuate significantly under the influence of soil resistance. In Fig. 4a–e, the curve oscillations of the four groups of CH₄ in red, blue, green, and purple at the initial leakage stage are relatively obvious, which is considered to be caused by the decrease of pipeline pressure with the increase of leakage time in the initial leakage stage of the buried pipeline. The closer the leakage point is, the more obvious this phenomenon becomes.

Analysis of CH4 molar concentration at the monitoring point above the pipeline

The gas leakage and diffusion characteristics of the buried natural gas pipeline under 1 m burial depth and pressures of 0.8 MPa, 1.6 MPa, 2.0 MPa, 4.0 MPa, and 6.0 MPa were simulated, and the change of CH₄ gas mole fraction at the monitoring point directly above the leakage hole of the buried natural gas pipeline under different pressure conditions at 1 m burial depth was analyzed. The CH₄ gas mole fraction curve at the monitoring point directly above the leak hole of the buried natural gas pipeline is shown in Fig. 5.

Fig. 5.

Mole fraction diagram of CH₄ gas at the monitoring point directly above the leak hole of the buried natural gas pipeline: (a) 0.8 MPa pressure 1 m buried depth; (b) 1.6 MPa pressure 1 m burial depth; (c) 2.0 MPa pressure 1 m burial depth; (d) 4.0 MPa pressure 1 m buried depth; (e) 6.0 MPa pressure 1 m buried depth.

It can be seen from Fig. 5 that the change of CH₄ gas mole fraction curve at the monitoring point above the buried natural gas pipeline under different pressure conditions of 1 m buried depth. In Fig. 5a, the CH₄ gas mole fraction curve of each monitoring point shows a gradual decrease. With the increase of leakage monitoring distance, the CH₄ gas mole fraction of each monitoring point becomes lower and lower. The CH₄ gas mole fraction of 0.03 m and 0.05 m leak monitoring points is significantly higher than that of 0.1 m and 0.15 m. The CH₄ gas mole fraction at the four leakage detection points increased rapidly during 0–30 s, reaching 0.028, 0.025, 0.02, and 0.017, respectively. The first turning point occurred during 30–60 s, and the growth rate of each monitoring point decreased. The CH₄ gas mole fraction curve of each monitoring point increased steadily during the period of 60–200 s. The CH₄ gas mole fraction curves of the monitoring points in Fig. 5b–e are consistent with those in Fig. 5a, but the turning point time of the CH₄ gas mole fraction curves at each monitoring point is slightly different, and the difference of CH₄ gas mole fraction values at monitoring points at different distances gradually decreases with the increase of buried pipeline pressure. The comparison between Figs. 3 and 4 shows that the dynamic law of CH₄ gas mole fraction curve above and below the leak point of the buried pipeline is obviously different. The CH₄ gas mole fraction value of the area below the leak point is about 10 times that of the area above the leak point, and the CH₄ gas mole fraction of the monitoring point above the leak hole is significantly less affected by pressure than that of the monitoring point below the leak hole.

Pressure drop analysis of the right monitoring point of the pipeline

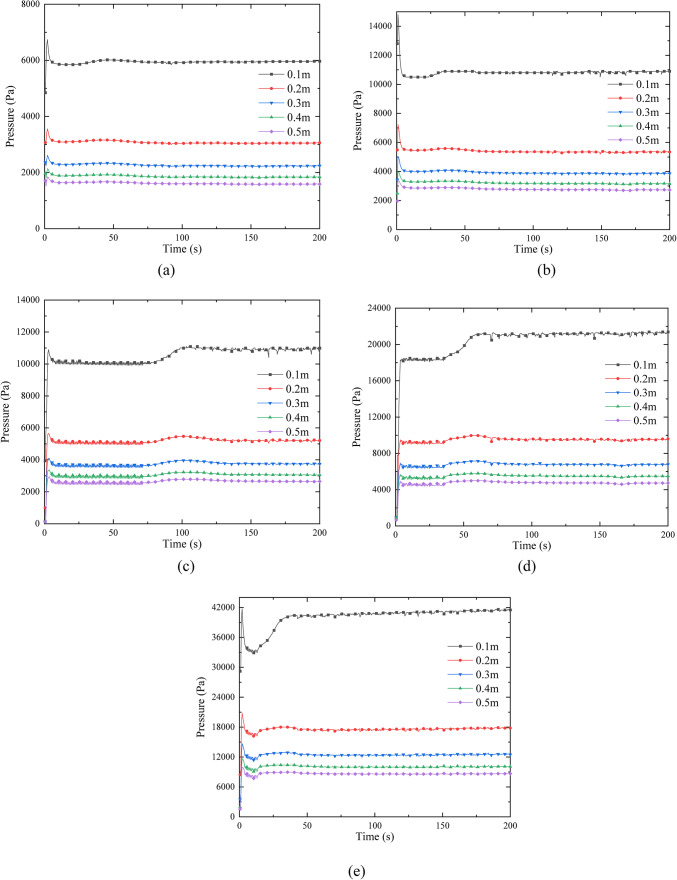
The pressure drop rule for buried natural gas pipelines was simulated under various conditions, including a buried depth of 1 m and pressures of 0.8 MPa, 1.6 MPa, 2.0 MPa, 4.0 MPa, and 6.0 MPa. The resulting pressure drop at the monitoring point on the right side of the leak hole was then analyzed. The pressure drop curve for this detection point is illustrated in Fig. 6.

Fig. 6.

Pressure drop curve of the detection point on the right side of the leakage hole of the buried natural gas pipeline: (a) 0.8 MPa pressure 1 m buried depth; (b) 1.6 MPa pressure 1 m burial depth; (c) 2.0 MPa pressure 1 m burial depth; (d) 4.0 MPa pressure 1 m buried depth; (e) 6.0 MPa pressure 1 m buried depth.

It can be seen from Fig. 6 that the pressure drop curve of the monitoring point on the right side of the buried natural gas pipeline changes under different pipeline pressure conditions at a 1 m buried depth. In Fig. 6a, the pressure change at the right side of the leak hole at 0.1 m presents a steady change trend after first increasing and then decreasing. In the 0–2 s period before the leak, the pressure rises rapidly, reaching about 6700 Pa, and then drops to about 6000 Pa. Under the influence of soil resistance, the pressure value at the 0.2 m leak hole drops rapidly, and the maximum pressure is about 3500 Pa. Meanwhile, the pressure fluctuation at this monitoring point is small, and the change trend is the same as that at the 0.1 m monitoring point. The variation trend of pressure drop at the leakage points 0.3 m, 0.4 m, and 0.5 m is basically the same, and the pressure value decreases successively. The pressure drop of each monitoring point in Fig. 6b is the same as that in Fig. 6a, but the pressure drop value is slightly different. The pressure drop of each monitoring point in Fig. 6c,d presents a trend of first increasing, then decreasing, then stabilizing, then rising slightly, and then stabilizing. However, the change time nodes of pressure drop in Fig. 6c,d are different, and the pressure drop trend of each monitoring point in Fig. 6c,d is different from that in Fig. 6a,b to some extent. In Fig. 6d, the pressure drop at each monitoring point presents a trend of first increasing, then decreasing, then increasing again, and then stabilizing. In Fig. 6e, under the working condition of 1 m buried depth of 6 MPa pipeline pressure, the value of the monitoring point near the leak hole is significantly higher than that in Figures a, b, c, and d. The oscillation range of the pressure curve of each monitoring point with time increases obviously, and the oscillation effect of each monitoring point is more pronounced in the period of 0–25 s. The pressure of the buried pipeline has a great influence on the variation trend of pressure drop at each monitoring point, but the increase of pipeline pressure has no obvious rule on the change of pressure drop near the leakage point, and the pressure drop value increases with the increase of the distance from the monitoring point.

CH4 gas mole fraction diffusion cloud image analysis in the x-axis direction of the pipeline

The gas leakage and diffusion characteristics of the buried natural gas pipeline under the conditions of 1 m buried depth, 0.8 MPa, 1.6 MPa, 2.0 MPa, 4.0 MPa, and 6.0 MPa are simulated. The gas diffusion patterns and distribution rules of buried natural gas pipelines under different pressure conditions at 1 m burial depth were analyzed during four periods (2 s, 40 s, 120 s, and 200 s) along the x-axis during 200 s. The CH4 gas mole fraction diffusion patterns along the x-axis of the buried natural gas pipelines are shown in Fig. 7.

Fig. 7.

Cloud image of CH₄ gas diffusion form on the x-axis direction of the pipeline.

It can be seen from Fig. 7 that the cloud image of CH₄ gas diffusion forms on the x-axis direction of the pipeline under different pipeline pressure conditions with a buried natural gas depth of 1 m. The CH₄ gas diffusion pattern at a pressure of 0.8 MPa and a buried depth of 1.0 m gradually expands downward with the increase of leakage time, and the CH₄ gas diffusion pattern is not obvious during the 2 s and 40 s of leakage, and the CH₄ gas leakage amount is small. During the 120 s of leakage, the CH₄ gas presents U-shaped diffusion under the pipeline. At 200 s of leakage, CH₄ gas diffused to the area above the pipe. CH₄ gas diffusion patterns at pressures of 0.8 MPa, 1.6 MPa, 2.0 MPa, 4.0 MPa, and 6.0 MPa with a buried depth of 1.0 m are basically the same as those at a pressure of 0.8 MPa and a buried depth of 1.0 m. However, with the increase of buried pipeline pressure, the CH₄ gas diffusion patterns near the leak hole show a trend of gradual expansion. The pressure grade of the pipeline has a great influence on the CH₄ gas leakage of the buried pipeline, while the pressures of 0.8 MPa, 1.6 MPa, and 2.0 MPa have little influence on the CH₄ gas leakage of the buried pipeline, especially the pressures of 4.0 MPa and 6.0 MPa have a serious influence on the CH₄ gas leakage of the buried pipeline.

Simulation of different buried depths

Analysis of CH4 molar concentration at the monitoring point below the pipeline

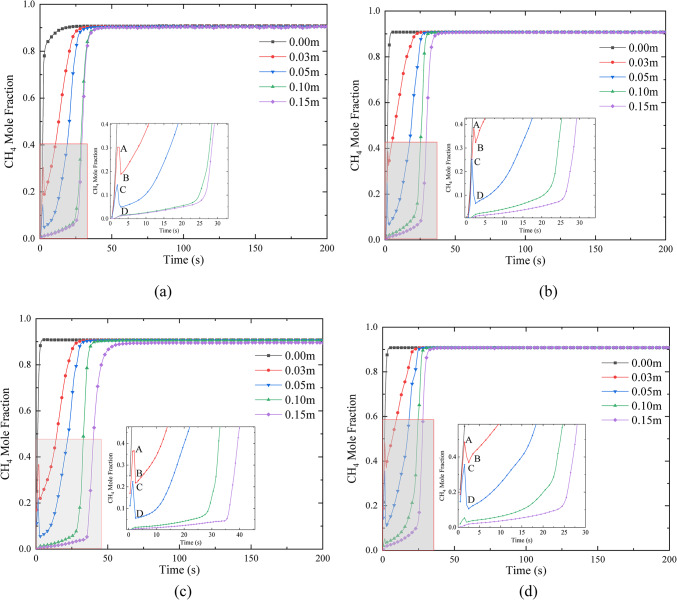
The gas leakage and diffusion patterns of buried natural gas pipelines under a pressure of 1.6 MPa and buried depths of 0.8 m, 1.0 m, 1.5 m, and 2.0 m were simulated, and the change in CH₄ gas mole fraction at the monitoring point directly below the leak hole of buried natural gas pipelines under different buried depth conditions of 1.6 MPa was analyzed. The CH₄ gas mole fraction curve at the monitoring point directly below the leak hole of the buried natural gas pipeline is shown in Fig. 8.

Fig. 8.

Mole fraction curve of CH₄ gas at the monitoring point directly below the leak hole of the buried natural gas pipeline: (a) 1.6 MPa pressure 0.8 m burial depth; (b) 1.6 MPa pressure 1.0 m buried depth (c) 1.6 MPa pressure 1.5 m buried depth; (d) 1.6 MPa pressure 2.0 m burial depth.

Figure 8a When leakage occurs in the buried pipeline, the gas mole fraction of the monitoring points at 0.00 m, 0.03 m, 0.5 m, 0.1 m, and 0.15 m directly in front of the leakage point reaches about 0.9 within 15 s, 18 s, 25 s, 27 s, and 28 s, respectively. In the four diagrams, the oscillations of CH₄ leakage curves in the red, blue, green, and purple groups are weakened, which shows that the influence of buried depth factors on the initial leakage of CH₄ is small, and the influence of buried depth factors and pressure factors on the CH₄ leakage curve is different, mainly reflected in the initial oscillation characteristics of the CH₄ leakage curves in the red, blue, green, and purple groups. The change trend of the four figures in Fig. 8a–d is basically the same, and the factor of pipeline buried depth has an obvious difference on the transition time node of the CH₄ leakage curve. When the buried pipeline leaks, the buried depth has a great influence on the leak point in the range of 0.05 m, and has little influence in the range of 0.05–1 m. The CH₄ gas mole fraction curve at each monitoring point reached a stable state within 48 s after leakage.

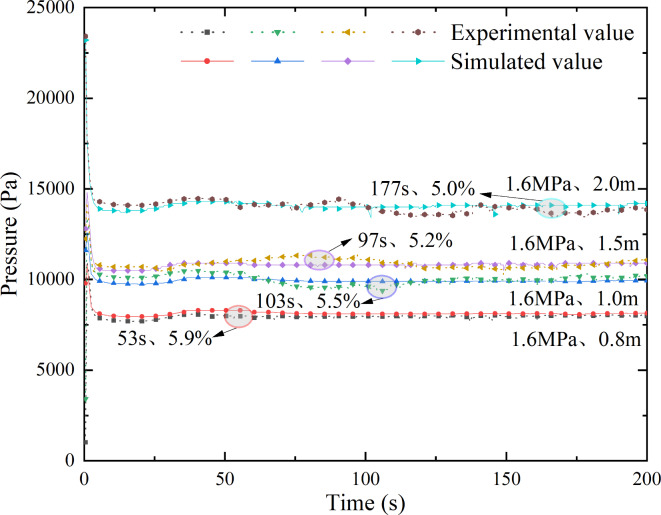
Analysis of CH4 molar concentration at the monitoring point above the pipeline

The gas leakage and diffusion patterns of buried natural gas pipelines under a pressure of 1.6 MPa and buried depths of 0.8 m, 1.0 m, 1.5 m, and 2.0 m were simulated, and the changes in CH₄ gas mole fraction at the monitoring point directly above the leakage hole of buried natural gas pipelines under different burial depths of 1.6 MPa were analyzed. The CH₄ gas mole fraction curve at the monitoring point directly above the buried natural gas pipeline is shown in Fig. 9.

Fig. 9.

Mole fraction of CH₄ gas at the monitoring point above the buried natural gas pipeline: (a) 1.6 MPa pressure 0.8 m burial depth; (b) 1.6 MPa pressure 1.0 m buried depth (c) 1.6 MPa pressure 1.5 m buried depth; (d) 1.6 MPa pressure 2.0 m burial depth.

It is not difficult to see from Fig. 9 that the CH₄ gas mole fraction curves at the four monitoring points in Fig. 9a–d show the same trend of change, and the CH₄ gas mole fraction curves at the four monitoring points show a trend of first increasing, then decreasing, then increasing, and then slowing down during the period from 0 to 45 s. However, the CH₄ gas mole fraction curve at each monitoring point shows an inflection point during 45–55 s. Considering that this may be caused by the gradual decrease of pipeline pressure with the increase of leakage time, the CH₄ gas mole fraction curve also shows a steady growth trend when the pressure is reduced to stability. During 55–200 s, the CH₄ gas mole fraction curve shows a steady growth trend. The growth rate of CH₄ gas mole fraction curve at each monitoring point decreased, and the value continued to increase. At the same time, the gas mole fraction of CH₄ gradually decreased with the increase of the distance from the monitoring point, and the change trend was more obvious with the increase of the leakage time. By comparing Figs. 7 and 8, it can be seen that the CH₄ gas mole fraction below the leak hole has a great influence on the pressure drop. The difference between the CH₄ gas mole fraction above and below the leak hole of the buried pipeline is nearly 10 times, and the change law of CH₄ gas mole fraction over time is also significantly different. Comparative analysis shows that pressure factors and buried factors have obvious differences in the variation trend of CH₄ gas mole fraction curve below the leak hole, which is mainly reflected in the CH₄ gas mole fraction curve after 60 s. Pressure factors have a greater impact than buried factors on the CH₄ gas mole fraction curve below the leak hole.

Pressure drop analysis of the right monitoring point of the pipeline

The pressure drop of the buried natural gas pipeline under the working conditions of 1.6 MPa pressure and buried depths of 0.8 m, 1.0 m, 1.5 m, and 2.0 m was simulated, and the pressure drop change at the monitoring point on the right of the leak hole of the buried natural gas pipeline under different buried depth conditions of 1.6 MPa was analyzed. The pressure drop curve of the monitoring point on the right side of the buried natural gas pipeline is shown in Fig. 10.

Fig. 10.

Pressure drop curve of the monitoring point on the right side of the leakage hole of the buried natural gas pipeline: (a) 1.6 MPa pressure 0.8 m burial depth; (b) 1.6 MPa pressure 1.0 m buried depth (c) 1.6 MPa pressure 1.5 m buried depth; (d) 1.6 MPa pressure 2.0 m burial depth.

It is not difficult to see from Fig. 10 that the pressure drop at each monitoring point increases first, then decreases, and then changes steadily. When a buried pipeline leaks, the pressure of each monitoring point will rise in a short time, and the closer the monitoring point is to the leak hole, the more obvious this phenomenon is. The pressure drop on the right side of the leakage hole of the buried pipeline is more significant in the range of 0.2 m, and the pressure drop in the range of 0.3–0.5 m is smaller. The pressure drop of the monitoring point at 0.1 m on the right side decreases from 11,000 Pa to about 8,000 Pa, while the pressure drop of the monitoring points at 0.2 m, 0.3 m, 0.4 m, and 0.5 m on the right side decreases successively. This phenomenon is mainly caused by the resistance of the soil to the pressure transfer of the leaking gas. With the increase of buried pipe depth, the pressure drop difference of each monitoring point increases, and the pressure drop duration around the leakage hole is shorter. Compared with the pressure factors, it is found that the influence of the buried depth factors on the pressure drop curve is less, and the influence of the pressure factors on the buried depth factors on the pressure drop curve is more serious; the most obvious is the change of the pressure drop curve in the period of 40 s to 100 s.

Test analysis

The results of the finite element simulation were compared and analyzed with the test results for different buried depths and a pressure of 1.6 MPa in the pipeline. The maximum error between the simulated and test values was calculated to verify the accuracy of the simulation. Figure 11 shows the comparison between the simulated and test values for different buried depths and a pressure of 1.6 MPa. The simulation and test values were compared for pressures of 1.6 MPa and buried depths of 0.8 m, 1.0 m, 1.5 m, and 2.0 m. In Fig. 11, the dashed line represents the test value and the solid line represents the simulation value. The pressure drop of the buried natural gas pipeline was analyzed for a leakage duration of 200 s.

Fig. 11.

Comparison of simulation values and test values under different buried depths of 1.6 MPa pipeline pressure.

As shown in Fig. 11, the comparison between the finite element simulation value and the test value during the 200-s time period of a buried natural gas pipeline leakage reveals that the pressure drop curves for both values are similar under different working conditions. At 1.6 MPa and 0.8 m, the maximum error for both values occurs at 53 s, with a difference of 5.9%. Overall, the test value is slightly lower than the finite element simulation value. Under 1.6 MPa and 1.0 m conditions, both the simulation and test values fluctuate to some extent, with the maximum error occurring at 103 s and a difference of 5.5%. However, the pressure drop curves for both values remain within the acceptable error range. For 1.6 MPa and 1.5 m conditions, the pressure drop curve shows two distinct parts: the first part (0–110 s) has a slightly higher test value compared to the simulation value, while the second part (110–200 s) has a slightly lower test value. The maximum error between the two occurs at 97 s, with a difference of 5.2%. Under 1.6 MPa and 2.0 m conditions, there is no clear pattern in the variation of the pressure drop curve between the simulation and test values, with the maximum error occurring at 177 s and a difference of 5.0%. Overall, the errors for both the finite element simulation value and the test value for the buried natural gas pipeline leakage pressure drop curve under all four working conditions are within an acceptable range, effectively verifying the accuracy of the finite element simulation results and the reliability of the buried natural gas pipeline leakage test.

Discussion

There are significant differences in the CH₄ gas mole fraction curves between the monitoring points above and below the leakage point at a buried depth of 1 m, under varying pressure conditions. At each monitoring point below the leak hole, the CH₄ gas mole fraction initially increases, then decreases, and then steadily increases again. On the other hand, the CH₄ gas mole fraction at each monitoring point above the leak hole shows a pattern of increasing, slowing down, and then steadily increasing. The pipeline pressure has a significant impact on the CH₄ gas mole fraction at the monitoring point below the leakage point. However, as the distance from the monitoring point increases and the soil resistance comes into play, the pipeline pressure decreases, resulting in the lowest CH₄ gas mole fraction at the monitoring points at 0.10 m and 0.15 m. At a buried depth of 1 m and under varying pressure conditions, the pressure drop curve at the monitoring point on the right side of the leak point initially rises rapidly, then stabilizes after decreasing. The pressure drop at the right side of the leak hole is most affected by the pipeline pressure at 0.1 m and 0.2 m, while it is least affected at 0.3 m, 0.4 m, and 0.5 m. However, as the pressure of the buried pipeline increases, the diffusion pattern of CH₄ gas near the leakage hole expands. The pressure of 0.8 MPa, 1.6 MPa, and 2.0 MPa has little influence on the CH₄ gas leakage of the buried pipeline, while the pressure of 4.0 MPa and 6.0 MPa has a more significant impact on the CH₄ gas leakage.

The CH₄ gas mole fraction curve at the monitoring point below the leak hole shows a trend of initially increasing, then decreasing, and then increasing again at a pipeline burial depth of 1.6 MPa pressure. Within 48 s of the leak, the CH₄ gas mole fraction curve at each monitoring point reaches a stable state, with the burial depth having a significant impact on the leak point within 0.05 m. However, the effect is negligible in the range of 0.05–1 m. On the other hand, the CH₄ gas mole fraction curve at the monitoring point above the leak hole exhibits a rapid increase followed by a steady rise after a turning point. Additionally, the CH₄ gas mole fraction gradually decreases with increasing distance from the monitoring point, and this trend becomes more pronounced over time. The difference in CH₄ gas molar fraction above and below the leak hole is nearly 10 times.

The pressure drop at the monitoring point on the right side of the leak hole under different burial depths of 1.6 MPa pressure shows a trend of initially increasing, then decreasing, and then stabilizing. This phenomenon becomes more apparent as the monitoring point gets closer to the leak hole. The pressure drop at the monitoring point decreases successively at 0.2 m, 0.3 m, 0.4 m, and 0.5 m. This is due to the soil’s resistance to the pressure transfer of the leaking gas, and the difference in pressure drop at each monitoring point increases with the depth of the buried pipeline. The CH₄ gas diffusion cloud image in the x-axis direction of the buried natural gas pipeline under different pipeline depths at 1.6 MPa pressure gradually increases over time. As the pipeline depth increases under the same pressure, the diffusion area of CH₄ gas in the soil along the x-axis becomes smaller, but this does not significantly affect the diffusion distribution pattern of CH₄ gas in the soil along the x-axis direction.

Under four working conditions, the errors between the finite element values and the test values of the leakage pressure drop curve of the buried natural gas pipeline are 5.9%, 5.5%, 5.2%, and 5.0%, respectively. The largest error between the simulation value and test value of the pressure drop curve is 5.9% under the working conditions of 1.6 MPa and 0.8 m. The error between the simulation value and test value of the pressure drop curve is at least 5.0% under the conditions of 1.6 MPa and 2.0 m. However, the finite element values and test values of the four groups of pressure drop curves are all within the allowable error range, effectively verifying the correctness of the finite element calculation results and the reliability of the test.

Conclusions

The trend of CH₄ gas mole fraction curve above and below the leakage point of a buried natural gas pipeline varies to some extent. The CH₄ gas mole fraction curve in the area below the leak point reaches a stable state within 50 s. However, at the monitoring points 0.03 m and 0.05 m below the leak point, the CH₄ gas mole fraction curve fluctuates sharply for 2 to 3 s, with a fluctuation of approximately 7%. The depth at which the pipeline is buried has the greatest influence on CH₄ levels at the leak point, with a nearly 10-fold difference in numerical value between the levels above and below the leak hole. Additionally, the pressure of the pipeline has a greater impact on CH₄ gas leakage than the depth at which it is buried. The pressure of the pipeline affects the pressure drop near the leak point, while the depth at which it is buried has little impact on the pressure drop further away from the leak point. As the depth of the buried pipeline increases, the pressure drop at monitoring points 0.1 m, 0.2 m, 0.3 m, 0.4 m, and 0.5 m decreases by 27.64%, 24.02%, 21.52%, 17.65%, and 17.11%, respectively. The larger the pipe pressure, the larger the area of CH₄ gas diffusion on the x-axis section, and the deeper the pipe is buried, the smaller the area of CH₄ gas diffusion on the x-axis section. The diffusion of CH₄ gas in the soil in the x-axis direction is U-shaped, and after 200 s of leakage, the gas diffuses to the top of the pipe. The errors between the finite element values and the test values of the buried natural gas pipeline leakage pressure drop curve under four working conditions are 5.9%, 5.5%, 5.2%, and 5.0%, respectively. These error values are within the allowable range, which verifies the correctness of the finite element calculation results and the reliability of the test. The research results are expected to provide valuable references for monitoring and safety design of buried natural gas pipelines.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author contributions

C.Z. and Y.H. methodology, C.Z. software, Y.H. validation, Z.D., Z.Y. and D.Y. formal analysis, Z.D. investigation, Z.Y. resources, D.Y. data curation, Z.Y. writing—original draft preparation, Y.H. writing—review and editing. All authors have read and agreed to the published version of the manuscript.

Data availability

The research data supporting this publication are provided within this paper.Please refer to the supplementary materials for the simulation and test data in the paper.

Declarations

Competing interests

The authors declare no competing interests.