Dual-role ion dynamics in ferroionic CuInP₂S₆: revealing the transition from ferroelectric to ionic switching mechanisms

Abstract

Due to its “ferroionic” nature, CuInP₂S₆ combines switchable ferroelectric polarization with highly mobile Cu ions, allowing for multiple resistance states. Its conductive mechanism involves ferroelectric switching, ion migration, and corresponding intercoupling, which are highly sensitive to external electric field. Distinguishing the dominant contribution of either ferroelectric switching or ion migration to dynamic conductivity remains a challenge and the conductive mechanism is not clear yet. Here, based on polarization switching analyses and first-principles calculations, this work demonstrates that the Cu ion migration pathways enable the formation of a quadruple-well state, determining the conductive mechanism. Accordingly, it favors the manipulation of Cu ion transport in the intralayer and interlayer in a controlled manner, and makes a transition from ferroelectric-dominated to ion-migration-dominated conductivity, by tailoring the electric fields. This work deepens the understanding of ion migration dynamics and conductive switching in ferroionic systems, which is critical for the advancement of memristor-based neuromorphic computing.

The authors find that the Cu ion migration pathways determine the conductive mechanism of van der Waals ferroelectric CuInP₂S₆. By tailoring the electric field, they manipulate Cu ions transport within and between layers, revealing the transition from ferroelectric to ionic switching mechanisms.

Introduction

In recent years, there has been a surge of interest in memristor-based neuromorphic computing technologies^1–3. Two-dimensional ferroelectric materials have emerged as highly promising candidates in these fields due to their atomically thin structure and switchable polarization by manipulating the electric field, enabling the energy-efficient information processing and synaptic-like functionalities^4–8.

Among these materials, CuInP₂S₆ (CIPS) is particularly noteworthy as it exhibits “ferroionic” properties^9–11, that is the combination of switchable ferroelectric polarization with mobile ions. This characteristic allows for the dynamic adjustment of resistance states and self-rectification in memristive devices that are pivotal in memory and logic operations^12–16. This dual functionality is primarily attributed to the copper (Cu) ions in CIPS, which contribute to both the ferroelectricity characterized by off-center ordering and the ionic conduction, characterized by long-range disordered migration^17–21. Their close correlation endows this material with novel phenomena, including the existence of quadruple-or sextuple well states^22–25, polarization reversal against the electric field^23,26, anomalous photocurrent reversal²⁷, remarkable ionic conduction¹², etc. For example, Brehm et al. ²² revealed that along the direction of the electric field, Cu ions can be migrated from intralayer to a stable interlayer position in the van der Waals (vdW) gap, thereby forming an additional pair of highly polarization states. Neumayer et al. ²⁶ further revealed that the application of electric field can also drive the Cu ions across the vdW gap, which leads to polarization alignment against the electric field. Although these outstanding works have provided a deep understanding of Cu ion migration dynamics and multiple-well states through switching spectroscopy-PFM (SS-PFM) measurements supplemented with density functional theory (DFT) calculations, the relationship between Cu ion migration dynamics and the conductive mechanisms was not addressed, leaving it unclear in this field. Given that Cu ions dynamics induce the ferroelectric switching simultaneously with Cu ions migration in CIPS, the conductive mechanism involves ferroelectric switching, ion migration, and their coupling, all of which are highly sensitive to electric field conditions^23,26. It remains a challenge to accurately distinguish whether it is ferroelectric or ion migration that primarily contributes to the dynamic conductivity under varied electric field strengths, directions, and time duration. The concrete evidence linking the dual-role ion dynamics to the conductive mechanisms should be further established, which is the focus of our work.

Recent works have shown that applying an electric field through nanometer tip provides an effective approach to investigate the ionic migration effect and conductive behavior. For polarization switching, Cu ions maintain a relatively ordered position in the lattice^18,28,29, while the localized strong electric field under the nanometer conductive tip would lead to the reversible accumulation and depletion of Cu ions under the tip and even complete disordering of Cu ion positions^30,31. Another benefit of using nanometer tip is providing a highly asymmetric electrode configuration³², where the conducting behavior is primarily influenced by the nanometer-sized tip and the macroscopic counter-electrode has a minimal impact, greatly reducing the complexity of understanding the mechanisms at play¹².

In this work, we used CIPS as the memristor layer and constructed a prototype device with a macroscopic Au bottom electrode and a conductive Pt nanometer tip as the top electrode. Based on the tip-based SS-PFM and first-principles calculations, this work confirms the control of Cu ion transport properties in multiple wells states and reveals their roles in determining the conductive behaviors. It reveals that the intralayer migration leads to ferroelectric-dominated conduction and interlayer migration contributes to ion migration-controlled conduction. The Cu ion migration pathways in the quadruple state can be manipulated in a controlled manner depending on the electric fields, achieving a controlled transition from ferroelectric to ion migration-dominated conductive mechanism. Finally, it also demonstrates that the Cu ion migration can be effectively modulated by the application of mechanical load. Our work provides unique insights into the switching of conductive mechanisms in the ferroionic CIPS.

Results

Ferroelectric-/ion migration-modulated conductive switching behavior

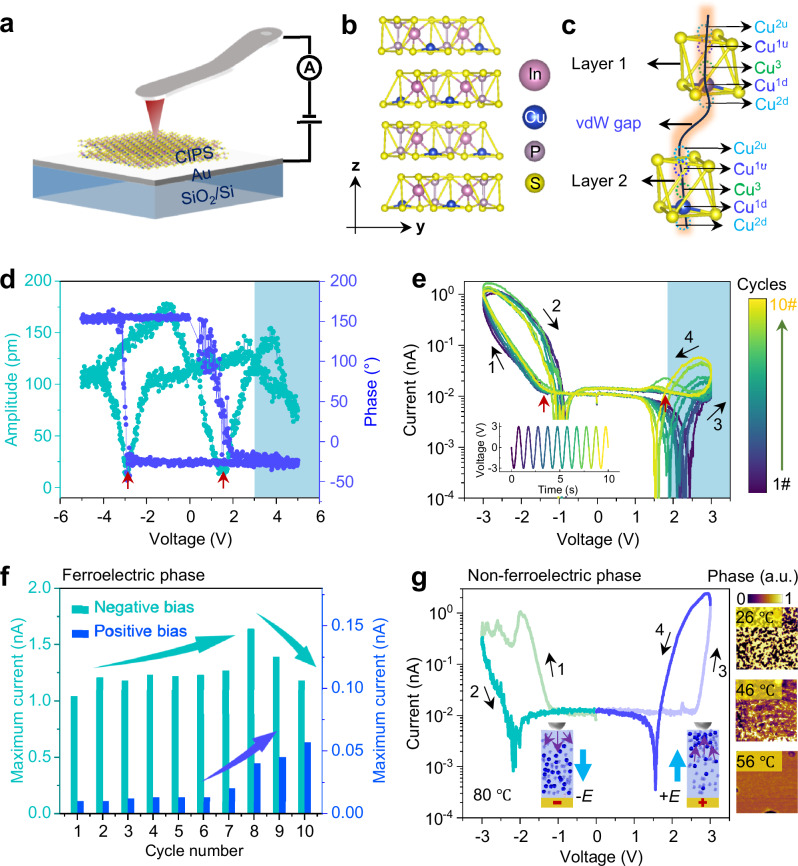
The highly asymmetric electrode configuration was presented in Fig. 1a, where a macroscopic Au was used as bottom electrode and a conducting Pt nanometer tip as the top electrode. The exfoliated CIPS flake was used as memristor layer. The crystal structure can be described as a sulfur framework, with metal cations (Cu and In) and P–P pairs occupying the octahedral voids²⁰, as depicted in Fig. 1b. The unstable Cu ions can occupy three crystallographic sites⁹, as presented in Fig. 1c: (1) intralayer position Cu¹ (upward Cu^1u and downward Cu^1d), which shifted from the centers of the octahedra, (2) octahedral Cu² (Cu^2u and Cu^2d), which located in the centers of the octahedra, and (3) nearly interlayer positions Cu³ (Cu^3u and Cu^3d), which located in the vdW gap. Under external electric field, Cu ions migrate and can occupy these possible positions, forming multiple wells states. In this work, we aim to investigate the control of Cu ion transport properties in multiple wells states and their roles in determining the conductive mechanisms.

Fig. 1. Ferroelectric-/ion-modulated conductive switching in ferroionic CuInP₂S₆.

a The schematic of AFM tip/CIPS/Au on SiO₂/Si substrate for electrical measurement. b, c Schematic of layered structured CIPS and possible copper positions labeled Cu¹, Cu², and Cu³. d The switching spectroscopy-PFM (SS-PFM) at ambient environment (~26 °C), with a testing time duration of 10 s. e Ten fast scans of I–V curves with a time duration of 1 s for each I–V cycle at ambient temperature. The numbers and arrows represent the bias scanning sequence and direction, respectively. The raw data in (e) is adapted from our previous work¹⁶ under a Creative Commons licence CC BY 4.0. f The maximum current change with the cycles in two bias direction according to the results of (e). g The I–V curves measured at 80 °C with a time duration of 1 s (left panel) and PFM phase at different temperature (right panel).

Figure 1d shows the SS-PFM performed at ambient environment (~26 °C), with a testing time duration of 10 s. Both phase and amplitude reveal hysteresis loops (off-field, V_dc  =  0). A ~180° phase contrast corresponds to the two opposite polarization directions perpendicular to the layer surface. The amplitude signal shows two minima (the red arrow) at the threshold voltage for polarization switching in a double potential wells due to the Cu ions hopping between the intralayer Cu^1u and Cu^1d positions¹⁸. Interestingly, above a threshold voltage of ~+3 V, the amplitude once again shows a trend towards minima (the shaded region), suggesting the onset of quadruple-well due to Cu ion migration across vdW layers^18,26. Notably, the activation of quadruple states also significantly influences the conductive behavior. As shown in Fig. 1e and Supplementary Fig. 1, 10 fast scans of full-cycle current–voltage (I–V) curves were conducted with a time duration of 1 s for each cycle. Asymmetric conductive switching was observed with the current being larger in negative bias than positive bias due to the asymmetric electrode configurations³². The current in negative bias exhibits a resistive switching window at a threshold voltage of ~−1.5 V and a current peak in positive bias is observed at a threshold voltage of ~+1.5 V due to the dominating ferroelectric switching in a double wells state³⁰. Interestingly, a resistive switching window forms at higher voltages and significantly expands with increased cycles (the shaded region), which identifies the activation of quadruple states due to the enhanced Cu ions migration across the vdW gap. As presented in Fig. 1f and Supplementary Fig. 2, with increased scanning cycles, the current first increases and then starts to decrease after cycle#8 in negative bias direction. Conversely, the current significantly increases after cycle#8 in positive bias direction. Applying a large V, or long t also leads to a rapid current decrease in negative bias direction and a significant current increase in positive bias direction (Supplementary Figs. 3–5). The significant change in conductive behavior after the turning point under both positive and negative bias serves as proof Cu ion migration across vdW gap and the emergence of the quadruple-well states. In this scenario, ferroelectric polarization charge control of the conductive mechanism is no longer applicable, and ion migration becomes the primary contribution.

The ion migration mechanism was further confirmed by elevating the temperature above the Curie temperature (T_c) to eliminate ferroelectricity. As shown in Fig. 1g and Supplementary Fig. 6, the non-ferroelectric phase can be obtained when the temperature reaches 56 °C, higher than T_c of CIPS. Subsequently, I–V curves were measured at higher temperature such as 80 °C, which is sufficient to ensure the non-ferroelectricity. It was strongly confirmed in the non-ferroelectric phase that applying negative bias dramatically decreases the current with low-resistance state (LRS) switching to a high-resistance state (HRS) in a counterclockwise sequence from 1 to 2. Conversely, applying positive bias significantly increases the current with a large resistive switching from HRS to LRS state. This result strongly indicates the ion migration control of conductive behavior. The pronounced accumulation and depletion of Cu ions beneath the nanometer tip¹² drastically influences the conduction in two different bias directions in an opposite manner. The current rectification of I–V curves can be dynamically manipulated and effectively switched by varying the bias conditions such as voltage magnitude or time duration to activate Cu ion migration (Supplementary Fig. 7).

The abnormal ferroelectric polarization switching behaviors under an electric field

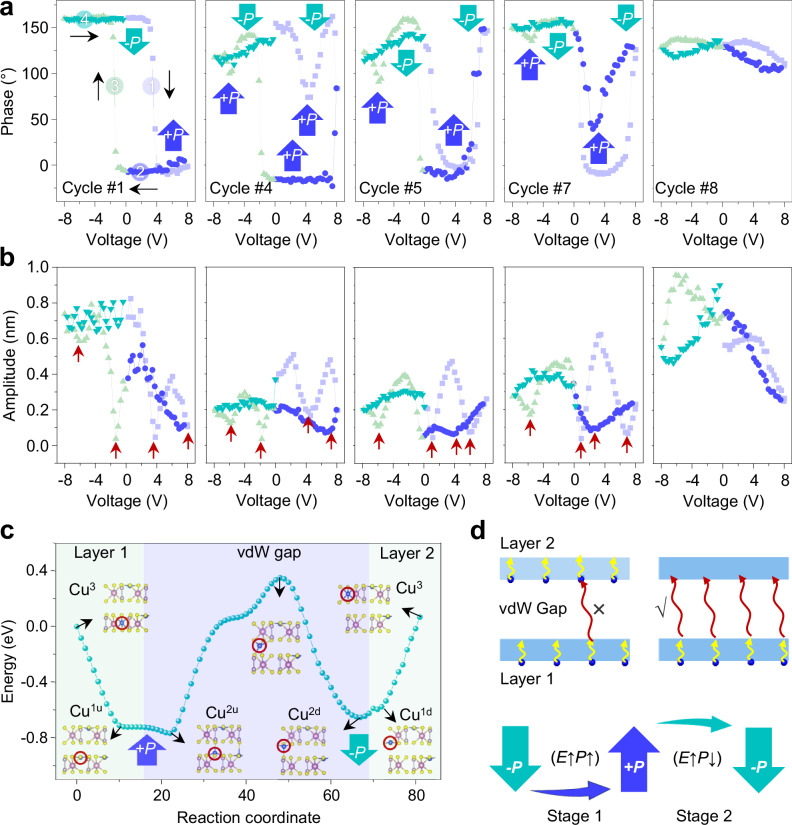
For further investigation on the Cu ion migration dynamics under external electric field, SS-PFM technique was employed³³. Ten SS-PFM were performed at a specific location with time duration of 1 s for each cycle (Supplementary Fig. 8). The phase and amplitude at different test cycles are representatively presented in Fig. 2a and b, respectively. For cycle #1, the phase shows the typical hysteresis loops for double wells states. For example, downward polarization (P↓) can be switched to upward polarization P↑ by a positive electric field (E↑) at threshold voltage of ～+3 V. P↑ can be switched back to P↓ by applying a negative electric field (E↓) at threshold voltage of ～−1.5 V. The polarization aligns with the positive E-field (E↑P↑ or E↓P↓) and this behavior is attributed to Cu ions hopping between the intralayer Cu^1u and Cu^1d positions^18,20,34.

Fig. 2. The Cu ion migration dynamics and abnormal switching behaviors under an electric field.

a, b The phase and amplitude of SS-PFM at different test cycles, respectively. The numbers 1–4 and black arrows represent the bias scanning sequence and direction, respectively. c The calculated potential barrier during Cu ion migration across the vdW layer by nudged elastic band (NEB) method. d The schematic of two stages for the migration Cu ions paths.

Interestingly, for cycle #4, the phase shows the non-typical hysteresis loops. At a threshold voltage of ～+3 V, P↓ was firstly switched to P↑, and then immediately switched back to P↓ by the E↑, where the polarization aligns against the electric field (E↑P↓), which is the evidence of quadruple-well states due to the Cu ions migration across the vdW gap^23,26,35. With further increasing cycles, the threshold voltage for switching from P↓ to P↑ reduces progressively due to the redistributed Cu ions, and down to～1 V for cycle #7. At a threshold voltage of ～+6 V, P↑ can be switched back to P↓ by the E↑(E↑P↓). Under negative E-field E↓, the polarization also partially aligns against the field (E↓P↑) but not as prominently as at positive E-field E↑. A major difference between them lies in the fact that applying the negative bias firstly promotes the polarization switching (E↓P↑) from cycle#1 to cycle#5 and then depresses this process after cycle#5. However, applying positive bias continuously promotes the polarization switching (E↑P↓) with the repeated cycles and higher bias voltage. These results are excellently in agreement with the conduction behavior in the positive and negative bias direction, which are solid evidence of the contribution of Cu ions migration across the vdW gap to the conductive mechanism. For cycle #8, polarization switching becomes invisible because the long-range migration across the vdW gap significantly disrupts the ferroelectric order³⁰, which is further confirmed by the formation of topographic bulges up to 30 nm after 10 cycles (Supplementary Fig. 9). Applying a higher V_max can also induce polarization alignment opposite to the applied electric field (Supplementary Fig. 10).

Figure 2c further shows the migration scenario and the migration barriers during Cu ion migration across the vdW layers. The initial Cu ion is in the central symmetric position of the [S₆] cage. The system energy continues to decrease during the process of Cu ion moving to gap and reaches two local minimum energy minimums in the layer 1, which correspond to the Cu^1u and Cu^2u positions with the P↑, respectively. The barrier energy reaches the maximum when Cu ions are in vdW gap. Subsequently, Cu ions enter the two local energy minimum in the adjacent vdW layer 2, which corresponds to Cu^2d and Cu^1d positions with the P↓, respectively. Overall, the barrier for the intralayer hopping between the Cu^1u and Cu^2u, or Cu^1d and Cu^2d is about 0.05 eV. The barrier for the intralayer hopping between the Cu^1u and Cu^1d positions is about 0.7 eV. The barrier for the interlayer migration between the Cu^2u and Cu^2d positions is about 1.1 eV. The Cu ion migration pathways can be feasibly manipulated by varying electric field to surpass the migration barrier. As presented in Fig. 2d, two stages can be proposed to illustrate the Cu ions migration pathways under an electric field E (V, t, N), including bias voltage V, time duration t, and repeated cycles N. At stage 1, under low V, short t, or few N, Cu ions can only hop up and down in the intralayer without energy across the vdW gap. At stage 2, with further increased V, t, or N, Cu ions can migrate across the vdW gaps to reach the adjacent layer or the entire layers.

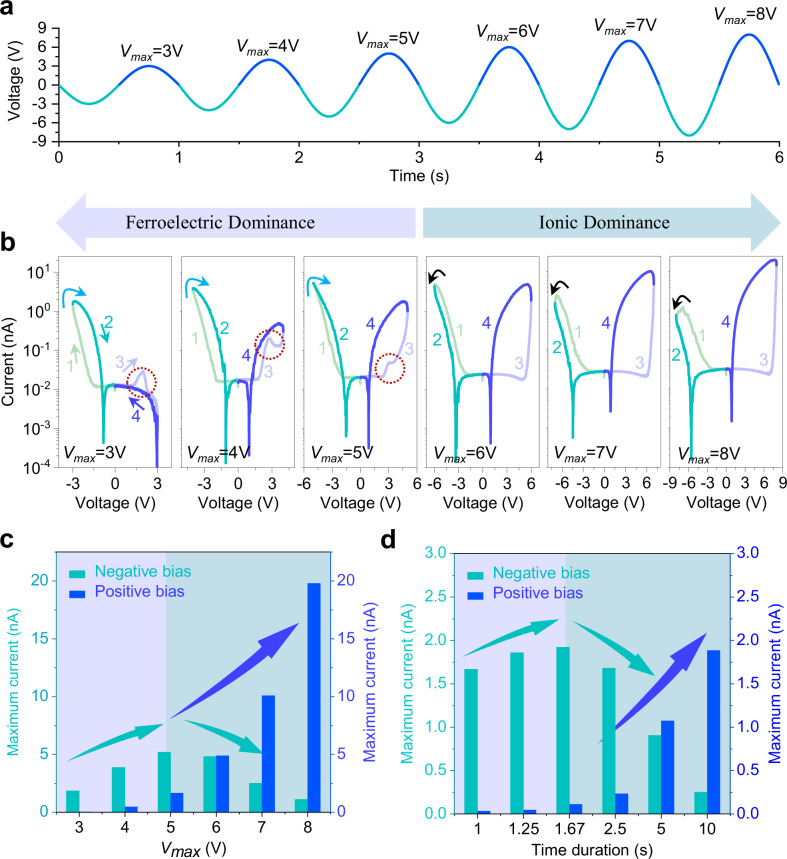
The dynamic conductive behavior under varying electric field

The conductive switching manipulated by the ionic migration dynamics was further confirmed by precise adjustments of electric field E (V, t, N). It is revealed that the intralayer and interlayer Cu ions migration in a quadruple-well state determines the conductive mechanisms. Figure 3a shows the six sinusoidal voltage sweeping cycles varying the bias voltage magnitude and the time taken for six sinusoidal cycles. The corresponding six sets of full-cycle semilog I–V curves and the maximum current in two bias directions are presented in Fig. 3b and c, respectively. It has been revealed that the turning point of the conductive mechanism occurs around V_max = 5 V. Before V_max = 5 V, the conductive mechanism is primarily dominated by ferroelectric effects due to the intralayer Cu ions hopping. In this range, the current under negative bias is greater than that under positive bias and increases with the increased V_max. The resistive switching occurs from the HRS to the LRS in a clockwise sequence from 1 to 2. Under positive bias, a distinct current peak can be observed at small positive bias due to ferroelectric switching³⁰. This is especially identified to be the sharp peak of the switching current through the semilog I–t curves (Supplementary Fig. 11). When V_max exceeds the turning point of V_max = 5 V, the conductive mechanism shifts to being dominated by interlayer Cu ion migration across the vdW gap. The current under negative bias begins to decrease sharply, and the resistive switching occurs from the LRS to the HRS in a counterclockwise sequence from 1 to 2. Conversely, under positive bias, the current peak from ferroelectric switching becomes invisible. The current starts to increase significantly and forms a large hysteresis window at a large threshold voltage above 5 V. This result is highly consistent with the Cu ions migration dynamics in a quadruple-well states as confirmed by the polarization switching results in Fig. 2, where at a large threshold voltage of å 5 V, Cu ions start to migrate across the vdW gap or through the entire layers, as evidenced by the alignment of ferroelectric polarization against the electric field. The long-range migration of Cu⁺ ions can be also verified from the topographic changes where a slightly topographic bump (~2 nm) appears with one semi-cycle (0 V→+5 V→0 V) I–V measurement (Supplementary Fig. 12).

Fig. 3. The dynamic transition from ferroelectric to ion migration-dominated conductive behavior under varying electric fields.

The raw data are adapted from our previous work¹⁶ under a Creative Commons licence CC BY 4.0. a The six sinusoidal voltage sweeping cycles varying the bias voltage magnitude and the time taken for six cycles. The time duration is 1 s for each cycle. b The corresponding six full-cycle of semilog I–V curves varying bias voltage magnitude. The numbers#1–4 and black arrows represent the bias scanning sequence and direction, respectively. The current change with the six cycles c varying bias voltage and d varying time duration in positive and negative bias direction.

In addition to bias voltage V, the time duration t also significantly influences the Cu ions migration across the vdW gap in a similar manner. Six sets of full-cycle semilog I–V curves varying time duration of each cycle are also plotted in Supplementary Fig. 13. The maximum current in negative bias direction is presented in Fig. 3d. With longer time duration, the current first increases and then starts to decrease rapidly in negative bias direction. Conversely, the current significantly increases in positive bias direction. The turning point of the conductive mechanism switching from ferroelectric to ionic migration effect occurs around time duration t = 1.65 s.

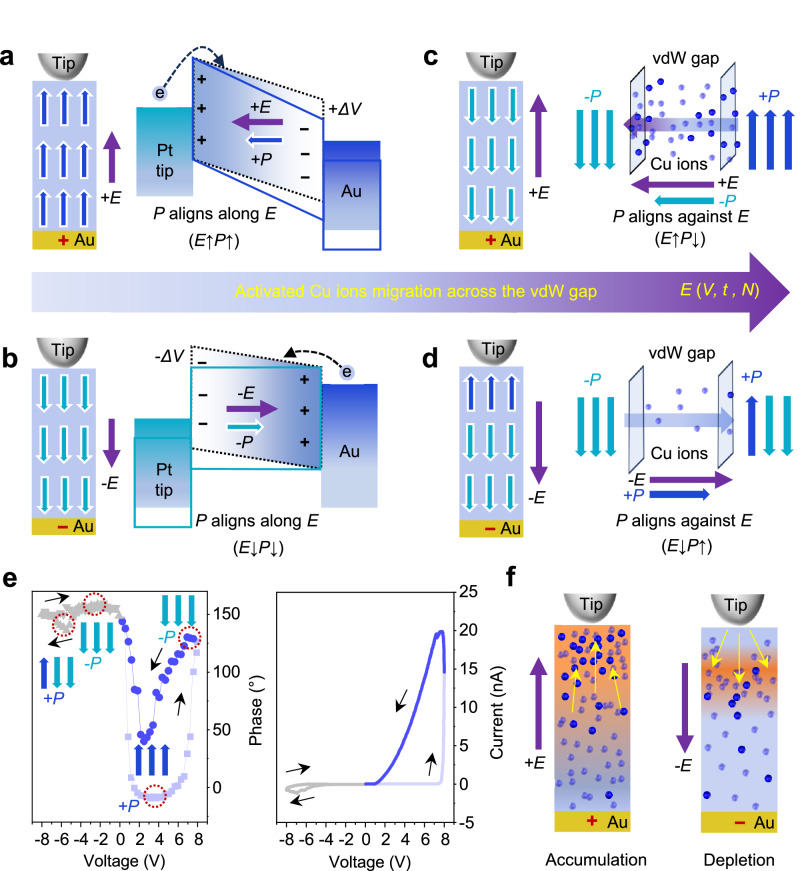
The asymmetric Cu ions migration and conductive mechanisms

The conductive switching mechanism under the varied electric field E (V, t, N) can be comprehensively understood by the Cu ion migration dynamics in a quadruple state. At low V, short t, or few N, Cu ions are restricted to hop up or down in the intralayer, unable to migrate across the vdW gap. In this scenario, ferroelectric polarization aligns with the electric field direction, and becomes the dominant conductive switching mechanism. As illustrated in Fig. 4a, when a positive electric field is applied through the bottom Au electrode, the energy band on the Au side shifts downward, where electrons are transported to the Au electrode more difficult due to a higher interface barrier and smaller contact area at the Pt tip/CIPS. Conversely, as shown in Fig. 4b, applying a negative electric field through the top Pt tip electrode shifts downward the energy band on the Pt side, where electrons are easier transported to the Pt tip electrode due to a lower interface barrier and larger contact area at the CIPS/Au side.

Fig. 4. The conductive mechanisms and the asymmetric Cu ions migration across the vdW gap in two opposite bias direction.

Band diagrams according to the work function of Pt (5.6 eV)^50,51, Au (5.1 eV)⁵¹, and electron affinity of CIPS (3.7 eV)⁵ under positive (a) and negative bias (b) with low bias magnitude or short time duration. The schematic of the Cu ions migration across the vdW gap in positive (c) and negative (d) bias direction with high bias magnitude, long time duration or multiple cycles. e The excellent agreement between I–V curves and the polarization switching curve due to the Cu ions migration across the vdW gap. The polarization switching curve is taken from that for Cycle #7 in Fig. 2a. The I–V curve is the linear plot of semilog I–V curve with V_max = 8 V in Fig. 3b. f The diagram of the accumulation and depletion of Cu ions at interfaces in positive and negative bias direction.

As V, t, or N reaches a certain threshold, Cu ions can migrate across the vdW gaps to adjacent layers or even across the entire layers and this migration process can be evidenced by the ferroelectric polarization aligning against the electric field (E↓P↑) or (E↑P↓). In this scenario, the interlayer Cu ions migration across the vdW gap becomes the primary contribution to the conductive mechanism. As illustrated in Fig. 4c, d, this migration is significantly more pronounced under positive bias and particularly weak under negative bias. This asymmetry is confirmed by the stronger (E↑P↓) switching under positive bias compared to (E↓P↑) switching under negative bias in Fig. 2. Figure 4e shows the excellent agreement between conductive behavior and Cu⁺ migration across the vdW gap. Especially in the positive bias region of the I–V curve, Cu ions begin to migrate across the vdW gap at a large threshold voltage, where the current also increases significantly. This result confirms that the extent of this migration determines the conductive behavior. However, distinguishing electronic and ionic conductivity remains challenging due to their strong coupling. Ion migration influences electronic conductivity by forming internal electric fields and modifying Schottky barriers^10–12. Conversely, electron transport also affects ion migration. When electron transport is hindered due to interfacial barrier, the effective voltage applied inside the bulk decreases, making ion migration more difficult. The time-resolved current on different time scales may be useful to distinguish their contributions. According to the current in response to 10 cycles of 5 V pulse voltage with pulse widths of 0.01 and 0.1 s, a simple estimate suggests that the ionic current is approximately five times greater than the electronic current (Supplementary Fig. 14).

Cu ion transport modulated by the strain engineering

The asymmetric Cu ions migration across the vdW gap under positive and negative biases arises from the asymmetric distribution of Cu ions. Specifically, this involves the local accumulation of Cu ions beneath the tip under positive bias and their depletion under negative bias, as depicted in Fig. 4f. The Cu ions accumulation effectively lowers the contact barrier at the Pt/CIPS side^14,15,36 and further facilitates Cu ions migration over long distance. In contrast, the depletion of Cu increases the contact barrier at the Pt/CIPS side, and thus prevents the Cu ions migration over long distance. Therefore, at large V, long t or multiple N, the asymmetric Cu ions migration leads to the opposite conductive manner in two opposite bias directions. Specifically, this means that the current increases significantly under positive bias and decreases sharply under negative bias.

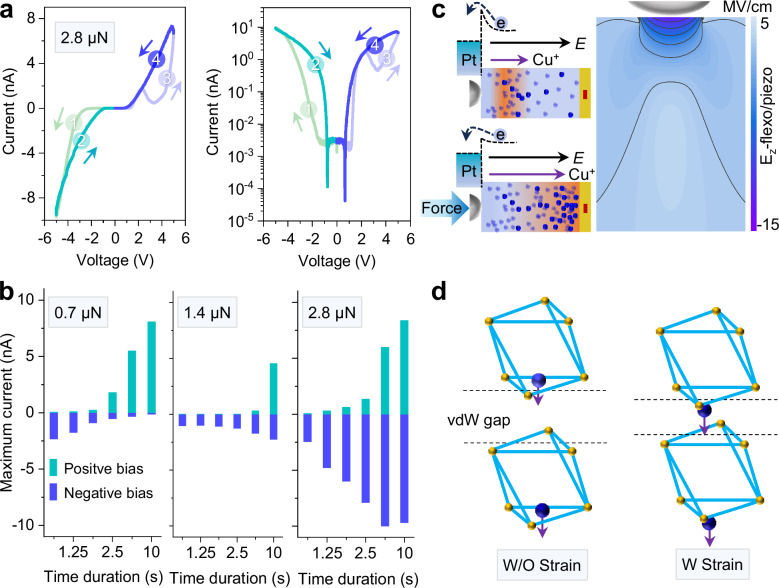
As discussed earlier, the asymmetric Cu ions migration in two opposite bias directions arises from the interfacial contact barrier. Tip force is an effective means of modulating the interfacial barrier through electromechanical coupling effects, including the piezo- and flexo-electric effect due to the non-uniform strain under the tip^34,37–39. Here, the AFM tip acts as the top electrode and strain source. The I–V curves varying time duration are conducted under different tip forces (Supplementary Fig. 15). The linear and semilog I–V curves under ~2.8 µN tip force and a time duration of 10 s are representatively shown in Fig. 5a. It is revealed that the tip force significantly increases the current under negative bias to a level that even exceeds the current under positive bias. This effect is more clearly presented in Fig. 5b and Supplementary Fig. 16. At 0.7 µN, as the time duration extends, the current significantly increases under positive bias and rapidly decreases under negative bias due to the accumulation and depletion of Cu ions beneath the tip. This severe depletion of Cu ions leads to lower currents under negative bias at 1.4 µN compared to the currents at 0.7 µN during short time duration. Increasing the tip force significantly prevents the rapid current decrease under negative bias and instead significantly increases the current as time duration extends. The modulation is driven by two key contributions through the synergistic effects of interfacial and bulk effects mechanisms. On one hand, the interfacial barrier can be reduced under non-uniform strain via piezoelectric and flexoelectric effects. As shown in Fig. 5c, under a force of 2.8 µN, the piezoelectric and flexoelectric effects can generate a net downward-pointing strong electric field of up to the MV/cm level. On the other hand, as shown in Fig. 5d, the vdW gap distance can be reduced and the migration of Cu ions into interlayer sites can be facilitated under strain^22,40. Overall, the tunable Cu ion migration, responsive to varied electric fields and mechanical loads, highlights its significant potential for multi-state memristor applications.

Fig. 5. Deterministic Cu ion transport via strain engineering.

a The linear and semilog I–V curves with ~2.8 µN tip force and a time duration of 10 s. b The maximum current (I_max) under different tip forces and time duration. c The schematic of modulating Cu ions transport via the piezo- and flexo-electric effect. d The schematic of the reduced vdW gap distance and enhanced ionic migration across the vdW gap under the condition without strain (W/O strain) and with strain (W strain).

Discussion

This work investigates the Cu ion dynamics in a quadruple-well state in ferroionic CIPS and the conductive switching mechanisms. It unveils the Cu ions migration dynamics and their interactions with ferroelectric switching, using advanced tip-based SS-PFM and first-principles calculations. It confirms that the intralayer and interlayer migration of Cu ions leads to the formation of a quadruple-well state and determines the conductive mechanisms. The intralayer migration leads to ferroelectric-dominated conduction and interlayer migration triggers a shift to ion migration-controlled conduction. Through precise control of electric field parameters E(V, t, N)—bias voltage (V), time duration (t), and repeated cycles (N)—this work demonstrates an ability to manipulate the transport properties of Cu ions in the quadruple-well state, achieving a controlled transition from ferroelectric to ion migration-dominated conductive mechanism under varying electric field. Finally, this work also demonstrates the significantly modulated Cu ion migration by the application of mechanical strain. The tunable Cu ion migration, responsive to varied electric fields and mechanical loads, highlights its significant potential for multi-state memristor applications.

Methods

Crystal growth and sample preparation

CIPS single crystals were grown by the chemical vapor transport method²⁰. The stoichiometric elemental precursors were encapsulated in a vacuum-sealed quartz tube (vacuum at the level of ~10⁻³ Pa). In two-zone tube furnace, the hot zone was kept at ~650 °C and a cold zone at ~600 °C for a reaction time of ~212 h, respectively. For electrical measurement, the as-grown CIPS crystal was mechanically exfoliated and transferred on Au/SiO₂/Si substrates. In this work, the thickness of CIPS nanoflakes is ~120 nm.

Switching spectroscopy-PFM (SS-PFM)

The variable-temperature PFM measurements were conducted using a commercial atomic force microscope (Asylum Research MFP-3D) equipped with a temperature controller. The ferroelectric domains were imaged by the Pt/Ir-coated Si cantilever tip driven with an ac voltage (V_ac = 2 V) and the drive frequency of ≈350 kHz. The localized hysteresis loops of CIPS were collected using the SS-PFM mode. Pulsed triangular dc driving voltage (V_dc) was used and the dc pulse width was set to 10 ms. A high-frequency ac voltage (V_ac = 2 V) was superimposed on the dc voltage. A hysteresis loop consists of 100 pulses as the time duration is 1 s. To void the ambiguity from the electrostatic force for on-field (dc voltage is on) measurements, we focused on the off-field (remanent) data for our analyses. Multiple cycles of hysteresis loops were collected for each measurement at a specific location.

Conductive atomic force microscopy (c-AFM)

In c-AFM measurement, single point I–V measurements were performed with ORCA module with compliance current of 20 nA. The Pt/Ir-coated Si cantilever tip was used as the top electrode. The voltage was applied to the conducting Au bottom electrode, which was continuously swept to simultaneously read the current. Multiple cycles of I–V measurements were conducted by varying bias voltage magnitude and time duration of each cycle at a specific location.

Piezoelectric and flexoelectric calculation

The strain and strain gradient distributions in CIPS flakes were obtained from theoretical simulations with a tip-force model under a tip force of 2.8 μN⁴¹. The Pt/Ir-coated silicon tip was considered as the rigid sphere, tip radius is 25 nm. The Young’s modulus and Poisson’s ratio of CIPS are 25 GPa and −0.06, respectively. For simplicity, the piezoelectric coefficient d₃₃ was set to be −85 pm/V based on previous literature⁴², and the effective flexoelectric coefficient μ_eff was set to be 1 nC/m, which is close to the reported values of two-dimensional materials⁴³. The piezoelectric and flexoelectric fields were obtained by using the linear piezoelectric equation and the flexoelectric constitutive equation, respectively.

Density functional theory simulation

To investigate the mechanism of electric field regulation, we employed DFT using the Vienna Ab initio Simulation Package^44–46. We examined the Cu ion migration barriers between different atomic layers in CIPS and evaluated the minimum energy path using the nudged elastic band (NEB) method⁴⁷. The effects of various electron exchange–correlation functionals and vdW corrections on the lattice parameters (a, b, c, and β) and lattice volume V are calculated and results are listed in Supplementary Table 1. The Perdew–Burke–Ernzerhof formulation of the generalized gradient approximation⁴⁸ was chosen to describe the exchange–correlation interaction of electrons, and the DFT-D3 (Becke–Johnson) vdW formulation was used to describe vdW interactions between layers. Wave functions were expanded in a plane-wave basis set with an energy cutoff of 680 eV for structural relaxation and 520 eV for electronic structure calculations. The force convergence criterion for each ion was set to less than 10⁻³ eV/Å, and a total energy minimization precision of 10⁻⁶ eV was adopted. In NEB calculations, one Cu ion was removed to accommodate the migrating ion, with the force convergence criterion tightened to less than 0.04 eV/Å. For the unit cell, we used the 8 × 4 × 4 k-mesh in the Monkhorst–Park scheme in reciprocal space to ensure the convergence for the total energy self-consistent calculations. Valence electrons were defined as follows: Cu: 3p⁶3d¹⁰4s¹, In 4d¹⁰5s²5p¹, P 3s²3p³, and S 3s²3p⁴. Crystal structures were visualized using VESTA software⁴⁹.

Author contributions

X.L.W., X.Y.W., and W.Y. conceived the idea and directed the project. X.J. prepared the samples with the help of J.D. X.J. performed the I–V, the PFM measurements, and data analysis. X.Z. performed the analysis of piezo- and flexo-electric field calculation. Z.D. conducted the DFT calculations. X.J., X.Y.W., and W.Y. co-wrote the manuscript. All authors discussed the data and contributed to the manuscript.

Peer review

Peer review information

Nature Communications thanks Wenwu Li and Nikita Ter-Oganessian for their contribution to the peer review of this work. A peer review file is available.

Data availability

The authors declare that all the relevant data within this paper and its Supplementary Information file are available from the corresponding author upon request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-55160-7.