Abstract
A theoretical investigation of spin-orbit coupling effect on magnetotransport of a monolayer graphene system having the geometry of Aharonov–Bohm interferometer is presented. The spin-orbit interaction is considered in the form of Rashba spin-orbit (RSO) coupling. The problem is studied within atomistic tight-binding approximation in combination with non-equilibrium Green’s functions formalism. The influence of RSO coupling on quantum interference effects is investigated within linear response limit in terms of transmission function and magnetoconductance as functions of Fermi energy, RSO coupling, magnetic flux and the number of transmission-modes as well as beyond this limit in terms of current-flow, under finite bias conditions. The Fourier power spectra of corresponding response functions are also obtained. The possibility of an effective control the two-terminal spin resolved resistances of the system and the spin polarization of equilibrium charge current as well as a nonequilibrium net current by means of RSO coupling and magnetic flux through the system, leading to an increase of the functionality of graphene in potential electronic applications, has been demonstrated.
Subject terms: Nanoscience and technology, Graphene, Nanoscale devices
Introduction
Oscillatory phenomena in mesoscopic systems can be regarded to as the hallmark of the quantum world and they are interesting themselves, but also provide a basis for exploring other effects, where electron phase modulation leads to a change in the measurable interference pattern. The AB effect appears in this case as an orthodox example of a oscillatory phenomenon exhibiting quantum interference1–3. In recent time, the AB effect has attracted significant attention in the field of mesoscopic physics in connection with the study, among others, the electron transport in two-dimensional materials. The reason for this is that the observable magnetoconductance oscillations being a result of interference of electron waves are very sensitive to the change in magnetic flux. On the other hand, direct numerical simulation leads to the observation that the effect of a magnetic field on transmission function of a graphene nanoribbon with a regular geometry is very weak, for typical magnetic fields, used in the laboratory. To obtain observable effect on the transport properties of a graphene nanoribbon, it is necessary to use magnetic fields at least of several hundred of teslas. The use of a graphene ring coupled to graphene electrodes changes the situation significantly, because interference effects are involved, which are very sensitive to even small changes in the magnetic field, but not depend on its value. In this way, the importance of the magnetic field as a factor that can influence the transport properties of a graphene, increases and thus increases up the functionality of graphene. As an example of the system, in which tunable breaking of valley degeneracy can be performed by means of magnetic flux, an isolated graphene ring i.e. not connected to external electrodes has been considered4. The rings of circular and hexagonal geometries have been there investigated. The effect of magnetic field, the shot noise power and related quantities for the AB rings and the Corbino disks in graphene, have been studied analytically within continuum model of the graphene5. The Aharonov–Bohm effect and valley polarization in nanoscopic graphene ring were studied in a tight-binding model of graphene6. In this context, a quantum Hall analogue of the Fabry–Pérot interferometer, utilizing the AB effect, has been proposed recently as a tool for detection fractionally charged quasiparticles, known as skyrmions7–10. Interplay of the AB effect and Klein tunneling in graphene has been investigated using a TB model with nearest-neighbor couplings11. Electron transport through the Corbino disk in graphene has been studied in the presence of uniform magnetic fields at the Dirac point within analytical approach12.
Another important area of interest in mesoscopic physics are spin-related effects, including the spin-orbit interaction. Among others, effects induced by RSO coupling in low-dimensional systems are of particular interest due to possibility of controlling the electron dynamics by its spin orientation manipulation13. The intensity of the RSO coupling can be tuned due to built-in electric field induced by inversion asymmetry of the nanostructure or by the gate voltage change. Many investigations have been performed for the RSO induced effects on various properties in different systems14–31.
The purpose of this paper is a theoretical investigation the influence of the spin-orbit interaction in the form of RSO coupling on AB effect in graphene. To this end, coherent transport regime is supposed which requires the electron coherence length to be comparable with the graphene ring size. We note that the AB conductance oscillations in a graphene ring has been observed experimentally at temperatures below 1K and there was estimated that the electron coherence length is comparable or larger than the size of the ring having the inner and outer radii of 350 and 500 nm, respectively32. This fact justifies used in the present paper assumption regarding to the coherent transport regime. The problem is studied within linear response limit where RSO coupling effect on equilibrium transmission and spin dependent characteristics of the system for different types of electrodes edges is determined as well as beyond this limit where the RSO effect and finite temperature effect on current–volatage characteristics of the system under finite bias are investigated.
The model
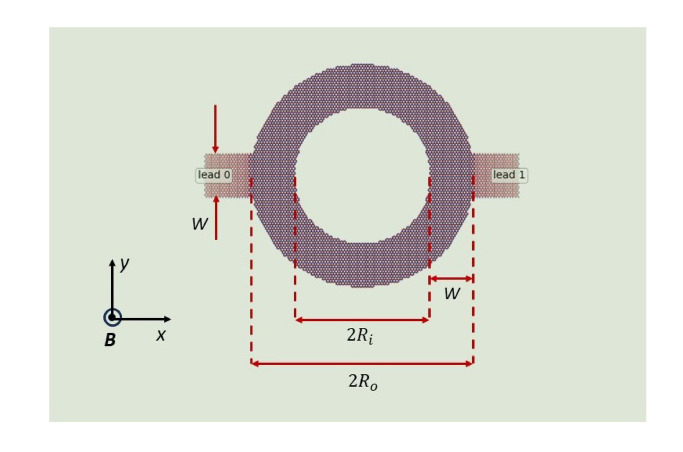
The system under study is sketched in Fig. 1. Although there are many other configurations, defining the AB system we confine ourselves to the cases, in which the width of the central graphene ring, defined as relevant radii difference, is the same as the width of external graphene electrodes, oriented along the zigzag or armchair direction. This configuration is characterized by well defined number of transmission modes related to the electrodes width and does not introduced additional scattering due to eventual contractions in the contact regions. The external magnetic field perpendicular to the plane of the system and the RSO coupling are applied to the central ring as well as to the semi-infinite leads.
Fig. 1.
Sketch of the system under study. The width of the ring and semi-infinite leads denoted as lead0 and lead1 is defined as 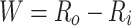 , where
, where 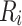 and
and 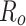 are the inner and outer radii of the ring, respectively. The leads are oriented along zigzag direction in the graphene.
are the inner and outer radii of the ring, respectively. The leads are oriented along zigzag direction in the graphene.
TB Hamiltonian
The Hamiltonian of the system is constructed within a single-orbital TB approximation. The single orbital is the 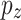 atomic orbital of carbon, that is decoupled from the in-plane
atomic orbital of carbon, that is decoupled from the in-plane 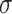 orbitals (formed by s,
orbitals (formed by s, 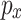 and
and 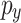 orbitals). Using the first-nearest-neighbors approximation the Hamiltonian including spin-orbit interaction and external magnetic field may be written in the form
orbitals). Using the first-nearest-neighbors approximation the Hamiltonian including spin-orbit interaction and external magnetic field may be written in the form 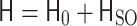 , where
, where
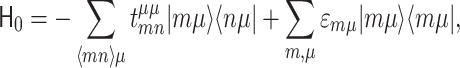 |
1 |
is the single-orbital (including spin), semi-empirical TB Hamiltonian, where 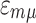 is the on-site energy and
is the on-site energy and 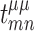 is the transfer (spin–diagonal) hopping energy. Using the restriction of electron hopping only between first-nearest neighbors, the hopping parameters without the magnetic field are supposed to be all equal and reduced to
is the transfer (spin–diagonal) hopping energy. Using the restriction of electron hopping only between first-nearest neighbors, the hopping parameters without the magnetic field are supposed to be all equal and reduced to  eV. In the presence of RSO coupling also spin-off-diagonal hoppings
eV. In the presence of RSO coupling also spin-off-diagonal hoppings 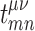 (
(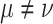 ) are non zero. In the presence of a magnetic field the hopping parameters are modified according to the Peierls substitution, described below. In order to simplify the formulation, on-site energies are conventionally set to zero,
) are non zero. In the presence of a magnetic field the hopping parameters are modified according to the Peierls substitution, described below. In order to simplify the formulation, on-site energies are conventionally set to zero, 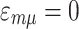 . The Zeeman term is not explicitly included here but it is taken into account in the context of spin resolved characteristics of the system. The Rashba spin-orbit coupling within first-nearest-neighbors approximation is represented by the operator33
. The Zeeman term is not explicitly included here but it is taken into account in the context of spin resolved characteristics of the system. The Rashba spin-orbit coupling within first-nearest-neighbors approximation is represented by the operator33
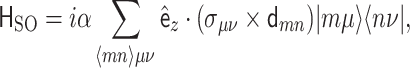 |
2 |
where 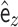 is unit vector pointing in z-direction and
is unit vector pointing in z-direction and 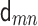 is unit vector pointing from site m to site n. In the above formula,
is unit vector pointing from site m to site n. In the above formula, 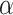 denotes RSO coupling strength (in units of eV) and
denotes RSO coupling strength (in units of eV) and  denotes vector of Pauli matrices. Thus, in order to incorporate RSO coupling into TB Hamiltonian it is sufficient to define spin-dependent hoppings according to
denotes vector of Pauli matrices. Thus, in order to incorporate RSO coupling into TB Hamiltonian it is sufficient to define spin-dependent hoppings according to 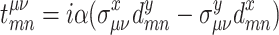 . Note that since Pauli matrices
. Note that since Pauli matrices 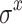 and
and 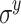 are off-diagonal, hoppings with
are off-diagonal, hoppings with 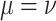 are not modified. The magnetic field is represented by in-plane vector potential, in the Landau gauge
are not modified. The magnetic field is represented by in-plane vector potential, in the Landau gauge 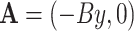 . The interaction with the magnetic field is introduced by Peierls substitution34,
. The interaction with the magnetic field is introduced by Peierls substitution34, 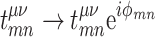 , where phases
, where phases
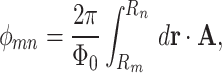 |
3 |
are spin-independent and 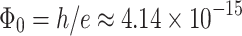 Wb is the flux quantum (FQ). For a graphene lattice, after simple calculations one obtains
Wb is the flux quantum (FQ). For a graphene lattice, after simple calculations one obtains
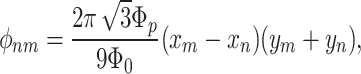 |
4 |
where 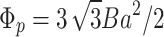 is magnetic flux through the area of benzene ring, where
is magnetic flux through the area of benzene ring, where 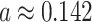 nm is the distance between two neighbor carbon atoms. In the formula (4) numbers (
nm is the distance between two neighbor carbon atoms. In the formula (4) numbers (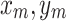 ) indicate lattice points coordinates, given in units of a. The numbers are dimensionless.
) indicate lattice points coordinates, given in units of a. The numbers are dimensionless.
Phase difference quantization
It is convenient for the analysis of phase difference quantization to rewrite the vector potential in polar coordinates,
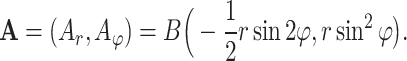 |
5 |
Phase shift along any path 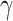 is given by the real number
is given by the real number 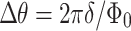 , where
, where
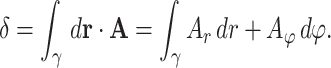 |
6 |
For closed path one obtains, 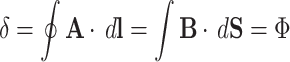 , where
, where 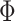 is the magnetic flux piercing the surface limited by the closed path
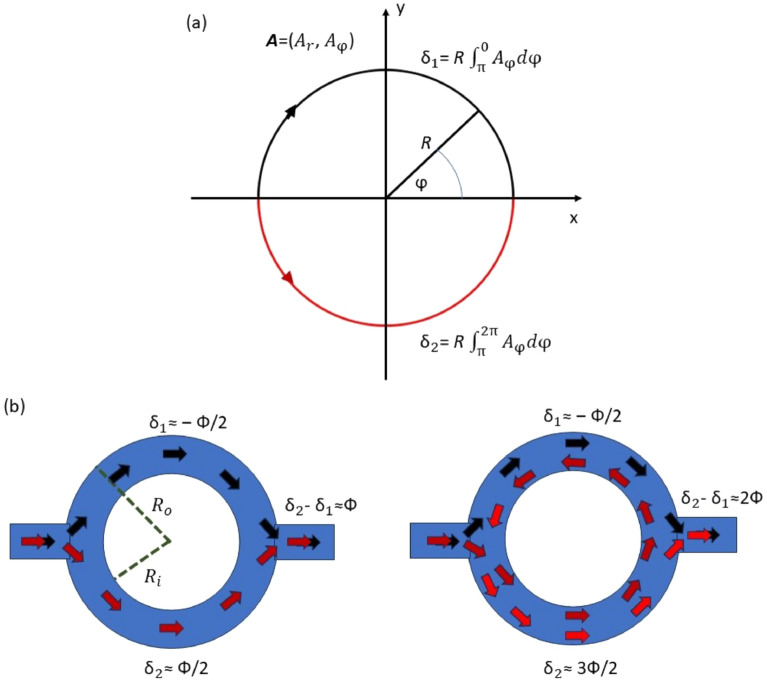
is the magnetic flux piercing the surface limited by the closed path 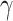 . For a strictly one-dimensional circular ring, with the radius R (see Fig. 2a) we obtain, for the upper arm
. For a strictly one-dimensional circular ring, with the radius R (see Fig. 2a) we obtain, for the upper arm 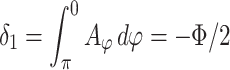 and for the lower arm
and for the lower arm 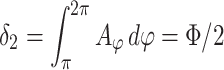 , where
, where 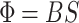 with
with 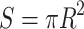 . This gives the phase difference for conjugated trajectories summing to a one full cycle,
. This gives the phase difference for conjugated trajectories summing to a one full cycle, 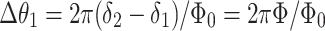 . In general, for conjugated trajectories summing to N full cycles, one obtains, the quantization condition for the phase difference,
. In general, for conjugated trajectories summing to N full cycles, one obtains, the quantization condition for the phase difference, 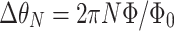 . When this phase difference happen for some magnetic field, for which
. When this phase difference happen for some magnetic field, for which 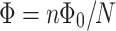 , then
, then 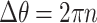 . This means that any characteristic of the system, reflecting interference effects induced by magnetic flux change, such as transmission or conductance being a function of
. This means that any characteristic of the system, reflecting interference effects induced by magnetic flux change, such as transmission or conductance being a function of 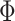 , should include superpositions of sinusoidal signals, having periods
, should include superpositions of sinusoidal signals, having periods 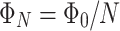 or equivalently, having characteristic frequencies
or equivalently, having characteristic frequencies
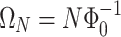 . Note that for extremely thin ring the frequency
. Note that for extremely thin ring the frequency 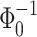 is dominant or equivalently the period of oscillations is
is dominant or equivalently the period of oscillations is 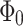 . In the other words, for a very thin ring the higher number of cycles performed by trajectories propagating along two arms of the interferometer is less probably due to high probability of the interference after one cycle. For the ring having a finite width (see Fig. 2b) the phase difference quantization condition remains valid in an average sense. In this case however higher harmonics in the Fourier power spectra are also expected. For an arbitrary (non-intersecting) trajectory
. In the other words, for a very thin ring the higher number of cycles performed by trajectories propagating along two arms of the interferometer is less probably due to high probability of the interference after one cycle. For the ring having a finite width (see Fig. 2b) the phase difference quantization condition remains valid in an average sense. In this case however higher harmonics in the Fourier power spectra are also expected. For an arbitrary (non-intersecting) trajectory 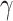 , laying in the region between
, laying in the region between 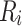 and
and  , we have
, we have 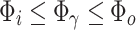 , where in the case of uniform magnetic field,
, where in the case of uniform magnetic field, 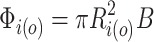 . For any
. For any 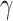 we can find such
we can find such 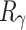 , between
, between 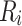 and
and 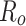 , giving
, giving 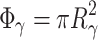 . For N full cycles performed by closed trajectories
. For N full cycles performed by closed trajectories 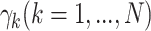 we can write
we can write 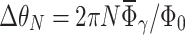 , where
, where 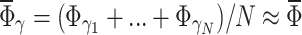 , where
, where 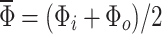 . Numerical calculations presented in this paper show that this approximation works very well, giving peaks in Fourier transform of conductance as function of
. Numerical calculations presented in this paper show that this approximation works very well, giving peaks in Fourier transform of conductance as function of 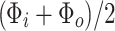 exactly at positions
exactly at positions 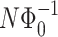 . This means that
. This means that 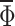 accurately represents the effective flux through the finite width ring. In further part of the work, the average value
accurately represents the effective flux through the finite width ring. In further part of the work, the average value 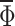 is simply denoted by
is simply denoted by 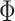 . Other trajectories, not summing to full cycles, lead to broadening of peaks appearing in the Fourier power spectrum.
. Other trajectories, not summing to full cycles, lead to broadening of peaks appearing in the Fourier power spectrum.
Fig. 2.
Phase difference quantization diagrams: (a) splitted electron waves along two arms of one-dimensional AB interferometer and phase shifts for conjugated trajectories summing to a one full cycle; (b) splitted electron waves along AB interferometer with finite width and phase shifts for conjugated trajectories summing to a one- and two full cycles, respectively.
Transport formalism
The quantum transport properties of the system with geometry presented in Fig. 1 are investigated using atomistic TB model coupled to the NEGF technique35,36. As we can see in Fig. 1, the entire system is divided into three parts: semi-infinite left lead, the central region (device) having the geometry of graphene ring and semi-infinite right lead. The leads are taken in the form of zigzag graphene nanoribbons of the width equal to the width of the central ring. We note that transport properties of the system are mainly determined by number of transmission modes which in turn are dependent on the size W, but not on particular values of 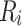 and
and 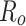 . The magnetic field and the RSO coupling are applied to whole the system. The leads are supposed to be strictly periodic structures, with respect to the transport direction. The Hamiltonian matrix of the entire system can be written in the block form
. The magnetic field and the RSO coupling are applied to whole the system. The leads are supposed to be strictly periodic structures, with respect to the transport direction. The Hamiltonian matrix of the entire system can be written in the block form
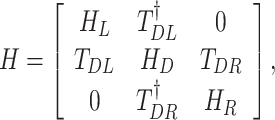 |
7 |
where 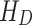 and
and 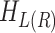 denote the Hamiltonian matrix of the device and left (right) lead, respectively. The matrix
denote the Hamiltonian matrix of the device and left (right) lead, respectively. The matrix 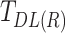 is the hopping matrix responsible for the coupling between the device and the left (right) lead. All the matrices are given in TB representation. The electron transmission function at energy E within the NEGF formalism is given by36
is the hopping matrix responsible for the coupling between the device and the left (right) lead. All the matrices are given in TB representation. The electron transmission function at energy E within the NEGF formalism is given by36
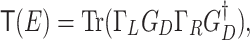 |
8 |
where 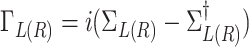 is the broadening matrix and
is the broadening matrix and 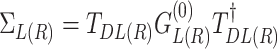 denotes self-energy matrix, describing the effect of coupling to the left (right) lead. The matrix
denotes self-energy matrix, describing the effect of coupling to the left (right) lead. The matrix 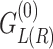 represents the Green’s function of an isolated left (right) lead. The matrix
represents the Green’s function of an isolated left (right) lead. The matrix 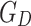 is the Green’s function of the device including the coupling to semi-infinite leads
is the Green’s function of the device including the coupling to semi-infinite leads
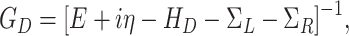 |
9 |
where an infinitesimal positive number 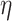 is introduced to incorporate appropriate boundary conditions for retarded Green’s function36. The Green’s functions of the device region and semi-infinite leads were calculated numerically, using recursive techniques presented in37. We note that equilibrium conductance is directly obtained from the transmission function as
is introduced to incorporate appropriate boundary conditions for retarded Green’s function36. The Green’s functions of the device region and semi-infinite leads were calculated numerically, using recursive techniques presented in37. We note that equilibrium conductance is directly obtained from the transmission function as 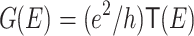 . In further part of the work the Fermi energy in most cases is fixed. Thus, we will write explicitly only the dependence on RSO coupling and the magnetic field.
. In further part of the work the Fermi energy in most cases is fixed. Thus, we will write explicitly only the dependence on RSO coupling and the magnetic field.
Results and discussion
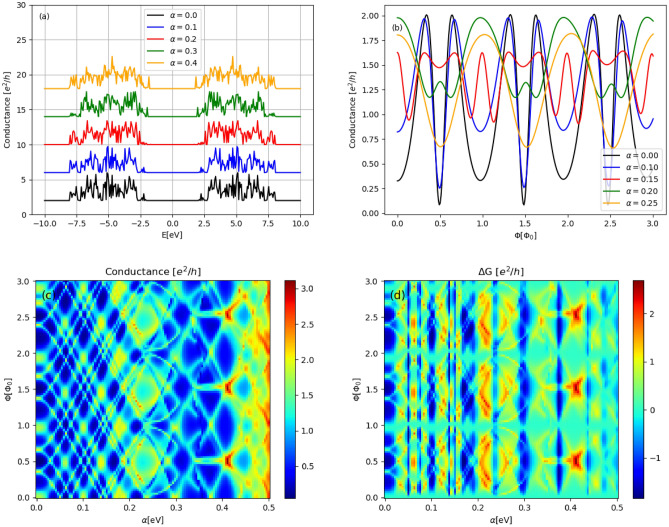
We start our analysis from the discussion of some general transport properties of the AB interferometer, based on a graphene ring. First, it is necessary to find the energy range in which the comparison of energy-dependent quantities for the system under different external conditions, is possible. We should therefore estimate whether the considered energy range giving nonzero transmission function does not change significantly when changing the model parameters. Figure 3a shows conductance as a function of Fermi energy, in field-free limit. The central graphene ring (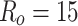 nm) and semi-infinite zigzag-edge graphene leads are taken with the width
nm) and semi-infinite zigzag-edge graphene leads are taken with the width 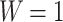 nm, which gives
nm, which gives 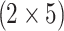 transmission modes (including spin). The energy range corresponding to nonzero conductance of the system is related to the subbands structure of isolated leads. As we can see this range is stable versus the RSO coupling variation. The presence of energy gap in the transmission spectrum is due to nonuniform geometry of the entire system and disappears for a single semi-infinite zigzag-shaped graphene nanoribbon. Nonuniform geometry enhances scattering processes, leading to strong oscillations of conductance in function of energy. For the uniform graphene nanoribbon well known regular step-like behavior of conductance spectrum can be observed. Figure 3b shows the conductance as a function of effective magnetic flux through the central ring, for several RSO coupling constants. We can see that almost perfect periodicity of conductance oscillations is observed, with the fundamental period
transmission modes (including spin). The energy range corresponding to nonzero conductance of the system is related to the subbands structure of isolated leads. As we can see this range is stable versus the RSO coupling variation. The presence of energy gap in the transmission spectrum is due to nonuniform geometry of the entire system and disappears for a single semi-infinite zigzag-shaped graphene nanoribbon. Nonuniform geometry enhances scattering processes, leading to strong oscillations of conductance in function of energy. For the uniform graphene nanoribbon well known regular step-like behavior of conductance spectrum can be observed. Figure 3b shows the conductance as a function of effective magnetic flux through the central ring, for several RSO coupling constants. We can see that almost perfect periodicity of conductance oscillations is observed, with the fundamental period 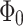 . Particularly interesting is that the period does not depend on RSO coupling. We can see that RSO coupling leads to damping of the amplitude of the conductance oscillations, but it may lead to increase or decrease of an average value of the conductance. In general, the dependence
. Particularly interesting is that the period does not depend on RSO coupling. We can see that RSO coupling leads to damping of the amplitude of the conductance oscillations, but it may lead to increase or decrease of an average value of the conductance. In general, the dependence 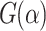 is strongly nonmonotonic and discloses nonperiodic oscillations. This is well demonstrated in Fig. 3c, in which the density map of G as function of
is strongly nonmonotonic and discloses nonperiodic oscillations. This is well demonstrated in Fig. 3c, in which the density map of G as function of 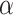 and
and 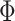 is given. We see that along the
is given. We see that along the 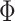 -axis the conductance oscillates approximately with the period
-axis the conductance oscillates approximately with the period 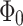 while along the
while along the 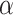 -axis oscillations are nonperiodic. There are islands in the map characterized by high conductance surrounded by regions with low conductance. One should be noted, that for
-axis oscillations are nonperiodic. There are islands in the map characterized by high conductance surrounded by regions with low conductance. One should be noted, that for 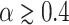 the amplification of G is observed, for a half-integer multiple of
the amplification of G is observed, for a half-integer multiple of 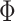 (in units of
(in units of 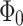 ). Figure 3d presents the density map for magnetoconductance, defined as the difference
). Figure 3d presents the density map for magnetoconductance, defined as the difference 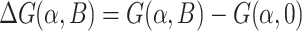 . We can see that RSO coupling generates well defined regions localized between subsequent
. We can see that RSO coupling generates well defined regions localized between subsequent 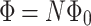 , corresponding to positive or negative magnetoconductance, depending on
, corresponding to positive or negative magnetoconductance, depending on 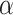 -value. For
-value. For 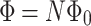 , there are regions in the map with
, there are regions in the map with 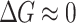 for arbitrary RSO coupling.
for arbitrary RSO coupling.
Fig. 3.
Results for AB system with (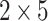 )-transmission modes: (a) conductance spectra for several values of RSO coupling (in units of eV) and
)-transmission modes: (a) conductance spectra for several values of RSO coupling (in units of eV) and 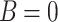 (to distinguish the curves artificial shifts are added; in fact, the flat parts in every curve correspond to vanishing conductance); (b) conductance oscillations in function of effective magnetic flux through the central ring, with Fermi energy
(to distinguish the curves artificial shifts are added; in fact, the flat parts in every curve correspond to vanishing conductance); (b) conductance oscillations in function of effective magnetic flux through the central ring, with Fermi energy 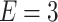 eV; (c) color map of conductance as a function of magnetic flux and RSO coupling for
eV; (c) color map of conductance as a function of magnetic flux and RSO coupling for 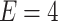 eV; (d) color map of magnetoconductance as a function of magnetic flux and RSO coupling for
eV; (d) color map of magnetoconductance as a function of magnetic flux and RSO coupling for 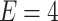 eV.
eV.
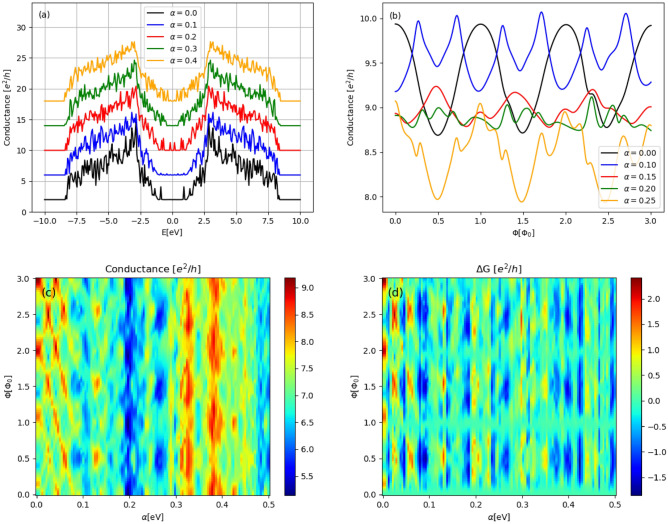
In Fig. 4a are plotted conductance spectra of field-free system having 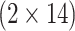 transmission modes, corresponding to the characteristic width
transmission modes, corresponding to the characteristic width 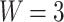 nm (
nm (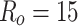 nm) of the zigzag-edge electrodes. In comparison to the narrow ring discussed above, the system with
nm) of the zigzag-edge electrodes. In comparison to the narrow ring discussed above, the system with 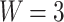 nm is characterized by approximately three-times higher conductance. In this case, the central transmission gap becomes closed due to the presence of peaks induced by RSO coupling. One can also be observed that the magnetic field does not change the energy range corresponding to the non-zero-transmission of the system. This allows for consideration the continuous evolution of the system with increasing magnetic field at Fermi level fixed on the value corresponding to the nonvanishing conductance in field-free limit. Figure 4b shows the conductance for
nm is characterized by approximately three-times higher conductance. In this case, the central transmission gap becomes closed due to the presence of peaks induced by RSO coupling. One can also be observed that the magnetic field does not change the energy range corresponding to the non-zero-transmission of the system. This allows for consideration the continuous evolution of the system with increasing magnetic field at Fermi level fixed on the value corresponding to the nonvanishing conductance in field-free limit. Figure 4b shows the conductance for 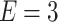 eV as a function of the effective magnetic flux, for several strengths of RSO coupling. We can see that increasing transverse size of the system leads to increase of conductance with approximately the same oscillation amplitudes, as in a case of narrow ring. Almost perfect periodicity in conductance oscillations is also observed. One should be noted here that the RSO coupling gives amplification (
eV as a function of the effective magnetic flux, for several strengths of RSO coupling. We can see that increasing transverse size of the system leads to increase of conductance with approximately the same oscillation amplitudes, as in a case of narrow ring. Almost perfect periodicity in conductance oscillations is also observed. One should be noted here that the RSO coupling gives amplification (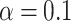 ) or damping (
) or damping (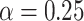 ) of the conductance, relatively to the system without spin-orbit interaction. Continuous distributions of G and
) of the conductance, relatively to the system without spin-orbit interaction. Continuous distributions of G and 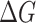 in a (
in a (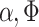 )-plane are presented in Fig. 4c and d, respectively. The Fermi level is fixed at
)-plane are presented in Fig. 4c and d, respectively. The Fermi level is fixed at 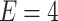 eV. As we can see in Fig. 4c, the RSO coupling significantly changes the amplitude of G-oscillations giving regions with large (
eV. As we can see in Fig. 4c, the RSO coupling significantly changes the amplitude of G-oscillations giving regions with large (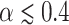 ) and low amplitudes (
) and low amplitudes (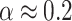 ). The influence of magnetic field on conductance in terms of
). The influence of magnetic field on conductance in terms of 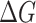 is demonstrated in Fig. 4d. We can see that similarly to a few-mode AB interferometer, the RSO coupling introduces irregular oscillations in magnetoconductance. In particular, it is possible to set the difference
is demonstrated in Fig. 4d. We can see that similarly to a few-mode AB interferometer, the RSO coupling introduces irregular oscillations in magnetoconductance. In particular, it is possible to set the difference 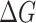 to be positive, negative or zero by proper choice of
to be positive, negative or zero by proper choice of 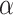 .
.
Fig. 4.
Results for AB system with (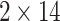 )-transmission modes: (a) conductance spectra for several values of RSO coupling (in units of eV) and
)-transmission modes: (a) conductance spectra for several values of RSO coupling (in units of eV) and 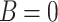 (to distinguish the curves artificial shifts are added; in fact, the flat parts in every curve correspond to vanishing conductance); (b) conductance oscillations in function of effective magnetic flux through the central ring, with Fermi energy
(to distinguish the curves artificial shifts are added; in fact, the flat parts in every curve correspond to vanishing conductance); (b) conductance oscillations in function of effective magnetic flux through the central ring, with Fermi energy 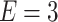 eV; (c) color map of conductance as a function of magnetic flux and RSO coupling for
eV; (c) color map of conductance as a function of magnetic flux and RSO coupling for 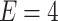 eV; (d) color map of magnetoconductance as a function of magnetic flux and RSO coupling for
eV; (d) color map of magnetoconductance as a function of magnetic flux and RSO coupling for 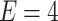 eV.
eV.
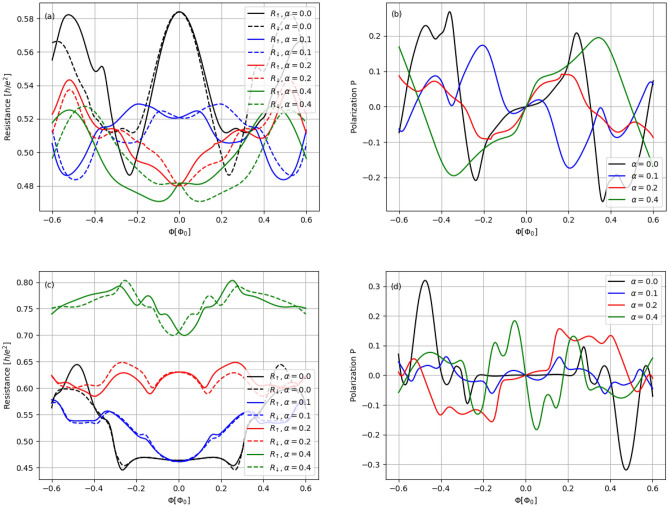
Figure 5 presents spin resolved equilibrium characteristics of the AB systems with graphene nanoribbon electrodes having different types of edges. In Fig. 5a are shown low-bias spin resolved resistances 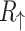 and
and 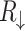 as functions of magnetic flux through the system with zigzag shaped electrodes (
as functions of magnetic flux through the system with zigzag shaped electrodes (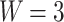 nm). In the linear response approximation, the spin resolved resistances can be defined as
nm). In the linear response approximation, the spin resolved resistances can be defined as 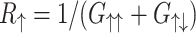 and
and 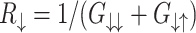 , where spin resolved conductances
, where spin resolved conductances 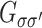 are proportional to the spin resolved transmission function, given by
are proportional to the spin resolved transmission function, given by 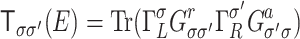 , where
, where 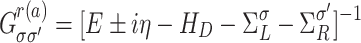 is retarded (advanced) Green’s function of the device and coupling matrices
is retarded (advanced) Green’s function of the device and coupling matrices 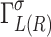 are defined as non-hermitian parts of corresponding spin-diagonal self-energies33,38,39. The spin resolved transmission gives the probability that an electron with energy E and spin
are defined as non-hermitian parts of corresponding spin-diagonal self-energies33,38,39. The spin resolved transmission gives the probability that an electron with energy E and spin 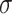 in the left lead reaches right lead with spin
in the left lead reaches right lead with spin 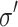 . One can be observed that
. One can be observed that 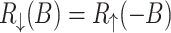 , which gives
, which gives  , for
, for 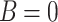 . These properties are a consequence of Kramer’s degeneracy theory, which states that for a time-reversal symmetric system with half-integer spin, for every energy eigenstate, the time reversed state has the same energy. Since time reversal reverses spins, by reversing spins for
. These properties are a consequence of Kramer’s degeneracy theory, which states that for a time-reversal symmetric system with half-integer spin, for every energy eigenstate, the time reversed state has the same energy. Since time reversal reverses spins, by reversing spins for 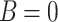 we obtain the same system and
we obtain the same system and  . On the other hands, if
. On the other hands, if 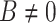 the time reversal symmetry is broken and
the time reversal symmetry is broken and 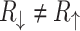 . Since states with opposite spins are related by time inversion and a magnetic field change the sign under time reversal (when it is consider as a part of the system) we expect the symmetry
. Since states with opposite spins are related by time inversion and a magnetic field change the sign under time reversal (when it is consider as a part of the system) we expect the symmetry 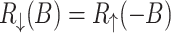 , which is really observed. We can see that the difference between both spin components of the system resistance strongly depends on the RSO coupling. The presence of the difference
, which is really observed. We can see that the difference between both spin components of the system resistance strongly depends on the RSO coupling. The presence of the difference 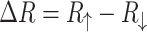 determines the difference in charge currents
determines the difference in charge currents 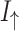 and
and 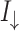 , defined by
, defined by 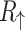 and
and 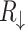 , respectively. This means that initially unpolarized charge current flowing from left to right contact becomes partially spin polarized in the right contact. In the low-bias limit, the currents are proportional to the source-drain voltage
, respectively. This means that initially unpolarized charge current flowing from left to right contact becomes partially spin polarized in the right contact. In the low-bias limit, the currents are proportional to the source-drain voltage 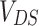 ,
, 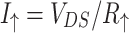 and
and 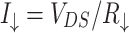 . Thus, the spin polarization of the charge current may be defined as
. Thus, the spin polarization of the charge current may be defined as 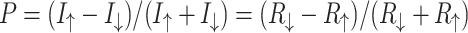 . Note that this definition directly follows from the definition of spin polarization of the conductance33. Figure 5b shows the effect of spin polarization of the charge current, modulated by AB interference effects, for several values of RSO couplings. We can see that for low magnetic fields (important for experimental investigations) a significant amplification of spin polarization (with respect to the z-direction) is generated by increasing RSO coupling and the polarization reaches the value of about
. Note that this definition directly follows from the definition of spin polarization of the conductance33. Figure 5b shows the effect of spin polarization of the charge current, modulated by AB interference effects, for several values of RSO couplings. We can see that for low magnetic fields (important for experimental investigations) a significant amplification of spin polarization (with respect to the z-direction) is generated by increasing RSO coupling and the polarization reaches the value of about 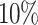 , for
, for 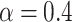 . In Fig. 5c are shown low-bias spin resolved resistances
. In Fig. 5c are shown low-bias spin resolved resistances 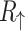 and
and 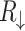 as functions of magnetic flux through the system with armchair shaped electrodes. We can observe that contrary to the zigzag case, the system resistances increase with increasing
as functions of magnetic flux through the system with armchair shaped electrodes. We can observe that contrary to the zigzag case, the system resistances increase with increasing 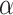 , for a weak magnetic field. Figure 5d presents the effect of spin polarization of the charge current for increasing RSO couplings. We can see that the polarization increases rapidly for
, for a weak magnetic field. Figure 5d presents the effect of spin polarization of the charge current for increasing RSO couplings. We can see that the polarization increases rapidly for 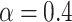 and reaches the value of about
and reaches the value of about 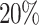 in the weak magnetic field limit.
in the weak magnetic field limit.
Fig. 5.
Equilibrium spin-dependent characteristics of the system (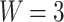 nm) as functions of magnetic flux for equilibrium electrochemical potential
nm) as functions of magnetic flux for equilibrium electrochemical potential 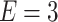 eV and for several
eV and for several 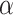 -values: (a) and (c) spin-resolved resistances
-values: (a) and (c) spin-resolved resistances 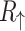 (solid) and
(solid) and 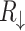 (dashed) for zigzag- and armchair shaped graphene electrodes, respectively; (b) and (d) spin polarization of source to drain charge current
(dashed) for zigzag- and armchair shaped graphene electrodes, respectively; (b) and (d) spin polarization of source to drain charge current 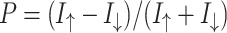 for zigzag- and armchair shaped graphene electrodes, respectively.
for zigzag- and armchair shaped graphene electrodes, respectively.
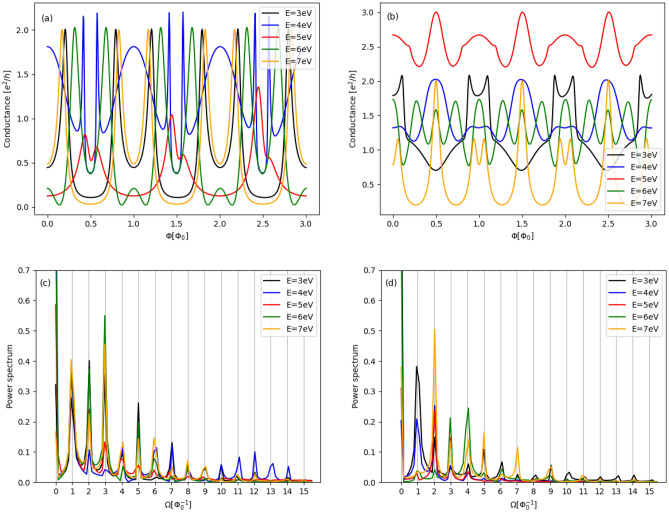
Figure 6a,b show conductance of AB system with 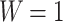 nm and zigzag-edge graphene electrodes as a function of average magnetic flux
nm and zigzag-edge graphene electrodes as a function of average magnetic flux 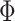 , for
, for 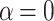 and
and 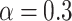 , respectively. The conductances are plotted for several values of Fermi energy. Corresponding Fourier power spectra (absolute values) are given in Fig. 6c,d. One can see that
, respectively. The conductances are plotted for several values of Fermi energy. Corresponding Fourier power spectra (absolute values) are given in Fig. 6c,d. One can see that 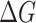 -curves significantly differs in the shape and amplitude depending on E and
-curves significantly differs in the shape and amplitude depending on E and 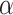 , but they disclose the same periodicity in function of
, but they disclose the same periodicity in function of 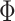 . This periodicity property is reflected in the Fourier power spectra, calculated using DFT method40. We can also see that the peaks in the Fourier spectrum are located perfectly at frequencies
. This periodicity property is reflected in the Fourier power spectra, calculated using DFT method40. We can also see that the peaks in the Fourier spectrum are located perfectly at frequencies
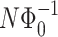 , which is in agreement with the semi-qualitative discussion given in previous section. In other words, the existence of peaks in Fourier power spectrum is the evidence of the fact that the conductance (signal) treated as function of
, which is in agreement with the semi-qualitative discussion given in previous section. In other words, the existence of peaks in Fourier power spectrum is the evidence of the fact that the conductance (signal) treated as function of 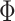 (time domain) is composed mainly from waves with discrete values of
(time domain) is composed mainly from waves with discrete values of 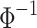 (frequency domain). In turn, this is a consequence of phases difference quantization induced by AB effect and it is expected for any ring system in a magnetic field on the ground of semiclassical trajectories consideration, discussed in the section “The model”. The amplitudes between peaks are small but non-zero, which means that not only trajectories with well-defined quantized phases difference contribute to the transport but also other ones with arbitrary phases. Therefore, periodicity of conductance should also be expected for the net current, as a function of the magnetic flux through the system. The net current for the two-terminal device is defined by the integral of transmission function over the transport window, defined by bias voltage35
(frequency domain). In turn, this is a consequence of phases difference quantization induced by AB effect and it is expected for any ring system in a magnetic field on the ground of semiclassical trajectories consideration, discussed in the section “The model”. The amplitudes between peaks are small but non-zero, which means that not only trajectories with well-defined quantized phases difference contribute to the transport but also other ones with arbitrary phases. Therefore, periodicity of conductance should also be expected for the net current, as a function of the magnetic flux through the system. The net current for the two-terminal device is defined by the integral of transmission function over the transport window, defined by bias voltage35
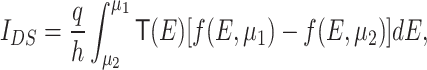 |
10 |
where 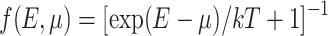 is Fermi distribution function and q is absolute value of the electron charge. Supposing symmetric bias
is Fermi distribution function and q is absolute value of the electron charge. Supposing symmetric bias 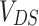 , the electrochemical potentials of the leads are taken as
, the electrochemical potentials of the leads are taken as 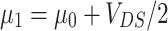 and
and 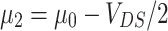 , respectively. Here kT denotes thermal energy, that is supposed to be close to zero.
, respectively. Here kT denotes thermal energy, that is supposed to be close to zero.
Fig. 6.
Conductance as a function of magnetic flux for several Fermi energies and corresponding Fourier spectra for AB systems: (a) and (c) with 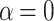 ; (b) and (d) with
; (b) and (d) with  eV. The number of transmission modes is (
eV. The number of transmission modes is (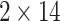 ).
).
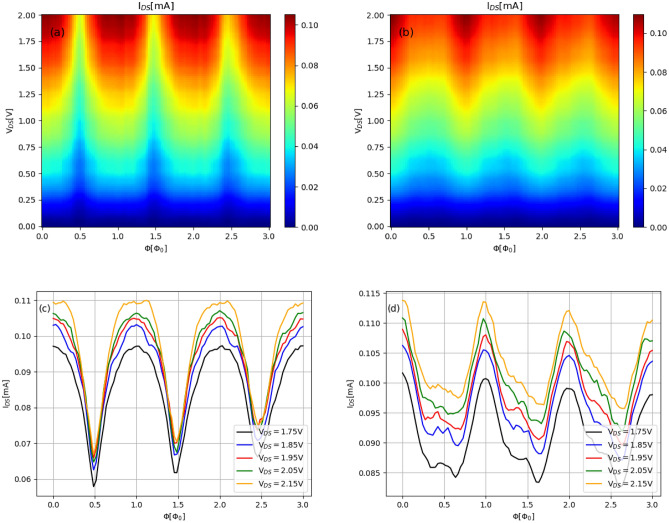
Figure 7a,b show the maps of the net current calculated using Eq. (10) for the two-terminal device with the ring geometry and zigzag-edge electrodes, for 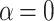 and
and 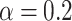 respectively. As expected, with increasing bias, the current increases. Particularly important is that the current discloses periodicity in the
respectively. As expected, with increasing bias, the current increases. Particularly important is that the current discloses periodicity in the 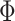 -direction. We can see that maxima of
-direction. We can see that maxima of 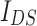 are localized around integer multiples of
are localized around integer multiples of 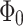 . On the other hand, the minima are localized around half-integer multiples of
. On the other hand, the minima are localized around half-integer multiples of 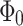 . As can be seen in Fig. 7b, the maxima become more localized for non-zero
. As can be seen in Fig. 7b, the maxima become more localized for non-zero 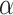 . The voltage-resolved currents as functions of
. The voltage-resolved currents as functions of 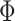 are shown in Fig. 7c,d, for
are shown in Fig. 7c,d, for 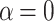 and
and 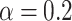 , respectively. We see that broadened maxima corresponding to the system without spin-orbit interactions become more sharp if RSO coupling is present. This property is of particular interest from the point of view of potential application of the system as a sensor of magnetic field intensity. The presence of well defined distances between successive maxima allows for an accurate determination of the change in magnetic flux corresponding to one FQ. Importantly, this can be done by current–voltage measurement.
, respectively. We see that broadened maxima corresponding to the system without spin-orbit interactions become more sharp if RSO coupling is present. This property is of particular interest from the point of view of potential application of the system as a sensor of magnetic field intensity. The presence of well defined distances between successive maxima allows for an accurate determination of the change in magnetic flux corresponding to one FQ. Importantly, this can be done by current–voltage measurement.
Fig. 7.
Color maps of the net current as a function of magnetic flux and bias voltage and corresponding voltage-resolved currents: (a) and (c) with 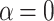 ; (b) and (d) with
; (b) and (d) with 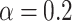 eV. The number of transmission modes is (
eV. The number of transmission modes is (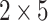 ), the equilibrium electrochemical potential
), the equilibrium electrochemical potential 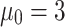 eV.
eV.
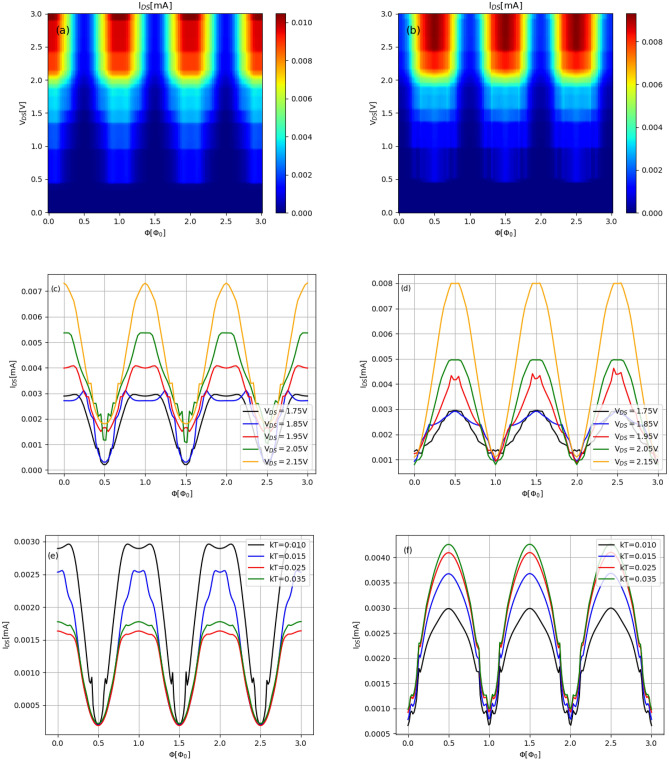
Figure 8a,b show the maps of the net current for extremely thin ring (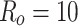 nm,
nm, 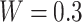 nm) with (
nm) with (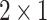 )-transmission modes. The maps correspond to
)-transmission modes. The maps correspond to 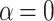 and
and 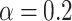 , respectively. The effect of the spin-orbit interaction manifests itself in this case as a shift of the current maxima centred at integer multiple of the FQ to positions corresponding to the half-integer multiple of the FQ. Figure 8c,d give the voltage-resolved currents for the cases
, respectively. The effect of the spin-orbit interaction manifests itself in this case as a shift of the current maxima centred at integer multiple of the FQ to positions corresponding to the half-integer multiple of the FQ. Figure 8c,d give the voltage-resolved currents for the cases 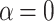 and
and 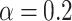 , respectively. We can see that in the case of quasi-one-dimensional system the local minima of
, respectively. We can see that in the case of quasi-one-dimensional system the local minima of 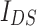 are perfectly localized while local maxima become well localized when the bias voltages increase. One should be noted that for
are perfectly localized while local maxima become well localized when the bias voltages increase. One should be noted that for 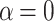 and
and 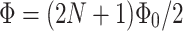 , the voltage-resolved currents take minima but for
, the voltage-resolved currents take minima but for 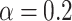 they take local maxima, according to the previous observation. For
they take local maxima, according to the previous observation. For 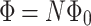 the situation is reversed. In the other words, the resistance of the system is strongly correlated with RSO coupling due to presence of interference effects induced by magnetic field. One should be added here that minimum values of
the situation is reversed. In the other words, the resistance of the system is strongly correlated with RSO coupling due to presence of interference effects induced by magnetic field. One should be added here that minimum values of 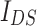 in the case of nonzero RSO coupling corresponding to
in the case of nonzero RSO coupling corresponding to 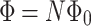 are only weakly dependent on bias voltage. On the other hand, in the system without spin-orbit interaction the minima of the currents at
are only weakly dependent on bias voltage. On the other hand, in the system without spin-orbit interaction the minima of the currents at 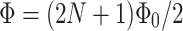 significantly increase with increasing
significantly increase with increasing 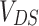 . We can also observe that by changing magnetic flux from
. We can also observe that by changing magnetic flux from 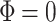 to
to 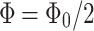 , the resistance of the system with
, the resistance of the system with 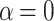 increases while for the system with
increases while for the system with 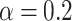 decreases. This indicates that the spin-orbit correlation significantly affects the electronic properties of the AB system. The correlation may be detected by the charge-current experimental measurements. We considered the system in a coherent transport regime, which means that effects of inelastic scattering have been neglected. This approximation is in accordance with experimental situation until the temperature is close to zero. At higher temperatures the effects of electron scattering on phonons increase and to model transport properties of the system, taking into account these effects within NEGF formalism, it is necessary to include into the device Green’s function an additional self-energy term, responsible for inelastic scattering. However, in the low-temperatures limit we can estimate the influence of the temperature effect on transport properties of the system utilizing only temperature dependence of the Fermi distribution function. Figure 8e,f present temperature effect on
decreases. This indicates that the spin-orbit correlation significantly affects the electronic properties of the AB system. The correlation may be detected by the charge-current experimental measurements. We considered the system in a coherent transport regime, which means that effects of inelastic scattering have been neglected. This approximation is in accordance with experimental situation until the temperature is close to zero. At higher temperatures the effects of electron scattering on phonons increase and to model transport properties of the system, taking into account these effects within NEGF formalism, it is necessary to include into the device Green’s function an additional self-energy term, responsible for inelastic scattering. However, in the low-temperatures limit we can estimate the influence of the temperature effect on transport properties of the system utilizing only temperature dependence of the Fermi distribution function. Figure 8e,f present temperature effect on 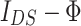 characteristic at fixed bias
characteristic at fixed bias 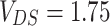 V, for
V, for 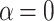 and
and 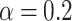 , respectively. We can see that in general the temperature effects modify the maxima of the net current, without significant change the shape of the characteristic. In particular, for
, respectively. We can see that in general the temperature effects modify the maxima of the net current, without significant change the shape of the characteristic. In particular, for 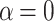 we can observe non-monotonic decrease of
we can observe non-monotonic decrease of 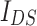 with increasing temperatures, while for
with increasing temperatures, while for 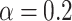 ,
, 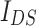 discloses at maxima an monotonic increase for increasing kT.
discloses at maxima an monotonic increase for increasing kT.
Fig. 8.
Color maps of the net current as a function of magnetic flux and bias voltage and corresponding voltage-resolved currents: (a) and (c) with 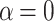 ; (b) and (d) with
; (b) and (d) with 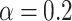 eV; (e) temperature dependence of the net current for
eV; (e) temperature dependence of the net current for 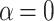 and
and 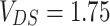 V; (f) temperature dependence of the net current for
V; (f) temperature dependence of the net current for 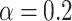 eV and
eV and 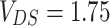 V. The number of transmission modes is (
V. The number of transmission modes is (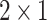 ), the equilibrium electrochemical potential
), the equilibrium electrochemical potential 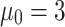 eV.
eV.
Summary
We have shown that the Rashba spin-orbit coupling significantly modifies coherent transport properties of the graphene system of Aharonov–Bohm interferometer geometry. The problem has been investigated theoretically in combination with numerical simulation of the quantum transport based on a single-orbital atomistic TB approximation and NEGF method. The influence of RSO coupling on the amplitude and the range of conductance oscillations for various system geometries, manifested by a different number of transmission modes, was demonstrated. Results for different sets of characteristic model parameters were presented. One of the main results obtained is the observation that the equilibrium resistance of the system becomes spin-dependent when the magnetic field is applied. The interplaying of the AB geometry and RSO coupling yields a significant difference between spin-resolved resistances which leads to spin polarization of the initially unpolarized charge current. In the low-magnetic fields limit, important from the point of view of experimental investigations, the spin polarization of the equilibrium charge current is mainly determined by RSO coupling The polarization strongly depends on the type of the graphene electrodes and for the armchair type electrodes, in weak magnetic field, the increase of the polarization is more efficient with increasing RSO coupling than for the zigzag type electrodes. It is also important to note that quantum oscillations in conductance translate into nonequilibrium net current oscillations as a function of the magnetic flux through the system. This is possible because the Fourier power spectra of conductance at different energies cover the same frequencies for a wide range of Fermi energies. In turn, the current is proportional to the integral of the transmission function over the energy range, defined by an external bias voltage. In this way, the oscillations of the electron transmission function are transformed into oscillations of the net current as a function of the magnetic flux. One should be pointed out that, current–voltage measurements provide a bridge between theory and experiment and allows for experimental verification of theoretical predictions regarding the impact of various effects on the transport properties of the system. The example of the relationship between classical characteristics of the system such as current–voltage characteristic and fundamental microscopic phenomena as quantum interference effects has been presented in this paper. In conclusion, we can say that the use of a graphene ring in the nanotransistor-like structure increases functionality of the graphene nanoribbons in potential electronic applications by utilizing the quantum interference effect and RSO coupling.
Author contributions
A.P. wrote the main manuscript text, prepared all figures and reviewed the manuscript.
Data availability
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Aharonov, Y. & Bohm, D. Significance of electromagnetic potentials in the quantum theory. Phys. Rev.115, 485–491. 10.1103/PhysRev.115.485 (1959). [Google Scholar]
-
2.Webb, R. A., Washburn, S., Umbach, C. P. & Laibowitz, R. B. Observation of
 Aharonov–Bohm oscillations in normal-metal rings. Phys. Rev. Lett.54, 2696–2699. 10.1103/PhysRevLett.54.2696 (1985).
[DOI] [PubMed] [Google Scholar]
Aharonov–Bohm oscillations in normal-metal rings. Phys. Rev. Lett.54, 2696–2699. 10.1103/PhysRevLett.54.2696 (1985).
[DOI] [PubMed] [Google Scholar] - 3.Washburn, S. & Webb, R. A. Aharonov–Bohm effect in normal metal quantum coherence and transport. Adv. Phys.35(4), 375–422. 10.1080/00018738600101921 (1986). [Google Scholar]
- 4.Recher, P. et al. Aharonov–Bohm effect and broken valley degeneracy in graphene rings. Phys. Rev. B76, 235404. 10.1103/PhysRevB.76.235404 (2007). [Google Scholar]
- 5.Rycerz, A. Aharonov–Bohm and relativistic corbino effects in graphene: A comparative study of two quantum interference phenomena. Acta Phys. Pol. A121, 1242 (2012). [Google Scholar]
- 6.Rycerz, A. Aharonov–Bohm effect and valley polarization in nanoscopic graphene rings. Acta Phys. Pol. A115, 322 (2009). [Google Scholar]
- 7.von Keyserlingk, C. W., Simon, S. H. & Rosenow, B. Enhanced bulk-edge Coulomb coupling in fractional Fabry-Perot interferometers. Phys. Rev. Lett.115, 126807. 10.1103/PhysRevLett.115.126807 (2015). [DOI] [PubMed] [Google Scholar]
- 8.Levkivskyi, I. P., Fröhlich, J. & Sukhorukov, E. V. Theory of fractional quantum Hall interferometers. Phys. Rev. B86, 245105. 10.1103/PhysRevB.86.245105 (2012). [Google Scholar]
- 9.Rosenow, B. & Simon, S. H. Telegraph noise and the Fabry-Perot quantum Hall interferometer. Phys. Rev. B85, 201302. 10.1103/PhysRevB.85.201302 (2012). [Google Scholar]
- 10.Halperin, B. I., Stern, A., Neder, I. & Rosenow, B. Theory of the Fabry-Pérot quantum Hall interferometer. Phys. Rev. B83, 155440. 10.1103/PhysRevB.83.155440 (2011). [Google Scholar]
- 11.Schelter, J., Bohr, D. & Trauzettel, B. Interplay of the Aharonov–Bohm effect and Klein tunneling in graphene. Phys. Rev. B81, 195441. 10.1103/PhysRevB.81.195441 (2010). [Google Scholar]
- 12.Rycerz, A. Magnetoconductance of the Corbino disk in graphene. Phys. Rev. B81, 121404. 10.1103/PhysRevB.81.121404 (2010). [Google Scholar]
- 13.Winkler, R. Spin-orbit Coupling Effects in Two-Dimensional Electron and Hole Systems, Springer Tracts in Modern Physics. New York[SPACE]10.1007/b13586 (2003).
-
14.Nitta, J., Akazaki, T., Takayanagi, H. & Enoki, T. Gate control of spin-orbit interaction in an inverted I
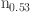 G
G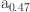 As/I
As/I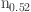 A
A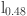 As heterostructure. Phys. Rev. Lett.78, 1335–1338 (1997). [Google Scholar]
As heterostructure. Phys. Rev. Lett.78, 1335–1338 (1997). [Google Scholar] - 15.Destefani, C. F., Ulloa, S. E. & Marques, G. E. Spin-orbit coupling and intrinsic spin mixing in quantum dots. Phys. Rev. B69, 125302. 10.1103/PhysRevB.69.125302 (2004). [Google Scholar]
- 16.Szafran, B., Nowak, M. P., Bednarek, S., Chwiej, T. & Peeters, F. M. Selective suppression of Dresselhaus or Rashba spin-orbit coupling effects by the Zeeman interaction in quantum dots. Phys. Rev. B79, 235303. 10.1103/PhysRevB.79.235303 (2009). [Google Scholar]
- 17.Dyrdał, A., Inglot, M., Dugaev, V. K. & Barnaś, J. Thermally induced spin polarization of a two-dimensional electron gas. Phys. Rev. B87, 245309. 10.1103/PhysRevB.87.245309 (2013). [Google Scholar]
- 18.Governale, M. Quantum dots with Rashba spin-orbit coupling. Phys. Rev. Lett.89, 206802. 10.1103/PhysRevLett.89.206802 (2002). [DOI] [PubMed] [Google Scholar]
- 19.Bouziani, M. E., Houça, R. & Jellal, A. A confined system with Rashba coupling in a constant magnetic field. J. Phys. A: Math. Theor.45(50), 505306. 10.1088/1751-8113/45/50/505306 (2012). [Google Scholar]
- 20.Bednarek, S. & Szafran, B. Spin rotations induced by an electron running in closed trajectories in gated semiconductor nanodevices. Phys. Rev. Lett.101, 216805. 10.1103/PhysRevLett.101.216805 (2008). [DOI] [PubMed] [Google Scholar]
- 21.Poszwa, A. Electric field induced effects for two-electron quantum dot in presence of magnetic field. Acta Phys. Pol. A138, 477 (2020). [Google Scholar]
- 22.Poszwa, A. Enhancement of spin current polarization in 2d ferromagnetic/insulator/heavy fermion material tunnel junction induced by Rashba spin-orbit coupling. Acta Phys. Pol. A141, 55. 10.12693/143.55 (2023). [Google Scholar]
- 23.Poszwa, A. Numerical simulation of Rashba spin-orbit coupling effect on quantum Hall resistivity within tight-binding approximation. Phys. E: Low-Dimens. Syst. Nanostr.162, 115977. 10.1016/j.physe.2024.115977 (2024). [Google Scholar]
- 24.Poszwa, A. Two-dimensional hydrogen-like atom in magnetic field in the presence of Rashba spin-orbit coupling. Phys. E: Low-Dimens. Syst. Nanostr.124, 114247. 10.1016/j.physe.2020.114247 (2020). [Google Scholar]
- 25.Dossa, A. F. & Avossevou, G. Y. H. Analytical spectrum for a Hamiltonian of quantum dots with Rashba spin-orbit coupling. Phys.Scripta89(12), 125803. 10.1088/0031-8949/89/12/125803 (2014). [Google Scholar]
- 26.Voskoboynikov, O., Bauga, O., Lee, C. P. & Tretyak, O. Magnetic properties of parabolic quantum dots in the presence of the spin-orbit interaction. J. Appl. Phys.94(9), 5891–5895. 10.1063/1.1614426 (2003). [Google Scholar]
- 27.Tsitsishvili, E., Lozano, G. S. & Gogolin, A. O. Rashba coupling in quantum dots: An exact solution. Phys. Rev. B70, 115316. 10.1103/PhysRevB.70.115316 (2004). [Google Scholar]
- 28.Weiss, S. & Egger, R. Path-integral Monte Carlo simulations for interacting few-electron quantum dots with spin-orbit coupling. Phys. Rev. B72, 245301. 10.1103/PhysRevB.72.245301 (2005). [Google Scholar]
- 29.Weiss, S., Thorwart, M. & Egger, R. Charge qubit entanglement in double quantum dots. Europhys. Lett.76(5), 905. 10.1209/epl/i2006-10342-y (2006). [Google Scholar]
- 30.Trif, M., Golovach, V. N. & Loss, D. Spin-spin coupling in electrostatically coupled quantum dots. Phys. Rev. B75, 085307. 10.1103/PhysRevB.75.085307 (2007). [Google Scholar]
- 31.Sinitsyn, N. A., Hankiewicz, E. M., Teizer, W. & Sinova, J. Spin Hall and spin-diagonal conductivity in the presence of Rashba and Dresselhaus spin-orbit coupling. Phys. Rev. B70, 081312. 10.1103/PhysRevB.70.081312 (2004). [Google Scholar]
- 32.Russo, S. et al. Observation of Aharonov–Bohm conductance oscillations in a graphene ring. Phys. Rev. B77, 085413. 10.1103/PhysRevB.77.085413 (2008). [Google Scholar]
- 33.Santos, H., Chico, L., Alvarellos, J. E. & Latgé, A. Defect-enhanced Rashba spin-polarized currents in carbon nanotubes. Phys. Rev. B96, 165401. 10.1103/PhysRevB.96.165401 (2017). [Google Scholar]
- 34.Cresti, A. Convenient Peierls phase choice for periodic atomistic systems under magnetic field. Phys. Rev. B103, 045402. 10.1103/PhysRevB.103.045402 (2021). [Google Scholar]
- 35.Datta, S. Quantum Transport: Atom to Transistor. Cambridge University Press, 10.1017/CBO9781139164313,(2005).
- 36.Datta, S. Electronic transport in mesoscopic systems (Cambridge University Press, Cambridge, 1995). [Google Scholar]
- 37.Lewenkopf, C. & Mucciolo, E. The recursive Green’s function method for graphene. J. Comput. Electron12, 203–231. 10.1007/s10825-013-0458-7 (2013). [Google Scholar]
- 38.Diniz, G. S., Latgé, A. & Ulloa, S. E. Helicoidal fields and spin polarized currents in carbon nanotube-DNA hybrids. Phys. Rev. Lett.108, 126601. 10.1103/PhysRevLett.108.126601 (2012). [DOI] [PubMed] [Google Scholar]
- 39.Xu, F., Li, B., Pan, H. & Zhu, J.-L. Spin-orbit coupling effects on transport in carbon nanotubes with adatoms. Phys. Rev. B75, 085431. 10.1103/PhysRevB.75.085431 (2007). [Google Scholar]
- 40.Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. Numerical Recipes 3rd Edition: The Art of Scientific Computing 3rd edn. (Cambridge University Press, USA, 2007).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.