Deep learning-based automated tool for diagnosing diabetic peripheral neuropathy

Abstract

Background

Diabetic peripheral neuropathy (DPN) is a common complication of diabetes, and its early identification is crucial for improving patient outcomes. Corneal confocal microscopy (CCM) can non-invasively detect changes in corneal nerve fibers (CNFs), making it a potential tool for the early diagnosis of DPN. However, the existing CNF analysis methods have certain limitations, highlighting the need to develop a reliable automated analysis tool.

Methods

This study is based on data from two independent clinical centers. Various popular deep learning (DL) models have been trained and evaluated for their performance in CCM image segmentation using DL-based image segmentation techniques. Subsequently, an image processing algorithm was designed to automatically extract and quantify various morphological parameters of CNFs. To validate the effectiveness of this tool, it was compared with manually annotated datasets and ACCMetrics, and the consistency of the results was assessed using Bland­–Altman analysis and intraclass correlation coefficient (ICC).

Results

The U2Net model performed the best in the CCM image segmentation task, achieving a mean Intersection over Union (mIoU) of 0.8115. The automated analysis tool based on U2Net demonstrated a significantly higher consistency with the manually annotated results in the quantitative analysis of various CNF morphological parameters than the previously popular automated tool ACCMetrics. The area under the curve for classifying DPN using the CNF morphology parameters calculated by this tool reached 0.75.

Conclusions

The DL-based automated tool developed in this study can effectively segment and quantify the CNF parameters in CCM images. This tool has the potential to be used for the early diagnosis of DPN, and further research will help validate its practical application value in clinical settings.

Introduction

The prevalence of diabetes continues to increase globally. As of 2021, the global prevalence of diabetes among adults was approximately 10.5%.1 Diabetic peripheral neuropathy (DPN) is a common chronic complication of diabetes that affects approximately 50% of patients. Early identification and treatment of DPN are crucial for improving prognosis.2 However, current common diagnostic methods for DPN have certain limitations. The “gold standard” clinical diagnostic method for DPN, nerve conduction studies, has shortcomings such as the inability to diagnose small nerve fiber neuropathy, insufficient sensitivity, high variability, and the need for standardization of testing methods and results.3 Although skin biopsy allows for direct observation of nerve fiber damage, it is an invasive procedure with high costs.4 Clinical symptoms, physical examination, and questionnaires, such as the Neuropathy Symptom Score and Michigan Neuropathy Screening Instrument, are highly subjective and have poor reproducibility.5

Recently, increasing emphasis has been placed on the relationship between changes in corneal nerve fibers (CNFs) and DPN. Studies have revealed that morphological changes in CNF are closely related to the severity of DPN and can occur in the early stages of DPN.6 Corneal confocal microscopy (CCM) enables the non-invasive and rapid detection of CNF changes, making it possible to analyze CNF morphological alterations. This method offers advantages such as being rapid, non-invasive, quantitative, highly reproducible, and highly sensitive.^7,8 Labor-intensive manual annotation is usually required to accurately quantify the morphological parameters of CNFs. This process is time-consuming and relies on the subjectivity of the analyst.9 Therefore, an objective, accurate, and rapidly automated analytical tool is required.

With the continuous development of deep learning (DL), neural network models for image segmentation have been widely used in medicine, including in tumor and cell segmentation.^10,11 Some DL-based image segmentation approaches have been applied to corneal nerve images, including convolutional neural network (CNN) models12 and U-Net models^.13 Compared with non-DL-based automated analysis algorithms, these methods have significantly improved recognition accuracy and stability.14 Additionally, compared with manual annotation, they enhance objectivity and detection efficiency, alleviating the labor-intensive burden.14 However, current studies still have certain limitations. Studies comparing the recognition capabilities of different models of corneal nerve images are lacking. Furthermore, DL-based tools capable of directly calculating CNF morphological parameters are facing a shortage, making it difficult to apply these tools in clinical auxiliary diagnosis.

This study aims to train and evaluate different DL neural network models for segmenting CCM images and design image processing algorithms based on the optimal DL model to accurately and automatically analyze the morphological parameters of CNF. This study also compares these results with those obtained from the widely used and validated automated image analysis software, ACCMetrics, to verify the clinical efficacy.

Materials and methods

Study design and population

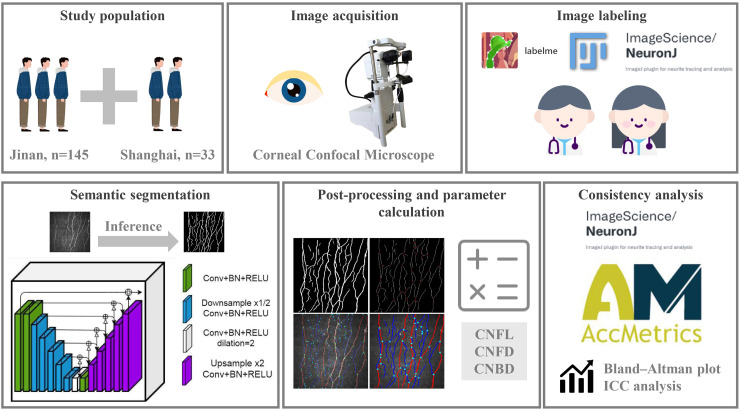
The overall study design is illustrated in Figure 1. First, we included 1454 CCM images of 175 healthy volunteers and patients with diabetes from two independent clinical research centers. Among them, 34 healthy participants and 108 patients with diabetes were selected from the Qilu Hospital of Shandong University in Jinan, with a total of 1274 images. Another 30 healthy participants and 3 diabetic patients were from Shanghai, contributing a total of 196 images. According to the current consensus,^15,16 accurate assessment of DPN requires evaluating 5–8 non-overlapping images from the apex of the cornea, where the sub-basal nerve plexus is most dense. Our image selection process was consistent with this consensus.

Figure 1.

Schematic of the study design. Participants were recruited from two independent research centers, and corneal nerve images were captured using CCM. The dataset was annotated by two experienced specialists. Afterward, the corneal nerve images were segmented using a semantic segmentation neural network model, followed by postprocessing to calculate relevant morphological parameters. Finally, statistical analyses were performed to evaluate the consistency with manually annotated datasets and ACCMetrics.

Participants were selected from healthy individuals or patients aged 18–80 years, with diabetes diagnosis and classification based on the American Diabetes Association (ADA) criteria (2024 edition).17 Participants were evaluated for peripheral neurological symptoms and nerve conduction examinations, and a diagnosis of peripheral neuropathy was made according to the Toronto criteria.18 All participants voluntarily signed an informed consent form. The exclusion criteria included a history of acute illness, chronic gastrointestinal disease, hypertension, cerebrovascular disease, malignant tumors, autoimmune diseases (such as systemic lupus erythematosus, systemic sclerosis, and Crohn's disease), vitamin B12 or folate deficiency, hypothyroidism, liver or kidney dysfunction, cervical or lumbar spine disease, and central neurodegenerative diseases (including Parkinson's disease, multiple sclerosis, Alzheimer's disease, Huntington's disease, and dementia). Volunteers with genetic diseases (including but not limited to hereditary neuropathy), a history of eye trauma, disease, corneal disease, surgery, contact lens wear, alcohol abuse, and exposure to toxic or chemotherapeutic drugs were also excluded. Pregnant or breastfeeding women and vegetarians were excluded.

Image acquisition and annotation

CCM (HRT-II or HRT-III, Heidelberg Rostock Cornea Module, Heidelberg Engineering Inc., Germany) is performed using confocal laser scanning technology. The primary device is a Rostock corneal microscope objective equipped with a helium–neon laser source at a wavelength of 670 nm. The horizontal and vertical resolutions of the microscope are both 1 µm, with a magnification of 800× and a viewing area of 400 µm × 400 µm. The images were captured and stored using a fully digital image acquisition system. Carbomer eye gel (Berlin, Germany) was used as a coupling agent between the microscope lens and corneal contact cap, and 0.4% oxybuprocaine hydrochloride was used for surface anesthesia of the eye under examination. During the CCM examination, the head of the participant was fixed in front of the microscope lens and focused straight ahead. The lens was gradually moved forward until the corneal contact cap touched the corneal center, and the focus was adjusted to obtain images of the corneal sub-basal nerve plexus. Nerve images were obtained at five locations: near the corneal center, slightly above, below, to the left, and to the right of the center. Several images were captured and stored at each location. The image size was 384 × 384 pixels, with a pixel size of 1.0417 µm.

Two experienced professional physicians performed the following tasks. For the dataset from healthy people from Jinan (n = 210), one physician used the Labelme tool to delineate the boundaries between nerve fibers and the background in CCM images, completing the initial image segmentation annotation task. The annotations were thereafter reviewed and modified by a more senior physician. The final annotation results were achieved through consensus between the two physicians. For the dataset from Shanghai (n = 196), CNF tracking, quantification, and analysis were first performed using the NeuronJ plugin in the ImageJ image processing software.19 The original images were quantified, and relevant parameters were calculated for corneal nerve morphology using the fully automated analysis software ACCMetrics.20 The remaining dataset of 1048 images from Jinan diabetic patients was used to evaluate the efficacy of the tool for diagnosing DPN.

Deep learning-based semantic segmentation

To perform CCM corneal nerve image segmentation efficiently, we selected several different DL-based semantic segmentation models, including UNet,21 UNet++,22 U2Net,23 SegNet,24 ESPNet,25 Deeplabv3+,26 and PSPNet.27 UNet is the earliest CNN architecture proposed for medical image segmentation and is characterized by a symmetric U-shaped structure for feature extraction and reconstruction, comprising an encoder and a decoder. UNet++ is an improved version of UNet, and its main improvement is the design of skip connections. U2Net employs a deeper U-Net structure in which each U-Net unit comprises multiple U-Nets. SegNet is a classic CNN for semantic segmentation, whose core idea is asymmetric decoding using max-pooling indices. ESPNet is a lightweight segmentation network that focuses on computational efficiency by introducing an efficient spatial pyramid (ESP) module. PSPNet introduces a pyramid pooling module that captures the global contextual information of an image using pooling operations at different scales. Deeplabv3+ combines the advantages of atrous convolution and spatial pyramid pooling, with further optimization of the decoder.

To evaluate and compare the performance of the seven network models, model training and prediction were implemented using Python 3.10.13 and the PaddleSeg 2.9 framework, and iterative training was performed on an NVIDIA GeForce RTX 3090 GPU. Using a Python script, the annotated CCM image dataset, comprising 210 images, was randomly split into 60% (n = 126) for training, 20% (n = 42) for testing, and 20% (n = 42) for validation.

During training, the optimizer used was stochastic gradient descent with a momentum of 0.9 and a weight decay of 4.0e-5. The learning rate scheduler employed a polynomial decay strategy with an initial learning rate of 0.01, final learning rate of 0, and decay power of 0.9. This configuration helps to stabilize the training process and gradually reduces the learning rate to avoid overfitting.

Given that nerve fibers (i.e., the foreground) occupy only a small portion of the entire image, the Dice Loss was selected as the loss function to address the class imbalance issue commonly encountered in this task. For model performance evaluation, the mean Intersection over Union (mIoU) was used as the primary metric. mIoU is a commonly used image segmentation metric that quantitatively assesses the segmentation accuracy of a model by calculating the ratio of the intersection to the union of the predicted and ground truth areas. The higher the mIoU value, the better the segmentation performance of the model. Additionally, the accuracy, Cohen's Kappa coefficient, and Dice coefficient were calculated. To ensure the robustness and generalizability of the results, five-fold cross-validation was performed, and the average value was taken as the final evaluation result for comparison. If the best validation mIoU did not improve after 1000 iterations during the model training, the training was terminated. The optimal model was selected for the subsequent semantic image segmentation tasks.

Quantitative detection of corneal nerve fibers

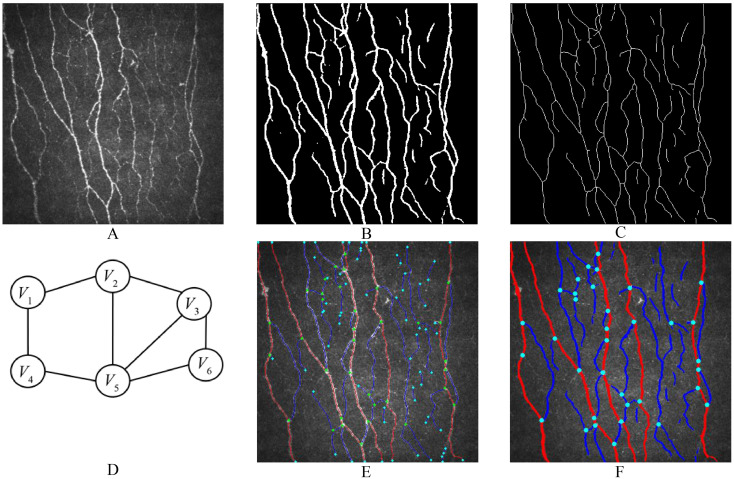
After inferring the original images (Figure 2(a)) using the semantic segmentation neural network model from the previous step, binarized images were obtained (Figure 2(b)). An image processing algorithm was designed for the quantitative detection of CNFs. The Zhang–Suen algorithm is a classic thinning algorithm widely used in image processing and computer vision, particularly in shape analysis.28 This algorithm, implemented through the skimage.morphology.skeletonize function, was used to thin the binarized images to extract the skeletal structure of the nerve fibers (Figure 2(c)). The skeletonization procedure is based on the 8-connection method, implying that it considers each pixel's eight neighboring pixels to generate the skeletal structure. To further enhance the image quality, noise was first filtered out, and then a 3 × 3 operator with a center value of 10 and surrounding values of 1 was used for a two-dimensional convolution to determine the classification of each pixel. These classifications included endpoints (n = 11), nerve fiber segments (n = 12), and branch points (n = 13).

Figure 2.

Workflow of image processing. (a) is the original image, which is segmented by the DL model to obtain the binary image (b). Afterward, image thinning and skeleton extraction algorithms are applied, resulting in the CNF skeleton image (c). (d) illustrates the construction of an undirected graph from each CNF segment and branching point for trunk or branch determination. (e) and (f) respectively depict images showing the skeleton of the CNF or the entire processed result.

Next, the skeleton image was segmented based on the branch points, and a unique index was assigned to each segment. Inverse convolution operations were performed using affine transformation to retrieve detailed information on the location, area, and width of each segment. All the interconnected segments and nodes were constructed into an undirected graph, where each node corresponded to a node number, each edge corresponded to a segment number, and the length of the segment was used as the weight parameter of the edge (Figure 2(d)).

Dijkstra's algorithm is a classic and effective method for solving path optimization problems. It can find the shortest path from the source node to all other nodes in a graph with non-negative edge weights. The linearity, length, and average width of each shortest path were calculated, and the shortest paths with lengths and linearities within a certain threshold range were selected as candidate trunks. Using dynamic programming (DP), non-overlapping trunks with the highest average linearity and width were identified; the segments on these paths were considered trunk segments, whereas the remainder were considered branch segments (Figure 2(e) and (f)).

Parameter calculation and consistency test

Three commonly used CNF parameters were calculated: (1) Corneal nerve fiber density (CNFD, n/mm²), the number of nerve trunk fibers per square millimeter; (2) Corneal nerve branch density (CNBD, n/mm²), the number of branches originating from the main nerve per square millimeter; and (3) Corneal nerve fiber length (CNFL, mm/mm²), the total length of all nerve fibers per square millimeter.29

The parameters calculated using the software proposed in this study were compared with those obtained using the automated parameter recognition tool ACCMetrics, and manually annotated parameters using the NeuronJ plugin tool. Various methods were used to evaluate the consistency between the results obtained using different measurement methods and manually annotated results.

Statistical analysis

Statistical analysis was performed using R 4.2.1, with a two-sided p-value of <0.05 considered statistically significant.

To evaluate the consistency between the different measurement methods and manual annotations, a Bland–Altman plot was used to visually present the bias and limits of agreement between the two measurement methods (the proposed software and ACCMetrics) and manual annotations. Additionally, the intraclass correlation coefficient (ICC) was calculated to quantitatively assess the degree of consistency between the different measurement methods and the manual annotations.

CNFL, CNFD, and CNBD parameters were calculated using the tools of our research as well as ACCMetrics on 1048 CCM images of 51 diabetic patients with combined DPN and 57 diabetic patients without DPN, respectively. Subsequently, the subjects’ working curves (ROC) were plotted, the area under the curve (AUC) was calculated, and the three parameters were used for joint prediction by constructing a logistic regression model. Delong analysis was performed to compare the performance of the two ROC curves for any significant differences.

Results

Comparison of identification results

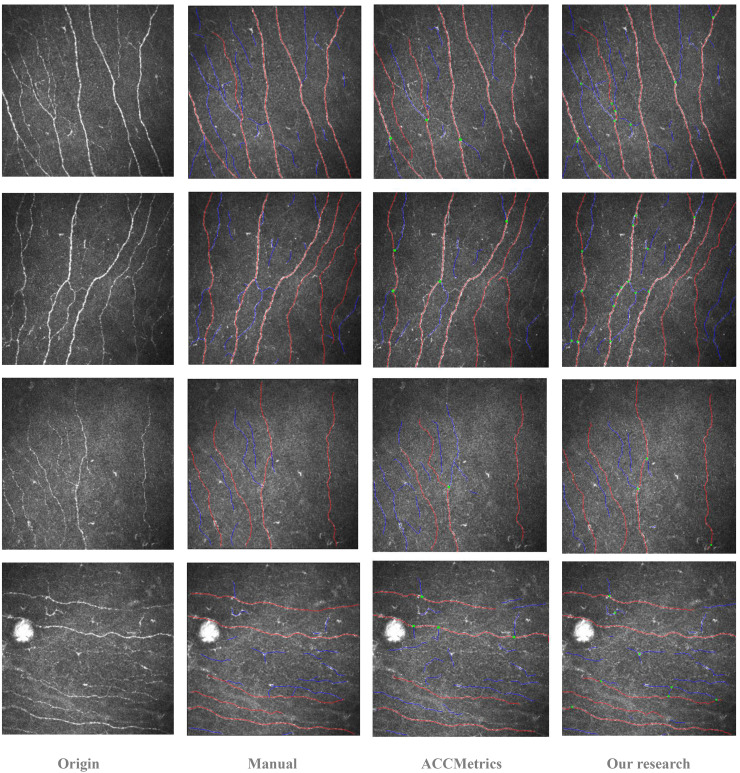
Figure 3 presents a comparison of the original CCM corneal nerve images, manual annotations, predictions from ACCMetrics, and predictions from this study, arranged in rows. Overall, the number of main trunks predicted by both automated tools was similar. However, this study demonstrates an advantage in identifying the finer details of CNF, as it can detect a greater number of branches in the main CNF trunks. Notably, in regions where the contrast between nerve fibers and the background is less distinct, or where significant noise is present, the algorithm proposed in this study identifies CNF segments that ACCMetrics fails to detect.

Figure 3.

Comparison of processing results for four example images. Each row, from left to right, shows the original image, manual annotation result, ACCMetrics prediction result, and the ACCMetrics from the algorithm in this study.

Evaluation of image segmentation performance of different deep learning models

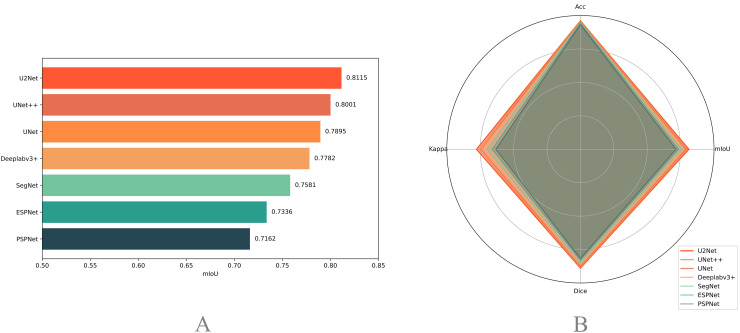
The evaluation results for the test set are shown in Figure 4. Generally, most models exhibit strong segmentation capabilities. U2Net performed the best, achieving an mIoU of 0.8115, accuracy of 0.9607, Kappa coefficient of 0.7774, and Dice coefficient of 0.8887, highlighting its significant advantages in handling this type of image segmentation task. UNet++ and UNet followed closely with mIoUs of 0.8001 and 0.7895, respectively. In comparison, although Deeplabv3+ and SegNet performed well, their mIoUs were slightly lower at 0.7782 and 0.7581, respectively. The lightweight ESPNet had an mIoU of 0.7336, which, despite its computational efficiency, exhibited relatively lower segmentation accuracy. PSPNet exhibited the lowest mIoU (0.7162). Overall, these models performed well, achieving an mIoU above 0.7, with U2Net performing the best on the test set.

Figure 4.

Evaluation of image segmentation performance across different DL models. The left plot (a) ranks the mIoU of each model on the test dataset in descending order. The right plot (b) presents a radar chart comparing the mIoU, Dice, Kappa, and Acc metrics of each model.

Consistency evaluation of nerve fiber quantification

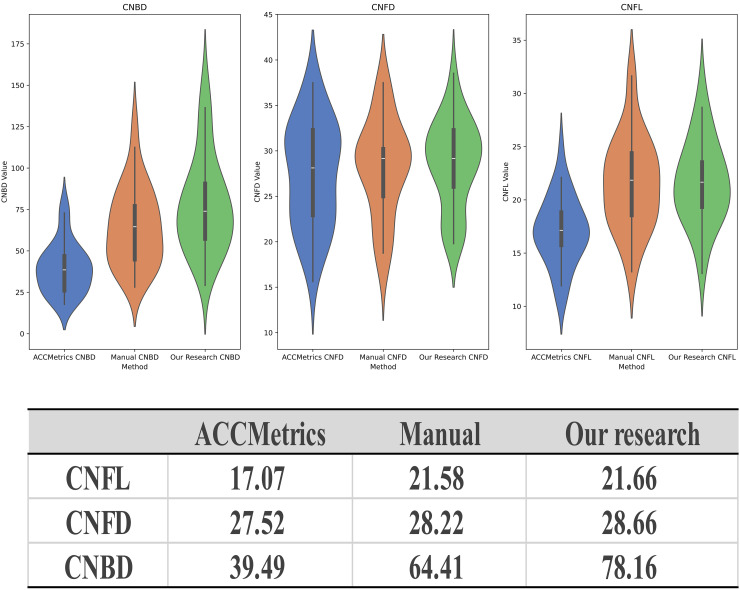
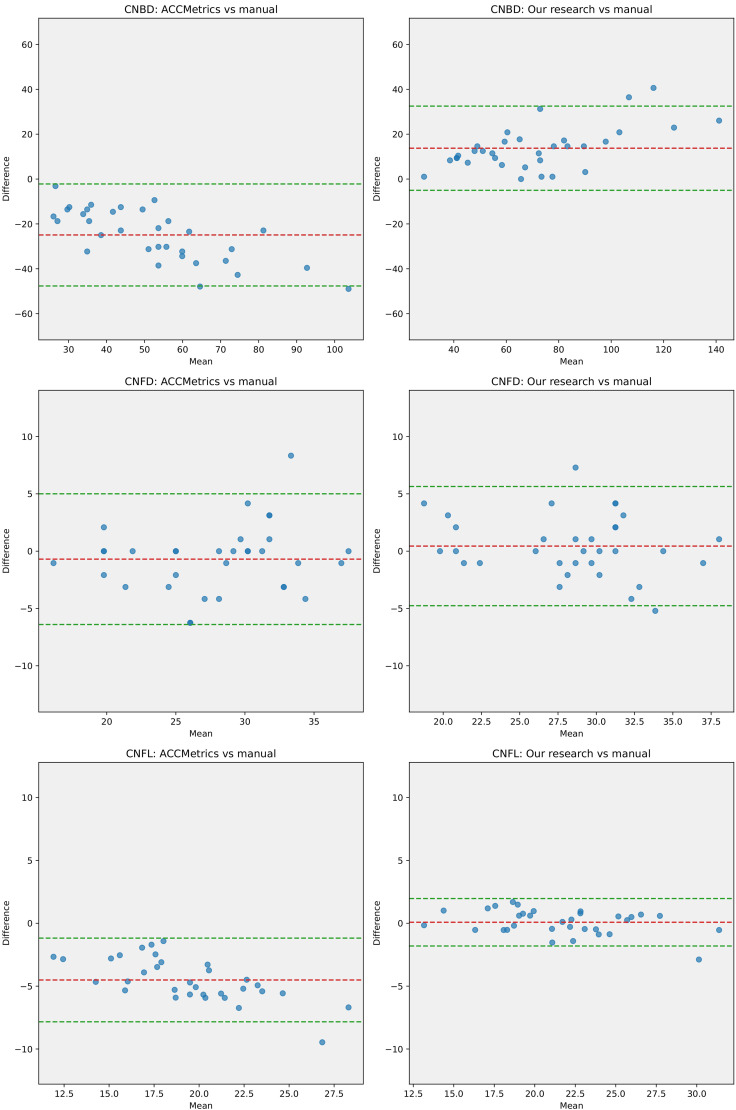
As mentioned earlier, we selected the U2Net model, which demonstrated the best performance, as the basis for extracting the binary images of nerve fibers. Analysis of the dataset from Shanghai indicated that, compared with ACCMetrics, the CNFL and CNBD detected by the new algorithm were closer to the manually annotated dataset, whereas CNFD exhibited minimal differences among the three methods. This suggests that the new algorithm has the advantage of recognizing the total length of the CNF and the number of primary branches (Figure 5). The Bland–Altman plots indicate that, compared with manual annotations, the mean difference in the results from the new algorithm is closer to zero, and the limits of agreement are narrower (Figure 6). This indicates that the CNF length, number of main trunks, and number of primary branches analyzed by the new algorithm are closer to the results from manual annotations, with less heterogeneity.

Figure 5.

Results of quantitative analysis of CNF images. The upper violin plots compare the results of ACCMetrics, manual annotations, and the algorithm proposed in this study for CNBD, CNFD, and CNFL, respectively. The table below lists the mean values of the quantitative analysis results.

Figure 6.

Bland­–Altman plots. From top to bottom, the Bland–Altman plots display the results of ACCMetrics versus manual annotations and the algorithm proposed in this study versus manual annotations for CNBD, CNFD, and CNFL. Evidently, the mean difference between the algorithm proposed in this study and manual annotations is closer to 0, with narrower limits of agreement.

Using the manually annotated dataset as a reference, ICC values were calculated for the two methods and three parameters. ICC values of <0.5, 0.5–0.75, 0.75–0.9, and >0.90 indicate poor, moderate, good, and excellent reliability, respectively. The ICC coefficients of the proposed algorithm for CNFL, CNFD, and CNBD using the manually annotated datasets were 0.974, 0.861, and 0.828, respectively. In contrast, the ICC coefficients of ACCMetrics were 0.534, 0.858, and 0.470, respectively. As the results indicate, the proposed algorithm exhibits higher consistency with the manually annotated dataset in all aspects, outperforming ACCMetrics in terms of identification capability.

Assessment of diagnostic effectiveness

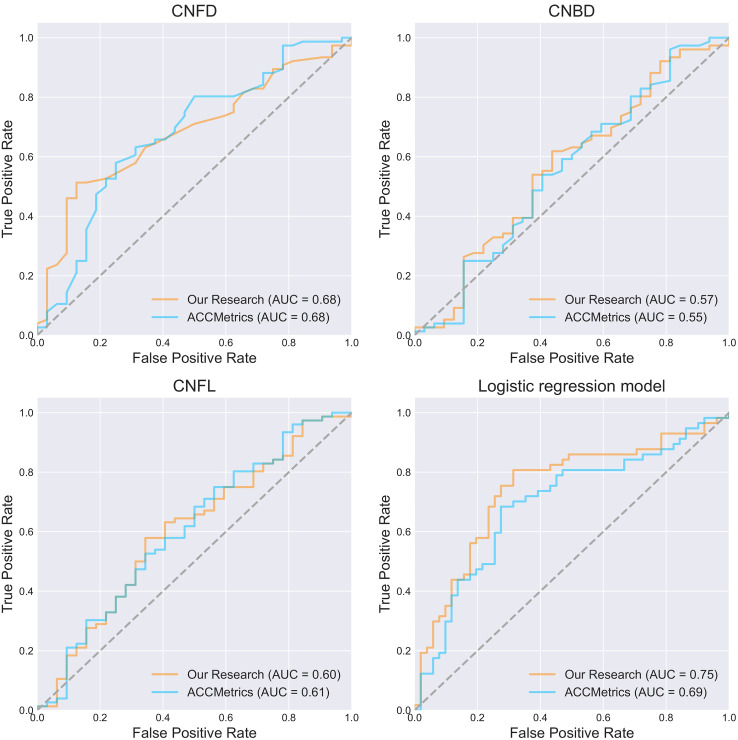
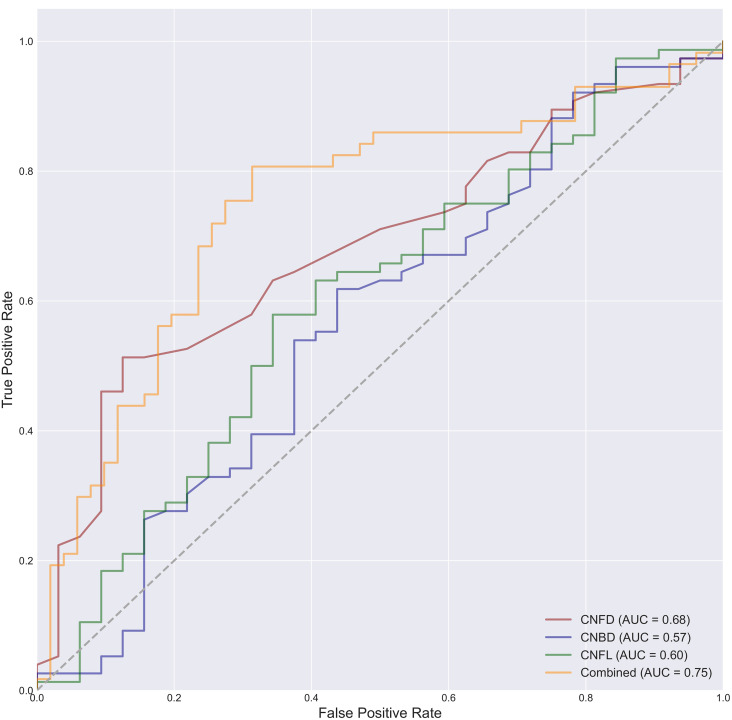
The AUCs were 0.68, 0.57, and 0.60 for classification using only the CNFD, CNBD, and CNFL parameters calculated by our studied tool alone. The AUCs were 0.68, 0.55, and 0.61 for classification using only the CNFD, CNBD, and CNFL parameters calculated by ACCMetrics alone. The AUCs were 0.75 and 0.69 for classification using our studied tool in conjunction with the three parameters obtained from ACCMetrics for classification, the AUCs obtained were 0.75 and 0.69 (Figure 7). However, the Delong test on the ROC curves of the two logistic regression models showed a P-value of .293, which is not a significant difference between the two. Thereafter, Delong's test was performed on the ROC curves of the combined classification of the three parameters computed by the tools of our study, compared to the ROC curves of the classification using CNFD, CNBD, and CNFL alone, respectively. The P-values of the Delong test results are 0.024, 0.007, and 0.011, respectively, which indicates that the combined use of the three parameters provides significantly better classification performance than any of them alone (Figure 8).

Figure 7.

ROC plots of the three parameters CNFD, CNBD, and CNFL alone and the combined three to classify the presence or absence of DPN in participants, respectively. The best classification efficacy was achieved using the three parameters jointly.

Figure 8.

ROC curves for classification using the joint three parameters of CNFD, CNBD, and CNFL alone are shown. As shown, the classification performance of the joint three parameters is better than using any of them alone.

When performing the above task of quantitative parametric analysis of the CCM image dataset on a personal PC with a CPU of Intel i5-11300H, ACCMetrics took 8932 s, whereas our research tool took 1450 s, an overall increase in the speed of the analysis by a factor of approximately 6.

In addition, we performed the same operation on a dataset of healthy people in Jinan. Healthy people were used as a control group to compare with NDPN and DPN patients respectively, and relevant results can be obtained in supplementary materials (sFigure 1, 2).

Discussion

In this study, we developed an automatic analysis tool for CCM corneal nerve images based on DL to accurately quantify the morphological parameters of CNF. Statistical analyses showed that the tool proposed in this study was in high agreement with manual annotation and had better efficacy in diagnosing DPN.

Numerous studies have shown a correlation between CNF morphological parameters and DPN. Although traditional manual tracing methods can provide valuable insights, their complex and time-consuming nature limits their widespread use in clinical settings. Therefore, clinicians typically rely on a simplified approach, namely, automated parameter quantification tools. This study aims to propose a solution that is more accurate, robust, and efficient than the currently popular tools.

First, we evaluated the segmentation performance of seven different DL models on CCM corneal nerve images, among which the models based on U-Net and its variants (U-Net, U-Net++, and U2Net) performed the best. U-Net was initially designed specifically for medical image segmentation tasks.21 Considering the common issue of limited medical image data, the unique network architecture of U-Net allows for good segmentation performance even with a small amount of data. The U-Net model also features a symmetrical encoder–decoder structure that effectively captures both local and global features in the image, which is particularly important for complex and subtle structures, such as corneal nerves. U2Net, the best-performing model, has each basic unit as a small U-Net nested together, forming a recursive U-Net structure that significantly increases the network depth and feature extraction capability.23 Therefore, compared with the basic U-Net model, U2Net may be more suitable for the segmentation of CCM corneal nerve images.

Because semantic segmentation models can finely determine the classification of each pixel, they can directly obtain CNF width data rather than estimating or predicting them. Using a DP algorithm, the thickest fibers in the undirected graph constructed using the CNF and branch points are selected as the main trunk, thereby increasing the interpretability of the analysis. Compared with ACCMetrics, this study exhibited significant improvements in CNF length and primary branch count.

Several studies on the quantitative analysis of CCM images based on DL models have been conducted.14 Williams et al. achieved satisfactory results using an improved U-Net model.13 Scarpa et al. evaluated CCM image density and tortuosity information through CNNs.12 Oakley et al. achieved automatic tracking of CNFs in monkey CCM images using an extension of U-Net.30 Nevertheless, current related studies have been limited to CNF segmentation and skeleton refinement without the capability to further calculate various corneal nerve parameters (such as CNFD and CNBD). The results of the ROC analysis showed that the efficacy of using the three parameters, CNFL, CNFD, and CNBD, to jointly classify DPN was superior to using any of them alone and that the computational power of a wider range of parameters resulted in stronger clinical diagnostic efficacy.

This study has certain limitations. First, the overall prediction of the CNBD parameter was higher than that of the manually annotated results because the CNF segmentation results produced by the semantic segmentation model had interruptions, resulting in a higher number of identified primary branches of the CNF. Increasing the number of datasets used for training will help improve the segmentation efficiency. It must be acknowledged that the number of datasets used was not large, which may also explain the insufficient performance of some DL models. In addition, the calculation of the parameters depends on the post-processing of the segmentation results. In future studies, we plan to explore end-to-end DL models to further improve the performance and address these limitations.

To the best of our knowledge, this is an automated tool based on a DL image segmentation model capable of quantifying commonly used CNF parameters. We also evaluated the ability of different types of DL network models to segment CCM corneal nerve images and identified the most suitable specific models for such tasks. In summary, further research is required to determine the applicability of this tool in clinical settings.

Conclusion

DL-based automated tools can effectively quantify nerve fiber parameters in CCM images. This tool has potential applications in the early diagnosis of DPN, but further clinical validation is required to ensure its practical feasibility.