Skip to main content
PMC home page
RSC Advances logoLink to RSC Advances
. 2025 Jan 2;15(1):337–347. doi: 10.1039/d4ra05327c

DFT study of alkaline earth metals NaXH3 (X = Be, Mg, Ca, Sr) for hydrogen storage capacity

Danial Tufail a, Umair Ahmed a, Mazhar Haleem a, Bin Amin a, Muhammad Shafiq a,✉
PMCID: PMC11694718  PMID: 39758900

Abstract

The potential application of materials referred to as perovskite hydrides in hydrogen storage – a crucial element of renewable energy systems – has sparked a great deal of interest. We use density functional theory (DFT) to investigate the structural, formation energy, hydrogen storage, electronics, thermoelectric and elastic properties of NaXH3 (X = Be, Mg, Ca, and Sr) hydrides. The band gap is calculated using WC-GGA and WC-GGA+mBJ potentials. WC-GGA+mBJ potentials show improvement in band gap values. The thermoelectric properties of these compound are studied using post-DFT Boltzmann's techniques. The elastic constants and mechanical properties of the hydrides, such as their Shear modulus, Young’s modulus, Pugh ratio, Poisson ratios, anisotropic index and micro-hardness, are also calculated. Our findings show that all materials are mechanically stable and satisfy the Born criteria. The higher gravimetric ratios of all materials are good enough for storing hydrogen and can be used for advanced future applications. Furthermore, NaSrH3 is the perfect candidate for thermoelectric applications due to its higher power factor and figures of merit ZT (≈ 1).

We use DFT to investigate the structural, formation energy, hydrogen storage, electronics, thermoelectric and elastic properties of NaXH3 (X = Be, Mg, Ca, and Sr) hydrides as potential hydrogen storage materials.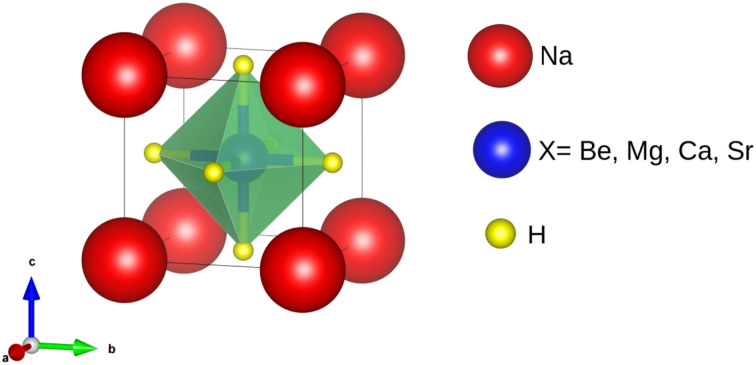graphic file with name d4ra05327c-ga.jpg

1. Introduction

With the rise in population, there has been a significant increase in global energy consumption. Hydrogen is considered one of the most promising energy carriers.1 In order to provide humanity with cutting-edge facilities, research and technology must provide solutions to the demand for the day by day energy increases.2 Most energy generated comes from fossil fuels, which are non-renewable and take longer to replenish or return to their starting form.3 As the world's energy needs increase, innovative strategies and research on sustainable energy are also updated.4 Although hydrogen has a few obstacles to overcome, it is undoubtedly a fantastic alternative to fossil fuels like coal, oil and natural gas.5 Because of environmental contamination and the use of fossil fuels, there is an increasing need for clean and economical energy sources. Renewable and electrified energy sources are being studied extensively.6,7 Hydrogen presents itself as an exceptional gas for use as a source of energy, but the most challenging aspect currently is storing hydrogen.8 For cars, computers, and mobile devices, hydrogen is a promising energy source that has the potential to displace non-renewable petroleum derivatives. Burning hydrogen can lower carbon dioxide emissions and is environmentally friendly, efficient and sustainable.9 Numerous materials have been investigated for the storage of hydrogen, such as complex hydrides, nanomaterials, and graphene-based materials. A high rate of hydrogen is needed for practical use in order to make it a viable alternative to fossil fuels.10 Researchers are working on a variety of perovskite materials that have exceptional hydrogen storage capacity. Hydrogen storage materials are made up of specific metals, compounds, and a special form of nano structured hydrides, which is made up of microscopic particles.11 Certain parameters must be met by the material used for energy storage, including a high volumetric and gravimetric ratio, good kinetic energy, noteworthy mechanical qualities, and the capacity to release hydrogen under normal circumstances.12,13 ABH3 perovskite is a hydride perovskite with a structure in which B is a light element that replaces one of the O-atoms in the BO6 octahedral, such as carbon (C), oxygen (O), or nitrogen (N). When lighter elements are substituted for oxygen, hydrogen forms more bonding sites, resulting in high storage capacity.14,15 They are different categories as the elements in groups 1 and 2 of the periodic table can be used to create A and B. The second class of hydrides of the perovskite type is produced by combining monovalent alkali or divalent metals A and B.16,17 This category consists of SrPdH3, LiCuH3, LiFeH3, MgFeH3, CaNiH3, MgCoH3, CaCoH3 and KCuH3.18,19 Due to their high gravimetric densities, light metal hydrides are among the most promising materials for on-board hydrogen storage.20 Metal hydrides are examples of functional compounds that aid in the absorption of hydrogen.21 Hydrogen is stored in vast amounts in the intermetallic phases of various metals through chemical bonding.22

NaMgH3 and Na0.9K0.1MgH3 have been experimentally synthesized using a high-energy ball milling method, which revealed that adding different concentrations of K on Na enhanced the dehydriding kinetic properties and increased the amount of hydrogen desorbed.23 Song et al.24 found that the gravimetric hydrogen storage capacities of NaMnH3, KMnH3, and RbMnH3 compounds are 3.74, 3.12, and 2.11 wt%. Li et al.25 studied the electronic structure of NaMgH3 and reported that it behaves as a metal, while Bouhadda et al.,21 Fornari et al.26 and Vajeeston et al.27 found theoretically that NaMgH3 must be a semiconductor. In this paper we reported the electronic behavior of NaMgH3 using a different exchange correlation potential in order to accurately treat the band structure.

The need for clean and renewable energy sources has become a serious challenge. In this regard, thermoelectric materials and hydrogen are very popular as a potentially broad, effective, and sustainable energy source. By solving the heating problems linked to storing hydrogen, thermoelectric properties can help make hydrogen a successful and sustainable energy source in the long term. Also, it has been found that thermoelectric devices can be used as hydrogen solid storage tanks.28 In contrast to compressed gas or liquid hydrogen, perovskite hydrides of the type NaXH3 (X = Be, Mg, Ca and Sr) are considered safer options for storing hydrogen. This study provides important information that could improve the efficiency and safety of hydrogen storage technologies in the future by examining the characteristics of these materials. For hydrogen storage applications we calculated the gravimetric ratio and formation energy. Furthermore, other important properties such as structural, electronic, mechanical and thermoelectric characteristics of NaXH3 (X = Be, Mg, Ca, Sr) hydride perovskites are also calculated and studied in this article.

2. Computational details

Density functional theory (DFT) and an approach known as full-potential linearized augmented plane wave plus local orbitals (FP-LAPW+lo) implemented in WEIN2k code is used in the first principles calculations of NaXH3 (X = Be, Mg, Ca, and Sr).29,30 We used WC-GGA as an accurate exchange-correlation potential in our calculations.31 To ascertain these properties, the WC-GGA is employed in conjunction with the modified Beck-Johnson (mBJ) approach.32 mBJ is one of the best density functional approaches (error of about 2%) to treat the electronic band structure of perovskites and various semiconductor materials.33 We use the finer, 7 × 7 × 7 and the denser 10 × 10 × 10 k-mesh to determine the structural and electronic properties. To obtain the elastic constant, the energy strain approach which is included in the WEIN2k package was applied.34 By subjecting the cubic lattice to deformation, only three independent elastic constants C11, C12 and C44 can be calculated. Thermoelectric characteristics including figure of merit (ZT), power factor (PF), electronic thermal conductivity (κ), electrical conductivity (σ), and Seebeck coefficient (S) were investigated utilizing WC-GGA+mBJ through the extended semi-classical BoltzTraP package.35 Different possible geometries are designed and visualized using VESTA, with the assist of vesta code we obtained the polyhedral structure of these perovskite materials.36

3. Results and discussion

3.1. Structural properties

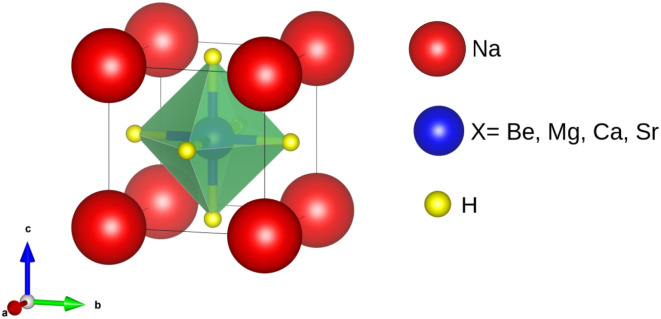
NaXH3 (X = Be, Mg, Ca, Sr) hydrides have the Pm3̄m (221) space group. The unit cells of these compounds were figured out using fractional coordinates. The Na-atom is found at the corner position (0, 0, 0), the X metal atom is located at the center position (0.5, 0.5, 0.5) and the H-atom occupies the center position of the face of the octahedral sites (0.5, 0, 0), (0, 0.5, 0) and (0, 0, 0.5). In Fig. 1, the structural arrangement is presented.

Fig. 1. Crystal structure of NaXH3 (X = Be, Mg, Ca, Sr) perovskite-type hydrides.

Fig. 1

Open in a new tab

Fig. 1 shows that the Na-atoms (red sphere) are cations which occupy the corner of a cube. The X-atom (blue sphere) (X = Be, Mg, Ca, Sr) also serves as a cation but with a position at the center. The face of the cube is occupied by hydrogen atoms (yellow sphere) serving as anions.

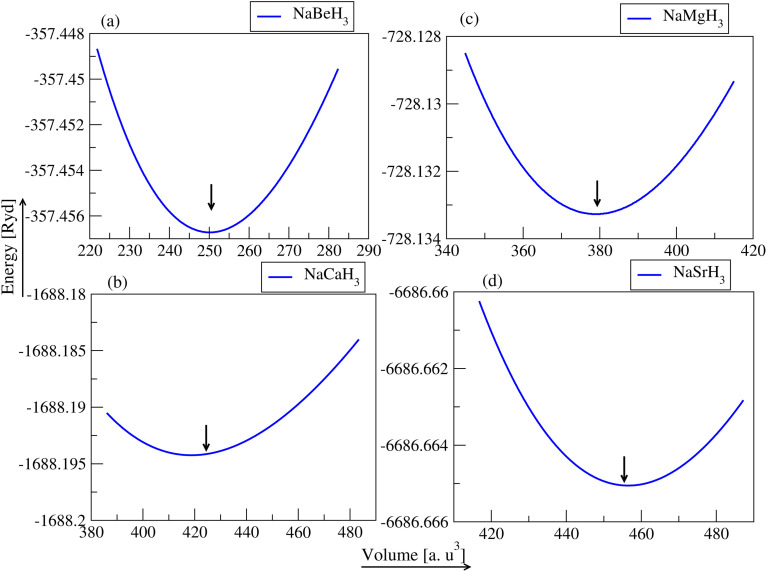
The structural stability of perovskite materials can be understood using energy–volume curves. The E–V curves for NaXH3 (X = Be, Mg, Ca, Sr) are shown in Fig. 2(a)–(d). The E–V plot for any material provides very valuable information about its mechanical structure and dynamic stability. Achieving a ground state is the first step in the stability of any physical compound that can be found by plotting an energy graph in terms of its volume.37 Forces were firstly calculated, using the WC-GGA function. The system was unfastened until the forces acting on the atoms were negligible. The optimized lattice constants were obtained using the Birch–Murnaghan equation of state,38

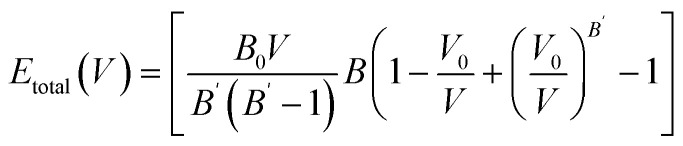3.1. 1

where in eqn (1)B0, B′, V0 and E(V) are the bulk modulus, first derivative of B, unit cell volume and energy at equilibrium ground states, respectively. Fig. 2 shows the evolution of the total energy as a function of the unit cell volume of cubic perovskite-type NaXH3. The equilibrium lattice parameter was computed also from the structural optimization, using the Birch–Murnaghan equation of state listed in Table 1. The E–V plot is generated by varying the lattice constant and calculating the minimal energy point – the lowest point of the curve where the arrow is set – which shows where the structure is dynamically stable. E–V plot provides important details regarding the properties and structural stability of the NaXH3 (X = Be, Mg, Ca, Sr) material. Table 1 shows that the calculated lattice constants are in agreement with other reported values. The previous studies20–22 on the same type of hydrides show that these materials may be used for hydrogen storage applications. When a substance absorbs hydrogen, its stability may be ascertained using the E–V curve. A material is said to be capable of efficiently storing hydrogen if its energy dramatically drops as its volume increases. This connection guarantees that the material stays stable and effective for storage while demonstrating how well it can withstand the changes that occur during hydrogen absorption, which could be employed in hydrogen storage applications.

Fig. 2. E–V curve of NaXH3 (X = Be, Mg, Ca, Sr), arrow shows the minimum energy point.

Fig. 2

Open in a new tab

Table 1. The calculated lattice constants (Å), bulk's modulus B (GPa), volume (Å3), formation energy (ΔHf) and gravimetric ratio (Cwt%) of perovskite hydride NaXH3 (X = Be, Mg, Ca, Sr).

Compound a (Å) C wt% ΔHf (eV per atom)
Present work Previous work
NaBeH3 3.397 3.281 (ref. 20) 8.6 −0.285
NaMgH3 3.879 2.009 (ref. 21) 6.0 −0.241
NaCaH3 3.958 — 4.5 −0.134
NaSrH3 4.077 — 2.6 −0.107
Open in a new tab

3.2. Formation energy and hydrogen storage

To compute the thermodynamical stability of NaXH3 (X = Be, Mg, Ca, Sr) their formation energies ΔHf are determined using the equation:39

ΔHf(NaXH3) = [Etotal(NaXH3) − Es(Na) − Es(X) − 3/2(EsH2)]. 2

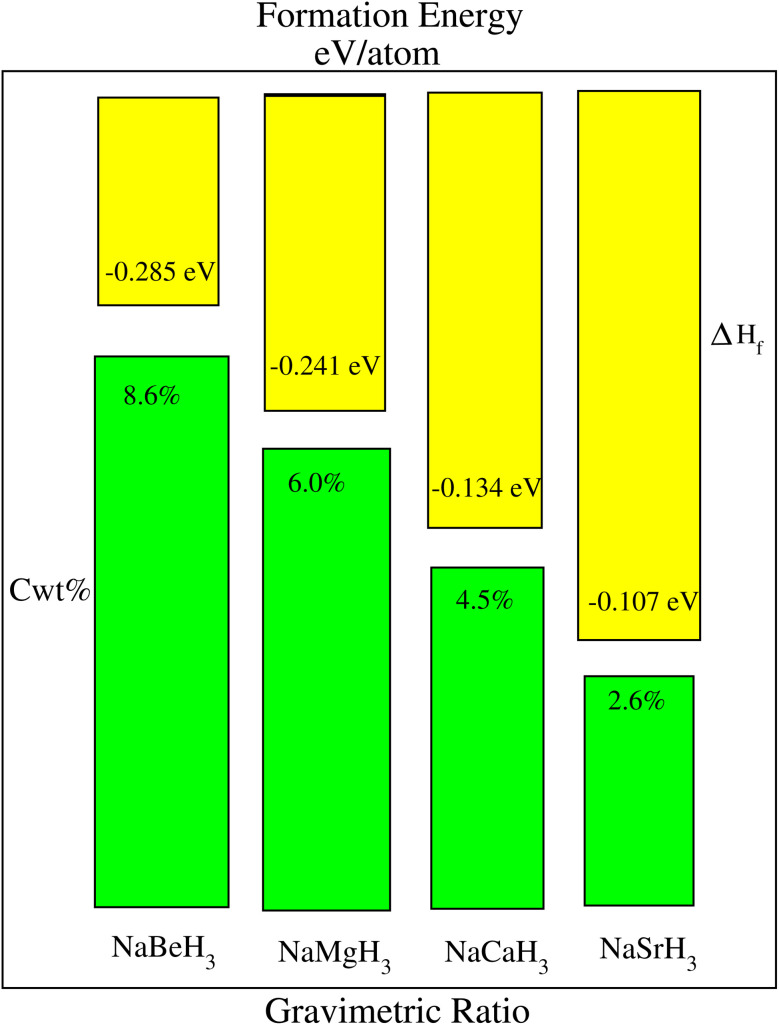
In eqn (2) the individual ground state energies Es(Na), Es(X) and EsH2, as well as Etotal(NaXH3), the energy of the whole compound, are used. The stability formalisms for the formation energies of NaXH3 perovskite materials are shown in Fig. 3. The figure shows that the calculated value of all materials have a negative formation energy (yellow bar), indicating that these materials are thermodynamically stable. The negative formation energy of NaXH3 is also listed in Table 1. NaBeH3 has the lowest formation energy (−0.285) among all the materials under consideration and is the most thermodynamically stable material along with NaCaH3 and NaMgH3.

Fig. 3. Formation energy ΔHf (yellow bars) and gravimetric storage capacity Cwt% (green bars) of NaXH3 (X = Be, Mg, Ca, Sr).

Fig. 3

Open in a new tab

The potential for hydrogen storage applications of NaXH3 (X = Be, Mg, Ca, Sr) hydride perovskites has been assessed by calculating their gravimetric storage capacity using eqn (3), the hydrogen deposited is represented by the gravimetric ratios. The algorithm utilized to assess the cwt% for gravimetric ratio is given by:40,41

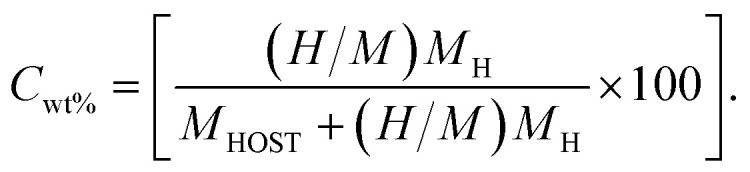3.2. 3

In eqn (3), MH represents the weight of hydrogen atoms, MHOST represents the weight of the material it's in and H/M is the ratio of hydrogen atoms to material atoms. Fig. 3 represents the weight percentage of the gravimetric capacity of perovskite hydrides NaXH3 (X = Be, Mg, Ca, Sr) in which NaBeH3 can hold the most at 8.6% and NaMgH3 can hold 6.0%. Also, NaCaH3 can store 4.5% but NaSrH3 can only store 2.6%. Therefore, NaBeH3, NaMgH3, and NaCaH3 have good gravimetric ratios. The energy–volume curve demonstrates a material's stability by displaying how its energy varies with volume. Lower energy states correspond with lower formation energies, making the material better suited for hydrogen storage. The lowest formation energy of NaBeH3 compounds allows hydrogen to enter and exit more easily compared to other compounds, and achieves a hydrogen gravimetric capacity of 8.6%. High formation energy can make hydrogen storage less efficient. These principles work together to determine the best materials for successful hydrogen storage applications.42,43

3.3. Electronic properties

Examining the electronic structure of compounds allows us to better comprehend their solid form. Several major characteristics of materials can be better understood thanks to such studies. Both the band structure and the total density of electronic states are important in the study of solid construction.

3.3.1. Band structure

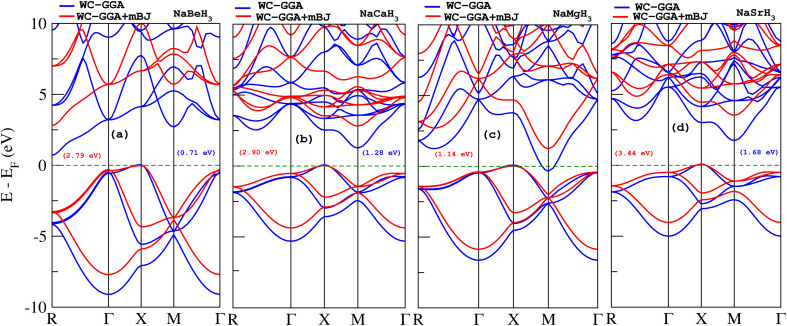
The band structure for the NaXH3 (X = Be, Mg, Ca, Sr) cubic phase has been calculated along the high symmetry directions in the first Brillouin zone, with WC-GGA and WC-GGA+mBJ exchange potential method. Fig. (4a–d) display the band structure of NaXH3. We notice that the minima and maxima of the conduction and valence band are not situated at the same point of symmetry. Therefore, these materials have an indirect band gap transition in both correlations. The material NaBeH3 has Γ–R and NaMgH3, NaCaH3 and NaSrH3 have X–M direction, which validates that our materials have semiconductor nature. The calculated band gaps for all considered materials are given in Table 2.

Fig. 4. The band structure of NaXH3 (X = Be, Mg, Ca, Sr) with WC-GGA and WC-GGA+mBJ.

Fig. 4

Open in a new tab
Table 2. Calculated band gap with WC-GGA and WC-GGA+mBJ NaXH3 (X = Be, Mg, Ca, Sr).
Compound Present work Other work
WC-GGA WC-GGA+mBJ WC-GGA GGA+mBJ
NaBeH3 0.71 eV 2.79 eV 0.76 eV 3.1 eV (ref. 20)
NaMgH3 0.0 eV 1.14 eV — —
NaCaH3 1.28 eV 2.90 eV — —
NaSrH3 1.68 eV 3.44 eV — —
Open in a new tab

Using the WC-GGA approximation (blue lines in Fig. 4), the Eg values for NaBeH3, NaCaH3 and NaSrH3 compounds are found to be 0.71 eV, 1.28 eV, 1.68 eV, respectively, while NaMgH3 shows metallic nature using WC-GGA. Whereas the WC-GGA+mBJ approach (red lines in Fig. 4) changes the band gap nature of NaMgH3 material from metallic to semiconductor with a band gap value of 1.14 eV. Similarly, the improved band gap of NaBeH3, NaCaH3 and NaSrH3 are 2.79 eV, 2.90 eV and 3.44 eV, respectively.

The electronic band gap has a major impact on the capacity to store hydrogen. To permit ideal electron transport between the material and hydrogen from the valence to conduction band, a modest band gap that increases binding energy is required, as in our computed data for NaBeH3, explaining its better hydrogen intake of up to 8.6%. Additionally, such a band gap enhances electrical conductivity, which promotes the passage of hydrogen. The band gap also helps predict phase stability during the absorption and desorption of hydrogen.

3.3.2. Density of states

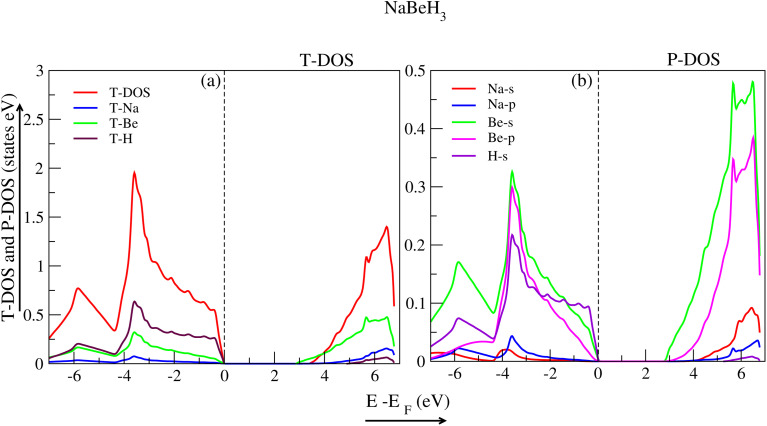
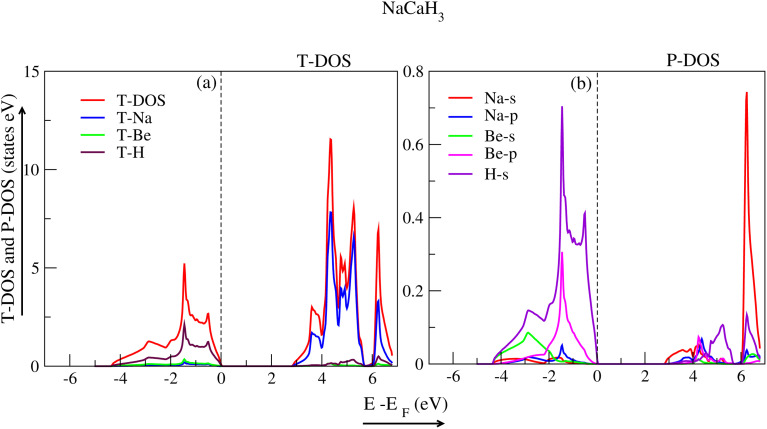
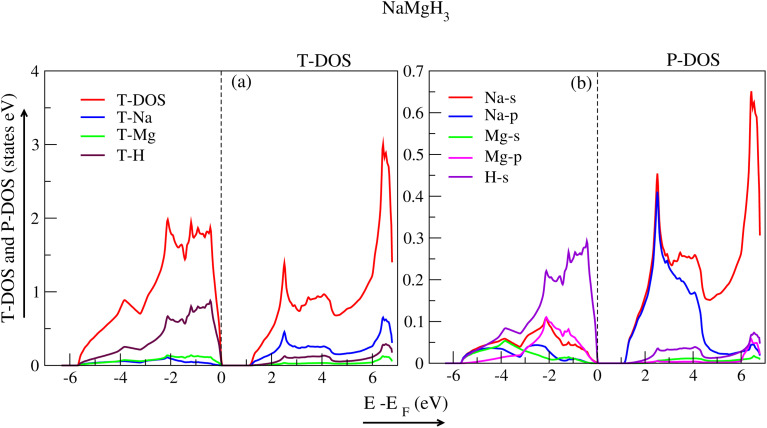
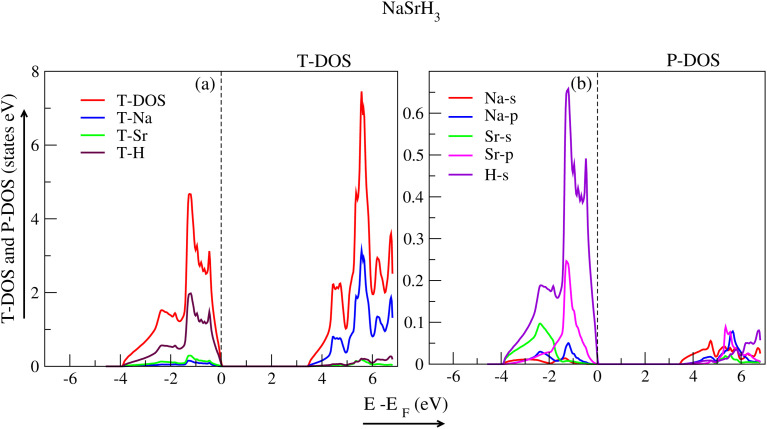
Density of states (DOS) is used to scrutinize how electronic band structure is affected due to atomic exchange and relaxation distribution of energy levels. By examining DOS, one can discern if a material contributes metallic or semiconductor behaviour. The partial density of states (P-DOS) gives insight into the role of an electron's orbital in the conduction and valence band. The DOS for each material were examined using WC-GGA+mBJ. The total density of states (T-DOS) and P-DOS for the hydride perovskite NaXH3 materials are displayed in Fig. 5–8. Strong hybridization between hydrogen, sodium and the X atom (X= X = Be, Mg, Ca, Sr) is found, as expected. Therefore, hydrogen interaction with other atoms increases the stability of the compounds as shown in the E–V plots (Fig. 2).

Fig. 5. Total and partial density of states for NaBeH3.

Fig. 5

Open in a new tab
Fig. 6. Total and partial density of states for NaCaH3.

Fig. 6

Open in a new tab
Fig. 7. Total and partial density of states for NaMgH3.

Fig. 7

Open in a new tab
Fig. 8. Total and partial density of states for NaSrH3.

Fig. 8

Open in a new tab

Fig. 5(a) shows the T-DOS of NaBeH3 (red line). Fig. 5(a) reveals the primary influence of the individual atoms (Na, Be and H) in both the valence band (VB) and conduction band (CB). The P-DOS of NaBeH3 in Fig. 5(b) shows that the VB and CB can be attributed to the s and p-orbitals of the Be-atom, while the VB can also be attributed to the s-orbital of the H-atom. Fig. 6(a) represents the T-DOS of NaCaH3. The CB can be attributed to the dominant peak of the Na-atom (blue peak); the T-DOS are depicted by (red peaks). Fig. 6(b) shows the P-DOS of NaCaH3, where the s-orbital of the H-atom and p-orbital of the Be-atom have major influence on the VB (violet and magenta peak), while in CB the s-orbital of the Na-atom plays a vital role.

The T-DOS of NaMgH3 are presented in Fig. 7(a), where the significant contribution of the H-atom in the VB and Na-atom in the CB are shown with the maroon and blue peaks, respectively. The P-DOS of NaMgH3 is presented in Fig. 7(b), where the s-orbital of the H-atom has a major contribution to the VB, and the CB can be attributed to the s and p-orbitals of the Na-atom. Fig. 8(a) shows the T-DOS of NaSrH3 with major contribution of the H-atom to the VB (maroon peak), and Na-atom (blue peak) to the CB, while the red peak indicates the T-DOS. Fig. 8(b) shows that the P-DOS of NaSrH3 has a significant contribution from the s-orbital of the H-atom and p-orbital of the Sr-atom, and the VB is contributed by the p-orbital of Na and Sr-atom in CB.

DOS is significant for hydrogen storage because it indicates the availability of electronic states suitable for hydrogen binding. A high DOS near the Fermi level suggests that a material has more binding sites, which boosts its capacity to absorb hydrogen; in the present work NaBeH3 has the highest DOS. Furthermore, the DOS structure affects the energy levels associated with hydrogen interactions, which in turn affects binding energies. An optimal DOS promotes efficient charge transfer, which stabilizes hydride phases during absorption and desorption. Overall, a positive DOS contributes to improved reaction kinetics and stability, making it important for efficient hydrogen storage.44

3.4. Thermoelectric properties

Thermoelectric properties play a crucial role in heat transfer, such properties have diverse applications in storing energy effectively and providing solutions to various problems. Thermoelectric materials are especially valuable in thermoelectric devices as they can convert waste heat into usable electrical energy. By employing thermoelectric devices to harness and utilize wasted engine heat, significant cost savings can be achieved. The use of thermoelectric materials holds promise in addressing society's energy challenges. Examples of different types of thermoelectric properties include Seebeck coefficients, electrical conductivity and thermal conductivity.

3.4.1. Seebeck coefficient (S)

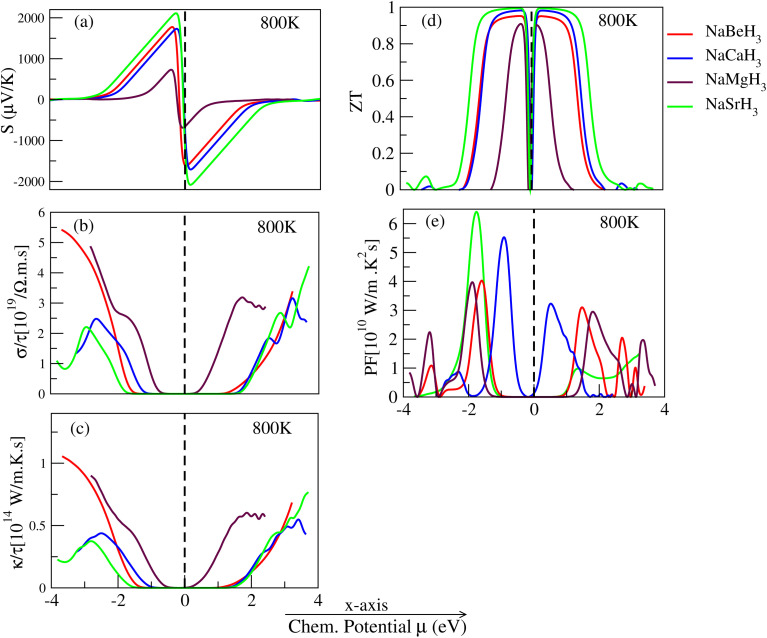
How much voltage is transferred from a junction that is hotter to one that is colder is known as the thermo power. Varying temperature causes changes in the Seebeck coefficient. With rising temperatures, it gets smaller in the range 100 V K−1 to +1000 V K−1. Thermoelectric applications require substances with high Seebeck values. The Seebeck coefficient is the ability of a material to have a temperature gradient which produces a thermoelectric voltage. The Seebeck coefficient of NaBeH3, NaCaH3, NaSrH3 is presented in Fig. 9(a), at 800 K. The Seebeck coefficient values for NaBeH3, NaMgH3, NaCaH3, NaSrH3 are given in Table 3 and 4 for p-type and n-type doping, respectively. From Table 3 and 4 and Fig. 9(a), we show that NaSrH3 has the larger value at 800 K in n-type regions.

Fig. 9. Thermoelectric properties of NaXH3 (X = Be, Mg, Ca, Sr).

Fig. 9

Open in a new tab
Table 3. Calculated values of Seebeck coefficient (S), electrical conductivity(σ), power factor (P), thermal conductivity (K) and figure of merit (ZT) in (p-type) region of thermoelectric property of NaBeH3, NaCaH3, NaMgH3, NaSrH3.
Compound p-type S (V K−1) K (W m−1 K−1 s−1) σ (Ω−1 ms−1) P (W mK−2 s−1) ZT
NaBeH3 800 K 1700 0.61 3.4 2.9 0.945
NaCaH3 800 K 1730 0.54 3.1 3.2 0.977
NaMgH3 800 K 693 0.59 3.0 2.7 0.881
NaSrH3 800 K 2014 0.71 4.1 1.4 0.988
Open in a new tab
Table 4. Calculated values of Seebeck coefficient (S), electrical conductivity (σ), power factor (P), thermal conductivity (K) and figure of merit (ZT) in (n-type) region of thermoelectric property of NaBeH3, NaCaH3, NaMgH3, NaSrH3.
Compound n-type S (V K−1) K (W m−1 K−1 s−1) σ (Ω−1 ms−1) P (W m K−2 s−1) ZT
NaBeH3 800 K 1757 1.04 5.3 4.0 0.951
NaCaH3 800 K 1790 0.44 2.5 5.4 0.972
NaMgH3 800 K 710 0.88 4.3 3.8 0.891
NaSrH3 800 K 2114 0.37 2.1 6.4 0.998
Open in a new tab

3.4.2. Electrical conductivity (σ)

Electrical conductivity is a term for how a material can conduct electric currents. Using the strength of the electrical field to determine the current density ratio. While a thermoelectric material possesses a high electrical conductivity, the influence of joule heating should be minimum. Materials are categorized according on how well they conduct electricity; in contrast to insulators, conductors have a relatively high electrical conductivity. The Fermi level is nearer to the conduction band in a conductor than it is in a semiconductor, it is positioned in the middle of the valence band and conduction band. The Fermi level is nearer to the conduction band in p-type semiconductors than it is in n-type semiconductors, and vice versa. Temperature has a significant impact on electrical conductivity. Conductivity is 0 at absolute zero (K) temperatures, but it goes up exponentially as temperature goes up. The calculated electrical conductivities of NaBeH3, NaMgH3, NaCaH3, NaSrH3 are shown in Fig. 9(b) at 800 K and are listed in Table 3 and 4 at 800 K. The greatest electrical conductivity values are found for NaBeH3 at 800 K in the n-type region.

3.4.3. Thermal conductivity (κ)

A material can conduct heat differently, and its ability to do so is called thermal conductivity. Heat means being warm or hot. Some materials do not let heat move very fast, while others let heat move quickly. Metals can usually let heat pass through them easily. Good conductors easily move heat while insulating materials do not – for instance, Styrofoam or rock wool. Materials that cannot transfer heat well are often used in things that need to stay cold and in things that stop heat from getting through. The calculated thermal conductivities of NaBeH3, NaMgH3, NaCaH3 and NaSrH3 are shown in Fig. 9(c) at 800 K and the calculated values of thermal conductivity of NaBeH3, NaMgH3, NaCaH3, NaSrH3 are presented in Table 3 and 4 at 800 K.

3.4.4. Figure of merit (ZT)

The term “figure of merit” is a general concept used in various fields to quantify and compare the performance of a system or a device. The figure of merit is a number that shows how well the system works. In the particular study of materials that can conduct heat or convert it into electricity, scientists often use the figure of merit to measure how well a thermoelectric material will work. We use an equation to calculate it:

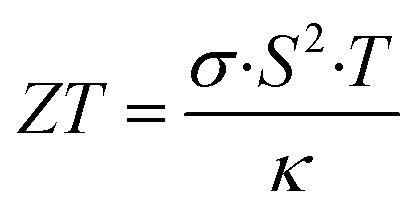3.4.4. 4

where T is the temperature; κ is the material's heat conductivity; σ is its electrical conductivity; S is its electrical generating capacity. To put it simply, a higher ZT value indicates that the material has superior heat-controlling capabilities, useful in appliances that run on electricity for heating or cooling. Fig. 9(d) illustrates the degree to which NaBeH3, NaMgH3, NaCaH3, NaSrH3 function at varying temperatures. Table 3 and 4 illustrate the observed values for NaXH3 (X = Be, Ca, Mg, Sr) for temperatures at 800 K. NaSrH3 has the maximum value in the n-type region, 0.998.

3.4.5. Power factor (PF)

To calculate the thermoelectric power factor of a material, one of the best parameters to consider is the power factor (PF). PF = σS2, here ‘S’ represents the Seebeck coefficient and ‘σ’ represents the electrical conductivity of the material. The calculated power factor of NaBeH3, NaMgH3, NaCaH3, NaSrH3 are shown in Fig. 9(e) at 800 K, and the calculated power factor values are presented in Table 3 and 4. Further, it is shown in Fig. 9(e), that the n-type NaSrH3 has the largest value of PF making it favorable for thermoelectric applications. Among NaBeH3, NaCaH3, NaMgH3 and NaSrH3, the NaSrH3 is the perfect candidate for use in thermoelectric applications because it has the highest PF and high ZT in n-type doping.

To obtain a high ZT value, the material will have a large Seebeck coefficient, high electrical conductivity, and low thermal conductivity. It is evident from Table 3 and 4 that the value of Seebeck coefficient is close to unity. Therefore, all of these materials could be used in thermoelectric power generators.45 The thermoelectrical behavior of materials, including conductivity, energy band gaps, power factor and figure of merit, are essential for promoting the absorption and desorption of hydrogen. Positive thermoelectric characteristics may also help with heat control during the hydrogen cycle, which would boost storage efficiency even more. Furthermore, improving the interaction of electrical conductivity, thermal conductivity, and the Seebeck coefficient, can result in sophisticated materials that excel at both hydrogen storage and thermoelectric conversion. This integration promotes the development of sustainable energy solutions by increasing energy efficiency in hydrogen-based systems.

3.5. Elastic and mechanical properties

The strain-dependent matrix of second-order elastic constants (Cij), equilibrium volume and crystal energy are some of the parameters that affect a lattice's elastic behavior. The elastic stiffness tensor for NaXH3 (X = Be, Mg, Ca, Sr) compounds displaying the symmetry features of the Pm3̄m space group is composed of three separate components, denoted by Young’s notation as C11, C12, and C44.46,47 The calculated values of C11, C12 and C44 for NaXH3 (X = Be, Mg, Ca, Sr) perovskites are listed in Table 5. It is evident from the table that our calculated values of elastic constants fulfil the Born stability criteria, commonly known as the mechanical stability conditions.48,49

Table 5. Computed elastic constants (Cij) and Cauchy's pressure (Cp) of NaXH3 (X = Be, Mg, Ca, Sr).

Compound C 11 C 12 C 44 C p
NaBeH3 84.738 35.037 61.473 −26.436
NaMgH3 119.26 16.062 0.1182 15.944
NaCaH3 76.264 1.326 12.816 −11.49
NaSrH3 75.222 2.759 12.707 −14.944
Open in a new tab

The positive/negative of Cauchy’s pressure (Cp = C12 − C44) can be used to evaluate whether a material exhibits ductile/brittle behavior. The data presented in the Table 5 indicate that NaXH3 (X= Be, Mg, Ca, Sr) display brittle behaviour, which is empirically determinable. The bulk modulus (B), Shear modulus (G), Young's modulus (E), Poisson's proportion (v) and Pugh’s ratio (B/G) are illustrations of the mechanical properties of the materials, calculated using the elastic constant (Cij), shown in Table 6, using equations given in ref. 50 and 51. The bulk modulus of a material indicates the maximum pressure it can bear without changing shape. The shear modulus shows how well a material can withstand pressure without losing its shape. The expansion and deformation of materials are due to their bulk and shear moduli. Young's modulus is a measure of a material's stiffness that compares how much it expands when pushed, to the amount of force applied to it. Table 6 shows that, in comparison to other materials, the material considered that has the largest bulk modulus B value is NaBeH3. The second column of results in the table indicate the shear G distortion, the compound with the greatest value for G was found to be NaBeH3. The values of B and G were used to calculate the young modulus E. In our calculations, a high Young's modulus E indicates that NaBeH3 is tougher than other materials.52,53 Materials that can bend a lot and do not break easily have a B/G ratio of more than 1.75, showing the ductile behaviour of the material. When Poisson's ratio gets close to 0.5, the material is likely to become difficult to compress. When v = 0.5, it is almost impossible to compress. Compared to other materials that can change shape easily, our estimated values for v range from 0.05 to 0.06, which shows that NaSrH3 is a material that is hard to compress. Table 6 provides the obtained values of anisotropic (A) for cubic NaXH3. The values of A significantly deviate from unity, indicating that these cubic materials, NaXH3, are anisotropic. Micro-hardness (H) is a measure of a material’s resistance to compression. According to the results in Table 6, NaBeH3 has a higher micro-hardness than other materials, which means it is more resistant to being compressed by small components.54

Table 6. Calculated bulk modulus (B), Shear modulus (G), Young’s modulus (E), Pugh's ratio (B/G), Poisson ratio (v), anisotropic index (A) and micro-hardness (H), of NaXH3 (X = Be, Mg, Ca, Sr).

Compound B (GPa) G (GPa) E (GPa) B/G v A H (GPa)
NaBeH3 51.60 58.35 127.14 0.88 0.05 2.47 17.64
NaMgH3 50.46 17.35 46.72 2.90 0.23 0.02 3.40
NaCaH3 27.59 27.59 59.65 0.95 0.07 0.34 7.88
NaSrH3 26.91 32.06 68.84 0.83 0.06 0.48 9.60
Open in a new tab

4. Conclusion

In summary we considered the structural, formation energy, hydrogen storage, electronics, thermoelectric and elastic properties of NaXH3 (X = Be, Ca, Mg, and Sr) cubic hydride perovskites. The formation energy and elastic stability criteria confirm their mechanical stability. The band of the materials are increased by applying the mBJ correction. For NaXH3 (X = Be, Mg, Ca, and Sr), the computed hydrogen storage capacities are 8.6, 6.0, 4.6, and 2.6 wt%, respectively. Therefore, NaBeH3, NaMgH3, and NaCaH3 are considered to be potential materials for hydrogen storage applications. For NaSrH3, the power factor at negative chemical potentials is about 25–30% higher than positive chemical potentials, which indicates that the n-type doping is more efficient and the material could be suitable for thermoelectric applications.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of interest

There are no conflicts to declare.

References

  1. Pan Y. Exploring the structural, physical properties and hydrogen storage properties of LiBHx (x= 1 and 4) lithium borohydrides. Ceram. Int. 2024;50(2):3837–3842. [Google Scholar]
  2. Ahmed B. Tahir M. B. Li A. Sagir M. First principles screening of structural, electronic, optical and elastic properties of Cu-based hydrides-perovskites XCuH3 (X= Ca and Sr) for hydrogen storage applications. Int. J. Hydrogen Energy. 2024;54:1001–1007. [Google Scholar]
  3. Shang L. Chen X. Liu B. Tao Q. Chen R. Formation of eutectic structure and de/hydriding kinetics properties: A novel Ti-Hf-V-Mn multi principal element alloy. Int. J. Hydrogen Energy. 2024;50:1152–1163. [Google Scholar]
  4. Achqraoui M. El-Akkel M. Bekkioui N. Ez-Zahraouy H. First principles calculation of perovskite-type hydrides KXH3 (X= Al, Cu) for hydrogen storage applications. E3S Web Conf. 2023;469:00067. [Google Scholar]
  5. Klopčič N. Grimmer I. Winkler F. Sartory M. Trattner A. A review on metal hydride material for hydrogen storage. J. Energy Storage. 2023;72:108456. [Google Scholar]
  6. Shahi R. R. Gupta A. K. Amit K. Kumari P. Prespective of high entropy alloys as hydrogen storage materials. Int. J. Hydrogen Energy. 2023;48(56):21412–21428. [Google Scholar]
  7. Garara M. Benzidi H. Abdellaoui M. Lakhal M. Benyoussef A. Mounkachi O. Loulid M. Hydrogen storage properties of perovskite type-MgCoH3 under strain effect. Mater. Chem. Phys. 2020;254:123417. [Google Scholar]
  8. Hailong Y. Wenzhi W. Wang Q. Liu J. Kong D. Yachen G. Unusual luminescence and its decay behavior of CH3 NH3 PbBr3 single crystals at orthorhombic phase. Mater. Today Phys. 2022;22:100621. [Google Scholar]
  9. Baishya R. Unique Solution of Unpolarized Evolution Equations. J. Appl. Sci. 2022;9:44. [Google Scholar]
  10. Surucu G. Gencer A. Candan A. Gullu H. H. Isik M. CaXH3 (X= Mn, Fe, Co) perovskite type hydrides for hydrogen storage applications. Int. J. Energy Res. 2020;44(3):2345–2354. [Google Scholar]
  11. Shah S. F. A. Murtaza G. Ismail K. Raza H. H. Khan I. M. First principles investigation of transition metal hydrides LiXH3 (X= Ti, Mn, and Cu) for hydrogen storage. J. Comput. Electron. 2023;22(4):921–929. [Google Scholar]
  12. Nagar R. Srivastava S. et al., Recent developments in state-of-the-art hydrogen energy technologies–review of hydrogen storage materials. Solar Compass. 2023;5:100033. [Google Scholar]
  13. Kong L. Liu G. Synchrotron-based infrared microspectroscopy under high pressure: An introduction. Matter Radiat. Extremes. 2021;6(6):068202. [Google Scholar]
  14. Zhang X. Tang Y. Zhang F. Lee C. S. A novel aluminum-graphite dual-ion battery. Adv. Energy Mater. 2016;6(11):1502588. [Google Scholar]
  15. Wang M. Jiang C. Zhang S. Song X. Tang Y. Cheng H. M. Reversible calcium alloying enables a practical room-temperature rechargeable calcium-ion battery with a high discharge voltage. Nat. Chem. 2018;10(6):667–672. doi: 10.1038/s41557-018-0045-4. [DOI] [PubMed] [Google Scholar]
  16. Schouwink P. Ley M. B. Tissot A. Hagemann H. Jensen T. R. Smrčok L. Černý R. Structure and properties of complex hydride perovskite materials. Nat. Commun. 2014;5:5706. doi: 10.1038/ncomms6706. [DOI] [PubMed] [Google Scholar]
  17. Rehman Z. Rehman M. A. Rehman B. Amjad M. Awais M. Iqbal I. Rafique A. A DFT study of structural, electronic, mechanical, phonon, thermodynamic, and H2 storage properties of lead-free perovskite hydride MgXH3 (X= Cr, Fe, Mn) J. Phys. Chem. Solids. 2024;186(1):111801. [Google Scholar]
  18. Sato R. Saitoh H. Endo N. Takagi S. Matsuo M. Aoki K. Orimo S. I. Formation process of perovskite-type hydride LiNiH3: In situ synchrotron radiation X-ray diffraction study. Appl. Phys. Lett. 2013;102(9):091901. [Google Scholar]
  19. Sun C. Alonso J. A. Bian J. Recent advances in perovskite-type oxides for energy conversion and storage applications. Adv. Energy Mater. 2021;11(2):2000459. [Google Scholar]
  20. Rehmat B. Rafiq M. A. Javed Y. Irshad Z. Ahmed N. Mirza S. M. Elastic properties of perovskite-type hydrides LiBeH3 and NaBeH3 for hydrogen storage. Int. J. Hydrogen Energy. 2017;42(15):10038–10046. [Google Scholar]
  21. Bouhadda Y. Bououdina M. Fenineche N. Boudouma Y. Elastic properties of perovskite-type hydride NaMgH3 for hydrogen storage. Int. J. Hydrogen Energy. 2013;38(3):1484–1489. [Google Scholar]
  22. Bouhadda Y. Djellab S. Bououdina M. Fenineche N. Boudouma Y. Structural and elastic properties of LiBH4 for hydrogen storage applications. J. Alloys Compd. 2012;534:20–24. [Google Scholar]
  23. Tao S. mi Wang Z. Wan Z. Z. Deng J. Q. Zhou H. Yao Q. Enhancing the dehydriding properties of perovskite-type NaMgH3 by introducing potassium as dopant. Int. J. Hydrogen Energy. 2017;42(6):3716–3722. [Google Scholar]
  24. Song R. Xu N. Chen Y. Chen S. Dai W. Zhang W. First-principles investigation for the hydrogen storage, mechanical, electronic, optical, dynamic, and thermodynamic properties of XMnH3 (X= Na, K, Rb) perovskites for hydrogen storage applications. Vacuum. 2024;222:113007. [Google Scholar]
  25. Li Y. Rao B. K. McMullen T. Jena P. Khowash P. K. Electronic structure of the LiMgH3 class of compounds: cluster calculations. Phys. Rev. B:Condens. Matter Mater. Phys. 1991;44(12):6030e6. doi: 10.1103/physrevb.44.6030. [DOI] [PubMed] [Google Scholar]
  26. Fornari M. Subedi A. Singh D. J. Structure and dynamics of perovskite hydrides AMgH3 (A1/4Na, K, Rb) in relation to the corresponding fluorides: a first-principles study. Phys. Rev. B: Condens. Matter Mater. Phys. 2007;76(21):214118. [Google Scholar]
  27. Vajeeston P. Ravindran P. Kjekshus A. Fjellvag H. First- principles investigations of the MMgH3 (M=Li, Na, K, Rb, Cs) series. J. Alloys Compd. 2008;450(1–2):327–337. [Google Scholar]
  28. Lahmer K. Numerical investigation of thermal and electrical management during hydrogen reversible solid-state storage using a novel heat exchanger based on thermoelectric modules. Int. J. Hydrogen Energy. 2022;47(71):30580–30591. [Google Scholar]
  29. Blaha P. Schwarz K. Tran F. Laskowski R. Madsen G. K. Marks L. D. WIEN2k: An APW+ lo program for calculating the properties of solids. J. Chem. Phys. 2020;152(7):123411–123417. doi: 10.1063/1.5143061. [DOI] [PubMed] [Google Scholar]
  30. McCabe C. J. Halvorson M. A. King K. M. Cao X. Kim D. S. Interpreting interaction effects in generalized linear models of nonlinear probabilities and counts. Multivar. Behav. Res. 2022;57(2–3):243–263. doi: 10.1080/00273171.2020.1868966. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Wu Z. Cohen R. E. More accurate generalized gradient approximation for solids. Phys. Rev. B: Condens. Matter Mater. Phys. 2006;73(23):235116. [Google Scholar]
  32. Tran F. Blaha P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 2009;102(22):226401. doi: 10.1103/PhysRevLett.102.226401. [DOI] [PubMed] [Google Scholar]
  33. Barlido P. Aull T. Huran A. W. Tran F. Marques M. A. L. Large-scale benchmark of exchange-correlation functionals for the detremination of electronic band gaps of solids. J. Chem. Theory Comput. 2019;15:5069–5079. doi: 10.1021/acs.jctc.9b00322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Charpin T., A Package for Calculating Elastic Tensors of Cubic Phase Using WIEN, Laboratory of geometrix F-75252 Paris, France, 2001 [Google Scholar]
  35. Madsen G. K. H. Singh D. J. BoltzTraP. A code for calculating band-structure dependen quantities. Comput. Phys. Commun. 2006;175:67–71. [Google Scholar]
  36. Momma K. Izumi F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011;44(6):1272–1276. [Google Scholar]
  37. Othman M. S. Sadeghi M. A Vahabzadeh N. Boochani A. Amiri M. Hydrogen effect on half-metallic and thermoelectric properties of CoRhMnSi [001] film. Int. J. Energy Res. 2021:1–16. [Google Scholar]
  38. Birch F. Finite elastic strain of cubic crystals. Phys. Rev. 1947;71(11):809. [Google Scholar]
  39. Shakoor S. A. Murtazaa G. Raza H. H. Ahmad N. Rehman S. A. Structural, thermoelectric, elastic, and electronic properties of XPdH3 (X= Li, Na, K) for hydrogen storage application: A first principle study. J. Comput. Electron. 2023;1234(1):114528. [Google Scholar]
  40. Surucu G. Candan A. Gencer A. Isik M. First-principle investigation for the hydrogen storage properties of NaXH3 (X= Mn, Fe, Co) perovskite type hydrides. Int. J. Hydrogen Energy. 2019;44(57):30218–30225. [Google Scholar]
  41. Wang M. Jiang C. Zhang S. Song X. Tang Y. Cheng H. M. Reversible calcium alloying enables a practical room-temperature rechargeable calcium-ion battery with a high discharge voltage. Nat. Chem. 2018;10(6):667–672. doi: 10.1038/s41557-018-0045-4. [DOI] [PubMed] [Google Scholar]
  42. Chaib H. Mohammedi L. Benmebrouk L. Boukraa A. Daoudi B. Achouri A. Effect of metal atom substitutions in Li based hydrides for hydrogen storage. Int. J. Hydrogen Energy. 2020;45(53):28920–28929. [Google Scholar]
  43. Rizwan M. Ullah H. M. N. Usman Z. Ysain M. W. Ali Q. Ali S. S. Effect of electronic alteration on hydrogen storage and optical response in NaMgF3 using DFT approach. Int. J. Hydrogen Energy. 2023;48(86):33599–33609. [Google Scholar]
  44. Rehman Z. Rehman M. A. Chaudhry H. Awais M. Ab initio insight into the structural, vibrational, electronic, optical, magnetic, and thermal properties of lead-free perovskite Cs3Sb2Cl9 for solar cell application. J. Phys. Chem. Solids. 2023;182:111548. [Google Scholar]
  45. Ahiska R. Mamur H. Development and Application of a New Power Analysis System for Testing of Geothermal Thermoelectric Generators. Int. J. Green Energy. 2016;13(7):672–681. [Google Scholar]
  46. Wu Z. J. Zhao E. J. Xiang H. P. Hao X. F. Liu X. J. Meng J. Crystal structures and elastic properties of superhard IrN2 and Ir N3 from first principles. Phys. Rev. B: Condens. Matter Mater. Phys. 2007;76(5):054115. [Google Scholar]
  47. Born M. On the stability of crystal lattices. I. InMathematical Proceedings of the Cambridge Philosophical Society. Soc. 1940;36(2):160–172. [Google Scholar]
  48. Gencer A. Surucu G. Al S. MgTiO3Hx and CaTiO3Hx perovskite compounds for hydrogen storage applications. Int. J. Hydrogen Energy. 2019;44(23):11930–11938. [Google Scholar]
  49. Shafiq M. Arif S. Ahmad I. Asadabadi S. J. Maqbool M. Aliabad H. A. Elastic and mechanical properties of lanthanide monoxides. J. Alloys Compd. 2015;618:292–298. [Google Scholar]
  50. Shafiq M. Ahmad I. Jalali Asadabadi S. Mechanical properties and variation in SOC going from La to Nd in intermetallics RIn3 and RSn3 (R= La, Ce, Pr, Nd) RSC Adv. 2015;5:39416. [Google Scholar]
  51. Hill R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc., London, Sect. A. 1952;65(5):349. [Google Scholar]
  52. Yu F. Y S. Li C C. Li Z. et al., Molecular engineerig of biometric donor acceptor conjugateed microporous polymers with full spectrum response and an unusual electronic shuttle for enhanced uranium (vi) photoreduction. Chem. Eng. J. 2023;466:143285. [Google Scholar]
  53. Voigt W.. Lehrbuch der kristallphysik, Teubner, Leipzig, 1928 [Google Scholar]
  54. Reuss A. Angew Z. Berechnung der Fliegrenze von Mischkristallen auf Grund der Plastizittsbedingungfr Einkristalle. Math. Mech. 1929;9:49–58. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

The authors confirm that the data supporting the findings of this study are available within the article.

Articles from RSC Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES