Integrating electronic health records and GWAS summary statistics to predict the progression of autoimmune diseases from preclinical stages

Abstract

Autoimmune diseases often exhibit a preclinical stage before diagnosis. Electronic health record (EHR) based-biobanks contain genetic data and diagnostic information, which can identify preclinical individuals at risk for progression. Biobanks typically have small numbers of cases, which are not sufficient to construct accurate polygenic risk scores (PRS). Importantly, progression and case-control phenotypes may have shared genetic basis, which we can exploit to improve prediction accuracy. We propose a novel method Genetic Progression Score (GPS) that integrates biobank and case-control study to predict the disease progression risk. Via penalized regression, GPS incorporates PRS weights for case-control studies as prior and forces model parameters to be similar to the prior if the prior improves prediction accuracy. In simulations, GPS consistently yields better prediction accuracy than alternative strategies relying on biobank or case-control samples only and those combining biobank and case-control samples. The improvement is particularly evident when biobank sample is smaller or the genetic correlation is lower. We derive PRS for the progression from preclinical rheumatoid arthritis and systemic lupus erythematosus in the BioVU biobank and validate them in All of Us. For both diseases, GPS achieves the highest prediction $R^2$ and the resulting PRS yields the strongest correlation with progression prevalence.

The authors propose a Genetic Progression Score (GPS) model to predict autoimmune disease progression from preclinical stages, integrating genome-wide association study summary statistics and electronic health records from the All of Us and BioVU biobanks.

Introduction

Many autoimmune diseases have a preclinical phase where early symptoms or serology precede the manifestation of complete disease state^1,2. In the preclinical stage, the immune system is activated, and autoantibodies can be detected. For example, in patients with rheumatoid arthritis (RA), circulating auto-antibodies such as anti-citrullinated protein antibodies or rheumatoid factor (RF) can be detected 5 years prior to the onset of symptoms². Joint pain and swelling are also reported for preclinical RA patients². Patients who progress to systemic lupus erythematosus (SLE), may develop anti-nuclear antibody (ANA), antiphospholipid, anti-Ro (SS-A), and anti-La antibodies (SS-B) in the preclinical phase^2,3. Only a fraction of preclinical individuals will advance to complete disease states, while others may remain in a stable preclinical phase or remit without clinical consequence⁴. Developing biomarkers to inform disease progression from preclinical stage will facilitate early intervention, which is critical for mitigating symptoms, slowing down the progression, and improving the quality of life^3,5–8.

Electronic health record (EHR)-based biobanks contain rich information of genetic variants, lab tests, and clinical diagnosis, which can be used to identify preclinical individuals at risk for progression⁹. As germline genetic information usually does not change during the lifetime, it is an ideal instrument for early diagnosis. Our previous work shows that genetic risk scores for SLE, when used together with ANA and anti-dsDNA tests, improve disease diagnosis and help stratify patients at risk for progressions¹⁰. Notably, the progression from preclinical stage to full-blown SLE may have shared yet distinct genetic basis from the case-control (CC) phenotype comparing SLE cases vs controls. PRS models constructed from CC studies may not be ideal for predicting disease progressions. Novel PRS models that integrate information from EHR-based biobanks and CC studies can more accurately predict preclinical to disease progressions.

Compared to standard CC genome-wide association studies (GWAS), EHR-based biobanks have fewer disease cases and fewer number of individuals in the preclinical phase. Progression PRS models constructed using biobanks only will have limited accuracy. Integrating large CC studies and biobanks will borrow strengths from the large sample sizes of CC studies and improve prediction accuracy.

Different methods exist to combine studies measuring CC and progression phenotypes. These methods include (1) cross-trait meta-analysis (e.g., MTAG)¹¹ to get more precise genetic effect estimates for progression and use them to construct PRS for progression phenotypes; (2) methods based on transfer learning which refines PRS models constructed from CC studies for predicting progression phenotypes¹²; (3) methods based on weighted combination (i.e., stacking) of PRS models from biobank and CC studies; and (4) methods based on multivariate extension of regression methods^13,14, which also require genetic correlation between traits as input.

While existing methods can potentially improve accuracy over the methods that rely on CC or biobank datasets only, they all have limitations. For example, existing multivariate methods that jointly consider CC and progression phenotypes often lack the flexibility of accommodating different genetic architectures for the trait, e.g., sparse or polygenic. Current stacking and transfer learning-based methods may not be effective in combining the CC and biobank datasets, and may perform worse than using either dataset alone in certain scenarios. There is considerable room and needs for further improvements.

In this article, to combine the large sample sizes of CC GWAS studies and detailed phenotypes in EHR-based biobanks, we propose a novel method called Genetic Progression Score (GPS) to predict disease progressions from preclinical stages. GPS incorporates PRS weights for the CC phenotype as prior via a penalty term. The penalty term forces the model parameters to be similar to the prior if it helps improve the prediction accuracy. As a result, GPS can borrow strength from the large sample sizes of CC studies, while accommodating potential genetic effect differences between CC and progression phenotypes.

Via extensive simulations, we show that GPS consistently achieves the highest or comparable prediction accuracy. The improvement offered by GPS is particularly significant, leading to more than two folds improvements in the prediction $R^2$, when genetic correlation between CC and progression trait is low or when the biobank has a limited sample size. Furthermore, as applications, we constructed PRS models in the Vanderbilt University biobank (BioVU) to predict preclinical to disease progressions for RA and SLE. For RA, we focus on the progression from preclinical RA with positive RF antibody. For SLE, we study the progression from preclinical SLE with positive antinuclear antibody (ANA). We validate the progression risk scores in the All of Us biobank. For both autoimmune disorders, GPS demonstrated much-improved prediction $R^2$ compared to alternative methods. Resulting risk scores from GPS models also showed the strongest association with the progression phenotype in the All of Us biobank.

Results

Overview of GPS

GPS is a penalized regression method aiming to improve the prediction accuracy by integrating information from both biobanks and CC studies. To borrow information from large-scale CC study, we first train a PRS model for CC phenotype using summary statistics. Any PRS method can be used. This allows using the best-performing PRS models as weights which is critical for the accuracy of predicting progression phenotypes. GPS then takes the trained PRS models as prior and uses a penalty term to penalize the deviation of the parameter estimates from the prior. The model hence forces the model parameters to resemble the prior, if the prior helps improve the prediction accuracy for progression. Besides, it also uses extra $L_1$ and $L_2$ penalty terms to impose shrinkage and sparsity of the model parameters.

There are three tuning parameters in the GPS model, including the parameters that control the shrinkage ($\lambda$), the mixing ratio of L1 and L2 penalty ($\alpha$), and the tuning parameter controlling the contribution of prior ($\eta$). These tuning parameters will be estimated using a validation dataset with individual-level genotype and phenotype data. We use three established PRS methods as baseline methods, i.e., Lassosum¹⁵, LDpred2¹⁶, and PRS-CS¹⁷, to construct priors from CC study and use them in GPS to improve prediction accuracy. A workflow for GPS is presented in Fig. 1. Detailed methodology about GPS can be found in Methods.

Fig. 1. Detailed workflow of GPS.

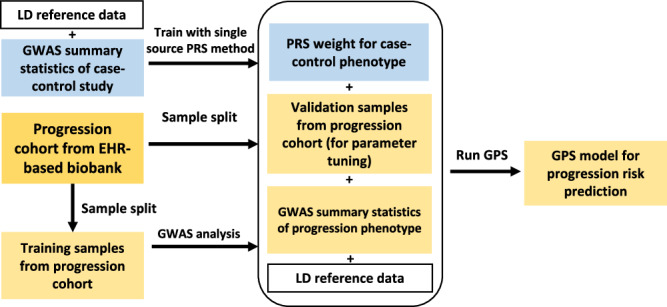
GPS combines CC GWAS data and EHR-based biobanks to construct PRS models for predicting the risk of preclinical → disease progression.

We compare GPS with a few alternative PRS strategies for predicting the progression from preclinical to disease stage:

1. using CC study alone to calculate a PRS and use it to predict preclinical to disease progressions (CC).

2. using biobank data alone to calculate a PRS for preclinical to disease progression phenotype (PROG).

3. using cross-trait meta-analysis (e.g., MTAG¹⁸) to improve marginal genetic effect estimates for the progression phenotype and use improved marginal genetic effects to construct PRS models for progression.

4. using transfer learning¹² to refine PRS models constructed from CC studies by integrating preclinical to disease progression phenotype and genetic data in a biobank (TL-PRS).

5. using stacking to create a weighted combination of PRSs from biobank and CC datasets (STACKING).

6. using multivariate Lassosum¹³, a PRS method that extends the original Lassosum method. It combines multivariate linear mixed model and L1 penalty to jointly model genetically correlated traits. The multivariate Lassosum method is referred to as MVL throughout this paper.

7. Super stacking methods: Besides, for each combination strategy, we further consider stacking the PRS from different baseline methods (i.e., LDPred2, PRS-CS, and Lassosum), which we call super-stacking. Specifically, super-stacking includes stacking of all GPS PRSs (GPS_stacking), stacking of all MTAG PRSs (MTAG_stacking), stacking of all TL-PRSs (TL-PRS_stacking) models, and stacking all baseline methods (ALL-BASE_stacking).

In total, 23 PRS models (3 GPS-based models and 20 alternative models) are evaluated. Further details can be found in Supplementary Data 1.

Connections with other methods

Our method has connections with existing approaches. Broadly speaking, our method is conceptually similar to the methods that incorporate priors, including transfer learning. Yet, it differs from other methods in the way prior information is modeled and incorporated. It has some similarities with fused lasso and its adaptations^19–21. Fused lasso jointly fits the model for multiple traits using an $L_1$ penalty to impose sparsity and another $L_2$ penalty to enforce similarity of weights. In comparison, our method uses PRS weights estimated from a CC study as input. It can flexibly accommodate more accurate risk scores as prior instead of sticking with a pre-specified model, e.g., lasso/elastic net-based model¹³ or Bayesian linear mixed model¹⁴. Given that not a single baseline PRS performs consistently the best, the flexibility of incorporating different baseline methods is critical for improving the prediction accuracy, which is evident from our simulation evaluations and real data analysis. Instead of using $L_1$ penalty for the prior, we use $L_2$ penalty to enable continuous shrinkage toward the prior if the prior is helpful for improving the prediction accuracy. Finally, our approach can analyze summary statistics as input while the fused lasso, in its original form, requires individual-level data.

Overview of simulation studies

We simulate progression and CC summary statistics as training data. We also simulate individual-level validation and test data for hyperparameter tuning and model evaluation. Briefly, we assume the progression and CC phenotypes to be genetically correlated with possibly different effect sizes or possibly different causal variants. We vary the sample sizes for biobank datasets with progression phenotype, the genetic correlations and proportions of shared causal variants between CC and progression phenotypes, and the number of causal variants. The sample size for the simulated CC study is fixed and assumed to be at least more than ten times larger than the number of preclinical individuals from biobanks, which reflects the sample sizes we observe for commonly studied autoimmune diseases. We simulate 20 replicates for each simulation scenario. In total, 23 different PRS models are included in the comparison (see Methods). For strategies that combine biobank and CC studies, they can be used with different baseline PRS methods, so we name them after both the integration strategy and the baseline PRS methods. For example, for the stacking method that combines PRS-CS risk scores from CC and progression cohorts, we name it as STACKING-PRS-CS. Detailed explanations of all models can be found in Supplementary Data 1.

Simulation comparison of different PRS strategies for predicting progressions

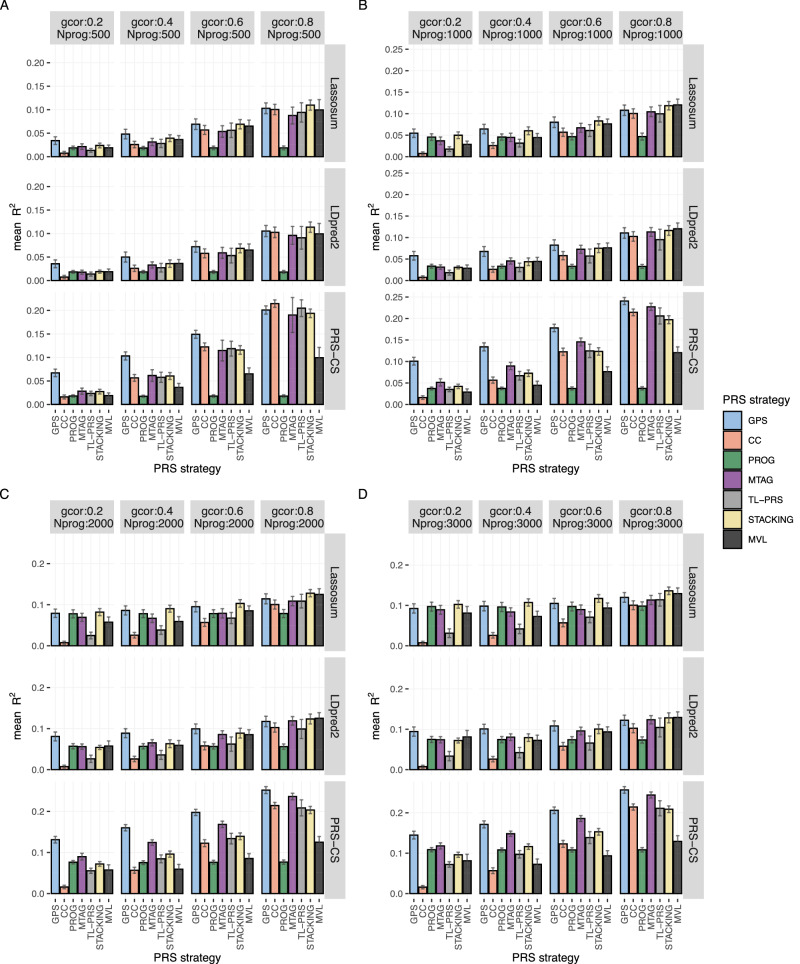
Prediction accuracy is evaluated using prediction $R^2$. Figure 2 shows the simulation results for all non-super-stacking PRS models when 200 variants are causal for the trait. Simulation results with 500 causal variants are presented in Supplementary Fig. 1. All causal variants are shared between two traits in these simulations. The results when CC and progression traits have different causal variants remain similar. They are shown in Supplementary Fig. 2. PRS from CC study only performs well when genetic correlation is high. The sample size of progression phenotype is small (Fig. 2A, with genetic correlation = 0.8). In contrast, PROG models usually have lower accuracy than models that borrow strength from CC studies, unless genetic correlation is low and the sample size of progression cohort is large (Fig. 2D, with genetic correlation = 0.2).

Fig. 2. Prediction accuracy of different PRS models in simulations (200 causal variants).

All causal variants are shared between progression and case-control phenotypes in this simulation. The prediction accuracy is evaluated by the mean prediction ${\mathit{R}}^{\mathit{2}}$ across 20 simulated replicates. The error bar indicates the standard deviation of prediction ${\mathit{R}}^{\mathit{2}}$ across 20 simulation replicates. Each row represents different PRS models using the same baseline PRS method. MVL uses Lassosum as baseline framework, so it cannot accommodate alternative baseline PRS methods. To facilitate comparisons, we estimate the prediction ${\mathit{R}}^{\mathit{2}}$ of MVL by repeating across the scenarios in different rows and taking the average. The sample size of the progression cohort is 500 in (A), 1000 in (B), 2000 in (C), and 3000 in (D). The number of causal variants is set as 200. gcor genetic correlation, Nprog sample size of biobank study of progression phenotype. Super-stacking models are not included here but are shown in Supplementary Fig. 3. Scenarios with different causal variants between case-control and progression phenotypes are given in Supplementary Fig. 1.

GPS, TL-PRS, and STACKING models use different strategies to incorporate PRS from CC studies. GPS models have the highest or comparable prediction accuracy in all simulation scenarios. When the sample size of progression cohort is fixed, GPS’s advantage in prediction accuracy is larger when genetic correlation is smaller. For example, when the sample size of biobank cohort is set as 500 and genetic correlation is set as 0.2, among models using PRS-CS as the baseline method, GPS has prediction $R^2$ 0.067, which is 2.4-fold higher than the second-best model MTAG-PRS-CS (0.028) (Fig. 2A). In contrast, when genetic correlation is 0.8 and progression cohort sample size as 500, GPS-PRS-CS’s prediction $R^2$ (0.20) becomes comparable to CC-PRS-CS ($R^2=0.21$) (Fig. 2A). This is not surprising, as when genetic correlation between CC and progression phenotype is high, the genetic effects for the two traits will become very similar (up to a scalar) and CC risk scores would by itself be sufficient for predicting the progression phenotype.

When genetic correlation is fixed, the advantages of GPS over alternative methods is larger when sample size of the biobank study is smaller. For example, when the genetic correlation is 0.4 and sample size of biobank cohort is 500, the prediction $R^2$ is 0.10 for GPS-PRS-CS and 0.061 for the second-best model MTAG-PRS-CS. GPS-PRS-CS’s $R^2$ is 1.6-fold of that of the second-best method MTAG-PRS-CS (Fig. 2A). However, when the sample size of progression cohort is 3000 and genetic correlation remains to be 0.4, the prediction $R^2$ of GPS-PRS-CS is only 1.1-fold of that of the second-best method MTAG-PRS-CS i.e., 0.17 vs 0.15 (Fig. 2D). It should be noted that for the current sample sizes, most biobanks contain fewer than 3000 preclinical individuals. The presented scenario with 3000 preclinical individuals may be viewed as an uncommon and worst-case scenario for GPS.

MTAG analysis requires reliable genetic correlation estimates for jointly analyzed traits. As expected, applying baselines PRS methods to MTAG results yields low prediction accuracy when the biobank dataset with progression phenotype is small (Fig. 2A). MTAG models only yield higher or comparable prediction accuracy when genetic correlation is high or when the biobank cohort is large (Fig. 2B–D). Our results show that cross-trait meta-analysis strategy using MTAG may not be suitable for predicting preclinical phase to disease stage progressions.

TL-PRS is a recently proposed transfer learning-based PRS method. By integrating data from a smaller target sample, it can fine-tune pretrained PRS models constructed from large samples. Our simulation results indicate that TL-PRS models perform worse than models trained using biobank only, when the genetic correlation is low or when progression cohort is large (Fig. 2D). When genetic correlation is high (e.g., genetic correlation = 0.8), TL-PRS models also perform worse than models trained using CC studies only, across all sample sizes of progression cohorts (Fig. 2A–D). Similarly, the STACKING models only perform well when genetic correlation between CC and progression phenotype is high (Fig. 2A–D), demonstrating a lack of robustness of the stacking method.

Similar to MTAG, MVL also requires genetic covariance estimates to jointly analyze multiple traits. It extends the Lassosum framework to estimate joint effects of multiple SNPs. It thus cannot accommodate other PRS methods as priors. Compared to other combination strategies using Lassosum and LDpred2 as baseline methods, MVL has much lower prediction $R^2$ unless the genetic correlation is high (e.g., genetic correlation = 0.8). MVL has lower prediction $R^2$ than methods using PRS-CS as the baseline method in almost all scenarios (except for TL-PRS when genetic correlation is low and sample size of progression cohort is large) (Fig. 2). The results remain similar for scenarios with 500 causal variants (Supplementary Fig. 1). This comparison further demonstrates the importance of having the flexibility of using different PRS methods as the baseline.

Prediction accuracy results of super-stacking models are shown in Supplementary Figs. 3 and 4. The accuracies of these super-stacking methods are similar to the best-performing models that are stacked. GPS-stacking remains the best-performing super-stacking method.

Lastly, when only a portion of causal variants are shared between the CC phenotype and progression phenotype (Supplementary Fig. 2), GPS models continue to outperform alternative models which is consistent with scenarios where CC and progression phenotype share the same set of causal variants.

Constructing and evaluating different PRS models for progression risk of autoimmune disorders

We apply GPS as well as other PRS methods in the BioVU biobank to construct PRS for predicting the progression from RF positive to RA and the progression from ANA positive to SLE. To evaluate the prediction accuracy of the trained PRS models, we further build progression patient cohort using the All of Us biobank as the test dataset. The sample sizes and demographics of the BioVU and the All of Us cohorts can be found in Supplementary Data 2. Further details of the analyses can be found in Methods.

GPS gives the highest prediction accuracy for progression risk of autoimmune diseases

We evaluate the accuracy using Nagelkerke’s $R^2$ on the liability scale²². We need disease prevalence as input when converting the observed scale $R^2$ to liability scale. In our analysis, the disease progression is set to be the fraction of individuals with positive biomarkers who progress to the disease states. According to published studies of RF test and ANA test^23,24, we set the progression prevalence estimates to be 25% for RA and 15% for SLE.

Table 1 summarizes the performance of different PRS models for predicting the risk of progressing from RF positive to RA in the All of Us biobank. The GPS models yield the top three $R^2$ estimates, with GPS-lassosum model being the best performing model for predicting RA progression risk ($R^2$ = 0.124). All GPS models have $R^2$ significantly greater than zero. Among all other 16 models, only CC-PRS-CS, PROG-Lassosum, STACKING-Lassosum, and STACKING-PRS-CS give $R^2$ estimates that are significantly larger than zero. For RA, we find that the STACKING-Lassosum score is exactly the same as PROG-Lassosum score as the weights assigned to CC risk scores is zero. It indicates that the stacking fails to borrow strength from CC study of RA. GPS, on the other hand, presents itself as a more effective approach to integrate prior and improves over CC risk scores. All MTAG-based models, TL-PRS-based models, and the MVL model fail to yield $R^2$ that are statistically significantly different from 0.

Table 1.

The accuracy for predicting RF positive to RA progressions in the All of Us biobank

Method	$R^2$	AUPRC	AUC
CC-Lassosum	0.038 (−0.003, 0.079)	0.312 (0.234, 0.419)	0.571 (0.495, 0.653)
CC-LDpred2	0.043 (0, 0.086)	0.296 (0.225, 0.393)	0.576 (0.508, 0.659)
CC-PRS-CS	0.053 (0.005, 0.1)	0.33 (0.248, 0.445)	0.586 (0.512, 0.666)
PROG-Lassosum	0.118 (0.052, 0.184)	0.366 (0.273, 0.462)	0.638 (0.557, 0.711)
PROG-LDPred2	0.011 (−0.012, 0.034)	0.272 (0.212, 0.365)	0.535 (0.455, 0.608)
PROG-PRS-CS	0.011 (−0.012, 0.034)	0.26 (0.205, 0.342)	0.538 (0.464, 0.612)
GPS-Lassosum	0.124 (0.057, 0.191)	0.376 (0.279, 0.486)	0.634 (0.557, 0.706)
GPS-LDpred2	0.119 (0.053, 0.185)	0.397 (0.294, 0.499)	0.634 (0.558, 0.707)
GPS-PRS-CS	0.122 (0.055, 0.188)	0.384 (0.289, 0.494)	0.635 (0.559, 0.708)
MTAG-Lassosum	0 (−0.002, 0.003)	0.239 (0.188, 0.315)	0.497 (0.421, 0.573)
MTAG-LDpred2	0.001 (−0.007, 0.01)	0.259 (0.201, 0.348)	0.513 (0.439, 0.587)
MTAG-PRS-CS	0.001 (−0.006, 0.008)	0.242 (0.191, 0.315)	0.509 (0.434, 0.583)
TL-PRS-Lassosum	0 (−0.004, 0.005)	0.24 (0.186, 0.309)	0.513 (0.439, 0.582)
TL-PRS-LDpred2	0.001 (−0.005, 0.007)	0.261 (0.204, 0.346)	0.513 (0.434, 0.589)
TL-PRS-PRS-CS	0.025 (−0.009, 0.058)	0.284 (0.215, 0.361)	0.56 (0.486, 0.629)
STACKING-Lassosum	0.118 (0.052, 0.184)	0.366 (0.273, 0.462)	0.638 (0.557, 0.711)
STACKING-LDpred2	0.011 (−0.012, 0.034)	0.272 (0.212, 0.365)	0.535 (0.455, 0.608)
STACKING-PRS-CS	0.053 (0.005, 0.1)	0.33 (0.248, 0.445)	0.586 (0.512, 0.666)
MVL	0.009 (−0.011, 0.03)	0.275 (0.213, 0.371)	0.533 (0.460, 0.615)

We report the Nagelkerke’s $R^2$, AUPRC (area under the precision recall curve), and AUC (area under the receiver operating characteristic curve). The 95% confidence intervals for different estimates are listed in the parenthesis. The top two methods for each metric are displayed in bold and italic font.

GPS models also outperform other PRS models for predicting the risk of progression from ANA positive to SLE. As shown in Table 2, GPS-Lassosum and GPS-PRS-CS models yield the top two $R^2$ estimates, with GPS-lassosum model giving the highest $R^2$ estimate (0.044). All GPS models for SLE progression have statistically significant $R^2$ estimates. Models based on stacking improves over single source models that rely on the biobank or CC data alone. STACKING-PRS-CS model yields the best $R^2$ estimate (0.039) among non-GPS models. However, similar to the observations in RA, MTAG, TL-PRS, and MVL-based models yield lower $R^2$ estimates for ANA positive to SLE progressions and both MTAG and MVL models fail to yield $R^2$ that are significantly different from zero. Although TL-PRS-Lassosum and TL-PRS-PRS-CS models give significantly positive $R^2$ estimates (0.028 and 0.027), they both have lower accuracy compared to the PRS constructed using only CC studies ($R^2$ 0.033 for CC-Lassosum and $R^2$ 0.032 for CC-PRS-CS). While TL-PRS seeks to refine CC-Lassosum and CC-PRS-CS, it fails to outperform these baseline methods. For both RA and SLE, we also calculated the area under the precision-recall curve (AUPRC) as additional metrics for evaluating PRS models for progression risk (Tables 1–2). We observe that GPS-LDpred2 model yields the best AUPRC for RF positive to RA progression and GPS-Lassosum model gives the best AUPRC for ANA positive to SLE progression.

Table 2.

The accuracy of PRS models for predicting ANA positive to SLE progressions in the All of Us biobank

Model	$R^2$	AUPRC	AUC
CC-Lassosum	0.033 (0.015, 0.052)	0.112 (0.088, 0.15)	0.568 (0.506, 0.628)
CC-LDpred2	0.01 (0, 0.021)	0.096 (0.077, 0.123)	0.540 (0.482, 0.596)
CC-PRS-CS	0.032 (0.014, 0.05)	0.11 (0.087, 0.146)	0.566 (0.508, 0.625)
PROG-Lassosum	0.001 (−0.002, 0.004)	0.093 (0.076, 0.127)	0.519 (0.465, 0.575)
PROG-LDpred2	0.019 (0.005, 0.033)	0.096 (0.079, 0.12)	0.554 (0.498, 0.606)
PROG-PRS-CS	0.01 (0, 0.021)	0.095 (0.078, 0.119)	0.543 (0.488, 0.592)
MTAG-Lassosum	0.001 (−0.002, 0.003)	0.091 (0.074, 0.116)	0.516 (0.455, 0.573)
MTAG-LDpred2	0.005 (−0.002, 0.012)	0.09 (0.075, 0.11)	0.533 (0.479, 0.583)
MTAG-PRS-CS	0.003 (−0.003, 0.008)	0.091 (0.076, 0.113)	0.528 (0.471, 0.576)
GPS-Lassosum	0.044 (0.023, 0.065)	0.124 (0.091, 0.171)	0.568 (0.511, 0.622)
GPS-LDpred2	0.037 (0.018, 0.056)	0.117 (0.089, 0.167)	0.566 (0.513, 0.623)
GPS-PRS-CS	0.042 (0.021, 0.062)	0.119 (0.09, 0.163)	0.566 (0.51, 0.623)
TL-PRS-Lassosum	0.028 (0.011, 0.044)	0.102 (0.084, 0.131)	0.561 (0.507, 0.612)
TL-PRS-LDpred2	0.007 (−0.002, 0.016)	0.093 (0.077, 0.118)	0.527 (0.477, 0.578)
TL-PRS-PRS-CS	0.027 (0.011, 0.044)	0.100 (0.083, 0.126)	0.558 (0.509, 0.605)
STACKING-Lassosum	0.034 (0.016, 0.053)	0.111 (0.088, 0.148)	0.570 (0.51, 0.63)
STACKING-LDpred2	0.028 (0.011, 0.046)	0.103 (0.082, 0.131)	0.558 (0.499, 0.611)
STACKING-PRS-CS	0.039 (0.019, 0.059)	0.112 (0.089, 0.149)	0.569 (0.51, 0.626)
MVL	0.0046 (−0.0025, 0.012)	0.090 (0.075, 0.113)	0.529 (0.476, 0.579)

We report the Nagelkerke’s $R^{\mathit{2}}$, AUPRC (area under the precision recall curve), and AUC (area under the receiver operating characteristic curve). The 95% confidence intervals for the estimates are listed in the parenthesis. The top two methods for each metric are displayed in bold and italic font.

The prediction accuracies of super-stacking models are presented in Supplementary Data 3 and 4. Among these four models, GPS-stacking yields the highest $R^2$ estimates for predicting progression risk of RA (0.119) and SLE (0.042). ALL-BASE_stacking model achieves the second-best prediction $R^2$ (0.107 for RA and 0.0385 for SLE). For both autoimmune diseases, the GPS-stacking model does not outperform the top two GPS models, i.e. GPS-PRS-CS and GPS-Lassosum, in predicting their progression risk.

Moreover, it is understood now that genetic risk scores can be more informative for identifying individuals with high and low-risk scores. We also confirmed this observation in GPS. According to the best performing GPS, preclinical patients with progression PRS scores in the top 10th percentiles have ~3.8 and ~2.3 folds elevated progression risk for RA and SLE compared to the medians among preclinical individuals. These significantly elevated risks underscore the importance of early interventions to slow down the progression and mitigate the disease risk, as autoimmunity can quickly lead to irreversible organ damages.

Association with progression prevalence of autoimmune diseases in All of Us

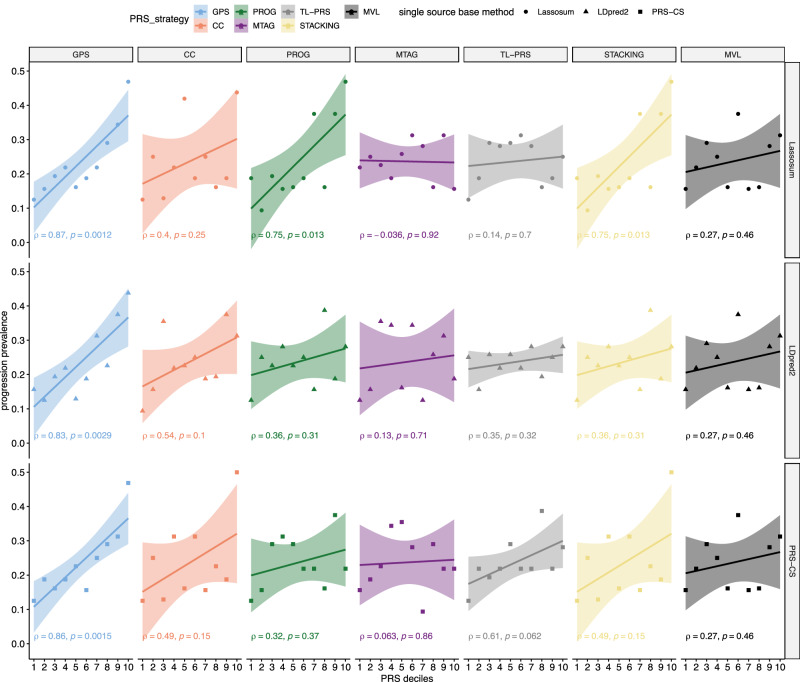
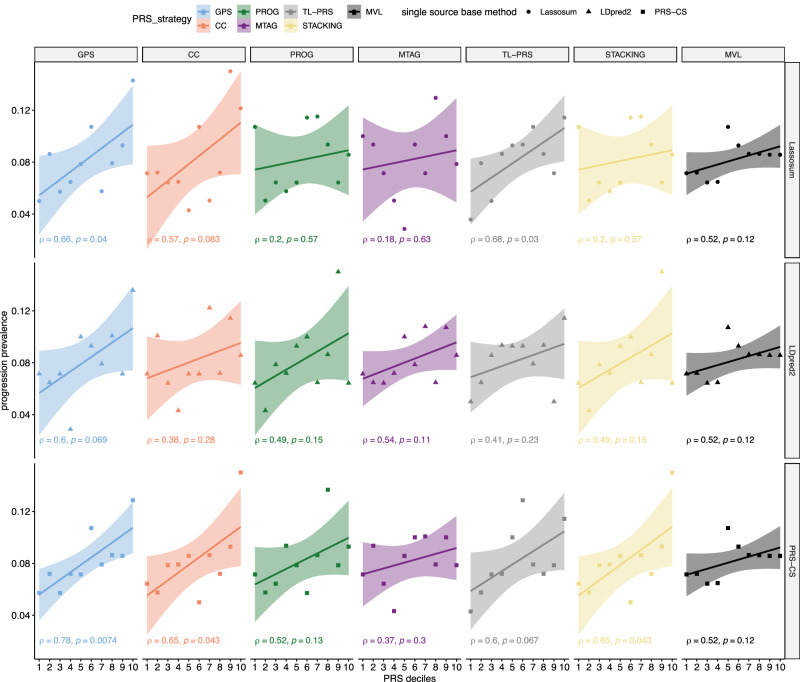
Next, we evaluated the associations between the different PRS scores and the progression prevalence for RA and SLE in the All of Us study. We plot deciles of PRS scores versus the progression prevalence and calculate Pearson’s correlation coefficients ($\rho$) between them. As shown in Fig. 3, for RA, GPS-Lassosum, GPS-LDpred2, and GPS-PRS-CS yield the top three most significant correlations, [i.e., $\rho$ = 0.87 (p-value = 0.0012), 0.83 (p-value = 0.0029), and 0.86 (p-value = 0.0015)]. Alternative methods have much lower accuracy, among which, PROG-Lassosum and STACKING-Lassosum yield the highest accuracy ($\rho =0.75$, p-value = 0.013). This is consistent with the comparison using liability scale $R^2$. For SLE, GPS-PRS-CS model yields the strongest correlation between PRS and observed progression prevalence ($\rho =0.78$, p-value = 0.0074), whereas TL-PRS-Lassosum yields the second-best yet much lower correlation ($\rho =0.68,$ p-value = 0.03) (Fig. 4).

Fig. 3. The association between PRS and the prevalence of RF positive → RA progressions in the All of Us data.

The All of Us data is not used to train genetic risk scores. The Pearson correlation coefficient (and corresponding p-values from two-sided t-test) between PRS and the progression prevalence at each decile in the All of Us data are labeled on the plot. The error bands represent 95% confidence intervals of fitted linear regression lines. MVL uses Lassosum as baseline framework. The prediction accuracy of MVL is obtained by repeating across the scenarios of different rows and taking the average. It is clear that GPS consistently yields stronger and more significant correlations between predicted and observed progression in the independent test dataset, which demonstrates improved accuracy. Super-stacking models are shown in Supplementary Fig. 5.

Fig. 4. The association between PRS and the prevalence of ANA positive → SLE progressions in the All of Us data.

The All of Us data is not used to train genetic risk scores. The Pearson correlation coefficient (and corresponding p-values from two-sided t-test) between PRS and the progression prevalence at each decile in the All of Us data are labeled on the plot. The error bands represent 95% confidence intervals of fitted linear regression lines. MVL uses Lassosum as baseline framework. The prediction accuracy of MVL is obtained by repeating across the scenarios of different rows and taking the average. It is clear that GPS consistently yields stronger and more significant correlations between the predicted and observed progression prevalence in the independent test dataset, which demonstrates improved accuracy. Super-stacking models are shown in Supplementary Fig. 6.

Among the four super-stacking models, similar to when evaluating with liability scale $R^2$, GPS_stacking demonstrates the strongest correlation ($\rho =$0.83 for RA and $\rho =0.78$ for SLE) while ALL-BASE_stacking being the second best super-stacking method ($\rho =$0.82 for RA and $\rho =0.56$ for SLE) as shown in Supplementary Figs. 5 and 6.

GPS models select variants that help distinguish preclinical patients

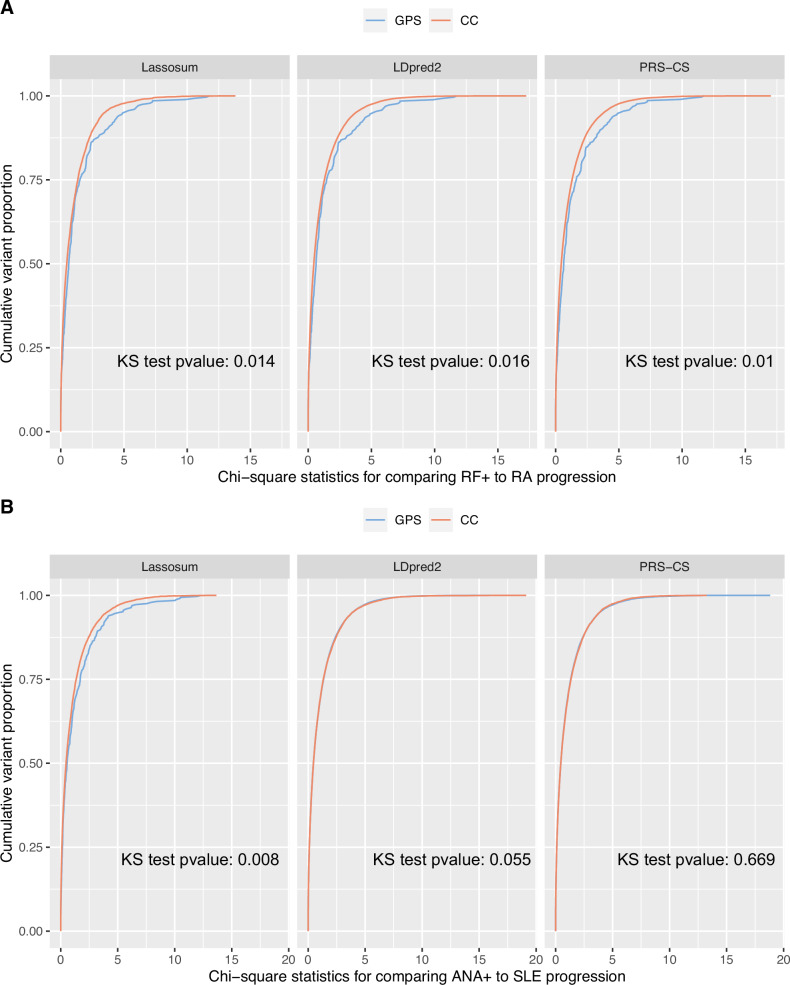
We further investigate the advantage offered by GPS models over the risk scores calculated using summary statistics from CC studies. To do so, for variants selected by the GPS models and by the models using CC samples only, we plot the distributions of marginal association ${\chi }^2$ statistics testing for control → preclinical association and the marginal association ${\chi }^2$ statistics testing for preclinical → cases associations in the All of Us biobank, which is an independent dataset not used for training the risk scores. Figure 5A shows the comparison of risk scores calculated for RF positive to RA progressions. For each quantile, the marginal ${\chi }^2$ statistics for variants in the GPS models are always bigger than those in the risk scores based on CC samples. It indicates variants selected by GPS models are more significantly associated with RF positive → RA progressions, compared to variants in the models trained with CC data. Variants selected by the GPS models are also more significantly associated with control vs preclinical status (Supplementary Fig. 7A, B). Overall, our comparison shows that GPS helps to select variants that can better distinguish preclinical individuals from both case and healthy controls. It helps explain why it yields better prediction accuracy. It should also be noted that our study here only explores marginal association statistics. It remains to be explored using larger datasets and more rigorous colocalization methods (e.g., coloc²⁵) whether the causal variants influencing control → preclinical progression and those influencing preclinical → disease progressions are identical.

Fig. 5. Cumulative distributions of marginal association statistics testing the association with preclinical to disease progressions in the All of Us dataset.

We trained the progression risk scores in the BioVU biobank. We also performed GWAS, comparing preclinical to disease cases, in the All of Us data, which is not used in model training. For variants selected by GPS or the risk scores using CC samples only, we compare the distribution of the marginal ${\chi }^2$ statistics testing genetic associations with preclinical → disease progression. The cumulative distribution functions of the marginal ${\chi }^2$ statistics are plotted for A RF positive to RA progressions and B ANA positive to SLE progressions, for the variants selected by the risk scores. Two-sided Kolmogorov-Smirnov (KS) tests were performed to compare the distributions and the p-values are labeled on each subpanel. At each quantile, the variants selected by GPS are often more significantly associated with the progression phenotype compared to variants selected by risk scores based on CC studies. This comparison explains why GPS is more accurate for predicting preclinical to disease progressions. Cumulative distributions of marginal association statistics contrasting healthy control with preclinical disease are given in Supplementary Fig. 7.

PheWAS analysis in the UK Biobank and All of Us

We conduct phenome wide association study (PheWAS) in UK Biobank to explore which PheWAS codes are associated with PRS calculated from CC studies and from GPS models (See “Methods”). PRS calculated using GPS-Lassosum and CC-Lassosum models are denoted as GPS-PRS and CC-PRS, respectively.

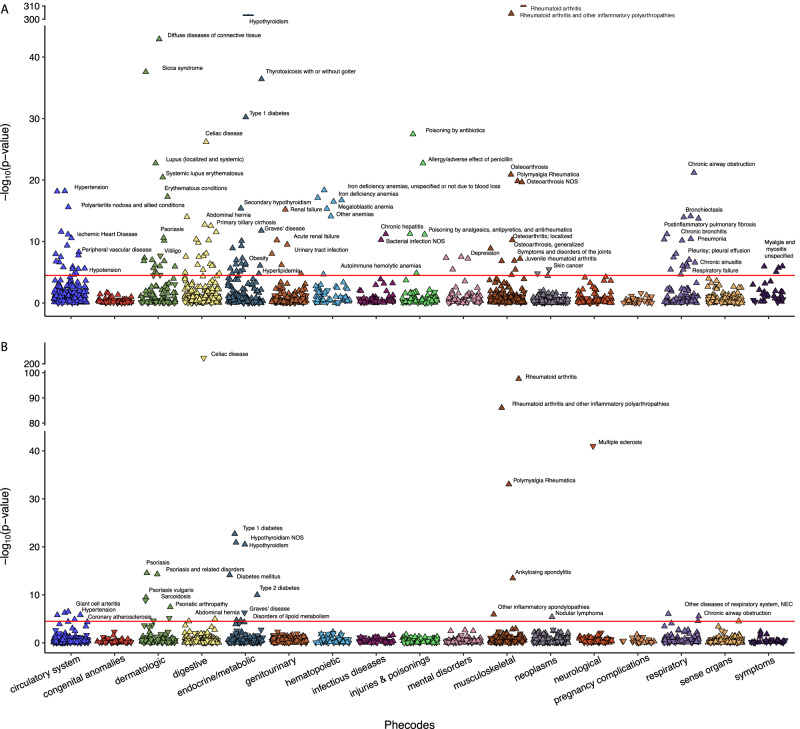
In UK Biobank for RA, out of a total of 1405 PheWAS codes analyzed, CC-PRS and GPS-PRS are significantly associated with 141 and 34 PheWAS codes, respectively, (Bonferroni corrected p-value < 0.05, Supplementary Data 5, Fig. 6). PheWAS code for RA is significantly associated with both CC-PRS (OR = 3.49, p-value < 1 × 10⁻³²⁰) and GPS-PRS (OR = 1.82, p-value = 2.66 × 10⁻⁹⁸). Among the 34 PheWAS codes significantly associated with GPS-PRS, a majority (28) are also significantly associated with RA CC-PRS. Five of the six PheWAS codes uniquely associated to RA GPS-PRS include nodular lymphoma (p-value = 4.3 × 10⁻⁶), multiple sclerosis (p-value = 1.0 × 10⁻⁴¹), glaucoma (p-value = 3.3 × 10⁻⁵), other inflammatory spondylopathies (p-value = 1.2 × 10⁻⁶), and ankylosing spondylitis (p-value = 3.6 × 10⁻⁶). Four out of five PheWAS codes were replicated for RA GPS-PRS in All of Us: nodular lymphoma (p-value = 0.0037), multiple sclerosis (p-value = 1.09 × 10⁻²²), other inflammatory spondylopathies (p-value = 0.018), and ankylosing spondylitis (p-value = 0.0002) (Supplementary Data 6). All five of these PheWAS codes remained insignificant for RA CC-PRS in All of Us (p-value > 0.05). Patients with RA have been reported to have a greater risk of lymphoma and glaucoma^26–28 and patients with multiple sclerosis are at an increased risk of developing RA²⁹. Lastly, various studies also suggested RA and ankylosing spondylitis have overlapping etiologies and are closely related^30,31. In UK Biobank, the 114 PheWAS codes uniquely associated with RA CC-PRS are either related to other less similar diseases (e.g., SLE, osteoarthritis, primary biliary cirrhosis, or idiopathic pulmonary fibrosis) or to comorbidities frequently observed due to RA treatment (e.g., thyroid disease, anemias, renal failure, or lung disease)^32–34. Thus, phenotypes associated with GPS-PRS are more specific to RA compared to those associated with CC-PRS. Our results suggest that GPS-PRS provides better clinical utility to predict patients who will progress to RA with positive RF test.

Fig. 6. PheWAS results for RA case-control and progression risk scores in UK Biobank.

A PheWAS results from CC-PRS of RA. B PheWAS results from GPS-PRS of RA. The y-axis represents the −log10(p-value) for each PheWAS code, derived using a two-sided Chi-square test after fitting a multivariate logistic regression model. The x-axis displays different PheWAS code categories. Each point corresponds to a specific PheWAS code, with downward and upward pointing triangles indicating negative and positive associations between disease status defined by the PheWAS code and the PRS, respectively.

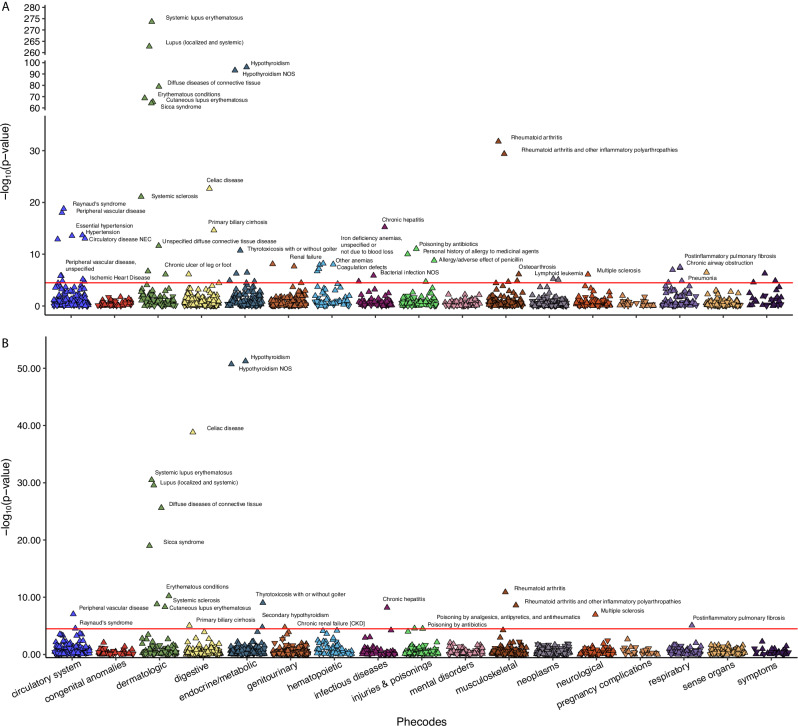
Similarly, in UK Biobank, for SLE, CC-PRS and GPS-PRS are significantly associated with 64 and 23 PheWAS codes (with Bonferroni corrected p-value < 0.05, Supplementary Data 7, Fig. 7). As expected, SLE is among the most significantly associated PheWAS codes with SLE CC-PRS (OR = 2.91, p-value = 2.35 × 10⁻²⁷⁴) and GPS-PRS (OR = 2.83, p-value = 3.31 × 10⁻³¹). All 23 PheWAS codes significantly associated with SLE GPS-PRS are also associated with SLE CC-PRS, while SLE CC-PRS is associated with an additional 41 PheWAS codes. Among the 23 PheWAS codes associated with SLE GPS-PRS in UK Biobank, 17 were replicated for SLE GPS-PRS in All of Us (p-value < 0.05) (Supplementary Data 8). Furthermore, out of the 41 PheWAS codes uniquely associated with SLE CC-PRS in UK Biobank, 15 were replicated for SLE CC-PRS in All of Us (p-value < 0.05) and 27 remained insignificant for SLE GPS-PRS in All of Us (p-value ≥ 0.05) (Supplementary Data 8). The PheWAS codes associated with both PRSs are often for closely related autoimmune diseases (e.g., Celiac disease, RA, Systemic Sclerosis, Multiple Sclerosis, Sicca Syndrome, or Multiple Sclerosis)^35–37. The 41 PheWAS codes uniquely associated with SLE CC-PRS usually involve less related phenotypes (e.g., hypertension, anemias, gastroenteritis, myalgia/myositis, chronic ulcer of skin, or lymphoid leukemia). This suggests that phenotypes associated with CC-PRS are less relevant for SLE when compared to those associated with GPS-PRS. Thus, SLE GPS-PRS can provide better clinical utility when compared to SLE CC-PRS, as its higher specificity would allow increased certainty in eventual SLE diagnosis in individuals with positive ANA test.

Fig. 7. PheWAS results for SLE case-control and progression risk scores in UK Biobank.

A PheWAS results for CC-PRS of SLE. B PheWAS results from GPS-PRS of SLE. The y-axis represents the −log10(p-value) for each PheWAS code, derived using a two-sided Chi-square test after fitting a multivariate logistic regression model. The x-axis displays different PheWAS code categories. Each point corresponds to a specific PheWAS code, with downward and upward-pointing triangles indicating negative and positive associations between the disease status defined by the PheWAS code and the PRS, respectively.

We also examine whether PheWAS effects in the All of Us and UK Biobank are concordant (See Methods). Among the PheWAS results with p-value < 0.05 in UK Biobank, we observed a significant correlation between effect sizes in UK Biobank and All of Us (RA CC-PRS r² = 0.53, p-value < 2.2 × 10⁻¹⁶; RA GPS-PRS r² = 0.6, p-value < 2.2 × 10⁻¹⁶; SLE CC-PRS r² = 0.70, p-value = <2.2 × 10⁻¹⁶; SLE GPS-PRS r² = 0.44, p-value = 5 × 10⁻⁹) (Supplementary Figs. 8 and 9, Supplementary Data 5–8). These findings demonstrate that the PheWAS effect sizes observed in UK Biobank are consistent with that in All of Us, supporting the validity of the UK Biobank PheWAS results.

To ensure GPS-related PRS for both RA and SLE were more specific to RA and SLE, respectively, when compared to other PRS methods, we conducted PheWAS in UK Biobank and All of Us for the PRS calculated from the remaining 21 alternative methods for RA and SLE (Supplementary Data 5–8). Overall, for both RA and SLE, GPS scores continue to be associated with more biologically relevant PheWAS codes that are specific to RA and SLE, respectively, when compared to non-GPS PRS methods (See Supplementary Material for more details). This observation was similar in UK Biobank and All of Us, which provide further support of the specificity of GPS-related PRS (Supplementary Figs. 10–13).

Discussion

In this article, we investigate different strategies to construct genetic risk scores to predict the progression from preclinical to disease states and apply them to study several autoimmune diseases where we have sufficient sample sizes. Using our newly developed method GPS, we are able to synthesize information from both biobank studies that measure progression phenotypes and large-scale studies for CC phenotypes. GPS outperforms other methods that analyze either biobank or CC studies alone, methods that perform cross-trait meta-analysis, methods that use transfer learning to refine risk scores from CC studies, methods based on multivariate extension of regression models, and methods that combine risk scores from biobanks and CC studies through stacking. Individuals with high GPS scores have much-elevated risk of progressing to disease states and would benefit the most from early interventions. Moreover, we showed via PheWAS that GPS scores are more likely to be associated with closely related autoimmune diseases compared to risk scores calculated from CC studies and other methods, suggesting that the selected predictors in the model may be more relevant to disease etiology.

Predicting the progression from preclinical stage to diseases can be more clinically meaningful and actionable than predicting disease outcomes alone. Progression PRS is conceptually different from most PRS focused on predicting dichotomous disease status contrasting disease cases and healthy controls. For relatively rare diseases such as SLE (1 in 2500 among people of European ancestry), a 3× fold increase in the risk is still low for the general population and cannot justify clinical action for an at risk individual who is otherwise healthy. Instead, decisions for clinical intervention are necessary for individuals in the preclinical stage when early symptoms already start to show, autoantibodies can be detected, and autoimmunity is already activated³⁸. As autoimmune diseases may quickly lead to irreversible organ damages, early clinical interventions for individuals with high progression risk scores are critical, as those individuals may have ~3× elevated risk. Germline genetic variants usually do not change over the lifetime, which can capture the underlying risk at very early stages³⁹. Stratifying patients by their risk of disease progression allows healthcare providers to give early intervention, targeted monitoring, personalized treatment decisions, which also helps improve clinical trial designs⁴⁰.

It is intriguing to see that CC studies comparing disease vs. healthy (or population) controls yield suboptimal prediction accuracy for the progression from preclinical phases even though it measures the same end point (i.e., the disease states). The difference lies in the control groups. Variants that separate healthy controls from diseases cases tend to have different marginal effects compared to variants that separate preclinical individuals from disease cases. Our analysis indicates that GPS models for progression risk prediction preferably select variants that distinguish preclinical patients from patients with full-blown disease and healthy individuals. According to the results of PheWAS analysis, PRS for progression traits are more uniquely associated with related autoimmune diseases. On the other hand, PRS scores calculated from CC studies are more broadly associated with many traits, including many diseases that may co-occur with SLE or RA treatment, e.g., infection, acute renal failure, or hypertension. At the current sample size, there is not sufficient power to examine if the actual causal variants differ between CC and progression phenotypes. Yet, the results from our study underscore the importance of defining a reference group for genetic studies (e.g., preclinical individual vs. healthy controls), even when the end points (i.e., disease states) are the same.

Our results suggest new direction of research using EHR-based biobanks, which have become a valuable resource for genetic research, owing to their extensive collection of lab tests, clinical diagnosis, and medications⁴¹. Leveraging these comprehensive and detailed phenotypic data, researchers can effectively identify patients in preclinical stages of diseases, enabling in-depth investigations into the genetics of disease progression. While our research focuses on autoimmune conditions, similar framework would benefit the study of other progression phenotypes.

As all other studies, our research also has limitations. Due to small sample sizes, we do not have the power to analyze non-European samples. Limited exploration of transferability of the GPS scores yields noisy and inconclusive results (Supplementary Data 9 and 10). This is an unfortunate omission. As bigger datasets of diverse ancestries start to appear, our method can be similarly applied to non-European studies. Importantly, the same idea presented in GPS can be adapted to improve PRS across ancestries, where PRS constructed from the European ancestry may serve as prior to improve the accuracy of non-European PRS. Besides, we only use ANA and RF biomarkers to define preclinical phase. In practice, the preclinical phase may also be characterized by the presence of other autoantibodies including anti-rho, anti-double-strand DNA, etc. Yet, those biomarkers are measured in a very small number of individuals in current biobanks. As more EHR-based biobanks become available, our studies can be extended to include other biomarkers to more precisely define preclinical individuals.

In summary, we explore the utility of PRS to predict the progression from preclinical phase to disease states. Early diagnosis, treatment, and intervention can greatly alleviate disease symptoms, slow down progression, and improve the quality of life. The GPS method proposed in this paper outperforms alternative methods and leads to more accurate prediction of progression. It will become a useful tool for studying many diseases and will play a key role in extending utility of PRS in the era of precision medicine.

Methods

Study approval

This study is deemed non-human subject research and approved by Penn State College of Medicine IRB.

Below, we first provide the mathematical details of the GPS model and the details of model fitting algorithm. We then describe our simulation study, the applications to autoimmune diseases, and the follow-up PheWAS studies.

GPS model

We denote the progression phenotype as $\mathbf{Y}=\left(y_1,\dots ,y_n\right)\prime$, which is a $n\times 1$ vector of 0–1 values, with 0 being the baseline preclinical status and 1 being the disease state. $\mathbf{X}$ is a $n\times p$ matrix of genotypes. We encode genotypes by the number of alternative alleles in each position (i.e., 0, 1, or 2) or by allelic dosage for imputed genotypes. To facilitate presentation of the methods, we assume the genotypes are mean-centered. We use ${\mathbf{X}}_{i\cdot }$ to represent the genotype vector for individual $i$. $\mathbf{\beta }$ denotes $p\times 1$ vector of prediction weights. The model for the progression phenotype is given by

$$\mathrm{logit}\left(P\left(Y_i=1\mid {\mathbf{X}}_{i\cdot }\right)\right)={\mathbf{X}}_{i\cdot }\mathbf{\beta }$$

The likelihood function is given by

$$l\left(\mathbf{Y}\mid \mathbf{X};\mathbf{\beta }\right)={\prod }_i\sigma {\left({\mathbf{X}}_{i\cdot }\mathbf{\beta }\right)}^{I\left(Y_i=1\right)}{\left(1-\sigma \left({\mathbf{X}}_{i\cdot }\mathbf{\beta }\right)\right)}^{I\left(Y_i=0\right)}$$

where $\sigma$ is the logistic link function (or equivalently the sigmoid function), i.e.,

$$\sigma \left({\mathbf{X}}_{i\cdot }\mathbf{\beta }\right)=\frac{\exp \left({\mathbf{X}}_{i\cdot }\mathbf{\beta }\right)}{1+\exp \left({\mathbf{X}}_{i\cdot }\mathbf{\beta }\right)}$$

Expanding the likelihood at $\mathbf{\beta }=\mathit{0}$, the likelihood can be approximated by

$$l\left(\mathbf{\beta }\right)\approx {\mathbf{\beta }}^{\prime }{\mathbf{X}}^{\prime }\left(\mathbf{Y}-{\mathbf{Y}}_{\mathbf{0}}\right)-1/2\times {\mathbf{\beta }}^{\prime }{\mathbf{X}}^{\prime }\mathbf{WX}\mathbf{\beta }$$

${\mathbf{Y}}_{\mathbf{0}}$ is a vector of constant $\sigma \left({\beta }_0\right)$, representing the intercept of the model. $\mathbf{W}$ is a diagonal matrix with diagonal entries being ${\mathbf{Y}}_{\mathbf{0}}*\left(1-{\mathbf{Y}}_{\mathbf{0}}\right)$, where * is element-wise product. It is clear that maximizing the approximate likelihood is equivalent to minimizing the following loss function:

$$l^{*}\left(\mathbf{\beta }\right)=-{\mathbf{\beta }}^{\prime }{\mathbf{X}}^{\prime }\mathbf{Y}+1/2\times {\mathbf{\beta }}^{\prime }{\mathbf{X}}^{\prime }\mathbf{X}\mathbf{\beta }$$

To properly estimate the joint effects, we impose $L_1$ and $L_2$ penalties on the regression parameters, i.e., ${\mid \mid \mathbf{\beta }\mid \mid }_1^1$ and ${\mid \mid \mathbf{\beta }\mid \mid }_2^2$. To further borrow strength from large genetic studies of CC phenotypes, we use the PRS weights from CC studies as priors, i.e., ${\widehat{\mathbf{\beta }}}_{\mathbf{cc}}$. We introduce another $L_2$ penalty term to penalize the deviation between the prior and the parameters of the PRS model. It will force the model parameter to be similar to the prior, if it helps improve the prediction accuracy. Together, the loss function of the model is given by

$$L_{\mathrm{GPS}}\left(\mathbf{\beta };\alpha ,\lambda ,\eta \right)=\frac{1}{2\mathrm{N}}\left(-{\mathbf{\beta }}^{\prime }{\mathbf{X}}^{\prime }\mathbf{Y}+1/2\times {\mathbf{\beta }}^{\prime }{\mathbf{X}}^{\prime }\mathbf{X}\mathbf{\beta }\right)+\lambda \times \alpha {\mid \mid \mathbf{\beta }\mid \mid }_1^1+0.5\times \lambda \times \left(1-\alpha \right){\mid \mid \mathbf{\beta }\mid \mid }_2^2+\eta {\mid \mid {\widehat{\mathbf{\beta }}}_{\mathbf{cc}}-\mathbf{\beta }\mid \mid }_2^2$$

$\lambda$ denotes the shrinkage parameter and $\alpha$ denotes the mixing parameter that controls the weight of $L_1$ penalty relative to $L_2$ penalty. ${\mid \mid {\widehat{\mathbf{\beta }}}_{\mathbf{cc}}-\mathbf{\beta }\mid \mid }_2^2$ denotes the penalty term for the prior. The choice of $L_2$ norm allows for small differences between prior and parameters of progression PRS model. Here, $\eta$ is the corresponding tuning parameter for the new penalty term controlling for the contribution of the prior, which can be determined by cross validation. If the prior is helpful for improving progression risk prediction, the penalty term and the optimization algorithm will force parameter estimates to be similar to the CC prior. In contrast, if the prior does not help, the optimal $\eta$ will be small, and the influence of the prior will be reduced. Established methods exist to approximate ${\mathbf{X}}^{\prime }\mathbf{Y}$ and ${\mathbf{X}}^{\prime }\mathbf{X}$ using summary statistics of marginal associations and a reference panel with matched ancestries^42,43. The solutions of $L_{\mathrm{GPS}}\left(\mathbf{\beta };\alpha ,\lambda ,\eta \right)$ will be sparse as it uses a combination of $L_1$ and $L_2$ penalty.

While our method is not Bayesian, it has a Bayesian interpretation as in lasso or ridge regression models. Specifically, we can consider an equal mixture of three distributions, i.e., $N\left({\widehat{\mathbf{\beta }}}_{\mathbf{cc}},\frac{1}{\lambda }\mathbf{I}\right)$, which corresponds to the prior from CC studies, $N\left(\mathbf{0},\frac{2}{\lambda \left(1-\alpha \right)}\mathbf{I}\right)$ which corresponds to the $L_2$ penalty, and a Laplace distribution (or double exponential distribution) $Laplace\left(\lambda \right)$, which corresponds to the $L_1$ penalty. Minimizing the loss function is equivalent to maximizing the joint likelihood.

Model fitting for GPS

For notational convenience, we define $\mathbf{\Sigma }={\mathbf{X}}^{\mathbf{T}}\mathbf{X}$ as a $p\times p$ matrix and $\mathbf{\varphi }={\mathbf{X}}^{\mathbf{T}}\mathbf{Y}$ as a $p\times 1$ vector. The prior weight for variant $k$ is denoted by ${\widehat{\beta }}_{\mathit{c}{\mathit{c}}_{\mathit{k}}}$. To minimize the loss function $L_{\mathrm{GPS}}$, we employ a coordinate descent algorithm to find the solution by iteratively updating each element in $\mathbf{\beta }=\left({\beta }_1,{\beta }_2,\dots ,{\beta }_k,{\dots \beta }_p\right)$.

In iteration $t$, we update ${\beta }_k$ by

$${\beta }_k^{\left(t\right)}=\left\{\begin{array}{c}\hfill \frac{u_k^{\left(t\right)}-n\lambda \alpha }{{\mathrm{\Sigma }}_{kk}+n\lambda \left(1-\alpha \right)+n\eta },if{u}_k^{\left(t\right)}>n\lambda \alpha \hfill \\ \hfill \frac{u_k^{\left(t\right)}+n\lambda \alpha }{{\mathrm{\Sigma }}_{kk}+n\lambda \left(1-\alpha \right)+n\eta },if{u}_k^{\left(t\right)}<-n\lambda \alpha \hfill \\ \hfill 0,if{\mid u}_k^{\left(t\right)}\mid <n\lambda \alpha \hfill \end{array}\right)$$

$$u_k^{\left(t\right)}={\varphi }_k-{\sum }_{j=1,j\ne k}^{j=p}{\beta }_j{\mathrm{\Sigma }}_{kj}+n\eta {\widehat{\beta }}_{c{c}_k}$$

For variants without corresponding prior PRS weights (e.g., when the variant is not measured in the training data), we ignore the penalty term in the loss function. The optimal combination of tuning parameters $\left(\alpha ,\lambda ,\eta \right)$ that minimize the loss function in a validation dataset will be chosen and used in the final prediction model.

To improve computational efficiency, GPS models are fitted separately for each linkage disequilibrium (LD) block. For samples of European ancestry, we obtain the LD correlation matrix calculated by using 1000 Genomes project phase 3 European samples and provided by PRS-CS¹⁷. Variants in different LD blocks are considered independent. The tuning parameters $\left(\alpha ,\lambda ,\eta \right)$ are assumed to be shared across all LD blocks.

Generating simulation data

For validation and test cohorts, we simulate correlated quantitative liability scores for progression phenotype and CC phenotype using real genotypes in UK biobank. We focus only on individuals of European ancestry and use Hapmap3 variants in the simulation. We randomly select 200 or 500 causal variants for each trait. The total heritability $h^2$ is set as 0.4 for both the CC and progression phenotypes, mimicking the estimates from RA and SLE.

To generate genetically correlated liability scores, we first simulate pairs of causal variant effects from a bivariate normal distribution denoted below,

$$\left({\beta }_j^{prog},{\beta }_j^{cc}\right)~MVN\left(\right)\left(0,0\right),\mathbf{\Sigma }\left)\right)$$

$$\mathbf{\Sigma }=\left[\begin{array}{cc}\hfill \frac{h^2}{M}\hfill & \hfill \frac{h^2}{M}*\rho \hfill \\ \hfill \frac{h^2}{M}*\rho \hfill & \hfill \frac{h^2}{M}\hfill \end{array}\right]$$

Where ${\beta }_j^{prog}$ and ${\beta }_j^{cc}$ are the true effects of a causal variant $j$ for progression and CC phenotype, respectively. For non-causal variants, their true effects are set to 0. $M$ denotes the total number of causal variants and $\rho$ denotes the genetic correlation between the two phenotypes. We vary the values of $\rho$ between 0.2, 0.4, 0.6, and 0.8.

Next, to simulate individual-level phenotype information (e.g., in the validation and test cohorts), the liability scores for the CC and progression phenotypes are generated according to a linear model, i.e., $\left(y_i^{cc},y_i^{prog}\right)={\sum }_j{X}_{ij}\left({\beta }_j^{cc},{\beta }_j^{prog}\right)+\left({ϵ}_i^{cc},{ϵ}_i^{prog}\right)$, where $X_{ij}~N\left(\mathrm{0,\; 1}\right)$, and ${ϵ}_i^{cc},{ϵ}_i^{prog}~\left(0,1-h^2\right)$ $y_i$ and $X_i$ represent the simulated liability and genotype vector of individual $i$. ${ϵ}_i$ denotes the residuals. ${\beta }_j$’s represent the causal effects from the progression or CC phenotypes. Binary disease outcomes can be obtained by dichotomizing the liability score according to the disease prevalence. For both phenotypes, we simulate a validation cohort of 2000 unrelated individuals to estimate tuning parameters. For the progression phenotype, we simulate an additional test cohort of 2000 individuals to evaluate the prediction accuracy.

For training cohorts, summary level statistics of marginal effects are simulated from normal distributions ${\mathbf{\beta }}_{marginal}^{prog}~\mathrm{MVN}\left(\mathbf{D}{\mathbf{\beta }}^{\mathrm{prog}},\mathbf{D}/N_{prog}\right)$ and ${\widehat{\mathbf{\beta }}}_{marginal}^{cc}~\mathrm{MVN}\left(\mathbf{D}{\mathbf{\beta }}^{cc},\mathbf{D}/N_{cc}\right)$, where $\mathbf{D}$ denotes the LD correlation matrix. In this paper, we used precalculated LD correlation matrices based on the UK biobank samples of European ancestry, as provided by Privé et al. ¹⁶. We set the sample size of CC dataset $N_{cc}$ to be 50000. Despite the large sample sizes of biobanks, the number of preclinical individuals is often small. We vary the progression sample size $N_{prog}$ between 500, 1000, 2000, 3000, which mimics the sample sizes of preclinical individuals in biobanks such as All of Us and BioVU.

We also consider scenarios where only a portion of causal variants are shared by progression and CC phenotypes. For these scenarios, $M$, $\rho$, and $N_{prog}$ are set to be 200, 0.4, and 1000, respectively, and we vary the proportion of shared causal variants between 0.25, 0.5, and 0.75. For each simulation scenario, we simulate 20 replicates with individual-level genotype and phenotype data and calculate the marginal association summary statistics.

Building PRS models on simulation data

We use three popular PRS methods, i.e., Lassosum, LDpred2, and PRS-CS to construct baseline PRS from biobanks and CC studies. We also combine them using GPS, MTAG, transfer learning, multivariate Lassosum, and stacking strategies, as in the “Overview of GPS” section of the Results, to construct the progression PRS.

Different combinations of baseline PRS methods and progression PRS construction strategies are considered, resulting in 23 PRS models to be compared, including models from 6 combination strategies (CC, PROG, GPS, MTAG, TL-PRS, STACKING) used together with 3 baseline methods (Lassosum, LDpred2 and PRS-CS), the MVL model and four super stacking models (GPS_stacking, MTAG_stacking, TL-PRS_stacking, and ALL-BASE_stacking). More methodology details can be found in Supplementary Data 1. As input to different PRS methods, we also use the European LD correlation matrix calculated based on the 1000 Genomes project phase 3 samples, as provided by PRS-CS¹⁷. The prediction $R^2$ (i.e., the squared Pearson correlation coefficients between observed and predicted progression outcome) is used to evaluate model performance on independently simulated testing data.

GWAS summary statistics of case-control phenotypes of autoimmune disorders

For CC phenotypes, we assembled published GWAS summary statistics from studies of European ancestry for RA and SLE^44–50. Non-European individuals are excluded as the sample sizes are not sufficient for calculating polygenic risk scores or because the number of preclinical samples in biobanks is not sufficient for constructing progression risk scores. Details about the included CC studies can be found in Supplementary Data 11. We performed fixed-effect meta-analysis using rareGWAMA^51,52 to synthesize results from multiple cohorts. The resulting effective sample size is 37,828 for RA and 16,654 for SLE. We use fixed effect meta-analysis results to construct genetic risk scores.

Sample selection in Vanderbilt University Biobank (BioVU) and All of Us dataset

In the BioVU biobank, we first determined the ancestry of each sample via ADMIXTURE⁵³ using the 1000 Genome Project Phase 3 data as the reference panel. We only included samples with >90% European ancestry composition for subsequent analyses. In the All of Us biobank, we utilized the pre-calculated genetic ancestry and only included samples of European ancestry.

We then performed quality control following the recommendation by Marees et al. ⁵⁴. Specifically, with PLINK, we excluded (1) SNPs with low genotyping rate (--geno 0.01), (2) individuals who have high rates of genotype missingness (--mind 0.01), (3) SNPs with low minor allele frequency (--maf 0.05), (4) SNPs that deviate from Hardy-Weinberg equilibrium (--hwe 1e-6), (5) individuals with high or low heterozygosity rates, (6) individuals that have first or second-degree relatives in the sample (--rel-cutoff 0.125), and (7) SNPs not within the HapMap3 SNP set. Next, we select seropositive individuals from the biobanks to construct genetic risk scores, i.e., the individuals with positive ANA biomarker for SLE^3,8 and with positive RF biomarker for RA^5–7, respectively. For ANA and RF test results reported as titers, we considered titers $\ge$ 1:80 (e.g., 1:80, 1:160, 1:320, etc.) as positive, and the other values as negative (e.g., negative status, 1:40, 1:20, and etc.), following established protocols^10,55. For binary ANA and RF test results (i.e., reported as either positive or negative), we considered positive tests as positive and negative tests as negative. Lastly, for RF reported in the unit of IU/mL, we considered values > 15 IU/mL as positive and values ≤ 15 IU/mL as negative.

Defining individuals with preclinical and disease status and GWAS analysis

To define progression phenotypes for RA and SLE in BioVU and All of Us, we use patients who had positive biomarker test results (RF positive for RA and ANA positive for SLE) and relevant PheWAS codes for SLE or RA phenotype as progressed cases, following established algorithms⁵⁶ (Table 3). The remaining seropositive individuals that were followed up in the biobank but without the disease PheWAS code were used as non-progressed. The summary of sample size and demographic information for diseased and preclinical individuals from BioVU and All of Us cohorts are provided in Supplementary Data 2.

Table 3.

ICD codes used to define RA and SLE disease status

Disease	ICD codes
Rheumatoid Arthritis (RA)	ICD9: 714.0, 714.1, 714.2, 714.81 ICD10: M05*, M06.8*, M06.9
Systemic lupus erythematosus (SLE)	ICD9: 710.0 ICD10: M32.8, M32.9, M32.1*

Seropositive (ANA or RF positive) Individuals with relevant diagnostic codes are defined as disease cases⁵⁶, following established algorithms. The remaining seropositive individuals with no diagnostic codes for the disease at any time in the EHR but being followed up are considered non-progressed controls.

ICD codes ending in “*” include all sub-level codes. e.g., M32.1* code contains all sublevel codes such as M32.10, M32.11, M32.12, M32.13, M32.14, etc.

Given the diseased and preclinical status definition, we performed GWAS analysis in the training dataset using REGENIE v2.2.4⁵⁷, adjusting for sex, year of birth ($YOB$), $YO{B}^2$, $sex\times YOB$, $sex\times YO{B}^2$, and 20 genotype principal components. The resulting GWAS summary statistics are used to construct progression risk scores.

Building PRS models for progression risk of autoimmune disorders

As in simulation studies, 23 different PRS models are used to predict the progression risks for two autoimmune disorders, i.e., RA and SLE. Models were constructed in the same way as in simulation studies. For methods that need tuning parameters, we randomly split BioVU cohort into training samples (70%) and validation samples (30%). Training samples are used to generate GWAS summary statistic for progression phenotype and validation samples are used for selecting tuning parameters. After tuning parameters are selected, we retrain the model using the whole BioVU dataset and use the All of Us data as our test data to evaluate the accuracy of different risk scores.

To evaluate different PRS models, Nagelkerke’s ${\mathit{R}}^{\mathit{2}}$ on the liability scale²² are calculated. 95% confidence intervals of the Nagelkerke’s ${\mathit{R}}^{\mathit{2}}$ estimates are calculated using the CI.Rsq function in the psychometric R package (version 2.3). This function constructs confidence intervals for ${\mathit{R}}^{\mathit{2}}$ based on an approximated standard error estimates⁵⁸. We also calculated area under the precision recall curve (AURPC) and area under the receiver operating characteristic curve (AUC) using ROCR⁵⁹ package (version 1.0-11). 95% confidence intervals for AUPRC and AUC are calculated by 1000-fold bootstrapping on the testing dataset.

Comparing marginal association statistics of progression phenotypes in All of Us

GWAS analysis of progression phenotypes in the All of Us biobank was conducted in the same way as the analysis of the BioVU biobank. For variants selected by GPS and PRS models trained with CC studies, we examined how strongly they are associated with the control → preclinical and preclinical → disease progression phenotypes in the independent test dataset All of Us. We plotted the cumulative distribution functions of the marginal ${\chi }^2$ statistics testing for the genetic association with control vs preclinical states and with preclinical → disease progressions. Two-sided Kolmogorov-Smirnov tests were conducted to compare the distributions of marginal ${\chi }^2$ statistics.

PheWAS analysis in UK biobank and All of Us

PheWAS was conducted in the UK Biobank and All of Us data. We obtained the 23 trained PRS models of preclinical to disease progressions for RA and SLE. For 16 non-stacking-based PRS models, we calculated risk scores for all UK Biobank and All of Us individuals using the “score” function of plink2. For 7 stacking-based PRS models, we calculated their risk score by weighted sum of individual non-stacked PRS models included within each stacked-based PRS model. PheWAS codes were assigned to each participant based on the reported ICD-9 and ICD-10 codes from the EHR, using the createPhenotypes function from the PheWAS R package (https://github.com/PheWAS/PheWAS). Default parameters were used. We limit our analyses to samples of European ancestry (UK Biobank n = 458,878 and All of Us n = 97,016) and only analyze PheWAS codes that occur in at least 0.1% of individuals. In total, we included 1405 and 1282 PheWAS codes in the UK Biobank and All of Us analysis, respectively. We estimated the association between PheWAS codes with PRS using logistic regression models, controlling for $sex$, year of birth ($YOB$), $YO{B}^2$, $sex\times YOB$, $sex\times YO{B}^2$, and the top 20 genotype PCs as covariates.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

C.W., H.M., B.J., and D.J.L. conceived the study and developed the statistical model. C.W. and H.M. led the data analysis. C.W., H.M., A.R.D., C.K., and X.W. conducted analyses. L.C., B.L., Xue Z., G.T.F., and N.J.O. helped with data interpretation. Xiaowei Z. helped with coding and programming. C.W., H.M., and D.J.L. prepared the manuscript. All authors contributed to manuscript editing and approved the manuscript. B.J. and D.J.L. jointly supervised the project.

Peer review

Peer review information

Nature Communications thanks Wanling Yang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The GWAS summary statistics for CC studies of autoimmune diseases are publicly available and their corresponding PubMed IDs can be found in Supplementary Data 11. GWAS summary statistics constructed in this study from data of the BioVU and the All of Us biobank will be available upon request from the author. The individual-level EHR lab test, diagnosis and genotype data of patients from the All of Us (https://www.researchallofus.org) biobank can be accessed upon application. The individual-level EHR lab test, diagnosis, and genotype data of patients from the BioVU biobank (https://victr.vumc.org/biovu-description) can be accessed via collaborations with Vanderbilt University. All other data supporting the findings described in this manuscript are available in the article and its Supplementary Information files.

Code availability

Code for constructing baseline PRS models or combining different PRS models can be found at https://github.com/wangc29/GPS_paper_script. We also use the following software to construct PRS, including Lassosum (version 0.4.5), LDpred2 (version 1.12.2) and PRS-CS (version 1.1.0), MTAG (version 2017-04-07), TL-PRS (version 1.0.0), and multivariate Lassosum (version 1.0.0). All other methods were implemented with their default settings and tuning parameters are selected by optimizing the prediction $R^2$ in validation dataset. An R package implementing the GPS method can be found at https://github.com/wangc29/gps and the linked Zenodo repository (10.5281/zenodo.14176980)⁶⁰. As presented in Fig. 1, GPS takes four pieces of information as input including the weights of a pretrained CC PRS model, GWAS summary statistics of a progression phenotype, a validation dataset with individual level genotype and phenotype information for the progression phenotype, and an LD correlation matrix from the matched ancestry. The final output is a trained GPS model that can be used to predict disease progression risk.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-55636-6.