Compact wearable microstrip antenna design using hybrid quasi-Newton and Taguchi optimization

Abstract

A novel approach is introduced for designing a miniaturized wearable antenna. Utilizing Taguchi’s philosophy typically entails numerous experimentations runs, but our method significantly reduces these by employing a quasi-Newton approach with gradient descent to estimate process parameter ranges. This hybrid technique expedites convergence by streamlining experiments. Additionally, the Taguchi array ensures a balanced design, equalizing factor weights. Unlike conventional Taguchi methods, which risk trapping optimized results at local minima with increased repetitions, our modified technique mitigates this issue by adjusting level differences, aiming for global minima. Antenna design often involves competing objectives, such as size, impedance matching, cross-polarization, directivity, and frequency range. This study addresses these multiobjective challenges using a hybrid approach. The proposed method is applied to design and fabricate a biosafe miniaturized antenna for integration into clothing. The comparison of computed and measured antenna parameters confirms the accuracy of our solution while demonstrating a reduction in the required number of experiments. This innovative approach significantly advances the efficient design of wearable antennas. The biosafe wearable antenna demonstrated compliant specific absorption rate (SAR) (1.2 W/kg), robust mechanical performance (up to 40° bending), and underwent human body effect investigation. Comparison of computed and measured antenna parameters confirms solution accuracy. By implementing the proposed hybrid approach, computational time is significantly reduced by 98%, outperforming electromagnetic (EM) solvers’ built-in optimization.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-83864-9.

Introduction

Designing contemporary antenna systems is challenging due to evolving requirements¹. Global optimization methodologies are extensively employed in antenna design due to their ability to address complex specifications². These methodologies become invaluable tools when closed-form solutions are unavailable for attributes like gain characteristics and impedance. Practical constraints, such as device profile and miniaturization needs, often restrict antenna design³. However, downsizing can compromise electrical and field performance, necessitating careful trade-offs⁴. Traditional approaches like equivalent network models or experience-based research are inadequate for managing multiple design objectives^5–7. Thorough numerical optimization is recommended instead⁸. Nature-inspired algorithms are popular for global optimization^9,10. Despite their ease of execution, they can be cost-ineffective. Alternatively, machine learning techniques have been explored, but they suffer from dimensionality issues and can alter antenna characteristics significantly¹¹. Numerous studies have focused on synthesis and optimization to enhance antenna design efficacy. For example, Genetic Algorithms (GA) and moment concepts have been used to increase the bandwidth of patch antennas¹². GA has also been employed to optimize miniaturized patch antenna for gain and bandwidth maximization¹³. Other techniques, such as Particle Swarm Optimization (PSO) with neighborhood redispatch, have been applied to design ultra-wideband slot antennas¹⁴. While various optimization techniques exist^15,16, Taguchi’s method, based on orthogonal arrays¹⁷, is preferred for its systematic parameter selection, reducing experimentation time and resources¹⁸. However, Taguchi’s method has limitations, including overlooking certain parameter combinations and requiring expertise in experimental design and analysis. Quasi-Newton methods have shown fast convergence rates for local minima, but their impact on optimal parameter range generation in antenna design remains unexplored. This study aims to incorporate a technique for determining the ideal range of process parameters to minimize trial experiments, adhere to Taguchi’s philosophy, and ensure quick convergence in flexible antenna design.

Methodology

The characteristics of an antenna are closely tied to its application scenarios, with the antenna’s size determined by factors such as operating frequency, substrate thickness, and dielectric constant. However, reducing antenna size while maintaining performance parameters like bandwidth, gain, impedance matching, VSWR, directivity, and resonant frequency presents a challenge. After identifying independent parameters based on substrate choice and frequency, control parameters such as ground plane size, feed position, and width were identified as process parameters for experimentation. The range of these parameters was determined using the quasi-Newton approach, which involves moving in the gradient direction to locate maxima and in the opposite direction to find minima. Simulation was conducted for all process parameters using the HFSS tool to establish their ranges.

Trial and error approach

A flexible rectangular patch antenna was developed using textile polyester flexible substrate material, featuring a dielectric constant (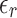) of 2.75 and a thickness (h) of 1.5 mm for 2.45 GHz frequency (f_r). The antenna’s dimensions were calculated using conventional patch parameter formulas as shown in Eqs. (1) to (7)¹⁹, resulting in a size of 53.89 × 62.71 mm². Achieving a resonant frequency of 2.43 GHz, the antenna demonstrated a |S11| of − 22.46 dB and a gain of 6.75 dBi. Given the importance of compactness in wearable applications, parametric modifications were necessary to attain the desired outcomes within a reduced size. The trial-and-error method adjusted antenna parameters, including patch width, ground plane size, and feed slot inset. Parameter variations spanned from the upper range determined by traditional formulas to 10% reductions, with step sizes ranging from 0.03 to 0.005 mm. 160 trial-and-error experiments were conducted, documented in an annexed table, and analyzed based on the desired resonant frequency, |S11|, and antenna gain. This iterative process allowed for fine-tuning antenna parameters to meet performance requirements while accommodating compactness constraints for wearable applications.

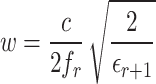1

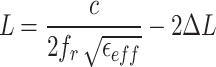2

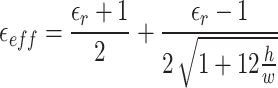3

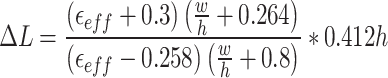4

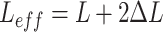5

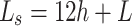6

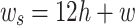7

Quasi-Newton method

The iterative process relies on gradient information to update an approximation of the Hessian matrix, enhancing optimization when combined with gradient descent. Unlike Newton’s method, the quasi-Newton algorithm doesn’t necessitate matrix inversion or equation system solutions, utilizing an estimated inverse Hessian matrix. The process initiates with formulating the objective function for controlling parameter minimization or maximization, along with setting the maximum iteration count, convergence criteria, and step size. Subsequently, quasi-Newton with Gradient Descent is implemented through the following steps:

1. Starting with an initial solution estimate, denoted as 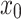, the gradient of the objective function at the current estimate  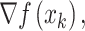(where k denotes the current iteration) is computed.

2. The estimate using a combination of the gradient and an approximation of the Hessian matrix is updated as

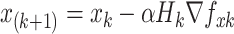
   8

   where α is the step size, and 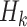approximates the Hessian matrix for kth iteration.

3. Based on the estimated solution and variations in the gradient, 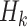is updated at each iteration. The Broyden-Fletcher-Goldfarb-Shanno (BFGS) approximation is employed. The iteration process continues until a small gradient magnitude is reached. The results are estimated based on the maximum and minimum values of the function. The technique potentially converges to a minimum point even if the starting guess for 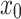Is set. The only prerequisites for the initial approximation of the inverse Hessian, or 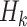, are that it must be symmetric, positive definite, and real.

Taguchi’s method for optimization

To initialize Taguchi’s method for optimization after deriving the control parameter range, the first step is to initialize the orthogonal array. The orthogonal array is represented in the form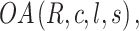

Where R—Number of orthogonal array rows, c—Number of design variables, l—levels of parameters, s—strength .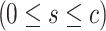

Taguchi’s method of process flow includes the creation of the orthogonal array, Rao’s inequalities equation is used to decide the number of experiments to perform based on the finalized orthogonal array²⁰. The orthogonal array parameters need to satisfy the following equations of existence/construction:

if s = 2x; x > 0 then:

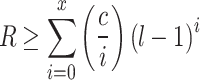9

and if s = 2x + 1; x ≥ 0 then:

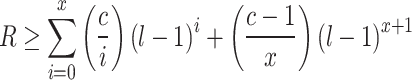10

Hybrid approach: quasi-Newton with Taguchi’s orthogonal array method

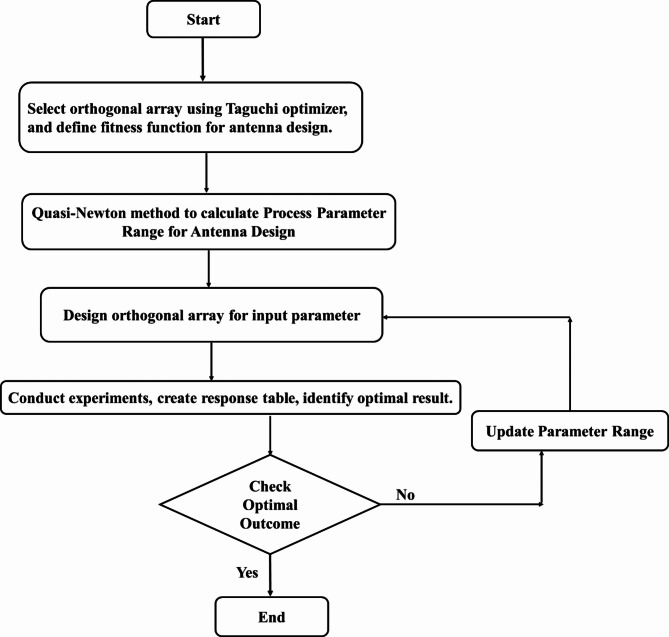
One of the significant limitations of Taguchi’s method is that it does not consider every possible combination of the orthogonal array’s parameters. Also, the Taguchi method has some other limitations for optimization, such as requiring a high level of expertise and knowledge in designing and analyzing experiments and optimizing the performance characteristics within the combination of the process parameters. The use of Taguchi’s philosophy requires more experimentation runs which is considerably reduced by using quasi-Newton with gradient descent approach to estimate the process parameter range. The effect of the quasi-Newton method, on the optimal generation of the process parameter range was applied to search local minimums. Hence, employing the Taguchi method integrated quasi-Newton algorithm for determining the ideal range of process parameters will decrease the number of trial experiments, and guarantee quick convergence to obtain the optimum results. The process flow of a proposed hybrid method of Taguchi with a quasi-Newton algorithm is shown in Fig. 1.

Fig. 1.

The flow of the proposed hybrid approach of Taguchi with the quasi-Newton method.

In the proposed work, the five control factors, including patch width, ground width, ground length, feed width, and feed slot, were identified with the sole objective of miniaturization, as given in Tables 1 and 2 for the first and second iterations, respectively. These five parameters were considered for five different levels, and the orthogonal array 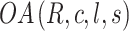is designed for R = 25, c = 5, l = 5, and s = 2, as shown in Tables 3 and 4 for the first and second iterations, respectively. Textile material, with a dielectric constant of 2.75- and 1.5-mm thickness, serves as the substrate for flexible antenna design.

Table 1.

Control factors of antenna for miniaturization for the first iteration.

Factor levels	Patch width (mm)	Ground width (mm)	Ground length (mm)	Feed width (mm)	Feed slot (mm)
	f1	f2	f3	f4	f5
	(u)	(v)	(w)	(x)	(y)
1	44.71	62.71	53.89	0.25	8.97
2	39.12	57.12	49.39	0.37	8.22
3	33.53	51.53	44.89	0.5	7.47
4	27.94	45.94	40.39	0.62	6.72
5	22.35	40.35	36	0.75	5.98

Table 2.

Control factors of antenna for miniaturization for the second iteration.

Factor levels	Patch width (mm)	Ground width (mm)	Ground length (mm)	Feed width (mm)	Feed slot (mm)
	f1	f2	f3	f4	f5
	(u)	(v)	(w)	(x)	(y)
1	44.71	62.71	53.89	0.25	8.97
2	41.91	57.12	51.64	0.37	8.22
3	39.12	51.53	49.39	0.5	7.47
4	36.32	45.94	47.14	0.62	6.72
5	33.53	40.35	44.89	0.75	5.98

Table 3.

Orthogonal array of first iteration designed for R = 25, c = 5, l = 5, s = 2.

Experiment	Patch width (mm)	Ground width (mm)	Ground length (mm)	Feed width (mm)	Feed slot (mm)
	f1	f2	f3	f4	f5
	(u)	(v)	(w)	(x)	(y)
D1	44.71	62.71	53.89	0.25	8.97
D2	44.71	57.12	49.39	0.37	8.22
D3	44.71	51.53	44.89	0.5	7.47
D4	44.71	45.94	40.39	0.62	6.72
D5	44.71	45	36	0.75	5.98
D6	39.12	62.71	49.39	0.5	6.72
D7	39.12	57.12	44.89	0.62	5.98
D8	39.12	51.53	40.39	0.75	8.97
D9	39.12	45.94	36	0.25	8.22
D10	39.12	40.35	53.89	0.37	7.47
D11	33.53	62.71	44.89	0.75	8.22
D12	33.53	57.12	40.39	0.25	7.47
D13	33.53	51.53	36	0.37	6.72
D14	33.53	45.94	53.89	0.5	5.98
D15	33.53	40.35	49.39	0.62	8.97
D16	27.94	62.71	40.39	0.37	5.98
D17	27.94	57.12	36	0.5	8.97
D18	27.94	51.53	53.89	0.62	8.22
D19	27.94	45.94	49.39	0.75	7.47
D20	27.94	40.35	44.89	0.25	6.72
D21	22.35	62.71	36	0.62	7.47
D22	22.35	57.12	53.89	0.75	6.72
D23	22.35	51.53	49.39	0.25	5.98
D24	22.35	45.94	44.89	0.37	8.97
D25	22.35	40.35	40.39	0.5	8.22

Table 4.

Orthogonal array of second iteration designed for R = 25, c = 5, l = 5, s = 2.

Experiment	Patch width (mm)	Ground width (mm)	Ground length (mm)	Feed width (mm)	Feed slot (mm)
	f1	f2	f3	f4	f5
	(u)	(v)	(w)	(x)	(y)
D1	44.71	62.71	53.89	0.25	8.97
D2	44.71	57.12	51.64	0.37	8.22
D3	44.71	51.53	49.39	0.5	7.47
D4	44.71	45.94	47.14	0.62	6.72
D5	44.71	45	44.89	0.75	5.98
D6	41.91	62.71	51.64	0.5	6.72
D7	41.91	57.12	49.39	0.62	5.98
D8	41.91	51.53	47.14	0.75	8.97
D9	41.91	45.94	44.89	0.25	8.22
D10	41.91	40.35	53.89	0.37	7.47
D11	39.12	62.71	49.39	0.75	8.22
D12	39.12	57.12	47.14	0.25	7.47
D13	39.12	51.53	44.89	0.37	6.72
D14	39.12	45.94	53.89	0.5	5.98
D15	39.12	40.35	51.64	0.62	8.97
D16	36.32	62.71	47.14	0.37	5.98
D17	36.32	57.12	44.89	0.5	8.97
D18	36.32	51.53	53.89	0.62	8.22
D19	36.32	45.94	51.64	0.75	7.47
D20	36.32	40.35	47.14	0.25	6.72
D21	33.53	62.71	44.89	0.62	7.47
D22	33.53	57.12	53.89	0.75	6.72
D23	33.53	51.53	51.64	0.25	5.98
D24	33.53	45.94	49.39	0.37	8.97
D25	33.53	40.35	47.14	0.5	8.22

Resonant frequency, high signal-to-noise ratio, and minimum fitness function which uses |S11| parameters are considered while evaluating optimization results. The fitness function used is the |S11| parameter, resonant frequency, and compactness. In comparison to the size of 53.89 × 62.71 mm² that is obtained after considering the traditional method, the identified fifteenth design experiment (Table 1) from the first iteration gives the |S11| of − 17.39 dB at a resonant frequency of 2.46 GHz for a compact size of 49.39 × 40.35 mm². This indicates a 41.02% reduction in the size. The optimization range for subsequent iterations is iteratively refined by scaling the current level difference by a reduction factor (ρ) between 0.5 and 1, tailored to specific requirements. The optimal level for each iteration serves as the centroid for the next iteration’s search space, ensuring convergence within the predefined bounded region. So, for the (i + 1)th iteration.

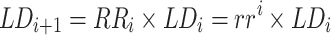11

Where 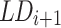is called a level difference of the next iteration; 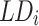is the level difference of the ith iteration; 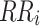is the reduced rate of the ith iteration; 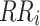= 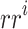termed the reduced function. Reducing the optimization range and performing the second iteration, the identified twenty-fifth design experiment (Table 3) from the second iteration the |S11| found is − 12.12 dB, the resonant frequency is 2.46 GHz with a reduced size of 47.14 × 40.35 mm² with 43.71% reduction in the size. It is observed that the optimal fitness is located in a short time, with the use of the estimated parameter values derived using the quasi-Newton method with a reduced number of experiments as given in Tables 3 and 4 of the first and second iterations respectively.

Result and discussion

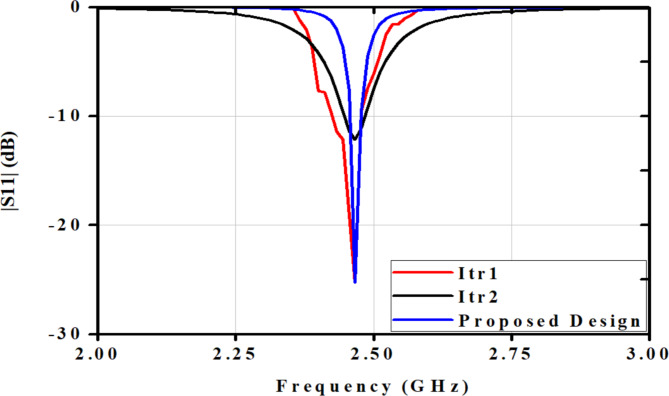
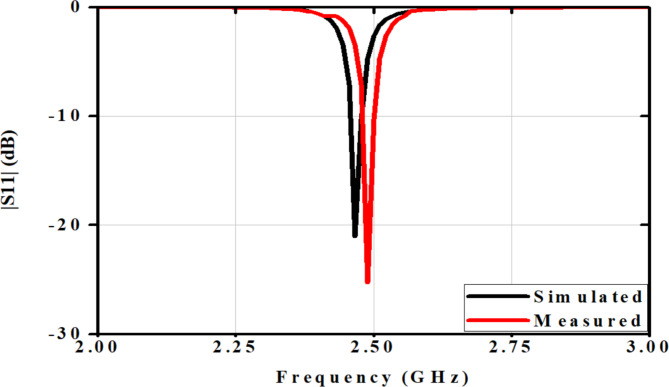
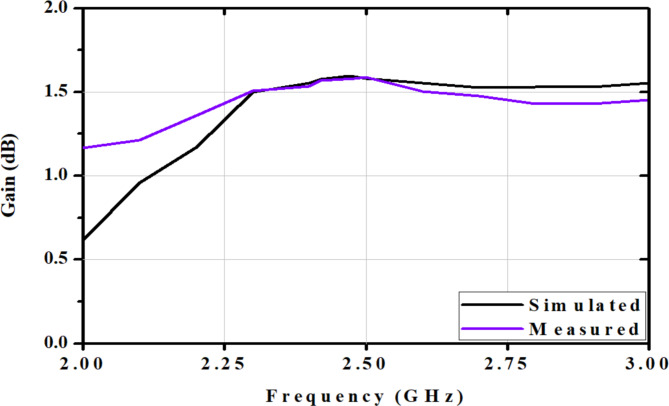
The preceding outcomes were a foundation for refining the design to align with predefined objectives. A modified design was formulated, featuring shorting posts across the patch width and a halved patch length compared to the optimized design, derived from the twenty-fifth design experiment of the second iteration. This modified design was utilized to validate the proposed hybrid concept, depicted in Fig. 2a. Fabrication of the antenna was executed using textile material, illustrated in Fig. 2b–e. This paper utilizes graphs generated using OriginPro software to visualize and analyze the data. Characterization of the fabricated antenna was conducted using a vector network analyzer (VNA) from the Keysight streamline series P9370A (300 MHz to 4 GHz), as illustrated in Fig. 3a. Additionally, testing was conducted in an anechoic environment, as Fig. 3b depicts. The analysis of frequency and |S11| for both iterations of the Taguchi method and the proposed design is presented in Table 5; Fig. 4, respectively. Observations show iterative size reduction in antenna design: Taguchi’s iterations achieved 41.02% and 43.71% reductions, while the proposed design with shorting vias achieved a substantial 71.85% reduction. The |S11| versus frequency plot and gain versus frequency plot were examined for the fabricated flexible antenna with shorting posts, illustrated in Figs. 5 and 6, respectively. A comparative analysis between the simulated and measured results of the proposed antenna design is provided in Table 6. The proposed antenna demonstrated close agreement between simulated and measured results, with resonant frequency at 2.466 GHz, |S11| of − 21.03 dB (simulated) and − 25.29 dB (measured), and gain of 1.83 dB (simulated) and 1.73 dB (measured). Additionally, the E/H-Co/Cross polarization plots for both simulated and measured designs were analyzed, as depicted in Figs. 7 and 8. Simulations were performed using High Frequency Structure Simulator (HFSS) EM solvers on an Intel Core i5-10210U (1.60 GHz, 8 GB RAM, 11 GB virtual memory, Windows 10). Table 7 presents a comparative analysis of convergence time and efficiency metric parameter for the Fast Frequency Sweep (FFS) solver at 2.45 GHz, employing a mesh density of λ/15. Conventional trial and error methods necessitate an indefinite number of attempts, quasi-Newton optimization demands 3125 experiments, the Taguchi method involves 225 trials. In contrast, the hybrid approach requires merely 50 experiments, effectively balancing optimization accuracy with computational efficiency. Furthermore, Table 8 compares the analysis of textile substrate material antennas reported in the literature and the proposed optimized design. From Table 8, it is clear that recently reported pioneer state of the art utilized flexible substrates with resonance frequencies ranging from 2.4 to 5.25 GHz and antenna sizes varying from 38.5 mm × 25 mm to 140 mm × 70 mm, exhibiting medium to high design complexity. In contrast, the proposed design achieves 2.49 GHz resonance with a smaller, simpler antenna size of 40.35 mm × 23.57 mm.

Fig. 2.

(a) Dimensional details of the optimized miniaturized antenna structure (b) Optimized miniaturized antenna front view (c) Optimized miniaturized antenna back view (d) Optimized miniaturized antenna front perspective view (e) Optimized miniaturized antenna back perspective view.

Fig. 3.

(a) Characterization of fabricated optimized miniaturized antenna using VNA (b) Fabricated optimized miniaturized antenna placed in an anechoic chamber for testing.

Table 5.

Comparative analysis of the proposed antenna and Taguchi’s iterations.

Technique	Size of antenna (mm2)	Reduction in size with respect to size of antenna considering traditional method (%)
Taguchi’s first iteration (15th design experiment)	49.39 × 40.35	41.02
Taguchi’s second iteration (25th design experiment)	47.14 × 40.35	43.71
Proposed design with shorting vias	23.57 × 40.35	71.85

Fig. 4.

|S11| and frequency graph.

Fig. 5.

|S11| and frequency graph of optimized miniaturized antenna for simulated and measured cases.

Fig. 6.

Gain versus frequency plot of optimized miniaturized antenna for simulated and measured cases.

Table 6.

Validation of optimized miniaturized antenna for simulated and experimental results.

Proposed antenna	Resonant frequency (GHz)	|S11| (dB)	Gain (dB)
Simulated results	2.46	− 21.03	1.83
Measured results	2.49	− 25.29	1.73

Fig. 7.

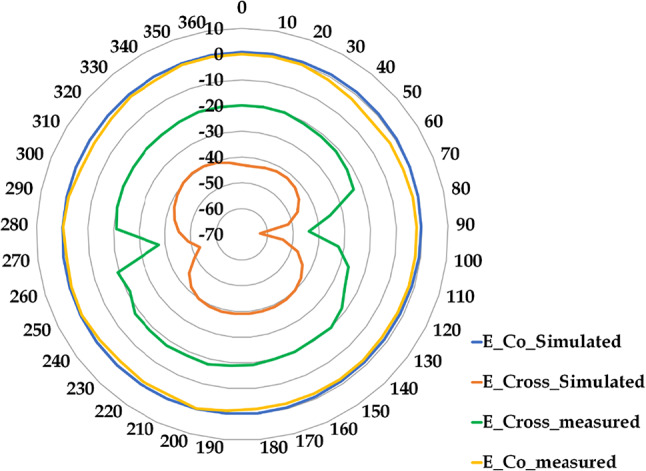
E-co/cross polarization plots of simulated and measured results of optimized miniaturized antenna.

Fig. 8.

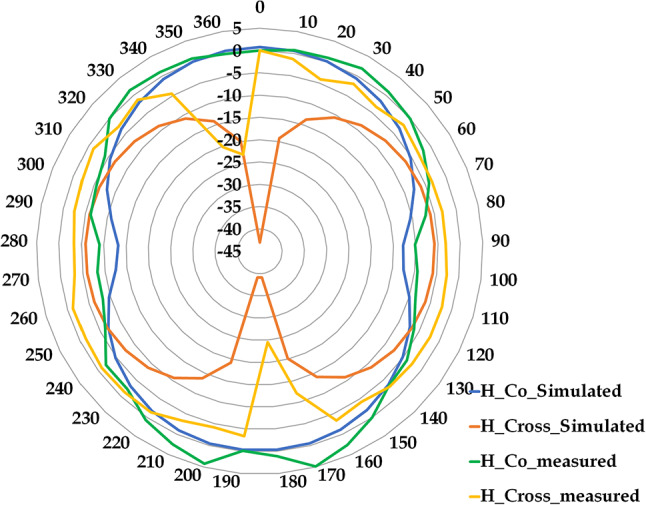
H-co/cross polarization plots of simulated and measured results of optimized miniaturized antenna.

Table 7.

Comparative analysis of convergence time and no. of experiments in different techniques.

Technique	No. of experimentations	Convergence time and computation efficiency metric elements
Quasi-Newton (EM solvers build-in optimization)	3125 (5 antenna parameters for five different levels)	Mesh generation: 0.42 min Solver setup: 0.28 min Convergence time: 93.22 min Total convergence time: 93.92 min Simulation time/iteration: 0.03 min
Taguchi method	225 (Nine iterations of 25 experiments each)	Mesh generation: 0.42 min Solver setup: 0.28 min Convergence time: 9.50 min Total convergence time: 10.20 min Simulation time/iteration: 0.045 min
Hybrid approach: quasi-Newton + Taguchi orthogonal array	50 (Two iterations of 25 experiments each)	Mesh generation: 0.42 min Solver setup: 0.28 min Convergence time: 1.15 min Total convergence time: 1.85 min Simulation time/iteration: 0.037 min

Table 8.

Comparative analysis of fabricated prototype with recent pioneer state of art.

Refs.	Substrate material	Number of bands	Resonance frequency (GHz)	Gain (dB)	Size of antenna (mm2)	Design type	Design complexity
21	Textile	Single	2.45	6.2	72.4 × 65.5	Electromagnetically-coupled patch	Medium
22	Textile	Dual	0.915 2.45	6.84	48 × 52	Patch with monopole	Medium
23	Textile	Single	2.45	4.7	140 × 70	Dual Patch	Simple
24	Textile	Single	2.4	1	Patch size: 40.1 × 40.1	Square patch	Medium
25	Textile	Single	2.45	7.46	82.4 × 35.4	EBG structure	Medium
26	Polyimide	Triple	1.31 3.55 5.25	4.39	55 × 42	Toroidal	Medium
27	Polyethylene	Single	2.45	–	38.5 × 25	Coplanar	High
28	Ultra-lam 3850	Dual	2.4 7.48	2.36 3.1	50 × 35	Slotted circular disc patch with partial ground	Medium
Proposed design	Textile	Single	2.5	1.73	40.35 × 23.57	Rectangular	Simple

The wearable flexible compact antenna is analyzed for working on the human body, its Specific Absorption Rate (SAR), and bending analysis.

Performance evaluation of the antenna on human body phantom

The human body’s presence substantially impacts antenna performance due to its complex and energy-absorbing properties. Human body effects on antenna performance were investigated using a four-layered phantom (muscle, fat, bone, and skin) and measurements on a human hand with VNA. Results, shown in Fig. 9a and b. The phantom’s electrical properties at 2.45 GHz were: Bone: ε = 11.41, σ = 0.385 S/m, thickness = 28 mm; Muscle: ε = 54.9, σ = 0.96 S/m, thickness = 10 mm; Fat: ε = 5.4, σ = 0.05 S/m, thickness = 4 mm; Skin: ε = 41.4, σ = 0.88 S/m, thickness = 2 mm.

Fig. 9.

(a) Performance analysis of the proposed antenna positioned to the equivalent human torso in simulation environment. (b) Performance analysis of the proposed antenna positioned on human hand.

Investigation of specific abortion rate of the antenna

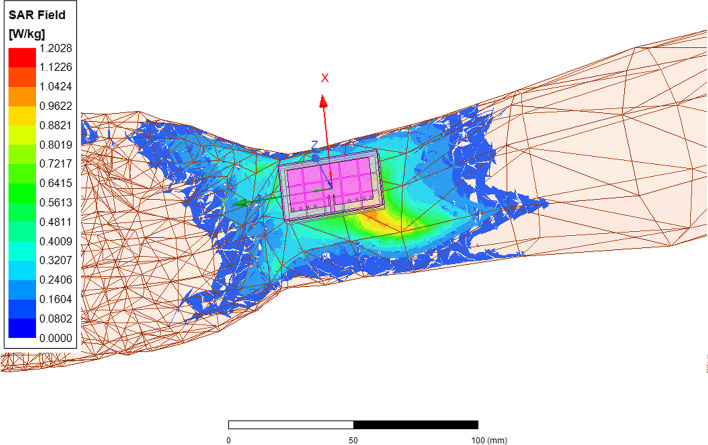
The proposed antenna’s SAR was simulated on the human torso hand using HFSS as shown in Fig. 10. Results show the antenna’s SAR (1.2 W/kg at 1 mm spacing) complies with International Commission on Non-ionizing Protection guidelines (ICNIRP) 2 W/kg limit for 10 g tissue.

Fig. 10.

SAR analysis of the proposed antenna positioned on the human torso.

Investigation of antenna conformality

The proposed antenna’s performance was tested in wearable scenarios, including bending and flexing. Figure 11 shows the antenna wrapped around a cylinder. The results (Table 9) demonstrate that the antenna maintains its performance even when bent at angles up to 40°, making it suitable for wearable applications.

Fig. 11.

Investigation of antenna conformality.

Table 9.

Investigation of antenna conformality for different bending conditions.

Bending angle in degrees	Frequency (GHz)	|S11| (dB)	Frequency deviation with respect to non-bend antenna (%)
10	2.4493	− 27.581	0.02
20	2.4432	− 26.8468	0.28
30	2.4385	− 25.3401	0.46
40	2.431	− 24.0228	0.78

Benchmarking different optimization models

The optimization of antenna designs requires efficient computational methods to reduce design time and enhance performance. Various approaches have been explored as shown in Table 10, including deep learning surrogate models²⁹, surrogate-assisted particle swarm optimization³⁰, Taguchi methods³¹, fast global sensitivity analysis-based surrogate-assisted machine learning³², support vector machines³³, and online data-driven enhanced-XGBoost³⁴. While these methods demonstrate some computational efficiency, the proposed hybrid approach, combining Taguchi and quasi-Newton methods, achieves a remarkable 98% average cost reduction. This significant reduction corresponds to a substantial decrease in total computational time compared to EM solvers’ built-in optimization, as demonstrated using HFSS. The proposed hybrid approach reduces the initial computational effort required for building the training dataset, thereby accelerating the overall design optimization process for antenna designs. In contrast, existing methods exhibit varying degrees of computational efficiency, ranging from 39 to 85% reductions. The Proposed Hybrid approach offers a substantial advantage in reducing computational time and enhancing design optimization for antenna designs, making it an attractive solution for efficient antenna design.

Table 10.

Benchmarking different optimization models: results and insights.

Refs.	Antenna type	Model used for optimization	EM simulator used	Average cost reduction	Details
Proposed hybrid approach	Patch with shorting posts	Hybrid method: Taguchi with quasi Newton metod	HFSS	98% (corresponds to a total computational time of EM solvers build-in optimization and proposed hybrid approach)	The proposed approach can reduce the initial computational effort required for building the data set to be used for training the models thereby accelerating the overall design optimization process for antenna designs
29	Microstrip	Deep learning surrogate model	CST	50% (corresponds to a total computational time of EM solvers build-in optimization and surrogate model)	The dataset is generated for a deep learning-based surrogate model using EM simulator
30	SIW cavity backed slot antenna	Surrogate-assisted particle swarm optimization with mixed prescreening	HFSS	39% (60 Simulations for optimization considering best case of Surrogate-assisted particle swarm optimization with mixed pre-screening and 98.5 simulations of ten runs optimization)
31	Microstrip patch antenna	Taguchi method	COMSOL	–	81 (Three trials of 27) experiments required for Taguchi compared to the trial-and-error approach
32	Dipole antenna	Fast global sensitivity analysis-based surrogate-assisted machine-learning	CST	85% (corresponds to the total computational duration required for EM solvers’ built-in optimization and surrogate model)	The dataset enables a surrogate-based optimization framework for antenna design, employing particle swarm optimization and kriging interpolation, with electromagnetic simulations providing the necessary data
33	Circular patch	Support vector machine (SVM)	CST	–	1000 simulation are used to generate dataset for proposed SVM model
34	Resonator antenna	Online data-driven enhanced-XGBoost (E-XGBoost) Method consists of input variable filter module (IVFM) and an antenna optimization module (AOM)	HFSS	80% (max) (Time overhead compared to ML methods)	The dataset is generated for a machine learning-based model using EM simulator. The enhanced-XGBoost method is used for antenna optimization model

Conclusion

The proposed work presents a computationally efficient antenna design optimization technique using novel hybrid approach combining Taguchi philosophy and the quasi-Newton method. The technique is validated using a simple wearable flexible rectangular patch antenna geometry for easy modeling, simulation, and prototype development. Key innovations include methodology development, design space exploration, and multi-objective optimization. The technique offers efficient design space exploration and reduced computational cost, making it applicable to complex antenna geometries with multiple variables. Future research avenues could explore further enhancements in the effectiveness and efficiency of Machine Learning models through integrating quasi-Newton optimization and Taguchi methods, focusing on sustainability and resource conservation. Additionally, investigations into the synergistic use of these approaches with evolutionary or reinforcement strategies may provide valuable insights for addressing optimization challenges in real-world scenarios.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author contributions

(1) Archna Tiwari: Wrote the main manuscript. (2) Aleefia A. Khurshid: Review and measurement (3) Kanhaiya Sharma: Supervision, analysis, and review.

Data availability

The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.

Declarations

Competing interests

The authors declare no competing interests.