ABSTRACT
Soybean (Glycine max) is the single most important global source of vegetable protein. Yield improvements per unit land area are needed to avoid further expansion onto natural systems. Mesophyll conductance (g m ) quantifies the ease with which CO2 can diffuse from the sub‐stomatal cavity to Rubisco. Increasing g m is attractive since it increases photosynthesis without increasing water use. Most measurements of g m have been made during steady‐state light saturated photosynthesis. In field crop canopies, light fluctuations are frequent and the speed with which g m can increase following shade to sun transitions affects crop carbon gain. Is there variability in g m within soybean germplasm? If so, indirect selection may have indirectly increased g m during domestication and subsequent breeding for sustainability and yield. A modern elite cultivar (LD11) was compared with four ancestor accessions of Glycine soja from the assumed area of domestication by concurrent measurements of gas exchange and carbon isotope discrimination (∆13C). g m was a significant limitation to soybean photosynthesis both at steady state and through light induction but was twice the value of the ancestors in LD11. This corresponded to a substantial increase in leaf photosynthetic CO2 uptake and water use efficiency.
Keywords: crop domestication, crop improvement, food security, mesophyll conductance, photosynthetic CO2 assimilation, photosynthetic induction, soybean, water use efficiency
Summary statement
Mesophyll conductance (g m ) describes the ease of CO2 transfer from the sub‐stomatal cavity to Rubisco, improvement would increase photosynthesis without additional water loss. g m likely doubled in soybean domestication, suggesting variation within the germplasm for exploitation by direct selection.
1. Introduction
Soybean (Glycine max [L.] Merr.) is among the most important agricultural seed crops globally as the largest single source of vegetable protein and the second largest source of vegetable oils. The major areas of production are North and South America, and eastern Asia (Specht et al. 2014; Anderson et al. 2019). Improved agronomic practices and intensive breeding programmes have resulted in sustained soybean yield increases. However, these have not been sufficient to satisfy increasing demand which has resulted in expansion onto more natural land (Specht et al. 2014; Anderson et al. 2019; Williams et al. 2021). Increasing photosynthetic efficiency, especially if this can be achieved without more water, may be one way to supplement breeding efforts and achieve more yield within existing land of cultivation (Burgess et al. 2023; Long, Marshall‐Colon, and Zhu 2015; Murchie, Pinto, and Horton 2009). In an agricultural setting, crop canopy leaves consistently experience light intensity fluctuations due to changing solar angles, cloud cover, wind and intraspecific shading (Pearcy 1990; Long et al. 2022). Soybean is also a common understory legume crop in intercropping systems where such light fluctuations are intensified by interspecific shading (Adeniyan and Ayoola 2006; Kamara et al. 2019; Li et al. 2020; Mbah, Muoneke, and Okpara 2009; Pelech, Alexander, and Bernacchi 2021; Pelech et al. 2023). However, the response of photosynthesis to fluctuating light is not instant and the resulting loss may cost up to 13% of potential carbon assimilation in soybean (Wang et al. 2020). Exploring the factors limiting photosynthesis under both dynamic and steady‐state light conditions may aid a sustainable improvement of soybean productivity.
Leaf photosynthetic CO2 assimilation (A) shows a slow rise or induction on shade to sun transitions before reaching steady state. Both induction and steady‐state photosynthesis can each be limited by (1) conductance of CO2 from the air around the leaf to the site of assimilation in the chloroplast, (2) the maximum rate of ribulose 1,5‐biphosphate (RuBP) carboxylation (V cmax) and (3) electron transport rate for the regeneration of RuBP (J). The CO2 diffusion path is characterised by two spatially sequential components, stomatal conductance (g s ) and mesophyll conductance (g m ). The path from the leaf boundary layer to the intercellular airspaces across the stomata defines g sw , whereas g m in C3 crops is the gas to liquid phase CO2 diffusion path between leaf intercellular airspaces to Rubisco within the chloroplast stroma of the mesophyll cells (Flexas et al. 2008). Across studies and crop species, significant variations in the speed of stomatal opening during light induction exist (Acevedo‐Siaca et al. 2020; De Souza et al. 2020; Long et al. 2022), limiting photosynthetic rates between 10% and 15% (McAusland et al. 2016). On the other hand, the understanding of the limitation imposed by g m to A during induction and steady state has rarely been evaluated due to greater difficulty of estimating g m , especially under dynamic light conditions (Leverett and Kromdijk 2024; Salesse‐Smith, Driever, and Clarke 2022).
The response of g m to shade to sun transitions has been quantified using two techniques: (1) combined measurements of gas exchange and chlorophyll fluorescence or (2) simultaneous measurements of gas exchange with carbon isotope discrimination (∆13C). Kaiser et al. (2017) used the ‘Variable J’ method (Harley et al. 1992) with the former technique. The study refrained from quantifying the limitation to A during induction due to the assumptions and estimation bias with the Variable J method, but the steady‐state values compared well to other techniques (Bernacchi et al. 2002; Flexas et al. 2008; von Caemmerer and Evans 2015). Using the ∆13C technique has been suggested a more accurate method of estimating g m due to the high sensitivity and specificity of tunable‐diode laser (TDL) absorption spectroscopy (Flexas et al. 2018; Leverett and Kromdijk 2024). A mechanistic model has been used to determine g m under dynamic conditions that relates ∆13C to the multiple carbon isotope fractionation events. This utilizes the different speeds at which the two CO2 isotopologues (12CO2 and 13CO2) diffuse and/or are processed in biochemical reactions. This technique was used to measure g m in Arabidopsis and tobacco under non‐photorespiratory conditions by Sakoda et al. (2021) who found that the limitation of g m to A was the smallest compared to the limitations imposed by g sw , V cmax and J through induction. However, Liu et al. (2022) used the same technique in two Arabidopsis lines and found the relative limitation g m imposed on A during induction was > 35%. Liu et al. (2022) also re‐analysed the limitation data presented in Sakoda et al. (2021) by time integration and found a > 20% g m limitation on A during induction.
Whether g m imposes a significant limitation to A during light induction and/or at steady state in soybean remains to be explored. Soybean was domesticated from Glycine soja [Siebold & Zucc] in China 6000–9000 years ago (Kim et al. 2012) which is a vining plant that would have escaped much shade compared to the considerable self‐shading and sun‐flecking that occurs in today's dense soybean crop canopies, which can have a leaf area index of over six (Dermody, Long, and DeLucia 2006). In selecting for higher yield or water use efficiency, indirect selection for higher g m could be expected if there is variation in g m within the germplasm. Determining whether variation exists is key to understanding if there is sufficient variation to allow for direct breeding selection for increased g m , and in turn increased productivity and water use efficiency (Specht et al. 2014; Anderson et al. 2019). This study tests the question of whether during domestication and subsequent breeding an inadvertent selection for increased g m occurred, given its pivotal role in both crop photosynthetic efficiency and use of water. The hypotheses tested are: (1) g m is a significant limitation to soybean photosynthesis both during light induction and at steady state and (2) domestication and selection have both increased g m , corresponding with increased leaf photosynthesis and water use efficiency.
2. Methods and Materials
2.1. Accession Selection
Ancestral soybean accessions G. soja [Siebold & Zucc] were selected from the U.S. National Plant Germplasm System (https://npgsweb.ars-grin.gov/gringlobal/search). The G. soja accessions were chosen from locations in the assumed regions of N.E. China where the germplasm, subsequently introduced into N. America, was domesticated (Liu et al. 2020). Four such accessions in maturity groups II through IV were selected (Table 2). The domesticated high‐yielding elite cultivar LD11‐2170 of G. max [L.] Merr was used for comparison.
Table 2.
Summary of soybean accession information.
| Species | Accession | Maturity group | Country of origin |
|---|---|---|---|
| Glycine soja Siebold & Zucc | Anc297 (PI 407297)a | II | Liaoning Sheng, China |
| Anc460 A (PI 483460 A)a | III | Liaoning Sheng, China | |
| Anc460 B (PI 483460 B)a | III | Liaoning Sheng, China | |
| Anc399 B (PI 468399 B)a | IV | Shandong Sheng, China | |
| Glycine max (L.) Merr | LD11 (LD11‐2170)b | III | Illinois, United States |
U.S. National Plant Germplasm System (https://npgsweb.ars-grin.gov/gringlobal/search).
Cai and Brock (2021).
2.2. Growth Conditions
To allow imbibition, the seed coats of ancestral accessions were cut, and the seed placed on wet paper towels for 1 week before sowing. Accessions were sown on 15 April 2022, at the University of Illinois Champaign‐Urbana in pots of 0.1 m depth filled with germination growing medium (Cultivation Nation Seventy Thirty Growing Media, Fox Farm, USA). Four to six seedlings of each accession were then transplanted after 7–10 days into 6‐L pots filled with the same growing medium as for germination but supplemented with 30 mL of slow‐release fertiliser (Osmocote Plus 15‐9‐12, ICL‐US). Once the ancestral accessions had established in the 6‐L pots, a 1 m wire tomato cage was inserted to each pot support tendril development (Supporting Information S1: Figure 1B). LD‐11‐2170 was grown alongside the ancestral accessions. Plants were watered twice daily. The average temperature of the greenhouse was 29.2°C with a 14‐h photoperiod.
2.3. Concurrent Measurements of Gas Exchange and Carbon Isotope Discrimination
Leaf gas exchange and photosynthetic carbon isotope discrimination were measured concurrently using an open‐gas exchange system (LI‐6800, LI‐COR Environmental, Lincoln, NE, USA) incorporating a clear‐top controlled environment small leaf chamber (6800‐17, LI‐COR Environmental, Lincoln, NE, USA) with the small LED light source (6800‐02, LI‐COR Environmental, Lincoln, NE, USA) enclosing 6 cm2 of leaf (Supporting Information S1: Figure 1A). On enclosure of the leaf, the settings were: chamber inlet [CO2] at 400 μmol mol−1, initial photosynthetic photon flux density (PPFD) 0 μmol m−2 s−1, flow rate 350 μmol s−1, air temperature at 25°C, vapour pressure deficit at 1.2 kPa and [O2] 1.97 kPa (2%). Once respiration was stable, six consecutive measurements were logged manually to measure dark respiration. Next, the auto programme was initiated where PPFD was set to 100 μmol m−2 s−1 for 24 min before increasing to 1800 μmol m−2 s−1 for 48 min. Measurements were recorded at 10 s intervals.
The gas‐exchange system was coupled to a TDL system (TDL; TGA200a, Campbell Scientific, Inc., Logan, UT, USA) for concurrent measurements of both [12CO2] and [13CO2], allowing estimation of δ13C (Bowling et al. 2003; Evans and Von Caemmerer 2013; Wang et al. 2022). The TDL was connected to the LI‐6800 reference air stream using the reference port on the back of the sensor head while the port on the front of the head supplied air from the leaf chamber (Jaikumar et al. 2021). CO2‐free air with 1.97 kPa [O2] and balance N2 was produced by mixing two gas streams using precision mass flow controllers (Omega Engineering Inc., Stamford, CT, USA) with a portion of the supply going to the gas exchange system while the remainder was used to calibrate and to correct for drift in the TDL (Jaikumar et al. 2021; Wang et al. 2022; Salesse‐Smith et al. 2024).
The TDL was calibrated using the concentration series method, described in detail in Wang et al. (2022). Briefly a 10% CO2 calibration cylinder was diluted in the N2/O2 stream to produce different [CO2] with the same isotopic composition (Tazoe et al. 2011; Ubierna et al. 2013; Wang et al. 2022). The measurement sequence consisted of eight gas streams: CO2‐free air, followed by three different [CO2] of the same isotopic signature, air from a calibration tank with a known [12CO2], [13CO2] and δ13C composition (NOAA Global Monitoring Laboratory, Boulder, CO, USA), the IRGA reference and leaf chamber air streams, and the IRGA reference again. As in Wang et al. (2022), each step had a duration of 20 s, except for the leaf chamber air, which had a duration of 600 s with a total cycle time of 740 s. Measurements were collected at 10 Hz and averaged over 10 s into a single data point. The first 10 s of each gas stream was excluded, except for the sample line which produced 59 data points each cycle according to Wang et al. (2022).
Before measurement, plants were kept in the dark overnight, and then transferred to a low PPFD of ca.10 µmol m−2 s−1. Between two and four 8–9‐week‐old plants of each accession in their vegetative growth phase were used for measurements. The youngest fully expanded trifoliate was selected. Given the vining architecture of the ancestral accessions, the youngest fully expanded trifoliate not overlapped by a neighbouring trifoliate or tendril was chosen. In some cases, the tendril with the selected trifoliate had to be disentangled to reach the leaf chamber (Supporting Information S1: Figure 1B).
2.4. Calculations of photosynthetic discrimination (Δ13Cobs) and mesophyll conductance (g m )
On‐line photosynthetic discrimination (Δ13Cobs) was calculated according to Evans et al. 1986:
| (1) |
where δ13Csamp and δ13Cref are the carbon isotope compositions of the leaf chamber and reference air in the LI‐6800 and ξ is
| (2) |
where C ref and C samp are the CO2 concentrations of dry air entering and exiting the leaf chamber, respectively, measured by the TDL. A full list of symbols can be found in Table 1.
Table 1.
Summary abbreviations and their definitions and units.
| Variable | Definition | Units | Notes | |
|---|---|---|---|---|
| a s | Fractionation across the stomata | ‰ | 4.4 | |
| a b | Fractionation across the boundary layer | ‰ | 2.9 | |
| a i | Fractionation factor for dissolution and diffusion through water | ‰ | 1.8 | |
| a′ | Combined fractionation factor through the leaf boundary layer and stomata | ‰ | Equation (5) | |
| A | Net CO2 assimilation rate | μmol m−2 s−1 | ||
| A c | Rubisco‐limited net CO2 assimilation rate | μmol m−2 s−1 | Equation (15) | |
| A j | RuBP‐regeneration‐limited net CO2 assimilation rate | μmol m−2 s−1 | Equation (16) | |
|
|
Modelled assimilation rate expected to occur if stomatal conductance to CO2 diffusion were infinite | μmol m−2 s−1 | Equation (11) | |
|
|
Modelled assimilation rate expected to occur if mesophyll conductance to CO2 diffusion were infinite | μmol m−2 s−1 | Equation (12) | |
| b | Fractionation associated with Rubisco carboxylation | ‰ | 29 (Roeske and O'Leary 1984) | |
| C a | Ambient CO2 partial pressure | µmol mol−1 | ||
| C c | Chloroplastic CO2 partial pressure/mole fraction | µmol mol−1 | ||
|
|
Value of expected to occur if stomatal conductance to CO2 diffusion were infinite | Pa/µmol−1 | Equation (13) | |
|
|
Value of expected to occur if mesophyll conductance to CO2 diffusion were infinite | Pa/µmol−1 | Equation (14) | |
| C i | Intercellular CO2 partial pressure/mole fraction | µmol mol−1 | ||
| C s | CO2 partial pressure at the leaf surface | µmol mol−1 | ||
| e | Respiratory fractionation during decarboxylation (respiratory fractionation) | ‰ | 0 (Ubierna et al. 2013) | |
| e′ | Fractionation during decarboxylation including measurement artefacts | ‰ | Equation (6) | |
| E | Transpiration rate | mol H2O m−2 s−1 | ||
| f | Fractionation during photorespiration | ‰ | 11.6 in this study | |
| g m | Mesophyll conductance | μmol m−2 s−1 Pa or bar−1 | Equation (3) | |
| g sc | Stomatal conductance to CO2 diffusion; | mol m−2 s−1 | ||
| g sw | Stomatal conductance to water vapour | mol m−2 s−1 | ||
| g t ac | Total conductance to CO2 diffusion between boundary layer and stomatal conductance | mol total m−2 s−1 | ||
| J | Light‐dependent RuBP regeneration rate | μmol m−2 s−1 | Equation (18) | |
|
|
Relative limiting factor due to stomatal conductance in the Warren et al. (2003) framework | % | Equation (11) | |
|
|
Relative limiting factor due to mesophyll conductance in the Warren et al. (2003) framework | % | Equation (12) | |
| O | O2 partial pressure | Pa | ||
| PPFD | Photosynthetic Photon Flux Density | µmol m−2 s−1 | ||
| R d | Mitochondrial respiration in the light | μmol CO2 m−2 s−1 | ||
| Sc/o | Rubisco specificity factor | mol CO2/mol O2 | ||
| t | Ternary effect | ‰ | Equation (4) | |
|
|
time taken for mesophyll conductance to reach 50% of its steady‐state value | minutes | ||
|
|
time taken for mesophyll conductance to reach 90% of its steady‐state value | minutes | ||
| V cmax | Maximum Rubisco carboxylation rate | μmol m−2 s−1 | Equation ((15), (17)) | |
| WUEi | Intrinsic water‐use efficiency | mol CO2 mol−1 H2O | A/g sw | |
| Δ13Cobs | Photosynthetic discrimination | ‰ | Equation (1) | |
| Δ e | Fraction associated with respiration | ‰ | Equation (8) | |
| Δ f | Fractionation associated with photorespiration | ‰ | Equation (9) | |
| Δ i | Fractionation if C i = C c in the absence of any respiratory fraction | ‰ | Equation (7) | |
| Γ* | CO2 compensation point in the absence of mitochondrial respiration in the light | Pa or bar | Equation (10) | |
| ξ | Ratio of 12CO2 mole fraction in the dry air coming into the gas‐exchange cuvette over the difference in 12CO2 mole fractions of air in and out of the cuvette | unitless | Equation (2) |
Mesophyll conductance was estimated according to Evans and Von Caemmerer (2013), accounting for the ternary effect (Farquhar and Cernusak 2012):
| (3) |
where b is fractionation associated with Rubisco carboxylation (29‰, Roeske and O'Leary 1984), a i (1.8‰) denotes the fractionation factor for dissolution and diffusion through water, e denotes the apparent fractionation factor associated with decarboxylation, R d is the rate of mitochondrial respiration in the light (assumed to be equal to respiration in the dark) and A is the rate of net leaf CO2 assimilation. Carbon dioxide diffusion from the boundary layer to the sub‐stomatal cavity is affected by collisions of the isotopologues of CO2 with air and with water vapour, a process referred to as the ternary effect. Without accounting for this, conductance would be overestimated. Following Farquhar and Cernusak (2012) the ternary correction factor (t) is obtained as
| (4) |
where E is the rate of transpiration, g t ac is the total conductance to CO2 diffusion in the gas phase including boundary layer and stomatal conductance (von Caemmerer and Farquhar 1981) and a′ denotes the combined fractionation factor through the leaf boundary layer and stomata:
| (5) |
where C a , C s and C i are the ambient, leaf surface and intercellular CO2 partial pressures, a b (2.9‰) is the fractionation occurring through diffusion in the boundary layer and a s (4.4‰) is the fractionation due to diffusion in the air (Evans et al. 1986).
The apparent fractionation during decarboxylation includes two terms, such that e = e′ + e 0. The first term e′ represents the influence of measurement artifacts, defined as
| (6) |
while e 0 is the respiratory fractionation during decarboxylation, taken to be 0‰ in this study (Evans and Von Caemmerer 2013; Ubierna et al. 2013). δ13Cref is the isotopic signature of the CO2 entering the LI‐6800 reference and δ13C gatm (−8‰) is the isotopic compositions of the CO2 where the plants are grown. Δ i is the discriminations that would occur if C i = C c in the absence of any respiratory fractionation (e = 0):
| (7) |
Δ e is the fractionation associated with respiration:
| (8) |
is the fractionation associated with photorespiration:
| (9) |
where f is the photorespiratory fractionation factor assumed to be 11.2‰ (Lanigan et al. 2008) and Δ f is linearly related to O2 concentration via the CO2 compensation point in the absence of respiration ():
| (10) |
where O is the [O2] in partial pressure and S c/o is the Rubisco specificity factor (von Caemmerer, 2000).
2.5. Calculations of Limiting Factors
Dimensionless factors representing the limitations placed on the photosynthetic CO2 assimilation rate by CO2 diffusion or biochemistry were calculated using two different frameworks (Warren et al. 2003; Grassi and Magnani 2005) using the calculate_c3_limitations_warren and calculate_c3_limitations_grassi functions from the PhotoGEA R package (Lochocki 2024). Here, we describe the Warren et al. (2003) framework, the Grassi and Magnani (2005) framework can be found in Supporting Information S1: Methods.
Limiting factors during induction were calculated using the 4‐min averages of A, g sw , g m , C i and C c , as described in detail below. The Warren et al. (2003) framework defines limiting factors due to stomatal and mesophyll conductance, which we refer to here as and :
| (11) |
| (12) |
where A is the measured assimilation rate and and are modelled assimilation rates expected to occur if g sc (stomatal conductance to CO2 diffusion g sc = g sw /1.6) or g m were infinite, respectively. These modelled rates can be calculated by first defining corresponding values of C c using C c = C a – ∆C s −∆C m , where ∆C s = C a − C i and ∆C m = C i − C c are the [CO2] drawdowns across the stomata and mesophyll, respectively, and C a , C i and C c are the measured ambient, intercellular and chloroplast [CO2], respectively. If conductance across a barrier (stomata or mesophyll) is infinite, the drawdown across it is zero:
| (13) |
| (14) |
where and are chloroplast [CO2] that expected to occur if g sc or g m were infinite, respectively. With these, it is possible to calculate the modelled assimilation rates using the Farquhar‐von‐Caemmerer‐Berry model (von Caemmerer, 2000) under two scenarios, where assimilation is either Rubisco‐limited A c or RuBP‐regeneration‐limited A j :
| (15) |
| (16) |
where V cmax is the maximum Rubisco carboxylation rate, J is the light‐dependent whole chain electron transport rate, is the effective Michaelis–Menten constant for Rubisco carboxylation, K c and K o are the Michaelis–Menten constants for [CO2] and [O2], and is the oxygen concentration in the chloroplast (assumed to be 1.97 kPa, equal to the ambient value in the leaf chamber). Values of K c and K o were calculated from the leaf temperature as described previously (Bernacchi et al. 2001).
Both frameworks require values of V cmax and J, which can be estimated from the measured values of A n , C c , and R d by assuming either Rubisco‐limited or RuBP‐regeneration‐limited assimilation and solving Equations (15) and (16) for V cmax and J, respectively:
| (17) |
| (18) |
The induction curves measured here do not provide enough information to determine whether assimilation is limited by Rubisco or RuBP regeneration, so each set of limiting factors was calculated under each scenario. However, prior work with soybean cultivars have suggested Rubisco and not RubP regeneration is the predominant biochemical limitation throughout induction (Soleh et al. 2016, 2017; Taylor and Long 2017). Note, that as written, Equations (11) and (12) calculate dimensionless limiting factors, which are multiplied by 100 to express them as percentages.
2.6. Data Processing and Statistical Analysis
An automatic data processing and g m calculation tool was developed in MATLAB (v2019a, Mathworks, https://uk.mathworks.com). MATLAB used the pretreated gas exchange data files (csv file with parameters needed for calculation) and the raw TDL data files to calculate the g m through the photosynthetic induction, with the equations described earlier. The data that support the findings of this study are available at: https://doi.org/10.13012/B2IDB-7809185_V2.
Unreasonable values of g m (g m ≥ 1 or g m ≤ 0 and those associated with ξ ≥ 50 or ξ ≤ 0) were removed before analysis. Data points were grouped into 4‐min intervals and the interquartile range was calculated to remove outliers within each interval before averaging. Due to noise within each replicate, the moving average of g m was then calculated. Values of A, C i , C c , g sw and WUEi were also grouped and averaged into 4‐min intervals. Only the response of photosynthetic parameters after the increase in PPFD from 100 to 1800 was evaluated; therefore, values of light induction and steady state were calculated as the average of the initial and last 12 min (three 4‐min intervals) after the increase in light intensity. Statistical analyses (p < 0.1 significance level) were performed using repeated measures ANOVA where accession and time were main effects. The residuals were checked for normality and constant variance, box Cox transformations were conducted if these criteria were unmet. Means comparison Dunnett test using LD11 as the control was performed if there was a significant accession effect and/or significant interaction between accession and time (R software, R Core Team 2021). Curve fitting (3 parameter Sigmoidal Hill) was conducted in SigmaPlot (SigmaPlot 15, Systat Software) for the calculation of the time taken for g m to reach 50% () and 90% () of its steady‐state value where a one‐way ANOVA was conducted for statistical analysis (Supporting Information S1: Figures 2–6).
3. Results
3.1. The Response of Mesophyll Conductance (g m ) and Other Photosynthetic Parameters after an Increase in Light Intensity
Steady‐state g m was significantly greater (ca. 70%) in the elite modern cultivar (LD11) than the average of the four ancestors (Figure 1A,B and Supporting Information S1: Table S1). Despite attaining this higher g m , induction in LD11 was as rapid as in the ancestors (Figure 1C and Supporting Information S1: Figures 2‐6). Steady‐state net leaf CO2 assimilation rate (A) of LD11 was significantly higher and almost twice that of the ancestral accessions, as was the average A over the first 12 min of induction following transfer from low to high light (Figure 2). At steady state and throughout induction intercellular and stromal [CO2] (C i and C c , respectively) were substantially lower in the modern elite (LD11) (Figure 3). C i and C c briefly decreased after the increase in light intensity before reaching a plateau, which was close to the shade value for the ancestral accessions, but below that for LD11 (Figure 3). In contrast to g m , stomatal conductance (g sw ) was not significantly higher than the ancestral accessions, both at steady state and through induction (Figure 4). Coincided with this and the higher A of the elite is a higher leaf instantaneous water use efficiency (Figure 4).
Figure 1.
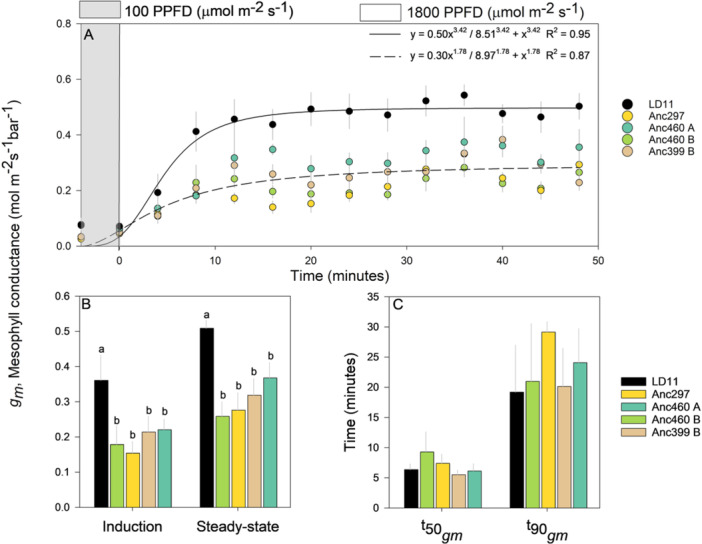
Comparisons among domesticated high‐yielding elite LD11 (Glycine max (L.) Merr) and four ancestor accessions (Glycine soja Siebold & Zucc) illustrated as (A) the average temporal response of mesophyll conductance (g m ) after a transition in photosynthetic photon flux density (PPFD) from 100 (grey area) to 1800 (white area) where data points represent 4‐min moving averages, solid black line and dashed black line represent the fitted sigmoidal Hill regression of the elite and ancestors, respectively, (B) the average response of g m during light induction and at steady state, and (C) the time taken for g m to reach 50% () and 90% () of its steady‐state value. Light induction and steady state were defined as the initial and last 12 min (three 4‐min intervals) after an increase in light intensity, respectively. Different letters indicate significant differences (p < 0.1, repeated measures ANOVA, n = 12) and error bars indicate standard error.
Figure 2.
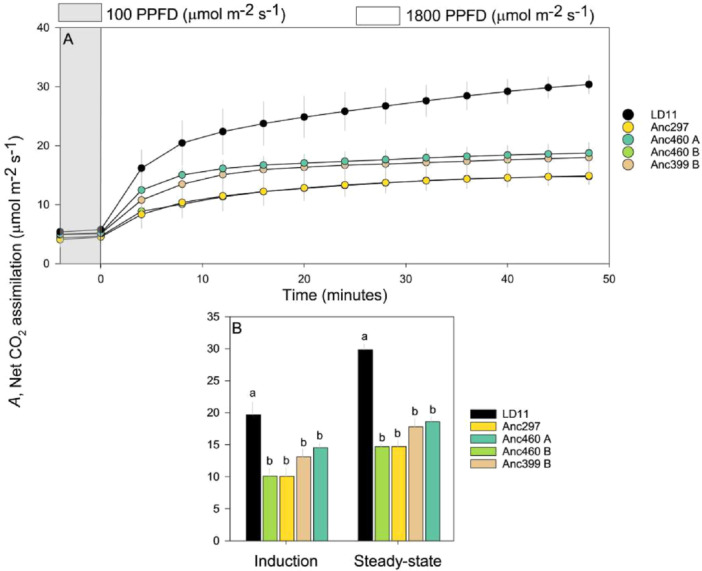
Comparisons among domesticated high‐yielding elite LD11 (Glycine max (L.) Merr) and four ancestor accessions (Glycine soja Siebold & Zucc) illustrated as (A) the average temporal response of net CO2 assimilation (A) after a transition in photosynthetic photon flux density (PPFD) from 100 (grey area) to 1800 (white area) where data points represent 4‐min averages, (B) the average response of A during light induction and at steady state. Light induction and steady state were defined as the initial and last 12 min (three 4‐min intervals) after an increase in light intensity, respectively. Different letters indicate significant differences (p < 0.1, repeated measures ANOVA, n = 12) and error bars indicate standard error. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 3.
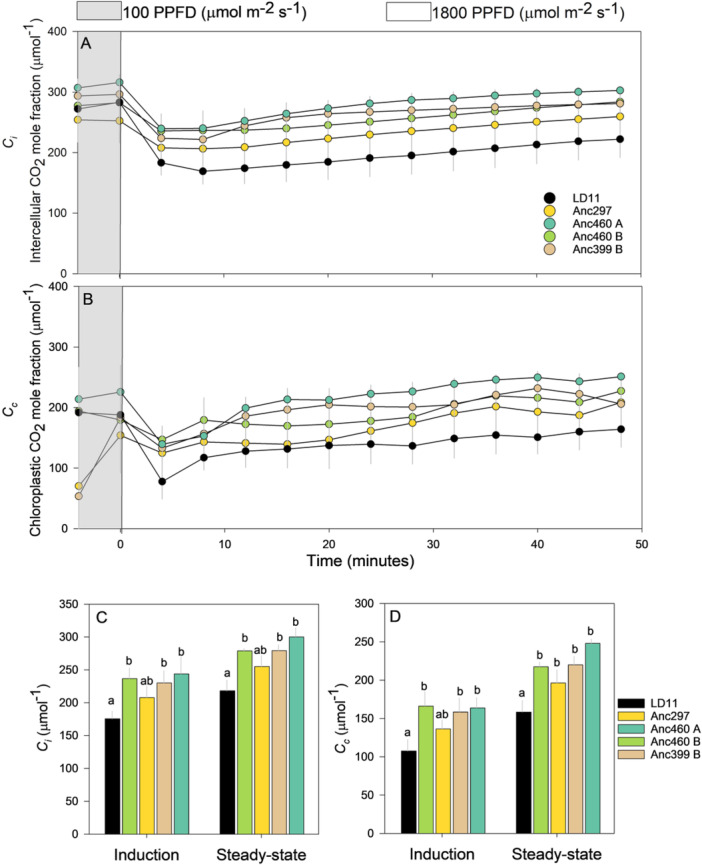
Comparisons among domesticated high‐yielding elite LD11 (Glycine max (L.) Merr) and four ancestor accessions (Glycine soja Siebold & Zucc) illustrated as the average temporal response of (A) intercellular CO2 mole fraction (C i ) and (B) chloroplastic CO2 mole fraction (C c ) after a transition in photosynthetic photon flux density (PPFD) from 100 (grey area) to 1800 (white area) where data points represent 4‐min averages, the average response of (C) C i and (D) C c during light induction and at steady state. Light induction and steady state were defined as the initial and last 12 min (three 4‐min intervals) after an increase in light intensity, respectively. Different letters indicate significant differences (p < 0.1, repeated measures ANOVA, n = 12) and error bars indicate standard error. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 4.
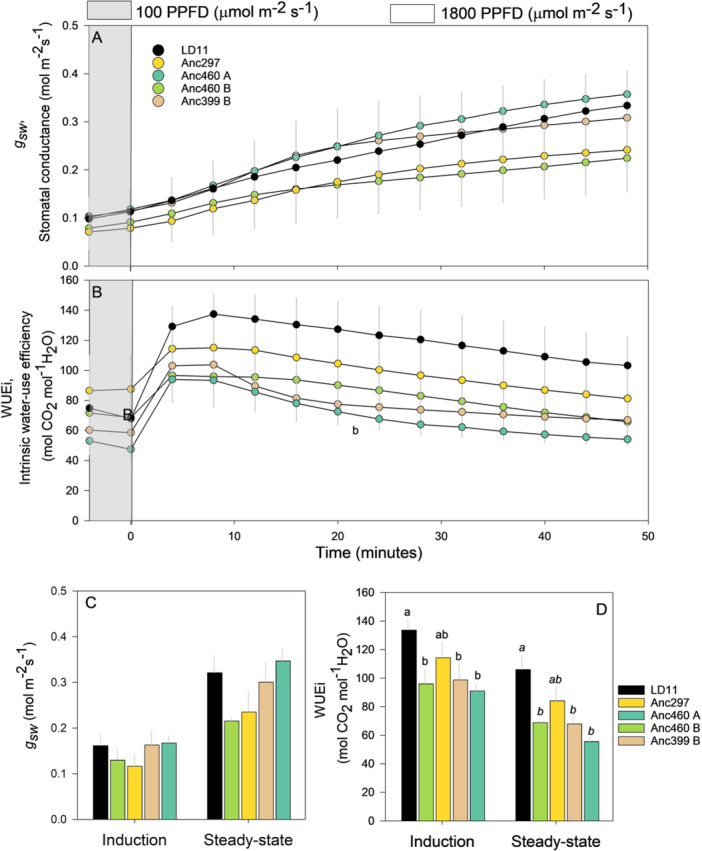
Comparisons among domesticated high‐yielding elite LD11 (Glycine max (L.) Merr) and four ancestor accessions (Glycine soja Siebold & Zucc) illustrated as the average temporal response of (A) stomatal conductance (g sw ) and (B) intrinsic water‐use efficiency (WUEi) after a transition in photosynthetic photon flux density (PPFD) from 100 (grey area) to 1800 (white area) where data points represent 4‐min averages, the average response of (C) g sw and (D) WUEi during light induction and at steady state. Light induction and steady state were defined as the initial and last 12 min (three 4‐min intervals) after an increase in light intensity, respectively. Different letters indicate significant differences (p < 0.1, repeated measures ANOVA, n = 12, where italic letters indicate p = 0.12) and error bars indicate standard error. [Color figure can be viewed at wileyonlinelibrary.com]
3.2. The Limitation on Net CO2 Assimilation Rate (A)
The dynamics of the two gas diffusional limiting factors (g m and g sw ) affecting A under the assumption of RuBP regeneration (J) and Rubisco carboxylation (V cmax) biochemical limitation were evaluated using the methods described in Warren et al. (2003). Since g m and A of LD11 were found to be significantly higher than for all four ancestral accessions, the limitation comparisons were made between species where the response of all four ancestral accessions was represented by a combined average (G. max and G. soja, respectively).
Limitations analysis showed that regardless of whether RubP regeneration or Rubisco carboxylation was assumed as the biochemical limitation, the limitations on A imposed by both stomatal and mesophyll conductance were greater in the elite modern soybean at steady state and through induction (Figure 5). The limitations on A by both g m and g sw followed similar trends but were more severe under carboxylation than regeneration biochemical limitation through induction and at steady state (Figure 5). The limitation of g sw was also greater than g m under both biochemical limitation assumptions (Figure 5C,D). Limitations calculated using the methods described in Grassi and Magnani (2005), although different in scale, compare well to the conclusions from the Warren et al. (2003) method (Supporting Information S1: Figures 7AB and 8AB). The Grassi and Magnani (2005) framework also calculates biochemical limitations in addition to diffusion limitations; limitations imposed by J or V cmax on A were higher for G. soja than G. max during both the induction and steady‐state phases (Supporting Information S1: Figures 7C and 8C).
Figure 5.
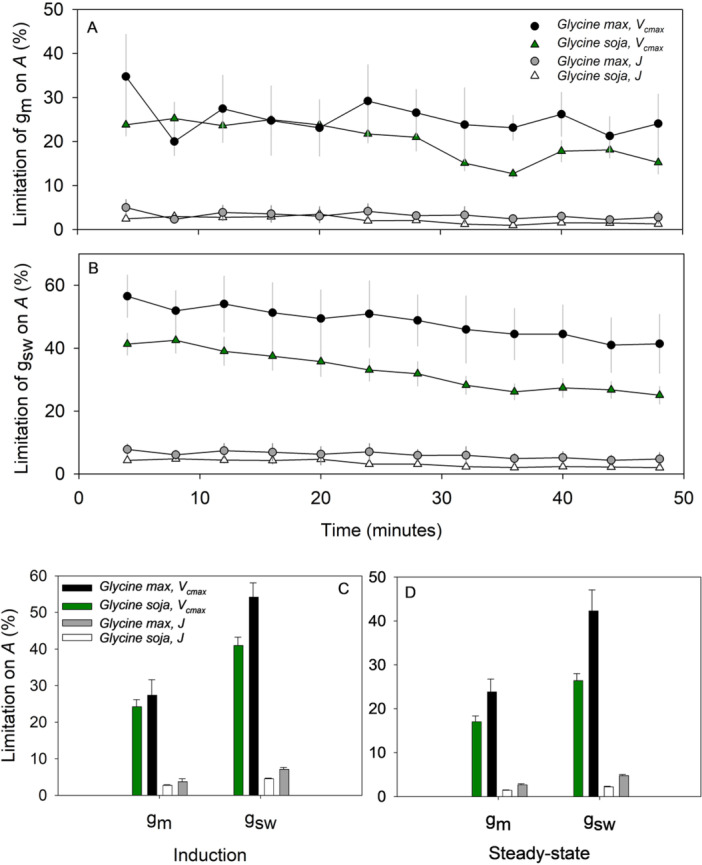
The limitation of mesophyll conductance (g m ) and stomatal conductance (g sw ) on net CO2 assimilation rate (A) after an increase in light intensity over time (A, B), and the average limitation during light induction (C) and steady state (D) assuming the biochemical limitations of ribulose 1,5‐biphosphosphate (RuBP) carboxylation (V cmax) and regeneration (J). Limitation calculations were made using the methods described in Warren et al. (2003). The comparisons are between domesticated high‐yielding elite LD11 (Glycine max (L.) Merr, n = 4) and the average of four ancestor accessions (Glycine soja Siebold & Zucc, n = 16). Light induction and steady state were defined as the initial and last 12 min (three 4‐min intervals) after an increase in light intensity, respectively. Error bars indicate standard error. [Color figure can be viewed at wileyonlinelibrary.com]
4. Discussion
This study tested two hypotheses concerning the domestication and subsequent improvement of soybean, both are strongly supported by the results obtained. (1) Mesophyll conductance (g m ) was shown to be a significant limitation to soybean photosynthesis both at steady state and through light induction especially when the major biochemical limitation was in vivo Rubisco activity (V cmax) (Figure 5). (2) Compared to the ancestral accessions, the elite soybean cultivar showed a near doubling and significant increase in g m at both steady state and through light induction (Figure 1), which also corresponded to a substantial increase in leaf CO2 assimilation (A) and leaf level water use efficiency (WUEi, Figures 2 and 4). It also shows that domestication and breeder selection for yield had resulted in a large increase in leaf photosynthetic rate (Figure 2).
Further examination investigating the g m response to light induction across a broader range of ancestral accessions as well as different domesticated accessions of soybean by year of release may strengthen the conclusions here. Previous research has explored historical soybean accessions between 1923 and 2007 where steady‐state A/C i responses using the Variable J method revealed that g m has not changed consistently with release date (Koester et al. 2016). Evaluation under dynamic light conditions with the isotopic discrimination technique may challenge these conclusions. We acknowledge that the equations used here to calculate g m (Evans and Von Caemmerer 2013) are not the most recent. Busch et al. (2020) modified the assumptions related to the mitochondrial respiration fractionation component which improved the accuracy of g m when intercellular [CO2] (C i ) values are low (< 100 µmol mol−1). Here, C i did not drop below 150 µmol mol−1 during light induction (Figure 3A) and Supporting Information S1: Figure 9 shows negligible differences between g m calculated of Busch et al. (2020) relative to Evans and Von Caemmerer (2013) under the measurement conditions used in this study. More replicate power may also reduce the noise associated with the speed of g m response to light induction (Figure 1C and Supporting Information S1: Figures 2–6). Nonetheless, such techniques require proficiency and specialized equipment where labour and costs may need to be compromised in screening large amounts of germplasm.
Mesophyll conductance is a suggested target for improvement, since it would result in higher rates of CO2 assimilation per unit leaf area, without any increased cost in terms of water use, so potentially providing a sustainable increase in crop productivity (Flexas et al. 2013; Lundgren and Fleming 2020; Long et al. 2022; Salesse‐Smith et al. 2024). Here, it was shown to be a substantial limitation to light‐saturated A at steady state (ca. 20%) and more so in the elite LD11 than the ancestral accessions when V c,max was the major biochemical limitation (Figure 5). Most previous studies have estimated g m under steady‐state conditions. However, the light environment in dense modern crop canopies is rarely constant, with most leaves experiencing many fluctuations in light over the course of a day (Long et al. 2022). On transition of leaves from shade to sun, g sw and g m increase over several minutes, and contribute to the slow increase in A. Under these conditions the limitation attributable to g m (ca. 25%) was even greater than at steady state, showing the importance of considering light fluctuation for field crops. The limitation, at both steady state and through induction, was only slight when regeneration of RuBP, governed by the maximum rate of whole chain electron transport (J), is assumed the biochemical limitation (Figure 5). However, previous analyses of A/C i responses of a range of soybean germplasm showed that in the current atmosphere, V c,max and not J max as the exclusive biochemical limitation at both light‐saturated steady‐state A and through light‐induction (Sakoda et al. 2016; Soleh et al. 2016, 2017). The results therefore suggest a strong limitation on assimilation by g m ; a limitation which has decreased through selection in domestication and subsequent breeding.
As a major limitation to assimilation under current and past atmospheric [CO2], it might be expected that domestication and breeding would have indirectly selected for increased g m , particularly for the most recent soybean releases, which appear strongly source limited (Ainsworth and Long, 2021). The ca. 70% increase in g m in LD11 compared to the ancestral accessions, corresponds to a near doubling of light‐saturated A (Figures 1 and 2) implying that g m has scaled with increase in A. However, while increased g m and the associated increased WUEi may have indirectly resulted from selection of more productive accessions, it appears that g m has not kept pace with increased A. Despite higher g m in the elite cultivar, C i was ca. 60 µmol mol−1 lower at light‐saturated steady state (Figure 3) which would substantially increase photorespiration and decrease the rate of carboxylation. This finding implies that improvement of g m has been less than the increase in biochemical capacity for CO2 assimilation, and suggests g m is an important target for improving both productivity and water use efficiency in soybean.
Manipulation of cell wall porosity has been suggested as one means to substantially increase g m (Evans 2021). In tobacco, transgenic upregulation of a pectin methyltransferase increased cell wall porosity, with concomitant significantly increased g m and A, suggest one way to achieve this in soybean (Salesse‐Smith et al. 2024). However, the large differences in g m found here between the wild ancestors and an elite line suggest that there may be substantial variation within soybean germplasm that might be exploited through marker‐assisted breeding, genomic selection, or direct selection through measurement of g m . Substantial variation in g m and associated improvement in WUE has been shown in other crops (Barbour et al. 2010; Jahan et al. 2014; Tomás et al. 2014). In soybean, a survey of 12 cultivars showed a two‐fold variation in g m . This was strongly and positively correlated with variation in A, where 38% of the variation was due to cultivar (Tomeo and Rosenthal 2017). These results suggest g m has unexplored potential within soybean breeding to deliver increased productivity and water use efficiency.
Supporting information
Supporting information.
Acknowledgements
We thank the late Theodore Hymowitz for guidance on selecting accessions (Glycine soja Siebold & Zucc) considered the closest to the ancestor of the soybean accessions introduced to N. America (Glycine max (L.) Merr). We thank Brighid Zelko, Ben Thompson, Andy Wszalek and David Drag for plant care and management, Ryan Boyd for advice on the calculation of mesophyll conductance and Lynn Doran for advice on statistical analysis. We also thank Liana Acevedo‐Siaca and Shellie Wall for their advice on interpreting light induction curves. This work was supported by the research project Realizing Increased Photosynthetic Efficiency (RIPE), which was funded by the Bill & Melinda Gates Foundation, Foundation for Food and Agriculture Research and U.K. Foreign, Commonwealth & Development Office under grant no. OPP1172157. This work is licensed under a Creative Commons Attribution 4.0 International (CC BY 4.0) license, which permits unrestricted use, distribution and reproduction in any medium, provided the original work is properly cited. To view a copy of this license, visit https://creativecommons.org/licenses/by/4.0/. This license does not apply to figures/photos/artwork or other contents included in the article that is credited to a third party; obtain authorization from the rights holder before using such material.
Contributor Information
Elena A. Pelech, Email: pelech@illinois.edu.
Stephen P. Long, Email: slong@illinois.edu.
Data Availability Statement
The data that support the findings of this study are openly available in Soybean/Soja mesophyll conductance during light induction at https://doi.org/10.13012/B2IDB-7809185_V2.
References
- Acevedo‐Siaca, L. G. , Coe R., Wang Y., Kromdijk J., Quick W. P., and Long S. P.. 2020. “Variation in Photosynthetic Induction Between Rice Accessions and Its Potential for Improving Productivity.” New Phytologist 227: 1097–1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adeniyan, O. N. , and Ayoola O. T.. 2006. “Growth and Yield Performance of Some Improved Soybean Varieties as Influenced by Intercropping with Maize and Cassava in Two Contrasting Locations in Southwest Nigeria.” African Journal of Biotechnology 5: 1886–1889. [Google Scholar]
- Ainsworth, E. A. , and Long S. P.. 2021. “30 Years of Free‐Air Carbon Dioxide Enrichment (FACE): What Have We Learned about Future Crop Productivity and Its Potential for Adaptation?”Global Change Biology 27: 27–49. [DOI] [PubMed] [Google Scholar]
- Anderson, E. J. , Ali M. L., Beavis W. D., et al. 2019. “Soybean Glycine max (L.) Merr. Breeding: History, Improvement, Production and Future Opportunities.” Advances in Plant Breeding Strategies: Legumes 7: 431–516. [Google Scholar]
- Barbour, M. M. , Warren C. R., Farquhar G. D., Forrester G., and Brown H.. 2010. “Variability in Mesophyll Conductance Between Barley Genotypes, and Effects on Transpiration Efficiency and Carbon Isotope Discrimination.” Plant Cell Environment 33: 1176–1185. [DOI] [PubMed] [Google Scholar]
- Bernacchi, C. J. , Portis A. R., Nakano H., von Caemmerer S., and Long S. P.. 2002. “Temperature Response of Mesophyll Conductance. Implications for the Determination of Rubisco Enzyme Kinetics and for Limitations to Photosynthesis in Vivo.” Plant Physiology 130: 1992–1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernacchi, C. J. , Singsaas E. L., Pimentel C., A. R. Portis, Jr. , and Long S. P.. 2001. “Improved Temperature Response Functions for Models of Rubisco‐Limited Photosynthesis.” Plant, Cell & Environment 24: 253–259. [Google Scholar]
- Bowling, D. R. , Sargent S. D., Tanner B. D., and Ehleringer J. R.. 2003. “Tunable Diode Laser Absorption Spectroscopy for Stable Isotope Studies of Ecosystem‐Atmosphere CO2 Exchange.” Agricultural and Forest Meteorology 118: 1–19. [Google Scholar]
- Burgess, A. J. , Masclaux‐Daubresse C., Strittmatter G., et al. 2023. “Improving Crop Yield Potential: Underlying Biological Processes and Future Prospects.” Food and Energy Security 12: e435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busch, F. A. , Holloway‐Phillips M., Stuart‐Williams H., and Farquhar G. D.. 2020. “Revisiting Carbon Isotope Discrimination in C3 Plants Shows Respiration Rules When Photosynthesis Is Low.” Nature Plants 6: 245–258. [DOI] [PubMed] [Google Scholar]
- von Caemmerer, S. 2000. Biochemical Models of Leaf Photosynthesis. Clayton, VIC: CSIRO Publishing. [Google Scholar]
- von Caemmerer, S. , and Evans J. R.. 2015. “Temperature Responses of Mesophyll Conductance Differ Greatly between Species.” Plant, Cell & Environment 38: 629–637. [DOI] [PubMed] [Google Scholar]
- von Caemmerer, S. , and Farquhar G. D.. 1981. “Some Relationships between the Biochemistry of Photosynthesis and the Gas Exchange of Leaves.” Planta 153: 376–387. [DOI] [PubMed] [Google Scholar]
- Cai, G. , and Brock A. 2021. “The Uniform Soybean Tests: Northern Regions 2021, 404.” West Lafyette, IN: USDA‐ARS.
- Dermody, O. , Long S. P., and DeLucia E. H.. 2006. “How Does Elevated CO2 or Ozone Affect the Leaf‐Area Index of Soybean When Applied Independently.” New Phytologist 169: 145–155. [DOI] [PubMed] [Google Scholar]
- Evans, J. R. 2021. “Mesophyll Conductance: Walls, Membranes and Spatial Complexity.” New Phytologist 229: 1864–1876. [DOI] [PubMed] [Google Scholar]
- Evans, J. R. , and Von Caemmerer S.. 2013. “Temperature Response of Carbon Isotope Discrimination and Mesophyll Conductance in Tobacco.” Plant, Cell & Environment 36: 745–756. [DOI] [PubMed] [Google Scholar]
- Evans, J. R. , Sharkey T. D., Berry J. A., and Farquhar G. D.. 1986. “Carbon Isotope Discrimination Measured Concurrently with Gas‐Exchange to Investigate CO2 Diffusion in Leaves of Higher Plants.” Australian Journal of Plant Physiology 13: 281–292. [Google Scholar]
- Farquhar, G. D. , and Cernusak L. A.. 2012. “Ternary Effects on the Exchange of Isotopologues of Carbon Dioxide.” Plant, Cell & Environment 35: 1221–1231. [DOI] [PubMed] [Google Scholar]
- Flexas, J. , Carriquí M., and Cano F. J., et al. 2018. “CO2 Diffusion Inside Photosynthetic Organs.” In Leaf: A Platform for Performing Photosynthesis, edited by AdamsI W. W. and Terashima I., 163–208. Springer International Publishing AG. [Google Scholar]
- Flexas, J. , Niinemets Ü., Gallé A., et al. 2013. “Diffusional Conductances to CO2 as a Target for Increasing Photosynthesis and Photosynthetic Water‐Use Efficiency.” Photosynthesis Research 117: 45–59. [DOI] [PubMed] [Google Scholar]
- Flexas, J. , Ribas‐carbó M., Diaz‐espejo A., Galmés J., and Medrano H.. 2008. “Mesophyll Conductance to CO2: Current Knowledge and Future Prospects.” Plant, Cell & Environment 31: 602–621. [DOI] [PubMed] [Google Scholar]
- Grassi, G. , and Magnani F.. 2005. “Stomatal, Mesophyll Conductance and Biochemical Limitations to Photosynthesis as Affected by Drought and Leaf Ontogeny in Ash and Oak Trees.” Plant, Cell & Environment 28: 834–849. [Google Scholar]
- Harley, P. C. , Loreto F., Dimarco G., and Sharkey T. D.. 1992. “Theoretical Considerations When Estimating the Mesophyll Conductance to CO2 Flux by Analysis of the Response of Photosynthesis to CO2 .” Plant Physiology 98: 1429–1436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jahan, E. , Amthor J. S., Farquhar G. D., Trethowan R., and Barbour M. M.. 2014. “Variation in Mesophyll Conductance Among Australian Wheat Genotypes.” Functional Plant Biology 41: 568–580. [DOI] [PubMed] [Google Scholar]
- Jaikumar, N. S. , Stutz S. S., Fernandes S. B., et al. 2021. “Can Improved Canopy Light Transmission Ameliorate Loss of Photosynthetic Efficiency in the Shade? An Investigation of Natural Variation in Sorghum bicolor .” Journal of Experimental Botany 72: 4965–4980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser, E. , Kromdijk J., Harbinson J., Heuvelink E., and Marcelis L. F. M.. 2017. “Photosynthetic Induction and Its Diffusional, Carboxylation and Electron Transport Processes as Affected by CO2 Partial Pressure, Temperature, Air Humidity and Blue Irradiance.” Annals of Botany 119: 191–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamara, A. Y. , Tofa A. I., Ademulegun T., et al. 2019. “Maize‐Soybean Intercropping for Sustainable Intensification of Cereal‐Legume Cropping Systems in Northern Nigeria.” Experimental Agriculture 55: 73–87. [Google Scholar]
- Kim, M. Y. , Van K., Kang Y. J., Kim K. H., and Lee S.‐H.. 2012. “Tracing Soybean Domestication History: From Nucleotide to Genome.” Breeding Science 61: 445–452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koester, R. P. , Nohl B. M., Diers B. W., and Ainsworth E. A.. 2016. “Has Photosynthetic Capacity Increased with 80 years of Soybean Breeding? An Examination of Historical Soybean Cultivars.” Plant, Cell & Environment 39: 1058–1067. [DOI] [PubMed] [Google Scholar]
- Lanigan, G. J. , Betson N., Griffiths H., and Seibt U.. 2008. “Carbon Isotope Fractionation during Photorespiration and Carboxylation in Senecio .” Plant Physiology 148: 2013–2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leverett, A. , and Kromdijk J.. 2024. “The Long and Tortuous Path Towards Improving Photosynthesis by Engineering Elevated Mesophyll Conductance.” Plant, Cell & Environment 47: 3411–3427. [DOI] [PubMed] [Google Scholar]
- Li, C. , Hoffland E., Kuyper T. W., et al. 2020. “Syndromes of Production in Intercropping Impact Yield Gains.” Nature Plants 6: 653–660. [DOI] [PubMed] [Google Scholar]
- Liu, T. , Barbour M. M., Yu D., Rao S., and Song X.. 2022. “Mesophyll Conductance Exerts a Significant Limitation on Photosynthesis during Light Induction.” New Phytologist 233: 360–372. [DOI] [PubMed] [Google Scholar]
- Liu, X. , He J., Wang Y., et al. 2020. “Geographic Differentiation and Phylogeographic Relationships Among World Soybean Populations.” Crop Journal 8: 260–272. [Google Scholar]
- Lochocki, E. B. 2024. “PhotoGEA: Photosynthetic Gas Exchange Analysis.” R package version 1.0.0”. https://eloch216.github.io/PhotoGEA.
- Long, S. P. , Marshall‐Colon A., and Zhu X. G.. 2015. “Meeting the Global Food Demand of the Future by Engineering Crop Photosynthesis and Yield Potential.” Cell 161: 56–66. [DOI] [PubMed] [Google Scholar]
- Long, S. P. , Taylor S. H., Burgess S. J., et al. 2022. “Into the Shadows and Back into Sunlight: Photosynthesis in Fluctuating Light.” Annual Review of Plant Biology 73: 617–648. [DOI] [PubMed] [Google Scholar]
- Lundgren, M. R. , and Fleming A. J.. 2020. “Cellular Perspectives for Improving Mesophyll Conductance.” The Plant Journal 101: 845–857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mbah, E. U. , Muoneke C. O., and Okpara D. A.. 2009. “Evaluation of Cassava Manihot esculenta Manihot Esculenta (Crantz) Planting Methods and Soybean Glycine max (L.) Merrill Sowing Dates on the Yield Performance of the Component Species in Cassava/Soybean Intercrop under the Humid Tropical Lowlands of Southeastern Nigeria.” African Journal of Biotechnology 8: 42–47. [Google Scholar]
- McAusland, L. , Vialet‐Chabrand S., Davey P., Baker N. R., Brendel O., and Lawson T.. 2016. “Effects of Kinetics of Light‐Induced Stomatal Responses on Photosynthesis and Water‐Use Efficiency.” New Phytologist 211: 1209–1220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murchie, E. H. , Pinto M., and Horton P.. 2009. “Agriculture and the New Challenges for Photosynthesis Research.” New Phytologist 181: 532–552. [DOI] [PubMed] [Google Scholar]
- Pearcy, R. W. 1990. “Sunflecks and Photosynthesis in Plant Canopies.” Annual Review of Plant Physiology and Plant Molecular Biology 41: 421–453. [Google Scholar]
- Pelech, E. A. , Alexander B. C. S., and Bernacchi C. J.. 2021. “Photosynthesis, Yield, Energy Balance, and Water‐Use of Intercropped Maize and Soybean.” Plant Direct 5, no. 12: e365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelech, E. A. , Evers J. B., Pederson T. L., Drag D. W., Fu P., and Bernacchi C. J.. 2023. “Leaf, Plant, to Canopy: A Mechanistic Study on Aboveground Plasticity and Plant Density Within a Maize‐Soybean Intercrop System for the Midwest, USA.” Plant, Cell & Environment 46: 405–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team . 2021. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. http://www.R‐project.org/. [Google Scholar]
- Roeske, C. A. , and O'Leary M. H.. 1984. “Carbon Isotope Effects on Enzyme‐Catalyzed Carboxylation of Ribulose Bisphosphate.” Biochemistry 23: 6275–6284. [DOI] [PubMed] [Google Scholar]
- Sakoda, K. , Tanaka Y., Long S. P., and Shiraiwa T.. 2016. “Genetic and Physiological Diversity in the Leaf Photosynthetic Capacity of Soybean.” Crop Science 56: 2731–2741. [Google Scholar]
- Sakoda, K. , Yamori W., Groszmann M., and Evans J. R.. 2021. “Stomatal, Mesophyll Conductance, and Biochemical Limitations to Photosynthesis during Induction.” Plant Physiology 185: 146–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salesse‐Smith, C. E. , Driever S. M., and Clarke V. C.. 2022. “Modifying Mesophyll Conductance to Optimise Photosynthesis in Crops.” In Burleigh Dodds Series In Agricultural Science, Vol. 27. Sawston, UK: Burleigh Dodds Science Publishing. [Google Scholar]
- Salesse‐Smith, C. E. , Lochocki E. B., Doran L., Haas B. E., Stutz S. S., and Long S. P.. 2024. “Greater Mesophyll Conductance and Leaf Photosynthesis in the Field through Modified Cell Wall Porosity and Thickness via AtCGR3 Expression in Tobacco.” Plant Biotechnology Journal 22: 2504–2517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soleh, M. A. , Tanaka Y., Kim S. Y., Huber S. C., Sakoda K., and Shiraiwa T.. 2017. “Identification of Large Variation in the Photosynthetic Induction Response Among 37 Soybean [Glycine max (L.) Merr.] Genotypes That Is not Correlated with Steady‐State Photosynthetic Capacity.” Photosynthesis Research 131: 305–315. [DOI] [PubMed] [Google Scholar]
- Soleh, M. A. , Tanaka Y., Nomoto Y., et al. 2016. “Factors Underlying Genotypic Differences in the Induction of Photosynthesis in Soybean [Glycine max (L.) Merr.].” Plant, Cell & Environment 39: 685–693. [DOI] [PubMed] [Google Scholar]
- De Souza, A. P. , Wang Y., Orr D. J., Carmo‐Silva E., and Long S. P.. 2020. “Photosynthesis Across African Cassava Germplasm Is Limited by Rubisco and Mesophyll Conductance at Steady State, but by Stomatal Conductance in Fluctuating Light.” New Phytologist 225: 2498–2512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Specht, J. E. , Diers B. W., Nelson R. L., Ferraz de Toledo J. F., Torrion J. A., and Grassini P.. 2014. “Soybean.” In Yield Gains in Major U.S. Field Crops, edited by Smith S., Diers B., Specht J., and Carver B., 311–355. [Google Scholar]
- Taylor, S. H. , and Long S. P.. 2017. “Slow Induction of Photosynthesis on Shade to Sun Transitions in Wheat May Cost at Least 21% of Productivity.” Philosophical Transactions of the Royal Society B: Biological Sciences 372: 20160543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tazoe, Y. , VON Caemmerer S., Estavillo G. M., and Evans J. R.. 2011. “Using Tunable Diode Laser Spectroscopy to Measure Carbon Isotope Discrimination and Mesophyll Conductance to CO2 Diffusion Dynamically at Different CO2 Concentrations.” Plant, Cell & Environment 34: 580–591. [DOI] [PubMed] [Google Scholar]
- Tomás, M. , Medrano H., Brugnoli E., et al. 2014. “Variability of Mesophyll Conductance in Grapevine Cultivars under Water Stress Conditions in Relation to Leaf Anatomy and Water Use Efficiency.” Australian Journal of Grape and Wine Research 20: 272–280. [Google Scholar]
- Tomeo, N. J. , and Rosenthal D. M.. 2017. “Variable Mesophyll Conductance Among Soybean Cultivars Sets a Tradeoff Between Photosynthesis and Water‐Use‐Efficiency.” Plant Physiology 174: 241–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ubierna, N. , Sun W., Kramer D. M., and Cousins A. B.. 2013. “The Efficiency of C4 Photosynthesis under Low Light Conditions in Zea mays, Miscanthus x giganteus and Flaveria bidentis .” Plant, Cell & Environment 36: 365–381. [DOI] [PubMed] [Google Scholar]
- Wang, Y. , Burgess S. J., de Becker E. M., and Long S. P.. 2020. “Photosynthesis in the Fleeting Shadows: an Overlooked Opportunity for Increasing Crop Productivity.” Plant Journal 101: 874–884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, Y. , Stutz S. S., Bernacchi C. J., Boyd R. A., Ort D. R., and Long S. P.. 2022. “Increased Bundle‐Sheath Leakiness of CO2 during Photosynthetic Induction Shows a Lack of Coordination between the C4 and C3 Cycles.” New Phytologist 236: 1661–1675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren, C. R. , Ethier G. J., Livingston N. J., et al. 2003. “Transfer Conductance in Second Growth Douglas‐Fir (Pseudotsuga menziesii (Mirb.)Franco) Canopies.” Plant, Cell & Environment 26: 1215–1227. [Google Scholar]
- Williams, D. R. , Clark M., Buchanan G. M., Ficetola G. F., Rondinini C., and Tilman D.. 2021. “Proactive Conservation to Prevent Habitat Losses to Agricultural Expansion.” Nature Sustainability 4: 314–322. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting information.
Data Availability Statement
The data that support the findings of this study are openly available in Soybean/Soja mesophyll conductance during light induction at https://doi.org/10.13012/B2IDB-7809185_V2.


