Ultra robust negative differential resistance memristor for hardware neuron circuit implementation

Abstract

Neuromorphic computing holds immense promise for developing highly efficient computational approaches. Memristor-based artificial neurons, known for due to their straightforward structure, high energy efficiency, and superior scalability, which enable them to successfully mimic biological neurons with electrical devices. However, the reliability of memristors has always been a major obstacle in neuromorphic computing. Here, we propose an ultra-robust and efficient neuron of negative differential resistance (NDR) memristor based on AlAs/In_0.8Ga_0.2As/AlAs quantum well (QW) structure, which has super stable performance such as low variation (0.264%), high temperature resistance (400 °C) and high endurance. The NDR devices can cycle more than 10¹¹ switching cycles at room temperature and more than 10⁹ switching cycles even at a high temperature of 400 °C, which means that the device can operate for more than 310 years at 10 Hz update frequency. Furthermore, the NDR memristor implements the integration feature of the neuronal membrane and avoids using external capacitors, and successfully apply it to the self-designed super reduced neuron circuit. Moreover, we have successfully constructed Fitz Hugh Nagumo (FN) neuron circuit, reduced hardware costs of FN neuron circuit and enabling diverse neuron dynamics and nine neuron functions. Meanwhile, based on the high temperature stability of the device, a voltage-temperature fused multimodal impulse neural network was constructed to achieve 91.74% accuracy in classifying digital images with different temperature labels. This work offers a novel approach to build FN neuron circuits using NDR memristors, and provides a more competitive method to build a highly reliable neuromorphic hardware system.

The reliability of memristors has always been a major obstacle in neuromorphic computing. This work reports a negative differential resistance memristor based on quantum well structure for neuron circuit implementation, which shows low performance variation (0.264%), high temperature resistance at 400 °C.

Introduction

The exponential growth in data volume and computational demand, coupled with the performance limitations of transistor-based computing systems, has spurred interest in alternative computing paradigms¹. Researchers have proposed neuromorphic computing hardware that simulates the behavior of brain and biological neural network, which can produce greater performance improvements than digital computing in the rapidly growing field of massive data sets, information recognition, and classification^2,3. Currently, the Leaky Integrate and Fire (LIF) and Hodgkin-Huxley (HH) models are predominant in neuron simulation. The LIF model, being the simplest, is widely used for spike neuron simulations but lacks the ability to replicate many biologically relevant neuron features critical for computational neuroscience⁴. The CMOS-based HH model accurately replicates biological neuron behavior but necessitates a complex circuit design⁵. Neurons in the brain exhibit oscillatory behavior and multiple neurons can oscillate synchronously. The Fitz-Hugh Nagumo (FN) model, a simplification of the HH model, is optimal for neural networks exhibiting synchronous neuron oscillation⁶. Besides, FN neuron model can simulate the operation of biological neurons more accurately than LIF neurons. Furthermore, the neural network with FN neurons can be used to solve many complex computational problems and can also be used to study the work of the human brain. Therefore, the FN neuron model is considered one of the most successful models in computational neuroscience⁷. However, digital transistor-based chips attempt to model complex equations representing neuron-rich nonlinear dynamics, thereby complicating them, and these models are currently hampered by computational bottlenecks^8,9.

On the other hand, various new devices have been used to simulate biological neurons, benefiting from their greater biological similarity and scalability than digital transistors. Usually, FN neural circuits require N-type negative differential resistance (NDR) memristors to be implemented¹⁰, while traditional S-type NDR memristors including threshold switch memristors¹¹, phase change memristors¹², and Mott memristors⁸ are difficult to support the implementation of FN neural circuits. On the other hand, due to the randomness of conductive filaments and nucleation sites^13–15, these traditional NDR memristor devices are often unstable and typically require capacitors to integrate neurons, which limits their practical applications in large-scale neural morphology computing systems. Therefore, finding more stable N-type NDR devices to construct neural circuits is a very necessary task. Fortunately, the resonant tunneling diode (RTD) is a typical N-type NDR device that adopts band controlled tunneling mechanism and is less affected by temperature, which makes it have better device stability¹⁶. Therefore, combining the NDR effect of RTD and the hysteresis characteristics of memristors is a new idea to develop suitable devices for neuron circuits.

Here, we have carefully designed a memristor with NDR effect to construct the electronic equivalent of biological neurons. The NDR memristor functional layer is assumed by AlAs/In_0.8Ga_0.2As/AlAs with quantum-well (QW) structure via metal-organic vapour phase epitaxy (MOVPE) ensures device stability and reproducibility, which displays a volatile resistance switch and is locally activated under the state of a hysteresis NDR with current-voltage characteristics. A new fabrication technique based on conventional i-line photolithography for micron-scale high current density NDR memristor devices is also developed with accurate control over the hence characteristics. The NDR memristor shows high reliability and temperature stability and can be cycled stably at room temperature and 10⁹ cycles at 400 °C. The NDR memristor is used to construct a simple Fitz Hugh Nagumo (FN) neuron circuit, which effectively proves the feasibility and advantages of designing neuron circuit without capacitor. This design not only reduces hardware costs but also enables diverse neuron dynamics and functionality. The new FN neuron circuit designed by us realizes 9 kinds of neuron functions, including phasic spiking, anodal break excitation, spike accommodation, subthreshold oscillations, class 1 excitable, all or nothing firing, tonic bursting, refractory period, and accommodation. We constructed an edge detection device based on FN neurons, which showed better characteristics than other edge detection techniques by comparison. A voltage-temperature fused multimodal impulse neural network is also constructed based on the high-temperature stability of the device, and the results show that our system can distinguish images with different temperature labels. With excellent device performance and simple neuron circuit design, it opens a road to the neuromorphic computing with full memristor.

Results

Negative differential resistance (NDR) memristor device activation Fitz-Hugh Nagumo (FN) neuron

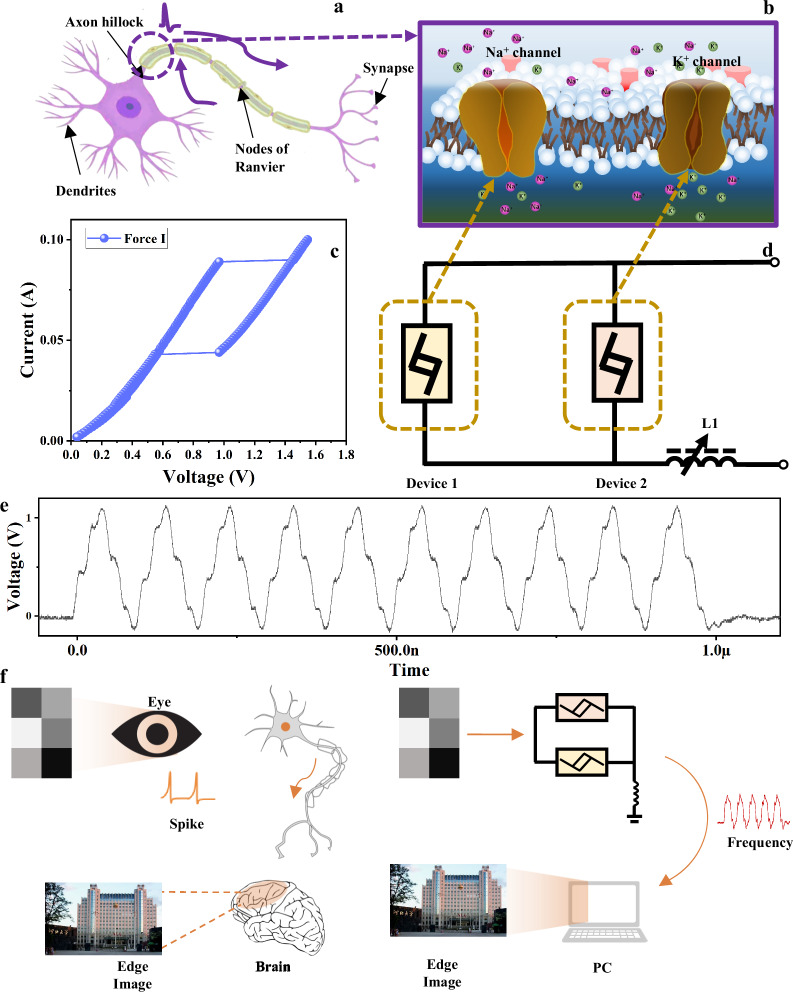
The neurons in the brain show oscillatory behavior, and the synchronous oscillation of neurons plays a crucial role in many human operations¹⁷. Neural networks with FN neurons can be used to solve many complex computing problems, and even to study the work of human brain. Therefore, the FN neuron model is considered one of the most successful models in computational neuroscience¹⁸. The importance of synchronous oscillation in brain operation inspires the realization of coupled oscillators without modeling neuron operations. However, oscillators themselves cannot simulate many neuron characteristics, which will affect the system’s computing power. Therefore, people need to ideally use circuits that can accurately simulate the operation of biological neurons. Figure 1a demonstrates the working principle of our afferent nerve and the analogy with its biological counterpart. The prototype circuit is composed of NDR memristors with different switching voltages as shown in Fig. 1c. The parallel NDR memristors are connected in series with an inductor L1. Two NDR memristors with different switching voltages simulate voltage gated Na⁺ and K⁺ membrane protein ion channels like Fig. 1b, which can also be regarded as the equivalent of neuron membrane potential. Through the I–V characteristics of the components force by current (Fig. 1d), the device not only reflects the NDR characteristics, but also shows the box type hysteresis characteristics. The two I–V characteristic curves under voltage force are shown in Fig. S1. The N-type NDR exhibited by the memristor and the oscillation voltage difference between the two devices are important reasons for the successful implementation of the FN neuron circuit¹⁹. The constructed neuronal circuits exhibit oscillatory behavior similar to that of biological neurons at a prescribed range of inputs, as shown in Fig. 1e. Based on the typical oscillatory behavior of neurons, we designed an edge detection device based on the constructed neuronal circuit to mimic the extraction of image edges by living organisms, and the schematic of the edge detection is shown in Fig. 1f.

Fig. 1. Biological neurons and artificial neurons.

a Schematic structure of a biological neuron, showing that an action potential is fired near the axon hillock (under sufficient input stimulus) and propagates along the cell axon toward the output synapses. b Mechanism of voltage-gated Na⁺ and K⁺ ion flows across the cell membrane. c Basic circuit of a two-channel NDR memristor devices neuron to emulate the Fitz-Hugh Nagumo (FN) neuron. d The typical I–V characteristic curve of NDR memristor devices, where two devices with different switching voltages simulate Na⁺ and K⁺ ion channels, respectively. e The output signal of the circuit in (a) exhibits oscillatory behavior similar to that of neurons. f FN neuron circuit applied to image edge detection.

Structure and model analysis of NDR memristor devices

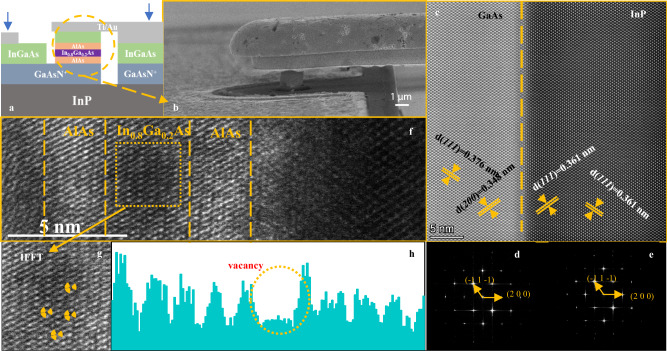
Figure 2a is a schematic diagram of the device cross-section, showing the structure of the NDR memristor device. The entire process includes, based on the air bridge technology, standard i-line lithography and wet chemical etching, a technology for manufacturing NDR memristor with high current density has been developed. Figure 2b is the SEM image of the yellow circle in Fig. 2a. The process details are described in detail in the Supplementary Information (Section 1) as shown in Fig. S2. The high-quality InP and GaAsN⁺ based epitaxial layers have been obtained by metal-organic vapour phase epitaxy (MOVPE). Figure 2c shows the high angle annular dark field image InP/GaAs heterostructure of GaAs cross section. GaAs layer has perfect epitaxial (111) relationship. Figure 2d, e show the crystal structure and corresponding Fast Fourier Transform (FFT) images in Fig. 2c. The relative angle and distance between two lattice planes and diffraction spots indicate the existence of (111) oriented tetragonal F42m phase. The Fig. S3 in Supplementary Information shows that the arrangement of As atoms (yellow dots) and Ga atoms (red dots) is very regular, and the lattice constants are 3.76 Å and 3.48 Å, which can reduce the formation of interface states between GaAs layers and AlAs layers, as well as between GaAs layers and InP substrates. As shown in Fig. 2f, the TEM image of the enlarged cross section of AlAs/In_0.8Ga_0.2As/AlAs QW shows the layer-by-layer growth of the film with good interfaces between AlAs and In_0.8Ga_0.2As. Excellent film quality not only reduces the formation of interfacial states between layers, but also has better thermal conductivity and thermal expansion matching, which helps to reduce thermal stress and thermal gradient, and improve the overall thermal stability of the device^20,21. In addition, the thickness of In_0.8Ga_0.2As layer is determined to be about 3 nm, which is smaller than the carrier thermal de Broglie wavelength. Discrete energy levels were created in the well which led to a NDR characteristic²², which details are described in the Supplementary Information Section 1.1. Resonant tunneling of electrons was easy to produce in a double barrier heterostructure with a thin In_0.8Ga_0.2As layer sandwiched between two AlAs barriers. The electronic resonance tunneling behavior used in the switching process of the device does not change the distribution of internal ions and crystal structure, so it can improve the stability of the device and make the device more uniform^23,24. The Fig. 2g is the inverse FFT of the yellow box in the Fig. 2f diagram, and a small number of vacancies can be observed locally. Figure 2h the yellow dotted contour area is empty. The important reason why the IV curve reflects the box type hysteresis is that there are a few vacancies in the In_0.8Ga_0.2As film, which makes the device a key feature in the application of neuron circuits.

Fig. 2. NDR memristor device analysis.

a Device structure diagram, the yellow circle part is the quantum well (QW) structure. b SEM image of “air bridge” structure. c High-angle annular dark field scanning TEM image of InP and GaAs structure. d, e corresponding to the fast Fourier transform of GaAs and InP, respectively. f High resolution TEM image of QW structure in (a). g In the inverse FFT image of In_0.8Ga_0.2As, it can clearly see the defects marked in the yellow circle. h Line profiles of the areas with and without atomic vacancies in In_0.8Ga_0.2As.

Device characteristics and modeling

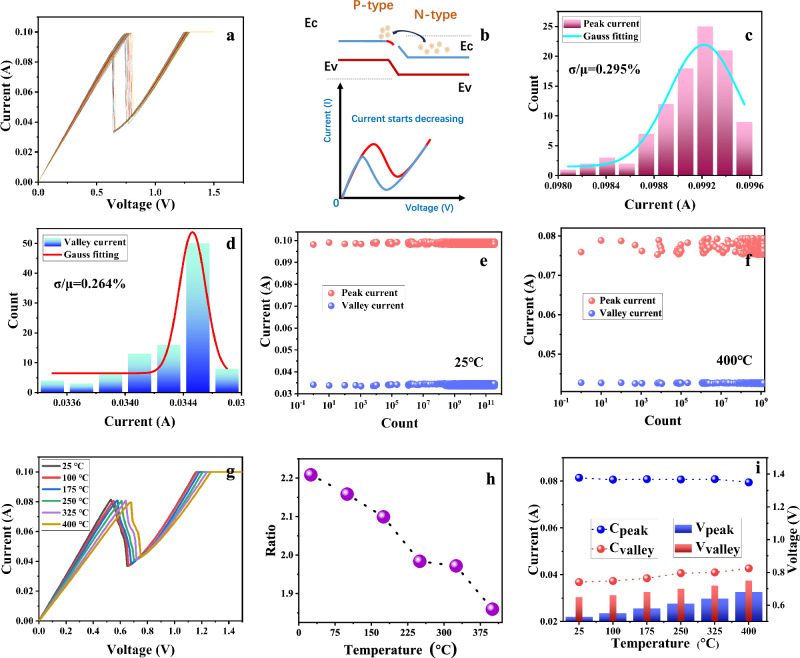
The NDR memristor is powered by connecting a digital meter at two electrodes. Figure 3a shows the I–V characteristic curve of the device at room temperature. After 100 cycles of scanning, the device has no obvious fluctuation, showing excellent uniformity. Unlike traditional RTD devices, the voltage gradually increases, causing electrons in the N-type region to cross the potential barrier and enter the P-type region. In the NDR devices, the application of an external voltage facilitates electron tunneling within the device’s structure, leading to the generation of a tunneling current²⁵. Due to internal defects in semiconductor materials, electrons are captured, resulting in a certain accumulation of electrons at the interface. This accumulation of electrons will reduce the energy band at the interface. When the current decreases, the captured electrons are released, resulting in a hysteresis phenomenon²⁶. Therefore, as the voltage decreases, the switching voltage will decrease to a certain extent and a certain window will appear (Fig. 3b). The equivalent circuit diagram of the component is shown in Fig. S4. Among them, L_s and R_s are the series inductance and series resistance from the lead and contact, R_n and C are the negative resistance and intrinsic capacitance of the double barrier single well structure, C_p is the parallel parasitic capacitance related to the device structure and lead, and L_QW is the intrinsic inductance related to the time constant τ_QW related to the local energy level of the potential well. The quantum-well inductance (L_QW) represents the electron dwell time in quantum well and will not limit the oscillator frequency. The maximum oscillation frequency (f_max) of the NDR memristor is defined as the frequency where R(f) becomes zero, as given by Eq. 1²⁷.

$$f_{\max }=\frac{1}{2\pi }\sqrt{\frac{1}{2L_{QW}^2{C}_n}}\sqrt{\left\{2L_{QW}-\frac{C_n}{C_n^2}+\sqrt{\left[{\left(\frac{C_n}{C_n^2}-2L_{QW}\right)}^2-\frac{4L_{QW}\left(1+R_s{G}_n\right)}{R_s{G}_n}\right]}\right\}}$$ 1

Therefore, the electrical characteristics of NDR memristor devices can be changed by adjusting device technology, material growth conditions, device size, etc. The I–V curve of NDR memristor devices shows obvious NDR and box type hysteresis, in which the NDR memristor device negative resistance (R_n) is given by

$$R_n=\frac{2\mathrm{\Delta }V}{3\mathrm{\Delta }I}$$ 2

Where ΔV = V_p-V_v, ΔI = I_p-I_v. In DC mode, NDR memristor shows ultra-high reproduction performance. To check the uniformity of the device, the statistical data of Gaussian fitting histogram of peak current and valley current are analyzed in the Fig. 3c, d. The device shows only a 0.29 % temporal variation (σ/μ) during 100 consecutive DC cycles, which is nearly 5 times higher than the currently reported high reliability devices²⁸. Similarly, the statistical data of Gaussian fitting histogram of peak voltage and valley voltage are analyzed in Fig. S5. We also calculated the ratio of peak current to valley current under 100 DC scans, which is almost stable at about 2.94 as shown in Fig. S6. Stable peak to valley ratio can contribute stable output frequency in neuron circuit. Temperature correlation measurement is carried out to study the thermal correlation of V–I characteristics of NDR devices. The operating temperature is controlled by the heating table. Fig. S7 shows the 100 cycles of I–V cycles of the device at 400 °C, which still shows good stability. The statistical data of Gaussian fitting histogram of peak current and valley current are analyzed in Fig. S8. Endurance is also an important indicator to measure the stability of devices. Figure 3e shows that NDR devices can cycle more than 10¹¹ switching cycles at room temperature and Fig. 3f shows that NDR devices can cycle more than 10⁹ switching cycles even at a high temperature of 400 °C, which means that the device can operate for more than 310 years at 10 Hz update frequency. Fig. S9 shows the yield of components under different graphical conditions. The yield of components in each area is greater than 95%, and that in some areas is 100%. To demonstrate the uniformity between devices from different batches, we randomly selected 10 batches of device and tested ten I–V characteristic cycle for each device. Fig. S10 show that the devices from different batches had good uniformity. From the perspective of manufacturing, high yield of high-performance NDR devices requires not only uniform doping concentration, but also uniform QW layer thickness. Rapid, non-destructive evaluation of epitaxial materials is valuable for optimizing and monitoring the growth process, which in turn can maximize device output. To better study the relationship between the electrical characteristics of devices and temperature changes, we selected devices with smaller linewidth to study small current changes. Figure 3g shows the I–V characteristics of NDRs (line weight is 1 μm) measured as a function of temperature from 25 °C to 400 °C, the details of peak and valley currents are presented in Fig. S11. The peak current is essentially unchanged, but the valley current increases when the temperature is raised from 25 °C to 400 °C. As the valley current increases more rapidly than the peak current, the ratio peak and valley currents reduce from 2.94 to 1.86 as shown in Fig. 3h. The valley current is known to depend on elastic and inelastic electron scattering processes, such as interface roughness, impurity scattering, phonon scattering, and thermally assisted tunneling through higher resonances^29,30. The peak current reduces and valley current increases with temperature due to enlarged phonon scattering which degrades the peak tunneling current and broadens the resonant transmission probability³¹.The peak current measured in Fig. 3g increases slightly with temperature, probably due to thermal assisted electron tunneling through higher resonance energy levels³². Figure 3i shows the peak to valley current and peak to valley voltage variation of NDR devices at 25 °C–400 °C. The relationship between voltage and current and temperature is shown in Fig. S12. Those observations are very consistent with previous work on the temperature dependent transmission probability of heterostructures³². This result not only proves the transmission mechanism of the NDR device, but also strongly proves that the device has good working stability at high temperatures. The excellent robustness of NDR memristor devices under high temperature conditions can be attributed to the high thermal stability of the AlAs/In_0.8Ga_0.2As/AlAs quantum well structure. By using a double barrier structure for resonant tunneling, efficient electron transfer can be achieved at specific energy levels, which is insensitive to temperature changes and helps maintain stability at high temperatures^33,34. This NDR device has shown intentional stability and durability compared to threshold switching devices used in neuronal circuits in recent years. (Table S1)

Fig. 3. Electrical performance measurement of devices.

a The 100 cycles of I–V characteristic curve of NDR device at room temperature. Illustrations are pictures of devices under an optical microscope. b The working mechanism of NDR memristor devices. c The peak current distribution histogram, blue line is a Gaussian fitting curve. d The valley current distribution histogram, the red line is a Gaussian fitting curve. e The NDR devices undergo more than 10¹¹ switching cycles at room temperature. f The NDR devices undergo more than 10⁹ switching cycles at 400 °C. g The illustration of single I–V curve at 25–400 °C. h The statistics of peak valley current ratio at different temperatures. i Statistics and change trend of peak current (valley current) and peak voltage (valley voltage) at 25–400 °C.

Spike behavior of NDR based FN neurons

An action potential in a biological neuron consists of three events, corresponding to four states as shown in Fig. 4a. The four processes correspond to, 1, Resting state. 2, Depolarization. 3, Re- and hyper-polarization. 4, Refractory period³⁵. Here we will provide a detailed description of the working process of the circuit and its association with neurons. In the resting state, both the Na⁺ and K⁺ channels are closed, both Device 1 (D1) and Device 2 (D2) are in the low resistance state. When subjected to an input voltage stimulation exceeding the threshold, D1 enters the high resistance state, causing the membrane potential to rise and exhibit depolarization behavior. Subsequently, the increase in membrane potential triggers D2 to enter the high resistance state, causing the membrane potential to further increase (further depolarization). Then the current flowing through the inductor decreases, the voltage (membrane potential) on both D1 and D2 decreases. Once the voltage drops below the hold value of D2, the D2 goes back to a low resistance state and speeds up the decrease of membrane potential. Once the voltage drops below the hold voltage of D1, the D1 goes back to the low resistance state, the membrane potential further decreases and drops to a negative value, corresponding to re-polarization and hyperpolarization. It should be noted that, the hold voltage of D2 is higher than the threshold voltage of D1, just as the stages shown in Fig. 4a. At this point, both D1 and D2 return to the initial. An FN model can be used to mimic the spiking and bursting behavior of cortical neurons. FN neuron models are described by (3)³⁶

$$z=f\left(x\right)+\frac{dx}{cdt}+y$$ 3a

$$c\frac{dy}{dt}=x-a-by$$ 3b

this circuit has certain similarity with FN neurons in model (Table S2). In Eq. (3), a, b, and c are defined such that, for no injected current, the neuron membrane potential will be constant. In the FN neuron model, $f\left(x\right)=-x+x^3/3$, device I–V is also sufficient that function $f\left(x\right)$ has a shape like the one shown in Fig. S13. Because only when both devices are unstable, the FN neuron circuit is in an oscillatory working state, and the input voltage is less than the active value and does not oscillate, while the input voltage is higher than the active value and generates an oscillation (Fig. 4b–d). This active range is affected by the device itself and the series inductance, and the device parameters are not easy to change. Figure 4e shows the relationship between the active voltage and the output frequency when the series inductance is different. Figure 4f–n summarizes 9 experimentally proven spike behaviors in FN neurons and uses simulation methods to verify the experimental results. The 9 neuron behaviors are described in detail in the supplementary information (section 2.2). All behaviors are measured from the neuron circuit independently designed in this work. The phasic spiking, anodal break excitation, spike accommodation, subthreshold oscillations, class 1 excitable, all or nothing firing, and Tonic bursting behavior has the circuit diagram in Fig. 1 copied, the refractory period and accommodation behavior are improved based on Fig. 1, and the circuit diagram is shown in Fig. S14. Some results are verified by software simulation (Fig. S15). This circuit is only composed of two NDR memristor devices and inductance elements, which greatly reduces the complexity compared with the previous neuron circuit (Table S3).

Fig. 4. Biological neuron behavior modeling and experimental measurement.

a Four dynamical events during the electrical impulse (1–4) are marked. 1 Resting state, both Na⁺ and K⁺ channels are closed. 2 Depolarization, the hyperpolarization caused by the activation of Na⁺ channels make the membrane potential move in the negative direction. 3 Re- and hyper-polarization, the depolarization caused by the activation of K⁺ channel drives the membrane potential to the positive direction. 4, Refractory period, neurons are recovering and have no response to another stimulus. b–d The relationship between input voltage and output voltage of FN neuron circuit. e The relationship between effective voltage and output frequency when the series inductance is different. f–n The experiment demonstrated 9 biological neuron spike behaviors in FN neuron circuits based on NDR memristors. f phasic spiking, g anodal break excitation, h spike accommodation, i subthreshold oscillations, j class 1 excitable, k all or nothing firing, l tonic bursting, m refractory period, n accommodation.

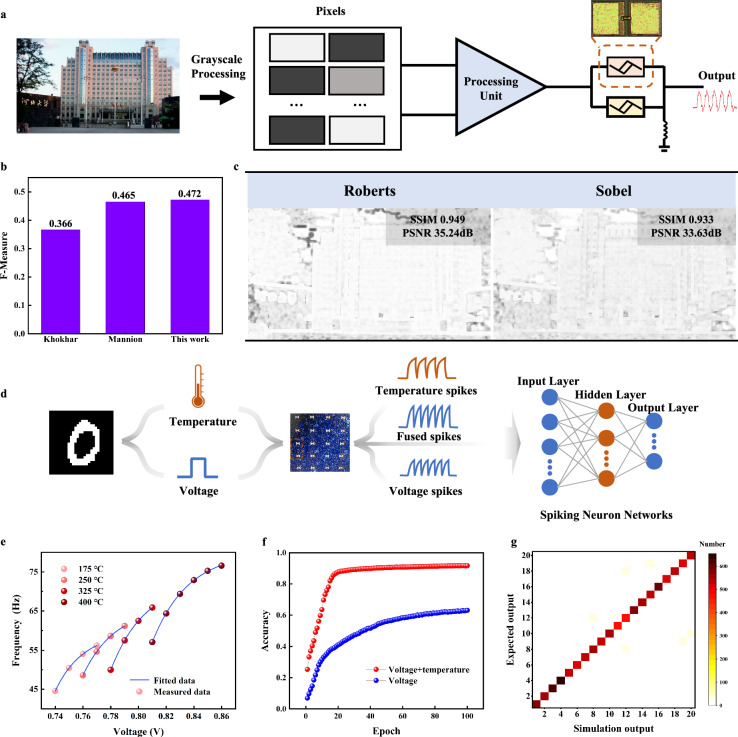
Considering the unique relationship between the input voltage and output voltage of the constructed FN neurons, we have developed an edge detection device³⁷, as illustrated in Fig. 5a. The grayscale image is first processed, mapping pixel values from 0 to 255 to voltage, with a potential difference of 0.83V–0.94 V between any two points. After being processed by the processing unit, the input is fed into the constructed FN neurons. The neuron’s output yields the pixel gradient values, detecting gradients in both X and Y directions to generate edge images, as shown in Fig. S16. These are eventually integrated into the final edge image, with the processing unit depicted in Fig. S17. The evaluation of this work’s edge detection results using the BSD500³⁸ dataset yielded an F-measure of 0.472 as shown in Fig. 5b. The F-Measure is a weighted summed average of accuracy and recall and is a commonly used comprehensive evaluation metric, a higher value of the F-Measure indicates a better performance in edge detection, its value ranges from 0 to 1, with 1 indicating perfect performance³⁹. The F-Measure indicates that the edge detection results of this work outperform other memristor-based edge detection works. The FN neurons serve as the core detection unit, with the neuron outputting a single spike pulse when the input exceeds 0.93 V. All single spike pulse outputs are classified as edges, enhancing the image edges. This outperforms Mannion et al.‘s use of LIF neurons for edge detection^40,41, which is the fundamental reason for the higher F- Measure compared to Mannion et al.‘s work. Meanwhile, the FN neuron circuit performed the edge detection work using the same way as the software operator, which is the convolutional edge detection method. The edge detection was compared using two evaluation metrics, SSIM and PSNR, and the principle is demonstrated in Supplementary Information (Section 1.3). The results show that the neuron-based edge detection compared to the software operator results in SSIM of 0.949 (Roberts) and 0.933 (Sobel), shown in Fig. 5c respectively, which produces a small amount of error, but this result is acceptable. On one hand, the convolution operation performed by software is executed on the CPU. The energy consumption of the CPU and neuron circuits during the edge detection process was assessed (Both calculate the energy consumed to complete a convolution operation using a 3 × 3 convolution kernel), the MATLAB-based estimation determined that the energy consumption for the CPU to perform a single convolution operation is ~138.02 µJ, whereas the neuron circuits consume about 4.11 nJ for the same task. This represents an energy reduction of 5 to 6 orders of magnitude when using neuron circuits compared to the CPU. On the other hand, this FN neuron circuit is a basic unit circuit that can be easily embedded into other circuits to form more complex neuromorphic computing circuits to perform various real-time computational tasks, which cannot be accomplished by traditional computing chips such as CPUs.

Fig. 5. Neuromorphic computation based on neurons.

a Schematic representation of the principle of edge detection by FN neurons. b Comparative analysis of edge detection performance based on the BSDS500 dataset. c Metrics evaluation of edge detection images using SSIM and PSNR. d Schematic diagram of voltage-temperature multimodal image recognition system. e Input voltage versus output frequency curves at four different temperatures. f Accuracy of the network after 100 epochs using only voltage mode and voltage-temperature fusion mode. g Confusion matrix of real and desired outputs in voltage-temperature fusion mode.

Meanwhile, a voltage-temperature fused multimodal spiking neural network system was constructed using FN neurons based on the high-temperature stability characteristics of the device, as shown in Fig. 5d. The MNIST⁴² dataset was processed and temperature information was introduced, the specific processing is shown in methods, the frequency mapping diagrams of some of the datasets processed by the FN neurons are shown in Fig. S18. Then the image pixel information was mapped as the input voltage to the FN neurons, and the spiking signals fusing the voltage and the temperature were obtained after neuron processing, and then entered a spiking neural network for classification, with a network structure of 28 × 28 neurons in the input layer, 128 neurons in the hidden layer, and the output layer of 20 neurons. Figure 5e displays the curves of the relationship between the input voltage and the output frequency for four temperatures, where the output frequency gradually increases as the temperature increases, thus allowing easy decoupling of the temperature and pressure information in the fusion spikes. Under the same network structure, the results of training with voltage spikes signals alone and voltage-temperature fused spikes signals respectively are shown in Fig. 5f. After 100 epochs of training, the accuracy of the network trained with voltage-temperature fused spikes signals reaches 91.74%, while the accuracy of the network trained with voltage spikes signals alone is only 63.1%. Figure 5g shows the confusion matrix heat map of the network trained by voltage-temperature fusion spikes, which shows that the network achieves excellent classification results and only few samples are misclassified. In summary, it is proved by simulation that our system can complete the classification of images at high temperatures, and at the same time, it can distinguish between different temperatures.

Discussion

In summary, we have developed an ultra-robust NDR memristor using the AlAs/In_0.8Ga_0.2As/AlAs quantum well (QW) structure, which possesses low variation, high temperature resistance, high temperature and high yield for a memristor-based neuromorphic system. This NDR memristor exhibits exceptional stability, including low variation, high temperature resistance, and endurance exceeding 10¹¹ cycles, making it ideal for neuromorphic computing. The innovative aspect of this memristor is its ability to integrate the neuronal membrane’s functionality, eliminating the need for external capacitors in the neuron circuit. The research successfully demonstrates the construction of a Fitz Hugh Nagumo (FN) neuron circuit using two NDR memristors and an inductor. This approach significantly reduces the hardware cost and complexity of FN neuron circuits, while offering versatility in neuron dynamics and functions. Finally, we applied this FN neuron to a voltage-temperature fusion multimodal image recognition system that can classify images with different temperature labels at high temperatures with a classification accuracy of 91.74%. This work presents a groundbreaking method to build FN neuron circuits with NDR memristors, contributing to the development of highly reliable neuromorphic hardware systems, specifically addressing the challenges of computational efficiency and reliability.

Methods

Device fabrication

The growth was performed in a vertical Thomas Swan 6 × 2′′ close-coupled shower head MOVPE reactor on (100) semi-insulating InP substrates with a 0.07^o offcut at a pressure of 100 mTorr. A Laytec EpiTT pyrometer (calibrated using an Absolut probe) was used to control the growth temperature to 560 ^°C. The wafer was heated by three stationary resistive graphite heaters located underneath the wafer carrier which was rotated at 100 rpm in the clockwise direction. Trimethylgallium (TMG), trimcethylaluminium (TMA) and trimethylindium (TMI), housed in stainless steel bubblers, were used as group-III precursors and arsine (AsH₃) and phosphine (PH₃) as the group-V source materials. Epison TM gas phase analysers were used to accurately control the concentration of the gas phase. To achieve high n-doping concentrations (up to 2 × 10¹⁹cm^-3), a comparatively low growth rate of 6 nm/min was used to maximize the incorporation of the silicon dopant in the crystal.

The epitaxy of the NDR structure consisted of a 100 nm InP buffer layer, followed by 400 nm highly n-doped GaAs (2 × 10¹⁹cm⁻³Si) to serve as the lower contact. An In_0.80Ga_0.20As quantum well was formed between two AlAs barriers. To minimize the parasitic capacitance of NDR devices, low resistance Ohmic contacts are required to reduce the self-heating effect in the device, which is beneficial for optimizing device performance and reliability. The epitaxy was terminated with 15 nm n-doped In_0.53Ga_0.47As to enhance the formation of a low-resistance ohmic contact. NDR structures were grown with varying QW thicknesses of 4.5 nm. Finally, a specific contact resistivity of 6.3 Ω/m² was obtained for a Ti (20 nm)/Au (200 nm) non-alloyed ohmic contact on In_0.53Ga_0.47As. The surface preparation procedure for the optimum contact consisted of a 10 min. O₃ treatment followed by a 15 s dip in 1.25% ammonium hydroxide after which the sample was blown dry using N₂. A Ti (20 nm)/Au (200 nm) metal stack was deposited onto the samples in a metal evaporator. After the deposition, a post-metallization anneal at 275 ^°C was carried out for the duration of 35 min. to obtain a specific contact resistivity of 6.3 Ω/m².

These inverted air-bridge structures were fabricated on n+ InGaAs film using the photolithography mask. Metallic strips, with dimensions matching contact gaps, were created through a metal evaporation and lift-off process. Subsequently, etching of InGaAs and InP was performed using H₃PO₄:H₂O₂:H₂O (1:1:18) and HCl, respectively. This etching process formed “tunnels” beneath metallic stripes.

Dataset processing

The ten categories in the MNIST dataset were divided equally, with half of them labeled 175 °C and the other 325 °C, to form a new twenty-category dataset.

Author contributions

Y.P. and X.Y. designed the experiments. B.Y. developed the edge detection. Q.L., P.C., and X.Z. designed the circuit. Y. P., H.H., Z.W., and J. Z., test device and circuit performance. S.X.L., N.S., and G.G. grown the materials. Y. S. performed TEM measurement. Y.P., B.Y., S.S.L., and X.Y. wrote and revised the paper. All the authors discussed the data and results.

Peer review

Peer review information

Nature Communications thanks Ki Jun Yu who co-revied with Kyowon Kang; Ye Zhou and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

All data supporting this study and its findings are available within the article, its Supplementary Information and associated files. All source data in the article image is saved in 10.5281/zenodo.14054388

Code availability

The code used for simulation in the article is stored in 10.5281/zenodo.14203073.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-55293-9.