Abstract
We integrate monolayer TMDCs into silicon-on-insulation (SOI) waveguides and dielectric-loaded surface plasmon polariton (DLSPP) waveguides to enhance nonlinear parameters (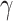 ) of silicon-based waveguides. By optimizing the waveguide geometry, we have achieved significantly improved
) of silicon-based waveguides. By optimizing the waveguide geometry, we have achieved significantly improved 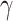 . In MoSe2-on-SOI and MoSe2-in-DLSPP waveguide with optimized geometry, the maximum
. In MoSe2-on-SOI and MoSe2-in-DLSPP waveguide with optimized geometry, the maximum 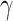 at the excitonic resonant peak (
at the excitonic resonant peak (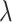 p) is 5001.87 W−1m−1 and 119111.94 W−1m−1 respectively for each case. Based on this, we designed all-optical TMDCs-on-SOI phase and extinction waveguide modulators, achieving
p) is 5001.87 W−1m−1 and 119111.94 W−1m−1 respectively for each case. Based on this, we designed all-optical TMDCs-on-SOI phase and extinction waveguide modulators, achieving 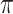 -phase and 3 dB modulation with millimeter-scale modulation lengths under an optical pump intensity of 1 GW/
-phase and 3 dB modulation with millimeter-scale modulation lengths under an optical pump intensity of 1 GW/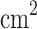 at the optical communication wavelengths of 1310 nm and 1550 nm. At the
at the optical communication wavelengths of 1310 nm and 1550 nm. At the 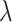 p of MoSe2, a modulation length of only 75
p of MoSe2, a modulation length of only 75 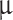 m is required for
m is required for 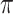 -phase modulation, while a modulation length of 1.36 mm is sufficient for 3 dB modulation. Our work provides new insights for achieving miniaturized and low-power optical communication and networking applications.
-phase modulation, while a modulation length of 1.36 mm is sufficient for 3 dB modulation. Our work provides new insights for achieving miniaturized and low-power optical communication and networking applications.
Subject terms: Applied physics, Optical physics, Nonlinear optics, Nanophotonics and plasmonics
Introduction
Silicon-based electronic microprocessors have experienced a flourishing period of 40 years. However, with the rapid advancement in advanced engineering computing, data analytics, and cloud computing, silicon-based electronic processors are no longer capable of meeting the escalating demand for ultra-fast and energy-efficient computation1. In this regard, silicon photonics emerges as an appealing solution due to its low cost and excellent compatibility with mature CMOS industry. Modulation in all-optical computing for silicon photonics is achieved through nonlinear phenomena. Nevertheless, it should be noted that silicon possesses a relatively low Kerr coefficient (n2)2. Consequently, achieving a satisfactory optical modulation effect requires excessively high light intensity and necessitates lengthy device lengths. To overcome these limitations effectively, integration of novel materials exhibiting exceptional nonlinear-optical coefficients into silicon photonic platforms has been identified as an ideal approach3–6. For instance, waveguides integrated with graphene have achieved high nonlinear parameters7, high-performance vertical van der Waals heterostructure-based photodetectors are successfully integrated on a silicon photonics platform8, and silicon nitride-on-silicon waveguide photodetectors integrated in a visible light photonic platform on silicon have attained a high external quantum efficiency9.
Two-dimensional transition metal dichalcogenides (TMDCs) are a highly promising class of two-dimensional nanomaterials. The chemical composition of TMDCs can be expressed as MX2 (M = Mo, W, etc.; X = S, Se, etc.), with the M layer sandwiched between two X layers10. Due to their unique two-dimensional confinement of electron motion and absence of interlayer perturbation, TMDCs have found extensive applications in photodetectors11, photocatalysis12, and mode lockers13. Theoretical calculations and experimental measurements have revealed that monolayer TMDCs exhibit significant binding energy (0.5 - 1 eV) for their two-dimensional excitons14. This large binding energy enables a series of exciton levels to serve as final or even intermediate states for optical parametric amplification (OPA) or two-photon absorption (2PA)15,16. Notably, studies have demonstrated that TMDCs possess substantial nonlinear coefficients in certain near-infrared regions. In comparison with zero-bandgap graphene, the considerable bandgaps of monolayer TMDCs prevent them from significant linear absorption loss at infrared telecommunication wavelengths3,17. It is anticipated that by integrating TMDCs into silicon waveguides instead of graphene, one can mitigate the high optical losses associated with graphene while harnessing the remarkable n2 offered by TMDCs.
In this paper, we integrate monolayer TMDCs into silicon-on-insulator (SOI) waveguides and dielectric-loaded surface plasmon polariton (DLSPP) waveguides. We exploit the excitonic resonant enhanced 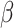 and n2 of monolayer TMDCs to enhance the nonlinear parameter (
and n2 of monolayer TMDCs to enhance the nonlinear parameter (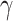 ) of silicon waveguides. By optimizing the geometry of the TMDCs-based waveguide, we achieve a substantial enhancement in
) of silicon waveguides. By optimizing the geometry of the TMDCs-based waveguide, we achieve a substantial enhancement in 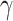 of the waveguide at the excitonic resonant peak (
of the waveguide at the excitonic resonant peak (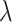 p = 1172 nm) and telecommunications wavelength of 1310 nm, 1550 nm. Subsequently, we conduct further investigation on the
p = 1172 nm) and telecommunications wavelength of 1310 nm, 1550 nm. Subsequently, we conduct further investigation on the 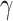 maxima of TMDCs-based waveguides within the wavelength range from 1100 to 1550 nm, employing optimized waveguide geometry. Further, the giant
maxima of TMDCs-based waveguides within the wavelength range from 1100 to 1550 nm, employing optimized waveguide geometry. Further, the giant 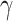 and long-range waveguiding properties of the acquired integrated waveguides with optimized structures are used as both extinction and phase modulators to demonstrate superb all-optical switching performance. Finally, we present the phase and extinction modulation performance of TMDCs-on-SOI waveguides in optimized structures. Significantly, this study may enable novel ways for next-generation nonlinear all-optical modulation applications.
and long-range waveguiding properties of the acquired integrated waveguides with optimized structures are used as both extinction and phase modulators to demonstrate superb all-optical switching performance. Finally, we present the phase and extinction modulation performance of TMDCs-on-SOI waveguides in optimized structures. Significantly, this study may enable novel ways for next-generation nonlinear all-optical modulation applications.
Results and discussion
Characterization of monolayer TMDCs
In monolayer TMDCs, the refractive index of the material offers the most fundamental description of light-matter interaction. Ellipsometry has been proven to be an effective non-destructive method for characterizing the optical properties of monolayer TMDCs, offering crucial insights into film refractive index, extinction coefficient, and thickness18. In recent years, a large number of studies have employed ellipsometry to measure the complex refractive index of TMDCs19–21. The theoretical treatment of TMDCs’ optical properties is complex, notably due to spin-orbit coupling and strong excitonic effects resulting from electron-hole interactions22,23. Therefore, in the simulations conducted in this study, we directly utilize the experimental values of monolayer TMDCs refractive index obtained at room temperature, as reported in the Ref.24.
Within monolayer TMDCs, there exist two characteristic excitonic states known as exciton A and exciton B. Recently, Ji et al. conducted a systematic theoretical study based on quantum perturbation theory, revealing that the strong excitonic resonant effects in highly-crystalline monolayer TMDCs lead to significantly enhanced 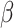 15,16. Based on second-order, time-dependent quantum perturbation theory,
15,16. Based on second-order, time-dependent quantum perturbation theory, 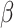 of monolayer TMDCs can be calculated by:
of monolayer TMDCs can be calculated by:
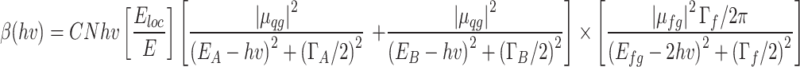 |
1 |
where h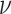 is the photon energy, N represents the density of active unit cells, Eloc/E refers to the local-field correction factor, Ei and
is the photon energy, N represents the density of active unit cells, Eloc/E refers to the local-field correction factor, Ei and 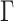 i correspond to transition energy of a certain energy level and its linewidth, respectively,
i correspond to transition energy of a certain energy level and its linewidth, respectively, 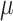 ij denotes the transition dipole moment, C is a material-independent constant. By substituting eq.1 into Kramers-Krönig transformation, we can obtain n2 of the monolayer TMDCs. it is assumed that only the 2p excited states are involved in the 2PA process, while other excitonic states are completely ignored25. The spectra of n2 and
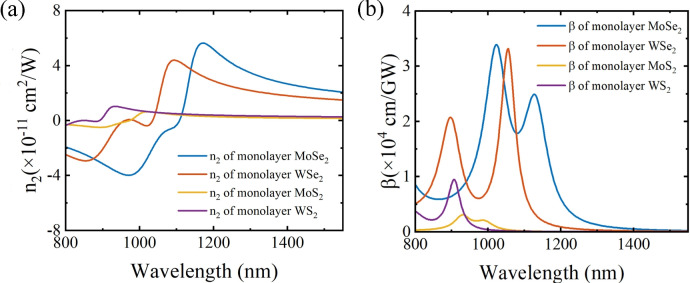
ij denotes the transition dipole moment, C is a material-independent constant. By substituting eq.1 into Kramers-Krönig transformation, we can obtain n2 of the monolayer TMDCs. it is assumed that only the 2p excited states are involved in the 2PA process, while other excitonic states are completely ignored25. The spectra of n2 and 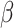 are shown in Fig. 1.
are shown in Fig. 1.
Fig. 1.
(a) Kerr coefficients n2 of the monolayer TMDCs in 800 - 1550 nm. (b) Two-photon absorption coefficients 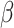 of the monolayer TMDCs in 800 - 1550 nm.
of the monolayer TMDCs in 800 - 1550 nm.
Giant nonlinear parameters of the monolayer-TMDCs-silicon waveguides
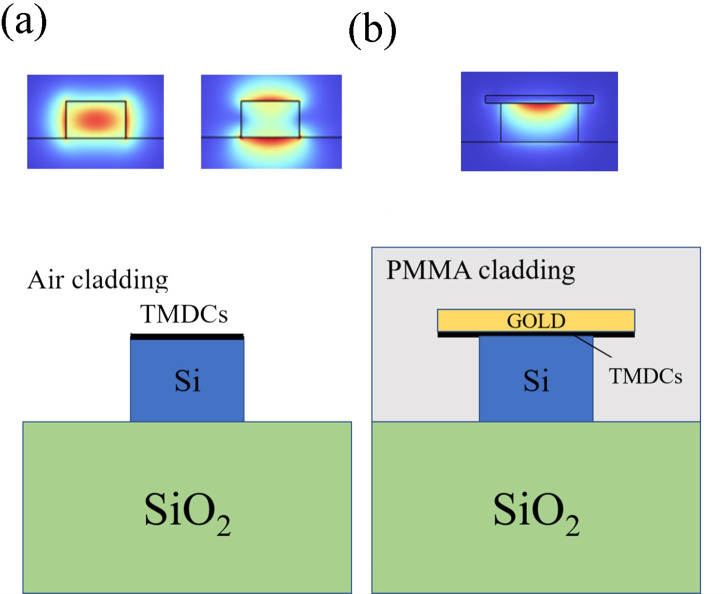
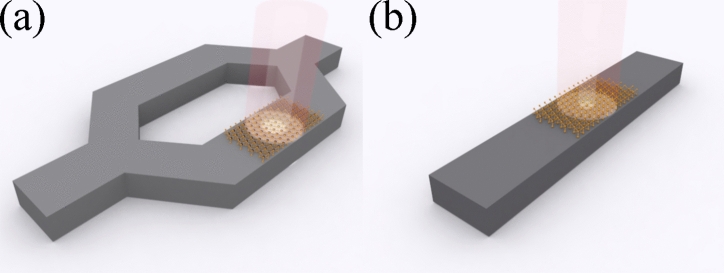
As shown in Fig. 2, Two typical photonic and plasmonic silicon-waveguide structures have been made use of to optimize electric-field interaction with monolayer TMDCs and maximize the 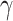 . Firstly, the representative SOI waveguide is employed, which is a photonic waveguide and composed of SiO2 substrate beneath a silicon slab with air as the overcladding. Monolayer TMDCs are deposited on top of the silicon slab and cover the prime mode-area of the silicon slab. Both the fundamental quasi-TM and quasi-TE modes are considered. Secondly, to concentrate optical modes intensity on the top surface of the SOI waveguide and achieve greater interaction between monolayer TMDCs and fundamental optical modes, a DLSPP waveguide is employed. In the DLSPP waveguide integrated with monolayer TMDCs, 50 nm of gold is added on top of the first waveguide configuration and the overcladding is replaced by PMMA, whose refractive index is close to that of SiO2. Only TM-like surface plasmon polaritons parallel to the boundary between gold and Si are supported in the DLSPP waveguide.
. Firstly, the representative SOI waveguide is employed, which is a photonic waveguide and composed of SiO2 substrate beneath a silicon slab with air as the overcladding. Monolayer TMDCs are deposited on top of the silicon slab and cover the prime mode-area of the silicon slab. Both the fundamental quasi-TM and quasi-TE modes are considered. Secondly, to concentrate optical modes intensity on the top surface of the SOI waveguide and achieve greater interaction between monolayer TMDCs and fundamental optical modes, a DLSPP waveguide is employed. In the DLSPP waveguide integrated with monolayer TMDCs, 50 nm of gold is added on top of the first waveguide configuration and the overcladding is replaced by PMMA, whose refractive index is close to that of SiO2. Only TM-like surface plasmon polaritons parallel to the boundary between gold and Si are supported in the DLSPP waveguide.
Fig. 2.
(a) Schematic diagram of silicon channel waveguide with monolayer TMDCs (the upper inset shows the electric-field distribution 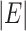 in quasi-TE and quasi-TM modes for a silicon channel waveguide). (b) Schematic diagram of DLSPP waveguide consisting of a silicon core, monolayer of TMDCs, PMMA cladding, and a 50 nm Au layer (the upper inset shows the electric-field distribution
in quasi-TE and quasi-TM modes for a silicon channel waveguide). (b) Schematic diagram of DLSPP waveguide consisting of a silicon core, monolayer of TMDCs, PMMA cladding, and a 50 nm Au layer (the upper inset shows the electric-field distribution 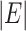 in TM mode for a DLSPP waveguide).
in TM mode for a DLSPP waveguide).
The effective third-order nonlinearity of the integrated waveguides is characterized by their 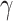 , which takes account of both the transverse dependence of the nonlinear coefficients and the effective optical mode area (Aeff) of the waveguide. Taking consideration of the large refractive index contrast in the integrated waveguides,
, which takes account of both the transverse dependence of the nonlinear coefficients and the effective optical mode area (Aeff) of the waveguide. Taking consideration of the large refractive index contrast in the integrated waveguides, 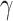 could be quantitatively evaluated by26:
could be quantitatively evaluated by26:
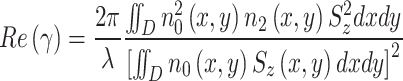 |
2 |
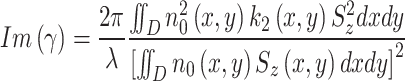 |
3 |
where Sz is time-averaged Poynting vector, D refers to the integral of the electric-field over the material regions, n0 corresponds to linear refractive index of material, n2 denotes the Kerr coefficients of material, k2 is nonlinear extinction coefficients. The definition of  highlights the importance of waveguide design in achieving optimal electric-field interaction with monolayer TMDCs. We carry out the calculations over a broad wavelength range from the first
highlights the importance of waveguide design in achieving optimal electric-field interaction with monolayer TMDCs. We carry out the calculations over a broad wavelength range from the first  p wavelength to the telecommunication wavelength of 1550 nm. In the subsequent calculations, the values of n2 and
p wavelength to the telecommunication wavelength of 1550 nm. In the subsequent calculations, the values of n2 and 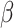 for silicon are obtained from Ref.2. Additionally, the values of n0 and k0 for silicon, SiO2, PMMA are obtained from the experimentally determined results in Refs.26–28, respectively.
for silicon are obtained from Ref.2. Additionally, the values of n0 and k0 for silicon, SiO2, PMMA are obtained from the experimentally determined results in Refs.26–28, respectively.
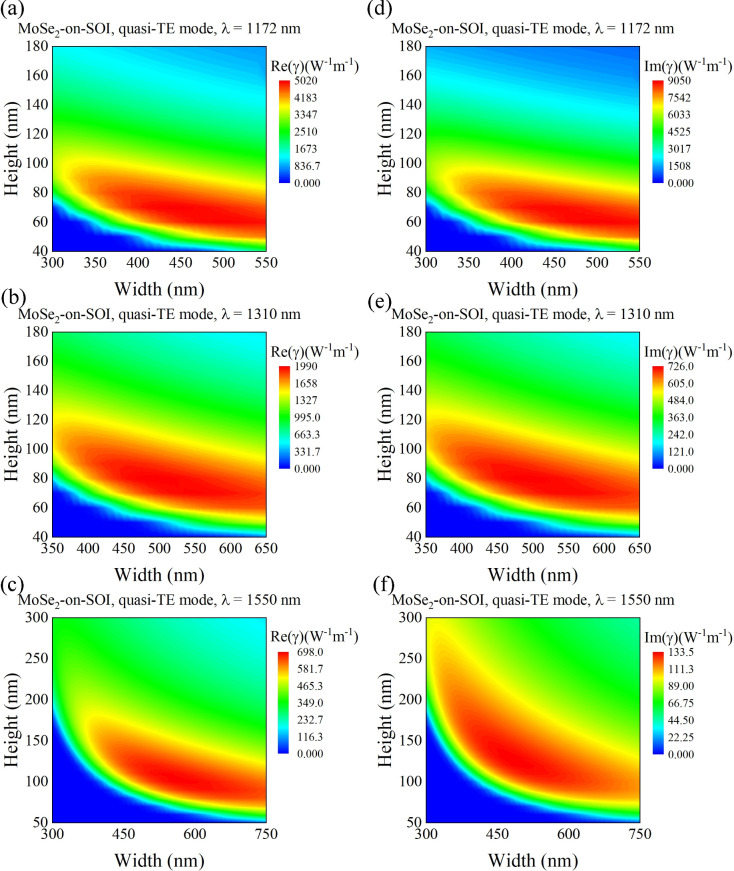
Firstly, we investigate the optimization of geometry for the monolayer-TMDCs-on-SOI waveguides so as to attain the optimal Re(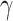 ) and Im(
) and Im(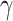 ), as demonstrated in Fig. 3. Taking monolayer-MoSe2-on-SOI waveguides as an example, Fig. 3a–f demonstrate the dependence of Re(
), as demonstrated in Fig. 3. Taking monolayer-MoSe2-on-SOI waveguides as an example, Fig. 3a–f demonstrate the dependence of Re(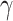 ) and Im(
) and Im(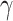 ) for the fundamental quasi-TE mode on the geometry at three representative wavelengths (
) for the fundamental quasi-TE mode on the geometry at three representative wavelengths (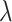 p = 1172 nm and telecommunication wavelength
p = 1172 nm and telecommunication wavelength 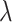 = 1310 nm, 1550 nm), respectively. At 1172 nm, the waveguide geometry is optimized to be 440
= 1310 nm, 1550 nm), respectively. At 1172 nm, the waveguide geometry is optimized to be 440 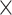 70 nm to achieve the maximized absolute values of Re(
70 nm to achieve the maximized absolute values of Re(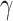 ) and Im(
) and Im(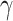 ) reaching up to 5.00
) reaching up to 5.00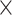 103 and 8.91
103 and 8.91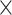 103 W−1m−1. In addition, under the excitation at 1310 nm, the largest absolute values of Re(
103 W−1m−1. In addition, under the excitation at 1310 nm, the largest absolute values of Re(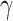 ) and Im(
) and Im(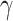 ) up to 1.98
) up to 1.98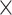 103 W−1m−1 and 7.25
103 W−1m−1 and 7.25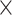 102 W−1m−1 have been attained at the optimal waveguide geometry of 490
102 W−1m−1 have been attained at the optimal waveguide geometry of 490 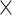 80 nm. Furthermore, the best waveguide geometry of 580
80 nm. Furthermore, the best waveguide geometry of 580 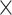 100 nm and 480
100 nm and 480 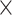 130 nm are exploited to realize the highest absolute values of Re(
130 nm are exploited to realize the highest absolute values of Re(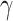 ) and Im(
) and Im(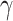 ) up to 7.51
) up to 7.51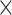 102 W−1m−1 and 1.13
102 W−1m−1 and 1.13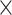 102 W−1m−1 at the mostly used telecommunication wavelength of 1550 nm. Importantly, the achieved Re(
102 W−1m−1 at the mostly used telecommunication wavelength of 1550 nm. Importantly, the achieved Re(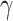 ) and Im(
) and Im(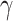 ) at the three wavelengths have been significantly improved in comparison to that of pure SOI waveguides, especially in
) at the three wavelengths have been significantly improved in comparison to that of pure SOI waveguides, especially in 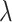 p, as revealed in the Fig. 4. Simultaneously, we conduct a tolerance analysis on the monolayer-MoSe2-on-SOI waveguide optimized geometry, as shown in Table S1 (see the Supplementary Material) . On the other side, the considerable bandgaps of monolayer TMDCs can exempt our waveguides from large linear absorption loss, which is remarkable in graphene-silicon waveguides. In the comparison among the maximized Re(
p, as revealed in the Fig. 4. Simultaneously, we conduct a tolerance analysis on the monolayer-MoSe2-on-SOI waveguide optimized geometry, as shown in Table S1 (see the Supplementary Material) . On the other side, the considerable bandgaps of monolayer TMDCs can exempt our waveguides from large linear absorption loss, which is remarkable in graphene-silicon waveguides. In the comparison among the maximized Re(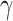 ) and Im(
) and Im(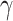 ) at the three distinct wavelengths, the greatest values attained at 1172 nm result from the enhanced n2 together with the best electric-field overlap with monolayer MoSe2 laterally and the strongest optical-mode confinement. It has been disclosed that smaller optimized waveguide geometry at shorter wavelengths lead to superior electric-field overlap with monolayer TMDCs laterally and more intense optical-mode confinement. This in combination with the larger n2 at 1310 nm results in about 3 times greater Re(
) at the three distinct wavelengths, the greatest values attained at 1172 nm result from the enhanced n2 together with the best electric-field overlap with monolayer MoSe2 laterally and the strongest optical-mode confinement. It has been disclosed that smaller optimized waveguide geometry at shorter wavelengths lead to superior electric-field overlap with monolayer TMDCs laterally and more intense optical-mode confinement. This in combination with the larger n2 at 1310 nm results in about 3 times greater Re(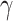 ) than that at 1550 nm. Therefore, the interplay of three factors originating from wavelength-dependent n2, electric-field overlap with monolayer MoSe2 laterally, and optical-mode confinement gives rise to the spectral dependence of the maximized Re(
) than that at 1550 nm. Therefore, the interplay of three factors originating from wavelength-dependent n2, electric-field overlap with monolayer MoSe2 laterally, and optical-mode confinement gives rise to the spectral dependence of the maximized Re(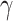 ) and Im(
) and Im(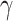 ) of the MoSe2-on-SOI waveguides over a broad wavelength range from 1100 to 1550 nm, as shown in Fig. S1 (see the Supplementary Material). In comparison with the quasi-TE mode, quasi-TM mode for the waveguides exhibits significantly reduced optical intensity and the resultant much weaker electric-field interaction with monolayer TMDCs. As a consequence, the nonlinear parameters for the quasi-TM mode are several times smaller than those for the quasi-TE mode, as demonstrated in Fig. S5 (see the Supplementary Material).
) of the MoSe2-on-SOI waveguides over a broad wavelength range from 1100 to 1550 nm, as shown in Fig. S1 (see the Supplementary Material). In comparison with the quasi-TE mode, quasi-TM mode for the waveguides exhibits significantly reduced optical intensity and the resultant much weaker electric-field interaction with monolayer TMDCs. As a consequence, the nonlinear parameters for the quasi-TM mode are several times smaller than those for the quasi-TE mode, as demonstrated in Fig. S5 (see the Supplementary Material).
Fig. 3.
Real part of nonlinear parameters of monolayer-MoSe2-on-SOI waveguide in quasi-TE mode as a function of waveguide core width (x-axis) and height (y-axis) at (a) 1172 nm, (b) 1310 nm, (c) 1550 nm, and imaginary part of nonlinear parameters at (d) 1172 nm, (e) 1310 nm, and (f) 1550 nm. The insets show the waveguide cross sections when the maximum nonlinear parameter is taken at the respective wavelengths, respectively.
Fig. 4.
(a) Maximum nonlinear parameters obtained at three different wavelengths exciton resonance peak 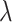 p = 1172 nm, communication wavelength
p = 1172 nm, communication wavelength 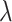 = 1310 nm, 1550 nm) in the quasi-TE mode of the monolayer-MoSe2-on-SOI waveguide, and (b) its comparison with the nonlinear parameters of the pure SOI waveguide.
= 1310 nm, 1550 nm) in the quasi-TE mode of the monolayer-MoSe2-on-SOI waveguide, and (b) its comparison with the nonlinear parameters of the pure SOI waveguide.
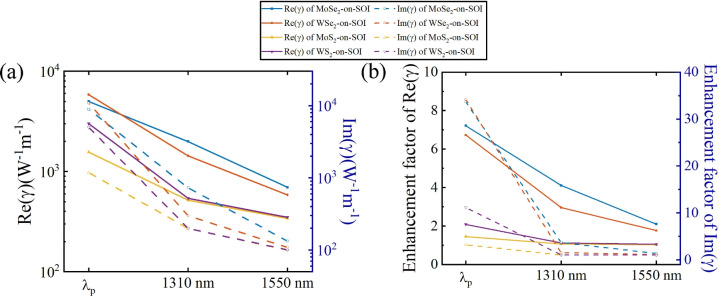
In order to fully understand the nonlinear optical interaction in the monolayer-TMDCs-on-SOI waveguides and optimize their performance, we further study the nonlinear parameters of monolayer MoS2-, WS2-, WSe2-on-SOI waveguides. Fig. 4 also illustrates the summary and comparison of the maximum Re(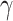 ) and Im(
) and Im(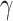 ) for the essential quasi-TE mode of the monolayer MoS2-, MoSe2- WS2-, WSe2-on-SOI waveguides at the three representative wavelengths (
) for the essential quasi-TE mode of the monolayer MoS2-, MoSe2- WS2-, WSe2-on-SOI waveguides at the three representative wavelengths (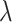 p, telecommunication wavelength
p, telecommunication wavelength 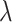 = 1310 nm, 1550 nm). As a result of the superb NLO characteristics of monolayer-TMDCs, all the monolayer-TMDs-on-SOI waveguides exhibit much superior nonlinear parameters compared to that of pure SOI waveguides. Moreover, Figs. S2-S4 (see the Supplementary Material) demonstrate the spectral dependence of the maximized Re(
= 1310 nm, 1550 nm). As a result of the superb NLO characteristics of monolayer-TMDCs, all the monolayer-TMDs-on-SOI waveguides exhibit much superior nonlinear parameters compared to that of pure SOI waveguides. Moreover, Figs. S2-S4 (see the Supplementary Material) demonstrate the spectral dependence of the maximized Re(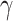 ) and Im(
) and Im(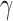 ) of monolayer- MoS2-, WS2-, WSe2-on-SOI waveguides over a wide wavelength range from 1100 to 1550 nm. Similar to the case in monolayer-MoSe2-on-SOI waveguides, the quasi-TM mode for the MoS2-, WS2-, WSe2-on-SOI waveguides possess substantially reduced electric-field intensity and the resultant much weaker electric-field interaction with monolayer TMDCs. Hence, the nonlinear parameters and the contribution from nonlinearity of TMDCs layers for the quasi-TM mode are much smaller than that for the quasi-TE mode, as demonstrated in Fig. S6 (see the Supplementary Material).
) of monolayer- MoS2-, WS2-, WSe2-on-SOI waveguides over a wide wavelength range from 1100 to 1550 nm. Similar to the case in monolayer-MoSe2-on-SOI waveguides, the quasi-TM mode for the MoS2-, WS2-, WSe2-on-SOI waveguides possess substantially reduced electric-field intensity and the resultant much weaker electric-field interaction with monolayer TMDCs. Hence, the nonlinear parameters and the contribution from nonlinearity of TMDCs layers for the quasi-TM mode are much smaller than that for the quasi-TE mode, as demonstrated in Fig. S6 (see the Supplementary Material).
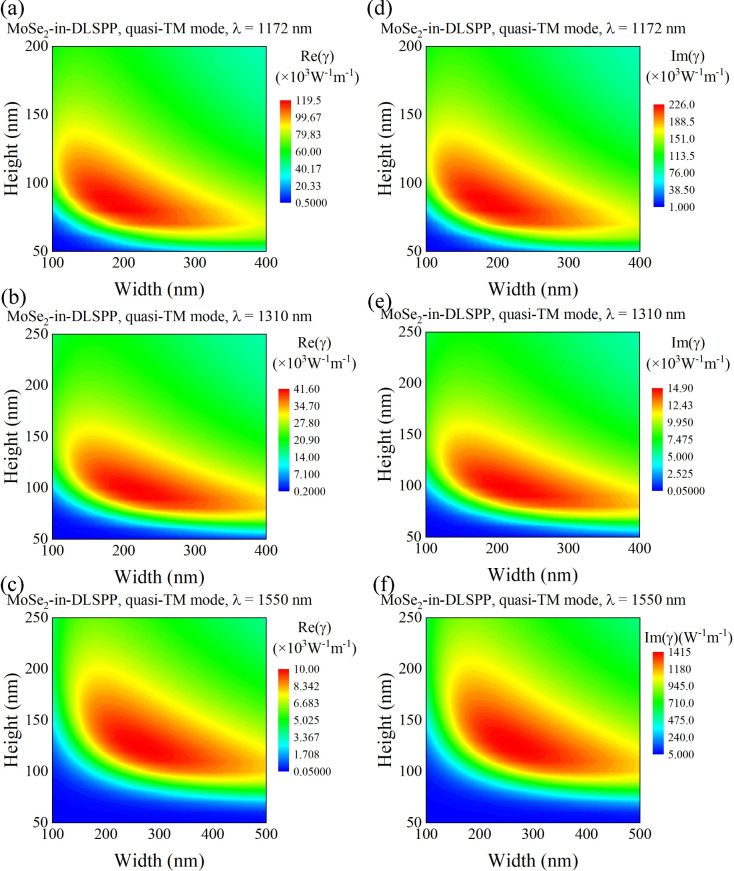
Secondly, we utilize the DLSPP waveguide to concentrate the electric-field intensity to the boundary between gold and silicon significantly enhancing the electric-field interaction with monolayer MoSe2. This enhancement could further promote the nonlinear parameters of the waveguides. Similar to the above case, we optimize the geometry of the DLSPP waveguides to obtain the best Re(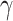 ) and Im(
) and Im(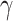 ), as shown in Fig. 5. The electric-field is intensely confined in the gold-Si interface where the monolayer MoSe2 resides. The excellent overlap between monolayer MoSe2 and the electric-field could lead to optimal light-matter interaction. Thanks to the strong optical confinement and the great electric-field overlap with monolayer TMDCs laterally, the resultant nonlinear parameters of monolayer-TMDCs-integrated-DLSPP waveguides are up to two orders of magnitude superior than that of the monolayer-TMDCs-on-SOI waveguides. Especially, the optimized geometry of 200
), as shown in Fig. 5. The electric-field is intensely confined in the gold-Si interface where the monolayer MoSe2 resides. The excellent overlap between monolayer MoSe2 and the electric-field could lead to optimal light-matter interaction. Thanks to the strong optical confinement and the great electric-field overlap with monolayer TMDCs laterally, the resultant nonlinear parameters of monolayer-TMDCs-integrated-DLSPP waveguides are up to two orders of magnitude superior than that of the monolayer-TMDCs-on-SOI waveguides. Especially, the optimized geometry of 200 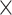 80 nm for the monolayer-MoSe2-in-DLSPP waveguide has been employed to attain the maximized absolute values of Re(
80 nm for the monolayer-MoSe2-in-DLSPP waveguide has been employed to attain the maximized absolute values of Re(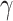 ) and Im(
) and Im(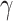 ) at 1172 nm, which reach up to 1.19
) at 1172 nm, which reach up to 1.19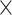 105 W−1m−1 and 2.25
105 W−1m−1 and 2.25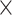 105 W−1m−1. These values are more than approximately 20 and 25 times higher compared to those of the monolayer-MoSe2-on-SOI waveguides, respectively. In addition, the highest absolute values of Re(
105 W−1m−1. These values are more than approximately 20 and 25 times higher compared to those of the monolayer-MoSe2-on-SOI waveguides, respectively. In addition, the highest absolute values of Re(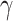 ) and Im(
) and Im(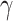 ) up to 4.15
) up to 4.15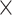 104 W−1m−1 and 1.48
104 W−1m−1 and 1.48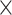 104 W−1m−1 have been achieved at 1310 nm, which are approximately 20 times superior compared to that of the monolayer-MoSe2-on-SOI waveguides. Moreover, at the mostly used telecommunication wavelength of 1550 nm, the realized greatest absolute values of Re(
104 W−1m−1 have been achieved at 1310 nm, which are approximately 20 times superior compared to that of the monolayer-MoSe2-on-SOI waveguides. Moreover, at the mostly used telecommunication wavelength of 1550 nm, the realized greatest absolute values of Re(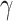 ) and Im(
) and Im(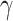 ) reach 9.97
) reach 9.97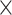 103 W−1m−1 and 1.41
103 W−1m−1 and 1.41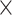 102 W−1m−1, respectively, which are 14 and 10 times larger than that of the monolayer-MoSe2-on-SOI waveguides. We conduct a tolerance analysis on the monolayer-MoSe2-in-DLSPP waveguide optimized geometry, as shown in Table S2 (see the Supplementary Material). Simultaneously, we summarize and compare the maximum absolute values of Re(
102 W−1m−1, respectively, which are 14 and 10 times larger than that of the monolayer-MoSe2-on-SOI waveguides. We conduct a tolerance analysis on the monolayer-MoSe2-in-DLSPP waveguide optimized geometry, as shown in Table S2 (see the Supplementary Material). Simultaneously, we summarize and compare the maximum absolute values of Re(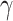 ) and Im(
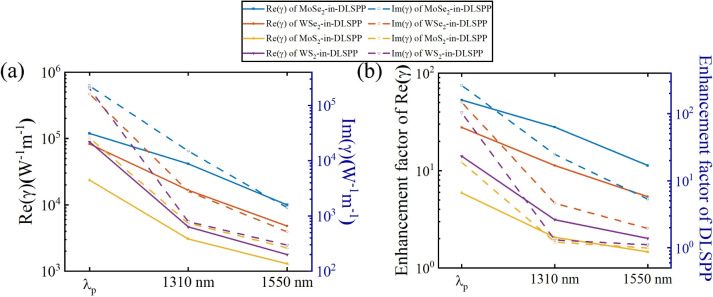
) and Im(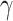 ) for the monolayer-MoS2-, WS2-, MoSe2-, WSe2-in-DLSPP waveguides at the three representative wavelengths, as shown in Fig. 6. Due to the eminent NLO characteristics of monolayer TMDCs, all the monolayer-TMDCs-in-DLSPP waveguides possess much greater absolute values of Re(
) for the monolayer-MoS2-, WS2-, MoSe2-, WSe2-in-DLSPP waveguides at the three representative wavelengths, as shown in Fig. 6. Due to the eminent NLO characteristics of monolayer TMDCs, all the monolayer-TMDCs-in-DLSPP waveguides possess much greater absolute values of Re(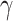 ) and Im(
) and Im(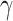 ) than that of pure DLSPP waveguides. Furthermore, spectral dependence of the maximized absolute values of Re(
) than that of pure DLSPP waveguides. Furthermore, spectral dependence of the maximized absolute values of Re(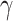 ) and Im(
) and Im(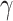 ) for all the monolayer-TMDCs-in-DLSPP waveguides are quantitatively studied over a broad wavelength range from 1100 to 1550 nm, as illustrated in Figs. S7-S10 (see the Supplementary Material). Finally, the propagation losses of pure SOI and TMDCs-on-SOI waveguides, as well as DLSPP and TMDCs-in-DLSPP waveguides, are calculated, as shown in Table S3 (see the Supplementary Material).
) for all the monolayer-TMDCs-in-DLSPP waveguides are quantitatively studied over a broad wavelength range from 1100 to 1550 nm, as illustrated in Figs. S7-S10 (see the Supplementary Material). Finally, the propagation losses of pure SOI and TMDCs-on-SOI waveguides, as well as DLSPP and TMDCs-in-DLSPP waveguides, are calculated, as shown in Table S3 (see the Supplementary Material).
Fig. 5.
Real part of nonlinear parameters of monolayer-MoSe2-in-DLSPP waveguide in quasi-TM mode as a function of waveguide core width (x-axis) and height (y-axis) at (a) 1172 nm, (b) 1310 nm, (c) 1550 nm, and imaginary part of nonlinear parameters at (d) 1172 nm, (e) 1310 nm, and (f) 1550 nm. The insets show the waveguide cross sections when the maximum nonlinear parameter is taken at the respective wavelengths, respectively.
Fig. 6.
(a) Maximum nonlinear parameters obtained at three different wavelengths (exciton resonance peak 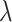 p = 1172 nm, communication wavelength
p = 1172 nm, communication wavelength 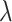 = 1310 nm, 1550 nm) in quasi-TE mode of the monolayer-MoSe2-in-DLSPP waveguide, and (b) its comparison with nonlinear parameters of the pure DLSPP waveguide.
= 1310 nm, 1550 nm) in quasi-TE mode of the monolayer-MoSe2-in-DLSPP waveguide, and (b) its comparison with nonlinear parameters of the pure DLSPP waveguide.
Superb performance of all-optical modulators based on the waveguides
In this section, we utilize the above results to demonstrate the phase modulation and extinction modulation performance of waveguides integrated with monolayer-TMDCs. Despite the promising potential of monolayer-TMDCs-in-DLSPP waveguides with their giant nonlinear parameters, their practical application is hindered by significant linear losses caused by the metal layer. As a consequence, we exploit the monolayer-TMDCs-on-SOI with the optimized geometry to construct the all-optical nonlinear phase and extinction modulators, which is easier to interact with optical pump. As can be seen from Fig. 7a, in the nonlinear phase modulator, one arm of the Mach-Zehnder interferometer (MZI) is integrated with monolayer TMDCs to attain a 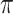 -phase shift, in order to achieve the constructive/destructive interference and the resultant maximized contrast between the on/off states. The reason why we only integrate one arm of MZI with monolayer TMDCs is to minimize the insertion loss29. Initially, the results of the coupling loss of MZI integrated with monolayer TMDCs indicate low loss value, demonstrating efficient light propagation within the modulator and confirming the feasibility of MZI, as shown in Fig. S11-S13 (see the Supplementary Material). Thus we can calculate its modulation efficiency, i.e., the phase modulation effect per unit length, as
-phase shift, in order to achieve the constructive/destructive interference and the resultant maximized contrast between the on/off states. The reason why we only integrate one arm of MZI with monolayer TMDCs is to minimize the insertion loss29. Initially, the results of the coupling loss of MZI integrated with monolayer TMDCs indicate low loss value, demonstrating efficient light propagation within the modulator and confirming the feasibility of MZI, as shown in Fig. S11-S13 (see the Supplementary Material). Thus we can calculate its modulation efficiency, i.e., the phase modulation effect per unit length, as
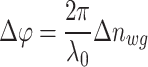 |
4 |
where  is the variation of the waveguide phase coefficient, due to maximum and minimum applied local optical intensity, n2eff refers to the nonlinear refractive index of the waveguide and is another way to characterize the nonlinear refractive properties of a waveguide, I is the optical pump intensity. The maximum phase shift of the nonlinear phase modulator can be calculated by30:
is the variation of the waveguide phase coefficient, due to maximum and minimum applied local optical intensity, n2eff refers to the nonlinear refractive index of the waveguide and is another way to characterize the nonlinear refractive properties of a waveguide, I is the optical pump intensity. The maximum phase shift of the nonlinear phase modulator can be calculated by30:
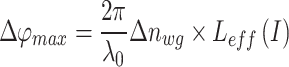 |
5 |
where 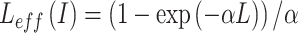 is effective length of the waveguide,
is effective length of the waveguide, 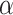 (I) refers to the damping factor of the waveguide.
(I) refers to the damping factor of the waveguide.
Fig. 7.
Schematic of (a) MZI phase modulator, (b) extinction modulator based on the monolayer-TMDCs-on-SOI waveguide.
The all-optical absorption modulator is an optical device used to achieve all-optical domain signal modulation and control without the need for an applied voltage. It utilizes the absorption and nonlinear optical effects of light in materials to realize modulation of optical signals, as shown in Fig. 7b. The optical loss per unit length can be written as
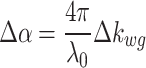 |
6 |
where 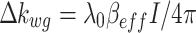 is the variation of the waveguide extinction coefficient, due to maximum and minimum applied local optical intensity,
is the variation of the waveguide extinction coefficient, due to maximum and minimum applied local optical intensity, 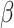 eff denotes the
eff denotes the 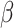 of the waveguide. The maximum extinction change of the nonlinear extinction modulator could be computed as
of the waveguide. The maximum extinction change of the nonlinear extinction modulator could be computed as
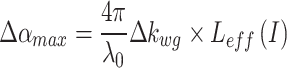 |
7 |
the optical pump intensity used in the following calculation will be much smaller than the saturation term of monolayer TMDCs 2PA31,32, therefore we will ignore the saturation term of monolayer TMDCs 2PA below.
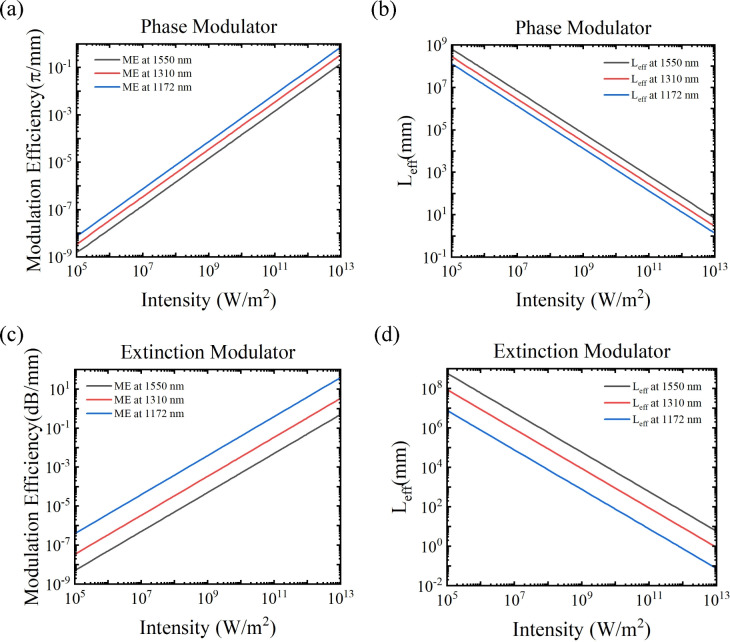
Taking monolayer-MoSe2-on-SOI waveguides as examples, we characterize and optimize the performance of the corresponding all-optical nonlinear modulators at the three representative wavelengths. First of all, we investigate the properties of all-optical nonlinear phase modulators based on MZI. Fig. 8a demonstrates the modulation efficiency of a phase modulator based on monolayer-MoSe2-on-SOI as a function of the optical pump intensity at three characteristic wavelengths, which can be calculated by Eq. 4. It can be observed that since monolayer MoSe2 is a material without saturable absorption, the modulation efficiency increases with increasing optical power without any saturation effects. The modulator based on integrated silicon waveguides with monolayer MoSe2 exhibits modulation efficiencies of 0.73 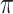 /mm at the
/mm at the 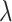 p, 0.35
p, 0.35 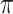 /mm at 1310 nm, and 0.15
/mm at 1310 nm, and 0.15 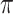 /mm at 1550 nm under an optical pump intensity of 1 GW/cm2. Figure 8b shows the Leff required to achieve a
/mm at 1550 nm under an optical pump intensity of 1 GW/cm2. Figure 8b shows the Leff required to achieve a 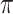 -phase modulation in an all-optical phase modulator under different optical pump intensities at three characteristic wavelengths. Based on a monolayer MoSe2-integrated silicon waveguide all-optical phase modulator, the required Leff to achieve
-phase modulation in an all-optical phase modulator under different optical pump intensities at three characteristic wavelengths. Based on a monolayer MoSe2-integrated silicon waveguide all-optical phase modulator, the required Leff to achieve 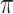 -phase modulation is 1.36 mm, 2.83 mm, and 6.79 mm at the
-phase modulation is 1.36 mm, 2.83 mm, and 6.79 mm at the 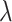 p, 1310 nm, and 1550 nm, respectively, when the optical pump intensity is 1 GW/cm2. In addition to this, we summarize the modulation efficiency and effective modulation length of four monolayer-TMDCs-on-SOI waveguide modulators at an optical pump intensity of 1 GW/cm2 in Tables S4 and S5 (see the Supplementary Material), respectively.
p, 1310 nm, and 1550 nm, respectively, when the optical pump intensity is 1 GW/cm2. In addition to this, we summarize the modulation efficiency and effective modulation length of four monolayer-TMDCs-on-SOI waveguide modulators at an optical pump intensity of 1 GW/cm2 in Tables S4 and S5 (see the Supplementary Material), respectively.
Fig. 8.
(a) Modulation efficiency and (b) effective modulation length of monolayer-MoSe2-on-SOI all-optical phase modulator as a function of optical pump intensity at three characteristic wavelengths. (c) Modulation efficiency and (d) effective modulation length of monolayer-MoSe2-on-SOI all-optical extinction modulator as a function of optical pump intensity at three characteristic wavelengths.
The extinction modulation efficiency of silicon waveguides integrated with monolayer TMDCs can be calculated using Eq. 6. Similar to all-optical phase modulators, the all-optical extinction modulation efficiency increases with increasing optical intensity, as shown in Fig. 8c. For a monolayer-MoSe2-on-SOI waveguide all-optical extinction modulator, the modulation efficiencies under an optical pump intensity of 1 GW/cm2 are 39.92 dB/mm, 3.45 dB/mm, and 0.51 dB/mm at 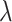 p, 1310 nm and 1550 nm, respectively. Figure 8d illustrates the required Leff for achieving 3 dB extinction modulation in an all-optical phase modulator at three characteristic wavelengths as a function of the optical pump intensity. For an all-optical extinction modulator based on a monolayer-MoSe2-on-SOI waveguide, the required Leff to achieve 3 dB extinction modulation is 5.85 mm, 0.87 mm, and 75
p, 1310 nm and 1550 nm, respectively. Figure 8d illustrates the required Leff for achieving 3 dB extinction modulation in an all-optical phase modulator at three characteristic wavelengths as a function of the optical pump intensity. For an all-optical extinction modulator based on a monolayer-MoSe2-on-SOI waveguide, the required Leff to achieve 3 dB extinction modulation is 5.85 mm, 0.87 mm, and 75 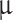 m at the
m at the 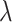 p, 1310 nm, and 1550 nm, respectively, under an optical pump intensity of 1 GW/cm2. Furthermore, we present a summary of the modulation efffciency, effective modulation length and extinction ration of four monolayer-TMDCs-on-SOI waveguide modulators under an optical pump intensity of 1 GW/cm2 in Tables S6, S7 and S8 (see the Supplementary Material), respectively.
p, 1310 nm, and 1550 nm, respectively, under an optical pump intensity of 1 GW/cm2. Furthermore, we present a summary of the modulation efffciency, effective modulation length and extinction ration of four monolayer-TMDCs-on-SOI waveguide modulators under an optical pump intensity of 1 GW/cm2 in Tables S6, S7 and S8 (see the Supplementary Material), respectively.
A comparative performance evaluation was conducted for monolayer-MoSe2-on-SOI waveguide devices against a typical nonlinear graphene-based waveguide. The graphene-on-silicon (GOS) waveguide phase modulator is required to achieve a 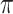 -phase modulation with a modulation length of 1.5 cm under an optical intensity of 0.3 GW/cm2
33. Our designed phase modulator requires a modulation length nearly an order of magnitude smaller than the modulation length required for the GOS waveguide phase modulator under an optical intensity of 1 GW/cm2. Furthermore, the GOS waveguide phase modulator requires 220
-phase modulation with a modulation length of 1.5 cm under an optical intensity of 0.3 GW/cm2
33. Our designed phase modulator requires a modulation length nearly an order of magnitude smaller than the modulation length required for the GOS waveguide phase modulator under an optical intensity of 1 GW/cm2. Furthermore, the GOS waveguide phase modulator requires 220 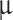 m to achieve 3 dB extinction modulation under an optical intensity of 10 MW/cm2. At the
m to achieve 3 dB extinction modulation under an optical intensity of 10 MW/cm2. At the 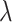 p, the modulation length of our designed modulator is shorter than that required for GOS extinction modulators. Although the optical pump intensity required for our designed monolayer-MoSe2-on-SOI waveguide is slightly higher, our designed waveguides circumvent the issue of linear loss observed in GOS waveguides. Additionally, we have summarized the information in Tables S8 and S9 (see the Supplementary Material). In summary, compared to graphene-based nonlinear modulators, our designed nonlinear modulator based on monolayer MoSe2 exhibits excellent performance in both phase modulation and extinction modulation. The increase in optical intensity allows for a further reduction in the length of the modulator, enhancing flexibility and adjustability in system design. This indicates that monolayer-TMDCs-on-SOI waveguides can achieve compact and efficient optical modulators, supporting applications in the optical communication and networking fields.
p, the modulation length of our designed modulator is shorter than that required for GOS extinction modulators. Although the optical pump intensity required for our designed monolayer-MoSe2-on-SOI waveguide is slightly higher, our designed waveguides circumvent the issue of linear loss observed in GOS waveguides. Additionally, we have summarized the information in Tables S8 and S9 (see the Supplementary Material). In summary, compared to graphene-based nonlinear modulators, our designed nonlinear modulator based on monolayer MoSe2 exhibits excellent performance in both phase modulation and extinction modulation. The increase in optical intensity allows for a further reduction in the length of the modulator, enhancing flexibility and adjustability in system design. This indicates that monolayer-TMDCs-on-SOI waveguides can achieve compact and efficient optical modulators, supporting applications in the optical communication and networking fields.
Conclusion
We investigated the influence of monolayer TMDCs on the nonlinear parameters of silicon photonic waveguides and gold-based DLSPP waveguides over a wide spectral range from the excitonic resonant peak (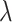 p) to 1550 nm. Taking monolayer MoSe2 as an example, after integrating it into SOI waveguides, we obtained a maximum Re(
p) to 1550 nm. Taking monolayer MoSe2 as an example, after integrating it into SOI waveguides, we obtained a maximum Re(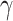 ) of 5001.87 W−1m−1 and a maximum imaginary part of 8910.76 W−1m−1 at the
) of 5001.87 W−1m−1 and a maximum imaginary part of 8910.76 W−1m−1 at the 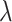 p in the quasi-TE mode. These values exceed those of SOI waveguides without monolayer MoSe2 by more than 7 times and 33 times, respectively. The nonlinear parameters in the quasi-TM mode are much lower than those in the quasi-TE mode, mainly due to the extremely low optical field intensity at the core-cladding boundary where monolayer MoSe2 is located. For the monolayer-MoSe2-in-DLSPP waveguide at the
p in the quasi-TE mode. These values exceed those of SOI waveguides without monolayer MoSe2 by more than 7 times and 33 times, respectively. The nonlinear parameters in the quasi-TM mode are much lower than those in the quasi-TE mode, mainly due to the extremely low optical field intensity at the core-cladding boundary where monolayer MoSe2 is located. For the monolayer-MoSe2-in-DLSPP waveguide at the 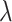 p, optimized geometry yielded a real part of the nonlinear parameter of 119111.94 −1m−1 and an imaginary part of 225534.04 −1m−1, which are 53 times and 262 times larger, respectively, than those of DLSPP waveguides without monolayer MoSe2.
p, optimized geometry yielded a real part of the nonlinear parameter of 119111.94 −1m−1 and an imaginary part of 225534.04 −1m−1, which are 53 times and 262 times larger, respectively, than those of DLSPP waveguides without monolayer MoSe2.
Furthermore, based on the optimized two-dimensional TMDCs-silicon waveguide composite structure, we further investigated the all-optical modulation performance of the monolayer-MoSe2-on-SOI waveguide. Based on a monolayer MoSe2-integrated silicon waveguide all-optical phase modulator, the required Leff to achieve 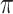 -phase modulation is 1.36 mm, 2.83 mm, and 6.79 mm at the
-phase modulation is 1.36 mm, 2.83 mm, and 6.79 mm at the 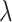 p, 1310 nm, and 1550 nm, respectively, when the optical pump intensity is 1 GW/cm2. For an all-optical extinction modulator based on a monolayer-MoSe2-on-SOI waveguide, the required
p, 1310 nm, and 1550 nm, respectively, when the optical pump intensity is 1 GW/cm2. For an all-optical extinction modulator based on a monolayer-MoSe2-on-SOI waveguide, the required 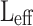 to achieve 3 dB extinction modulation is 5.85 mm, 0.87 mm, and 75
to achieve 3 dB extinction modulation is 5.85 mm, 0.87 mm, and 75 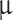 m at the
m at the 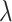 p, 1310 nm, and 1550 nm, respectively, under an optical pump intensity of 1 GW/cm2. Our designed waveguides circumvent the issue of linear loss observed in GOS waveguides. It is worth noting that with increasing optical intensity, the length of the modulator can be further reduced, providing greater flexibility and tunability for system design in practical applications. This implies that integrated waveguides based on monolayer TMDCs can achieve more compact and efficient optical modulators, providing strong support for applications in the optical communication and networks.
p, 1310 nm, and 1550 nm, respectively, under an optical pump intensity of 1 GW/cm2. Our designed waveguides circumvent the issue of linear loss observed in GOS waveguides. It is worth noting that with increasing optical intensity, the length of the modulator can be further reduced, providing greater flexibility and tunability for system design in practical applications. This implies that integrated waveguides based on monolayer TMDCs can achieve more compact and efficient optical modulators, providing strong support for applications in the optical communication and networks.
Methods
The interaction between light and TMDCs within the waveguide optical modes is characterized by the nonlinear parameter. The parameter was calculated using a two-dimensional full-vector finite element method (FEM) in COMSOL Multiphysics 6.0. Simulations were performed at free-space wavelengths of 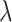 = 1550 nm, 1310 nm, and at the exciton resonance peaks of the TMDCs. In all COMSOL simulations, the monolayer thicknesses were set to 0.97 nm for MoSe2, 0.76 nm for WSe2, 0.71 nm for MoS2, and 0.81 nm for WS2. The waveguide substrate made of SOI was sized at 10
= 1550 nm, 1310 nm, and at the exciton resonance peaks of the TMDCs. In all COMSOL simulations, the monolayer thicknesses were set to 0.97 nm for MoSe2, 0.76 nm for WSe2, 0.71 nm for MoS2, and 0.81 nm for WS2. The waveguide substrate made of SOI was sized at 10 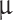 m
m 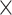 5
5 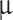 m, with an air (or PMMA) cladding of the same dimensions. Additionally, an 800 nm perfectly matched layer (PML) was placed around the air (PMMA) cladding and SOI substrate to simulate an open boundary with no reflections. The mesh was controlled by the physics-controlled network, with the element size set to ”Extremely fine.”
m, with an air (or PMMA) cladding of the same dimensions. Additionally, an 800 nm perfectly matched layer (PML) was placed around the air (PMMA) cladding and SOI substrate to simulate an open boundary with no reflections. The mesh was controlled by the physics-controlled network, with the element size set to ”Extremely fine.”
Supplementary Information
The supplementary material contains ten supplementary figures, cited in the test as Figs. S1–S10, and four tables, cited as Tables S1–S4.
Supplementary Information
Author contributions
Tianyang Ding conducted simulations and wrote the manuscript. All authors reviewed the manuscript.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-83898-z.
References
- 1.Santos, I., Castro, L., Rodriguez-Fernandez, N., Torrente-Patiño, Á. & Carballal, A. Artificial neural networks and deep learning in the visual arts: A review10.1007/s00521-020-05565-4 (2021).
- 2.Bristow, A. D., Rotenberg, N. & Van Driel, H. M. Two-photon absorption and Kerr coefficients of silicon for 850–2200 nm. [Appl. Phys. Lett.10.1063/1.2737359 (2007). [Google Scholar]
- 3.Chhowalla, M., Liu, Z. & Zhang, H. Two-dimensional transition metal dichalcogenide (TMD) nanosheets. Chem. Soc. Rev.44, 2584–2586. 10.1039/c5cs90037a (2015). [DOI] [PubMed] [Google Scholar]
- 4.Li, W. et al. Ultrafast all-optical graphene modulator. Nano Lett.14, 955–959. 10.1021/nl404356t (2014). [DOI] [PubMed] [Google Scholar]
- 5.Yu, S. et al. All-optical graphene modulator based on optical kerr phase shift. Optica3, 541–544. 10.1364/OPTICA.3.000541 (2016). [Google Scholar]
- 6.He, X. et al. On-chip two-dimensional material-based waveguide-integrated photodetectors. J. Mater. Chem. C12, 2279–2316. 10.1039/D3TC03679K (2024). [Google Scholar]
- 7.Ooi, K. J. A., Ang, L. K. & Tan, D. T. H. Waveguide engineering of graphene’s nonlinearity. Appl. Phys. Lett.105, 111110 (2014). [Google Scholar]
- 8.Flöry, N. et al. Waveguide-integrated van der waals heterostructure photodetector at telecom wavelengths with high speed and high responsivity. Nat. Nanotechnol.15, 118–124. 10.1038/s41565-019-0602-z (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lin, Y. et al. Monolithically integrated, broadband, high-efficiency silicon nitride-on-silicon waveguide photodetectors in a visible-light integrated photonics platform. Nat. Commun.13, 6362. 10.1038/s41467-022-34100-3 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol.7, 699–712. 10.1038/nnano.2012.193 (2012). [DOI] [PubMed] [Google Scholar]
- 11.Koppens, F. H. L. et al. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotechnol.9, 780–793. 10.1038/nnano.2014.215 (2014). [DOI] [PubMed] [Google Scholar]
-
12.Weng, B., Zhang, X., Zhang, N., Tang, Z. R. & Xu, Y. J. Two-dimensional
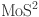 nanosheet-coated
nanosheet-coated 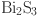 Discoids: Synthesis, formation mechanism, and photocatalytic application. Langmuir31, 4314–4322. 10.1021/la504549y (2015).
[DOI] [PubMed] [Google Scholar]
Discoids: Synthesis, formation mechanism, and photocatalytic application. Langmuir31, 4314–4322. 10.1021/la504549y (2015).
[DOI] [PubMed] [Google Scholar] -
13.Koo, J. et al. Near-infrared saturable absorption of defective bulk-structured
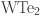 for femtosecond laser mode-Locking. Adv. Funct. Mater.26, 7454–7461. 10.1002/adfm.201602664 (2016). [Google Scholar]
for femtosecond laser mode-Locking. Adv. Funct. Mater.26, 7454–7461. 10.1002/adfm.201602664 (2016). [Google Scholar] - 14.Mueller, T. & Malic, E. Exciton physics and device application of two-dimensional transition metal dichalcogenide semiconductors. npj 2D Mater. Appl.2, 29, 10.1038/s41699-018-0074-2 (2018).
- 15.Zhou, F., Kua, J. H., Lu, S. & Ji, W. Two-photon absorption arises from two-dimensional excitons. Opt. Exp.26, 16093. 10.1364/oe.26.016093 (2018). [DOI] [PubMed] [Google Scholar]
-
16.Zhou, F. & Ji, W. Two-photon absorption and subband photodetection in monolayer
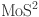 . Opt. Lett.42, 3113. 10.1364/ol.42.003113 (2017).
[DOI] [PubMed] [Google Scholar]
. Opt. Lett.42, 3113. 10.1364/ol.42.003113 (2017).
[DOI] [PubMed] [Google Scholar] - 17.Cunningham, G. et al. Solvent exfoliation of transition metal dichalcogenides: Dispersibility of exfoliated nanosheets varies only weakly between compounds. ACS Nano6, 3468–3480. 10.1021/nn300503e (2012). [DOI] [PubMed] [Google Scholar]
- 18.Liu, H. L. et al. Optical properties of monolayer transition metal dichalcogenides probed by spectroscopic ellipsometry. Appl. Phys. Lett.[SPACE]10.1063/1.4901836 (2014).25565707 [Google Scholar]
-
19.Yim, C. et al. Investigation of the optical properties of
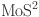 thin films using spectroscopic ellipsometry. Appl. Phys. Lett.104, 103114. 10.1063/1.4868108 (2014). [Google Scholar]
thin films using spectroscopic ellipsometry. Appl. Phys. Lett.104, 103114. 10.1063/1.4868108 (2014). [Google Scholar] -
20.Eichfeld, S. M., Eichfeld, C. M., Lin, Y.-C., Hossain, L. & Robinson, J. A. Rapid, non-destructive evaluation of ultrathin
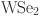 using spectroscopic ellipsometry. APL Mater.[SPACE]10.1063/1.4893961 (2014). [Google Scholar]
using spectroscopic ellipsometry. APL Mater.[SPACE]10.1063/1.4893961 (2014). [Google Scholar] -
21.Park, H. G. et al. Temperature dependence of the critical points of monolayer
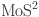 by ellipsometry. Appl. Spectro. Rev.51, 621–635. 10.1080/05704928.2016.1166436 (2016). [Google Scholar]
by ellipsometry. Appl. Spectro. Rev.51, 621–635. 10.1080/05704928.2016.1166436 (2016). [Google Scholar] -
22.Qiu, D. Y., da Jornada, F. H. & Louie, S. G. Optical spectrum of
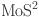 : Many-body effects and diversity of exciton states. Phys. Rev. Lett.111, 216805. 10.1103/PhysRevLett.111.216805 (2013).
[DOI] [PubMed] [Google Scholar]
: Many-body effects and diversity of exciton states. Phys. Rev. Lett.111, 216805. 10.1103/PhysRevLett.111.216805 (2013).
[DOI] [PubMed] [Google Scholar] -
23.Molina-Sánchez, A., Sangalli, D., Hummer, K., Marini, A. & Wirtz, L. Effect of spin-orbit interaction on the optical spectra of single-layer, double-layer, and bulk
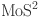 . Phys. Rev. B88, 045412. 10.1103/PhysRevB.88.045412 (2013). [Google Scholar]
. Phys. Rev. B88, 045412. 10.1103/PhysRevB.88.045412 (2013). [Google Scholar] -
24.Liu, H. L. et al. Temperature-dependent optical constants of monolayer
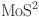 ,
,  ,
,  , and
, and  : spectroscopic ellipsometry and first-principles calculations. Sci. Rep.10, 15282. 10.1038/s41598-020-71808-y (2020).
[DOI] [PMC free article] [PubMed] [Google Scholar]
: spectroscopic ellipsometry and first-principles calculations. Sci. Rep.10, 15282. 10.1038/s41598-020-71808-y (2020).
[DOI] [PMC free article] [PubMed] [Google Scholar] - 25.Zhou, F., Nieva, C. J., Fan, D., Lu, S. & Ji, W. Superior optical Kerr effects induced by two-dimensional excitons. Photon. Res.10, 834. 10.1364/prj.447029 (2022). [Google Scholar]
- 26.Zhang, X., Qiu, J., Li, X., Zhao, J. & Liu, L. Complex refractive indices measurements of polymers in visible and near-infrared bands. Appl. Opt.59, 2337. 10.1364/ao.383831 (2020). [DOI] [PubMed] [Google Scholar]
- 27.Schinke, C. et al. Uncertainty analysis for the coefficient of band-to-band absorption of crystalline silicon. AIP Adv.[SPACE]10.1063/1.4923379 (2015). [Google Scholar]
-
28.Malitson, I. H. Interspecimen comparison of the refractive index of fused silica*,
 . J. Opt. Soc. Am.55, 1205. 10.1364/josa.55.001205 (1965). [Google Scholar]
. J. Opt. Soc. Am.55, 1205. 10.1364/josa.55.001205 (1965). [Google Scholar] - 29.Ji, Y. et al. An electronic Mach-Zehnder interferometer. Nature422, 415–418. 10.1038/nature01503 (2003). [DOI] [PubMed] [Google Scholar]
- 30.Ojaghi, S., Golmohammadi, S. & Soofi, H. All-optical graphene-on-silicon slot waveguide modulator based on graphene’s Kerr effect. Appl. Opt.60, 7945. 10.1364/ao.427755 (2021). [DOI] [PubMed] [Google Scholar]
- 31.Dong, N. et al. Saturation of two-photon absorption in layered transition metal dichalcogenides: Experiment and theory. ACS Photon.5, 1558–1565. 10.1021/acsphotonics.8b00010 (2018). [Google Scholar]
-
32.Zhang, S. et al. Direct observation of degenerate two-photon absorption and its saturation in
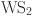 and
and 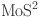 monolayer and few-layer films. ACS Nano9, 7142–7150. 10.1021/acsnano.5b03480 (2015).
[DOI] [PubMed] [Google Scholar]
monolayer and few-layer films. ACS Nano9, 7142–7150. 10.1021/acsnano.5b03480 (2015).
[DOI] [PubMed] [Google Scholar] - 33.Ooi, K. J. A., Leong, P. C., Ang, L. K. & Tan, D. T. H. All-optical control on a graphene-on-silicon waveguide modulator. Sci. Rep.7, 12748. 10.1038/s41598-017-13213-6 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.