Lossless and reference-free compression of FASTQ/A files using GeneSqueeze

Abstract

As sequencing becomes more accessible, there is an acute need for novel compression methods to efficiently store sequencing files. Omics analytics can leverage sequencing technologies to enhance biomedical research and individualize patient care, but sequencing files demand immense storage capabilities, particularly when sequencing is utilized for longitudinal studies. Addressing the storage challenges posed by these technologies is crucial for omics analytics to achieve their full potential. We present a novel lossless, reference-free compression algorithm, GeneSqueeze, that leverages the patterns inherent in the underlying components of FASTQ files to solve this need. GeneSqueeze’s benefits include an auto-tuning compression protocol based on each file’s distribution, lossless preservation of IUPAC nucleotides and read identifiers, and unrestricted FASTQ/A file attributes (i.e., read length, number of reads, or read identifier format). We compared GeneSqueeze to the general-purpose compressor, gzip, and to a domain-specific compressor, SPRING, to assess performance. Due to GeneSqueeze’s current Python implementation, GeneSqueeze underperformed as compared to gzip and SPRING in the time domain. GeneSqueeze and gzip achieved 100% lossless compression across all elements of the FASTQ files (i.e. the read identifier, sequence, quality score and ‘ + ’ lines). GeneSqueeze and gzip compressed all files losslessly, while both SPRING’s traditional and lossless modes exhibited data loss of non-ACGTN IUPAC nucleotides and of metadata following the ‘ + ’ on the separator line. GeneSqueeze showed up to three times higher compression ratios as compared to gzip, regardless of read length, number of reads, or file size, and had comparable compression ratios to SPRING across a variety of factors. Overall, GeneSqueeze represents a competitive and specialized compression method for FASTQ/A files containing nucleotide sequences. As such, GeneSqueeze has the potential to significantly reduce the storage and transmission costs associated with large omics datasets without sacrificing data integrity.

Introduction

The field of genomics, due to advancements in high-throughput sequencing technologies, has experienced a revolution in the past two decades, with almost a million-fold reduction (from 1 billion to hundreds of dollars) in the cost of sequencing¹. The increase in accessibility has led to an increase in the quantity of omics data, with estimations predicting that 2–40 exabytes of data will be generated within the next decade². Unfortunately, storage technology is advancing at a much slower pace, leading to critical technical and economic bottlenecks for omics-based discovery and their applications in biomedical or clinical research. Omics data is essential in personalized medicine, which relies on accurate omics data to extract biomarkers or signatures that can individualize a patient’s preventative measures, diagnoses, treatments, and monitoring³. To be practically used in biomedical research and patient care, omics data needs to be stored, retrieved, and transmitted in a manner that is cost-effective, time-efficient, and lossless for analysis and dissemination. Therefore, specialized compressors for omics data are needed to continue to support advancements in medicine.

Nucleotide-based omics data (i.e., genomics, transcriptomics, epigenomics) are commonly stored in FASTQ or FASTA text-based formats. FASTA format contains a read identifier line followed by either nucleotide or amino acid sequences. These nucleotide sequences can contain the classical A, C, G, and T nucleotides as well as non-ACGT IUPAC nucleotides⁴. Non-ACGT IUPAC nucleotides aid in representing ambiguity in DNA sequences and therefore are often used during the genome assembly process. These bases are useful in metagenomics studies, for use in accurately representing the genetic composition of complex microbial communities^5,6, and in clinical diagnostics—notably in cancer genomics—to denote mutations and genomic variations^7–9. Additionally, in the context of continual discoveries of new species, the need for efficient storage of genome assembly files continues to rise¹⁰. The FASTQ format is derived from FASTA and additionally stores the quality scores output by sequencing platforms (e.g., Illumina) which reflect the level of confidence in the read of each base in a sequence³. The maintenance of quality scores during storage is critical for analyses such as variant detection, in which accuracy and reliability of the base calls are foundational^11,12. Both FASTA and FASTQ files can be large, particularly for high-coverage sequencing data, which makes them difficult to store and process efficiently. Therefore, FASTQ/A files are routinely compressed for more practical storage, management, and transfer. The similarities in structure between FASTA and FASTQ files led us to develop one algorithm which can be utilized across both file types, accommodating the non-ACGT IUPAC bases that are specifically noted in FASTA files.

The current standard practice for FASTQ/A compression across the omics industry is the general compressor gzip¹³, a general-purpose algorithm that combines Huffman encoding¹⁴ and LZ77¹⁵ to create a dictionary tailored to the frequency of word repetitions in the data. Unfortunately, gzip performs poorly on genomic data compression when compared to omics domain-specific compressors^16–18, which leverage the inherent repetitive characteristics of FASTQ files. Despite this, gzip remains the de facto standard in the biomedical research domain due to its stability and popularity. gzipped files are accepted as input by various sequencing analysis tools and are used by public repositories of genomic data¹⁹. However, domain-specific algorithms that leverage the redundancy in FASTQ files have shown promise in reducing storage volume by achieving high compression ratios while maintaining high accuracy for downstream analysis. As clinical utilization of omics data increases, it appears likely that a need for highly accurate, domain-specific compression algorithms with great compression abilities will arise.

Various domain-specific genomic data compressors such as FaStore²⁰, SPRING¹⁶, FQSqueezer²¹, PetaGene²², Genozip²³, ColoRd²⁴, repaq²⁵, DSRC^18,26, and MZPAQ²⁷ have shown significant promise in addressing data size challenges within the domain. Unfortunately, each of the existing domain-specific compression methods exhibit one or more drawbacks which have precluded their widespread adoption in the space. Examples of these drawbacks include relatively poor compression ratios^18,25–27, large memory and time requirements²¹, loss of read order²⁰, lossiness for non-ACTGN IUPAC bases¹⁶, and not being open source^22,23. As such, there is still a need for efficient domain-specific methods for next-generation sequencing (NGS) data compression.

Given the needs of the field, we chose to create a novel reference-free compressor, GeneSqueeze, which uses read-reordering-based compression methodology¹⁴ to maximally compress FASTQ files while maintaining complete data integrity, as verified by MD5²⁸ matching. To assess GeneSqueeze’s functionality as compared to the field, we chose to examine its performance as compared to the industry standard compressor, gzip¹³, and SPRING¹⁶, a ‘state of the art’³ open source compressor which supports lossless compression (with the exception of certain cases such as FASTQ/A files containing rare IUPAC nucleotides or specific read identifier formats), and has fast speeds and small compression ratios^11,27.

GeneSqueeze algorithm

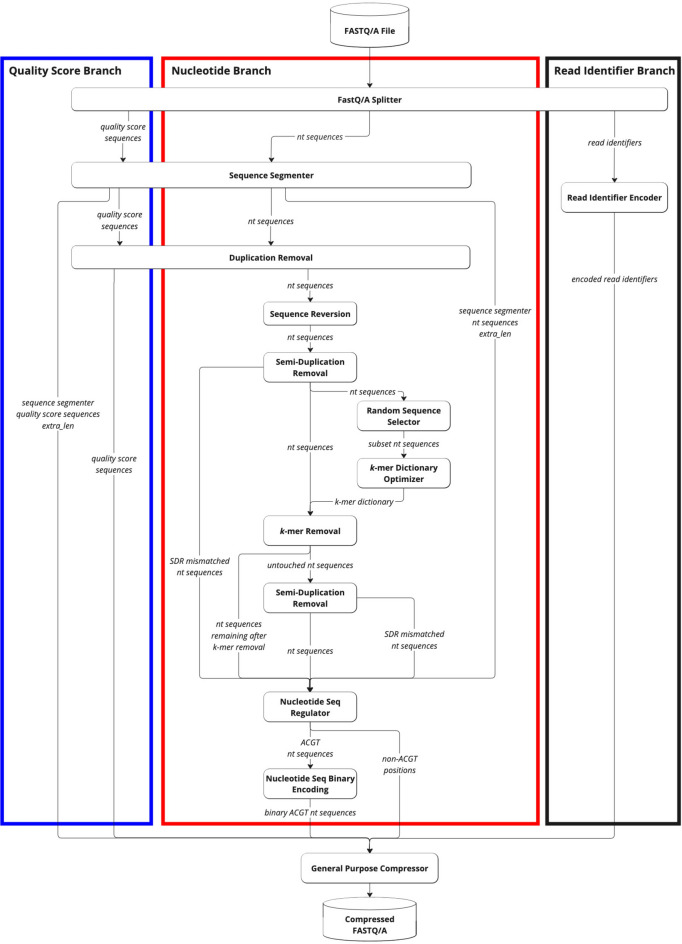
The GeneSqueeze algorithm is designed to fully leverage the inherent repetitions of FASTQ/A files and thus independently reduces the instances of k-mers within the nucleotide sequences prior to further compression of the nucleotides, quality scores, and read identifier sequences using a general compressor (Fig. 1) Within each branch of the algorithm, specific groups of activity are described as ‘blocks’ to provide greater clarity of overall function. Each block is explained below. Additionally, the GeneSqueeze algorithm processes each file independently, under the assumption that files will have a more similar distribution of sequences within a file than within a dataset containing multiple files from multiple disparate samples from disparate sources.

Fig. 1.

GeneSqueeze compression flow-diagram. A diagram depicting the overall methodology of the GeneSqueeze algorithm. A blue outline denotes the quality score branch, a red outline indicates the nucleotide sequence branch, and a black outline designates the read identifier branch. The duplication removal, semi-duplication removal, k-mer removal, and nucleotide sequence regulator all output auxiliary information, which refers to all of the information necessary to losslessly decompress the file.

FASTQ/A splitter

The GeneSqueeze algorithm begins with the FASTQ/A Splitter block which loads and reads the FASTQ/A files to memory. As FASTQ/A files can be large, the FASTQ/A Splitter block breaks large files (≥ 50 GB) into smaller sub-files to facilitate their loading into memory. Once files are in memory, the files are then parsed into their nucleotide sequences, read identifiers, and quality score sequences (for FASTQ only). For large datasets, all sub-files proceed through the algorithm individually and are restored to the single original FASTQ/A file during the decoding step.

Sequence segmenter

Once FASTQ/A file components are held in their own lists, the Sequence Segmenter splits nucleotide sequences and quality score sequences from longer reads into smaller segments. The Sequence Segmenter is designed this way for two reasons: (1) similar to our design to split files into chunks small enough to hold in memory, our Sequence Segmenter splits reads into lengths small enough to be held in memory and which our algorithm can easily process and enables the algorithm to be functional across all read sizes, (2) our preliminary studies found that there exists an ideal sequence segment length (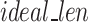) for maximal GeneSqueeze compression efficiency.

Utilizing a fixed value for the hyperparameter 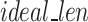, the Sequence Segmenter then calculates the number of segments (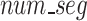, Eq. 1) each sequence will be split into and the length of each segment (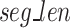, Eq. 2).

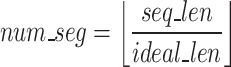1

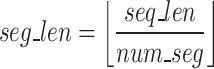2

The algorithm necessitates all segments are of equal length for use in downstream blocks and thus, if 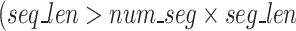), the remainder ( 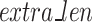characters, Eq. 3) of the sequences are separated and concatenated together to make a long sequence to be processed separately.

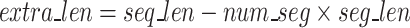3

The following is a numerical example:

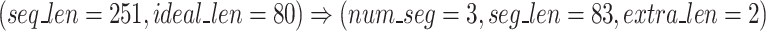After processing the nucleotide and quality score components to the desired lengths, these components of the FASTQ/A file are sent to their specific branches of the GeneSqueeze algorithm for further processing.

Nucleotide compression branch

The segmented nucleotide sequences are passed to the nucleotide sequence compression branch of the algorithm, which consists of the following blocks: Duplication Removal (DR), Sequence Reversion, Random Sequence Selector, k-mer Dictionary Optimizer, k-mer Removal, Semi-Duplication Removal (SDR), Nucleotide Sequence Regulator, and Nucleotide Sequence Binary Encoding. This branch utilizes block-constrained read-reordering-based methodology to reduce computational load while maintaining overall read order¹⁵.

Duplication removal (nucleotide branch)

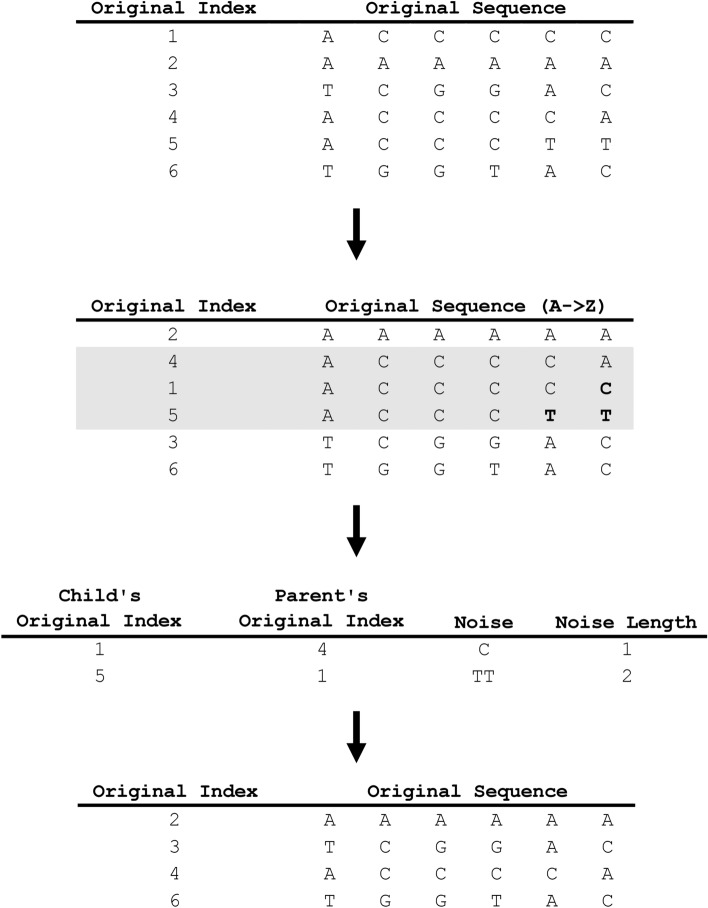
The nucleotide branch begins with the Duplication Removal block, which finds, groups, encodes, and removes all duplicative reads within a given set of sequences. The duplication removal workflow (Fig. 2) first creates an array containing all sequences and a temporary index value, called original_index, for each sequence, to preserve a reference to the original sequence order. The sequences are then sorted alphabetically and identical sequences are grouped. Within a group of identical sequences, the first instance of a sequence is labeled as a parent sequence and any subsequent instances of the same sequence are designated as child sequences. Parent sequences with child sequences are given a separate designation from parent sequences without any associated child sequences. This designation is stored in the dr_identifier variable to enable the retrieval of all parent and child sequences during decompression. The child sequences are then removed from the sequences array, followed by the re-sorting of the parent sequences using their original indices, prior to deletion of the original_index.

Fig. 2.

GeneSqueeze duplication removal process. An example of this process is depicted, showing the initial creation of an index for the original order of the sequences. The process then illustrates the alphabetical re-ordering of the sequences based on the first nucleotide of the sequence, and the retention of the original index position of each sequence. The original index position of duplicate sequences is then associated with the original index identifier for the sequence that is the initial occurrence of the duplicate sequences (the ‘parent’ sequence). The duplicate sequences are then removed from the data frame, and an index of the original identifiers, and the duplication removal identifiers is created to store the identity and relationships between the retained sequences and any removed duplicate sequences. S denotes a parent with no duplicates. M denotes a parent with duplicate ‘child’ sequences. For the duplicated sequences, the DR_Identifier indicates the original index identifier of their parent sequence.

The pseudocode presented below shows the duplication removal process:

The dr_identifier is encoded as a string and directed to the General-Purpose Compressor and the parent sequences are passed to the Sequence Reversion and then to the Semi-Duplication Removal (SDR) blocks for further processing.

Semi-duplication removal (SDR)

The semi-duplication removal block finds similar, but not identical, nucleotide sequences, in order to encode their similarities and differences to enable removal of the similar subsequences within each group in a manner that efficiently reduces the compression ratio. The semi-duplication removal workflow is depicted in Fig. 3. In this context, two subsequences are considered semi-identical if their initial non-identical character falls within a certain number of characters from their respective beginnings, defined as the sdr_threshold.

Fig. 3.

Semi-duplication removal (SDR) process. An example of this process is depicted, showing the creation of an array of sequences and their associated indices. The sequences are then sorted alphabetically while retaining their original indices (OI). Semi-duplicative sequences are identified and grouped (grey background). Within the semi-duplicative sequence group, the first sequence (OI #4) is identified as the first parent sequence, with the second sequence (OI #1) as its child sequence. The mismatch between parent OI #4 and child OI #1 is C, which is encoded as noise. The SDR block then identifies OI#1 as a parent to OI#5 with a mismatch of TT, which is encoded as the child’s noise. The child sequences are then removed from the array, with the parent sequences and their original indices retained as the output of the SDR block.

In SDR operation, the sequences are first ordered alphabetically while retaining their original indices. Once sorted, semi-duplicate nucleotide sequences are referred to as groups. For each group, the first instance of the sequence is designated as the parent sequence and is assigned a parent_index. The remaining semi-duplicate sequences within the group are designated as the child_sequences. Each child sequence is assigned a child_index associated with the parent_index to which it belongs. GeneSqueeze then examines the non-identical nucleotides between the parent sequence and the child sequence. GeneSqueeze identifies the first non-identical character in the child sequence and encodes the sub-subsequence from the first non-identical character to the last character of the sequence as noise (noise). The GeneSqueeze algorithm continues to iterate through the group, identifying noise between the first child and its parent and between any subsequent child with its preceding child. The length of the noise_sequence is also encoded as noise_length. Noise length along with child identifier indices are passed to the General-Purpose Compressor (noise_length, child_index). Meanwhile, the noise_sequences are directed to the Nucleotide Sequence Regulator block. Finally, the parent_sequences are resorted using their original indices and directed to either the Sequence Reversion or the Nucleotide Sequence Regulator, for the first or second SDR operation, respectively.

The pseudocode presented below shows the semi-duplication removal process:

FUNCTION semi_duplication_removal(sequences, sdr_threshold).

1. Convert sequences to an array.

2. Sort the sequences and keep track of their original indices.

3. Calculate the differences between adjacent sorted sequences.

4. Prepare data structure to store information about sequences, groups, noise sequence, and noise lengths.

5. Create groups of sequences based on the cut points.

6. Identify the first sequence in each group as parent sequence and rest of the sequences as child sequences.

7. Calculate the noises between each sequence and its previous sequence for each group.

8. Calculate the length of obtained noises.

9. Build a DataFrame to organize the information for the child indices.

10. Sort sequences by original indices.

11. Extract the indices of the child sequences as child indices.

12. Join noise sequences as a single string.

13. Return the child indices, noise lengths, noise sequences, and the parent sequences.

Sequence reversion

As mentioned in the semi-duplication removal block, the GeneSqueeze SDR block is crafted to identify and eliminate sequences that exhibit semi-duplication at the beginning of a sequence. To ensure the maximum removal of semi-duplicate sequences across the entire sequence, this block reverses the sequences prior to sending the sequences back through the SDR block. After passing through SDR, the output parent sequences are reverted to their original orientation using the Sequence Reversion block before being sent to the k-mer Dictionary Optimizer. The Sequence Reversion block is only utilized for the first instance of the SDR process.

Random sequences selector

To reduce computational load, we utilized the random sequence selector block, which randomly selects a subset of nucleotide sequences to be used in the k-mer dictionary optimizer block. The percentage of sequences selected is defined by the hyperparameter, random_subset %.

k-mer dictionary optimizer

The k-mer dictionary optimizer block utilizes a k-mer dictionary to encode k-mers by replacing the k-mers with short indices to maximize the compression ratio. Theoretically, the k-mer dictionary could contain many k-mers of numerous k lengths. Given the myriad of potential combinations, the creation and storage of this dictionary can be an expensive process. There is a trade-off between the optimal length k of each k-mer, the optimal frequency of k-mers, and the optimal total number of k-mer–index pairs in the k-mer dictionary. The elimination of longer k-mers can result in larger deletions overall, but only if these k-mers are sufficiently high in frequency. Removing shorter k-mers results in removing less information per sequence; however, given their higher likelihood of occurrence, removal of high frequency short k-mers can lead to a greater number of nucleotides being eliminated. The addition of each k-mer to the dictionary adds to the dictionary length and increases the total amount of data required for compression. Given this intrinsic linkage, these factors require simultaneous computation. Additionally, the problem is further complicated by the removal of each k-mer sequence from the original sequences, as this may affect the frequency of other k-mers within the remaining sequences. This requires the algorithm to iteratively select the ‘best’ remaining k-mer to add to the k-mer dictionary. Moreover, the removal of k-mers from within a read often leaves a preceding sequence and a succeeding sequence, which are henceforth referred to as prefix and suffix sequences, respectively.

Overall, this leads to a complex multi-objective optimization problem which balances k-mer length, k-mer frequency, and both prefix and suffix length and content to maximize compression ratio and reduce the computational costs of compression. Importantly, the storage space required for both the k-mer dictionary and the additional encoding information needed for k-mer removal must not exceed the space saved by removing the k-mers. This constraint provides ideal stopping criteria for the algorithm.

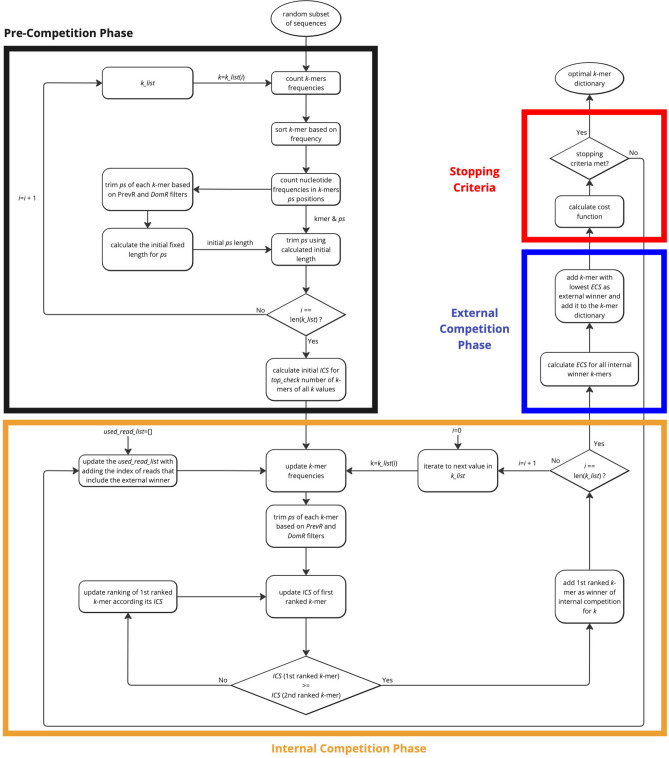
Given the numerous coupled factors and computational iterations involved in k-mer dictionary creation, the GeneSqueeze algorithm works to reduce overall computation requirements by identifying the k-mer dictionary from the randomly selected sequences generated by the Random Sequence Selector in the following 4 main phases: the pre-competition phase, the internal competition phase, the external competition phase, and stopping criteria phase as depicted in Fig. 4.

Fig. 4.

GeneSqueeze k-mer dictionary optimizer process. A sequence diagram depicting the methodology of the k-mer dictionary optimization flow diagram. The black block denotes the Pre-Competition Phase. The orange block outlines the Internal Competition Phase. The dark blue block indicates the external competition phase, and the red block depicts the Stopping Criteria Phase.

The k-mer dictionary optimizer block’s pre-competition phase creates an initial list of k-mers utilizing the sequences output by the Random Sequence Selector. A pre-selected list of k values, referred to as k_list, is used for the k-mer selection process. As previously noted, there exists a trade-off between the length of the k-mer (k) and the frequency of the k-mers. Correctly balancing the interplay between these values is crucial to ascertain the optimal k-mers. As sequencing is related to sequences from the genome, the k-mers and their preceding and succeeding sequences should align to specific locations in a reference genome. This means they are inherently not randomly distributed, meaning that when we expand our examination from the k-mers to the surrounding sequences, it is likely that we will find highly similar sequences. This biological context can be leveraged in the optimization process to further reduce the compression ratio. Henceforth, we refer to a k-mers preceding sequence as the prefix, and their succeeding sequences as the suffix, with the goal of removing the most highly represented similar sequences (prefix—k-mer—suffix) to enhance compression ratio (example in Fig. 5).

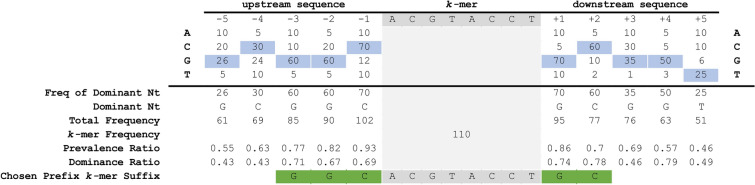
Fig. 5.

GeneSqueeze prefix and suffix identification process. An example is depicted with prevalence_ratio_threshold = 0.6 and dominance_ratio_threshold = 0.5. Grey highlight indicates the selected k-mer. Blue highlight indicates the dominant nucleotide at each position before and after the selected k-mer. Nucleotides highlighted in green are shown to have surpassed both the prevalence ratio and dominance ratio thresholds and have been selected as the k-mer prefix and suffix.

To decide which k-mer sequence of length k is more qualified to be added to the k-mer dictionary, we begin by calculating the frequencies (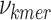) of all the individual k-mers of length k in the dictionary. GeneSqueeze then ranks each k-mer based on their frequency to obtain a ranked k-mer list. The top ranked k-mers, which are the number of k-mers defined by the hyperparameter top_check, then proceed to the prefix and suffix sequence identification stage.

To identify which prefix and suffix sequences are most highly represented within all sequences, we first calculate the prevalence_ratio (Eq. 6) for each nucleotide (A, C, T, G) at each position in the concatenated prefix and suffix sequence, 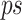, associated with every instance of a given k-mer using Eq. 4, wherein the prevalence_ratio (PrevR) for position i ( 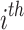character) of the 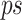, , 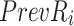is defined as the total frequency of the nucleotides A, C, T, or G in position i , 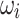, over the frequency of the k-mer itself, .

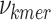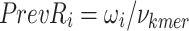4

To maximize the number of potential removed prefix and suffix sequences, we then identify the nucleotide which is most prevalent in a given position within 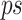using Eq. 5, the dominance_ratio (DomR) equation, in which the DomR for position i of concatenated prefix and suffix, 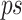, is the frequency of the dominant nucleotide at position i, 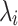, over the total frequency of all bases in position i of the concatenated prefix and suffix of the k-mer affix, 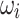. An example is shown in Fig. 5.

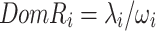5

Unlike k-mers, which our algorithm requires to be 100% identical, GeneSqueeze does not constrain the prefixes and suffixes of a prefix–k-mer–suffix sequence to be identical to the prefix–k-mer–suffix sequence in the optimal k-mer dictionary. Instead, the GeneSqueeze algorithm encodes the non-identical nucleotides in the ps sequence as noise. GeneSqueeze utilizes a prevalence_ratio_threshold and a dominance_ratio_threshold for PrevR and DomR, respectively, to ensure that the chosen ps sequence will lead to sufficient compression even including the resultant encoded noise.

The length of the final ps sequences of the top ranked k-mers of length k is then averaged and assigned as the initial ps length for all k-mers. This averaged calculation aids in the reduction of computational load across the dataset, as calculation of all true optimal ps sequences would be computationally expensive.

An internal competition score (ICS), is calculated for each prefix–k-mer–suffix of length k to estimate the optimality of removing these prefix—k-mer—suffix subsequences from each sequence. In the ICS equation, as defined in Eq. 6, 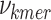represents the frequency of a k-mer, 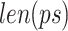represents the length of the concatenated prefix and suffix sequences (ps), and 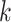represents the length of the k-mer. The optimal k-mer for each k value in the k_list is defined as the prefix–k-mer–suffix sequence with the highest ICS.

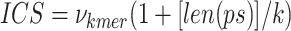6

After initialization of the ps length, all of the k-mers then enter the internal competition phase. In the first step of the internal competition phase, the true ICS value is calculated for the top ranked k-mer. The top ranked k-mer’s ps length is again calculated using the PrevR and DomR equations prior to calculation of the k-mers’ ICS. The ICS of the top ranked k-mer is then updated and compared to the averaged initialized ICS of the second ranked k-mer. If the top ranked k-mer’s ICS is greater than the ICS of the second ranked k-mer, then the top ranked k-mer is declared the winner of the internal competition and sent to the external competition phase. If the recalculation using the updated ps length for the top ranked k-mer leads to the top ranked k-mer’s ICS being less than that of the second ranked k-mer’s ICS based on the second ranked k-mers initialized ps length, then the top ranked k-mer is moved to its new ranking in the list and all k-mers now above the inserted k-mer are promoted. This means the second ranked k-mer is promoted to the first ranked position, the third ranked k-mer is promoted to the second rank position, and the internal competition restarts between the new first and second ranked k-mers. The internal competition process concludes with a declaration of an internal competition winner when the first ranked k-mer’s ICS ranking is greater than the second ranked k-mer, as depicted in the internal competition phase section of Fig. 4.

The winners of each internal competition (one winner for each k value in the k_list) then participate in an external competition to determine the overall optimal k-mer for inclusion in the k-mer dictionary. This external competition evaluates which k-mer among the most qualified candidates from all k-values in the k_list is most suitable for inclusion in the final optimal k-mer dictionary, using the external competition score (ECS), which is defined in Eq. 7.

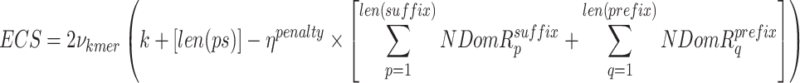7

where, 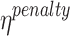is the penalty factor for the fraction of nucleotides that do not match the prefix and/or suffix, 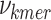represents the frequency of the k-mer, 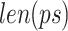represents the length of the concatenated prefix and suffix sequences ps, 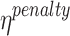represents the cost of encoding prefix and/or suffix mismatch (i.e. noise), and NDomR is defined in Eq. 8 as the non-dominance ratio for position i of ps and where DomR is the dominance ratio for position i of ps. The NDomR identifies all the locations in the ps for a given k-mer where mismatches will be found and thus noise will need to be encoded; as such, NDomR acts as a penalty against the given k-mer.

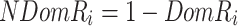8

The winning prefix–k-mer–suffix sequence of the external competition is added to the optimal k-mer dictionary. The external winner is then removed from the list of candidate k-mers that are available to participate in future internal competitions and all sequences which contain the winning k-mer are removed from the future internal competition rounds. The removal of these sequences may alter the frequencies of the remaining k-mers. Consequently, for each k value within the k_list, the internal competition process continues to update the frequency of the highest ranked k-mer (i.e. the k-mer with the highest ICS in the previous round who did not win the external competition) and revise its ICS value after the external competition winner k-mer is removed. The external competition phase is then repeated to identify the next external winner, which will be the next k-mer added to the optimal dictionary.

This process persists until one of the following stopping criteria is fulfilled:

1. The number of consecutive cycles with an increase in cost function score exceeds the tolerance_threshold.

2. The length of the k-mer dictionary reaches the limit set in hyperparameter max_dict_len, which defines the maximum allowed length of the k-mer dictionary.

The cost function, referred to as the 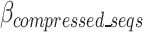, is defined in Eq. 9 and further expanded into component equations in Eqs. 10–19. The 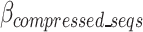equation is designed to provide an estimation in bits, assuming all bases are regular (A,C,T,G) of the encoded size ( 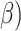of the 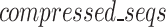as a function of 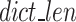for the existing distribution of k-mers in the FASTQ/A file. GeneSqueeze allows for temporary increases in the 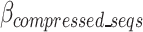over a set number of cycles, set in the hyperparameter tolerance_threshold, assuming that temporary increases in 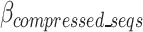may be resolved after the removal of an additional k-mer. When the number of consecutive cycles in which 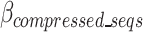is greater than the tolerance_threshold , all competitions are stopped and all k-mers which when added to the k-mer dictionary led to an increase in the cost function over the tolerance_threshold are removed. The optimal k-mer dictionary is now finalized and the finalized dictionary is sent to the k-mer Removal block.

The 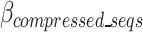is defined in Eq. 9, where 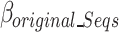represents the estimated size of encoding all remaining original sequences as defined in Eq. 10, 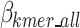represents the estimated size to encode all k-mers, and 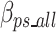represents the estimated size to encode all ps sequences as defined by Eq. 17.

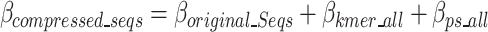9

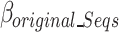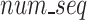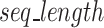Equation 10 defines as the estimated size of the binary-encoded input nucleotide sequences of this block in bits in which and are the number and length of the input nucleotide sequences, respectively.

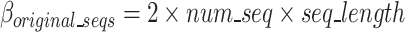10

Equation 11 defines 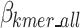as the estimated size of encoding of all k-mers that are selected and included in the optimal k-mer dictionary, where 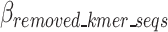represents the total bit size of all removed k-mer sequences as defined in Eq. 12, 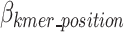represents the bits required to encoded each k-mers position as defined in Eq. 13, 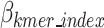represents the bits encoded for each index as defined in Eq. 14, 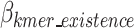represents the total bits of the 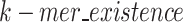binary vector of length 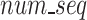to show which nucleotide sequence includes any k-mer of the final dictionary as defined in Eq. 15, and 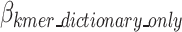represents the bits required to encode k-mers into the optimal k-mer dictionary, as defined in Eq. 16.

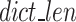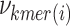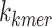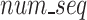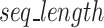In Eqs. 12–16, HI stands for the binary code length of Huffman encoded k-mer in k-mer dictionary, denotes the number of k-mers added to the dictionary, denotes the frequency of each k-mer, represents the length of a given k-mer, and are the number and length of the input nucleotide sequences, respectively.

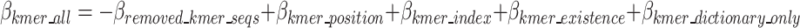11

In Eq. 11, the contribution of removed k-mers to the encoding size (compared to a scenario without these k-mers having been removed) is negative, hence the negative sign for 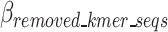which indicates it is better to remove k-mers and encode the relevant information to decode the k-mers as opposed to encoding the original sequence. Conversely, the remaining k-mer elements, which need to be encoded into the compressed file, are positive and are calculated in Eqs. 13–16. Meanwhile, the absolute value of 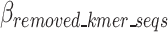is calculated in Eq. 12.

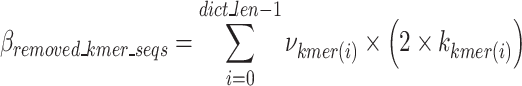12

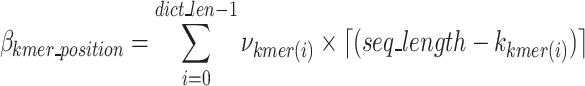13

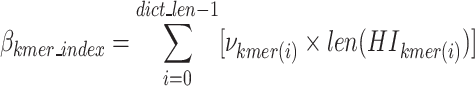14

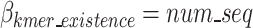15

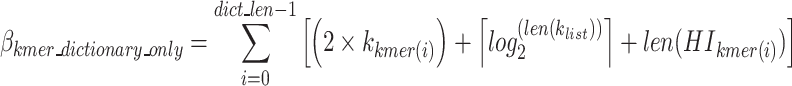16

Equation 17 defines 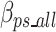as the estimated size required to encode all of the concatenated prefixes and suffixes sequences (ps) associated with the k-mers defined in the optimal k-mer dictionary, where 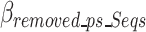represents the bits of the ps sequences removed from the final sequence array, 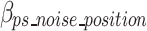represents the bits for all the information encoded as noise for a given ps, 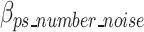represents the bits the number of mismatched ‘noise’ nucleotides in a ps sequence, 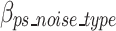represents the bits for storing the noisy nucleotides in the ps sequence, 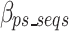represents the bits not used to store the removed sequences penalized by the bits necessary to store all non-dominant nucleotides as noise as defined in Eq. 18, and.

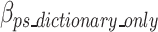represents the bits necessary to store the ps sequences in the optimal k-mer dictionary. Similar to the removed k-mers in Eq. 11, the contribution of removed prefix and suffix nucleotides to the ultimate encoding size is negative compared to a scenario without the removed prefix and suffix nucleotides, which is why 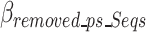has a negative sign in Eq. 17.

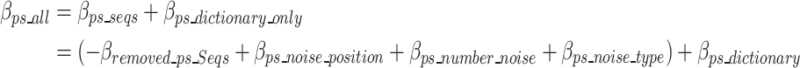17

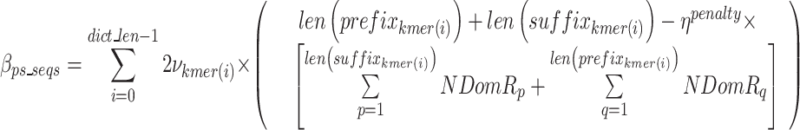18

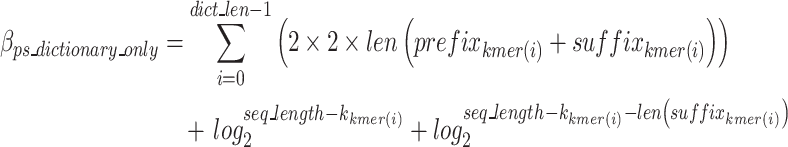19

Once the stopping criteria is met and the optimal k-mer dictionary is found, the GeneSqueeze algorithm sends the optimal k-mer dictionary and the current non-duplicative, non-semi-duplicative array of nucleotides sequences to the k-mer Removal block for removal of k-mers.

K-mer removal

The k-mer removal block utilizes the final k-mer dictionary to remove duplicative k-mers in the sequence array. The function first checks each nucleotide sequence of the input sequences to determine if there is a full match for the k-mers in the finalized dictionary. If there is a match, it removes the prefix–k-mer–suffix sequence and encodes its existence (one bit per nucleotide sequence), the k-mer index, the k-mer position in original nucleotide sequence and its index (dictionary value), as well as any noise in the prefix and suffixes. After removal of the prefix–k-mer–suffix sequence, the subsequences before and after the removed part of the sequence are concatenated and sent to the Nucleotide Sequence Regulator block. The untouched nucleotide sequences (nucleotide sequences with no identified k-mers) are passed to the Semi-Duplication Removal block to remove any additional semi-duplicative sequences. The indices, positions, and other values necessary to encode the removed prefix–k-mer–suffix sequences are sent to the General-Purpose Compressor block. An example of the k-mer removal process is shown in Fig. 6.

Fig. 6.

GeneSqueeze k-mer removal process. An example of the k-mer removal process is depicted, illustrating the identification and encoding of k-mers, as well as the outcome for sequences that contain no k-mers (untouched sequences) or mismatches (post k-mer removal nt). The initial array shows the original indices and original sequences, with the k-mers highlighted in yellow, the prefixes and suffixes highlighted in green, and noise highlighted in red. The second array illustrates the k-mer dictionary. The third table illustrates the presence or absence of k-mers in each sequence, as well as the position and type of any noise detected in each sequence.

Nucleotide sequence regulator

This block encodes any nucleotides other than A, C, G and T. The input for this block is the output of all other blocks that are in the nucleotide sequence branch. Given that the predominant characters in nucleotide sequences are usually A, C, G, and T, and considering that four characters can be encoded using only two bits in binary, this block encodes the information of non-ACGT characters separately and then replaces them with A in the nucleotide sequence. Therefore, the output of this block is the nucleotide sequences that only include A, C, G and T, as well as the position of non-ACGT characters. They are directed to Nucleotide Sequence Binary Encoding and General-Purpose Compressor blocks, respectively.

This block assumes by default that all irregular (non-ACGT) nucleotides characters are N- (which is the most common irregular nucleotide) and encodes their nucleotide sequence position. In cases where any irregular non-N nucleotide is observed, its actual character is also encoded in addition to the position.

Nucleotide sequence binary encoding

The nucleotide sequences are then encoded in binary using the hash table presented in Table 1. As mentioned in the Nucleotide Sequence Regulator block, irregular nucleotides are encoded as A: [0 0] since their information is recorded separately. The hash table is then sent to the General-Purpose Compressor block for further compression.

Table 1.

Nucleotides binary encoding hash table.

Nucleotide	Binary code
A	00
C	01
G	10
T	11

Quality score compression branch

The segmented quality scores are passed to the quality score compression branch of the algorithm, which has one block dedicated to duplication removal.

Duplication removal (quality score)

After quality scores are segmented in the Sequence Segmenter block, they proceed through the duplication removal block. This block searches across the quality score sequences to find and group identical sequences and encodes only the first instance of a specific quality score sequence of each group, which is designated as the parent sequence. The other sequences of each group are designated as child sequences following the same methodology as defined in the nucleotide compression Branch. The encoded files are sent to the general-purpose compressor.

Read identifier compression branch

The segmented read identifiers are passed through the read identifier compression branch of the algorithm which has one block in which the read identifiers are encoded.

Read identifier encoder

The read identifier encoder block stores the first read identifier. The block then identifies which portions of the identifier are fixed or variable and subsequently encodes only the change in variables for each ensuing read. The encoded information is then sent to the general-purpose compressor to be further compressed.

General-purpose compressor

All the generated files are then sent to a general-purpose compressor to achieve a higher compression ratio. GeneSqueeze uses BSC, which is a general-purpose compressor built based on the Burrows–Wheeler Transform (BWT)²⁴.

Methods

Dataset

We tested the performance of each compression algorithm on a collection of 283 FASTQ files totaling 1572 GB (uncompressed). The largest file size was 56 GB and the longest read length was 202 bases. The full list of the datasets used for experiments is found in Supplemental Table 1 and the ranges for read length (Table 2), number of reads (Table 3), and file size (Table 4) can be found in Tables 2, 3 and 4, respectively. In the following experiments using GeneSqueeze, each FASTQ file is compressed independently. The characteristics of each dataset can directly affect the performance of a compression algorithm, thus the algorithm performance was analyzed in the context of each dataset’s characteristics. Natively, these datasets contained N nucleotides but did not contain non-N irregular nucleotides, thus to test the losslessness of non-N irregular IUPAC nucleotides, two N characters were replaced with non-ACGTN IUPAC characters in a FASTQ file.

Table 2.

FASTQ file size (GB) of the datasets used for experiments.

FASTQ file size (GB)	Number of files
0–4	156
4–8	75
8–12	48
54–57	4

Table 3.

Number of reads (million reads per sample) of the datasets used for experiments.

Number of reads (million reads per sample)	Number of files
1–20	172
20–35	40
35–65	67
215–224	4

Table 4.

Read length (nucleotide sequence) of the datasets used for experiments.

Read length (nucleotide sequence)	Number of files
35–36	106
50–51	107
100–101	63
202	7

Resource conditions

We utilized SPRING version 1.1.1 in lossless mode, enabling the lossless compression of non-ACTGN IUPAC nucleotides and gzip version 1.9. All results were generated using a n2-highmem-80 virtual machine on Google Cloud Platform, equipped with 80 cores (vCPUs), 640 GB of RAM, and 600 HDD, facilitating the concurrent processing of files.

Hyperparameters

The values of the hyperparameters for GeneSqueeze are presented in Table 5. GeneSqueeze’s k-mer Dictionary Optimizer block selected the optimal length of the k-mer dictionary and the k-mers via the optimization process presented in the Methods section (k-mer Dictionary Optimization block). In the current version of GeneSqueeze, we employed a static value for the rest of the hyperparameters. Our current use of this static value is not optimized. As such, our future directions include upgrading the algorithm to dynamically determine and adapt the values of the hyperparameters for each dataset or sample to further improve our compression ratios.

Table 5.

Hyperparameter values used by the GeneSqueeze algorithm.

Hyperparameter	Value
k_list	[10, 25]
random_subset	1%
EI_threshold	0.1
DI_threshold	0.5
tolerance_threshold	10
max_dict_len	64
top_check	10
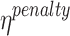	6
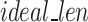	80
sdr_threshold (1st SDR block)	5
sdr_threshold (2nd SDR block)	10

Evaluation metrics

We measured the performance of GeneSqueeze against gzip and SPRING using the evaluation metrics presented in Eqs. 20 and 21:

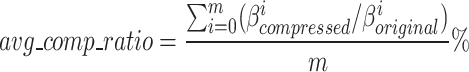20

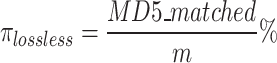21

where 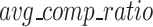and 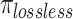are average compression ratio (%) and losslessness ratio (%), respectively. Here, 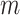represents the total number of FASTQ files in the test set, while 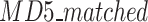denotes the number of files with matched MD5 sums. The metric compression ratio was chosen to assess the total reduction in file size after compression, and losslessness ratio was chosen to understand if total data integrity was preserved after compression. These represent important factors in the overall efficiency and integrity of each compression algorithm.

Results

All three algorithms were able to significantly compress the datasets. The individual metrics for all 273 files in the dataset across all algorithms can be found in Supplementary Table 2. Overall, the average compression ratios of SPRING and GeneSqueeze were similar (7.61% vs 7.70%), and both were significantly lower than gzip (21.20%) (Table 6). FASTQ files can vary in size, number of reads, and read length, which were characteristics that we hypothesized could lead to changes in algorithmic efficiency.

Table 6.

Average compression ratio (%), average compression time per sample (sec/GB) and average decompression time per sample (sec/GB) using gzip, SPRING, or GeneSqueeze algorithms.

	Gzip	SPRING	GeneSqueeze
Average compression ratio (%)	21.20%	7.61%	7.70%
Average compression time (sec/GB)	44.4	36.7	550.3
Average Decompression time (sec/GB)	5.2	5.6	606.5

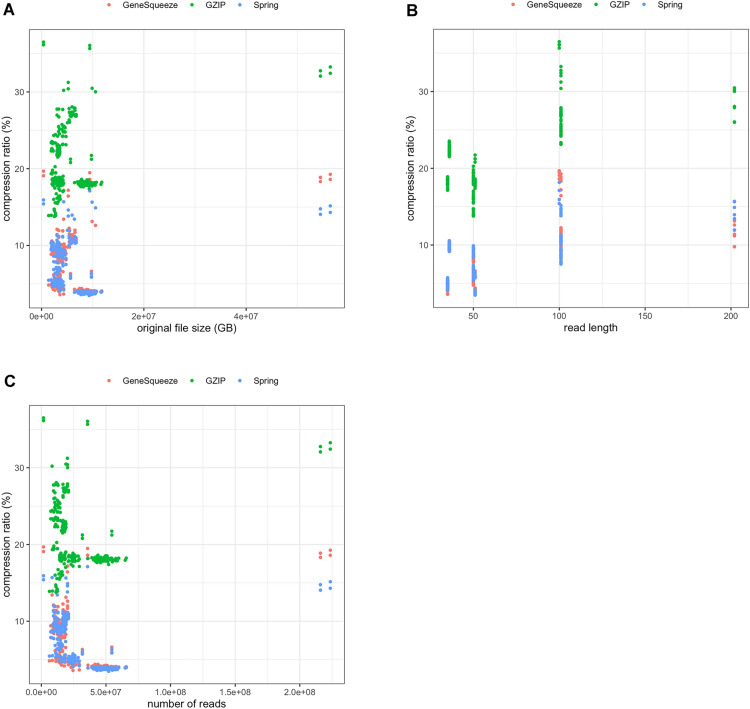
To understand which FASTQ files GeneSqueeze excelled at compressing, we examined compression ratio amongst FASTQ files with differing dataset sizes (Table 7), number of reads (Table 8), and read lengths (Table 9). We found that both GeneSqueeze and SPRING outperformed gzip in all categories. We found that GeneSqueeze compressed files of size 8–12 GB most efficiently and was least efficient at compressing large files (54–57 GB). Notably, GeneSqueeze compressed smaller files (0–4 GB) better than SPRING (Table 7). When examining GeneSqueeze’s performance on files with differing number of reads, we found that GeneSqueeze was best at compressing files with 35–65 million reads and performed worst when compressing files with 215–224 million reads. GeneSqueeze outperformed SPRING when compressing files with 1–20 and 20–35 million reads (Table 8). Next, we examined the compression ratio based on read length. We found that GeneSqueeze had the greatest compression on files with read lengths of 50–51 nucleotides and the least compression on reads of 100–101 nucleotides. GeneSqueeze outperformed SPRING on files with read lengths of 35–36, 50–51, and 202 nucleotides (Table 9). Figure 7 presents a comprehensive analysis of these factors influencing compression ratio across various datasets. In Fig. 7a, a scatter plot visually represents the relationship between dataset size and compression ratio, highlighting how the compression ratio varies with sample size. The data indicate that GeneSqueeze and SPRING are similar in their compression ratio of samples in similar file sizes up to approximately 12 GB, and that both of these algorithms outperformed gzip in compression ratio across files irrespective of file size. In terms of compression ratios on files above 50 GB, it appears that GeneSqueeze suffers from drawbacks likely related to implementation limitations, as its compression ratio falls behind that of SPRING when compressing these larger files. Additionally, Fig. 7b and c provide further insights by illustrating the fluctuations in compression ratio relative to read length and the number of reads, respectively. Both figures illustrate similar trends, with GeneSqueeze and SPRING demonstrating similar compression ratios at lower read lengths and smaller numbers of reads, outstripping gzip, and with SPRING outperforming GeneSqueeze when applied to files with read lengths in excess of 200 bp and numbers of reads above 200 million.

Table 7.

Average compression ratio (%) of samples by FASTQ file size (GB).

FASTQ file size (GB)	Gzip (%)	SPRING (%)	GeneSqueeze (%)
0–4	20.50	8.01	7.90
4–8	23.17	8.10	8.35
8–12	19.42	4.96	5.12
54–57	32.63	14.56	18.76

Table 8.

Average compression ratio (%) of samples by differing number of reads (million reads per sample).

Number of reads	Gzip (%)	SPRING (%)	GeneSqueeze (%)
1–20	22.11	9.01	8.99
20–35	20.33	6.43	6.25
35–65	18.69	4.31	4.57
215–224	32.63	14.56	18.76

Table 9.

Average compression ratio (%) of samples by read length.

Read length	Gzip (%)	SPRING (%)	GeneSqueeze (%)
35–36	20.59	7.69	7.56
50–51	17.82	5.36	5.25
100–101	27.16	10.60	11.64
202	28.39	13.93	11.62

Fig. 7.

Compression ratio distribution across files. Scatter plots depicting compression ratio variations across files in relation to (a) original file size, (b) read length, and (c) number of reads in FASTQ files.

The average compression times (sec/GB) of SPRING and gzip were similar at 36.7 and 44.4 s/GB, respectively, and both were significantly faster than GeneSqueeze, which averaged 550.3 s/GB (Table 6). Similarly, the average decompression times (sec/GB) for SPRING and gzip were 5.2 and 5.6 s/GB, respectively, much lower than GeneSqueeze’s 605.5 s/GB (Table 6). This indicates that GeneSqueeze’s current Python implementation has significant speed drawbacks compared to SPRING and gzip, which are predominantly implemented in C/C +  + .

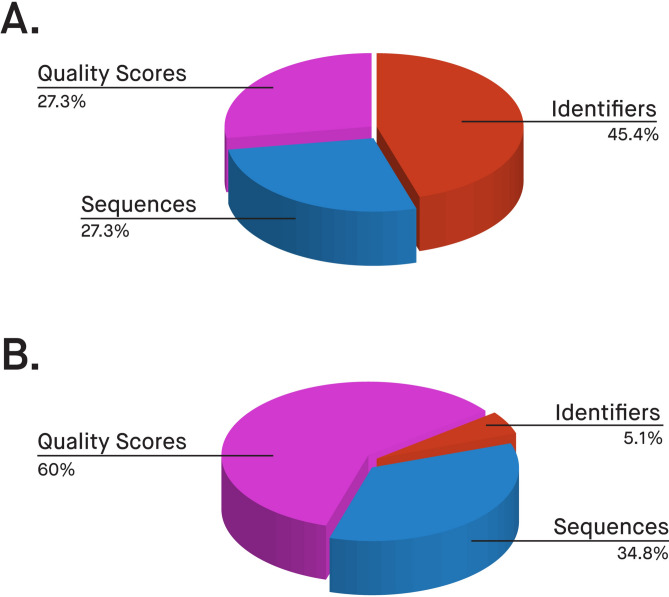
Quality scores are typically more challenging to compress than nucleotide sequences³. Thus, quality score compression represents an area with opportunities for further improvement in the field. GeneSqueeze uniquely pre-compresses quality scores with a domain-specific compression process and then feeds that to the general-purpose compressor. Our method allows us to further reduce the file size dedicated to quality scores without any loss or impact on downstream analysis. The pie charts in Fig. 8 indicate how much—on average—each component of a FASTQ file contributes to the total size, before and after GeneSqueeze compression. The difficulty in compressing quality scores is indicated by 60% of GeneSqueezed FASTQ file sizes, on average, being allotted to quality scores (Fig. 8). We observed that read identifiers were the easiest to compress due to their fixed template.

Fig. 8.

Contribution to File Size. Average contribution of each of the three parts of FASTQ files to final file sizes in (a) uncompressed files and (b) GeneSqueezed files. Pink illustrates the contribution of quality scores. Red indicates the contribution of read identifiers. Blue depicts the contribution of the nucleotide sequences.

We also investigated the ability of GeneSqueeze to recapitulate original data upon compression and decompression. In order to do so, we cross-referenced MD5 checksums for 283 FASTQ files before and after their compression via GeneSqueeze and found that 100% of the files showed were identical to their original format, showing lossless compression and decompression. To compare, we performed the same experiment using SPRING on the same 283 files and found that only 10 of the files (3.5%) maintained the same MD5 hash before and after the experiment. We investigated what these files had in common with one another, and found that in each of these 10 files, the separator line solely contained a ‘ + ,’ whereas in the other 273 files there was additional information following the ‘ + .’ This behavior is expected according to SPRING, as the algorithm discards information following the ‘ + ’ after compression even in the ‘lossless’ mode of SPRING, which leads to technical “loss” in the decompressed files^16,29. While the information typically following the ‘ + ’ in these files is not generally considered essential for performing downstream analysis, we considered it critical to recapitulate the entirety of the original files for the purposes of maintaining perfect losslessness.

As our datasets did not natively include non-N irregularities, we changed two nucleotides in a FASTQ file to non-N irregularities in a separate experiment to confirm which of the algorithms tested could perfectly recapitulate the original file. We observed that SPRING was not able to decode the non-ACGTN letters that existed in the IUPAC nucleotide code, but that both GeneSqueeze and gzip losslessly encoded and decoded the file, with matching MD5 hashes for the original and decoded files.

Discussion

Nucleotide sequencing data contains intricate patterns of redundancy and variation that require specialized data compression techniques. The unique features of nucleotide sequences, such as hierarchical structure and redundancy, can be utilized to achieve high compression ratios while minimizing loss of information. Developing effective compression algorithms for sequencing data requires a deep understanding of the data and the biological processes that generate it. The GeneSqueeze algorithm is capable of compressing FASTQ and FASTA data containing nucleotide sequences and is designed to be lossless for all parts of the FASTQ format, including the read identifier, quality score, and nucleotide sequence. GeneSqueeze relies on reducing the dimension and redundancy in genomic data in a unique and efficient way prior to data storage in binary format.

The results of our comparison demonstrate the effectiveness and efficiency of our novel data compressor, which showed both high compression ratios and accurate data recapitulation in our experiments.

This algorithm’s unique key features are:

1. Presenting a dynamic protocol for efficiently encoding high frequency k-mers.

2. Leveraging the innate redundancy in quality scores before passing them to the general-purpose compressor.

3. Encoding and losslessly decoding all IUPAC characters.

4. Expressing no capability limitations in context of read length and number of reads, allowing for flexibility in long-read / high-throughput FASTQ/As compression.

5. Compatible with all FASTQ/As sequence identifier formats.

Overall, we observed that GeneSqueeze performed competitively against a domain-specific comparison algorithm, SPRING, with both GeneSqueeze and SPRING performing better than the general-purpose compressor, gzip, for compression ratios. GeneSqueeze and gzip maintained losslessness when decompressing compressed files, whereas SPRING exhibited loss in the files which contained data following the “ + ” in the separator lines, as assessed via MD5 sums. Our goal in this version of the GeneSqueeze algorithm was to present a new methodology for genomic compression which prioritizes losslessness and compression ratio and allows for future iterations which address speed and memory in a manner which enables further reductions in compression ratios. Due to this, and in particular to GeneSqueeze’s current Python implementation, our current version of GeneSqueeze has drawbacks in speed and memory usage when compared to SPRING and gzip, which are predominantly implemented in C/C + + . Despite these drawbacks, GeneSqueeze’s novel approach, competitive performance, and complete preservation of genomic data ensures that GeneSqueeze is able to support the growing applications of omics technologies in the biomedical and clinical research space. Our forthcoming emphasis will be focused on: improving GeneSqueeze’s speed and memory via implementation in a more efficient programming language, upgrading the algorithm to dynamically optimize the values of hyperparameters across multiple blocks, upgrading the usability for general practitioners to enable the setting of individual thresholds and algorithm priorities such as compression ratio or speed, ensuring optimal adaptation for each dataset, sample, or file, and testing GeneSqueeze’s performance when used on other sequencing types, such as whole metagenome sequencing or functional genomics data. The efforts put forth in these future endeavors will expand GeneSqueeze’s ability to serve the needs of the biomedical space.

Author contributions

Algorithm development: F.N. Implementation: F.N., S.P. Figure Generation: F.N., M.L., A.S., E.K.M., G.S. Pseudocode Generation: F.N., R.C. Conceptualization: F.N., S.P., E.K.M., G.S. Manuscript Writing: F.N., M.L., R.C., E.K.M., G.S., A.S. Review: F.N., S.P., E.K.M., G.S., M.L., R.C., A.S. All authors revised and approved the manuscript.

Data availability

Datasets are sourced from the public databases listed in Table 1 in the Supplementary data. Also, the details of the results are presented in Table 2 in the Supplementary data.

Declarations

Competing interests

The authors declare the following competing interests: All authors (F.N., S.P., M.L., A.S., R.C., G.S., and E.K.M.) were employed by Rajant Health Incorporated. F.N., S.P., G.S., and E.K.M. have a patent pending for the GeneSqueeze compressor: “Fastq/fasta compression systems and methods,” 2022-11-18: Application filed by Rajant Health Incorporated. 2023-05-25: Publication of WO2023092086A2. 2024-04-25: Publication of US20240134825A1. F.N., S.P., M. L., G.S., and E.K.M. have a provisional patent submitted for the GeneSqueeze compressor: “GeneSqueeze: A Novel Method for Compression of FASTQ/A Files,” Application filed by Rajant Health Incorporated. 2024-02-16: Application No. 63/554,788.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-79258-6.