Many-body van der Waals interactions in multilayer structures studied by atomic force microscopy

Abstract

Van der Waals interaction in multilayer structures was predicted to be of many-body character, almost in parallel with the establishment of Lifshitz theory. However, the diminishing interaction between layers separated by a finite-thickness intermediate layer prevents experimental verification of the many-body nature. Here we verify the substrate contribution at the adhesion between the atomic force microscopy tip and the supported graphene, by taking advantage of the atomic-scale proximity of two objects separated by graphene. While the pairwise dispersion theory overestimates the substrate contribution at critical adhesive pressures, the many-body dispersion theory remedies this deficiency, highlighting the non-additivity nature of substrate contribution. The many-body effect is further understood through the energy spectrum of charge density fluctuations. These findings open the door to modulating the van der Waals interaction on two-dimensional material surfaces, which would be relevant to various technologies, including microelectromechanical systems and surface molecular assembly.

Many-body van-der-Waals interaction in multilayer structures has long been predicted but is difficult to be observed experimentally. Here the authors verify it in a tip graphene-substrate system benefiting from atomically thin intermediate graphene.

Introduction

Originating from quantum-mechanical fluctuations of materials charges, Van der Waals (vdW) interaction is ubiquitous in nature and relevant to a wide range of disciplines including condensed matter, nanoelectromechanical devices, bio-systems and so on^1–10. It is intrinsically a many-body phenomenon, namely, the total energy of multiple bodies is not a summation of two-body energies, since multiple scattering must be considered¹¹. The many-body effect was frequently manifested in atomic systems, such as parallel atomic wires¹², molecular crystals¹³, and atomic pairs within a carbon tube¹⁴, but typically revealed indirectly through inconsistencies in structural parameters, like lattice constant and geometrical configuration.

Although the many-body effect is also predicted to exist in continuum objects, such as multilayer systems^15–18, this effect is relatively easy to predict theoretically but challenging to detect since the total energy is predominantly dominated by the two closest layers due to the rapid decay of vdW interactions with separation. The emerging two-dimensional (2D) materials, such as graphene¹⁹, are the thinnest substances in nature. Crucially, they can separate objects by mere vdW gaps. It offers a brand-new opportunity to directly measure the many-body interaction in a tri-layer system, typically consisting of an object on graphene with substrates.

In contrast to the intensive efforts devoted to investigating the substrate effect on the electrical properties of graphene^20–22, the understanding of how the underlying substrate shapes its vdW interaction with other objects is lagging behind. Conspicuous theoretical works predicted a Faraday cage like screening effect on the vdW interaction between an object located above graphene and an underlying substrate^23–25. However, the extent to which vdW interaction can be screened off largely depends on the theoretical method applied, highlighting the compelling importance of quantitative experimental probing of the many-body effect. The attempt to measure the degree of transparency of graphene to vdW interactions can be traced back to the study of its wetting properties²⁶. However, the H-π interaction between graphene and water molecules complicates the matter considerably, as the interaction is not solely dominated by vdW interactions^27–29.

Atomic force microscope (AFM) has become a promising tool to evaluate the interfacial vdW interactions³⁰. Recent milestone works have precisely revealed the cleavage energy of graphite³¹, the lattice orientation specificity of vdW interaction³², the superlubricity at the vdW interface^33–35 as well as their adhesion strength^36,37. However, most of them focused on the measurement of vdW interactions between two homogeneous objects. By probing the force exerted on an AFM tip by substrate-supported graphene, Tsoi et al. and Chiou et al. pioneered the study of substrate effect on the vdW interaction between AFM tip and graphene^38,39. While Tsoi et al. demonstrated the capability of graphene to shield the interaction between the AFM tip and underlying SiO₂ substrate, Chiou et al. found a contribution of substrate on the graphene surface. The inconsistent findings could originate from the different testing environments applied and the oversimplified pairwise interaction or Hamaker approximation applied to interpret the experimental data. Besides, these works were performed in a gaseous environment, and factors including contaminants and surface water film inevitably lead to notable distortion and complexity, affecting the interpretation of experimental results^40,41.

The work presented here provides a comprehensive study that not only examines the substrate contribution, but also delves deeper into the many-body effect of vdW interaction in the tip-graphene-substrate tri-layer system, through both experimental measurements and theoretical calculations. We quantify the critical adhesion force exerted on an AFM tip by a freestanding graphene, bulk graphite as well as graphene supported on metal substrates in vacuum, and find that it increases in order. The atomically smooth sample surfaces, the absence of impurities on sample surfaces and interfaces guarantee the robustness of the findings. Density functional theory (DFT) simulations verify that the vdW interaction between substrate and tip is indispensable for the observed variation in adhesion force. It is shown that the pairwise vdW theory assuming additivity, significantly overestimates the substrate contribution and the many-body dispersion (MBD) theory amends this deficiency. The non-additive vdW interaction in the tip-graphene-substrate tri-layer system is understood through analyzing the energy spectrum of the MBD oscillation modes.

Results

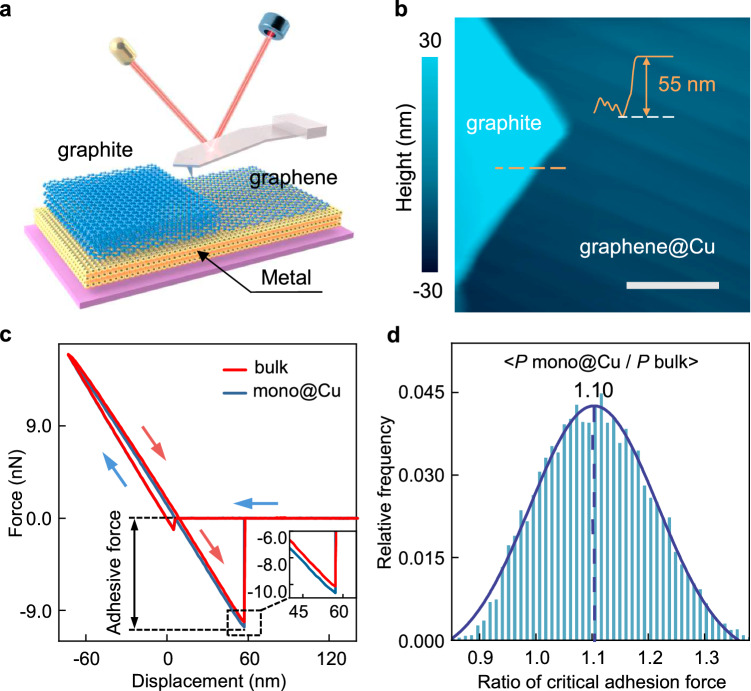
Figure 1a illustrates the sample architecture, where copper was employed as the substrate due to its weak bonding and limited charge transfer with graphene^20,25. High-quality monolayer graphene on copper (mono@Cu) was prepared through chemical vapor deposition (see “Methods” section). The surface reconstruction of Cu substrate during the growth offers Cu steps of atomically flatness comparable to that of bulk graphite, guaranteeing reliable tip-sample contact during force curve measurements, as illustrated in Supplementary Fig. 1. This advantage allows for a quantitative comparison between the adhesion force measured on mono@Cu and that measured on bulk graphite. Layer number of graphene and its high quality was verified through Raman spectrum as shown in Supplementary Fig. 3. A neighboring exfoliated bulk graphite flake, as shown in Fig. 1b, was utilized as a reference sample for all AFM mechanical tests, enabling reliable comparisons between different samples and measurements. Mechanical tests were conducted under high vacuum, and the silicon tips and samples were thermally annealed in situ to eliminate the effects of water capillary and surface contamination. The results of attenuated total reflection Fourier transform infrared spectroscopy convincingly illustrated the operational validity⁴¹, as shown in Supplementary Note 2 and Fig. 4. In addition, to further remove the potential hydrocarbon residuals, contact mode imaging was performed at large normal loads before the force curve measurements⁴². All samples and the AFM tips were grounded to eliminate the influence of electrostatic charge.

Fig. 1. Critical adhesion of monolayer graphene supported on substrates.

a Schematic representation of the AFM force measurement carried over bulk graphite and monolayer graphene supported on metal substrate. b Topography image of graphene grown on Cu substrate with an exfoliated neighboring graphite flake for controlled measurements. Inset is the height profile of the graphite sheet. The white line denotes scale bar, 1 μm. c Typical force versus displacement curves measured on top of monolayer graphene grown on Cu (mono@Cu) and bulk graphite (bulk). Inset is an enlarged view to highlight the variation in the critical adhesion force, P. d Histogram distribution of the ratio of critical adhesion forces measured on top of mono@Cu (P_mono@Cu) to those measured on top of bulk graphite (P_bulk). The blue curve is a Gaussian fit with a mean value of 1.10 and a standard deviation of 0.113.

Although dynamic force spectroscopy techniques, such as the bimodal and amplitude modulation techniques adapted by Chiou et al.³⁸, have shown great advantages in reconstructing the tip-sample force and high throughput mapping of Hamaker coefficient, quantitative interpretation of the force-distance relationship for such multilayer systems is challenging as it is expected to differ from that well established for two homogeneous bodies (Supplementary Note 3.1 and Fig. 5). Thus, we focus on investigating the critical adhesion force, which can be facilely determined from quasi-static force curves following Hooke’s law. The substrate contribution to the critical adhesion force is also more notable, as the vdW interaction decays rapidly with distance. Figure 1c presents typical force versus displacement curves taken over mono@Cu and bulk graphite during the loading (blue arrow) and unloading (red arrows) cycles. To determine the adhesion force with a high accuracy, soft AFM cantilevers with a low spring constant close to 0.2 N/m was adapted in our tests. This low spring constant leads to ‘snap-to-contact’ in the large tip-sample distance, which happens when the surface force gradient exceeds the cantilever’s spring constant. At such large tip-sample distances, the vdW force between the tip and the sample is buried within the noise level of our setup (±0.03 nN, Supplementary Note 3.2 and Fig. 6). Thus, during the loading process, there is not notable difference between these two curves. We note that the AFM cantilever does not deform notably while the tip is positioned 10 nm away from the sample surface, indicating the absence of long-range electrostatic force and the neutrality of both the tip and the sample. During the unloading stage, the AFM tip would jump off the sample surface once the elastic force applied to the cantilever exceeded the critical adhesion force, P, between the tip and the sample. The variation in P indicates that mono@Cu exerts a stronger adhesion force on the tip compared to the force exerted by bulk graphite (see Fig. 1c inset).

To quantitatively analyze the differences in P, we measured 100 sets of force curves on both mono@Cu and bulk graphite, 10 by 10 circularly on each region. The stability of P throughout the measurements indicates that the tip apex geometry did not notable change during the measurements, which was further confirmed by the critical amplitude method⁴³ (Supplementary Fig. 7 and Fig. 8). The histogram distribution of the ratio of P measured over mono@Cu (P_mono@Cu) to that measured over bulk graphite (P_bulk) is presented in Fig. 1d, which follows a Gaussian distribution with a mean value of P_mono@Cu/P_bulk located around 1.10. Measurements conducted on different samples gave close values, indicating the reliability of the deduced ratio (Supplementary Fig. 7). The measurements obtained by replacing the silicon tip with a coated tip are also close to 1.10 (Supplementary Fig. 9). We note that only tips made of inert materials, i.e. passivated silicon and diamond-like carbon, were adapted to suppress the charge transfer between tip and the sample. This ensures that the critical adhesion force is dominated by vdW interaction, as will be discussed below. The critical adhesion force of monolayer graphene exfoliated on sputtered Au film was also determined to be stronger than that of bulk graphite, with a ratio of 1.06 (Supplementary Fig. 10). We note that the roughness of the graphene-Au surface (~4 Å), is larger than those of atomically flat bulk graphite and mono@Cu, which may lead to  an underestimation of the adhesion strength ratio P_mono@Au/P_bulk^44,45 (Supplementary Note 3.2 and Fig. 10). Nevertheless, these results clearly indicate that the interaction between monolayer graphene and the AFM tip shows a remarkable dependence on the substrate, in consistence with the results revealed by Chiou et al. in ambient³⁸, and graphene supported on metal substrates generally applies a stronger adhesion force to the tip compared to the force applied by bulk graphite. However, we note the importance of the surface cleanness in determining the intrinsic vdW adhesion, and found a significant increase in adhesion force and a decrease in the ratio of P_mono@Cu/P_bulk due to air exposure, as shown in Supplementary Fig. 11. The distortion induced by air exposure would prevent a clear interpretation of the intrinsic vdW interaction at the interface, and consequently the many-body effects.

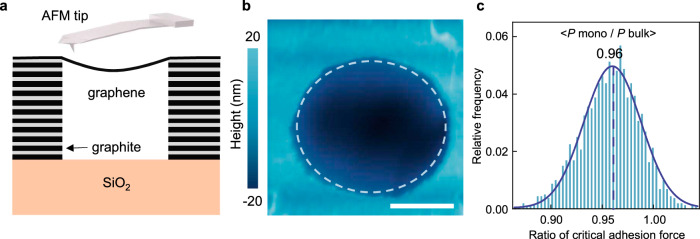
The dependence of the critical adhesion force on the graphene substrates implies a substrate contribution penetrating monolayer graphene, at least partially. To directly verify the substrate contribution, we utilized a monolayer graphene suspended on a graphite microwell, as schematically illustrated in Fig. 2a (see “Methods” section). Spontaneous self-cleaning process at the graphene/graphite interface ensures atomically clean interface^46,47. Force curve measurements on the freestanding graphene were performed in regions nearly 100 nm away from the graphite edge, as highlighted by the dashed circle in Fig. 2b, where the vdW force from the graphite was expected to be attenuated due to its rapid decayed with distance. Additionally, at the hole edge, the influence of graphene elastic deformation on the adhesion force was also minimized, compared to that determined at the hole center⁴⁸(Supplementary Fig. 12). The critical adhesion force measured on free-standing graphene, P_mono, is notably lower than P_bulk, as shown in Fig. 2c. These results again confirm the substrate contribution to the graphene-tip adhesion.

Fig. 2. Critical adhesion of suspended graphene compared to that of bulk graphite.

a Schematic of the AFM measurements taken over suspended graphene. b AFM topography of graphene suspended over a graphite hole of 2.5 μm diameter. The white line denotes scale bar, 1 μm. c Histogram distribution of the ratio of critical adhesion forces measured on top of suspended monolayer graphene (P_mono) to P_bulk. The blue curve is a Gaussian fit with a mean value of 0.96 and a standard deviation of 0.028.

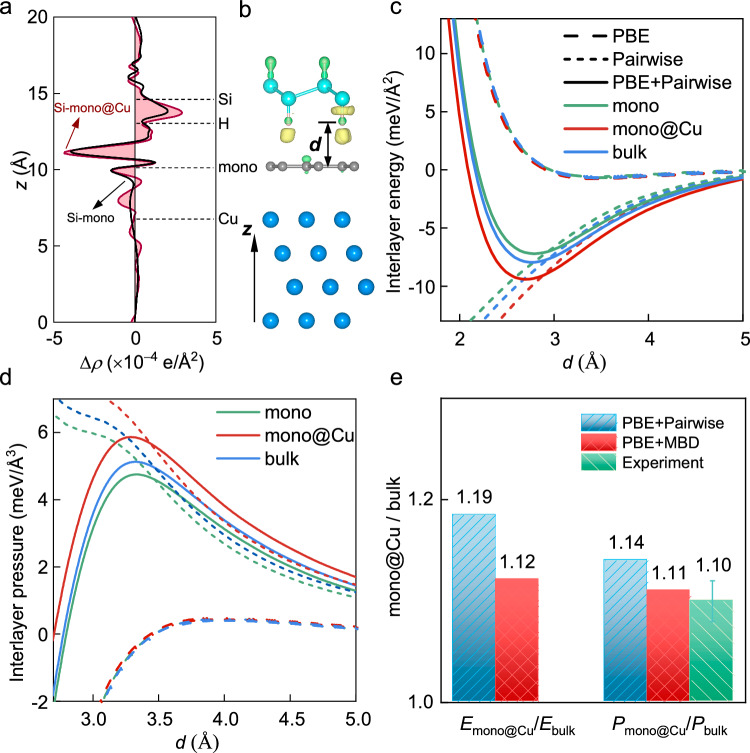
The DFT simulations based on the Perdew-Burke-Ernzernhof (PBE) exchange-correlation functional were performed to elucidate how the substrate modulates the tip-graphene adhesion force^49–52. The vdW interactions were considered using the semiempirical correction pairwise or the MBD theory⁵³. To improve the accuracy of the pairwise theory, the C₆ coefficient of graphene was derived from its dielectric functions via a Clausius-Mossotti relation dedicated to two-dimensional materials, and those of Cu and Si were derived from their dielectric functions via conventional Clausius-Mossotti relations^20,54,55. Even so, the non-additive nature of the interlayer vdW interaction was completely neglected by the pairwise theory. The MBD theory treats the vdW energy as the zero-point energy of coupled quantum harmonic oscillators⁵⁶, thus can properly handle the collective effect. In the simulations, four metal atom layers, four graphene layers and one H-passivated silicon layer were applied to mimic the metal substrate, bulk graphite and the AFM tip, respectively (see Methods). We note that, although the Lifshitz theory can also reflect the many-body effect (Supplementary Note 5 and Fig. 15), it is not suitable for a quantitative description of systems with atomic scale feature sizes/separations, due to the assumption of continuum dielectric media.

To consider the influence of charge transfer between tip and graphene, Fig. 3a presents the plane-average charge density differences (Δρ) at the interface. At the equilibrium separation (d = 2.7 Å), the charge transfer between tip and graphene is insignificant and almost unaffected by the appearance of Cu substrate. At the separation of critical pressure (d = ~3.3 Å), the charge transfer would be further reduced. The limited and substrate-insensitive interfacial charge transfer leaves the difference in interface interaction dominated by the vdW component contributed by the substrates, as will be discussed below.

Fig. 3. DFT results for the interlayer interaction between a hydrogen-passivated silicon layer and (supported) graphene.

a Plane-average charge density differences upon the formations of tip and monolayer graphene complex (Si-mono) or tip and monolayer graphene on Cu substrate complex (Si-mono@Cu), Δρ (Δρ is defined as the charge density of the coupled system subtracts those of the isolated components). The vertical positions of the atomic layers in a are marked by the dashed lines. b Surface charge density difference (0.00015 e/A³). Charge accumulation and depletion regions are labeled by yellow and green isosurfaces, respectively. c Binding energy densities as a function of interlayer distance d, defined as the vertical separation between the top graphene and the bottom hydrogen layer of the passivated silicon layer shown in b. The short and long dashed lines denote the pairwise and PBE energies, respectively. d Adhesive pressures as a function of d. e Ratios of equilibrium binding energies (left) and critical adhesive pressures (right) of the tip-mono@Cu interfaces relative to those of the tip-bulk interface, calculated by the pairwise and MBD theories. The error bar represents the standard deviation of the experiment.

Figure 3c, d present the binding energy densities and adhesive pressures predicted by the pairwise theory, as a function of the tip-graphene separation, d. The binding energy and adhesive pressure appear to be influenced by the appearance of a substrate, in consistency with Chiou et al.’s DFT-D2 result that increasing the number of graphene layers enhances the surface adhesion force. Both the equilibrium binding energies and critical adhesive pressures of the tip-mono@Cu interface and of the tip-bulk interface are larger than those of the tip-mono interface. To highlight the dominant role of vdW interaction in the enhanced binding energy and adhesive pressure under the appearance of metal substrate, Figs. 3c and 3d show the energies and pressures contributed separately by the vdW and PBE interactions. Evidently, the enhanced critical adhesive pressures under the appearance of Cu mainly predominantly originate from the vdW interaction between the tip and underlying metal substrate. The obtained ratio of equilibrium binding energy E_mono@Cu/E_bulk and ratio of critical adhesive pressures P_mono@Cu/P_bulk are 1.19 and 1.14, respectively, as shown in Fig. 3e. Notably, the ratio P_mono@Cu/P_bulk is overestimated compared to the measured value, indicating that the substrate contributions are overestimated by the pairwise theory. The MBD theory is seen to amend this deficiency, with P_mono@Cu/P_bulk modified to 1.11.

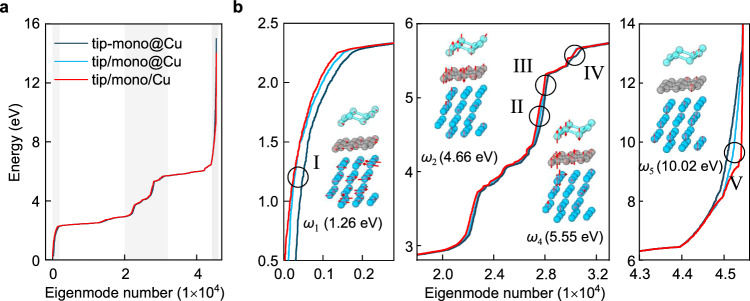
To gain further verification and deeper physical insight into the many-body vdW interaction between the tip and the supported graphene, Fig. 4a presents the energy spectrum of MBD oscillation modes of the coupled tip-graphene-Cu tri-layer (tip-mono@Cu), the combined spectrum of isolated tip and Cu-supported graphene (tip/mono@Cu), as well as the combined spectrum of isolated tip, isolated graphene, and isolated Cu (tip/mono/Cu). As the reciprocal-space implementation of the MBD approach⁵⁷ is applied with a k-point mesh of 15 × 15 × 1, the spectrum of the N-atoms system corresponds to 675 N modes. It is seen that the energy differences between most coupled modes and corresponding uncoupled modes are modest. The underlying reason is that the interlayer dipole-dipole couplings are weaker than the intralayer ones. Thus, the spectra are mainly shaped by the intralayer couplings. Nevertheless, in regions I, II, and IV, as zoomed in Fig. 4b, the energies of coupled modes are visibly shifted downwards with respect to the uncoupled ones. The summation of the energy differences over all modes contributes the vdW binding energy between the tip and the supported graphene.

Fig. 4. MBD oscillation modes of charge density fluctuations.

a Energy spectrum for the coupled tip-graphene-Cu tri-layer (tip-mono@Cu), plotted in ascending order. The combined spectrum of isolated tip and Cu-supported graphene (tip/mono@Cu), and the combined spectrum of isolated tip, isolated graphene and isolated Cu (tip/mono/Cu) are presented for comparison. The shaded areas in a correspond to the zoomed panels in b. b Zoomed spectra for the shadowed regions in a, and illustrations of coupled modes evidently shifted from corresponding uncoupled modes. The red arrows represent the dipole displacements of the atoms. Hydrogen atoms with minute dipole displacements are hidden for clarity.

Insets in Fig. 4b show the dipole displacements of four representative coupled modes. The dipole displacements seem more complex than those for one-dimensional carbyne wires as revealed by Ambrosetti et al.¹², due to the reduced symmetry of the tri-layer here. However, one can still figure out how the eigen-energies are lowered via interlayer coupling. As a typical plasmonic character of charge density fluctuations, low-frequency modes (i.e. ω₁) are delocalized, while high-frequency modes (i.e. ω₅) are more localized. In agreement with previous findings^12,58, low-frequency and high-frequency modes are seen to contribute attractive and repulsive interactions, respectively. In mode ω₄, Si atoms are polarized in the normal direction with an out-of-phase arrangement of dipole displacements in SiH layer. The dipole displacements of C atoms are also aligned along the normal direction and tend to be in phase with the nearest Si atoms, contributing positively to the attraction between the tip and graphene. The normal polarizations of underlying Cu are less significant, indicating a negligible coupling between Cu and graphene (or tip) and rationalizing that at region IV the spectrum of tip-mono@Cu is not evidently split from the combined spectrum of tip/mono@Cu. In mode ω₂, SiH, graphene and Cu are polarized simultaneously, indicating a direct three-body coupling, that is, the appearance of Cu substrate has an influence on tip-graphene interaction. Also, there are modes not participated by SiH (i.e. ω₃) without contribution to the tip-graphene interaction.

Discussion

In conclusion, many-body effect in vdW interaction of tri-layer systems is verified through AFM force measurements in combination with theoretical simulations, taking tip-graphene-substrate as a model system. The atomically narrow gap between the substrate and the tip allows a notable enhancement in surficial adhesion of graphene on AFM tip due to the substrate contribution. On the contrary, the many-body effect weakens the tip-sample interaction compared to that predicted by pairwise theory. The strategy to modulate the surface adhesion of graphene here is expected to be applicable to a broader range of substrates and two-dimensional materials, shedding a new light on modulating surface molecular assembly and hybrid structure construction via vdW interaction. Moreover, other factors, such as the interlayer charge transfer and spacing is expected to provide additional degrees to modulate the surficial interactions of such tri-layer systems, and deserve further investigations.

Methods

Graphene growth

The monolayer graphene on Cu substrate was directly grown by chemical vapor deposition on Cu foil (Alfa Aesar, 0.025 mm thick, 99.8 % purity). Before being loaded into a quartz tube, the Cu foil was electrochemically polished in phosphoric acid followed by rinsing with deionized water. When the growth system was pumped down to the base pressure around 1 Pa, a 20 sccm H₂ flow was introduced into the chamber and then annealed at 1025 °C for 2 h. Deposition of monolayer graphene was carried out by introducing 5 sccm CH₄, the growth lasted 5 min at 1025 °C before opening the furnace to let it cool down to room temperature quickly.

Suspended graphene preparations

The suspended graphene samples were made through transferring monolayer graphene nanosheets onto graphite flakes with pre-fabricated micro-wells of 2.5 μm diameter. The monolayer graphene was firstly exfoliated onto a polymer bilayer film on a Si wafer. The film consists of a water-soluble bottom layer (polyvinyl alcohol, PVA) and a top layer of PMMA (polymethyl methacrylate, molecular weight 495 K). The graphene/PMMA film was released from the substrate by dissolving PVA in de-ionized water and then picked up by a washer. Following that, the graphene was aligned and placed over the graphite micro-well, and the PMMA film was removed through vacuum annealing at 400 ^oC for 3 h. Graphite micro-wells were prepared by exfoliating single crystal graphite flakes on SiO₂/Si substrates, followed by lithographic definition of 2.5 μm round islands on a photoresist layer. An aluminum film was deposited as the etched mask. Reactive ion etching created 100 nm deep graphite micro-wells, and the aluminum mask was dissolved using NaOH, followed by de-ionized water rinsing, as shown in Supplementary Fig. 2.

AFM measurements

Static force curve measurements were carried out using an AFM (SPI SPA 300) with inert silicon AFM tips (AN-CSG01, ~0.2 N/m) or diamond-like carbon coated tips (ContDLC, ~0.2 N/m) in vacuum at room temperature. Before the experiment, the samples were annealed in situ under vacuum (pressure ~10⁻⁵Pa) at 200 ^oC for 30 min, and then the AFM tip was brought into contact with the sample for annealing at 200 ^oC for another 30 min to remove possible adsorption of impurities. The cantilevers’ spring constant (k) were calibrated by the thermal noise method and the sensitivity of the optical lever system was calibrated on hard SiO₂ samples with limited deformation. Quasi-static force curves were collected through recording the cantilever bending displacement (z) while sweeping the piezo displacement (d) at a fixed range from 0 nm to 200 nm with a speed of 40 nm/s. The recorded z (d) are converted into force curve based on F = k ∙ z.

DFT simulations

Theoretical studies on the substrate contributions to the surficial adhesive pressures were performed using the FHI-AIMS simulation package^57,59. DFT calculations were carried out with the PBE functional^49–52 using the ‘tight’ Gaussian-type bases. VdW interactions were considered using either the semiempirical pairwise correction^53,60 or the MBD theory^57,59. It is worthy of mentioning that the performance of the MBD in describing interlayer interactions of vdW materials has been justified previously^24,61. Supplementary Fig. 13a, b and c illustrate the structural models used to simulate the tip-mono@Cu, tip-bulk, tip-mono interfaces, respectively. Due to the limitation of computational cost, four Cu atomic layers, four graphene layers and one H-passivated silicon layer were used to mimic the Cu (111) substrate, the bulk graphite and the AFM tip, respectively. The commensurability condition was realized by compressing or stretching 3 × 3 graphite, 2 × 2 H-Si and 3 × 3 Cu (111) supercells by no more than 4.1%. A vacuum layer of 35 Å was used to avoid any spurious interaction between periodic images. A 2 × 2 × 1 k-point mesh was adopted for the momentum space sampling. Prior to calculating the binding energy as a function of the distance between H-Si and graphene, the separation between graphene and Cu substrate was relaxed to its equilibrium value and the structure of H-Si layer was fully optimized. Atomic coordinates of the three systems (Si-mono, Si-bulk and Si-mono@Cu) are presented in Source Data File. Notably, the MBD applied here has not included the effect of electrical conductivity, which is important to the asymptotic behavior of vdW interaction in long ranges⁶² but less crucial to the short-range interaction studied here.

Author contributions

J.Y. and X.Liu. conceived the project. W.G. supervised the project. X.W. performed the experiments with assistances from R.Q., X.Li, Y.L., and B.L.; Z.K. performed the theoretical studies under supervision of X.Liu. X.W., Z.K., X.Liu., and J.Y. wrote the paper. All the authors discussed the results and reviewed the manuscript. X.W. and Z.K. contributed equally to this work.

Peer review

Peer review information

Nature Communications thanks Matteo Chiesa, Haitao Liu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

All source data generated in this study are provided in the Source Data file. Source data are provided with this paper.

Code availability

The numerical methods related to this work is encoded within the FHI-aims and the pyMBD. Further explanation of our methodology is available upon request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-54484-8.