Combining Fundamental Kinetics and Standard Alkylation Assays to Prioritize Lead-Like KRAS G12C Inhibitors

Abstract

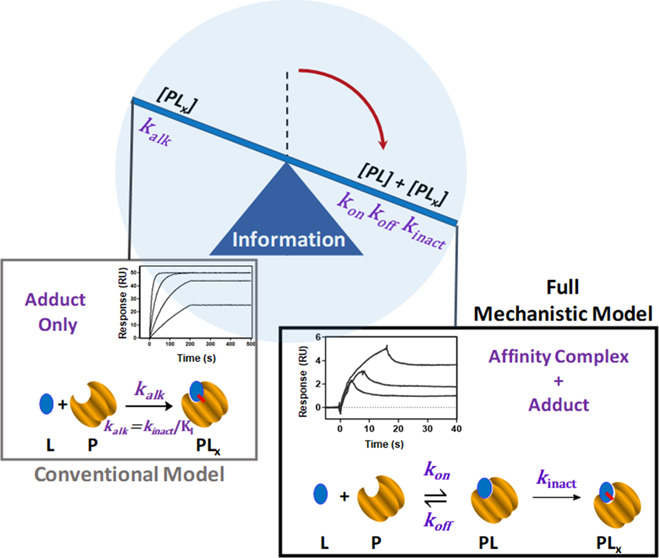
We measure the fundamental rate constants of internally discovered KRAS G12C inhibitors to demonstrate how kinetic analyses can be integrated with standard biochemical and cell-based assays for more optimal biophysical compound prioritization. In this proof-of-principle study, we characterize three irreversible covalent inhibitors targeting the mutant cysteine at the switch II binding pocket. We estimate the three fundamental kinetic rate constants (k_on, k_off, k_inact) that define the contributions of affinity and inactivation to the overall alkylation rate for a more complete biophysical characterization. These parameters are typically unavailable and are generally approximated by a single overall alkylation rate constant (k_alk), where the relative contributions of affinity and inactivation remain unknown. We demonstrate that the alkylation rate constant sacrifices valuable mechanistic information leading to higher risk of suboptimal compound prioritization. Estimation of the three fundamental kinetic rate constants was made possible by developing label-free surface plasmon resonance (SPR) methodologies adapted to measure transient binding using standard SPR equipment. Binding enthalpy was measured by Eyring transition state analysis, which can also benefit compound prioritization. We illustrate how these methodologies can enable more reliable prioritization of lead-like compounds when combined with standard orthogonal assays in a typical lead optimization setting.

Irreversible covalent inhibitors often produce high therapeutic efficacy despite lower systemic exposure by inactivating target proteins through a combination of affinity binding and covalent adduct formation.¹ This decouples target occupancy from the usual equilibrium constraints that apply to affinity-driven drugs. Assuming nonlimiting pharmacokinetics (PK) then occupancy proceeds kinetically until all target is inactivated such that only target resynthesis can negate inhibition. The discovery and optimization of such covalent inhibitors^2,3 are more complex relative to affinity binding inhibitors, yet recent success in inhibiting challenging targets such as mutant KRAS⁴ has established covalent inhibitors as a valuable modality for difficult to drug targets. Here, we focus on enhancing the mechanistic characterization of early lead compounds through direct kinetic binding employing SPR detection and we will show how this can improve compound selection and optimization.

We first introduce the basic reaction theory required to understand how the familiar overall alkylation rate constant (k_alk) relates to the three fundamental rate constants. Microscopically, the formation of a simple affinity complex follows a conformational ensemble model⁵ and combines aspects of both conformational selection and induced fit, where multiple transition states may exist.⁶ In practice, SPR systems sample a large population of binding events over a large sensing region, producing intrinsically averaged affinity binding curves that exhibit monophasic exponential decay. This monophasic decay reflects the accumulation of the affinity complex at a rate determined by the slowest rate limiting kinetic step and is therefore insensitive to any transient intermediate states that might exist microscopically. A simple 1:1 affinity binding reaction is given in Reaction (1)

R1

A ligand (L) is bound by an active target protein (P) to form an affinity complex (PL), according to an association rate constant (k_on, units: M^–1 s^–1) and a dissociation rate constant (k_off, units: s^–1) with a dissociation affinity constant K_D given by eq 1 and is often denoted as K_i for covalent inhibitors.

1

Assuming a pseudo-first-order approximation applies, a mechanistic model describing Reaction (1) is given by the ordinary differential equation (ODE) shown in eq 2.

2

In some cases simple binding can be followed by a slow conformational change of the affinity complex forming a more stable affinity complex (PL_x). This two-state mechanism⁷ requires additional forward rate constant (k_f, units: s^–1) and reverse rate constants (k_r, units: s^–1) as shown in Reaction (2).

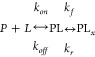R2

Assuming a pseudo-first-order approximation holds, the affinity constant for the two-state mechanism is given by eq 3 where the term in brackets defines the fraction of PL that proceeds to form PL_x.

3

This general two-state model applies when the second bound state results from either covalent,⁷ or noncovalent interactions.

Interactions governed by the two-state model generally produce biphasic time course curves for both association and dissociation phases, distinguishing them from the monophasic time course curves produced by the simple 1:1 binding model. However, this distinction is rarely possible to resolve in early discovery since target occupancy is typically dominated by the accumulation of the more stable state (PL_x) because the affinity complex (PL) is transient (i.e., k_off > 0.1).

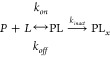
For irreversible covalent inhibitors (i.e., where k_r = 0), k_f is generally referred to as the target inactivation rate constant, k_inact (units: s^–1), as shown in Reaction (3) because adduct (PL_x) formation results in permanent inactivation.

R3

As in the simple 1:1 model, formation of PL is defined by eq 2 but eq 4 is coupled in order to account for adduct formation.

4

Reaction (3) can then be fit to SPR curves by coupling eqs 2 and eq 4 allowing all three fundamental kinetic rate constants to be estimated. In the case of transient affinity binding there is usually inadequate information in the curves to estimate all three rate constants. To avoid overfitting, a rapid steady-state assumption can be assumed where [PL] = constant, reducing the alkylation kinetics to a single pseudo-first-order alkylation rate constant (k_alk), as shown in Reaction (4) and eqs 5–8.

R4

5

6

K_I is the inactivation constant and specifies the concentration of inhibitor that inactivates the enzyme at a rate equal to k_inact/2 and is given by eq 7.

7

Importantly, the three fundamental rate constants k_on, k_off and k_inact are generally unknown, which limits the information content available for compound prioritization. The reaction mechanisms specified by the ODEs defined above can be fit to SPR binding curves through numerical integration coupled with nonlinear least-squares regression curve fitting, which is the industry standard in label-free biosensing. This enables estimation of the kinetic constants without being burdened by the assumptions and approximations that are often required for analytical solutions to complex binding mechanisms. k_alk has also been previously expressed by Schwartz⁸ as shown in eq 8, where the term in brackets represents the compounds commitment to covalency (C_c), which is the probability of PL proceeding to form PL_x. The application of this metric to compound prioritization using conventional SPR methodology has been demonstrated elsewhere.⁹

8

More general application of the SPR methodology has likely been hindered by the extremely transient nature of affinity binding in early covalent inhibitors and the limiting throughput of the early methodology. These limitations in SPR methodology are addressed in this current work though here we focus on demonstrating the value of fundamental rate constants in optimal compound prioritization. k_alk alone is widely used for estimation of on-target potency of irreversible covalent inhibitors as it can be readily measured and applied broadly.^10,11k_alk alone does not provide optimal biophysical ranking since the contributions of affinity and inactivation to the overall alkylation process are not resolved. We overcome these limitations by estimating all three fundamental rate constants k_on, k_off and k_inact in a fully kinetic regime. The fundamental rate constants in turn allowed enthalpic contributions to be quantified through Eyring transition state analysis.¹² Despite complex enthalpy/entropy compensation effects^13,14 it has been reported that thermodynamic characterization of irreversible covalent binders may promote development of higher quality therapeutics with particular focus on increased binding enthalpy.^15,16 Kinetic measurements were made possible by developing SPR-based assays tailored to measure transient binding on standard SPR equipment that can also provide sufficient throughput for application in a drug discovery project team setting.

Results and Discussion

Affinity Ranking Using k_alk

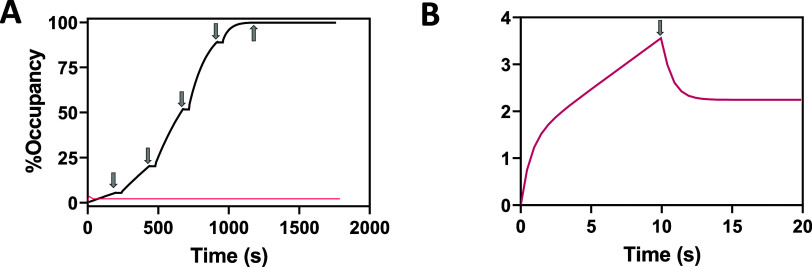
The interpretation of SPR curves obtained for covalent inhibitors generally deviates significantly from curves obtained for reversible inhibitors. Therefore, we simulated a Single Cycle Kinetic (SCK) curve expected for an irreversible inhibitor according to Reaction (3) and employed standard compound dosing and contact times as shown in Figure 1A. Dissociation is near completely absent from the accumulative SCK titration curve because the reversible transient affinity complex contributes <1% to the accumulative response, with the remainder being irreversibly bound adduct. This near-complete absence of accumulated affinity complex demonstrates why reversible kinetic rate constants cannot be resolved when the affinity complex is transient. Therefore, to avoid overfitting, it becomes necessary to combine the fundamental rate constants, giving k_alk, which is estimated by fitting Reaction (4). In the simulation, dramatically lowering the compound exposure time while also increasing the compound concentration produced a very different result (Figure 1B). A single concentration of compound was injected for a very brief contact time (10s), producing very low occupancy (<5%). Under these conditions, both reversible affinity binding and alkylation contribute nearly equally to the accumulative SPR curve, allowing all three fundamental binding constants to be recovered when back-fitted to Reaction (3). In summary, the simulations in Figure 1 demonstrate why kinetic analyses of reversible covalent inhibitors are largely reliant on estimating k_alk and also show how transient reversible affinity binding can be resolved by using nonstandard SPR assays.

Figure 1.

Simulations facilitating the interpretation of SPR curves for characterization of covalent inhibitors binding to an immobilized target. Arrows indicate the end of each injection, which is followed by continuous buffer flow, allowing a dissociation phase to be measured. A response of 1 RU = 1 pg/mm² and here is expressed in terms of protein occupancy, where % Occupancy = (Response/Saturation Response). Curves were simulated by numerical integration of coupled eqs 2 and 4 assuming rate constants k_on = 2.2 × 10⁵ M^–1 s^–1, k_off = 1.27 s^–1, k_f= k_inact = 0.15 s^–1 and k_r = 0 s^–1. (A) Simulated binding/alkylation curve (black) for exposure of an irreversible covalent inhibitor to surface-bound protein. Repeated injections of inhibitor are simulated over five serial-tripling concentrations to a maximum concentration of 1 μM. (B) Simulated binding/alkylation curve where a single concentration (100 nM) of compound was injected for 10 s thereby limiting occupancy to <4% which resolves affinity binding (i.e., rapid rise/fall at start/stop of exposure) from accumulation of adduct (linear association segment and irreversible baseline increase). Note that this curve is also plotted in A (red) for comparison.

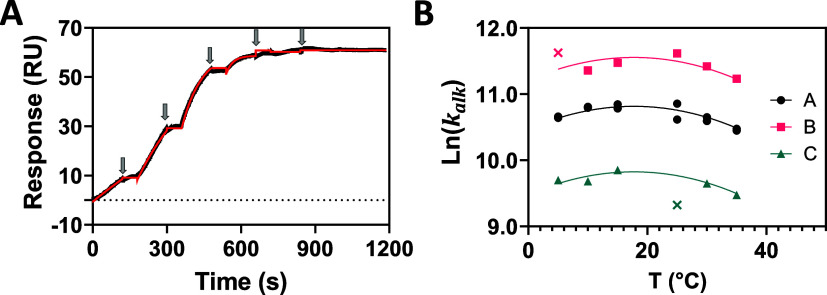
As already mentioned, it is not possible to quantify the affinity component of k_alk. However, we reasoned that an enthalpy-driven compound might show a measurable temperature dependence in k_alk and might therefore provide a crude affinity rank order since enthalpy is itself highly temperature-dependent. Warhead reactivity has an opposing temperature dependence (see Supplemental eq S1) that might interfere with resolution of any enthalpy-dependence. This hypothesis was evaluated experimentally as follows. Three KRAS G12C inhibitors were injected for 200s over an SPR surface coated with recombinant KRAS G12C protein, and a single exemplary SCK curve is shown in Figure 2A.

Figure 2.

Experimental estimation of k_alk. (A) Measured SCK titration curves obtained under the same conditions as described in Figure 1A for analysis of compound C alkylating KRAS G12C at 25 °C. (B) Temperature (T) dependence of k_alk for compounds A, B and C. Compound A was run in duplicate, while B and C were run as singletons. Outliers are indicated by × on the graph.

The SPR curve was fit to eq 5 assuming pseudo-first-order kinetics by coupled numerical integration and nonlinear least-squares regression returning an estimate of k_alk. This analysis was repeated at six temperatures from 5 to 35 °C revealing the temperature dependence of k_alk. This entire sequence was repeated for compounds B and C producing the fitted curves in Supplemental Figure S1 and the associated parameter estimates in Supplemental Table S1. The maximum relative CV with respect to k_alk was <0.35% and the global average goodness of fit was χ² = 0.015 (±0.01) RU². We plotted the estimated k_alk against temperature (Figure 2B) for the three compounds and fitted the data by robust regression to a second order polynomial eq 9.

9

It is obvious that the three curves are near identical in curvature other than being offset with respect to the Y-axis. Coefficient B₀ (Y-intercept) defines the nontemperature dependent variability in k_alk between compounds, returning 10.47 ± 0.07, 11.21 ± 0.08 and 9.48 ± 0.07 for compounds A, B and C, respectively. Even small differences in curvature caused by any variable temperature dependence in k_alk between compounds would result in different values of coefficients B₁ and B₂ between compounds. Negligible variation in temperature dependence between the compounds was observed as the three curves share the same values of B₁ and B₂. Least-squares regression returned globally fitted values B₁ = 0.039 ± 0.008 and B₂ = 0.0011 ± 0.0002 with excellent goodness of fit (R² = 0.99, χ² = 0.07). The statistical robust global fit eliminates the possibility of significant variation in temperature dependence. Had variation existed then the global constraint would have been inappropriate and would require local fitting of B₁ and B₂ to produce a robust fit. Full experimental details are found in Supplemental Methods S1 and S4.

We hypothesized that the observed low temperature dependence might be caused by kinetic compensation effects, where a proportional increases in both k_inact and k_off with increasing temperature would produce little change in k_alk as both of these fundamental kinetic constants act antagonistically with respect to target alkylation (see eq 7). Such low temperature dependence is convenient in that k_alk applies over a broad range, and values reported from a biochemical assay at room temperature should be reasonable approximations of k_alk in cells at 37 °C. Assuming transient affinity binding, then the time to achieve any given fractional alkylation (f) using inhibitor (I) can be estimated from eq 10.

10

We employ a Cell_EC₅₀ assay (Supplemental Method S5) to estimate compound potency, where cells were incubated with compound for 18 h. Using eq 10, we predict 95% alkylation, assuming t_alk = 18 h, k_alk = 3.13 × 10⁴ M^–1 s^–1 and compound concentration [I] = 10 nM. As mentioned earlier, irreversible covalent inhibitors alkylate in a kinetic regime without tending toward an equilibrium, or steady-state.

Prediction of expected fractional alkylation from k_alk for any given incubation time and compound concentration is useful in interpreting potency readings from the various assays that contribute to compound prioritization. This can also be useful in setting an effective target coverage profile. For example, t_alk can be compared to the target resynthesize time in cells in order to set a minimum k_alk threshold capable of producing sustained target inhibition in cells.

Determining Accurate Fundamental Kinetic Parameters

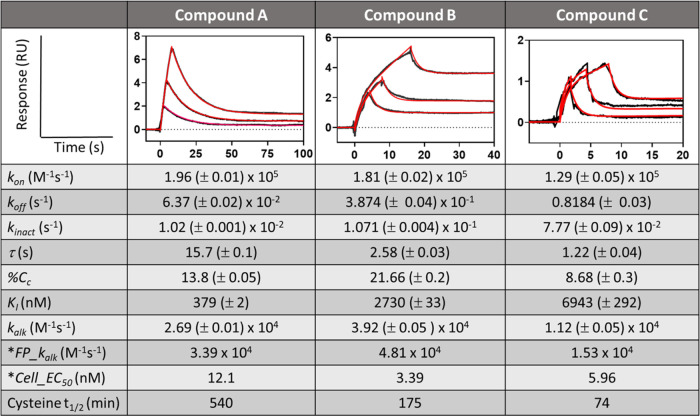
We next sought to estimate the fundamental kinetic parameters in order to demonstrate how a full mechanistic analysis enables improved decision-making in progressing compounds. As expected from Eyring theory (see Supplemental eq S1), lower temperatures decrease the thermal motion of molecules, thereby favoring higher binding affinity for enthalpy-driven interactions. Conversely, lower temperatures decrease the energy required to overcome the activation energy barrier toward covalent adduct formation. This implies that affinity of enthalpy-driven compound binding will be more readily resolved at lower temperature. An SPR assay adapted to measure transient binding was developed using commercially available instruments and was run at 5 °C to enhance enthalpy. Briefly, 100 nM compound was injected at maximum flow rate (100 μL/min) for a brief contact time (≤16 s) to better resolve transient affinity binding compounds, which exhibit low residence times (e.g., τ ∼ 0.2 s). Figure 3 shows the resulting SPR curves fitted to coupled eqs 2 and 4, where interaction constants were constrained to global values. For all SPR curves, the fractional occupancy resulting from accumulation of adduct remained <10% of the saturation capacity (R_max), allowing R_max to be assumed approximately constant, equal to 60 RU for compound A and 63 RU for compounds B and C (Refer to Supplemental Method S2 for full experimental details).

Figure 3.

Experimental estimation of fundamental interaction constants for compounds A, B, and C. The SE associated with each fitted parameter is specified in brackets (value ± SE) and the goodness of fit for all fits was χ² < 0.01 RU². %C_c = 100(k_inact)/(k_inact + k_off). *FP_k_inact/K_I was obtained from a fluorescent polarization biochemical assay (Supplemental Method S6) and *Cell_EC₅₀ was obtained from a cell activity assay (Supplemental Method S5).

The interaction constants returned from the fit along with k_alk from the fluorescent polarization biochemical assay (FP_k_alk) and cell potency (Cell_EC₅₀) are also given in Figure 3. We found that k_alk calculated from the fundamental kinetics correlated linearly with FP_k_alk and k_inact from SPR correlated with Cell_EC₅₀ (see supplemental Figure S3). This suggests that k_inact accounts for the variation (∼3-fold) in Cell_EC₅₀ between these compounds. In addition, the relative magnitude of the differences in Cell_EC₅₀ are comparable in scale to the differences in k_alk between the compounds, which are relatively small. However, compound C gave a ∼7-fold higher cysteine reactivity half-life (see Supplemental Method S7) relative to compound A and was therefore deprioritized given the associated high risk of off-target alkylation. Compound A appears superior to compound B given its 6.6-fold higher affinity while retaining a comparable C_c and k_alk (i.e., both within 1.6-fold). C_c measures the efficiency of alkylation resulting from the competing effects of k_inact and k_off. Higher C_c coupled with lower cysteine reactivity suggests higher synergy between the affinity bound conformation and adduct formation. Now reconsidering this analysis in the absence of the three fundamental rate constants, we find insufficient information to prioritize one compound over the other as their k_alk values are similar. As mentioned earlier, enthalpy rich affinity contacts are known to be correlated to greater success in the clinic^14,15 and could further support prioritization of compound A. We therefore applied transition state analysis to confirm that compound A is an enthalpy-driven inhibitor.

Transition State Analysis

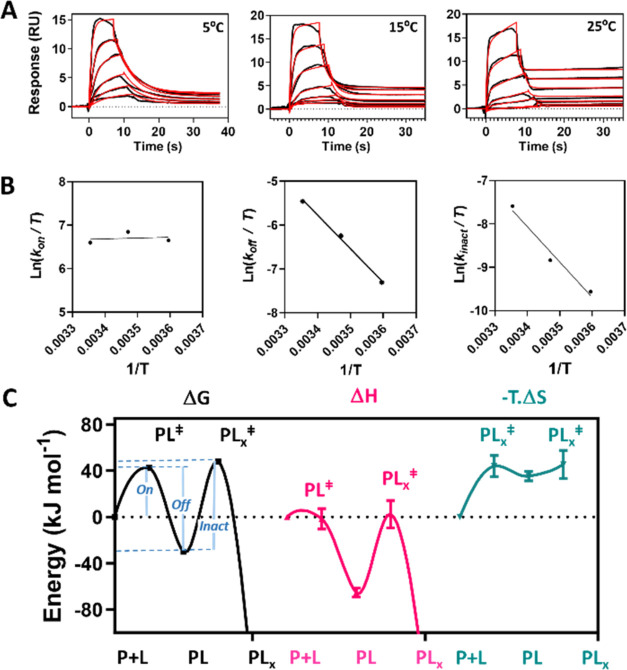
We next performed transition state analysis¹⁷ in order to resolve the thermodynamic binding energies for compound A. We repeated the SPR analysis format described in Figure 3 at three different temperatures, and here KRAS G12C was automatically recaptured after each compound injection. The method (see Supplemental Method S3) employs a protein G-functionalized SPR sensing surface to support an affinity-capture stack built by sequential injections of antistreptavidin mAb, streptavidin, KRAS G12C-biotinylated and finally compound A. The surface was regenerated on exposure to weak acid (pH ∼ 1.5), allowing a fresh stack to be constructed for the next sample. This target recapture method¹⁸ enables long assay run times and facilitates a continuous sampling rate of over 6 compounds/hour/SPR channel, which is sufficient to support general hit-to-lead or lead development campaigns. Target recapture enabled a fixed R_max over the assay run producing high quality SPR sensograms as shown in Figure 4A. The interaction constants for each curve set are reported in Supplemental Table S2. A comparatively low accumulation of adduct (7.7–lower k_inact) is apparent at 5 °C (278 K) relative to 25 °C (298 K) and is consistent with lower warhead reactivity allowing the affinity component to dominate. In contrast, biphasic association–dissociation curves are apparent at 25 °C indicating that accumulated affinity complex and adduct contribute near equally to occupancy. Linear temperature dependences were observed from Eyring plots (Figure 4B) for both k_off and k_inact showing comparable increases that act antagonistically causing k_alk to remain relatively stable (<12% variation). Interestingly, k_on remained relatively unchanged suggesting additional thermodynamic compensation effects.

Figure 4.

Kinetic characterization of compound A at three temperatures and associated thermodynamic analysis. (A) SPR sensograms at various temperatures showing binding a serial doubling dose–response series of compound A from 5 μM with variable contact times (black) with respect to concentration. Reaction (3) was fitted to the data (red) through numerical integration of coupled eqs 3 and 4 assuming pseudo-first-order reaction kinetics. The relative SE associated with each fitted parameter were <0.6% other than for k_off, where the maximum relative SE was 7.2%. All χ² < 0.1 RU. (B) Eyring transition state model was fitted to the fundamental kinetic constants obtained from analysis in (A) with error bars indicating ± SE of the fit obtained in (A). (C) Energy transitions in ΔG^⧧, ΔH^⧧ and TΔS^⧧ at 25 °C (chosen standard temperature) for compound A binding KRAS G12C on the reaction coordinate. The free energy barrier associated with each transition state is defined by the energy difference between the reactants, indicated along the reaction coordinate (x-axis) and the corresponding transition state, designated with superscript (⧧). The error bars represent the SE of the fit associated with each thermodynamic quantity returned from the fit in (B). The correspondence between transition state free energy ΔG^⧧ and the fundamental kinetic rate constants are indicated by on, off and inact, respectively. The relative SE was insignificant (<1%) for estimation of ΔG^⧧ but higher (see visible error bars) for its components ΔH^⧧ and TΔS^⧧.

The component binding energies associated with each fundamental rate constant were obtained by fitting the Eyring eq (Supplemental eq S1) and are listed in Supplemental Table S3. These data were then used to estimate the energy transitions (Supplemental Table S4) for binding of compound A to KRAS G12C in terms of ΔG^⧧, ΔH^⧧ and TΔS^⧧ at a standard temperature of 25 °C and are plotted on the reaction coordinate (Figure 4C). Full experimental details are found in Supplemental Method S3. The reaction coordinate plot indicates that activation of the transition state PL^⧧ toward formation of the affinity complex PL requires overcoming unfavorable entropy (−TΔS^⧧ ≈ 44 kJ mol^–1), which dominates the energy barrier and is typical of a diffusion-limited association process. The association process is enthalpy-driven (ΔH ≈ −64 kJ mol^–1) while enthalpy–entropy compensation¹⁹ results in moderate affinity binding (ΔG ≈ – 30 kJ mol^–1). Unfavorable enthalpy (ΔH^⧧ ≈ 68 kJ mol^–1) dominates formation of the adduct transition state PL_x^⧧ suggesting that partial reconfiguration of the affinity complex may be required to form the adduct PL_x. This analysis confirms the enthalpy-driven affinity binding of Compound A and justifies selection of compound A over B.

Conclusions

Direct kinetic analyses of irreversible covalent binders using k_alk is straightforward and can be done by SPR, biochemical or MS assays⁸ but it lacks the mechanistic insights that are possible from knowledge of the component fundamental rate constants. We measured negligible relative temperature variation in k_alk for all three compounds and this was found to be related to opposing relative increases in both k_off and k_inact which negate each other. While it was possible to deprioritize compound C due to its high cysteine reactivity it was not possible to unambiguously distinguish compounds A and B which had similar k_alk values. We showed that all three compounds follow the same mechanistic model which revealed the three fundamental rate constants (k_on, k_off, k_inact) allowing compound A to be clearly identified as superior. The higher C_c for compound A and its low cysteine reactivity is consistent with higher efficiency where the affinity bound conformation supports adduct formation. Eyring transition state analysis showed that the association process for compound A is enthalpy-driven yet the adduct transition state PL_x^⧧ exhibited unfavorable enthalpy suggesting partial reconfiguration of the affinity complex to form adduct PL_x. While not performed here, our optimized methodology could also be used to estimate K_i, k_alk and therefore k_inact for early hits that bind weakly and alkylate slowly. This would allow for early compound prioritization based on affinity (K_i) and mitigate the risk of highly reactive compounds with weak affinity that are difficult to optimize. In conclusion, we provide a proof-of-principle for routine and thorough kinetic and thermodynamic characterization of early covalent inhibitors for more optimal prioritization and optimization using commercially available instrumentation. The final SPR assay is scalable and can be rapidly implemented by drug discovery teams without any further guidance. The methods described eliminate the need to synthesize compounds without their reactive warhead, often used as proxies to estimate the affinity parameters without interference for alkylation. Integrating these SPR methodologies with standard biochemical and cell-based assays provides a more reliable biophysical approach to compound prioritization, ultimately contributing to the development of higher quality therapeutics.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.4c08774.

• All compounds are >95% pure by HPLC analysis. The Supporting Information contains Material and Methods and supplemental data (Table S5) along with the HPLC chromatograms (Figures S4–S6) showing the purity of the three compounds (PDF)

Author Present Address

^§ Gilead, 333 Lakeside Drive, Foster City, California 94404, United States

Author Contributions

J.G.Q. and A.F. conceived the approach, A.F. conducted SPR experiments, J.G.Q. performed all numerical simulations and N.F.E., L.K.N., and M.S. contributed to planning and execution of the cellular and biochemical experiments. The manuscript was written through contributions of J.G.Q., A.F., and M.M.M.

The authors declare no competing financial interest.