A bi-level optimization strategy of electricity-hydrogen-carbon integrated energy system considering photovoltaic and wind power uncertainty and demand response

Abstract

To address the power supply-demand imbalance caused by the uncertainty in wind turbine and photovoltaic power generation in the regional integrated energy system, this study proposes a bi-level optimization strategy that considers the uncertainties in photovoltaic and wind turbine power generation as well as demand response. The upper-level model analyzes these uncertainties by modeling short-term and long-term output errors using robust optimization theory, applies an improved stepwise carbon trading model to control carbon emissions, and finally constructs an electricity-hydrogen-carbon cooperative scheduling optimization model to reduce wind and carbon emissions. The lower-level model incentivizes users to participate in integrated demand response through dynamic energy pricing, thereby reducing the annual consumption cost of load aggregator. The Karush-Kuhn-Tucker conditions and the Big-M method are used to solve the bi-level optimization model. Simulation results indicate that the improved carbon trading model reduces carbon emissions by approximately 40.12 tons per year, a decrease of 1.1%; the prediction accuracy of the short-term error model improves by 6.77%, and the prediction accuracy of the long-term error model improves by 15.16%; the electricity-hydrogen-carbon synergistic dispatch optimization model enhances the total profit of integrated energy system operator by 14.07% and reduces the total cost of load aggregator by 10.06%.

Introduction

With the increasing prominence of global energy shortages and environmental pollution, regional integrated energy system (RIES) have received extensive attention from countries around the world due to their advantages of high efficiency, cleanliness, and low carbon emissions¹. RIES are capable of efficiently integrating various distributed energy sources, including photovoltaic (PV) power generation, wind turbine (WT) power generation, combined cooling-heating-power (CCHP), and energy storage, among others². However, RIES face two major challenges: first, the uncertainty in WT and PV power generation leads to poor reliability of supply-demand balance³; second, the dual pressure of energy shortages and environmental pollution⁴. Therefore, it is crucial to effectively reduce the error between the actual and predicted values of WT and PV power generation, to enhance the reliability of the supply-demand balance in RIES, and to minimize carbon dioxide emissions for sustainable development.

The instability of WT and PV power generation significantly impacts the operational stability and reliability of RIES⁵. When the actual output of WT and PV power exceeds the predicted value, RIES need to reduce the capacity of conventional generating units to avoid energy waste and ensure efficient utilization⁶; conversely, when the actual output is lower than the predicted value, it may lead to load loss⁷. To address these issues, many scholars have conducted extensive research. Dong et al.⁸ proposes a new hybrid robust interval optimization framework aimed at promoting flexible and robust planning while reducing operating costs of integrated energy system (IES). Wang et al.⁹ developed a multi-timescale optimal scheduling model for day-ahead and intraday operations using multi-scenario techniques and fuzzy chance-constrained planning theory, considering source-load uncertainties. Zhang et al.¹⁰ proposed a distributed robust joint opportunity constrained model to simulate a two-phase energy and reserve economic dispatch problem in an islanded microgrid. Chen et al.¹¹ developed a cooperative optimal operation and dispatch model for an integrated e-mobility network that accounts for the uncertainty of traffic demand and PV forecasting errors, incorporating them into grid load-side and source-side uncertainties. Zhou et al.¹² also introduced information gap decision theory to model bilateral uncertainties in the network. Chen et al.¹³ proposed a robust optimization-based planning method for IES with cooperative grid-side and source-side planning to handle uncertainties in renewable energy sources through robust optimization. Wu et al.¹⁴ developed a distributionally robust optimization model with scenario robust fuzzy sets to solve the scaling planning problem of integrated PV-building systems, effectively addressing uncertainties in load demand and solar irradiance. Liu et al.¹⁵ proposed a multidimensional spatio-temporal correlation scenario generation method to more accurately characterize short-time scale uncertainties caused by renewable energy and load fluctuations, capturing the least representative scenarios and their stochastic features.

Although these studies have explored methods to address the uncertainty in WT and PV power generation from multiple perspectives, they have not fully considered the short-term impact of weather factors on forecast accuracy and the long-term impact of equipment performance on forecast accuracy. In addition, as the reduction of carbon emissions has become a global consensus, RIES, as a significant source of carbon emissions, need urgent attention. However, existing studies have not yet simultaneously considered these two aspects.

The carbon trading mechanism plays a crucial role in promoting sustainable energy development and protecting the ecological environment¹⁶. Introducing a sensible carbon trading mechanism in RIES can significantly reduce carbon dioxide emissions¹⁷. Huo et al.¹⁸ proposed a seasonal carbon trading mechanism that considers the carbon emission characteristics of each cycle in the system, optimizing the stepped carbon price model and carbon quota allocation method. Shi et al.¹⁹ employed a more accurate carbon emission model to account for the actual carbon emissions of gas loads and introduced a stepped carbon trading mechanism to constrain the carbon emissions of the IES. Zhang et al.²⁰ examined the impacts of demand response and carbon trading mechanisms on the system, constructing an integrated demand response model for electricity-heat-gas loads and a stepped carbon trading model that considers the entire carbon emission process, respectively. Wang et al.²¹ proposed a coupled interaction mechanism by combining green certificates with stepped carbon trading. Gao et al.²² introduced a multi-energy coupled IES optimal scheduling model that integrates the stepped carbon trading mechanism and demand response, and explored the potential interactions between the coupling capacity of multiple heterogeneous energy sources and carbon emissions using a reward-penalty model combined with the effects of carbon capture equipment. Luo et al.²³ incorporated the carbon emissions trading mechanism into the optimal scheduling of the IES, establishing a stepwise carbon emission costing model based on distinct rewards and penalties to strictly control carbon emissions. Gao et al.²⁴ proposed an IES multi-energy trading strategy that simultaneously considers carbon emissions trading and green certificates to further promote low-carbon energy development. Duan et al.²⁵ quantified carbon trading costs using a reward-penalty ladder carbon trading mechanism and constructed an IES low-carbon economic optimization model integrating electricity-to-gas and demand response.

Despite these studies fully demonstrating that the carbon trading mechanism can effectively reduce carbon emissions in IES, the carbon trading models they employed use a fixed price ladder and apply a constant carbon price across different carbon trading quota zones. This fixed-price mechanism lacks flexibility and cannot be adjusted according to the dynamic changes in actual carbon emissions, thereby limiting its effectiveness in reducing systemic carbon emissions. For example, when systematic carbon emissions fall within a specific interval, the same carbon price is used for trading, regardless of whether actual emissions are near the lower or upper limit of the interval. This inability to accurately incentivize enterprises to further reduce carbon emissions is a significant drawback.

Existing studies have shown that combining power-to-gas (P2G) technology²⁶, carbon capture and storage (CCS)²⁷, and carbon trading mechanisms can bring significant economic and environmental benefits to RIES. Yang et al.²⁸ developed a low-carbon economic dispatch model incorporating CCS, two-stage P2G, and combined heat and power units, using a stepwise carbon trading model to constrain the carbon emissions of RIES. Zhao et al.²⁹ proposed a cooperative optimal scheduling strategy for multi-microgrid power systems based on stepped carbon trading, hydrogen-doped natural gas, and coupled P2G-CCS operations. Wu et al.³⁰ established a framework for operating a hydrogen-based integrated energy system that includes P2G and CCS under a carbon trading system. Gao et al.³¹ proposed a multi-timescale, low-carbon optimal scheduling strategy for an IES with high degrees of coupling between combined heat and power, CCS, P2G, and hydrogen. Wang et al.³² developed a low-carbon optimal dispatch model for integrated energy stations (IES) that considers carbon capture and hydrogen energy demand, effectively solving the carbon source problem for P2G, reducing net carbon emissions, and converting carbon transaction costs into profit. The above studies demonstrate the feasibility of integrating P2G, CCS, and carbon trading mechanisms into RIES.

However, most of these studies treat RIES as a unified whole without optimizing the supply side and demand side separately. Therefore, this paper optimizes both the supply side and the demand side separately. On the supply side, an electricity-hydrogen-carbon co-dispatch optimization model is established to achieve the coupled conversion between electricity, hydrogen, and carbon. The structure of the P2G-CCS system is shown in Fig. 1. It includes CCS, fuel cell (FC), electrolyzer (EL), hydrogen storage tank (HST), methane reactor (MR) and gas storage tank (GST).

Figure 1.

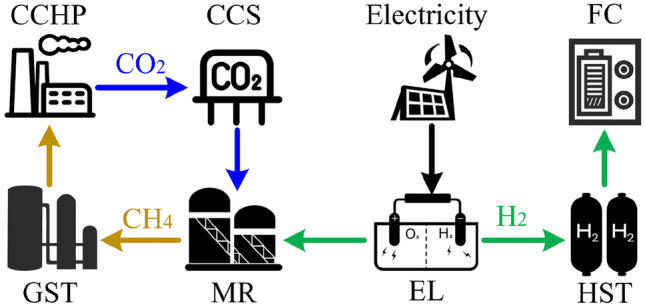
P2G-CCS cooperative scheduling system.

In summary, this study addresses the power supply-demand imbalance caused by the uncertainty of WT and PV power generation in RIES. It proposes a two-tier optimization strategy for an integrated electricity-hydrogen-carbon energy system that accounts for the uncertainty of PV and WT power as well as demand response. The strategy fully considers the short-term impact of weather factors on forecast accuracy and the long-term impact of equipment performance on forecast accuracy. It further improves the traditional stepwise carbon trading model by combining P2G and CCS technologies with the carbon trading mechanism. The goal is to enhance the reliability of the supply-demand balance, increase the utilization rate of renewable power generation, and reduce carbon emissions from RIES. The main contributions of this study are summarized below:

1) In this study, the uncertainty of WT and PV power generation is addressed, along with the influence of weather factors on short-term prediction accuracy and the influence of equipment performance on long-term prediction accuracy. This comprehensive consideration makes the scheduling model more accurate and reliable.

2) By enhancing the traditional stepwise carbon trading model, a more flexible carbon trading mechanism is proposed. This mechanism can dynamically adjust the carbon price based on actual carbon emissions, thereby more accurately incentivizing enterprises and users to reduce their carbon emissions.

3) A bi-level optimization strategy combining P2G-CCS-IDR is proposed to optimize the system from both the supply side and the demand side. This approach enhances the operational efficiency and reliability of the entire system in a more comprehensive manner. The utilization of renewable energy and the system’s low-carbon performance are effectively improved.

The rest of the paper is organized as follows. “Structure and model of RIES” describes the system architecture and device model of IES. A B-L optimization model is developed in “A B-L optimization model for RIES”. Robust stochastic optimization theory is introduced in “Uncertainty modeling of RIES” to deal with the associated uncertainties, and a model is constructed for short and long-term prediction deviations as a function of time-lapse. “Model solving methods” presents a methodology for solving this model. “Example analysis” presents a case study. “Conclusion” presents the main conclusions and suggests future work.

Structure and model of RIES

Structure of RIES

In this paper, we take the RIES as the research object, and the region contains many types of energy sources such as electricity, heat, cold, natural gas, hydrogen, etc., and its structure is shown in Fig. 2. Four components are included in the system: energy supply, conversion, storage, and consumption. The energy supply component includes power networks (PN), gas network (GN), PV, and WT; The energy conversion part mainly includes gas turbine (GT), gas boiler (GB), waste heat boiler (WHB), absorption chiller(AC), electric chiller (EC), and P2G-CCS; The energy storage system mainly consists of electricity storage system (ESS), heat storage system (HSS), gas storage tanks (GST), and hydrogen storage tanks (HST). Since the cold load can be converted by electricity and heat, no cold storage equipment is installed in the system to minimize energy loss and reduce costs.

Figure 2.

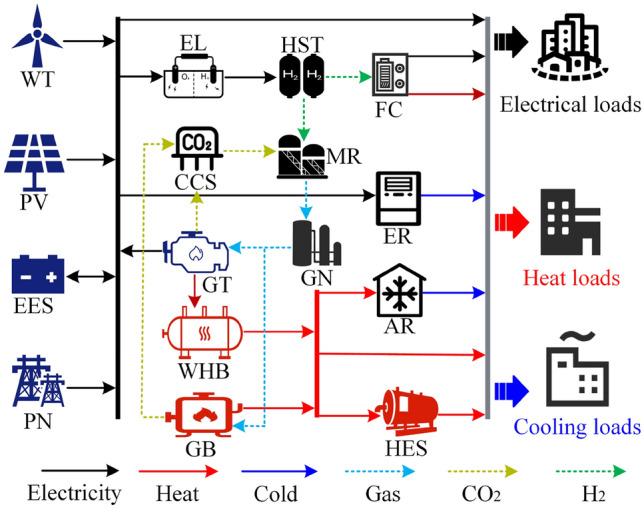
Structure of RIES.

PV and WT generation by the weather has uncertainty, although ESS can alleviate the problem of uncertainty brought about by PV and WT generation, ESS can only be the short-cycle power supply and demand balance adjustment, if you need to carry out a large-scale new energy across the seasons, long cycle of energy storage, ESS capacity limitations will be relatively obvious. In contrast, the biggest advantage of hydrogen storage tanks is a longer range, larger system capacity, and lower investment cost per unit capacity. Combined with their low self-decay rate, high energy density, and other characteristics, hydrogen storage tanks have obvious advantages in multi-day continuous peaking and quarterly peaking.

During the low power consumption period, the P2G unit is utilized to convert the excess power into hydrogen, which is stored in the HST; during the peak power consumption period hydrogen is used as the fuel, and the FC is utilized to generate electricity, and heat to meet the user’s demand, thus promoting the consumption of renewable energy, which has a similar functional role to that of the ESS. It is also possible to use hydrogen and carbon dioxide to make methane, and the resulting methane is injected into the GN for use in other energy conversion equipment, improving energy efficiency and reducing carbon dioxide emissions to some extent. In addition, the operation of GT and GB generates a large amount of carbon dioxide, and CCS captures a portion of this carbon dioxide to be traded in the carbon trading market, the carbon trading mechanism is a key support for IES to achieve its low-carbon goals. To further limit IES carbon emissions, this paper introduces an improved stepped carbon trading mechanism.

Model of RIES

Model of energy supply equipment

(1) Operational model of WT

The operation state and output power of the WT depend mainly on the wind speed, e.g., at higher wind speeds, it will produce greater output power. The relationship between WT output and wind speed is:

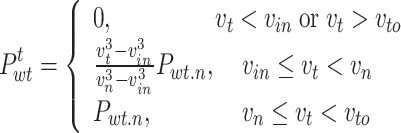1

where 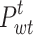indicates the predicted power of the WT; 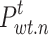indicates the rated output power of the fan; 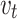indicates real-time wind speed; 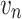, , 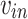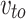are the rated wind speed, cut-in wind speed, and cut-out wind speed of the WT, respectively.

(2) Model of PV

The operation state and output power of PV are mainly affected by temperature and light intensity, and the output power of PV power generation can be expressed as:

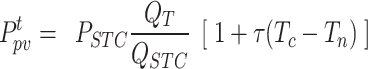2

where 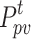, , 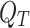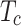are the PV output power, light radiation, and temperature, respectively; 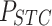, , 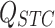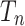are the PV rated output power, rated light radiation, and rated temperature standard conditions, respectively; 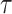denotes the power temperature coefficient.

(3) Model of GT

3

where 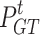denotes the power generated by the GT; 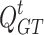denotes the natural gas consumption of the GT; 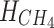denotes the low calorific value of natural gas; 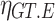denotes the power generation efficiency of the GT.

(4) Model of WHB

The GT generates a large amount of waste heat that is recovered by the WHB, and the relationship between the amount of waste heat recovered and the output electric power of the GT can be expressed as follows.

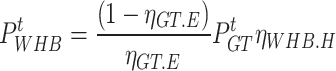4

where 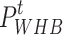denotes the output power of the WHB; 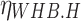denotes the working efficiency of the WHB.

(5) Model of GB

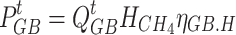5

where 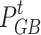denotes the output power of the GB, 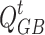denotes the amount of natural gas consumed by the GB, and 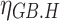denotes the operating efficiency of the GB.

(6) Model of EC

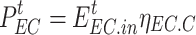6

where 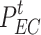is the output power of the EC; 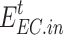is the power consumption of the EC; 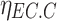is the working efficiency of the EC.

(7) Model of AC

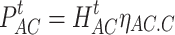7

where 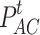is the output power of the AC; 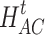is the heat consumed by the AC; 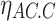is the working efficiency of the AC.

Model of energy storage equipment

Energy storage types of equipment in IES mainly have ESS, HSS, HST, and GST, among which the mathematical models of ESS and HSS are similar. Taking ESS as an example, the running model is as follows.

When the ESS is charging:

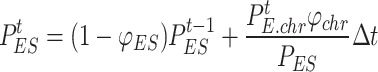8

When the ESS is discharging:

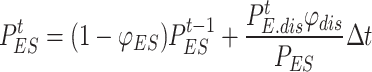9

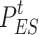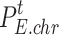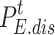where denotes the SOC of the ESS at time t ; and are the charging power and discharging power of the ESS at time t , respectively; 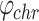and 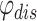are the charging efficiency and discharging efficiency of the ESS, respectively; 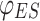denotes the self-depletion rate of the ESS; 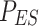denotes the rated capacity of the ESS; and 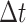denotes the running time of the unit.

The mathematical model is similar between HST and GST. Taking HST as an example, the model is as follows.

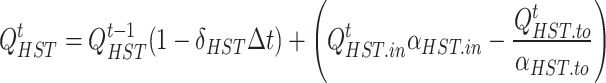10

where 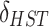, 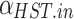and 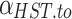are the self-depletion rate, charging efficiency, and discharging efficiency of the hydrogen storage tank, respectively; 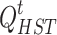and 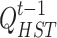are the amount of hydrogen stored in period t and period t-1, respectively; 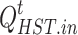and are the charging and discharging power of the hydrogen storage tank in period t, respectively.

Model of P2G-CCS

Currently, CCS technology has certain shortcomings, such as the fact that it is very expensive to transport captured carbon dioxide over long distances to a safe location for storage and that there is still a risk of possible leakage of the stored carbon dioxide. At the same time, the carbon dioxide generally required for synthesizing methane needs to be purchased from the carbon trading market, which will greatly increase the operating costs of the system and lead to poor economics. Therefore, this paper considers the combination of P2G and CCS to realize the local utilization of carbon dioxide generated by carbon capture, which not only reduces the carbon emission and carbon trading costs of the IES but also avoids the costs and risks associated with the transmission of sequestered carbon dioxide. The presence of CCS effectively reduces the amount of carbon dioxide purchased for the synthesis of methane in the electrically converted gas, which in turn reduces the operating cost of the entire system, as shown in the coupled P2G-CCS model below.

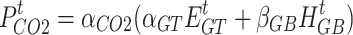11

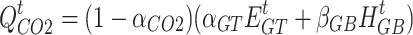12

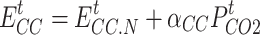13

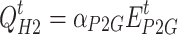14

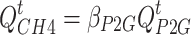15

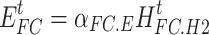16

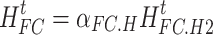17

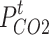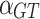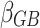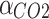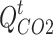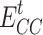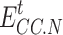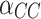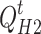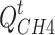where is the carbon dioxide captured by CCS; and are the carbon emissions per unit output power of GT and GB; is the working efficiency of CCS; is the carbon dioxide not captured by CCS; and are the energy consumption of CCS operation and stationary energy consumption, respectively; is the energy consumption coefficient of CCS; and are the hydrogen and methane produced by P2G, respectively; 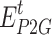is the electric power consumed for hydrogen production; 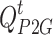is the hydrogen power consumed for methane production; 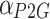is the efficiency of hydrogen production by electricity; 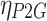is the efficiency of methane production by hydrogen; 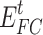and a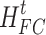re the power generation and heating power of the FC, respectively; 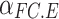and 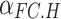are the power generation and heating efficiencies of the FC, respectively; 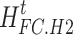is the hydrogen power input into the FC.

Improved cascade carbon trading model

The sources of carbon emissions in the IES of this paper are GT, GB, electricity purchased from the grid and fuel purchases. Carbon emission allowances are modeled as follows.

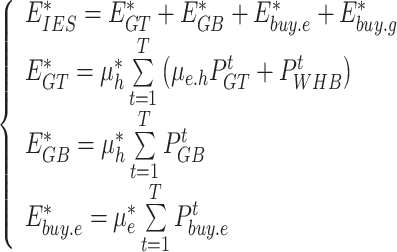18

where 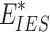denotes the total carbon emission allowances of IES; 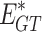, 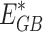and 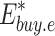denote the carbon emission allowances of GT, GB and electricity purchased from the grid respectively; 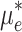and 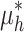denote the carbon emission allowances obtained from the production of electricity and heat power respectively; and denotes the conversion factor of electricity and heat for GT.

It is set that all electricity purchased from the grid is produced by coal-fired units, and at the same time, some carbon dioxide is absorbed when the P2G equipment is operated. The actual carbon emissions are modeled as follows.

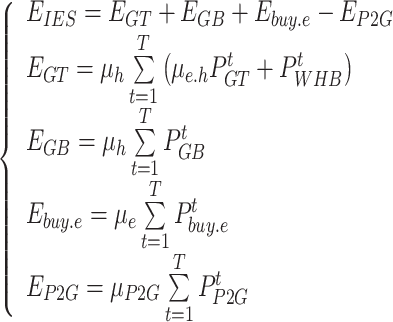19

Where 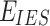denotes the actual carbon emissions from IES; 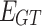, , 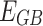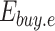denote the actual carbon emissions from GT, GB, and electricity purchased from the grid, respectively; 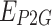denotes the actual carbon emissions from the consumption of P2G units; 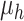, 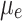denote the actual carbon emissions from the production of units of electric power and thermal power, respectively; and 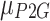denotes the actual carbon emissions from the consumption of units of P2G equipment.

In a carbon trading settlement cycle, the amount of IES ’participation in the carbon trading market is determined by the difference between IES’ actual carbon emissions and carbon emission allowances.

20

The traditional stepped carbon trading mechanism limits systematic carbon emissions by setting a stepped carbon price at different carbon trading allowance bands. Whenever the carbon trading volume rises by one interval, the base price of carbon trading in the corresponding interval will rise to achieve the purpose of limiting carbon emissions. In this paper, we refer to the literature³³, based on the traditional laddered carbon price, the carbon price is further optimized in each carbon trading amount interval, we further optimize the processing and introduce an improved carbon trading mechanism with the following formula.

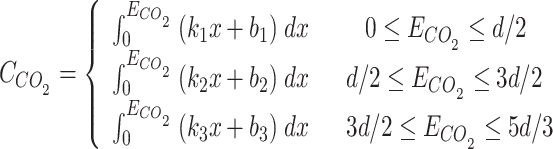21

where 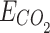is the carbon trading quota; 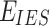is the actual carbon emissions of IES; 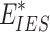is the carbon emission quota of IES; 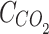is the carbon trading cost; d is the carbon trading quota range; k is the growth slope of the price function; b is the intercept of the price function.

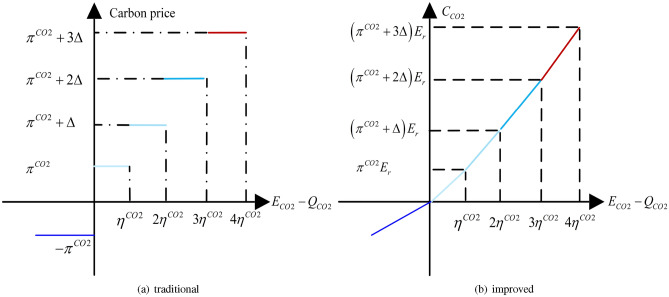
The improved stepped carbon trading price is a four-stage linear function with a sequentially increasing slope. When the system’s carbon emissions are less than the corresponding standard carbon emission range, the traditional stepped carbon trading mechanism uses the standard carbon base price for carbon trading. The improved carbon trading price is not fixed but increases linearly with the volume of carbon traded to limit carbon emissions. For example, when carbon emissions are in stages 0 to d, the improved carbon trading price is lower than the traditional carbon trading price when carbon emissions are less than d/2 , and the improved carbon trading price is higher than the traditional carbon trading price when carbon emissions are greater than d/2, and similarly when carbon emissions are in other stages, to achieve the purpose of limiting carbon emissions . The comparison of the traditional laddered carbon trading mechanism and the improved laddered carbon trading mechanism is shown in Fig. 3.

Figure 3.

Comparison of two carbon trading mechanisms.

In the traditional stepped carbon trading model, a fixed price step is set based on carbon emissions. The improved model, however, introduces a dynamic pricing mechanism. When carbon emissions fall below a certain threshold (e.g., d/2), the carbon trading price in the improved model is lower than in the traditional model. Once emissions exceed that threshold, the carbon trading price in the improved model rises above the traditional model’s price. This dynamic approach is designed to more effectively discourage high emissions and encourage low emissions, promoting better economic and environmentally friendly carbon management. This improvement ensures that the price is adjusted dynamically according to the level of emissions at different stages, allowing carbon emissions to be better controlled and managed.

Model of IDR

The IDR model of loads studied in this paper includes transferable electric loads, curtailable electric loads, curtailable heat loads, and curtailable cold loads. Transferable electric load refers to the transfer of the electric load of certain equipment at a certain time to another time to balance the load demand of the power system and ensure the stability and reliability of the power supply. Curtailable load refers to the reduction of IES load demand by various means to alleviate the problem of overloading the system, which can lead to energy saving, balancing supply and demand, and improving the stability of the IES.

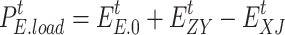22

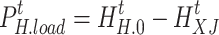23

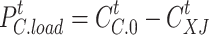24

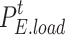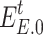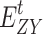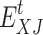where is the electric load after participating in demand response; is the initial electric load; and are the transferred and curtailed electric load, respectively; 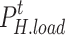is the heat load after participating in demand response; 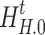is the initial heat load; 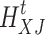is the curtailed heat load; 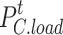is the cold load after participating in demand response; 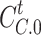is the initial cold load; and 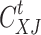is the curtailed cold load, respectively.

A B-L optimization model for RIES

B-L optimization model of RIES

The B-L optimization problem has an obvious recursive structure, the upper and lower problems have their objective functions, decision variables, and constraints, but there is a strong coupling relationship between them, and the upper-level and lower-level influence each other. In the B-L optimization problem, the first decision maker is called the leader, the later decision maker is called the follower, and the follower makes a reaction decision according to the leader’s decision. The decision model can be expressed as follows:

Leader Decision Model:

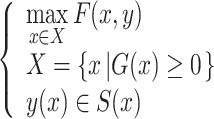25

Follower Decision Model:

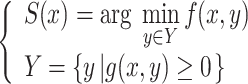26

where x , y denote the leader’s and follower’s strategies, X , Y denote the leader’s and follower’s strategy sets, respectively; F(x, y) , f(x, y) denote the leader’s and follower’s objective functions, respectively; G(x) , g(x, y) denote the leader’s and follower’s constraints, respectively; and S(x) denotes the set of optimal solutions to the follower’s problem with x as a parameter.

In this paper, IESO is the leader and LA is the follower. IESO and LA make decisions in a non-cooperative sequential manner, with IESO choosing strategy x and LA choosing its strategy y based on IESO’s strategy x, the strategy of IESO not only affects the objective function f(x, y) of LA but also affects the set of strategies Y(x) of LA. Although the LA’s strategy y also affects the IESO’s objective function, the IESO can anticipate the LA’s reaction y(x) when it adopts a strategy x, Therefore, IESO need to consider responses from LAs when making decisions.

Upper-level optimization model

The upper-level optimization model begins by analyzing the economic aspects of IESO operation, taking into account important factors like fuel procurement and carbon trading. The objective function of the upper-level model aims to maximize the annual operating revenue of IESO. Moreover, the model must comply with various constraints, such as maintaining system power balance and ensuring efficient energy supply and storage operations. These constraints are integral to the overall optimization process of the upper-level model.

Objective function

In the upper-level optimization model, the objective function is designed to maximize the annual operating revenue of the IESO. Consequently, equipment investment costs are not taken into account. Additionally, the maintenance costs of individual equipment are relatively low compared to the annual operating costs, and therefore, they are not considered either. The operating costs of the IESO primarily include fuel costs, purchased power costs, expenses related to demand response resources, and costs associated with carbon trading. These factors play a crucial role in determining the overall operating costs of the IESO within the optimization model.

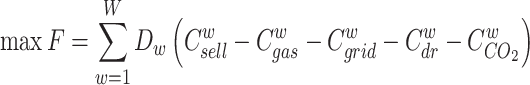27

where W denotes the type of typical days, including spring, summer, fall, and winter, 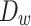denotes the number of typical days.

(1) Sales income

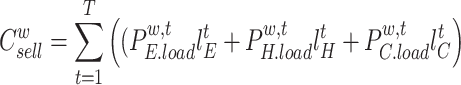28

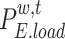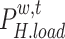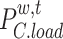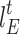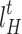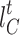where , , and denote the electricity, heat, and cold loads purchased by LA; , and denote the electric, heat, and cold prices, respectively.

(2) DR Cost

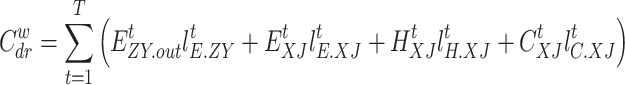29

where 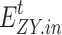, 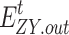and 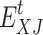denote the amount of electric load transfer, transfer out, and reduction, respectively; 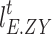and 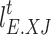denote the unit price of electric load transfer compensation and reduction compensation, respectively; 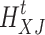and 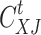denote the amount of reduction of heat load and cold load, respectively; 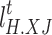and 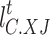denote the unit price of reduction compensation of heat load and cold load, respectively.

(3) Gas purchase cost

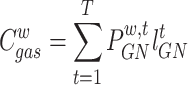30

where 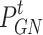indicates the gas purchased by IESO from the gas grid; 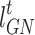indicates the unit price of natural gas.

(4) Electricity purchasing cost

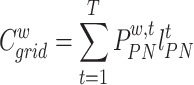31

where 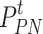indicates the electric power purchased by IESO from the grid; 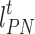indicates the grid time-of-day tariff.

(5) Carbon trading

The cost of carbon trading has been analyzed in the previous model. Since the addition of CCS and P2G devices makes the carbon emission quota larger than the actual carbon emission, carbon trading can be regarded as income.

Constraint conditions

The key constraints involved in the upper-level optimization model mainly include the requirement to ensure the balance between energy supply and demand, equipment operation constraints, power purchase constraints, and gas purchase constraints.

(1) Energy supply and demand balance constraints

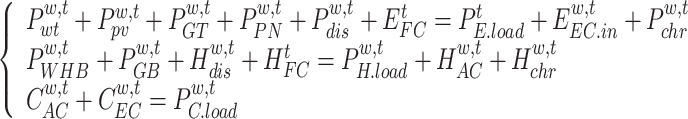32

(2) GT operational constraints

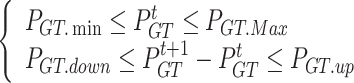33

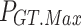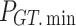where and denote the upper and lower limits of GT power; 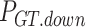and 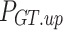denote the downward and upward climb power limits of GT respectively.

(3) GB operational constraints

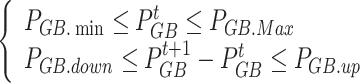34

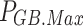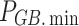where and denote the upper and lower limits of GT power, respectively; 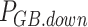and 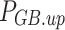denote the downward and upward climb power limits of GT, respectively.

(4) Energy storage device operational constraints

Considering the cyclicality and technical characteristics of the operation of the energy storage device, the initial SOC of the ESS is the same as the final SOC, and charging and discharging cannot be performed simultaneously. The same applies to other energy storage devices.

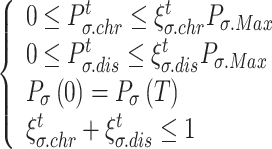35

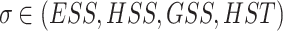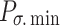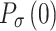where , and denote the minimum and maximum capacities of the energy storage device, respectively, and 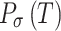denote the beginning and end SOC of the energy storage device, respectively.

The GST and HST are used to store natural gas and hydrogen converted by the P2G unit, respectively. Therefore, to maintain balance, their filling power must be less than or equal to the gas production power of the P2G unit.

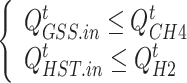36

where 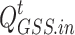denotes the filling power of the GST; 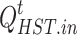denotes the filling power of the HST.

(5) Other equipment operating constraints

37

where , 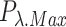and 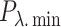denote the upper and lower limits of the device 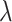power, respectively.

(6) Price constraints

To remain competitive, IESOs must sell energy at prices lower than grid time-of-day tariffs so that they can attract more market share. The same applies to cold and heat.

38

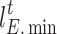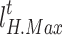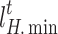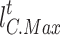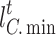where and denote the upper and lower limits of electricity price, respectively; and denote the upper and lower limits of heat price; and are the upper and lower limits of cold price, respectively.

(7) External power and gas purchase constraints

Due to the pressure limitations of the natural gas network and the power limitations of the grid, the power purchased by IESO for electricity and natural gas should not exceed the limitations.

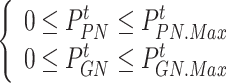39

where 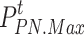and 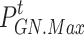represent the maximum power limits for purchasing electricity and natural gas, respectively.

(8) Other constraints

Since the power consumed by P2G mainly comes from abandoned WT and PV, the power consumed by P2G should be less than the sum of abandoned WT and PV.

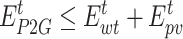40

where 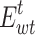and 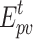denote the abandoned WT and PV, respectively.

Lower-level optimization model

The lower-level optimization model considers the economic aspects for the user, taking into account the cost of procuring energy and the revenue generated from selling IDR resources. The objective is to minimize the LA’s annual consumption cost while satisfying the constraints associated with load demand response.

Objective function

The LA’s target benefit is the cost of purchasing electricity, heat, and cold energy minus the benefit from IDR. The objective function can be expressed as:

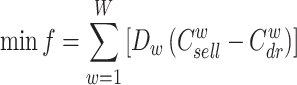41

where f denotes the annual consumption cost of the LA.

Constraint conditions

The constraints of the lower-level optimization model mainly include electrical load transfer constraints, electrical load curtailment constraints, heat load curtailment constraints, and cold load curtailment constraints.

(1) Electricity load transfer constraints Load transfer constraints include load transfer-in constraints and load transfer-out constraints, firstly, the amount of load transferred in at the moment t must be transferred out at the moment t+a ; secondly, at the same moment of the same cycle, load transfers in and load transfers out can’t be carried out at the same time, and the number of loads transferred in and load transfers out should be smaller than its upper limit.

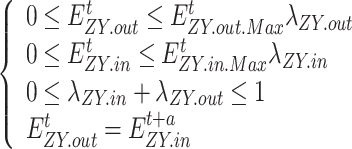42

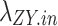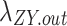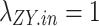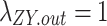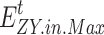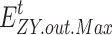where, and denote the 0-1 variable, when , it means that the load is transferred, and when , it means that the load is transferred out; and denote the upper limit of the amount of electricity load transferred in and transferred out, respectively.

(2) Electricity load curtailment constraints

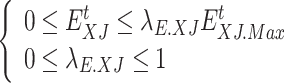43

where denotes the 0-1 variable, and 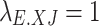indicates that electricity load curtailment occurs. 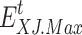is the upper limit of electricity load curtailment.

(3) Heat load curtailment constraints

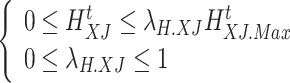44

where 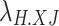denotes the 0-1 variable, and 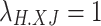indicates that heat load curtailment occurs. 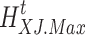is the upper limit of heat load curtailment.

(4) Cold load curtailment constraints

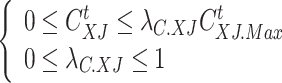45

where 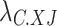denotes the 0-1 variable, and 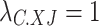indicates that cold load curtailment occurs. 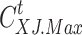is the upper limit of cold load curtailment.

Uncertainty modeling of RIES

Robust stochastic optimization model

Affected by natural factors, WT and PV has certain randomness, volatility, and uncertainty, which brings certain threat to the smooth operation of the power system, to avoid the risk of WT and PV uncertainty to the RIES, this paper adopts the combination of interval linear programming and robust optimization to establish the uncertainty model of WT and PV. The WT and PV in the uncertain form are as follows³⁴.

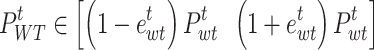46

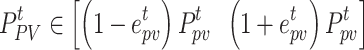47

where 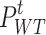and 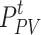denote the uncertainty forms of WT and PV, respectively; 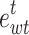and 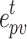denote the error coefficients of WT and PV, respectively; Converting the above uncertainty model into an equational form, it can be expressed as:

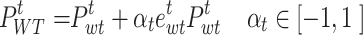48

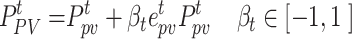49

Guarantee the electricity demand, the power supplied has to be greater than or equal to the power used, so the supply-demand balance constraint can be converted into the following inequality constraint:

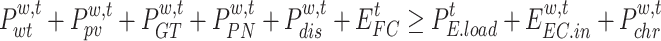50

Assuming that 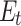is the net load of the RIES, the net load can be expressed as follows, which can then be obtained by substituting the above uncertainty model into the above equation:

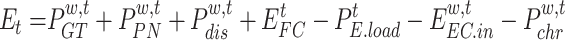51

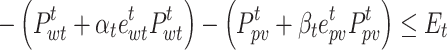52

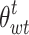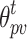However, the above inequality is highly uncertain and almost impossible to reach the extremes. Assuming that and denote the boundary thresholds where the actual output power of WT and PV is in the prediction interval, respectively, and 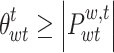, , 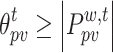then the robust coefficients 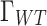, , 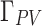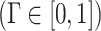are introduced:

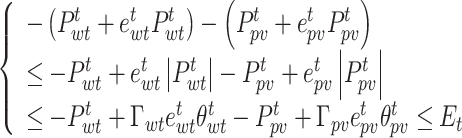53

Combined with the above model, the robust stochastic optimization-based operation optimization model for the RIES is developed as follows:

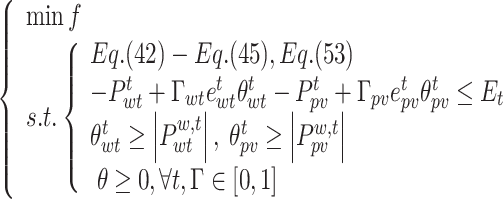54

Robust stochastic optimization model considering the effect of prediction times

Traditional WT and PV unit output prediction only considers the impact of wind speed on WT power generation and the impact of environmental factors such as irradiance, ambient temperature, relative humidity, and dust on PV. However, over time, the performance of WT and PV unit equipment changes, and changes in equipment performance also affect unit output, which in turn affects the prediction of WT and PV unit output. The researchers found that WT in operation for 10 years experienced an average annual decline in output of up to 3.6 percent. As a result, the power generation performance of WT and PV units gradually decays over time until they become obsolete. The output power of WT and PV at each cycle must satisfy the following conditions³⁵.

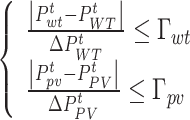55

where 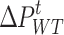and 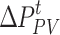are the allowable deviations of WT and PV generation forecasts, respectively.

Short-term intra-day predictive analysis

WT and PV are most affected by weather factors primarily, and the accuracy of weather forecasts decreases over time, leading to a gradual decrease in the accuracy of wind and PV forecasts

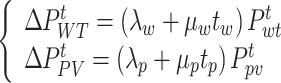56

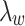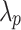where and denote the intercept of the linear function, respectively; 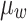and 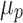denote the slope of the linear function, respectively.

Long-term intra-year forecast analysis

Since the actual output of WT and PV decreases gradually with the long-term operation of the equipment, the prediction error between the predicted and actual values of WT and PV increases gradually with time, and the permissible deviation of the prediction of WT and PV will also increase gradually, which is nonlinearly related to time.

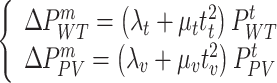57

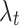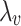where and denote the intercept of the linear function, respectively; 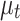and 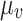denote the slope of the linear function, respectively.

Model solving methods

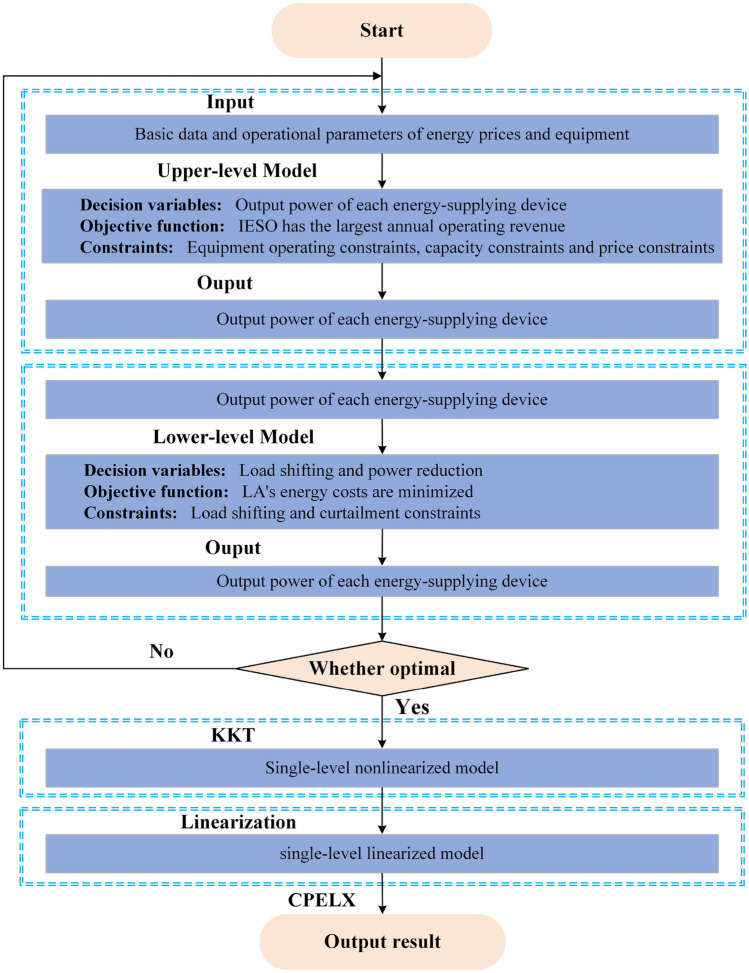
Analytical methods and heuristic algorithms are currently the two mainstream methods for solving B-L optimization problems. The KKT condition was used by the analytic method to transform a B-L optimization problem into a sl-L optimization problem, which is then solved directly using the well-established solver CLPEX. Compared with the analytical method, the heuristic algorithm needs to repeat the search for many iterations, which increases the difficulty of solving and does not guarantee the optimal solution. In contrast, the analytic method can find the optimal solution quickly and accurately and does not require multiple iterations. Therefore, this paper adopts the analytical method to solve the B-L model, and compared with the heuristic algorithm in the literature^36,37, the method used in this paper eliminates the need for multiple iterations and allows the optimal solution of the model to be determined simultaneously in a short time. The solution flow is shown in Fig. 4.

Figure 4.

Flowchart for solving the B-L optimization model.

Using the KKT condition to use the lower model as an additional constraint to the upper model, the objective function and constraints of the lower model are multiplied by the Lagrange multipliers, the Lagrangian function model as follows:

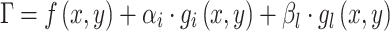58

The B-L optimization model (25)–(26) is then converted to a single-level optimization model (59).

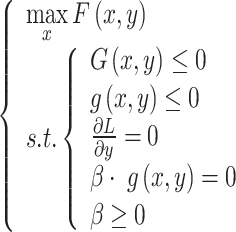59

Introducing a sufficiently large constant M and a binary variable v with a value of 0 or 1 converts the nonlinear term to a linear term. The magnitude of the value of M is relative to and g(x, y) .

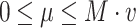60

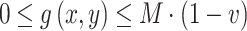61

In this section, the lower-level optimization problem is equivalently transformed through the KKT condition, which in turn transforms the original B-L model into a Single-level nonlinear optimization problem.

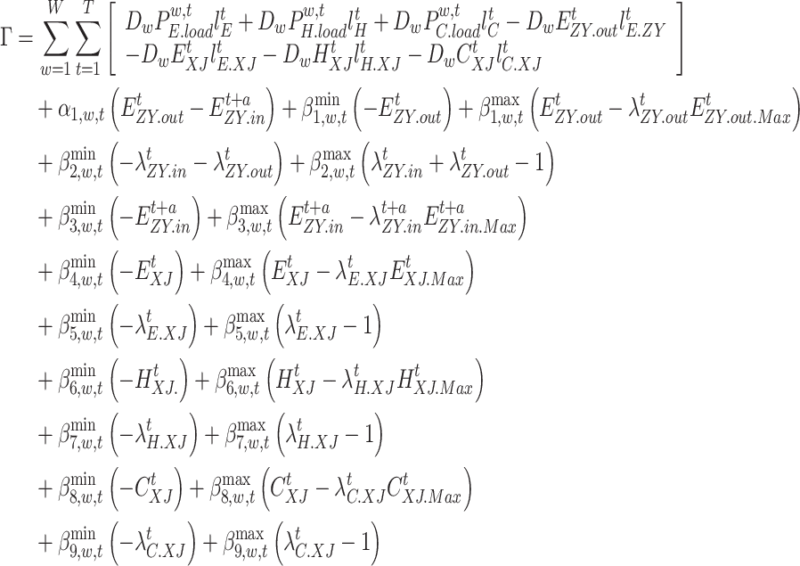62

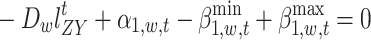63

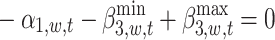64

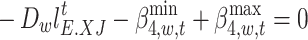65

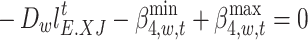66

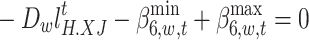67

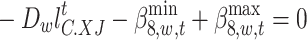68

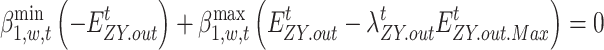69

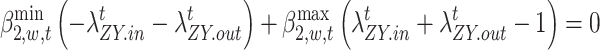70

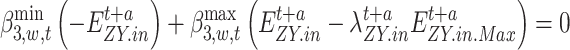71

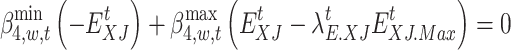72

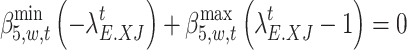73

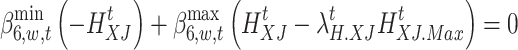74

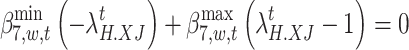75

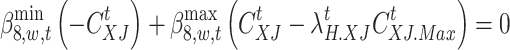76

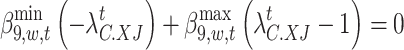77

In this paper, nonlinear constraints are transformed into linear constraints by introducing Boolean variables and Big M. The category is equations (69)–(77). Taking Eq. (69) as an example, it can be transformed into Eq. (78). The rest of the transformation process is the same and can be expressed as follows:

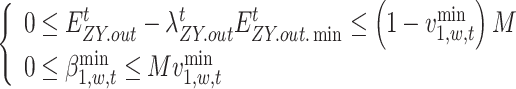78

Example analysis

Basic data

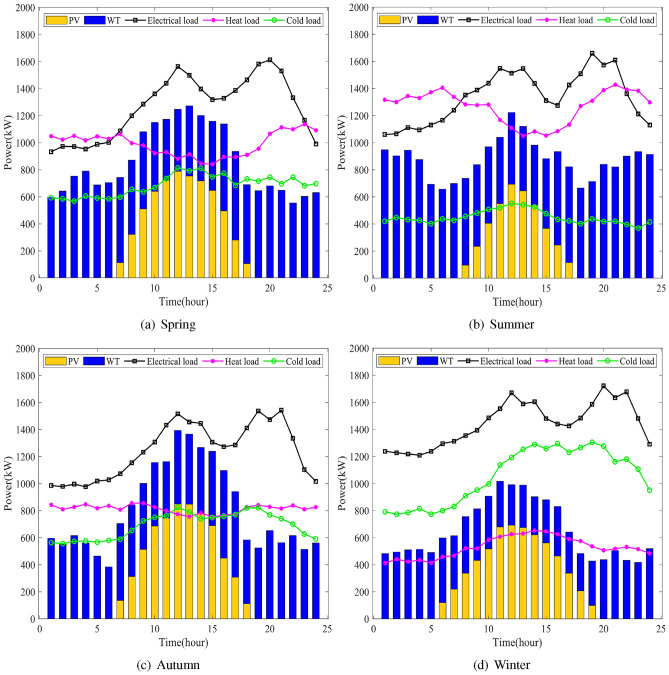
In this paper, a CCHP type RIES in northern China is taken as the object of study. The region’s electrical, heat, and cold loads and the predicted four-season production of PV and WT are shown in Fig. 5. The annual scheduling cycle consists of four seasons, spring, summer, autumn, and winter, each lasting 91 days. Also, the daily scheduling cycle is 24 hours. The calorific value of natural gas is 9.97 kW/; IESO purchases natural gas at 2.50 ¥/; The unit price of compensation for electric load transfer is 0.8 ¥/kW; the unit price of curtailment for electrical load reduction is 1.2 ¥/kW; the unit price of curtailment for heat load reduction is 0.6 ¥/kW; and the unit price of curtailment for cold load reduction is 0.4 ¥/kW; The cut-in, rated and cut-out wind speeds for WT are 3 m/s, 12 m/s, and 22 m/s, respectively. The allowable deviation rate at the initial time for PV and WT is 1%, and the slope of the PV and WT error to the prediction time is 0.01. The initial robustness factor is set to 1. The equipment operating parameters are given in Tables 1, 2 and 3, and carbon trading parameters are given in Table 4.

Figure 5.

Electrical, heat, and cold loads and the predicted four-season production of PV and WT.

Table 1.

Energy trading prices.

Energy	Peak hour prices/¥ (9:00-12:00,17:00-21:00)	Prices for general hours/¥ (7:00-8:00,13:00-16:00,22:00-23:00)	Prices at the trough/¥ (24:00-6:00)
Electricity	1.2	0.8	0.4
Heat	0.6	0.5	0.4
Cold	0.4	0.3	0.2

Table 2.

Equipment parameters.

Equipment	Rated power/kW	Operation efficiency/%	Climbing/kW
GT	1000	35	− 200,200
GB	800	85	− 160,160
P2G	300	60	− 60,60
FC	200	60	− 40,40
WHB	1200	90	*
EC	1000	320	*
AC	800	120	*
CCS	1000	80	*

Table 3.

Energy storage parameters.

Types	Charging efficiency /%	Discharging efficiency/%	Minimum SOC/%	Maximum SOC/%	Initial SOC/%	Rated power/ kW
ESS	95	95	10	90	50	500
HSS	95	95	10	90	50	500
HST	95	95	10	90	50	500
GST	95	95	10	90	50	500

Table 4.

Carbon emission parameters.

Parameters	Numerical value
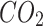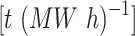
emissions per unit of electricity /	1.08
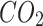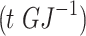
emissions per unit of heat /	0.065
Carbon credit allowance factors for natural gas units /	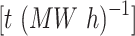0.367
Carbon credit allowance factors for coal-fired units /	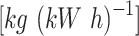0.728
Electricity-heat conversion factor /	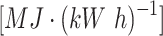6
Length of interval per unit of carbon emissions /kg	5000
Carbon trading base price C1 /¥	0.2
Carbon trading base price C2 /¥	C1+0.25
Carbon trading base price C3 /¥	C2+0.30
Carbon trading base price C4 /¥	C3+0.35

Solution results of B-L optimization model

The above parameters were input into the model and after 4.54s of solving, the optimal solutions for the upper and lower models were obtained. Table 5 shows the operating benefits and costs of IESO and LA during the four seasons. In addition to this, we can also see the carbon emissions and the utilization of WT and PV. The abandonment of WT and PV can be converted to hydrogen and methane by P2G to be reused, so the wind and solar utilization rate is 100% in all four seasons. As the total amount of new energy generation is relatively low in summer, while the demand for electric and cooling loads is relatively high, it is necessary to purchase power from external grids, thus generating more .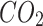

Upper-level optimization model solution results

Based on the influence of the lower model on the decisions of the upper model, with the overall economics of the IESO as the starting point, the decision variables of the upper optimization model are the output of each unit of equipment. The objective is to maximize the annual operating revenue of the IESO. Based on the results of the lower-level model, the optimal operating solution solution of the upper-level model is derived, which is shown in Table 6. The objective function value for the upper model is 10,339,319.9 ¥, which means that the annual operating revenue of IESO is 10,339,319.9 ¥.

Table 5.

Costs and benefits of a typical day’s operation for four seasons.

Energy	Benefit IESO (¥)	Cost LA (¥/kW)	Emission (kg)	Utilization (%)
Spring	29,613.18	41,514.10	10,327.09	100
Summer	26,206.22	41,266.92	15,139.04	100
Autumn	27,278.87	38,907.50	9,939.32	100
Winter	30,520.63	43,684.74	11,785.24	100
Total	113,618.9	165,373.26	47,190.69	100

According to the data in Table 6, the power supply units within IESO can meet the main power demand under the typical day’s power load in spring without purchasing power from the higher grid. In North China, on the other hand, due to the persistent cold climate, the heat demand is higher, so GT generation is mainly used for heating, and only a small portion of the heat is absorbed by the AC units for cooling. The cold load is mainly supplied by the EC unit, which consumes 4266.5 kW.

Table 6.

IESO four-season typical day operating scenario for each equipment.

Typical day	Electricity (kW)							Heat (kW)					Cold (kW)
	WT	PV	GT	EC	FC	ESS	Buy	WHB	GB	FC	HSS	AC	AC	EC
Spring	14,515	6063	14,328	− 4266.5	61.2	940.8	0	22,087	2061.1	61.2	1220.9	− 1780.9	2137.1	13,652
Summer	9700	5960	18,030	− 1551.5	50.7	850.6	2385.4	27,792	0	50.7	818.9	− 15690	18,828.1	4964.9
Autumn	12,942	6431	14,120	− 3311	19.7	1130.3	0	21,765	1118	19.7	736.8	− 4440.4	5328.5	10,595.3
Winter	17,162	3893	14,413	− 2986	73.8	1013.1	0	22,217	7045.7	73.8	1184.9	− 635.9	763.1	9556.6

The electricity load is higher on a typical summer day, and the WT output is lower due to lower wind speeds in the summer. Summer is hot and rainy, and PV is not the highest all year round, so it is necessary to purchase 2385.4 kW of electricity from the grid to ensure that the electricity load demand is met. Due to the low heat load in summer, the GT generates a large amount of waste heat sufficient to supply the heat load, so the GB does not need to run. However, in summer, when the cold load is relatively high, the GT generates waste heat, which is converted to cold except for supplying the heat load, and the PV power generation is higher from 10:00 to 14:00, so the GT output is lower in this period and the EC output will increase.

The electrical load on a typical day in the Autumn is supplied primarily through the various power supply units within the IESO, and there is also no need to purchase power from the higher grid. Since it remains hot in the fall, its cold demand is relatively high, with one-third of the cold load being supplied by AC and the rest by ER, which consumes 3311 kW of electricity.

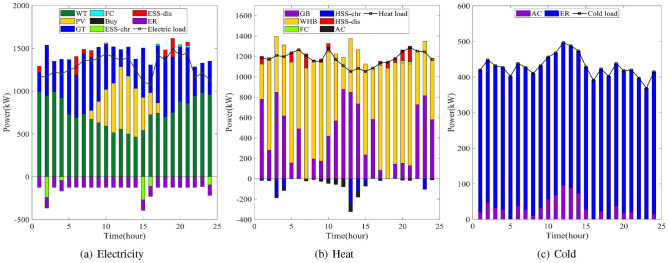
According to the analysis results, the operation scheme obtained by the B-L optimization model is consistent with the real-life operation rules, thus verifying the effectiveness of the proposed model. The designed CCHP system is capable of flexible scheduling according to the load characteristics of different seasons and realizes the coordinated and complementary supply of multiple energy sources. However, in the actual operation of IESO, the operation decision of the equipment must take into account the actual load demand per hour to realize fine management and economic operation. Figure 6 shows the optimized scheduling results of IESO for a typical day in winter.

Figure 6.

Optimal scheduling results for a typical winter day.

Compared to other seasons, winter days are characterized by higher WT at night and lower PV during the day. Electricity loads show a “double peak” pattern from 11:00 to 13:00 and from 18:00 to 22:00. Electricity load demand is mainly met by WT, PV, and GT, which are abundant and do not need to buy electricity from the grid. When there is an excess supply of electricity during periods of low electricity consumption, part of the excess electricity is stored by the battery, and the other part is converted into hydrogen for use in FC or into methane for use in gas-fired equipment through the P2G. With a robustness factor of 1, the utilization rate of WT and PV on a typical winter day is 93.4%. Although WT and PV cannot be fully used for electricity supply, the remaining electricity from WT and PV is made into methane and hydrogen by P2G, and there is no WT and PV abandonment.

The supply of heat load mainly depends on the WHB, in addition to the WT and PV to supply the electric load demand, the shortfall is mainly supplied by the GT, which generates a lot of waste heat during operation, to promote the gradient utilization of energy, these waste heat will be recycled through the WHB, and after treatment to supply the heat load. However, during the night, when the WT output is high and the electrical load demand is low, the reduced output of the GT results in less heat being produced by the WHB, making it necessary to start up the GB to meet the remaining heat load demand. During the 10:00 to 14:00, although the GT generates less power, the PV will supply a large amount of electricity at this time, which will also lead to a reduction in the GT output, and therefore the GB will need to be activated as well to meet the residual heat load demand.

During the 11:00 to 15:00, the heat load demand is relatively low and the cold load demand is relatively high. Part of the excess heat energy at this stage is utilized by the AC to be converted into cold energy to supply the cold load, and the other part is stored by the HSS to supply the heat load in the peak heat demand period; According to the analysis, most of the cooling load is supplied by EC, except for part of the cooling load supplied by AC. The daily electricity consumption of EC is relatively uniform and is not affected by the peak of the cooling load, so it does not lead to dramatic fluctuations in electricity consumption. By analyzing the results of the 24-h optimal scheduling for a typical day in winter, it can be concluded that IES has a reasonable structure of electricity, heat, and cooling energy supply, and can realize the coordinated supply and complementarity of various energy sources.IES is conducive to the flexible allocation and full use of energy, and the designed B-L optimization model can reasonably allocate resources and reduce the operating costs of IESO.

Lower-level optimization model solution results

Based on the influence of the upper model on the lower model’s decision, the decision variables of the lower model include load shifting and curtailment, and the objective function aims to minimize the cost of load demand. The optimal strategy for the lower model is obtained from the solution, as shown in Table 7. The objective function value of the lower model is 15,048,966.66 ¥, which means that the annual energy cost of the LA is 15,048,966.66 ¥.

Table 7.

LA’s Four-season typical day demand response program.

Energy	Elec. transfer (kW)	Elec. curtail. (kW)	Heat curtail. (kW)	Cold curtail. (kW)
Spring	690.8	1068.7	1377.8	663.1
Summer	1177.4	1123.4	612.4	1528.9
Autumn	705.8	1037.1	1076.3	675.2
Winter	786.8	1095.7	1756.9	449.3

As can be seen in Table 7, the electrical load demands in spring and fall are roughly the same, and the electrical load transfers and curtailments are close to each other. Since spring transitions from winter and autumn transitions from summer, the heat load demand in spring is higher than that in autumn, and the cold load demand in autumn is higher than that in spring; therefore, the heat load curtailment is higher in spring than in autumn, and the cold load curtailment is higher in autumn than in spring; The heat load demand is higher in winter and therefore the heat load reductions are higher in winter; the cold load demand is higher in summer and the cold load reductions are higher in summer. At the same time, the amount of transfer or curtailment of load participation in demand response is maintained within 2 MW to satisfy customer comfort.

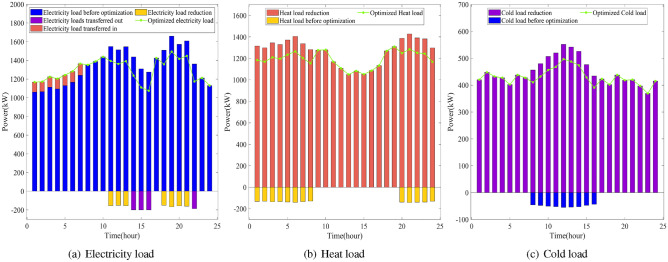
According to the electric, heat, and cold load curves shown in Fig. 7, it can be observed that in the case before and after the demand response, the electricity load from 10:00 to 22:00 shows an obvious double-peak characteristic. To reduce the total cost of electricity, the optimized load profile shows the characteristic of “peak shaving and valley filling”. The original load profile has obvious peak loads during the peak hours of 11:00 to 13:00 and 18:00 to 22:00 when electricity prices are higher. Through the optimization adjustment on the customer side, the peak load is significantly reduced, and part of the peak load is shifted to 0 8:00 hours when the electricity price is lower. Such optimization adjustment makes the load curve fluctuation significantly reduced.

Figure 7.

Load changes before and after user-side demand response.

In winter, the heat load demand is higher at night, and the optimized heat load demand is reduced from 20:00 to 8:00, while at 10:00-17:00, the original heat load demand is lower, and the heat load is not reduced to ensure the comfort of the users. After the reduction, the heat load at each time of the day remains basically at the same level, and the fluctuation of the heat load curve is significantly reduced. Similarly, on winter days, due to lower temperatures, the cold load demand is very small, only during the daytime the cold demand is relatively high, which is significantly reduced by the optimization, and at night when the temperature is lower, the cold load demand is fluctuating slightly at the same level, the cold load demand for each period throughout the day also remained at the same level.

Comparative analysis of multiple cases

To verify the effectiveness of the model proposed in this paper, the following five scenarios are set up for comparative analysis.

Scenario 1: General model without P2G-CCS and IDR.

Scenario 2: Building on Scenario 1, consider P2G-CCS (traditional stepped carbon trading mechanism) and IDR.

Scenario 3: Building on Scenario 1, consider P2G-CCS (improved stepped carbon trading mechanism) and IDR.

Scenario 4: Considering the uncertainty of WT and PV based on Scenario 3.

Scenario 5: Based on Scenario 4, the intra-day prediction accuracy for short-term weather effects and the intra-year prediction accuracy for long-term equipment performance effects were further considered.

Comparing Scenario 1 and Scenario 2, in Scenario 2, the incorporation of the P2G-CCS greatly improves the utilization of WT and PV. The hydrogen produced can be sold directly or used to make FC, and the remainder is stored in hydrogen storage tanks. The incorporation of the P2G-CCS improves the utilization of WT and PV, and reduces the GT and GB output, thus reducing the cost of WT and PV abandonment and carbon emissions. In addition, the CCS can capture the carbon dioxide emitted by the system to be traded in the carbon trading market, which has obvious environmental and economic benefits. With the synergistic operation optimization of the P2G-CCS, the operating cost of the whole system is further reduced. As the carbon trading market continues to develop and improve, the economic and environmental benefits of Scenario 2 will further increase. Table 8 shows a comparison of the relevant data for Scenario 1 and Scenario 2.

Table 8.

Comparison of Scenario 1 and Scenario 2.

Typical day	Benefits of IESO (¥)		Cost of LA (¥)		Carbon emission (kg)		WT and PV utilization (%)
	Scenario 1	Scenario 2	Scenario 1	Scenario 2	Scenario 1	Scenario 2	Scenario 1	Scenario 2
Spring	25,805.04	29,513.11	45,742.60	41,514.10	21,291.39	9644.08	75.24	100
Summer	21,585.42	26,206.22	46,332.56	41,556.32	29,249.19	14,557.72	74.91	100
Autumn	24,364.72	27,113.34	42,908.80	38,762.10	20,819.19	9298.73	75.17	100
Winter	25,877.56	30,073.60	48,233.70	43,684.74	22,738.02	11111.68	74.87	100

Comparing Scenario 3 and Scenario 2, it can be seen from Table 9 that the improved stepped carbon trading mechanism reduces carbon emissions to a much lower level and the benefits from carbon trading are further enhanced. The improved laddered carbon trading model reduces annual carbon emissions by roughly 40123.5375 kg.

Table 9.

Comparison of Scenario 2 and Scenario 3.

Typical day	Benefits of IESO (¥)		Cost of LA (¥)		Carbon emission (kg)		Revenue from carbon trading (¥)
	Scenario 2	Scenario 3	Scenario 2	Scenario 3	Scenario 2	Scenario 3	Scenario 2	Scenario 3
Spring	29,513.11	29,520.92	41,514.10	41,317.78	9644.08	9565.28	5929.08	5973.75
Summer	26,206.22	26,489.22	41,556.32	41,196.75	14,557.72	14,355.43	8148.01	8170.98
Autumn	27,113.34	27,304.26	38,762.10	38,653.45	9298.73	9184.71	5576.67	5600.65
Winter	30,073.60	30,304.11	43,684.74	43,530.00	11,111.68	11,067.08	7091.78	7171.53

Scenario 3 does not take into account the uncertainty of the renewable energy output, and the optimization results are too conservative from the actual. Scenario 4 further considers the uncertainty of WT and PV based on Scenario 3 and introduces robust stochastic optimization to deal with the impact of the uncertainty of WT and PV on the power stability of the system. The results were analyzed with both 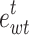and 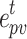at 0.05; 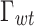and 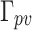at 0.5, 1, 1.5, and 2 respectively. In addition, P2G technology improves the ability of IES to absorb PV and WT. When the capacity of P2G is large enough, it can fully absorb excess energy from PV and WT, realizing zero PV and WT abandonment. At the same time, P2G utilizes 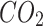to produce natural gas, which helps to reduce the carbon emissions of the system and promotes sustainable energy use and environmental protection.

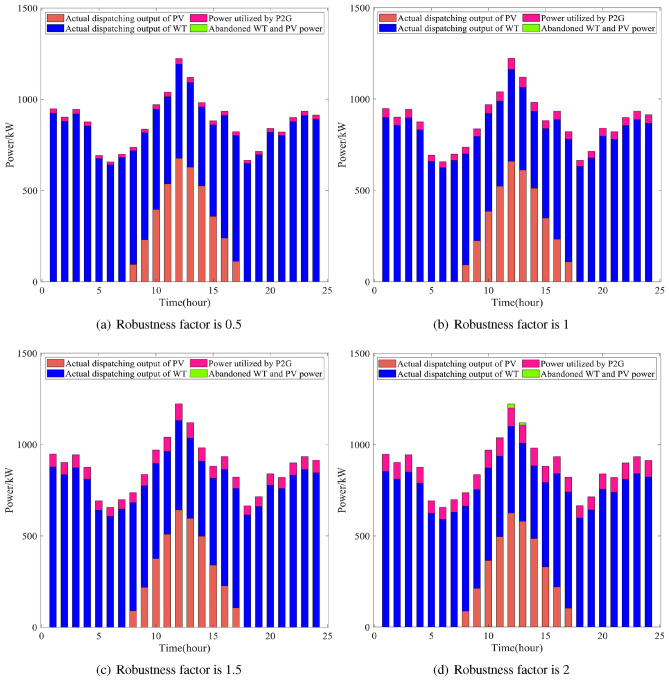
According to Fig. 5, WT production is higher in winter, taking a typical winter day as an example, Fig. 8 shows the WT and PV utilization under different robustness coefficients for a typical day in winter. From the Fig. 8, it can be seen that WT and PV abandonment become more and more serious as the robustness coefficient increases. When 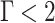the remaining unscheduled WT and PV are used by the P2G system without wastage; 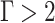, The abandoned WT and PV exceed the rated power for P2G operation and cannot be fully utilized. Abandonment of WT and PV phenomenon mainly occurs from 1:00 to 4:00 a.m. and during the day from 10:00 to 14:00 two time periods, the main original is the winter day and night WT is significantly higher than during the day, and at noon PV is larger, WT and PV increases lead to the difficulty of the system’s actual scheduling.

Figure 8.

WT and PV utilization without considering the influence of prediction time.

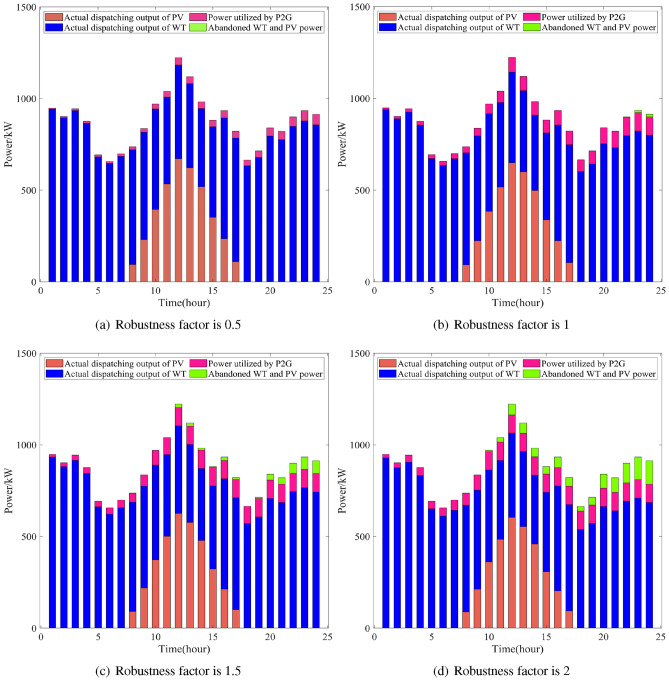
In Fig. 8, the abandonment of wind and PV power occurs only when the robustness factor is greater than 2, while the wind and PV energy sources are fully utilized in the other cases. However, we need to point out that the optimization results in Fig. 8 may be overly optimistic and not entirely accurate for the actual operation of the IES. First of all, the analysis of the intraday short-term forecasts shows that the weather has a significant impact on wind and PV power generation because the accuracy of the weather forecasts decreases as the forecast time increases. This results in the forecast bias of wind and PV power generation showing distributional differences at different times of the day. Figure 9 illustrates the actual dispatch of wind and PV considering the effect of weather forecasts. During the day, as the accuracy of weather forecasts decreases, the deviation between the predicted and actual dispatch values of wind and PV gradually increases, which leads to increasingly severe wind and PV abandonment. Therefore, these influencing factors must be considered in the optimization model to more accurately reflect the actual operation of the IES. The WT and PV runs considering the effect of short forecast times are shown in Table 10

Figure 9.

Utilization of WT and PV on a typical winter day with different robust coefficients.

Table 10.

WT and PV unit operation analysis with different robustness coefficients.

Robust coef.	Benefit IESO (¥)	Cost LA (¥)	Emission (kg)	Utilization (%)	GT (kW)	ESS (kW)	P2G (kW)	Curtail rate (%)
0.5	30,635.09	43,196.79	11,755.83	100	13,701.08	684.44	712.35	0
1.0	30,544.84	43,160.07	11,785.24	100	14,413.43	710.01	1394.86	0
1.5	30,520.63	43,139.21	11,821.30	98.3	15,125.77	806.62	1784.21	1.7
2.0	30,168.47	42,979.40	11,966.42	95.6	15,838.12	873.50	1921.10	4.4

As the robustness factor increases, the utilization of WT and PV power gradually decreases. Meanwhile, an increase in the output power of GT leads to an increase in carbon emissions, while the output power of ESS and P2G also increases. Therefore, to minimize the reduction of renewable energy output and to improve the stability of the energy supply and demand balance, the capacity of GT, ESS, and P2G devices should be increased appropriately while increasing robustness. However, long-term operation leads to a gradual degradation of the performance of WT and PV equipment, and considering only the weather factor also introduces errors in the forecasting of WT and PV power generation. Therefore, this study continues to consider the impact of wind and PV equipment performance loss on the actual dispatch as the operation time increases.

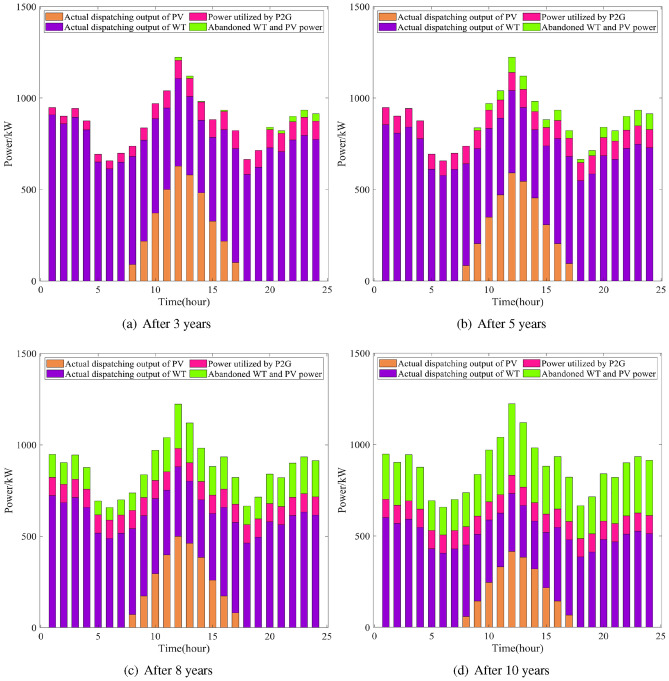
Figure 9 shows the variation of PV and WT output over time for a robustness factor of 1, taking into account the intraday short-term weather factor and long-term equipment operating losses. Figure 10 also considers the case of wind and PV plants operating for 3, 5, 8, and 10 years, the running data is shown in Table 11 Compared to the case with a robustness factor of 1 in Fig. 9, when the equipment is operated for 3 years, the change in the output power of the PV and wind farms is small, and the excess wind and PV power can be absorbed by the capacity planned by the P2G. However, as the equipment operation time grows to 5 years, the deviation between the actual output power and the predicted value starts to increase, and the fully loaded P2G equipment is no longer able to fully absorb the excess power. After 8 years of operation, the deviation between the actual output power and the predicted value becomes more obvious; and after 10 years of operation, the deviation between the actual output power and the predicted value reaches one-third of the initial value. Therefore, in the case of long-term operation of WT and PV equipment, considering only the deviations caused by short-term daily weather factors without considering the effects of equipment performance degradation will lead to a very large deviation between the total annual forecast and the actual annual dispatch.

Figure 10.

Analysis of WT and PV considering the effect of equipment wear and tear.

Table 11.

Operation analysis of WT and PV in different years.

Years	Benefit IESO (¥)	Cost LA (¥)	Emission (kg)	Util. (%)	GT (kW)	ESS (kW)	P2G (kW)	Curtail. rate (%)
3	30,440.09	43,684.74	11,764.96	99.7	15,049.42	520.96	1887.11	0.3
5	30,281.75	43,553.32	11,886.78	95.9	16,180.07	665.69	2332.42	4.1
8	29,970.53	43,484.74	12,707.89	83.3	18,807.00	694.72	2400.00	16.7
10	28,663.45	43,393.50	13,793.28	71.1	20,524.55	752.75	2400.00	29.9

In response to the deviation problem brought about by the long-term operation of WT and PV equipment, we can consider the following measures: (1). Regular monitoring and evaluation of equipment performance: Conduct regular performance evaluation of WT and PV equipment, including power output, efficiency, and other indicators, and track the long-term operation of the equipment. This can help us understand the degree of degradation of equipment performance and take timely measures to repair or upgrade equipment. (2). More accurate weather forecasting: Improve the accuracy of weather forecasting, especially for short time scales. Advanced weather modeling and data analysis methods, combined with real-time monitoring data, provide more accurate weather forecasts and reduce the impact of weather factors on wind and PV power generation. (3). Diversified energy mix: Introducing a hybrid mix of other renewable energy sources and traditional energy sources to build a more flexible and diverse energy system. By combining WT, PV, hydropower, biomass, and other energy sources, they can compensate each other for the volatility of a particular energy source and increase the stability and reliability of the system. (4). The application of energy storage technology: the use of energy storage technology, such as battery storage, pump storage, compressed air storage, etc, the WT and PV power generation of excess energy stored, and released when needed. This increases the system’s regulation capability and balances the fluctuations between energy supply and demand. (5). Optimized scheduling strategy: Intelligent energy scheduling and optimization algorithms are used to accurately schedule WT and PV power generation by combining real-time data and prediction models. By rationally arranging the working status and output power of each energy component, we maximize the use of renewable energy, reduce the demand for traditional energy, and ensure the balance between energy supply and demand. With adequate analysis, we can better cope with the deviation problems brought about by the long-term operation of WT and PV equipment, and improve the stability and sustainability of the energy system.

Conclusion

To solve the supply-demand balance operation problem in the IES, this paper describes the overall structure and model of the IES and constructs an IES that considers the IDR scheme and the P2G-CCS synergistic scheduling operation. The upper-level IESO is considered the leader and the lower-level user is seen as the follower. In the solution of the B-L optimization model with multiple variable types and nonlinear constraints, the Lagrangian function for the lower model is created using the KKT condition. This function is then transformed into constraints for the upper model, and subsequently, the nonlinear term is linearized, the B-L optimization model for P2G-CCS co-scheduling and multiple load demand response is constructed. The main conclusions are as follows:

(1) Under the optimal solution of the B-L optimization model, the IESO can achieve a maximum annual operating revenue of 10,339,319.9 ¥, while the LA can achieve a minimum annual consumption cost of 15,048,966.66 ¥. The model takes into account the operating rules of the IES equipment on typical days in different seasons and demonstrates flexible scheduling capabilities during high cooling loads in summer and high heating loads in winter. The energy supply in the system exhibits coordination. According to the model results, when the robustness factor is less than 1, the undispatched wind and PV generation can be absorbed by the P2G technology and no wind and PV curtailment is required. When the robustness factor is greater than 1, the curtailment power of wind and PV power increases with the robustness factor.

(2) From the perspective of economic benefits, the model proposed in this paper brings significant benefits to both IESO and LA. In the case of IESO, the adoption of the model in this paper leads to an increase in the total profit of IESO by 14.07%. As for LA, the adoption of the model in this paper led to a 10.06% reduction in their total costs.

(3) From the perspective of environmental benefits, the model proposed in this paper reduces 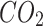emissions by 44.28% and improves the utilization of wind and light resources. The results reflect the positive impact of P2G-CCS synergistic dispatch optimization and IDR scheme under the B-L energy trading model on the improvement of environmental benefits.

Overall, the optimization model proposed in this paper achieves high economic and environmental benefits while balancing supply and demand under the premise of ensuring the economics of both the supply side and the energy use side. However, this study only considered the overall operational benefits of IES and did not consider the distribution of benefits among the subjects within IES. Our future research will focus on developing a fair and reasonable benefit distribution scheme that takes into account the contribution of each subject. We will work on the development of models and algorithms to ensure that the benefits among the parties in the IES are fairly distributed, reflecting the contributions and interests of each subject.

Author contributions

M.L.: Conceived and wrote the manuscript and conducted simulation experiments. Y.T.: Provided methodological and writing guidance and reviewed the manuscript. Z.C.: Reviewed the manuscript. Y.S.: Reviewed the manuscript.

Data availability

All data generated or analysed during this study are included in this published article.

Declarations

Competing interests

The authors declare no competing interests.