Creation of a stable vector vortex beam with dual fractional orbital angular momentum

Abstract

Recently, vortex beams have been widely studied and applied because they carry orbital angular momentum (OAM). It is widely acknowledged in the scientific community that fractional OAM does not typically exhibit stable propagation; notably, the notion of achieving stable propagation with dual-fractional OAM within a single optical vortex has been deemed impracticable. Here, we address the scientific problem through the combined modulation of phase and polarization, resulting in the generation of a dual-fractional OAM vector vortex beam that can stably exist in free space. Applying this unique characteristic, we derive an integrated analytical model to calculate the focused electromagnetic fields and Poynting vector distributions based on Debye vector diffraction integral. Utilizing phase stitching technology, this research combines two fractional topological charges to investigate the properties of dual-fractional OAM optical vortices with diverse polarization conditions. Furthermore, the transmission characteristics of these optical vortices are meticulously analyzed. This work not only enriches the types of vortex beams but also provides a novel optical tool, potentially transformative for applications in optical communications, optical manipulation, and optical imaging.

Introduction

The optical vortex (OV) refers to the beam with helical phase distribution in the optical axis direction of the wavefront^1,2, which can be quantitatively described by the phase factor exp(ilψ), where l is the topological charge (TC) and ψ is the azimuth angle. The OV carries orbital angular momentum (OAM), and each photon carries a lħ OAM (ħ is the reduced Planck’s constant). Due to the singularity of the central phase, the OV has an obvious doughnut intensity structure³, and this novel discovery leads to the generation of singularity optics^4,5. OV also plays a vital role in various applications such as optical communication^6,7, optical imaging^8,9, particle manipulation^10,11, quantum information^12,13 and optical detection^14,15 because of their unique physical properties. Therefore, the research of OV is scientifically important for scientific applications. In previous studies, TC of OV is always constrained to an integer. In fact, the value of TC can also be non-integer and is called fractional OV^16,17. As an indispensable supplement to integer OV, fractional OV exhibits more unique physical properties. These include complex phase structure, radial dark opening intensity distribution, and more complex OAM modulation dimensions.

For a long time, it has been a consensus that fractional OV cannot propagate stably in free space, because fractional OV in the process of propagation will produce phase singularity splitting, reconstruction^18,19, beam shape rotation²⁰, TC jump²¹ and OAM oscillation^22,23. However, with the deepening of the research, the vector characteristics of the beam^24,25 and the non-local characteristics of the transmission medium²⁶ have been proved to stabilize the transmission of fractional OV. Furthermore, fractional OV offers more possibilities for a wide range of applications due to their unusual properties. For example, in optical communication, the unique non-integer OAM state of fractional vortex beams can overcome the limitation of aperture size and greatly expand the communication capacity^27,28. In microscopic imaging, fractional-order vortex beams have better anti-noise ability and can achieve anisotropic edge enhancement to improve imaging effect^29,30. In addition, fractional vortex beams also show unprecedented advantages in the fields of optical manipulation^31,32 and quantum optics^33,34. Current research on fractional OV predominantly focuses on single OAM. Using a method of extracting arbitrary polarization modes³⁵ and “Optical Pen” technology³⁶, a propagating fractional-order vortex beam with a single OAM was generated^37,38. However, research on complex fractional OV with mixed OAM is comparatively limited. The fractional OV with dual OAM encodes a greater amount of information, thereby presenting novel avenues for the application of vortex beams.

In this paper, we employ a phase splicing technique to generate a stable vector vortex beam with dual-fractional OAM, and we systematically investigate the focusing and transmission characteristics of this beam under radial, azimuthal, and 0.5-order vectorial polarization conditions. The mathematical descriptions of the energy-flow and the focused electromagnetic field are theoretically analyzed. The fundamental aspects of vector vortex beam with dual-fractional OAM and its distinctive polarization states are examined in depth. This research demonstrates that vector vortex beams with dual-fractional OAM maintain stability under 0.5-order vector polarization, confirming that multiple OAM states can coexist within a single OV. This work not only provides new optical tools for applications in optical communication, optical manipulation, and optical imaging, but also offers innovative methodological guidance for optical field modulation techniques, which can be extended to any type of OAM beams.

Principle

This paper demonstrates the creation of a dual-fractional OAM vector vortex beam that can stably exist in free space through the application of phase stitching technology within the focusing region of the objective lens, as illustrated in Fig. 1. In Fig. 1(A), a collimated incident beam propagating along the optical axis is focused by the objective lens (OL) following appropriate phase modulation. Figure 1(B) delineates the detailed process of phase stitching technology, exemplified by a TC of ± 2.5. Specifically, Fig. 1(a) represents the + 2.5-order phase, while Fig. 1(b) depicts the − 2.5-order phase. The resulting ± 2.5-order phase obtained through phase stitching is illustrated in Fig. 1(c). The composite topological charge obtained through phase stitching technology is referred to as the “dual-topological charge”. Specifically, within the phase distribution range of 0-π, the topological charge is denoted as l, while within the phase distribution range of π-2π, the topological charge is denoted as -l. Here, the phase is positioned at the pupil plane of the OL to achieve focusing characteristics at varying transmission distances. P is the pupil filter in front of the wave of the OL. The assembled phase (c) was applied to P, and through the focusing lens, focused optical fields of the dual-fractional OAM vector vortex beam were obtained at three distinct propagation planes: z = 0λ, z = 5000λ, and z = 10000λ, as illustrated in Fig. 1(d).

Fig. 1.

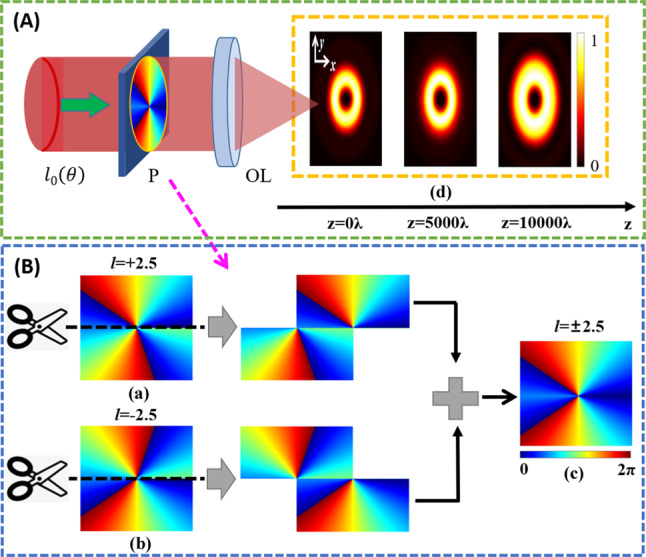
Schematic illustration of a system for generating a stable vector vortex beam with dual-fractional OAM using phase stitching technology. Subfigure (A) illustrates the creation of dual-fractional OAM vortex beams that can propagate on three different planes at z = 0λ, z = 5000λ, and z = 10000λ, made possible by the phase stitching technique shown in (B). P is the pupil filter in front of the wave of the objective lens (OL).

Specifically, based on the Debye vector diffraction theory, the distribution of the electromagnetic field in the focal region of OL in Fig. 1 can be expressed as³⁹:

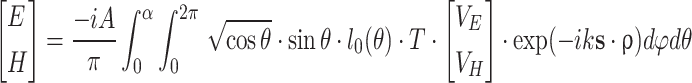1

where A is a normalized constant. θ and φ are the convergent angle and azimuthal angle, respectively. α = arcsin(NA/n), where NA is the numerical aperture of the object lens, n is the refractive index in the focusing space. The wavenumber k = 2nπ/λ, where λ is the wavelength of the incident vector vortex beams, and ρ=(rcosΦ, rsinΦ, z) represents the position vector of an arbitrary points in the focused field, and r represents the distance from the origin of the projection of arbitrary point on the xoy plane. Φ is x axis and y axis angle, s=(-sinθcosφ, -sinθsinφ, cosθ) represents the unit vector along the ray in spherical coordinates, T = exp(iΨ) represents the transmittance function of pupil filter, Ψ represents the phase distribution of the optical pupil filter. l₀(θ) is the electric field amplitude of the incident beam. When l₀(θ) is the Gauss amplitude, the expression is⁴⁰:

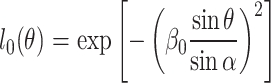2

Here, β₀ is the ratio of the pupil radius to the incident beam waist.

In Eq. (1), V_E denotes the unit vector of the electric field propagated by the incident beam after passing through the lens. Vector beams with different polarization modes can be obtained by modulating V_E. This paper investigates the transmission and focusing properties of dual-fractional OAM vector vortex beams with radial polarization, azimuthal polarization, and 0.5-order vector polarization. Radially polarized beam and azimuthally polarized beam are both vector beams of polarization order 1, with their polarization states exhibiting axial symmetry in the cross-sectional distribution. Both can be viewed as superpositions of positive vortices encoded in left circularly polarized beams and negative vortices encoded in right circularly polarized beams. The key distinction lies in the relative phase shift between the left and right circular polarizations: for radially polarized beam, the relative phase shift is 0, whereas for azimuthally polarized beam, it is π. Consequently, the polarization direction of radially polarized beam is always parallel to the radial direction, while the polarization direction of azimuthally polarized beam is always perpendicular to the radial direction⁴¹.

According to Debye diffraction theory, when the incident beam is radially polarized, V_E can be expressed as³⁹:

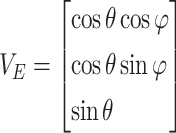3

According to Debye diffraction theory, when the incident beam is azimuthally polarized, V_E can be expressed as³⁹:

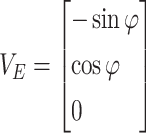4

A vector beam with a non-uniform polarization state can be represented as a combination of two orthogonal polarization modes. These two polarization modes can be considered as a combination of x-line polarization and y-line polarization³⁸. When the incident beam exhibits a vector polarization of order (m + 0.5), V_E can be expressed as^42,43:

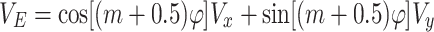5

where V_x and V_y are electric vectors of the x and y line polarization modes, i.e. the components of the x and y axes of the global frame reference along the axes of the local frame reference integral with the optical rays. V_x and V_y can be expressed as^42,43:

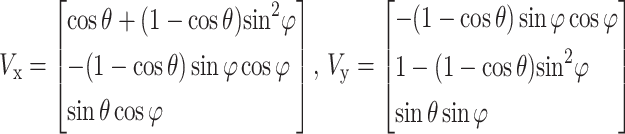6

According to reference³⁸, the vortex beam with a natural non-integer TC can be expressed as:

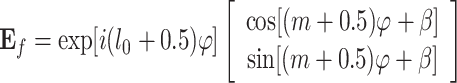7

where l₀ and m are two integers related to the TC and polarization order of the vector vortex beam, φ is the azimuthal angle, and β determines the polarization direction of the m + 0.5 order vector vortex beam.

Equation (7) can be divided into two different forms, which can be expressed as³⁸:

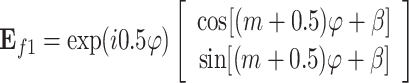8

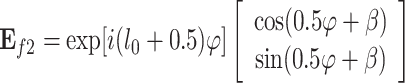9

To ensure stable propagation of such beams in free space, in accordance with the previous discussion, the condition specified in Eq. (9) must be satisfied. When the polarization is of the 0.5-order, the value of the TC can be manipulated to achieve stable transmission of fractional-order vector vortex beams. Therefore, in this paper, m = 0, where m denotes the polarization order of the vector vortex beam. Consequently, when the incident beam exhibits 0.5-order vector polarization, V_E can be expressed as:

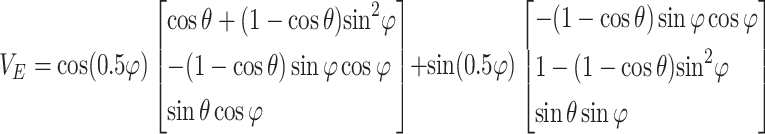10

In Eq. (1), V_H denotes the unit vector of the magnetic field propagated by the incident beam after passing through the lens. Based on the relationship between the magnetic and electric fields, V_H can be expressed as^42,43:

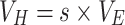11

The topological charge (TC) of a vortex beam refers to the orbital angular momentum (OAM) quantum number, which indicates the number of times the phase of the vortex beam rotates around the axis. This rotation is associated with the helical wavefront of the beam. In conventional vortex beams, the TC refers to the multiple of 2π phase change encountered over one complete revolution around the beam’s center, where the phase is undefined at the center of the closed loop, thus forming a phase singularity. The definition of TC in vortex beams can be expressed as the closed path integral of the phase gradient of the wavefield on the cross-sectional plane, and can be written as⁴⁴:

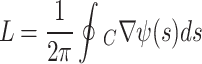12

where L represents the topological charge, ψ(s) denotes the wave field phase, C refers to a closed path, and ∇ is the vector differential operator. This equation indicates that the TC is an integer multiple of 2π, and such classical vortex beams are commonly referred to as regular vortex beams.

Reference⁴⁵ introduces a noncanonical vortex beam with a phase gradient and replaces the line integral of the TC along a closed curve with a stepwise integration approach. This method leverages the additivity property of integrals to decompose the TC, yielding:

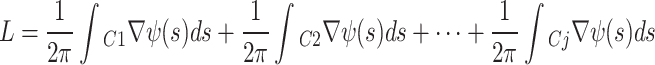13

According to the reference⁴⁵, the stepwise integration method is only applicable when the phase gradient ∇ψ(s) is continuous along a closed path (i.e., with a variation of 0 to 2π at the boundaries), and the path itself is closed. Furthermore, the decomposed TC cannot be expressed as a conventional numerical value to describe the TC of the complete vortex beam. It can only be represented by a piecewise function to describe the overall phase.

According to the calculation based on Eq. (13), the total TC before the optical phase is indeed zero. However, when dealing with fractional TCs and phase stitching, the phase distribution is not entirely continuous, as there is a phase discontinuity at the stitching points. This disruption leads to the violation of the closed path during integration. As a result, the traditional definition of TC—defined as the integral of the phase gradient along a closed path—becomes inapplicable. Consequently, a conventional numerical value for the complete TC cannot be directly obtained using this definition. Therefore, the use of a piecewise function is most appropriate in this paper, as it mathematically represents the distribution of the overall phase. According to Fig. 1(B), phase splicing is obtained by combining two upper and lower parts with fractional TCs, and in order to ensure the consistency of the spliced optical field, the two fractional TCs are equal in size and opposite in direction, and the phase function can be expressed as:

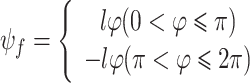14

where l represents the fractional topological charge, l = 0.5, 1.5, 2.5, …. Eventually, the intensity distribution of the propagable vector vortex beams with dual-fractional OAM can be obtained using  I = |E²|.

In terms of the time-dependent electric and magnetic fields, the energy flux is defined by the time-averaged Poynting vector^39,46:

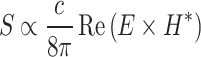15

where the asterisk denotes the complex conjugation, and c is the velocity of light in vacuum.

Results and discussions

In the subsequent investigation of the focusing and transmission characteristics, several distinct polarization modes of the dual-fractional OAM vector vortex beams were generated with the conditions of NA = 0.01 and n = 1. The parameter β₀ is set to 1 in Eq. (2), the unit of length in all figures is the wavelength λ and the light intensities of the dual-fractional OAM vector vortex beams are normalized to a unit value.

The focusing results with radial polarization

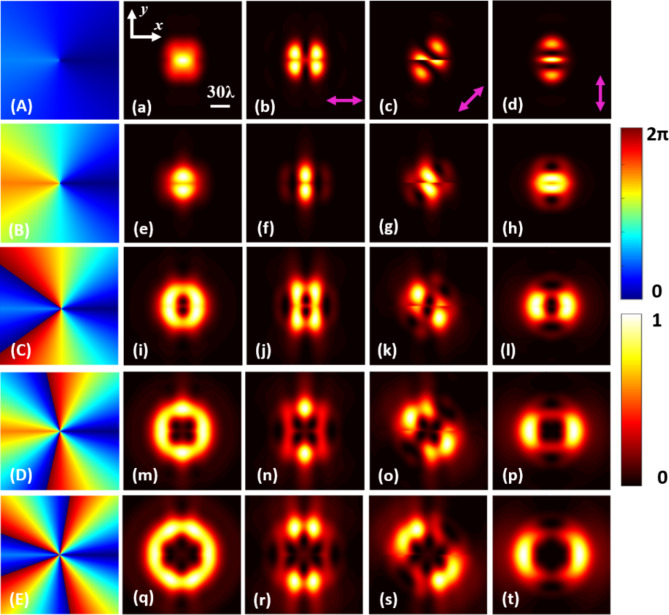
Based on Eqs. (1) and (3), this paper studies the focusing results of dual-fractional OAM vector vortex beams under different TC with radial polarization, as illustrated in Fig. 2, where (a) l = ± 0.5, (e) l = ± 1.5, (i) l = ± 2.5, (m) l = ± 3.5, (q) l = ± 4.5. The different splicing phases encoded in P-SLM³⁵ are included, as shown in Fig. 2 (A, B, C, D, E). According to the results, when the polarization is radial, the focusing fields of dual-fractional vector vortex beams obtained by the phase stitching technique are not a regular circle, as shown in Fig. 2(a, e, i, m, q).

Fig. 2.

Light intensity diagram under different TC with radial polarization. (a) l = ± 0.5, (e) l = ± 1.5, (i) l = ± 2.5, (m) l = ± 3.5, (q)l = ± 4.5 vector vortex beams respectively by splicing phase (A, B, C, D, E) to create. The subgraph (b-d, f-h, j-l, n-p, r-t) shows the light intensity of the vector vortex beams (a, e, i, m, q) through the polarizer with purple arrows. The light intensities are normalized to a unit value, and the phase scale is 0–2π.

In addition, we present the focused optical field patterns as the polarizer is rotated. When l = ± 0.5, the focusing field is an irregular solid dot, which shows different shapes of focused optical fields after passing through the polarizer at different angles. At a polarizer rotation angle of 0°, the focal spot exhibits a left-right symmetrical distribution, resembling the shape of butterfly wings, as illustrated in Fig. 2(b). At a polarizer rotation angle of 45°, the shape of the focused optical spot is irregular and asymmetric, as depicted in Fig. 2(c). At a polarizer rotation angle of 90°, the focal spot takes the form of three flattened solid bright points, displaying an upper-lower symmetrical configuration, as shown in Fig. 2(d). When l = ± 1.5, the focused optical field gradually diffuses from a solid point to both sides into two irregular solid points with upper and lower symmetry, and also shows different shapes of focused optical spots after passing through different angles of polarizers. When the polarizer is oriented at an angle of 0°, the focused optical field is elongated in the vertical direction, resulting in the formation of two irregularly shaped, solid bright spots that are symmetrically arranged, as depicted in Fig. 2(f). When the polarizer is rotated to an angle of 45°, the shape of the focused optical field becomes irregular and asymmetric, as shown in Fig. 2(g). When the polarizer is oriented at an angle of 90°, the entire focused optical field is compressed in the vertical direction, exhibiting a flattened circular shape that remains symmetric, as illustrated in Fig. 2(h).

When l ≥ ± 2.5, the focused optical field transitions from one or two solid points to a left-right symmetric irregular hollow ring, evolving gradually with an increase in topological charge. Notably, this configuration does not represent a vortex beam, as shown in Fig. 2(i, m, q). Furthermore, the shape of the focused optical field remains irregular upon the introduction of polarizers at various angles, as illustrated in Fig. 2 (j-l, n-p, r-t). Consequently, vortex beams possessing dual-fractional OAM, which are generated through phase stitching techniques, cannot stably exist in free space when radially polarized.

The focusing results with azimuthal polarization

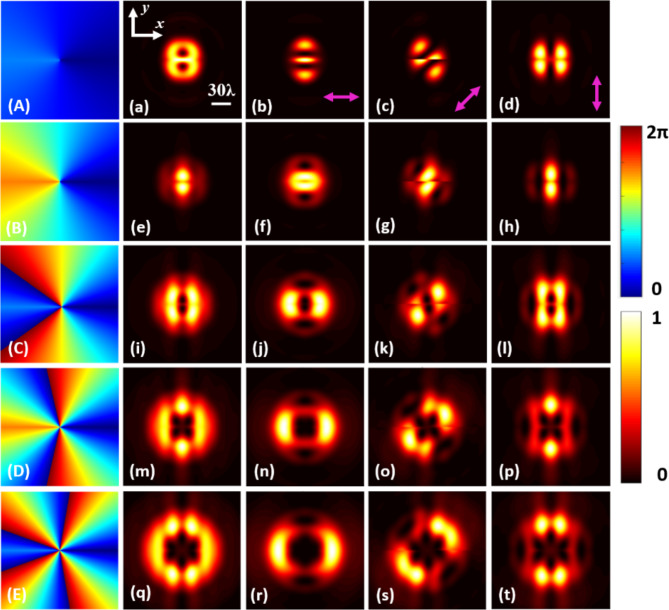
According to Eqs. (1) and (4), this paper analyzes the focusing results of dual-fractional OAM vector vortex beams under different TC with azimuthal polarization, as depicted in Fig. 3. The focal configurations correspond to topological charges of (a) l = ± 0.5, (e) l = ± 1.5, (i) l = ± 2.5, (m) l = ± 3.5, (q) l = ± 4.5. Additionally, Fig. 3 panels (A, B, C, D, E) illustrate the various splicing phases encoded in P-SLM.

Fig. 3.

Light intensity diagram under different TC with azimuthal polarization. Subgraphs (a, e, i, m, q) are vector vortex beams generated with azimuthal polarization, (a) l = ± 0.5, (e) l = ± 1.5, (i) l = ± 2.5, (m) l = ± 3.5, (q) l = ± 4.5, which created by phase encoded in P-SLM (A, B, C, D, E). The subgraph (b-d, f-h, j-l, n-p, r-t) shows the light intensity of the vector vortex beams (a, e, i, m, q) passing through the polarizer with purple arrows. The light intensities are normalized to a unit value, and the phase scale is 0–2π.

Similar to radial polarization, the focused optical field of the dual-fractional OAM vector vortex beam, obtained through phase-stitching techniques in the azimuthal polarization, does not exhibit a regular circular shape. Specifically, when l = ± 0.5and l = ± 1.5, the focused optical field exhibits two vertically symmetric yet irregular shapes, as illustrated in Fig. 3(a, e). For l ≥ ± 2.5, the focused optical field takes on an irregular ring shape, and as the absolute value of the TC increases, the radius of the focused optical field progressively enlarges. However, the surrounding light intensity is not continuous, indicating that it is not classified as a vortex beam, as demonstrated in Fig. 3(i, m, q). Furthermore, we provide illustrations of the focused optical field corresponding to various angles of polarization rotation, as shown in Fig. 3(b-d, f-h, j-l, n-p, r-t). Due to the symmetry relationship between radial and azimuthal polarization, a comparison between Figs. 2 and 3 reveals that the focused optical field shapes under radial polarization at 0° and azimuthal polarization at 90° are identical, and vice versa.

The focusing results with 0.5-order vector polarization

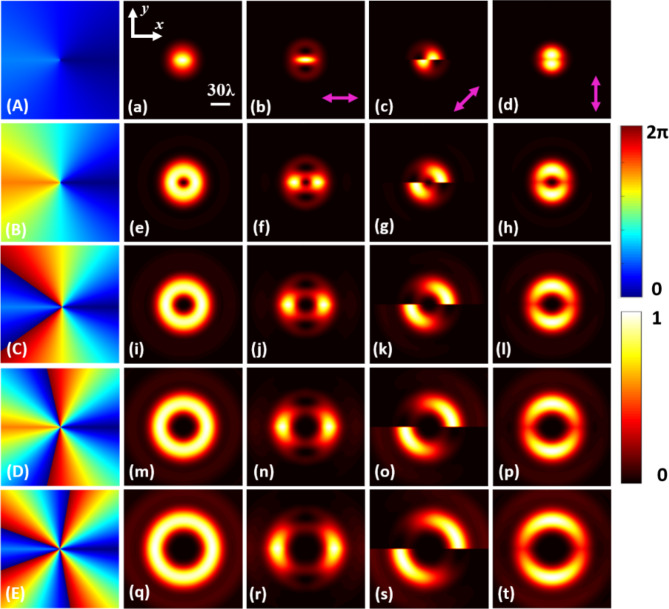
Utilizing on Eqs. (1) and (10), this study investigates the focusing properties of dual-fractional OAM vector vortex beams under different TC with 0.5-order vector polarization, as depicted in Fig. 4. The results include topological charges of (a) l = ± 0.5, (e) l = ± 1.5, (i) l = ± 2.5, (m) l = ± 3.5, (q) l = ± 4.5. Additionally, Fig. 4 panels (A, B, C, D, E) depict the various splicing phases encoded in P-SLM. Figure 4 illustrates the focused optical fields under varying TC. When l = ± 0.5, the focused optical field manifests as a solid optical point, as depicted in Fig. 4(a). When l ≥ ± 1.5, the focused optical field assumes the characteristic shape of a well-defined hollow circular vortex beam. Moreover, both the radius of the optical spot and the radius of the dark core exhibit a systematic increase with the absolute value of the TC, as shown in Fig. 4(e, i, m, q).

Fig. 4.

Light intensity diagram under different TC with 0.5-order vector polarization. Subgraphs (a, e, i, m, q) are vector vortex beams generated with 0.5-order vector polarization, (a) l = ± 0.5, (e) l = ± 1.5, (i) l = ± 2.5, (m) l = ± 3.5, (q) l = ± 4.5, which created by phase encoded in P-SLM (A, B, C, D, E). The subgraph (b-d, f-h, j-l, n-p, r-t) shows the light intensity of the vector vortex beams (a, e, i, m, q) passing through the polarizer with purple arrows. The light intensities are normalized to a unit value, and the phase scale is 0–2π.

Additionally, Fig. 4 presents the focused optical field images when the polarizer is rotated. At a polarizer rotation angle of 0°, the focused optical spots for l = ± 0.5 exhibit a flat, solid spot shape, as illustrated in Fig. 4(b). When l ≥ ± 1.5, the focused optical spots display two symmetrically positioned bright spots with a central dark ring, with the radius of the spots increasing systematically with the absolute value of the TC, as shown in Fig. 4(f, j, n, r). When the polarizer is rotated to an angle of 45°, the focused optical field for l = ± 0.5 reveal a solid semicircular shape, displaced and oriented along the 45° direction, as depicted in Fig. 4(c). When l ≥ ± 1.5, the focused optical spots exhibit two quarter-ring shaped patterns, also displaced and oriented along the 45° direction, with a central dark ring. The radius of these spots consistently increases with the absolute value of the TC, as demonstrated in Fig. 4(g, k, o, s). At a polarizer rotation angle of 90°, the focused optical field for l = ± 0.5 manifest as two symmetrically aligned small solid bright spots, as shown in Fig. 4(d). When l ≥ ± 1.5, the optical spots exhibit two interconnected arc-shaped patterns with a central dark ring, maintaining symmetry in the vertical direction. The radius of these spots also increases systematically with the absolute value of the TC, as illustrated in Fig. 4(h, l, p, t). Therefore, it can be concluded that the dual-fractional OAM vector vortex beams with 0.5-order vector polarization exhibit stable vortex patterns.

Building on the preceding analysis, we further investigated the energy flow (Poynting vector) of focused optical fields under varying TC with 0.5-order vector polarization, as illustrated in Fig. 5. For the ± 0.5-order focused optical field, the direction of energy flow progresses from the right of the spot, traversing through the central bright region and flowing towards the left. Subsequently, the flow bifurcates vertically, resulting in a symmetric closed-loop energy flow pattern above and below the center of the spot. Notably, the energy flow amplitude in the central region surpasses that of the surrounding areas, as depicted in Fig. 5(a). In contrast, for the ± 1.5-order focused optical field, the presence of a dark core alters the direction of energy flow compared to the ± 0.5-order case. Energy emanates from the left side of the spot, gradually forming a vertically symmetric bifurcation into semi-circular energy flows. Ultimately, these flows converge at the right side of the spot, resulting in a high-flow-density focused hollow annular energy stream, as illustrated in Fig. 5(b). For the ± 2.5-order, ± 3.5-order, and ± 4.5-order focused optical field, the increase in the absolute value of the TC significantly affects the dimensions of the dark core region. As the radius of the dark ring progressively enlarges, the energy flow ring is gradually eroded by the dark ring, leading to the formation of a hollow energy flow ring with an increasing radius, while maintaining the same flow direction, as shown in Fig. 5(c, d, e). This unique characteristic facilitates the capture of particles of varying radii, which subsequently rotate in a uniform direction, indicating the robust manipulation capabilities of optical tweezers. It is noteworthy that the energy flow direction and pattern at ± 0.5-order exhibit slight differences compared to other orders, enabling the control of particle chirality, thereby further enriching the application potential of dual-fractional OAM vortex beams.

Fig. 5.

Poynting vector of dual-fractional OAM vector vortex beams. Subfigures (a, b, c, d, e) illustrate the total energy flow of dual-fractional OAM vector vortex beams corresponding to TC of l = ± 0.5, ± 1.5, ± 2.5, ± 3.5, and ± 4.5, respectively. The light intensities are normalized to a unit value.

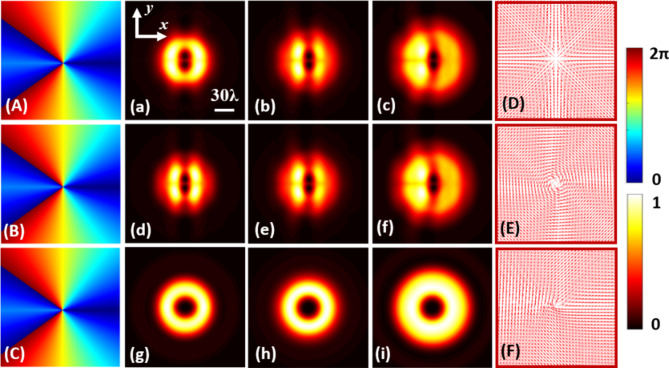
To investigate the transmission characteristics of the dual-fractional OAM vector vortex beams with radial polarization, azimuthal polarization, and 0.5-order vector polarization, we exemplify with a TC value of l = ± 2.5. The focused optical field patterns for the three distinct polarizations are presented at various distances along the propagation axis (z-axis), as illustrated in Fig. 6. Specifically, Fig. 6 (a-c), (d-f), and (g-i) depict the focused optical field patterns for radial polarization, azimuthal polarization, and 0.5-order vector polarization, respectively, under varying propagation axes (z-axis). These results are created by phase (A, B, C) and polarization (D, E, F), respectively. Figure 6 (a, d, g) (b, e, h) (c, f, i) shows the focused light intensity diagram at z = 0λ, 5000λ, 10000λ, respectively. Figure 6 clearly illustrates that as the transmission axis (z-axis) distance increases, the focused optical field of the dual-fractional OAM vector vortex beam experiences diffraction with the azimuthal and radial polarization. With the increasing transmission distance, the patterns of the focused optical field progressively separate, and the light intensity distribution becomes increasingly non-uniform. In both cases, the dual-fractional OAM vector vortex beam cannot maintain stability, as demonstrated in Fig. 6 (a-f). In contrast, the focused optical field remains stable in the form of optical vortices as the transmission distance increases with the 0.5-order vector polarization, thereby demonstrating its capability for stable transmission within a specific spatial range.

Fig. 6.

Light intensity diagram of different transmission fields (z-axis) with different polarizations for TC l = ± 2.5. Subgraphs (a-c), (d-f), (g-i) are focusing graphs under different transmission fields (z-axis) with radial polarization, azimuthal polarization and 0.5-order vector polarization respectively. These results are created by phase (A, B, C) and polarization (D, E, F). The subgraphs (a, d, g), (b, e, h) and (c, f, i) are the focused light intensity graphs at z = 0λ, 5000λ and 10000λ, respectively. The light intensities are normalized to a unit value, and the phase scale is 0–2π.

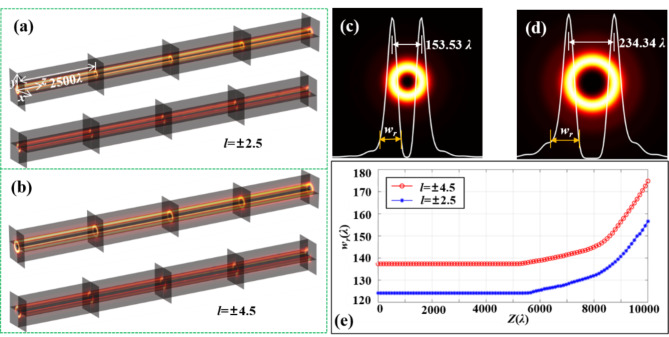
Finally, the transmission stability of the dual-fractional OAM vector vortex beams under TC of l = ± 2.5and l = ± 4.5 is analyzed with 0.5-order vector polarization. Figure 7 presents the results of the transmission stability of dual-fractional OAM vector vortex beams. Panels (a) and (b) illustrate the three-dimensional reconstruction of the beams during free-space transmission for TC of l = ± 2.5 and l = ± 4.5, respectively. Panels (c) and (d) depict the half-width at half maximum (HWHM) and the ring width for the respective topological charges. Panel (e) illustrates the relationship between the ring width and transmission distance within the range of 0-10000λ. The study focuses on the transmission over a distance range of 0-10000λ. In panels (a) and (b), the upper sections depict the reconstruction results of the total field transmission, while the lower sections present the reconstruction results when the polarizer is set at 45°. The dual-fractional OAM vector vortex beams are capable of maintaining stable optical field modes during transmission in free space. Cross-sections of the transmission process were extracted to analyze the variations in the HWHM and ring width. According to the results presented in panels (c) and (d), it is evident that the HWHM of the beams remains constant within the range of 0-10000λ. Specifically, the HWHM is measured at 153.53λ for the TC of ± 2.5 and 234.34λ of ± 4.5. However, the beams exhibit gradual divergence during transmission, resulting in variations in the ring width as the transmission distance increases. The ring width of the beams is defined as w_r, as depicted in panel (e), which illustrates the relationship between w_r and the transmission distance. The analysis indicates that within the range of 0-6000λ, the ring width remains stable. Within the range of 6000–8000λ, the beams begin to diverge, with a gradual increase in ring width; however, the extent of divergence remains minimal, and the growth of the ring width is relatively slow. Beyond 8,000λ, the beams exhibit accelerated divergence, leading to a rapid increase in ring width, while the central singularity gradually contracts.

Fig. 7.

Transmission stability of dual-fractional OAM vector vortex beams. Subfigures (a, b) are the three-dimensional reconstructions of the dual-fractional OAM vector vortex beams with TC of l = ± 2.5, ± 4.5 when transmitted in free space. Subfigures (c, d) are the HWHM and ring width of the beams. (e) is the ring width versus distance in the range 0-10000λ.

Conclusion

In conclusion, it has been demonstrated that the generation of a stable dual-fractional OAM vector vortex beam in free space is indeed feasible. This paper innovatively employs phase stitching techniques to combine two fractional topological charges, investigating the characteristics of dual-fractional OAM optical vortices with various polarizations. This research substantiates the existence of multiple OAMs within a single optical vortex. The dual-fractional OAM vector vortex beam not only enrich the types of fractional OV, but also carry more optical information, which promotes the application of spin and orbital angular momentum of vortex beams and its application in basic disciplines such as optics and electromagnetism.

Methods

Simulations

Based on the Debye vector diffraction theory, the “Principle” section of the paper provides a comprehensive formulation of the focused electromagnetic field distribution, expressions for different polarization states, the stitching phase function, and the computational method for energy flux (Poynting vector). Employing this comprehensive theoretical model, the paper numerically simulates the focused intensity distribution and transmission characteristic of a dual fractional orbital angular momentum (OAM) vector vortex beam under radial, azimuthal, and 0.5-order vector polarizations. The generation of these beams is facilitated by encoding different stitching phases onto a polarization-spatial light modulator (P-SLM).

Phase stitching

The “phase stitching technique” mentioned refers to the combination of two or more helical phase profiles of optical vortex beams, thereby generating a vortex beam that carries multiple orbital angular momenta. In this study, we stitch together two fractional-order topological charges of equal magnitude but opposite directions. Specifically, within the 0-π half phase distribution, the topological charge is designated as l, and within the π-2π half phase distribution, the charge is -l, resulting in a new composite phase, as illustrated in Fig. 1(B). By applying the composite phase to the pupil filter (P) of the OL wavefront depicted in Fig. 1(A), and focusing through a lens, the focused intensity distribution of the dual fractional OAM vector vortex beam across various propagation planes can be obtained.

Author contributions

Lingyu Wang: Conceiving the method, verifing the theoretical feasibility, investigation, writing first draft, simulation, visualization, analysis. Guanxue Wang: Conceiving the method, Proofreading English, proofreading the results. Xiangmei Dong: analysis, proofreading English. Xiumin Gao and Songlin Zhuang: analysis, validation, supervision. All authors reviewed the manuscript.

Funding

Parts of this work were supported by the National Key Research and Development Program of China (2018YFC1313803).

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request. Corresponding author: Xiumin Gao (Email: gxm@usst.edu.cn; Addresses: University of Shanghai for Science and Technology, Shanghai, 200093, China).

Declarations

Competing interests

The authors declare no competing interests.