Abstract
Two-Dimensional transition metal dichalcogenides have been the subject of extensive attention thanks to their unique properties and atomically thin structure. Because of its unprecedented room-temperature magnetic properties, iron-doped MoS2 (Fe:MoS2) is considered the next-generation quantum and magnetic material. It is essential to understand Fe:MoS2’s thermal behavior since temperature and thermal load/activation are crucial for their magnetic properties and the current nano and quantum devices have been severely limited by thermal management. In this work, Fe:MoS2 is synthesized by doping Fe atoms into MoS2 using the chemical vapor deposition synthesis and a refined version of opto-thermal Raman technique is used to study the thermal transport properties of Fe:MoS2 in the forms of single (1L), bilayer (2L), and tri-layer (3L). In the Opto-thermal Raman technique, a laser is focused on the center of a thin film and used to measure the peak position of a Raman-active mode. The lateral thermal conductivity of 1-3L of Fe:MoS2 and the interfacial thermal conductance between Fe:MoS2 and the substrate were obtained by analyzing the temperature-dependent and power-dependent Raman measurement, laser power absorption coefficient, and laser spot sizes. At the room temperature, the lateral thermal conductivity of 1-3L Fe:MoS2 were discovered as 24 ± 11, 18 ± 9, and 16 ± 8 W/m·K, respectively which presents a decreasing trend from 1 to 3L and is about 40% lower than that of MoS2. The interfacial thermal conductance of between Fe:MoS2 and the substrate were discovered to be 0.3 ± 0.2, 1.1 ± 0.7, and 3.0 ± 2.3 MW/m2⋅K for 1L to 3L respectively. We also characterized Fe:MoS2’s thermal transport at high temperature, and calculated Fe:MoS2’s thermal transport by density theory function. These findings will shed light on the thermal management and thermoelectric designs for Fe:MoS2 based nano and quantum electronic devices.
Subject terms: Materials science, Nanoscience and technology
Introduction
Two-dimensional (2D) materials and their unique properties have attracted significant attention in recent years. With the discovery of graphene1, transition metal dichalcogenides (TMDCs)2,3 have been researched extensively due to their interesting thermal4–8, electrical9, thermoelectric10, and optical11,12 properties. Among them, MoS2 is a layered semiconductor composed of covalently bonded transition-metal atoms (Mo) and chalcogen atoms (S)13 with important applications in optoelectronic14 and nano-electronic devices15. The thermal transport properties of 2D MoS2 are very different from the bulk. Due to higher efficiency, thin layer MoS2 are promising electronic devices16. Impurities, such as vacancies, chemical doping, and grain boundaries, can lead to phonon scattering17–20 and, as a result, thermal conductivity reduction. Green’s function suggests the higher likeliness of short wavelength or high-frequency phonon modes scattering by defects. Jenisha et al.14 revealed the reduction of thermal conductivity for Ni-doped MoS2. They observed two times smaller thermal conductivity of about 0.48 W/m⋅K for 7.5% of Ni-doped MoS2 than undoped MoS2. Mao et al.15 reported a significant increase in electric conductivity and reduction in thermal conductivity for 1–10% vanadium atoms doped in MoS2 lattice structure. Also, the thermal conductivity was significantly reduced due to point defects and interface scattering. Structural, optical, electrical, and phonon properties of V-doped and Ti-doped 2D MoS2 were studied by Williamson et al.21 They revealed the concentration of 2.083% Ti is the most effective due to effective dopant isolation. The research indicated that Ti dopant impacts the phonon properties greater than V-doped; however, V-dopant has a great phonon anharmonicity due to shorter bond length and weaker covalent bonds.
Modifying the magnetic properties of MoS2 nanosheets is crucial for expanding their applications in nanoelectronics22 and spintronics23 using the diluted magnetic semiconductor (DMS) concept. MoS2 nanosheets, however, are intrinsically nonmagnetic. Therefore, it is highly desirable to realize stable magnetism in MoS2. Iron-doped Molybdenum disulfide (Fe:MoS2) is considered a quantum material thanks to its intriguing properties, such as magnetic properties, lower mobility, more lattice impurities, and imperfections. Iron (Fe) doping into MoS2 lattice structure has been reported to facilitate DMS formation24, with Scanning Transmission Electron Microscopy (STEM), X-ray Photoelectron Spectroscopy (XPS), and Magnetic circular Dchroism (MCD) Spectroscopy characterizations of the Fe doping. The magnetic and electronic properties of Fe-doping monolayer MoS2 have been studied using a combination of density functional theory by Shu et al.25 They reported that the stability of Fe dopant in MoS2 lattice structure depends on the layer number and chemical potential. In another work, Mishra et al.26 investigated the electronic and magnetic properties of the Fe atom doped on the MoS2 and MoS2 using first-principal function theory. They reported that the dopant significantly changes magnetic moments, magnetic anisotropic energy, and charge transfer which counts as electronic properties. Wang et al.11 compared undoped and Fe-doped MoS2 chemical vapor deposition (CVD) grown optical and electrical properties. They observed longer carrier lifetime and lower mobility for Fe:MoS2 compared to MoS2. Despite all the studies on Fe:MoS2, the thermal transport properties of Fe:MoS2 has not been extensively investigated. The findings could be used to design Fe doped MoS2 electronic devices in the future.
In this work, we report the in-plane thermal conductivity of 1L, 2L, and 3L Fe:MoS2 and the interfacial thermal conductance between the Fe:MoS2 and SiO2 substrate for the first time. The opto-thermal Raman technique is employed to measure the thermal properties27,28 of Fe:MoS2. This technique is contactless, with no fabrication requirement and capable of directly measuring thermal conductivity without changing the physical properties of pristine samples. It is particularly ideal for measuring 2D materials due to their sub-nanometer thickness. The result has been confirmed by the computational method, density theory function.
Results
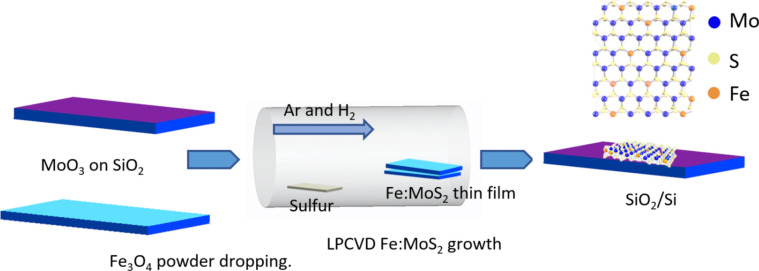
MoS2 monolayers were synthesized via Low pressure chemical vapor deposition (LPCVD). The schematic of growth using the chemical vapor deposition is shown in Fig. 1, and the details are described in the Methods section.
Fig. 1.
Schematic of chemical vapor deposition (CVD) growth process for Fe:MoS2.
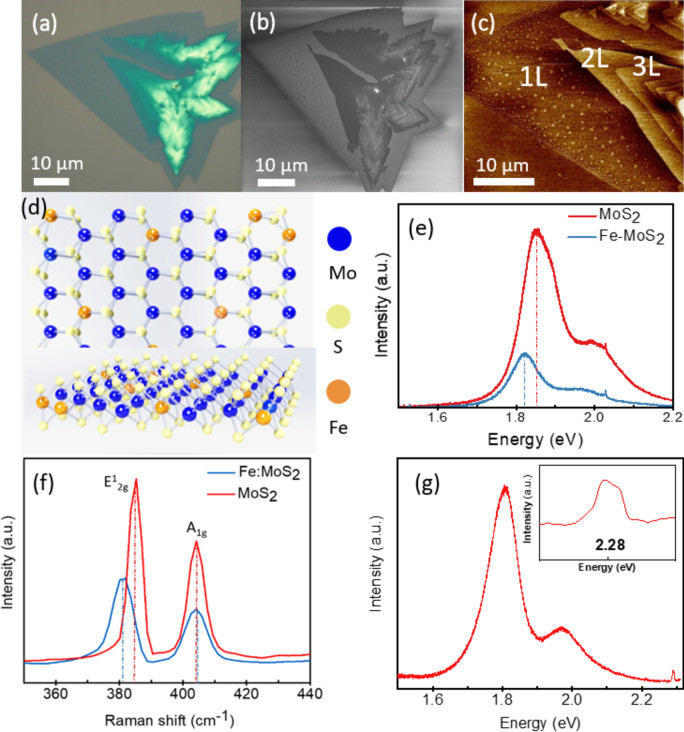
The morphology of the Fe:MoS2 samples was characterized by optical microscopy and scanning electron microscopy as shown in Figs. 2a and b, respectively. To confirm the growth of 1-3L Fe:MoS2 domains, the sample is characterized by the atomic force microscopy (AFM) peak force mode (Bruker Dimension) as shown in Fig. 2c. The thicknesses of 1L, 2L, and 3L Fe:MoS2 are 0.8 nm, 1.6 nm, and 2.4 nm. The AFM image also confirms that there is no Fe3O4 residual remaining on the surface of Fe:MoS2 after wet cleaning and thermal annealing. Figure 2d is the top view schematic of crystal structure of Fe:MoS2.
Fig. 2.
(a) Optical microscopy image of 1–3L Fe:MoS2. (b) Scanning electron microscopy image of 1-3L Fe:MoS2. (c) Atomic force microscopy image of 1–3L Fe:MoS2. (d) Top view schematic of crystal structure of Fe:MoS2. (e) Photoluminescent spectra and (f) Raman spectra comparing MoS2 and Fe:MoS2 monolayers. (g) PL spectra of 1L Fe:MoS2 at 300 K. Only Fe:MoS2 monolayers exhibit Fe-related emission (2.28 eV), whereas undoped MoS2 with Fe and Fe3O4 clusters on top does not. This finding suggests that only substitutional incorporation of Fe can produce this transition.
Raman and photoluminescence (PL) spectroscopy provide evidence that Fe is incorporated into the lattice (Fig. 2). To demonstrate the success of doping MoS2 with Fe, the photoluminescence (PL) spectra of the 1L MoS2 and Fe:MoS2 were characterized under a 405 nm laser excitation with 5 mW power at 300 K. There are two broad bands in the PL spectrum associated with two excitons peaks formed by spin–orbit coupling in the valence band (direct excitonic transition). The left PL peak at 1.86 eV represents MoS2 and the right peak at 1.49 eV represents Fe in Fe:MoS2. The red-shift of 0.37 eV caused by defect in MoS2 lattice structure. Figure 2e shows that the PL intensity of the Fe:MoS2 sample dropped significantly compared to the MoS2 sample. This optical quenching results from the MoS2 lattice distortion due to the introducing of the Fe dopants into the lattice and the existence of additional nonradiative channels known as trap states11,29.
Due to the highly mobile charges and wide access to shallow trap states, MoS2 is expected to have more electron concentration when Fe dopants are introduced. Fe is an n-type dopant, so Fe-doping is expected to increase electron concentrations in Fe:MoS2 monolayers. Due to the reduction in neutral excitons and the increase in negative trion emission, the peak position of the PL would be redshifted, as previous studies demonstrated30. The spectra of 1L MoS2 and 1L Fe:MoS2 samples were collected using a micro-Raman spectrometer (Renishaw InVia Raman Microscope system) under 514 nm laser excitation. Both spectra demonstrate the in-plane E12g and out-of-plane A1g vibration modes of MoS2 as shown in Fig. 2f. The E12g and A1g models of the pristine MoS2 sample are at 385.4 cm−1 and 404.6 cm−1, respectively. The A1g model of the Fe:MoS2 is at 404.2 cm−1, which is like that of the pristine MoS2. However, the E12g model of the Fe:MoS2 is at 381.1 cm−1, indicating a red shift as compared with that of the MoS2. The observed red-shift can be related to the defect in MoS2 lattice structure16. In addition, Raman spectroscopy was employed to further confirm that Fe incorporates into the MoS2 lattice. Figure 2g presents a comparison of PL emission for MoS2 and Fe:MoS2. It is clear from this figure that the Fe-related emission at 2.28 eV can only be observed from 1L Fe:MoS216, which also validates the substitution of Mo by Fe atoms and there is no peak at 2.28 eV for 1L MoS2. This peak is only observable for 1L Fe:MoS2 at room temperature since 2.28 eV peak is considered as PL emission and is affected by band gap. The band gap changes from direct to indirect as the layer number increases from monolayer to thicker samples. Therefore, the quench for the 2.28 eV peak disappears for samples thicker than 1L31.
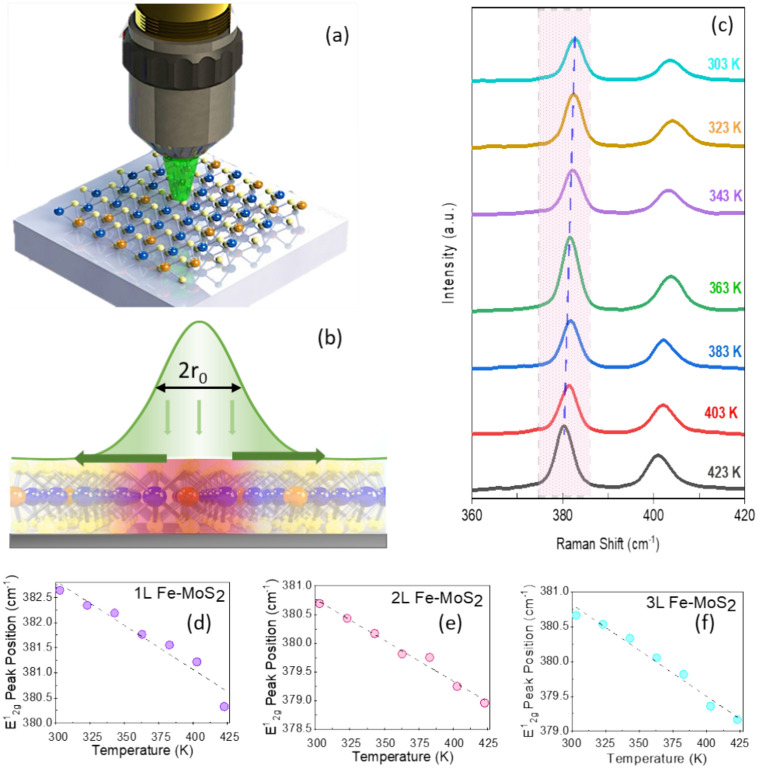
Figure 3a presents a schematic of the experimental setup for the Fe:MoS2 sample by the opto-thermal Raman technique, while in Fig. 3b a schematic of the Raman laser and thermal transport profiles can be observed. At temperatures ranging from 303 to 423 K, we calibrated the Raman E12g peak position shift rate. A laser with a wavelength λ of 514 nm was used. A Raman spectrum of 1L Fe:MoS2 with temperature dependence is shown in Fig. 3c.
Fig. 3.
(a) Schematic of the experimental setup for the Fe:MoS2 sample by the opto-thermal Raman technique. (b) Schematic of the Raman laser and thermal transport profiles. (c) Raman spectra of 1L Fe:MoS2 recorded at temperatures from 303 to 423 K. (d) The temperature-dependent E12g Raman peak shift measured on the 1L Fe:MoS2, (e) 2L Fe:MoS2, and (f) 3L Fe:MoS2.
To acquire 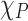 (power-dependent coefficient), the E12g mode shift of the Fe:MoS2 samples was also measured using the micro-Raman system under the 514 nm laser excitation. Then the power dependent coefficient can be derived from the equation of
(power-dependent coefficient), the E12g mode shift of the Fe:MoS2 samples was also measured using the micro-Raman system under the 514 nm laser excitation. Then the power dependent coefficient can be derived from the equation of 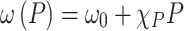 , where
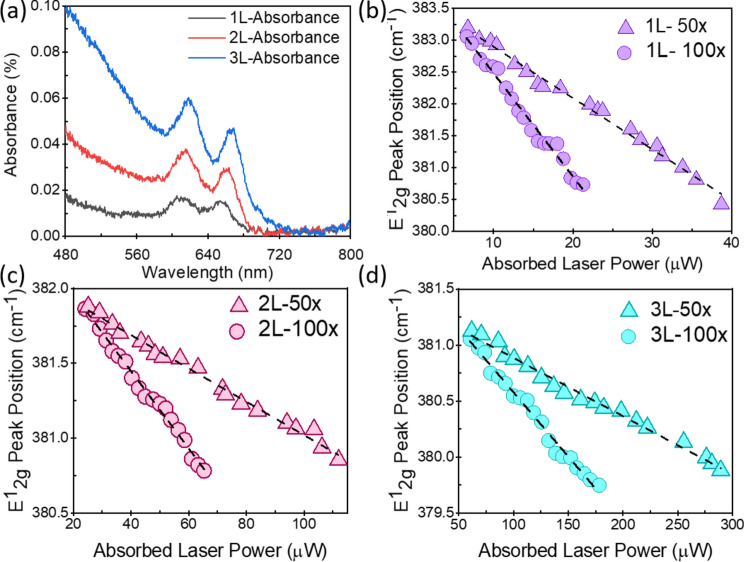
, where 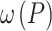 is the Raman peak frequency at absorbed laser power P,
is the Raman peak frequency at absorbed laser power P, 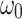 is the Raman peak frequency at power 0 and P is the absorbed laser power. The absorbed laser power can be calculated by multiplying the incident laser power with the absorbance (α) of the samples. The confocal absorption spectra were recorded with a Nikon Eclipse TE2 equipped with an Acton 500 spectrograph and a PIXIS 100 CCD camera (NT&C Consulting, Germany). Figure 4a shows the absorbance of the 1L, 2L, and 3L Fe:MoS2 as a function of wavelength. We used the interpolated method to extract the absorbance at 514 nm wavelength. The absorbance values of 1L, 2L, and 3L Fe:MoS2 are 0.0127, 0.0344, and 0.0831, respectively. 1L-3L Fe:MoS2 were prepared on a transparent quartz substrate, and the transmittance T of 1L-3L Fe:MoS2 at the wavelength of 480 nm – 800 nm were characterized. The absorbance A were calculated as
is the Raman peak frequency at power 0 and P is the absorbed laser power. The absorbed laser power can be calculated by multiplying the incident laser power with the absorbance (α) of the samples. The confocal absorption spectra were recorded with a Nikon Eclipse TE2 equipped with an Acton 500 spectrograph and a PIXIS 100 CCD camera (NT&C Consulting, Germany). Figure 4a shows the absorbance of the 1L, 2L, and 3L Fe:MoS2 as a function of wavelength. We used the interpolated method to extract the absorbance at 514 nm wavelength. The absorbance values of 1L, 2L, and 3L Fe:MoS2 are 0.0127, 0.0344, and 0.0831, respectively. 1L-3L Fe:MoS2 were prepared on a transparent quartz substrate, and the transmittance T of 1L-3L Fe:MoS2 at the wavelength of 480 nm – 800 nm were characterized. The absorbance A were calculated as 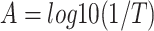 . The E12g peak position as a function of the absorbed laser power was characterized using both 100
. The E12g peak position as a function of the absorbed laser power was characterized using both 100 and 50
and 50 objective lens of the Raman system as shown in Fig. 4b, c, and d. The laser light acted as both the thermometer and the heat source for the Fe:MoS2 flakes. It can be observed that the E12g peak of all the samples decreases almost linearly as a function of the absorbed laser power. This is because the local temperature rise induced by the laser heating resulted in red shift due to the phonon softening effect. The convection through the air is negligible since it is less than 0.01% for all the measured samples18. Both
objective lens of the Raman system as shown in Fig. 4b, c, and d. The laser light acted as both the thermometer and the heat source for the Fe:MoS2 flakes. It can be observed that the E12g peak of all the samples decreases almost linearly as a function of the absorbed laser power. This is because the local temperature rise induced by the laser heating resulted in red shift due to the phonon softening effect. The convection through the air is negligible since it is less than 0.01% for all the measured samples18. Both 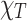 and
and 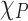 are extracted via linear regression and summarized in Table 1.
are extracted via linear regression and summarized in Table 1.
Fig. 4.
(a) Absorbance of 1-3L Fe:MoS2 at wavelengths from 480 to 800 nm. (b) Power-dependent E2g1 Raman peak shift characterized using two different laser spot sizes, on the 1L Fe:MoS2, (c) 2L Fe:MoS2, and (d) 3L Fe:MoS2.
Table 1.
First-order temperature coefficients, absorbance, and power shift rates of 1–3L Fe:MoS2.
| Temperature coefficient (cm−1/K) | Absorbance (%) | Absorbed power shift rate (cm−1/µw) | ||
|---|---|---|---|---|
| 0.18 µm spot size | 0.31 µm spot size | |||
| 1L Fe:MoS2 | −0.0176 ± 0.0020 | 1.27 | −0.1185 ± 0.0036 | −0.0644 ± 0.00150 |
| 2L Fe:MoS2 | −0.0143 ± 0.0008 | 3.44 | −0.0383 ± 0.0009 | −0.0182 ± 0.00004 |
| 3L Fe:MoS2 | −0.0131 ± 0.0008 | 8.31 | −0.0158 ± 0.0004 | −0.0067 ± 0.00004 |
To calculate the thermal conductivity, one also need to know the laser spot size of the Raman system. The laser spot size of both 100 and 50
and 50 objective lenses was measured using the knife-edge method32. In this method, the laser moves across a sharp edge and using the Raman mapping feature the Si peak is monitored. The Si peak intensity as a function of position had been studied with Gaussian distribution as mentioned in equation below
objective lenses was measured using the knife-edge method32. In this method, the laser moves across a sharp edge and using the Raman mapping feature the Si peak is monitored. The Si peak intensity as a function of position had been studied with Gaussian distribution as mentioned in equation below
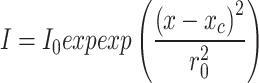 |
1 |
where r0 is the laser spot size, xc is the center of peak position, and I0 is the initial intensity. The laser spot size passing through 100× and 50× was 0.18 µm and 0.31 µm, respectively. The measurements were made in the air at ambient temperature. Laser spot size can also be estimated from the numerical aperture. 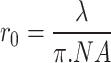 where λ is the laser wavelength and NA is the numerical aperture. For 100× and 50×, the calculated result using the numerical aperture is 0.19 µm and 0.22 µm, respectively. The substrate interaction can make the mean free paths of phonons in Fe:MoS2 smaller than the laser beam size, especially for long-wavelength phonons33. In the cylindrical coordinate T(r), the temperature distribution is related to the in-plane thermal conductivity, interfacial thermal conductance between the flake and substrate, and the absorbed laser power. The volumetric laser heating power density q’’’(r) based on the Gaussian profile of the laser equation below is
where λ is the laser wavelength and NA is the numerical aperture. For 100× and 50×, the calculated result using the numerical aperture is 0.19 µm and 0.22 µm, respectively. The substrate interaction can make the mean free paths of phonons in Fe:MoS2 smaller than the laser beam size, especially for long-wavelength phonons33. In the cylindrical coordinate T(r), the temperature distribution is related to the in-plane thermal conductivity, interfacial thermal conductance between the flake and substrate, and the absorbed laser power. The volumetric laser heating power density q’’’(r) based on the Gaussian profile of the laser equation below is
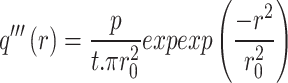 |
2 |
where P is the absorbed laser power, t is the thickness of the flake, and r0 is the laser spot size. After taking the interfacial thermal conductance between the flake and the substrate into consideration, T(r) is presented by the equation below
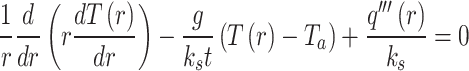 |
3 |
where g is the interfacial thermal conductance between the flake and the substrate, Ks is the in-plane thermal conductivity of Fe:MoS2 and Ta is the ambient temperature. The weighted result can be calculated by considering the Gaussian profile of the laser spot. The equation below is the average temperature.
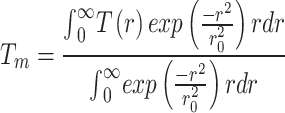 |
4 |
To solve the equations, boundary conditions need to be defined. Based on the Gaussian profile of the laser 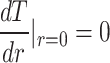 , the maximum temperature is in the center where the laser shines on the sample (
, the maximum temperature is in the center where the laser shines on the sample (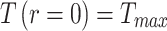 and further away from the center, the temperature is the ambient temperature
and further away from the center, the temperature is the ambient temperature 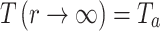 . We also need to calculate the thermal resistance of Fe:MoS2, which can be calculated as
. We also need to calculate the thermal resistance of Fe:MoS2, which can be calculated as 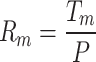 and relate the thermal resistance to the thermal conductivity and the interfacial thermal conductance between the flake and the substrate. The ratio of two Rm characterized from two laser spot sizes is a function of g/Ks. The calculated results are Ks = 24 ± 11 W/m⋅K, and g = 0.3 ± 0.2 MW/m2⋅K for 1L Fe:MoS2, Ks = 18 ± 9 W/m⋅K, and g = 1.1 ± 0.7 MW/m2⋅K for 2L Fe:MoS2, and Ks = 16 ± 8 W/m⋅K, and g = 3.0 ± 2.3 MW/m2⋅K for 3L Fe:MoS2.
and relate the thermal resistance to the thermal conductivity and the interfacial thermal conductance between the flake and the substrate. The ratio of two Rm characterized from two laser spot sizes is a function of g/Ks. The calculated results are Ks = 24 ± 11 W/m⋅K, and g = 0.3 ± 0.2 MW/m2⋅K for 1L Fe:MoS2, Ks = 18 ± 9 W/m⋅K, and g = 1.1 ± 0.7 MW/m2⋅K for 2L Fe:MoS2, and Ks = 16 ± 8 W/m⋅K, and g = 3.0 ± 2.3 MW/m2⋅K for 3L Fe:MoS2.
To obtain the relationship between Raman peak shift and temperature rise, we also heated the samples from room temperature to 500 K on the heating platform. The optothermal Raman characterizations were conducted with a Raman laser of low power (100 μW). The thermal conductivity and interfacial thermal conductance between the flake and substrate are summarized in Table 2.
Table 2.
Thermal conductivities of 1–3L Fe:MoS2 at room temperature (300 K) and at 500 K, and their interfacial thermal conductance.
| Thermal conductivity (W/m⋅K) | Interfacial thermal conductance (MW/m2⋅K) | ||
|---|---|---|---|
| At 300 K | At 500 K | ||
| 1L Fe:MoS2 | 24 ± 11 | 19 ± 10 | 0.3 ± 0.2 |
| 2L Fe:MoS2 | 18 ± 9 | 11 ± 6 | 1.1 ± 0.7 |
| 3L Fe:MoS2 | 16 ± 8 | 8 ± 3 | 3.0 ± 2.3 |
Discussion
Thermal conductivities of 1-3L Fe:MoS2 have been explored and found in the range of 16–24 W/m⋅K which is about 40% lower than the reported values for MoS218. This value is also smaller than other TMDC materials, such as MoS2, MoSe2, and WSe2, due to the imperfect lattice structure of MoS2 from the doping engineering. The iron doped MoS2 causes imperfection in the lattice structure, leading to phonon scattering and a further reduction in thermal conductivity. The phonon scattering rate caused by imperfections can be derived from Green’s function approach or calculated using Fermi’s golden rule34,35. The phonon scattering rate for 2D materials can be estimated by the formula 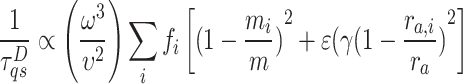 , where m and ra are the average atom mass and radius,
, where m and ra are the average atom mass and radius, 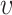 is the phonon group velocity,
is the phonon group velocity, 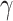 is the Gruneisen parameter, mi, ra, i, and fi are the mass, radius, and fraction concentration of type i atom, and
is the Gruneisen parameter, mi, ra, i, and fi are the mass, radius, and fraction concentration of type i atom, and 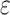 is a parameter for defect scattering due to lattice distortion and mass difference. This expression indicates the likelihood of high-frequency phonon modes scattering by defects. Since the Fe atoms substitute the Mo atoms in MoS2 lattice structure, the difference between the atomic radius and the atomic mass of these two materials cause a change in phonon scattering rate36.
is a parameter for defect scattering due to lattice distortion and mass difference. This expression indicates the likelihood of high-frequency phonon modes scattering by defects. Since the Fe atoms substitute the Mo atoms in MoS2 lattice structure, the difference between the atomic radius and the atomic mass of these two materials cause a change in phonon scattering rate36.
A decreasing trend of thermal conductivities and an increasing trend in interfacial thermal conductance have been observed with increasing layer numbers of Fe:MoS2. The decreasing trend of thermal conductivities from thinner layer to thicker layer is due to the stronger phonon-boundary scattering. The strength of boundary condition scattering, which is defined as 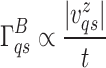 where t is the thickness, decreases in the layered 2D crystals due to the weak van der Waals interaction 36. In addition, the decreasing trend is associated with the Umkkalpp phonon scattering, crystal’s phonon anharmonicity, and reduction of ballistic resistance that affects phonon mean free path for thicker flakes. Other studies on the MoS2, MoSe2, WSe2, and hBN also faced the decreasing trend of thermal conductivity with increasing the number of layers18,37,38. The increasing trend in interfacial thermal conductance could be explained that as the number of layers increases, the interface between 2D materials and the substrate becomes more tightly coupled. In addition, there are less defects in 2D materials with increased layers because more layers can act as “bridge” between 2D materials and the substrate. We also compared to the undoped CVD MoS2 that we synthesized with the Fe doped CVD MoS2 in this work(with Fe concentration 0.3–0.5%), and found the Fe doped CVD MoS2’s thermal conductivity is ~ 30% smaller. This decrease in thermal conductivity is due to the defects in the material created during the doping process.
where t is the thickness, decreases in the layered 2D crystals due to the weak van der Waals interaction 36. In addition, the decreasing trend is associated with the Umkkalpp phonon scattering, crystal’s phonon anharmonicity, and reduction of ballistic resistance that affects phonon mean free path for thicker flakes. Other studies on the MoS2, MoSe2, WSe2, and hBN also faced the decreasing trend of thermal conductivity with increasing the number of layers18,37,38. The increasing trend in interfacial thermal conductance could be explained that as the number of layers increases, the interface between 2D materials and the substrate becomes more tightly coupled. In addition, there are less defects in 2D materials with increased layers because more layers can act as “bridge” between 2D materials and the substrate. We also compared to the undoped CVD MoS2 that we synthesized with the Fe doped CVD MoS2 in this work(with Fe concentration 0.3–0.5%), and found the Fe doped CVD MoS2’s thermal conductivity is ~ 30% smaller. This decrease in thermal conductivity is due to the defects in the material created during the doping process.
Computational studies were carried out in parallel to verify the experimental results. we utilized a combination of phonopy, thirdorder, and ShengBTE software, integrated with VASP first-principles DFT calculations, to compute the thermal conductivity of Fe-doped MoS2. The second- and third-order interatomic force constants were extracted and employed to solve the phonon Boltzmann transport equation. For this, we constructed a 4 × 4 × 1 supercell of monolayer MoS₂, with one Mo atom substituted by an Fe atom to introduce doping. Following structural optimization, the atomic configuration corresponding to the minimum energy was identified. The cutoff energy for plane-wave basis sets was set to 400 eV, ensuring sufficient accuracy, while the energy convergence criterion was set to 1 × 10⁻⁶ eV, which provided precise structural optimization. Additionally, we used a Γ-centered k-point mesh of 6 × 6 × 1 for Brillouin zone sampling and employed a Methfessel-Paxton smearing method with a width of 0.05 eV to ensure electronic structure convergence during the relaxation process. the cutoff distance was set to 0.3 Å in the calculation of third-order force constants for neighboring atoms. We employed a 10 × 10 × 10 q-grid to more accurately estimate phonon frequencies and phonon lifetimes, ensuring better resolution of the phonon characteristics for our calculations.
The thermal conductivity results revealed that for the monolayer Fe-doped MoS₂, the in-plane thermal conductivity was 28.3 W/mK. In contrast, for the bilayer Fe-doped MoS₂, the in-plane thermal conductivity dropped to 20.3 W/mK. The in-plane thermal conductivity of the 3L material is 18.8 W/mK. The computational results are in good agreement with the experimental findings. These findings indicate that the significant reduction in thermal conductivity for multilayered 2D materials, as compared to their monolayer counterparts, can be attributed to the poor efficiency of interlayer thermal transport. The out-of-plane thermal conductivity remains several orders of magnitude lower than the in-plane thermal conductivity, which is primarily responsible for the observed suppression of thermal transport in the multilayer structure.
Methods
MoS2 monolayers were synthesized via Low pressure chemical vapor deposition (LPCVD). Before growth, a thin MoO3 layer was prepared using physical vapor deposition (PVD) of e-beam evaporating MoO3 pellet onto a Si substrate with 300 nm-thick thermal oxides. Subsequently, the MoO3-deposited substrate was in direct contact with a different SiO2/Si substrate. On the SiO2/Si substrate, monolayers of Fe:MoS2 were grown. The following steps were taken to dope the Fe atoms: the MoO3-deposited substrate was rinsed with deionized (DI) water to deposit a thin layer of water on the SiO2 surface to ensure that the Fe3O4 particles were distributed uniformly. Fe3O4 particles were uniformly cast onto the SiO2/Si substrate and then the substrate was baked at 110 °C for 5 min. During the growth, the furnace was heated with a ramping rate of 18 ˚C/min and held for 15 min at 850 ˚C. Upon the heating procedure, an argon gas (30 sccm) was supplied at 300 ˚C, and a hydrogen gas (15 sccm) was delivered at 760 ˚C. Sulfur was supplied when the furnace temperature reached 790 ˚C. After the growth, a few millimeters of Fe:MoS2 monolayers were obtained.
Conclusion
It is the first work to explore the thermal transport properties of the novel magnetic 2D material Fe:MoS2 in its 1L to 3L forms, both experimentally and computationally. Fe:MoS2 is produced via the LPCVD method, with Fe atoms in the lattice structure of Fe:MoS2 characterized by Raman spectroscopy and photoluminescence. Our refined opto-thermal Raman method was used to characterize the in-plane thermal conductivity and interfacial thermal conductance of Fe:MoS2. A decreasing trend has been observed for thermal conductivities of Fe:MoS2 as the layer number increases. The in-plane thermal conductivities of 1L, 2L, and 3L Fe:MoS2 are 24 ± 11 W/m⋅K, 18 ± 9 W/m⋅K, and 16 ± 8 W/m⋅K and the interfacial thermal conductivity are 0.3 ± 0.2 MW/m2⋅K, 1.1 ± 0.7 MW/m2⋅K, and 3.0 ± 2.3 MW/m2⋅K respectively. These values will help us to understand their thermal behavior, the critical factor that has a significant limitation on nano- and quantum devices. Experimental results show a layer-dependent trend of thermal conductivity.
Acknowledgements
This work was supported by the National Science Foundation CAREER Award (Grant CBET-2145417) and LEAPS Award (Grant DMR-2137883).
Author contributions
X.Z. contributed to the conceptualization and the methodology. E.E. and X.Z. contributed to the investigation. M.F. and E.Y. contributed to the material synthesis. M.L. contributed to the optical characterization. E.Y. contributed to writing the original draft. X.Z. contributed to writing the review and editing. All authors have given approval to the final version of the manuscript.
Funding
National Science Foundation CAREER Award (Grant CBET-2145417) and LEAPS Award (Grant DMR-2137883).
Data availability
The datasets used and analysed during the current study available from the corresponding author on reasonable request.
Declarations
Competing interests
The authors declare no conflict of interest.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science306(5696), 666–669 (2004). [DOI] [PubMed] [Google Scholar]
- 2.Amani, M. et al. Recombination kinetics and effects of superacid treatment in sulfur- and selenium-based transition metal dichalcogenides. Nano Lett.16(4), 2786–2791 (2016). [DOI] [PubMed] [Google Scholar]
- 3.Ahmed, S. & Yi, J. Two-dimensional transition metal dichalcogenides and their charge carrier mobilities in field-effect transistors. Nano-Micro Lett.9(4), 50 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kandemir, A., Yapicioglu, H., Kinaci, A., Çağın, T. & Sevik, C. Thermal transport properties of MoS2 and MoSe2 monolayers. Nanotechnology27(5), 055703 (2016). [DOI] [PubMed] [Google Scholar]
- 5.Wang, Y. & Zhang, X. Thermal transport in graphene under large mechanical strains. J. Appl. Phys.136(7), 074302 (2024). [Google Scholar]
- 6.Ye, F., Liu, Q., Xu, B., Feng, P. X. L. & Zhang, X. Ultra-high interfacial thermal conductance via double hBN encapsulation for efficient thermal management of 2D electronics. Small19(12), 2205726 (2023). [DOI] [PubMed] [Google Scholar]
- 7.Kalantari, M. H., Zhang, X. Thermal transport in 2D materials. Nanomaterials [Online] (2023). [DOI] [PMC free article] [PubMed]
- 8.Wang, Y. & Zhang, X. On the role of crystal defects on the lattice thermal conductivity of monolayer WSe2 (P63/mmc) thermoelectric materials by DFT calculation. Superlattices Microstruct.160, 107057 (2021). [Google Scholar]
- 9.Seyler, K. L. et al. Electrical control of second-harmonic generation in a WSe2 monolayer transistor. Nature Nanotechnol.10(5), 407–411 (2015). [DOI] [PubMed] [Google Scholar]
- 10.Babaei, H., Khodadadi, J. M. & Sinha, S. Large theoretical thermoelectric power factor of suspended single-layer MoS2. Appl. Phys. Lett.105(19), 193901 (2014). [Google Scholar]
- 11.Wang, S. Y., Ko, T. S., Huang, C. C., Lin, D. Y. & Huang, Y. S. Optical and electrical properties of MoS2 and Fe-doped MoS2. Japanese J. Appl. Phys.53(4S), 04EH07 (2014). [Google Scholar]
- 12.Wang, Y., Zhang, X. Experimental and theoretical investigations of direct and indirect band gaps of WSe2 Micromachines [Online] (2024). [DOI] [PMC free article] [PubMed]
- 13.Mas-Ballesté, R., Gómez-Navarro, C., Gómez-Herrero, J. & Zamora, F. 2D materials: To graphene and beyond. Nanoscale3(1), 20–30 (2011). [DOI] [PubMed] [Google Scholar]
- 14.Jenisha, M. A. et al. Interfacial engineering effect and bipolar conduction of Ni- doped MoS2 nanostructures for thermoelectric application. J. Alloys Compd.895, 162493 (2022). [Google Scholar]
- 15.Mao, Y., Fang, Y., Yuan, K. & Huang, F. Effect of vanadium doping on the thermoelectric properties of MoS2. J. Alloys Compd.903, 163921 (2022). [Google Scholar]
- 16.Chen, Y. et al. Tuning electronic structure of single layer MoS2 through defect and interface engineering. ACS Nano12(3), 2569–2579 (2018). [DOI] [PubMed] [Google Scholar]
- 17.Zhou, W.-X. et al. Thermal conductivity of amorphous materials. Adv. Funct. Mater.30(8), 1903829 (2020). [Google Scholar]
- 18.Chen, X.-K., Zhang, E.-M., Wu, D. & Chen, K.-Q. Strain-induced medium-temperature thermoelectric performance of Cu4TiSe4: The role of four-phonon scattering. Phys. Rev. Appl.19(4), 044052 (2023). [Google Scholar]
- 19.Chen, X.-K. et al. Large contributions from optical phonons to thermal transport in hexagonal carbon-boron-nitrogen monolayers. Phys Rev B108(23), 235420 (2023). [Google Scholar]
- 20.Kuang, H.-L., Wu, C.-W., Zeng, Y.-J., Chen, X.-K. & Zhou, W.-X. The amplification effect of four-phonon scattering in CdX (X=Se, Te): The role of mid-frequency phonons. Int. J. Thermal Sci.205, 109254 (2024). [Google Scholar]
- 21.Williamson, I. et al. Structural, electrical, phonon, and optical properties of Ti- and V-doped two-dimensional MoS2. Chem. Phys. Lett.674, 157–163 (2017). [Google Scholar]
- 22.Yokoo, A. Nanoelectrode lithography. Jpn. J. Appl. Phys.42(2A), L92 (2003). [Google Scholar]
- 23.Zibouche, N., Kuc, A., Musfeldt, J. & Heine, T. Transition-metal dichalcogenides for spintronic applications. Ann. der Phys.526(9–10), 395–401 (2014). [Google Scholar]
- 24.Fu, S. et al. Enabling room temperature ferromagnetism in monolayer MoS2 via in situ iron-doping. Nature Commun.11(1), 2034 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Shu, H., Luo, P., Liang, P., Cao, D. & Chen, X. Layer-dependent dopant stability and magnetic exchange coupling of iron-doped MoS2 nanosheets. ACS Appl. Mater. Interfaces7(14), 7534–7541 (2015). [DOI] [PubMed] [Google Scholar]
- 26.Mishra, N., Pandey, B. P. & Kumar, S. Impact of Mn- and Fe-doping on electronic and magnetic properties of MoX₂ (X = S, Se) monolayer. IEEE Trans. Electron Devices69(3), 1553–1560 (2022). [Google Scholar]
- 27.Zhang, X. et al. Measurement of lateral and interfacial thermal conductivity of single- and bilayer MoS2 and MoSe2 using refined optothermal Raman technique. ACS Appl. Mater. Interfaces7(46), 25923–25929 (2015). [DOI] [PubMed] [Google Scholar]
- 28.Easy, E. et al. Experimental and computational investigation of layer-dependent thermal conductivities and interfacial thermal conductance of one- to three-layer WSe2. ACS Appl. Mater. Interfaces13(11), 13063–13071 (2021). [DOI] [PubMed] [Google Scholar]
- 29.Zhang, S. et al. Controllable, wide-ranging n-doping and p-doping of monolayer group 6 transition-metal disulfides and diselenides. Adv. Mater.30(50), 1806345 (2018). [DOI] [PubMed] [Google Scholar]
- 30.Mouri, S., Miyauchi, Y. & Matsuda, K. Tunable photoluminescence of monolayer MoS2 via chemical doping. Nano Lett.13(12), 5944–5948 (2013). [DOI] [PubMed] [Google Scholar]
- 31.Zhang, K. et al. Tuning the electronic and photonic properties of monolayer MoS2 via in situ rhenium substitutional doping. Adv. Funct. Mater.28(16), 1706950 (2018). [Google Scholar]
- 32.Suzaki, Y. & Tachibana, A. Measurement of the μm sized radius of Gaussian laser beam using the scanning knife-edge. Appl. Opt.14(12), 2809–2810 (1975). [DOI] [PubMed] [Google Scholar]
- 33.Xiaokun Gu, R. Y. Phonon transport and thermal conductivity in two-dimensional materials. In: Annual Review of Heat Transfer, Begell: 2016.
- 34.Klemens, P. G., The scattering of low-frequency lattice waves by static imperfections. Proceedings of the Physical Society. Section A1955,68 (12), 1113.
- 35.Klemens, P. G. Theory of the a-plane thermal conductivity of graphite. J. Wide Bandgap Mater.7, 332–339 (2000). [Google Scholar]
- 36.Yarali, M. et al. Effects of defects on the temperature-dependent thermal conductivity of suspended monolayer molybdenum disulfide grown by chemical vapor deposition. Adv. Funct. Mater.27(46), 1704357 (2017). [Google Scholar]
- 37.Cai, Q., Scullion, D., Gan, W., Falin, A., Zhang, S., Watanabe, K., Taniguchi, T., Chen, Y., Santos, E. J. G., Li, L. H. High thermal conductivity of high-quality monolayer boron nitride and its thermal expansion. Sci. Adv. 5(6), eaav0129. [DOI] [PMC free article] [PubMed]
- 38.Yuan, P., Wang, R., Wang, T., Wang, X., Xie, Y. Nonmonotonic thickness-dependence of in-plane thermal conductivity of few-layered MoS2: 2.4 to 37.8 nm. Phys. Chem. Chem. Phys. 2018, 20(40), 25752–25761. [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and analysed during the current study available from the corresponding author on reasonable request.