Abstract
Monovalent salts are generally believed to stabilize DNA duplex by weakening inter-strand electrostatic repulsion. Unexpectedly, our force-induced hairpin unzipping experiments and thermal melting experiments show that LiCl, NaCl, KCl, RbCl, and CsCl at concentrations beyond ~1 M destabilize DNA, RNA, and RNA-DNA duplexes. The two types of experiments yield different changes in free energy during melting, while the results that high concentration monovalent salts destabilize duplexes are common. The effects of these monovalent ions are similar but also have noticeable differences. From 1 M to 4 M, DNA duplex is destabilized by about 0.3 kBT/bp and the melting temperature decreases by about 10 oC. Our all-atom simulations reveal this effect is caused by overcharging, where excessive ion absorption inverts the effective DNA charge from negative to positive. Furthermore, our coarse-grained simulations obtain a phase diagram that indicates whether DNA overcharging occurs at a given cation valence and concentration. These findings challenge the traditional belief that DNA overcharging occurs only with multivalent ions and have significant implications for polyelectrolyte theory, DNA nanomaterials, DNA nanotechnology, and DNA biophysics.
Subject terms: Single-molecule biophysics, Computational biophysics, DNA, RNA, Computational models
Experiments and simulations suggest monovalent salts destabilize DNA/RNA because of overcharging. These findings challenge views that overcharging requires multivalent ions, with implications for nanomaterials, nanotechnology, and biophysics.
Introduction
Ion-nucleic acid interactions play essential roles in biological processes, because nucleic acids, including DNA and RNA, carry high-density negative charges (see a review in ref. 1). One important role of ions, such as Na+ and K+, is screening the repulsions among negative charges in nucleic acids2–6. Without such screening, DNA duplex would be unstable, and RNA folding would not occur due to the strong repulsions in nucleic acids1.
In this work, our experiments surprisingly find that monovalent cations destabilize DNA duplexes when salt concentration , is beyond a critical concentration . Such destabilization by ions is opposite to the stabilization caused by electrostatic screening7–9. And such DNA destabilization occurs for LiCl, NaCl, KCl, RbCl, and CsCl. Furthermore, the destabilization by monovalent ions also occurs for other nucleic acids (NA) including RNA and RNA-DNA hybrid (RDH) duplexes, which suggests the phenomenon is general, independent of the structural details of NA duplexes.
Previous studies have observed many salt effects on DNA that go beyond electrostatic screening. For example, multivalent ions can induce DNA-DNA attraction10,11, which is manifested by DNA condensation, and reversal of DNA electrophoretic direction12. However, these experimental phenomena occur only with multivalent ions, such as cobalt hexamine (CoHex3+), but not with monovalent ions. Theories have been developed to explain multivalent ion-induced DNA-DNA attraction and DNA charge inversion observed in experiments13,14. According to the theory based on the Wigner crystal, the interactions between multivalent ions are so strong that they form a strongly correlated liquid or Wigner crystal, which causes DNA-DNA attraction and DNA charge inversion13,14. According to this theory, the interactions between monovalent ions are not strong enough to induce a Wigner crystal. Simulations have observed DNA charge inversion15, and DNA-DNA attraction induced by multivalent ions16. In terms of monovalent effects beyond electrostatic screening, simulations have observed DNA-DNA attraction induced by high concentrations of NaCl17. This phenomenon is different from the DNA destabilization with monovalent ions, because the former is about inter-DNA interaction, while the latter is about intra-DNA interaction18. In addition, DNA overcharging induced by monovalent ions has been observed in coarse-grained (CG) simulations and theoretical calculations19. In these simulations and calculations, DNA was modeled as a cylinder and water molecules were not considered. It is not sure that the phenomenon in such a simple model can be applied to realistic DNA molecules. After two decades of this work, no experimental results have confirmed that DNA overcharging can occur with monovalent ions. Whether DNA overcharging by monovalent ions can occur remains unclear.
DNA thermal melting experiments by Tomac et al. 20 and Khimji et al. 2 observed that DNA duplex is destabilized at high concentrations of Na+. Khimji et al. 2 did not discuss the mechanism of DNA destabilization because their focus was on the effect of polyanions on DNA stability. Their experiments used only one monovalent ion, Na+. It is unclear whether any ion-specific effects cause DNA destabilization under high salt concentrations. Later, a theoretical work by Maity, Singh, and Singh5 reproduced the DNA destabilization at high salt concentrations by assuming the effective base-pairing hydrogen bonds weaken at high salt concentrations. This assumption has not yet been validated.
In this work, we perform precise and systematic measurements for DNA, RNA, and RDH duplex stabilities across wide ranges of for LiCl, NaCl, KCl, RbCl, and CsCl. The experiments constantly show duplex destabilization by high concentrations of monovalent ions. Furthermore, we reveal that such duplex destabilization is caused by overcharging using extensive all-atom molecular dynamics (MD) and CG Langevin dynamics simulations, as well as Wigner crystal theory. In addition, we discovered that overcharging can also occur for ssDNA through experiments and simulations.
Results
Monovalent cations at high concentrations destabilize DNA duplexes in single-molecule experiments
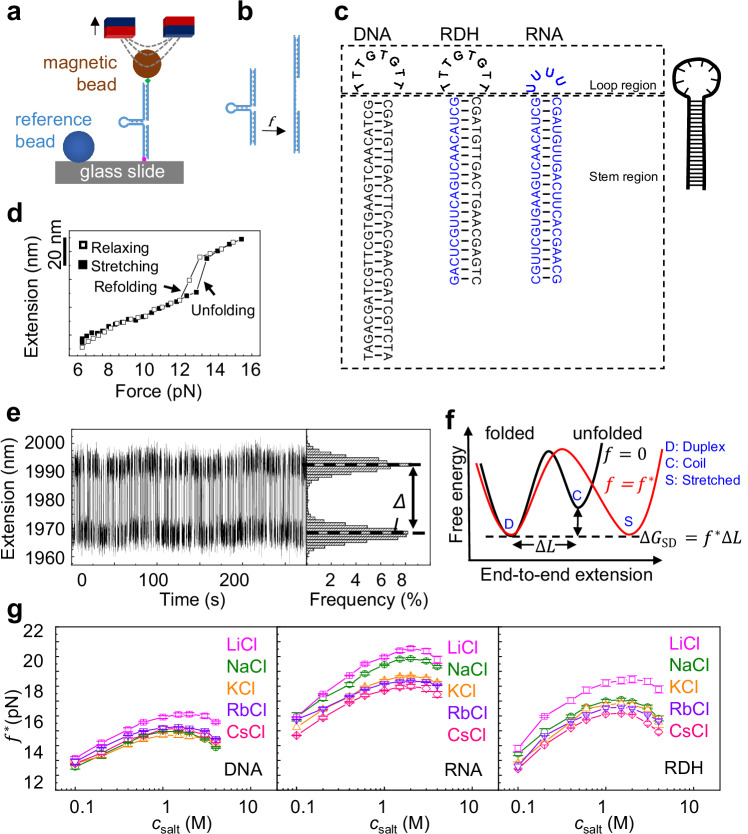
We first measured the stabilities of NA duplexes by unzipping short NA hairpins using magnetic tweezers (MT) experiments (Fig. 1a, b), similar to previous works21–24, while we focused on the variation of the NA duplexes stability with monovalent salt concentrations. For each salt condition, we first measured the extension of the NA construct through a force-cycle containing a stretching process followed by a relaxing process. The NA hairpin unfolded during stretching and refolded during relaxing, which provided the unfolding and refolding forces (arrows, Fig. 1d), respectively. Within the range from the refolding force to the unfolding force, we searched for a transition force, , where the folded and stretched states of the NA hairpin had the same probability (Fig. 1e). The free energy cost of hairpin unfolding equals the change in the external potential, (Fig. 1f), where is the change in the DNA extension during the hairpin unfolding (Supplementary Fig. 1a). The transition is between the duplex state and the stretched state, and we denote the free energy cost as . Note that varying salt concentration affects the refractive index of the buffer (up to 4%). We have considered this factor in the measurement of using a previous method25. Ultimately, we found that very weakly depends on the salt condition (Supplementary Fig. 1b).
Fig. 1. Measurement of NA duplex stability by MT experiments.
Source are provided as a Source Data file. a Manipulation of NA hairpin using magnetic tweezers. b The NA hairpin is unfolded by the external force. c Illustration of the construct of three types of NA hairpins. Black for DNA bases and blue for RNA bases. d The unfolding and folding of an NA hairpin are indicated by abrupt changes in DNA extension during stretching and relaxing, respectively. e At the transition force , the NA hairpin hops between the folded and stretched states with equal probability. f The free energy difference between the folded and unfolded hairpin. g Transition force as a function of salt concentration. The averages and standard errors from several molecules (four for CsCl and three for other ions) are plotted as data points and error bars.
Figure 1g shows reaches a peak at a critical salt concentration, which is denoted as . The values of are always between 1 M and 2 M. Figure 2a shows NA duplex stabilities as functions of , which is calculated as . Because we focus on the dependence of on , we shift the curves to offset the peak values of in Fig. 2b for NaCl (a similar plot for KCl is shown in Supplementary Fig. 2). From to 4 M, DNA duplex is destabilized by about . Such magnitude of duplex destabilization roughly equals the case from to . Similar results were observed for RNA for five salt types (Fig. 2c, d). The values of for RNA are typically slightly lower than those for DNA. Under a given high , the magnitude of destabilization for RNA is smaller than the case of DNA. The differences between RNA and DNA are possibly caused by different charge densities and ion distribution patterns26 (Supplementary Fig. 3). Previous ion counting experiments have also observed that ion distributions around RNA and DNA are different1,27.
Fig. 2. Comparison of experimental and simulation results.
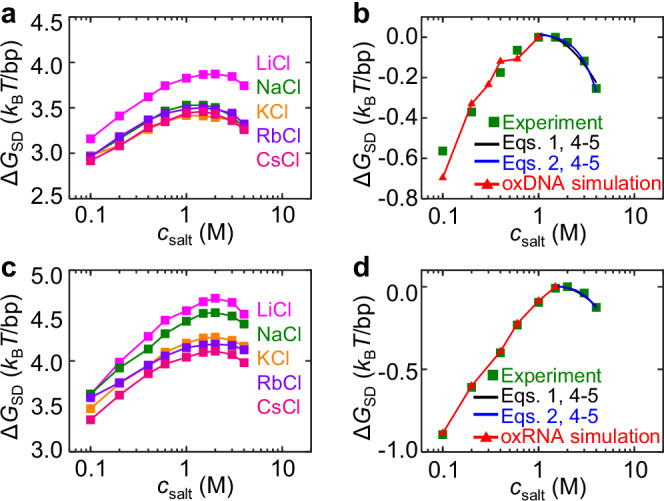
In MT experiments, the averages and standard errors from three molecules are plotted as data points and error bars. In MD simulations, the averages and standard errors from five equal intervals after equilibrium are plotted as data points and error bars. Source data are provided as a Source Data file. a The free energy difference between duplex and stretched single-stranded DNA states () as a function of salt concentration ) from MT experiments. b Variation of , . The red curve is obtained from oxDNA simulation. c, d Similar results for RNA duplex stability and the red curve are obtained from oxRNA simulation. In (b) and (d), all experimental curves are shifted to make at for the salt type of NaCl, and the black curves are calculated from Eqs. 1, 4–5, and the blue curves from Eqs. 2, 4–5.
Measurement of duplex stability by thermal melting
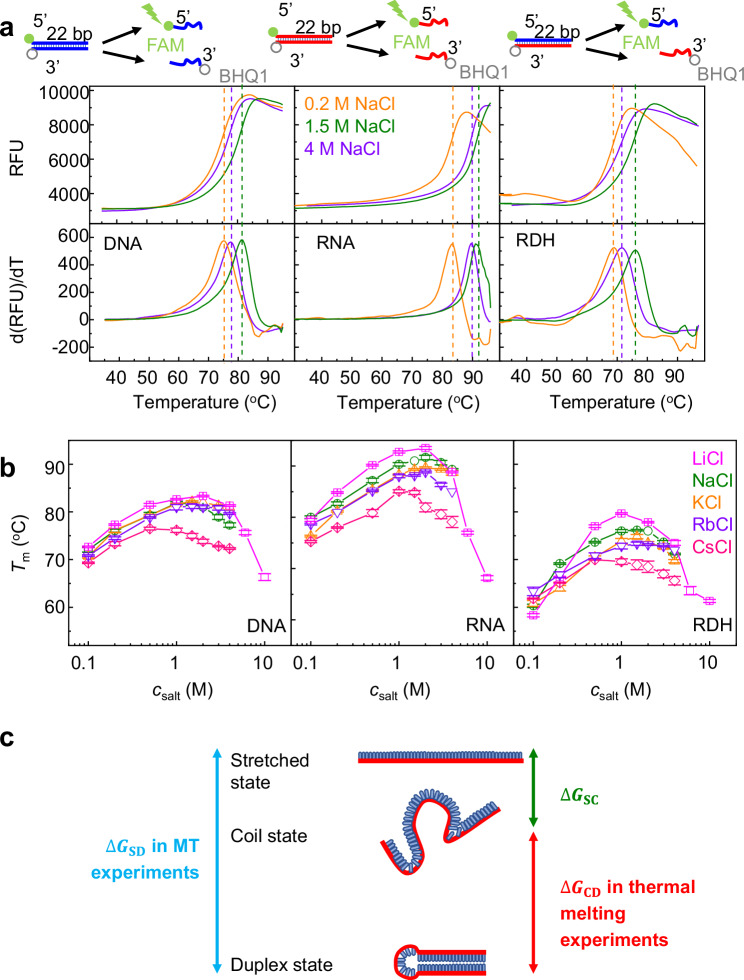
We measured the melting temperature (Tm) of NA duplexes at various using a fluorescence quenching test, as detailed in the “Methods” section (Fig. 3 and Supplementary Fig. 4). In the duplex state, the BHQ1 quencher on one strand effectively suppressed the proximate FAM fluorescence on the complementary strand. We raised the temperature incrementally at a rate of 0.1 oC/s. As the NA duplex gradually melted and the FAM strand separated from the BHQ1 strand, we observed a corresponding increase in fluorescence intensity. The peak of the derivative of the fluorescence intensity determined the Tm under each salt condition28.
Fig. 3. Measurement of NA duplex stability by thermal melting.
Source data are provided as a Source Data file. a Representative melting curves obtained from a fluorescence quenching test. The top panels are the fluorescence intensity as a function of temperature, and the bottom panels are the derivative of fluorescent intensity versus temperature. b Melting temperature Tm as functions of . The averages and standard errors from several independent experiments (six for NaCl and three for other ions) are plotted as data points and error bars. c Two different transitions in MT and thermal melting experiments.
As shown in Fig. 3b, Tm exhibits a non-monotonic change with , in agreement with the MT results in Fig. 1g. DNA destabilization at high consistently occurs for different DNA lengths from 12 to 400 bp and different GC percentages in thermal melting experiments (Supplementary Figs. 5 and 6). From these curves, we determined the critical salt concentrations, , corresponding to the maximum melting temperature. The values of are also between 1 and 2 M for all three NA duplexes and four types of monovalent salts, except for CsCl whose is below 1 M. The smaller for CsCl may be caused by stronger binding of Cs+ to DNA than other cations.
The curves in MT experiments (Fig. 1g) are smoother and the error bars are smaller than those in thermal melting experiments (Fig. 3b). It is worth noting that the conformational transitions in MT and thermal melting experiments are slightly different (Fig. 3c). In MT experiments, NA hairpins transition between the folded duplex state and unfolded stretched state under tension, and the free energy difference is denoted as . In thermal melting experiments, NA duplexes transit between the duplex state and a single-stranded random-coiled state, and the free energy difference is denoted as . As shown in Fig. 3c, we have , where is the free energy difference between the stretched state and coil state.
The value of can be estimated through the integration of the force-extension curve from the coil state to the stretched state. Here, and are the extensions of the stretched and coil states, respectively, and is the stretching force at a given extension, . After approximating ssDNA as a worm-like chain29, the dependence of the force on the extension is described by the Marko–Siggia equation . Here, is the ssDNA persistence length, is the ssDNA contour length, N = 64 is the number of nucleotides for DNA hairpin in MT experiments, and is the contour length per nucleotide30,31. Previous experiments have obtained 0.94 nm, 1.08 nm, and 1.6 nm at 1 M, 0.5 M, and 0.1 M NaCl, respectively. Based on the Marko–Siggia equation and = 12.5, 14.4, and 15 pN at 0.1, 0.5, and 1 M NaCl, we can obtain the values of . Eventually, we obtained , 0.89, and 0.95 kBT/bp at 0.1, 0.5, and 1 M NaCl, correspondingly. Here, 28 is the number of base pairs of the DNA stem region in MT experiments. As illustrated in Fig. 3c, we expect . To examine this relationship, we calculated using the nearest-neighbor model32 and obtained at 1 M NaCl (Supplementary Method 1). With at 1 M NaCl from Fig. 2a and from the Marko–Siggia equation, we find that at 1 M NaCl, , which is close to and confirms .
The increase of with likely explains why the peak locations in Fig. 3b, i.e. , are generally smaller than the peak locations in Fig. 1g, considering that MT and thermal melting experiments correspond to , and , respectively, which differ by
The value of depends not only on , but may also depend on the ion species. Ions may mediate intra-strand interaction in the random-coiled state and thus affect the effective ssDNA persistence length or make the force-extension curve deviate from the worm-like chain behavior29. For example, the smaller for Na+ and Cs+ at high concentrations in Fig. 3b may be caused by greater intra-strand attraction mediated by Na+ and Cs+, which enhances the dependence of on .
Mechanism of DNA duplex destabilization by monovalent ions
We propose that DNA duplex destabilization at high concentrations of monovalent salts is caused by DNA overcharging. In the following paragraphs, we will elaborate on this mechanism and provide evidence of this mechanism.
As increases, more and more counterions are absorbed on DNA and the effective DNA charge, , undergoes the transition from to and eventually to . Here, means that the absorbed counterions carry the same amount but opposite charges as DNA, and DNA is effectively neutral. Under the condition of , inter-strand electrostatic repulsion vanishes, and duplex stability is maximized. The condition of is referred to as DNA overcharging which reintroduces inter-strand electrostatic repulsion and reduces duplex stability. It is worth noting that corresponds to the total charges of DNA and ions within a certain short distance around DNA, because the total charges of DNA and all ions, i.e., the entire system, are always zero.
Simulations of DNA with monovalent ions
While DNA overcharging with high-valent ions has been observed in experiments12 and explained by theory13,14, DNA overcharging by monovalent ions is much less explored19 and whether it can occur remains unclear. To quantitatively understand it, we performed three types of simulations with different resolutions, (i) all-atom MD simulations, (ii) oxDNA simulations, and (iii) CG Langevin dynamics simulations, as each simulation method has its own advantages and disadvantages. All-atom MD simulations can capture DNA overcharging but cannot capture the equilibrium transition of DNA strand separation. The oxDNA simulation is based on a CG DNA model whose resolution is lower than all-atom but higher than typical CG simulations33. The oxDNA simulations can capture the equilibrium transition of DNA strand separation but cannot capture DNA overcharging because there are no explicit ion particles in oxDNA simulations, and the effect of ion particles is considered through Debye screening. Our CG Langevin dynamics simulations, which are described in the “Methods” section, can dramatically improve computational efficiency and allow freedom to vary ion parameters but cannot capture many effects caused by water molecules, such as ion hydration. CG simulations are suitable for building a phase diagram of DNA overcharging.
We first present oxDNA simulation results. The red curve in Fig. 2b shows that oxDNA simulation can quantitatively capture the effect of on DNA duplex stability in the range of within the framework of the classic Debye screening, which supports that the variation of electrostatic interactions, rather than hydrogen bonds and base stacking, is the primary factor for the variation of DNA duplex stability within the range we consider here. Similar oxRNA simulations were performed and the results agree with experiments for (red curve in Fig. 2d). Note that the entire oxDNA (as well as oxRNA) parameterization is based on implicit ions with the Debye screening to reproduce a double-helical DNA structure with properties close to experimental results. Due to the absence of explicit ions, the oxDNA model cannot capture DNA overcharging by ions.
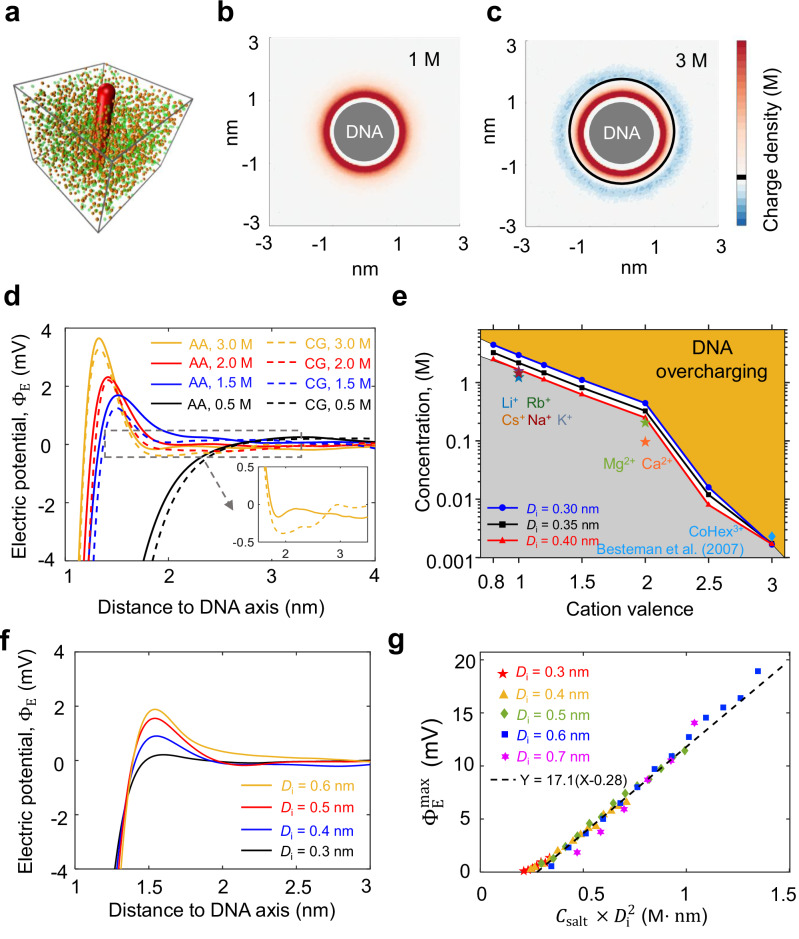
Next, we present all-atom MD simulations of a DNA duplex with NaCl, KCl, or CsCl. Our simulations reveal DNA overcharging in three aspects. First, we calculated , the total charge of DNA atoms, Na+, and Cl− within a cylinder around DNA (Fig. 4a). For , is always negative, as expected from mean-field theory. However, for , becomes positive at , which indicates DNA overcharging (Fig. 4b). For each , we recorded the maximum of , which is denoted as . The radial distances corresponding to usually located at the first or second layer of ions absorbed on DNA. Figure 4c shows that when , increases roughly linearly with . Here, is normalized for one base pair. According to the theory by Shklovskii et al. 13,14, the dependence of on can be approximated by
| 1 |
Here, is a fitting parameter. See more about Eq. 1 in Supplementary Method 2. As shown by the blue line in Fig. 4c, the fit of Eq. 1 to our simulation results yield = 0.163 and = 1.02 M. Because the simulation data in Fig. 4c appears to follow a linear relationship, we also fit the data by
| 2 |
Fig. 4. Ion distribution around the DNA from MD simulations.
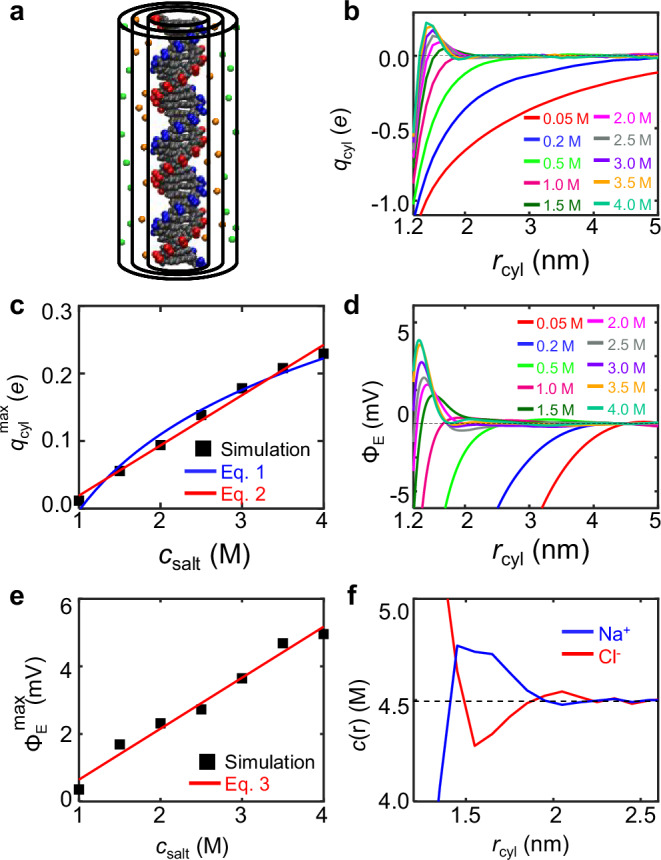
Source data are provided as a Source Data file. a Total charge, , within a cylinder around DNA. The smallest cylinder has a radius of 1 nm, corresponding to DNA radius. The middle cylinder has a radius of 1.5 nm, corresponding to the position of the maximum overcharging. The largest cylinder has a radius of 2 nm, where the ion concentrations approach the bulk values. b as a function of the cylindrical radius. c Maximum of , , as a function of NaCl concentration. d Electric potential, , as a function of radial distance. e Maximum of , , as a function of NaCl concentration. f Radial distribution of Na+ and Cl− at 4.5 M NaCl.
Note that the above linear equation is just for convenient usage, not based on rigorous mathematical simplification of Eq. 1.
Second, from the same simulation results of monovalent ion distribution, we calculated the electric field around DNA using Gauss’s law, i.e., the strength of the electric field at determined by . Integration of the electric field over the radial distance, we obtained the electric potential around DNA, (Fig. 4d). For , is always negative as expected from mean-field theory. For , becomes positive at , which indicates DNA overcharging. For each , we recorded the maximum of which is denoted as . Figure 4e shows that also increases with linearly after the critical concentration
| 3 |
Alternatively, we can approximate from in Eq. 2. By approximating the thickness of the overcharging layer as 0.71 nm, we can obtain from Eq. 2, which is close to the result in Eq. 3. Note that due to Gauss’s law, the linear behavior of the accumulated charge in Eq. 2 can lead to a linear behavior of the electrical potential.
Third, the radial distributions of Na+ and Cl− in Fig. 4f reveal DNA overcharging. The concentration of Na+ at is less than the Na+ concentration far from DNA, indicating a positive electric potential at . Similarly, the concentration of Cl− at is larger than the Cl− concentration far from DNA.
To quantify the effect of overcharging on DNA strand-strand electrostatic interaction, we make several crude approximations. First, we use to approximate the effective DNA charge per nucleotide. Second, we calculate the electrostatic interaction between two charges separated by a distance of (the inter-strand P–P distance or DNA diameter)
| 4 |
Here, is the elementary charge, is the vacuum permittivity, is the dielectric constant inside DNA34, and is the distance between two charges or the DNA diameter. We use the unit of for an easy comparison with experimental results in Fig. 2b.
The above calculation makes many approximations. Accordingly, we add a coefficient
| 5 |
Here, is the effect of DNA overcharging on inter-strand electrostatic interaction. The fit of Eq. 5 to the experimental results yields , as shown by the black curve in Fig. 2b. One reason that causes is that the calculation of only considers the charge-charge interaction within a base pair, and actually the charge on a DNA strand can interact with all charges on the other DNA strand.
We did similar all-atom MD simulations for DNA in other monovalent salts. We obtained and with KCl (Supplementary Figs. 2 and 7) and and with CsCl (Supplementary Figs. 8 and 9). We also carried out similar all-atom MD simulations and analysis for RNA with NaCl (Supplementary Fig. 10) and obtained the black curve in Fig. 2d, which explains RNA duplex destabilization by monovalent ions. For RNA with NaCl, we obtained and . These results suggest that NA duplexes overcharging with monovalent ions is a common phenomenon. Please see Supplementary Table 1 for the determined Eqs. 1–3 and 5 for different monovalent ions on DNA.
Phase diagram of DNA overcharging with n-valent ions
The DNA overcharging with monovalent and high-valent ions inspires us to think about the criterion of DNA overcharging. What is the minimum ion valence that can induce DNA overcharging? To find the answer, we used CG simulations, which greatly accelerate simulations and allow for freedom to vary ion parameters (Fig. 5a). In these CG Langevin dynamics simulations, DNA is modeled as a charged rod with diameter, = 1.8 nm. The linear charge density of the rod is per . Ions are modeled as hard spheres with different diameters, = 0.3, 0.35, or 0.4 nm. We examined whether DNA overcharging occurs by analyzing the charge distribution and the electric potential around the DNA rod. When the monovalent ion concentration is greater than 1.6 M, DNA overcharging occurs (Supplementary Fig. 11 and Supplementary Method 3). Although the CG simulations ignore explicit water molecules and DNA structural details, we found that the CG simulations with suitable parameterization can quantitatively capture DNA overcharging observed in all-atom MD simulations (Fig. 5d).
Fig. 5. Criterion of DNA overcharging.
Source data are provided as a Source Data file. a Coarse-grained simulation setup. b Diagram of charge distribution around DNA at 1 M NaCl from CG simulations. c Diagram of DNA overcharging from CG simulations with a DNA diameter of 2 nm and an ion diameter of 0.3 nm. d Electric potential, , as a function of radial distance obtained from all-atom and CG MD simulations. e Phase diagram of DNA overcharging. The symbols represent experimental data from our work and a previous study12. Ions are modeled as hard spheres with different diameters, . f The overcharging electric potential for different ion diameters. g Maximum of versus for different ion diameters.
From systematic CG simulation results, we obtained a phase diagram for the conditions of DNA overcharging (Fig. 5e). The critical concentrations of Mg2+ and Ca2+ where Tm reverses were obtained by thermal melting experiments (Supplementary Fig. 12). For a lower cation valence, is higher. Our theoretical phase boundary for = 0.4 nm (red line in Fig. 5e) agrees with our experimental results for monovalent ions, Li+, Na+, K+, Rb+, and Cs+. Our theoretical phase boundaries are above the experimental results for divalent ions, Mg2+ and Ca2+, possibly because the hydrated ion diameters of Mg2+ and Ca2+ are larger than 0.4 nm. Our theoretical phase boundaries are close to a previous experimental result12 for CoHex3+. For a realistic salt solution, there is an upper limit of , which is the saturated salt concentration. When we set the maximum as 3 M, the minimum ion valence for DNA overcharging is about 0.8 for short DNA segments with straight rod conformations.
The reason for DNA overcharging has been investigated in previous studies13,14,35,36. It has been proposed that the excluded volume interaction between cations causes the positional correlations of cations around DNA. This correlation leads to an arrangement of cations where the cations of the second layer interlace with the cations of the first layer around DNA, resembling a crystal. Such arrangement significantly weakens the repulsions between cations in the first and second layers and allows excessive cations on the second or following layers, which results in DNA overcharging. In this mechanism, the excluded volume interaction between cations plays a crucial role in DNA overcharging, supported by the fact that the modified Poisson-Boltzmann equation considering the excluded volume interaction between cations can reproduce overcharging36. Our CG simulations also find that increasing ion diameter can reduce the minimum salt concentration for DNA overcharging, as seen by comparing the blue, black, and red curves in Fig. 5e. As shown in Fig. 5f, with the decrease of ion diameter, the overcharging electric potential decreases toward zero. Additionally, our CG simulations demonstrate the of DNA overcharging appears to have a universal dependence on (Fig. 5g), which indicates the critical role of the excluded volume interaction of ions in DNA overcharging.
Discussion
Due to the high charge density of DNA, salt concentration strongly affects DNA stability. It is generally believed that monovalent ions weaken DNA-DNA electrostatic interactions by Debye screening and hence enhance DNA duplex stability. In contrast to the common belief, our experiments reveal that high concentrations of monovalent salts destabilize DNA duplexes. This counterintuitive behavior, consistent across DNA, RNA, and RDH duplexes and various monovalent salts (LiCl, NaCl, KCl, RbCl, and CsCl), points to a universal physical phenomenon rather than duplex-structure-specific or ion-specific effects. Our all-atom and CG simulations showed this destabilization is caused by DNA overcharging. The magnitude of DNA destabilization by overcharging is significant, which can be per base pair. Such magnitude decreases the melting temperature by about 10 °C.
The physical mechanism for DNA overcharging has been investigated previously using the Wigner crystal model14. In the classical mean-field treatment, when DNA charges are fully compensated by absorbed counterions, DNA cannot attract additional counterions because the absorbed counterions repel the additional counterions. The mean-field treatment assumes absorbed counterions distribute continuously on the DNA surface, while in real cases, counterions are discrete and may form a crystal-like structure on the DNA surface when the repulsions between counterions are strong. The crystal-like structure weakens the repulsions between absorbed counterions and other counterions, which allows neutralized DNA to absorb additional counterions. Please see Supplementary Method 2 and Supplementary Fig. 13 for the theoretical calculation of DNA overcharging using this theory and a simplified explanation for DNA overcharging, respectively. It is worth pointing out that Wigner crystal theory was developed for multivalent ions because the strong repulsions among multivalent ions favor the formations of crystal-like structures. Here, we applied the theory to monovalent ions and found the functional form, the logarithmic function in Eq. 1, seems to work, but the quantitative values, such as , deviate greatly from the prediction of the theory. Such deviation is not surprising, because monovalent ions do not form a Wigner crystal, as shown by the liquid-like structure in Fig. 4f. In addition to the Wigner crystal theory, a previous study has added two salt-dependent energetic terms for inter-strand interaction to capture DNA destabilization under high salt concentrations5 (Supplementary Fig. 14 and Supplementary Method 4).
DNA overcharging is supported by several DNA phenomena observed in the literature. First, DNA overcharging is evidenced by the reversal of the electrophoretic direction of DNA with high-valent () ions12. Under normal salt conditions, DNA carries negative charges and migrates toward the anode. When CoHex3+ exceeds a critical concentration (), DNA absorbs excessive CoHex3+ ions and migrates toward the cathode12.
Second, DNA overcharging can weaken the attraction between two double-stranded DNA molecules. Previous experiments have observed that with the increasing concentration of high-valent ions such as CoHex3+, DNA first condensed, indicating DNA-DNA attraction, and then dissolved at even higher concentrations, indicating DNA-DNA repulsion10,11,37. Previous theoretical studies have explained it by following mechanisms13,14,35. There are two contributions of electrostatic interactions between two DNA molecules. The first contribution is the classical electrostatic repulsion between two DNA molecules, which can be understood in the mean-field treatment or Debye screening. The second contribution is the like-charge attraction caused by ion correlation. With the increase of high-valent ion concentration, the first contribution switches from repulsion to zero and eventually to repulsion again due to DNA overcharging. After assuming the second contribution does not vary much with , DNA overcharging can explain the experimental phenomena of DNA dissolution, condensation, and re-dissolution with the increase of . Similarly, DNA condensation resists the maximum stretching force around the critical salt concentration of charge inversion because inter-DNA electrostatic repulsion vanishes12,38. A difference between those experiments and our experiment is that these experiments deal with the interaction between two double-stranded DNA fragments, while our work focuses on the inter-strand interaction within a duplex. Nevertheless, DNA overcharging should strengthen the repulsion within a duplex or between DNA duplexes. Our experiments and all-atom simulations also observed single-stranded DNA overcharging at large (Supplementary Figs. 15 and 16 and Supplementary Method 5).
DNA destabilization induced by monovalent ions has significant implications in polyelectrolyte theory, DNA nanomaterials, DNA nanotechnology, and DNA biophysics. First, DNA destabilization induced by monovalent ions inspires us to clarify the criterion of DNA overcharging. It is generally believed that DNA overcharging occurs for multivalent ions but not monovalent ions. Our experimental and simulation results refresh the understanding. Broadly speaking, the precise experimental results of DNA help advance polyelectrolyte theory. In the past decades, DNA, as a model polymer and a model polyelectrolyte, has greatly facilitated the advance of polymer physics theory in terms of providing quantitative results, such as the scaling behavior of single polymers in confinement39–41, and polyelectrolyte theory, such as like-charge attraction and overcharging11,14. There are several advantages for DNA as a model polymer and a model polyelectrolyte, including mature biotechnology to prepare high-quality DNA samples42,43 and well-established single-DNA experiments by MT44.
Second, DNA has been widely applied in nanomaterial design, which takes advantage of the base-pairing attraction to achieve well-defined nanostructures45–47. Such nanomaterial design requires DNA duplex formation, and the material stability depends on DNA duplex stability. Our quantitative results of DNA duplex stability as a function of salt concentration can be applied to rationally control the stability of such nanomaterials.
Third, high concentrations of monovalent salts, such as LiCl and KCl, are commonly used in DNA-nanopore experiments in order to enhance the precision of electrical signals48–50. In addition, strand separation is often involved in nanopore experiments51,52. In such cases, DNA destabilization induced by monovalent salt at high concentrations should be considered.
Lastly, DNA destabilization under high salt concentration may be biologically relevant. For example, some halophilic archaea cells prefer a high salt environment and can even grow on NaCl crystals53.
In conclusion, we summarize the overall results of this work, (i) precisely measuring DNA, RNA, and RDH destabilization by Li+, Na+, K+, Rb+, Cs+; (ii) demonstrating DNA destabilization by high concentrations of monovalent ions is a common phenomenon, not ion-specific; (iii) revealing that such DNA destabilization is caused by DNA overcharging using extensive all-atom and CG simulations, as well as Wigner crystal theory. Our results have both fundamental and practical values, (i) Fundamentally, we advance the polyelectrolyte theory of overcharging using DNA as a model polyelectrolyte. We highlight that the single-DNA technique can achieve a high precision (~0.01 pN & 1 nm) that is unachievable in traditional experiments for other polyelectrolytes. (ii) Practically, our systematical experimental data of DNA, RNA, and RHD duplexes stabilization under various salt concentrations act as the table of physical-chemical data for nucleic acids, which can be used in many bio-nanotechnological applications, such as DNA origami, and DNA-nanopore sequencing.
Method
Buffer solutions
We prepared the near-saturation concentration of monovalent salt mother liquor which undergoes filtration, DEPC treatment, and autoclaving. The concentration of the mother liquor was 10 M for LiCl, 5 M for NaCl, 4 M for KCl, 5 M for RbCl, and 5 M for CsCl. Before each experiment, we used DEPC-treated deionized water to dilute the mother liquor to different salt concentrations. We used a buffer system comprising a final concentration of 10 mM Tris-HCl to ensure a consistent pH of 7.5.
MT experiments
Each NA (DNA, RNA, or RDH) hairpin construct was labeled with digoxigenin at one end and labeled with biotin at the other end (Fig. 1a). The loop regions have 8 nucleotides for DNA and RDH hairpins but 4 nucleotides for RNA hairpin. Because RNA transitions between folded and unfolded states more slowly than DNA under equilibrium, we designed shorter loop regions for RNA to accelerate the transition rate21,24. A previous study21 has found that reducing the loop-region length has no obvious effect on shown in Fig. 1f. See the illustrations of hairpins in Fig. 1c. We made the DNA and RNA constructs by one-sided PCR54 and made the RDH construct by ligation (Supplementary Fig. 17 and Supplementary Method 6).
We sequentially coated the piranha-cleaned glass slides with 1% APTES, 2% glutaraldehyde, 1 mg/mL anti-digoxigenin and passivated the slides with 2% bovine serum albumin. After coating glutaraldehyde on the glass slides, we attached the polystyrene microbeads as references. In a flow cell, we attached the digoxigenin-labeled end of the NA hairpin construct to the anti-digoxigenin-coated glass slide and attached its biotin-labeled end to a streptavidin-coated paramagnetic microbead (Dynabeads M-270). We used a pair of neodymium magnets to exert force to stretch the NA hairpin construct and controlled the stretching force using a linear motor (L-509, Physik Instrument). We viewed the microbeads by a 100× oil immersion objective (Olympus), captured the images with a CCD camera (MER2-230-168U3M, Daheng Imaging), and calculated the positions of the microbeads based on their diffraction pattern55. We conducted the experiments in an ultra-clean room with a stable temperature of 22 °C.
Thermal melting measurement through fluorescence quenching
We measured Tm of NA duplexes using the fluorescence quenching test (FQT), similar to a previous study28. We designed two complementary paired single-strand NA. One strand was labeled with the FAM group at the 5′ end and its complementary strand was labeled with the BHQ1 group at the 3′ end. When the two single-stranded oligos were annealed into double-stranded NA, BHQ1 quenched the FAM fluorescence. When the NA duplexes melted during heating up, the fluorescence intensity increased due to the release of the BHQ1 strand. The peak of the derivative of the fluorescence intensity gave the Tm. The two DNA strands were FAM-GACGATCGTTCGTGAAGTCAAC and BHQ1-GTTGACTTCACGAACGATCGTG. The RNA strands have the same sequence as DNA except T bases are replaced by rU bases.
All-atom MD simulations
We performed all-atom MD simulations to probe the ion atmosphere of monovalent salts (NaCl, KCl, and CsCl) at gradient bulk concentrations (0.05 to 4 M) around DNA and RNA duplexes. We conducted the simulations using the GROMACS 2021 simulation package56, where the OL15 force field was used to describe DNA57 and the OL3 force field was used to represent RNA58. The monovalent ions were described by the parameters from the Joung and Cheatham model59. We ran the simulations for 600 ns after energy minimization and equilibration at 295 K and 1 bar. We used the last 500 ns of the simulation trajectory for data analysis.
oxDNA simulations
To explain how DNA duplex stability changes with salt concentration in the range of , we conducted the CG Brownian dynamics simulations using the oxDNA simulation package33. The oxDNA model describes DNA electrostatic interaction using the Debye screening and has successfully reproduced many DNA properties such as DNA melting temperature (Tm). In our oxDNA simulations, the sequence of DNA hairpin is TTTTCTGGTATTTTTTTACCAGTTTT. The temperature was set to T = 295 K. In each simulation, we specified a salt concentration and ran steps. At each salt concentration, we tuned the stretching force and observed the equilibrium DNA hairpin opening/closing (Supplementary Fig. 18). We determined the critical force corresponding to the equal probability between hairpin and stretched state (Supplementary Fig. 19), same as the experimental results in Fig. 1e. We also use oxRNA model60 to observe the zipping/unzipping of RNA hairpin. In oxRNA simulations, the sequence of the RNA is similar to that of oxDNA simulation except T is replaced by U.
CG simulations
To obtain ion distributions around DNA efficiently, we also performed CG Langevin dynamics simulations using the LAMMPS 2020 simulation package61. The DNA molecule was modeled as a cylinder with a uniform linear charge density of −1e per 0.17 nm, and ions were modeled as hard-sphere particles. We used a simulation box. Ions were then added to mimic salt conditions employed in MT experiments.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Source data
Acknowledgements
We are grateful to financial support from the National Natural Science Foundation of China (No. 12074294 and 12374216 to X.-H.Z.; No. 12304254 to C.Z; No. 22273080 to L.D.), the Research Grants Council of Hong Kong (No. 11313322, 11307224 and PDFS2425-1S09), Guangdong Basic and Applied Basic Research Fund (project no. 2022A1515010484), Super Computing Center of Wuhan University, and the National Supercomputer Center in Guangzhou.
Author contributions
X.-H.Z. and L.D. conceived the idea. C.Z., J.-H.Z., W.W., and W.-Q.W. performed the experiments. L.D., F.T., H.-W.Z., and Q.-Y.Q. performed the simulations. L.D., X.-H.Z., F.T., Y.Z., Z.-J T., and W.-Q.W. analyzed the data. All authors wrote the paper.
Peer review
Peer review information
Nature Communications thanks Jan Lipfert, Antonio Trovato, and the other, anonymous, reviewers for their contribution to the peer review of this work. A peer review file is available.
Data availability
All data needed to evaluate the conclusions in the paper are present in the paper and the Supplementary Information. Source data for figures are provided with this paper. Source data are provided with this paper.
Code availability
The source code for MD simulations can be found via GitHub [https://github.com/cityuBiophysics/Double-stranded-Nucleic-acid-charge-inversion].
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Chen Zhang, Fu-Jia Tian, Hong-Wei Zuo.
Contributor Information
Yan Zhang, Email: peneyyan@whu.edu.cn.
Wen-Qiang Wu, Email: wuwenqiang@henu.edu.cn.
Liang Dai, Email: liangdai@cityu.edu.hk.
Xing-Hua Zhang, Email: zhxh@whu.edu.cn.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-55404-6.
References
- 1.Lipfert, J., Doniach, S., Das, R. & Herschlag, D. Understanding nucleic acid–ion interactions. Annu. Rev. Biochem.83, 813–841 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Khimji, I., Shin, J. & Liu, J. DNA duplex stabilization in crowded polyanion solutions. Chem. Commun.49, 1306–1308 (2013). [DOI] [PubMed] [Google Scholar]
- 3.Owczarzy, R., Moreira, B. G., You, Y., Behlke, M. A. & Walder, J. A. Predicting stability of DNA duplexes in solutions containing magnesium and monovalent cations. Biochemistry47, 5336–5353 (2008). [DOI] [PubMed] [Google Scholar]
- 4.Vlassakis, J. et al. Probing the mechanical stability of DNA in the presence of monovalent cations. J. Am. Chem. Soc.130, 5004–5005 (2008). [DOI] [PubMed] [Google Scholar]
- 5.Maity, A., Singh, A. & Singh, N. Differential stability of DNA based on salt concentration. Eur. Biophysics. J.46, 33–40 (2017). [DOI] [PubMed] [Google Scholar]
- 6.Bai, Y., Das, R., Millett, I. S., Herschlag, D. & Doniach, S. Probing counterion modulated repulsion and attraction between nucleic acid duplexes in solution. Proc. Natl Acad. Sci. USA102, 1035–1040 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gruenwedel, D. W. & Hsu, C.-H. Salt effects on the denaturation of DNA. Biopolymers7, 557–570 (1969). [DOI] [PubMed] [Google Scholar]
- 8.Bizarro, C. V., Alemany, A. & Ritort, F. Non-specific binding of Na + and Mg 2+ to RNA determined by force spectroscopy methods. Nucleic Acids Res.40, 6922–6935 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tan, Z.-J. & Chen, S.-J. Salt contribution to RNA tertiary structure folding stability. Biophys. J.101, 176–187 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bloomfield, V. A. DNA condensation. Curr. Opin. Struct. Biol.6, 334–341 (1996). [DOI] [PubMed] [Google Scholar]
- 11.Bloomfield, V. A. DNA condensation by multivalent cations. Biopolymers44, 269–282 (1997). [DOI] [PubMed] [Google Scholar]
- 12.Besteman, K., Van Eijk, K. & Lemay, S. G. Charge inversion accompanies DNA condensation by multivalent ions. Nat. Phys.3, 641–644 (2007). [Google Scholar]
- 13.Shklovskii, B. I. Wigner crystal model of counterion induced bundle formation of rodlike polyelectrolytes. Phys. Rev. Lett.82, 3268–3271 (1999). [Google Scholar]
- 14.Grosberg, A. Y., Nguyen, T. T. & Shklovskii, B. I. Colloquium: the physics of charge inversion in chemical and biological systems. Rev. Mod. Phys.74, 329–345 (2002). [Google Scholar]
- 15.Hsiao, P.-Y. Overcharging, charge inversion, and reentrant condensation: using highly charged polyelectrolytes in tetravalent salt solutions as an example of study. J. Phys. Chem. B112, 7347–7350 (2008). [DOI] [PubMed] [Google Scholar]
- 16.Dai, L., Mu, Y., Nordenskiöld, L. & van der Maarel, J. R. C. Molecular dynamics simulation of multivalent-ion mediated attraction between DNA molecules. Phys. Rev. Lett.100, 118301 (2008). [DOI] [PubMed] [Google Scholar]
- 17.Luan, B. & Aksimentiev, A. DNA attraction in monovalent and divalent electrolytes. J. Am. Chem. Soc.130, 15754–15755 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sarkar, S., Maity, A., Sarma Phukon, A., Ghosh, S. & Chakrabarti, R. Salt induced structural collapse, swelling, and signature of aggregation of two ssDNA strands: insights from molecular dynamics simulation. J. Phys. Chem. B123, 47–56 (2019). [DOI] [PubMed] [Google Scholar]
- 19.Deserno, M., Jiménez-Ángeles, F., Holm, C. & Lozada-Cassou, M. Overcharging of DNA in the Presence of Salt: theory and Simulation. J. Phys. Chem. B105, 10983–10991 (2001). [Google Scholar]
- 20.Tomac, S. et al. Ionic effects on the stability and conformation of peptide nucleic acid complexes. J. Am. Chem. Soc.118, 5544–5552 (1996). [Google Scholar]
- 21.Woodside, M. T. et al. Nanomechanical measurements of the sequence-dependent folding landscapes of single nucleic acid hairpins. Proc. Natl Acad. Sci. USA103, 6190–6195 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Huguet, J. M. et al. Single-molecule derivation of salt dependent base-pair free energies in DNA. Proc. Natl Acad. Sci. USA107, 15431–15436 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Stephenson, W. et al. Combining temperature and force to study folding of an RNA hairpin. Phys. Chem. Chem. Phys.16, 906–917 (2014). [DOI] [PubMed] [Google Scholar]
- 24.Bercy, M. & Bockelmann, U. Hairpins under tension: RNA versus DNA. Nucleic Acids Res.43, 9928–9936 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tian, F.-J. et al. Universality in RNA and DNA deformations induced by salt, temperature change, stretching force, and protein binding. Proc. Natl Acad. Sci. USA120, e2218425120 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dong, H.-L. et al. The origin of different bending stiffness between double-stranded RNA and DNA revealed by magnetic tweezers and simulations. Nucleic Acids Res.120, 2519–2529 (2024). [DOI] [PMC free article] [PubMed]
- 27.Gebala, M. & Herschlag, D. Quantitative studies of an RNA duplex electrostatics by ion counting. Biophys. J.117, 1116–1124 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.You, Y., Tataurov, A. V. & Owczarzy, R. Measuring thermodynamic details of DNA hybridization using fluorescence. Biopolymers95, 472–486 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Saleh, O. A., McIntosh, D. B., Pincus, P. & Ribeck, N. Nonlinear low-force elasticity of single-stranded DNA molecules. Phys. Rev. Lett.102, 068301 (2009). [DOI] [PubMed] [Google Scholar]
- 30.Chen, H. et al. Ionic strength-dependent persistence lengths of single-stranded RNA and DNA. Proc. Natl Acad. Sci. USA109, 799–804 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sim, A. Y. L., Lipfert, J., Herschlag, D. & Doniach, S. Salt dependence of the radius of gyration and flexibility of single-stranded DNA in solution probed by small-angle x-ray scattering. Phys. Rev. E86, 021901 (2012). [DOI] [PubMed] [Google Scholar]
- 32.SantaLucia, J. A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl Acad. Sci. USA95, 1460–1465 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Šulc, P. et al. Sequence-dependent thermodynamics of a coarse-grained DNA model. J. Chem. Phys.137, 135101 (2012). [DOI] [PubMed] [Google Scholar]
- 34.Cuervo, A. et al. Direct measurement of the dielectric polarization properties of DNA. Proc. Natl Acad. Sci. USA111, E3624–E3630 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nguyen, T. T., Rouzina, I. & Shklovskii, B. I. Reentrant condensation of DNA induced by multivalent counterions. J. Chem. Phys.112, 2562–2568 (2000). [Google Scholar]
- 36.Gupta, A., Govind Rajan, A., Carter, E. A. & Stone, H. A. Ionic layering and overcharging in electrical double layers in a Poisson-Boltzmann model. Phys. Rev. Lett.125, 188004 (2020). [DOI] [PubMed] [Google Scholar]
- 37.Pelta, J., Livolant, F. & Sikorav, J.-L. DNA aggregation induced by polyamines and cobalthexamine (∗). J. Biol. Chem.271, 5656–5662 (1996). [DOI] [PubMed] [Google Scholar]
- 38.Yang, Y. J. et al. Cytosine methylation enhances DNA condensation revealed by equilibrium measurements using magnetic tweezers. J. Am. Chem. Soc.142, 9203–9209 (2020). [DOI] [PubMed] [Google Scholar]
- 39.Dai, L., Renner, C. B. & Doyle, P. S. The polymer physics of single DNA confined in nanochannels. Adv. Colloid Interface Sci.232, 80–100 (2016). [DOI] [PubMed] [Google Scholar]
- 40.Tang, J. et al. Revisiting the conformation and dynamics of DNA in slitlike confinement. Macromolecules43, 7368–7377 (2010). [Google Scholar]
- 41.Gupta, D. et al. Experimental evidence of weak excluded volume effects for nanochannel confined DNA. ACS Macro Lett.4, 759–763 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Thind, A. K. et al. Rapid cloning of genes in hexaploid wheat using cultivar-specific long-range chromosome assembly. Nat. Biotechnol.35, 793–796 (2017). [DOI] [PubMed] [Google Scholar]
- 43.Moss, E. L., Maghini, D. G. & Bhatt, A. S. Complete, closed bacterial genomes from microbiomes using nanopore sequencing. Nat. Biotechnol.38, 701–707 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rittich, B. & Španová, A. SPE and purification of DNA using magnetic particles. J. Sep. Sci.36, 2472–2485 (2013). [DOI] [PubMed] [Google Scholar]
- 45.Aldaye, F. A., Palmer, A. L. & Sleiman, H. F. Assembling materials with DNA as the guide. Science321, 1795–1799 (2008). [DOI] [PubMed] [Google Scholar]
- 46.Yang, D. et al. DNA materials: bridging nanotechnology and biotechnology. Acc. Chem. Res.47, 1902–1911 (2014). [DOI] [PubMed] [Google Scholar]
- 47.Jones, M. R., Seeman, N. C. & Mirkin, C. A. Programmable materials and the nature of the DNA bond. Science347, 1260901 (2015). [DOI] [PubMed] [Google Scholar]
- 48.Kumar Sharma, R., Agrawal, I., Dai, L., Doyle, P. S. & Garaj, S. Complex DNA knots detected with a nanopore sensor. Nat. Commun.10, 4473 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sharma, R. K., Agrawal, I., Dai, L., Doyle, P. & Garaj, S. DNA knot malleability in single-digit nanopores. Nano Lett.21, 3772–3779 (2021). [DOI] [PubMed] [Google Scholar]
- 50.Smeets, R. M. M. et al. Salt dependence of ion transport and DNA translocation through solid-state nanopores. Nano Lett.6, 89–95 (2006). [DOI] [PubMed] [Google Scholar]
- 51.Howorka, S., Cheley, S. & Bayley, H. Sequence-specific detection of individual DNA strands using engineered nanopores. Nat. Biotechnol.19, 636–639 (2001). [DOI] [PubMed] [Google Scholar]
- 52.Derrington, I. M. et al. Nanopore DNA sequencing with MspA. Proc. Natl Acad. Sci. USA107, 16060–16065 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Oren, A. Microbial life at high salt concentrations: phylogenetic and metabolic diversity. Saline Syst.4, 2 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Yang, Y. J. et al. A universal assay for making DNA, RNA, and RNA-DNA hybrid configurations for single-molecule manipulation in two or three steps without ligation. ACS Synth. Biol.8, 1663–1672 (2019). [DOI] [PubMed] [Google Scholar]
- 55.van Loenhout, M. T. J., Kerssemakers, J. W. J., De Vlaminck, I. & Dekker, C. Non-bias-limited tracking of spherical particles, enabling nanometer resolution at low magnification. Biophys. J.102, 2362–2371 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Abraham, M. J. et al. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX1–2, 19–25 (2015). [Google Scholar]
- 57.Zgarbová, M. et al. Refinement of the sugar–phosphate backbone torsion beta for AMBER force fields improves the description of Z- and B-DNA. J. Chem. Theory Comput.11, 5723–5736 (2015). [DOI] [PubMed] [Google Scholar]
- 58.Zgarbová, M. et al. Refinement of the Cornell et al. nucleic acids force field based on reference quantum chemical calculations of glycosidic torsion profiles. J. Chem. Theory Comput.7, 2886–2902 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Joung, I. S. & Cheatham, T. E. III. Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B112, 9020–9041 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Matek, C., Šulc, P., Randisi, F., Doye, J. P. K. & Louis, A. A. Coarse-grained modelling of supercoiled RNA. J. Chem. Phys.143, 243122 (2015). [DOI] [PubMed] [Google Scholar]
- 61.Thompson, A. P. et al. LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun.271, 108171 (2022). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data needed to evaluate the conclusions in the paper are present in the paper and the Supplementary Information. Source data for figures are provided with this paper. Source data are provided with this paper.
The source code for MD simulations can be found via GitHub [https://github.com/cityuBiophysics/Double-stranded-Nucleic-acid-charge-inversion].